The influence of scattering correction effect based on optical path distribution on CO2 retrieval

Yun Jiang; Fenghua Duan; Yue Pan; Gen Wang; Chuanyu Fan; Xin Qiao

doi:10.1515/phys-2025-0245

Article Open Access

The influence of scattering correction effect based on optical path distribution on CO₂ retrieval

Yun Jiang , Fenghua Duan , Yue Pan , Gen Wang , Chuanyu Fan and Xin Qiao

Published/Copyright: December 16, 2025

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

From the journal Open Physics Volume 23 Issue 1

Abstract

Based on the Photonpath-length Probability Density Function (PPDF) model and traditional DOAS method, the correction factor (α, ρ, h, γ) is introduced for atmospheric scattering on optical paths. The scattering correction of PPDF factor on 1.6μm band radiation and CO₂ retrieval is analyzed. The results show that the influence of α, ρ on radiance is greater than that of h, γ. Increasing α, h will increase the results, and increasing α by 0.1 will increase the retrieval result by about 3 ppm. Increasing ρ, γ will decrease CO₂ retrieval, and increasing ρ by 0.1 will decrease the retrieval result by 2 ppm. At the same time, as the surface reflectance increases, its impact on CO₂ retrieval becomes smaller and smaller. However, as the aerosol optical thickness increases, the retrieval error increases, which significantly affects the accuracy of CO₂ retrieval. The influence of aerosols cannot be ignored and should be corrected to improve the accuracy of CO₂ retrieval. The scattering correction of PPDF is verified using the measured GOSAT spectrum, with retrieval accuracy within 0.7 %. Due to the lack of scattering correction in the DOAS method, the scattering correction effect of the PPDF method is also verified.

Keywords: carbon dioxide; photon probability density function; atmospheric scattering; retrieval

1 Introduction

Since the industrialization of human society, the greenhouse effect caused by greenhouse gases such as CO₂ has become serious, affecting global environment, economy and social development. It has brought significant challenges and threats to human life [1], 2]. Real-time monitoring of CO₂ is crucial for studying climate change [3]. However, traditional ground-based greenhouse gas monitoring systems have limitations in spatial scale and coverage, and satellite observations of greenhouse gases can help address these shortcomings [4], 5]. Therefore, satellite monitoring of greenhouse gases has become an important and effective method for addressing these challenges [6], 7]. The defect of using satellite to monitor CO₂ gas lies in its retrieval accuracy. Satellite observations in the shortwave infrared band are greatly affected by aerosols and cirrus clouds, and CO₂ observation and retrieval accuracy will be significantly affected by scattering. In 2020, Sanghavi et al. [8] pointed out that if the influence of cirrus and aerosol scattering on CO₂ retrieval is ignored, the retrieval error can reach 15 ppm. In the desert area with high surface reflectivity, the retrieval error is even as high as 40 ppm [9]. In 2014, Jiang et al. [10] also pointed out that different scattering correction methods have different effects on CO₂ retrieval. They pointed out that the PPDF method has a significant effect on correcting the optical path caused by scattering, which can greatly improve the retrieval accuracy. Huo and Duan [11] pointed out that under dust-type fine particle aerosols, aerosol misestimation of 0.1 will cause a retrieval deviation of 4–5 ppm. Ye et al. [12] pointed out that as the surface reflectance in the CO₂ band increases, the impact on the retrieval results will be smaller and smaller. Therefore, aerosol scattering effect is important in short-wave near-infrared remote sensing. How to effectively correct aerosol scattering is the key to achieve high-precision satellite remote sensing of CO₂.

To achieve high-precision of CO₂ retrieval, Crisp has developed a full-physical method [13]. SCIMACHY also developed the retrieval method of WFM-DOAS [14]. A CO₂ retrieval algorithm based on PPDF model was developed with the Japanese GOSAT satellite [15]. One of the important factors affecting the accuracy of CO₂ retrieval in these mainstream algorithms is the correction of scattering, and the correction effect is directly related to the accuracy of CO₂ retrieval. Although the PPDF method can avoid the complex scattering process, the accuracy of PPDF factor in describing the scattering effect of aerosol is directly related to the retrieval accuracy of CO₂ concentration. Therefore, it is necessary to analyze the influencing factors of the scattering effect of the PPDF method.

Based on the principle of PPDF, the influence of optical path correction factor on CO₂ radiance spectrum is first analyzed, and then the error of optical path correction factor on CO₂ retrieval. Finally, the influence of PPDF scattering correction effect on CO₂ retrieval under different atmospheric conditions is analyzed, aiming to provide a theoretical foundation for achieving high-precision CO₂ retrieval.

2 Materials and methods

The PPDF model is a greenhouse gas retrieval method based on the equivalence theory. Cloud and aerosol scattering essentially affects the distribution of photon paths. Due to cloud and aerosol scattering, the photon paths are stretched or shortened, leading to an underestimation or overestimation of CO₂ concentration. In regions with high surface reflectance, ignoring this path correction effect may result in a particularly noticeable overestimation. Studies have pointed out that in desert areas, ignoring photon path correction can lead to a deviation of more than 15 ppm in CO₂. Considering the photon path correction factor in the PPDF model, this method can overcome the limitations of the DOAS method in dealing with scattering. The traditional DOAS method treats gas absorption as a fast-varying component, and aerosol and other influences as slow-varying components for spectral separation. In contrast, the PPDF model converts scattering into fast-varying components through the PPDF factor, thereby theoretically correcting the errors caused by atmospheric scattering in CO₂ retrieval. The model diagram is shown in Figure 1.

(1) T eff = α c T 3 + 1 − α c T 12 c T a T 3

(2) T 3 = exp − Ψ τ 3

(3) T 12 c = exp − Ψ 1 + σ c τ 12

(4) T a = 1 − α a exp − Ψ τ a σ a + α a ⁡ exp Ψ τ a

(5) τ a = ∫ 0 h a k ( h ) d h , τ 12 = ∫ 0 h c k ( h ) d h , τ 3 = ∫ h c H atom k ( h ) d h

(6) Ψ = 1 cos ( θ ) + 1 cos ( θ 1 )

(7) σ a = ρ a ⁡ exp − γ a τ a , σ c = ρ c ⁡ exp − γ c τ 12

where α _a, α _c, ρ _a, ρ _c, h _a, h _c, γ _a, and γ _c are 8 PPDF parameters; k is the molecular absorption coefficient; T _eff is the effective transmittance of the whole atmosphere; θ and θ1 are the solar zenith angle and the satellite observation angle, respectively. These PPDF parameters treat the scattering of clouds and aerosols as stretching or shortening the optical path, thereby changing the effective transmittance of the entire atmosphere.

Figure 1:

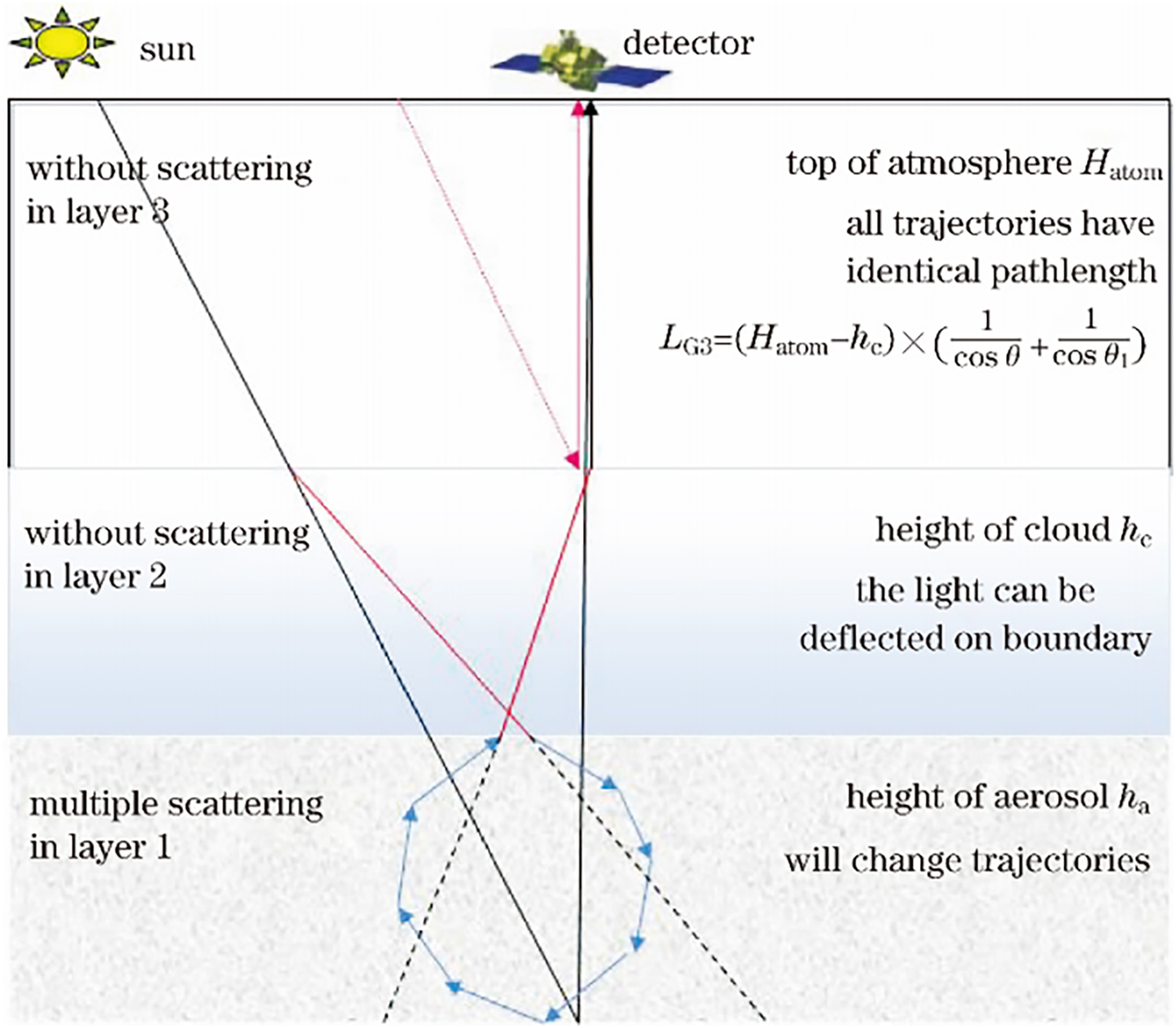
The three-layer PPDF model.

According to the transmittance of Eq. (1) and the instrument response of the detector, the radiance spectrum received by the satellite is as follows:

(8) R = S ∗ T eff

where R is the radiance spectrum of CO₂ in the 1.6 µm band; S is the solar spectrum outside the atmosphere, and < > is the convolution with the instrument linear function.

The scattering is corrected using eight PPDF factors, and the correction effect is directly related to the retrieval accuracy of CO₂. The actual effective transmittance of the atmosphere is shown in Eq. (1), and the effect of scattering correction is the deviation of the eight PPDF factors from their true states. Since the PPDF factors of the upper scattering layers α _c , ρ _c , h _c , γ _c and α _a , ρ _a , h _a , γ _a basically have the same effect on the spectrum, the influence of α _c , ρ _c , h _c , γ _c on the effective transmittance in Eq. (1) is discussed. To analyze the influence of α _c , ρ _c , h _c , γ _c on radiance, the effect of a small perturbation of a PPDF factor on its effective transmittance is first taken into account, as described by Eqs. (1)– (7). Assuming that α _c can change Δα _c, the resulting change in transmittance is as follows:

(9) Δ T 1 = Δ α c 1 − T 12 c ∗ T a T 3

If ρ _c changes Δρ _c, the change in transmittance is as follows:

(10) Δ T 2 = 1 − α c ∗ T a ∗ T 3 ∗ exp − Ψ 1 + ρ c + Δ ρ c ∗ exp − γ c ∗ τ 12 − 1 − α c ∗ T a ∗ T 3 ∗ exp − Ψ 1 + ρ c ∗ exp − γ c ∗ τ 12

If h _c changes Δh _c, Δ τ 12 = ∫ h c h c + Δ h c k ( h ) d h . Therefore, the effective transmittance is changed to:

(11) Δ T 3 = 1 − α c ∗ T a ∗ T 3 ∗ exp − Ψ 1 + σ c ∗ τ 12 + Δ τ 12 − 1 − α c ∗ T a ∗ T 3 ∗ exp − Ψ 1 + σ c ∗ τ 12

If γ _c changes Δγ _c, the transmittance is as follows:

(12) Δ T 4 = 1 − α c ∗ T a ∗ T 3 ∗ exp − Ψ 1 + ρ c ∗ exp − ( γ c + Δ γ c ) ∗ τ 12 − 1 − α c ∗ T a ∗ T 3 ∗ exp − Ψ 1 + ρ c ∗ exp − γ c ∗ τ 12

Therefore, the influence of α _c , ρ _c , h _c , γ _c on radiance depends on the values of ΔT ₁, ΔT ₂, ΔT ₃, ΔT ₄. If Δα _c > 0, then ΔT ₁ > 0, the spectrum received by the satellite is enhanced, and the absorption peak becomes shallow. This makes the results of CO₂ retrieval larger; otherwise, it is small. If Δρ _c > 0, then ΔT ₂ < 0, the spectrum received by the satellite weakens and the absorption peak becomes deeper. This makes the CO₂ retrieval result smaller; otherwise, the retrieval result is larger. Similarly, the effect of Δh _c is similar to that of Δα _c, and the effect of Δγ _c is similar to that of Δρ _c.

The disturbance of the PPDF factor will increase or decrease the effective transmittance in Eq. (1). Consequently, the radiance received by the satellite will also increase or decrease, making the CO₂ retrieval result smaller or larger. Therefore, the influence of the scattering correction of the PPDF model on CO₂ retrieval is discussed.

3 Results and analysis

3.1 Effect of PPDF factor on 1.6 µm band radiance and CO₂ retrieval

From Eqs. (1)– (7) in the PPDF model, it can be seen that the PPDF factor is directly related to the construction of the simulated spectrum and has significant impact on the retrieval accuracy of CO₂. The weight of each PPDF factor on the 1.6 µm band radiance of CO₂ is obtained using Eqs. (1)– (7). The simulated spectrum is expressed as follows:

(13) Y = − ln ( R ) = − ln ( < S ∗ T eff > ) + P 2 ( λ )

The weight function is expressed as follows:

(14) ∂ ( R ) ∂ ( X ) = ∂ ( R ) ∂ ( Y ) ∗ ∂ ( Y ) ∂ ( X ) = − R ∗ S ∗ ∂ T eff ∂ ( X ) S ∗ T eff

where X is each PPDF factor, and T _eff is the calculation result of Eq. (1). The second-order polynomial is calculated as follows:

(15) P 2 ( λ ) = a 1 + a 2 λ − λ j + a 3 λ − λ j 2

which is used to fit other slow components except scattering.

The simulated spectral calculation conditions are shown in Table 1. The weight of each PPDF factor and the CO₂ mixing ratio at 1.6 µm are calculated by using Eq. (14). The weight is shown in Figure 2. The x-axis represents the corresponding wave number, and the y-axis represents the weight of each PPDF factor and CO₂ mixing ratio.

Table 1:

Simulated spectral factors.

Parameters	Variation range
Viewing zenith angle	10°
Albedo (1.6 μm)	0.3
AOD (1.6 μm)	0.5
Solar zenith angle	65°
Atmospheric profile	76-year standard atmospheric profile

Figure 2:

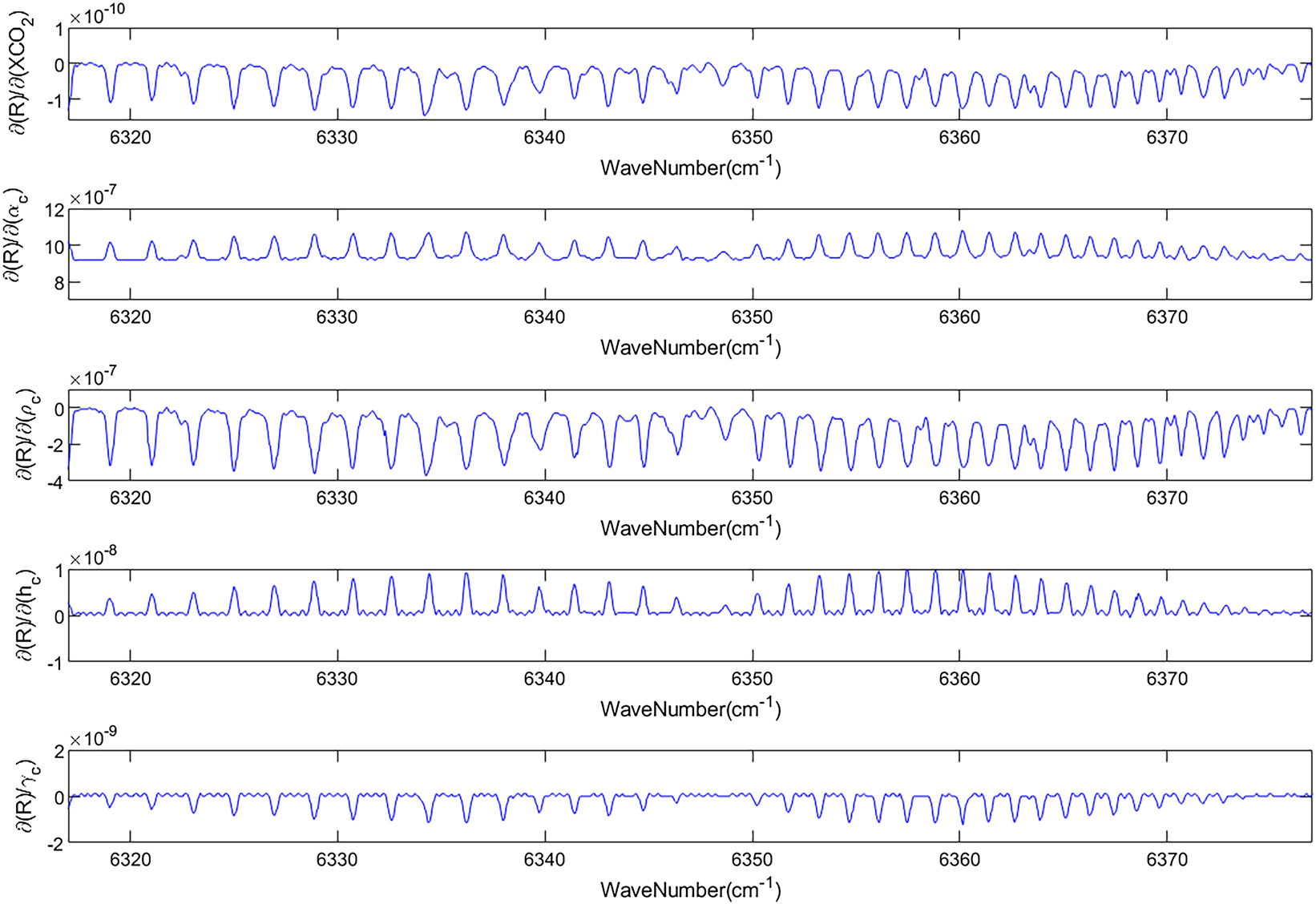
Weight of CO₂ and PPDF factors.

As shown in Figure 2, the weight of each factor is different in the 1.6 µm band. For magnitude, the influence of α _c , ρ _c on the 1.6 µm band radiance is greater than that on the CO₂ column concentration, while the influence of h _c , γ _c on the 1.6 µm band radiance and the CO₂ column concentration is similar. In terms of the impact on CO₂ retrieval, α _c , h _c have the same effect on the spectrum, resulting in shallow absorption peaks in the simulated spectrum and overestimating the retrieval results. On the other hand, ρ _c , γ _c deepens the absorption peaks in the spectrum, resulting in an underestimation of the retrieval results. Based on the PPDF model, the above results can be understood as: parameter photons are directly scattered back to the satellite by the scattering layer, thereby shortening the actual optical path. This leads to a reduction in CO₂ absorption, manifested as a shallower absorption peak, resulting in an increase in the retrieval results. ρ _c represents the stretching of the optical path due to atmospheric scattering. The more significant the stretching, the deeper the absorption peak, and the smaller the retrieval result. h _c represents the height of the scattering layer. The higher the scattering layer, the lower the absolute probability of photon absorption, the shallower the absorption peak, and the larger the retrieval result. γ _c represents the shape of probability distribution of the optical path. The larger γ _c, the more photons are stretched due to scattering, the deeper the absorption peak, and the smaller the retrieval.

Based on the influence of the weight function (Figure 2) on the radiance of each PPDF factor, how each PPDF factor affects CO₂ retrieval is further investigated. In this study, one factor is changed at a time. Since α _c , ρ _c are usually small and randomly changes between 0 and 0.1, h _c is between 0 and 5 km and γ _c is between 0 and 2. In the same way, the influence of α _c , ρ _c , h _c , and γ _c on CO₂ retrieval can be explored. In actual PPDF retrieval, the column concentration is 393.2145 ppm. Figure 3 shows the difference between the retrieved values and the actual PPDF under different factors, helping to determine the influence of each PPDF factor on CO₂ retrieval.

Figure 3:

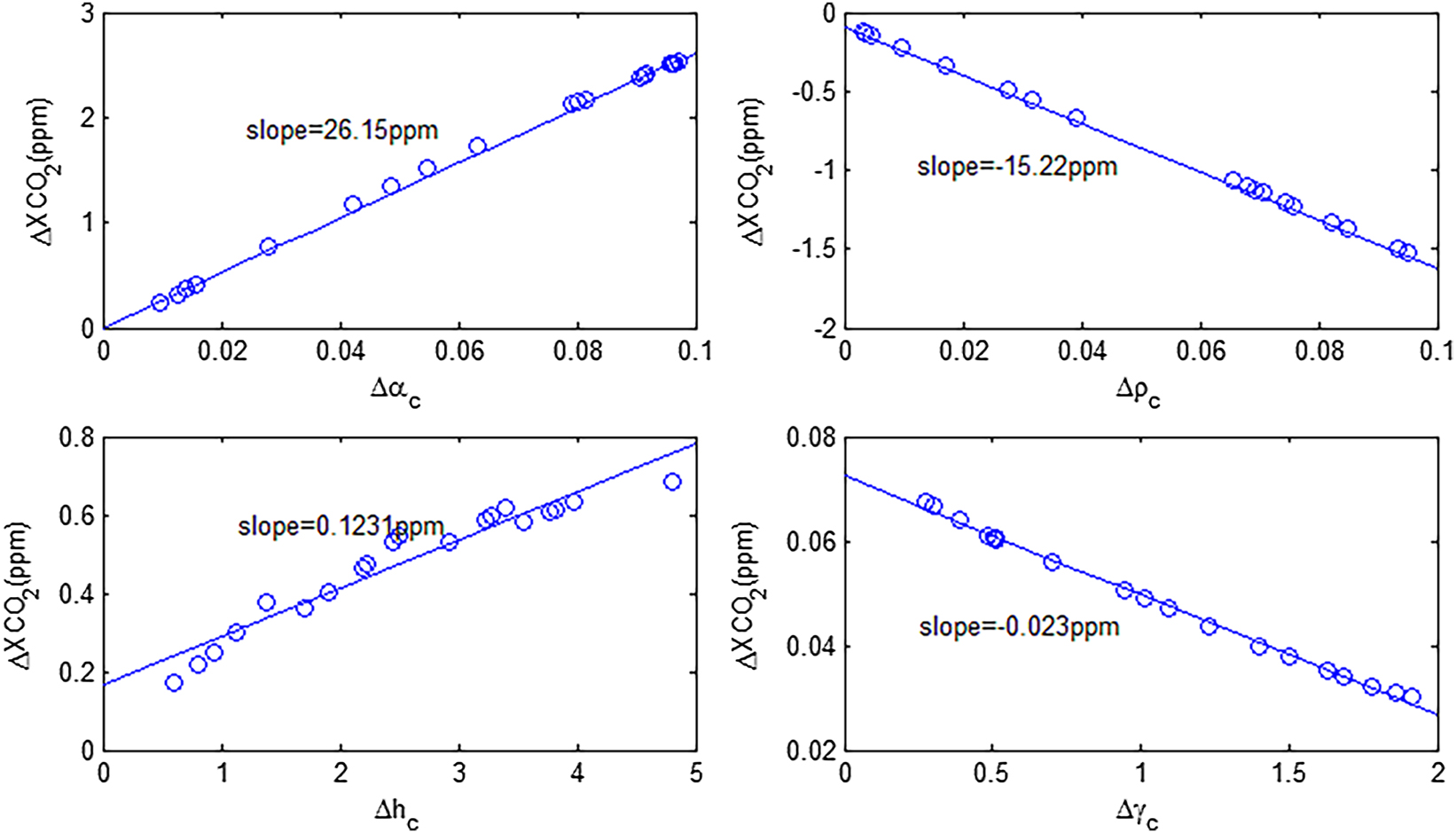
The relationship between PPDF factor and the deviation of CO₂ retrieval value.

As shown in Figure 3, the impact of α _c, ρ _c, h _c, and γ _c on CO₂ retrieval is approximately linear. A linear fit is performed on the above retrieval results, and the slope of α _c, h _c is greater than 0. This indicates that as α _c, h _c increases, the retrieval results become larger and larger, and the retrieved value is greater than the real value of ρ _c, γ _c ; on the contrary, this is consistent with the conclusion of the weight. From the absolute value of the slope, the slope of α _c, ρ _c is much larger than that of h _c, γ _c, which means that the sensitivity of α _c, ρ _c to CO₂ retrieval is much stronger than that of h _c, γ _c. Therefore, to ensure retrieval accuracy during the inversion process, variable transformations are introduced to constrain the parameters: α = e − x 2 _ α and perform retrieval on x_α _. Similarly, ρ = e − x 2 _ ρ and retrieve the corresponding x_ρ.

3.2 Effects of surface reflectance and aerosol on CO₂ retrieval

Temperature, pressure, and aerosol optical thickness have a significant impact on the optical path during photon transport. These factors will influence the scattering, absorption, and transmission of photons through the atmosphere, thereby affecting the retrieval of CO₂ concentrations. In addition, the surface reflectance characterizes the ability of the Earth’s surface to reflect solar radiation. The coupling of these atmospheric conditions and surface reflectance will influence the accuracy of CO₂ retrievals. The PPDF method is used to further analyze the impact of atmospheric parameters and surface reflectance on CO₂ retrieval. Table 1 can be used for simulation (The aerosol optical depth is modified to 0.05). The PPDF method is used to retrieve CO₂ by changing different temperature, pressure, surface reflectance and aerosol optical thickness. The retrieval results are shown in Figure 4.

Figure 4:

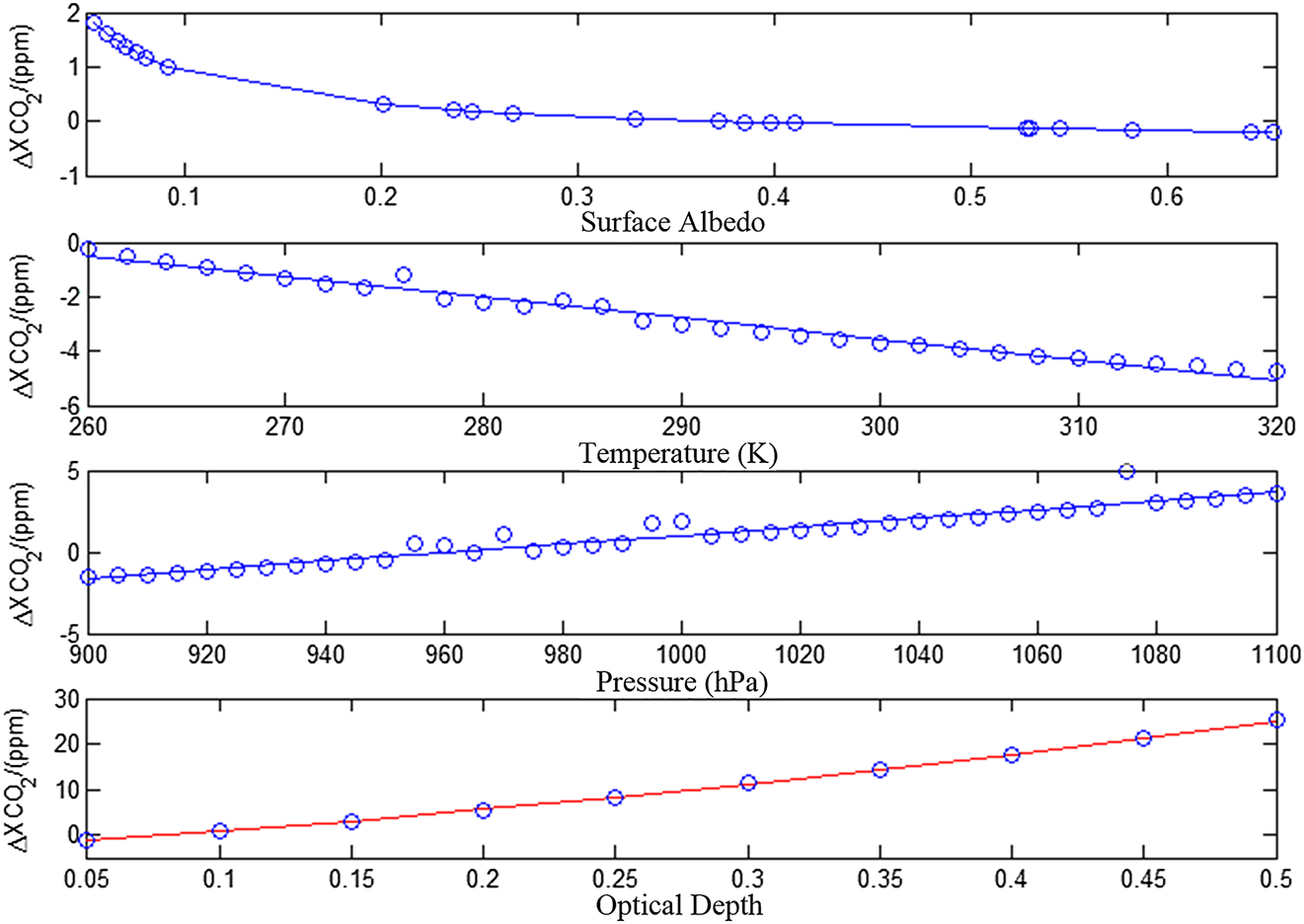
Errors of PPDF retrieval under different conditions.

According to the linear fitting of the temperature and surface pressure impacts on the CO₂ retrieval results, it is found that the slope of surface pressure is 0.025 ppm/hPa and that of temperature is −0.0753 ppm/K. This means that a pressure difference of 40 hPa from the true value will cause a 1 ppm CO₂ retrieval error. About 14 K temperature difference from the true value will result in a 1 ppm CO₂ retrieval error. These errors are usually within the acceptable limits in most remote sensing applications. The influence of optical thickness and surface reflectance is not simply linear. As the surface reflectance increase, its influence on CO₂ retrieval is small. As the optical thickness increases, the retrieval error increases in the form of quadratic function. To more clearly reflect the retrieval deviation under different surface reflectance and optical thickness conditions, according to the statistical results of MODIS, the deviation of optical thickness can be approximately expressed as Δτ = 0.05 + 0.15τ. The deviation of surface reflectance is usually smaller than 60 %. According to Figure 4, Tables 2 and 3 show the retrieval error caused by optical thickness and surface reflectivity in practical applications.

Table 2:

Retrieval errors of different surface reflectivity.

Surface reflectivity	0.1	0.2	0.3	0.4
ΔXCO₂ (ppm)	0.7–1.8	0.15–0.88	0.56–0.32	0.19–0.33

Table 3:

Retrieval errors of different aerosol optical thickness.

Aerosol optical depth	0.1	0.2	0.3	0.4
ΔXCO₂ (ppm)	2.97	4.14	6.15	8.17

From Tables 2 and 3, as the surface reflectivity increases, its influence on the retrieval becomes small. However, as the aerosol optical thickness increases, the retrieval error will increase, which has a significant impact on the CO₂ retrieval accuracy.

4 Verification of measured data

To analyze the scattering correction performance of the PPDF method, GOSAT land data from April, June, October, and December, 2022 were selected to represent the four seasons: spring, summer, autumn, and winter. The retrieval deviations of the PPDF results are shown in Figure 5. The results show that the PPDF retrieval show significant fluctuations in June. This is mainly due to high temperatures in summer, increased convective activity, and increased aerosol concentrations of complex types such as biomass burning and urban pollution, resulting in a significant decrease in retrieval accuracy. Most errors are in the range of 0.8–1%. There is also a clear latitudinal variation in retrieval accuracy: the retrieval errors of the PPDF method significantly increase in areas between 30°N and 60°N (temperate continental zone). There are two main reasons for this: (1) This region includes many industrialized countries and densely populated areas. Anthropogenic emission sources such as coal-fired power plants, transportation, and agriculture enhance the near-surface CO₂ concentration gradient, which may introduce retrieval bias. In addition, human activities release large amounts of aerosols and pollutants, significantly increasing the uncertainty in atmospheric scattering and absorption; (2) High solar zenith angle in this region increases the complexity of atmospheric scattering, aerosol interference, and surface reflection, thereby greatly affecting the effective detection of CO₂ absorption signals.

Figure 5:

Retrieval deviations of the PPDF method in different seasons.

Due to the time-consuming nature of the DOAS retrieval method, this study only applied it to a subset of data in low-latitude regions in May. The retrieval results are compared with those obtained using the PPDF method, as shown in Figure 6, and corresponding means and variances shown in Table 2.

Figure 6:

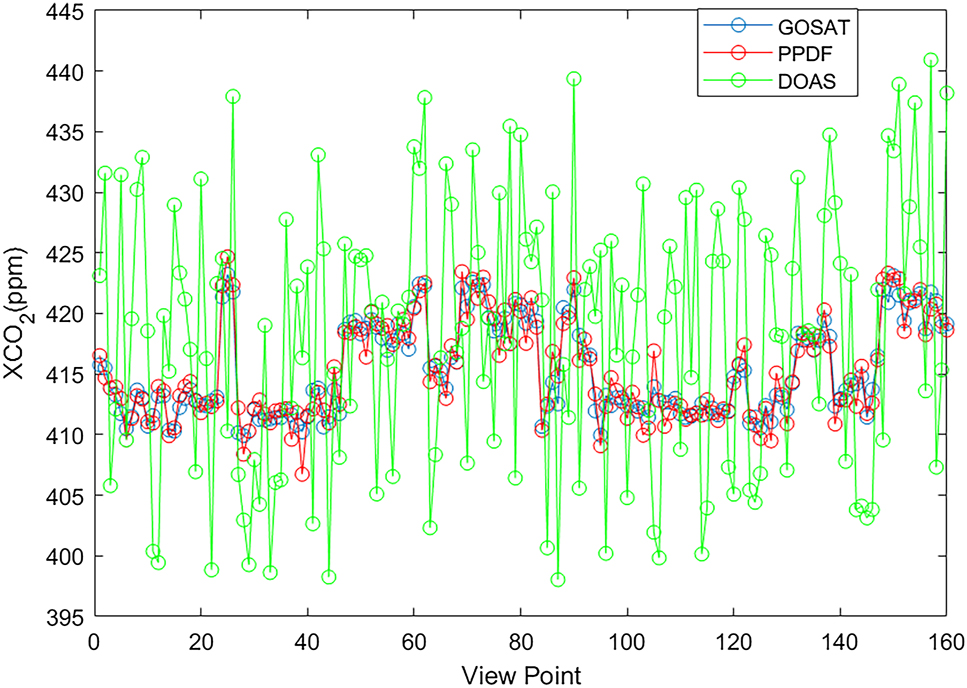
Retrieval results of CO₂ infusion concentration obtained by different retrieval methods and GOSAT.

As shown in Figure 6 and Table 4, the deviation between PPDF search results and GOSAT level 2 products is within 0.7 %, and the mean and variance are close to those of GOSAT. This level of retrieval accuracy is suitable for climate studies. In contrast, the DOAS method yields retrieval deviations ranging from 2 to 5 %, with a variance as high as 121, not meeting the accuracy requirements for climate.

Table 4:

Retrieval error of different aerosol optical thickness.

	GOSAT	PPDF	DOAS
Mean/ppm	415.29	415.31	418.35
Variance/ppm	14.85	16.37	21.34

Based on the modeling of photon path length distribution, the PPDF method can better capture multiple scattering effects and significantly reduce retrieval biases under strong atmospheric scattering conditions. It can simplify complex radiative transfer into an integration over path distributions with low computation, making it suitable for large-scale operational processing. It shows high adaptability to different surface albedos and aerosol conditions, reducing sensitivity to scene-dependent parameters. It can also be embedded as a scattering correction module within existing retrieval pipelines without altering the overall framework. These results demonstrate that the PPDF method can correct scattering effects and improve the retrieval accuracy, and it is applicable.

5 Conclusions

Aerosol scattering effect has a significant impact on CO₂ satellite remote sensing observation. How to correct aerosol scattering effect is a key scientific problem. Based on the principle of PPDF, the influence of optical path correction factor on CO₂ retrieval is analyzed. From the retrieval results, the sensitivity of α, ρ to CO₂ in the retrieval process is much stronger than that of h, γ. The influence of α, ρ, h, γ on CO₂ retrieval is approximately linear. Increasing α by 0.1 will make the retrieval result increase by about 3 ppm; increasing ρ by 0.1 will make the retrieval results decrease by about 2 ppm; increasing h by 1 km will only increase the retrieval result by 0.12 ppm; increasing γ by 1 km makes the retrieval result decrease by 0.023 ppm. The inversion accuracy of PPDF factor is related to the effect of scattering correction, which further affects the accuracy of CO₂ retrieval. To improve the accuracy of CO₂ retrieval, the scattering correction effect should be guaranteed in the subsequent retrieval process. To verify the effect of scattering correction, the global data of GOSAT in 2022 is selected for retrieval. The deviation of PPDF retrieval is within 0.7 %, which is better than the accuracy of traditional DOAS method (2–5 %), verifying the effect of scattering correction. Since this method was developed based on GOSAT data, it is also applicable to OCO-2 data. For this case, further validation and some algorithm modifications are still required, and this is also the focus in the future work.

Corresponding author: Yun Jiang, College of Electronic Engineering, Chaohu University, Hefei, China, E-mail: yjg4i1@163.com

Funding information: The authors acknowledge the Key Scientific Research Project of Anhui Education Department (2023AH052104, 2022AH051712, 2023AH052099, KJ2021A1027), The Start-up Fund for High-level Talents (KYDQ-202207, KYQD-202208), College Students’ Innovation and Entrepreneurship Training Program (S202510380077), the Natural Science Foundation of Anhui province (2408085MD102) and the Anhui Provincial Colleges Science Foundation for Distinguished Young Scholars (2022AH020093).
Author contribution: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors state no conflict of interest.
Data availability statement: All data generated or analysed during this study are included in this published article.

References

1. Sun, ZQ, Wang, XH, Ye, HH, Li, C, An, Y, Sun, EC, et al.. Fast retrieval method of atmospheric CO2 based on GF-5 satellite remote sensing data. Acta Opt Sin 2024;44:281–90. https://doi.org/10.3788/AOS231995.Search in Google Scholar

2. Kiel, M, Eldering, A, Roten, DD, Lin, JC, Feng, S, Lei, R, et al.. Urban-focused satellite CO2 observations from the orbiting carbon observatory-3: a first look at the Los Angeles megacity. Rem Sens Environ 2021;258:112314. https://doi.org/10.1016/j.rse.2021.112314.Search in Google Scholar

3. Li, ZQ, Xie, YS, Shi, YS, Li, Q, Jason, C, Zhang, YZ, et al.. A review of collaborative remote sensing observation of greenhouse gases and aerosol with atmospheric environment satellites. Natl Remote Sens Bull 2022;26:795–816. https://doi.org/10.11834/jrs.20221387.Search in Google Scholar

4. Somkuti, P, Bösch, H, Parker, RJ. The significance of fast radiative transfer for hyperspectral SWIR XCO2 retrievals. Atmosphere 2020;11:1219. https://doi.org/10.3390/atmos11111219.Search in Google Scholar

5. Bertaux, JL, Hauchecorne, A, Lefèvre, F, Bréon, FM, Blanot, L, Jouglet, D, et al.. The use of the 1.27 µm O2 absorption band for greenhouse gas monitoring from space and application to MicroCarb. Atmos Meas Tech 2020;13:3329–74. https://doi.org/10.5194/amt-13-3329-2020.Search in Google Scholar

6. Lee, KS, Lee, CS, Seo, M, Choi, S, Seong, NH, Jin, D, et al.. Improvements of 6S look-uptable based surface reflectance employing minimum curvature surface method. Asia-Pac J Atmos Sci 2020;56:235–48. https://doi.org/10.1007/s13143-019-00164-3.Search in Google Scholar

7. Clarisse, L, Van damme, M, Hurtmans, D, Franco, B, Clerbaux, C, Coheur, PF. The diel cycle of NH3 observed from the FY-4A geostationary interferometric infrared sounder (GIIRS). Geophys Res Lett 2021;48:e2021GL093010. https://doi.org/10.1029/2021GL093010.Search in Google Scholar

8. Sanghavi, S, Nelson, R, Frankenberg, C, Gunson, M. Aerosols in OCO-2/GOSAT retrievals of XCO2: an information content and error analysis. Rem Sens Environ 2020;251:112053. https://doi.org/10.1016/j.rse.2020.112053.Search in Google Scholar

9. Sinyuk, A, Holben, BN, Eck, TF, Giles, DM, Slutsker, I, Korkin, S, et al.. The AERONET version 3 aerosol retrieval algorithm, associated uncertainties and comparisons to version 2. Atmos Meas Tech 2020;13:3375–411. https://doi.org/10.5194/amt-13-3375-2020.Search in Google Scholar

10. Jiang, XH, Wang, XH, Ye, HH, Wei, QY, Li, ZW, Bu, TT. Correction method of atmospheric scattering effect through optical path in CO2 retrieval. Acta Opt Sin 2014;34:235–41. https://doi.org/10.3788/AOS201434.0801005.Search in Google Scholar

11. Huo, YF, Duan, MZ. Sensitivity studies for CO2 retrieval of aerosol optical depth, type and profile. Remote Sens Technol Appl 2014;29:33–9. https://doi.org/10.11873/j.issn.1004-0323.2014.0033.Search in Google Scholar

12. Ye, H, Shi, H, Li, C, Wang, X, Xiong, W, An, Y, et al.. A coupled BRDF CO2 retrieval method for the GF-5 GMI and improvements in the correction of atmospheric scattering. Remote Sens 2022;14:488. https://doi.org/10.3390/rs14030488.Search in Google Scholar

13. Crisp, D, O’dell, C, Granat, R. Orbiting carbon observatory-2 & 3 (OCO-2 & OCO-3) level 2 full physics retrieval algorithm theoretical basis document. NASA Jet Propulsion Laboratory; 2021. Report No. OCO D-55207. https://disc.gsfc.nasa.gov/information/documents?title=OCO-2%20Documents&utm_source=chatgpt.com.Search in Google Scholar

14. Heymann, J, Reuter, M, Hilker, M, Buchwitz, M, Schneising, O, Bovensmann, H, et al.. Consistent satellite XCO2 retrials from SCIAMACHY and GOSAT using the BESD algorithm. Atmos Meas Tech 2015;8:2961–80. https://doi.org/10.5194/amt-8-2961-2015.Search in Google Scholar

15. Jiang, F, Wang, H, Chen, JM, Ju, W, Tian, X, Feng, S, et al.. Regional CO2 fluxes from 2010 to 2015 in‐ferred from GOSAT XCO2 retrievals using a new version of the global carbon assimilation system. Atmos Chem Phys 2021;21:1963–85. https://doi.org/10.5194/acp-21-1963-2021.Search in Google Scholar

Received: 2025-03-24

Accepted: 2025-11-06

Published Online: 2025-12-16

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/phys-2025-0245

Keywords for this article

carbon dioxide; photon probability density function; atmospheric scattering; retrieval

Creative Commons

BY 4.0

The influence of scattering correction effect based on optical path distribution on CO2 retrieval

Article

Abstract

1 Introduction

2 Materials and methods

3 Results and analysis

3.1 Effect of PPDF factor on 1.6 µm band radiance and CO2 retrieval

3.2 Effects of surface reflectance and aerosol on CO2 retrieval

4 Verification of measured data

5 Conclusions

References

Articles in the same Issue

Articles in the same Issue

Articles in the same Issue

The influence of scattering correction effect based on optical path distribution on CO₂ retrieval

3.1 Effect of PPDF factor on 1.6 µm band radiance and CO₂ retrieval

3.2 Effects of surface reflectance and aerosol on CO₂ retrieval