Numerical study of flow and heat transfer in the air-side metal foam partially filled channels of panel-type radiator under forced convection

Nomenclature

a _sf

area per unit volume of metal foam (m²/m³)

A _f

heat transfer area (m²)

c _p

specific heat capacity (J/(kg K))

C _f

inertia coefficient

d _f

fiber thickness (m)

D _h

hydraulic diameter (m)

f

friction factor

h

convective heat transfer coefficient (W/(m² K))

h _sf

interfacial heat transfer coefficient (W/(m² K))

H

panel spacing (m)

k

turbulent kinetic energy (m²/s²)

K

permeability (m²)

L

panel length (m)

L ₁

length of entrance section (m)

L ₂

length of outlet section (m)

L _p

length of porous filling area (m)

m

mass flow rate (kg/s)

Nu

Nusselt number

p

pressure (pa)

Pr

Prandtl number

q _w

wall heat flux (W/m²)

Re

Reynolds number

t

thickness of porous foam panels (m)

T

temperature (K)

T _x,y

local temperature on panel surface (K)

u

velocity (m/s)

u _interface

average velocity at porous interface (m/s)

u _m

average inlet velocity (m/s)

V _p

metal foam filling ratio

w

width of porous fins (m)

W

panel width (m)

Greek letters

ε

turbulent dissipation rate (m²/s³)

λ

thermal conductivity (W/(m K))

μ

dynamic viscosity (Pa s)

ν

kinematic viscosity (m²/s)

ρ

density (kg/m³)

ρ _p

relative density

φ

porosity

ω

pore density (PPI)

Abbreviations

PEC

performance evaluation criterion

PFF

porous fin filled

PPI

pores per inch

PTLF

porous thin-layer filled

Subscripts

avg

average

eff

effective

f

fluid

fe

fluid effective

in

inlet

i,j

tensor

max

maximum

out

outlet

s

solid

se

solid effective

t

turbulent

w

wall

0

base case

1 Introduction

Oil-immersed transformers are vital components of the electrical power system, which are essential for the efficient transmission, flexible distribution, and secure utilization of electrical energy [1]. With the increasing demand for electricity, the phenomenon of internal overheating in transformers has become more prevalent [2], thereby necessitating enhanced requirements for cooling systems. Since panel-type radiators are the predominant choice for oil-immersed transformers, it is essential to improve their cooling efficiency.

To improve the heat dissipation efficiency of panel-type radiators, researchers have conducted relevant studies. Taghikhani et al. [3] numerically investigated the impact of incorporating alumina nanoparticles into pure transformer oil on the system’s cooling performance. It was found that, when using the oil-based alumina nanofluid, the hotspot temperature of the transformer was decreased by approximately 4% under the oil-natural air-natural (ONAN) mode and by about 1% under the oil-forced air-natural mode compared to pure transformer oil. Tian et al. [4] numerically investigated the effect of chimney structure on the radiator’s cooling performance in ONAN mode, finding that the cooling capacity increased by 14.76% and the oil temperature decreased by 6.72°C. Garelli et al. [5] utilized a delta wing array in the air channel between two panels under ONAN mode, and the numerical results indicated a 12% improvement in the radiator’s heat dissipation performance. Li et al. [6] conducted a comparative study on the effects of fan cooling versus falling film cooling on the top oil temperature and hotspot temperature of transformers. They found that falling film cooling is a more effective heat dissipation method, reducing the top oil temperature and hotspot temperature by 31.2 and 28.7°C, respectively, compared to natural convection cooling. Paramane et al. [7] conducted a numerical study on the transformer air cooling system under the oil-natural air-forced (ONAF) mode. It was found that the horizontal blowing method achieved higher cooling efficiency than the vertical blowing method, which was attributed to reduced lateral air leakage. Although enhanced heat dissipation measures have been proposed for panel-type radiators, most are implemented in the ONAN mode. In contrast, the focus in the ONAF mode remains primarily on optimizing fan placement [7,8], with limited attention given to structural improvements of the radiator body.

Porous media, such as metal foam, have garnered significant attention from researchers due to their unique flow and heat transfer characteristics. Open-cell metal foams, with their interconnected voids, can disrupt the boundary layer, inducing turbulence within the pores and thereby enhancing convective heat transfer. Additionally, open-cell metal foams are characterized by low density, high strength, high rigidity, high thermal conductivity, and a large heat transfer surface area per unit volume [9]. Noh et al. [10] conducted experimental research on forced convection heat transfer in annular channels filled with aluminum foam, deriving correlations for the friction factor and Nusselt number, which were subsequently applied to thermal design. Leong et al. [11] conducted experimental and numerical studies on forced convection heat transfer in graphite foam channels with various configurations. It was found that the best performance was achieved using a solid block of foam, although this configuration also resulted in the largest pressure drop. Therefore, channels fully filled with porous foam can achieve optimal heat transfer performance, but can also significantly increase the flow resistance, leading to higher power consumption when using fans or pumps. Employing partially filled porous foam channels effectively addresses the issue of excessive pressure drop in open-cell foam-filled channels. These partially filled channels are typically categorized into two types: porous layer filled and porous fin filled (PFF) configurations. Lu et al. [12] proposed an analytical solution for fully developed forced convection heat transfer in flat channels that are partially filled with metal foam. Their study revealed the influence of metal foam characteristics, including relative height, porosity, and pore density, on flow distribution and heat transfer performance within the channels. Additionally, the solid-fluid thermal conductivity ratio and Reynolds number are also critical parameters for heat transfer performance. Anuar et al. [13] conducted flow visualization experiments in channels that were partially filled with metal foam blocks of different pore densities. It found that the channel filled with 5 PPI metal foam exhibited a higher pressure drop compared with those filled with 10 and 30 PPI metal foam. Moreover, the development of boundary layers at the porous interface was observed. Jadhav et al. [14] numerically investigated the flow and heat transfer characteristics of a tube partially filled with aluminum foam. It was found that the tube core arrangement of aluminum foam exhibited lower resistance loss but also lower heat transfer performance as compared with the tube wall arrangement of aluminum foam. The optimal overall heat transfer performance of the pipe was attained by minimizing the thickness of the aluminum foam in the tube wall arrangement. Furthermore, Jiang et al. [15] numerically investigated the flow and heat transfer characteristics of hydrocarbon fuel in a partially filled tube with metal foam under supercritical pressure. The tube wall and tube core arrangement of the metal foam were analyzed, and the heat transfer effect of the gradient-filled metal foam was compared. It was found that partially filled metal foam effectively enhanced heat transfer performance. Additionally, the utilization of gradient-filled metal foam was found to effectively prevent potential overheating phenomena that may occur in thermal protection systems. As for porous fin filling, Alfellag et al. [16] numerically investigated metal foam pin-fin heat sinks (MFPFHS) with both uniform and variable cross-sections. It was found that MFPFHS exhibited superior heat dissipation performance and lower drag losses as compared with solid pin-fins. Moreover, the utilization of variable cross-section pin-fins can further enhance the overall heat dissipation performance of the heat sink. Akbarnataj et al. [17] numerically investigated the heat transfer characteristics of a porous longitudinal ribbed counter flow double tube heat exchanger and optimized the number of fins to obtain the highest heat transfer to pressure drop ratio. They found that decreasing the porosity significantly increased both heat transfer and flow resistance, and the overall thermal performance was optimal when the number of fins was set to 40. Salehi and Fattahi [18] numerically investigated hydrogen/air jet impingement cooling of heated surfaces. The effects of inserting solid or porous fins, as well as inline and staggered fin configurations, were compared. They found that the temperature drop on the hot surface with porous fins was larger than that with solid fins or without fins. The convective heat transfer coefficient of the air coolant increased by 10% with staggered fin distribution as compared with in-line fins.

In summary, studies on enhanced heat dissipation in panel-type radiators under air-side forced convection conditions are limited. The application of metal foam filling technology is regarded as a feasible solution. Previous studies have mainly investigated the usage of metal foam filling technology in pipes and heat sinks, with limited exploration of its application in panel-type radiators. Moreover, these studies often use metal foam with filling rates larger than 50% to improve heat transfer efficiency, while the heat transfer characteristics in the channel with low filling rates (<20%) are still unclear. In addition, there is also lack of comparative studies on the effects of different metal foam filling methods in the air-side channel of panel-type radiators, and further analysis for the related effects of the filling method is quite necessary.

Therefore, to enhance the overall heat transfer performance of the panel type radiator, this study developed a strategy of partially filling the air-side channel with metal foam and numerically investigated its flow and heat transfer performances under forced convection conditions. The effects of metal foam porous thin layer filled (PTLF) method versus PFF method and the filling rate V _p were analyzed. Besides, the flow and heat transfer characteristics in the metal foam-filled channels with different metal foam materials, porosities, and pore densities were also discussed. This research would be meaningful for the selection and arrangement of metal foams to achieve heat transfer enhancement at the air-side channel of panel-type radiators.

2 Physical model and computational methods

2.1 Physical model

The simplified physical model of the panel-type radiator is shown in Figure 1, where Figure 1(a) represents the panel-type radiator, with baffles arranged on both sides to form closed channels between the panels, preventing lateral airflow leakage [7]. Figure 1(b) shows the radiator unit extracted from the panel-type radiator. Considering the symmetry of the model, a quarter of the air-side channel of the radiator unit is used as the computational model, which is symmetric with respect to y = 0 and z = H/2 surfaces, as shown in Figure 1(c). The geometry of the computational domain is identical to the model in Garelli et al. [5], where the spacing between panels is H = 45 mm, the width of the panel is W = 450 mm, and the length is L = 1,524 mm. The panel surface contains several trapezoidal oil channel structures, and the detailed dimensions are referenced to the literature of Min et al. [19]. Since most of the area in the channel is fully developed, the entry and exit sections are set according to the ASHARE standard to eliminate inlet and outlet effects. The length of the entry section L ₁ should be greater than 5 WH , and the length of the exit section L ₂ should be greater than 2.5 WH [20]. Thus, L ₁ = 800 mm and L ₂ = 500 mm are adopted. This study focuses on enhancing heat dissipation by partially filling metal foam in the air-side channels of the panel-type radiator. Since the actual panel ends lack trapezoidal oil channel structures, the filling area is located in the middle of the panel surface, with L _p = 1,420 mm. The metal foam filling method can be classified into two categories: PTLF and PFF. As shown in Figure 2, the PTLF method is to install the porous metal foam plate with thickness t on the panel surface directly, and the PFF method is to install six porous metal foam fins with width w along the y-direction on the oil channel protrusions. Both the porous metal foam plate and porous metal foam fins have uniform cross-sections along the x-direction, with their lengths equal to the filling area length L _p. The metal foam filling rate (V _p) is defined as the area proportion of the porous region in the yz cross-section. Table 1 lists the geometrical parameters for PTLF and PFF methods at different filling rates.

Figure 1

Panel-type radiator and simplified physical model of air channel between panels: (a) panel-type radiator, (b) radiator unit, and (c) computational domain.

Figure 2

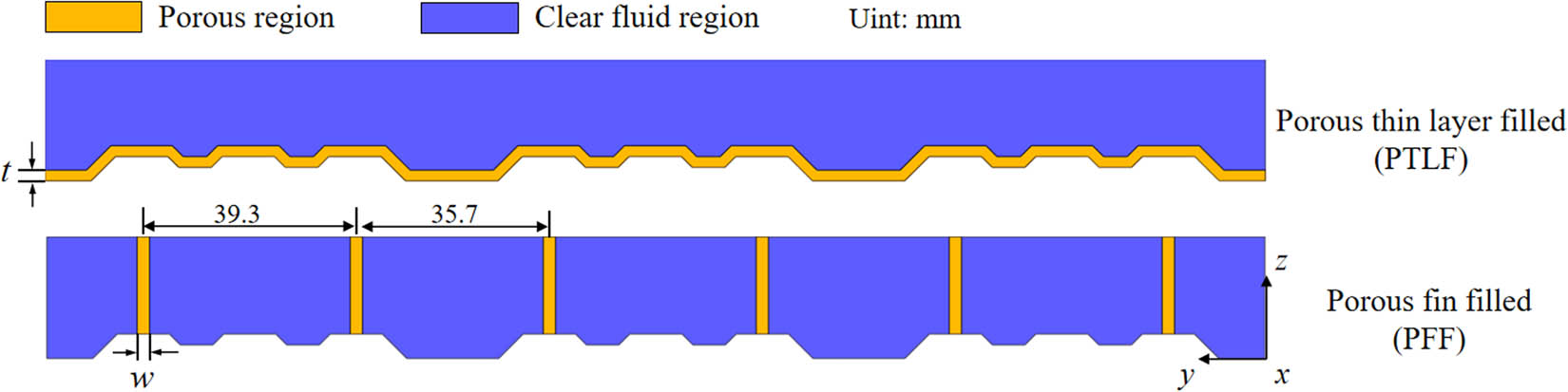
Metal foam filling method (yz-plane).

Table 1

Geometrical parameters of two partially filled models at different filling rates

V p (%)	t/(mm)	w/(mm)
5.55	1	2.28
11.1	2	4.56
16.6	3	6.84
22.2	4	9.12

This study considers the effect of the filling rate on the flow and heat transfer characteristics of the channel and compares the flow and heat transfer performance of aluminum and copper foam channels under different porosities (φ) and pore densities (ω). The ranges of porosity and pore density for the samples are from 0.903 to 0.956 and from 10 to 40 PPI, respectively. Table 2 lists the geometrical parameters of the metal foam samples. The naming of the samples in Table 2 is consistent with the studies of Mancin et al. [21,22,23]. Taking sample Al-10-4.4 as an example, Al represents the material of the sample, 10 indicates a pore density of 10 PPI, and 4.4 denotes a relative density (ρ _p) of 4.4%, where the sum of ρ _p and porosity (φ) is 1.

Table 2

Geometrical parameters of aluminum foam and copper foam samples [21,22,23]

Sample	Pore density ω (PPI)	Porosity φ	Area per unit volume a sf (m2/m3)	Fiber thickness d f (mm)	Permeability K (10−7 m2)	Inertia coefficient (C f)
Al-10-4.4	10	0.956	537	0.445	1.82	0.102
Al-10-6.6	10	0.934	692	0.450	1.87	0.082
Al-10-9.7	10	0.903	839	0.529	1.90	0.074
Al-20-6.8	20	0.932	1,156	0.367	0.824	0.065
Al-40-7.0	40	0.930	1,679	0.324	0.634	0.086
Cu-10-6.7	10	0.933	698	0.390	2.09	0.091
Cu-10-9.5	10	0.905	831	0.403	1.21	0.056
Cu-20-6.7	20	0.933	1,148	0.293	0.41	0.039
Cu-40-6.6	40	0.934	1,635	0.262	0.44	0.060

3 Grid independence test and model validations

3.1 Grid independence test

To ensure the accuracy of the numerical simulation, the computational mesh is tested for grid independence. A 3D hybrid mesh, consisting of hexahedral, polyhedral, and prismatic cells, is generated using Fluent Meshing software. The mesh is refined at the near-wall and porous interfaces, as shown in Figure 3. In the case of PFF with the metal foam sample Al-10-4.4 and fin width of 4.56 mm, six grid sets are tested to assess grid independence, using the Nu and f as evaluation targets. As shown in Figure 4, it is found that the relative deviation in Nu and f under grid with 8,118,446 elements is only 1.4 and 0.7%, respectively, compared with the grid of 11,654,793 elements. Therefore, it can be concluded that the grid with 8,118,446 elements is sufficient to obtain the grid-independent results, and this grid set is adopted for the following studies.

Figure 3

Computational grid.

Figure 4

Variations of Nu and f at different computational grids (Re = 5,125).

3.2 Model validations

To validate the accuracy of the numerical model and computational method, the model validation is carried out. First, the radial dimensionless velocity variation in the metal foam partially filled channel is verified. As shown in Figure 5(a), the computational results of the dimensionless velocity along the dimensionless height of the channel are in good agreement with the simulation results of Kotresha and Gnanasekaran [26]. Subsequently, a comparison is also conducted with the experimental results of Mancin et al. [21,22,23], where channels are fully filled with aluminum and copper metal foams of different porosities and pore densities. The computational pressure drop per unit length can also agree well with the experimental results, as shown in Figure 5(b), where the Cu-20-6.7 case shows a larger deviation as compared with the other two cases, and the average deviation for Cu-20-6.7 case is 6.36%.

Figure 5

(a) Comparison of dimensionless velocity and (b) comparison of pressure drop.

Moreover, the accuracy of the heat transfer results is also verified. Figure 6(a) presents the experimental results of fully filled uniform porous media of Mancin et al. [22,23]. Comparing the average wall temperatures for aluminum foam and copper foam fully filled channels with different porosities and pore densities, it shows that the simulation results of present study are in good agreement with the experimental results. The Al-10-4.4 case shows a relatively larger deviation than other cases, and its average deviation is 8.10%. Additionally, a comparison is also conducted with the simulation results of partially filled gradient metal foam of Jadhav et al. [9], as shown in Figure 6(b). The radial temperature of fluid in the metal foam partially filled tube is validated, and the computational results are in good agreement with the simulations of Jadhav et al. [9]. In summary, the numerical model and computational method used in this study are reliable, which can be used for the subsequent analysis of flow and heat transfer characteristics of metal foam partially filled channels.

Figure 6

(a) Comparison of averaged wall temperature and (b) comparison of fluid radial temperature distribution.

4 Results and discussion

Figure 7 demonstrates the local velocity distribution in PTLF and PFF channels at the yz-plane (x = 762 mm) for different filling rates. It shows that the air velocity is higher in the clear fluid region as compared with the porous region. Compared with the PTLF channel, the interface area between the porous fins and the fluid is larger in the PFF channel, which will lead to greater fluid permeation inside the porous region. As the filling rate increases, the air velocity in the clear fluid region increases, while the proportion of low-speed fluid within the porous region increases. It is attributed to the high flow resistance in the porous region, which will lead most of the fluid flow into the clear fluid region. Meanwhile, the average velocity at the porous interface (u _interface) indicates that as the filling rate increases, the fluid permeation within the porous region of the PTLF channel increases significantly, while in the PFF channel, the variation is small. At the same filling rate, the width of the porous fin in the PFF channel is obviously larger than the thickness of the porous thin layer. Consequently, the permeation resistance within the porous fins will restrict the increase of fluid permeation.

Figure 7

Local velocity distributions at the yz-plane (x = 762 mm) in PTLF and PFF channels (Re = 10,250, Al-10-9.7): (a) V _p = 11.1% and (b) V _p = 22.2%.

Figure 8 illustrates the local turbulence kinetic energy distribution in PTLF and PFF channels at the yz-plane (x = 762 mm) for different filling rates. It shows that the local turbulence kinetic energy is higher at the porous interface, while it is relatively low at other regions. As described by Chandesris et al. [29], large flow velocity differences at the porous interfaces and the presence of solid matrix inside porous region will induce Kelvin–Helmholtz instabilities, where vortices generation and dissipation are remarkable. Compared with the PTLF channel, the maximum turbulence kinetic energy (k _max) at the porous interface in the PFF channel is larger. In conjunction with Figure 7, it can be seen that this is due to the large velocity difference between inside and outside of porous region in the PFF channel. Furthermore, as the filling rate increases, the turbulence effects at the porous interface become more pronounced, which is due to the increased velocity difference between the porous and clear regions.

Figure 8

Local turbulence kinetic energy distributions at the yz-plane (x = 762 mm) in PTLF and PFF channels (Re = 10,250, Al-10-9.7): (a) V _p = 11.1% and (b) V _p = 22.2%.

Figure 9 presents the local fluid temperature distribution in PTLF and PFF channels at the yz-plane (x = 762 mm) for different filling rates. Compared with the PTLF channel, the PFF channel has a higher average temperature (T _avg) and a smaller maximum temperature difference (ΔT _max) at the cross-section, indicating better flow mixing and heat transfer capabilities. This is attributed to the larger interface area between porous fins and clear fluid regions, as well as the enhanced turbulence intensity at the porous interface. As the filling rate increases, the average temperature of the channel cross-section, T _avg, increases for both filling methods, which is due to the increased heat transfer area within the porous region and the enhanced turbulence intensity at the interfaces.

Figure 9

Local fluid temperature distributions at the yz-plane (x = 762 mm) in PTLF and PFF channels (Re = 10,250, Al-10-9.7): (a) V _p = 11.1% and (b) V _p = 22.2%.

Figure 10 illustrates the variations of the average heat flux (q _w) on the heating surface and the temperature difference between the inlet and outlet (ΔT) with Reynolds number (Re) in PTLF and PFF channels at different filling rates. As shown in Figure 10(a), when Re increases, the temperature difference in the PTLF channel changes little. However, the temperature difference in the PFF channel changes greatly, which is larger than that in the PTLF channel at the same filling ratio. The metal foam fins in the PFF channel can go deep into the middle of the channel, to exchange heat with the cold fluid. In contrast, the metal foam plate in the PTLF channel only exchanges heat with the near-wall cold fluid and has a limited effect on the center fluid. As shown in Figure 10(b), when Re increases, the average heat flux will increase on the heating surface in both PTLF and PFF channels, indicating heat transfer improvement. Additionally, the effect of filling rate is more remarkable on temperature difference and heat flux in the PTLF channel, whereas it is relatively small for the PFF channel. This is due to relatively small variation of fluid permeation in the porous region of PFF channel as filling rate changes. Therefore, increasing filling rate can effectively enhance heat transfer in the PTLF channel, while it has less effect on the PFF channel.

Figure 10

Variations of temperature difference between inlet and outlet and heat flux on the heating wall with Re in PTLF and PFF channels (Al-10-9.7): (a) ΔT and (b) q _w.

Figure 11 illustrates the variations of Nusselt number (Nu), friction factor (f), and PEC with Re for both PTLF and PFF channels. As Re increases, Nu increases in both channels, the variation of f in the PTLF channel is small, while f decreases in the PFF channel. This is due to the small spacing between porous fins, where the flow boundary layer between two fins may interact with each other, and the f in the PFF channel would be more sensitive as Re changes. When the filling rate increases, both Nu and f increase in PTLF and PFF channels, indicating an increase in both heat transfer performance and flow resistance. As porous region increases in the channel, the heat transfer surface area is larger within the metal foam, together with more fibers, which would lead to higher heat transfer performance and flow resistance. The impact of V _p on Nu in PFF channels is small compared with the PTLF channels. The previous analyses indicate that the fluid permeability in the porous region of the PFF channel changes little as V _p changes. Therefore, the heat transfer enhancement is not obvious. Furthermore, difference in the f is also observed at different V _p in the PFF channels. It is noted that the f for the case of V _p = 22.2% is much higher than that of other cases. This is potentially due to the reduced spacing between adjacent porous fins at this filling rate, and it may lead to mutual interference of flow boundary layers. When compared with both the PTLF channels and unfilled channels, PFF channels demonstrate higher Nu and f values, which should be related to the factors, such as the interfacial area between porous and clear fluid regions, fluid permeation rate in the porous region, and turbulence intensity at the interfaces. In summary, the overall heat transfer performance of PFF channels is generally better than that of PTLF channels. The PEC of PTLF channels increases with V _p, while the PEC of PFF channels changes little with V _p. It is noted that the PEC of PFF channel with V _p = 11.1% is generally higher than those of the PTLF channels and PFF channels at other filling rates. Although the PTLF channel with V _p = 22.2% exhibits slightly higher PEC values at high Re, its metal foam usage is twice that in the PFF channel with V _p = 11.1%. Within the range of Re = 5,125–15,375, compared with the PTLF channel under V _p = 11.1%, the Nu, f, and PEC of the PFF channel under V _p = 11.1% are increased by 37.5–82.6%, 85.2–172.0%, and 12.0–30.8%, respectively, and its PEC value is from 2.07 to 2.16.

Figure 11

Variations of Nu, f, and PEC with Re in PTLF and PFF channels (Al-10-9.7): (a) Nu, (b) f, and (c) PEC.

4.1 Effect of porosity and pore density of metal foams on flow and heat transfer in PFF channel

4.1.1 Effect of porosity

Figure 12 presents the local velocity distributions at the yz-plane (x = 762 mm) in PFF channels (V _p = 11.1%), where the metal foams have different porosities (φ) but the same pore density (ω). In aluminum foam PFF channels, fluid permeation in the porous region increases as φ decreases. In contrast, for copper foam PFF channels, fluid permeation decreases as φ decreases. The fluid permeation in the porous region is directly related to the sample’s permeability. The higher permeability, the lower flow resistance in the porous region, and the higher fluid permeation. As indicated in Table 2, under the same pore density conditions, the permeability of aluminum metal foam increases as φ decreases, while the opposite trend is observed for copper metal foam. The difference in permeability between the cases of Al-10-6.6 and Al-10-9.7 is small, which would lead to similar velocity distributions at the cross-section of different channels. Furthermore, the permeability of both metal foam materials varies with φ. According to Mancin et al. [21], an increase in φ will lead to a reduction in solid material in the aluminum foam, decrease fiber thickness, and potentially change the fiber cross-section from circular to triangular shape. Such changes in the fiber cross-section may introduce additional resistance and reduce the permeability.

Figure 12

Local fluid temperature distributions at the yz-plane (x = 762 mm) in PFF channels under different porosities (Re = 10,250).

Figure 13 illustrates the variations of Nusselt number (Nu), friction factor (f), and PEC with Reynolds number (Re) in PFF channels (V _p = 11.1%) under different porosity rates (φ) but certain pore density (ω). It is observed that as Re increases, Nu increases while f decreases. As shown in Figure 13(a), when φ decreases, the Nu of the PFF channel increases for both aluminum and copper foams. Since the area per unit volume of the metal foam skeleton (a _sf) will increase as φ decreases, which would be beneficial for the heat transfer in porous region. Conversely, the fluid permeation in the porous region of the copper foam PFF channel will decrease as φ decreases, which will weaken the heat transfer in the porous region. The results indicate that the effect of a _sf on the heat transfer is more significant than the effect of permeability K. In the range of Re = 5,125–15,375, with the same ω, the Nu for the case of Cu-10-6.7 is increased by 4.6–11.2% as compared with the case of Al-10-6.6, while for the case of Cu-10-9.5, it is increased by 3.9–9.4% as compared with the case of Al-10-9.7, which is benefited from copper’s higher thermal conductivity. As shown in Figure 13(b), it is found that f decreases when φ decreases in the aluminum foam PFF channel, while it increases in the copper foam PFF channel, which is due to the permeability of the metal foams. The higher the permeability, the lower the flow resistance in the porous region and the lower the total flow resistance in the channel. As shown in Table 2, the permeability of the aluminum foam samples increases when φ decreases under the same ω, while this trend is reversed for copper foam. Furthermore, due to the similar permeability of the aluminum foams, the flow resistance differences among different aluminum foam PFF channels are small. As shown in Figure 13(c), in the range of Re = 5,125–15,375, when Re increases, the PEC in copper foam PFF channels increases, while that in aluminum foam PFF channels increases first and then decreases slightly. At high Re, the variations of PEC for the cases of Al-10-6.6 and Al-10-9.7 are small, while the variation of PEC for the case of Al-10-4.4 is remarkable. When φ decreases, the PEC in both aluminum foam and copper foam PFF channels increases, and the variation of PEC in the aluminum foam PFF channel is more obvious. Overall, in the range of Re = 5,125–15,375, the PEC in the copper foam PFF channel is larger as compared with that in the aluminum foam PFF channel, and the Al-10-9.7 and Cu-10-9.5 samples are the best samples among the two metal foam materials at the same ω, where the PEC values of Al-10-9.7 and Cu-10-9.5 are 2.07-2.16 and 2.12-2.32, respectively. Compared with the Al-10-9.7 PFF channel, the PEC in the Cu-10-9.5 PFF channel is increased by 2.4–7.4%.

Figure 13

Variations of Nu, f, and PEC with Re in PFF channel channels under different porosities: (a) Nu, (b) f, and (c) PEC.

4.1.2 Effect of pore density

Figure 14 illustrates the variations of Nusselt number (Nu), friction factor (f), and PEC in PFF channels (V _p = 11.1%) with Re under similar porosity (φ) and different pore densities (ω). It is observed that as Re increases, Nu increases while f decreases. As shown in Figure 14(a), when ω increases, the Nu of the PFF channel increases for both aluminum and copper foams. This is due to the area per unit volume of the metal foam sample, a _sf, which is positively correlated with ω, as shown in Table 2. In the range of Re = 5,125–15,375, with similar φ, as ω increases from 10 to 40 PPI, the Nu in copper PFF channels will increase by 4.6–11.2%, 3.0–11.1%, and 3.5–10.8% as compared with aluminum PFF channels. Figure 14(b) shows that, among copper PFF channels, the PFF channel filled with Cu-10-6.7 sample has the smallest pressure drop, and the other two samples show small differences. In the aluminum foam PFF channels, f increases as ω increases, which is also related to the permeability of the metal foams, as shown in Table 2. Overall, in the range of Re = 5,125–15,375, PFF channels filled with Cu-10-6.7 and Al-10-6.6 foams have the smallest flow resistance. As compared with those filled with Cu-20-6.7 and Al-40-7 foams, the f of Cu-10-6.7 and Al-10-6.6 foams are decreased by 10.7–12.4% and 8.7–9.5%, respectively. Figure 14(c) indicates that, in copper PFF channels, the PFF channel filled with Cu-10-6.7 foam can achieve the maximum PEC at low Re, while the PFF channel filled with Cu-40-6.6 foam can achieve the maximum PEC at relatively high Re. In the aluminum foam PFF channel, the PEC increases with pore density. Overall, as compared with aluminum foam PFF channels, copper foam PFF channels would have better overall heat transfer performance. The Al-40-7 and Cu-40-6.6 foams are the best samples among the two types of metal foams, respectively. Under similar φ, in the range of Re = 5,125–15,375, the PEC values of Al-40-7 and Cu-40-6.6 foams are 2.02-2.11 and 2.09-2.29, respectively. Compared with the PFF channels filled with Al-40-7, the PEC of the PFF channel filled with Cu-40-6.6 is increased by 3.5–8.5%.

Figure 14

Variations of Nu, f, and PEC with Re in PFF channels under different pore densities: (a) Nu, (b) f, and (c) PEC.

4.2 Comparison with previous work

Due to the limited research on heat transfer enhancement at the air side of panel-type radiator, and since the heat exchange channels of solar air heaters are similar to the models studied here, which can be regarded as closed rectangular channels, the findings of the present study on air-side closed channel flow and heat transfer are compared with those in the field of heat transfer enhancement for solar air heaters. Figure 15 shows a comparison of the present results with those from previous research under optimal conditions for the variations of PEC in the channel with Re. Enhanced heat transfer measures in the related studies include miniature and dimple combination [30], inclined trapezoidal vortex generators [20], multi-row vortex generator [31], perforated-winglet-type vortex generator [32], hole-punched wings [33], quarter-circular ribs [34], multi-V-shaped baffle [35], and wavy-groove and perforated-delta wing combination [36]. The PFF channels of Cu-10-9.5 and Al-10-9.7 (V _p = 11.1%) in this study are selected for the comparison. When Re is low, the PEC in the PFF channel of this study is slightly lower than that in the channel with combined wavy-groove and perforated-delta wing as reported in Skullong et al. [36], but it is still higher than that in the other heat transfer enhancement channels. At high Re, the overall heat transfer performance of this study is significantly improved as compared with the previous studies.

Figure 15

Comparison of present study with previous relevant studies.

5 Conclusions

In this study, the flow and heat transfer characteristics of copper and aluminum metal foams in the air-side closed channel of panel-type radiator for transformers are numerically investigated. The effects of the PTLF and PFF methods of metal foams and the filling rate V _p are analyzed, and the variations of the flow and heat transfer in the channel for different metal foam materials, porosities (φ), and pore densities (ω) are discussed. The main conclusions are as follows:

1. Compared with the PTLF channel, the fluid permeation in the porous region and the maximum turbulent kinetic energy k _max at the porous interface of the PFF channel are larger, so the flow mixing and heat transfer in the PFF channel are better. As the filling rate V _p increases, the heat transfer area in the porous region increases, and the turbulence intensity at the porous interface is enhanced, which can promote the flow mixing and heat transfer.

2. In the range of Re = 5,125–15,375, the PFF channel has larger Nu and f, which are less affected by V _p as compared with the PTLF and unfilled channels. The overall heat transfer performance (PEC) in the PFF channel is generally better than that in the PTLF channel at the same V _p. Compared with the PTLF channel, the Nu, f, and PEC in the PFF channel are increased by 37.5–82.6%, 85.2–172.0%, and 12.0–30.8%, respectively, and the PEC values of the PFF channel are in the range of 2.07–2.16, when Al-10-9.7 sample is used as filling material and V _p = 11.1%.

3. With the same pore density, as the porosity decreases, the area per unit volume of the metal foam a _sf increases and the Nu in the PFF channels increases. The flow resistance within the channels is related to the permeability of the metal foam samples. The PEC in the PFF channels increases as metal foam porosity decreases, and the PEC is higher in the copper foam PFF channels as compared with the aluminum foam PFF channels. In the range of Re = 5,125–15,375, when V _p = 11.1%, the PEC in Cu-10-9.5 PFF channels is increased by 2.4–7.4% as compared with Al-10-9.7 PFF channels.

4. With similar porosity rates, as the pore density increases, the Nu in the PFF channels increases. The flow resistance in the Cu-10-6.7 and Al-10-6.6 PFF channels is the smallest. Compared with the aluminum foam PFF channels, the copper foam PFF channels have better overall heat transfer performance. In the range of Re = 5,125–15,375, when V _p = 11.1%, the PEC in Cu-40-6.6 PFF channels is increased by 3.5–8.5% as compared with Al-40-7 PFF channels.