Modeling and analysis of quantum communication channel in airborne platforms with boundary layer effects

Zhi-Feng Deng; Hao-Ran Hu; Ya Wang; Jia-Hao Li; Jia-Hua Wei; Hui-Cun Yu; Lei Shi

doi:10.1515/phys-2025-0133

Artikel Open Access

Modeling and analysis of quantum communication channel in airborne platforms with boundary layer effects

Zhi-Feng Deng , Hao-Ran Hu , Ya Wang , Jia-Hao Li , Jia-Hua Wei , Hui-Cun Yu und Lei Shi

Veröffentlicht/Copyright: 14. März 2025

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen Erkunden Sie dieses Fachgebiet

Aus der Zeitschrift Open Physics Band 23 Heft 1

Abstract

The establishment of secure global communication links is fundamentally dependent on the support of airborne platforms. However, the transmission of quantum signals from these platforms faces significant challenges related to boundary layer (BL) effects. This article presents an improved channel loss calculation model that effectively incorporates these BL effects in airborne environment. The model takes into account detailed variations in beam width, scintillation index, and transmission efficiency within the airborne environment. The results indicate that BL effects have an impact on the beam width and scintillation index, highlighting the need to maximize the receiver aperture within payload capacity constraints. In addition, the analysis shows that the supersonic BL results in greater losses and higher error rates compared to the transonic BL. Furthermore, atmospheric turbulence is identified as the primary factor that reduces transmission efficiency when transmitting over long distances in the airborne environment.

Keywords: airborne quantum key distribution; boundary layer effects; free space optical

1 Introduction

In recent years, the field of secure communications has seen a growing interest in quantum communication, which is based on the principles of quantum mechanics and has made significant progress over the past decade [1–3]. However, it has become evident that fiber-optic quantum communication cannot achieve ultra-long distance communication without ground relays. Furthermore, due to geographical constraints, global quantum communication cannot be achieved by ground-based relays alone [4,5]. Consequently, the use of airborne platforms is a potential way to overcome the distance limitations of quantum communication and thus enable a global quantum network [6,7].

Airborne quantum communication systems are strategically valuable for secure military and emergency communications, offering advantages such as high security, high maneuverability, and low latency [6–8]. A significant amount of research and experimental works on airborne quantum key distribution (QKD) have been reported [9–11]. Nauerth et al. successfully integrated a BB84 system into an airborne platform, enabling air-to-ground QKD experiments [9]. Wang et al. conducted experiments on a floating moving platform to investigate the feasibility of QKD using entanglement states [10]. Pugh et al. conducted QKD experiments between an aircraft and an optical ground station utilizing a quantum up link, with experimental error rates ranging from 2.66 to 5.08% [11]. These results provide a technical basis for the practical implementation of airborne quantum communication platforms. However, in both free-space optical and quantum communication systems, atmospheric turbulence is an unavoidable problem [12–16]. Moreover, when the speed of the aircraft exceeds 0.3 Mach, the geometry of the optical window can lead to the formation of complex turbulent flows. As the optical signal traverses the flow field, boundary layer (BL) effects such as optical distortion and interference occur.

The investigation of BL effects in airborne laser systems has become crucial [17–24]. The Airborne Aero-Optics Laboratory has conducted experiments on transonic plane window turntables to study the BL effect of outer pod windows under high-speed flight conditions [17–19]. Smith et al. conducted an analysis of the optical distortion caused by turbulence at flight speeds of 0.4 to 0.6 Ma, thereby confirming the frozen flow hypothesis of the BL [20]. Morrida et al. investigated the influence of shockwaves and wakes generated by conical windows and planar windows on the laser beam when the Mach number between 0.5 and 0.8 Ma [21]. Sun et al. investigated the simulation and verification methods of aero-optic effects in supersonic turbulent BLs, demonstrating that numerical coding and appropriate grid scales are effective for both turbulence and aero-optic statistical results [22]. Zhao et al. conducted flight experiments in the BL, with a particular focus on the potential of lens compensation to counteract detector defocus caused by the BL [23]. Dang et al. proposed a method to reduce dynamic aberrations by designing the inner surface of a conformal dome [24]. Similarly, in the context of airborne quantum communication, the BL introduces a degree of random offsets and jitter to the transmitted photons, which has the potential to disrupt their modes. Previous studies have analyzed the performance of BL effects on QKD systems in airborne environments, covering air-to-ground, air-to-air, satellite-to-aircraft, as well as measured supersonic BLs [25–28]. However, these studies often overlook the significant influence of the BL and do not fully consider the general conditions of atmospheric turbulence in airborne communication links.

In this article, the influence of atmospheric turbulence and BL effects on quantum channels in the airborne environment is comprehensively investigated. In Section 2, the BL effects of the airborne platform are introduced, and the relevant formulas for the beam width caused by the BL effects are derived. In Section 3, the model of typical atmospheric turbulence effects is introduced, and the BL effects are incorporated into the typical atmospheric turbulence model. In Section 4, the corresponding estimation results for beam width, scintillation index, and transmission efficiency are presented. By considering the combined influence of BL effects and atmospheric turbulence, this work provides a reference for the design and optimization of airborne quantum communication systems in real scenarios.

2 Channel model

The airborne platform plays a key role in the integrated quantum communication network, serving as both a receiver for satellite signals and a transmitter to establish temporary communication with ground stations, as illustrated in Figure 1. When a moving airborne platform is incorporated into the communication system, the BL is formed around the optical window surface of the airborne platform. The substantial reduction in received intensity and signal loss can be attributed to atmospheric turbulence along the propagation path and the BL surrounding the aircraft. The present study is concerned with the air-to-ground communication scenario, in which the BL exerts an influence on the transmitter.

Figure 1

Schematic diagram of the quantum network based on the airborne platform. (a) Satellite to aircraft, (b) air to air, and (c) air to ground.

2.1 Effects of aero-optical BL

The BL surrounding a moving aircraft is typically confined to a few centimeters near the fuselage. Consequently, it can be modeled using a phase screen. The phase screen is characterized by the Kolmogorov spectral model of refractive index fluctuations, with the refractive index structure constant C n 2 employed to describe its characteristics [29]. As illustrated in Figure 2, the photon source is positioned within the airborne environment. It traverses the BL and atmospheric turbulence, ultimately reaching the receiver. In the context of the transmission channel, two primary aspects of loss are considered: the increase in beam width and the decay of light intensity. The decay of light intensity can be appropriately expressed by the scintillation index and the Strehl ratio (SR). The optical evaluation of light transmitted in the convective field is based on the optical path difference (OPD). By performing a root mean square calculation on the OPD, it is possible to relate it to aero-optical statistical quantities. To gain a deeper understanding of these effects, phase screen models and optical evaluation methods can be employed to calculate transmission efficiency.

$Figure 2 Schematic diagram of the transmitted photons in the airborne environment. The black dashed lines represent the transmitted beams affected only by diffraction effects, and the red line represents the transmitted beam under the combined effect of the BL and atmospheric turbulence.$

Figure 2

Schematic diagram of the transmitted photons in the airborne environment. The black dashed lines represent the transmitted beams affected only by diffraction effects, and the red line represents the transmitted beam under the combined effect of the BL and atmospheric turbulence.

2.1.1 Beam broadening

In the airborne environment, considering the scintillation caused by atmospheric turbulence and BL effects, the long-distance transmission beam radius expressions under the condition of weak and strong fluctuations are obtained, respectively, as follows [29]:

(1) w L = W 1 + T 1 + T BL ( weak fluctuations ) W 1 + T 2 + T BL ( strong fluctuations ) ,

where W represents the beam radius resulting from pure diffraction for a collimated beam, which can be expressed by the beam radius at the transmitter output aperture w 0 , the transmission distance L , and the wave-vector k [30]:

(2) W = w 0 1 + 2 L k w 0 2 2 ,

where the broadening coefficients T 1 and T 2 , which are due to turbulence of different fluctuations, are given by the expressions T 1 = 1.33 σ R 2 Λ 5 ∕ 6 and T 2 = 1.63 σ R 2 Λ 5 ∕ 6 , respectively. T BL represents the broadening coefficient due to the BL, expressed as T BL = 1.93 σ BL 2 Λ 5 ∕ 6 , and Λ denotes the diffraction beam parameter at the receiver [25]. σ R 2 represents the Rytov index with σ R 2 = 1.23 C n 2 k 7 ∕ 6 L 11 ∕ 6 , and C n 2 meets the Clear 1 model [31], as shown in Table 1. σ BL 2 represents the modified Rytov index considering only BL effects, with

(3) σ BL 2 = 1.23 C n , BL 2 k 7 ∕ 6 L 11 ∕ 6 ,

where C n , BL 2 represents the effective refractive index structure constant under the BL effects, setting that C n , BL 2 = 2 × 1 0 − 16 m − 2 ∕ 3 .

Table 1

Clear 1 model [31]

Altitude (km)	C n 2 ( h )
1.23 < h ≤ 2.13	log 10 [ C n 2 ( h ) ] = − 10.7025 − 4.3507 h + 0.8141 h 2
2.13 < h ≤ 10.34	log 10 [ C n 2 ( h ) ] = − 16.2897 + 0.0335 h − 0.0134 h 2
10.34 < h ≤ 30	log 10 [ C n 2 ( h ) ] = − 17.0577 − 0.0449 h − 0.0005 h 2 + 0.6181 exp [ − 0.5 ( ( h − 15.5617 ) ∕ 3.4666 ) 2 ]
h > 30	C n 2 ( h ) = 0

2.2 Beam width and scintillation index

2.2.1 Scintillation index

The scintillation index of the Gaussian beam at the receiving end in the direction of the optical axis can be obtained according to Rytov theory in the case of weak turbulence and the Kolmogorov spectrum model [32] by considering the influence of the BL effects as follows:

(4) σ B 2 = 3.86 σ R 2 Re i 5 ∕ 6 F 1 2 − 5 6 , 11 6 ; 17 6 ; 1 − Θ + i Λ − 2.64 σ R 2 Λ 5 ∕ + σ BL 2 ( L ) ,

where Θ represents the diffraction beam parameter at the receiver [30]. The term Re represents the real part of the function. The expression i = F 1 2 ( a , b ; c ; x ) denotes a generalized hypergeometric function. σ BL 2 denotes the increasing term of the scintillation index, which is affected by the BL effect, expressed as follows:

(5) σ BL 2 ( L ) = 3.87 σ R , B L 2 ( ( Θ 2 + Λ 2 ) 5 ∕ 12 × cos 5 6 tan − 1 Θ Λ − Λ 5 ∕ 6 .

For moderate-to-strong turbulence conditions, the scintillation index along the optical axis can be expressed by the Gamma–Gamma model:

(6) σ I 2 ( 0 , L ) = exp ( P 1 + P 2 ) − 1

where P 1 = 0.49 σ B 2 [ 1 + 0.56 ( 1 + Θ ) σ B 12 ∕ 5 ] 7 ∕ 6 , P 2 = 0.51 σ B 2 [ 1 + 0.69 σ B 12 ∕ 5 ] 5 ∕ 6 .

Eq. (6) is valid when the receiving aperture is smaller than the Fresnel scale or the spatial coherence length. When the aperture at the receiving end is a fixed length D, the scintillation index can be expressed as follows:

(7) σ I 2 ( 0 , L ; D ) = exp [ σ ln X 2 ( D ) + σ ln Y 2 ( D ) ] − 1 , Ω > Λ ,

where σ ln X 2 ( D ) , σ ln Y 2 ( D ) are the large-scale and small-scale logarithmic variances [26], respectively, which can be expressed as follows:

(8) σ ln X 2 ( D ) = 0.49 Ω − Λ Ω + Λ 2 σ B 2 [ 1 + P 3 + 0.56 ( 1 + Θ ) σ B 12 ∕ 5 ] ,

(9) σ ln Y 2 ( D ) = 0.51 σ B 2 ( 1 + 0.69 σ B 12 ∕ 5 ) 5 ∕ 6 1 + 1.20 ( σ R ∕ σ B ) 12 ∕ 5 + 0.83 σ B 12 ∕ 5 Ω + Λ ,

where P 3 = 0.4 ( 2 − Θ ¯ ) ( σ B ∕ σ R ) 12 ∕ 7 ( Ω + λ ) 1 3 − 1 2 Θ ¯ + 1 5 Θ ¯ 2 6 ∕ 7 , and Ω is a dimensionless parameter describing the aperture at the receiving end and can be expressed as Ω = 16 L ∕ k D 2 .

2.2.2 Strehl ratio

The Strehl ratio is a measure of the on-axis beam intensity at the target (far field receiver) relative to the intensity for a perfect on-axis intensity at the target. It is calculated by dividing the on-axis beam intensity I r by the intensity for a perfect on-axis intensity I 0 using the Marechal approximation [33]:

(10) SR = I r I 0 ≈ exp ( − ϕ rms 2 ) = exp − 2 π OPD rms λ 2 ,

where OPD rms represents the root mean square of the optical path difference. With the ideal environment and a low flight speed, the SR value is approximately equal to 1.0.

There are various methods to calculate OPD. In experimental settings, the most commonly used wavefront aberration measurement methods include Malley probes, Shack–Hartmann sensors, small aperture beam techniques, sensors based on Background Oriented Schlieren-based wavefront sensing, and nano-tracer-based planar laser scattering [34,35]. In a simulation, the corresponding flow field is typically obtained using computational fluid dynamics (CFD) software, and then the OPD is calculated using ray tracing methods [36]. The density distribution of a flow field determines its optical refractive properties, and the density distribution is not directly applicable to optical calculations. The interface between fluid dynamics and optics is the Gladstone–Dale equation [25]:

(11) n = 1 + ρ K GD ,

where n is the gradient refractive index and ρ is the density of flow field. K GD is the Gladstone–Dale constant decided only the wavelength λ of photons [25]:

(12) K GD = 2.23 × 1 0 − 4 × 1 + 7.52 × 1 0 − 3 λ 2 .

Based on extensive data, OPD rms can be linked to aero-optic statistics, and multiple scaling arguments for the root mean square phase distortion have been proposed [36–38]. For the sake of computational convenience, we adopt the scaling argument as follows [37]:

(13) OPD rms = δ K GD ρ ∞ C w r 2 − 3 ∕ 2 M a ∞ 2 C f ,

where δ represents the BL thickness, K GD is the Gaussian-Dörfler constant, ρ ∞ and M a ∞ , respectively, denote the density and Mach number of the free stream, C w is the model parameter, typically taken as 0.34, and 0.7 under hypersonic conditions, and C f is the skin friction coefficient. For a heated wall, the parameter r 2 can be expressed as follows:

(14) r 2 = 1 + M a ∞ 2 ( γ − 1 ) ( 1 − r r 1 2 ) ∕ 2 ,

where r is the recovery factor, taken as 0.9. The parameter γ is equal to 1.4. For the subsonic BL, r 1 is equal to 0.82. For the supersonic BL, r 1 is equal to 0.84.

2.3 Channel transmittance models

In a previous study [39–41], the mathematical expression for the free-space quantum communication channel was presented, with the transmittance η representing the linear losses of the channel. This transmittance is composed of three factors [39]: the deterministic attenuation due to optical absorption and scattering η l , the random fluctuations caused by time-varying atmospheric turbulence near the ground I a , and the inconclusive fraction of received power collected by a certain diameter of a telescope, accounting for pointing errors-induced fluctuations and beam broadening-induced geometrical loss η p . Since the three factors are statistically independent, η can be expressed as follows:

(15) η = η l I a η p .

The systematic effects encompass predictable physical processes that disrupt and attenuate the signal. These effects include the refraction of the beam in different atmospheric layers and the reduction of light due to absorption or scattering by air molecules or aerosols. When the zenith angle is below 6 0 ∘ , the elongation effect has a negligible impact on the quantum communication process, allowing η l to be simply scaled as τ zen [42]. The scaling of τ zen falls within the range of [0, 1], indicating the determined transmission efficiency at a specific zenith angle, a value that can be conveniently determined using the MODTRAN code [43].

In examining the effect of random atmospheric turbulence, it is possible to select from a range of statistical probability distributions, with a specific choice depending on the intensity of the turbulence. In situations where turbulence is relatively weak, the log-normal (LN) probability distribution is a suitable option [44], expressed as follows:

(16) f ( I a ) = 1 I a 2 π σ R 2 exp − ( ln ( I a ) + σ R 2 ∕ 2 ) 2 2 σ R 2 .

The n th order statistical moment of the LN random variable is given by the following equation:

(17) E [ I a n ] = exp σ R 2 n ( n − 1 ) 2 .

On the other hand, the moderate-to-strong turbulence condition is the consequence of both large-scale and small-scale fluctuations, which can be modeled using a Gamma–Gamma distribution for the I a with the following probability density function [45]:

(18) f ( I a ) = 2 Γ ( α ) Γ ( β ) I a ( α β I a ) ( α + β ) ∕ 2 K α − β ( 2 α β I a ) ,

where Γ ( ⋅ ) is the gamma function, K v ( ⋅ ) is the modified Bessel function of the second kind, and the parameters α and β are defined as follows:

(19) α = 1 exp [ σ ln X 2 ( D ) ] − 1 , β = 1 exp [ σ ln Y 2 ( D ) ] − 1 .

The n th order moment under the Gamma–Gamma model can be expressed as follows:

(20) E [ I a n ] = Γ ( α + n ) Γ ( β + n ) ( α β ) n Γ ( α ) Γ ( β ) .

In free-space quantum communication, the width of the optical beam increases as it propagates over distances of tens to hundreds of kilometers. A reduction in beam size requires higher precision for the pointing and tracking mechanisms. This is of particular importance in the context of quantum communication, given that the smaller footprint of the beam significantly reduces losses when received through a finite-aperture telescope. Furthermore, mechanical errors in the tracking and pointing systems, as well as vibrations of the airborne platform, can lead to random beam jitter, resulting in fluctuation losses. In the case of a Gaussian beam, the normalized spatial distribution of the emission intensity at a distance L from the transmitter is given by the following equation [46]:

(21) I ( ρ s , L ) = 2 π w L 2 exp − 2 ∥ ρ s ∥ 2 w L 2 ,

where ρ s denotes the radial vector from the beam center with ∥ ⋅ ∥ the norm of a vector, and w L is the beam radius calculated at a distance L .

Assuming a circular receiving telescope aperture with an opening area C , η p can be given as follows:

(22) η p = ∫ C I ( ρ − s , L ) d ρ ,

where s represents the radial vector that signifies random beam displacements, while η p is defined as the fraction of power collected when coupling the received beam to a finite receiving aperture. Given the symmetry of the beam shape and receiver area, the characterization of η p depends solely on the radial jitter distance ∥ s ∥ . A commonly used approximation of η p can be expressed as follows [47]:

(23) η p ≈ A 0 exp − 2 s 2 w LP 2 ,

where A 0 = [ erf ( v ) ] 2 represents the maximum fraction of collected power on the receiving aperture when there is no pointing error ( s = 0 ). Meanwhile, v = π a ∕ 2 w L represents deterministic geometric loss, and erf ( x ) = 2 π ∫ 0 x exp ( − t 2 ) d t represents Gauss error function. In addition, it is important to note that w LP is the calculated equivalent beam radius and can be expressed as follows:

(24) w LP 2 = w L 2 π erf ( ν ) 2 ν exp ( − ν 2 ) .

To ascertain the probability density function of η p , it is necessary to determine the distribution of s , considering the random jitter on the horizontal x -axis and the elevation angle y -axis. Previous studies on quantum atmospheric channels have assumed that s follows a Gaussian, Rayleigh, Rician, or Beckmann distribution [39,48–50], where the jitters on the x and y axes are two independent Gaussian random variables, and the distribution model of s can be expressed as follows:

(25) f s ( s ) = s 2 π σ x σ y × ∫ 0 2 π exp × − ( r cos ( Θ ) − μ x ) 2 2 σ x 2 − ( r sin ( Θ ) − μ y ) 2 2 σ y 2 d Θ ,

where μ x and μ y represent the mean jitters on the x and y axes, respectively, while σ x and σ y represent the standard deviations of the jitters on the x and y axes, respectively. The first statistical moment of η p is given by the following equation.

(26) E [ η p ] ∈ 0 , A 0 exp − ( μ x 2 + μ y 2 ) w LP 2 .

In airborne quantum communication systems, the photon transmission efficiency η p is reduced due to the BL effects when the optical beam passes through the BL and is then received by the telescope at the receiving end. It can be modified as η p ′ [40]:

(27) η p ′ = SR ⋅ η p ≈ SR ⋅ A 0 exp − 2 s 2 w LP 2 .

The overall transmission efficiency, accounting for BL effects, can be determined as follows:

(28) η ′ = η l I a η p ′ .

From Eq. (28), it can be seen that the first statistical moment of η ′ is given by E [ η ′ ] = η l E [ I a ] E [ η p ′ ] , where η l ∈ [0, 1], E [ I a ] = 1 , and E [ η p ′ ] ∈ [0, 1]. Therefore, E [ η ′ ] ∈ [0, 1], satisfies the exchange relation between the transmitted and received quantum states. Subsequently, by substituting the calculated transmission efficiency into the decoy-state BB84 protocol [51], the gain of the signal states here can be calculated as follows:

(29) Q μ = Y 0 + 1 − e − η μ ,

where Y 0 is the dark count rate of QKD systems, and μ is the intensity of the signal state. Thus, the quantum bit error rate (QBER) of airborne QKD under BL effects can be determined as follows:

(30) E μ = E μ Q μ ∕ Q μ ,

where E μ Q μ represents the error gain of signal quantum states, with

(31) E μ Q μ = e 0 Y 0 + e d ( 1 − e − η μ ) ,

where e 0 = 0.5 is the error rate of dark counts, and e d is the detection error rate of QKD systems.

3 Simulation results

3.1 Parameters setting

In this section, we focus on the beam broadening caused by BL effects in the airborne environment, the increase in beam width, scintillation index, and the corresponding changes in transmission efficiency. It is worth noting that, for computational convenience, the eigenvalues of the statistical components are considered when estimating the transmission efficiency, with a primary focus on the BL effects. Given the detailed aircraft description with 0.7 Ma velocity, the BL will be generated around the hemisphere-on-cylinder turret and its refractive index distribution can be calculated by Eqs (11) and (12), shown in Figure 3. The relevant parameters are presented in Table 2.

$Figure 3 Cross section of the evaluated refractive index distribution of the hemisphere-on-cylinder turret.$

Figure 3

Cross section of the evaluated refractive index distribution of the hemisphere-on-cylinder turret.

Table 2

Parameters of airborne QKD

Category	Parameter	Description	Value
BL	M	Flight speed	0.8 Ma/1.5 Ma
	δ	BL thickness	0.025 m
	ρ h	Air density	0.525 kg/m 3
	C w	Modelling parameters	0.34/0.7
	C f	Skin friction coefficient	0.0026
Atmosphere turbulence	C n 2	Refractive index	CLEAR 1 model [31]
	τ zen	Deterministic attenuation	0.75
Photon source	w 0	Waist radius	0.05 m
	λ	Transmitter wavelength	1,550 mm
	r 0	Fried parameter in zenith	0.2 m
Receiver	D	Diameter of the receiver telescope	0.3 m
	e d	system detection error rate	0.01
Protocol	μ	Intensity of signal states	0.8
	v	Intensity of decoy states	0.1
	N	System repetition rate	100 MHz
	P s	Sent probability of signal states	0.5
	P d	Sent probability of decoy states	0.25
	P v	Sent probability of vacuum states	0.25

3.2 Beam width and scintillation index

By employing Eqs (1)–(3) and substituting the relevant parameters, it is feasible to determine the curve between the beam radius of the transmitted beam in the airborne environment and the transmission distance for varying wavelengths and altitudes, as illustrated in Figure 4. For longer transmission distances, the BL effects result in a greater degree of beam broadening for the 1,060 nm beam compared to the 1,550 nm beam. Furthermore, the results show that as the transmission distance increases, the beam radius continues to expand. When the altitude is maintained at a constant value, the beam with a wavelength of 1,550 nm exhibits a greater transmitted beam radius than the 1,060 nm beam. Conversely, as shown in Figure 4(b), when the wavelength is maintained at a constant value, an increase in altitude results in a reduction in the size of the transmitted beam radius. It is worth noting that the beam radius with the BL effects is larger than that observed in the absence of such effects. Therefore, in the engineering practice of quantum communications on airborne platforms, it is advisable to consider the combined effects of the BL and atmospheric turbulence on beam radius. This can be achieved by using a beacon beam with a shorter wavelength to mitigate the impact of these effects.

Figure 4

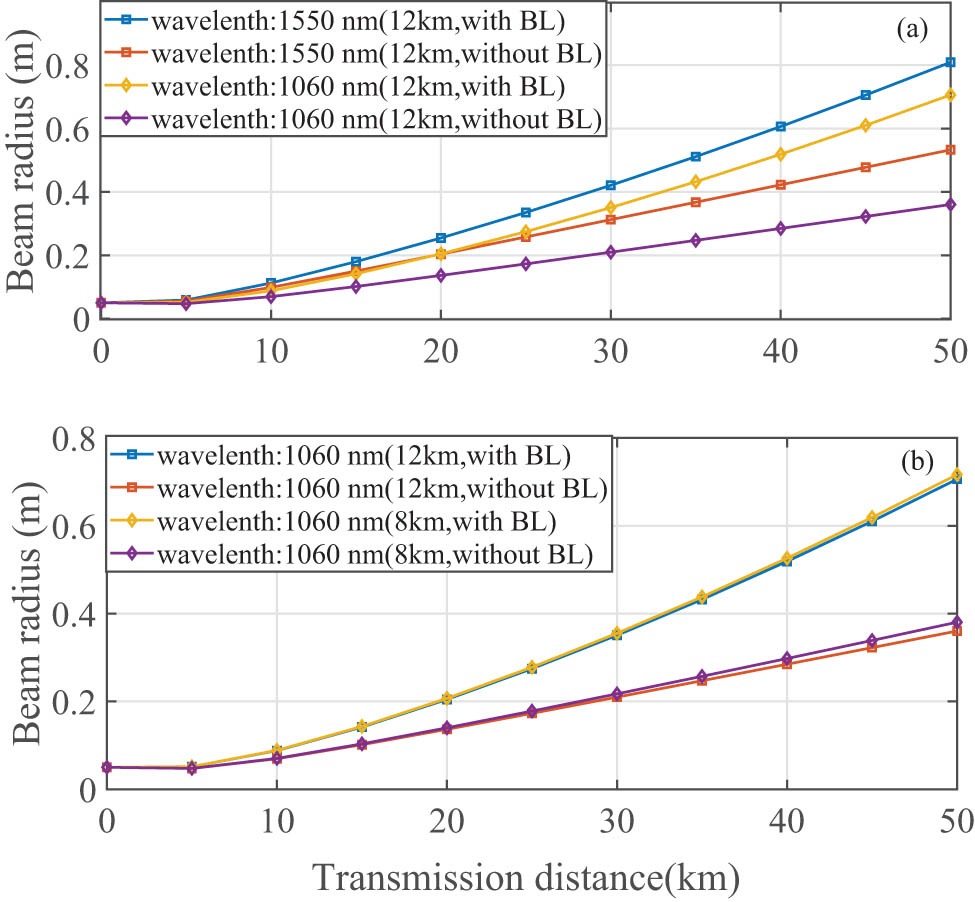
The beam radius varies with the transmission distance at different altitudes and wavelengths: (a) the same altitudes and (b) the same wavelength.

Figure 5 presents the scintillation index varying with the transmission distance in an airborne environment. It can be observed that as the transmission distance increases, the scintillation index also increases. At the same altitude, the increase in the scintillation index to the transmission distance is relatively smaller for the 1,550 nm wavelength compared to the 1,060 nm wavelength. Similarly, at an altitude of 12 km, the increase in the scintillation index relative to the transmission distance is less pronounced than at an altitude of 8 km. Additionally, the BL effects cause an increase in the scintillation index under the same conditions, with the largest increase occurring at 12 km and 1,550 nm.

Figure 5

The scintillation index varies with the transmission distance at different altitudes and wavelengths: (a) the same altitudes and (b) the same wavelength.

In the airborne environment, the payload capacity of the aircraft platform limits the capabilities of the communications system, especially when the aircraft platform serves as the receiving end. In such scenarios, the size of the receiving telescope will impose limitations on its capabilities. Accordingly, it is essential to examine the variation of the scintillation index with transmission distance for diverse receiving apertures, as illustrated in Figure 6. For the same receiving aperture, it can be seen that lower altitudes result in higher scintillation indices. Similarly, at the same altitude, larger receiving apertures lead to smaller scintillation indices. Furthermore, considering the overall performance of the system, it can be advised that larger receiving apertures should be used within the payload capacity of the airborne platform.

Figure 6

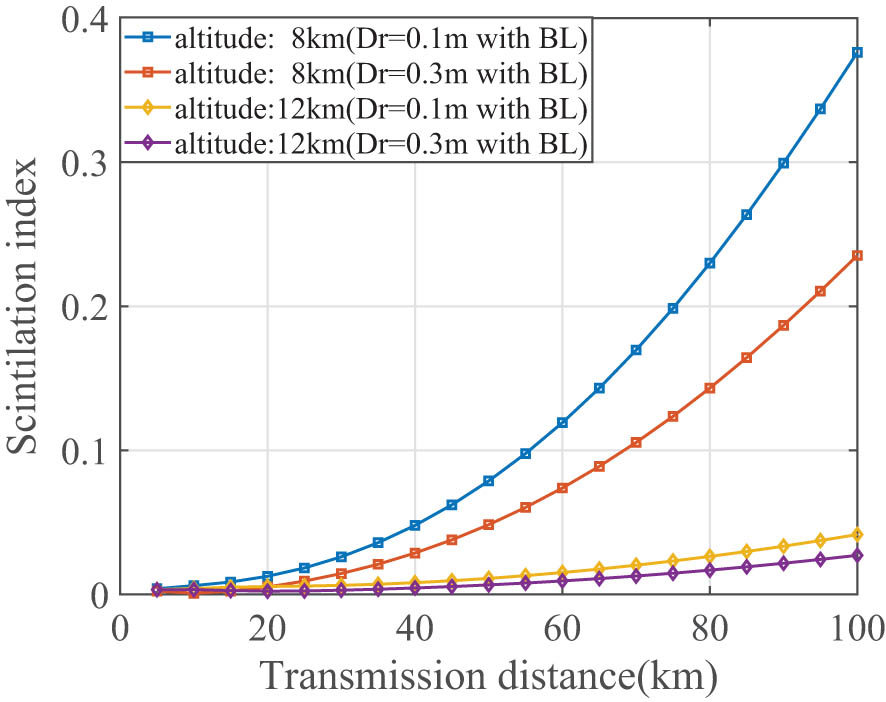
The scintillation index varies with transmission distance at different altitudes and diameters of the receiver.

3.3 Transmission efficiency

In Figure 7, the curve between the transmission efficiency of the system in the airborne environment and the transmission distance can be quantified for different receiver apertures. It can be seen that an increase in transmission distance is accompanied by a gradual decrease in transmission efficiency. When the level of BL effects remains constant, a reduction in the size of the receiving aperture results in a more rapid decline in transmission efficiency, even if the transmission distance remains unchanged. It can be concluded that larger receiving apertures can maintain a higher transmission efficiency, which is consistent with the results for the beam radius. Figure 7(b) presents a comparison of transmission efficiency and receiving aperture with and without the BL effects. It can be seen that the transmission efficiency continues to improve as the receiving aperture increases. At this point, altitude is not the main factor for affecting transmission efficiency, and the BL becomes dominant.

Figure 7

The transmission efficiency varies with (a) transmission distance and (b) diameter of the receiver.

Figure 8 shows the curve between the transmission efficiency of a beam in the airborne environment and the transmission distance under the influence of varying intensities of BL effects (expressed as the ratio of OPD ∕ λ and the evaluated refractive index) in both subsonic and supersonic conditions. It can be observed that, except for the initial value, the trend of the transmission efficiency η p ′ obtained from the simulated flow field calculation is basically the same as that of the scaling argument. Furthermore, in the subsonic conditions, the transmission efficiency is slightly lower in the short range compared to the scenario in where there is no BL effect. This is due to the fact that it is mainly influenced by SR, and the beam divergence is smaller. As the transmission distance increases, the influence of the beam divergence gradually increases, resulting in a significant decrease in transmission efficiency compared to that observed at shorter distances. In the context of supersonic conditions, the transmission efficiency initially drops to half of the value in the absence of BL effects, due to the pronounced reduction in SR. As the transmission distance increases, the transmission efficiency continues to decrease, eventually reaching a value that is comparable to that observed under subsonic conditions. This suggests that both subsonic and supersonic conditions have a considerable influence on the transmission efficiency over long distances.

Figure 8

The transmission efficiency varies with transmission distance.

By incorporating the calculated transmission efficiency into the vacuum and weak decoy BB84 protocol and using the given parameters, it is feasible to calculate the total transmission loss and the QBER value of the system as the transmission distance increases, as shown in Figure 9. It can be observed that the total loss due to the hemisphere-on-cylinder turret and the QBER trend are essentially the same as in the case of the scaling argument. Furthermore, under supersonic conditions, the system initially experiences significant losses due to BL effects, although this is not significantly reflected in the QBER. As the transmission distance increases, the rate of loss increase is initially relatively slow. However, after a certain transmission distance is reached, both the transmission loss and the QBER value increase rapidly. The influence of the supersonic BL (OPD/ λ = 0.13 ) results in an increase in transmission loss of up to 9.8 dB compared to the case without BL effects, and an increase in QBER of up to 0.22.

Figure 9

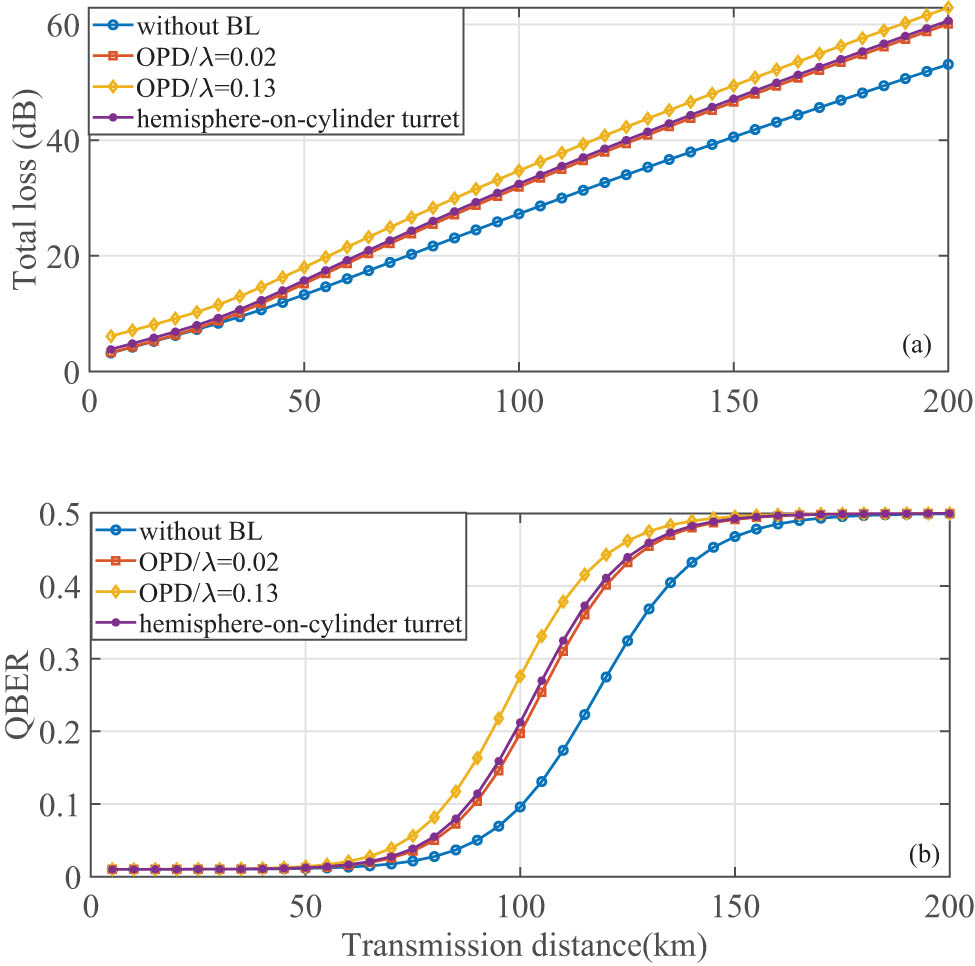
The performance varies with transmission distance: (a) the total loss and (b) the QBER.

4 Conclusion

This article presents an improved channel loss calculation model that incorporates BL effects in airborne environment. By incorporating scaling arguments, this model facilitates the rapid implementation of adaptive compensation for BL effects. Modeling the BL as a thin phase screen allows the derivation of beam width and scintillation index under the combined effects of atmospheric turbulence and BL. The results show that the BL has a significant effect on the beam width, highlighting the importance of selecting the largest possible receiving aperture within the constraints of payload capacity. Subsequently, the flow field around the hemisphere-on-cylinder turret was simulated using CFD and compared with scaling arguments. Furthermore, an investigation of QBER was also carried out using the decoy-state BB84 protocol, showing that BL effects consistently reducing transmission efficiency, with a more pronounced reduction observed at higher altitudes. The analysis also shows that the supersonic BL results in greater losses and higher error rates compared to the transonic BL. While atmospheric turbulence has been identified as a primary factor in the reduction of transmission efficiency, it is important to recognize the significant impact of BL effects, which deserves considerable attention. Overall, our results provide valuable technical support for the implementation of airborne quantum communication.

Acknowledgments

The authors acknowledge the support by the National Natural Science Foundation of China (Grants No. 61971436, No. 62401621), the Natural Science Basic Research Plan in Shaanxi Province of China (Grant No. 2023JC-QN-0674).

Funding information: This work was supported by the National Natural Science Foundation of China (Grants No. 61971436, No. 62401621), the Natural Science Basic Research Plan in Shaanxi Province of China (Grant No. 2023JCQN-0674).
Author contributions: Zhi-Feng Deng: Writing – original draft, Software, Methodology, Formal analysis, Data curation. Hao-Ran Hu: Supervision, Project administration, Investigation. Ya Wang: Visualization, Validation, Conceptualization. Jia-Hao Li: Resources, Data curation, Investigation. Jia-Hua Wei： Data curation, Conceptualization. Validation. Hui-Cun Yu: Writing – review & editing, Supervision, Funding acquisition. Lei Shi: Writing – review & editing, Supervision, Funding acquisition. All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors state no conflict of interest.
Data availability statement: The datasets generated and/or analysed during the current study are available from the corresponding author on reasonable request.

References

[1] Lu CY, Cao Y, Peng CZ, Pan JW. Micius quantum experiments in space. Rev Mod Phys. 2022;94:035001. 10.1103/RevModPhys.94.035001Suche in Google Scholar

[2] Liu HY, Tian XH, Gu C, Fan P, Ni X, Yang R, et al. Drone-based entanglement distribution towards mobile quantum networks. Natl Sci Rev. 2020;7(5):921–8. 10.1093/nsr/nwz227Suche in Google Scholar PubMed PubMed Central

[3] Mehic M, Niemiec M, Rass S, Ma J, Peev M, Aguado A, et al. Quantum key distribution: a networking perspective. ACM Comput Surv. 2020;53(1):1–41. 10.1145/3402192Suche in Google Scholar

[4] Shen Q, Guan JY, Ren JG, Zeng T, Hou L, Li M, et al. 113 km free-space time-frequency dissemination at the 19th decimal instability. 2022. arXiv: http://arXiv.org/abs/arXiv:2203.11272. Suche in Google Scholar

[5] Wang BX, Mao Y, Shen L, Zhang L, Lan XB, Ge D, et al. Long-distance transmission of quantum key distribution coexisting with classical optical communication over a weakly-coupled few-mode fiber. Opt Express. 2020;28(9):12558–65. 10.1364/OE.388857Suche in Google Scholar PubMed

[6] Xue Y, Chen W, Wang S, Yin Z, Shi L, Han Z. Airborne quantum key distribution: a review. Chin Opt Lett. 2021;19(12):122702. 10.3788/COL202119.122702Suche in Google Scholar

[7] Dubey U, Bhole P, Dutta A, Behera DP, Losu V, Pandeeti GS, et al. A review on practical challenges of aerial quantum communication. Phys Open. 2024;19:100210. 10.1016/j.physo.2024.100210Suche in Google Scholar

[8] Quintana C, Sibson P, Erry G, Thueux Y, Kingston E, Ismail T, et al. Low size, weight and power quantum key distribution system for small form unmanned aerial vehicles. In: Free-Space Laser Communications XXXI. Vol. 10910. Bellingham, Washington, USA: SPIE; 2019. p. 240–6. 10.1117/12.2507669Suche in Google Scholar

[9] Nauerth S, Moll F, Rau M, Horwath J, Frick S, Fuchs C, et al. Air to ground quantum key distribution. In: Quantum Communications and Quantum Imaging X. Vol. 8518. Bellingham, Washington, USA: SPIE; 2012. p. 71–6. 10.1117/12.929790Suche in Google Scholar

[10] Wang JY, Yang B, Liao SK, Zhang L, Shen Q, Hu XF, et al. Direct and full-scale experimental verifications towards ground-satellite quantum key distribution. Nat Photonics. 2013;7(5):387–93. 10.1038/nphoton.2013.89Suche in Google Scholar

[11] Pugh CJ, Kaiser S, Bourgoin JP, Jin J, Sultana N, Agne S, et al. Airborne demonstration of a quantum key distribution receiver payload. Quantum Sci Technol. 2017;2(2):024009. 10.1088/2058-9565/aa701fSuche in Google Scholar

[12] Elsayed EE. Atmospheric turbulence mitigation of MIMO-RF/FSO DWDM communication systems using advanced diversity multiplexing with hybrid N-SM/OMI M-ary spatial pulse-position modulation schemes. Opt Commun. 2024;562:130558. 10.1016/j.optcom.2024.130558Suche in Google Scholar

[13] Elsayed EE, Hayal MR, Nurhidayat I. Coding techniques for diversity enhancement of dense wavelength division multiplexing MIMO-FSO fault protection protocols systems over atmospheric turbulence channels. IET Optoelectron. 2024;18(1–2):11–31. 10.1049/ote2.12111Suche in Google Scholar

[14] Elsayed EE. Performance enhancement of atmospheric turbulence channels in DWDM-FSO PON communication systems using M-ary hybrid DPPM-M-PAPM modulation schemes under pointing errors, ASE noise and interchannel crosstalk. J Opt. 2024;30:1–17. 10.1007/s12596-024-01908-9Suche in Google Scholar

[15] Yousif BB, Elsayed EE, Alzalabani MM. Atmospheric turbulence mitigation using spatial mode multiplexing and modified pulse position modulation in hybrid RF/FSO orbital-angular-momentum multiplexed based on MIMO wireless communications system. Opt Commun. 2019;436:197–208. 10.1016/j.optcom.2018.12.034Suche in Google Scholar

[16] Elsayed EE. Investigations on modified OOK and adaptive threshold for wavelength division multiplexing free-space optical systems impaired by interchannel crosstalk, atmospheric turbulence, and ASE noise. J Opt. 2024;30:1–14. 10.1007/s12596-024-01929-4Suche in Google Scholar

[17] Porter C, Gordeyev S, Zenk M, Jumper E. Flight measurements of aero-optical distortions from a flat-windowed turret on the airborne aero-optics laboratory (AAOL). In: 42nd AIAA Plasmadynamics and Lasers Conference. 2011. p. 3280. 10.2514/6.2011-3280Suche in Google Scholar

[18] Jumper EJ, Gordeyev S, Cavalieri D, Rollins P, Whiteley M, Krizo M. Airborne aero-optics laboratory-transonic (AAOL-T). In: 53rd AIAA Aerospace Sciences Meeting. 2015. p. 0675. 10.2514/6.2015-0675Suche in Google Scholar

[19] Kalensky M, Gordeyev S, Jumper EJ. In-flight studies of aero-optical distortions around AAOL-BC. In: AIAA Aviation 2019 Forum. 2019. p. 3253. 10.2514/6.2019-3253Suche in Google Scholar

[20] Smith A, Gordeyev S, Jumper E. Aperture effects on aero-optical distortions caused by subsonic boundary layers. In: 43rd AIAA Plasmadynamics and Lasers Conference. 2012. p. 2986. 10.2514/6.2012-2986Suche in Google Scholar

[21] Morrida J, Gordeyev S, De Lucca N, Jumper EJ. Shock-related effects on aero-optical environment for hemisphere-on-cylinder turrets at transonic speeds. Appl Opt. 2017;56(17):4814–24. 10.1364/AO.56.004814Suche in Google Scholar PubMed

[22] Sun XW, Yang XL, Liu W. Validation method of aero-optical effect simulation for supersonic turbulent boundary layer. AIAA J. 2021;59(2):410–6. 10.2514/1.J059583Suche in Google Scholar

[23] Zhao HW, Hou TJ, Zhu B, Deng M. Design analysis for optical dome and scanning mirror. J Appl Opt. 2010;6:898–903. Suche in Google Scholar

[24] Dang F, Chen S, Zhang W, Wang H, Fan Z. Optimized design method for the inner surface of a conformal dome based on the ray tracing approach. Appl Opt. 2017;56(28):8230–39. 10.1364/AO.56.008230Suche in Google Scholar PubMed

[25] Yu HC, Tang BY, Chen H, Xue Y, Tang J, Yu WR, et al. Airborne quantum key distribution with boundary layer effects. EPJ Quantum Technol. 2021;8:1–13. 10.1140/epjqt/s40507-021-00115-wSuche in Google Scholar

[26] Yu H, Tang B, Li J, Cao Y, Zhou H, Li S, et al. Satellite-to-aircraft quantum key distribution performance estimation with boundary layer effects. Chin Opt Lett. 2023;21(4):042702. 10.3788/COL202321.042702Suche in Google Scholar

[27] Yu H, Tang B, Ding H, Xue Y, Tang J, Wang X, et al. Airborne quantum key distribution performance analysis under supersonic boundary layer. Entropy. 2023;25(3):472. 10.3390/e25030472Suche in Google Scholar PubMed PubMed Central

[28] Deng Z, Yu H, Tang J, Li J, Cao Y, Hu H, et al. Air-to-air quantum key distribution with boundary layer effects. Results Phys. 2023;54:107020. 10.1016/j.rinp.2023.107020Suche in Google Scholar

[29] Zhao J, Zhao SH, Zhao WH, Cai J, Liu Y, Li X. BER performance analysis of M-ary PPM over exponentiated Weibull distribution for airborne laser communications. J Opt Technol. 2017;84(11):658–63. 10.1364/JOT.84.000658Suche in Google Scholar

[30] Andrews LC, Phillips RL. Laser beam propagation through random media. Bellingham, Washington: SPIE Press; 2005. 10.1117/3.626196Suche in Google Scholar

[31] Zhao J, Zhao SH, Zhao WH, Li YJ, Liu Y, Li X. Analysis of link performance and robustness of homodyne BPSK for airborne backbone laser communication system. Opt Commun. 2016;359:189–94. 10.1016/j.optcom.2015.09.082Suche in Google Scholar

[32] Andrews LC, Phillips RL, Wayne D, Sauer P, Leclerc T, Crabbs R. Creating a Cn2 profile as a function of altitude using scintillation measurements along a slant path. In: High Energy/Average Power Lasers and Intense Beam Applications VI; Atmospheric and Oceanic Propagation of Electromagnetic Waves VI. Vol. 8238. Bellingham, Washington, USA: SPIE; 2012:95–106. 10.1117/12.913756Suche in Google Scholar

[33] Ross TS. Limitations and applicability of the Maréchal approximation. Appl Opt. 2009;48(10):1812–8. 10.1364/AO.48.001812Suche in Google Scholar

[34] Zhao X, Yi S, Ding H. Experimental study on the influence of attitude angle on the aero-optical effects of a hypersonic optical dome. Optik. 2020;201:163448. 10.1016/j.ijleo.2019.163448Suche in Google Scholar

[35] Ding H, Yi S, Zhu Y, He L. Experimental investigation on aero-optics of supersonic turbulent boundary layers. Appl Opt. 2017;56(26):7604–10. 10.1364/AO.56.007604Suche in Google Scholar PubMed

[36] Wang M, Mani A, Gordeyev S. Physics and computation of aero-optics. Annu Rev Fluid Mech. 2012;44:299–321. 10.1146/annurev-fluid-120710-101152Suche in Google Scholar

[37] Wyckham CM, Smits AJ. Aero-optic distortion in transonic and hypersonic turbulent boundary layers. AIAA J. 2009;47(9):2158–68. 10.2514/1.41453Suche in Google Scholar

[38] Kalensky M, Jumper EJ, Gordeyev S. Extracting atmospheric optical turbulence parameters from AAOL-BC wavefront measurements. In: AIAA SCITECH 2022 Forum. 2022 Forum. 2022. p. 0829. 10.2514/6.2022-0829Suche in Google Scholar

[39] Trinh PV, Carrasco-Casado A, Takenaka H, Fujiwara M, Kitamura M, Sasaki M, et al. Statistical verifications and deep-learning predictions for satellite-to-ground quantum atmospheric channels. Commun Phys. 2022;5:225. 10.1038/s42005-022-01002-1Suche in Google Scholar

[40] Neumann SP, Joshi SK, Fink M, Ursin R. Quantum communications uplink to a 3U CubeSat. In: 2017 IEEE International Conference on Space Optical Systems and Applications (ICSOS). 2017:302–6. 10.1109/ICSOS.2017.8357431Suche in Google Scholar

[41] Vasylyev D, Vogel W, Moll F. Satellite-mediated quantum atmospheric links. Phys Rev A. 2019;99(5):053830. 10.1103/PhysRevA.99.053830Suche in Google Scholar

[42] Sayat M, Shajilal B, Kish SP, Assad SM, Symul T, Lam PK, et al. Satellite-to-ground continuous variable quantum key distribution: The Gaussian and discrete modulated protocols in low earth orbit. IEEE Trans Commun. 2024;72(2):4215–27.10.1109/TCOMM.2024.3359295Suche in Google Scholar

[43] Bourgoin JP, Meyer-Scott E, Higgins BL, Helou B, Erven C, Huebel H, et al. A comprehensive design and performance analysis of low Earth orbit satellite quantum communication. New J Phys. 2013;15:023006. 10.1088/1367-2630/15/2/023006Suche in Google Scholar

[44] Samimi H. New statistical model for atmospheric optical scintillation and its application. IET Optoelectron. 2013;7(1):31–7. 10.1049/iet-opt.2012.0004Suche in Google Scholar

[45] AlQuwaiee H, Yang HC, Alouini MS. On the asymptotic capacity of dual-aperture FSO systems with generalized pointing error model. IEEE Trans Wireless Commun. 2016;15(10):6502–12. 10.1109/TWC.2016.2585486Suche in Google Scholar

[46] Dickson LD. Characteristics of a propagating Gaussian beam. Appl Opt. 1970;9(8):1854–61. 10.1364/AO.9.001854Suche in Google Scholar PubMed

[47] Farid AA, Hranilovic S. Outage capacity optimization for free-space optical links with pointing errors. J Lightwave Technol. 2007;25(6):1702–10. 10.1109/JLT.2007.899174Suche in Google Scholar

[48] Vasylyev DY, Semenov AA, Vogel W. Toward global quantum communication: beam wandering preserves nonclassicality. Phys Rev Lett. 2012;108(22):220501. 10.1103/PhysRevLett.108.220501Suche in Google Scholar PubMed

[49] Vasylyev D, Semenov AA, Vogel W. Atmospheric quantum channels with weak and strong turbulence. Phys Rev Lett. 2016;117(9):090501. 10.1103/PhysRevLett.117.090501Suche in Google Scholar PubMed

[50] Vasylyev D, Vogel W, Semenov AA. Theory of atmospheric quantum channels based on the law of total probability. Phys Rev A. 2018;97(6):063852. 10.1103/PhysRevA.97.063852Suche in Google Scholar

[51] Ma X, Qi B, Zhao Y, Lo HK. Practical decoy state for quantum key distribution. Phys Rev A. 2005;72(1):012326. 10.1103/PhysRevA.72.012326Suche in Google Scholar

Received: 2024-10-22

Revised: 2024-12-26

Accepted: 2025-01-13

Published Online: 2025-03-14

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

https://doi.org/10.1515/phys-2025-0133

Schlagwörter für diesen Artikel

airborne quantum key distribution; boundary layer effects; free space optical

Creative Commons

BY 4.0