Home Modeling and heat transfer analysis of magnetized hybrid micropolar blood-based nanofluid flow in Darcy–Forchheimer porous stenosis narrow arteries
Article Open Access

Modeling and heat transfer analysis of magnetized hybrid micropolar blood-based nanofluid flow in Darcy–Forchheimer porous stenosis narrow arteries

  • Zahir Shah EMAIL logo , Muhammad Rooman , Naeem Ullah Khan , Muhammad Sulaiman , Mansoor H. Alshehri , Narcisa Vrinceanu EMAIL logo and Mihaela Racheriu
Published/Copyright: August 28, 2025
Download Article (PDF)
Open Physics
From the journal Open Physics Volume 23 Issue 1

Abstract

This article provides a concise comparative examination of how heat generation affects the flow of a magnetized micropolar blood-based hybrid nanofluid (HNF) via a stenotic artery. The effects of Joule heating and viscous dissipation are considered. The purpose of this model is to evaluate and contrast the efficiency of HNF models. Our objective is to comprehend the complex process of hybridization by studying the behavior of titanium dioxide (TiO2) and gold (Au) nanoparticles scattered in blood. The mathematical model has been converted into a dimensionless form by applying similarity transformations. This modified model is then efficiently solved using numerical methods, specifically bvp4c, which is a built-in command in MATLAB for solving boundary value problems, and facilitates the efficient handling of nonlinear ordinary differential equations with high accuracy and stability. The cylindrical surface is employed for the computation of flow measures, and the results are visually depicted using tables and graphs. This study makes a substantial contribution by uncovering previously unidentified flow characteristics. The use of Au nanoparticles demonstrates efficacy in improving the blood flow and offers a promising approach for addressing arterial disorders, as opposed to aluminum oxide nanoparticles. Moreover, an inquiry is carried out to examine the skin friction and heat transfer related to the dynamics of blood flow. The results demonstrate that the inclusion of Au and TiO2 nanoparticles enhances heat transfer compared to single-component nanofluids (NFs) while effectively moderating the velocity and temperature profiles under varying conditions. Also, the HNF shows a reduction in temperature rise compared to NFs with only Au nanoparticles, under specific parameter settings.

Keywords: computational modeling; hybrid nanofluid; heat source; Darcy–Forchheimer; curved surface; stenotic artery; vicious and Joule dissipation; blood; gold nanoparticles

Nomenclature

B

micro-inertia density parameter (kg m2)

Ec

Eckert number

F r

coefficient of inertia

K

micropolar material parameter

M

magnetic parameter

N

microrotation (rad/s)

P

pressure (Pa)

Pr

Prandtl number

S

unsteady parameter

T

temperature (K)

V

velocity vector (m/s)

k f

thermal conductivity (W/m K)

c p

specific heat of nanoparticles (J/Kg K)

Greek

α, β, and γ

gyroviscosity coefficients

κ

vortex viscosity (Pa s)

u f

dynamic viscosity (Pa s)

ρ p

density of nanoparticles (kg/m3)

σ e

electrical conductivity (mS/m)

Subscript

hnf

hybrid nanofluid

f

base fluid

1 Introduction

Micropolar fluids possess distinct microscopic properties and are characterized by the manifestation of rigid, spherical, or erratically oriented particles. When the microparticles are suspended in a thick liquid, they display distinct spins and little rotations. These are a class of polar fluids that possess a wide range of microscale activities, which are observed in a range of phenomena physically, such as blood circulation, liquid crystals, and bubbling liquids. As a result, this topic has gained significant recognition in the literature. Xu and Pop [1] have established a connection between advancements in nanofluids (NFs) and bioconvection through their latest study on micropolar fluids. Aziz et al. [2] proposed a theoretical model for the flow of an NF at the bio-convection boundary layer. Agarwal et al. [3] employed the finite element method to investigate the flow and heat transmission of a micropolar fluid over a stretching sheet. Hassanien and Gorla [4] studied the steady flow of boundary layers formed by permeable and impermeable sheets with micropolar movement. Rehman et al. [5] analyzed the stability influenced by shape factors in radiative magneto-hydrodynamic couple stress hybrid nanofluids (HNFs), and this work highlights how shape factors affect the stability of thermal and flow fields in complex fluids, with potential applications in industrial fluid systems.

The study conducted by Nadeem et al. [6] focused on examining the axisymmetric stagnation flow of a micropolar NF within a rotating cylinder. Balaram and Sastri [7] studied the natural flow of a micropolar fluid in a vertical tube with parallel plates. Lok et al. [8] constructed a continuous flow of data in two dimensions.

An HNF is a novel fusion of two or more dispersed nanoparticles in a base fluid. The objective of discovering HNFs is to optimize the heat transmission, enhance the thermal conductivity, and achieve stability by successfully merging the benefits and drawbacks of distinct suspensions. This is accomplished by the combined impact of nanomaterials, carefully adjusted proportions, an exceptional thermal network, and extensive utilization in diverse nuclear power-related domains, including generator cooling, machinery coolant, electronic cooling, and general cooling applications. The enhanced thermal conductivity exhibited by HNFs offers an opportunity to consider their potential application in addressing real-world thermal energy challenges. In their investigation, Waini et al. [9] investigated the effects of a hybrid nano-liquid on a surface that is both moving and permeable. The liquid included a constant volume portion for alumina nanoparticles and varying volume fraction for copper (Cu) nanoparticles. Ashwinkumar et al. [10] used non-linear thermal radiation to investigate the flow of an HNF consisting of CuO–Al2O3 in water. They specifically examined the parameters of the HNF flow past a vertical plate and a cone. Samrat and his team [11] investigated the impact of a stretched surface on heat transfer in the flow of dusty NF and HNF. Acharya [12] developed a simulation using spectral quasi-linearization to study the hydrothermal properties of HNFs when applied to a tilted spinning disc, and Sarwar and Hussain [13] worked on flow characteristics of the Au–blood NF in stenotic arteries. The results suggest that both the rotational speed of the disc and the proportion of nanoparticles in the volume have a significant influence on temperature distributions. Garia et al. [14] investigated the flow of HNFs on two different shapes. A mathematical correlation was constructed to quantify the magnitude of skin friction and the Nusselt number. The micro-polar liquid theory is a theoretical framework that considers the rotation of nanoparticles within a boundary layer. The studies of Eringen, Shah et al., and Deebani et al. [15,16,17] suggest that micropolar fluids can be regarded as an enhancement of the Navier–Stokes condition. These systems are considered a subset of microfluidics due to consideration of the microstructure and the inertial characteristics of the particles inside the fluid that enable the experiment. In their study, Hassanien and Gorla [18] examined the heat transportation process from a stretching sheet to a micropolar fluid. The time-dependent flow of micropolar magnetohydrodynamic (MHD) fluid in a penetrable medium on a two-dimensional plane was examined by Subhani and Nadeem [19]. Hasegan et al. [20,21,22] investigated the blood flow and medical applications. MHD fluid refers to a fluid that experiences the influence of magnetic and electromagnetic forces. Some applications that utilize MHD are solar panels, polymer synthesis, and efficient boilers. A comprehensive study was carried out in this area to examine the manipulation of NFs using electromagnetic forces, due to their considerable importance. Ghadikolaei et al. [23] investigated the manipulation of microliquid flow in a medium using magnetic field effects. The study conducted by Ullah et al. [24] investigated the impact of Newtonian heating and slip conditions on the MHD flow of a Casson fluid across a nonlinearly stretching sheet that is saturated in a porous medium. The study conducted by Gul et al. [25] investigated the heat transport in a fluid flow of ferrofluids with MHD mixed convection on a vertical passage. Saqib et al. [26] conducted a study on the natural convection channel flow of the CMC-based CNT NF. The results suggest that greater enhancement in heat transmission is achieved when lower volume fractions are used, matching the base fluid. Augmentation of the proportion of volume was demonstrated to lead to an elevation in the localized Nusselt number. A numerical examination of the MHD convection in NFs within a baffled U-shaped region was conducted by Ma et al. [27], whereas Khan et al. [28] studied how various models of nanoparticles influence the properties of peristaltic flow in MHD NFs in an irregular passage. Ghalambaz et al. [29] examined the presence of unstructured convection in an enclosed region containing a mix of nanoparticles of copper and aluminum oxide, recognized as Cu–Al2O3 HNFs. Zeb et al. [30] investigated the melting heat transfer and thermal radiation effects on MHD tangent hyperbolic NF flow, incorporating chemical reactions and activation energy. Das et al. [31] examined the production of entropy in the motion of Cu–Al2O3 HNFs in a porous channel under the effect of MHD. The findings indicate that when the volume fraction of nanoparticles increases, the production of entropy is reduced. The impact of viscous dissipation on the flow of micropolar fluids over a small stretching surface was explored by Anantha Kumar et al. [32], and they observed that as the value of micropolar parameters and viscous dissipation increase, the temperature decreases. Khan et al. [33] explored the dynamics of micropolar fluids within porous channels through a semi-analytical approach, focusing on the behaviors of fluids with micropolar characteristics and their interactions with porous structures. In studies of Hasegan et al., Mihai et al., Boicean et al., Pirvut et al., and Dawar et al. [20,21,34–36] the behavior of chemically reactive MHD flow in micropolar NFs was investigated. The researchers conducted a focused investigation on the impacts of velocity slips and fluctuations in the heat source/sink. The study demonstrated several applications, such as wire drawing, liquid composite molding, metal spinning, gas blowing, extrusion of polymer sheets, and manufacture of hot rolling and plastic films. Sakiadis [37] presented the results of a study investigating the characteristics of fluid flow over a solid border under constant conditions. Tsou et al. [38] explored the heat transfer onto a stretched sheet, and Crane [39] inspected an analytical solution for the flow of a viscous fluid generated by a surface that is linearly stretched. In their study, Gupta and Gupta [40] examined the impact of linear velocity on a flexible sheet while also considering the effects of suction or blowing. Grubka and Bobba [41] employed linear velocity in their investigation of heat transfer characteristics under different temperature distributions.

The flow of blood through arteries is a fundamental part of the cardiovascular system, responsible for distributing oxygen-rich blood from the heart to various tissues and organs throughout the body, which is not only crucial for the delivery of essential nutrients and oxygen but also plays a significant role in the removal of waste products and carbon dioxide. Recent work on blood through arteries includes the study of Das et al. [42] who examined the effects of Hall currents on blood flow through mildly stenosed, inclined arteries using a homotopy perturbation method, while Karmakar et al. [43] investigated the dynamics of blood containing trihybrid nanoparticles pumped through an eccentric endoscopic arterial canal using an electro-osmotic mechanism, which enhanced the understanding of targeted drug delivery systems within complex vascular architectures. More recently, Ali and Das [44] applied neuro-computing and fractional calculus to analyze blood flow carrying modified trihybrid nanoparticles in a diseased ciliated artery, and Paul et al. [45] demonstrated the use of a balloon catheter for angioplasty in arteries containing a tetra-hybrid nano-bloodstream under a magnetic field, analyzed via artificial neural networks, and their work contributes to the development of precision interventions in cardiology, particularly in magnetically influenced environments.

Fluid flow over curved surfaces is a highly intriguing subject in the field of fluid mechanics, having a wide range of practical uses in areas such as aerospace engineering and biomedical devices. When a fluid moves across a curved surface, various significant phenomena arise because of the interaction between the fluid and the curvature of the surface. Given the significance and practical relevance of fluid flow over curved surfaces, it has garnered considerable attention in the literature. Haq et al. [46] explored periodic heat transfer through extended surfaces, shedding light on the periodic nature of heat transfer processes and its implications for optimizing thermal management across diverse applications. A study conducted by Ahmed and Khan [47] investigated the causes of fluid flow on a curved surface with pores incorporating magneto-nanomaterials. Sheikholeslami et al. [48] formulated a mathematical model to describe the fluid flow of nanomaterials when employing MHD on an inclined surface. Additionally, Ahmed and Khan [44] conducted research in this area. Computational modeling of MHD flow of the Sisko NF past a curved surface in motion.

The aim of this work is to examine the characteristics of magnetized micropolar blood including Cu and gold (Au) nanoparticles in an HNF as it moves across a curved surface. This work demonstrates innovation and originality by integrating the following concepts:

  • Unsteady flow.

  • Magnetized micropolar blood-based NF.

  • An HNF that incorporates both Cu and Au nanoparticles.

  • Consideration of complicated geometry with curved surfaces.

  • The study examines different factors, including the Prandtl number, volume proportion of nanoparticles, and blood flow parameters.

The present study uniquely integrates MHD and micropolar fluid dynamics with HNFs in a medically relevant model of blood flow through stenotic arteries. Unlike previous studies, such as the exploration of HNF heat transfer over different geometries by Ashwinkumar et al. [10] or the experimental analysis of Au–blood NF flow in stenotic arteries by Sarwar and Hussain [13], this study introduces a comprehensive framework for modeling blood flow under the simultaneous influence of magnetic fields, slip effects, and porous stenosis conditions. Building on the foundational theory of micropolar fluids established by Eringen [15], it incorporates advanced numerical methods to capture the unsteady behavior of HNFs (blood–Au + TiO2), revealing significant improvements in heat transfer and flow dynamics. Additionally, the thermal performance findings of Waini et al. [9] and the axisymmetric flow explored by Nadeem et al. [6] are extended to address curved, porous surfaces, with specific attention to the implications for cardiovascular treatments. By unifying these elements, the current work advances the understanding of HNF dynamics in biomedical applications, offering new insights into optimizing drug delivery and managing arterial disorders. Additionally, Table 1 explains the novelty with reference to the available literature.

Table 1

Comparative summary of key features addressed in previous and current studies on hybrid nanofluid and methods applied

References MHD HNF Blood-based NF Micropolar dynamics Heat transfer Numerical methods Experimental methods Medical relevance
Ashwinkumar et al. [10] ✓ ✗ ✗ ✓ ✓ ✗ ✓
Sarwar and Hussain [13] ✓ ✓ ✗ ✓ ✓ ✓ ✓
Waini et al. [9] ✓ ✗ ✗ ✓ ✓ ✗ ✓
Ghalambaz et al. [29] ✓ ✗ ✗ ✓ ✓ ✗ ✓
Nadeem et al. [6] ✗ ✗ ✓ ✗ ✓ ✗ ✓
Eringen [15] ✗ ✗ ✓ ✗ ✗ ✗ ✗
Current study ✓ ✓ ✓ ✓ ✓ ✗ ✓

1.1 The investigation progresses in a systematic manner

First, the governing equations are solved with great attention to detail, resulting in a numerical solution achieved with MATLAB software. Afterward, a detailed representation of the physical measurements linked to various parameters is given by displaying graphs. The results of this research are highly relevant to a wide range of biomedical applications.

2 Formulation

2.1 Geometry and physical description of the model

The 2D flow model of a micropolar time-dependent hybrid magnetized NF moving through a stenosis artery is scrutinized in the present study context. We considered that blood flowing through an artery stenosis of length L 0 2 behaves like an incompressible unsteady Newtonian micropolar fluid flow. The blood flow is assumed to be along the x-axis and perpendicular to the r-axis. The artery has a cosine-shaped stenosis having a width of unobstructed region of 2 R 0 ° , where R ( x ) is the artery’s radius which is the stenosis’s greatest height. The following profile is adopted for the stenosed area (Figure 1) [13,45]:

(1) R ( x ) = R 0 − λ 2 1 + cos 4 π x L 0 , − L 0 4 < x < L 0 4 = R 0 ,  Otherwise ,

Figure 1 Geometrical demonstration of the problem.
Figure 1

Geometrical demonstration of the problem.

2.2 Assumptions

  • Blood behaves as a micropolar fluid with inherent microstructural behaviors.

  • The flow is unsteady, with varying flow characteristics over time.

  • The fluid is a magnetically influenced HNF.

  • Blood flow is assumed incompressible, maintaining constant density under pressure variations.

  • Artery stenosis is modeled with a cosine-shaped profile for precise geometric simulation.

  • Blood flow is directed along the x-axis and perpendicular to the r-axis, simplifying the analysis to two dimensions.

  • Incorporates gyration tensor, micro-inertia, and micro-stress in the fluid’s constitutive equations, reflecting complex internal and magnetic interactions.

2.3 Mathematical modeling

The vector form of the constitutive equations which describe the micropolar nature of the fluid is written by combining novel kinematic features, such as the gyration tensor and the micro-inertia, moment tensor, as well as the thoughts of micro-stress, body, and stress moments. These equations also consider the magnetic effect as follows [13,46]:

(2) ∇ ⋅ V = 0 ,

(3) ρ f ∂ V ∂ t + V ⋅ ∇ V = − ∇ p + ( μ f + k ⁎ ) ∇ 2 V + k ⁎ ( ∇ × v ) + μ u K + ρ f F u 2 + J × B ,

(4) ρ f j ∂ v ∂ t + v ⋅ ∇ v = ( α + β + γ ) ∇ ⋅ ∇ v − γ ( ∇ × ∇ × v ) + k ⁎ ( ∇ × v ) − 2 k v + J × B .

The inequalities are as follows [45]:

k ≥ 0 ,   2 μ f + k ≥ 0 ,   3 α + β + γ ≥ 0 ,   ∣ γ ∣ ≥ β .

The thermal energy and nanoparticle diffusion equations, which adhere to the Fourier and Fick laws, are expressed in accordance with Buongiorno’s model [13].

(5) ρ f c f ∂ T ∂ t + V ⋅ ∇ T = k f ∇ 2 T .

Here, ρ f and c f refer to the density and specific heat of nanoparticles, respectively. The variables in the given equation are given in Table 2.

Table 2

Variables used

Parameter Symbol
Velocity vector V = ( u , v , w )
Pressure p
Microrotation N
Current density J = σ e ( V × B )
Electrical conductivity σ e
Magnetic field B
Fluid density ρ f
Dynamic viscosity μ f
Vortex viscosity κ
Microinertia density j
Gyroviscosity coefficients α , β , γ
Temperature T
Specific heat c f
Thermal conductivity k f
Density nanoparticles ρ p
Specific heat of nanoparticles c p

2.4 Reduced equations after implementation of assumptions and boundary conditions

The equations that regulate the flow and heat transfer for Newtonian NFs in an unstable boundary layer are defined, assuming certain conditions [13,46]

(6) ∂ ∂ x ( r u ) + ∂ ∂ r ( r v ) = 0 ,

(7) ∂ u ∂ t + u ∂ u ∂ x + v ∂ u ∂ r = ( μ hnf + k ⁎ ) ρ hnf ∂ r ∂ r r ∂ u ∂ r − σ hnf B 0 2 ρ hnf u − μ hnf k 1 u − c b k 1 ( u 2 ) ,  

(8) ∂ N ∂ t + u ∂ N ∂ x + v ∂ N ∂ r = − γ ⁎ j ρ hnf 1 r ∂ N ∂ r + ∂ 2 N ∂ r 2 − k ⁎ j ρ hnf ∂ u ∂ r + 2 N ,

(9) ∂ T ∂ t + u ∂   T ∂ x + v ∂ T ∂ r = k hnf ( ρ C p ) hnf ∂ r ∂ r r ∂ T ∂ r + ( μ hnf + k ⁎ ) ( ρ C p ) hnf ∂ u ∂ r 2 + σ hnf B 0 2 ( ρ C p ) hnf u 2 .

For this model, the workable boundary conditions are [13]

u = u 0 ,   v = 0 ,   N = N 0  and  T = T 0  at  r = R ( x ) ,

(10) ∂ u ∂ r = 0 ,   ∂ N ∂ r = 0 ,  and  ∂ T ∂ r = 0 ,  as  r = 0 .

2.5 Hybrid nanomaterial properties

To accurately forecast the heat transmission characteristics of NFs, a thorough examination of their thermophysical properties is essential. Nanoparticles can significantly improve heat conductivity compared to larger particles in suspension, such as millimeter-sized and micrometer-sized particles. Empirical research has shown that the thermal conductivity of NFs is affected by various elements, such as the temperature, the composition of the base fluid, the percentage of particle volume, the material composition of the particles, the size of the particles, and the form of the particles. The influence of NF additions on the improvement of heat conductivity has been found to be dependent on their features, such as kind, amount, and acidity. The thermo-physical characteristics and relationship of nano and hybrid nanomaterials are shown in Tables 3 and 4, respectively. Diagrams for the preparation and factors influencing the HNFs and application of Au and titanium dioxide (TiO2) are given in Figure 2.

Table 3

Thermo-physical attributes of both the base fluid and the HNF Φ 1 + Φ 2 = Φ analyzed and reported in detail in previous studies [24,25,26]

Components c p  J kg K k  W m K σ m S m   ρ kg m 3    
Gold ( Au ) 129 318 4.1 × 106 19,300
Titanium dioxide (TiO2) 4,250 8.9538 6.27 × 10−5 686.20
Blood 3,594 0.492 6.67 × 10−1 1,063
Table 4

Thermo-physical interactions of NFs and HNFs [46]

Properties NF and HNF
Viscosity μ hnf μ bf = 1 ( 1 − ϕ g − ϕ TiO 2 ) 2.5
Density ρ hnf ρ bf = ϕ g ρ g ρ bf + ϕ TiO 2 ρ TiO 2 ρ bf + ( 1 − ϕ g − ϕ TiO 2 )
Thermal capacity ( ρ c p ) hnf ( ρ c p ) bf = ϕ g   ( ρ c p ) g ( ρ c p ) bf + ϕ TiO 2 ( ρ c p ) g ( ρ c p ) bf + ( 1 − ϕ g − ϕ TiO 2 )
Thermal conductivity k hnf k bf = ( ϕ g k g + ϕ TiO 2 k TiO 2 ) ϕ g + ϕ TiO 2 + 2 k bf + 2 ( ϕ g k g + ϕ TiO 2 k TiO 2 ) − 2 ( ϕ g + ϕ TiO 2 ) k bf ( ϕ g k g + ϕ TiO 2 k TiO 2 ) ϕ g + ϕ TiO 2 + 2 k bf − ( ϕ g k g + ϕ TiO 2 k TiO 2 ) + ( ϕ g + ϕ TiO 2 ) k bf
Electrical conductivity σ hnf σ bf = ( ϕ g σ g + ϕ TiO 2 σ TiO 2 ) ϕ g + ϕ TiO 2 + 2 σ bf + 2 ( ϕ g σ g + ϕ TiO 2 σ TiO 2 ) − 2 ( ϕ g + ϕ TiO 2 ) σ bf ( ϕ g k g + ϕ TiO 2 k TiO 2 ) ϕ g + ϕ TiO 2 + 2 σ bf − ( ϕ g σ g + ϕ TiO 2 σ TiO 2 ) + ( ϕ g + ϕ TiO 2 ) σ bf
Figure 2 (a) Diagram for the preparation of HNFs. (b) Factors impacting the HNF properties. (c) Application of TiO 2 {\text{TiO}}_{2} . (d) Applications of Au nanoparticles.
Figure 2

(a) Diagram for the preparation of HNFs. (b) Factors impacting the HNF properties. (c) Application of TiO 2 . (d) Applications of Au nanoparticles.

2.6 Similarity transformation

Similarity transformation is a technique used to simplify the solution of partial differential equations (PDEs) by identifying scaling properties that allow the equations to be transformed into a dimensionless form. The principle behind similarity transformations lies in recognizing that certain physical systems or phenomena exhibit self-similarity. We use similarity transformation to reduce the given modeled equation. The appropriate transformations of similarity are specified as follows:

u = a ( 1 − α t )   u 0 x L 0 F ′ ( η ) ,   v = − R r u 0 ϑ f a L 0 ( 1 − α t ) F ( η ) , η = r 2 − R 2 2 R u 0 a ϑ   f L 0 ( 1 − α t )   ,

(11) θ ( η ) = a ( 1 − α t ) T − T ∞ T w − T ∞ ,  and  N = u 0 a x u 0 a ϑ f L 0 ( 1 − α t ) g ( η ) .

2.7 Non-dimensional system of ordinary differential equations (ODEs)

After introducing similarity transformation, the following transformed governing equations are obtained.

(12) ( μ hnf + K ) μ f ( ( 1 + 2 η γ ) f ‴ + 2 γ f ″ ) − ρ hnf ρ f S 1 2 η f ″ + f ′ + ( f ' 2 − f f ″ ) − μ hnf μ f β 0 f ′ − F r f ' 2 − σ hnf σ f M f ′ = 0 ,

(13) S ( η g ′ + g ) + f ′ g − f g ′ + ρ f ρ nf ( 1 + K ) ( ( 1 + 2 η γ ) g ″ + 2 γ g ′ ) + ρ f ρ nf K ( ( 1 + 2 η γ ) 1 / 2 f ″ + 2 B g ) = 0 ,

(14) K nf K f [ ( 1 + 2 η γ ) θ ″ + 2 γ θ ′ ] + ( μ hnf + K ) μ f Pr Ec ( 1 + 2 η γ ) f ″ 2 + σ nf σ f M Pr Ec ( 1 + 2 η γ ) f ″ 2 − Pr ( ρ C p ) nf ( ρ C p ) f [ S ( η θ ′ − θ ) − f θ ′ ] = 0 .

The non-dimensional boundary conditions are as follows:

(15) f ( 0 ) = 0 , f ′ ( 0 ) = g ( 0 ) =   θ ( 0 ) = 1 , f ″ ( η ) = 0 ,   g ′ ( η ) = θ ′ ( η ) = 0  at  η = f .  

2.7.1 Obtained physical parameters

The dimensionless parameters after modeling in Eqs. (12)–(15) are given with details in Table 5.

Table 5

Physical parameters and details

Parameter Symbol Mathematical form
Micropolar material parameter K K = K ⁎ μ f
Micro-inertia density parameter B B = ϑ f ( 1 − α t ) L 0 a u 0 j  
Coefficient of inertia F r F r = F x ρ f = C b x k ρ f
Unsteady parameter S S = α L 0 a u 0
Curvature parameter γ γ = L 0 ( 1 − α t ) ϑ f u 0 a R 2
Eckert number Ec Ec = u 0 2 a 3 x 2 ( 1 − α t ) 2 L 0 2 C p ( T w − T ∞ )
Prandtl number Pr Pr = k f ( μ C p ) f
Magnetic parameter M M = σ f B 0 2 L 0 ( 1 − α t ) ρ f a u 0
Porosity parameter β 0 β 0 = μ f L 0 ( 1 − α t ) ρ f a u 0 K

3 Calculation of physical quantities

The Nusselt number is a dimensionless parameter which is used in heat transfer analysis to describe the convective heat transfer between a fluid and a solid surface. It represents the ratio of convective heat transfer to conductive heat transfer over the thermal boundary layer. The Nusselt number essentially indicates the efficiency of convective heat transfer relative to conductive heat transfer. A higher Nusselt number signifies a higher convective heat transfer rate relative to conduction, indicating more efficient heat transfer. The Nusselt number is used to design and optimize heat exchangers, cooling systems, and other thermal devices.

Skin friction is another primary concept in the study of fluid flow. Skin friction refers to the drag force exerted by the fluid on a solid surface due to viscous shear stresses within the boundary layer. It is essential in various engineering applications, including hydrodynamics, aerodynamics, and heat transfer. The skin friction coefficient depends on the flow conditions, geometry of the surface, and properties of the fluid. Skin friction plays a role in convective heat transfer, particularly in forced convection where fluid flow over a surface enhances heat transfer. Comprehension and precise calculation of skin friction are essential for designing efficient vehicles, aircrafts, ships, and other structures where minimizing drag is crucial for performance and fuel efficiency. The physical quantities, i.e., skin friction coefficient C f and heat transfer coefficient Nu of the flow field are defined as:

(16) C f = τ w 1 2 ρ f U w 2 ,  Nu = x q w k f ( T w − T ∞ ) ,

where shear stress τ w   and q w are

(17) τ w = ( μ h n f + K ) μ f ∂ u ∂ r r = R ,  Re x 1 / 2 C f = ( μ hnf + K ) μ f F ″ ( 0 ) .

q w = − k hnf ∂ T ∂ r r = R ,  Re x 1 / 2 Nu x = − k hnf k ( θ ' ) ,

where Re x − 1 / 2 is the local Reynolds number.

4 Solution methodology

In this section, the solution procedure for this model is determined by using a shooting method with the bvp4c solver. The model’s ODEs are numerically solved using the MATLAB tool’s bvp4c solver, which uses a shooting strategy. The first step in using this method is to convert the higher-order system into a first-order system. To complete this conversion, several guidelines will be followed:

(18) f = y 1 ,   f ′ = y 2 , f ″ = y 3 ,   g = y 4 ,   g ′ = y 5 ,   y 6 = θ ,   y 7 = θ ′ ,

(19) y 3 ′ = − 2 γ 1 + 2 η γ y 3 + 1 ( 1 + 2 η γ ) D 1 D 2 S 1 2 η y 3 + y 2 + ( y 2 2 − y 1 y 3 ) + ( D 1 β 0 + D 5 M ) y 2 + F γ y 2 2 ,

(20) y 5 ′ = − 2 γ 1 + 2 η γ y 5 − 1 ( 1 + K ) ( 1 + 2 η γ ) [ D 2 { S ( η y 5 + y 4 ) + y 2 y 4 − y 1 y 5 } + K ( 1 + 2 η γ ) 1 / 2 y 3 + 2 B y 4 ] ,

(21) y 7 ′ = − 2 γ 1 + 2 η γ y 7 + 1 D 4 ( 1 + 2 η γ ) [ Pr D 3 ( S ( η y 7 − y 6 ) − y 1 y 7 ) − D 1 P r E c ( 1 + 2 η γ ) y 3 2 − D 5 Pr Ec M ( 1 + 2 η γ ) y 3 2 ] .

5 Results and discussion

This study presents a detailed scrutiny of the impact of heat generation on the unsteady magnetized micropolar blood-based HNF flow through a porous stenotic artery. The bvp4c method was used to compute results numerically in a nonlinear system. To attribute influential parameters on velocity, microrotation and temperature profiles are examined in this section.

5.1 Velocity profile

Figure 3 indicates the effects of the β 0 porosity parameter on f ′ ( η ) for the HNF (blood–Au + TiO2) and the NF (blood–Au). It is observed that f ′ ( η ) decreases for both fluids as the porosity parameter increases. This is attributed to the fact that introducing more pores on the porous surface creates additional resistance to fluid flow. The velocity behavior is almost the same for both NFs which is clearly reflected in the graph. Figure 4 showcases the relation between the coefficient of inertia F r and velocity profile f ′ ( η ) . When the coefficient of inertia F r is increased, the velocity decreases for both the HNF and NF because the fluid’s resistance to acceleration or velocity changes may rise with a higher coefficient of inertia. In regions where the flow is changing, this higher resistance may cause a drop in the overall velocity profile. Variations in this coefficient can have an impact on the equations’ acceleration terms, which in turn can have an impact on the velocity profile. Higher inertia coefficients increase resistance to changes in motion, thus decreasing velocity as the fluid struggles to accelerate. Figure 5 illustrates the effect of curvature parameter γ on the velocity profile f ′ ( η ) . The velocity declines for increasing values of curvature parameter γ because centripetal acceleration is a factor in fluid flow along a curved surface. This acceleration is aimed at the center of curvature and acts perpendicular to the velocity direction. The centripetal acceleration rises with increasing curvature, causing the total velocity to decrease. Increased curvature enhances centripetal forces acting perpendicular to the flow, reducing the velocity due to higher directional force requirements. Figure 6 portrays the influence of the micropolar material parameter K on the velocity profile f ′ ( η ) , that is, when the material parameter K increases, the micropolar velocity profile decreases for both the HNF and NF. The micropolar material parameter, often referred to as the spin gradient viscosity or microinertia, is represented by the parameter K in the context of micropolar fluid theory. It measures the impact of the fluid’s microrotations. A rise in K indicates a corresponding increase in the fluid’s microinertia, or resistance to micro-rotations. The fluid therefore becomes more resilient to internal deformations or small-scale rotating movements. This higher resistance has the tendency to restrict the micro-rotations, which has an impact on the fluid’s overall velocity profile. Figure 7 depicts the relation between the magnetic parameter M and velocity profile; it can be noted that for higher values of magnetic parameter M , the velocity profile decreases for both the HNF and NF because the Lorentz force is an important component of MHD. The interaction of the magnetic field with the fluid’s generated electric currents produces this force. The fluid motion may encounter resistance from the Lorentz force, which would affect the velocity. In Figure 8, the impact of volume fraction ϕ on the velocity profile is displayed, and it is revealed that for increasing values of ϕ the velocity profile enhances for both the HNFs and NFs. This is due to the change in thermal as well as dynamic viscosity of the fluids. Also, the increasing value of ϕ enhances the concentration rate which further increases the fluid convection. This increasing trend of convection further increases the velocity profile. Particularly, when the volume fraction ϕ of TiO2 nanoparticles is increased while maintaining the volume fraction ϕ of Au constant, the velocity profile in the HNF is observed to sharply increase. This observation implies that, under the given conditions, TiO2 nanoparticles may have a more pronounced effect on fluid dynamics than Au nanoparticles. Figure 9 manifests the fluctuations between the value of ϕ and velocity profile f ′ ( η ) . When the volume fraction ϕ is augmented, the velocity profile increases for both the HNF and NF because the viscosity and thermal conductivity of the NF may both be improved by adding Au nanoparticles. While higher viscosity may have an impact on fluid flow and perhaps increase velocity dispersion, enhanced thermal conductivity can result in better heat transfer. It appears that Au nanoparticles under these circumstances have a greater influence on the flow dynamics than TiO2 nanoparticles based on the observation that velocity increases by increasing the volume fraction ϕ of Au while maintaining the volume fraction ϕ of TiO2 in the HNF. Figure 10 highlights the effects between the ϕ and velocity profile. It is observed that for the boosted volume fraction ϕ the velocity profile increases for both the HNF and NF because, among other things, the addition of nanoparticles to a fluid can change its viscosity and thermal conductivity. When the volume fraction ϕ increases, the concentration of nanoparticles in the fluid also increases. The fluid’s behavior may alter because of this concentration increase, raising the velocity profile. Particularly, when the volume fraction ϕ of TiO2 nanoparticles is increased while maintaining the volume fraction ϕ of Au constant, the velocity profile in the HNF is observed to sharply increase. This observation implies that, under the given conditions, TiO2 nanoparticles may have a more pronounced effect on fluid dynamics than Au nanoparticles. Figure 11 exhibits the interdependence between the unsteady parameter S and velocity profile f ′ ( η ) . The velocity profile decreases for both the HNF and NF if the unsteady parameter S is increased because time-dependent variations in pressure and velocity are characteristics of unsteady flows. A higher level of unsteadiness in the flow is indicated by a rise in the unsteady parameter S . The velocity field may experience oscillations or changes as a result.

Figure 3 Effects of porosity parameter β 0 on the velocity profile f ' ( η ) f\text{'}(\eta ) for both the HNF (blood–Au + O2) and NF (blood–Au).
Figure 3

Effects of porosity parameter β 0 on the velocity profile f ' ( η ) for both the HNF (blood–Au + O2) and NF (blood–Au).

Figure 4 Influence of the coefficient of inertia F r {F}_{r} on the velocity profile f ' ( η ) f\text{'}(\eta ) for the HNF (blood–Au + TiO 2 {\text{TiO}}_{2} ) and NF (blood–Au).
Figure 4

Influence of the coefficient of inertia F r on the velocity profile f ' ( η ) for the HNF (blood–Au + TiO 2 ) and NF (blood–Au).

Figure 5 Impact of the curvature parameter γ \gamma on the velocity profile f ' ( η ) . {\boldsymbol{\text{'}}}(\eta ).
Figure 5

Impact of the curvature parameter γ on the velocity profile f ' ( η ) .

Figure 6 Variation of the velocity profile f ' ( η ) f\text{'}(\eta ) with the micropolar material parameter K K for the HNF (blood–Au + TiO2) and NF (blood–Au).
Figure 6

Variation of the velocity profile f ' ( η ) with the micropolar material parameter K for the HNF (blood–Au + TiO2) and NF (blood–Au).

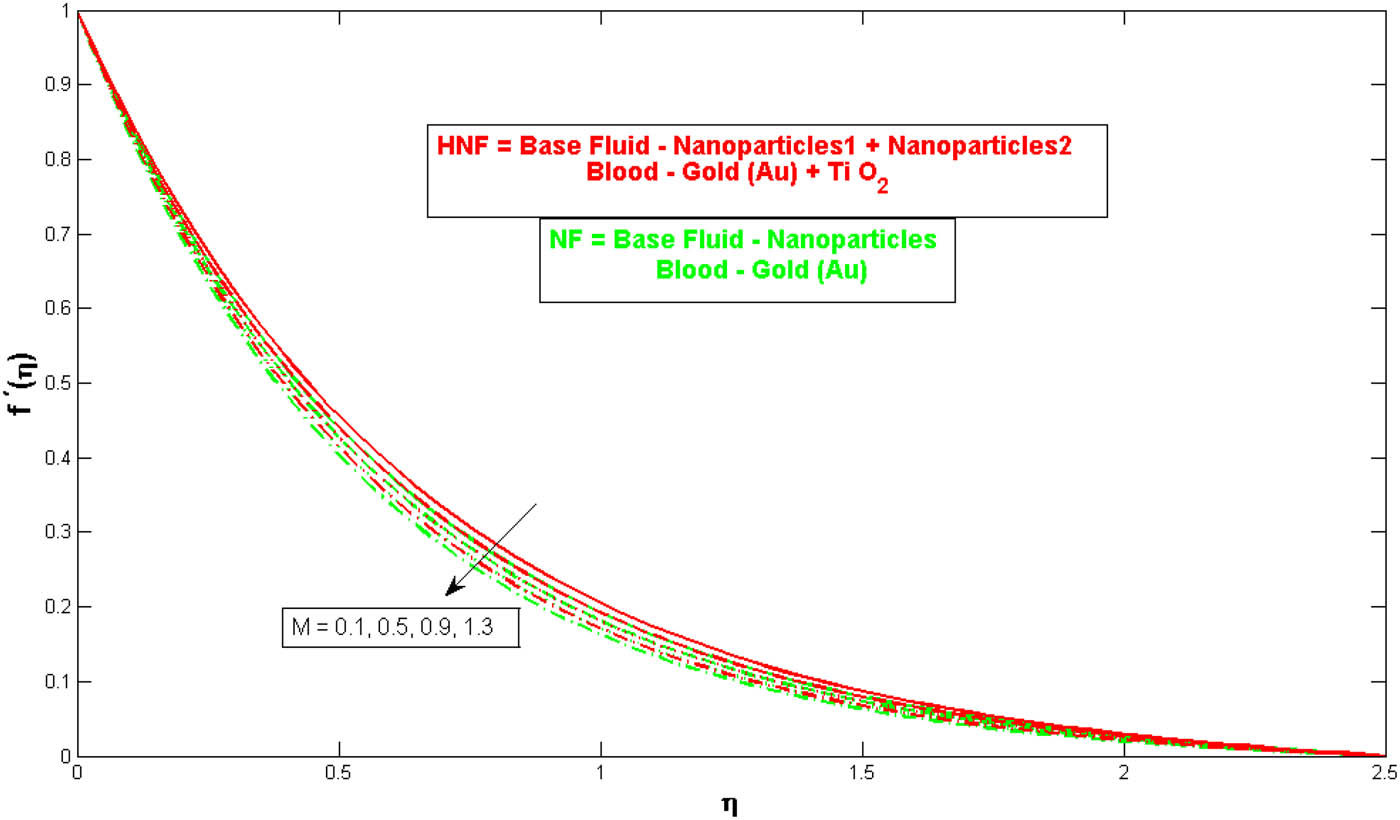
Figure 7 Relationship between the magnetic parameter M and the velocity profile f′(η).
Figure 7

Relationship between the magnetic parameter M and the velocity profile f′(η).

Figure 8 Effect of the volume fraction ϕ on the velocity profile f ' ( η ) f\text{'}(\eta ) for both the HNF (blood–Au + TiO2) and NF (blood–Au).
Figure 8

Effect of the volume fraction ϕ on the velocity profile f ' ( η ) for both the HNF (blood–Au + TiO2) and NF (blood–Au).

Figure 9 Influence of ϕ \phi \hspace{.25em} on the velocity for both the HNF (blood–Au + O2) and NF (blood–Au).
Figure 9

Influence of ϕ on the velocity for both the HNF (blood–Au + O2) and NF (blood–Au).

Figure 10 Variation of ϕ \phi on the f ′ ( η ) f^{\prime} (\eta )\hspace{.25em} for the HNF (blood−Au + TiO2) and NF (blood−Au).
Figure 10

Variation of ϕ on the f ′ ( η ) for the HNF (blood−Au + TiO2) and NF (blood−Au).

Figure 11 Variation of S S on f ′ ( η ) f^{\prime} (\eta )\hspace{.25em} for the HNF (blood–Au + TiO2) and NF (blood–Au).
Figure 11

Variation of S on f ′ ( η ) for the HNF (blood–Au + TiO2) and NF (blood–Au).

5.2 Temperature profile

It is recorded in Figure 12 that with the increase of the porosity parameter β 0 , the temperature increases for both the HNF and NF because the fluid’s and the porous medium’s interaction can be affected by the porosity parameter. Elevated temperature profiles may result from enhanced heat transfer between the fluid and solid due to a higher degree of contact between the fluid and the porous structure. The variation between the magnetic parameter M and temperature profile θ ( η ) is presented in Figure 13, and it is recognized that as fog enlarged the value of the magnetic parameter M the temperature profile increases for both the HNF and NF because the fluid’s ability to transmit heat can be improved by the magnetic field. This is especially true for NFs in which the base fluid contains scattered nanoparticles (like Au). These nanoparticles’ mobility may be influenced by the magnetic field, which can enhance heat conduction. The dominance of Ec on temperature profile θ ( η ) is shown in Figure 14; it is noted that the increment in the Ec causes an enhancement in the temperature for both the HNF and NF because an increase in the Ec indicates a higher kinetic energy relative to internal energy, which can lead to enhanced convective heat transfer and higher temperature profiles. The Ec is frequently associated with the balance between kinetic energy and internal energy (enthalpy) in a fluid flow. With the increase in the curvature parameter γ , the temperature decreases for both the HNF and NF, which is shown in Figure 15, because heat conduction and convective heat transmission can be balanced differently depending on curvature changes. Heat transmission away from the surface may be improved by higher curvature due to greater convective processes. However, lower temperature profiles might arise if this improvement is insufficient to offset any decrease in heat conduction. Figure 16 displays the modification between the unsteady parameter S and temperature profile θ ( η ) , which shows that with the increase in the unsteady parameter S the temperature increases for both the HNF and NF, because higher levels of unsteadiness in the flow are frequently indicated by a rise in the unsteady parameter. There might be more transient heat transfer processes because of this enhanced unsteadiness. Temperature variations can be caused by transient heat transfer, and under some circumstances the temperature profile may rise overall.

Figure 12 Effect of porosity parameter β 0 {\beta }_{0} on temperature, showing an increase in temperature with higher porosity due to improved fluid–porous medium interaction.
Figure 12

Effect of porosity parameter β 0 on temperature, showing an increase in temperature with higher porosity due to improved fluid–porous medium interaction.

Figure 13 Influence of the magnetic parameter M on temperature.
Figure 13

Influence of the magnetic parameter M on temperature.

Figure 14 Effect of the Ec on temperature, indicating that higher Ec increases the temperature by enhancing convective heat transfer.
Figure 14

Effect of the Ec on temperature, indicating that higher Ec increases the temperature by enhancing convective heat transfer.

Figure 15 Influence of the curvature parameter γ on temperature, showing a decrease in temperature with increasing curvature due to changes in heat transfer dynamics.
Figure 15

Influence of the curvature parameter γ on temperature, showing a decrease in temperature with increasing curvature due to changes in heat transfer dynamics.

Figure 16 Impact of the unsteady parameter S S on temperature, where an increase in S results in a higher temperature due to enhanced transient heat transfer.
Figure 16

Impact of the unsteady parameter S on temperature, where an increase in S results in a higher temperature due to enhanced transient heat transfer.

5.3 Micro-rotation profile

Figure 17 demonstrates the control of the micro-inertia density parameter B on micropolar profile g ( η ) ; with the increase of the micro-inertia density parameter B , the micropolar profile increases for both the HNF and NF because micro-inertia and nanoparticle dynamics may combine to provide a synergistic impact in an HNF that contains both micropolar effects and nanoparticles. In comparison to the conventional NF, the HNF may exhibit a greater rise in the micropolar profile due to the combined impact of micro-inertia and nanoparticle dispersion. Figure 18 highlights the variant linking the curvature parameter γ and micropolar profile g ( η ) . When the curvature γ is increased, the micropolar profile decreases for both the HNF and NF, because micro-rotation and micro-deformation effects are a result of the fluid’s micropolar character. A decrease in the micropolar profile g ( η ) can occur from modifications in the microstructure and flow patterns of the micropolar fluid caused by an increase in curvature γ . When the micropolar material parameter K is boosted, the micropolar profile decreases for both the HNF and NF as shown in Figure 19, because the degree of micro-deformation and micro-rotation in the fluid is characterized by the micropolar material parameter K . An increase in K can cause the fluid’s micro-deformation and micro-rotation to rise, which can alter the flow patterns and concentration profiles and decrease the micropolar profile g ( η ) . The persuasion of the unsteady parameter S on micropolar profile g ( η ) is displayed in Figure 20. When there is an increase in the unsteady parameter S , the micropolar profile increases for both the HNF and NF, because a more dynamic flow field is suggested by an increase in the unsteady parameter S . The micropolar profile g ( η ) increases because of increased mixing and transport caused by unsteady flows.

Figure 17 Effect of micro-inertia density parameter B on the micropolar profile g ( η ) , g(\eta ), showing an increase in profile with higher B for both hybrid and conventional NFs.
Figure 17

Effect of micro-inertia density parameter B on the micropolar profile g ( η ) , showing an increase in profile with higher B for both hybrid and conventional NFs.

Figure 18 Influence of the curvature parameter γ \gamma on the micropolar profile g(η).
Figure 18

Influence of the curvature parameter γ on the micropolar profile g(η).

Figure 19 Impact of the micropolar material parameter K on the micropolar profile g ( η ) . g(\eta ).
Figure 19

Impact of the micropolar material parameter K on the micropolar profile g ( η ) .

Figure 20 Effect of the unsteady parameter S on the micropolar profile g(η).
Figure 20

Effect of the unsteady parameter S on the micropolar profile g(η).

Table 6 exhibits the values of skin friction coefficient for numerous parameters. It is noteworthy that the skin friction coefficient drops for large values of porosity, unsteady, magnetic, and flow parameters. Table 7 highlights how the various parameters and the Nusselt number are interdependent. It is recorded that the Nusselt number lowers for large values of porosity parameter, Eckert number, flow parameter and unsteady parameter. Table 8 shows a comparison with the already published work, which shows the validity of our results. The comparison is made for different values of the parameters γ (shear parameter) and ϕ (volume fraction of nanoparticles) in terms of the dimensionless friction factor. The close agreement between the results of the present study and those from the published work validates the accuracy and reliability of the current model.

Table 6

Impact of different parameters on skin friction coefficient

β 0 S γ M NF HNF
0.10 0.10 0.10 −2.114507 −2.512631
0.20 −2.181286 −2.607065
0.30 −2.246348 −2.698726
0.1 0.1 0.1 −2.114507 −2.512631
0.2 −2.240494 −2.659066
0.3 −2.35676 −2.795233
0.1 0.1 0.1 −2.114507 −2.512631
0.2 −2.198743 −2.634848
0.3 −2.279811 −2.752537
0.1 −2.114507 −2.512631
0.2 −2.1593 −2.577853
0.3 −2.203312 −2.641736
Table 7

Influence of some parameters on the Nusselt number

β 0 Ec γ S NF HNF
0.1 1.0 1.0 0.1 0.6531922 2.177478
0.2 0.6358387 2.153595
0.3 0.6187621 2.130125
0.1 1.0 1.0 0.1 0.6531922 2.177478
1.1 0.5627625 2.063243
1.2 0.4723327 1.949009
0.1 1.0 1.0 0.1 0.6531922 2.177478
1.1 0.6807187 2.265521
0.706238 2.34732
0.1 1.0 1.0 0.1 0.6531922 2.177478
0.2 0.5178419 2.001518
0.3 0.3775971 1.821829
Table 8

Comparison of γ and ϕ values in the present work and the literature

γ ϕ Present work Re x 1 / 2 Re x 1 / 2 C f Published work [13] Re x 1 / 2 Re x 1 / 2 C f
0.1 0.0 −0.9352436 −0.939968
0.12 −0.9219889 −0.924794
0.14 −0.9099237 −0.911311
0.1 0.0 −0.9352436 −0.939968
0.05 −1.324139 −1.329552
0.1 −1.689456 −1.715985

6 Conclusions

In the present investigation, we developed a mathematical model to describe the unsteady magnetized flow of a micropolar fluid across a curved surface, considering the slip effects. The governing PDEs were transformed into nonlinear ODEs using the similarity transformation technique. The dimensionless system was then numerically solved using the BVP4C method in MATLAB. Various key parameters were systematically varied to analyze the behavior of velocity and temperature profiles. The following summarizes the main conclusions drawn from the current study:

  • The velocity profile of the HNF improves with increasing volume fraction ϕ, suggesting that the use of HNFs could enhance the blood flow through narrowed arteries by improving fluid dynamics.

  • Velocity decreases with higher values of porosity parameter, coefficient of inertia, curvature parameter, micropolar material parameter, unsteady parameter, and magnetic parameter. This indicates that the resistance to flow in a stenotic artery is influenced by these factors, affecting blood circulation in diseased or narrowed arteries.

  • The temperature profile of the fluid increases with the porosity parameter, Eckert number, and unsteady parameter, highlighting the importance of efficient heat transfer for thermal regulation in blood flow through arteries.

  • The HNF (blood–Au + TiO₂) demonstrates better heat transfer performance compared to the NF (blood–Au), especially with an increased porosity parameter. This suggests that the combination of TiO₂ and Au nanoparticles in HNFs can improve the thermal efficiency and offer potential for controlling temperature within arterial flow.

  • The curvature parameter influences the micropolar profile with an increase in curvature leading to a decrease in micropolar behavior, which reflects how the narrowing and curvature of arteries affect fluid dynamics in the region of stenosis.

  • Micropolar behavior is enhanced in HNFs (blood–Au + TiO₂), as compared to conventional NFs, under the influence of micro-inertia density and unsteady parameters. This behavior is critical in modeling blood flow in arteries where complex dynamics, such as micro-rotations and fluid deformations, are present.

The current study provides valuable insights into the flow dynamics of magnetized micropolar HNFS in stenotic arteries. However, several areas remain open for future exploration to further enhance our understanding and broaden the application of HNFs in medical contexts. While the current study employs numerical simulations, future research could focus on experimental studies to validate the numerical predictions of HNF behavior under real-world conditions. These experiments could focus on simulating arterial stenosis in laboratory settings and comparing results with computational models. Including biological factors such as red blood cell behavior, plasma blood viscosity, and the effects of pulsatile nature of blood flow could enhance the realism of the simulations and provide a more comprehensive understanding of blood flow dynamics in diseased arteries. By addressing these research directions, future studies could significantly contribute to the development of more effective medical treatments using HNFs for improving the blood flow, heat transfer, and overall vascular health.

Acknowledgments

This project was supported by the Ongoing Research Funding program, (ORF-2025-411), King Saud University, Riyadh, Saudi Arabia.

  1. Funding information: This study was supported by the “Project financed by Lucian Blaga University of Sibiu through the research grant LBUS-IRG-2024.”

  2. Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.

  3. Conflict of interest: The authors state no conflict of interest.

  4. Data availability statement: The datasets generated and/or analyzed during the current study are available from the corresponding author on reasonable request.

References

[1] Xu H, Pop I. Mixed convection flow of a nanofluid over a stretching surface with uniform free streamin the presence of both nanoparticles and gyrotactic microorganisms. Int J Heat Mass Transf. 2014;75:610–23.10.1016/j.ijheatmasstransfer.2014.03.086Search in Google Scholar

[2] Aziz A, Khan WA, Pop I. Free convection boundary layer flow past a horizontal flat plate embedded in porous medium filled by nanofluid containing gyrotactic microorganisms. Int J Therm Sci. 2012;56:48–57.10.1016/j.ijthermalsci.2012.01.011Search in Google Scholar

[3] Agarwal RS, Bhargava R, Balaji AVS. Finite element solution of flow and heat transfer of a micropolar fluid over a stretching sheet. Int J Eng Sci. 1989;27(11):1421–8.10.1016/0020-7225(89)90065-7Search in Google Scholar

[4] Hassanien IA, Gorla RSR. Heat transfer to a micropolar fluid from a non-isothermal stretching sheet with suction and blowing. Acta Mech. 1990;84(1–4):191–9.Search in Google Scholar

[5] Rehman A, Khun MC, Khan D, Shah K, Abdeljawad T. Stability analysis of the shape factor effect of radiative on MHD couple stress hybrid nanofluid. South Afr J Chem Eng. 2023;46:394–403.10.1016/j.sajce.2023.09.004Search in Google Scholar

[6] Nadeem S, Rehman A, Vajravelu K, Lee J, Lee C. Axisymmetric stagnation flow of a micropolar nanofluid in a moving cylinder. Math Probl Eng. 2012;2012:1–18.10.1155/2012/378259Search in Google Scholar

[7] Balaram M, Sastri VUK. Micropolar free convection flow. Int J Heat Mass Transf. 1973;16(2):437–41.10.1016/0017-9310(73)90070-7Search in Google Scholar

[8] Lok YY, Amin N, Pop I. Steady two-dimensional asymmetric stagnation point flow of a micropolar fluid. ZAMM - J Appl Math Mech/Z Angew Math Mech. 2003;83(9):594–602.10.1002/zamm.200310050Search in Google Scholar

[9] Waini I, Ishak A, Pop I. Hybrid nanofluid flow and heat transfer past a vertical thin needle with prescribed surface heat flux. Int J Numer Methods Heat Fluid Flow. 2019;29(12):4875–94.10.1108/HFF-04-2019-0277Search in Google Scholar

[10] Ashwinkumar GP, Samrat SP, Sandeep N. Convective heat transfer in MHD hybrid nanofluid flow over two different geometries. Int Commun Heat Mass Transf. 2021;127:105563.10.1016/j.icheatmasstransfer.2021.105563Search in Google Scholar

[11] Samrat S, Ashwinkumar GP, Sandeep N. Simultaneous solutions for convective heat transfer in dusty-nano- and dusty-hybrid nanoliquids. Proc Inst Mech Eng E: J Process Mech Eng. 2021;236(2):473–9.10.1177/09544089211043605Search in Google Scholar

[12] Acharya N. Spectral quasi linearization simulation on the hydrothermal behavior of hybrid nanofluid spraying on an inclined spinning disk. Partial Differ Equ Appl Math. 2021;4:100094.10.1016/j.padiff.2021.100094Search in Google Scholar

[13] Sarwar L, Hussain A. Flow characteristics of Au-blood nanofluid in stenotic artery. Int Commun Heat Mass Transf. 2021;127:105486.10.1016/j.icheatmasstransfer.2021.105486Search in Google Scholar

[14] Garia R, Rawat SK, Kumar M, Yaseen M. Hybrid nanofluid flow over two different geometries with Cattaneo–Christov heat flux model and heat generation: A model with correlation coefficient and probable error. Chin J Phys. 2021;74:421–39.10.1016/j.cjph.2021.10.030Search in Google Scholar

[15] Eringen AC. Theory of micropolar fluids. J Math Mech. 1966;16(1):1–18.10.1512/iumj.1967.16.16001Search in Google Scholar

[16] Shah Z, Sulaiman M, Dawar A, Alshehri MH, Vrinceanu N. Darcy–Forchheimer MHD rotationally symmetric micropolar hybrid-nanofluid flow with melting heat transfer over a radially stretchable porous rotating disk. J Therm Anal Calorim. 2024;149(24):14625–41. 10.1007/s10973-024-12986-z.Search in Google Scholar

[17] Deebani W, Shah Z, Rooman M, Khan NU, Vrinceanu N, Shutaywi M. Computational modelling of micropolar bloodbased magnetised hybrid nanofluid flow over a porous curved surface in the presence of artificial bacteria. Front Chem. 2024;12:1397066. 10.3389/fchem.2024.139706.Search in Google Scholar

[18] Hassanien IA, Gorla RSR. Heat transfers to a micropolar fluid from a non-isothermal stretching sheet with suction and blowing. Acta Mech. 1990;84(1–4):191–9.10.1007/BF01176097Search in Google Scholar

[19] Subhani M, Nadeem S. Numerical analysis of micropolar hybrid nanofluid. Appl Nanosci. 2019;9(4):447–59.10.1007/s13204-018-0926-2Search in Google Scholar

[20] Hasegan A, Mihai I, Teodoru CA, Matacuta IB, Dura H, Todor SB, et al. Exploring the challenges of using minimal invasive surgery to treat stress urinary incontinence: insights from a retrospective case-control study. Diagnostics. 2024;14(3):323. 10.3390/diagnostics14030323.Search in Google Scholar PubMed PubMed Central

[21] Mihai I, Dura H, Teodoru CA, Todor SB, Ichim C, Grigore N, et al. Intraoperative ultrasound, bridging the gap between laparoscopy and surgical precision during 3D laparoscopic partial nephrectomies. Diagnostics. 2024;14:942. 10.3390/diagnostics14090942.Search in Google Scholar PubMed PubMed Central

[22] Mihai I, Boicean A, Teodoru CA, Grigore N, Iancu GM, Dura H, et al. Laparoscopic adrenalectomy: tailoring approaches for the optimal resection of adrenal tumors. Diagnostics. 2023;13(21):3351. 10.3390/diagnostics13213351.Search in Google Scholar PubMed PubMed Central

[23] Ghadikolaei SS, Yassari M, Sadeghi H, Hosseinzadeh K, Ganji DD. Investigation on thermophysical properties of Tio2–Cu/H2O hybrid nanofluid transport dependent on shape factor in MHD stagnation point flow. Powder Technol. 2017;322:428–38.10.1016/j.powtec.2017.09.006Search in Google Scholar

[24] Ullah I, Shafie S, Khan I. Effects of slip condition and Newtonian heating on MHD flow of Casson fluid over a nonlinearly stretching sheet saturated in a porous medium. J King Saud Univ - Sci. 2017;29(2):250–9.10.1016/j.jksus.2016.05.003Search in Google Scholar

[25] Gul A, Khan I, Shafie S, Khalid A, Khan A. Heat transfer in MHD mixed convection flow of a ferrofluid along a vertical channel. PLOS ONE. 2015;10(11):e0141213.10.1371/journal.pone.0141213Search in Google Scholar PubMed PubMed Central

[26] Saqib M, Khan I, Shafie S. Natural convection channel flow of CMC-based CNTs nanofluid. Eur Phys J Plus. 2018;133(12):549.10.1140/epjp/i2018-12340-3Search in Google Scholar

[27] Ma Y, Mohebbi R, Rashidi MM, Yang Z, Sheremet MA. Numerical study of MHD nanofluid natural convection in a baffled U-shaped enclosure. Int J Heat Mass Transf. 2019;130:123–34.10.1016/j.ijheatmasstransfer.2018.10.072Search in Google Scholar

[28] Khan LA, Raza M, Mir NA, Ellahi R. Effects of different shapes of nanoparticles on peristaltic flow of MHD nanofluids filled in an asymmetric channel: A novel mode for heat transfer enhancement. J Therm Anal Calorim. 2020;140(3):879–90.10.1007/s10973-019-08348-9Search in Google Scholar

[29] Ghalambaz M, Mehryan SAM, Izadpanahi E, Chamkha AJ, Wen D. MHD natural convection of Cu–Al2O3 water hybrid nanofluids in a cavity equally divided into two parts by a vertical flexible partition membrane. J Therm Anal Calorim. 2019;138(2):1723–43.10.1007/s10973-019-08258-wSearch in Google Scholar

[30] Zeb S, Gul S, Shah K, Santina D, Mlaiki N. Melting heat transfer and thermal radiation effects MHD tangent hyperbolic nanofluid flow with chemical reaction and activation energy. Therm Sci. 2023;27(Spec. issue 1):253–61.10.2298/TSCI23S1253ZSearch in Google Scholar

[31] Das S, Jana RN, Makinde OD. MHD flow of Cu-Al2O3/water hybrid nanofluid in porous channel: Analysis of entropy generation. Defect Diffus Forum. 2017;377:42–61.10.4028/www.scientific.net/DDF.377.42Search in Google Scholar

[32] Anantha Kumar K, Sugunamma V, Sandeep N. Influence of viscous dissipation on MHD flow of micropolar fluid over a slendering stretching surface with modified heat flux model. J Therm Anal Calorim. 2020;139(6):3661–74.10.1007/s10973-019-08694-8Search in Google Scholar

[33] Khan A, Ullah S, Shah K, Alqudah MA, Abdeljawad T, Ghani F. Theory and semi-analytical study of micropolar fluid dynamics through a porous channel. CMES-Comput Model Eng Sci. 2023;136(2):1473–86.10.32604/cmes.2022.023019Search in Google Scholar

[34] Boicean A, Bratu D, Bacila C, Tanasescu C, Fleaca RS, Mohor CI, et al. Therapeutic perspectives for microbiota transplantation in digestive diseases and neoplasia – A literature review. Pathogens. 2023;12(6):766.10.3390/pathogens12060766Search in Google Scholar PubMed PubMed Central

[35] Pirvut V, Grigore N, Mihai I, Priporeanu AT, Racheru M, Cretu D, et al. Comparative study between polydioxanone unidirectional barbed suture and absorbable polyglactin running suture in partial nephrectomy. Rev Mater Plast. 2018;54:82–4.10.37358/MP.18.1.4968Search in Google Scholar

[36] Dawar A, Shah Z, Kumam P, Alrabaiah H, Khan W, Islam S, et al. Chemically reactive MHD micropolar nanofluid flow with velocity slips and variable heat source/sink. Sci Rep. 2020;10(1):20926.10.1038/s41598-020-77615-9Search in Google Scholar PubMed PubMed Central

[37] Sakiadis BC. Boundary-layer behavior on continuous solid surfaces: I. Boundary-layer equations for two-dimensional and axisymmetric flow. AIChE J. 1961;7(1):26–8.10.1002/aic.690070108Search in Google Scholar

[38] Tsou FK, Sparrow EM, Goldstein RJ. Flow and heat transfer in the boundary layer on a continuous moving surface. Int J Heat Mass Transf. 1967;10(2):219–35.10.1016/0017-9310(67)90100-7Search in Google Scholar

[39] Crane LJ. Flow past a stretching plate. ZAMP Z Angew Math Phys. 1970;21(4):645–7.10.1007/BF01587695Search in Google Scholar

[40] Gupta PS, Gupta AS. Heat and mass transfer on a stretching sheet with suction or blowing. Can J Chem Eng. 1977;55(6):744–6.10.1002/cjce.5450550619Search in Google Scholar

[41] Grubka LJ, Bobba KM. Heat transfer characteristics of a continuous, stretching surface with variable temperature. J Heat Transf. 1985;107(1):248–50.10.1115/1.3247387Search in Google Scholar

[42] Das S, Pal TK, Jana RN, Giri B. Significance of Hall currents on hybrid nano-blood flow through an inclined artery having mild stenosis: homotopy perturbation approach. Microvasc Res. 2021;137:104192.10.1016/j.mvr.2021.104192Search in Google Scholar PubMed

[43] Karmakar P, Ali A, Das S. Circulation of blood loaded with trihybrid nanoparticles via electro-osmotic pumping in an eccentric endoscopic arterial canal. Int Commun Heat Mass Transf. 2023;141:106593.10.1016/j.icheatmasstransfer.2022.106593Search in Google Scholar

[44] Ali A, Das S. Applications of neuro-computing and fractional calculus to blood streaming conveying modified trihybrid nanoparticles with interfacial nanolayer aspect inside a diseased ciliated artery under electroosmotic and Lorentz forces. Int Commun Heat Mass Transf. 2024;152:107313.10.1016/j.icheatmasstransfer.2024.107313Search in Google Scholar

[45] Paul P, Karmakar P, Das S, Das S. Demonstration of angioplasty using a balloon catheter in tetra-hybrid nano-bloodstream within an electrified stenotic arterial cavity under a magnetic field: Artificial neural network analysis. Biomed Signal Process Control. 2024;96:106549.10.1016/j.bspc.2024.106549Search in Google Scholar

[46] Haq F, Shah K, Abdeljawad T. Analysis of periodic heat transfer through extended surfaces. Therm Sci. 2023;27(4 Part A):2623–37.10.2298/TSCI220502184HSearch in Google Scholar

[47] Ahmad L, Khan M. Importance of activation energy in development of chemical covalent bonding in flow of Sisko magneto-nanofluids over a porous moving curved surface. Int J Hydrogen Energy. 2019;44(21):10197–206.10.1016/j.ijhydene.2019.02.162Search in Google Scholar

[48] Sheikholeslami M, Arabkoohsar A, Babazadeh H. Modeling of nanomaterial treatment through a porous space including magnetic forces. J Therm Anal Calorim. 2020;140(2):825–34.10.1007/s10973-019-08878-2Search in Google Scholar
Received: 2024-11-17
Revised: 2025-03-02
Accepted: 2025-03-12
Published Online: 2025-08-28

© 2025 the author(s), published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Research Articles
  2. Single-step fabrication of Ag2S/poly-2-mercaptoaniline nanoribbon photocathodes for green hydrogen generation from artificial and natural red-sea water
  3. Abundant new interaction solutions and nonlinear dynamics for the (3+1)-dimensional Hirota–Satsuma–Ito-like equation
  4. A novel gold and SiO2 material based planar 5-element high HPBW end-fire antenna array for 300 GHz applications
  5. Explicit exact solutions and bifurcation analysis for the mZK equation with truncated M-fractional derivatives utilizing two reliable methods
  6. Optical and laser damage resistance: Role of periodic cylindrical surfaces
  7. Numerical study of flow and heat transfer in the air-side metal foam partially filled channels of panel-type radiator under forced convection
  8. Water-based hybrid nanofluid flow containing CNT nanoparticles over an extending surface with velocity slips, thermal convective, and zero-mass flux conditions
  9. Dynamical wave structures for some diffusion--reaction equations with quadratic and quartic nonlinearities
  10. Solving an isotropic grey matter tumour model via a heat transfer equation
  11. Study on the penetration protection of a fiber-reinforced composite structure with CNTs/GFP clip STF/3DKevlar
  12. Influence of Hall current and acoustic pressure on nanostructured DPL thermoelastic plates under ramp heating in a double-temperature model
  13. Applications of the Belousov–Zhabotinsky reaction–diffusion system: Analytical and numerical approaches
  14. AC electroosmotic flow of Maxwell fluid in a pH-regulated parallel-plate silica nanochannel
  15. Interpreting optical effects with relativistic transformations adopting one-way synchronization to conserve simultaneity and space–time continuity
  16. Modeling and analysis of quantum communication channel in airborne platforms with boundary layer effects
  17. Theoretical and numerical investigation of a memristor system with a piecewise memductance under fractal–fractional derivatives
  18. Tuning the structure and electro-optical properties of α-Cr2O3 films by heat treatment/La doping for optoelectronic applications
  19. High-speed multi-spectral explosion temperature measurement using golden-section accelerated Pearson correlation algorithm
  20. Dynamic behavior and modulation instability of the generalized coupled fractional nonlinear Helmholtz equation with cubic–quintic term
  21. Study on the duration of laser-induced air plasma flash near thin film surface
  22. Exploring the dynamics of fractional-order nonlinear dispersive wave system through homotopy technique
  23. The mechanism of carbon monoxide fluorescence inside a femtosecond laser-induced plasma
  24. Numerical solution of a nonconstant coefficient advection diffusion equation in an irregular domain and analyses of numerical dispersion and dissipation
  25. Numerical examination of the chemically reactive MHD flow of hybrid nanofluids over a two-dimensional stretching surface with the Cattaneo–Christov model and slip conditions
  26. Impacts of sinusoidal heat flux and embraced heated rectangular cavity on natural convection within a square enclosure partially filled with porous medium and Casson-hybrid nanofluid
  27. Stability analysis of unsteady ternary nanofluid flow past a stretching/shrinking wedge
  28. Solitonic wave solutions of a Hamiltonian nonlinear atom chain model through the Hirota bilinear transformation method
  29. Bilinear form and soltion solutions for (3+1)-dimensional negative-order KdV-CBS equation
  30. Solitary chirp pulses and soliton control for variable coefficients cubic–quintic nonlinear Schrödinger equation in nonuniform management system
  31. Influence of decaying heat source and temperature-dependent thermal conductivity on photo-hydro-elasto semiconductor media
  32. Dissipative disorder optimization in the radiative thin film flow of partially ionized non-Newtonian hybrid nanofluid with second-order slip condition
  33. Bifurcation, chaotic behavior, and traveling wave solutions for the fractional (4+1)-dimensional Davey–Stewartson–Kadomtsev–Petviashvili model
  34. New investigation on soliton solutions of two nonlinear PDEs in mathematical physics with a dynamical property: Bifurcation analysis
  35. Mathematical analysis of nanoparticle type and volume fraction on heat transfer efficiency of nanofluids
  36. Creation of single-wing Lorenz-like attractors via a ten-ninths-degree term
  37. Optical soliton solutions, bifurcation analysis, chaotic behaviors of nonlinear Schrödinger equation and modulation instability in optical fiber
  38. Chaotic dynamics and some solutions for the (n + 1)-dimensional modified Zakharov–Kuznetsov equation in plasma physics
  39. Fractal formation and chaotic soliton phenomena in nonlinear conformable Heisenberg ferromagnetic spin chain equation
  40. Single-step fabrication of Mn(iv) oxide-Mn(ii) sulfide/poly-2-mercaptoaniline porous network nanocomposite for pseudo-supercapacitors and charge storage
  41. Novel constructed dynamical analytical solutions and conserved quantities of the new (2+1)-dimensional KdV model describing acoustic wave propagation
  42. Tavis–Cummings model in the presence of a deformed field and time-dependent coupling
  43. Spinning dynamics of stress-dependent viscosity of generalized Cross-nonlinear materials affected by gravitationally swirling disk
  44. Design and prediction of high optical density photovoltaic polymers using machine learning-DFT studies
  45. Robust control and preservation of quantum steering, nonlocality, and coherence in open atomic systems
  46. Coating thickness and process efficiency of reverse roll coating using a magnetized hybrid nanomaterial flow
  47. Dynamic analysis, circuit realization, and its synchronization of a new chaotic hyperjerk system
  48. Decoherence of steerability and coherence dynamics induced by nonlinear qubit–cavity interactions
  49. Finite element analysis of turbulent thermal enhancement in grooved channels with flat- and plus-shaped fins
  50. Modulational instability and associated ion-acoustic modulated envelope solitons in a quantum plasma having ion beams
  51. Statistical inference of constant-stress partially accelerated life tests under type II generalized hybrid censored data from Burr III distribution
  52. On solutions of the Dirac equation for 1D hydrogenic atoms or ions
  53. Entropy optimization for chemically reactive magnetized unsteady thin film hybrid nanofluid flow on inclined surface subject to nonlinear mixed convection and variable temperature
  54. Stability analysis, circuit simulation, and color image encryption of a novel four-dimensional hyperchaotic model with hidden and self-excited attractors
  55. A high-accuracy exponential time integration scheme for the Darcy–Forchheimer Williamson fluid flow with temperature-dependent conductivity
  56. Novel analysis of fractional regularized long-wave equation in plasma dynamics
  57. Development of a photoelectrode based on a bismuth(iii) oxyiodide/intercalated iodide-poly(1H-pyrrole) rough spherical nanocomposite for green hydrogen generation
  58. Investigation of solar radiation effects on the energy performance of the (Al2O3–CuO–Cu)/H2O ternary nanofluidic system through a convectively heated cylinder
  59. Quantum resources for a system of two atoms interacting with a deformed field in the presence of intensity-dependent coupling
  60. Studying bifurcations and chaotic dynamics in the generalized hyperelastic-rod wave equation through Hamiltonian mechanics
  61. A new numerical technique for the solution of time-fractional nonlinear Klein–Gordon equation involving Atangana–Baleanu derivative using cubic B-spline functions
  62. Interaction solutions of high-order breathers and lumps for a (3+1)-dimensional conformable fractional potential-YTSF-like model
  63. Hydraulic fracturing radioactive source tracing technology based on hydraulic fracturing tracing mechanics model
  64. Numerical solution and stability analysis of non-Newtonian hybrid nanofluid flow subject to exponential heat source/sink over a Riga sheet
  65. Numerical investigation of mixed convection and viscous dissipation in couple stress nanofluid flow: A merged Adomian decomposition method and Mohand transform
  66. Effectual quintic B-spline functions for solving the time fractional coupled Boussinesq–Burgers equation arising in shallow water waves
  67. Analysis of MHD hybrid nanofluid flow over cone and wedge with exponential and thermal heat source and activation energy
  68. Solitons and travelling waves structure for M-fractional Kairat-II equation using three explicit methods
  69. Impact of nanoparticle shapes on the heat transfer properties of Cu and CuO nanofluids flowing over a stretching surface with slip effects: A computational study
  70. Computational simulation of heat transfer and nanofluid flow for two-sided lid-driven square cavity under the influence of magnetic field
  71. Irreversibility analysis of a bioconvective two-phase nanofluid in a Maxwell (non-Newtonian) flow induced by a rotating disk with thermal radiation
  72. Hydrodynamic and sensitivity analysis of a polymeric calendering process for non-Newtonian fluids with temperature-dependent viscosity
  73. Exploring the peakon solitons molecules and solitary wave structure to the nonlinear damped Kortewege–de Vries equation through efficient technique
  74. Modeling and heat transfer analysis of magnetized hybrid micropolar blood-based nanofluid flow in Darcy–Forchheimer porous stenosis narrow arteries
  75. Activation energy and cross-diffusion effects on 3D rotating nanofluid flow in a Darcy–Forchheimer porous medium with radiation and convective heating
  76. Insights into chemical reactions occurring in generalized nanomaterials due to spinning surface with melting constraints
  77. Review Article
  78. Examination of the gamma radiation shielding properties of different clay and sand materials in the Adrar region
  79. Special Issue on Fundamental Physics from Atoms to Cosmos - Part II
  80. Possible explanation for the neutron lifetime puzzle
  81. Special Issue on Nanomaterial utilization and structural optimization - Part III
  82. Numerical investigation on fluid-thermal-electric performance of a thermoelectric-integrated helically coiled tube heat exchanger for coal mine air cooling
  83. Special Issue on Nonlinear Dynamics and Chaos in Physical Systems
  84. Analysis of the fractional relativistic isothermal gas sphere with application to neutron stars
  85. Abundant wave symmetries in the (3+1)-dimensional Chafee–Infante equation through the Hirota bilinear transformation technique
  86. Successive midpoint method for fractional differential equations with nonlocal kernels: Error analysis, stability, and applications
https://doi.org/10.1515/phys-2025-0139
Keywords for this article
computational modeling; hybrid nanofluid; heat source; Darcy–Forchheimer; curved surface; stenotic artery; vicious and Joule dissipation; blood; gold nanoparticles
Creative Commons
BY 4.0

Articles in the same Issue

  1. Research Articles
  2. Single-step fabrication of Ag2S/poly-2-mercaptoaniline nanoribbon photocathodes for green hydrogen generation from artificial and natural red-sea water
  3. Abundant new interaction solutions and nonlinear dynamics for the (3+1)-dimensional Hirota–Satsuma–Ito-like equation
  4. A novel gold and SiO2 material based planar 5-element high HPBW end-fire antenna array for 300 GHz applications
  5. Explicit exact solutions and bifurcation analysis for the mZK equation with truncated M-fractional derivatives utilizing two reliable methods
  6. Optical and laser damage resistance: Role of periodic cylindrical surfaces
  7. Numerical study of flow and heat transfer in the air-side metal foam partially filled channels of panel-type radiator under forced convection
  8. Water-based hybrid nanofluid flow containing CNT nanoparticles over an extending surface with velocity slips, thermal convective, and zero-mass flux conditions
  9. Dynamical wave structures for some diffusion--reaction equations with quadratic and quartic nonlinearities
  10. Solving an isotropic grey matter tumour model via a heat transfer equation
  11. Study on the penetration protection of a fiber-reinforced composite structure with CNTs/GFP clip STF/3DKevlar
  12. Influence of Hall current and acoustic pressure on nanostructured DPL thermoelastic plates under ramp heating in a double-temperature model
  13. Applications of the Belousov–Zhabotinsky reaction–diffusion system: Analytical and numerical approaches
  14. AC electroosmotic flow of Maxwell fluid in a pH-regulated parallel-plate silica nanochannel
  15. Interpreting optical effects with relativistic transformations adopting one-way synchronization to conserve simultaneity and space–time continuity
  16. Modeling and analysis of quantum communication channel in airborne platforms with boundary layer effects
  17. Theoretical and numerical investigation of a memristor system with a piecewise memductance under fractal–fractional derivatives
  18. Tuning the structure and electro-optical properties of α-Cr2O3 films by heat treatment/La doping for optoelectronic applications
  19. High-speed multi-spectral explosion temperature measurement using golden-section accelerated Pearson correlation algorithm
  20. Dynamic behavior and modulation instability of the generalized coupled fractional nonlinear Helmholtz equation with cubic–quintic term
  21. Study on the duration of laser-induced air plasma flash near thin film surface
  22. Exploring the dynamics of fractional-order nonlinear dispersive wave system through homotopy technique
  23. The mechanism of carbon monoxide fluorescence inside a femtosecond laser-induced plasma
  24. Numerical solution of a nonconstant coefficient advection diffusion equation in an irregular domain and analyses of numerical dispersion and dissipation
  25. Numerical examination of the chemically reactive MHD flow of hybrid nanofluids over a two-dimensional stretching surface with the Cattaneo–Christov model and slip conditions
  26. Impacts of sinusoidal heat flux and embraced heated rectangular cavity on natural convection within a square enclosure partially filled with porous medium and Casson-hybrid nanofluid
  27. Stability analysis of unsteady ternary nanofluid flow past a stretching/shrinking wedge
  28. Solitonic wave solutions of a Hamiltonian nonlinear atom chain model through the Hirota bilinear transformation method
  29. Bilinear form and soltion solutions for (3+1)-dimensional negative-order KdV-CBS equation
  30. Solitary chirp pulses and soliton control for variable coefficients cubic–quintic nonlinear Schrödinger equation in nonuniform management system
  31. Influence of decaying heat source and temperature-dependent thermal conductivity on photo-hydro-elasto semiconductor media
  32. Dissipative disorder optimization in the radiative thin film flow of partially ionized non-Newtonian hybrid nanofluid with second-order slip condition
  33. Bifurcation, chaotic behavior, and traveling wave solutions for the fractional (4+1)-dimensional Davey–Stewartson–Kadomtsev–Petviashvili model
  34. New investigation on soliton solutions of two nonlinear PDEs in mathematical physics with a dynamical property: Bifurcation analysis
  35. Mathematical analysis of nanoparticle type and volume fraction on heat transfer efficiency of nanofluids
  36. Creation of single-wing Lorenz-like attractors via a ten-ninths-degree term
  37. Optical soliton solutions, bifurcation analysis, chaotic behaviors of nonlinear Schrödinger equation and modulation instability in optical fiber
  38. Chaotic dynamics and some solutions for the (n + 1)-dimensional modified Zakharov–Kuznetsov equation in plasma physics
  39. Fractal formation and chaotic soliton phenomena in nonlinear conformable Heisenberg ferromagnetic spin chain equation
  40. Single-step fabrication of Mn(iv) oxide-Mn(ii) sulfide/poly-2-mercaptoaniline porous network nanocomposite for pseudo-supercapacitors and charge storage
  41. Novel constructed dynamical analytical solutions and conserved quantities of the new (2+1)-dimensional KdV model describing acoustic wave propagation
  42. Tavis–Cummings model in the presence of a deformed field and time-dependent coupling
  43. Spinning dynamics of stress-dependent viscosity of generalized Cross-nonlinear materials affected by gravitationally swirling disk
  44. Design and prediction of high optical density photovoltaic polymers using machine learning-DFT studies
  45. Robust control and preservation of quantum steering, nonlocality, and coherence in open atomic systems
  46. Coating thickness and process efficiency of reverse roll coating using a magnetized hybrid nanomaterial flow
  47. Dynamic analysis, circuit realization, and its synchronization of a new chaotic hyperjerk system
  48. Decoherence of steerability and coherence dynamics induced by nonlinear qubit–cavity interactions
  49. Finite element analysis of turbulent thermal enhancement in grooved channels with flat- and plus-shaped fins
  50. Modulational instability and associated ion-acoustic modulated envelope solitons in a quantum plasma having ion beams
  51. Statistical inference of constant-stress partially accelerated life tests under type II generalized hybrid censored data from Burr III distribution
  52. On solutions of the Dirac equation for 1D hydrogenic atoms or ions
  53. Entropy optimization for chemically reactive magnetized unsteady thin film hybrid nanofluid flow on inclined surface subject to nonlinear mixed convection and variable temperature
  54. Stability analysis, circuit simulation, and color image encryption of a novel four-dimensional hyperchaotic model with hidden and self-excited attractors
  55. A high-accuracy exponential time integration scheme for the Darcy–Forchheimer Williamson fluid flow with temperature-dependent conductivity
  56. Novel analysis of fractional regularized long-wave equation in plasma dynamics
  57. Development of a photoelectrode based on a bismuth(iii) oxyiodide/intercalated iodide-poly(1H-pyrrole) rough spherical nanocomposite for green hydrogen generation
  58. Investigation of solar radiation effects on the energy performance of the (Al2O3–CuO–Cu)/H2O ternary nanofluidic system through a convectively heated cylinder
  59. Quantum resources for a system of two atoms interacting with a deformed field in the presence of intensity-dependent coupling
  60. Studying bifurcations and chaotic dynamics in the generalized hyperelastic-rod wave equation through Hamiltonian mechanics
  61. A new numerical technique for the solution of time-fractional nonlinear Klein–Gordon equation involving Atangana–Baleanu derivative using cubic B-spline functions
  62. Interaction solutions of high-order breathers and lumps for a (3+1)-dimensional conformable fractional potential-YTSF-like model
  63. Hydraulic fracturing radioactive source tracing technology based on hydraulic fracturing tracing mechanics model
  64. Numerical solution and stability analysis of non-Newtonian hybrid nanofluid flow subject to exponential heat source/sink over a Riga sheet
  65. Numerical investigation of mixed convection and viscous dissipation in couple stress nanofluid flow: A merged Adomian decomposition method and Mohand transform
  66. Effectual quintic B-spline functions for solving the time fractional coupled Boussinesq–Burgers equation arising in shallow water waves
  67. Analysis of MHD hybrid nanofluid flow over cone and wedge with exponential and thermal heat source and activation energy
  68. Solitons and travelling waves structure for M-fractional Kairat-II equation using three explicit methods
  69. Impact of nanoparticle shapes on the heat transfer properties of Cu and CuO nanofluids flowing over a stretching surface with slip effects: A computational study
  70. Computational simulation of heat transfer and nanofluid flow for two-sided lid-driven square cavity under the influence of magnetic field
  71. Irreversibility analysis of a bioconvective two-phase nanofluid in a Maxwell (non-Newtonian) flow induced by a rotating disk with thermal radiation
  72. Hydrodynamic and sensitivity analysis of a polymeric calendering process for non-Newtonian fluids with temperature-dependent viscosity
  73. Exploring the peakon solitons molecules and solitary wave structure to the nonlinear damped Kortewege–de Vries equation through efficient technique
  74. Modeling and heat transfer analysis of magnetized hybrid micropolar blood-based nanofluid flow in Darcy–Forchheimer porous stenosis narrow arteries
  75. Activation energy and cross-diffusion effects on 3D rotating nanofluid flow in a Darcy–Forchheimer porous medium with radiation and convective heating
  76. Insights into chemical reactions occurring in generalized nanomaterials due to spinning surface with melting constraints
  77. Review Article
  78. Examination of the gamma radiation shielding properties of different clay and sand materials in the Adrar region
  79. Special Issue on Fundamental Physics from Atoms to Cosmos - Part II
  80. Possible explanation for the neutron lifetime puzzle
  81. Special Issue on Nanomaterial utilization and structural optimization - Part III
  82. Numerical investigation on fluid-thermal-electric performance of a thermoelectric-integrated helically coiled tube heat exchanger for coal mine air cooling
  83. Special Issue on Nonlinear Dynamics and Chaos in Physical Systems
  84. Analysis of the fractional relativistic isothermal gas sphere with application to neutron stars
  85. Abundant wave symmetries in the (3+1)-dimensional Chafee–Infante equation through the Hirota bilinear transformation technique
  86. Successive midpoint method for fractional differential equations with nonlocal kernels: Error analysis, stability, and applications
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 13.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/phys-2025-0139/html
Scroll to top button