Stability analysis, circuit simulation, and color image encryption of a novel four-dimensional hyperchaotic model with hidden and self-excited attractors

Tarek M. Abed-Elhameed; Mansour E. Ahmed

doi:10.1515/phys-2025-0179

Article Open Access

Stability analysis, circuit simulation, and color image encryption of a novel four-dimensional hyperchaotic model with hidden and self-excited attractors

Tarek M. Abed-Elhameed and Mansour E. Ahmed

Published/Copyright: July 22, 2025

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

From the journal Open Physics Volume 23 Issue 1

Abstract

A new four-dimensional hyperchaotic model (4-DHM) with eight parameters is examined in this work. Depending on how two of these parameters are chosen, this model may contain equilibrium points or not. Therefore, we may choose a value that will make the corresponding attractor either hidden or self-excited. In this model, we consider the two scenarios and analyze the dynamics of the two instances. The numerical simulation of the novel 4-DHM is shown together with bifurcation diagrams, the Lyapunov exponent, and an examination of equilibrium and stability. The novel 4-DHM may be used in many science and engineering applications, such as electronic circuits and image encryption. A physical implementation is added to the electronic circuit’s MATLAB Simulink to confirm that the new 4-DHM can be built. The results of the numerical analysis and electronic circuit simulation of our model were in a good agreement. The color image’s encryption, decryption, histogram analysis, information entropy, correlation coefficient, number of pixels change rate, and unified average changing intensity are examined using the proposed model.

Keywords: chaotic and hyperchaotic models; hidden attractors; Lyapunov exponents; nonlinear electronic circuit; color image encryption

List of Abbreviations

BDs: bifurcation diagrams
4-DHM: four-dimensional hyperchaotic model
LEs: lyapunov exponents
NPCR: number of pixel change rate
RGB: red, green, blue (color model)
UACI: unified average changing intensity

1 Introduction

Since Lorenz [1] discovered the first 3D autonomous chaotic system, chaos has adapted and grown significantly. Chaotic systems are important to dynamical systems due to their fascinating and complex dynamical properties. Some sciences, including biology, medicine, geology, image encoding, secure communication, and physics, may benefit from the study of chaotic systems [2–10]. Classical chaotic systems have already been identified in a number of instances over the past few decades [11–14]. Recently, many scientists have shown an increasing interest in studying chaotic and hyperchaotic dynamical systems [15–20]. For applications based on chaotic systems, hyperchaotic systems contribute to a crucial component [21–27].

Shilnikov’s criteria [28] state that there is a connection between chaotic attractors and the model equilibrium. In dissipative dynamical models, the presence of at least one unstable equilibrium point is a prerequisite for chaos. However, in order to confirm chaos in light of the finding of hidden attractors, the traditional Shilnikov criteria must be used. Attractors can be divided into two categories from a computational perspective: self-excited attractors and hidden attractors [29]. If any tiny neighborhoods of a stationary state are intersected by the basin of attraction of an attractor, it is referred to as a “self-excited attractor.” If not, it is called a hidden attraction. Hidden attractors are crucial in engineering applications because they enable unexpected and sometimes dangerous responses to perturbations in a structure, such as a bridge or an airplane wing [29–32].

Since the creation of Chua’s circuit [33], the study of chaotic circuits has attracted a lot of interest. Numerous chaotic (hyperchaotic)-producing nonlinear electronic circuits have been developed. A chaotic circuit is essentially a kind of chaotic system, and scholars usually use the electronic circuits to yield chaotic signals and demonstrate the physical existence of chaotic systems [34]. Some well-known examples of chaotic circuits are Chua’s circuit and the Lorenz system [35]. A hyperchaotic circuit is a chaotic circuit that has more than one positive Lyapunov exponent (LE), which means that it has more than one direction of instability and higher complexity [35]. Hyperchaos can be generated by adding some feedback controllers or nonlinear elements to the original chaotic circuits [35,36]. On the other hand, image encryption utilizing chaotic (or hyperchaotic) systems has garnered significant attention from researchers in recent years [37–39]. Masood et al. [37] introduced a novel approach for color image encryption based on DNA computing. Biban et al. explored image encryption employing an 8D hyperchaotic system combined with the Fibonacci Q-matrix [38]. Yan et al. introduced an innovative color image encryption technique utilizing a new three-dimensional chaotic mapping and DNA coding. As a result, applying chaotic (hyperchaotic) models to engineering practice through circuit implementation and image encryption has grown to be a crucial way for transferring chaotic (hyperchaotic) models from theory to practice. The circuit application and image encryption of chaotic (hyperchaotic) models have made significant progress up to this point.

Hu et al. [40] presented and studied a memristor-based VB2 chaotic model as

(1.1) u 1 ˙ = a u 2 + W ( u 2 ) u 3 , u 2 ˙ = b u 3 , u 3 ˙ = − c u 1 + d u 2 2 − e u 3 ,

where u i ; i = 1 , 2, 3 are the state variables, W ( u 2 ) = 0.08 + 0.2 u 2 2 , a , b , c , d , and e are constant parameters, and dots represent the derivatives with respect to time. Model (1.1) is chaotic with the parameter values e = 1 , d = 2.5 , c = 12 , b = 2 , and a = 0.34 and the initial values of u 10 = 2 , u 20 = 0 , and u 30 = 1 .

In this work, a new continuous-time, four-dimensional autonomous system is constructed, and its proposed scheme is obtained through the use of model (1.1). A new four-dimensional hyperchaotic model (4-DHM) based on model (1.1) is defined by

(1.2) u 1 ˙ = a u 2 + ( 0.08 + 0.2 u 2 2 ) u 3 , u 2 ˙ = b u 3 + h u 4 2 + f , u 3 ˙ = − c u 1 + d u 2 2 − e u 3 , u 4 ˙ = k u 3 ,

where u = ( u 1 , u 2 , u 3 , u 4 ) T are the state variables, a , b , c , d , e , and k are the positive constant parameters, and h and f are the constant parameters.

Our goal in this work is to introduce and investigate a new 4-DHM with self-excited and hidden attractors. The dynamics of the new 4-DHM with equilibrium or no equilibrium points are analyzed. Then, the LE, bifurcation diagram (BD), and phase portrait are used to examine the proposed hyperchaotic model. An electronic circuit for the new 4-DHM is being designed. The encryption, decryption, histogram analysis, information entropy, correlation coefficient, number of pixel change rate (NPCR), and Unified average changing intensity (UACI) of a color image are investigated based on the 4-DHM (1.2).

The rest of this work is arranged as follows: Section 2 provides a thorough examination of some basic dynamical properties of the 4-DHM (1.2). The 4-DHM (1.2) electronic circuit is found in Section 3. Comparing numerical and simulation findings, a good degree of agreement is obtained. Section 4 provides an analysis of encryption, decryption, histograms, information entropy, correlation coefficients, NPCR, and UACI for a color image using the 4-DHM (1.2). The conclusion of this research study is located in Section 5.

2 Basic dynamical properties of model (1.2)

In this section, we will study and discuss a few basic properties of the new 4-DHM model (1.2). Model (1.2) has eight parameters and nine terms, three of which are nonlinear. This model may or may not have equilibrium points, depending on how the parameters h and f are selected.

2.1 Equilibrium points

The equilibrium points of model (1.2) occur when u 1 ˙ = 0 , u 2 ˙ = 0 , u 3 ˙ = 0 , and u 4 ˙ = 0 .

(2.1) a u 2 + W ( u 2 ) u 3 = 0 , b u 3 + h u 4 2 + f = 0 , − c u 1 + d u 2 2 − e u 3 = 0 , k u 3 = 0 .

Clearly, one may derive u 1 = u 2 = u 3 = 0 from the first, third, and fourth equations in Eq. (2.1). It is simple to deduce that u 4 = ± − f h from Eq. (2.1) second equation, which means that there are no real solutions in (1.2) if h and f are both positive or both negative. But if h and f are chosen and one of them is positive and the other is negative, then model (1.2) has two equilibrium points E 1,2 = ( 0 , 0 , 0 , u 4 * ) and u 4 * = ± − f h . As a result, we confirm the potential of two different attractors for a fixed set of parameters in model (1.2), namely, the hidden attractors if h and f are both nonzero with the same signs and the self-excited attractors if h and f have opposite signs. While hidden attractors are associated with models with stable equilibrium points or no equilibrium points, self-excited attractors are related to models with unstable equilibrium points.

Remark 2.1

It is observed that one can attain hidden attractors or self-excited attractors for our model (1.2) by selecting suitable values for the model’s parameters h and f .

Remark 2.2

Model (1.1) is a special case of model (1.2) for the choice h = f = k = 0 and u 4 = c , c ∈ R .

2.2 Symmetry and dissipation

The new 4-DHM model (1.2) does not have symmetry since it changes independently of the coordinate transformation. Model (1.2) is dissipative under the condition e > 0 since

(2.2) ∇ ⋅ V = ∂ u 1 ˙ ∂ u 1 + ∂ u 2 ˙ ∂ u 2 + ∂ u 3 ˙ ∂ u 3 + ∂ u 4 ˙ ∂ u 4 = − e .

When ∇ ⋅ V < 0 , the model is dissipative, and the volume of the phase space gradually contracts to zero at an exponential rate because the model is dissipative.

2.3 Jacobian matrix and stability of equilibrium points

It is possible to determine the linear stability of the equilibrium points by computing the Jacobian matrix J ( E 1,2 ) as

(2.3) J ( E 1,2 ) = 0 a 0.08 0 0 0 b 2 h u 4 * − c 0 − e 0 0 0 k 0 .

The characteristic equation of (2.3) can be written as:

(2.4) f ( λ ) = λ 4 + e λ 3 + 0.08 c λ 2 + a b c λ + 2 a c h k u 4 * .

It is evident from the Routh–Hurwitz stability criterion that E 1 = ( 0 , 0 , 0 , − f h ) is stable if h > 0 and f < 0 , and E 2 = ( 0 , 0 , 0 , − − f h ) is stable if h < 0 and f > 0 .

2.4 Dynamics of model (1.2) with no equilibrium points

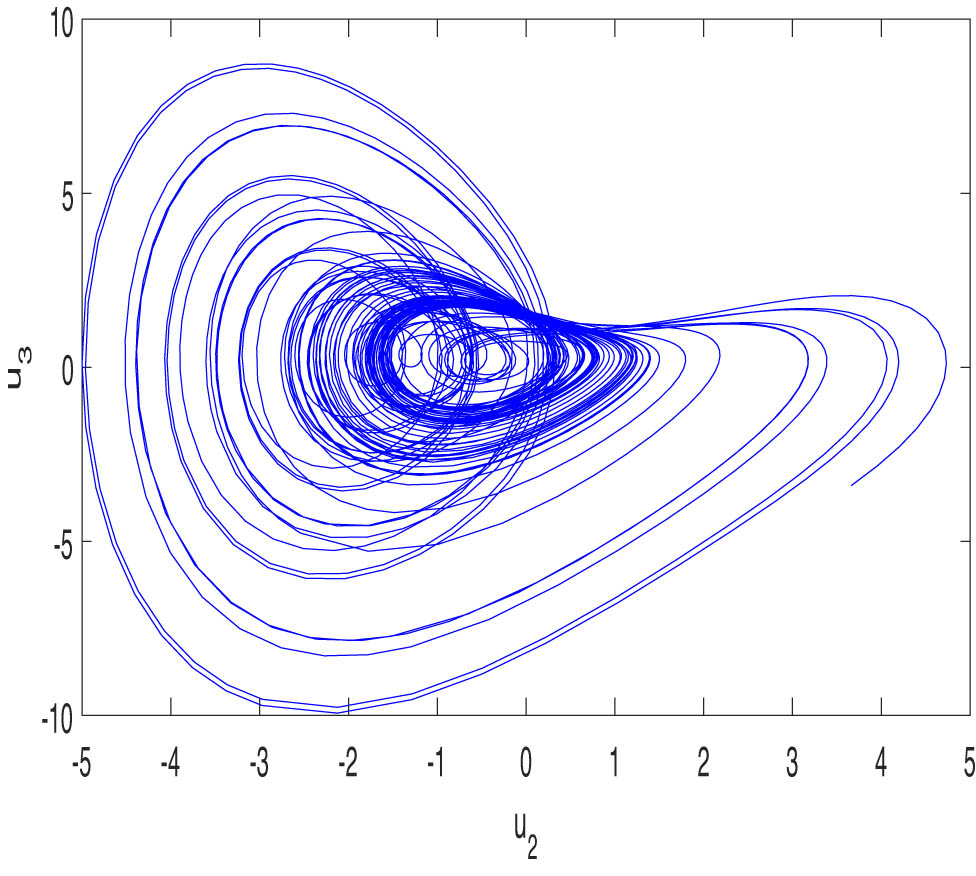
For the choice a = 0.34 , b = 2 , c = 12 , d = 2.5 , e = 1 , h = 1 , f = 0.411 , k = 0.01 , and the initial values ( 2 , 0 , 1 , 0.1 ) , the corresponding LEs are L E 1 = 0.0862 , L E 2 = 0.0453 , L E 3 = − 0.0746 , and L E 4 = − 1.0569 . This means that model (1.2) exhibits hyperchaotic hidden attractor, as illustrated in Figure 1. The LEs and BDs for the proposed hyperchaotic (chaotic) model (1.2) are provided for the same initial values in Figure 1 and the parameter values are

$Figure 1 Hyperchaotic hidden attractor of model (1.2) in the ( u 2 , u 1 , u 3 ) \left({u}_{2},{u}_{1},{u}_{3}) space for parameters e = 1 e=1 , d = 2.5 d=2.5 , c = 12 c=12 , b = 2 b=2 , a = 0.34 a=0.34 , h = 1 h=1 , f = 0.411 f=0.411 , k = 0.01 k=0.01 , and the initial values of u 10 = 2 {u}_{10}=2 , u 20 = 0 {u}_{20}=0 , u 30 = 1 {u}_{30}=1 and u 40 = 0.1 {u}_{40}=0.1 .$

Figure 1

Hyperchaotic hidden attractor of model (1.2) in the ( u 2 , u 1 , u 3 ) space for parameters e = 1 , d = 2.5 , c = 12 , b = 2 , a = 0.34 , h = 1 , f = 0.411 , k = 0.01 , and the initial values of u 10 = 2 , u 20 = 0 , u 30 = 1 and u 40 = 0.1 .

Fix e = 1 , d = 2.5 , c = 12 , b = 2 , h = 1 , f = 0.05 , and k = 0.01 and vary a ∈ ( 0 , 0.7 ) .

By calculating the LEs of model (1.2), it is clear that this model has chaotic and hyperchaotic solutions, as shown in Figure 2(a). The BD for the proposed hyperchaotic model is also provided in Figure 2(b) to indicate the path of chaos.

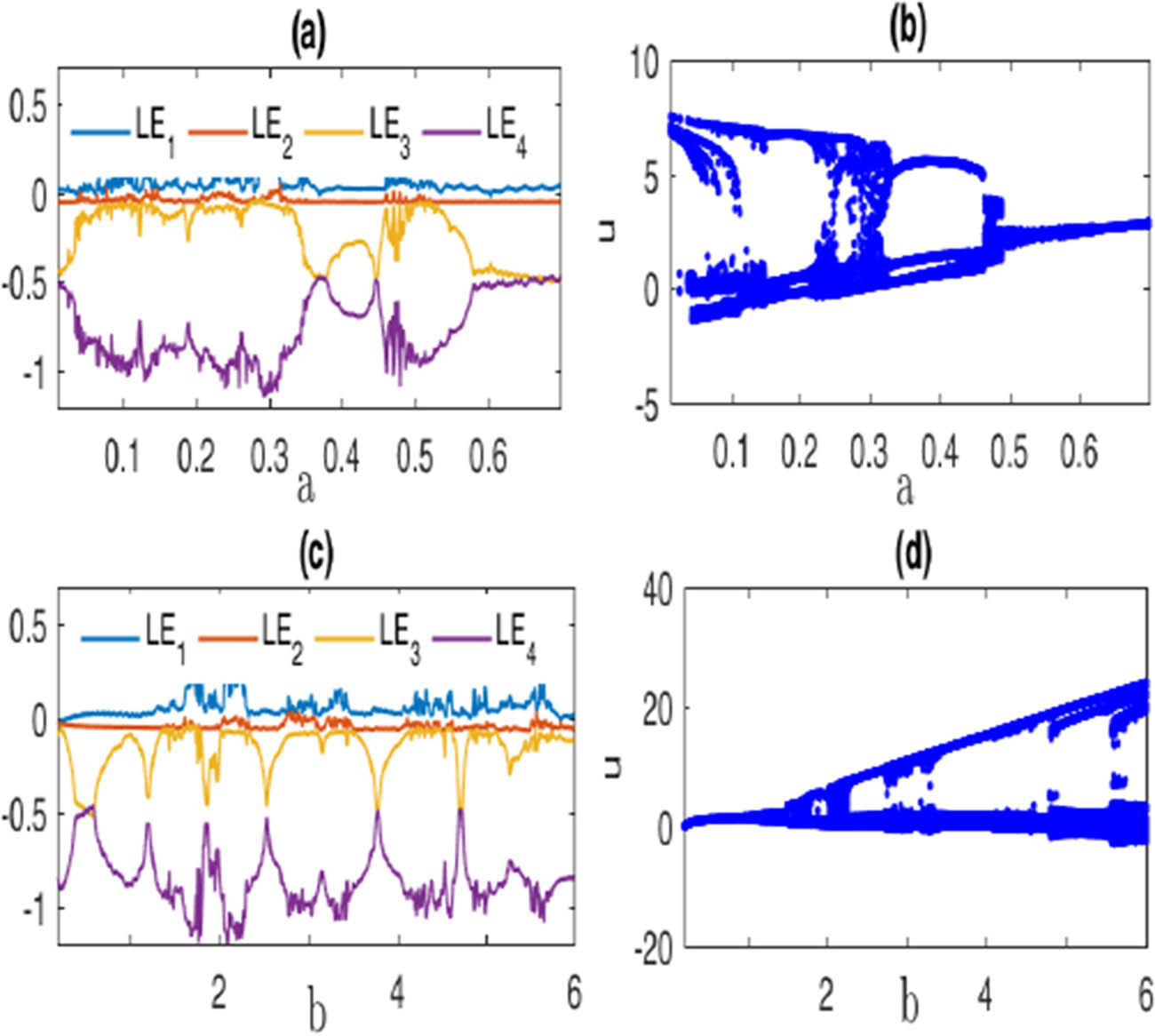
$Figure 2 Dynamics of model (1.2) with the same initial values as Figure 1: (a) The corresponding LE for the parameter values e = 1 e=1 , d = 2.5 d=2.5 , c = 12 c=12 , b = 2 b=2 , h = 1 , f = 0.05 , k = 0.01 h=1,f=0.05,k=0.01 and for a ∈ ( 0 , 0.7 ) a\in \left(0,0.7) , (b) BD for a ∈ ( 0 , 0.7 ) a\in \left(0,0.7) , (c) LE for parameters e = 1 e=1 , d = 2.5 d=2.5 , c = 12 c=12 , a = 0.34 a=0.34 , h = 1 h=1 , f = 0.05 f=0.05 , and k = 0.01 k=0.01 and for b ∈ ( 0 , 6 ) b\in \left(0,6) , and (d) BD for b ∈ ( 0 , 6 ) b\in \left(0,6) .$

Figure 2

Dynamics of model (1.2) with the same initial values as Figure 1: (a) The corresponding LE for the parameter values e = 1 , d = 2.5 , c = 12 , b = 2 , h = 1 , f = 0.05 , k = 0.01 and for a ∈ ( 0 , 0.7 ) , (b) BD for a ∈ ( 0 , 0.7 ) , (c) LE for parameters e = 1 , d = 2.5 , c = 12 , a = 0.34 , h = 1 , f = 0.05 , and k = 0.01 and for b ∈ ( 0 , 6 ) , and (d) BD for b ∈ ( 0 , 6 ) .

Fix e = 1 , d = 2.5 , c = 12 , a = 0.34 , h = 1 , f = 0.05 , and k = 0.01 , and vary b ∈ ( 0 , 6 ) . We showed the matching LEs for model (1.2) in Figure 2(c), while the corresponding BD for this model is given in Figure 2(d).

By the same way, Figures 3, 4, 5 show the LEs and BDs for the reminder parameters of model (1.2).

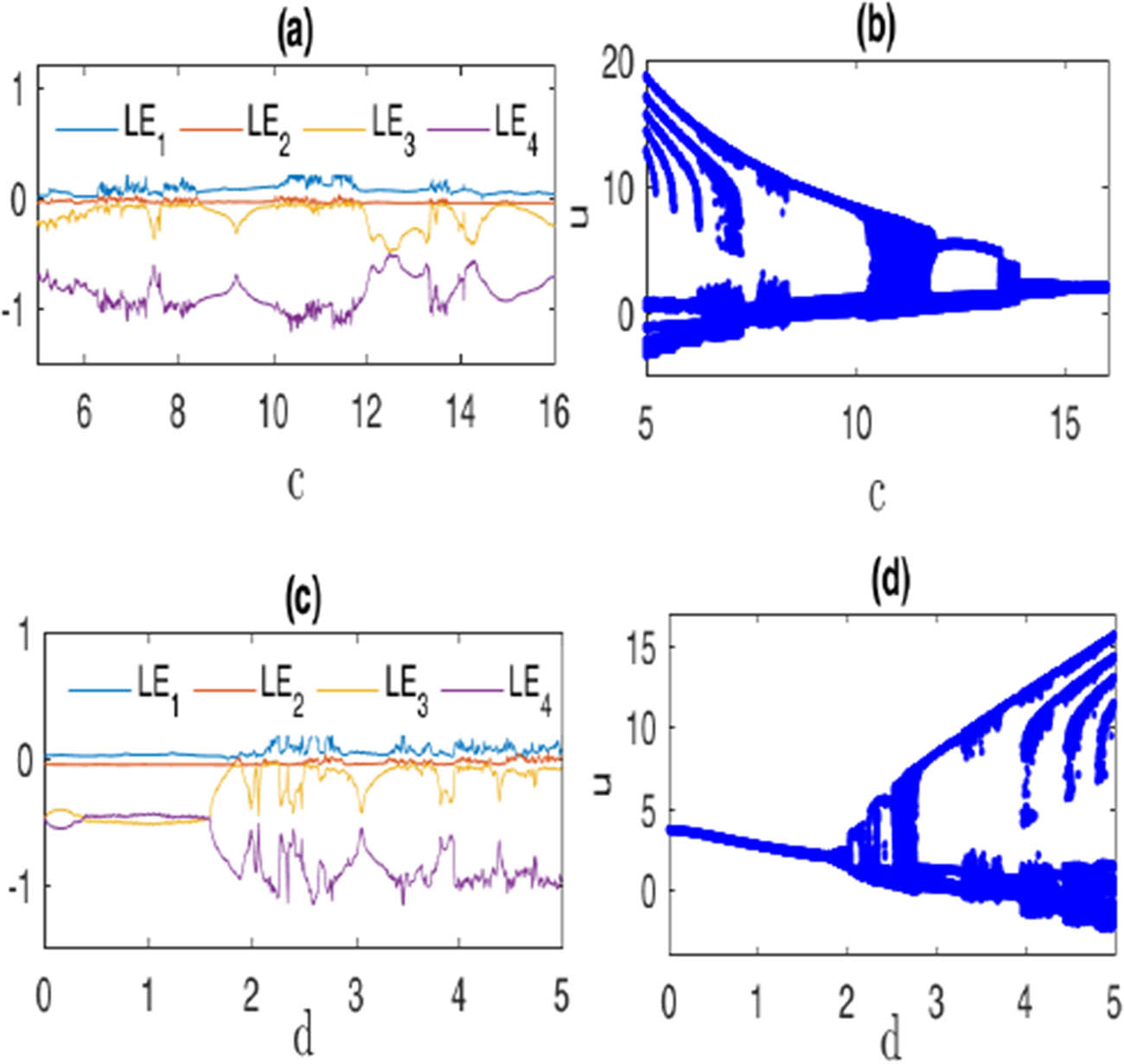
$Figure 3 LE and BD of model (1.2) with the same initial values as Figure 1: (a) LE for parameters e = 1 e=1 , d = 2.5 d=2.5 , b = 2 b=2 , a = 0.34 a=0.34 , h = 1 h=1 , f = 0.05 f=0.05 , k = 0.01 k=0.01 and for c ∈ ( 5 , 16 ) c\in \left(5,16) , (b) BD for b ∈ ( 5 , 16 ) b\in \left(5,16) , (c) LE for parameters e = 1 e=1 , c = 12 c=12 , b = 2 b=2 , a = 0.34 a=0.34 , h = 1 h=1 , f = 0.05 f=0.05 , k = 0.01 k=0.01 and for d ∈ ( 0 , 5 ) d\in \left(0,5) , and (d) BD for d ∈ ( 0 , 5 ) d\in \left(0,5) .$

Figure 3

LE and BD of model (1.2) with the same initial values as Figure 1: (a) LE for parameters e = 1 , d = 2.5 , b = 2 , a = 0.34 , h = 1 , f = 0.05 , k = 0.01 and for c ∈ ( 5 , 16 ) , (b) BD for b ∈ ( 5 , 16 ) , (c) LE for parameters e = 1 , c = 12 , b = 2 , a = 0.34 , h = 1 , f = 0.05 , k = 0.01 and for d ∈ ( 0 , 5 ) , and (d) BD for d ∈ ( 0 , 5 ) .

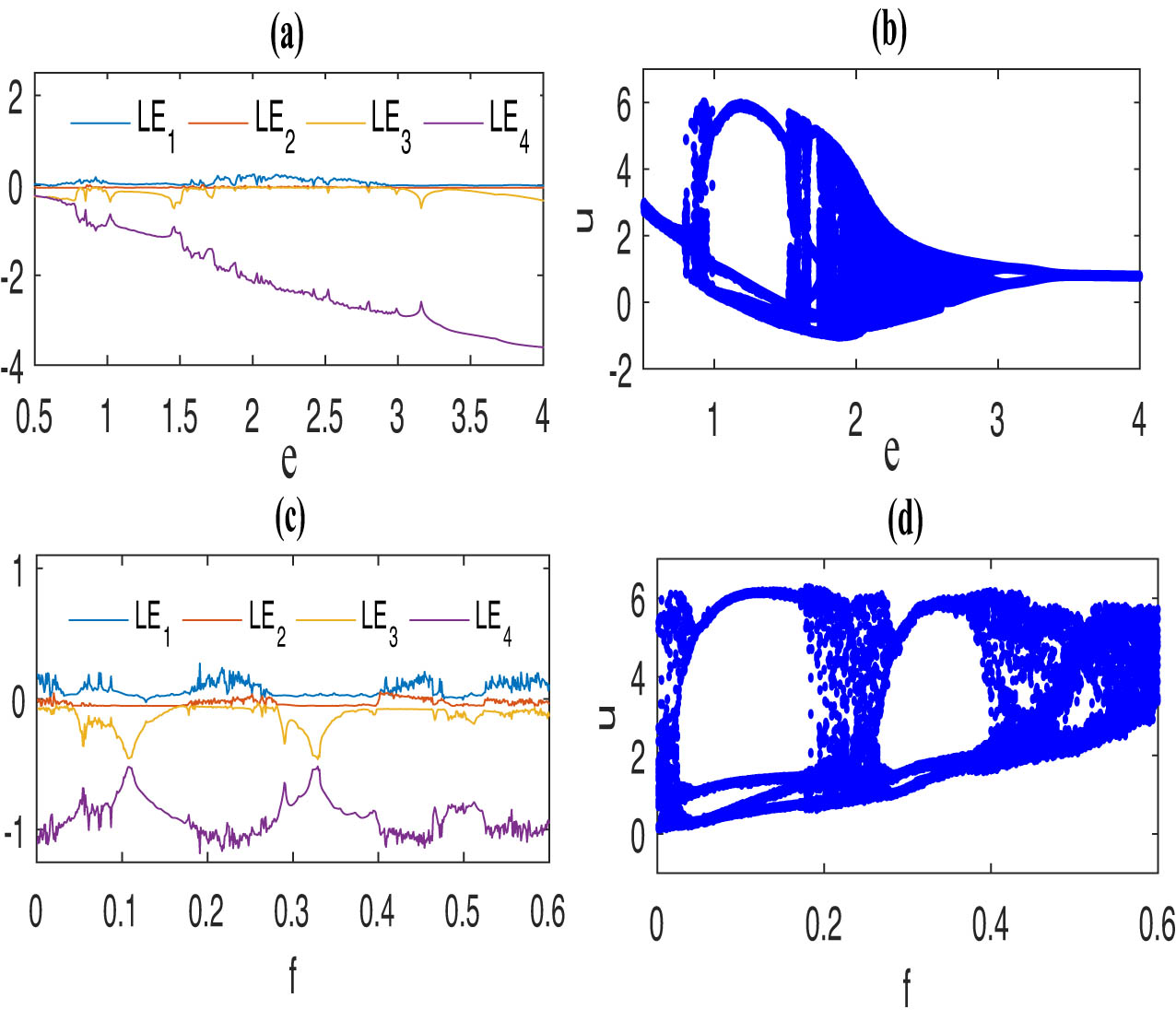
$Figure 4 LE and BD of model (1.2) with the same initial values as Figure 1: (a) LE for parameters d = 2.5 d=2.5 , c = 12 c=12 , b = 2 b=2 , a = 0.34 a=0.34 , h = 1 h=1 , f = 0.05 f=0.05 , k = 0.01 k=0.01 and for e ∈ ( 0 , 5 , 4 ) e\in \left(0,5,4) , (b) BD for e ∈ ( 0 , 5 , 4 ) e\in \left(0,5,4) , (c) LE for parameters e = 1 e=1 , d = 2.5 d=2.5 , c = 12 c=12 , b = 2 b=2 , a = 0.34 a=0.34 , h = 1 h=1 , k = 0.01 k=0.01 and for f ∈ ( 0 , 0.6 ) f\in \left(0,0.6) , and (d) BD for f ∈ ( 0 , 0.6 ) f\in \left(0,0.6) .$

Figure 4

LE and BD of model (1.2) with the same initial values as Figure 1: (a) LE for parameters d = 2.5 , c = 12 , b = 2 , a = 0.34 , h = 1 , f = 0.05 , k = 0.01 and for e ∈ ( 0 , 5 , 4 ) , (b) BD for e ∈ ( 0 , 5 , 4 ) , (c) LE for parameters e = 1 , d = 2.5 , c = 12 , b = 2 , a = 0.34 , h = 1 , k = 0.01 and for f ∈ ( 0 , 0.6 ) , and (d) BD for f ∈ ( 0 , 0.6 ) .

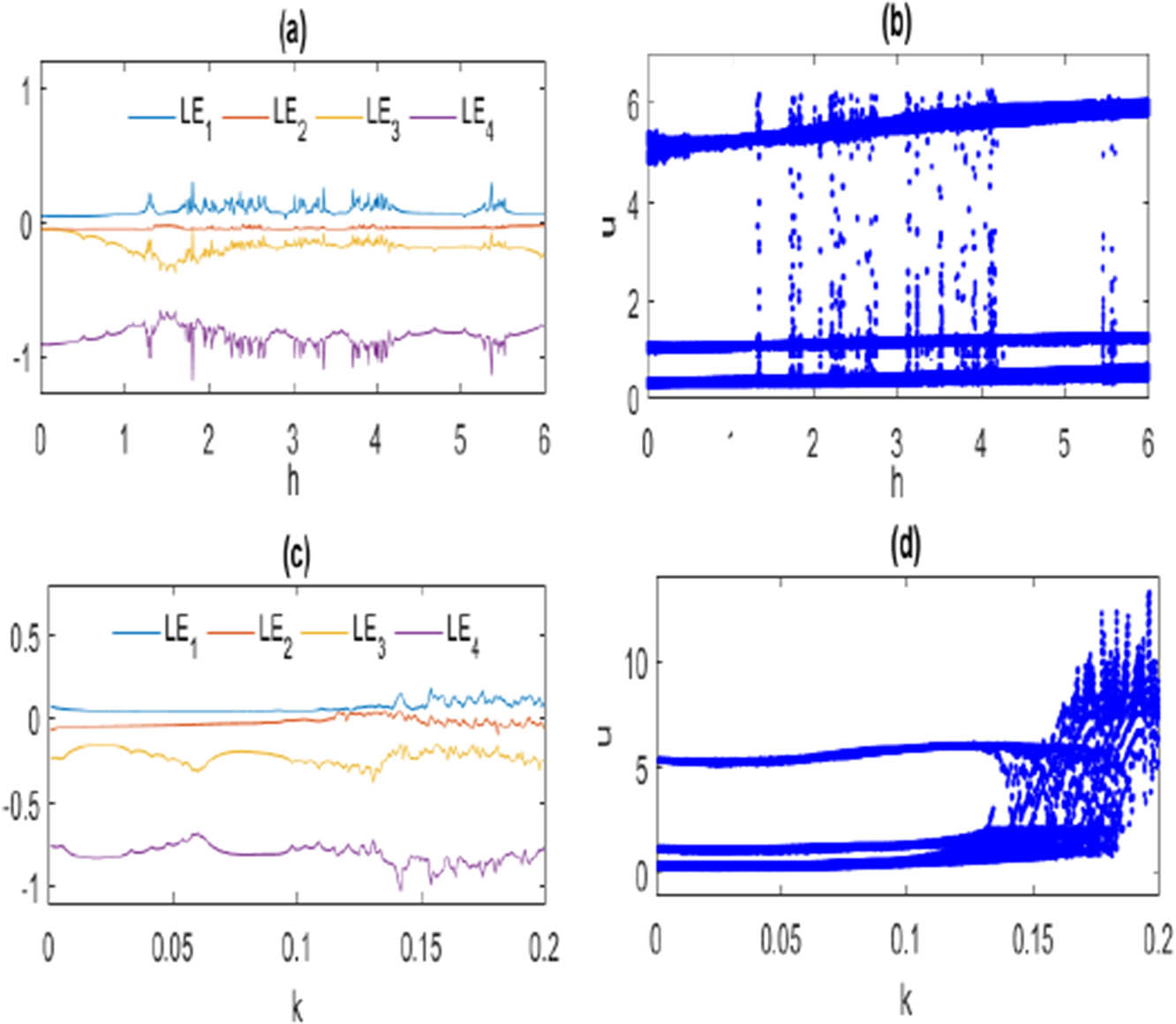
$Figure 5 LE and BD of model (1.2) with the same initial values as Figure 1: (a) LE for parameters e = 1 e=1 , d = 2.5 d=2.5 , c = 12 c=12 , b = 2 b=2 , a = 0.34 a=0.34 , f = 0.05 f=0.05 , k = 0.01 k=0.01 and for h ∈ ( 0 , 6 ) h\in \left(0,6) , (b) BD for h ∈ ( 0 , 6 ) h\in \left(0,6) , (c) LE for parameters e = 1 e=1 , d = 2.5 d=2.5 , c = 12 c=12 , b = 2 b=2 , a = 0.34 a=0.34 , h = 1 h=1 , f = 0.05 f=0.05 and for k ∈ ( 0 , 0.2 ) k\in \left(0,0.2) , and (d) BD for k ∈ ( 0 , 0.2 ) k\in \left(0,0.2) .$

Figure 5

LE and BD of model (1.2) with the same initial values as Figure 1: (a) LE for parameters e = 1 , d = 2.5 , c = 12 , b = 2 , a = 0.34 , f = 0.05 , k = 0.01 and for h ∈ ( 0 , 6 ) , (b) BD for h ∈ ( 0 , 6 ) , (c) LE for parameters e = 1 , d = 2.5 , c = 12 , b = 2 , a = 0.34 , h = 1 , f = 0.05 and for k ∈ ( 0 , 0.2 ) , and (d) BD for k ∈ ( 0 , 0.2 ) .

Remark 2.3

Model (1.2) has hyperchaotic solutions, while model (1.2) has only chaotic one.

2.5 Dynamics of model (1.2) with equilibrium points

Regarding the selection e = 1 , d = 2.5 , c = 12 , b = 2 , a = 0.34 , h = 1 , f = − 0.732 , k = 0.01 , and the same initial values of Figure 1, the corresponding LEs are L E 1 = 0.1369 , L E 2 = 0.0363 , L E 3 = − 0.0857 , and L E 4 = − 1.0876 . As shown in Figure 6, this indicates that model (1.2) displays hyperchaotic self-excited attractor.

$Figure 6 Hyperchaotic self-excited attractor of model (1.2) in the ( u 2 , u 3 ) \left({u}_{2},{u}_{3}) plane for the same initial values and the parameters in Figure 1 except f = − 0.732 f=-0.732 .$

Figure 6

Hyperchaotic self-excited attractor of model (1.2) in the ( u 2 , u 3 ) plane for the same initial values and the parameters in Figure 1 except f = − 0.732 .

The LEs and BDs for the proposed hyperchaotic (chaotic) model (1.2) are provided for the same initial values in Figure 1, and the parameter values are

Fix e = 1 , d = 2.5 , c = 12 , b = 2 , a = 0.34 , h = 1 , k = 0.01 , and vary f ∈ ( − 1 , 0 ) . By computing the LEs of model (1.2), this model has chaotic and hyperchaotic solutions, as shown in Figure 7(a). The BD for the proposed hyperchaotic model is also investigated in Figure 7(b).

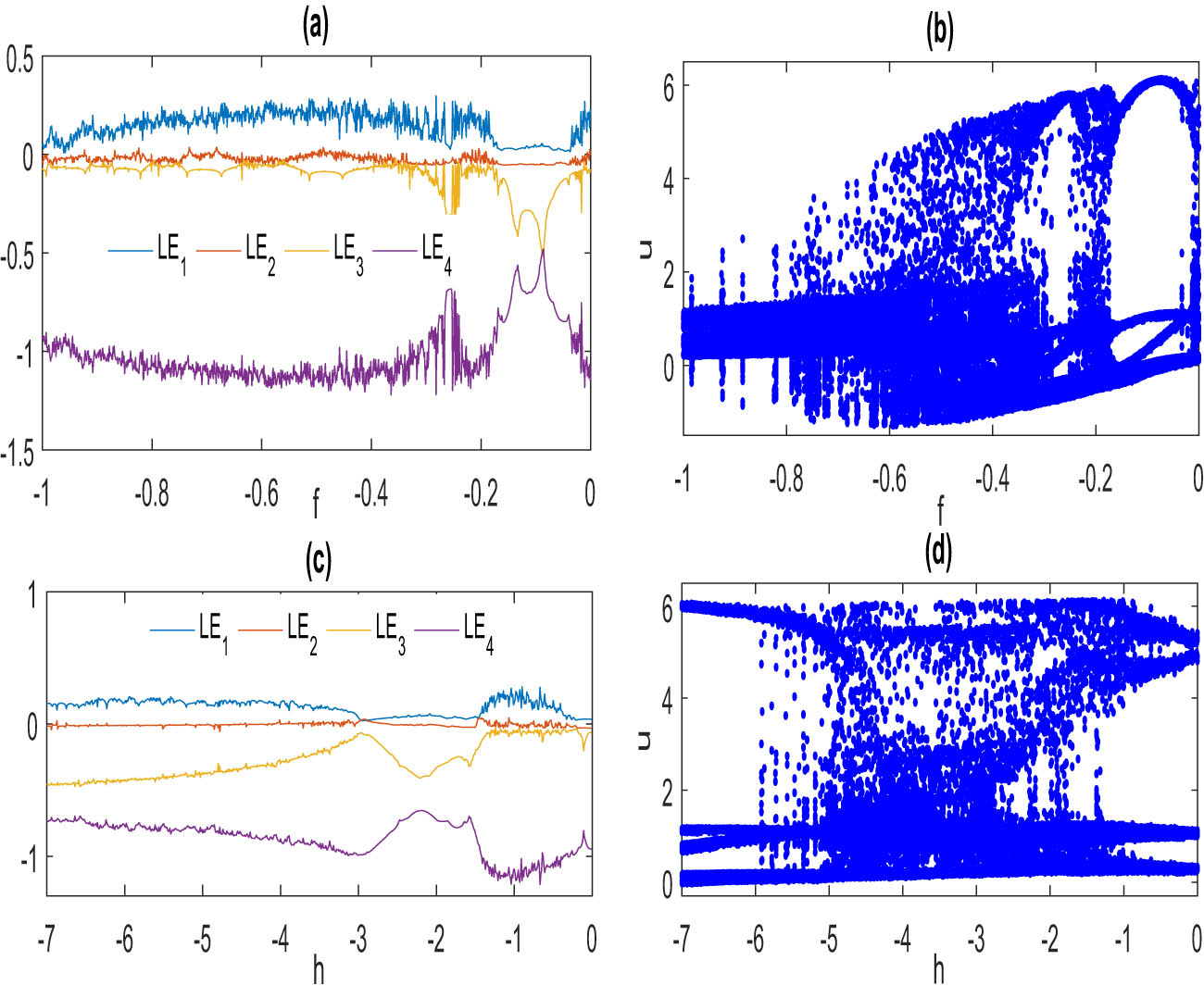
$Figure 7 LE and BD of model (1.2) with the same initial values as Figure 1: (a) LE for parameters e = 1 e=1 , d = 2.5 d=2.5 , c = 12 c=12 , b = 2 b=2 , a = 0.34 a=0.34 , h = 1 h=1 , k = 0.01 k=0.01 and for f ∈ ( − 1 , 0 ) f\in \left(-1,0) , (b) BD for f ∈ ( − 1 , 0 ) f\in \left(-1,0) , (c) LE for parameters e = 1 e=1 , d = 2.5 d=2.5 , c = 12 c=12 , b = 2 b=2 , a = 0.34 a=0.34 , f = 0.05 , k = 0.01 f=0.05,k=0.01 and for h ∈ ( − 7 , 0 ) h\in \left(-7,0) , and (d) BD for h ∈ ( − 7 , 0 ) h\in \left(-7,0) .$

Figure 7

LE and BD of model (1.2) with the same initial values as Figure 1: (a) LE for parameters e = 1 , d = 2.5 , c = 12 , b = 2 , a = 0.34 , h = 1 , k = 0.01 and for f ∈ ( − 1 , 0 ) , (b) BD for f ∈ ( − 1 , 0 ) , (c) LE for parameters e = 1 , d = 2.5 , c = 12 , b = 2 , a = 0.34 , f = 0.05 , k = 0.01 and for h ∈ ( − 7 , 0 ) , and (d) BD for h ∈ ( − 7 , 0 ) .

Fix e = 1 , d = 2.5 , c = 12 , b = 2 , a = 0.34 , f = 0.05 , k = 0.01 and vary h ∈ ( − 7 , 0 ) . Figure 7(c) shows the LEs for model (1.2), while the BD for this model is given in Figure 7(d).

By a similar way, the LEs and BDs for the reminder parameters of model (1.2) can be presented for this case.

3 Circuit implementation of model (1.2)

Examining equations of model (1.2) with a = 0.34 , b = 2 , c = 12 , d = 2.5 , e = 1 , h = 1 , k = 0.01 , and f = 0.411 , we can rewrite it as follows:

(3.1) u 1 ˙ = 0.34 u 2 + 0.08 u 3 + 0.2 u 2 2 u 3 , u 2 ˙ = 2 u 3 + u 4 2 + 0.05 , u 3 ˙ = − 12 u 1 − u 3 + 2.5 u 2 2 , u 4 ˙ = 0.01 u 3 .

We can implement the electronic circuit in Figure 8 using model (3.1), and the circuit equations in the Laplace domain are shown as

(3.2) s U 1 ( s ) = 1 C 1 1 R 1 U 2 ( s ) + 1 R 2 U 3 ( s ) + 1 R 3 L { u 2 ( t ) 2 u 3 } , s U 2 ( s ) = 1 C 2 1 R 4 U 3 ( s ) + 1 R 5 L { u 4 ( t ) 2 } + 1 R 6 , s U 3 ( s ) = 1 C 3 − 1 R 7 U 1 ( s ) − 1 R 8 U 3 ( s ) + 1 R 9 L { u 2 ( t ) 2 } , s U 4 ( s ) = 1 R 10 C 4 U 3 ( s ) ,

where L { ⋅ } is the Laplace transform, and the values of the resistors and the capacitors are R = R 5 = R 8 = 1 M Ω , R 1 = 2.9 M Ω , R 2 = 12.5 M Ω , R 3 = 5 M Ω , R 4 = 0.5 M Ω , R 6 = 2 M Ω , R 7 = 0.83 M Ω , R 9 = 0.4 M Ω , R 1 0 = 100 M Ω , and C 1 = C 2 = C 3 = C 4 = 1 μ F .

Figure 8

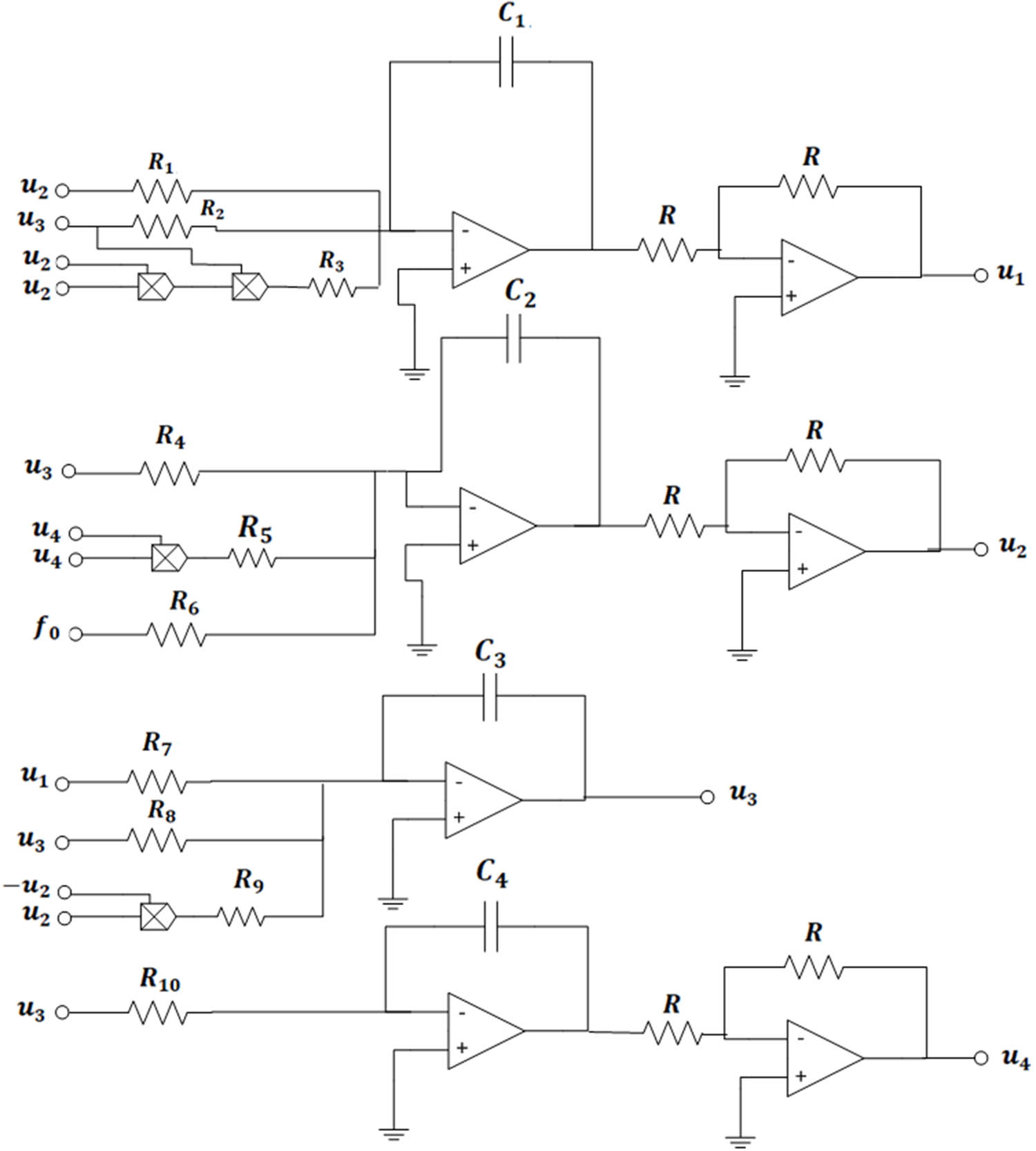
Circuit diagram of model (3.1).

On the MATLAB Simulink, the circuit implementation and simulations were performed. The observed circuit simulations of the chaotic system (3.1) in the ( u 2 , u 1 , u 3 ) spaces are shown in Figure 9. For the identical parameters and beginning circumstances, these simulations are in good agreement with the numerical solutions of Figure 1. On the other hand, for the case f = − 0.732 , the value of R 6 will change to R 6 = 1.4 M Ω , and the third term in the second equation will be negative. There is agreement between the circuit simulations and numerical solutions, as shown in Figures 6 and 10.

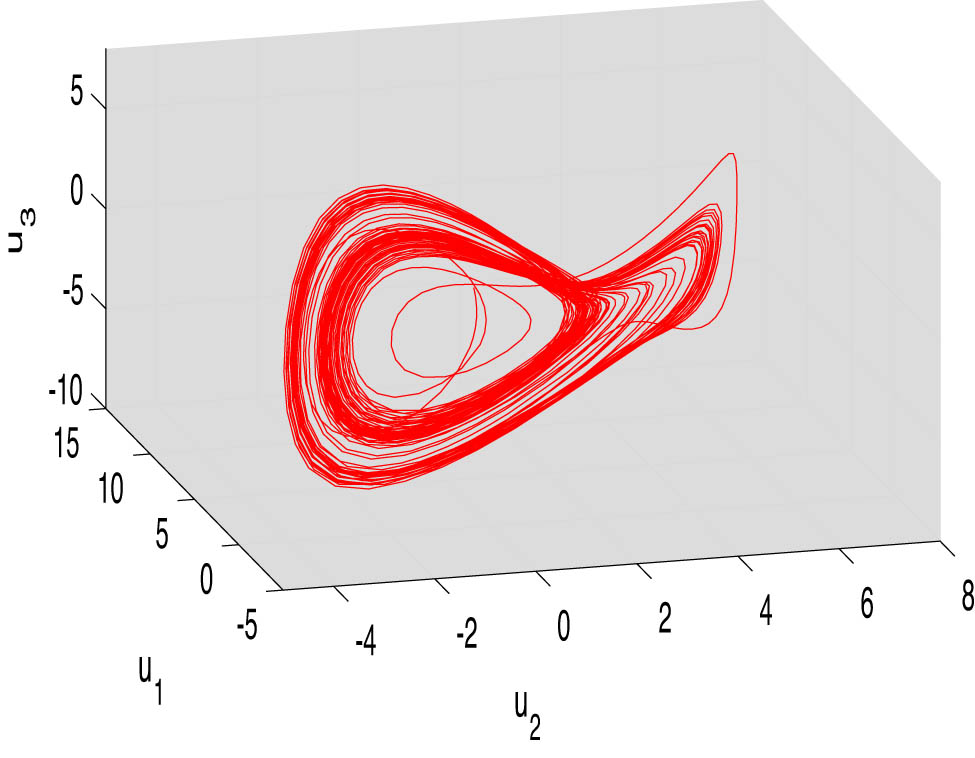
$Figure 9 Circuit simulation of model (3.1) in the ( u 2 , u 1 , u 3 ) \left({u}_{2},{u}_{1},{u}_{3}) plane for initial values of (2, 0, 1, 0.1) and for parameters a = 0.34 a=0.34 , b = 2 b=2 , c = 12 c=12 , d = 2.5 d=2.5 , e = 1 e=1 , h = 1 h=1 , f = 0.411 f=0.411 , and k = 0.01 k=0.01 .$

Figure 9

Circuit simulation of model (3.1) in the ( u 2 , u 1 , u 3 ) plane for initial values of (2, 0, 1, 0.1) and for parameters a = 0.34 , b = 2 , c = 12 , d = 2.5 , e = 1 , h = 1 , f = 0.411 , and k = 0.01 .

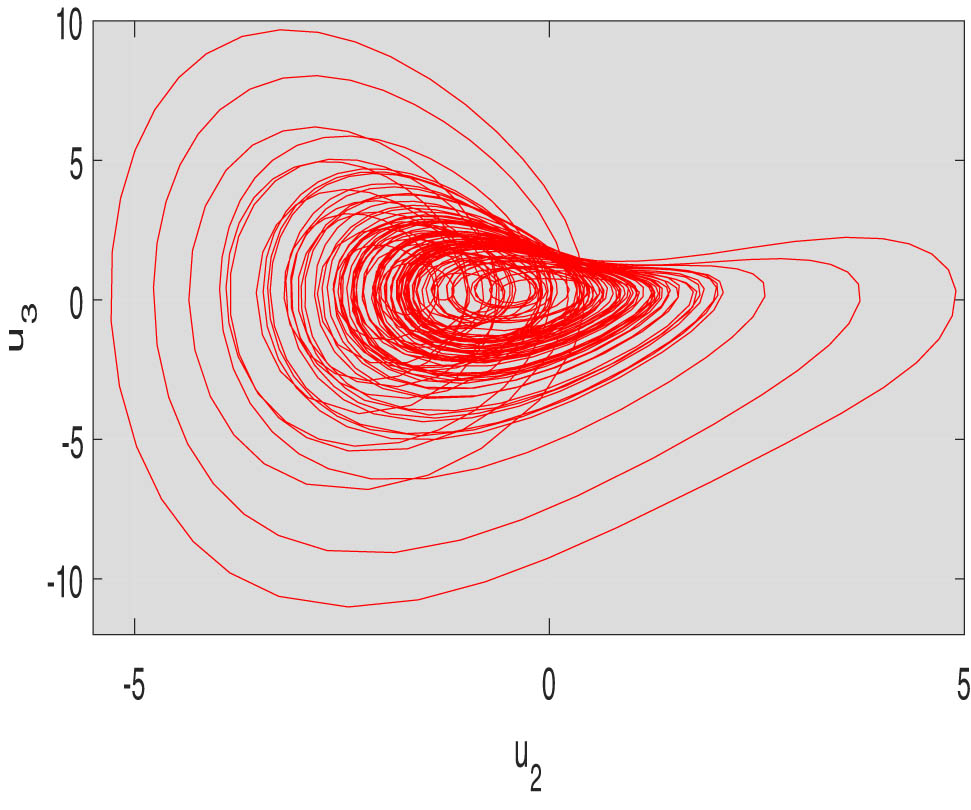
$Figure 10 Circuit simulation of model (3.1) in the ( u 2 , u 3 ) \left({u}_{2},{u}_{3}) plane for initial values of ( 2 , 0 , 1 , 0.1 ) \left(2,0,1,0.1) and for parameters a = 0.34 a=0.34 , b = 2 b=2 , c = 12 c=12 , d = 2.5 d=2.5 , e = 1 e=1 , h = 1 h=1 , f = − 0.732 f=-0.732 , and k = 0.01 k=0.01 .$

Figure 10

Circuit simulation of model (3.1) in the ( u 2 , u 3 ) plane for initial values of ( 2 , 0 , 1 , 0.1 ) and for parameters a = 0.34 , b = 2 , c = 12 , d = 2.5 , e = 1 , h = 1 , f = − 0.732 , and k = 0.01 .

4 Color image encryption using the hyperchaotic model (1.2)

Using the hyperchaotic model (1.2), the encryption and decryption process [41] entails a number of systematic steps to guarantee secure image transformation. Image preparation is the first step in the process, during which the color image is read and adjusted for further processing. Chaotic sequences are then generated using model (1.2) parameters and initial values, discretizing time for iterative calculations that create hyperchaotic sequences aligned with pixel positions. Channel-wise encryption follows, dividing the image into red, green, blue (color model) (RGB) channels and adjusting the chaotic sequences for each channel before applying encryption through simple addition and wrapping operations. Decryption reverses this process by subtracting the chaotic sequence and restoring the original pixel values. Image reconstruction merges decrypted channels to form the complete image.

In the experimental results, we utilize identical parameter values and initial values for model (1.2), as shown in Figure 1, along with the “House” image to evaluate the effectiveness of the image encryption technique. The original medical image, the encrypted one, and the decrypted image are shown in Figure 11. Figure 11(a)–(c) demonstrates how the encrypted image becomes unreadable during encryption and looks entirely different from the decrypted image. However, when visually compared, the original image and its decrypted version appear exactly the same.

Figure 11

Color image encryption of the “House” image using the hyperchaotic model (1.2): (a) the original image, (b) the encrypted image, and (c) the decrypted image.

Figure 11(a)–(c) shows that the red component of the encrypted image has a different histogram compared to the original and decrypted images. Similarly, Figure 11(d)–(f) displays differences in the green component, and Figure 11(g)–(i) shows changes in the blue component. This makes it hard for attackers to extract useful information or use statistical tools to figure out the original image.

The original “House” image has an information entropy of 7.0686, which indicates that the distribution of its pixels is very unpredictable. Following encryption, the entropy increases to 7.9970, which is close to the maximum value of 8 for an 8-bit image. This suggests that the encrypted image is extremely safe and disordered. After decryption, the entropy goes back to 7.0686, which corresponds to the original image and validates that the image was successfully recovered without any information being lost.

The original “House” image has a correlation coefficient of 0.9840, which shows that adjacent pixels are strongly correlated. The coefficient decreases to − 0.3221 during encryption, indicating a notable decrease in correlation and improved security; the decrypted image returns the correlation to 0.9840, verifying that the original structure was successfully recovered.

The NPCR for the encrypted “House” image is 100, indicating that 100% of the pixels have changed compared to the original image. This demonstrates the high sensitivity of the encryption process, ensuring strong security against differential attacks.

The encrypted “House” image has a UACI of 29.1854, meaning that there is an average intensity difference of about 29.19% between the original and encrypted photos. This value further validates the efficiency of the encryption process in reaching a high degree of security since it shows a notable change in pixel values.

While our encryption scheme demonstrates strong performance in NPCR (100%) and UACI (29%), we acknowledge that a complete cryptographic evaluation requires additional security analyses. In future work, we will conduct key sensitivity analysis with finer perturbations, evaluate resistance to known/chosen-plaintext attacks, perform key space analysis with formal entropy measurements, and benchmark against state-of-the-art chaos-based methods. These tests will further validate the robustness of our hyperchaos-driven encryption for real-world applications.

5 Conclusion

A new 4D hyperchaotic model is proposed that can produce hidden attractors or self-excited attractors depending on the value of model parameters. For the new 4-DHM model (1.2), some basic dynamical behaviors are investigated. LEs, phase portraits, and BDs have all been used to illustrate the new 4-DHM model’s complicated dynamical characteristics. Remarks 2.1–2.3 show the differences between the new 4-DHM model (1.2) and previous work. For the new 4-DHM model (1.2), an electronic circuit is designed. We think that our proposed model (1.2) is expected to find widespread use in a variety of physics, engineering, and computer science domains, including secure communication, information science, and laser systems. Figure 8 shows the electronic implementation of model (3.1). The simulation observations of our new electronic circuit of the new 4-DHM model (3.1) and those of numerical calculations were in good agreement, as illustrated in Figures 1–6 and 9–10. The encryption, decryption, histogram analysis, information entropy, correlation coefficient, NPCR, and UACI of the color (“House”) image are illustrated using the 4-DHM (1.2), and the results are depicted in Figures 11 and 12.

Figure 12

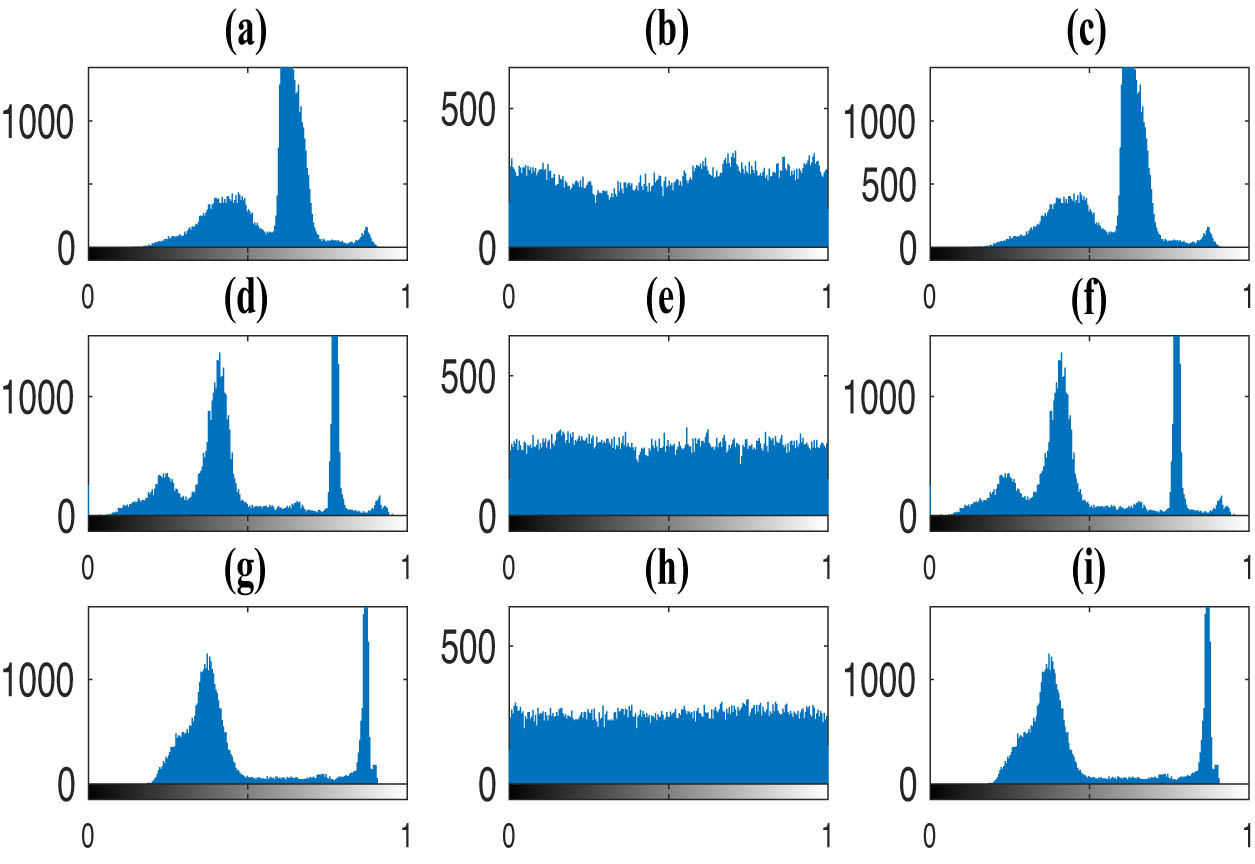
Histogram of color image encryption of the “House” image using the 4-DHM (1.2): (a) the histogram of the red component of the original image, (b) the histogram of the red component of the encrypted image, (c) the histograms of the red component of the decrypted image, (d)–(f) the histograms of the green components, and (g)–(i) the histograms of the blue components.

Funding information: The authors extend their appreciation to Prince Sattam bin Abdulaziz University for funding this research work through the Project Number (PSAU/2024/01/31725).
Author contributions: The study’s conception and design involved contributions from all authors. TMA wrote the initial draft of the manuscript. MEA conducted material preparation, data collection, and analysis. Through multiple iterations of manuscript revision, each author provided valuable insights and suggestions. The final version of the manuscript was reviewed thoroughly by all authors and unanimously approved for publication.
Conflict of interest: The authors state no conflict of interest.
Data availability statement: The datasets of the current study are available from the corresponding author on reasonable request.

References

[1] Lorenz EN. Deterministic nonperiodic flow. J Atmos Sci. 1963;20(2):130–41. 10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2Search in Google Scholar

[2] Heltberg ML, Krishna S, Jensen MH. On chaotic dynamics in transcription factors and the associated effects in differential gene regulation. Nat Commun. 2019;10(1):71. 10.1038/s41467-018-07932-1Search in Google Scholar

[3] Dharminder D, Kumar U, Gupta P. A construction of a conformal Chebyshev chaotic map based authentication protocol for healthcare telemedicine services. Complex Intell Syst. 2021;7(5):2531–42. 10.1007/s40747-021-00441-7Search in Google Scholar

[4] Li X, Jiang C, Xu R, Yang W, Wang H, Zou Y. Combining forecast of landslide displacement based on chaos theory. Arab J Geosci. 2021;14:1–10. 10.1007/s12517-021-06514-8Search in Google Scholar

[5] Mahmoud GM, Farghaly AA, Abed-Elhameed TM, Darwish MM. Adaptive dual synchronization of chaotic (hyperchaotic) complex systems with uncertain parameters and its application in image encryption. Acta Phys Polonica B. 2018;49(11):1923. 10.5506/APhysPolB.49.1923Search in Google Scholar

[6] Mahmoud GM, Bountis T, AbdEl-Latif G, Mahmoud EE. Chaos synchronization of two different chaotic complex Chen and Lü systems. Nonl Dyn. 2009;55:43–53. 10.1007/s11071-008-9343-5Search in Google Scholar

[7] Liao Y, Vikram A, Galitski V. Many-body level statistics of single-particle quantum chaos. Phys Rev Let. 2020;125(25):250601. 10.1103/PhysRevLett.125.250601Search in Google Scholar

[8] Awad E, Samir N. A closed-form solution for thermally induced affine deformation in unbounded domains with a temporally accelerated anomalous thermal conductivity. J Phys A Math Theoret. 2024;57(45):455202. 10.1088/1751-8121/ad878fSearch in Google Scholar

[9] Awad E. Modeling of anomalous thermal conduction in thermoelectric magnetohydrodynamics: Couette formulation with a multiphase pressure gradient. Phys Fluids. 2024;36(3):033608. 10.1063/5.0190970Search in Google Scholar

[10] Benkouider K, Sambas A, Bonny T, Al Nassan W, Moghrabi IA, Sulaiman IM, et al. A comprehensive study of the novel 4D hyperchaotic system with self-exited multistability and application in the voice encryption. Scientif Reports. 2024;14(1):12993. 10.1038/s41598-024-63779-1Search in Google Scholar

[11] Rössler OE. An equation for continuous chaos. Phys Lett A. 1976;57(5):397–8. 10.1016/0375-9601(76)90101-8Search in Google Scholar

[12] Matsumoto T. A chaotic attractor from Chuaas circuit. IEEE Trans Circuits Syst. 1984;31(12):1055–8. 10.1109/TCS.1984.1085459Search in Google Scholar

[13] Sprott JC. Some simple chaotic flows. Phys Rev E. 1994;50(2):R647. 10.1103/PhysRevE.50.R647Search in Google Scholar

[14] Chen G, Ueta T. Yet another chaotic attractor. Int J Bifurcat Chaos. 1999;9(7):1465–6. 10.1142/S0218127499001024Search in Google Scholar

[15] Zhu H, Ge J, Qi W, Zhang X, Lu X. Dynamic analysis and image encryption application of a sinusoidal-polynomial composite chaotic system. Math Comput Simulat. 2022;198:188–210. 10.1016/j.matcom.2022.02.029Search in Google Scholar

[16] Abed-Elhameed TM, Otefy M, Mahmoud GM. Dynamics of chaotic and hyperchaotic modified nonlinear Schrödinger equations and their compound synchronization. Phys Scr. 2024 Apr;99(5):055226. 10.1088/1402-4896/ad36edSearch in Google Scholar

[17] Laarem G. A new 4-D hyper chaotic system generated from the 3-D Rösslor chaotic system, dynamical analysis, chaos stabilization via an optimized linear feedback control, it’s fractional order model and chaos synchronization using optimized fractional order sliding mode control. Chaos Solitons Fractals. 2021;152:111437. 10.1016/j.chaos.2021.111437Search in Google Scholar

[18] Xiu C, Fang J, Liu Y. Design and circuit implementation of a novel 5D memristive CNN hyperchaotic system. Chaos Solitons Fractals. 2022;158:112040. 10.1016/j.chaos.2022.112040Search in Google Scholar

[19] Mahmoud GM, Abed-Elhameed TM, Khalaf H. Synchronization of hyperchaotic dynamical systems with different dimensions. Phys Scr. 2021;96(12):125244. 10.1088/1402-4896/ac3152Search in Google Scholar

[20] Guo Q, Wang N, Zhang G. A novel four-element RCLM hyperchaotic circuit based on current-controlled extended memristor. AEU-Int J Electron Commun. 2022;156:154391. 10.1016/j.aeue.2022.154391Search in Google Scholar

[21] Nguenjou LN, Kom G, Pone JM, Kengne J, Tiedeu A. A window of multistability in Genesio-Tesi chaotic system, synchronization and application for securing information. AEU-Int J Electron Commun. 2019;99:201–14. 10.1016/j.aeue.2018.11.033Search in Google Scholar

[22] Vaidyanathan S, Volos C. Advances and applications in chaotic systems. Vol. 636. Berlin, Germany: Springer; 2016. 10.1007/978-3-319-30279-9Search in Google Scholar

[23] Al Themairi A, Mahmoud GM, Farghaly AA, Abed-Elhameed TM. Complex Rayleigh-van-der-Pol-Duffing oscillators: dynamics, phase, antiphase synchronization, and image encryption. Fractal Fract. 2023;7(12):886. 10.3390/fractalfract7120886Search in Google Scholar

[24] Abed-Elhameed TM, Mahmoud GM, Elbadry MM, Ahmed ME. Nonlinear distributed-order models: Adaptive synchronization, image encryption and circuit implementation. Chaos Solitons Fractals. 2023;175:114039. 10.1016/j.chaos.2023.114039Search in Google Scholar

[25] Chai X, Tang Z, Gan Z, Lu Y, Wang B, Zhang Y. SE-NDEND: A novel symmetric watermarking framework with neural network-based chaotic encryption for Internet of medical things. Biomed Signal Proces Control. 2024;90:105877. 10.1016/j.bspc.2023.105877Search in Google Scholar

[26] Mahmoud GM, Khalaf H, Darwish MM, Abed-Elhameed TM. On the fractional-order simplified Lorenz models: Dynamics, synchronization, and medical image encryption. Math Meth Appl Sci. 2023;46(14):15706–25. 10.1002/mma.9422Search in Google Scholar

[27] Dou G, Guo W, Li Z, Wang C. Dynamics analysis of memristor chaotic circuit with coexisting hidden attractors. Europ Phys J Plus. 2024;139(4):1–17. 10.1140/epjp/s13360-024-05140-zSearch in Google Scholar

[28] Shilnikov LP. A case of the existence of a denumerable set of periodic motions. Sov Math Dokl. 1965;6:163–6. Search in Google Scholar

[29] Leonov G, Kuznetsov N, Mokaev T. Homoclinic orbits, and self-excited and hidden attractors in a Lorenz-like system describing convective fluid motion: Homoclinic orbits, and self-excited and hidden attractors. Europ Phys J Special Topics. 2015;224:1421–58. 10.1140/epjst/e2015-02470-3Search in Google Scholar

[30] Leonov GA, Kuznetsov NV, Mokaev TN. Hidden attractor and homoclinic orbit in Lorenz-like system describing convective fluid motion in rotating cavity. Commun Nonl Sci Numer Simulat. 2015;28(1–3):166–74. 10.1016/j.cnsns.2015.04.007Search in Google Scholar

[31] Sharma P, Shrimali M, Prasad A, Kuznetsov N, Leonov G. Control of multistability in hidden attractors. Europ Phys J Special Topics. 2015;224:1485–91. 10.1140/epjst/e2015-02474-ySearch in Google Scholar

[32] Abed-Elhameed TM, Mahmoud GM, Ahmed ME. On real and complex dynamical models with hidden attractors and their synchronization. Phys Scr. 2023;98(4):045223. 10.1088/1402-4896/acc490Search in Google Scholar

[33] Chua L, Komuro M, Matsumoto T. The double scroll family. IEEE Trans Circuits Syst. 1986;33(11):1072–118. 10.1109/TCS.1986.1085869Search in Google Scholar

[34] Lai Q, Bao B, Chen C, Kengne J, Akgul A. Circuit application of chaotic systems: modeling, dynamical analysis and control. Eur Phys J Special Topics. 2021;230:1691–4. 10.1140/epjs/s11734-021-00202-0Search in Google Scholar

[35] Gao T, Chen G, Chen Z, Cang S. The generation and circuit implementation of a new hyper-chaos based upon Lorenz system. Phys Lett A. 2007;361(1–2):78–86. 10.1016/j.physleta.2006.09.042Search in Google Scholar

[36] Ablay G. Novel chaotic delay systems and electronic circuit solutions. Nonl Dyn. 2015;81(4):1795–804. 10.1007/s11071-015-2107-0Search in Google Scholar

[37] Masood F, Masood J, Zhang L, Jamal SS, Boulila W, Rehman SU, et al. A new color image encryption technique using DNA computing and Chaos-based substitution box. Soft Comput. 2022;26:7461–77. 10.1007/s00500-021-06459-wSearch in Google Scholar

[38] Biban G, Chugh R, Panwar A. Image encryption based on 8D hyperchaotic system using Fibonacci Q-Matrix. Chaos Solitons Fractals. 2023;170:113396. 10.1016/j.chaos.2023.113396Search in Google Scholar

[39] Yan X, Hu Q, Teng L. A novel color image encryption method based on new three-dimensional chaotic mapping and DNA coding. Nonl Dyn. 2025;113(2):1799–826. 10.1007/s11071-024-10277-8Search in Google Scholar

[40] Hu C, Tian Z, Wang Q, Zhang X, Liang B, Jian C, et al. A memristor-based VB2 chaotic system: Dynamical analysis, circuit implementation, and image encryption. Optik. 2022;269:169878. 10.1016/j.ijleo.2022.169878Search in Google Scholar

[41] Guan ZH, Huang F, Guan W. Chaos-based image encryption algorithm. Phys Let A. 2005;346(1–3):153–7. 10.1016/j.physleta.2005.08.006Search in Google Scholar

Received: 2025-04-16

Revised: 2025-05-20

Accepted: 2025-05-23

Published Online: 2025-07-22

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/phys-2025-0179

Keywords for this article

chaotic and hyperchaotic models; hidden attractors; Lyapunov exponents; nonlinear electronic circuit; color image encryption

Creative Commons

BY 4.0