Tavis–Cummings model in the presence of a deformed field and time-dependent coupling

Mariam Algarni; Sayed Abdel-Khalek; Kamal Berrada

doi:10.1515/phys-2024-0118

Article Open Access

Tavis–Cummings model in the presence of a deformed field and time-dependent coupling

Mariam Algarni , Sayed Abdel-Khalek and Kamal Berrada

Published/Copyright: July 7, 2025

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

From the journal Open Physics Volume 23 Issue 1

Abstract

In this work, we introduce a model for a two-atom (T–A) system interacting with a field mode initially prepared in a coherent state of a Para Bose–field (P–F). The T–As are initially represented by a Bell state, and we present the quantum framework for the whole system by solving the dynamical equations. We investigate the time-dependent behavior of essential quantum resources relevant to various tasks in quantum optics and information science, including atomic population inversion, T–As entanglement, T–As-P–F entanglement, and the statistical properties of the P–F as they relate to the model parameters. Our analysis reveals how these quantum resources are affected by different parameters in the T–As-P–F model. Finally, we illustrate the evolving interdependencies among these quantum resources within the system.

Keywords: two atoms; Para–Bose field; quantum dynamics; entanglement; atomic inversion; statistical properties

1 Introduction

The interaction between light and matter is the main focus of quantum optics [1]. The primary and most widely used two models in quantum optics is the Jaynes (Tavis)-Cumming model J–CM (T–CM), which includes one atom and two atoms (T–As) in the presence of field modes [2,3]. The rotating wave approximation and dipole provided an exact solution. The J–CM (T–CM) model’s integrable Hamiltonian was solved to obtain the eigenvalues and eigenvectors of the system under various extensions and quantum effects. The intensity-dependent coupling [4] is one of these extensions. A multi-level atom is another extension, there have been discussions about three-level atoms with constant coupling [5,6,7], four-level atoms [8,9] and five-level atoms in previous literature [10,11,12,13] where nonlinear interactions are considered under different circumstances. A variety of quantum effects are expected within the framework of the J–CM. Examples include the collapse and revival of atomic population inversion, Rabi oscillations, and photon antibunching [14], photon switching [15,16], etc.

Quantum correlations (QCs) are a fundamental feature of quantum systems and serve as an essential tool in the field of quantum information science [17]. Quantum entanglement (QE), one of the most prominent types of QCs, proves valuable for numerous applications, including quantum teleportation [18], quantum key distribution [19], quantum metrology [20], and several others [21,22]. QCs provide precious resources for quantum information tasks. QE had rapid expansion in the last years [23,24], which was also the time when it became an important resource for quantum information processing (QIP). When atomic motion is considered, QIP may have significant applications for the advancement of quantum systems [25]. It has been shown that the von Neumann entropy changes periodically when the time-dependent (t-d) coupling is present. These findings have also been used for the examination of the entanglement that exists between a three-level trapped ion and a laser field [26]. A further extension that may be conducted is to investigate the ways in which the field-mode structure and t-d coupling alter the dynamic characteristics of the cavity field’s Wehrl entropy [27].

In recent decades, numerous researchers have explored extensions and deformations of the bosonic Fock-Heisenberg algebra (HA) to enhance various aspects of quantum field theory, with significant progress made in many areas. Various q-deformations of the simple harmonic oscillator (HO) have been proposed by several authors considering Jackson’s q-calculus [28], leading to the development of novel states associated with q-deformed Lie algebras, including q-coherent, q-squeezed, and q-cat states [29,30,31,32]. Another notable adaptation of the HA is the Wigner algebra, which incorporates the reflection operator R and the Wigner parameter λ in bosonic commutation relations and equations of motion. This algebra includes infinite-dimensional representations for parabosons and finite-dimensional representations for parafermions [33]. Concepts of parafields and parastatistics naturally emerge from these generalizations [34,35]. When λ is associated with the Calogero coupling constant, this algebra provides a symmetry framework for the reduced two-particle Calogero-Sutherland model or the pseudo-HO, useful in solving the quantum mechanical Calogero model [36,37,38,39]. Many systems within quantum optics can be characterized by this model [40], and its SU(1,1) dynamical symmetry has been examined in the study by Perelomov [41,42]. Additionally, when λ = p − 1 / 2 , this algebra transitions to the para-Bose oscillator algebra of order p [43,44], which offers a framework for describing particles that are neither bosons nor fermions. As λ → 0 , the algebra reduces to the standard bosonic algebra.

The concept of coherent states (CSs) have been widely used in quantum optics and information during the last several decades. Schrödinger first introduced CSs to describe systems with a Hamiltonian HO that minimizes quantum mechanical uncertainty [45,46]. Actually, two ways are considered for the construction of CSs known as Klauder–Perelomov and Barut–Girardello CSs [42,47,48]. Moreover, several investigations based on the standard creation and annihilation operators in original J–CM are generalized in the context of f-, q-, and λ-deformed operators [49–58]. Moreover, the conventional J–CM with intensity-dependent coupling and interaction of atoms with a field in the context of Holstein–Primakoff SU(2) and SU(1,1) CSs have been examined [59–61]. Some further extensions have been proposed and studied, including transitions between two or more photons [62] and Jaynes–Cummings–Hubbard model [63,64]. Based on the above consideration, in the present we develop the model of T–As interacting with a quantum field initially prepared in a CS of Para Bose–field (P–F). We examine the dynamic behavior of essential quantum resources relevant to various tasks in quantum optics and information. This includes examining atomic population inversion, T–As entanglement, T–As-P–F entanglement, and the statistical properties of P–F, all in relation to the parameters of the quantum model.

The rest of the article is structured as follows: Section 2 provides a description of the quantum system and outlines its dynamics. In Section 3, we discuss the numerical results alongside the measures of quantumness. Finally, our conclusion is summarized in Section 4.

2 Quantum model

This section represents the Hamiltonian of the interaction of one-mode P–F with T–As of an upper (lower) state | e j ⟩ ( | g j ⟩ )

(1) H ˆ int ( t ) = ∑ j = 1 2 C j ( t ) ( L ˆ | e j ⟩ ⟨ g j | + L ˆ + | g j ⟩ ⟨ e j | ) ,

where L ˆ + ( L ˆ ) is the creation (annihilation) operator of the P–F, acting on the Fock states as [65]

(2) L ˆ † | n ⟩ = h ( n + 1 ) | n + 1 ⟩ , L ˆ | n ⟩ = h ( n ) | n − 1 ⟩ ,

where h is a positive function and is equal to h ( n ) = n + 2 n + 1 2 − n 2 λ , where λ isa real parameter, so-called deformation parameter and [.] designs the integer part. Here the P–F is described through the P–F oscillator algebra that is a pseudo HO algebra characterized by the parameter λ . The function C j ( t ) is considered to describe the t-d coupling strength between the P–F and each one of the T–As. In this study, we concentrate on the case of identical coupling between the T–As and P–F, that is, C 1 ( t ) = C 2 ( t ) = C ( t ) , such that

(3) C ( t ) = ε sin ( t ) with t − d coupling ε without t − d coupling ,

where ε describes the coupling strength between P–F and each one of the T–As in the absence of t-d coupling.

The t-d state of the T–As-P–F system at any time τ > 0 , can be provided as

Next we proceed to solve the system’s equation of motion

(5) − i ℏ ∂ ∂ τ | ψ t - d ( τ ) 〉 = H ˆ int ( t ) | ψ t - d ( τ ) ⟩ ,

with initial system state

(6) | ψ ( 0 ) ⟩ = | ψ T − As ( 0 ) ⟩ ⊗ | ψ P – F ( 0 ) ⟩ = ( cos ⁡ ( θ ) | e 1 e 2 ⟩ + sin ( θ ) | g 1 g 2 ⟩ ) ⊗ ∑ n = 0 ∞ R n ( λ ) | n ⟩ ,

where R n is the amplitude of the superposition coefficients in the CSs of P–F and θ is a parameter characterizing the initial state of the T–As. The T–As is initially in the separable state for θ = 0 while the Bell state case can be obtained for θ = π / 4 .

By substituting the t-d state of the system into the motion equation and using the initial conditions, the functions D j ( n , τ ) are obtained to be

(7) D 1 ( n , τ ) = R n ( λ ) h ( n + 2 , λ ) + h ( n + 1 , λ ) [ cos θ { h ( n + 2 , λ ) + h ( n + 1 , λ ) cos ( d ( τ ) ξ n ( λ ) ) } + sin θ h ( n + 1 , λ ) h ( n + 2 , λ ) × { cos ( d ( τ ) ξ n ( λ ) ) − 1 } ] ,

(8) D 2 ( n , τ ) = − iR n ( λ ) sin ( d ( τ ) ξ n ( λ ) ) ξ n ( λ ) [ cos θ h ( n + 1 , λ ) + sin θ h ( n + 2 , λ ) ] ,

(9) D 4 ( n , τ ) = R n ( λ ) h ( n + 2 , λ ) + h ( n + 1 , λ ) [ h ( n + 1 , λ ) h ( n + 2 , λ ) × cos θ { cos ( d ( τ ) ξ n ( λ ) ) − 1 } + sin θ { h ( n + 2 , λ ) cos ( d ( τ ) ξ n ( λ ) ) + h ( n + 1 , λ ) } ] ,

with D 3 ( n , τ ) = D 2 ( n , τ ) and that

(10) ξ n ( λ ) = 2 h ( n + 2 , λ ) + 2 h ( n + 1 , λ ) ,

and

d ( τ ) = ∫ 0 τ C ( t ) d t .

The CSs corresponding to the P–F are introduced as [65]

(11) | Z , λ ⟩ = ∑ n = 0 ∞ R n ( λ ) | n ⟩ = exp − | Z | 2 2 4 λ ( λ ! ) 3 ( 2 λ ) ! ∑ n = 0 ∞ Z n λ + n 2 ! n 2 ! ( 2 λ + n ) ! × L λ n − 1 2 + 1 2 | Z | 2 2 | n ⟩ ,

where L λ m ( … ) is the associated Laguerre polynomials. In the limit λ = 0 , the CSs of P–F tends to the case of Glauber CSs.

The reduced density matrices of subsystems are obtained from the T–As-P–F density matrix, ρ t - d ( τ ) = | ψ t - d ( τ ) ⟩ ⟨ Ψ t - d ( τ ) | , as

(12) ρ T − As ( τ ) = Tr P – F { ρ t - d ( τ ) } = ∑ j = 1 4 ∑ n = 1 4 ρ jn | j ⟩ ⟨ n | ,

(13) ρ P – F ( τ ) = Tr T − A { ρ t - d ( τ ) } = ∑ k ∞ ρ k | k ⟩ ⟨ k | .

3 Quantum measures and their dynamical behavior

This section displays different measures for quantumness with their dynamical behavior discussion through the effect of t-d coupling ( C ( t ) ) and P–F deformation parameter ( λ ).

3.1 Atomic inversion

We begin by defining the population inversion for the T–As in terms of the functions D j ( n , τ ) as

(14) ρ z ( τ ) = ∑ m = 0 ∞ ( ⌈ D 1 ( m , τ ) ⌉ 2 + ⌈ D 2 ( m , τ ) ⌉ 2 − ⌈ D 3 ( m , τ ) ⌉ 2 − ⌈ D 4 ( m , τ ) ⌉ 2 ) .

In the case where the two atoms are identically coupled, we have D 2 ( m , τ ) = D 3 ( m , τ ) . Under this condition, the expression for the atomic inversion simplifies to

ρ z ( τ ) = ∑ m = 0 ∞ ( ⌈ D 1 ( m , τ ) ⌉ 2 − ⌈ D 4 ( m , τ ) ⌉ 2 ) .

The population inversion, ρ z of T–As with λ = 0 , λ = 1 , and λ = 5 is shown in the Figure 1. In general, it is evident that the parameter λ in the absence and presence of t–d coupling has an impact on the dynamics of the function ρ z . We can see that the function ρ z exhibits rapid oscillations with collapse and revival events in the case of C ( t ) = ε and λ = 0 . Here λ = 0 corresponds to the case of ordinary CSs. When the t-d effect is present, function ρ z oscillations take on a regular and periodic character. Furthermore, we can see that the collapse’s period doesn’t change during the dynamics. On the other hand, in both the absence and presence of the t-d coupling effect, the existence of the deformed field (P–F with λ = 1 and λ = 5 ) enhances the oscillations of the atomic inversion with the increase in their amplitude.

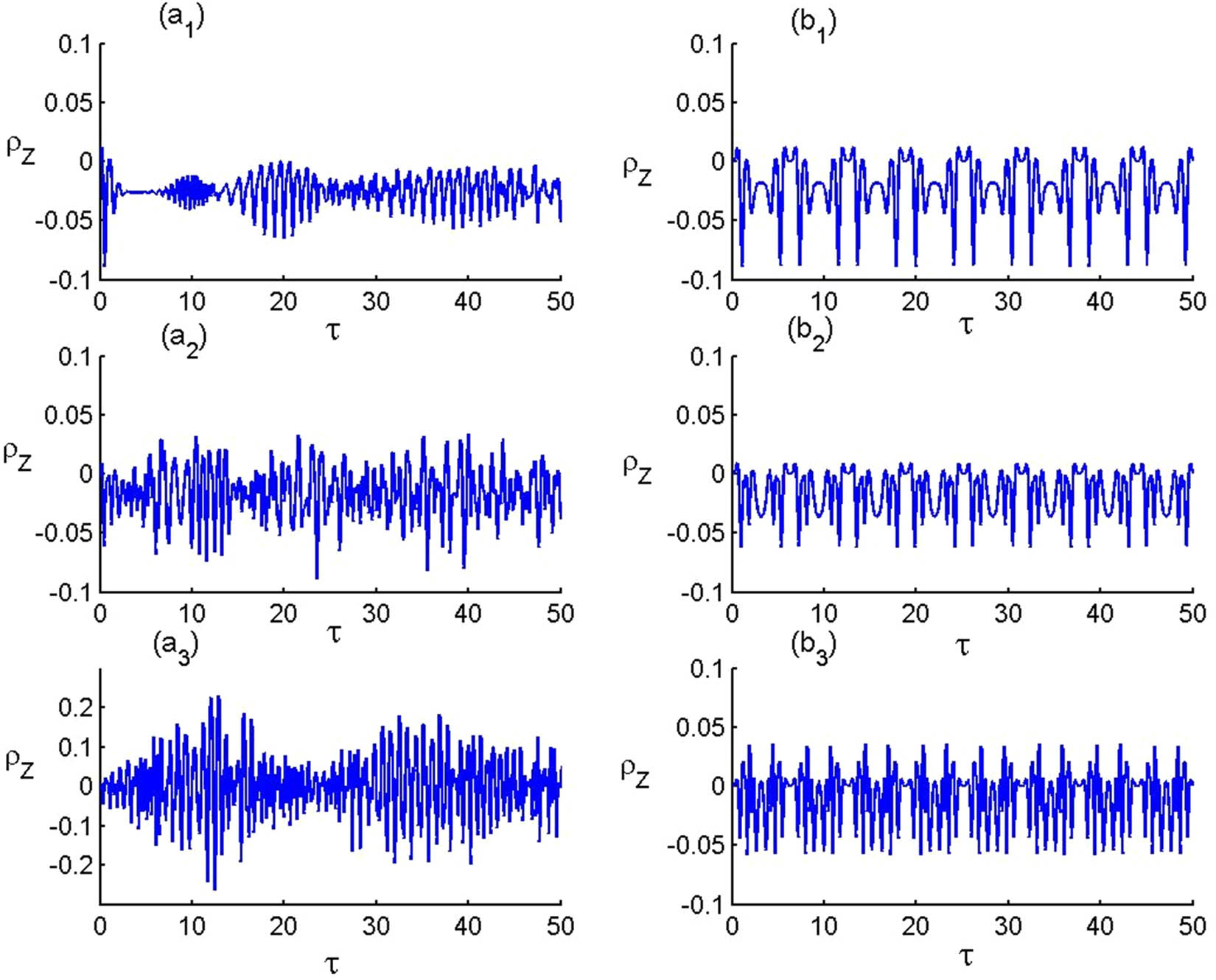
$Figure 1 Time evolution of ρ z {\rho }_{z} for T–As in the presence of P–F with z = 3 and θ = π / 4 . z=3\hspace{0.25em}{\rm{and}}\hspace{0.25em}\theta =\pi /4. Panels (a_i) and (b_i) represent the cases of constant t-d coupling ( C ( t ) = ε C(t)=\varepsilon ) and oscillating t-d coupling ( C ( t ) = ε sin ( t ) ) C(t)\left=\varepsilon \hspace{0.25em}\sin \left(t\left)) , respectively. Panels (a1, b1), (a2, b2), and (a3, b3) correspond to λ values of 0, 1, and 5, respectively.$

Figure 1

Time evolution of ρ z for T–As in the presence of P–F with z = 3 and θ = π / 4 . Panels (a_i) and (b_i) represent the cases of constant t-d coupling ( C ( t ) = ε ) and oscillating t-d coupling ( C ( t ) = ε sin ( t ) ) , respectively. Panels (a1, b1), (a2, b2), and (a3, b3) correspond to λ values of 0, 1, and 5, respectively.

3.2 T–As-P–F entanglement

To analyze the dynamics of the T–As-P–F entanglement, the Neumann entropy of the subsystems, T–A or P–F, is considered as a measure

(15) E P – F ( T − A ) = − Tr { ρ P – F ( T − A ) ln [ ρ P – F ( T − A ) ] } .

Here ρ P – F ( T − A ) represents the P – F ( T − A ) density operator given by Eqs. (14) and (15). The function E F ( T − A ) takes the form

(16) E P – F ( T − A ) = − ∑ l = 1 ∞ ( 4 ) η l P – F ( T − A ) ln η l P – F ( T − A ) ,

where η l P – F ( T − A ) are the eigenvalues of the state ρ P – F ( T − A ) .

In Figure 2, we illustrate the dynamic behavior of quantum entropy in relation to the parameter values of the physical model, using the same parameter settings as in Figure 1. The figure highlights significant physical scenarios based on the values of C ( t ) and λ . The E P – F ( T − A ) function shows t-d growth and oscillates, maintaining a steady oscillatory pattern over extended periods when λ → 0 limit and C ( t ) = ε . The QE of the T–As-P–F state stabilizes within a specific time range, mirroring the behavior of population inversion, and the T–As-P–F entanglement remains trapped by the P–F for large values of scaled time τ . On the other hand, with the t-d coupling effect, E P – F ( T − A ) oscillates periodically with period τ = 2 π , which agrees with the period of population inversion oscillations in the λ → 0 limit with the presence of t-d coupling effect. In the existence of the t-d effect, we discover that the T–As-P–F state approaches the maximum value of entanglement for λ → 5 . This means that the increase in the value of parameter λ results in an increase in the maximum amount of entanglement. Whereas, the behavior of the E P – F ( T − A ) function does not vary much over time in the absence of t-d coupling effect and the presence of field deformation ( λ ≠ 0 ). The obtained results illustrate that the manipulation of the T–As-P–F entanglement in the considered model can be achieved by convenable choice on the coupling function and deformation parameter.

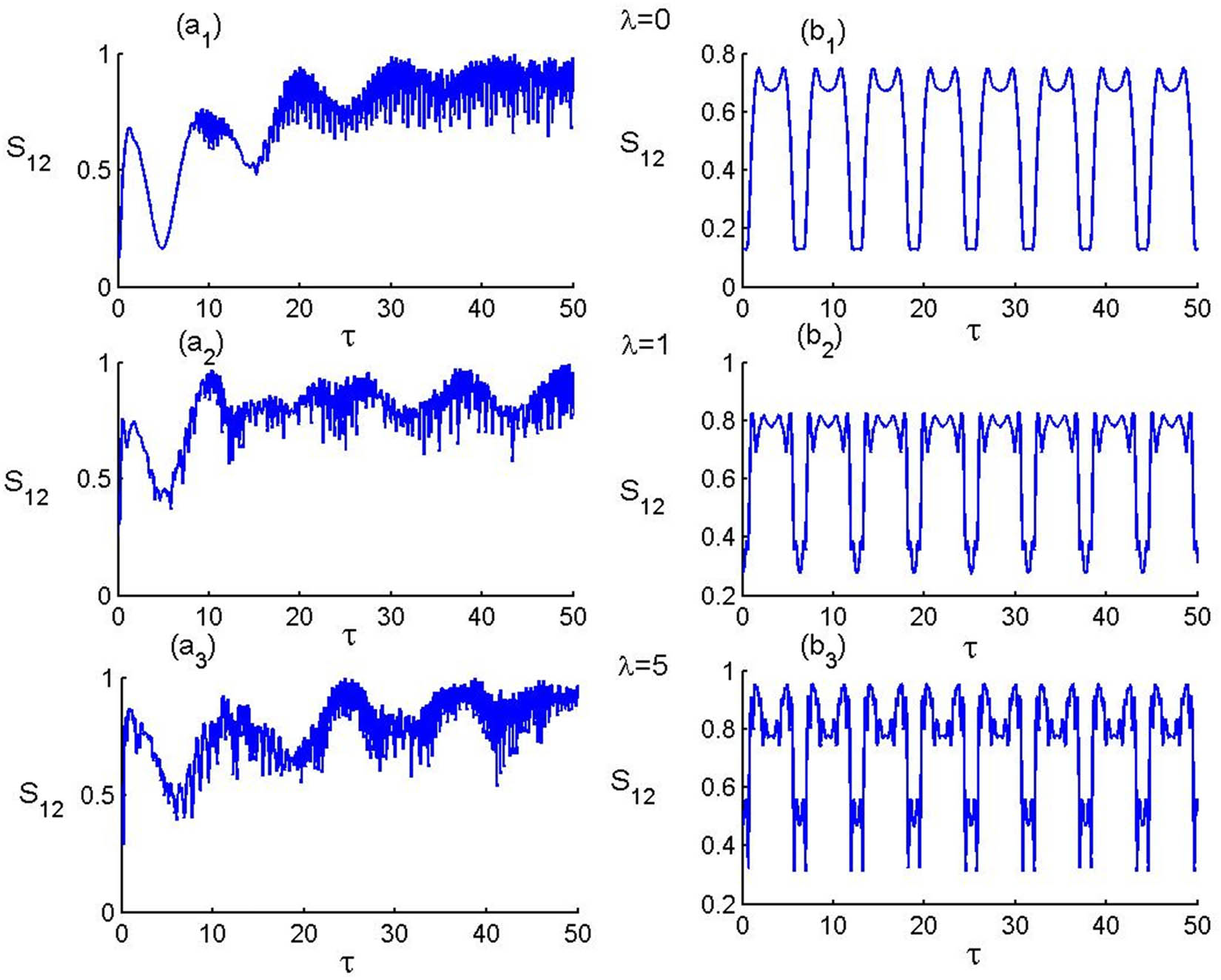
$Figure 2 Time evolution of T–As-P–F entanglement in the presence of P–F with z = 3 and θ = π / 4 . z=3\hspace{0.25em}{\rm{and}}\hspace{0.25em}\theta =\pi /4. Panels (a_i) and (b_i) represent the cases of constant t-d coupling ( C ( t ) = ε C(t)=\varepsilon ) and oscillating t-d coupling ( C ( t ) = ε sin ( t ) C(t)\left=\varepsilon \hspace{0.25em}\sin \left(t) ), respectively. Panels (a1, b1), (a2, b2), and (a3, b3) correspond to λ values of 0, 1, and 5, respectively.$

Figure 2

Time evolution of T–As-P–F entanglement in the presence of P–F with z = 3 and θ = π / 4 . Panels (a_i) and (b_i) represent the cases of constant t-d coupling ( C ( t ) = ε ) and oscillating t-d coupling ( C ( t ) = ε sin ( t ) ), respectively. Panels (a1, b1), (a2, b2), and (a3, b3) correspond to λ values of 0, 1, and 5, respectively.

3.3 T–As entanglement

To analyze the nonlocal correlation between the T–As, we utilize the concurrence that is given by [66]

(17) C 12 ≔ max { 0 , ϑ 1 − ϑ 2 − ϑ 3 − ϑ 4 } ,

where ϑ j represents the eigenvalues of the matrix ρ t - d ρ ∼ t - d , arranged in descending order, and ρ ∼ t - d denotes the density matrix associated with the Pauli matrix σ Y by

(18) ρ ∼ t − d = ( σ Y ⊗ σ Y ) ρ t − d * ( σ Y ⊗ σ Y ) .

Here ρ t − d * is the complex conjugate of ρ t − d . For C 12 = 0 , the T–As state is separable, while for C 12 = 1 , the T–As state is maximally entangled.

Figure 3 shows the time variation of concurrence with regard to the values of the T–As-P–F parameters. In general, it is evident that C ( t ) and λ have a significant impact on the dynamic behavior of the function C 12 . In the absence of t-d coupling and field deformation effects, the value of function C 12 ranges between 0 and 1 illustrating that the QE of the T–As state oscillates between a maximum and minimum value and cannot reach its maximum value at τ = 0 . Indeed, we observe that the function C 12 begins at its maximum value of 1, undergoes random oscillations, and then gradually decreases over time, eventually settling into a steady state of fluctuating oscillations. The function C 12 has a peculiar behavior during evolution, where it takes unexpectedly zero values for a brief time interval, exhibiting sudden birth and death phenomena of QE. The same behavior of the measure of QE can be obtained in the absence of t-d coupling with different values of λ . The periods of the sudden death phenomena remain constant throughout the dynamics when the t-d coupling effect is included, and the concurrence oscillations become regular, exhibiting periodic behavior. The sudden death phenomena of QE will disappear with a regular dynamic of concurrence in the presence of field deformation and t-d coupling effect. This finding suggests that the interaction between the T–As and the P–F in the present model is crucial for maintaining and controlling the QE of the T–As state, and that the dependence on the field’s deformation is considerable with respect to the t-d coupling effect.

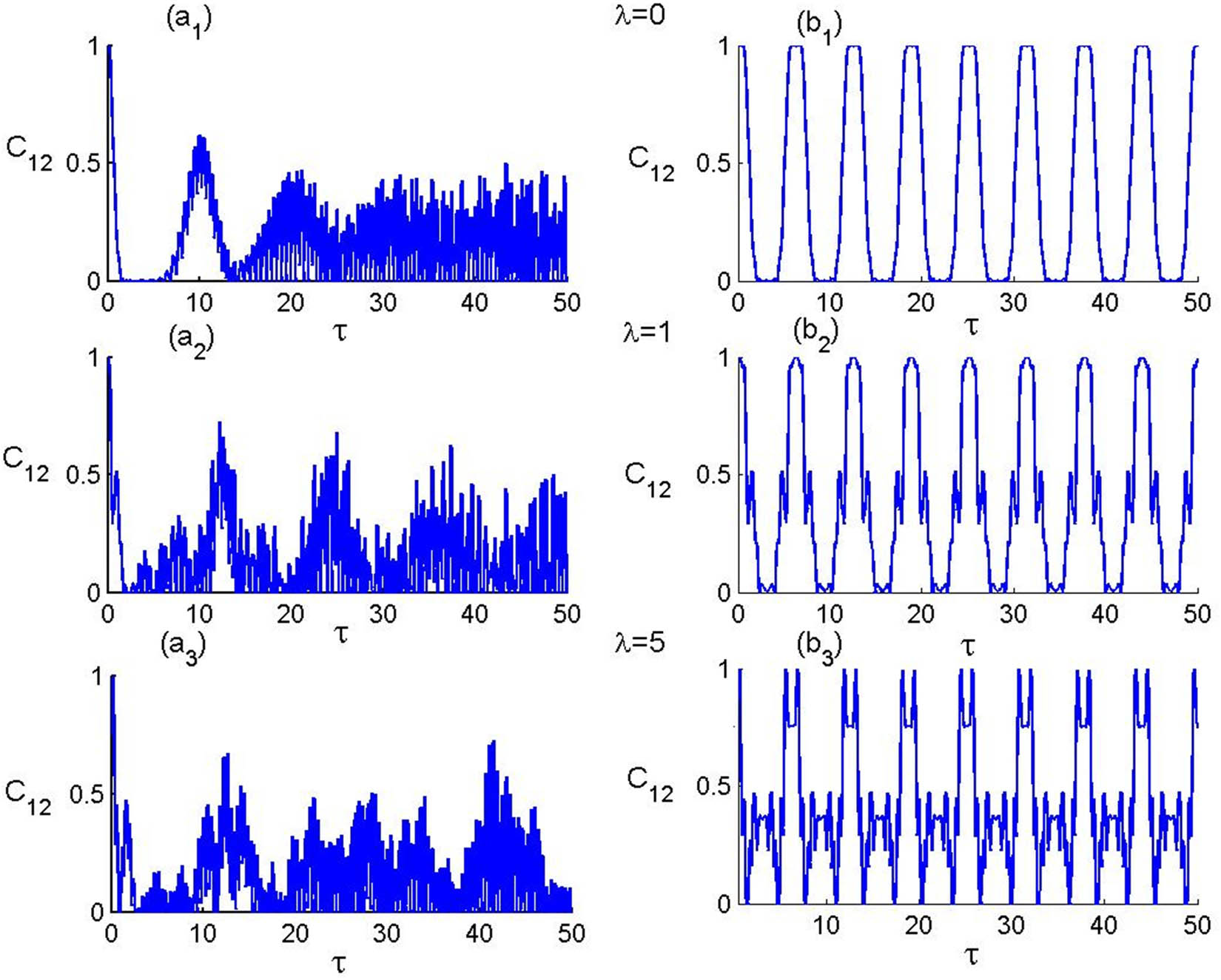
$Figure 3 Time evolution of T–As entanglement in the presence of P–F with z = 3 and θ = π / 4 . z=3\hspace{0.25em}{\rm{and}}\hspace{0.25em}\theta =\pi /4. Panels (a_i) and (b_i) represent the cases of constant t-d coupling ( C ( t ) = ε C(t)=\varepsilon ) and oscillating t-d coupling ( C ( t ) = ε sin ( t ) ) C(t)\left=\varepsilon \hspace{0.25em}\sin \left(t\left)) , respectively. Panels (a1, b1), (a2, b2), and (a3, b3) correspond to λ values of 0, 1, and 5, respectively.$

Figure 3

Time evolution of T–As entanglement in the presence of P–F with z = 3 and θ = π / 4 . Panels (a_i) and (b_i) represent the cases of constant t-d coupling ( C ( t ) = ε ) and oscillating t-d coupling ( C ( t ) = ε sin ( t ) ) , respectively. Panels (a1, b1), (a2, b2), and (a3, b3) correspond to λ values of 0, 1, and 5, respectively.

3.4 Statistical properties of the P–F

Now, we analyze the distribution of P–F photons using the Mandel parameter that is defined by [67,68]

(19) Q M = 1 Tr ( L ˆ † L ˆ ) { Tr ( L ˆ † L ˆ ) 2 − [ Tr ( L ˆ † L ˆ ) ] 2 − Tr ( L ˆ † L ˆ ) } .

The P–F exhibits the Poissonian statistics for Q M = 0 , while P–F has sub-Poissonian statistics for Q M < 0 , and governed by a super-Poissonian statistics when Q M > 0 . Figure 4 shows the dynamics of the Mandel parameter with regard to the values of the T–As-P–F parameters. It is clear that the parameter Q M < 0 and Q M > 0 during the dynamics for different choice of C ( t ) and λ , exhibiting a sub-Poissonian and super-Poissonian photon distribution. Notably, selecting suitable values for C ( t ) and λ can reduce the value of Q M .

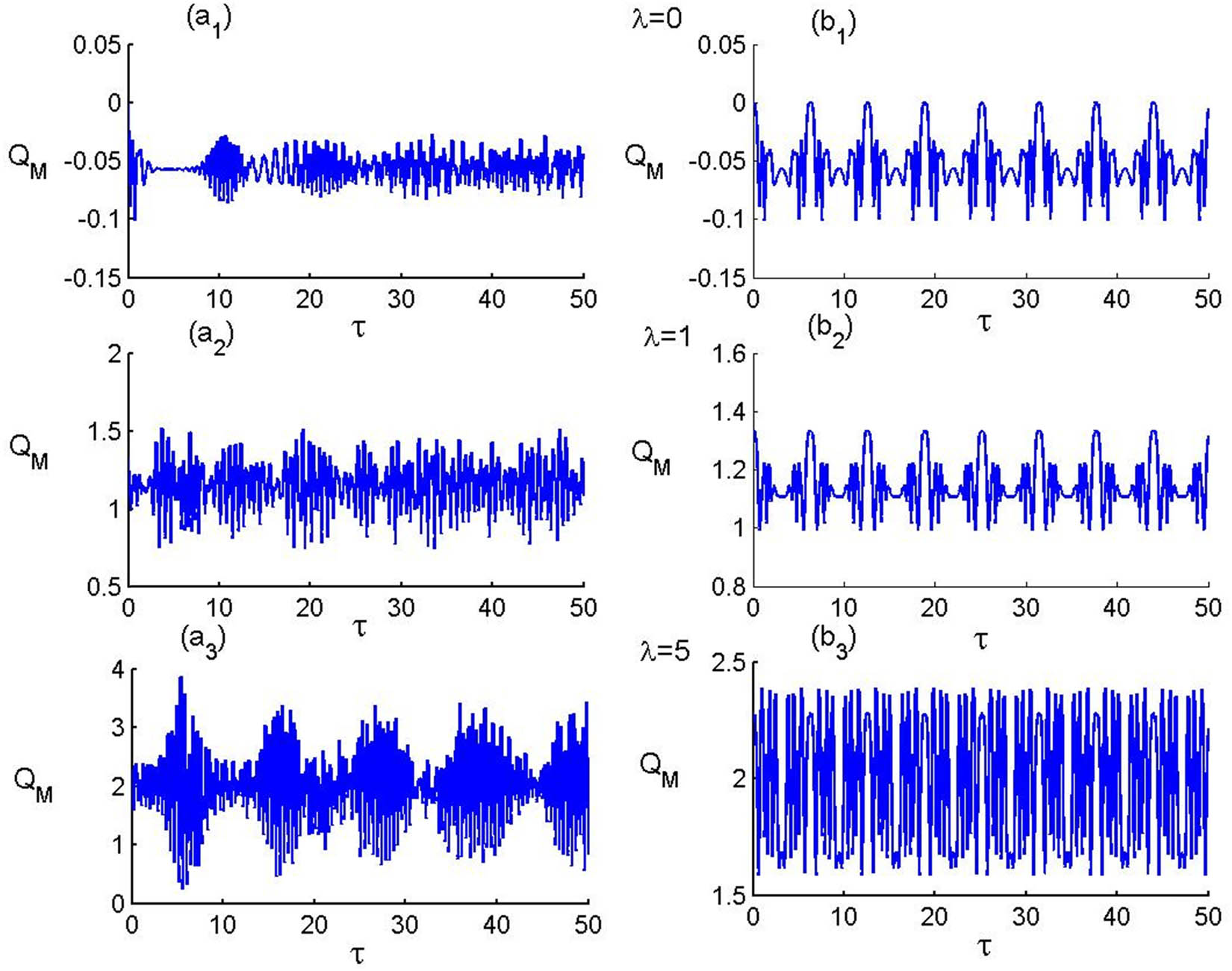
$Figure 4 The Mandel parameter for the P–F with z = 3 and θ = π / 4 . z=3\hspace{0.25em}{\rm{and}}\hspace{0.25em}\theta =\pi /4. Panels (a_i) and (b_i) represent the cases of constant t-d coupling ( C ( t ) = ε C(t)=\varepsilon ) and oscillating t-d coupling ( C ( t ) = ε sin ( t ) ) C(t)\left=\varepsilon \hspace{0.25em}\sin \left({\rm{t}}\left)) , respectively. Panels (a1, b1), (a2, b2), and (a3, b3) correspond to λ values of 0, 1, and 5, respectively.$

Figure 4

The Mandel parameter for the P–F with z = 3 and θ = π / 4 . Panels (a_i) and (b_i) represent the cases of constant t-d coupling ( C ( t ) = ε ) and oscillating t-d coupling ( C ( t ) = ε sin ( t ) ) , respectively. Panels (a1, b1), (a2, b2), and (a3, b3) correspond to λ values of 0, 1, and 5, respectively.

4 Conclusion

In this article, we have developed a model of T–As system that interacts with a field mode initially defined in a CS of P–F. We have considered that the T–As are initially described by a Bell state and display the quantum model of the whole system with the solution of the dynamics equation in the absence and presence of t-d coupling effect. We have examined the t-d behavior of essential quantum resources relevant to various tasks in quantum optics and information science, including atomic population inversion, T–As entanglement, T–As-P–F entanglement, and the statistical properties of the P–F as they relate to the model parameters. In this context, our analysis revealed how these quantum resources are affected by different parameters in the T–As-P–F model. Finally, we have illustrated the evolving interdependencies among these quantum resources within the quantum system.

Funding information: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R225), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors state no conflict of interest.
Data availability statement: All data generated or analyzed during this study are included in this published article.

References

[1] Jaynes ET, Cummings FW. Comparison of quantum and semiclassical radiation theories with applications to the beam maser. Proc IEEE. 1963;51:89.10.1109/PROC.1963.1664Search in Google Scholar

[2] Tavis M, Cummings FW. Exact solution for an N-molecule-radiation-field hamiltonian. Phys Rev. 1968;170:379.10.1103/PhysRev.170.379Search in Google Scholar

[3] Cummings FW. Stimulated emission of radiation in a single mode. Phys Rev A. 1965;140:A1051.10.1103/PhysRev.140.A1051Search in Google Scholar

[4] Chang Z. Generalized Jaynes-Cummings model with an intensity-dependent coupling interacting with a quantum group-theoretic coherent state. Phys Rev A. 1993;47:5017–23.10.1103/PhysRevA.47.5017Search in Google Scholar PubMed

[5] Yoo HI, Eberly JH. Dynamical theory of an atom with two or three levels interacting with quantized cavity fields. Phys Rep. 1985;118:239.10.1016/0370-1573(85)90015-8Search in Google Scholar

[6] Tavassoly MK, Yadollahi F. Dynamics of states in the nonlinear interaction regime between a three-level atom and generalized coherent states and their non-classical features. Int J Mod Phys B. 2012;26:1250027.10.1142/S0217979212500270Search in Google Scholar

[7] Fahgihi MJ, Tavassoly MK. Dynamics of entropy and nonclassical properties of the state of a Λ-type three-level atom interacting with a single-mode cavity field with intensity-dependent coupling in a Kerr medium. J Phys B: Mol Opt Phys. 2012;45:035502.10.1088/0953-4075/45/3/035502Search in Google Scholar

[8] Xu W, Gao JY. Absorption mechanism in a four-level system. Phys Rev A. 2003;67:033816–22.10.1103/PhysRevA.67.033816Search in Google Scholar

[9] Abdel-Wahab NH, Thabet L. Dynamics of N-configuration four-level atom interacting with one-mode cavity field. Eur Phys J Plus. 2014;129:1–10.10.1140/epjp/i2014-14144-9Search in Google Scholar

[10] Bhattacharyya D, Ray B, Ghosh PN. Theoretical study of electromagnetically induced transparency in a five-level atom and application to Doppler-broadened and Dopplerfree Rb atoms. J Phys B: At Mol Opt Phys. 2007;40:4061–70.10.1088/0953-4075/40/20/008Search in Google Scholar

[11] Nawaz SM, Tarak ND, Kanhaiya P. Microwave assisted transparency in M-system. J Phys B: At Mol Opt Phys. 2017;50:195502.10.1088/1361-6455/aa8a35Search in Google Scholar

[12] Amanjot K, Paramjit K. Dressed state analysis of electromagnetically induced transparency in a five-level X-type atomic system with wavelength mismatching effects. Phys Scr. 2018;93:115101–18.10.1088/1402-4896/aadec9Search in Google Scholar

[13] Li J, Ren-Gang W. Amplitude and phase-controlled absorption and dispersion of coherently driven five-level atom in double-band photonic crystal. Chin Phys B. 2019;28(2):024206–12.10.1088/1674-1056/28/2/024206Search in Google Scholar

[14] Ben1 L, Jing-Biao C. Photon antibunching. Rev Mod Phys. 1982;54:1061.10.1103/RevModPhys.54.1061Search in Google Scholar

[15] Harris SE, Yamamoto Y. Photon switching by quantum interference. Phys Rev Lett. 1998;81:3611–4.10.1103/PhysRevLett.81.3611Search in Google Scholar

[16] Yan M, Edward G, Zhu Y. Observation and absorptive photon switching by quantum interference. Phys Rev A. 2001;64:041801–4.10.1103/PhysRevA.64.041801Search in Google Scholar

[17] Bell JS. On the Einstein Podolsky Rosen paradox. Phys Phys Fiz. 1964;1(3):195.10.1103/PhysicsPhysiqueFizika.1.195Search in Google Scholar

[18] Bennett CH, Brassard G, Crépeau C, Jozsa R, Peres A, Wootters WK. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys Rev Lett. 1993;70(13):1895.10.1103/PhysRevLett.70.1895Search in Google Scholar PubMed

[19] Ekert AK. Quantum cryptography based on Bell’s theorem. Phys Rev Lett. 1991;67(6):661.10.1103/PhysRevLett.67.661Search in Google Scholar PubMed

[20] Maccone L. Intuitive reason for the usefulness of entanglement in quantum metrology. Phys Rev A. 2013;88(4):042109.10.1103/PhysRevA.88.042109Search in Google Scholar

[21] Horodecki R, Horodecki P, Horodecki M, Horodecki K. Quantum entanglement. Rev Mod Phys. 2009;81(2):865–942.10.1103/RevModPhys.81.865Search in Google Scholar

[22] Adesso G, Bromley TR, Cianciaruso M. Measures and applications of quantum correlations. J Phys A. 2016;49(47):473001.10.1088/1751-8113/49/47/473001Search in Google Scholar

[23] Brody J. Quantum entanglement. Cambridge, MA: The MIT Press Essential Knowledge series, Paperback–Illustrated; 2020.Search in Google Scholar

[24] Vedral V. Quantum entanglement. Nat Phys. 2014;10:256–8.10.1038/nphys2904Search in Google Scholar

[25] Gingrich RM, Christoph A. Quantum entanglement of moving bodies. Phys Rev Lett. 2002;89:270402.10.1103/PhysRevLett.89.270402Search in Google Scholar PubMed

[26] Abdel-Aty M, Wahiddin MR, Abdalla MS, Obada AS. Entanglement of a three-level trapped atom in the presence of another three-level trapped atom. Opt Commun. 2006;265:551–8.10.1016/j.optcom.2006.03.063Search in Google Scholar

[27] Abdel-Khalek S, Obada A-SF. The atomic Wehrl entropy of a V-type three-level atom interacting with two-mode squeezed vacuum state. J Russ Laser Res. 2009;30:146–56.10.1007/s10946-009-9066-1Search in Google Scholar

[28] Arik M, Coon DD. Hilbert spaces of analytic functions and generalized coherent states. J Math Phys. 1976;17:524.10.1063/1.522937Search in Google Scholar

[29] Fakhri H, Hashemi A. Nonclassical properties of the q-coherent and q-cat states of the Biedenharn–Macfarlane q oscillator with q > 1. Phys Rev A. 2016;93:013802.10.1103/PhysRevA.93.013802Search in Google Scholar

[30] Fakhri H, Sayyah-Fard M. Nonclassical properties of the Arik-Coon q−1-oscillator coherent states on the noncommutative complex plane Cq. Int J Geom Meth Mod Phys. 2017;14:1750165.Search in Google Scholar

[31] Fakhri H, Sayyah-Fard M. q-coherent states associated with the noncommutative complex plane C2 q for the Biedenharn–Macfarlane q-oscillator. Ann Phys. 2017;387:14.10.1142/S0219887817501651Search in Google Scholar

[32] Fakhri H, Sayyah-Fard M. Noncommutative photon-added squeezed vacuum states. Mod Phys Lett A. 2020;35:2050167.10.1142/S0217732320501679Search in Google Scholar

[33] Plyushchay MS. Deformed Heisenberg algebra with reflection. Nucl Phys B. 1997;491:619.10.1016/S0550-3213(97)00065-5Search in Google Scholar

[34] Green HS. A generalized method of field quantization. Phys Rev. 1953;90:270.10.1103/PhysRev.90.270Search in Google Scholar

[35] Ohnuki Y, Kamefuchi S. Quantum field theory and parastatistics. Tokyo: University Press of Tokyo; 1982.10.1007/978-3-642-68622-1Search in Google Scholar

[36] Polychronakos AP. Exchange operator formalism for integrable systems of particles. Phys Rev Lett. 1992;69:703.10.1103/PhysRevLett.69.703Search in Google Scholar PubMed

[37] Brink L, Hansson TH, Konstein S, Vasiliev MA. The Calogero model-anyonic representation, fermionic extension and supersymmetry. Nucl Phys B. 1993;401:591.10.1016/0550-3213(93)90315-GSearch in Google Scholar

[38] Mojaveri B, Dehghani A, Jafarzadeh R. Bahrbeig, Excitation on the para-Bose states: Nonclassical properties. Euro Phys J Plus. 2018;133:346.10.1140/epjp/i2018-12163-2Search in Google Scholar

[39] Dehghani A, Mojaveri B, Bahrbeig RJ, Nosrati F, Franco RL. Entanglement transfer in a noisy cavity network with parity-deformed fields. J Opt Soc Am B. 2019;36:1858.10.1364/JOSAB.36.001858Search in Google Scholar

[40] Mojaveri B, Dehghani A, Ahmadi Z. A quantum correlated heat engine based on the parity-deformed Jaynes–Cummings model: Achieving the classical Carnot efficiency by a local classical field. Phys Scr. 2021;96:115102.10.1088/1402-4896/ac1638Search in Google Scholar

[41] Perelomov AM. Generalized coherent states and some of their applications. Sov Phys Usp. 1977;20:703.10.1070/PU1977v020n09ABEH005459Search in Google Scholar

[42] Perelomov AM. Generalized coherent states and their applications. Berlin: Springer; 1986.10.1007/978-3-642-61629-7Search in Google Scholar

[43] Alderete CH, Vergara LV, Rodriguez-Lara BM. Nonclassical and semiclassical para-Bose states. Phys Rev A. 2017;95:043835.10.1103/PhysRevA.95.043835Search in Google Scholar

[44] Huerta Alderete C, Rodriguez-Lara BM. Simulating para-Fermi oscillators. Sci Rep. 2018;8:11572.10.1038/s41598-018-29771-2Search in Google Scholar PubMed PubMed Central

[45] Shrödinger E. The constant crossover of micro-to macro-mechanics. Naturwissenschaftler. 1926;14:664.Search in Google Scholar

[46] Glauber RJ. Coherent and incoherent states of the radiation field. Phys Rev. 1963;131:2766–88.10.1103/PhysRev.131.2766Search in Google Scholar

[47] Ali ST, Antoine JP, Gazeau JP. Coherent states, wavelets and their generalizations. Berlin: Springer; 2000.10.1007/978-1-4612-1258-4Search in Google Scholar

[48] Man’ko VI, Marmo G, Sudarshan ECG, Zaccaria F. f-Oscillators and nonlinear coherent states. Phys Scr. 1997;55:528.10.1088/0031-8949/55/5/004Search in Google Scholar

[49] Dehghani A, Mojaveri B, Shirin S, Amiri Faseghandis, S. Parity deformed Jaynes-Cummings Model: “Robust maximally entangled states. Sci Rep. 2016;6:38069.10.1038/srep38069Search in Google Scholar PubMed PubMed Central

[50] de los Santos-Sanchez O, Recamier J. f-deformed Jaynes–Cummings model and its nonlinear coherent states. J Phys B. 2012;45:015502.10.1088/0953-4075/45/1/015502Search in Google Scholar

[51] Cordero S, Nahmad-Achar E, Castaños O, López-Peña R. A general system of n levels interacting with electromagnetic modes. Phys Scr. 2017;92:044004.10.1088/1402-4896/aa6363Search in Google Scholar

[52] Cordero S, Castaños O, López-Peña R, Nahmad-Achar E. Variational study of λ and N atomic configurations interacting with an electromagnetic field of two modes. Phys Rev A. 2016;94:013802.10.1103/PhysRevA.94.013802Search in Google Scholar

[53] Castaños O, Cordero S, Nahmad-Achar E, López-Peña R. Coupling n-level atoms with l-modes of quantised light in a resonator. J Phys: Conf Ser. 2016;698(1):012006. IOP Publishing.10.1088/1742-6596/698/1/012006Search in Google Scholar

[54] Cordero S, Nahmad-Achar E, López-Peña R, Castaños O. Polychromatic phase diagram for n-level atoms interacting with ℓ modes of an electromagnetic field. Phys Rev A. 2015;92:053843.10.1103/PhysRevA.92.053843Search in Google Scholar

[55] Medina-Armendariz MA, Quezada LF, Sun GH, Dong SH. Exploring entanglement dynamics in an optomechanical cavity with a type-V qutrit and quantized two-mode field. Phys A: Stat Mech Appl. 2024;635:129514.10.2139/ssrn.4619729Search in Google Scholar

[56] Quezada LF, Zhang GQ, Martín-Ruiz A, Dong. SH. Exploring quantum critical phenomena in a nonlinear Dicke model through algebraic deformation. Results Phys. 2023;55:107157‏.10.1016/j.rinp.2023.107157Search in Google Scholar

[57] Fakhri H, Mirzaei S, Sayyah-Fard M. Two-photon Jaynes–Cummings model: a two-level atom interacting with the para-Bose field. Quantum Inf Process. 2021;23:398.10.1007/s11128-021-03338-zSearch in Google Scholar

[58] Mojaveri B, Dehghani A, Ahmadi Z, Amiri Faseghandis S. Interaction of a para-Bose state with two two-level atoms: control of dissipation by a local classical field. Eur Phys J Plus. 2020;135:1–25.10.1140/epjp/s13360-020-00236-8Search in Google Scholar

[59] Buzek V. Jaynes–Cummings model with intensity-dependent coupling interacting with Holstein–Primak of SU(1, 1) coherent state. Phys Rev A. 1989;39:3196.10.1103/PhysRevA.39.3196Search in Google Scholar

[60] Buzek V. SU(1,1) squeezing of SU(1,1) generalized coherent states. J Mod Opt. 1990;37:303.10.1080/09500349014550371Search in Google Scholar

[61] Gerry CC, Welc RF. Dynamics of a two-mode two-photon Jaynes–Cummings model interacting with correlated SU(1, 1) coherent states. J Opt Soc Am B. 1992;9:290.10.1364/JOSAB.9.000290Search in Google Scholar

[62] Abdel-Khalek S, Berrada K, Eleuch H, Abel-Aty M. Dynamics of Wehrl entropy of a degenerate two-photon process with a nonlinear medium‏. Opt Quantum Electron. 2011;42:887–97.10.1007/s11082-011-9498-zSearch in Google Scholar

[63] Li C, Zhang XZ, Song Z. Equivalent spin-orbit interaction in the two-polariton Jaynes–Cummings–Hubbard model. Sci Rep. 2015;5:11945.10.1038/srep11945Search in Google Scholar PubMed PubMed Central

[64] Prasad SB, Martin AM. Effective three-body interactions in Jaynes–Cummings–Hubbard systems. Sci Rep. 2018;8:16253.10.1038/s41598-018-33907-9Search in Google Scholar PubMed PubMed Central

[65] Fakhri H, Sayyah‑Fard M. The Jaynes–Cummings model of a two-level atom in a single-mode para-Bose cavity field. Sci Reports. 2021;11:22861.10.1038/s41598-021-02150-0Search in Google Scholar PubMed PubMed Central

[66] Wootters WK. Entanglement of formation and concurrence. Quantum Inf Comput. 2001;1:27.10.26421/QIC1.1-3Search in Google Scholar

[67] Singh S. Field statistics in some generalized Jaynes-Cummings models. Phys Rev A. 1982;25:3206.10.1103/PhysRevA.25.3206Search in Google Scholar

[68] Mandel L, Wolf E. Optical coherent and quantum optics. Cambridge: Cambridge University Press; 1955.Search in Google Scholar

Received: 2024-06-30

Revised: 2024-11-10

Accepted: 2024-11-29

Published Online: 2025-07-07

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/phys-2024-0118

Keywords for this article

two atoms; Para–Bose field; quantum dynamics; entanglement; atomic inversion; statistical properties

Creative Commons

BY 4.0