A comparative study of quantum resources in bipartite Lipkin–Meshkov–Glick model under DM interaction and Zeeman splitting

Mourad Benzahra; Heba Allhibi; Fahad Aljuaydi; Mostafa Mansour; Abdel-Baset A. Mohamed

doi:10.1515/phys-2025-0216

Article Open Access

A comparative study of quantum resources in bipartite Lipkin–Meshkov–Glick model under DM interaction and Zeeman splitting

Mourad Benzahra , Heba Allhibi , Fahad Aljuaydi , Mostafa Mansour and Abdel-Baset A. Mohamed

Published/Copyright: November 4, 2025

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

From the journal Open Physics Volume 23 Issue 1

Abstract

We assess the thermal resilience of key quantum resources-( ℓ 1 )-norm coherence ( Q ), quantum discord ( D ), logarithmic negativity ( ℒN ), Bell nonlocality ( ℬ ), and quantum steering ( S )-in a bipartite Lipkin–Meshkov–Glick (LMG) spin system subject to competing Dzyaloshinskii–Moriya (DM) interactions and Zeeman splitting. By varying temperature ( T ), spin–spin coupling ( λ ), magnetic field strength ( B 0 ), and DM amplitude ( D z ), we reveal a clear hierarchy of thermal stability: coherence and discord remain robust well beyond the temperatures at which nonlocality ( ℬ ), steering ( S ), and bipartite entanglement ( ℒN ) undergo successive thermal collapse. Stronger spin–spin coupling λ and nonzero DM strength D z ≥ 0 not only amplify overall quantum correlations but also elevate the critical temperatures T c for the survival of each resource. In contrast, a large B 0 polarizes the spins into paramagnetic states, thereby suppressing all quantum features at fixed T . Notably, high amplitude of DM interactions preserves residual coherence and discord even in the high-temperature limit ( T ≫ T c ) . These results establish practical operating thresholds for LMG-based quantum technologies in thermal environments and highlight D z as a powerful tuning parameter for engineering thermally robust quantum resources.

Keywords: Lipkin–Meshkov–Glick model; quantum coherence; quantum discord; quantum steering; Bell nonlocality; DM interaction

1 Introduction

Quantum coherence, emerging from the superposition of quantum states, serves as the foundation for all nonclassical phenomena, quantified by the off-diagonal elements of the density matrix within a specified basis [1,2]. This coherence is formalized through a resource-theoretic framework, where the l 1 -norm acts as a well-established measure [2]. Hierarchically, coherence underpins entanglement, a stronger form of correlations characterized by nonlocal state collapse upon subsystem measurement. Entanglement can be measured by entanglement of formation [3], concurrence [4], negativity [5], and resource theories that constrain its manipulation under local operations [6,7]. Quantum discord, capture correlations inaccessible to classical observers [8,9]. Quantum discord diverges from entanglement in mixed states, highlighting its distinct role in quantum information processing [10–12].

Nonlocality, validated through Bell inequality violations in photonic [13] and superconducting circuits [14], challenges classical realism by rejecting local hidden variable models [15]. However, its relationship with entanglement is nuanced, illustrating their ambiguous correspondence [16,17]. Steering [18–20], an asymmetric phenomenon in which one party remotely manipulates another’s state through local measurements, further stratifies these correlations [19,21,22]. The coexistence of coherence, entanglement, Bell nonlocality, quantum discord, and quantum steering resists unambiguous distinction even in bipartite systems. The lack of connections between these measures, combined with the inherent difficulty of separating entangled and separable states – implies that optimizing one resource does not inherently amplify others. This necessitates a multimeasure approach, as distinct correlations dominate in specific parameter regimes. Within the bipartite Lipkin–Meshkov–Glick (LMG) framework, we map their hierarchical relationships, identifying critical thresholds where spin–spin coupling ( λ ), anisotropy δ , Dzyaloshinskii–Moriya (DM) interaction ( D z ), external magnetic field B 0 , and thermal fluctuations ( T ) dictate the prominence of specific correlations for practical quantum protocols. The LMG model [23–25], an exactly solvable system, originated in nuclear physics to describe shape phase transitions through collective spin interactions. The model is used, initially for testing nuclear many-body approximations like Hartree–Fock and random phase approximations (RPA) [26–29], and was later recognized as a geometric analog of a quantum top in a magnetic field [30,31] and enabling description of diverse systems: double-well potentials, and infinite-range spin systems [32]. This duality propelled its adoption across disciplines. In the condensed matter, it models macroscopic single molecular magnets [33,34] and transitions in Bose–Einstein condensates [35].

In the field of quantum information science, the LMG model has served as a prominent platform for investigating quantum correlations, particularly in the context of quantum phase transitions (QPTs). Extensive studies have been conducted on two-spin entanglement [36–39], entanglement entropy [40,41], and multipartite entanglement [42–44], alongside analyses of multipartite nonlocality [45], quantum discord [46,47], and quantum correlations [48]. Furthermore, critical phenomena in the ( ℒℳG ) model have been thoroughly examined using measures such as fidelity susceptibility [49,50], quantum Fisher information [51], and dynamical indicators including the Loschmidt echo and fidelity [52]. The LMG model is also employed as the working medium in quantum Otto engines based on a two-site configuration, subjected to external magnetic fields and symmetric cross-interactions [53]. It is also worth highlighting that the LMG model has garnered considerable attention not only from a theoretical standpoint but also in terms of potential experimental realizations. Proposals have been made to implement the model using Bose–Einstein condensates in double-well potentials [54], cavity-based quantum optical systems [55,56], and circuit quantum electrodynamics (circuit QED) platforms [57]. More recently, significant progress has been achieved in simulating ( ℒℳG ) dynamics with all-to-all interactions in trapped-ion setups [58,59], nitrogen-vacancy center ensembles [60], and superconducting qubit networks [61], where the dynamical phase transition has been experimentally demonstrated [61].

We investigate the intricate dynamics of quantum resources: ℓ 1 -norm coherence Q , quantum discord ( D ), logarithmic negativity ( ℒN ), Bell nonlocality ( ℬ ), and quantum steering ( S ), within the ℒℳG model, focusing on their behavior under the influence of thermal noise, external magnetic fields, DM interaction, and variations in system parameters.

This paper is organized as follows. Section 2 introduces the used quantifiers, including coherence, discord, entanglement, Bell nonlocality, and steering. Section 3 investigates the Hamiltonian structure and the thermal density matrix of the bipartite LMG system. In Section 4, the interplay between system parameters and key measures dynamics is investigated, with theoretical insights supported by numerical simulations. Finally, Section 5 summarizes key findings, discusses implications for emerging quantum technologies, and outlines promising avenues for future research.

2 Quantum resources

This section investigates quantum resources within the bipartite LMG model. Entanglement is measured using the LN, while quantum discord evaluates nonclassical correlations that extend beyond entanglement. Bell nonlocality is identified through violations of the Clauser–Horne–Shimony–Holt (CHSH) inequality, and quantum steering is assessed via the Cavalcanti–Jones–Wiseman–Reid steering criterion [62]. These metrics are examined as functions of temperature T , spin–spin coupling strength λ , DM interaction parameter D z , and Zeeman splitting B 0 .

2.1 l 1 -norm of coherence function

Quantum coherence is an important feature derived from the principle of superposition in quantum physics. A well-established framework for quantifying coherence, has been extensively developed in recent studies [1,2]. This theory determines the set of incoherent states J that are diagonal in a taken basis { ∣ j ⟩ } :

(1) γ ∈ J ⇔ γ = ∑ j γ j ∣ j ⟩ ⟨ j ∣ .

Incoherent operations that transform incoherent states into other incoherent states are known as free operations. Detecting and quantifying quantum coherence plays a vital role in enabling quantum correlations and facilitating information processing in the quantum system. In this sense, Baumgratz et al. [2] introduced the l 1 -norm of coherence as a metric for measuring coherence, which is defined as follows:

(2) Q ( ρ ) = ∑ i ≠ j ∣ ⟨ i ∣ ρ ∣ j ⟩ ∣ = ∑ i , j ∣ ρ i j ∣ − ∑ i ∣ ρ ii ∣ ,

with ρ representing the density matrix in the system under consideration.

2.2 Quantum discord function

Quantum discord (QD) [8] provides a rigorous measure of nonclassical correlations that persist even in separable quantum states. For a bipartite system, QD is operationally defined as the discrepancy between total quantum mutual information ℐ ( ϱ ) and classical correlations C ( ϱ ) :

(3) D ( ϱ ) = ℐ ( ϱ ) − C ( ϱ ) ,

where ℐ ( ϱ ) represents the quantum mutual information quantifies total correlations giving by

(4) ℐ ( ϱ ) = S ( ϱ A ) + S ( ϱ B ) − S ( ϱ ) ,

and C ( ϱ ) represents the classical correlations obtained via measurement optimization:

(5) C ( ϱ ) = S ( ϱ A ) − min { Π i B } ∑ i p i S ( ϱ A ∣ i ) .

Here, S ( ϱ ) = − Tr ( ϱ log 2 ϱ ) denotes the von Neumann entropy, ϱ A ∣ i = Tr B ( Π i B ϱ Π i B ) ∕ p i represents post-measurement states on subsystem A with probability p i = Tr ( Π i B ϱ ) , and { Π i B } forms a complete set of orthogonal projectors on subsystem B . Rewriting QD through conditional entropy minimization [63,64] yields:

(6) D ( ϱ ) = min { Π B i } [ S ( ϱ ∣ { Π B i } ) + S ( ϱ B ) − S ( ϱ ) ] .

The computational complexity of this minimization restricts analytical solutions to specific state classes. For the bipartite X-state, the density matrix adopts the structured form:

(7) ρ X = ρ 11 0 0 ρ 14 0 ρ 22 ρ 23 0 0 ρ 23 * ρ 33 0 ρ 14 * 0 0 ρ 44 ,

where the diagonal elements ρ i i represent classical state populations, while the off-diagonal terms ρ 14 and ρ 23 govern quantum coherence. For such X-states, quantum discord (QD) can be expressed in a closed form [10,64] as follows:

(8) D ( ρ X ) = min { d 1 , d 2 } ,

with correlation measures:

(9) d j = F ( ρ 11 + ρ 33 ) + ∑ n = 1 4 λ n log 2 λ n + w j ,

where { λ n } are eigenvalues of ρ X , and the measurement-dependent terms:

(10) w 1 = F ( ξ ) ,

(11) w 2 = − F ( ρ 11 + ρ 33 ) − ∑ n = 1 4 ρ n n log 2 ρ n n ,

employ the binary entropy function:

(12) F ( ξ ) = − ξ log 2 ξ − ( 1 − ξ ) log 2 ( 1 − ξ ) .

The critical parameter ξ encapsulates the competition between off-diagonal terms ∣ ρ 14 ∣ + ∣ ρ 23 ∣ and the considered state populations ρ 33 + ρ 44 :

(13) ξ = 1 2 ( [ 1 − 2 ( ρ 33 + ρ 44 ) ] 2 + 4 ( ∣ ρ 14 ∣ + ∣ ρ 23 ∣ ) 2 + 1 ) .

2.3 LN function

LN serves as a practical entanglement quantifier due to its computational simplicity and operational interpretation [5,7]. For a bipartite system described by the density matrix ρ , LN is defined as follows [5]:

(14) LN ( ρ ) = log 2 ‖ ρ T B ‖ 1 ,

where ρ T B denotes the partial transpose of ρ with respect to subsystem B , and ‖ ⋅ ‖ 1 represents the trace norm. This norm, equivalent to the sum of singular values, is computed as ‖ ξ ‖ 1 = Tr ( ξ † ξ ) for any operator ξ . The connection between LN and the negativity measure N ( ρ ) is established through [5]:

(15) N ( ρ ) = ‖ ρ T B ‖ 1 − 1 2 ,

which quantifies the degree of positive partial transpose violation [65]. Equivalently, negativity can be expressed using the eigenvalues { ν i } of ρ T B :

(16) N ( ρ ) = ∑ i ∣ ν i ∣ − ν i 2 ,

where negative eigenvalues ( ν i < 0 ) directly signal entanglement. By combining these expressions, LN becomes:

(17) LN ( ρ ) = log 2 ( 2 N ( ρ ) + 1 ) .

Entanglement, as quantified by LN ( ρ ) , reflects the fundamental quantum inseparability of subsystems: LN ( ρ ) = 0 , corresponds to fully separable states describable through local operations and classical communication, while LN ( ρ ) > 0 certifies genuine quantum correlations.

2.4 Bell nonlocality function

To assess the nonlocality in our system, one can use the Bell inequality violation [66–69]. Bell nonlocality provides a stricter criterion for quantumness through experimentally testable inequalities. Here, we employ the CHSH inequality for any system of two qubits [68]

(18) ∣ Tr ( ρ B CHSH ) ∣ ≤ 2 ,

where B CHSH denotes the Bell operator defined as follows:

(19) B CHSH = x → ′ ⋅ σ → ⊗ ( y → − y → ′ ) ⋅ σ → + x → ⋅ σ → ⊗ ( y → + y → ′ ) ⋅ σ → .

In order to achieve the maximal value for the B CHSH in the bipartite state ρ , we optimize over the unit vectors x → , x → ′ , y → , and Y → ′ which refer to the measurements on subparties X and Y , respectively. It follows that [68]

(20) max B CHSH Tr ( ρ B CHSH ) ∣ = 2 W ( ρ ) ,

where W ( ρ ) = max l < m { α l + α m } ≤ 2 , with α m (m = 1, 2, 3) represent the eigenvalues of the operator U = T ⊤ T . Here, T ( i , j ) = Tr [ ρ ( σ i ⊗ σ j ) ] is the correlation matrix. Accordingly, the violation of inequality (18) can be quantified using a new formula for Bell’s operator B ( ρ ) , which is given by

(21) B ( ρ ) ≡ max ( W ( ρ ) − 1,0 ) ,

0 ≤ B ( ρ ) ≤ 1 as long as W ( ρ ) ≤ 2 . B ( ρ ) = 1 for a maximal violation of the inequality, and B ( ρ ) = 0 means that the states considered admit the local hidden variable theory. For any state of the form X as given in Eq. (7), the quantity W ( ρ X ) is expressed as follows:

(22) W ( ρ X ) = max { α 1 + α 2 , α 2 + α 3 } = max { 8 ( ∣ ρ 14 ∣ 2 + ∣ ρ 23 ∣ 2 ) , 4 ( ∣ ρ 14 ∣ − ∣ ρ 23 ∣ ) 2 + ( ρ 11 − ρ 22 − ρ 33 + ρ 44 ) 2 } .

2.5 Quantum steering function

The notion of steering, an extension of the Einstein–Podolsky–Rosen paradox, was introduced by Schrödinger [18]. Quantum states that exhibit steering offer key advantages in various applications, including secure quantum teleportation [70], device-independent quantum cryptography [71], and randomness certification [72]. A fundamental approach to identifying and quantifying steering, particularly in two-qubit systems, is the three-setting linear steering inequality [62,73]. This formulation assumes that both Alice and Bob can conduct three distinct measurements on their respective subsystems. The inequality is formulated as follows [73]:

(23) 1 3 ∑ n = 1 3 Tr ( X n ⊗ Y n ρ ) ≤ 1 .

Here, the operators X n = x n ⋅ σ and Y n = y n ⋅ σ act respectively on qubits X and Y , where, x n , y n ∈ R 3 symbolize the unit vectors, with the set { y 1 , y 2 , y 3 } forming an orthonormal basis, while σ = ( σ 1 , σ 2 , σ 3 ) represents the Pauli operators. When inequality (23) is violated, it indicates that the state ρ exhibits steerability, with the extent of the violation serving as a measure of this property [73]. Specifically, the inequality’s maximum violation is written as follows:

(24) S ( ρ ) = max { X n , Y n } 1 3 ∑ n = 1 3 Tr ( X n ⊗ Y n ρ ) ,

which quantifies the degree of steering present in the system. The steerability S ( ρ ) is then determined as follows [73]:

(25) S ( ρ ) = max 0 , F ( ρ ) − 1 3 − 1 ,

where

(26) F ( ρ ) = w 1 2 + w 2 2 + w 3 2 ,

such that { w 1 , w 2 , w 3 } are the singular values of the matrix T = [ T n m ] , with T representing the correlation matrix. The elements of T are defined as T n m = Tr [ ρ ( σ n ⊗ σ m ) ] , where σ k (k = 1, 2, 3) denotes the Pauli operators.

3 LMG model

The LMG model [23–25] represents a fully connected system of spin-1/2 particles, characterized by infinite-range interactions and a tunable anisotropy parameter δ in the x y plane. The ensemble is subjected to a uniform transverse magnetic field B 0 aligned along the z -axis. The competition between collective spin–spin interactions and the external magnetic field gives rise to QPTs, which can be of first or second order depending on the control parameters [36,37,74]. The critical properties of the LMG model have been extensively analyzed using quantum information-theoretic approaches, including finite-size scaling analyses [75,76]. Originally proposed in the context of nuclear many-body theory, the model has since become a cornerstone in the study of collective quantum phenomena, providing a fertile ground for investigating symmetry breaking, quantum criticality, and nonclassical correlations in many-body systems. The Hamiltonian governing the anisotropic version of the LMG model is given by [23,53,77]:

(27) H 0 = − λ N ( S x 2 + δ S y 2 ) − B 0 S z ,

where λ is the coupling constant, N denotes the total number of spins, and S ν = ∑ i = 1 N σ i ν ∕ 2 are the collective spin operators for ν ∈ { x , y , z } , with σ i ν being the Pauli matrices acting on the i th spin. The normalization factor 1 ∕ N ensures that the energy per spin remains finite in the thermodynamic limit.

Owing to its inherent symmetries and infinite-range interactions, the LMG model has emerged as a paradigmatic testbed in quantum information science, underpinning studies of entanglement scaling, quantum coherence, and the intricate hierarchy of many-body correlations. Notably, experimental breakthroughs have begun to bridge theory and practice: superconducting quantum circuits have demonstrated spontaneous symmetry breaking alongside the generation of multipartite entanglement [78], while neutral-atom quantum processors have accurately reconstructed LMG ground-state properties via variational algorithms [79]. Complementing these advances, recent quantum-computational investigations have further illuminated LMG physics: the ground-state energy of a two-spin system was computed on the IBM quantum experience [77], the energy spectrum of systems up to four spins was resolved [80], a suite of hybrid quantum-classical simulation strategies of the LMG model has been formulated [81–83]. In this article, we consider the bipartite LMG model (N = 2), where the Hamiltonian (27) writes as follows:

(28) H ˆ = − λ 4 ( σ 1 x σ 2 x + δ σ 1 y σ 2 y + ( δ + 1 ) I 4 ) − B 0 2 ( σ 1 z + σ 2 z ) .

The parameter λ governs the strength of the spin–spin interaction, while δ introduces anisotropy. The term λ 4 ( δ + 1 ) I 4 contributes a constant energy shift to the spectrum without influencing the system’s dynamics. In this work, we investigate an extended version of the LMG model incorporating an antisymmetric DM interaction, described by the following Hamiltonian:

(29) H = − λ 4 ( σ 1 x σ 2 x + δ σ 1 y σ 2 y + ( δ + 1 ) I 4 ) − B 0 2 ( σ 1 z + σ 2 z ) + D → 2 ( σ → 1 ∧ σ → 2 ) .

The DM interaction, characterized by the vector D → = ( D x , D y , D z ) , represents an antisymmetric exchange coupling that originates from spin–orbit interactions in magnetic systems lacking inversion symmetry. This mechanism introduces chirality into the spin dynamics, favoring twisted or helical spin configurations within noncentrosymmetric crystal lattices [84]. Beyond its role in classical magnetism, the DM interaction has drawn considerable attention in quantum information science, particularly for its impact on the behavior of quantum correlations in low-dimensional systems. Notably, several studies have investigated the influence of DM interaction on the dynamics of quantum resources, such as entanglement, discord, and coherence in bipartite Heisenberg XXZ models [85–87]. These analyses reveal that the DM-induced spin–orbit coupling can act as a tunable source of quantum correlations, even in thermally noisy environments. Assuming the D M interaction is aligned with the z -axis ( D → = ( 0 , 0 , D z ) ) , the Hamiltonian (29) writes as follows:

(30) H ˆ = − λ 4 ( σ 1 x σ 2 x + δ σ 1 y σ 2 y + ( δ + 1 ) I 4 ) − B 0 2 ( σ 1 z + σ 2 z ) + D z 2 ( σ 1 x σ 2 y − σ 1 y σ 2 x ) .

Thus, the matrix representation of H in the computational basis of product states ∣ i 1 ⟩ ⊗ ∣ j 2 ⟩ ( i , j = 0 , 1) is given by:

(31) H ˆ = − λ 4 ( 1 + δ ) − B 0 0 0 − λ 4 ( 1 − δ ) 0 − λ 4 ( 1 + δ ) − λ 4 ( 1 + δ ) + i D z 0 0 − λ 4 ( 1 + δ ) − i D z − λ 4 ( 1 + δ ) 0 − λ 4 ( 1 − δ ) 0 0 − λ 4 ( 1 + δ ) + B 0 .

The eigenvalues Λ i ( i = 1 , 2, 3, 4) and the corresponding eigenvectors ∣ χ Λ i ⟩ of H ˆ are provided as follows:

(32) Λ 1 = − λ ( δ + 1 ) 4 − μ 4 , ∣ χ Λ 1 ⟩ = − 4 B 0 − μ λ ( δ − 1 ) ∣ 4 B 0 + μ λ ( δ − 1 ) ∣ 2 + 1 ∣ 00 ⟩ + 1 ∣ 4 B 0 + μ λ ( δ − 1 ) ∣ 2 + 1 ∣ 11 ⟩ ,

(33) Λ 2 = − λ ( δ + 1 ) 4 + μ 4 , ∣ χ Λ 2 ⟩ = − 4 B 0 + μ λ ( δ − 1 ) ∣ 4 B 0 − μ λ ( δ − 1 ) ∣ 2 + 1 ∣ 00 ⟩ + 1 ∣ 4 B 0 − μ λ ( δ − 1 ) ∣ 2 + 1 ∣ 11 ⟩ ,

(34) Λ 3 = − λ ( δ + 1 ) 4 − κ 4 , ∣ χ Λ 3 ⟩ = − i κ ( 4 D z − i λ ( δ + 1 ) ) 1 + ∣ κ 4 D z − i λ ( δ + 1 ) ∣ 2 ∣ 01 ⟩ + 1 1 + ∣ κ 4 D z − i λ ( δ + 1 ) ∣ 2 ∣ 10 ⟩ ,

(35) Λ 4 = − λ ( δ + 1 ) 4 + κ 4 , ∣ χ Λ 4 ⟩ = i κ ( 4 D z − i λ ( δ + 1 ) ) 1 + ∣ κ 4 D z − i λ ( δ + 1 ) ∣ 2 ∣ 01 ⟩ + 1 1 + ∣ κ 4 D z − i λ ( δ + 1 ) ∣ 2 ∣ 10 ⟩ ,

where μ ≔ ( δ − 1 ) 2 λ 2 + 16 B 0 2 and κ ≔ ( δ + 1 ) 2 λ 2 + 16 D z 2 .

At zero temperature ( T = 0 ), the behavior of all quantum resources is fully governed by the Hamiltonian’s ground state, corresponding to the lowest eigenvalue ( Λ 1 or Λ 3 ) depending on the competition between Zeeman splitting ( B 0 ) and DM interaction ( D z ). For weak external fields ( B 0 ), the interplay of symmetric spin–spin coupling ( λ ) and antisymmetric DM interaction ( D z ) stabilizes the eigenstate ∣ χ Λ 3 ⟩ , where κ = ( δ + 1 ) 2 λ 2 + 16 D z 2 governs spin–orbit-induced chirality, enhancing quantum coherence and entanglement. In contrast, for high strengths of the field B 0 , the Zeeman effect dominates, polarizing the system into separable eigenstates (e.g., ∣ 00 ⟩ ) and suppressing all nonclassical correlations, marking a quantum-to-classical crossover into a paramagnetic regime. The distinct behaviors of quantum resources at low B 0 and classical separability at high B 0 highlight the tunability of quantum properties through external parameters, with the ground state acting as the linchpin for zero-temperature quantum resource engineering. At finite temperatures, the density matrix ρ ( T ) is determined by the Gibbs ensemble:

(36) ρ ( T ) = e − H ˆ ∕ k B T Z , with Z = Tr [ e − H ˆ ∕ k B T ] ,

where H ˆ is the system Hamiltonian and k B the Boltzmann constant (set to unity, k B = 1 , for dimensionless analysis). In the computational basis { ∣ 0 ⟩ 1 ⊗ ∣ 0 ⟩ 2 , ∣ 0 ⟩ 1 ⊗ ∣ 1 ⟩ 2 , ∣ 1 ⟩ 1 ⊗ ∣ 0 ⟩ 2 , ∣ 1 ⟩ 1 ⊗ ∣ 1 ⟩ 2 } , the thermal state ρ ( T ) assumes an X -structure:

(37) ρ ( T ) = ρ 11 0 0 ρ 14 0 ρ 22 ρ 23 0 0 ρ 23 * ρ 33 0 ρ 14 * 0 0 ρ 44 ,

with matrix elements parameterized by spin–spin coupling λ , DM interaction D z , Zeeman field B 0 , and anisotropy δ :

ρ 11 = e ( δ + 1 ) λ 4 T Z 4 B 0 sinh μ 4 T μ + cosh μ 4 T , ρ 14 = − ( δ − 1 ) λ e ( δ + 1 ) λ 4 T Z μ sinh μ 4 T , ρ 22 = e ( δ + 1 ) λ 4 T Z cosh κ 4 T , ρ 23 = [ ( δ + 1 ) λ − 4 i D z ] e ( δ + 1 ) λ 4 T Z κ sinh κ 4 T , ρ 32 = ρ 23 * , ρ 33 = ρ 22 , ρ 41 = ρ 14 , ρ 44 = e ( δ + 1 ) λ 4 T Z − 4 B 0 sinh μ 4 T μ + cosh μ 4 T ,

where the partition function Z and interaction parameters μ , κ are defined as follows:

(38) Z = 2 e ( δ + 1 ) λ 4 T cosh μ 4 T + cosh κ 4 T ,

(39) μ ≡ ( 4 B 0 ) 2 + [ ( δ − 1 ) λ ] 2 , κ ≡ [ ( δ + 1 ) λ ] 2 + ( 4 D z ) 2 .

The parameter μ governs field-anisotropy competition, while κ encodes spin–orbit coupling effects from D z . After we explore the anisotropic LMG model ( δ = 0.5 ) to explore the interplay between spin–spin couplings, DM interaction, and external magnetic fields under thermal fluctuations. The parameter B 0 is tuned across 0 ≤ B 0 ≤ 3 , a regime chosen to identify critical thresholds where magnetic polarization suppresses anisotropic quantum correlations.

4 Results and discussion

This section examines how critical parameters, spin–spin coupling strength ( λ ), external magnetic field ( B 0 ), DM interaction ( D z ), and temperature ( T ), govern the dynamical evolution of quantum coherence and correlations in a two-qubit LMG system.

4.1 The impact of spin–spin coupling strength λ

We illustrate in Figure 1, the influence of the coupling strength, λ , on the key quantifiers. These include the l 1 -norm of quantum coherence Q ( ρ ( T ) ) , quantum discord D ( ρ ( T ) ) , LN LN ( ρ ( T ) ) , Bell nonlocality B ( ρ ( T ) ) , and quantum steering S ( ρ ( T ) ) . All quantifiers are evaluated as functions of temperature T , with the remaining parameters fixed at δ = 0.5 , B 0 = 0.4 , and D z = 1 , ensuring a consistent anisotropic and magnetically biased environment.

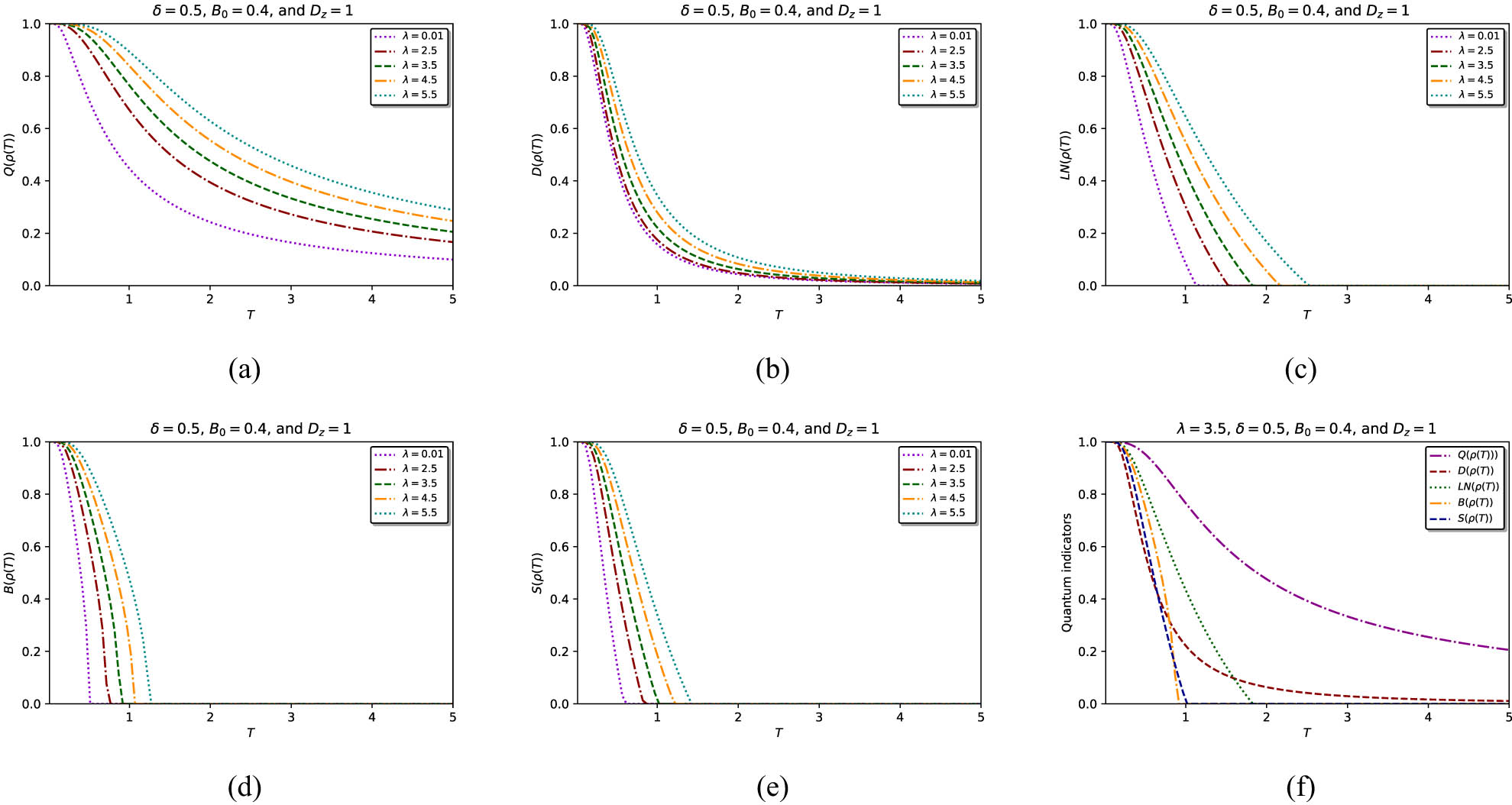
$Figure 1 Dynamics of quantum coherence (a), quantum discord (b), entanglement (c), nonlocality (d), and quantum steering (e) versus T T for different values of λ \lambda when δ = 0.5 \delta =0.5 , B 0 = 0.4 {B}_{0}=0.4 , and D z = 1 {D}_{z}=1 . (f) shows the comparative evolution of the five indicators at λ = 3.5 \lambda =3.5 .$

Figure 1

Dynamics of quantum coherence (a), quantum discord (b), entanglement (c), nonlocality (d), and quantum steering (e) versus T for different values of λ when δ = 0.5 , B 0 = 0.4 , and D z = 1 . (f) shows the comparative evolution of the five indicators at λ = 3.5 .

By varying the spin–spin coupling strength λ , we characterize the thermal resilience of each quantum resource. As evidenced in Figure 1(a)–(e), all measures universally attain their maximum value of 1 at T = 0 , revealing that the quantumness of ground state is not affected by the thermal noise. This maximum persists irrespective of λ , underscoring the dominance of quantum correlations at absolute zero. At low temperatures, these metrics exhibit a plateau-like persistence of nonclassicality, a signature of suppressed thermal decoherence. Crucially, the plateau width scales with λ : stronger spin–spin couplings broaden the temperature range over which quantum resources remain robust, delaying their collapse to classical limits. However, LN ( ρ ( T ) ) , B ( ρ ( T ) ) , and S ( ρ ( T ) ) are seen to vanish completely at a critical temperature T c , which varies depending on the value of λ . The critical temperature T c at which LN ℒN ( ρ ( T ) ) , Bell nonlocality ℬ ( ρ ( T ) ) , and quantum steering S ( ρ ( T ) ) vanish depends strongly on the coupling strength λ . For instance, ℒN ( ρ ( T ) ) collapses at T c = 1.831 for λ = 3.5 but persists until T c = 2.526 when λ = 5.5 . Similarly, ℬ ( ρ ( T ) ) disappears at T c = 0.879 for λ = 3.5 and survives up to T c = 1.238 for λ = 5.5 , while S ( ρ ( T ) ) vanishes at T c = 1.014 and T c = 1.425 for λ = 3.5 and λ = 5.5 , respectively. This consistent λ -dependent scaling underscores how stronger spin–spin couplings enhance thermal resilience of entanglement and nonlocal correlations. Figure 1(a)–(b) demonstrate that increasing the spin–spin coupling strength λ enhances the thermal robustness of quantum coherence ( Q ( ρ ( T ) ) ) and quantum discord ( D ( ρ ( T ) ) ). Notably, even when entanglement ( ℒN ( ρ ( T ) ) ), nonlocality ( ℬ ( ρ ( T ) ) ), and steering ( S ( ρ ( T ) ) ) collapse to zero at elevated temperatures, residual coherence ( Q ( ρ ( T ) ) > 0 ) and discord ( D ( ρ ( T ) ) > 0 ) persist, with Q ( ρ ( T ) ) > D ( ρ ( T ) ) across all T . This persistence highlights the hierarchical resilience of quantum resources. Figure 1(f) explores a comparative analysis between Q ( ρ ( T ) ) , D ( ρ ( T ) ) , LN ( ρ ( T ) ) , B ( ρ ( T ) ) , and S ( ρ ( T ) ) for λ = 3 , δ = 0.5 , B 0 = 0.25 , and D z = 1 . For low temperatures, the sudden death phenomenon occurs more quickly for Bell nonlocality, followed by steerability, and finally, entanglement compared to quantum discord. In summary, stronger spin–spin coupling enhances the resilience of quantum resources against degradation induced by thermal effects. We observed a distinct hierarchy among nonclassical resources: the l 1 norm of coherence surpasses quantum discord, which exceeds LN for intermediate and high temperatures, followed by quantum steering, and finally, Bell nonlocality. Hence, we can conclude that quantum coherence is the most robust measure in this study, while quantum nonlocality is the most fragile among the nonclassical properties investigated.

4.2 The impact of the Zeeman splitting B 0

Next, we examine the roles of Zeeman splitting ( B 0 ) and temperature ( T ) in shaping quantum correlations in the LMG model (Figure 2). Fixed parameters λ = 2 (spin–spin coupling), δ = 0.5 (anisotropy), and D z = 2 (DM interaction) isolate the interplay between thermal fluctuations ( k B T ) and magnetic polarization ( B 0 ). Here, fixing D z enables direct analysis of how T and B 0 affect coherence, entanglement, discord, and nonlocal correlations ( B ) and ( S ).

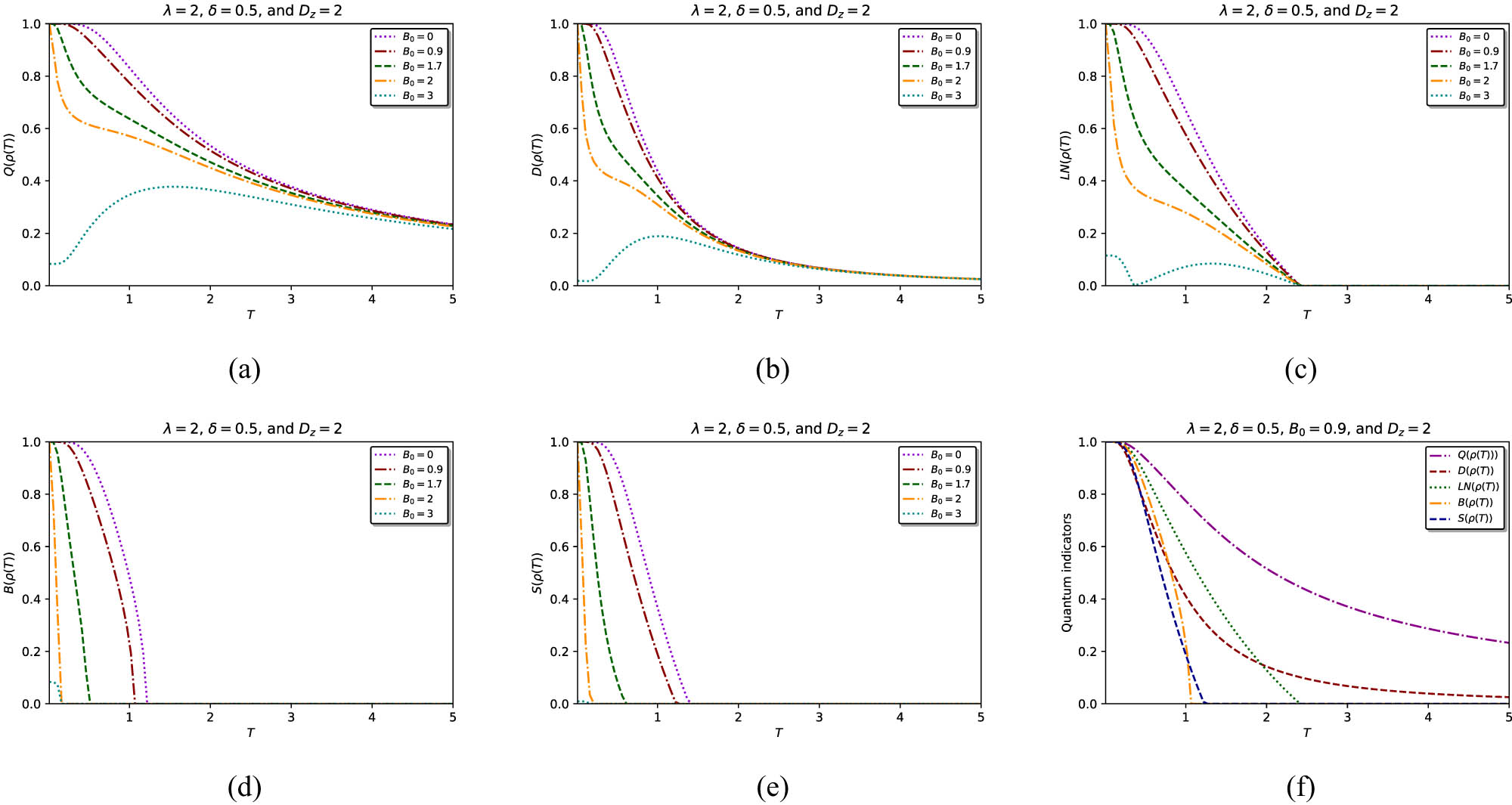
$Figure 2 Evolution of quantum coherence (a), quantum discord (b), entanglement (c), nonlocality (d), and quantum steering (e) versus temperature T T for different values of B 0 {B}_{0} when λ = 2 \lambda =2 , δ = 0.5 \delta =0.5 , and D z = 2 {D}_{z}=2 , (f) illustrates the comparative evolution of the five indicators at B 0 = 0.9 {B}_{0}=0.9 .$

Figure 2

Evolution of quantum coherence (a), quantum discord (b), entanglement (c), nonlocality (d), and quantum steering (e) versus temperature T for different values of B 0 when λ = 2 , δ = 0.5 , and D z = 2 , (f) illustrates the comparative evolution of the five indicators at B 0 = 0.9 .

Figure 2 investigates how quantum resources in the bipartite LMG model are influenced by the DM interaction ( D z = 2 ), Zeeman field ( B 0 ), and temperature ( T ). At absolute zero ( T = 0 ), all resources–coherence ( Q ), quantum discord ( D ), LN (LN, entanglement), Bell nonlocality ( B ), and steering ( S ) – attain maximal values for B 0 < 2 , aligning with the dominance of spin–spin correlations in the ground state (Figure 1). However, when B 0 = 3 > D z , a stark contrast emerges at T = 0 : Q and D drop to near-zero levels due to field-induced polarization into separable eigenstates (e.g., ∣ 00 ⟩ ). Intriguingly, these resources exhibit significant nonmonotonic behavior at finite T , peaking at intermediate critical temperatures ( T Q = 1.543 for coherence and T D = 1.015 for discord) before decaying to residual plateaus. Entanglement vanishes at a first critical temperature T c 1 LN = 0.351 , resurges and picks near T ≈ 1.45 and ultimately collapses at a second critical temperature T c 2 LN = 2.406 . In contrast, nonlocality ( B ) and steering ( S ), already suppressed at T = 0 , are entirely extinguished at infinitesimal T , revealing their fragility compared to Q and D . Across all regimes, the Zeeman field reduces the overall quantum resource capacity, while increasing ( D z ) counteracts this by enhancing and stabilizing quantum correlations with the system. This stabilization enhances the robustness of Q and D , allowing them to persist even at T ≫ T c 2 LN . A universal hierarchy of thermal resilience emerges: Q > D > LN > S > B (Figure 2f), with coherence ( Q ) enduring as the most robust resource and Bell nonlocality ( B ) the most fragile. Increasing B 0 suppresses T c 1 LN , yet the reentrant regime broadens the effective thermal lifetime of entanglement (LN). The DM interaction’s spin–orbit chirality further amplifies these effects, positioning the LMG model as a versatile platform for engineering noise resilient quantum protocols. By tuning external parameters ( B 0 , D z ), resource availability can be modulated under thermal noisy environment.

4.3 The impact of the interaction DM

Finally, we analyze the impact of the DM interaction on the dynamics of quantum resources as shown in Figure 3. The selected metrics are plotted as functions of temperature for varying DM interaction strengths D z , while keeping fixed parameters λ = 3 , δ = 0.5 , and B 0 = 0.5 . This parameter regime emphasizes the competition between symmetric exchange ( λ ) and antisymmetric DM interactions ( D z ), with the Zeeman field ( B 0 ) setting the energy scale for spin polarization.

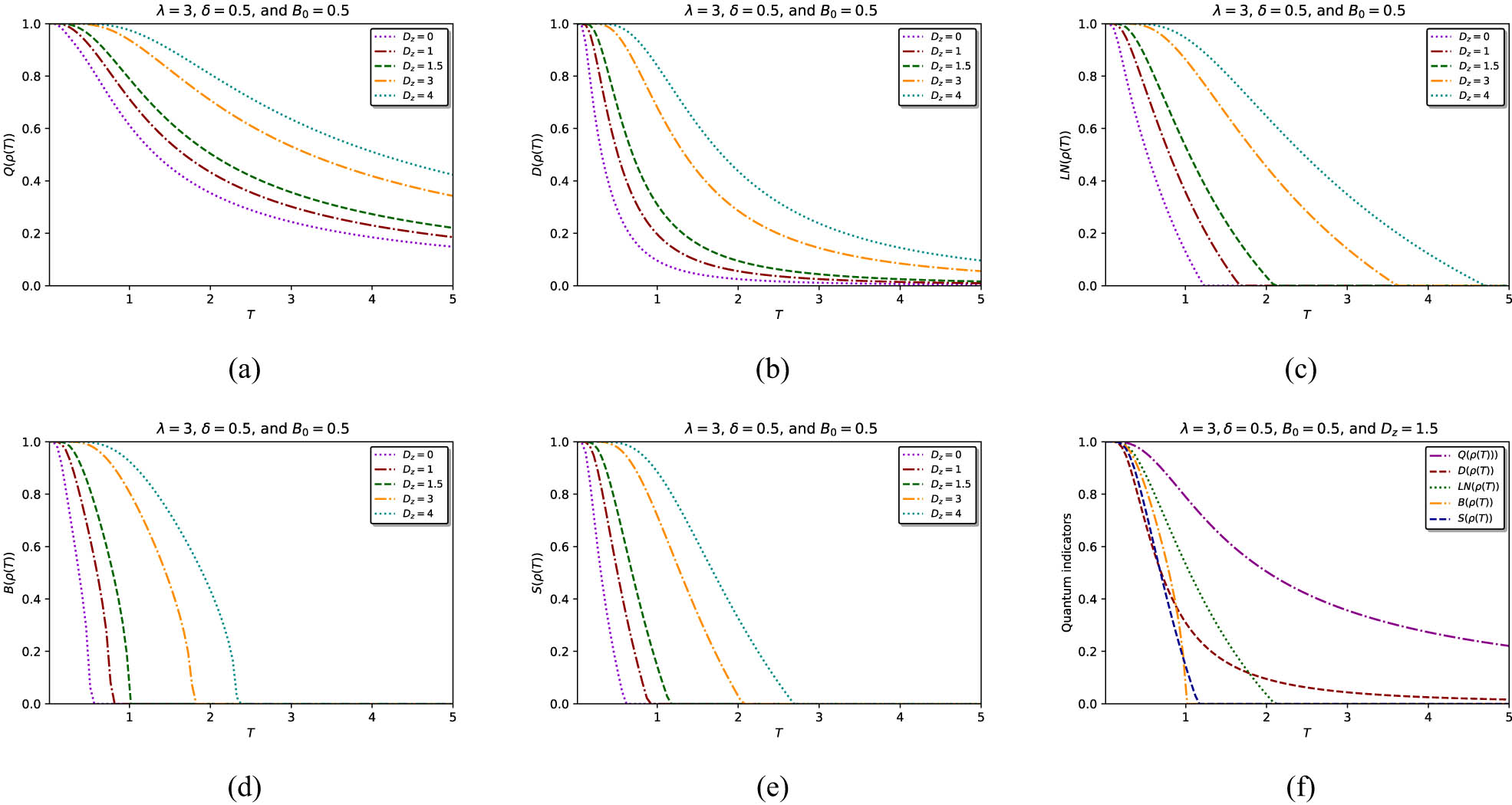
$Figure 3 Dynamics of quantum coherence (a), quantum discord (b), entanglement (c), nonlocality (d), and quantum steering (e) versus temperature T T for different values of D z {D}_{z} when λ = 3 \lambda =3 , δ = 0.5 \delta =0.5 , and B 0 = 0.5 {B}_{0}=0.5 . (f) The comparative evolution of the five indicators at D z = 1.5 {D}_{z}=1.5 .$

Figure 3

Dynamics of quantum coherence (a), quantum discord (b), entanglement (c), nonlocality (d), and quantum steering (e) versus temperature T for different values of D z when λ = 3 , δ = 0.5 , and B 0 = 0.5 . (f) The comparative evolution of the five indicators at D z = 1.5 .

As evidenced by the temperature-dependent evolution of quantum resources in Figure 3, all measures, coherence Q ( ρ ( T ) ) , discord D ( ρ ( T ) ) , entanglement LN ( ρ ( T ) ) , Bell nonlocality B ( ρ ( T ) ) , and steering S ( ρ ( T ) ) , attain their maximum value of 1 at zero temperature ( T → 0 ), independent of the DM interaction strength D z . However, their thermal resilience diverges sharply: increasing D z elevates the critical temperature T c at which each resource vanishes. For instance, Bell nonlocality B ( ρ ( T ) ) collapses at T c = 0.776 for D z = 1 but persists up to T c = 2.334 for D z = 4 , a trend mirrored by entanglement LN ( ρ ( T ) ) collapses at T c = 1.680 for D z = 1 vs T c = 4.710 for D z = 4 and steering ( S ( ρ ( T ) ) ) vanishes at T c = 0.896 for D z = 1 vs T c = 2.688 for D z = 4 . Figure 3(a) and (b) demonstrate that stronger DM interaction D z enhances the thermal robustness of coherence Q ( ρ ( T ) ) and discord D ( ρ ( T ) ) , with Q ( ρ ( T ) ) > D ( ρ ( T ) ) > 0 persisting even when LN ( ρ ( T ) ) , B ( ρ ( T ) ) , and S ( ρ ( T ) ) collapse at elevated T . A strict sensitivity hierarchy emerges: B > S > LN > D > Q (Figure 3(f)), where nonlocality vanishes first, followed by steering, entanglement, discord, and finally coherence. At high T ≫ T c , residual Q ( ρ ( T ) ) > D ( ρ ( T ) ) > 0 highlights basis-dependent coherence as the most robust resource. Stronger DM interactions ( D z ) universally enhance all resources by suppressing decoherence, while preserving the hierarchy. These findings position the DM-LMG model as a versatile platform for engineering noise-resilient protocols, where tunable D z sustains nonclassicality in thermal environments.

5 Conclusion

In this work, we examined how key quantum resources, Bell nonlocality, quantum steering, entanglement (via LN N ), and coherence (via the ℓ 1 -norm), behave in the LMG model subject to DM interactions and thermal noise. We find a clear hierarchy of thermal fragility: Bell nonlocality disappears first at the lowest critical temperature T c , followed by steering and then entanglement, whereas quantum discord and coherence endure far above T c , remaining nonzero even at T ≫ T c . Strengthening either the spin–spin coupling λ or the DM strength D decouples local thermal fluctuations from global quantum correlations, thereby enhancing all resources. The Zeeman field B 0 offers further control: as B 0 increases, entanglement reappears at intermediate temperatures before eventually decaying at higher T , while coherence shows no such sudden death and sudden birth. Importantly, at any fixed temperature, a stronger field uniformly suppresses all quantum resources, highlighting a nontrivial competition between thermal decoherence and magnetic tuning. Although our analysis is restricted to the bipartite case ( N = 2 ), it gives a first step to understand of how key system parameters, spin–spin coupling λ , magnetic field B 0 , and DM interaction D z govern the dynamics of non-classical correlations under thermal noises. In the thermodynamic limit ( N → ∞ ), collective quantum phenomena become dominant, and critical temperatures associated with entanglement, coherence, and nonlocality typically sharpen into true phase transitions. Prior studies have shown that in this limit, quantities such as entanglement entropy exhibit universal scaling laws governed by conformal symmetry and finite-size corrections. We anticipate that the hierarchy of robustness identified here will persist qualitatively, but with sharper resource thresholds and critical scaling behavior near QPTs. Extending the present formalism to N ≫ 1 via semiclassical approximations or mean-field theory is a promising direction for future work and would facilitate direct comparison with recent experiments in large atomic ensembles and superconducting simulators. LMG implementations span Bose–Einstein condensates in double wells [54], cavity QED [55,56], and circuit QED [57]. Recent advances, including superconducting circuits that exhibit symmetry breaking and multipartite entanglement [78], neutral-atom processors reconstructing LMG ground states [79], and IBM quantum experience demonstrations of two-spin energies and four-spin spectra [77,80], underscore the feasibility of experimentally testing our predictions.

Acknowledgments

The authors are very grateful to the referees for their important remarks which improve the manuscript. This work was supported by the Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R906), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. This study is supported via funding from Prince sattam bin Abdulaziz University project number (PSAU/2024/R/1446).

Funding information: This work was supported by the Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R906), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Author contributions: M.B., H.A, and F.A. contributed to the writing of the manuscript and played a role in software development and conceptualization. M.M. and ABA.M. provided supervision throughout the process and carefully reviewed the manuscript. M.B., H.A,F.A., M.M., and ABA.M. revised final draft of the manuscript. All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors state no conflict of interest.
Data availability statement: Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.

References

[1] Streltsov A, Adesso G, Plenio MB. Colloquium: Quantum coherence as a resource. Rev Modern Phys. 2017;89(4):041003. 10.1103/RevModPhys.89.041003Search in Google Scholar

[2] Baumgratz T, Cramer M, Plenio MB. Quantifying coherence. Phys Rev Lett. 2014;113(14):140401. 10.1103/PhysRevLett.113.140401Search in Google Scholar PubMed

[3] Wootters WK. Entanglement of formation of an arbitrary state of two qubits. Phys Rev Lett. 1998;80(10):2245. 10.1103/PhysRevLett.80.2245Search in Google Scholar

[4] Wootters WK. Entanglement of formation and concurrence. Quantum Inf Comput. 2001;1(1):27–44. 10.26421/QIC1.1-3Search in Google Scholar

[5] Vidal G, Werner RF. Computable measure of entanglement. Phys Rev A. 2002;65(3):032314. 10.1103/PhysRevA.65.032314Search in Google Scholar

[6] Horodecki M, Horodecki P, Horodecki R. On the necessary and sufficient conditions for separability of mixed quantum states. Phys Lett A. 1996;223(1):1–8. 10.1016/S0375-9601(96)00706-2Search in Google Scholar

[7] Plenio MB, Virmani SS. An introduction to entanglement theory. In: Quantum information and coherence. Scottish Graduate Series. Cham: Springer; 2014. p. 173–209. 10.1007/978-3-319-04063-9_8Search in Google Scholar

[8] Ollivier H, Zurek WH. Quantum discord: a measure of the quantumness of correlations. Phys Rev Lett. 2001;88(1):017901. 10.1103/PhysRevLett.88.017901Search in Google Scholar PubMed

[9] Ali M, Rau A, Alber G. Quantum discord for two-qubit X states. Phys Rev A-Atomic Mol Opt Phys. 2010;81(4):042105. 10.1103/PhysRevA.81.042105Search in Google Scholar

[10] Luo S. Quantum discord for two-qubit systems. Phys Rev A-Atomic Mol Opt Phys. 2008;77(4):042303. 10.1103/PhysRevA.77.042303Search in Google Scholar

[11] Dahbi Z, Oumennana M, Mansour M. Intrinsic decoherence effects on correlated coherence and quantum discord in XXZ Heisenberg model. Opt Quant Electr. 2023;55(5):412. 10.1007/s11082-023-04604-3Search in Google Scholar

[12] Baba H, Kaydi W, Daoud M, Mansour M. Entanglement of formation and quantum discord in multipartite j-spin coherent states. Int J Modern Phys B. 2020;34(26):2050237. 10.1142/S0217979220502379Search in Google Scholar

[13] Aspect A, Dalibard J, Roger G. Experimental test of Bell’s inequalities using time-varying analyzers. Phys Rev Lett. 1982;49(25):1804. 10.1103/PhysRevLett.49.1804Search in Google Scholar

[14] Storz S, Schär J, Kulikov A, Magnard P, Kurpiers P, Lütolf J, et al. Loophole-free Bell inequality violation with superconducting circuits. Nature. 2023;617(7960):265–70. 10.1038/s41586-023-05885-0Search in Google Scholar PubMed PubMed Central

[15] Bell JS. On the einstein podolsky rosen paradox. Phys Phys Fizika. 1964;1(3):195. 10.1103/PhysicsPhysiqueFizika.1.195Search in Google Scholar

[16] Bennett CH, DiVincenzo DP, Fuchs CA, Mor T, Rains E, Shor PW, et al. Quantum nonlocality without entanglement. Phys Rev A. 1999;59(2):1070. 10.1103/PhysRevA.59.1070Search in Google Scholar

[17] Halder S, Banik M, Agrawal S, Bandyopadhyay S. Strong quantum nonlocality without entanglement. Phys Rev Lett. 2019;122(4):040403. 10.1103/PhysRevLett.122.040403Search in Google Scholar PubMed

[18] Schrödinger E. Discussion of probability relations between separated systems. In: Mathematical Proceedings of the Cambridge Philosophical Society. vol. 31. Cambridge, United Kingdom: Cambridge University Press; 1935. p. 555–63. 10.1017/S0305004100013554Search in Google Scholar

[19] Uola R, Costa AC, Nguyen HC, Gühne O. Quantum steering. Rev Modern Phys. 2020;92(1):015001. 10.1103/RevModPhys.92.015001Search in Google Scholar

[20] Duuuu MM, Tong D. Relationship between first-order coherence and the maximum violation of the three-setting linear steering inequality for a two-qubit system. Phys Rev A. 2021;103(3):032407. 10.1103/PhysRevA.103.032407Search in Google Scholar

[21] Obada AS, Abd-Rabbou MY, Haddadi S. Does conditional entropy squeezing indicate normalized entropic uncertainty relation steering? Quant Inform Proces. 2024;23(3):90. 10.1007/s11128-024-04298-wSearch in Google Scholar

[22] Chouiba A, Elghaayda S, Ait Chlih A, Mansour M. Unveiling quantum resources in dimeric perylene-based arrays. J Phys A Math Theoret. 2025;58(12):125302. 10.1088/1751-8121/adbf77Search in Google Scholar

[23] Lipkin HJ, Meshkov N, Glick A. Validity of many-body approximation methods for a solvable model: (I). Exact solutions and perturbation theory. Nuclear Phys. 1965;62(2):188–98. 10.1016/0029-5582(65)90862-XSearch in Google Scholar

[24] Meshkov N, Glick A, Lipkin H. Validity of many-body approximation methods for a solvable model: (II). Linearization procedures. Nuclear Phys. 1965;62(2):199–210. 10.1016/0029-5582(65)90863-1Search in Google Scholar

[25] Glick A, Lipkin H, Meshkov N. Validity of many-body approximation methods for a solvable model: (III). Diagram summations. Nuclear Phys. 1965;62(2):211–24. 10.1016/0029-5582(65)90864-3Search in Google Scholar

[26] Dreiss GJ, Klein A. The algebra of currents as a complete dynamical method in the nuclear many-body problem: Application to an exactly soluble model. Nuclear Phys A. 1969;139(1):81–99. 10.1016/0375-9474(69)90261-9Search in Google Scholar

[27] Schuck P, Ethofer S. Self-consistent (nuclear) phonons. Nuclear Phys A. 1973;212(2):269–86. 10.1016/0375-9474(73)90563-0Search in Google Scholar

[28] Catara F, Dang ND, Sambataro M. Ground-state correlations beyond RPA. Nuclear Phys A. 1994;579(1–2):1–12. 10.1016/0375-9474(94)90790-0Search in Google Scholar

[29] Wahlen-Strothman JM, Henderson TM, Hermes MR, Degroote M, Qiu Y, Zhao J, et al. Merging symmetry projection methods with coupled cluster theory: Lessons from the Lipkin model Hamiltonian. J Chem Phys. 2017;146:054110. 10.1063/1.4974989Search in Google Scholar PubMed

[30] Turbiner A. Quasi-exactly-solvable problems and sl (2) algebra. Commun Math Phys. 1988;118:467–74. 10.1007/BF01466727Search in Google Scholar

[31] Ulyanov V, Zaslavskii O. New methods in the theory of quantum spin systems. Phys Reports. 1992;216(4):179–251. 10.1016/0370-1573(92)90158-VSearch in Google Scholar

[32] Botet R, Jullien R. Large-size critical behavior of infinitely coordinated systems. Phys Rev B. 1983;28(7):3955. 10.1103/PhysRevB.28.3955Search in Google Scholar

[33] Gatteschi D, Sessoli R, Villain J. Molecular Nanomagnets. Oxford, United Kingdom: Oxford University Press; 2006. 10.1093/acprof:oso/9780198567530.001.0001Search in Google Scholar

[34] Bogani L, Wernsdorfer W. Molecular spintronics using single-molecule magnets. Nature Materials. 2008;7(3):179–86. 10.1038/nmat2133Search in Google Scholar PubMed

[35] Cirac JI, Lewenstein M, Mølmer K, Zoller P. Quantum superposition states of Bose–Einstein condensates. Phys Rev A. 1998;57(2):1208. 10.1103/PhysRevA.57.1208Search in Google Scholar

[36] Vidal J, Palacios G, Mosseri R. Entanglement in a second-order quantum phase transition. Phys Rev A. 2004;69(2):022107. 10.1103/PhysRevA.69.022107Search in Google Scholar

[37] Vidal J, Mosseri R, Dukelsky J. Entanglement in a first-order quantum phase transition. Phys Rev A Atomic Mol Opt Phys. 2004;69(5):054101. 10.1103/PhysRevA.69.054101Search in Google Scholar

[38] Vidal J. Concurrence in collective models. Phys Rev A Atomic Mol Opt Phys. 2006;73(6):062318. 10.1103/PhysRevA.73.062318Search in Google Scholar

[39] Vidal J, Palacios G, Aslangul C. Entanglement dynamics in the Lipkin-Meshkov-Glick model. Phys Rev A Atomic Mol Opt Phys. 2004;70(6):062304. 10.1103/PhysRevA.70.062304Search in Google Scholar

[40] Latorre JI, Orús R, Rico E, Vidal J. Entanglement entropy in the Lipkin-Meshkov-Glick model. Phys Rev A Atomic Mol Opt Phys. 2005;71(6):064101. 10.1103/PhysRevA.71.064101Search in Google Scholar

[41] Barthel T, Dusuel S, Vidal J. Entanglement entropy beyond the free case. Phys Rev Lett. 2006;97(22):220402. 10.1103/PhysRevLett.97.220402Search in Google Scholar PubMed

[42] Cui H. Multiparticle entanglement in the Lipkin-Meshkov-Glick model. Phys Rev A Atomic Mol Opt Phys. 2008;77(5):052105. 10.1103/PhysRevA.77.052105Search in Google Scholar

[43] Lourenço AC, Calegari S, Maciel TO, Debarba T, Landi GT, Duzzioni EI. Genuine multipartite correlations distribution in the criticality of the Lipkin-Meshkov-Glick model. Phys Rev B. 2020;101(5):054431. 10.1103/PhysRevB.101.054431Search in Google Scholar

[44] Orús R, Dusuel S, Vidal J. Equivalence of critical scaling laws for many-body entanglement in the Lipkin–Meshkov–Glick model. Phys Rev Lett 2008;101(2):025701. 10.1103/PhysRevLett.101.025701Search in Google Scholar PubMed

[45] Bao J, Guo B, Cheng HG, Zhou M, Fu J, Deng YC, et al. Multipartite nonlocality in the Lipkin-Meshkov-Glick model. Phys Rev A. 2020;101(1):012110. 10.1103/PhysRevA.101.012110Search in Google Scholar

[46] Sarandy MS. Classical correlation and quantum discord in critical systems. Phys Rev A Atomic Mol Opt Phys. 2009;80(2):022108. 10.1103/PhysRevA.80.022108Search in Google Scholar

[47] Wang C, Zhang YY, Chen QH. Quantum correlations in collective spin systems. Phys Rev A Atomic Mol Opt Phys. 2012;85(5):052112. 10.1103/PhysRevA.85.052112Search in Google Scholar

[48] Ye BL, Li B, Li-Jost X, Fei SM. Quantum correlations in critical XXZ system and LMG model. Int J Quant Inform. 2018;16(03):1850029. 10.1142/S0219749918500296Search in Google Scholar

[49] Kwok HM, Ning WQ, Gu SJ, Lin HQ. Quantum criticality of the Lipkin-Meshkov-Glick model in terms of fidelity susceptibility. Phys Rev E-Stat Nonl Soft Matter Phys. 2008;78(3):032103. 10.1103/PhysRevE.78.032103Search in Google Scholar PubMed

[50] Ma J, Xu L, Xiong HN, Wang X. Reduced fidelity susceptibility and its finite-size scaling behaviors in the Lipkin-Meshkov-Glick model. Phys Rev E Stat Nonl Soft Matter Phys. 2008;78(5):051126. 10.1103/PhysRevE.78.051126Search in Google Scholar PubMed

[51] Ma J, Wang X. Fisher information and spin squeezing in the Lipkin-Meshkov-Glick model. Phys Rev A Atomic Mol Opt Phys. 2009;80(1):012318. 10.1103/PhysRevA.80.012318Search in Google Scholar

[52] Wang Q, Wang P, Yang Y, Wang WG. Decay of quantum Loschmidt echo and fidelity in the broken phase of the Lipkin-Meshkov-Glick model. Phys Rev A. 2015;91(4):042102. 10.1103/PhysRevA.91.042102Search in Google Scholar

[53] Abd-Rabbou M, Khalil E, Al-Awfi S. Quantum otto machine in Lipkin-Meshkov-Glick model with magnetic field and a symmetric cross interaction. Opt Quantum Electron. 2024;56(6):940. 10.1007/s11082-024-06444-1Search in Google Scholar

[54] Micheli A, Jaksch D, Cirac JI, Zoller P. Many-particle entanglement in two-component Bose–Einstein condensates. Phys Rev A. 2003;67(1):013607. 10.1103/PhysRevA.67.013607Search in Google Scholar

[55] Morrison S, Parkins A. Dynamical quantum phase transitions in the dissipative Lipkin–Meshkov–Glick Model with proposed realization in optical cavity QED. Phys Rev Lett. 2008;100(4):040403. 10.1103/PhysRevLett.100.040403Search in Google Scholar PubMed

[56] Chen G, Liang JQ, Jia S. Interaction-induced Lipkin-Meshkov-Glick model in a Bose–Einstein condensate inside an optical cavity. Optics Express. 2009;17(22):19682–90. 10.1364/OE.17.019682Search in Google Scholar PubMed

[57] Larson J. Circuit QED scheme for the realization of the Lipkin-Meshkov-Glick model. Europhys Lett. 2010;90(5):54001. 10.1209/0295-5075/90/54001Search in Google Scholar

[58] Unanyan R, Fleischhauer M. Decoherence-free generation of many-particle entanglement by adiabatic ground-state transitions. Phys Rev Lett. 2003;90(13):133601. 10.1103/PhysRevLett.90.133601Search in Google Scholar PubMed

[59] Russomanno A, Iemini F, Dalmonte M, Fazio R. Floquet time crystal in the Lipkin-Meshkov-Glick model. Phys Rev B. 2017;95(21):214307. 10.1103/PhysRevB.95.214307Search in Google Scholar

[60] Zhou Y, Ma SL, Li B, Li XX, Li FL, Li PB. Simulating the Lipkin-Meshkov-Glick model in a hybrid quantum system. Phys Rev A. 2017;96(6):062333. 10.1103/PhysRevA.96.062333Search in Google Scholar

[61] Xu K, Sun ZH, Liu W, Zhang YR, Li H, Dong H, et al. Probing dynamical phase transitions with a superconducting quantum simulator. Sci Adv. 2020;6(25):eaba4935. 10.1126/sciadv.aba4935Search in Google Scholar PubMed PubMed Central

[62] Cavalcanti EG, Jones SJ, Wiseman HM, Reid MD. Experimental criteria for steering and the Einstein-Podolsky-Rosen paradox. Phys Rev A Atomic Mol Opt Phys. 2009;80(3):032112. 10.1103/PhysRevA.80.032112Search in Google Scholar

[63] Henderson L, Vedral V. Classical, quantum and total correlations. J Phys A Math General. 2001;34(35):6899. 10.1088/0305-4470/34/35/315Search in Google Scholar

[64] Fanchini F, Werlang T, Brasil C, Arruda L, Caldeira A. Non-Markovian dynamics of quantum discord. Phys Rev A Atomic Mol Opt Phys. 2010;81(5):052107. 10.1103/PhysRevA.81.052107Search in Google Scholar

[65] Peres A. Separability criterion for density matrices. Phys Rev Lett. 1996;77(8):1413. 10.1103/PhysRevLett.77.1413Search in Google Scholar PubMed

[66] Bartkiewicz K, Horst B, Lemr K, Miranowicz A. Entanglement estimation from Bell inequality violation. Phys Rev A Atomic Mol Opt Phys. 2013;88(5):052105. 10.1103/PhysRevA.88.052105Search in Google Scholar

[67] Bartkiewicz K, Lemr K, Černoch A, Miranowicz A. Bell nonlocality and fully entangled fraction measured in an entanglement-swapping device without quantum state tomography. Phys Rev A. 2017;95(3):030102. 10.1103/PhysRevA.95.030102Search in Google Scholar

[68] Horodecki R, Horodecki P, Horodecki M. Violating Bell inequality by mixed spin-12 states: necessary and sufficient condition. Phys Lett A. 1995;200(5):340–4. 10.1016/0375-9601(95)00214-NSearch in Google Scholar

[69] Huuuu ML. Relations between entanglement, Bell-inequality violation and teleportation fidelity for the two-qubit X states. Quant Inform Proces. 2013;12(1):229–36. 10.1007/s11128-012-0371-1Search in Google Scholar

[70] He Q, Rosales-Zárate L, Adesso G, Reid MD. Secure continuous variable teleportation and Einstein-Podolsky-Rosen steering. Phys Rev Lett. 2015;115(18):180502. 10.1103/PhysRevLett.115.180502Search in Google Scholar PubMed

[71] Branciard C, Cavalcanti EG, Walborn SP, Scarani V, Wiseman HM. One-sided device-independent quantum key distribution: Security, feasibility, and the connection with steering. Phys RevA Atomic Mol Opt Phys. 2012;85(1):010301. 10.1103/PhysRevA.85.010301Search in Google Scholar

[72] Law YZ, Bancal JD, Scarani V, et al. Quantum randomness extraction for various levels of characterization of the devices. J Phys A Math Theoret. 2014;47(42):424028. 10.1088/1751-8113/47/42/424028Search in Google Scholar

[73] Costa A, Angelo R. Quantification of Einstein-Podolsky-Rosen steering for two-qubit states. Phys Rev A. 2016;93(2):020103. 10.1103/PhysRevA.93.020103Search in Google Scholar

[74] Vidal J, Dusuel S, Barthel T. Entanglement entropy in collective models. J Stat Mech Theory Experiment. 2007;2007(1):P01015. 10.1088/1742-5468/2007/01/P01015Search in Google Scholar

[75] Dusuel S, Vidal J. Finite-size scaling exponents of the Lipkin-Meshkov-Glick model. Phys Rev Lett. 2004;93(23):237204. 10.1103/PhysRevLett.93.237204Search in Google Scholar PubMed

[76] Dusuel S, Vidal J. Continuous unitary transformations and finite-size scaling exponents in the Lipkin-Meshkov-Glick model. Phys Rev B-Condensed Matter Materials Phys. 2005;71(22):224420. 10.1103/PhysRevB.71.224420Search in Google Scholar

[77] Cervia MJ, Balantekin A, Coppersmith S, Johnson CW, Love PJ, Poole C, et al. Lipkin model on a quantum computer. Phys Rev C. 2021;104(2):024305. 10.1103/PhysRevC.104.024305Search in Google Scholar

[78] Zheng RH, Ning W, Lü JH, Yu XJ, Wu F, Deng CL, et al. Experimental demonstration of spontaneous symmetry breaking with emergent multiqubit entanglement. Phys Rev Lett. 2025;134(15):150406. 10.1103/PhysRevLett.134.150406Search in Google Scholar PubMed

[79] Chinnarasu R, Poole C, Phuttitarn L, Noori A, Graham T, Coppersmith S, et al. Variational simulation of the Lipkin-Meshkov-Glick model on a neutral atom quantum computer. 2025. arXiv: http://arXiv.org/abs/arXiv:250106097. 10.1103/PRXQuantum.6.020350Search in Google Scholar

[80] Hlatshwayo MQ, Zhang Y, Wibowo H, LaRose R, Lacroix D, Litvinova E. Simulating excited states of the Lipkin model on a quantum computer. Phys Rev C. 2022;106(2):024319. 10.1103/PhysRevC.106.024319Search in Google Scholar

[81] Hengstenberg SM, Robin CE, Savage MJ. Multi-body entanglement and information rearrangement in nuclear many-body systems: a study of the Lipkin-Meshkov-Glick model. Europ Phys J A. 2023;59(10):231. 10.1140/epja/s10050-023-01145-xSearch in Google Scholar

[82] Robin CE, Savage MJ. Quantum simulations in effective model spaces: Hamiltonian-learning variational quantum eigensolver using digital quantum computers and application to the Lipkin-Meshkov-Glick model. Phys Rev C. 2023;108(2):024313. 10.1103/PhysRevC.108.024313Search in Google Scholar

[83] Beaujeault-Taudière Y, Lacroix D. Solving the Lipkin model using quantum computers with two qubits only with a hybrid quantum-classical technique based on the generator coordinate method. Phys Rev C. 2024;109(2):024327. 10.1103/PhysRevC.109.024327Search in Google Scholar

[84] Chen G, Robertson M, Hoffmann M, Ophus C, Fernandes Cauduro AL, Lo Conte R, et al. Observation of hydrogen-induced Dzyaloshinskii-Moriya interaction and reversible switching of magnetic chirality. Phys Rev X. 2021;11(2):021015. 10.1103/PhysRevX.11.021015Search in Google Scholar

[85] Oumennana M, Rahman AU, Mansour M. Quantum coherence versus non-classical correlations in XXZ spin-chain under Dzyaloshinsky-Moriya (DM) and KSEA interactions. Appl Phys B. 2022;128(9):162. 10.1007/s00340-022-07881-0Search in Google Scholar

[86] Oumennana M, Dahbi Z, Mansour M, Khedif Y. Geometric measures of quantum correlations in a two-qubit heisenberg xxz model under multiple interactions effects. J Russian Laser Res. 2022;43(5):533–45. 10.1007/s10946-022-10079-6Search in Google Scholar

[87] Bouafia Z, Oumennana M, Mansour M, Ouchni F. Thermal entanglement versus quantum-memory-assisted entropic uncertainty relation in a two-qubit Heisenberg system with Herring-Flicker coupling under Dzyaloshinsky-Moriya interaction. Appl Phys B. 2024;130(6):94. 10.1007/s00340-024-08228-7Search in Google Scholar

Received: 2025-04-20

Revised: 2025-06-03

Accepted: 2025-06-12

Published Online: 2025-11-04

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/phys-2025-0216

Keywords for this article

Lipkin–Meshkov–Glick model; quantum coherence; quantum discord; quantum steering; Bell nonlocality; DM interaction

Creative Commons

BY 4.0