Tunable double plasmon-induced transparency based on monolayer patterned graphene metamaterial

1 Introduction

Over the recent years, the scientific community has witnessed a remarkable upsurge in the research enthusiasm regarding surface plasmon polaritons (SPPs). This burgeoning interest stems from their unique capacity to surmount the constraints imposed by traditional optical diffraction [1], 2]. Specifically, SPPs hold great promise for manipulating light at the sub-wavelength scale, which has far-reaching implications for various fields such as nanophotonics [3], all-optical switch [4], and integrated optical circuits [5]. As a result, numerous studies have been dedicated to exploring the fundamental properties of SPPs, as well as devising novel strategies to harness and control them for practical applications [6], [7], [8].

Graphene has several remarkable attributes, namely its dynamic tunability, an extensive frequency operating range, and a substantially more pronounced locality of SPPs [9], 10]. Notably, the SPPs propagating along the surface of graphene exhibit properties that outshine those on metal surfaces. For instance, owing to the absence of a saturation point in the dispersion relation of graphene surface plasmons, a broadband optical response spanning from the mid-infrared to the THz regime is enabled [11]. Additionally, when the Fermi level of graphene is elevated to a higher value, the loss associated with graphene SPPs waves is significantly mitigated [12]. Experimental investigations have demonstrated that the graphene Fermi level can be effectively modulated by applying an appropriate applied voltage [13]. In light of these advantageous characteristics, graphene has emerged as the preeminent candidate in the development of plasmonic metamaterials. Consequently, graphene plasmonics has found significant applications in diverse areas such as light sensing [14], absorption [15], switching [16], and the generation of slow light [17], [18], [19]. In many instances, these applications are predicated on the mechanism of plasmonically induced transparency (PIT) [20], 21].

PIT arises from the quantum interference effects induced by the coupling between the bright-state and dark-state plasmons. A key feature of PIT is the presence of distinct transparent windows within the transmission spectra. This window effectively nullifies the resonance absorption that would otherwise be generated by Fano interference occurring in intense local fields [22]. To date, an extensive array of PIT based plasmonic devices has been put forward. These include optical switches, holographic imaging systems, and structures enabling ultra-slow light propagation [23]. The designs of these plasmonic devices exhibit great diversity. For example, they can be based on single-layer graphene, nanostructured metamaterials, or waveguide-graphene hybrid metamaterials. Nevertheless, the majority of these plasmonic devices are rather complex in their construction and pose challenges in terms of practical implementation [24]. Moreover, they predominantly display only a single PIT effect, limiting their functionality and versatility in more advanced applications [25]. This situation calls for the development of more simplified yet efficient strategies for fabricating PIT-based plasmonic devices with enhanced multi-functionality.

This study presents a novel graphene-based metastructure featuring a single-layer structure. At terahertz frequencies, the Double-PIT (DPIT) effect is attained via the interaction between a graphene rectangle and three graphene nanostrips within the structure. The metamaterial under investigation is modeled as an ideal, perfectly periodic patterned configuration. The outcomes from Finite-Difference Time-Domain (FDTD) numerical simulations are in close accordance with those derived from the coupled mode theory (CMT). When the proposed structure is contrasted with other existing structures, this particular graphene-based metamaterial showcases distinct advantages with regard to its simple structure and relative ease of manufacturing. By modulating the Fermi energy of graphene, active control over the DPIT windows can be effectively realized, thereby obviating the need for structural redesign. Additionally, this structure demonstrates excellent slow light performance. As a result, the proposed graphene-based metastructure holds great promise for enabling the development of modulation devices, slow light devices, and other associated devices, contributing to the advancement of terahertz based optoelectronic applications.

2 Model and theoretical method

The schematic diagram of the proposed periodic structure of the graphene metamaterial is shown in Figure 1(a). The Fermi levels E _f of the graphene structures can be dynamically tuned by gate voltage V _g between the electrode and the monolayer graphene, as illustrated in Figure 1(b). To achieve uniform impact of the gate voltage on all graphene sheets, they are linked with thin metal wires, ensuring consistent modulation across the entire graphene structure. As shown in Figure 1(c), the periodic unit is depicted from an overhead perspective. The monolayer graphene structures discussed in the article include a graphene rectangle (GR), a vertical graphene strip (VGS), and two aligned horizontal graphene strips (HGSs). Dielectric silicon layers with relative permittivity of 11.7, each having a thicknesses of 0.05 μm for top level and 0.25 μm for bottom level, encase the monolayer graphene. Details of the geometric parameters are given below: L = 6.0 μm, L ₁ = 0.6 μm, L ₂ = 3.0 μm, L ₃ = 2.7 μm, L ₄ = 2.0 μm, and L ₅ = 0.5 μm.

Figure 1:

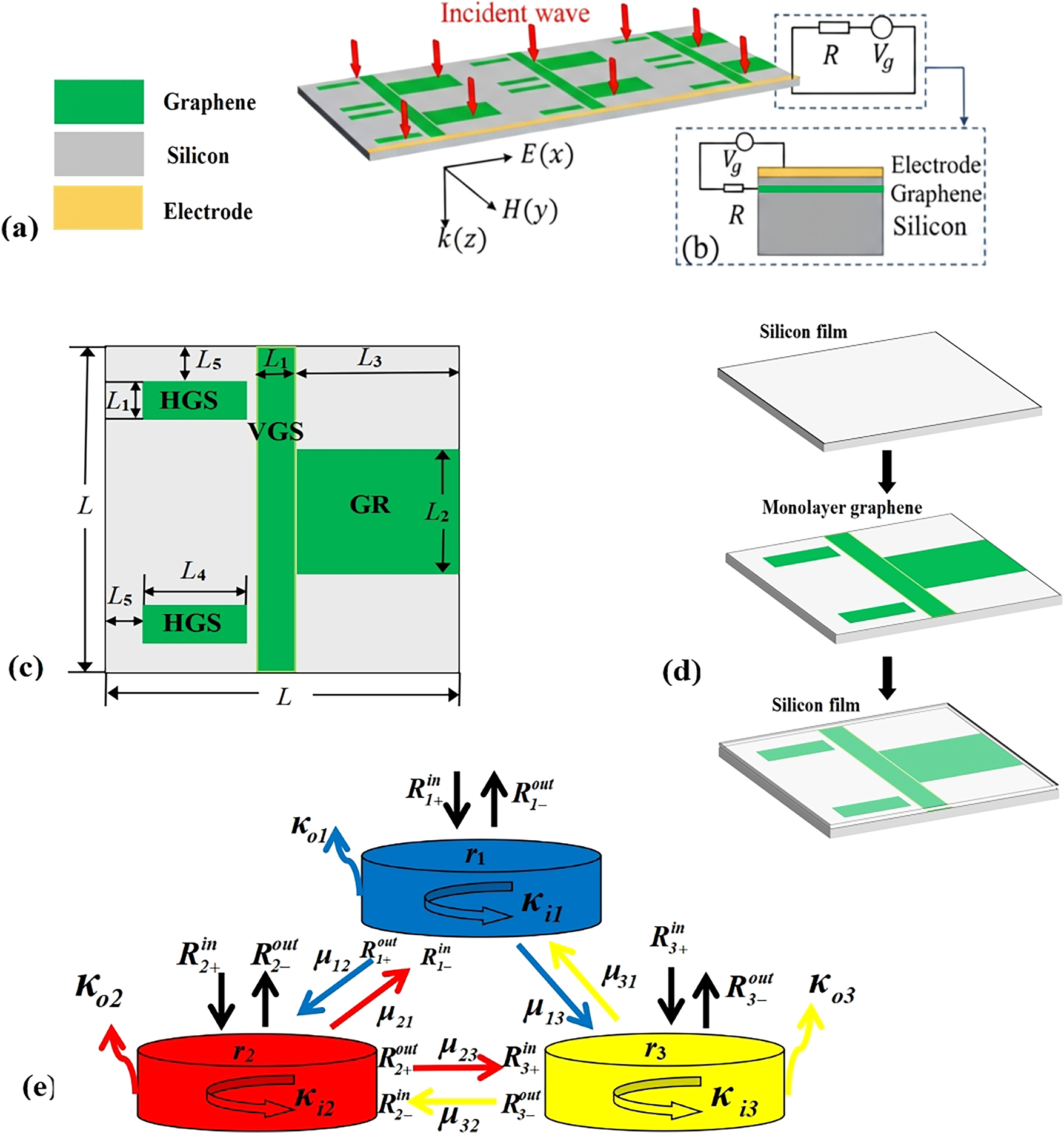
Schematic diagrams of the periodic metamaterial structure, Fermi energy-voltage relation, fabrication process and CMT representation. (a) Three-dimension illustration of the proposed periodic metastructure. (b) A diagram of the variation of the Fermi energy in relation to voltage. (c) Overhead view of a structural unit. (d) Fabrication process schematic of the designed metamaterial structure. (e) Schematic representation of CMT.

The fabrication process for our proposed structure is outlined in the schematic of Figure 1(d), which provides key information about how the structure is assembled. First, a graphene layer is grown on a copper foil via chemical vapor deposition, with the process carried out at a temperature of 1,050 °C [26]. After this step, the graphene is carefully transferred onto a 250 nm-thick silicon substrate, and acetone is used to remove any leftover photoresist from its surface [27]. Subsequently, following the approach detailed by reference [28], a 50 nm-thick silicon layer is accurately deposited on top of the graphene. These sequential steps help clarify the detailed preparation work involved in creating the structure.

In FDTD simulation calculations, the input x-polarized plane light wave propagates in the z-axis. Along the z-coordinate axis, perfectly matched layer (PML) boundary conditions are implemented, while periodic boundary conditions are imposed to the x and y directional boundaries. For the grid of the entire simulated structure, an accuracy of 50 nm is specified. A simulated environmental temperature of 300 K is adopted in the study. Under the above conditions, the conductivity σ _g of graphene layer can be written as:

Here, the electron charge corresponds to e, the graphene Fermi level is indicated by E _f , the angular frequency of incident light is reflected by ω, and the carrier relaxation time is embodied by τ = μ E f e v F 2 [29]. Here, v _F  = 10⁶ m/s indicates the Fermi velocity and the carrier mobility of graphene. Given that the graphene is embedded in the silicon layer, the propagation constant of graphene SPPs can be calculated by the following equation [30]:

Here, k ₀ denotes the electromagnetic wave vector transmitting in vacuum, ɛ _d signifies permittivity of dielectric layer silicon, and Z ₀ represents the intrinsic impedance in free space. Thus, it’s possible to determine the effective refractive index n eff = β k 0 .

Using the multi-mode interference CMT, investigation of transmission characteristics is also feasible. CMT stands out in photonic research for its notable strengths. It simplifies complex electromagnetic analyses by focusing on key resonant modes, avoiding computationally heavy full-wave simulations. As a well-developed theoretical research approach, CMT is capable of investigating the coupling interactions between two or more resonant modes, and it has been extensively applied in numerous academic studies [31], [32], [33]. In the diagram of Figure 1(e), we assume that the three resonators represent three modes. The notation R n ± i n / o u t n = 1,2,3 represent the input (denoted by superscript “in”) or output (denoted by superscript “in”) wave of the nth mode, where the subscripts “−” and “+” denote the wave’s positive or negative propagation direction. Correspondingly, the wave amplitudes of the three modes are designated as r ₁, r ₂, and r ₃ to match the respective resonators. The interrelation among the three resonators can be easily derived [34]:

Here, μ _nm (m = 1, 2, 3, n = 1, 2, 3, m ≠ n) indicates the resonator-to-resonator coupling coefficients, κ n = i ω − κ o n − κ i n − i ω n n = 1,2,3 denotes the net loss factor for the nth mode. Furthermore, κ o n = ω n 2 Q o n and κ i n = ω n 2 Q i n indicate the extra-loss and inter-loss coefficients, respectively. Meanwhile, Q _on and Q _in denote the external and internal loss quality factors of the nth mode. Q _in can be obtained by Q i n = Re n eff Im n eff ( Re n eff , Im n eff are the real and imaginary parts of the effective refractive index). The total quality factor Q _tn of the nth mode can be represented by: 1 Q t n = 1 Q o n + 1 Q i n , and 1 Q t n = f Δ f . Here, f and Δf are the resonance frequency of the nth mode as well as full width of half maximum (FWHM), respectively. As a beam of light wave is released from R ₁ and lastly emanates from R ₃, the relationship among three modes can be deduced via energy conservation:

Here, the phase difference of the plasmonic wave between R ₁ and R ₂, as well as R ₂ and R ₃, is represented by φ ₁ and φ ₂. Due to the fact that the three resonators are positioned in the identical plane, there is no phase difference among them. Thus, the aforementioned relationship can be utilized to determine the total transmission coefficient across the system:

Here,

Ultimately, the CMT can be used to determine the system transmittance: T = t ².

3 Results and theoretical analysis

In this section, we will discuss different impacts of parameters E _f , L ₂ and μ on the transparency windows. When the terahertz light is directly irradiated onto the proposed structure, different graphene structures have various spectral transmissions, as demonstrated in Figure 2(a) with E _f  = 1 eV, μ = 1.0 m 2 / V s , L ₂ = 3 μm. A detailed examination of each monolayer graphene’s function in the proposed structure is necessary to comprehend the physical process underlying DPIT. The spectra denoted by red and yellow lines show evident Lorentzian curves, which are the results of the HGSs and GR being directly excited by the incident wave. Thus, two transmission valleys located at 4.6143 THz (red line) and 4.6793 THz (yellow line) form in the spectra. And the two resonant frequencies are labeled by f ₁ (marked by red arrow) and f ₂ (marked by yellow arrow), respectively. Whereas, the transmittance of the VGS-generated blue line shows no significant alteration upon exposure to the incident wave. Its transmittance remains nearly constant at approximately 1.0. Apparently, both graphene HGSs and GR are identified as bright modes owing to the broad linewidths of their resonance dips in the transmission spectrum (as shown by the red and yellow lines in Figure 2(a)), while graphene VGS is characterized as a dark mode owing to the narrow linewidth of its resonance dip (as shown by the blue line in Figure 2(a)). When x-polarized terahertz incident light irradiates the metamaterial, the bright modes can be directly coupled with the incident light. The oscillating electric field of the light drives the charge carriers in HGSs and GR to oscillate collectively, exciting their plasmonic modes – these modes readily interact with the incident light. In contrast, due to the mismatch between the vertical structure of VGS and the direction of the x-polarized light, VGS cannot be directly excited by the incident light, so its plasmonic modes remain inactive initially. However, VGS can be indirectly excited by the near-field generated from the interaction between the bright modes and the incident light. When the resonance frequency of the bright modes matches the monopole resonance frequency of the dark mode, PIT phenomenon occurs, as shown by the black line in Figure 2(a). Two transparent windows with 0.907 and 0.79 transmittance are located at f _peak1 = 4.0991 THz (labeled as peak1) and f _peak2 = 4.997 THz (labeled as peak2). Correspondingly, three valleys appearing on the spectrum of combined graphene structure are denoted by dip1, dip2 and dip3, respectively. Moreover, Figure 2(b) shows a high degree of concordance between the theoretical calculations of CMT and the simulation findings of FDTD.

Figure 2:

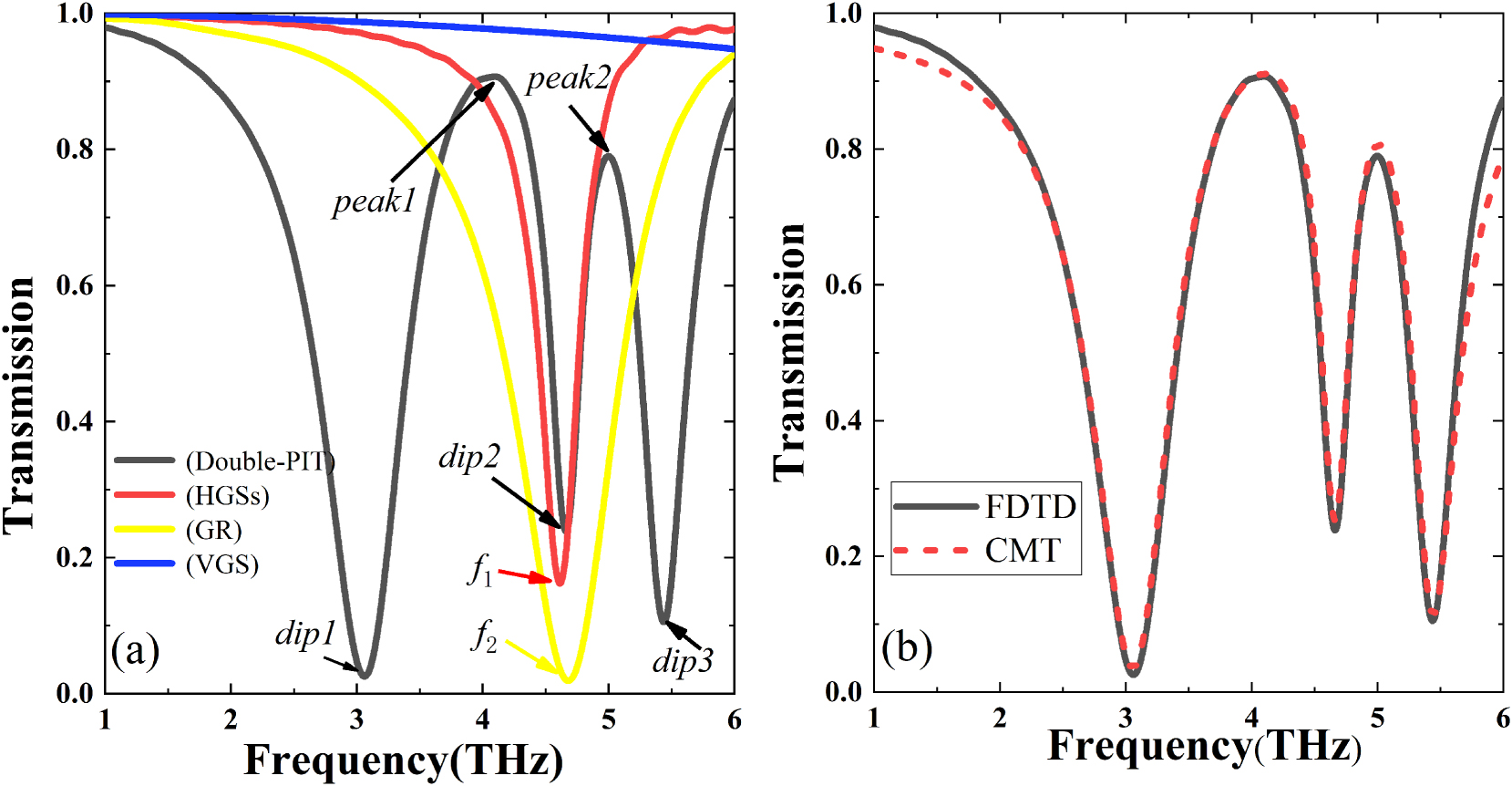
Transmission spectra of various graphene configurations and FDTD-CMT comparisons. (a) Transmission spectra of HGSs (red line), GR (yellow line), VGS (blue line), and combined graphene structure (black line). (b) Transmission spectra of FDTD simulation result and CMT theory. (E _f  = 1 eV, μ = 1.0 m 2 / V s , l ₂ = 3 μm).

The underlying physical mechanism of the double PIT production is reflected in the structural electric field distribution at the relevant resonant frequencies. Figure 3 displays the distribution of the electric field E (XY plane) at different resonance frequencies marked by arrows in Figure 2. For two independent bright modes, the weak electric field E is restricted to the region around graphene HGSs and GR, as shown in Figure 3(a) and (b), and the electric field energy around them is in equilibrium. However, when VGS (dark mode) is added to this system, the electric field balance around HGSs and GR (bright modes) is disrupted. At this moment, due to the coupling effect between them, the electric field around the bright modes are enhanced, and the dark mode is also excited by the near-field. Concerning the DPIT effect-induced dips, within subplots (c), (e), and (g) of Figure 3, the electric field is predominantly located at the corners of HGSs and GR, and stronger electric fields are localized in the gap between the HGSs (bright mode) and the VGS (dark mode). As depicted in the diagram of Figure 3(d), the electric field’s concentration shifts to the two sides of VGS, which means the peak located at f = 4.0991 THz is formed by the interaction between two bright modes and dark mode. At the resonance frequency peak2, the weak electric field largely emerges at the angular points of HGSs and the left side of VGS, as depicted in Figure 3(f). This observation suggests the resonant peak2 stems from the coupling effect between HGSs and GR.

Figure 3:

The electric field distributions of different resonant frequencies which are marked by arrows in Figure 2.

Because of its low ohmic losses and flexible modulation characteristics, graphene metamaterial is widely used and provides notable benefits in a variety of applications. Common techniques for achieving these tuning characteristics include chemical doping and field-based tuning via electric and magnetic field. A widely adopted method consists of utilizing a gate voltage V _g to modify the Fermi levels of graphene metamaterial [35], 36]. The relation between V _g and E _f can be given by [37]

Where ɛ ₀ represents the vacuum dielectric constant, and d denotes the distance separating the electrode from the graphene plane. Figure 4 illustrates various DPIT spectral lines produced by the proposed structure for different Fermi levels to demonstrate the tunability of PIT windows. It is clear that with the increase of the Fermi levels, two transparency windows shift gradually toward higher frequencies. For example, when E _f increases from 0.95 eV to 1.20 eV, peak1 shifts from 3.9815 THz to 4.4342 THz, and peak2 blue-shifts from 4.8694 THz to 5.4772 THz, respectively. This phenomenon stems from the requirement that graphene electrons necessitate a higher energy input to resonate with increasing Fermi level. It is evident that Figure 4 demonstrates the adjustability of transparency windows through the manipulation of the Fermi level.

Figure 4:

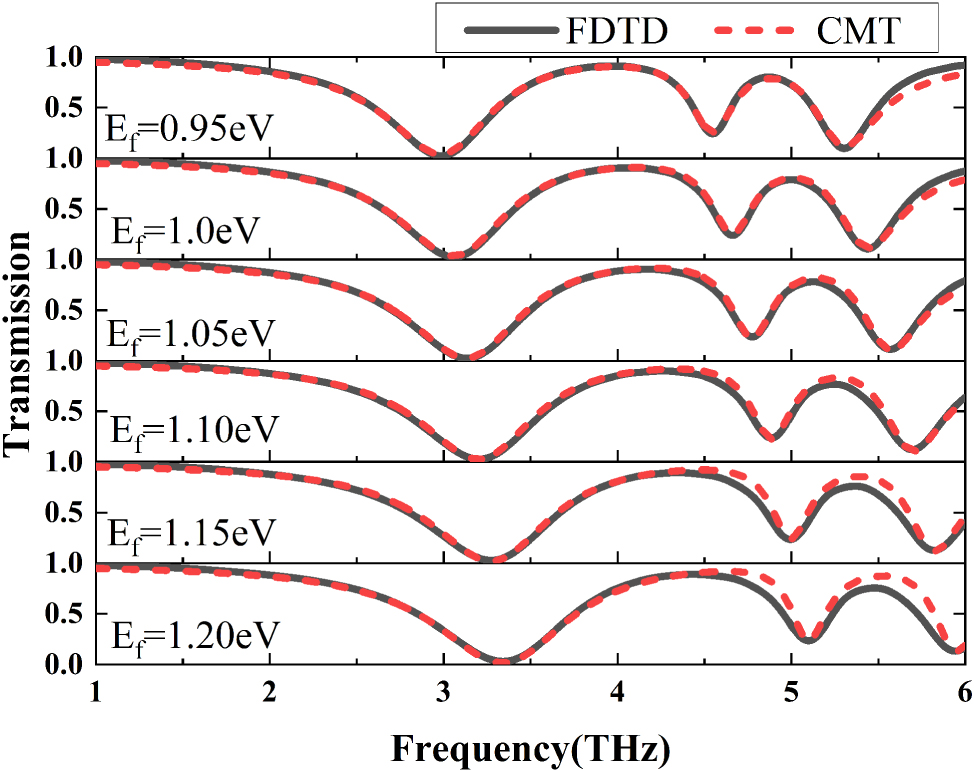
Transmission spectra of FDTD results and CMT data at different Fermi levels. ( μ = 1.0 m 2 / V s , L ₂ = 3 μm).

Analogous to the atomic system, the plasmonic system exhibits the capability to reduce group velocities. Leveraging the notable dispersion characteristics of monolayer graphene, we can utilize it in plasmonic nanostructures to manipulate electromagnetic fields. Regarding adjustable slow-light phenomena, controllable group delay is feasible via Fermi level modulation. Theoretical calculation of the group index (n _g ), which signifies the slow-light effect, is performed using the following formula [38]:

Here c is the light speed in vacuum, the group velocity is denoted by v _g , h stands for the thickness of the proposed nanostructure, and φ is the transmission phase shift. The graphs in Figure 5 display the modulation of group index and phase shift across frequencies when the graphene Fermi level is tuned from 0.95 eV to 1.2 eV. It reveals that the group index demonstrates a stable increase with the escalation of the Fermi level of graphene, on the condition that the remaining parameters remain constant. The group index is observed to be 239 when the Fermi level is at 0.95 eV, whereas the value increases to 270 as the Fermi level ascends to 1.20 eV. The sharp phase shift and intense dispersion of the SP wave, originating from the near-field interaction of bright-dark mode coupling, result in a remarkable augmentation of the group index close to the DPIT windows.

Figure 5:

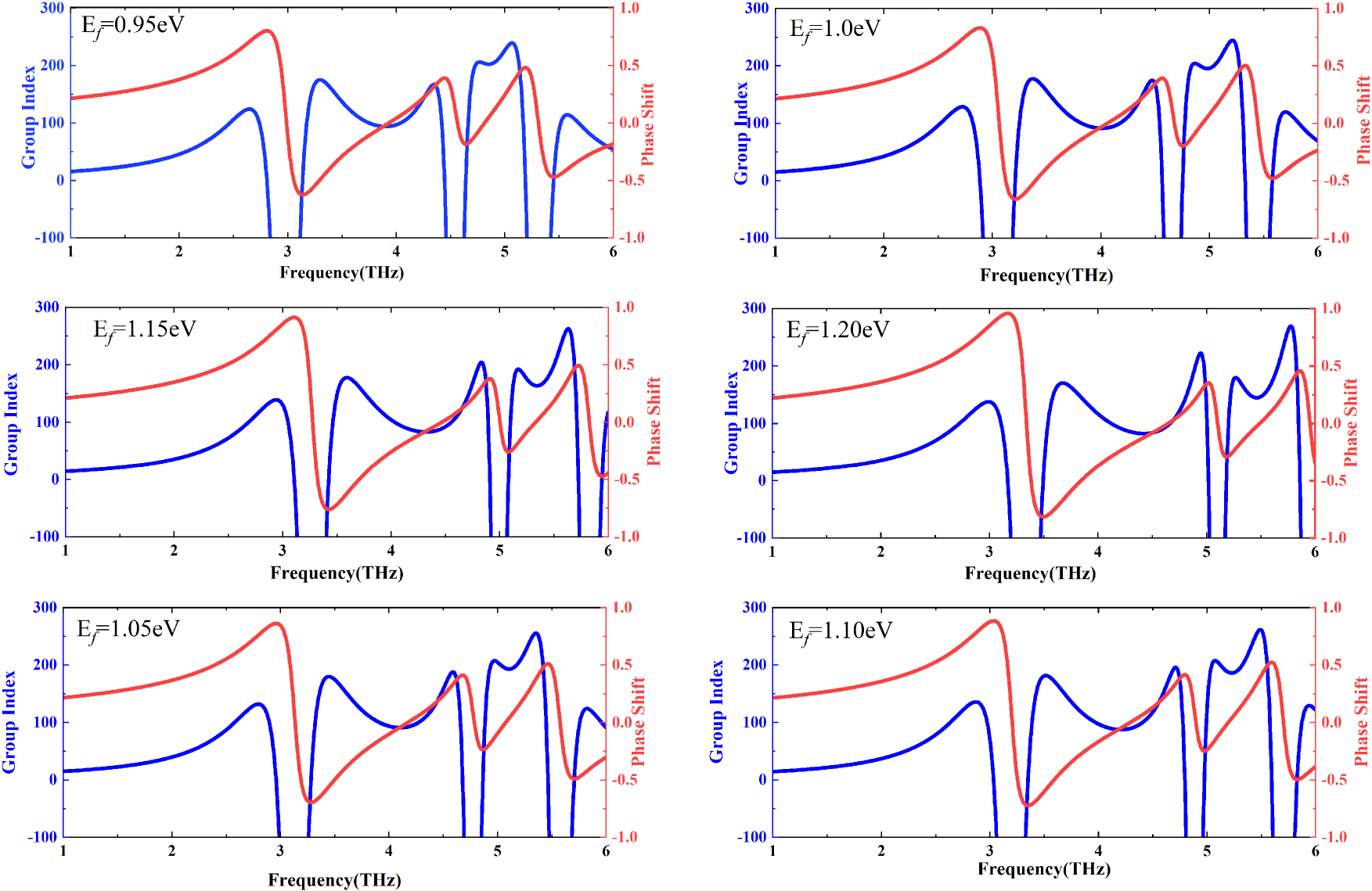
Frequency-dependent modulation of group index and phase shift during the transition of graphene Fermi level from 0.95 eV to 1.2 eV.

To investigate how structure geometry impacts DPIT windows, we set the Fermi level at 1.0 eV. The transmission characteristics of the graphene nanostructure for varying lengths of L ₂ are illustrated in Figure 6. It can be seen that with the gradual increase of L ₂, the transmission spectrum exhibits a minor blue shift. Additionally, the magnitude of peak1 experiences a slight diminishment, whereas the magnitude of peak2 undergoes a minor augmentation. Even in the presence of L ₂ variations of ±200 nm, the alterations to the transmission spectrum are minor. This observation indicates that during the fabrication process, the performance of this graphene structure exhibits resilience to minor discrepancies that potentially occur. The robustness has a certain value in practical implementations where maintaining consistent precision can be challenging.

Figure 6:

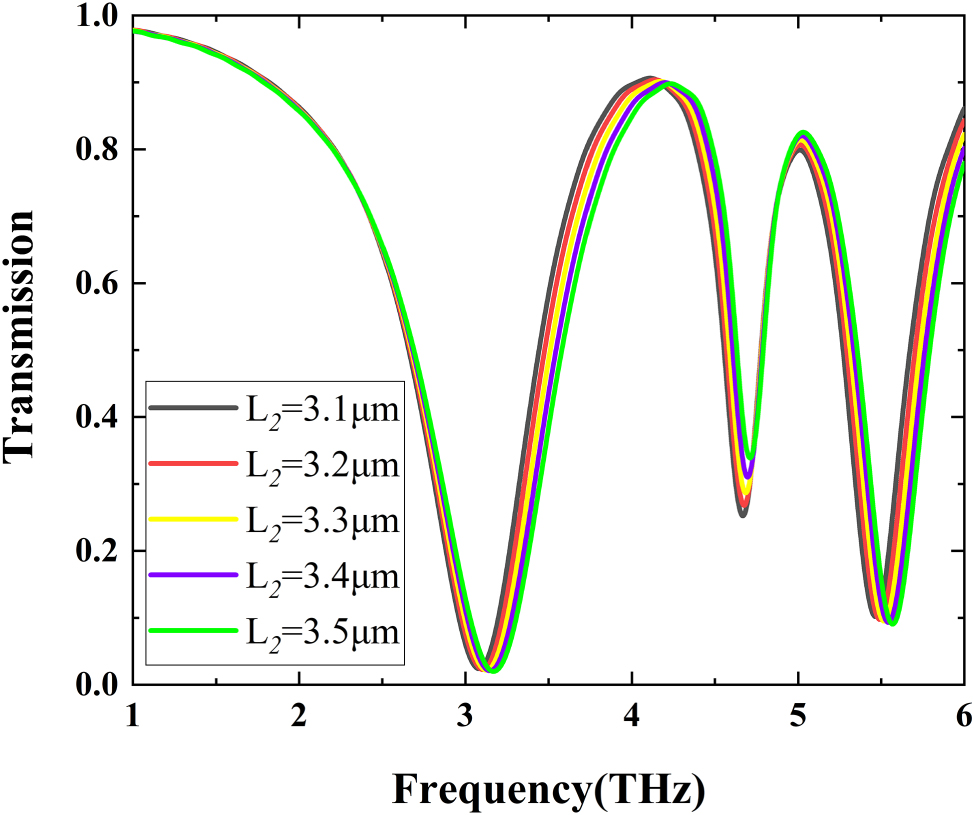
Transmission spectra of FDTD results at different lengths of L ₂. ( μ = 1.0 m 2 / V s , E _f  = 1 eV).

Chemical doping can modify the carrier mobility within graphene, thereby influencing its spectral characteristics. In order to ascertain this correlation, we maintained the Fermi level at 1.0 eV while changing the graphene carrier mobility (µ). Figure 7 provides the transmission spectra of FDTD results and CMT data when the graphene carrier mobility is varied from 1.5 m 2 / V s to 3.0 m 2 / V s . As depicted in Figure 7, the transmittance spectral curve exhibits a weak low-frequency shift (red shift), accompanied by an increase in transmittance for the two PIT windows with the elevation of graphene’s carrier mobility. An increase in carrier mobility (μ) implies enhanced transport capability of charge carriers, which reflects strengthened metallicity and electronic activity of graphene; consequently, electrons can participate more efficiently in electromagnetic responses and undergo collective oscillations. Meanwhile, high carrier mobility implies high surface conductivity [39], allowing electrons to respond more quickly to changes in the electric field without the need for high-frequency electric field driving. These effects collectively indicate that electrons can complete collective oscillation processes at lower frequencies, resulting in a decrease in spectral line frequency (redshift) [40]. The combined effect of these improvements yields a superior quality factor and an enhancement in peak transmittance. Simultaneously, we also observe that the values of dip2 and dip3 decrease gradually. The intrinsic relationship between spectral properties and carrier mobility highlights the significance of carrier mobility in the design and practical application of graphene-based metamaterials.

Figure 7:

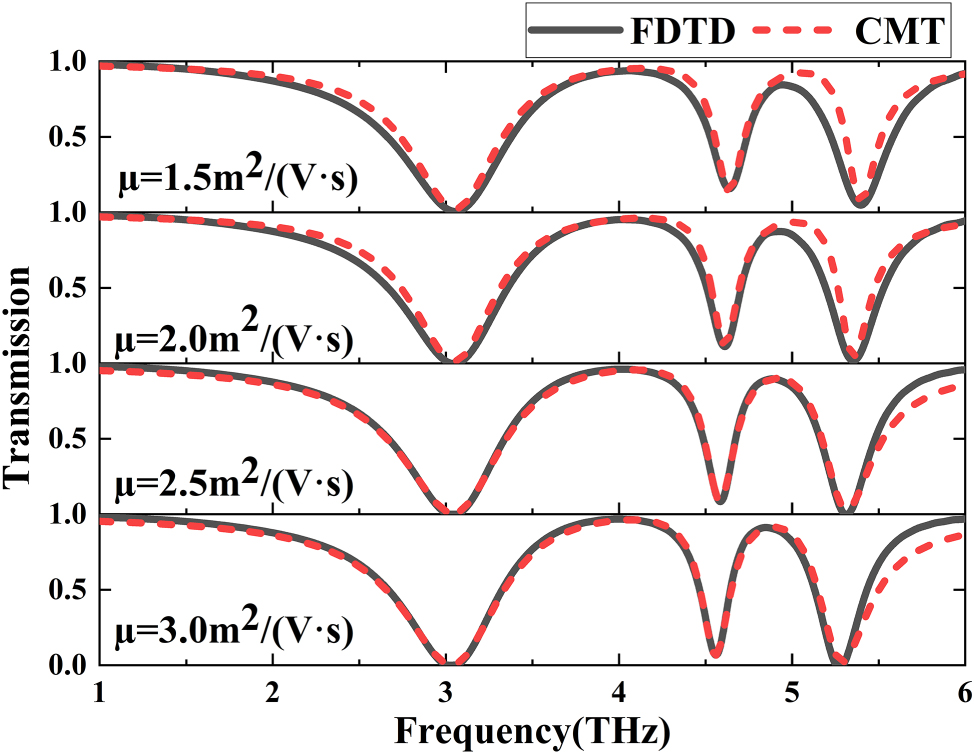
Transmission spectra of FDTD results and CMT data when the graphene carrier mobility is changed from  1.5 m 2 / V s to  3.0 m 2 / V s . (E _f  = 1.0 eV, L ₂ = 3 μm).

Figure 8 exhibits the variation of group index and phase shift in relation to frequency when the graphene carrier mobility is increased. It reveals that the group index of the proposed structure at the resonance points increases significantly with the Fermi level fixed at 1.0 eV. Notably, the group index even reaches 600 as μ = 3.0 m 2 / V s , and the value achieved in this way significantly surpasses the group index values obtained by adjusting the Fermi level of graphene. As shown in Table 1, this value is greater than that of other slow light effects relying on graphene metamaterials with comparable parameters. Additional experimental findings [41] corroborate that graphene exhibits a carrier mobility as high as 10 m 2 / V s at room temperature, a trait that remains invariant across temperature fluctuations and is predominantly constrained by impurity-mediated scattering processes. Consequently, it is viable to further reduce the group velocity by employing this methodology in reality.

Figure 8:

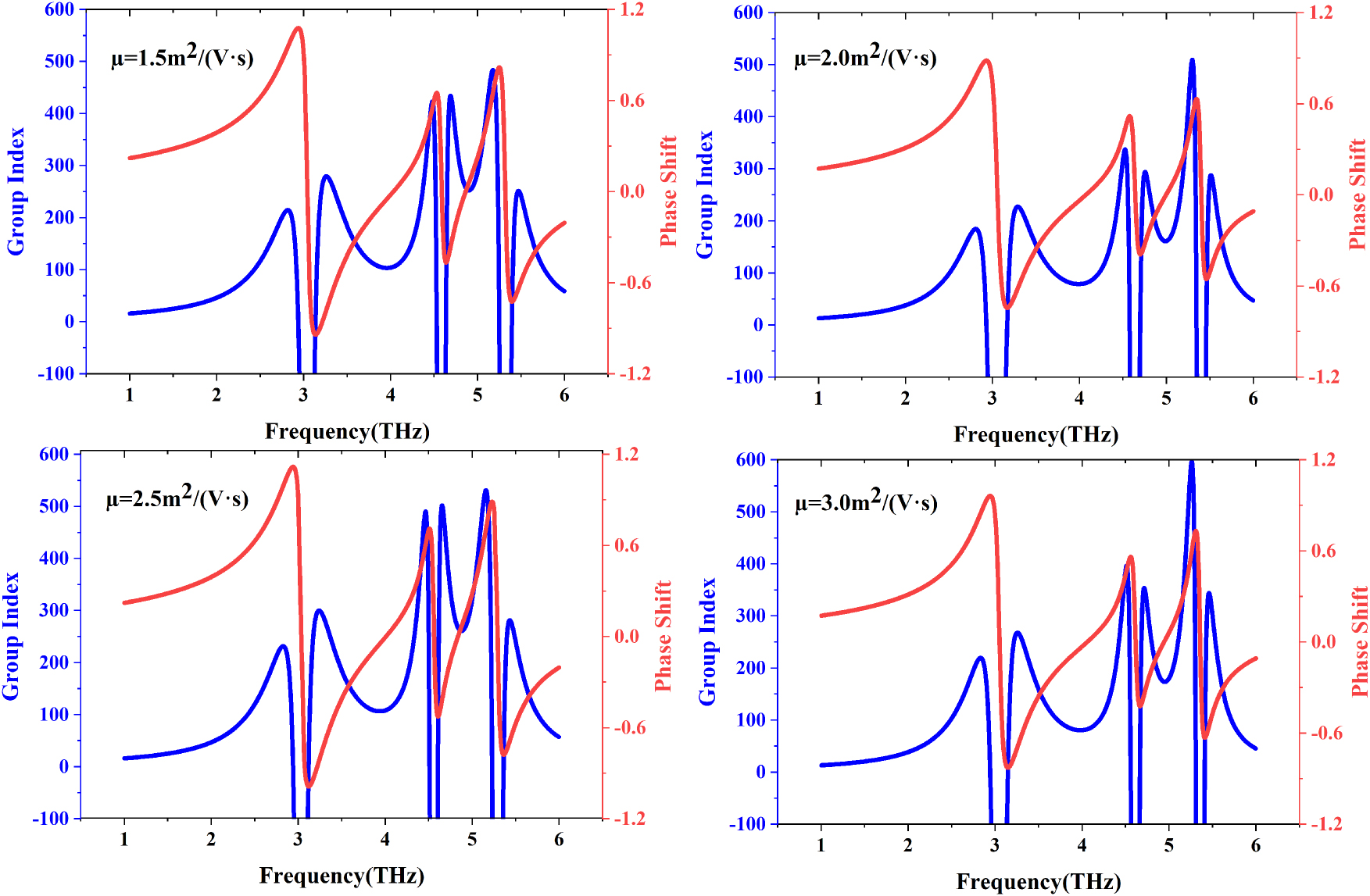
Frequency-dependent modulation of group index and phase shift during the transition of graphene carrier mobility from  1.5 m 2 / V s to  3.0 m 2 / V s .

4 Conclusions

In this work, we present a monolayer patterned graphene composed of three graphene nanostrips and a graphene rectangle for the realization of a DPIT, and explore its spectral properties with different geometrical parameters L ₂, Fermi energy level E _f , and carrier mobility μ. The spectral properties obtained from FDTD calculations show consistency with those derived from CMT theory calculations. In addition, we examine how adjusting the Fermi energy and carrier mobility influences the slow light phenomenon. Significantly, enhancing the mobility of carriers in graphene emerges as the most effective means to optimize the slow light effect. As demonstrated by the numerical results, the group index reaches 600 as μ = 3.0 m 2 / V s . In general, the findings of this work provide valuable guidance for slow light devices.