The search for the cosmological cold dark matter axion – A new refined narrow mass window and detection scheme

1 Introduction

To understand the constituent particles that form the matter in our universe, as well as explain the large-scale structure observed everywhere, it is necessary to get acquainted with the phenomenology of the elusive particles known as Axions or Axion-like particles (ALPs), which seem to lie outside the boundary of or beyond the current Standard Model (SM) of physics. These particles with interesting properties and fundamental importance in the SM also find possible liaisons within the current model of cosmology (the Concordance model or the Cold Dark Matter model), and therefore, have great potential in understanding the nature of matter (and possibly the nature of dark matter as well in our universe). Axions may also be radiated from primordial black holes (PBHs) as a result of their evaporation, as has been argued for some time if PBHs can be found [1,2]. Axion tomography can be carried out combined with gravitational wave detection [3] and their collective signatures could prove valuable in our understanding of the physical universe we inhabit.

A deep analysis of the theory of quantum chromodynamics (QCD), one of the cornerstone constituents of the SM Lagrangian, revealed that a problem existed with the vacuum structure in the theory (specifically by the virtue of the extremely small value of the vacuum angle or ( Θ ¯ ) parameter, also the minimum of the QCD Instanton potential, which is estimated at around less than 10⁻¹⁰ from the absence of neutron electric dipole moment) which allowed for the violation of Charge Conjugation and Parity (CP) symmetries in QCD interactions, a dilemma, which was later termed as the Strong CP problem [4]. Physicists Peccei and Quinn suggested an elegant mechanism to fix this problem with the suggestion of a new chiral symmetry ( U ( 1 ) P Q [5], which spontaneously broke to result in the emergence of an extremely light, virtually invisible, pseudo-Nambu-goldstone boson, named the Axion (although lately its variants have also been suggested, known as Axion-like particles or ALPs). These were also named and classified as the invisible dark matter particles by investigators during the early stages of the theory [6].

Axionic field replaced the small vacuum angle and emerged as a new quantum field among all the possible fields existing within the quantum vacuum; however, with extremely weak coupling to ordinary matter. It did not take long before axions were identified as plausible new candidates for the proposed (non-baryonic) cold dark matter dominating the matter density of our universe [7,8]. At the same time, nevertheless, it is becoming increasingly plausible after the recent astronomical observations that the unexplained matter responsible for the observed discrepancies in galactic rotation curves and cosmic microwave background (CMB) data could not be a non-baryonic dark matter but instead a conglomeration of ordinary baryonic matter (such as clumps of cold hydrogen gas agglomerating in galactic halos, etc.). The discussion of ordinary or dark matter and its possible forms is beyond the scope of this study, which specifically concentrates on the subject of axion mass and axion detection, and a recent review on the subject can be found elsewhere [8,9].

There has been a lot of theoretical investigation into the physics of axions, and countless models for their existence and properties have been suggested, including the recent suggestions of coherent zero-mode axionic oscillations around their minimum, possibly forming a Bose–Einstein condensate of axions [10,11].

Within the framework of QCD and the string theoretical framework [12], some ideas have been developed during the past three decades in an attempt to understand the formation and evolution of axions soon after the onset of inflation during the epoch. The detailed treatment of the primordial axion formation from the string networks is beyond the scope of this study and can be found in any detailed reviews, such as in previous studies [13,14]. In short, during the Planck epoch, soon after the PQ symmetry breaking, the fundamental axionic string networks form and give way to the formation of string-based domain walls that interact and annihilate around the time of the QCD phase transition [13–17], in turn producing axions that permeate the universe and reach the present epoch as non-thermal Relic Axions [18]. In the beginning, these axions are hot and have much higher kinetic energy; however, their temperatures subside as well as their speeds slow down as well and become non-relativistic (hence the term “cold” dark matter in contrast to the other supposed type, the relativistic or “hot” dark matter, such as neutrinos and other particles), and are thus considered to be one of the most ideal candidates for being the constituent particles of the dark matter. Only a cold form of dark matter could have contributed to the process of structure formation in the universe by agglomerating mass within galactic halos, leading to the formation of cosmic structures, such as galaxies and clusters, we observe today.

However, in addition, axions seem to evolve in a non-linear manner following the onset of QCD transition and have additional effects from cosmological factors, such as the Hubble expansion. Hence, it is difficult to predict their behavior owing to several mathematical and cosmological considerations. Besides, the axion field produced as a result of symmetry breaking (PQ) undergoes time-dependent random fluctuations as the universe evolves, and thus, the field takes the form of an oscillating field around a mean value. An important stage in axion field evolution is the onset and duration of inflation, whether the PQ symmetry is broken before (or during) the onset of inflation or post-inflation, once a minimum has been reached in the inflation, i.e., the inflation field has equilibrated to its minimum value in its potential valley, and the new episode of universe’s evolution, the Reheating, begins.

In this study, we contemplate the second scenario wherein the U(1) PQ symmetry breaks after the onset of inflation, while it has receded and the epoch of Reheating has commenced. As a result, the topological defects in the quantum vacuum produce a network of two-dimensional elementary objects, “Strings” and their corresponding “Domain Walls” [19], known as the “String–Wall” systems, which are formed at the onset of the QCD phase transition following the production of instantons. The formation of these systems and their subsequent collapse, later on through instantonic effects, in turn, produces several successive generations of cosmological axions, collectively forming a large number density of these particles, which later become the relic cold dark matter in our universe [20].

An important step in the cosmological evolution of the axion fields is that during the QCD transition, these fields become massive (as a result of the production of instantons) and undergo oscillations around the minimum of the field’s effective potential. Here, if the value of axion mass exceeds a certain threshold (which, in certain models, has been suggested to be around 5 μeV/c²), then the aforementioned mechanism can result in the production of an ensemble of cold and coherent light axions, forming the collective relic cold dark matter that has traveled since then in space and time to the current epoch. This is the ad hoc hypothesis of axion production from instantonic effects; in short, that is so far the most plausible scenario of the origins of axions in our universe. However, an appropriate detection mechanism and the knowledge of the right mass range are important to detect these particles. Axion mass and its particular value have non-trivial significance in not only the knowledge of elementary particle fields but also in cosmology, where another important parameter, the actual scalar field (that the axion field is a phase of, as explained later in the next section), enters the picture. The axion mass affects the role of the particle as a dark matter candidate as well as its interaction dynamics (mainly through the coupling to other particles and fields), whereas its associated scalar field determines the important elements in the cosmology of the universe, such as cosmic inflation and the equation of state. However, the axion field is a pseudo-scalar field, and the scalar field has different dynamics and interacts differently with other fields. Since we are not aware of the coupling strengths of the fields and also the mass of the axionic fields following mass generation, it is difficult to quantitatively describe the field dynamics as well as provide an experimental framework, which depends on the value of the couplings and an exact mass range.

Thus, we have a serious “axion mass problem” owing to our inability to estimate the mass range that these particles could exist in, which, in turn, determines another important parameter, the axion decay constant ( f a ), similar to decay constants of other particles, and also affects the coupling of axions to field mediating bosons, most importantly to photons. The correct knowledge of axion mass could help us determine both the decay constant of axions and their couplings to photons and other particles, such as pions. In addition, the axion mass window is paramount for the experimental detection of these particles, making it extremely difficult to find axions with precision in laboratory settings while being unaware of which mass window to look for them. Therefore, the parameter of axion mass is of fundamental importance in axion and related physics.

2 The model

The dynamics of a scalar field evolving in space-time in an expanding universe are described by the Friedmann equations, obtained from the Einstein field equations, using an appropriate metric. These equations laid down with the help of a spatially flat Friedmann–Lemaître–Robertson–Walker (FLRW) background, while incorporating the FLRW metric, can be expressed along with the metric as follows [21]:

where a s ( t ) is the scale factor, with each dot depicting one-time differentiation with respect to the cosmic time, G is the universal gravitational constant, ρ and p are the mass density and pressure of the fluid matter, respectively, and Λ is the cosmological constant.

We consider bosonic fields arising out of the spontaneous broken PQ symmetry that acquire mass and become axion (or ALPs) particles.

The interaction Lagrangian for these bosonic fields, often termed as the “invisible axion” particles, while ignoring the kinetic and other terms, is given by [6]

Here, J μ is the associated Noether current of the broken PQ global symmetry, whereas φ are the complex, pseudo-scalar bosonic fields (that become the axionic/ALP fields), and f a is the axion decay constant (a measure of axion–two-photon coupling, g a γ γ ), corresponding to the PQ symmetry breaking scale (also often written in the literature as f P Q ), and inversely proportional to the axion field’s mass.

The axion field, a ( x ) , itself is the phase of the complex scalar field φ , described by

The radial mode of this field, shown here as r ( x ) , is a massive field with mass m r . At high temperatures, after the QCD transition takes place, the axions have mass acquired from instanton effects, albeit negligible. The QCD phase transition (which sets the QCD temperature scale) involves the thermal transitory phase when the primordial quark and gluon condensate, created earlier in vacuum during the low-energy regime at zero temperature, has disappeared and the chiral symmetry is restored [10,11].

The most significant element of the PQ theory and a decisive factor in the emergence of axions is the decay constant, f a , which we shall limit our concentration to in this report.

The value of the axion decay constant is a free parameter in the theory under consideration here, with a broad range of mass values attributed to it. However, given the physical and cosmological considerations, a (broad) realistic window of the coupling’s possible range has been obtained as 3 × 10 9 ≥ f a ≤ 1 × 10 12 ( GeV ) [7,22], which approximately corresponds to an axion mass range of roughly ∼ 5.5 μeV ≥ m a ≤ 3.0 meV (with a somewhat lax lower bound, and conversely, a stringent bound on the upper limit). Hence, most of the axion searches are carried out within this parameter space.

The other main parameters in our model are the environmental factor, i.e., the misalignment angle, θ i , and the critical temperature ( T c ) at which the transition takes place.

Following the PQ symmetry breaking, the axion is created with a spectrum of misalignment angles in various disconnected regions; however, as the onset of inflation occurs during the post-inflation era, the instanton effects cause the value of the misalignment angle to fall to a universal value oscillating in its minimum potential. The accepted value of this minimum is the root-mean square value of 〈 ϑ a 〉 ≥ π 3 = 1.8137 , the lower bound around which the axion misalignment angle fluctuates (as existing in the current post-inflation epoch). Once the involved calculations are carried out, this corresponds to the value of axion coupling around f a = 2.82 × 10¹¹ GeV, thus making an upper bound on the axion mass. On the other hand, the lower value of the coupling finds a lower limit of f a > 10 8 , following stringent astrophysical considerations.

Based on earlier work, following a dilute gas approximation model conceived by Turner [23] (and further developed by Bae et al. [24]), assuming the axions to exist in the form of a dilute instanton gas following the onset of decoupling, the mass of axion/ALPs is described as follows for the dilute gas temperature Λ (in MeV):

The temperature at which the axions slow down and become the non-relativistic cold dark matter and undergo oscillations, as based on the QCD equation of state, is found to be approximately equal to [25]

This corresponds to an upper limit of

However, in the post-inflation scenario, the coupling is endowed with the production of string networks and domain walls, and hence, it is restricted to a lower value, as discussed earlier:

As per the misalignment mechanism [26], the value of the initial misalignment angle, θ i , spans the region

This produces the viable axion window in the post-inflation scenario of

In view of the measured non-absence of neutron electric dipole moment (nEDM) [27], an upper bound of θ i < 10 − 10 is fixed for the value of the misalignment angle.

Two scenarios of PQ symmetry breaking and axion production are possible here and need to be considered. In the first scenario, the PQ symmetry breaks a priori to the epoch of inflation begins (called the pre-inflation scenario), while in the second one, the PQ symmetry breaks a posteriori when the epoch of inflation has already begun, as the nascent universe evolves during the ensuing highly accelerated inflation epoch, generally known as the post-inflation schemes.

The universal expansion (and, consequently, the change in the scale factor, which is generally gauged with the help of the Hubble parameter) has a direct correlation with the temperature of the universe, which in turn affects the value of the axion potential [11].

As the universe’s temperature decreases, the value of the Hubble parameter also decreases; however, the axion potential becomes deeper, and its value increases. According to the equation of motion (obtained from the Dilute Instanton Gas model approximation [28]), the dynamics of the axion’s field are governed by

As argued in detail in Di Cortona et al. [11], as the temperature cools down further, the attractive axion potential reaches the expansion-driven Hubble friction. When the value of the temperature-dependent axion mass approaches nearly three times the value of the Hubble parameter, the axion field undergoes oscillation at the axion Compton frequency corresponding to the axion mass value. This is soon followed by the axion number density becoming an adiabatic invariant and the axion taking the form of cold dark matter. This occurs assuming the scenario that the PQ symmetry breaks a priori to the epoch of inflation (the pre-inflation scenario), with the value of the misalignment angle ϑ settling down to a fixed place ϑ 0 in the potential valley’s bottom, as the nascent universe evolved during the highly accelerated inflation epoch.

In the alternate scenario, the post-inflation scheme, PQ symmetry breaks following the onset of inflation, as the accelerated episode of inflation begins and the universe undergoes its massive accelerated expansion, and it is not possible to determine the value of θ . The value, thus, has to be integrated numerically over all the possible values, and an average value is chosen, which is typically θ i ≅ 2.1 . In this scenario, the free parameter θ is eliminated, and one obtains instead the axion abundance Ω a as a function of the decay constant f a , as follows:

where n a ⁎ / S ⁎ is the ratio of post-axion oscillation values of the photon entropy density and the average axion density (and takes the value of a constant as soon as the axion field undergoes oscillation), and the ratio Ω γ / T γ is the photon abundance’s ratio to its temperature around the decoupling era (and as indirectly estimated today by the CMB).

The axion mass is bound within the μeV region owing to cosmological considerations (in order not to exceed the observed CDM density), which is known as the so-called “Anthropic window” [6]. This is, thus, the narrow window for ultra-light cold dark matter axion (and axion-like particle) searches:

The critical temperature ( T c ) in the calculations is defined as the temperature when the axion field undergoes coherent oscillations around its minimum value (at the particular moment, which is known as the “critical time,” or t _c ):

where m a ( T c ) is the mass of the axionic field at the transition temperature, and the Hubble parameter H , ^[1] as a function of the critical temperature, is given by a form of the Friedmann equation (with flat geometry and vanishing cosmological constant):

Here, g _c is the relative degrees of freedom at the critical time t, G is Newton’s gravitational constant (which can be alternatively written in terms of the Planck mass, M p ), and ρ c is the critical energy density of the universe at the onset of the transition to the critical temperature.

We follow an approach, similar to Buschmann et al. [29] and Hiramatsu et al. [30–32], in constructing an axion model taking into account the three fundamental mechanisms for axion production, viz., misalignment [33,34], global string decays [35], and domain wall decays [36] since all these three, especially the two principal mechanisms, the axion field misalignment mechanism and the decay of global axion strings and domain walls, equally contribute to post-inflation era axion production.

The energy density with the cosmological constant (Λ) and the susceptibility ( χ ) of topological charge at T = 0 are given by:

which suppresses the temperature dependence and fixes the value of the zero temperature axion mass as a function of the coupling constant alone, and can be described by the expression [14]

3 Fitting of the model to cosmological parameters

Similar to the earlier calculations by Wantz and Shellard [10], among others, we adopt a high-temperature cosmological model in an era soon after the decoupling has taken place, with a sufficiently high-temperature value of the decoupling temperature, around T = 400 MeV (far above the QCD transition).

We carry out our calculations around the accepted value of axion density ( Ω a ) [37] with the express assumption that it is equal to the total cold dark matter density ( Ω CDM ):

Based on the WMAP, BAO, and Type 1a Supernova (SNe) data, Ω CDM is estimated at around

On the other hand, the major component of the universe, i.e., the dark energy (or “quintessence”) density, Ω Λ , based upon a flat universe assumption, and using the Type 1 Supernovae data [38], is estimated at

In addition, it is also assumed in this model, similar to several earlier models, that the value of the radial mass ( m r ) is on the order of the axion decay constant, f a , which is well within the acceptance window of axion searches based on the cosmological observations and calculations.

We follow an axion string network-based theoretical model similar to the approach of Kawasaki et al. [36], Hindmarsh et al. [39], Yamaguchi et al. [13], Vilenkin [19], and Shellard [40,41], under the String theory framework, using results from their simulations, and work with the calculations and simulations similar in the form to those set up by Gorghetto et al. [14]. However, no string network simulations are carried out; instead, our calculations are set up around the results obtained from those simulations and make use of the accepted values of cosmological parameters, as determined by the latest results of the Planck collaboration [37].

We attempt to fit our calculated results to a power law to estimate the value of f a , as follows. We consider three main contributions to the total cold dark matter density, i.e., the density as a result of axions radiated from the strings ( Ω a str ) , the contribution from the ones radiated from the decay of string–wall systems ( Ω a dec ) , and the density owing to the axions produced from the misalignment mechanism ( Ω a mis ) . The calculations for our model are carried out as follows, using a fitting routine working around a set of parameters, which are presented in Table 1:

Following the approach by several investigators before us, we consider it appropriate to adopt a value of the power n as the starting value before parametrizing it:

These parameters were fed into a fitting program (written in C++ language) based upon a multi-parameter space least-squares approximation scheme, and a set of values was obtained for the required decay constant ( f A ) , n , and α , corresponding to the best-known cosmological bounds, as delineated at the beginning of this section.

As a result of our calculations and fitting the parameters to the current dark matter density, we obtain the values of α and κ (to go into Eq. (2.3a)) as

The theoretical value for α is usually obtained as a ratio n + 6 n + 4 = 7/6 or 1.166667 in calculations carried out elsewhere, such as by Hiramatsu et al. [30,31]; however, in our calculations here, the fitted value for α is obtained a bit different for the model, based on our fitting routine, as 1.174. This is an important outcome of our calculations and a major differing factor from all the earlier calculations carried out elsewhere, albeit within the same window. We expect that it could possibly have significance in estimating the correct axion mass window, although these are not far from the values obtained by Kawasaki et al., Buschmann et al., Hiramatsu et al., and others; they could help pinpoint a value for a cavity-based search, where a fixed frequency search is sought in view of experimental limitations.

Thus, the final expression for Ω a , using the above value of α, is obtained as

with the value of the axion decay constant ( f A ) obtained accordingly as

This helps us obtain the corresponding axion mass value as

The corresponding Compton frequency [42] for the suggested axion mass above is obtained appropriately, in a usual manner, as

These are the results we obtained from our calculations and fitting routines based on and modifying the pertinent calculations and simulations carried out elsewhere before us, thus making it feasible to devise a suitable experiment in a narrow frequency range resonant cavity setting.

4 Experiment design and prospective implementation

Based on the short frequency range (falling within the Ku microwave band) obtained from our calculations, the next step is to implement this value and these ideas and probe this tangible range in an actual axion search experiment.

A review of various axion detection strategies based on their electromagnetic detection can be found here [43]. The method here is not novel but just a modification of the usual cavity-based detection methodologies, using some innovations like introducing a resonant tunneling diode element in the detection chain and employing a simple RF-detection-based approach.

We adopt an approach similar to the one devised earlier by Bukhari and Shah [42], based upon the inverse of Primakoff effect [44], which was first discovered for pions, whereby an axion can interact with an ambient powerful magnetic field and convert into a pair of photons and the latter can be detected in an appropriate detection setting using any of various methods.

The two-photon axionic decay width (under this model) is given by

Figure 1 illustrates a magnetic field-induced resonant conversion of an axion into a microwave photon under the inverse Primakoff effect.

Figure 1

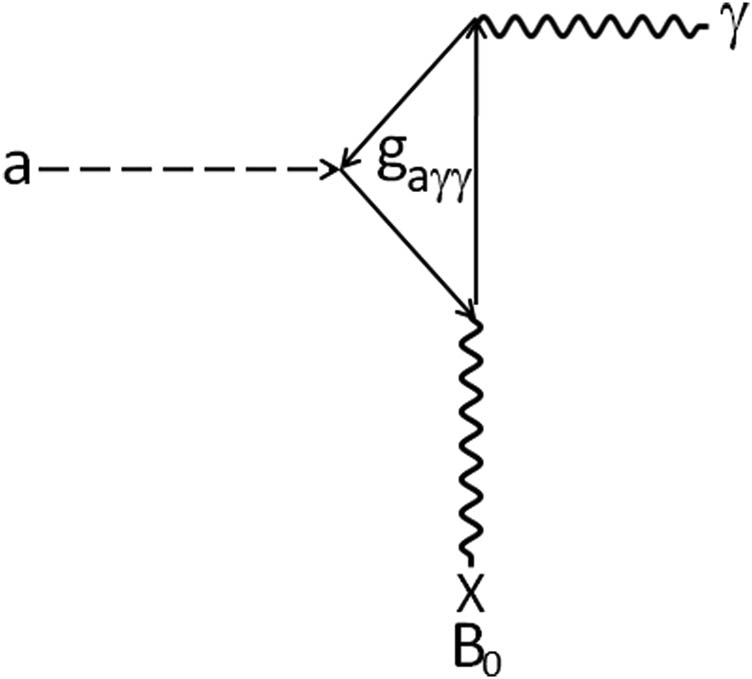
Magnetic field-mediated conversion of an axion into a photon under a process inverse to the well-known Primakoff effect.

The interaction is supposedly carried out between an axion and a photon by means of the axion’s two-photon vertex, as shown in the figure. This vertex facilitates a possible interaction of axions with electromagnetic fields, especially in the presence of very strong magnetic fields, as described by the Lagrangian:

Here, g a γ γ is the dimensionless axion-two-photon coupling, φ a , and F μ ν is the electromagnetic field tensor ( F ˜ μ ν = e μ ν λ ρ F λ ρ its dual, with e μ ν λ ρ being the Levi–Civita tensor with e 0123 = 1 ).

In terms of the vector electric and magnetic fields, this becomes

The model-dependent value of the coupling g a γ γ is obtained as

The coupling depends on the values of the electromagnetic and color anomalies, E and N, respectively, of the axion-associated axial current. We assume here E N = 0 under the Kim–Shifman–Vainshtein–Zakharov model [45].

Following these lines, the probability of an axion produced in a strong magnetic field, as a result of the inverse Primakoff effect, can be expressed as [42,44]

where B is the intensity of the applied magnetic field, L is the cavity length, and q is the momentum transfer [42].

The signal-to-noise ratio, an important parameter in the experimental detection of any signal, is given by the Dicke Radiometer equation, following the usual microwave signal measurement conventions, as follows [46]:

Here, k B is the Boltzmann constant, and t is the integration time.

Thus, in a nutshell, working under this theoretical framework, the possible detection of axions can be carried out if these particles or such excitations exist in nature.

4.1 Detection scheme

The central part of our detection scheme is a high-finesse resonant RF cavity and an antenna weakly coupled to it, while this setup is mounted in the bore of a high-intensity magnetic field. The output of the antenna is coupled to an extremely sensitive Josephson junction (JJ)-based amplifier device that can amplify the extremely faint electromagnetic signal arising from any possible axion–photon conversion event. To be detected by the antenna and to be read by a measurement system, a signal has to be of a sufficient level. Here, we introduce a new novel addition, which, to our knowledge, has never been used before in such an application: a tunnel diode device in an RF sensing setting. A Tunneling Diode (Resonant Mode) just after the antenna and before the JPA stage further amplifies the detected signal, while in resonance.

The particular JJ device reported here is a flux-driven JPA design [47], implemented with the help of a commercial SQUID-coupled pumped Niobium JPA chip. In addition, as described in an earlier report [42], we employ a new Resonant Tunneling Diode [48,49]-based amplification approach to further increase the sensitivity. We hope for a sensitivity up to around 10⁻¹⁸W with a noise spectral density down to the order of 10⁻¹⁸ to 10⁻¹⁹ W/Hz^1/2. At a highly uniform static magnetic field of approximately 8.0T < B < 10.0 T with a high-resolution (around δT/T < 1 ppb) and an operating temperature of ∼35–55 mK, and taking samples for sufficient longer times, we propose to achieve an operating window just above the Standard Quantum Limit and possibly detect any axion-induced signals within the cavity.

The pertinent parameters of the detection scheme are summarized in Table 2. An image of a simulated response of cavity electromagnetic field obtained from numerical methods (involving the solution of Maxwell equations using finite element method, with the help of COMSOL package, as outlined in our earlier paper [42]) in a transverse slice of the cavity is shown in Figure 2, with a cartoon of the Primakoff conversion process superimposed onto that.

Table 2

A summary of the cavity-based detection scheme parameters

Parameter	Value
Cavity resonance frequency (f)	17.00–18.99 GHz
Pin-point center frequency (f c)	18.999 GHz
Cavity length (l)	Tunable, variable
Mean operating temperature (cavity, T)	35.0 mK
Mean magnetic field (B)	9.0T (δB/B < 1 ppb)
Integration time	120–1,200 s
Transmon central frequency (ω/2π)	4.262 GHz
Sensitivity (P)	10−16 W
Mean spectral density (S)	10−18 W/Hz1/2

Figure 2

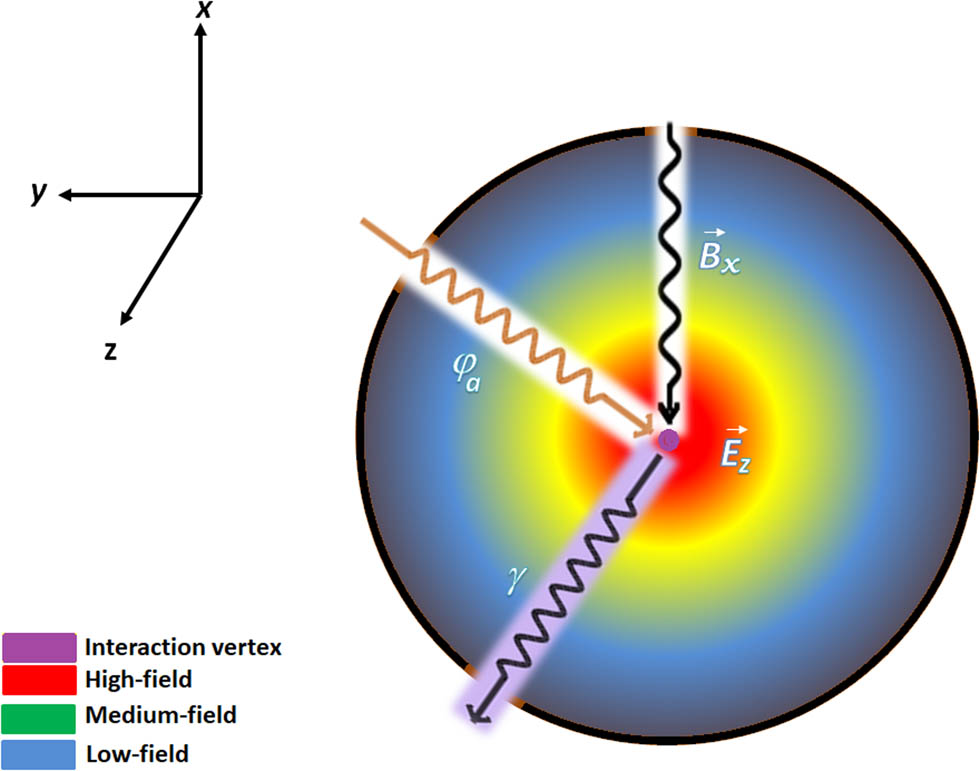
Cavity electromagnetic field distribution with a cartoon of an axion–photon conversion event facilitated by a strong magnetic field.

Note that the magnetic field (radial) direction is perpendicular to the direction of the electric field (axial).

Figure 3 illustrates an overview of the central element of the detection scheme, i.e., a JJ, and Figures 4 and 5 illustrate block diagrams for the detection scheme and detection electronics for the aforementioned frequency range, with the respective cryogenic and room-temperature sections in an isolated environment individually marked, especially with the cryogenic section (the cavity and cryogenic amplification section) in a low-temperature mu-metal chamber isolated from the strong magnetic field. More details of the experiment, various components, and relevant instrumentation may be found in our earlier report [42]; generic details on microwave measurements can be found elsewhere, such as in Feng et al. [50].

Figure 3

An overview of the superconducting JJ-based Parametric Amplifier (JPA), the central element of the detection scheme. The details are provided in an earlier report [42].

Figure 4

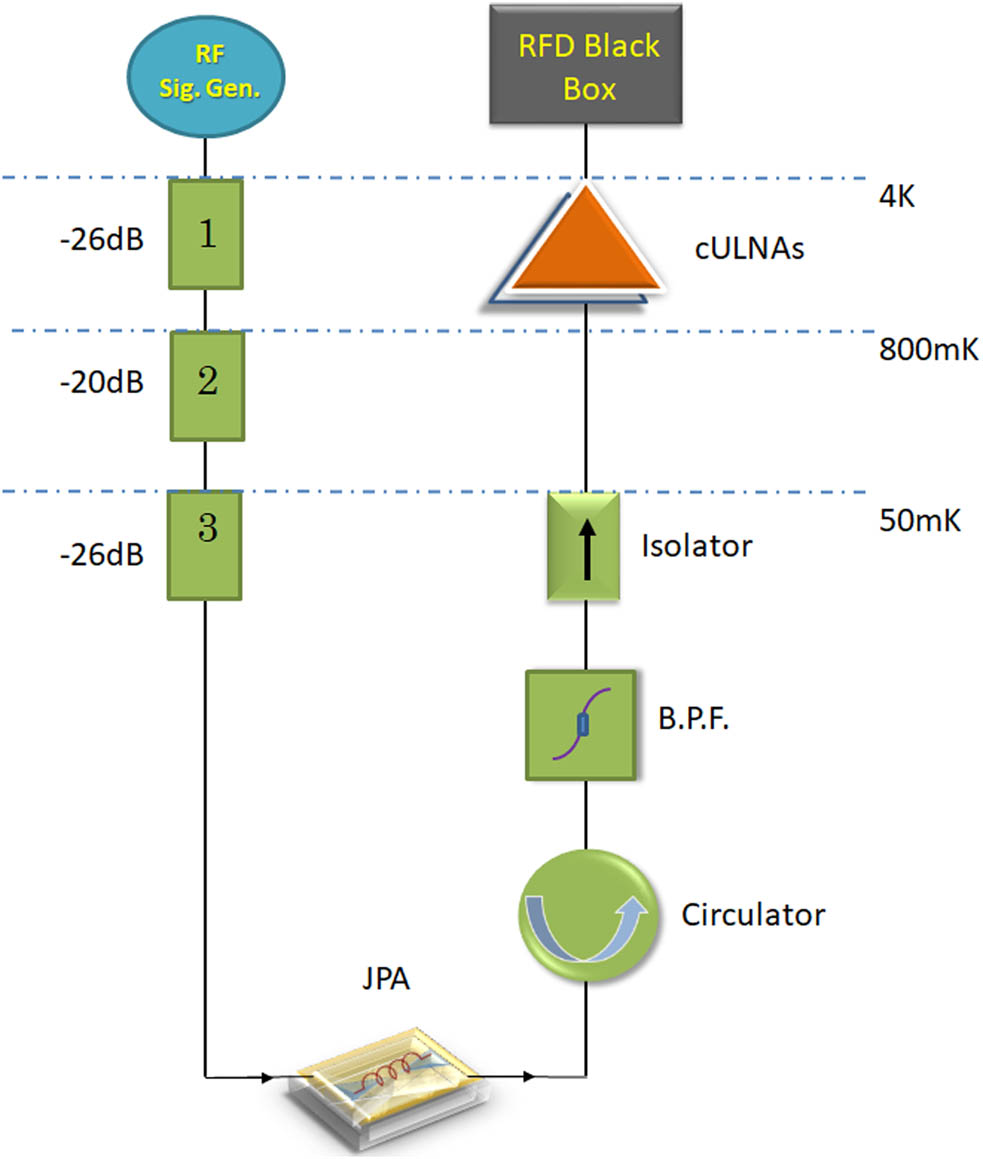
A block diagram of the detection components in the cryogenic measurement chain, including the respective operating temperatures.

Figure 5

A block schematic of the RF cavity, detection electronics, amplification and detection components, and relevant instrumentation. As explained in detail in an earlier report [42], a weak electromagnetic signal in the cavity (on resonance) is weakly coupled to a fine gold-plated copper antenna and amplified by a combination of a JJ-based parametric amplifier and a set of cryogenic LNAs in parallel, all operating at cryogenic temperatures, until the signal is amplified sufficiently to be readout by the room-temperature electronics (operated at 10°C). A test signal for calibration is fed from an RF Signal Generator (1–10 GHz). A home-made high-frequency Signal Sensing and Routing Hub (SRH), combines the detected signal with a carrier wave from an Ultra-Low-Distortion Signal Generator (1–100 kHz), feeding it to a Resonant Tunneling Diode (RTD) stage I of the detection chain. From RTD, the signal is amplified by a duo of high-gain Low-Noise Amplifiers until detected by an RF detector.

Figure 6 illustrates a spectral plot of a test signal, acting as a “false axion,” injected into the cavity and detected with the amplification system, showing the measured power spectral density ( W / H z ), as a function of frequency (measured in MHz) The image was prepared as a result of the measured signal (emulating a false axion event) obtained by weakly coupling an external signal from a high-frequency RF signal generator (Agilent) into the cavity means of an antenna, and carrying out the detection of aforementioned signal based upon the detection scheme outlined in Figures 5 and 6. Finally, the time-domain data were analyzed by converting them into a frequency-domain series using a FFT routine (in the Spectrum Analyzer), and the plot was obtained.

Figure 6

A simulated plot of a test signal spectral response, as measured by the detection scheme, measuring an injected ultra-weak signal from an RF generator (power spectral density in W/Hz^1/2 vs resonance frequency in MHz).

5 Discussion and conclusion

In this study (and the preprint before [51]), we present some calculations of axion mass and the coupling using standard methods and prescriptions. We assume that axions constitute the majority of the non-baryonic cold dark matter content of the universe, a reasonable assumption given the existing data, and consider three main contributions to axion production within the String theoretical framework, which are the field misalignment mechanism, the decay of global axion strings and domain walls, and the axions radiated from the strings. However, we consider the first two to be the major contributing factors to the total axion density in view of earlier reports. A viable axion mass window is obtained using our fitting routines, and a method to probe this window is also suggested using an approach presented earlier. The value of the axion mass is quite plausible since it is very close and within the window of calculations and simulations carried out in recent times, and also presents a specific center mass value for fixed resonance frequency cavity-based searches.

In particular, the results of our calculations are on similar lines as the recent simulations carried out by Borsanyi et al. [52], Gorghetto et al. [16], and Buschmann et al. [29], especially within the range of 40–180 μeV, as suggested by the important simulations by Buschmann et al. while employing a powerful “Adaptive Mesh Refinement” simulation approach [53]. The proposal of a further narrow axion mass range of around 73–83 μeV, with a center value of 78 μeV (and the corresponding frequency range of 18–20 Giga-Hertz), thus seems to be plausible and valuable to detect an axion, if appropriate experimental methods exist, and subject to the existence of these particles. Recently, Kawasaki et al. [22] have supported the value of f A ≥ 10 11 GeV , coinciding with the decay constant ( f A = 7.07 ( ± 0.47 ) × 10 11 GeV ) proposed here, and, in turn, with the corresponding mass range, as proposed by us. The next important thing is the availability of technology and experimental methods, and the sensitivity of our experiments to probe axions within this range. During the last decade, there have been significant developments in sub-Kelvin radiometry, especially with the advent of Josephson Amplifiers and Qubit-based methods of radio frequency signal detection and precision measurement, both increasing the dynamic range as well as facilitating the reduction in measurement noise. So far, weak signal detection with significant low-noise amplification within a few Giga-Hertz is quite possible and is routinely being made in laboratories, including us. Therefore, it is encouraging to have new and narrower mass ranges in order to build precision experiments to probe axions within the ranges suggested in this and other recent reports. The aim of this study, to come up with a narrow mass (and frequency) range to avoid expensive and cumbersome as well as noisy cavity frequency steering, is well-served by the range obtained by us and is now up to the experimenters to probe this by carrying out experiments at single-frequency values, starting with the two important frequency values of 18 and 19 GHz, all the way up to 21 GHz, using successive experiments done with the successive use of four resonant cavities (18, 19, 20, and 21 GHz), as these values may have great potential in view of our and other suggestions.

On the other hand, Chang and Cui, in their recent analysis of the dynamics of long-lived axion domain walls [54], have proposed a differing value of decay constant and mass window, one magnitude higher than those in our and other recent proposals. Kim et al. [55], while working on the similar lines of cosmic string networks formation in the post-inflation scenario, but with a new improvisation of the “Tetrahedralization of the Space,” provide their own measures of axion abundance. The mass range proposed by these methods and its corresponding frequencies, reaching the domain of TeraHertz (THz), however, is challenging and extremely difficult to experimentally probe with the precision and low-noise susceptibility of the measurement methods, if not impossible.

Working under a resonant cavity-based detection scheme, and making use of the Primakoff effect, as described in detail in one of our earlier reports [42] and in a recent arXiv report, we have made some viable suggestions for a search for the axions/ALPs to be carried out at or around this frequency, which is slightly difficult due to practical considerations but not impossible to achieve in the contemporary era. It must be mentioned here that this is an extraordinary frequency, just at the end of the microwave “Ku” band.

An important concern is the limitations imposed upon the measurement of the axion signal by the quantum nature of the measurement. These include the Standard Quantum Limit, the Back-Action Noise by the detector, and the quantum fluctuations inherent in the axion and electromagnetic quantum fields. A recent and quite pertinent discussion of these and the relevant parameters is available in the literature by Lasenby [56].