Home Physical Sciences Exact solutions of Einstein’s field equations via homothetic symmetries of non-static plane symmetric spacetime
Article Open Access

Exact solutions of Einstein’s field equations via homothetic symmetries of non-static plane symmetric spacetime

  • Tahir Hussain EMAIL logo , Muhammad Farhan , Kamran EMAIL logo , Ioan-Lucian Popa ORCID logo , Naveed Ahmad , Hadi Obaid Alshammari ORCID logo , Leila Jamel ORCID logo and Ibrahim Mahariq ORCID logo EMAIL logo
Published/Copyright: December 10, 2025
Download Article (PDF)
Open Physics
From the journal Open Physics Volume 23 Issue 1

Abstract

In this paper, we explore some non-static plane symmetric solutions of Einstein’s field equations (EFEs) that possess a specific scaling symmetry, known as homothetic symmetry. This symmetry helps in simplifying EFEs and reveals important patterns in gravitational systems. Using a systematic computational method, the Rif tree approach, we find some new exact solutions for expanding universes with plane symmetry. We classify these solutions according to their symmetry properties, finding spacetimes with 4-, 5-, 7-, and 11-dimensional symmetry structures. The physical viability is established through energy-momentum tensors, that reveal solutions describing anisotropic fluids, perfect fluids, and vacuum configurations. By analyzing energy conditions, we have identified which of the derived solutions are physically meaningful. The physical interpretation reveals important connections to some known models, including anisotropic Bianchi type universes, Kasner solutions, Szekeres inhomogeneities, and colliding plane wave geometries.

Keywords: exact solutions; spacetime symmetries; homothetic vector fields; plane symmetric spacetime; Rif tree approach

1 Introduction

In general relativity, spacetimes symmetries are crucial because they provide deep insights into the physical characteristics of gravitational fields as well as the mathematical structure of Einstein’s field equations. Among these symmetries, the isometries, conformal transformations and the homothetic vector fields are particularly important. These symmetries not only help in reducing the complexity of EFEs, enabling the search for their exact solutions, they also provide fundamental conservation laws and a greater understanding of the causal and geometric structure of spacetime.

A Killing vector field (KVF) is defined as a vector field η = (η 0, η 1, η 2, η 3) satisfying the condition [1]:

(1.1) L η g a b = 0 ,

where g ab denotes the spacetime metric and L is the Lie derivative operator. This condition is linked with the preservation of the metric of spacetime along the flow of the vector field. Killing vector fields are crucial in describing conserved quantities, such as energy, and linear and angular momentum.

If the metric of spacetime is preserved up to a constant scaling factor along the flow of a vector field η = (η 0, η 1, η 2, η 3), then such a vector field is defined as a homothetic vector field (HVF). These vector fields satisfy the relation [1]:

(1.2) L η g a b = 2 α g a b ,

where α is some constant. The above condition introduces a self-similarity or scaling symmetry in spacetime. If α = 0, a HVF reduces to a KVF. By a proper HVF, we mean a homothetic symmetry defined by Eq. (1.2) with non-zero α. Homothetic symmetries are central to studies involving self-similar solutions, cosmological models, and gravitational collapse, where scale invariance plays a key role.

In the broader context of spacetime symmetries, conformal vector fields (CVFs) preserve the metric up to a local scaling factor that depends on the spacetime coordinates. The CVFs are defined in a similar way by replacing α in Eq. (1.2) by a function of spacetime coordinates, that is:

(1.3) L η g a b = 2 ψ ( x a ) g a b ,

where ψ(x a ) is some smooth function. If ψ is a constant function, a CVF becomes a HVF and it reduces to a KVF for ψ = 0. A CVF that is neither Killing nor homothetic vector field is known as a proper CVF.

The symmetries of the Ricci and energy-momentum tensors are defined in a similar way by replacing g ab in Eqs. (1.1)- (1.3) by R ab and T ab respectively.

In addition to these spacetime symmetries, there is another important symmetry, called Noether symmetry. For a vector field V = η ∂ s + V a ∂ x a , its first prolongation is defined as V [ 1 ] = V + ( D V a − x a ̇ D η ) ∂ x a ̇ . A Noether symmetry of the Lagrangian L ( s , x a , x a ̇ ) is defined by the vector filed V if there exists a gauge function F(s, x a ) such that [2]:

(1.4) V [ 1 ] L + ( D s η ) L = D s F .

Here D s = ∂ s + x a ̇ ∂ x a , and η and V a are dependent on the geodesics parameter s. Moreover, the derivative with respect to s is denoted by a dot.

Noether symmetries are found to be valuable in the classification of Lagrangians associated with spacetime metrics and for analyzing differential equations. While solving complicated and nonlinear differential equations, Noether symmetries assist in the reduction of the number of independent variables and the order of higher order differential equations, and in the linearization of nonlinear differential equations. Moreover, Noether symmetries are also crucial from a physical standpoint because they are directly linked with conservation laws via Noether’s theorem.

There are some significant relations among Noether symmetries and other spacetime symmetries such as KVFs, HVFs and CVFs. For instance, all KVFs admitted by a spacetime metric are included in the collection of Noether symmetries of the associated Lagrangian. Similarly, if α denotes the homothety constant, then V + 2αs∂ s is a Noether symmetry of the lagrangian if and only if V is a HVF associated with the corresponding metric [3]. A Noether symmetry that is neither a KVF nor it is linked with a HVF is known as a proper Noether symmetry. For flat Minkowski spacetime, the set of 15 CVFs constitutes a subset of the collection of 17 Noether symmetries of the associated Lagrangian. However, for non-flat spacetimes no such general relationship is identified between CVFs and Noether symmetries.

All the above defined symmetries have been extensively explored in the literature for various spacetimes [4], [5], [6], [7], [8], [9], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19], [20]. However, most of this work has focused on simpler or static spacetimes due to the ease of their mathematical treatment and inherent simplicity. As a result, there has been less research done on non-static spacetimes, which are more complicated and harder to study. The difficulties of working with non-static metrics, like their changing nature and the complexity of solving the related equations, have made this area less studied.

In addition to the above mentioned references, the recent literature has highlighted the relevance of symmetry methods in the fields of cosmology and modified theories of gravity. Particularly, Noether symmetries are employed to f(R) and scalar-tensor cosmologies to identify the admissible forms of potentials and couplings, and to derive exact cosmological solutions describing late-time acceleration [21], [22], [23], [24], [25], [26]. Similarly, homothetic and conformal symmetries are also investigated in connection with anisotropic and inhomogeneous models, that provide deeper understanding of cosmological evolution and its observational implications [16]. Moreover, CVFs are explored in gravitational wave spacetimes, where related vacuum solutions show self-similar properties [27].

In this research, we investigate proper HVFs of non-static plane symmetric spacetime with the following most general metric [28].

(1.5) d s 2 = − f 2 ( t , x ) d t 2 + g 2 ( t , x ) d x 2 + h 2 ( t , x ) [ d y 2 + d z 2 ] ,

where f(t, x) ≠ 0, g(t, x) ≠ 0 and h(t, x) ≠ 0. Our goal is to extract all the non-static plane symmetric metrics that admit proper HVFs and to find the associated solutions to the EFEs. With a focus on anisotropic and perfect fluid sources, which are significant in many cosmological models and astrophysical scenarios, we discuss the physical implications of these symmetries.

The motivation behind selecting the metric (1.5) for our study is that it includes several important and well-studied solutions of EFEs. For example, when the metric coefficients f, g, and h depend only on x, the metric (1.5) signifies a static plane symmetric spacetime. Such metrics are essential in various contexts, particularly in deriving the Kasner’s and Taub solutions of EFEs. Moreover, when f, g, and h depend only on t, the metric (1.5) becomes the Bianchi type I metric. Bianchi type metrics are significant because they are homogeneous but not necessarily isotropic, offering key cosmological models that solve the EFEs, with different solutions based on the choice of scale factors. Additionally, when f = g = h = f(t), the metric (1.5) simplifies to the Friedmann metric, a fundamental model in cosmology. Therefore, this study naturally covers the classification of all these metrics in terms of their HVFs, as special cases.

In addition to this, the non-static plane symmetric metric (1.5) is a perfect model for studying gravitational waves, anisotropic gravitational fields, and cosmic evolution because of its symmetry in two spatial dimensions. This spacetime provides a simplified framework for investigating the solutions to EFEs since its metric is invariant under translations and rotations in the plane.

In order to explore the symmetries of a spacetime, one always needs to solve a system of determining equations representing these symmetries. The conventional method used to solve these determining equations is known as direct integration technique. In this method, the determining equations are decoupled and integrated directly to find the explicit form of symmetry vector fields. The process usually gives rise to a number of cases depending upon the conditions on the metric functions under which the spacetime under consideration admits the desired symmetries. It is a quite lengthy and cumbersome technique which may result in lack of potential spacetime metrics admitting the required symmetries.

In recent literature, the Rif tree approach has emerged as a powerful computational tool for analyzing systems of partial differential equations that govern the existence of symmetries in spacetimes. This algorithmic method transforms the system of determining equations into an involutive form, systematically solving them and allowing for the classification of vector fields such as HVFs. This method relies on a Maple algorithm (Rif algorithm), which is implemented using the Exterior package in Maple. The process begins by loading the “Exterior” package. Next, the system of differential equations defining HVFs is inserted using the command “sysDEs”. The third step involves applying the “symmetry, eq := findsymmetry” command, which analyzes the symmetry equations and identifies the conditions on the metric functions that allow for HVFs. The algorithm then displays these conditions. A graphical representation of these conditions can be viewed using the “caseplot(eq, pivots)” command, resulting in a tree shape, called Rif tree. The branches of the Rif tree illustrate the conditions under which the spacetime may admit HVFs. Finally, the symmetry equations are solved under these branch-specific conditions, yielding the explicit form of the HVFs. The novelty of this approach is that it gives a better classification of the spacetime through its symmetries. Recently, the Rif tree approach has been applied in the classification of HVFs and other symmetries, leading to the discovery of additional spacetime metrics that were previously unidentified using the conventional direct integration tecnique [29], [30], [31], [32], [33], [34].

In this paper, we focus on finding the HVFs of non-static plane symmetric spacetimes, using the Rif tree approach. We aim to identify all the non-static plane symmetric metrics for which proper homothetic symmetries exist and to derive the corresponding solutions to the EFEs for anisotropic or perfect fluid sources.

2 Homothetic symmetries

We apply the definition of HVFs given in Eq. (1.2) to the metric (1.5) to derive the following symmetry equations.

(2.1) f , t η 0 + f , x η 1 + f η , t 0 = α f ,

(2.2) g , t η 0 + g , x η 1 + g η , x 1 = α g ,

(2.3) h , t η 0 + h , x η 1 + h η , y 2 = α h ,

(2.4) h , t η 0 + h , x η 1 + h η , z 3 = α h ,

(2.5) f 2 η , x 0 − g 2 η , t 1 = 0 ,

(2.6) f 2 η , y 0 − h 2 η , t 2 = 0 ,

(2.7) f 2 η , z 0 − h 2 η , t 3 = 0 ,

(2.8) g 2 η , y 1 + h 2 η , x 2 = 0 ,

(2.9) g 2 η , z 1 + h 2 η , x 3 = 0 ,

(2.10) η , z 2 + η , y 3 = 0 ,

In order to find the exact form of the HVF η, we need to solve the above symmetry equations. For this, the metric coefficients f(t, x) g(t, x) and h(t, x) must be subject to some constraints. In order to obtain such constraints, we have analyzed Eqs. (2.1)– (2.10) using the commands of Rif algorithm, that are already explained in the introduction section. As a result, the algorithm generates the Rif tree given in Figure 1 along with its nodes (pivots) as presented in (2.11). Each branch of the Rif tree imposes certain restrictions on the functions f(t, x) g(t, x) and h(t, x). For example, in branch 1 both p1 and p2 are non-zero, that is h ,t ≠ 0 and h ,t g ,x  − h ,x g ,t ≠ 0. We have used these conditions to solve Eqs. (2.1)– (2.10). The same procedure is followed for the constraints of all 25 branches of the Rif tree. Consequently, we have obtained several metrics with 4, 5, 7, and 11-dimensional homothetic algebras. All these homothetic algebras include the set M 3 = {∂ y , ∂ z , y∂ z  − z∂ y } as a proper subset, which is the set of minimum KVFs admitted by the metric (1.5). Moreover, some cases produce only one proper HVF in addition to the three minimum KVFs, while the other metrics possess a proper HVF and some additional KVFs. The results of all 25 branches of the Rif tree are summarized in Table 1. In every case, the generator V 4 represents the proper homothety.

(2.11) p 1 = h , t p 2 = h , t g , x − h , x g , t p 3 = h , t f , x − h , x f , t p 4 = h , t h , t x − h , t t h , x p 5 = ( h , t ) 2 h , x x − 2 h , t x h , x + h , t t ( h , x ) 2 p 6 = ( h , t ) 2 h , t t x − 2 h , t h , t t h , t x − h , t h , x h , t t t + 2 ( h , t t ) 2 h , x p 7 = ( h , t ) 2 h , x x − h , t t ( h , x ) 2 p 8 = h , x p 9 = g , t p 10 = f , t p 11 = g , t f , x − g , x f , t p 12 = g , t g , t x − g , x g , t t p 13 = − ( g , t ) 2 g , x x + 2 g , t g , x g , t x − ( g , x ) 2 g , t t p 14 = g , t t t g , t g , x − ( g , t ) 2 g , t t x + 2 g , t g , t t g , t x − 2 g , x ( g , t t ) 2 p 15 = ( g , t ) 2 g , x x − ( g , x ) 2 g , t t p 16 = g x p 17 = f , t f , t x − f , x f , t t p 18 = ( f , t ) 2 f , x x − 2 f , t f , x f , t x + ( f , x ) 2 f , t t p 19 = ( f , t ) 2 f , t t x − f , t f , x f , t t t − 2 f , t f , t x f , t t + 2 f , x ( f , t t ) 2 p 20 = ( f , t ) 2 f , x x − ( f , x ) 2 f , t t p 21 = f , x

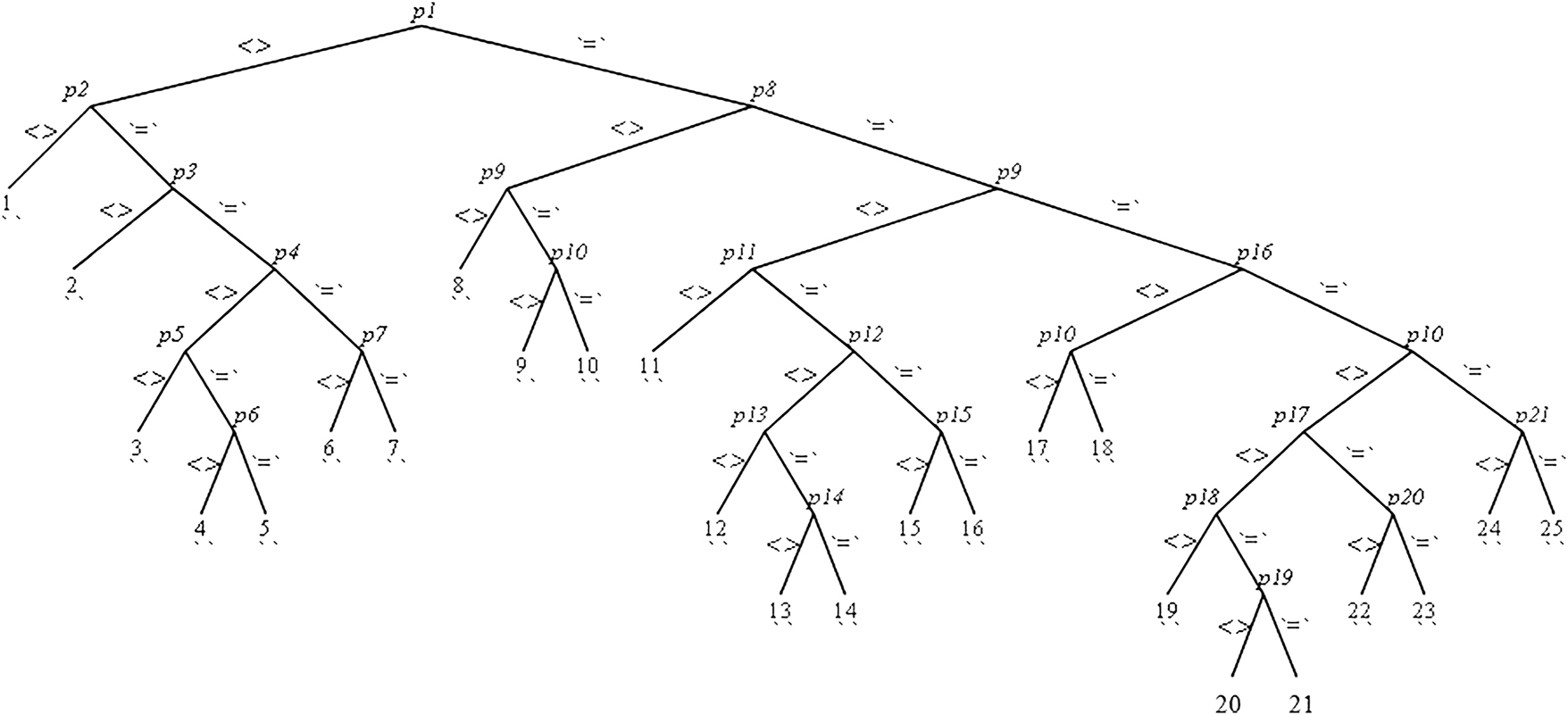
Figure 1: Rif tree.
Figure 1:

Rif tree.

Table 1:

Metrics and their homothetic symmetries.

Metric No./Branch no. Metric coefficients Proper HVF
4a f = Const., g = a 1 t + a 2, h = a 1 t + a 2 a 2 L ( x ) , V ( 4 ) = a 1 t + a 2 a 1 ∂ t
1 where a 1, a 2 are non-zero constants and L(x) is any function of x.
4b f = f(t), g = Const., h = − ( a 1 x + 2 a 2 ) 1 − 2 a 3 a 1 2 a 3 ( a 1 − 2 a 3 ) + ( a 1 ∫ f ( t ) d t + 2 a 4 ) 1 − 2 a 3 a 1 V ( 4 ) = ∫ f ( t ) d t f ( t ) ∂ t + x ∂ x ,
2 where f ,t (t) ≠ 0 a 1 ≠ 2a 3, a 1 ≠ 0, a 3 ≠ 0
4c f = ( a 1 x + 2 a 2 ) 1 − 2 a 3 a 1 , g = Const., h = ( 2 a 3 t + 2 a 4 ) a 1 − 2 a 5 2 a 3 V (4) = x∂ x
2 where a 1 ≠ 0, a 3 ≠ 0, a 1 ≠ 2a 3 ≠ 2a 5
4d f = a 1 x + a 2, g = Const., h = e ( a 3 − 2 a 4 ) t 2 a 5 V ( 4 ) = a 1 x + a 2 a 1 ∂ x ,
2 where a 3 ≠ 2a 4, and a 1 ≠ 0
4e f = a 1 x + a 2, g = Const., h = h ( t ) ≠ e ( a 3 − 2 a 4 ) t 2 a 5 , V ( 4 ) = a 1 x + a 2 a 1 ∂ x + y ∂ y + z ∂ z ,
2 where h ,t (t) ≠ 0 and a 1 ≠ 0
4f f = 2 a 1 x + 2 a 2 , g = Const., h = ( a 3 t + 4 a 4 ) 2 − 4 a 5 a 3 , V ( 4 ) = t 2 ∂ t + f 2 f , x ( x ) ∂ x .,
2 where a 3 ≠ 2a 5 and a 1 ≠ 0, a 3 ≠ 0
4g f = Const., g = Const., h = ( a 1 t + 2 a 2 ) 1 − 2 a 3 a 1 a 1 − 2 a 3 + ( a 1 x + 2 a 4 ) 1 − 2 a 3 a 1 , V (4) = t∂ t  + x∂ x ,
3 where a 1 ≠ 2a 3 and a 1, a 3 ≠ 0
4h f = Const., g = Const., h = 1 a 1 ln ( − a 1 x + a 2 a 1 t + a 3 ) , V ( 4 ) = ( a 1 t + a 3 ) a 1 ∂ t − ( − a 1 x + a 2 ) a 1 ∂ x + y ∂ y + z ∂ z
5 where a 1, a 2, a 3 are non-zero
4i f = Const., g = ( a 1 t + 2 a 2 ) 1 − a 3 + 2 a 3 a 5 a 1 , h = ( a 3 x + a 4 ) 1 a 3 , V (4) = t∂ t  + (a 3 x + a 5)∂ x
8 where a 1 ≠ 0, a 3 ≠ 0.
4j f = const., g = a 1 t + 2a 2, h = h ( x ) ≠ ( a 3 x + a 4 ) 1 a 3 , V (4) = t∂ t  + y∂ y  + z∂ z ,
8 where a 1 ≠ 0 and h ,x (x) ≠ 0
4k f = Const., g = 2 a 1 t + 2 a 2 , h = ( a 3 x + a 4 ) 1 a 3 , V ( 4 ) = g 2 ( t ) 2 a 1 ∂ t + h ( x ) 2 a 3 h , x ( x ) ∂ x + 2 a 3 − 1 2 a 3 ( y ∂ y + z ∂ z ) ,
8 where a 1 ≠ 0, a 3 ≠ 0
4l f = Const., g = t 2 a 2 a 1 , h = [ ( a 1 − 2 a 2 ) x ] a 1 − 2 a 3 a 1 − 2 a 2 V (4) = t∂ t  + x∂ x ,
8 where a 1 ≠ 0, a 1 ≠ 2a 2 and a 1 ≠ 2a 3
4m f = ( a 1 t + a 2 ) − 1 + a 3 2 a 1 + ( a 3 x + 2 a 4 ) 1 − 2 a 1 a 3 a 3 − 2 a 1 , g = Const.,  h = ( a 3 x + 2 a 4 ) 1 − 2 a 5 a 3 , V (4) = x∂ x ,
9 where a 3 ≠ 2a 1 ≠ 2a 5,
5a f = Const., g = a 1 t + a 2, h = a 3 e a 1 x + a 4 e − a 1 x ( a 1 t + a 2 ) a 2 , V ( 4 ) = h a 1 ∂ t ,
1 where a i ≠ 0 for i = 1, …, 4 V ( 5 ) = − a 2 h , x a 1 a 4 h ∂ t + a 2 h a 4 g 2 ∂ x ,
5b f = Const., g = g(x), h = a 1 t + a 2, V ( 4 ) = a 1 t + a 2 a 1 ∂ t + ∫ g ( x ) d x g ( x ) ∂ x
1 where g ,x (x) ≠ 0 and a 1 ≠ 0 V ( 5 ) = 1 g ( x ) ∂ x
5c f = f(t), g = const., h = a 1 x + a 2 ∫f(t)dt, V ( 4 ) = ∫ f ( t ) d t f ( t ) ∂ t + x ∂ x ,
2 where f ,t (t) ≠ 0, a 1 ≠ a 2, a 1 ≠ 0, a 2 ≠ 0 V ( 5 ) = 1 f ( t ) ∂ t − a 2 a 1 ∂ x
5d f = const., g = g(x), h = ( a 1 t + 2 a 2 ) 1 + a 3 a 1 a 1 + a 3 , V ( 4 ) = t ∂ t + ∫ g ( x ) d x g ( x ) ∂ x ,
1 where g ,x (x) ≠ 0, a 1 ≠ 0, a 1 ≠ − a 3 V ( 5 ) = 1 g ( x ) ∂ x
5e f = const., g = const., h = a 1 x + a 2 t, V (4) = t∂ t  + x∂ x
7 where a 1 ≠ a 2 and a 1 ≠ 0, a 2 ≠ 0. V ( 5 ) = − a 2 a 1 ∂ t + ∂ x
5f f = const., g = const., h = ( a 1 t + 2 a 2 ) 1 − 2 a 3 a 1 , V (4) = t∂ t  + x∂ x ,
7 where a 1 ≠ 0, a 1 ≠ 2a 3 V (5) = ∂ x
5g f = const., g = const., h = a 1 t + a 2, V ( 4 ) = a 1 t + a 2 a 1 ∂ t + x ∂ x ,
7 where a 1 ≠ 0 V (5) = ∂ x
5h f = const., g = a 2 t, h = ( a 1 t ) 1 − 2 a 3 a 1 , V (4) = t∂ t ,
7 where a 1 ≠ 0, a 2 ≠ 0 and a 1 ≠ 2a 3 V (5) = ∂ x
5i f = const., g = ( a 1 t + 2 a 2 ) 1 − 2 a 3 a 1 , h = ( a 1 t + 2 a 2 ) 1 − 2 a 4 a 1 , V (4) = t∂ t ,
7 where a 1 ≠ 0, a 1 ≠ 2a 3, a 1 ≠ 2a 4 V (5) = ∂ x
5j f = f(t), g = const., h = a 1 x + a 2, V ( 4 ) = ∫ f ( t ) d t f ( t ) ∂ t + a 1 x + a 2 2 a 1 ∂ x
9 where f ,t (t) ≠ 0 and a 1 ≠ 0 V ( 5 ) = 1 f ( t ) ∂ t
5k f = f(t), g = const., h = ( a 1 x + 2 a 2 ) 1 − 2 a 3 a 1 , V ( 4 ) = ∫ f ( t ) d t f ( t ) ∂ t + x ∂ x
9 where a 1 ≠ 2a 3, f ,t (t) ≠ 0, V ( 5 ) = 1 f ( t ) ∂ t
5l f = const., g = const., h = ( a 1 x + 2 a 2 ) 1 − 2 a 3 a 1 , V (4) = t∂ t  + x∂ x ,
10 where a 1 ≠ 0, a 1 ≠ 2a 3 V (5) = ∂ t
5m f = ( a 1 x + 2 a 2 ) 1 − 2 a 3 a 1 , g = const., h = ( a 1 x + 2 a 2 ) 1 − 2 a 4 a 1 , V (4) = x∂ x ,
10 where a 1 ≠ 0, a 1 ≠ 2a 3, a 1 ≠ 2a 4 V (5) = ∂ t
5n f = const., g = const., h = a 1 x + a 2, V ( 4 ) = t ∂ t + a 1 x + a 2 a 1 ∂ x
10 where a 1 ≠ 0 V (5) = ∂ t
5o f = ( a 1 ∫ g ( x ) d x + 2 a 2 ) 1 − 2 a 3 a 1 , g = g(x), h = const. V ( 4 ) = ∫ g ( x ) d x g ( x ) ∂ x + y ∂ y + z ∂ z ,
18 where g ,x (x) ≠ 0, a 1 ≠ 2a 3 and a 1 ≠ 0. V (5) = ∂ t
5p f = ( a 1 x + 2 a 2 ) 1 − 2 a 3 a 1 , g = const., h = const., V (4) = x∂ x  + y∂ y  + z∂ z ,
24 where a 1 ≠ 2a 3 and a 1 ≠ 0. V (5) = ∂ t
7a f = Const., g = a 1 t + a 2, h = ( a 1 t + a 2 ) a 2 e a 3 x , V ( 4 ) = a 1 t + a 2 a 1 ∂ t
1 where a 1 ≠ 0, a 2 ≠ 0, a 3 ≠ 0 V (5) = ∂ x  − a 3 y∂ y  − a 3 z∂ z
V ( 6 ) = y a 3 ∂ t + z 2 − y 2 2 + a 2 2 2 a 3 2 e 2 a 3 x ∂ y − y z ∂ z
V ( 7 ) = − z a 3 ∂ t + y z ∂ y + z 2 − y 2 2 − a 2 2 2 a 3 2 e 2 a 3 x ∂ z
7b f = Const., g = a 1 t, h = 1 a 2 t , V (4) = t∂ t
7 where a 1 ≠ 0, and a 2 ≠ 0. V (5) = ∂ x
V ( 6 ) = − y a 1 2 a 2 2 ∂ x + x ∂ y
V ( 7 ) = − z a 1 2 a 2 2 ∂ x + x ∂ z
7c f = const., g = h = ( a 1 t + 2 a 2 ) 1 − 2 a 3 a 1 , V (4) = t∂ t ,
7 where a 1 ≠ 2a 3, a 1 ≠ 0 V (5) = −y∂ x  + x∂ y
V (6) = −z∂ x  + x∂ z ,
V (7) = ∂ x
7d f = h = ( a 1 x + 2 a 2 ) 1 − 2 a 3 a 1 , V (4) = x∂ x ,
10 g = Const., V (5) = y∂ t  + t∂ y
where a 1 ≠ 2a 3 and a 1 ≠ 0 V (6) = z∂ t  + t∂ z ,
V (7) = ∂ t
7e f = a 1 x + a 2, g = Const., V ( 4 ) = a 1 x + a 2 a 1 ∂ x
10 h = a 1 x + a 2, V (5) = ∂ t
where a 1 ≠ 0. V (6) = y∂ t  + t∂ y
V (7) = z∂ t  + t∂ z
11a f = Const., V ( 4 ) = a 1 t + a 2 a 1 ∂ t
g = a 1 t + a 2, V (5) = ∂ x  − a 1 y∂ y  − a 1 z∂ z
1 h = a 1 t + a 2 a 2 e a 1 x , V ( 6 ) = e a 1 x ∂ t − e a 1 x a 1 t + a 2 ∂ x
where a 1 ≠ 0 V ( 7 ) = a 1 2 a 2 2 ( y 2 + z 2 ) e a 1 x + e − a 1 x ∂ t + − a 1 2 a 2 2 ( a 1 t + a 2 ) ( y 2 + z 2 ) e a 1 x + e − a 1 x a 1 t + a 2 ∂ x
and a 2 ≠ 0 − 2 a 1 y e − a 1 x a 1 t + a 2 ∂ y − 2 a 1 z e − a 1 x a 1 t + a 2 ∂ z ,
V ( 8 ) = y e a 1 x ∂ t − y e a 1 x ( a 1 t + a 2 ) ∂ x − a 2 2 a 1 ( a 1 t + a 2 ) e − a 1 x ∂ y ,
V ( 9 ) = z e a 1 x ∂ t − z e a 1 x ( a 1 t + a 2 ) ∂ x − a 2 2 a 1 ( a 1 t + a 2 ) e − a 1 x ∂ z ,
V ( 10 ) = y a 1 ∂ x + z 2 − y 2 2 + a 2 2 2 a 1 2 e − 2 a 1 x ∂ y − y z ∂ z
V ( 11 ) = − z a 1 ∂ x + y z ∂ y + z 2 − y 2 2 − a 2 2 2 a 1 2 e − 2 a 1 x ∂ z
11b f = f(t), g = Const., V ( 4 ) = ∫ f ( t ) d t f ( t ) ∂ t + x ∂ x
h = a 1 x + a 1 ∫f(t)dt, V ( 5 ) = − x f ( t ) ∂ t − ∫ f ( t ) d t ∂ x + y ∂ y + z ∂ z
2 where f ,t (t) ≠ 0 V ( 6 ) = a 1 2 ( y 2 + z 2 ) 2 f ( t ) + 1 f ( t ) ∂ t − a 1 2 ( y 2 + z 2 2 ) ∂ x − a 1 y h ( t , x ) ∂ y − a 1 z h ( t , x ) ∂ z
and a 1 ≠ 0 V ( 7 ) = ( y 2 + z 2 2 ) a 1 2 f ( t ) ∂ t + − a 1 2 ( y 2 + z 2 ) 2 + 1 ∂ x − a 1 y h ( t , x ) ∂ y − a 1 z h ( t , x ) ∂ z
V ( 8 ) = y f ( t ) − ∫ f ( t ) d t + h ( t , x ) a 1 ∂ t + y ∫ f ( t ) d t ∂ x + z 2 − y 2 2 + ∫ f ( t ) d t a 1 h ( t , x ) ∂ y − y z ∂ z
V ( 9 ) = z f ( t ) ∫ f ( t ) d t − h ( t , x ) a 1 ∂ t + z ∫ f ( t ) d t ∂ x + y z ∂ y + z 2 − y 2 2 − ∫ f ( t ) d t a 1 h ( t , x ) ∂ z
V ( 10 ) = y f ( t ) ∂ t − y ∂ x − 1 a 1 h ( t , x ) ∂ y
V ( 11 ) = z f ( t ) ∂ t − z ∂ x − 1 a 1 h ( t , x ) ∂ z
11c f = Const., V ( 4 ) = a 1 t + a 2 a 1 ∂ t + y ∂ y + z ∂ z
16 g = a 1 t + a 2, V ( 5 ) = y e a 1 x ∂ t − y e a 1 x a 1 t + a 2 ∂ x + a 1 t + a 2 a 1 e a 1 x ∂ y
h = Const., V ( 6 ) = y e − a 1 x ∂ t + y e − a 1 x a 1 t + a 2 ∂ x + a 1 t + a 2 a 1 e − a 1 x ∂ y
where a 1 ≠ 0 V ( 7 ) = z e a 1 x ∂ t − z e a 1 x a 1 t + a 2 ∂ x + a 1 t + a 2 a 1 e a 1 x ∂ z
V ( 8 ) = z e − a 1 x ∂ t + z e − a 1 x a 1 t + a 2 ∂ x + a 1 t + a 2 a 1 e − a 1 x ∂ z
V ( 9 ) = e a 1 x ∂ t − e a 1 x a 1 t + a 2 ∂ x
V ( 10 ) = e − a 1 x ∂ t + e − a 1 x a 1 t + a 2 ∂ x
V (11) = ∂ x
11d f = f(t), g = g(x), V ( 4 ) = ∫ f ( t ) d t f ( t ) ∂ t + ∫ g ( x ) d x ∂ x + y ∂ y + z ∂ z
17 h = const., V ( 5 ) = y f ( t ) ∂ t + ∫ f ( t ) d t ∂ y ,
where f ,t (t) ≠ 0 V ( 6 ) = z f ( t ) ∂ t + ∫ f ( t ) d t ∂ z ,
and g ,x (x) ≠ 0 V ( 7 ) = ∫ g ( x ) d x f ( t ) ∂ t + ∫ f ( t ) d t g ( x ) ∂ x ,
V ( 8 ) = − y g ( x ) ∂ x + ∫ g ( x ) d x ∂ y ,
V ( 9 ) = − z g ( x ) ∂ x + ∫ g ( x ) d x ∂ z ,
V ( 10 ) = 1 f ( t ) ∂ t
V ( 11 ) = 1 g ( x ) ∂ x
11e f = a 1 ∫g(x)dx, g = g(x), h = Const., V ( 4 ) = ∫ g ( x ) d x g ( x ) ∂ x + y ∂ y + z ∂ z
18 where a 1 ≠ 0 and g ,x (x) ≠ 0 V ( 5 ) = a 1 y e a 1 t f ( x ) ∂ t − a 1 y e a 1 t g ( x ) ∂ x + f ( x ) e a 1 t ∂ y ,
V ( 6 ) = − a 1 y e − a 1 t f ( x ) ∂ t − a 1 y e − a 1 t g ( x ) ∂ x + f ( x ) e − a 1 t ∂ y ,
V ( 7 ) = a 1 z e a 1 t f ( x ) ∂ t − a 1 z e a 1 t g ( x ) ∂ x + f ( x ) e a 1 t ∂ z ,
V ( 8 ) = − a 1 z e − a 1 t f ( x ) ∂ t − a 1 z e − a 1 t g ( x ) ∂ x + f ( x ) e − a 1 t ∂ z ,
V ( 9 ) = − e a 1 t ∫ g ( x ) d x ∂ t + a 1 e a 1 t g ( x ) ∂ x ,
V ( 10 ) = − e − a 1 t ∫ g ( x ) d x ∂ t − a 1 e − a 1 t g ( x ) ∂ x ,
V (11) = ∂ t
11f f = Const., g = g(x), h = Const., V ( 4 ) = t ∂ t + ∫ g ( x ) d x g ∂ x + y ∂ y + z ∂ z
18 where g ,x (x) ≠ 0 V (5) = y∂ t  + t∂ y ,
V (6) = z∂ t  + t∂ z ,
V ( 7 ) = ∫ g ( x ) d x ∂ t + t g ( x ) ∂ x ,
V ( 8 ) = − y g ( x ) ∂ x + ∫ g ( x ) d x ∂ y ,
V ( 9 ) = − z g ( x ) ∂ x + ∫ g ( x ) d x ∂ z ,
V (10) = ∂ t
V ( 11 ) = 1 g ( x ) ∂ x
11g f = f(t), g = Const. h = Const., V ( 4 ) = ∫ f ( t ) d t f ( t ) ∂ t + x ∂ x + y ∂ y + z ∂ z
23 where f ,t (t) ≠ 0 V ( 5 ) = y f ( t ) ∂ t + ∫ f ( t ) d t ∂ y ,
V ( 6 ) = z f ( t ) ∂ t + ∫ f ( t ) d t ∂ z ,
V ( 7 ) = x f ( t ) ∂ t + ∫ f ( t ) d t ∂ x ,
V (8) = −y∂ x  + x∂ y ,
V (9) = −z∂ x  + x∂ z ,
V ( 10 ) = 1 f ( t ) ∂ t
V (11) = ∂ x
11h f = a 1 x + a 2, g = Const., V ( 4 ) = a 1 x + a 2 a 1 ∂ x + y ∂ y + z ∂ z
24 h = Const., V ( 5 ) = y e a 1 t a 1 x + a 2 ∂ t − y e a 1 t ∂ x + a 1 x + a 2 a 1 e a 1 t ∂ y
where a 1 ≠ 0 V ( 6 ) = − y e − a 1 t a 1 x + a 2 ∂ t − y e − a 1 t ∂ x + a 1 x + a 2 a 1 e − a 1 t ∂ y
V ( 7 ) = z e a 1 t a 1 x + a 2 ∂ t − z e a 1 t ∂ x + a 1 x + a 2 a 1 e a 1 t ∂ z
V ( 8 ) = − z e − a 1 t a 1 x + a 2 ∂ t − z e − a 1 t ∂ x + a 1 x + a 2 a 1 e − a 1 t ∂ z
V ( 9 ) = − e a 1 t a 1 x + a 2 ∂ t + e a 1 t ∂ x
V ( 10 ) = e − a 1 t a 1 x + a 2 ∂ t + e − a 1 t ∂ x
V (11) = ∂ t

3 Solutions of the field equations

By solving the homothetic symmetry equations for non-static plane symmetric spacetime, we have derived various Lorentzian metrics with 4-, 5-, 7- and 11-dimensional homothetic algebras. Of these Lorentzian metrics, the exact solutions to the EFEs are given by those metrics that satisfy the EFEs and have the energy-momentum tensor associated with some known matter. The EFEs may be used to determine the energy-momentum tensor T ab , corresponding to each of these metrics. Additionally, T ab can be used to verify that these metrics satisfy different energy conditions and to evaluate the physical realism of the metrics. We follow this procedure to determine which of the acquired metrics are physically realistic solutions of EFEs. The metric (1.5) has four diagonal and one off-diagonal non-vanishing components of T ab , given by:

(3.1) T 00 = − 1 g 3 h 2 2 g f 2 h h , x x − g 3 ( h , t ) 2 − 2 g 2 h g , t h , t   + f 2 g ( h , x ) 2 − 2 f 2 g , x h h , x , T 01 = − 1 f g h 2 f g h , t x − f , x g h , t − f g , t h , x , T 11 = − 1 f 3 h 2 2 f g 2 h h , t t + f g 2 ( h , t ) 2 − 2 f , t g 2 h h , t   − f 3 ( h , x ) 2 − 2 f 2 f , x h h , x , T 22 = T 33 = h f 3 g 3 f 3 g h , x x − f g 3 h , t t − f g 2 h g , t t + f 2 f , x x g h + f , t g 3 h , t − f g 2 g , t h , t + f , t g 2 g , t h + f 2 f , x g h , x   − f 3 g , x h , x − f 2 f , x g , x h .

The energy-momentum tensor T ab has different structures for some known matter sources. For instance, if it is assumed that the matter source for the metric (1.5) is an anisotropic fluid, then the components of T ab are found to be T 00 = ρf 2(t, x), T 11 = p ‖ g 2(t, x), T 22 = T 33 = p ⊥ h 2(t, x), and T 01 = 0, where ρ is the density and p ‖ and p ⊥ are pressures in two directions. A perfect fluid is obtained when p ‖ = p ⊥ = p. Hence, among the classified metrics, those for which T 01 = 0 suggest anisotropic or perfect fluids. For all such metrics, ρ, p ‖, and p ⊥ can be calculated as:

(3.2) ρ = T 00 f 2 ( t , x ) , p ‖ = T 11 g 2 ( t , x ) , p ⊥ = T 22 h 2 ( t , x ) .

Out of the metrics obtained during the current study, all the metrics are anisotropic or perfect fluids with T 01 = 0, except the metrics 4c − 4f and 4i − 4l. However, in case of the metrics 4c − 4f, the condition T 00 > 0 is satisfied, ensuring that these metrics are physically realistic. For all other metrics, one can find the physical terms ρ, p ‖, and p ⊥ using Eq. (3.2), which can be subsequently used to check different energy conditions such as strong (SEC), weak (WEC), null (NEC) and dominant (DEC) energy conditions.

All the components of T ab vanish for the metrics possessing 11-dimensional homothetic algebra, labeled by 11a − 11h. Consequently, the terms ρ, p ‖ and p ⊥ also vanish for all these metrics and hence all the energy conditions are identically satisfied. Each of these metrics represents a vacuum solution of the EFEs. The metrics 5b and 5g give anisotropic solutions with ρ = a 1 2 ( a 1 t + a 2 ) 2 , p ‖ = −ρ and p ⊥ = 0, that satisfy all energy conditions. The metric 7b represents a perfect fluid solution with energy density ρ = 3 t 2 and pressure p ‖ = p ⊥ = − 1 t 2 . Like the previous two metrics, this metric also satisfies all the energy conditions.

Some of the derived metrics satisfy certain energy conditions if we further restrict the parameters in the metric coefficients. For example, the metrics 5c and 5e are anisotropic solutions with ρ = − p ‖ = a 2 2 − a 1 2 h 2 ( t , x ) and p ⊥ = 0. These models satisfy all energy conditions provided that a 2 2 − a 1 2 ≥ 0 . Similarly, the metric 7b gives a perfect fluid solution with ρ = 3 a 1 2 − a 3 2 ( a 1 t + a 2 ) 2 and p ‖ = p ⊥ = − ρ 3 , satisfying all energy conditions if a 1 2 − a 3 2 > 0 . For metrics 5o and 5p, both ρ and p ‖ vanish, while p ⊥ is found to be p ⊥ = 2 a 3 ( 2 a 3 − a 1 ) [ a 1 ∫ g ( x ) d x + 2 a 2 ] 2 and p ⊥ = 2 a 3 ( 2 a 3 − a 1 ) [ a 1 x + 2 a 2 ] 2 , respectively. If a 3(2a 3 − a 1) > 0, all energy conditions are satisfied for these two anisotropic fluid solutions. In Table 2, we give the details of energy conditions for some other metrics.

Table 2:

Energy conditions.

Metric no. Physical terms Energy conditions
5d ρ = ( a 1 + a 3 ) 2 ( a 1 t + a 2 ) 2 WEC, NEC and SEC are satisfied if
a 3(a 1 + a 3) < 0 and a 1(a 1 + a 3) > 0
p ‖ = − ( a 1 + a 3 ) ( a 1 + 3 a 3 ) ( a 1 t + a 2 ) 2 DEC is satisfied if a 3(a 1 + a 3) < 0,
p ⊥ = − a 3 ( a 1 + a 3 ) ( a 1 t + a 2 ) 2 a 1(a 1 + a 3) > 0 and (a 1 + a 3)(a 1 + 2a 3) > 0
5f ρ = ( a 1 − 2 a 3 ) 2 ( a 1 t + 2 a 2 ) 2 WEC, NEC and SEC are satisfied if a 3(a 1 − 2a 3) > 0
and a 1(a 1 − 2a 3) > 0
p ‖ = − ( a 1 − 2 a 3 ) ( a 1 − 6 a 3 ) ( a 1 t + 2 a 2 ) 2 DEC is satisfied if a 3(a 1 − 2a 3) > 0, a 1(a 1 − 2a 3) > 0
(a 1 − 2a 3)(a 1 − 4a 3) > 0
p ⊥ = 2 a 3 ( a 1 − 2 a 3 ) ( a 1 t + 2 a 2 ) 2
5k, 5l ρ = − ( a 1 − 2 a 3 ) ( a 1 − 6 a 3 ) ( a 1 x + 2 a 2 ) 2 WEC is satisfied if (a 1 − 2a 3)(a 1 − 6a 3) > 0, a 3(a 1 − 2a 3) > 0
(a 1 − 2a 3)(4a 3 − a 1) > 0
p ‖ = ( a 1 − 2 a 3 ) 2 ( a 1 x + 2 a 2 ) 2 NEC and SEC are satisfied if a 3(a 1 − 2a 3) > 0
and (a 1 − 2a 3)(4a 3 − a 1) > 0
p ⊥ = − 2 a 3 ( a 1 − 2 a 3 ) ( a 1 x + 2 a 2 ) 2 DEC is satisfied if a 3(a 1 − 2a 3) > 0
(a 1 − 2a 3)(4a 3 − a 1) > 0 and (a 1 − 2a 3)(8a 3 − a 1) > 0
5j, 5n ρ = − a 1 2 ( a 1 x + a 2 ) 2 An un-physical model with ρ < 0 and
p ‖ = −ρ satisfying none of the energy conditions
p ⊥ = 0
7c ρ = 3 ( a 1 − 2 a 3 ) 2 ( a 1 t + 2 a 2 ) 2 WEC and NEC satisfied if a 1(a 1 − 2a 3) > 0
p ‖ = p ⊥ = − ( a 1 − 2 a 3 ) ( a 1 − 6 a 3 ) ( a 1 t + 2 a 2 ) 2 SEC is satisfied ifa 1(a 1 − 2a 3) > 0
and a 3(a 1 − 2a 3) > 0
DEC is satisfied ifa 1(a 1 − 2a 3) > 0
and (a 1 − 3a 3)(a 1 − 2a 3) > 0
7e ρ = − a 1 2 ( a 1 x + a 2 ) 2 WEC and DEC are failed, while NEC and
p ‖ = 3 a 1 2 ( a 1 x + a 2 ) 2 SEC are satisfied
p ⊥ = −ρ

4 Physical interpretation and connection to known models

The classified metrics of the current study include many physically and geometrically important solutions of the field equations. For example, the metric labeled by 4a in Table 1 possesses a separable dependence on t and x in the transverse scale factor h(t, x). This metric resembles with the generalized Bianchi type I spacetimes with spatial inhomogeneity and anisotropic expansion. Similarly, the metric 4c admitting a 4-dimensional homothetic algebra exhibits generalized Kasner-like behavior in a non-comoving frame, similar to self-similar anisotropic cosmologies. The metric 4d, exhibiting an exponential evolution in the transverse directions is consistent with models that describe anisotropic inflation. With a square-root spatial character and a power-law time dependence, the metric 4f suggests connections to radiative or wave-like solutions. The moetric 4h, that involves a logarithmic coupling of space and time is structurally comparable to spacetimes occurring in the scalar field dynamics and colliding plane wave models.

Out of the metrics possessing five homothetic symmetries, the first metric labeled by 5a, includes a linear time scaling and the exponential spatial modulation, that are the features of the inhomogeneous generalized Szekeres-type models. The metric 5e has a linear mixing of time and space in the transverse direction and it captures directional anisotropy and evolving shear. The metric 5f involves power-law time dependent scale factor and it resembles the simplified anisotropic Bianchi type models. The metric 5g has spatial uniformity and linear time evolution in one direction and it corresponds to the plane symmetric analogues of locally rotationally symmetric Bianchi I spacetimes.

Among the metrics with seven homothetic symmetries, the metric labeled by 7a involves an exponential spatial dependence and its homothetic generators involve the transverse coordinates. It resembles generalized Szekeres-type geometries. The metric 7b exhibits uniform expansion in all directions, reflecting Milne-like or stiff fluid cosmologies. The metric 7c exhibits the same time dependency in both the spatial and transverse parts, it is therefore consistent with Kasner-type anisotropic models under self-similarity. The temporal and transverse scale factors of the metric 7d are spatially dependent, making it consistent with colliding plane wave geometries. Finally, the metric 7e is entirely a static metric with linear spatial inhomogeneity and it offers a symmetric vacuum configuration suitable for modeling non-evolving systems.

Out of the maximally symmetric metrics possessing 11 HVFs, the metric 11a involves exponential spatial dependence and its energy-momentum tensor vanishes. This metric resembles Robinson-Trautman type or plane wave solutions. The metric 11b combines spatially changing transverse scales with integrated time behavior and it is related to scalar field or wave-like cosmologies under self-similarity. The exponential symmetry generators acting on transverse directions for the metric 11c shows that this metric is suitable to model shear-free, plane symmetric vacuum fields. The metric 11g is homogeneous and purely dependent on time, it is consistent with the Milne limit of flat FLRW cosmologies. Lastly, the metric 11h is a spatially homogeneous and static metric, representing a symmetric configuration that is relevant for static interior solutions.

To provide a clearer overview, we provide schematic flow charts in Figures 2 and 3 to illustrate how our derived metrics correspond to vacuum, and perfect and anisotropic fluid configurations and how these metrics connect to some well known models in the literature.

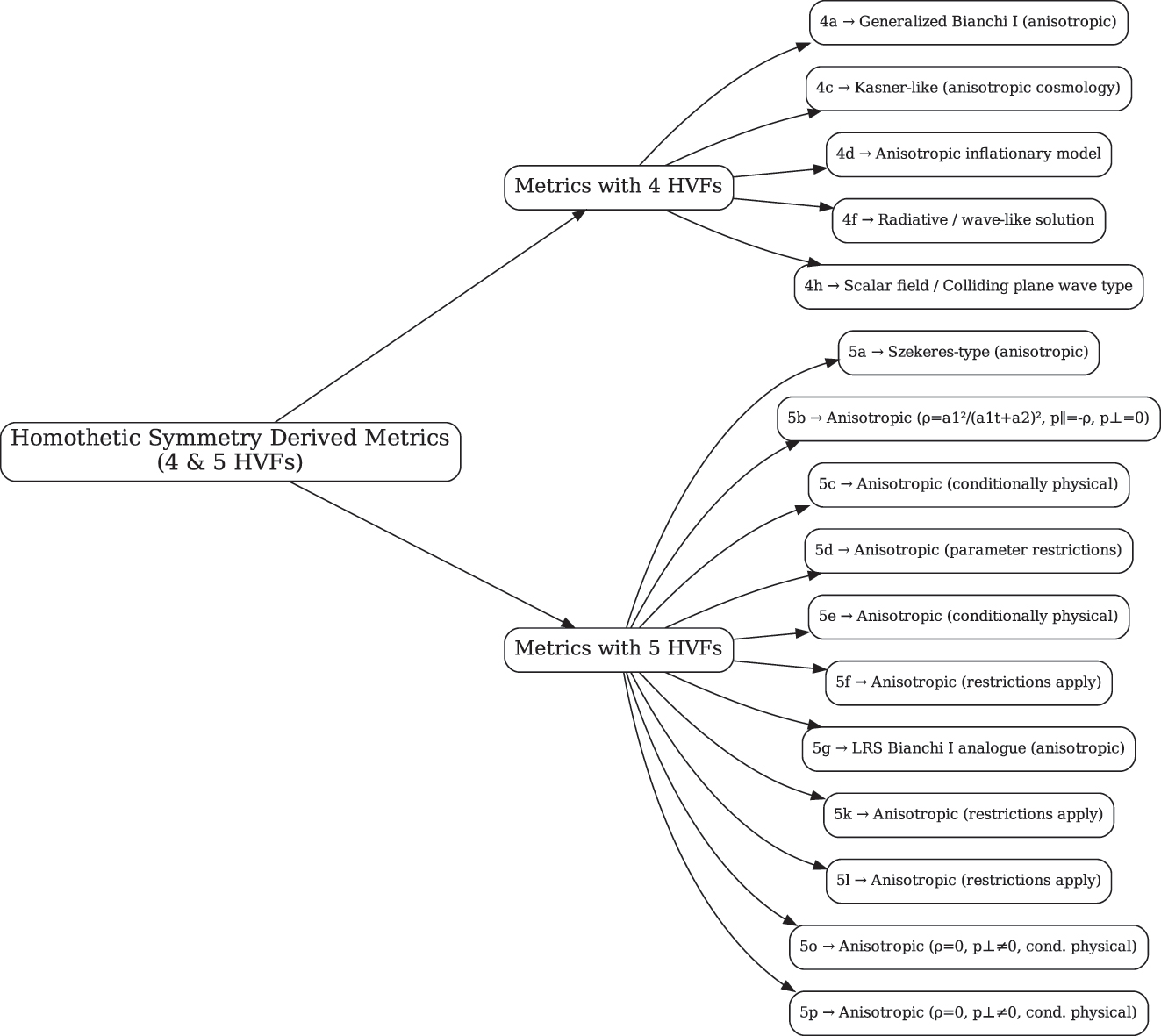
Figure 2: Schematic flow chart for metrics with 4 and 5 HVFs.
Figure 2:

Schematic flow chart for metrics with 4 and 5 HVFs.

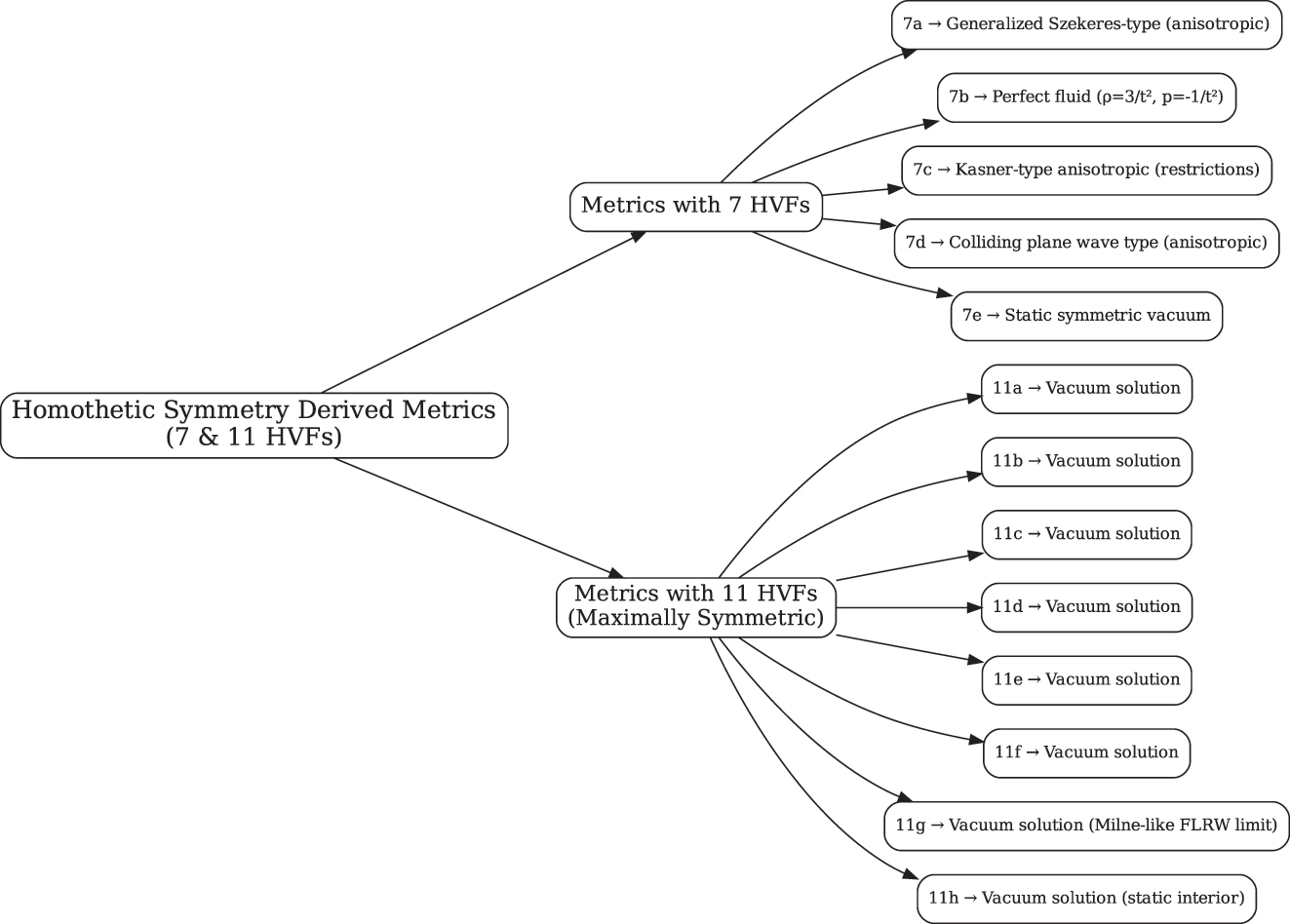
Figure 3: Schematic flow chart for metrics with 7 and 11 HVFs.
Figure 3:

Schematic flow chart for metrics with 7 and 11 HVFs.

Collectively, our derived results show that the obtained homothetic symmetries enrich the collection of known symmetries for plane symmetric non-static spacetimes and yield new possibilities for finding the exact solutions of EFEs. The derived models may also have applications in many current research areas in relativistic cosmology and gravitation. In anisotropic cosmological models, the spacetimes with planar symmetry provide important geometries for studying anisotropy and inhomogeneity, that play a pivotal role in Bianchi-type universes and in explaining possible deviations from isotropy in the cosmic microwave background. These solutions may further serve as toy models for the early universe, where anisotropic effects could have influenced pre-inflationary or inflationary dynamics. Moreover, non-static plane symmetric models are relevant in the study of gravitational collapse and black hole interiors, where anisotropic pressures and imperfect fluids naturally arise. In this way, the homothetic symmetries obtained in the present study may contribute to understanding self-similar structures that appear both in cosmology and in compact object models.

Anisotropic solutions of EFEs are of significant astrophysical importance. In compact stars, anisotropy can appear due to very high densities, phase transitions, superfluid states, or the presence of electromagnetic fields. Such anisotropic pressures influence the stability, mass-radius relation, and surface redshift of stellar configurations, making them more realistic than isotropic models. Beyond stellar interiors, anisotropic fluids are also relevant in exotic matter scenarios, including dark energy models and non-standard cosmological fluids. Therefore, the anisotropic plane symmetric solutions obtained in this work may provide useful toy models to explore situations where local anisotropy plays a fundamental role in the gravitational dynamics.

5 Conclusions

In this paper, we have explored how symmetries in spacetimes, particularly HVFs, can help us to solve the Einstein’s complex field equations more easily. These symmetries act like scaling rules that preserve the structure of spacetime while allowing it to evolve, making them a powerful tool for studying dynamic gravitational systems.

Using an advanced computational method, the Rif tree approach, we have classified a variety of exact solutions for non-static plane-symmetric spacetimes with 4-, 5-, 7-, and 11-dimensional homothetic algebras. Some of the obtained solutions describe universes filled with matter or radiation, while others represent vacuum regions. In addition, we have explored the physical and geometrical significance of many of the derived metrics by comparing their structure with some known solutions of EFEs. Several metrics were identified as generalized versions of Kasner, Szekeres, Bianchi type I, Milne-type, and Robinson-Trautman spacetimes. These results contribute new exact solutions and deepen the understanding of homothetic symmetry in modeling anisotropic, inhomogeneous, and self-similar cosmological geometries.

Corresponding authors: Tahir Hussain, Department of Mathematics, University of Peshawar, Khyber Pakhtunkhwa, Pakistan, E-mail: ; and Ibrahim Mahariq, Department of Mathematics, Saveetha School of Engineering, SIMATS, Saveetha University, Chennai 602105, Tamil Nadu, India; Department of Medical Research, China Medical University Hospital, China Medical University, Taichung, Taiwan; University College, Korea University, Seoul 02481, South Korea; and Applied Science Research Center, Applied Science Private University, Amman, Jordan, E-mail: ; and Kamran, Department of Mathematics, Islamia College University Peshawar, Khyber Pakhtunkhwa, Pakistan, E-mail:

  1. Funding Statement: The manuscript received no external funding.

  2. Conflicts of Interest: The authors declare no conflict of interest.

  3. Data availability Statement: No data was used for the research described in the article.

  4. Author Contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.

Acknowledgements

This work was supported by Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R897), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. The authors extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, KSA for funding this research work through the project number “NBU-FFR-2025-1902-05”.

References

1. Hall, GS. Symmetries and curvature structure in general relativity. United Kingdom: World Scientific; 2004.10.1142/1729Search in Google Scholar

2. Noether, E. Invariant variation problems. Nachr König Ges Wiss Göttingen Math-Phys Kl 1918;2:235. English translation in: Transport Theory Stat Phys 1971;1:186.10.1080/00411457108231446Search in Google Scholar

3. Hickman, M, Yazdan, S. Noether symmetries of Bianchi type II spacetimes. Gen Relat Gravit 2017;49:1–15. https://doi.org/10.1007/s10714-017-2228-5.Search in Google Scholar

4. Qadir, A, Ziad, M. Classification of static cylindrically symmetric space-times. Nuovo Cimento B 1995;110:277–90. https://doi.org/10.1007/bf02741369.Search in Google Scholar

5. Bokhari, AH, Qadir, A. Symmetries of static spherically symmetric space-times. J Math Phys 1987;28:1019–22. https://doi.org/10.1063/1.527594.Search in Google Scholar

6. Bokhari, AH, Qadir, A. Killing vectors of static spherically symmetric metrics. J Math Phys 1990;31:1463. https://doi.org/10.1063/1.528737.Search in Google Scholar

7. Bokhari, AH, Karim, M, Al-Sheikh, DN, Zaman, FD. Circularly symmetric static metric in three dimensions and its Killing symmetry. Int J Theor Phys 2008;47:2672–8. https://doi.org/10.1007/s10773-008-9704-3.Search in Google Scholar

8. Feroze, T, Qadir, A, Ziad, M. The classification of plane symmetric spacetimes by isometries. J Math Phys 2001;42:4947–55. https://doi.org/10.1063/1.1385175.Search in Google Scholar

9. Ziad, M. The classification of static plane-symmetric spacetime. Nuovo Cim B 1999;114:683–92.Search in Google Scholar

10. Ahmad, D, Ziad, M. Homothetic motions of spherically symmetric space-time. J Math Phys 1997;38:2547–52. https://doi.org/10.1063/1.531994.Search in Google Scholar

11. Moopanar, S, Maharaj, SD. Conformal symmetries of spherical spacetimes. Int J Theor Phys 2010;49:1878–85. https://doi.org/10.1007/s10773-010-0366-6.Search in Google Scholar

12. Maartens, R, Maharaj, SD. Conformal Killing vectors in Robertson–Walker spacetimes. Class Quan Grav 1986;3:1005–11. https://doi.org/10.1088/0264-9381/3/5/027.Search in Google Scholar

13. Moopanar, S, Maharaj, SD. Relativistic shear-free fluids with symmetry. J Eng Math 2013;82:125–31. https://doi.org/10.1007/s10665-012-9573-x.Search in Google Scholar

14. Duggal, KL, Sharma, R. Conformal Killing vector fields on spacetime solutions of Einstein’s equations and initial data. Nonlinear Anal 2005;63:447–54. https://doi.org/10.1016/j.na.2004.09.034.Search in Google Scholar

15. Khan, S, Hussain, T, Bokhari, AH, Khan, GA. Conformal Killing vectors of plane symmetric four-dimensional Lorentzian manifolds. Eur Phys J C 2015;75:523. https://doi.org/10.1140/epjc/s10052-015-3758-1.Search in Google Scholar

16. Hussain, F, Shabbir, G, Malik, S, Ramzan, M. Conformal vector fields for some vacuum classes of pp-wave spacetimes in ghost-free infinite derivative gravity. Int J Geomet Methods Mod Phys 2021;18:2150109. https://doi.org/10.1142/s0219887821501097.Search in Google Scholar

17. Qazi, S, Hussain, F, Shabbir, G. Exploring conformal vector fields of Bianchi type-I perfect fluid solutions in f(T) gravity. Int J Geomet Methods Mod Phys 2021;18:2150161. https://doi.org/10.1142/s0219887821501619.Search in Google Scholar

18. Shabbir, G, Khan, S. A note on proper teleparallel homothetic vector fields in non-static plane symmetric Lorentzian manifolds. Rom J Phys 2012;57:571–81.10.1140/epjp/i2012-12130-ySearch in Google Scholar

19. Ali, A, Khan, I, Khan, S. Conformal vector fields over Lyra manifold of locally rotationally symmetric Bianchi type I spacetimes. Eur Phys J Plus 2020;135:499. https://doi.org/10.1140/epjp/s13360-020-00518-1.Search in Google Scholar

20. Khan, S, Khan, GA, Amir, MJ. Teleparallel Killing motions of Bianchi type V spacetimes. Rom J Phys 2015;67:309–17.GoharSearch in Google Scholar

21. Capozziello, S, De Ritis, R, Rubano, C, Scudellaro, P. Noether symmetries in cosmology. Riv Nuovo Cim 1996;19:1–114. https://doi.org/10.1007/bf02742992.Search in Google Scholar

22. Capozziello, S, De Laurentis, M. Noether symmetries in extended gravity cosmology. Int J Geomet Methods Mod Phys 2014;11:1460004. https://doi.org/10.1142/s0219887814600044.Search in Google Scholar

23. Capozziello, S, Paliathanasis, A, Tsamparlis, M. Symmetries in scalar–tensor cosmology. Classical Quant Grav 2015;32:145006.10.1088/0264-9381/32/24/245006Search in Google Scholar

24. Miranda, M, Capozziello, S, Vernieri, D. General analysis of Noether symmetries in Horndeski gravity. Eur Phys J C 2024;84:1088. https://doi.org/10.1140/epjc/s10052-024-13088-8.Search in Google Scholar

25. Bajardi, F, Capozziello, S, Di Salvo, E, Spinnato, PF. The Noether symmetry approach: foundation and applications: the case of scalar–tensor Gauss–Bonnet gravity. Symmetry 2023;15:1625. https://doi.org/10.3390/sym15091625.Search in Google Scholar

26. Capozziello, S, Ferrara, S. The equivalence principle as a Noether symmetry. Int J Geomet Methods Mod Phys 2024;21:2450014. https://doi.org/10.1142/s0219887824400140.Search in Google Scholar

27. Podolsky, J, Ortaggio, M, Pravda, V. Conformally related vacuum gravitational waves and their symmetries. J High Energy Phys 2024;07:164.10.1007/JHEP07(2024)164Search in Google Scholar

28. Stephani, H, Kramer, D, Maccallum, M, Hoenselaers, C, Herlt, E. Exact solutions of Einstein’s field equations, 2nd ed. Cambridge: Cambridge University Press; 2003.10.1017/CBO9780511535185Search in Google Scholar

29. Albuhayr, MK, Bokhari, AH, Hussain, T. Killing vector fields of static cylindrically symmetric spacetime-A Rif tree approach. Symmetry 2023;15:1111. https://doi.org/10.3390/sym15051111.Search in Google Scholar

30. Bokhari, AH, Hussain, T, Hussain, W, Khan, F. Killing vector fields of Bianchi type I spacetimes via Rif tree approach. Mod Phys Lett A 2021;36:2150208. https://doi.org/10.1142/s0217732321502084.Search in Google Scholar

31. Ahmad, S, Hussain, T, Saqib, AB, Farhan, M, Farooq, M. Killing vector fields of locally rotationally symmetric Bianchi type V spacetime. Sci Rep 2024;14:10239. https://doi.org/10.1038/s41598-024-58560-3.Search in Google Scholar PubMed PubMed Central

32. Hussain, T, Bokhari, AH, Munawar, A. Lie symmetries of static spherically symmetric spacetimes by Rif tree approach. Eur Phys J Plus 2022;137:1322. https://doi.org/10.1140/epjp/s13360-022-03526-5.Search in Google Scholar

33. Hussain, T, Nasib, U, Farhan, M, Bokhari, AH. A study of energy conditions in Kantowski–Sachs spacetimes via homothetic vector fields. Int J Geomet Methods Mod Phys 2020;17:2050035. https://doi.org/10.1142/s0219887820500358.Search in Google Scholar

34. Bokhari, AH, Hussain, T, Khan, J, Nasib, U. Proper homothetic vector fields of Bianchi type I spacetimes via Rif tree approach. Results Phys 2021;25:104299. https://doi.org/10.1016/j.rinp.2021.104299.Search in Google Scholar
Received: 2025-08-16
Accepted: 2025-10-23
Published Online: 2025-12-10

© 2025 the author(s), published by De Gruyter, Berlin/Boston

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Research Articles
  2. Single-step fabrication of Ag2S/poly-2-mercaptoaniline nanoribbon photocathodes for green hydrogen generation from artificial and natural red-sea water
  3. Abundant new interaction solutions and nonlinear dynamics for the (3+1)-dimensional Hirota–Satsuma–Ito-like equation
  4. A novel gold and SiO2 material based planar 5-element high HPBW end-fire antenna array for 300 GHz applications
  5. Explicit exact solutions and bifurcation analysis for the mZK equation with truncated M-fractional derivatives utilizing two reliable methods
  6. Optical and laser damage resistance: Role of periodic cylindrical surfaces
  7. Numerical study of flow and heat transfer in the air-side metal foam partially filled channels of panel-type radiator under forced convection
  8. Water-based hybrid nanofluid flow containing CNT nanoparticles over an extending surface with velocity slips, thermal convective, and zero-mass flux conditions
  9. Dynamical wave structures for some diffusion--reaction equations with quadratic and quartic nonlinearities
  10. Solving an isotropic grey matter tumour model via a heat transfer equation
  11. Study on the penetration protection of a fiber-reinforced composite structure with CNTs/GFP clip STF/3DKevlar
  12. Influence of Hall current and acoustic pressure on nanostructured DPL thermoelastic plates under ramp heating in a double-temperature model
  13. Applications of the Belousov–Zhabotinsky reaction–diffusion system: Analytical and numerical approaches
  14. AC electroosmotic flow of Maxwell fluid in a pH-regulated parallel-plate silica nanochannel
  15. Interpreting optical effects with relativistic transformations adopting one-way synchronization to conserve simultaneity and space–time continuity
  16. Modeling and analysis of quantum communication channel in airborne platforms with boundary layer effects
  17. Theoretical and numerical investigation of a memristor system with a piecewise memductance under fractal–fractional derivatives
  18. Tuning the structure and electro-optical properties of α-Cr2O3 films by heat treatment/La doping for optoelectronic applications
  19. High-speed multi-spectral explosion temperature measurement using golden-section accelerated Pearson correlation algorithm
  20. Dynamic behavior and modulation instability of the generalized coupled fractional nonlinear Helmholtz equation with cubic–quintic term
  21. Study on the duration of laser-induced air plasma flash near thin film surface
  22. Exploring the dynamics of fractional-order nonlinear dispersive wave system through homotopy technique
  23. The mechanism of carbon monoxide fluorescence inside a femtosecond laser-induced plasma
  24. Numerical solution of a nonconstant coefficient advection diffusion equation in an irregular domain and analyses of numerical dispersion and dissipation
  25. Numerical examination of the chemically reactive MHD flow of hybrid nanofluids over a two-dimensional stretching surface with the Cattaneo–Christov model and slip conditions
  26. Impacts of sinusoidal heat flux and embraced heated rectangular cavity on natural convection within a square enclosure partially filled with porous medium and Casson-hybrid nanofluid
  27. Stability analysis of unsteady ternary nanofluid flow past a stretching/shrinking wedge
  28. Solitonic wave solutions of a Hamiltonian nonlinear atom chain model through the Hirota bilinear transformation method
  29. Bilinear form and soltion solutions for (3+1)-dimensional negative-order KdV-CBS equation
  30. Solitary chirp pulses and soliton control for variable coefficients cubic–quintic nonlinear Schrödinger equation in nonuniform management system
  31. Influence of decaying heat source and temperature-dependent thermal conductivity on photo-hydro-elasto semiconductor media
  32. Dissipative disorder optimization in the radiative thin film flow of partially ionized non-Newtonian hybrid nanofluid with second-order slip condition
  33. Bifurcation, chaotic behavior, and traveling wave solutions for the fractional (4+1)-dimensional Davey–Stewartson–Kadomtsev–Petviashvili model
  34. New investigation on soliton solutions of two nonlinear PDEs in mathematical physics with a dynamical property: Bifurcation analysis
  35. Mathematical analysis of nanoparticle type and volume fraction on heat transfer efficiency of nanofluids
  36. Creation of single-wing Lorenz-like attractors via a ten-ninths-degree term
  37. Optical soliton solutions, bifurcation analysis, chaotic behaviors of nonlinear Schrödinger equation and modulation instability in optical fiber
  38. Chaotic dynamics and some solutions for the (n + 1)-dimensional modified Zakharov–Kuznetsov equation in plasma physics
  39. Fractal formation and chaotic soliton phenomena in nonlinear conformable Heisenberg ferromagnetic spin chain equation
  40. Single-step fabrication of Mn(iv) oxide-Mn(ii) sulfide/poly-2-mercaptoaniline porous network nanocomposite for pseudo-supercapacitors and charge storage
  41. Novel constructed dynamical analytical solutions and conserved quantities of the new (2+1)-dimensional KdV model describing acoustic wave propagation
  42. Tavis–Cummings model in the presence of a deformed field and time-dependent coupling
  43. Spinning dynamics of stress-dependent viscosity of generalized Cross-nonlinear materials affected by gravitationally swirling disk
  44. Design and prediction of high optical density photovoltaic polymers using machine learning-DFT studies
  45. Robust control and preservation of quantum steering, nonlocality, and coherence in open atomic systems
  46. Coating thickness and process efficiency of reverse roll coating using a magnetized hybrid nanomaterial flow
  47. Dynamic analysis, circuit realization, and its synchronization of a new chaotic hyperjerk system
  48. Decoherence of steerability and coherence dynamics induced by nonlinear qubit–cavity interactions
  49. Finite element analysis of turbulent thermal enhancement in grooved channels with flat- and plus-shaped fins
  50. Modulational instability and associated ion-acoustic modulated envelope solitons in a quantum plasma having ion beams
  51. Statistical inference of constant-stress partially accelerated life tests under type II generalized hybrid censored data from Burr III distribution
  52. On solutions of the Dirac equation for 1D hydrogenic atoms or ions
  53. Entropy optimization for chemically reactive magnetized unsteady thin film hybrid nanofluid flow on inclined surface subject to nonlinear mixed convection and variable temperature
  54. Stability analysis, circuit simulation, and color image encryption of a novel four-dimensional hyperchaotic model with hidden and self-excited attractors
  55. A high-accuracy exponential time integration scheme for the Darcy–Forchheimer Williamson fluid flow with temperature-dependent conductivity
  56. Novel analysis of fractional regularized long-wave equation in plasma dynamics
  57. Development of a photoelectrode based on a bismuth(iii) oxyiodide/intercalated iodide-poly(1H-pyrrole) rough spherical nanocomposite for green hydrogen generation
  58. Investigation of solar radiation effects on the energy performance of the (Al2O3–CuO–Cu)/H2O ternary nanofluidic system through a convectively heated cylinder
  59. Quantum resources for a system of two atoms interacting with a deformed field in the presence of intensity-dependent coupling
  60. Studying bifurcations and chaotic dynamics in the generalized hyperelastic-rod wave equation through Hamiltonian mechanics
  61. A new numerical technique for the solution of time-fractional nonlinear Klein–Gordon equation involving Atangana–Baleanu derivative using cubic B-spline functions
  62. Interaction solutions of high-order breathers and lumps for a (3+1)-dimensional conformable fractional potential-YTSF-like model
  63. Hydraulic fracturing radioactive source tracing technology based on hydraulic fracturing tracing mechanics model
  64. Numerical solution and stability analysis of non-Newtonian hybrid nanofluid flow subject to exponential heat source/sink over a Riga sheet
  65. Numerical investigation of mixed convection and viscous dissipation in couple stress nanofluid flow: A merged Adomian decomposition method and Mohand transform
  66. Effectual quintic B-spline functions for solving the time fractional coupled Boussinesq–Burgers equation arising in shallow water waves
  67. Analysis of MHD hybrid nanofluid flow over cone and wedge with exponential and thermal heat source and activation energy
  68. Solitons and travelling waves structure for M-fractional Kairat-II equation using three explicit methods
  69. Impact of nanoparticle shapes on the heat transfer properties of Cu and CuO nanofluids flowing over a stretching surface with slip effects: A computational study
  70. Computational simulation of heat transfer and nanofluid flow for two-sided lid-driven square cavity under the influence of magnetic field
  71. Irreversibility analysis of a bioconvective two-phase nanofluid in a Maxwell (non-Newtonian) flow induced by a rotating disk with thermal radiation
  72. Hydrodynamic and sensitivity analysis of a polymeric calendering process for non-Newtonian fluids with temperature-dependent viscosity
  73. Exploring the peakon solitons molecules and solitary wave structure to the nonlinear damped Kortewege–de Vries equation through efficient technique
  74. Modeling and heat transfer analysis of magnetized hybrid micropolar blood-based nanofluid flow in Darcy–Forchheimer porous stenosis narrow arteries
  75. Activation energy and cross-diffusion effects on 3D rotating nanofluid flow in a Darcy–Forchheimer porous medium with radiation and convective heating
  76. Insights into chemical reactions occurring in generalized nanomaterials due to spinning surface with melting constraints
  77. Influence of a magnetic field on double-porosity photo-thermoelastic materials under Lord–Shulman theory
  78. Soliton-like solutions for a nonlinear doubly dispersive equation in an elastic Murnaghan's rod via Hirota's bilinear method
  79. Analytical and numerical investigation of exact wave patterns and chaotic dynamics in the extended improved Boussinesq equation
  80. Nonclassical correlation dynamics of Heisenberg XYZ states with (x, y)-spin--orbit interaction, x-magnetic field, and intrinsic decoherence effects
  81. Exact traveling wave and soliton solutions for chemotaxis model and (3+1)-dimensional Boiti–Leon–Manna–Pempinelli equation
  82. Unveiling the transformative role of samarium in ZnO: Exploring structural and optical modifications for advanced functional applications
  83. On the derivation of solitary wave solutions for the time-fractional Rosenau equation through two analytical techniques
  84. Analyzing the role of length and radius of MWCNTs in a nanofluid flow influenced by variable thermal conductivity and viscosity considering Marangoni convection
  85. Advanced mathematical analysis of heat and mass transfer in oscillatory micropolar bio-nanofluid flows via peristaltic waves and electroosmotic effects
  86. Exact bound state solutions of the radial Schrödinger equation for the Coulomb potential by conformable Nikiforov–Uvarov approach
  87. Some anisotropic and perfect fluid plane symmetric solutions of Einstein's field equations using killing symmetries
  88. Nonlinear dynamics of the dissipative ion-acoustic solitary waves in anisotropic rotating magnetoplasmas
  89. Curves in multiplicative equiaffine plane
  90. Exact solution of the three-dimensional (3D) Z2 lattice gauge theory
  91. Propagation properties of Airyprime pulses in relaxing nonlinear media
  92. Symbolic computation: Analytical solutions and dynamics of a shallow water wave equation in coastal engineering
  93. Wave propagation in nonlocal piezo-photo-hygrothermoelastic semiconductors subjected to heat and moisture flux
  94. Comparative reaction dynamics in rotating nanofluid systems: Quartic and cubic kinetics under MHD influence
  95. Laplace transform technique and probabilistic analysis-based hypothesis testing in medical and engineering applications
  96. Physical properties of ternary chloro-perovskites KTCl3 (T = Ge, Al) for optoelectronic applications
  97. Gravitational length stretching: Curvature-induced modulation of quantum probability densities
  98. The search for the cosmological cold dark matter axion – A new refined narrow mass window and detection scheme
  99. A comparative study of quantum resources in bipartite Lipkin–Meshkov–Glick model under DM interaction and Zeeman splitting
  100. PbO-doped K2O–BaO–Al2O3–B2O3–TeO2-glasses: Mechanical and shielding efficacy
  101. Nanospherical arsenic(iii) oxoiodide/iodide-intercalated poly(N-methylpyrrole) composite synthesis for broad-spectrum optical detection
  102. Sine power Burr X distribution with estimation and applications in physics and other fields
  103. Numerical modeling of enhanced reactive oxygen plasma in pulsed laser deposition of metal oxide thin films
  104. Dynamical analyses and dispersive soliton solutions to the nonlinear fractional model in stratified fluids
  105. Computation of exact analytical soliton solutions and their dynamics in advanced optical system
  106. An innovative approximation concerning the diffusion and electrical conductivity tensor at critical altitudes within the F-region of ionospheric plasma at low latitudes
  107. An analytical investigation to the (3+1)-dimensional Yu–Toda–Sassa–Fukuyama equation with dynamical analysis: Bifurcation
  108. Swirling-annular-flow-induced instability of a micro shell considering Knudsen number and viscosity effects
  109. Numerical analysis of non-similar convection flows of a two-phase nanofluid past a semi-infinite vertical plate with thermal radiation
  110. MgO NPs reinforced PCL/PVC nanocomposite films with enhanced UV shielding and thermal stability for packaging applications
  111. Optimal conditions for indoor air purification using non-thermal Corona discharge electrostatic precipitator
  112. Investigation of thermal conductivity and Raman spectra for HfAlB, TaAlB, and WAlB based on first-principles calculations
  113. Tunable double plasmon-induced transparency based on monolayer patterned graphene metamaterial
  114. DSC: depth data quality optimization framework for RGBD camouflaged object detection
  115. A new family of Poisson-exponential distributions with applications to cancer data and glass fiber reliability
  116. Numerical investigation of couple stress under slip conditions via modified Adomian decomposition method
  117. Monitoring plateau lake area changes in Yunnan province, southwestern China using medium-resolution remote sensing imagery: applicability of water indices and environmental dependencies
  118. Heterodyne interferometric fiber-optic gyroscope
  119. Exact solutions of Einstein’s field equations via homothetic symmetries of non-static plane symmetric spacetime
  120. A widespread study of discrete entropic model and its distribution along with fluctuations of energy
  121. Empirical model integration for accurate charge carrier mobility simulation in silicon MOSFETs
  122. The influence of scattering correction effect based on optical path distribution on CO2 retrieval
  123. Anisotropic dissociation and spectral response of 1-Bromo-4-chlorobenzene under static directional electric fields
  124. Role of tungsten oxide (WO3) on thermal and optical properties of smart polymer composites
  125. Analysis of iterative deblurring: no explicit noise
  126. Review Article
  127. Examination of the gamma radiation shielding properties of different clay and sand materials in the Adrar region
  128. Erratum
  129. Erratum to “On Soliton structures in optical fiber communications with Kundu–Mukherjee–Naskar model (Open Physics 2021;19:679–682)”
  130. Special Issue on Fundamental Physics from Atoms to Cosmos - Part II
  131. Possible explanation for the neutron lifetime puzzle
  132. Special Issue on Nanomaterial utilization and structural optimization - Part III
  133. Numerical investigation on fluid-thermal-electric performance of a thermoelectric-integrated helically coiled tube heat exchanger for coal mine air cooling
  134. Special Issue on Nonlinear Dynamics and Chaos in Physical Systems
  135. Analysis of the fractional relativistic isothermal gas sphere with application to neutron stars
  136. Abundant wave symmetries in the (3+1)-dimensional Chafee–Infante equation through the Hirota bilinear transformation technique
  137. Successive midpoint method for fractional differential equations with nonlocal kernels: Error analysis, stability, and applications
  138. Novel exact solitons to the fractional modified mixed-Korteweg--de Vries model with a stability analysis
https://doi.org/10.1515/phys-2025-0238
Keywords for this article
exact solutions; spacetime symmetries; homothetic vector fields; plane symmetric spacetime; Rif tree approach
Creative Commons
BY 4.0

Articles in the same Issue

  1. Research Articles
  2. Single-step fabrication of Ag2S/poly-2-mercaptoaniline nanoribbon photocathodes for green hydrogen generation from artificial and natural red-sea water
  3. Abundant new interaction solutions and nonlinear dynamics for the (3+1)-dimensional Hirota–Satsuma–Ito-like equation
  4. A novel gold and SiO2 material based planar 5-element high HPBW end-fire antenna array for 300 GHz applications
  5. Explicit exact solutions and bifurcation analysis for the mZK equation with truncated M-fractional derivatives utilizing two reliable methods
  6. Optical and laser damage resistance: Role of periodic cylindrical surfaces
  7. Numerical study of flow and heat transfer in the air-side metal foam partially filled channels of panel-type radiator under forced convection
  8. Water-based hybrid nanofluid flow containing CNT nanoparticles over an extending surface with velocity slips, thermal convective, and zero-mass flux conditions
  9. Dynamical wave structures for some diffusion--reaction equations with quadratic and quartic nonlinearities
  10. Solving an isotropic grey matter tumour model via a heat transfer equation
  11. Study on the penetration protection of a fiber-reinforced composite structure with CNTs/GFP clip STF/3DKevlar
  12. Influence of Hall current and acoustic pressure on nanostructured DPL thermoelastic plates under ramp heating in a double-temperature model
  13. Applications of the Belousov–Zhabotinsky reaction–diffusion system: Analytical and numerical approaches
  14. AC electroosmotic flow of Maxwell fluid in a pH-regulated parallel-plate silica nanochannel
  15. Interpreting optical effects with relativistic transformations adopting one-way synchronization to conserve simultaneity and space–time continuity
  16. Modeling and analysis of quantum communication channel in airborne platforms with boundary layer effects
  17. Theoretical and numerical investigation of a memristor system with a piecewise memductance under fractal–fractional derivatives
  18. Tuning the structure and electro-optical properties of α-Cr2O3 films by heat treatment/La doping for optoelectronic applications
  19. High-speed multi-spectral explosion temperature measurement using golden-section accelerated Pearson correlation algorithm
  20. Dynamic behavior and modulation instability of the generalized coupled fractional nonlinear Helmholtz equation with cubic–quintic term
  21. Study on the duration of laser-induced air plasma flash near thin film surface
  22. Exploring the dynamics of fractional-order nonlinear dispersive wave system through homotopy technique
  23. The mechanism of carbon monoxide fluorescence inside a femtosecond laser-induced plasma
  24. Numerical solution of a nonconstant coefficient advection diffusion equation in an irregular domain and analyses of numerical dispersion and dissipation
  25. Numerical examination of the chemically reactive MHD flow of hybrid nanofluids over a two-dimensional stretching surface with the Cattaneo–Christov model and slip conditions
  26. Impacts of sinusoidal heat flux and embraced heated rectangular cavity on natural convection within a square enclosure partially filled with porous medium and Casson-hybrid nanofluid
  27. Stability analysis of unsteady ternary nanofluid flow past a stretching/shrinking wedge
  28. Solitonic wave solutions of a Hamiltonian nonlinear atom chain model through the Hirota bilinear transformation method
  29. Bilinear form and soltion solutions for (3+1)-dimensional negative-order KdV-CBS equation
  30. Solitary chirp pulses and soliton control for variable coefficients cubic–quintic nonlinear Schrödinger equation in nonuniform management system
  31. Influence of decaying heat source and temperature-dependent thermal conductivity on photo-hydro-elasto semiconductor media
  32. Dissipative disorder optimization in the radiative thin film flow of partially ionized non-Newtonian hybrid nanofluid with second-order slip condition
  33. Bifurcation, chaotic behavior, and traveling wave solutions for the fractional (4+1)-dimensional Davey–Stewartson–Kadomtsev–Petviashvili model
  34. New investigation on soliton solutions of two nonlinear PDEs in mathematical physics with a dynamical property: Bifurcation analysis
  35. Mathematical analysis of nanoparticle type and volume fraction on heat transfer efficiency of nanofluids
  36. Creation of single-wing Lorenz-like attractors via a ten-ninths-degree term
  37. Optical soliton solutions, bifurcation analysis, chaotic behaviors of nonlinear Schrödinger equation and modulation instability in optical fiber
  38. Chaotic dynamics and some solutions for the (n + 1)-dimensional modified Zakharov–Kuznetsov equation in plasma physics
  39. Fractal formation and chaotic soliton phenomena in nonlinear conformable Heisenberg ferromagnetic spin chain equation
  40. Single-step fabrication of Mn(iv) oxide-Mn(ii) sulfide/poly-2-mercaptoaniline porous network nanocomposite for pseudo-supercapacitors and charge storage
  41. Novel constructed dynamical analytical solutions and conserved quantities of the new (2+1)-dimensional KdV model describing acoustic wave propagation
  42. Tavis–Cummings model in the presence of a deformed field and time-dependent coupling
  43. Spinning dynamics of stress-dependent viscosity of generalized Cross-nonlinear materials affected by gravitationally swirling disk
  44. Design and prediction of high optical density photovoltaic polymers using machine learning-DFT studies
  45. Robust control and preservation of quantum steering, nonlocality, and coherence in open atomic systems
  46. Coating thickness and process efficiency of reverse roll coating using a magnetized hybrid nanomaterial flow
  47. Dynamic analysis, circuit realization, and its synchronization of a new chaotic hyperjerk system
  48. Decoherence of steerability and coherence dynamics induced by nonlinear qubit–cavity interactions
  49. Finite element analysis of turbulent thermal enhancement in grooved channels with flat- and plus-shaped fins
  50. Modulational instability and associated ion-acoustic modulated envelope solitons in a quantum plasma having ion beams
  51. Statistical inference of constant-stress partially accelerated life tests under type II generalized hybrid censored data from Burr III distribution
  52. On solutions of the Dirac equation for 1D hydrogenic atoms or ions
  53. Entropy optimization for chemically reactive magnetized unsteady thin film hybrid nanofluid flow on inclined surface subject to nonlinear mixed convection and variable temperature
  54. Stability analysis, circuit simulation, and color image encryption of a novel four-dimensional hyperchaotic model with hidden and self-excited attractors
  55. A high-accuracy exponential time integration scheme for the Darcy–Forchheimer Williamson fluid flow with temperature-dependent conductivity
  56. Novel analysis of fractional regularized long-wave equation in plasma dynamics
  57. Development of a photoelectrode based on a bismuth(iii) oxyiodide/intercalated iodide-poly(1H-pyrrole) rough spherical nanocomposite for green hydrogen generation
  58. Investigation of solar radiation effects on the energy performance of the (Al2O3–CuO–Cu)/H2O ternary nanofluidic system through a convectively heated cylinder
  59. Quantum resources for a system of two atoms interacting with a deformed field in the presence of intensity-dependent coupling
  60. Studying bifurcations and chaotic dynamics in the generalized hyperelastic-rod wave equation through Hamiltonian mechanics
  61. A new numerical technique for the solution of time-fractional nonlinear Klein–Gordon equation involving Atangana–Baleanu derivative using cubic B-spline functions
  62. Interaction solutions of high-order breathers and lumps for a (3+1)-dimensional conformable fractional potential-YTSF-like model
  63. Hydraulic fracturing radioactive source tracing technology based on hydraulic fracturing tracing mechanics model
  64. Numerical solution and stability analysis of non-Newtonian hybrid nanofluid flow subject to exponential heat source/sink over a Riga sheet
  65. Numerical investigation of mixed convection and viscous dissipation in couple stress nanofluid flow: A merged Adomian decomposition method and Mohand transform
  66. Effectual quintic B-spline functions for solving the time fractional coupled Boussinesq–Burgers equation arising in shallow water waves
  67. Analysis of MHD hybrid nanofluid flow over cone and wedge with exponential and thermal heat source and activation energy
  68. Solitons and travelling waves structure for M-fractional Kairat-II equation using three explicit methods
  69. Impact of nanoparticle shapes on the heat transfer properties of Cu and CuO nanofluids flowing over a stretching surface with slip effects: A computational study
  70. Computational simulation of heat transfer and nanofluid flow for two-sided lid-driven square cavity under the influence of magnetic field
  71. Irreversibility analysis of a bioconvective two-phase nanofluid in a Maxwell (non-Newtonian) flow induced by a rotating disk with thermal radiation
  72. Hydrodynamic and sensitivity analysis of a polymeric calendering process for non-Newtonian fluids with temperature-dependent viscosity
  73. Exploring the peakon solitons molecules and solitary wave structure to the nonlinear damped Kortewege–de Vries equation through efficient technique
  74. Modeling and heat transfer analysis of magnetized hybrid micropolar blood-based nanofluid flow in Darcy–Forchheimer porous stenosis narrow arteries
  75. Activation energy and cross-diffusion effects on 3D rotating nanofluid flow in a Darcy–Forchheimer porous medium with radiation and convective heating
  76. Insights into chemical reactions occurring in generalized nanomaterials due to spinning surface with melting constraints
  77. Influence of a magnetic field on double-porosity photo-thermoelastic materials under Lord–Shulman theory
  78. Soliton-like solutions for a nonlinear doubly dispersive equation in an elastic Murnaghan's rod via Hirota's bilinear method
  79. Analytical and numerical investigation of exact wave patterns and chaotic dynamics in the extended improved Boussinesq equation
  80. Nonclassical correlation dynamics of Heisenberg XYZ states with (x, y)-spin--orbit interaction, x-magnetic field, and intrinsic decoherence effects
  81. Exact traveling wave and soliton solutions for chemotaxis model and (3+1)-dimensional Boiti–Leon–Manna–Pempinelli equation
  82. Unveiling the transformative role of samarium in ZnO: Exploring structural and optical modifications for advanced functional applications
  83. On the derivation of solitary wave solutions for the time-fractional Rosenau equation through two analytical techniques
  84. Analyzing the role of length and radius of MWCNTs in a nanofluid flow influenced by variable thermal conductivity and viscosity considering Marangoni convection
  85. Advanced mathematical analysis of heat and mass transfer in oscillatory micropolar bio-nanofluid flows via peristaltic waves and electroosmotic effects
  86. Exact bound state solutions of the radial Schrödinger equation for the Coulomb potential by conformable Nikiforov–Uvarov approach
  87. Some anisotropic and perfect fluid plane symmetric solutions of Einstein's field equations using killing symmetries
  88. Nonlinear dynamics of the dissipative ion-acoustic solitary waves in anisotropic rotating magnetoplasmas
  89. Curves in multiplicative equiaffine plane
  90. Exact solution of the three-dimensional (3D) Z2 lattice gauge theory
  91. Propagation properties of Airyprime pulses in relaxing nonlinear media
  92. Symbolic computation: Analytical solutions and dynamics of a shallow water wave equation in coastal engineering
  93. Wave propagation in nonlocal piezo-photo-hygrothermoelastic semiconductors subjected to heat and moisture flux
  94. Comparative reaction dynamics in rotating nanofluid systems: Quartic and cubic kinetics under MHD influence
  95. Laplace transform technique and probabilistic analysis-based hypothesis testing in medical and engineering applications
  96. Physical properties of ternary chloro-perovskites KTCl3 (T = Ge, Al) for optoelectronic applications
  97. Gravitational length stretching: Curvature-induced modulation of quantum probability densities
  98. The search for the cosmological cold dark matter axion – A new refined narrow mass window and detection scheme
  99. A comparative study of quantum resources in bipartite Lipkin–Meshkov–Glick model under DM interaction and Zeeman splitting
  100. PbO-doped K2O–BaO–Al2O3–B2O3–TeO2-glasses: Mechanical and shielding efficacy
  101. Nanospherical arsenic(iii) oxoiodide/iodide-intercalated poly(N-methylpyrrole) composite synthesis for broad-spectrum optical detection
  102. Sine power Burr X distribution with estimation and applications in physics and other fields
  103. Numerical modeling of enhanced reactive oxygen plasma in pulsed laser deposition of metal oxide thin films
  104. Dynamical analyses and dispersive soliton solutions to the nonlinear fractional model in stratified fluids
  105. Computation of exact analytical soliton solutions and their dynamics in advanced optical system
  106. An innovative approximation concerning the diffusion and electrical conductivity tensor at critical altitudes within the F-region of ionospheric plasma at low latitudes
  107. An analytical investigation to the (3+1)-dimensional Yu–Toda–Sassa–Fukuyama equation with dynamical analysis: Bifurcation
  108. Swirling-annular-flow-induced instability of a micro shell considering Knudsen number and viscosity effects
  109. Numerical analysis of non-similar convection flows of a two-phase nanofluid past a semi-infinite vertical plate with thermal radiation
  110. MgO NPs reinforced PCL/PVC nanocomposite films with enhanced UV shielding and thermal stability for packaging applications
  111. Optimal conditions for indoor air purification using non-thermal Corona discharge electrostatic precipitator
  112. Investigation of thermal conductivity and Raman spectra for HfAlB, TaAlB, and WAlB based on first-principles calculations
  113. Tunable double plasmon-induced transparency based on monolayer patterned graphene metamaterial
  114. DSC: depth data quality optimization framework for RGBD camouflaged object detection
  115. A new family of Poisson-exponential distributions with applications to cancer data and glass fiber reliability
  116. Numerical investigation of couple stress under slip conditions via modified Adomian decomposition method
  117. Monitoring plateau lake area changes in Yunnan province, southwestern China using medium-resolution remote sensing imagery: applicability of water indices and environmental dependencies
  118. Heterodyne interferometric fiber-optic gyroscope
  119. Exact solutions of Einstein’s field equations via homothetic symmetries of non-static plane symmetric spacetime
  120. A widespread study of discrete entropic model and its distribution along with fluctuations of energy
  121. Empirical model integration for accurate charge carrier mobility simulation in silicon MOSFETs
  122. The influence of scattering correction effect based on optical path distribution on CO2 retrieval
  123. Anisotropic dissociation and spectral response of 1-Bromo-4-chlorobenzene under static directional electric fields
  124. Role of tungsten oxide (WO3) on thermal and optical properties of smart polymer composites
  125. Analysis of iterative deblurring: no explicit noise
  126. Review Article
  127. Examination of the gamma radiation shielding properties of different clay and sand materials in the Adrar region
  128. Erratum
  129. Erratum to “On Soliton structures in optical fiber communications with Kundu–Mukherjee–Naskar model (Open Physics 2021;19:679–682)”
  130. Special Issue on Fundamental Physics from Atoms to Cosmos - Part II
  131. Possible explanation for the neutron lifetime puzzle
  132. Special Issue on Nanomaterial utilization and structural optimization - Part III
  133. Numerical investigation on fluid-thermal-electric performance of a thermoelectric-integrated helically coiled tube heat exchanger for coal mine air cooling
  134. Special Issue on Nonlinear Dynamics and Chaos in Physical Systems
  135. Analysis of the fractional relativistic isothermal gas sphere with application to neutron stars
  136. Abundant wave symmetries in the (3+1)-dimensional Chafee–Infante equation through the Hirota bilinear transformation technique
  137. Successive midpoint method for fractional differential equations with nonlocal kernels: Error analysis, stability, and applications
  138. Novel exact solitons to the fractional modified mixed-Korteweg--de Vries model with a stability analysis
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 31.12.2025 from https://www.degruyterbrill.com/document/doi/10.1515/phys-2025-0238/html
Scroll to top button