Solving an isotropic grey matter tumour model via a heat transfer equation

Sameerah Jamal

doi:10.1515/phys-2025-0120

Article Open Access

Solving an isotropic grey matter tumour model via a heat transfer equation

Sameerah Jamal

Published/Copyright: February 14, 2025

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

From the journal Open Physics Volume 23 Issue 1

Abstract

The prevalence and growth characteristics of glioma tumours in human tissues are often modelled by a parabolic partial differential equation. It is essential to analyse tumour growth factors to establish mathematical benchmarks in understanding cancer progression. In this tumour study, we consider factors such as the tumour proliferation rates and the anisotropy of the spatial diffusion tensor. We aim to solve the resulting model together with its initial condition, to provide realistic biological predictions into the mechanism of cancer invasion, metastasis and life expectancy after diagnosis. The solutions are inspired by transformations that we propose to convert the tumour model into a heat equation. A key component in understanding the physics of cancer phenomena, is through obtaining precise solutions. Lie symmetries provide the mechanism to obtain exact solutions.

Keywords: brain tumour; symmetries; initial conditions

1 Introduction

Tumours of the brain cause significant neurological problems and impact life expectancy dramatically. In particular, a glioma is a type of tumour that originates in the glial cells of the brain or spine. They are known to be aggressive, highly invasive, and are among the most common type afflicting human populations [1]. Unfortunately such tumours are heterogeneous and exhibit distinct molecular profiles – they vary widely in terms of growth rate and prognosis. Comprehensive research is ongoing on tumour biology and behaviour. The end goal is to find tools for prevention, a resistance to worsening health, or treatment mechanisms to avoid fatalities.

The mathematical modelling of tumours plays a crucial dynamic role in understanding tumour growth predictions and treatment response [2]. Mathematics offers an inexpensive approach to analyse tumour size and has applications in cancer treatment and surgical planning. Reaction–diffusion (or proliferative–invasive) equations offer an excellent baseline for modelling tumour growth.

It is true to state that mathematical models of tumours have limitations. Some tumour facets may not be accounted for in any given model, for example, the effects of oxygenation and nutrient concentration for cell hypoxia, the advance of necrosis, age, genetics, and/or environmental factors. However, despite these drawbacks, the exact solutions of such models are indispensable [3–8]. We discuss several reaction–diffusion models, mainly concentrating on the spread of untreated gliomas. One sees a general perspective of how parameters are extracted from medical modalities to encompass biological knowledge, and the proposed working models to simulate and optimise tumour investigations.

To our knowledge, a study of our main equation has not appeared elsewhere, in any prior mathematical context. For this reason, a discussion of its place among other tumour models is discussed in Section 2. In fact, despite the model being linear, it is non-trivial to solve it subject to initial data. This is precisely what our work has achieved, in a first and original study. It is also new and noteworthy that we prove that such a model is reducible to the classical heat equation.

Other parabolic equations, have been actively studied by symmetries, for example, the Vasicek model [9], the constant elasticity of variance model [10], the Kolmogorov equations [11], the time-dependent Black-Scholes [12], and many others.

We align our study to the existing literature through comparison with known results in the study of Burgess et al. [2]. Other leading mathematical analysis for tumour growth are the works of Woodward et al. [5,13,14]. Our approach has been cross-validated with these studies, ensuring that the solutions are reliable. We adopted the well-known conventions, such as time data, from the studies by Tracqui et al. [5] and Burgess et al. [2] to capture consistent and valid theoretical predictions, but we extend the existing results, providing insights into grey matter tumours specifically.

An important aspect of analysing problems in physics is deriving exact solutions to differential equations. In this regard, a mathematical framework provides powerful tools to effectively address and solve a wide range of physical problems. For example Shah et al. [15] discussed disease models in the field of physics, while under the mathematics of fractional derivatives.

The organisation of this investigation is as follows. Section 2 defines the basic assumptions of the model. In Section 3, we provide transformations that render the isotropic grey matter glioma model into the one-dimensional parabolic heat equation, followed by the determination of exact solutions by two vital methods. The first method is the standard Lie invariant method which includes the optimal system of one-dimensional subalgebras, and a second approach, is a solution of the initial-value problem. Section 4 provides the mathematical inferences of our study. The conclusion is given in Section 5.

2 The model

Suppose that the cellular flux obeys Fick’s law with proliferation descriptive of an exponential growth, so that we have the reaction–diffusion model [2]

∂ u ( x , t ) ∂ t = b ∇ 2 u + p u ,

where u ( x , t ) represents tumour cell concentration at radius x and time t , b is the constant diffusion coefficient that accounts for tumour invasiveness, and p is the tumour cell proliferation rate.

Experimental data from rats demonstrated that glioma cells disperse differently depending on its location in the brain matter, that is, grey vs white matter [16,17]. This spatial variation may be encompassed by the model proposed by Swanson et al. [18], which includes the spatial dependence of the diffusion coefficient, i.e. with b ( x ) , we have

(1) ∂ u ( x , t ) ∂ t = ∇ ⋅ ( b ∇ u ) + p u .

The two tissues found in the brain have distinct functions and characteristics. Abnormal growths may develop in either tissue, but this impacts modes of diagnosis and treatment. Gliomas in grey matter show symptoms that include seizures, headaches, and even cognitive issues depending on the tumour grade, location, and size. These factors also influence treatment aspects like surgery, radiation, and chemotherapy.

The diffusive term in equation (1) exhibits tensor properties, where grey matter is mostly isotropic while white matter is highly anisotropic [19]. Thus, in the case of grey matter, we have the model

(2) ∂ u ( x , t ) ∂ t = b ∇ 2 u + ∇ b ⋅ ∇ u + p u ,

where ∇ 2 is the Laplacian in a spherical coordinates system. The dynamics of this invasive and diffusive model translates to the parabolic equation

(3) ∂ u ( x , t ) ∂ t − b ( x ) ∂ 2 ∂ x ∂ x u ( x , t ) − 2 b ( x ) x + b ( x ) ∂ ∂ x u ( x , t ) − p u ( x , t ) = 0 , x ∈ R , t > 0 .

We may impose the initial condition (IC),

(4) u ( x , 0 ) = ζ ( x ) ,

in a three-dimensional unbounded domain. A typical IC includes, say N 0 , a constant related to the initial number of tumour cells. This model offers a solution for untreated gliomas and one of its advantages is that it contains a few parameters, for which patient data are easily extracted. On a computational level, we will propose simple ways to solve the model.

The primary contribution of this work is that we offer a poignant treatment of an important equation in medical biology. By simplifying a significant glioma model, we are able to find exact solutions and extract important theoretical observations predicted by the model.

3 Transformations and solutions

We prove how to transform (3) to the classical heat equation by an aptly chosen change in variables. This change provides a mathematical tool to solve (3) via interesting features of the classical heat equation. The discovery of such transformations are inspired by Lie’s [20] technique that allows for the classification of some equations to simple equations. However, this scope of his work is not trivial and not well-known. This is our approach below, where we seek simple transformations that are able to incorporate initial values.

But first, we require a meaningful connection between the diffusion and proliferation. Consider a mathematical expression for the diffusion coefficient, subject to the proliferation rate p . The Fisher approximation [21] is commonly applied in tumour modelling, to establish that a travelling wave solution propagates with a terminal velocity. It is given by

(5) v 2 = 4 p b ,

where v is the velocity measured at x ∕ n , where n refers to the number of days.

Hence, we prove the following result.

Theorem 1

Eq. (3) is converted to

(6) ω t − ω y y = 0 , ω ( y , t ) ∈ C ∞ ( R × ( 0 , ∞ ) ) ,

which is the 1 + 1 heat equation, under the spatial diffusion parameter

b ( x ) = v 2 4 p ,

coupled with the transformations

(7) y = 2 n p ln ( x ) ,

followed by

(8) u ( y , t ) = ω ( y , t ) exp e 3 y 4 n p − p t + 9 t 16 p n 2 .

Proof

An application of (7) renders Eq. (3) to the form

(9) ∂ ∂ t u ( y , t ) − ∂ 2 ∂ y 2 u ( y , t ) − 3 ∂ ∂ y u ( y , t ) 2 n 1 p − p u ( y , t ) = 0 .

Thereafter, the transformation (8) converts (9) to the heat equation (6).□

A simple extension of this theorem and its transformations to the IC (4) yields the following result.

Lemma 2

The invertible transformations of Theorem 1 converts IC (4) to

(10) ω ( y , 0 ) = exp 3 y 4 n p ζ ( y ) .

The above choice for the diffusion parameter is a biologically significant one, as this is generally how diffusion depends on proliferation. There are two possible paths to the solution of (3). First, we solve using the optimal system of subalgebras that provides non-equivalent classes of invariant solutions. Second, we solve the initial value problem by constructing a symmetry that incorporates the IC. Both approaches are important for the mathematical analysis of grey matter gliomas.

3.1 Exact solution via symmetries

The Lie point symmetries of (6) are well established, they are as follows:

(11) X 1 = ∂ ∂ y , X 2 = ∂ ∂ t , X 3 = ω ∂ ∂ ω , X 4 = y ∂ ∂ y + 2 t ∂ ∂ t , X 5 = 2 t ∂ ∂ y − y ω ∂ ∂ ω , X 6 = 4 t y ∂ ∂ y + 4 t 2 ∂ ∂ t − ( y 2 + 2 t ) ω ∂ ∂ ω , X α = α ( y , t ) ∂ ∂ ω .

The optimal one-dimensional subalgebra based on the above generators are [22] (p. 206)

X 1 , X 2 + c X 3 , X 2 − X 5 , X 2 + X 6 + c X 3 , X 4 + 2 c X 3 ,

where c ∈ R . Note that, compared to [22], we have omitted the subalgebra X 3 as it is not useful and of course, the subalgebra X 2 + X 5 is easily obtained from a discrete symmetry mapping of X 2 − X 5 . The invariant solutions based on the above subalgebras are split into five cases.

Case (i) X 1

This subalgebra yields the invariants m = t , ω = z ( m ) , which can be substituted into (6) to find a reduced equation that may be solved for z ( m ) and hence ω ( y , t ) .

In this regard, we obtain the exact solution of (6) as

(12) ω ( y , t ) = C 1 ,

where C 1 denotes an arbitrary constant hereunder. A reversal of the transformations from Theorem 1 gives the exact solution for (3), viz.

(13) u ( x , t ) = C 1 e p t e − 9 t 16 p n 2 x − 3 2 .

Case (ii) X 2 + c X 3

This subalgebra yields the invariants m = y , ω = z ( m ) e c t , and following the same procedure, an exact solution of (6) is

(14) ω ( y , t ) = ( C 1 e c y + C 2 e − c y ) e c t ,

where C 2 is also an arbitrary constant henceforth, so that from Theorem 1, we have the exact solution for (3), viz.

(15) u ( x , t ) = ( C 1 x 2 c n p + C 2 x − 2 c n p ) × e 1 16 p n 2 − 24 ln ( x ) p n 2 + 16 t − 9 16 + p ( c + p ) n 2 .

For c = 0 , we have the solution for (6) as

(16) ω ( y ) = C 1 y + C 2 ,

and Theorem 1 gives the exact solution for (3), viz.

(17) u ( x , t ) = ( 2 C 1 n p ln ( x ) + C 2 ) e − − 16 p 2 t n 2 + 24 ln ( x ) p n 2 + 9 t 16 p n 2 .

Case (iii) X 2 − X 5

The invariants of this case are m = y + t 2 , ω = z ( m ) e y t + 2 t 3 3 . An application of the invariants of this subalgebra produces the exact solution of (6) as

(18) ω ( y , t ) = ( C 1 Ai ( t 2 + y ) + C 2 Bi ( t 2 + y ) ) e y t + 2 t 3 3 ,

where Ai ( z ) and Bi ( z ) are the Airy Ai and Airy Bi functions, respectively. A reversal of the transformations from Theorem 1 gives the exact solution for (3), namely,

(19) u ( x , t ) = ( C 1 Ai ( t 2 + 2 n p ln ( x ) ) + C 2 Bi ( t 2 + 2 n p ln ( x ) ) ) × e 1 48 p n 2 ( 96 t n 3 p 3 ∕ 2 ln ( x ) + 32 t 3 p n 2 + 48 p 2 t n 2 − 72 ln ( x ) p n 2 − 27 t ) .

Case (iv) X 2 + X 6 + c X 3

The invariants of this case are m = 4 t 2 + 1 4 y 2 , ω = z ( m ) e y 2 8 t 2 + 2 − c ( 4 t 2 + 1 ) y 2 arctan 1 2 t − 2 t 1 y .

Thus, this subalgebra gives us the exact solution of (6), i.e.,

(20) ω ( y , t ) = C 1 M i 4 c , 1 4 i y 2 4 t 2 + 1 + C 2 W i 4 c , 1 4 i y 2 4 t 2 + 1 y × e 1 8 t 2 + 2 ( − 4 t 2 − 1 ) c arctan 1 2 t − 2 t y 2 ,

where W μ , ν ( z ) and M μ , ν ( z ) are Whittaker functions.

In this case, a reversal of the transformations from Theorem 1, gives the exact solution for (3), viz.

(21) u ( x , t ) = 2 2 C 1 M i 4 c , 1 4 4 i n 2 p ( ln ( x ) ) 2 4 t 2 + 1 + C 2 W i 4 c , 1 4 4 i n 2 p ( ln ( x ) ) 2 4 t 2 + 1 × e − 32 c p n 2 t 2 + 1 4 arctan 1 2 t − 64 ( ln ( x ) ) 2 n 4 p 2 t − 96 p n 2 t 2 + 1 4 ln ( x ) + ( 64 t 3 + 16 t ) p 2 n 2 − 36 t 3 − 9 t ( 64 t 2 + 16 ) p n 2 × 1 n p ln ( x ) .

For c = 0 , we find that

(22) ω ( y , t ) = 2 1 y C 1 J − 1 4 y 2 8 t 2 + 2 + C 2 Y − 1 4 y 2 8 t 2 + 2 e − t y 2 4 t 2 + 1 1 4 t 2 + 1 y 2 ,

where J v ( x ) and K v ( x ) are the Bessel functions of the first and second kind, respectively. Hence, an invariant solution to (3) is

(23) u ( x , t ) = 2 2 n p ln ( x ) C 1 J − 1 4 2 n 2 p ( ln ( x ) ) 2 4 t 2 + 1 + C 2 Y − 1 4 2 n 2 p ( ln ( x ) ) 2 4 t 2 + 1 × e 1 16 − 64 t n 4 p 2 ( ln ( x ) ) 2 − 96 ( t 2 + 1 ∕ 4 ) p n 2 ln ( x ) + 64 n 2 p 2 t 3 + 16 p 2 t n 2 − 36 t 3 − 9 t ( 4 t 2 + 1 ) p n 2 × 1 4 t 2 + 1 n 2 p ( ln ( x ) ) 2 .

Case (v) X 4 + 2 c X 3

Here the invariants are m = y 1 t , ω = z ( m ) t c . The symmetry invariants of the subalgebra produce the exact solution of (6) as

(24) ω ( y , t ) = e − y 2 4 t t y 2 c − 1 2 U c + 1 , 3 2 , y 2 4 t C 2 + M c + 1 , 3 2 , y 2 4 t C 1 y 2 c ,

where U ( μ , ν , z ) and M ( μ , ν , z ) are Kummer’s functions.

Finally, a reversal of the transformations of Theorem 1 gives the exact solution for (3), viz.

(25) u ( x , t ) = 2 e − 1 16 ( 4 ln ( x ) p n 2 − 4 n p t + 3 t ) ( 4 ln ( x ) p n 2 + 4 n p t + 3 t ) t p n 2 p ln ( x ) n × U 1 + c , 3 2 , n 2 p ( ln ( x ) ) 2 t C 2 + M 1 + c , 3 2 , n 2 p ( ln ( x ) ) 2 t C 1 t − 1 2 + c .

3.2 Initial-value solution via symmetries

To achieve the desired accuracies of solutions and simulate the complex behaviour of tumour growth over time, IC’s are crucial in solution processes. The heat equation is a perfect choice for study as it admits the heat kernel [23,24]. We demonstrate a technique to solve a Cauchy problem for (6) that involves Lie symmetries [25–28]. The main aim is to solve the original equation (3) subject to IC (4).

We recall that the fundamental solution of (6) is

(26) A ( y , t ) ≔ 1 4 π t e − y 2 4 t , ( y ∈ R , t > 0 ) , 0 , ( y ∈ R , t < 0 ) ,

which is singular at (0,0).

The symmetry generators of the heat Eq. (6) may be written as

(27) X = ξ ( y , t , ω ) ∂ ∂ y + η ( y , t , ω ) ∂ ∂ t + ϕ ( y , t , ω ) ∂ ∂ ω ,

so that the invariant surface condition (ISC) [22] is

(28) ξ ω y + η ω t − ϕ = 0 ,

where it is imposed that t = 0 and F ( y ) = ω ( y , 0 ) . Hence, the ISC becomes

(29) α ( y , 0 ) = ( c 1 y 2 + c 3 y − c 5 ) F ( y ) + ( c 2 y + c 4 ) F ′ ( y ) + c 6 F ″ ( y ) .

Eq. (29) is an IC (less restrictive) [29]. We now demonstrate a solution – more solutions exist and can be found by the same process.

We emphasise that the function α ( y , t ) is also a solution to (6), so we may design an initial problem for the heat equation, viz.

(30) α t − α y y = 0 , in R × ( 0 , ∞ ) , α ( y , 0 ) , on R × { t = 0 } .

If one can solve (30), we will find α ( y , t ) , which would give us a new symmetry that solves the original model (3) subject to its IC (4).

Let c 4 = 1 , c 1 = c 2 = c 3 = c 5 = c 6 = 0 (other solutions are possible from other c i ). Hence,

α ( y , 0 ) = F ′ ( y )

and

(31) X = ∂ ∂ y + α ( y , t ) ∂ ∂ ω .

Thus, via the ISC (28), we obtain that the solution to (6) is

(32) ω ( y , t ) = ∫ α ( y , t ) d y + H ( t ) .

We let H ( t ) = 0 for simplicity and use Theorem 1 to obtain an exact solution of (3) subject to its IC (4).

Let us consider a specific IC.

Case (vi) Consider the logarithmic growth function ζ ( x ) = N 0 ln ( x ) , which describes an initial rapid growth.

By the procedure described above, we find

(33) α ( y , t ) = N 0 e 3 ( 4 n p y + 3 t ) 16 n 2 p ( 8 n 2 p + 6 n p y + 9 t ) 16 n 3 p 3 ∕ 2 ,

and the heat equation’s solution is then

(34) ω ( y , t ) = N 0 e 3 ( 4 n p y + 3 t ) 16 n 2 p ( 2 n p y + 3 t ) 4 n 2 p .

Finally, the equation for grey matter gliomas has solution, subject to (4), as

(35) u ( x , t ) = e p t N 0 ( 3 t + 4 n 2 p ln ( x ) ) 4 n 2 p .

If we let t = 0 , we see that (35) is a solution of (3), subject to IC (4).

4 Mathematical analysis

In this section, we extract significant insights from the exact solutions. In this regard, some assumptions are necessary. First, we analyse high-grade tumours, characterised by high proliferation, at the value p = 0.012 [2]. This grade of tumour is known for fast and extensive growth, such that patients do not exhibit many initial symptoms. Active tumour cells invade the surrounding tissue, where growth resembles an explosion, i.e. a fast growing front wave seen on MRI scans.

The highest concentration of cells is near the centre x = 0 in most cases. The tumour grows from a point cell value N 0 = 1.2 × 1 0 6 , the radius x = 1.5 cm is equivalent to the time of diagnosis of the tumour ( t i ), a radius of x = 3 cm is equivalent to the time of death ( t d ) and a critical cell density value is 8.0 × 1 0 6 cells/cm 3 [2]. Above the critical cell density, the glioma is detectable by scans.

We present selected results from our cases in the figures and tables that follow. Figures 1 and 2 display the behaviour of cell density vs radius, for Cases (i)–(vi), where time of diagnosis is t i = 1.35 and time of death is t d = 1.84 (time data taken from [5] and [2]).

$Figure 1 Tumour cell density vs radius: (a) Case (i) with parameter selection C 1 = N 0 {C}_{1}={N}_{0} ; (b) Case (ii) with parameter selection C 1 = C 2 = N 0 {C}_{1}={C}_{2}={N}_{0} and c = 0 c=0 ; (c) Case (iii) with parameter selection C 1 = N 0 , C 2 = 0 {C}_{1}={N}_{0},{C}_{2}=0 ; and (d) Case (iv) with parameter selection C 1 = N 0 , C 2 = 0 {C}_{1}={N}_{0},{C}_{2}=0 .$

Figure 1

Tumour cell density vs radius: (a) Case (i) with parameter selection C 1 = N 0 ; (b) Case (ii) with parameter selection C 1 = C 2 = N 0 and c = 0 ; (c) Case (iii) with parameter selection C 1 = N 0 , C 2 = 0 ; and (d) Case (iv) with parameter selection C 1 = N 0 , C 2 = 0 .

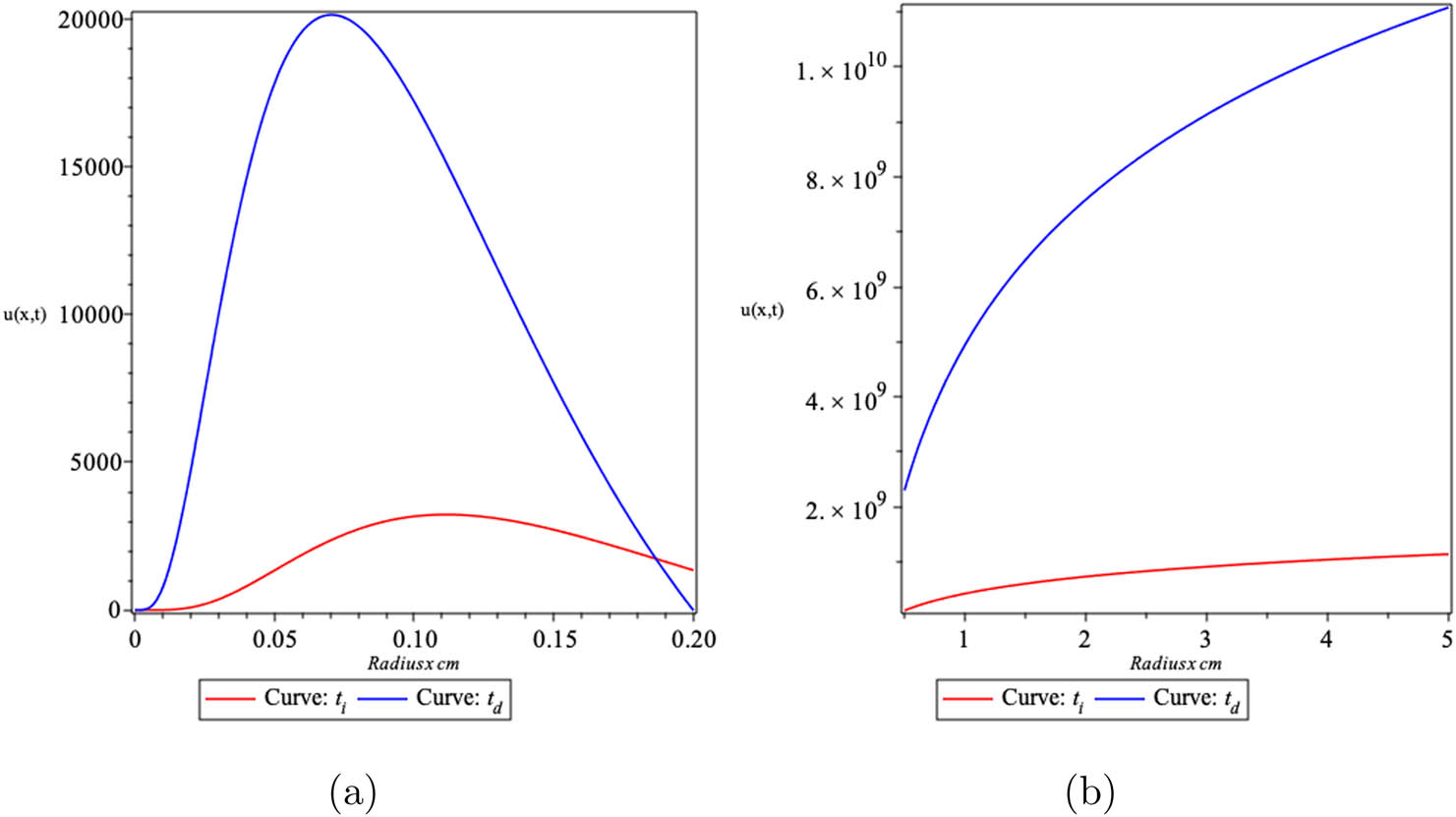
$Figure 2 Tumour cell density vs radius: (a) Case (v) with parameter selection C 1 = N 0 , C 2 = 0 {C}_{1}={N}_{0},{C}_{2}=0 and c = ‒ 2 c=‒2 and (b) Case (vi).$

Figure 2

Tumour cell density vs radius: (a) Case (v) with parameter selection C 1 = N 0 , C 2 = 0 and c = ‒ 2 and (b) Case (vi).

In Table 1, we determine the time of diagnosis and death given the critical cell density and the radii of x = 1.5 cm and x = 3 cm. This yields the predictions for survival years between diagnosis and death. We use the same parameter settings as in Figures 1 and 2, with the exception of c = 0 for Case (v).

Table 1

Expected survival of an untreated high-grade glioma

	(i)	(ii)	(vi)
t i	0.65	0.47	0.36
t d	0.92	0.74	0.50
Survival (years)	0.27	0.27	0.14

The expected cancer survival rate is vital in determining treatment options: side effects vs quality of life. Knowing the realistic survival can help patients prepare emotionally and realistically for the future.

Patients with a higher likelihood of survival may receive more aggressive treatments, while those with a lower chance of survival might focus on palliative care or supportive therapies.

In Table 2, we report on the tumour cell density under a high-grade glioma. For these results, we again utilise the time of diagnosis t i = 1.35 and time of death t d = 1.84 .

Table 2

Cell density under time of diagnosis and death

	(i)	(ii)	(iii)	(iv)	(v)	(vi)
Density at t i	1.19 × 1 0 8	2.37 × 1 0 8	1.34 × 1 0 6	7.67 × 1 0 6	8.19 × 1 0 7	6.04 × 1 0 8
Density at t d	2.78 × 1 0 8	5.55 × 1 0 8	1.54 × 1 0 6	8.69 × 1 0 6	3.75 × 1 0 8	9.13 × 1 0 9

Cell density constitutes vital data in experimental research assisting to replicate the tumour microenvironment more accurately. High cell density in tumours impact oxygen and nutrient levels. These microenvironmental conditions often interact with tumour growth and therapy response.

Some insights observed from the figures and tables are as follows. In Table 1, as expected, the high-grade gliomas have a very short life expectancy. The survival years reported by Tracqui et al. [5] and also applied by Burgess et al. [2], for high-grade gliomas with a constant diffusion coefficient is 0.49 years. Our expected survival is lower under a spatial diffusion coefficient, grey matter tumour model.

We observe from Figures 1 and 2, which provide the spatial profile of tumour cells at the time of diagnosis and death, that the cell densities around the centre approach between 10 and 10,000 times the critical cell density for most cases, with the exception of Cases (iii) and (v). In the former case, density around the centre is close to the critical cell density value but in the latter case, we see lower densities which would increase the difficulty in diagnosis.

From Table 2, we note that Case (iv) has cell density close to the critical cell density value, while most other cases predict 10- to 1,000-fold cell densities. We highlight from Table 1 that imposing the IC has a significant impact – it lowers life expectancy.

5 Conclusion

Gliomas can be challenging to diagnose accurately, especially within early stages. Research into glioma biology and the development of new diagnostic techniques are influenced by cell density studies. Accurate detection impacts treatment interventions and life expectancy.

Exact solutions to tumour models are pivotal in unravelling the complexities of gliomas, with symmetry analysis providing new and significant information in terms of (1) life expectancy/growth and (2) cell density. We highlight the correlation between the outcomes from the symmetry analysis and the underlying physics of diagnosis and tumour growth patterns:

Our contribution provides precise predictions in times of diagnosis, survival, and death for grey matter gliomas. The study’s innovative use of symmetries provides a breakthrough in proving lower life expectancy for isotropic grey matter tumours vs the full brain reported in the study by Tracqui et al. [5].
Symmetry analysis represents a major advancement in the understanding of the diagnosis capability of this model. Cell densities (Table 2) are comparable to findings reported by Burgess et al. [2], indicating grey matter tumours are mostly, as easily diagnosed as white plus grey matter brain tumours.
The dual relations between cell density and radius in the spatial profiles of Figures 1 and 2 support this notion, with cell density numbers significantly over the critical value, thus enabling tumour detection.
As a first, the addition of logarithmic growth in the IC of the model offers a reshaping of the way we model growth conditions, with lower survival predicted under this type of growth.

This is the first study of model (3), a grey matter isotropic model, hence it is the benchmark for any subsequent mathematical analysis. Our findings are robust and mathematically sound, as they are derived from a comprehensive analysis, ensuring the reliability of the results. Moreover the conclusions drawn implement Fishers’ approximation for the underlying model, as substantiated in the literature. This work represents some crucial contributions:

The novel approach presented offers a fresh perspective on solution approaches, by introducing new transformations to convert a tumour model to the simple heat equation. The transformations presented are tractable, and therefore, available to wide audiences.
Our conclusions are of practical importance, as they extend current theories and have potential implications for real-world medical theories.
The study of a specialised topic, such as grey matter tumours, is expected to stimulate further research and exploration in new avenues.

Mathematics and physics are deeply interconnected. In future, the theory presented here can be applied to similar models, offering effective methods for solving a broad spectrum of physical problems.

Acknowledgments

Opinions expressed and conclusions arrived at are those of the authors and are not necessarily to be attributed to the CoE-MaSS.

Funding information: The author states no funding involved.
Author contributions: The author has accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The author states no conflict of interest.
Data availability statement: All data generated or analysed during this study are included in this published article.

References

[1] Alvord EC. Shaw CM in the pathology of the aging human nervous system. Philadelphia: Lea & Febiger; 1991. Search in Google Scholar

[2] Burgess PK, Kulesa PM, Murray JD, Alvord EC. The interaction of growth rates and diffusion coefficients in a three-dimensional mathematical model of gliomas. J Neuropath Exp Neur. 1997;56:704–13. 10.1097/00005072-199706000-00008Search in Google Scholar

[3] Wein L, Koplow D. Mathematical modeling of brain cancer to identify promising combination treatments. Preprint, D Sloan School of Management. Cambridge, MA, USA: MIT. 1999. Search in Google Scholar

[4] Moyo S, Leach PGL. Symmetry methods applied to a mathematical model of a tumour of the brain. Proc. Inst. Math. NAS of Ukraine. 2004;50:204–10. Search in Google Scholar

[5] Tracqui P, Cruywagen GC, Woodward DE, Bartooll GT, Murray JD, Alvord EC. A mathematical model of glioma growth: the effect of chemotherapy on spatio-temporal growth. Cell Prolif. 1995;28:17–31. 10.1111/j.1365-2184.1995.tb00036.xSearch in Google Scholar PubMed

[6] Cruywagen GC, Woodward DE, Tracqui P, Bartoo GT, Murray JD, Alvord EC. The modelling of diffusive tumours, J Biol Syst. 1995;3:937–45. 10.1142/S0218339095000836Search in Google Scholar

[7] Jamal S. Prototype gliomas: Invariant solutions and expected survival times. Discrete Contin Dyn Syst - S. 10.3934/dcdss.2024113. Search in Google Scholar

[8] Swanson KR, Bridge C, Murray JD, Alvord EC. Virtual and real brain tumours: Using mathematical modeling to quantify glioma growth and invasion. J Neurol Sci. 2003;216:1–10. 10.1016/j.jns.2003.06.001Search in Google Scholar PubMed

[9] Sinkala W, Leach PGL, O’Hara JG. Embedding the Vasicek model into the Cox-Ingersoll-Ross model. Math Methods Appl Sci. 2011;34(2):152–9. 10.1002/mma.1342Search in Google Scholar

[10] Bakkaloglu A, Aziz T, Fatima A, Mahomed FM, Khalique CM. Invariant approach to optimal investment-consumption problem: the constant elasticity of variance (CEV) model. Math Methods Appl Sci. 2017;40(5):1382–95. 10.1002/mma.4060Search in Google Scholar

[11] Bluman GW, Shtelen V. Nonlocal transformations of Kolmogorov equations into the backward heat equation. J Math Anal Applic. 2004;291:419–37. 10.1016/j.jmaa.2003.11.028Search in Google Scholar

[12] Naz R, Johnpillai AG. Exact solutions via invariant approach for Black-Scholes model with time-dependent parameters. Math Meth Appl Sci. 2018;41:4417–27. 10.1002/mma.4903Search in Google Scholar

[13] Woodward DE, Cook J, Tracqui P, Cruywagen GC, Murray JD, Alvord EC. A mathematical model of glioma growth: the effect of extent of surgical resection. Cell Prolif. 1996;29(6):269–88. 10.1111/j.1365-2184.1996.tb01580.xSearch in Google Scholar PubMed

[14] Cook J, Woodward DE, Tracqui P, Murray JD. Resection of gliomas and life expectancy. J Neuro-Oncol. 1995;24(4):131–5. Search in Google Scholar

[15] Shah K, Ahmad I, Shafiullah, Mukheimer A, Abdeljawad T, Jeelani MB. On the existence and numerical simulation of Cholera epidemic model. Open Phys. 2024;22:20230165. 10.1515/phys-2023-0165Search in Google Scholar

[16] Chicoine MR, Silbergeld DL. Assessment of brain tumour cell motility in vivo and in vitro. J Neurosurg. 1995;82:615–22. 10.3171/jns.1995.82.4.0615Search in Google Scholar PubMed

[17] Giese A, Kluwe L, Laube B, Meissner H, Berens ME, Westphal M. Migration of human glioma cells on myelin. Neurosurgery 1996;38:755–64. 10.1227/00006123-199604000-00026Search in Google Scholar

[18] Swanson KR, Alvord EC, Murray JD. A quantitative model for differential motility of gliomas in grey and white matter. Cell Prolif. 2000;33:317–29. 10.1046/j.1365-2184.2000.00177.xSearch in Google Scholar PubMed PubMed Central

[19] Martín-Landrove M. Reaction–diffusion models for glioma tumour growth. arXiv:1707.09409v1. Search in Google Scholar

[20] Lie S. On integration of a class of linear partial differential equations by means of definite integrals. Arch Math Naturvidensk 1881;5:328–58. (German) Search in Google Scholar

[21] Fisher RA. The wave of advance of advantageous genes. Ann Eugenics. 1937;7:353–69. 10.1111/j.1469-1809.1937.tb02153.xSearch in Google Scholar

[22] Olver PJ. Applications of lie groups to differential equations. 2nd edition, New York: Springer; 1993. 10.1007/978-1-4612-4350-2Search in Google Scholar

[23] Evans LC. Partial differential equations. Graduate Studies in Mathematics. 2nd ed. Vol 19. Rhode Island: American Mathematical Society; 2010. 10.1090/gsm/019Search in Google Scholar

[24] Tikhonov AN. Uniqueness theorems for the heat equation. Dokl Akad Nauk SSSR 1935;1:294–300. (In Russian and French)Search in Google Scholar

[25] Champala R, Jamal S, Khan S. Fractional pricing models: transformations to a heat equation and Lie symmetries. Fractal Fract. 2023;7:632. 10.3390/fractalfract7080632Search in Google Scholar

[26] Jamal S, Maphanga R. A progressive approach to solving a CEV model via symmetry invariant surface conditions. AIMS Math. 2024;9(2):4326–36. 10.3934/math.2024214Search in Google Scholar

[27] Maphanga R, Jamal S. A terminal condition in linear bond-pricing under symmetry invariance. J Nonlinear Math Phys. 2023;30:1295–304. 10.1007/s44198-023-00132-6Search in Google Scholar

[28] Jamal S, Champala R, Khan S. Lie symmetries and the invariant solutions of the fractional Black-Scholes equation under time-dependent parameters. Fractal Fract. 2024;8:269. 10.3390/fractalfract8050269Search in Google Scholar

[29] Goard J. Noninvariant boundary conditions. Appl Anal. 2003;82:473–81. 10.1080/0003681031000109639Search in Google Scholar

Received: 2024-07-29

Revised: 2024-12-20

Accepted: 2025-01-21

Published Online: 2025-02-14

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/phys-2025-0120

Keywords for this article

brain tumour; symmetries; initial conditions

Creative Commons

BY 4.0