Startseite Improved GA for construction progress and cost management in construction projects
Artikel Open Access

Improved GA for construction progress and cost management in construction projects

  • Xudong Wang EMAIL logo
Veröffentlicht/Copyright: 28. August 2025
Artikel downloaden (PDF)
Veröffentlichen auch Sie bei De Gruyter Brill
Manuskript einreichen Informationen für Autor*innen
Nonlinear Engineering
Aus der Zeitschrift Nonlinear Engineering Band 14 Heft 1

Abstract

The construction progress and cost management (CPCM) of construction projects are key areas that need to be focused on when formulating construction plans and conducting on-site commands. A CPCM method is proposed based on the standard genetic algorithm. During the process, a serial operation strategy is introduced, a project valuation function is defined, and a CPCM resource library is constructed. The tangent function is used to simulate the key relationships in the construction process, and finally, the construction progress and cost are compressed and optimized. The experimental results indicate that in optimal fitness tests on the construction engineering cost standards (CECS) dataset, the proposed method reaches the upper limit of 20.9 in just 23 generations, 66.67% faster than multi-stage genetic algorithm’s (MGA’s) 72 generations and 51.06% faster than quantum genetic algorithm’s (QGA’s) 47 generations. For the building engineering dataset (BED) dataset, it achieves the upper limit of 21.2 in 30 generations, 33.33% faster than MGA’s 45 generations and 49.18% faster than QGA’s 61 generations. In MSE change tests, the proposed method’s MSE fluctuates within a range of 0.04 after 22 and 23 generations for the CECS and BED datasets, respectively, which is more stable than MGA and QGA. Additionally, when the number of engineering steps increases from 5 to 25, the calculation time of the proposed method increases by less than 30 s, demonstrating higher computational efficiency than that of MGA and QGA. When conducting cost compression, the research method generates a plan that reduced construction costs by 230 k yuan. This indicates that the research method has good computational efficiency and can effectively generate the reference of project construction cost management plans.

Keywords: construction progress; cost management; genetic algorithm; serial operation; multi-task scheduling

1 Introduction

In construction projects, construction progress and cost management (CPCM) are crucial tasks, and effective schedule cost management can improve project efficiency and economy, reduce cost and time waste [1,2]. The complexity of construction projects leads to the impact of multiple factors on construction progress and costs, such as resource allocation, task priority, and duration constraints, making it difficult to accurately plan and manage [3]. Traditional methods have certain limitations when considering interdependence and resource constraints between tasks, which cannot fully solve practical problems [4]. Genetic algorithm (GA) is an optimization algorithm based on biological evolution theory. It searches for the optimal solution by simulating the process of natural selection, crossover, and mutation [5]. The use of serial operations (SOs) and project valuation functions can comprehensively consider construction progress and costs, ensuring that the project is completed within a reasonable time and cost range. In this context, a project CPCM method based on improved GA is proposed to provide feasible technical references for the construction industry. The innovations of the research method are as follows. By introducing a SO strategy, the problems of a large initial population and a single coding method in traditional GAs have been avoided. The researchers defined the project evaluation function, highlighting the advantages of each objective in the chromosome, and constructed a resource library for construction progress and cost control, which improved the coordination efficiency when multiple tasks were carried out in parallel. The earliest possible start time and the earliest completion time of the task are obtained by decoding the chromosomes, with the goal of minimizing the total duration of the task. Meanwhile, the GA is improved by using multi-task scheduling (MTS) to preserve the optimal strategy and reduce the error probability. Furthermore, the genetic operation is completed by adopting the idea of discrete crossover operators, without the need for chromosome repair. The relative positions of the parents in each working cycle are retained, and the efficiency of the algorithm is improved. Finally, the tangent function is used to simulate the relationship between the project quality reliability and the subsystem cost during the construction process, and to construct the construction progress and cost optimization model.

The research mainly consists of four parts. The first part discusses and summarizes the current CPCM methods, as well as the relevant research results of GA. The second part mainly designs a project CPCM method based on the improved GA. The third part is an analysis of the effectiveness of the research method. The final part is a summary and discussion of the entire text.

2 Related works

Construction engineering is an indispensable link in the development of urban hardware facilities. With the growth of construction engineering, more scholars have realized the importance of project CPCM technology. Some scholars have conducted relevant research on project CPCM techniques. Alizadehsalehi and other scholars proposed a management framework based on digital twins to address the issue of automated construction progress management. In the process, building information modeling and extended reality technology were used to establish reality capture technology integration, and structural equation model was introduced to test assumptions. The experimental outcomes denoted that the proposed method had good data presentation ability [6]. Chen and other scholars proposed a management model based on radio frequency identification to address the issue of material supply in construction progress management. In the process, the building information modeling was introduced to build the database system, and the information of required materials was linked with the construction plan. The experiment findings indicated that the proposed method could effectively reduce the time consumption in material supply [7]. Scholars such as Ding proposed a cost management model based on neural networks to address the issue of cost management in construction. In the process, the project cost was analyzed, the neural network was introduced to predict the cost, and the building information modeling was added to control the cost. The experimental outcomes expressed that the proposed method could effectively reduce construction costs [8]. Scholars such as Annamalaisami CD proposed a cost management method based on causal mapping for cost control in construction. It needed to analyze and understand the construction scenario during the process and to predict possible future changes. The research results indicated that the proposed method could predict the risk of overspending [9]. Scholars such as Obi have proposed a management method based on expert review for the cost management of project construction. The cost-influencing factors during the process were analyzed, and experiments were conducted on the relationship between the factors through group meetings. The experimental results indicated that the proposed method could effectively evaluate construction costs [10].

Some scholars have conducted relevant research on the GA. Dharma and other scholars proposed a prediction model based on GA for inflation prediction. In the process, the historical consumer price index was analyzed, and the inflation level was predicted through the regression model. The research outcomes denoted that the proposed method could effectively predict inflation trends [11]. Rostami and other scholars proposed a feature selection method based on GA for feature selection in data preprocessing. During the process, feature similarity was calculated, features were redistributed in a cluster form, and finally, features were selected. The experiment findings expressed that the proposed method had high accuracy [12]. Scholars such as Jalali have proposed a design optimization strategy based on GA for sustainable design of buildings. It analyzed the physical performance of the building and its natural environment during the process, and conducted parametric modeling. The research outcomes showed that the proposed method had good design optimization effects [13]. Garud and other scholars proposed a prediction model based on GA for the performance prediction of solar photovoltaic systems. During the process, artificial intelligence technology was used to analyze various parameters of the solar photovoltaic system and detected faults. The experimental findings denoted that the proposed method had high performance prediction efficiency [14]. Chen proposed a GA-based optimization technique for parameter optimization problems. During the process, machines were used to learn the dataset, and the XGBoost model was introduced for parameter adjustment and encoding. The experimental results indicated that the proposed method had high computational performance [15].

In summary, the current methods have some deficiencies. For example, the management framework based on digital twins has high requirements for the real-time performance and accuracy of data, and data deviations will lead to a decline in management effects. The management model based on radio frequency identification relies on devices and tags. Device failure or tag damage can affect usage. The training process of the cost management model based on neural networks is complex, time-consuming, and requires a large amount of data. The cost management method based on causal mapping is complex in analysis and greatly influenced by subjective factors. The management method based on expert review relies on expert experience and lacks objectivity and universality. The research methods introduce SO strategies, construct project evaluation functions and construction progress cost control resource libraries, and adopt innovations such as MTS optimization GAs to avoid the problems of large initial populations and single coding methods in traditional GAs, improve the coordination efficiency of parallel task execution, and consider construction progress and cost factors more comprehensively. Furthermore, genetic operations are completed through the idea of discrete crossover operators without the need for chromosome repair, which can improve the algorithm efficiency, shorten the calculation time, and enhance the ability to adapt to changes in engineering steps, providing a more efficient and feasible technical reference for construction projects.

3 Design of CPCM method based on improved GA

The CPCM are the key points of construction projects. This section will focus on the technical means and development ideas used in the research and design of project CPCM methods based on improved GA.

3.1 Improvement design of standard GA algorithm and project scheduling model design

In the process of formulating the construction plan for infrastructure projects, in addition to considering whether the project progress can meet the construction needs of the group project, it is also necessary to control the cost of the project, ensuring that the construction project meets both the construction schedule and cost objectives of the project plan simultaneously [16,17]. Construction progress control includes the entire process of a project from start to finish, and suitable measurement methods need to be developed for different subprojects in order to clearly control the progress [18]. When conducting project cost management, it is necessary to balance three aspects: technological innovation, schedule management, and cost control. GA is derived from natural selection and genetic mechanism. It can use specific resource allocation strategies in task management and can be applied to construction schedule cost management. In practice, GA is shown in Figure 1.

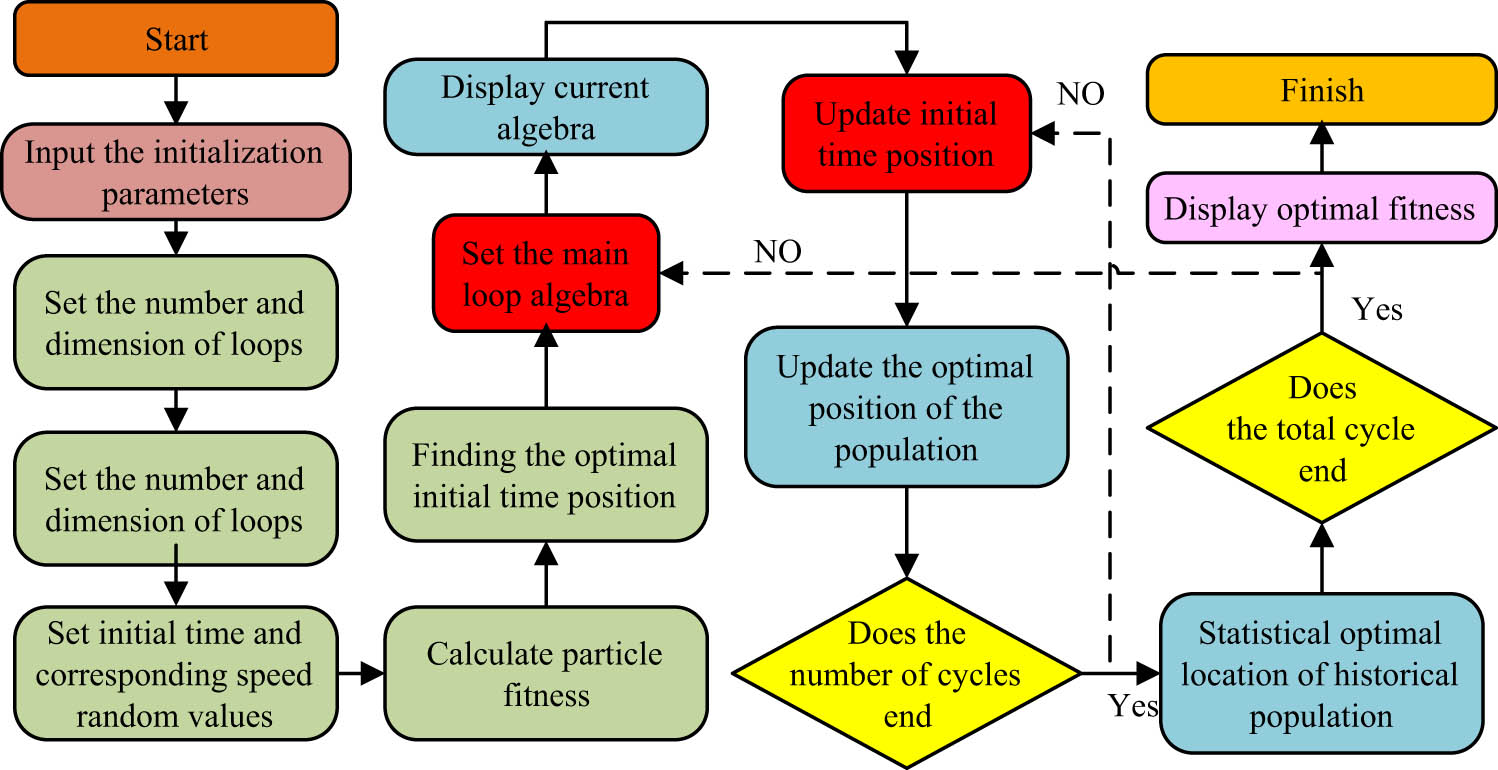
Figure 1 GA workflow.
Figure 1

GA workflow.

From Figure 1, GA first needs to set the basic coefficient, cycle dimension and number, initial time, and corresponding speed random values during operation. After the cycle ends, particle fitness is performed to obtain the optimal initial time position. It needs to initialize time and speed, set the main loop algebra, display the current algebra, start the loop, update the initial time position, and if the applicability of the obtained initial time is greater than the optimal position of the population, it needs to update the optimal position of the population. When the amount of cycles ends, the optimal position of the historical population is counted to determine whether the total cycle has reached the end condition. If it does not end, the main cycle algebra setting step is returned to continue the cycle. If it ends, the optimal fitness is displayed. The method of studying the selection coefficient is to highlight the advantages of each objective in the chromosome by defining the project evaluation function, and at the same time construct the construction progress and cost control resource library to improve the coordination efficiency when multiple tasks are carried out in parallel. The specific steps are as follows: first, determine the key factors that affect the project schedule and cost, such as resource allocation, task priority, and time constraints. Then, assign corresponding weights to these factors. The distribution of weights is based on the degree of influence of each factor on the project goals, and the total sum of the weights is 1. Then, each factor is scored, and the scoring criteria are formulated according to the actual project requirements. Then, calculate the weighted scores of each factor, i.e., multiply the scores by the weights. Finally, add up the weighted scores of all factors to obtain the total score of each task or scheme. The task or scheme with the highest total score is the optimal choice. Theoretically, the determination of the selection coefficient is based on the project characteristics and requirements to allocate weights, which has certain flexibility and adaptability and can be applied to projects different from the original research. The steps when using SOs for calculation are shown in Figure 2.

Figure 2 SO steps.
Figure 2

SO steps.

In Figure 2, when performing SOs, it is necessary to first encode the problem to be solved in the algorithm and then randomly initialize a population. Fitness search is conducted for each chromosome in the initialized population, and fitness represents the adaptability of the chromosome in the environment. Then, a new population is generated to expand the range that limited individuals in the algorithm can cover. It replaces the new group with the previous generation group. If the preset termination conditions are not met, it needs to go back to the fitness search step and cycle until the termination conditions are met, and the calculation ends. However, the initial population generated by traditional GA is huge, leading to an expansion of search space. Moreover, the encoding method of traditional GA is single, and there are multiple limitations in their application. Research is conducted on the improvement design of GA and a project evaluation function is defined, as shown in Eq. (1):

(1) g ( x ) = ∑ i = 1 k min f i ( x ) f i ( x ) × 100 2 ,

where g ( x ) means the project valuation, f i ( x ) denotes the cost of the target i , and min [ i ] indicates the scheduling problem for the i task in the MTS problem. The evaluation function highlights the advantages of each objective of the chromosome, avoiding the drawbacks of individual advantages that cannot be reflected [19]. A project scheduling model is established to improve coordination efficiency when multiple tasks are simultaneously carried out during project construction. Assuming that a shared resource library is used in the task during project schedule cost control, a resource library for construction progress cost control is constructed. In the constraint of construction resources, the collection of tasks simultaneously is shown in Eq. (2):

(2) I ( t ) = W k j ∈ ⋃ k = 1 P W k ∣ S k j ≤ t ≤ S k j + d k j ,

where ⋃ is used to describe that in the project scheduling process, the start time of a task must be greater than or equal to the union of the completion times of all its direct predecessor tasks; I ( t ) means a set of tasks that occur simultaneously at one time; W k j represents the jth task in the kth task; W k expresses the kth task; P denotes the set of immediate tasks; S k j indicates the start time of the task; and d k j refers to the duration of the task. The total task weight is shown in Eq. (3):

(3) ∑ k = 1 P ∂ k = 1 ,

where ∂ k stands for the weight of the k th task. It creates a two-dimensional array for the model structure, represents the benefit values of tasks on the processor, and then encodes and sorts the chromosome of the problem according to the work list. It represents the chromosomes of the population, as shown in Eq. (4):

(4) V K = [ L 1 i 1 , … , L 1 i i , … , L 1 i n , … , L k i 1 , … , L k i i , … , L k i n , … , L m i 1 , … , L m i i , … , L min ] ,

where V K indicates the Kth chromosomes within the population, and L represents different sequence number tasks at different positions in chromosomes. The set of activities corresponding to a portion of activities within a chromosome is represented by Eq. (5):

(5) Q t = { j ∣ P i ⊂ v k t } ,

where Q t denotes the set of activities, and v k t represents the part of the v chromosome that contains t motifs.

3.2 Optimization method for improving GA for CPCM

To calculate the shortest progress duration of multiple tasks, chromosomes can be decoded to obtain the earliest possible start time of work in the task and the earliest completion time of the task. The objective function is shown in Eq. (6):

(6) min ∑ k = 1 Y ∂ k × ( S k , n k + 1 ) ,

where ( S k , n k + 1 ) indicates the n k + 1 th tasks included in the kth task of the S k set, ( S k , n k + 1 ) clarifies a specific task within the set, and Y refers to the amount of mutually independent problems in MTS problems. In the MTS of construction projects, there exist multiple interrelated yet relatively independent problems such as resource allocation and task sequence arrangement. Y quantifies the number of these problems, which is helpful for grasping the complexity of MTS as a whole. The GA minimizes the total duration of a task and transforms the original objective function, as shown in Eq. (7):

(7) g ( v k ) = f max − f ( v k ) + ε f max − f min + ε ,

where g ( v k ) denotes the fitness function, f max expresses the maximum target value in the population, f ( v k ) indicates the original target value, and f min represents the minimum target value in the population. When conducting actual CPCM, using MTS to improve the GA can save the optimal strategy and reduce the probability of errors. The GA process for introducing MTS is shown in Figure 3.

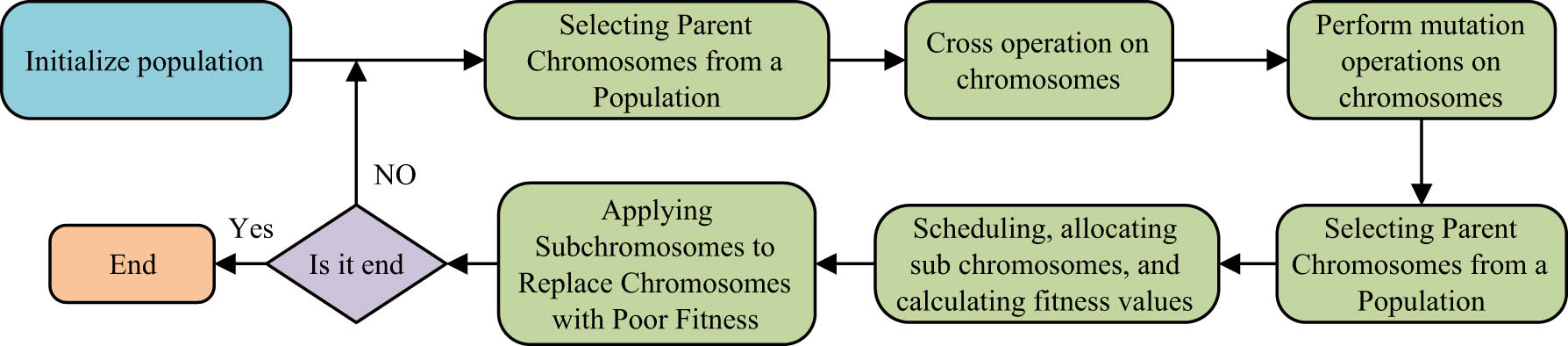
Figure 3 Introduction of GA algorithm flow for MTS.
Figure 3

Introduction of GA algorithm flow for MTS.

As shown in Figure 3, the GA that introduces MTS first needs to initialize the population before performing calculations, then select the parent chromosome in the population, perform crossover and mutation operations, update the population, and reselect the parent chromosome. It schedules and allocates sub-chromosomes, calculates corresponding fitness values, uses sub-chromosomes to replace those with poor fitness, and determines whether the cycle has ended. If not, it will continue the cycle. If it has ended, it will end the process and output the results. The standard GA is unable to solve non-cumulative workload problems, and research imitates the idea of discrete crossover operators to complete genetic operations without chromosome repair [20]. It performs cross-operation between the mother and father in GA to generate offspring and daughter offspring, and it carries out work inheritance in the work chain table, as shown in Eq. (8):

(8) N i D = N i M , ( i = 1 , 2 , … , q ) ,

where D denotes the work chain table, M expresses the matrix, q means the last work sequence number inherited, and N means the work that needs to be inherited. It preserves the relative positions of the parent body during each working period, as shown in Eq. (9):

(9) N i D = N k F , ( i = q + 1 , q + 2 , … , J ) ,

where F means the parent body. The expression of the task is shown in Eq. (10):

(10) k = min { k ∣ j k F ∉ { f 1 F , f 2 F , f 3 F , … , f k F } k = 1 , 2 , … , J } ,

where k expresses the task. The field technology and centralized search strategy are applied to search the genetic improved mutation operator. When executing the GA, the gene sequence violating the constraint relationship is directly discarded, which reduces the influence of the mutation operator on the field and improves the algorithmic efficiency. The tangent function, due to its specific mathematical characteristics and flexibility, can precisely fit complex nonlinear relationships. Its boundedness and monotonicity can simulate the situation where the cost growth tends to level off after the quality reliability improves to a certain extent. In the early stage of iteration, it can quickly approach the true characteristic function and accelerate the optimization convergence. In the study of nonlinear constitutive models of soil dynamics, the hyperbolic tangent function is used to construct the framework and hysteresis curves because its graph is similar to the measured soil framework curve, bounded and its derivatives are continuous. Similarly, in the management of construction progress and cost, the optimization model constructed by the tangent function can effectively capture the dynamic correlation between the project quality reliability and the cost of subsystems [21]. When optimizing the construction schedule cost, it is necessary to use the tangent function to simulate the relationship between the project quality reliability and the subsystem cost during the construction process, as shown in Eq. (11) [22]:

(11) C j ( R ( X j ) ) = C 0 ( X j ) t g π 2 × R ( X j ) α j , j = 1 , 2 , 3 , … , n

where C j ( R ( X j ) ) denotes the cost that the subsystem X j needs to consume when its reliability reaches R ( X j ) , C 0 ( X j ) represents basic expenses, R ( X j ) indicates the quality reliability of the subsystem X j , n refers to the number of subsystems, and α j stands for the cost growth index. It builds a construction schedule cost optimization model, as shown in Eq. (12):

(12) f ( R ( X j ) ) = min C s ∑ j = 1 n C j R ( X j ) s . t . R x i min < R ( X j ) < ( i = 1 , 2 , … , n ) R S min < R S ,

where C s refers to the total project cost, R S means the total reliability of project quality, R x i min stands for the lower limit of quality reliability in the subsystem, and SS indicates the lower reliability limit of the project subsystem. The study takes the construction of Viaduct project as an example to split the project construction schedule, as shown in Table 1.

Table 1

Construction work of Viaduct project

Job code Job name Immediate work Dependent tasks Duration (week)
A Construction preparation / B 11
B Pile foundation engineering A C 16
C Pier and abutment body construction B D, E 8
D Beam construction C F, G, H 13
E Beam support, binding steel bars C O 75
F Prestressed pouring beam D I 14
G Main structure D K 27
H External frame installation D L 42
I Masonry and backfill of viaduct F J 14
J Bridge deck and accessories I O 38
K Pier structure of viaduct G M 9
L Pouring H Q 46
M Box construction of viaduct K N 9
N Bridge deck decoration engineering M Q 17
O Pier column J Q 13
P Cast-in-place beams E Q 12
Q Pre-beam L, n, o, p R 10
R Completion acceptance Q / 5

From Table 1, each construction work step of viaduct project construction is separated separately, and each step is given a corresponding code, and the immediate work and immediate work of each work step are marked according to the construction process. It marks the individual duration of each work step according to the normal working speed to facilitate the development of construction plans. When the actual viaduct project construction schedule cost optimization is carried out, the GA mode based on the double code network is used to set the key process as the construction process with the free float of 0. It analyzes the progress cost critical path of the project and calculates it based on the process time and direct costs of the critical project.

In construction project management, the total cost TC is composed of direct cost TDC and indirect cost IC. Direct costs include expenses such as labor, materials, and equipment that are directly related to construction activities. Indirect costs are usually non-direct expenses such as management fees, venue rentals, and administrative expenditures, and their calculation should be based on industry practices or project experience. According to the common practices in the field of construction engineering (such as references [16,17]), the proportion of indirect costs in construction projects is usually between 0.15 and 0.25, and 20% is taken as the equilibrium value. Suppose the indirect cost is proportional to the direct cost. The calculation of the indirect cost is shown in Eq. (13):

(13) IC = TDC × 0 .2 .

The total project cost is shown in Eq. (14):

(14) TC = TDC × ( 1 + 0 .2) ,

where TC represents the total project cost, and T D C expresses the total direct cost. GA is utilized to search for the work path with the minimum total time difference, forming a critical control path for progress cost, and obtaining the theoretical construction period. The direct rate calculation is shown in Eq. (15):

(15) C i j , direct − C i j , normal = C i j L − C i j n t i j L − t i j N ,

where C i j , direct − C i j , normal refers to the direct rate of the project, C i j L − C i j n means the difference between the direct cost of using the shortest possible time and the direct cost of normal construction, and t i j L − t i j N expresses the difference between the normal construction time and the shortest time. The cost and time of each part of the work are introduced into the calculation to obtain data. When there is a deviation in the progress, the deviation can be analyzed, and the analysis process is shown in Figure 4.

Figure 4 Progress deviation analysis process.
Figure 4

Progress deviation analysis process.

From Figure 4, when conducting progress deviation analysis, the first step is to analyze whether the deviation occurs on the critical route. If it is on the critical route, it will affect the total construction period and adjustment measures need to be taken. If it is not on a critical route, it will analyze whether the deviation is greater than the total time difference. If the deviation is greater than the total time difference, it will affect the total construction period and adjustment measures need to be taken. If the deviation is not greater than the total time difference, it will analyze whether the deviation is greater than the free time difference. If it is greater than the free time difference, it needs to take adjustment measures. If it is not greater than the free time difference, it will directly return to the progress control system. After taking adjustment measures, it executes the new progress plan and returns to the progress control system. In optimization, it is necessary to determine whether the project progress is ahead of schedule, break down specific control tasks and personnel responsibilities, and establish a corresponding coding management system based on the actual progress of the project. A project schedule assurance system is developed based on GA combined with project quality control technology, as shown in Figure 5.

Figure 5 Project schedule guarantee system.
Figure 5

Project schedule guarantee system.

As shown in Figure 5, the project schedule guarantee system is divided into three categories: legal, institutional, and economic guarantees. The legal guarantee category includes content such as command system, leadership responsibility, and ideological education; the system assurance category includes construction plans, logistics support, settlement systems, and other contents; economic guarantee includes regular meeting systems, contracting mechanisms, and other contents. In the secondary optimization of project construction progress cost, the tipping rate processes in non-critical processes can be compressed, and genetic iteration can be carried out on the processes in order from small to large to obtain the minimum construction period. The total cost calculation during practical verification is shown in Eq. (16):

(16) TC = TDC × ( 1 + Δ C i j ) + ∑ Δ t i j ( Δ C i j o − Δ C i j ) × 10 ,

where Δ C i j refers to the indirect cost rate of the project, and Δ t i j means the compression time of the process.

4 Performance testing and application analysis of CPCM method based on improved GA

A good CPCM method can optimize the project’s duration and construction costs. This section will test the performance of the research method in CPCM and introduce real engineering projects for application effect analysis to determine the effectiveness of the method.

4.1 Performance testing of CPCM method based on improved GA

To analyze the effectiveness of the research institute’s design method in project CPCM for building engineering, performance testing and application analysis were conducted on the method. The construction engineering cost standards (CECS) and building engineering dataset (BED) were utilized as datasets, and it set the evolution algebra to 200, the population size to 20, the crossover probability to 0.4, and the mutation probability to 0.001. The optimal fitness was tested during the evolution of research methods, and they were compared with multi-stage genetic algorithm (MGA) and quantum genetic algorithm (QGA), as shown in Figure 6.

Figure 6 Best-fit evolution test: (a) CECS and (b) BED.
Figure 6

Best-fit evolution test: (a) CECS and (b) BED.

From Figure 6, during the best fitness test, the best fitness of all methods continuously increased with the increase of evolution times, stopped rising, and remained stable when reaching the upper limit of the best fitness. In the CECS dataset, MGA reached its optimal fitness upper limit of 20.9 when evolving to the 72nd generation; when QGA evolved to the 47th generation, it reached the upper limit of optimal fitness of 20.9, and there was a cross between the curve of optimal fitness and MGA during the upward process; the research method reached the optimal fitness limit of 20.9 when evolving to the 23rd generation. In the BED dataset, MGA reached its optimal fitness upper limit of 21.2 when evolving to the 45th generation; when QGA evolved to the 61st generation, it reached the upper limit of optimal fitness of 21.2, and there were multiple intersections with the curve of MGA during the rise of the optimal fitness curve; the research method reached the optimal fitness upper limit of 21.2 when evolving to the 30th generation. The research method had a faster rate of optimal fitness increase. It tested the mean squared error (MSE) change of the research method in the evolution process, as shown in Figure 7.

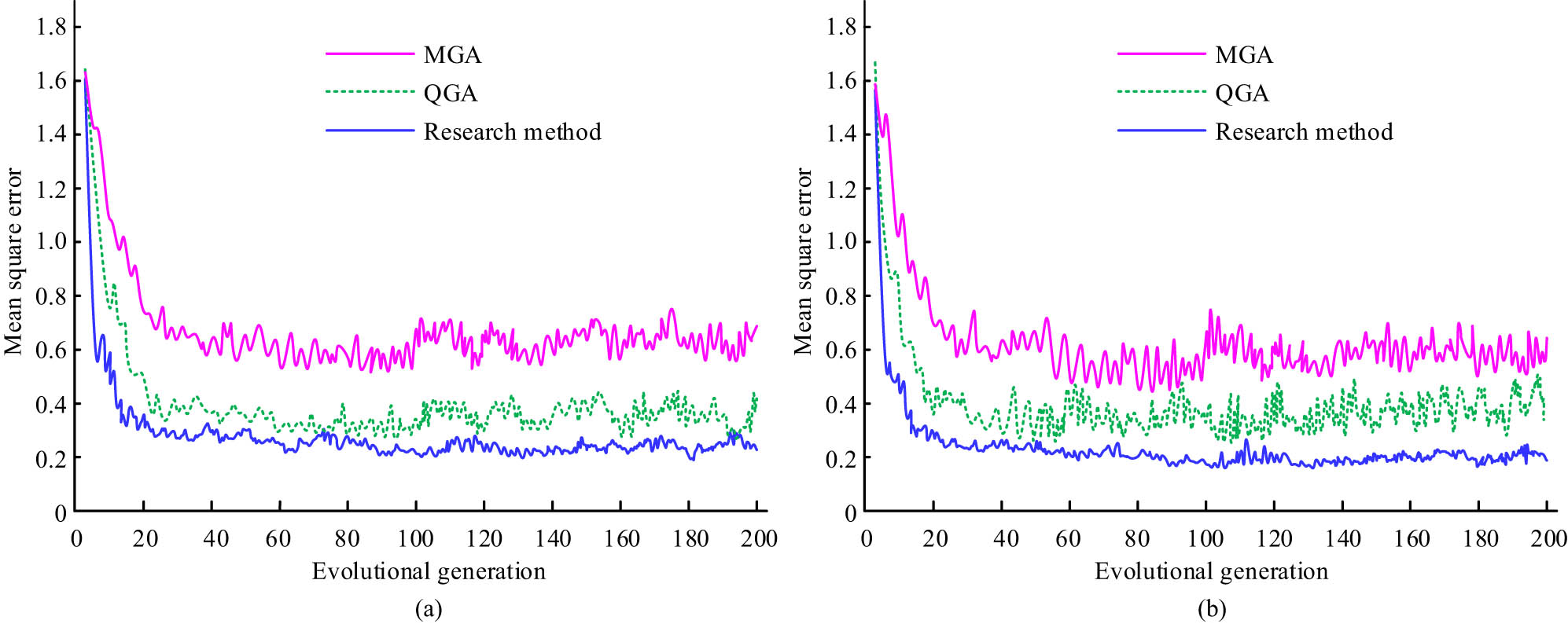
Figure 7 MSE change: (a) CECS and (b) BED.
Figure 7

MSE change: (a) CECS and (b) BED.

From Figure 7, the MSE of all methods decreased with the increase of evolution algebra. In the CECS dataset, the MSE of MGA ended its downward trend at the 36th evolution and then fluctuated around 0.64, with a fluctuation range of 0.12; the MSE of QGA ended its downward trend at the 27th evolution and then fluctuated around 0.37, with a fluctuation range of 0.07; the MSE of the research method ended its downward trend at the 22nd evolution and then fluctuated around 0.23, with a fluctuation range of 0.04. In the BED dataset, the MSE of MGA ended its downward trend at the 39th evolution and then fluctuated around 0.58, with a fluctuation range of 0.17; the MSE of QGA ended its downward trend at the 33rd evolution and then fluctuated around 0.37, with a fluctuation range of 0.12; the MSE of the research method ended its downward trend at the 23rd evolution and then fluctuated around 0.21, with a fluctuation range of 0.04. The MSE of the research method decreased faster and had stronger stability after reaching the lowest range. It tested the number of redundant individuals during the operation of the research method, as shown in Figure 8.

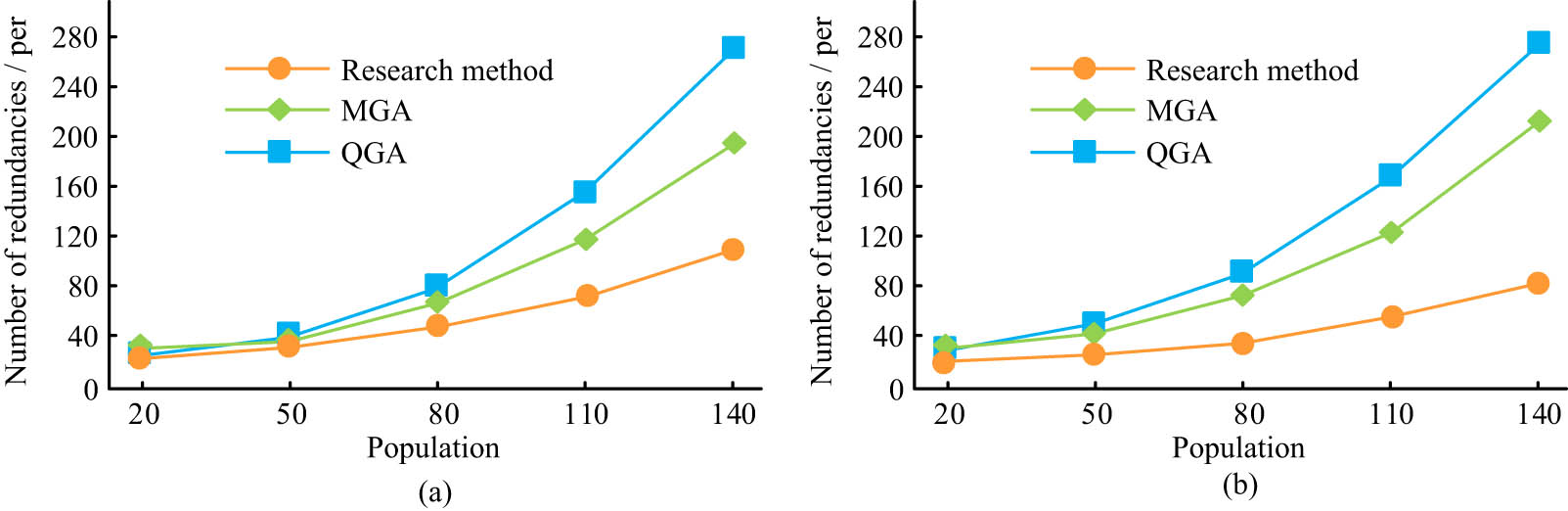
Figure 8 Number of redundant individuals: (a) CECS and (b) BED.
Figure 8

Number of redundant individuals: (a) CECS and (b) BED.

Figure 8 shows that in both the CECS and BED datasets, the number of redundant individuals for all methods increases with the increase in population size. In the CECS dataset, taking the QGA method as an example, when the population size increased from 20 to 140, the number of redundant individuals rose from 29 to 272, and other methods also showed a similar growth trend. The same is true in the BED dataset. For example, in the QGA method, there are 32 redundant individuals when the population size is 20, and it reaches 277 when it increases to 140. The number of redundant individuals in each method increases significantly with the expansion of the population size, reflecting a positive correlation between the population size and the number of redundant individuals. The reduction of redundant individuals means that the maintenance of population diversity is more effective, which helps the algorithm to explore more extensively in the search space and avoid premature convergence to the local optimal solution. When there are many redundant individuals, similar individuals in the population dominate, which limits the exploration ability of the algorithm and leads to the stagnation of the search process. The low-redundancy state can ensure the differences among individuals in the population, enabling the algorithm to continuously discover new and better solutions during the iterative process. Meanwhile, low redundancy also reduces unnecessary waste of computing resources because the algorithm no longer conducts repetitive fitness evaluations and genetic operations on a large number of similar individuals, thereby significantly improving the computing efficiency. This improvement in efficiency is particularly evident when dealing with large-scale or complex problems, enabling the algorithm to find satisfactory solutions in a shorter time. It tested the calculation time of the research method, as shown in Figure 9.

Figure 9 Computing time: (a) CECS and (b) BED.
Figure 9

Computing time: (a) CECS and (b) BED.

As shown in Figure 9, in both datasets, the calculation time of all methods increased with the number of engineering steps. In the CECS dataset, the calculation time of QGA was 16.9 s when the amount of engineering steps was 5, and increased to 68.2 s when the amount of engineering steps increased to 25; the calculation time for MGA was 24.8 s when the number of engineering steps was 5, and increased to 61.1 s when the amount of engineering steps increased to 25; the calculation time for the research method was 9.9 s when the number of engineering steps was 5, and increased to 33.7 s when the amount of engineering steps increased to 25. In the BED dataset, the calculation time of QGA was 19.7 s when the number of engineering steps was 5, and increased to 56.1 s when the number of engineering steps increased to 25; The calculation time for MGA was 28.1 s when the amount of engineering steps was 5, and increased to 27.8 s when the number of engineering steps increased to 25; the calculation time for the research method was 8.8 s when the number of engineering steps was 5, and increased to 28.2 s when the amount of engineering steps increased to 25. The research method had faster computational efficiency.

4.2 Application analysis of CPCM method based on improved GA

In the application analysis, the research took a viaduct construction project as the analysis object. The viaduct was an interchange double deck overpass, with a longitudinal bridge length of 1,400 linear meters and a transverse bridge length of 380 linear meters. The characteristics of the elevated bridge project dataset are shown in Table 2.

Table 2

Characteristics of the elevated bridge project dataset

Task name Duration (weeks) Task dependencies Resource requirements (unit) Task priority Earliest start time (weeks) Latest completion time (weeks)
Construction preparation 11.00 / 5.00 1 0.00 10.00
Pile foundation engineering 16.00 1 8.00 ２ 11.00 27.00
Pier and abutment body construction 8.00 ２ 6.00 3 27.00 35.00
Beam construction 13.00 3 7.00 4 35.00 48.00
Beam support, binding steel bars 75.00 3 10.00 ５ 35.00 110.00
Prestressed pouring beam 14.00 4 5.00 6 48.00 62.00
Main structure 27.00 4 9.00 7 48.00 75.00
External frame installation 42.00 4 7.00 8 48.00 90.00
Masonry and backfill of viaduct 14.00 6 6.00 9 62.00 76.00
Bridge deck and accessories 38.00 9 8.00 10 76.00 114.00
Pier structure of viaduct 9.00 7 5.00 11 75.00 84.00
Box construction of viaduct 9.00 11 4.00 12 84.00 93.00
Bridge deck decoration engineering 17.00 12 6.00 13 93.00 110.00
Pier column 13.00 10 5.00 14 114.00 127.00
Cast-in-place beams 12.00 5 6.00 15 110.00 122.00
Pre-beam 10.00 8, 13, 14, 15 8.00 16 127.00 137.00
Completion acceptance 5.00 16 3.00 17 137.00 142.00

The construction period compression test was carried out for each work of the viaduct, as shown in Figure 10.

Figure 10 Work duration compression.
Figure 10

Work duration compression.

From Figure 10, out of the 17 tasks, a total of nine tasks had their schedules compressed. The construction period of the pier and abutment body has been reduced from 8 weeks to 7 weeks; the construction period for brackets and binding steel bars has been reduced from 75 weeks to 73 weeks; the construction period of the main structure has been compressed from 27 weeks to 26 weeks; the construction period for the outer frame has been reduced from 42 weeks to 40 weeks; the construction period for the bridge deck and its accessories has been reduced from 38 weeks to 37 weeks; the pouring period has been reduced from 46 weeks to 45 weeks; the construction period of Viaduct box construction was reduced from 9 weeks to 8 weeks; the construction period for pier and abutment columns has been reduced from 13 weeks to 12 weeks. The research method effectively compressed the construction period. The cost compression was calculated in the context of schedule compression, as shown in Table 3.

Table 3

Project cost compression

Number of compressions Compression work Indirect rate adjustment (103 yuan/week) Direct cost slope (103 yuan/week) Reduce expenses (103 yuan) Total cost (103 yuan)
1 Beam construction −0.150 0.050 30 3,366
2 Pouring −0.130 0.067 40 3,326
3 Pre-beam −0.100 0.010 20 3,306
4 Beam support, binding steel bars −0.180 0.020 90 3,216
5 Masonry and backfill of viaduct −0.100 0.100 20 3,196
6 Bridge deck and accessories −0.063 0.130 20 3,176
7 Cast-in-place beams −0.050 0.150 10 3,166

From Table 3, the research method compressed the construction cost of the project in seven steps. When compressing the project duration at the same time, a total of 230k yuan in cost was reduced. The total construction period of viaduct was reduced from 149 weeks to 144 weeks, and the project construction cost was reduced from 3,366k to 3,166k yuan. The research method can effectively reduce the duration and cost of project construction. The experimental data were obtained from 30 independent repeated experiments, and the statistical test results of performance indexes are shown in Table 4.

Table 4

Statistical results of performance indicators

Performance index Data set Improved GA MGA QGA Statistical value p
Convergence algebra CECS 23.2 ± 1.8 72.5 ± 4.2 47.3 ± 3.1 F = 785.6 <0.001
BED 30.4 ± 2.1 45.1 ± 3.8 61.2 ± 5.3 F = 423.9 <0.001
MSE fluctuates steadily CECS 0.04 ± 0.006 0.12 ± 0.015 0.07 ± 0.009 t = 28.7 <0.001
BED 0.04 ± 0.005 0.17 ± 0.021 0.12 ± 0.018 t = 35.2 <0.001
Calculate the time increment (s) CECS 23.8 ± 2.3 61.4 ± 5.7 68.5 ± 6.2 H = 89.1 <0.001
(Steps 5 → 25) BED 19.4 ± 1.9 56.3 ± 4.8 47.6 ± 4.1 U = 0.0 <0.001
Cost reduction amount (104 yuan) Viaduct 23.0 ± 2.5 12.3 ± 3.1 15.8 ± 2.8 F = 49.2 <0.001

As can be seen from Table 4, the convergence algebra of Improved-GA on the CECS and BED datasets was 23.2 ± 1.8 and 30.4 ± 2.1, respectively, which was significantly superior to that of MGA and QGA. The MSE value is 0.04 on both the CECS and BED datasets, indicating that its convergence stability is higher. In terms of calculating the time increment, the performance of Improved-GA on the CECS and BED datasets is also superior to that of the other two algorithms. Especially when the engineering steps increase from 5 to 25, the calculation time increment is significantly smaller. Furthermore, in the elevated bridge project, the cost reduction of Improved-GA was 23.0 × 104 yuan, which was significantly higher than that of MGA and QGA. The statistical test results show that the differences among various performance indicators are highly significant (p < 0.001), proving the superiority and reliability of Improved-GA in the progress and cost management of construction projects. These results indicate that Improved-GA can effectively shorten the project cycle and reduce costs, while maintaining high computational efficiency and stability.

5 Conclusion

Conducting project CPCM can improve construction efficiency and reduce construction costs. A construction schedule and cost management method based on GA has been proposed for project construction cost management. By encoding the problem and performing SOs, the chromosome encoding was used to calculate the shortest duration of multiple tasks. Then, the optimal strategy was saved using MTS, and the project construction work was split and compressed separately. Finally, the effectiveness of the research method was tested. The experimental findings indicated that when testing the optimal fitness, the research method reached the upper limit of 20.9 in the_ 23rd generation of evolution in the CESE dataset; in the MSE test, the research method only needed 22 and 23 evolutions, respectively, in the two datasets to reach the lowest interval; when testing the amount of redundant individuals during runtime, the research method maintained the number of redundant individuals below 108 when the population reached 140; in the calculation time test of the research method, when the number of engineering steps in the BED dataset was 5, the calculation time was 8.8 s; when compressing the construction period, the research method compressed the construction period of 9 out of 17 tasks, with a maximum compression of 3 weeks for each individual task. The aforementioned results indicated that the research method had good model performance and could effectively compress the project construction period and cost.

Furthermore, the research method has the potential to be applied to non-elevated bridge projects, but it needs to be adjusted according to different building environments. For different building environments, if the project structure and process are different, the resource library and task relationship model need to be reconstructed. For instance, the number of building floors and functional zoning will change the task sequence and resource requirements. If there are differences in resource conditions, such as the speed of material supply and the number of laborers, the resource constraint equation and the cost calculation method should be adjusted. Meanwhile, it is also necessary to modify the optimization model constructed with the tangent function in combination with the quality standards and risk factors in the new environment to ensure the effectiveness of the method. However, the research still has limitations. First of all, although this method shows high efficiency when handling multiple tasks, its adaptability to the specific project environment still needs to be improved. Second, when dealing with large-scale projects, the computing time may still be relatively long. Future research can focus on further enhancing the universality and adaptability of algorithms to better address the challenges of different construction project environments. The research will explore how to customize and adjust the algorithm according to the specific requirements of the project and the characteristics of the environment. Meanwhile, combined with the real-time data monitoring and feedback mechanism, the response ability of the algorithm to the dynamic changes of the project is enhanced, enabling it to quickly adapt to the changes in project conditions. In addition, it is also possible to study how to optimize the computational efficiency of the algorithm to handle large-scale and complex projects more effectively. Through these improvements, it is expected that this method will play a greater role in the CPCM of construction projects.

  1. Funding information: The author states no funding involved.

  2. Author contributions: Xudong Wang: original draft preparation; methodology, review, and editing. The author has accepted responsibility for the entire content of this manuscript and approved its submission.

  3. Conflict of interest: The author states no conflict of interest.

  4. Data availability statement: All data generated or analyzed during this study are included in this published article.

References

[1] Dong Y, Zhang SL, Huang YL. Construction of educational quality evaluation index system based on project management. Int J Inf Syst Serv Sect (IJISSS). 2020;12(2):65–75.10.4018/IJISSS.2020040105Suche in Google Scholar

[2] Cassar DR, Santos GG, Zanotto ED. Designing optical glasses by machine learning coupled with a genetic algorithm. Ceram Int. 2021;47(8):10555–64.10.1016/j.ceramint.2020.12.167Suche in Google Scholar

[3] Kowalski M, Izdebski M, Żak J, Gołda P, Manerowski J. Planning and management of aircraft maintenance using a genetic algorithm. Eksploat i Niezawodn. 2021;23(1):143–53.10.17531/ein.2021.1.15Suche in Google Scholar

[4] Feng-Luan DU, Zhao CQ, Ding SN. Construction and recent progress of Z-scheme-based photoelectrochemical sensor. Chin J Anal Chem. 2021;49(8):1247–57.Suche in Google Scholar

[5] Yang Y, Song X. Research on face intelligent perception technology integrating deep learning under different illumination intensities. J Comput Cognit Eng. 2022;1(1):32–6.10.47852/bonviewJCCE19919Suche in Google Scholar

[6] Alizadehsalehi S, Yitmen I. Digital twin-based progress monitoring management model through reality capture to extended reality technologies (DRX). Smart Sustain Built Environ. 2023;12(1):200–36.10.1108/SASBE-01-2021-0016Suche in Google Scholar

[7] Chen Q, Adey BT, Haas C, Hall DM. Using look-ahead plans to improve material flow processes on construction projects when using BIM and RFID technologies. Constr Innov. 2020;20(3):471–508.10.1108/CI-11-2019-0133Suche in Google Scholar

[8] Ding X, Lu Q. Construction cost management strategy based on BIM technology and neural network model. J Intell Fuzzy Syst. 2021;40(4):6669–81.10.3233/JIFS-189502Suche in Google Scholar

[9] Annamalaisami CD, Kuppuswamy A. Reckoning construction cost overruns in building projects through methodological consequences. Int J Constr Manag. 2022;22(6):1079–89.10.1080/15623599.2019.1683689Suche in Google Scholar

[10] Obi LI, Arif M, Awuzie B, Islam R, Gupta AD, Walton R. Critical success factors for cost management in public-housing projects. Constr Innov. 2021;21(4):625–47.10.1108/CI-10-2020-0166Suche in Google Scholar

[11] Dharma F, Shabrina S, Noviana A, Tahir M, Hendrastuty N, Wahyono W. Prediction of Indonesian inflation rate using regression model based on genetic algorithms. J Online Inform. 2020;5(1):45–52.10.15575/join.v5i1.532Suche in Google Scholar

[12] Rostami M, Berahmand K, Forouzandeh S. A novel community detection based genetic algorithm for feature selection. J Big Data. 2021;8(1):1–27.10.1186/s40537-020-00398-3Suche in Google Scholar

[13] Jalali Z, Noorzai E, Heidari S. Design and optimization of form and facade of an office building using the genetic algorithm. Sci Technol Built Environ. 2020;26(2):128–40.10.1080/23744731.2019.1624095Suche in Google Scholar

[14] Garud KS, Jayaraj S, Lee MY. A review on modeling of solar photovoltaic systems using artificial neural networks, fuzzy logic, genetic algorithm and hybrid models. Int J Energy Res. 2021;45(1):6–35.10.1002/er.5608Suche in Google Scholar

[15] Chen J, Zhao F, Sun Y, Yin Y. Improved XGBoost model based on genetic algorithm. Int J Comput Appl Technol. 2020;62(3):240–5.10.1504/IJCAT.2020.106571Suche in Google Scholar

[16] Mello PP, Onofre RB, Rea M, Bierman A, Gadoury DM, Ivors K, et al. Design, construction, and evaluation of equipment for nighttime applications of UV-C for management of strawberry powdery Mildew in Florida and California. Plant Health Prog. 2022;23(3):321–7.10.1094/PHP-01-22-0002-RSSuche in Google Scholar

[17] Ranjithapriya R, Arulselvan S. Study on factors affecting equipment management and its effect on productivity in building construction. Int J Eng Res Technol (IJERT). 2020;9(4):223–30.10.17577/IJERTV9IS040176Suche in Google Scholar

[18] Vasko FJ, Lu Y, McNally B. A simple methodology that efficiently generates all optimal spanning trees for the cable-trench problem. J Comput Cognit Eng. 2022;1(1):13–20.10.47852/bonviewJCCE208918205514Suche in Google Scholar

[19] Ghezelbash R, Maghsoudi A, Shamekhi M, Pradhan B, Daviran M. Genetic algorithm to optimize the SVM and K-means algorithms for mapping of mineral prospectivity. Neural Comput Appl. 2023;35(1):719–33.10.1007/s00521-022-07766-5Suche in Google Scholar

[20] Protulipac DG, Nyabeeya EE, Karitanyi N, Vincent T, Panayotidis D. Construction progress at the Rusumo Falls hydro development in challenging times. Int J Hydropower Dams. 2020;27(5):91–5.Suche in Google Scholar

[21] Xu S, Chen H, Wang P, Nie R, Si J. An improved model predictive torque control for switched reluctance motors based on variable hyperbolic tangent function modeling. IEEE Trans Transp Electr. 2025;11(1):5029–41.10.1109/TTE.2024.3476037Suche in Google Scholar

[22] Mohammad S, Mendoza I. A new hyperbolic tangent family of distributions: Properties and applications. Ann Data Sci. 2025;12(2):457–80.10.1007/s40745-024-00516-5Suche in Google Scholar
Received: 2024-08-21
Revised: 2025-05-09
Accepted: 2025-05-21
Published Online: 2025-08-28

© 2025 the author(s), published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

  1. Research Articles
  2. Generalized (ψ,φ)-contraction to investigate Volterra integral inclusions and fractal fractional PDEs in super-metric space with numerical experiments
  3. Solitons in ultrasound imaging: Exploring applications and enhancements via the Westervelt equation
  4. Stochastic improved Simpson for solving nonlinear fractional-order systems using product integration rules
  5. Exploring dynamical features like bifurcation assessment, sensitivity visualization, and solitary wave solutions of the integrable Akbota equation
  6. Research on surface defect detection method and optimization of paper-plastic composite bag based on improved combined segmentation algorithm
  7. Impact the sulphur content in Iraqi crude oil on the mechanical properties and corrosion behaviour of carbon steel in various types of API 5L pipelines and ASTM 106 grade B
  8. Unravelling quiescent optical solitons: An exploration of the complex Ginzburg–Landau equation with nonlinear chromatic dispersion and self-phase modulation
  9. Perturbation-iteration approach for fractional-order logistic differential equations
  10. Variational formulations for the Euler and Navier–Stokes systems in fluid mechanics and related models
  11. Rotor response to unbalanced load and system performance considering variable bearing profile
  12. DeepFowl: Disease prediction from chicken excreta images using deep learning
  13. Channel flow of Ellis fluid due to cilia motion
  14. A case study of fractional-order varicella virus model to nonlinear dynamics strategy for control and prevalence
  15. Multi-point estimation weldment recognition and estimation of pose with data-driven robotics design
  16. Analysis of Hall current and nonuniform heating effects on magneto-convection between vertically aligned plates under the influence of electric and magnetic fields
  17. A comparative study on residual power series method and differential transform method through the time-fractional telegraph equation
  18. Insights from the nonlinear Schrödinger–Hirota equation with chromatic dispersion: Dynamics in fiber–optic communication
  19. Mathematical analysis of Jeffrey ferrofluid on stretching surface with the Darcy–Forchheimer model
  20. Exploring the interaction between lump, stripe and double-stripe, and periodic wave solutions of the Konopelchenko–Dubrovsky–Kaup–Kupershmidt system
  21. Computational investigation of tuberculosis and HIV/AIDS co-infection in fuzzy environment
  22. Signature verification by geometry and image processing
  23. Theoretical and numerical approach for quantifying sensitivity to system parameters of nonlinear systems
  24. Chaotic behaviors, stability, and solitary wave propagations of M-fractional LWE equation in magneto-electro-elastic circular rod
  25. Dynamic analysis and optimization of syphilis spread: Simulations, integrating treatment and public health interventions
  26. Visco-thermoelastic rectangular plate under uniform loading: A study of deflection
  27. Threshold dynamics and optimal control of an epidemiological smoking model
  28. Numerical computational model for an unsteady hybrid nanofluid flow in a porous medium past an MHD rotating sheet
  29. Regression prediction model of fabric brightness based on light and shadow reconstruction of layered images
  30. Dynamics and prevention of gemini virus infection in red chili crops studied with generalized fractional operator: Analysis and modeling
  31. Qualitative analysis on existence and stability of nonlinear fractional dynamic equations on time scales
  32. Fractional-order super-twisting sliding mode active disturbance rejection control for electro-hydraulic position servo systems
  33. Analytical exploration and parametric insights into optical solitons in magneto-optic waveguides: Advances in nonlinear dynamics for applied sciences
  34. Bifurcation dynamics and optical soliton structures in the nonlinear Schrödinger–Bopp–Podolsky system
  35. Review Article
  36. Haar wavelet collocation method for existence and numerical solutions of fourth-order integro-differential equations with bounded coefficients
  37. Special Issue: Nonlinear Analysis and Design of Communication Networks for IoT Applications - Part II
  38. Silicon-based all-optical wavelength converter for on-chip optical interconnection
  39. Research on a path-tracking control system of unmanned rollers based on an optimization algorithm and real-time feedback
  40. Analysis of the sports action recognition model based on the LSTM recurrent neural network
  41. Industrial robot trajectory error compensation based on enhanced transfer convolutional neural networks
  42. Research on IoT network performance prediction model of power grid warehouse based on nonlinear GA-BP neural network
  43. Interactive recommendation of social network communication between cities based on GNN and user preferences
  44. Application of improved P-BEM in time varying channel prediction in 5G high-speed mobile communication system
  45. Construction of a BIM smart building collaborative design model combining the Internet of Things
  46. Optimizing malicious website prediction: An advanced XGBoost-based machine learning model
  47. Economic operation analysis of the power grid combining communication network and distributed optimization algorithm
  48. Sports video temporal action detection technology based on an improved MSST algorithm
  49. Internet of things data security and privacy protection based on improved federated learning
  50. Enterprise power emission reduction technology based on the LSTM–SVM model
  51. Construction of multi-style face models based on artistic image generation algorithms
  52. Research and application of interactive digital twin monitoring system for photovoltaic power station based on global perception
  53. Special Issue: Decision and Control in Nonlinear Systems - Part II
  54. Animation video frame prediction based on ConvGRU fine-grained synthesis flow
  55. Application of GGNN inference propagation model for martial art intensity evaluation
  56. Benefit evaluation of building energy-saving renovation projects based on BWM weighting method
  57. Deep neural network application in real-time economic dispatch and frequency control of microgrids
  58. Real-time force/position control of soft growing robots: A data-driven model predictive approach
  59. Mechanical product design and manufacturing system based on CNN and server optimization algorithm
  60. Application of finite element analysis in the formal analysis of ancient architectural plaque section
  61. Research on territorial spatial planning based on data mining and geographic information visualization
  62. Fault diagnosis of agricultural sprinkler irrigation machinery equipment based on machine vision
  63. Closure technology of large span steel truss arch bridge with temporarily fixed edge supports
  64. Intelligent accounting question-answering robot based on a large language model and knowledge graph
  65. Analysis of manufacturing and retailer blockchain decision based on resource recyclability
  66. Flexible manufacturing workshop mechanical processing and product scheduling algorithm based on MES
  67. Exploration of indoor environment perception and design model based on virtual reality technology
  68. Tennis automatic ball-picking robot based on image object detection and positioning technology
  69. A new CNN deep learning model for computer-intelligent color matching
  70. Design of AR-based general computer technology experiment demonstration platform
  71. Indoor environment monitoring method based on the fusion of audio recognition and video patrol features
  72. Health condition prediction method of the computer numerical control machine tool parts by ensembling digital twins and improved LSTM networks
  73. Establishment of a green degree evaluation model for wall materials based on lifecycle
  74. Quantitative evaluation of college music teaching pronunciation based on nonlinear feature extraction
  75. Multi-index nonlinear robust virtual synchronous generator control method for microgrid inverters
  76. Manufacturing engineering production line scheduling management technology integrating availability constraints and heuristic rules
  77. Analysis of digital intelligent financial audit system based on improved BiLSTM neural network
  78. Attention community discovery model applied to complex network information analysis
  79. A neural collaborative filtering recommendation algorithm based on attention mechanism and contrastive learning
  80. Rehabilitation training method for motor dysfunction based on video stream matching
  81. Research on façade design for cold-region buildings based on artificial neural networks and parametric modeling techniques
  82. Intelligent implementation of muscle strain identification algorithm in Mi health exercise induced waist muscle strain
  83. Optimization design of urban rainwater and flood drainage system based on SWMM
  84. Improved GA for construction progress and cost management in construction projects
  85. Evaluation and prediction of SVM parameters in engineering cost based on random forest hybrid optimization
  86. Museum intelligent warning system based on wireless data module
  87. Optimization design and research of mechatronics based on torque motor control algorithm
  88. Special Issue: Nonlinear Engineering’s significance in Materials Science
  89. Experimental research on the degradation of chemical industrial wastewater by combined hydrodynamic cavitation based on nonlinear dynamic model
  90. Study on low-cycle fatigue life of nickel-based superalloy GH4586 at various temperatures
  91. Some results of solutions to neutral stochastic functional operator-differential equations
  92. Ultrasonic cavitation did not occur in high-pressure CO2 liquid
  93. Research on the performance of a novel type of cemented filler material for coal mine opening and filling
  94. Testing of recycled fine aggregate concrete’s mechanical properties using recycled fine aggregate concrete and research on technology for highway construction
  95. A modified fuzzy TOPSIS approach for the condition assessment of existing bridges
  96. Nonlinear structural and vibration analysis of straddle monorail pantograph under random excitations
  97. Achieving high efficiency and stability in blue OLEDs: Role of wide-gap hosts and emitter interactions
  98. Construction of teaching quality evaluation model of online dance teaching course based on improved PSO-BPNN
  99. Enhanced electrical conductivity and electromagnetic shielding properties of multi-component polymer/graphite nanocomposites prepared by solid-state shear milling
  100. Optimization of thermal characteristics of buried composite phase-change energy storage walls based on nonlinear engineering methods
  101. A higher-performance big data-based movie recommendation system
  102. Nonlinear impact of minimum wage on labor employment in China
  103. Nonlinear comprehensive evaluation method based on information entropy and discrimination optimization
  104. Application of numerical calculation methods in stability analysis of pile foundation under complex foundation conditions
  105. Research on the contribution of shale gas development and utilization in Sichuan Province to carbon peak based on the PSA process
  106. Characteristics of tight oil reservoirs and their impact on seepage flow from a nonlinear engineering perspective
  107. Nonlinear deformation decomposition and mode identification of plane structures via orthogonal theory
  108. Numerical simulation of damage mechanism in rock with cracks impacted by self-excited pulsed jet based on SPH-FEM coupling method: The perspective of nonlinear engineering and materials science
  109. Cross-scale modeling and collaborative optimization of ethanol-catalyzed coupling to produce C4 olefins: Nonlinear modeling and collaborative optimization strategies
  110. Unequal width T-node stress concentration factor analysis of stiffened rectangular steel pipe concrete
  111. Special Issue: Advances in Nonlinear Dynamics and Control
  112. Development of a cognitive blood glucose–insulin control strategy design for a nonlinear diabetic patient model
  113. Big data-based optimized model of building design in the context of rural revitalization
  114. Multi-UAV assisted air-to-ground data collection for ground sensors with unknown positions
  115. Design of urban and rural elderly care public areas integrating person-environment fit theory
  116. Application of lossless signal transmission technology in piano timbre recognition
  117. Application of improved GA in optimizing rural tourism routes
  118. Architectural animation generation system based on AL-GAN algorithm
  119. Advanced sentiment analysis in online shopping: Implementing LSTM models analyzing E-commerce user sentiments
  120. Intelligent recommendation algorithm for piano tracks based on the CNN model
  121. Visualization of large-scale user association feature data based on a nonlinear dimensionality reduction method
  122. Low-carbon economic optimization of microgrid clusters based on an energy interaction operation strategy
  123. Optimization effect of video data extraction and search based on Faster-RCNN hybrid model on intelligent information systems
  124. Construction of image segmentation system combining TC and swarm intelligence algorithm
  125. Particle swarm optimization and fuzzy C-means clustering algorithm for the adhesive layer defect detection
  126. Optimization of student learning status by instructional intervention decision-making techniques incorporating reinforcement learning
  127. Fuzzy model-based stabilization control and state estimation of nonlinear systems
  128. Optimization of distribution network scheduling based on BA and photovoltaic uncertainty
  129. Tai Chi movement segmentation and recognition on the grounds of multi-sensor data fusion and the DBSCAN algorithm
  130. Special Issue: Dynamic Engineering and Control Methods for the Nonlinear Systems - Part III
  131. Generalized numerical RKM method for solving sixth-order fractional partial differential equations
https://doi.org/10.1515/nleng-2025-0157
Schlagwörter für diesen Artikel
construction progress; cost management; genetic algorithm; serial operation; multi-task scheduling
Creative Commons
BY 4.0

Artikel in diesem Heft

  1. Research Articles
  2. Generalized (ψ,φ)-contraction to investigate Volterra integral inclusions and fractal fractional PDEs in super-metric space with numerical experiments
  3. Solitons in ultrasound imaging: Exploring applications and enhancements via the Westervelt equation
  4. Stochastic improved Simpson for solving nonlinear fractional-order systems using product integration rules
  5. Exploring dynamical features like bifurcation assessment, sensitivity visualization, and solitary wave solutions of the integrable Akbota equation
  6. Research on surface defect detection method and optimization of paper-plastic composite bag based on improved combined segmentation algorithm
  7. Impact the sulphur content in Iraqi crude oil on the mechanical properties and corrosion behaviour of carbon steel in various types of API 5L pipelines and ASTM 106 grade B
  8. Unravelling quiescent optical solitons: An exploration of the complex Ginzburg–Landau equation with nonlinear chromatic dispersion and self-phase modulation
  9. Perturbation-iteration approach for fractional-order logistic differential equations
  10. Variational formulations for the Euler and Navier–Stokes systems in fluid mechanics and related models
  11. Rotor response to unbalanced load and system performance considering variable bearing profile
  12. DeepFowl: Disease prediction from chicken excreta images using deep learning
  13. Channel flow of Ellis fluid due to cilia motion
  14. A case study of fractional-order varicella virus model to nonlinear dynamics strategy for control and prevalence
  15. Multi-point estimation weldment recognition and estimation of pose with data-driven robotics design
  16. Analysis of Hall current and nonuniform heating effects on magneto-convection between vertically aligned plates under the influence of electric and magnetic fields
  17. A comparative study on residual power series method and differential transform method through the time-fractional telegraph equation
  18. Insights from the nonlinear Schrödinger–Hirota equation with chromatic dispersion: Dynamics in fiber–optic communication
  19. Mathematical analysis of Jeffrey ferrofluid on stretching surface with the Darcy–Forchheimer model
  20. Exploring the interaction between lump, stripe and double-stripe, and periodic wave solutions of the Konopelchenko–Dubrovsky–Kaup–Kupershmidt system
  21. Computational investigation of tuberculosis and HIV/AIDS co-infection in fuzzy environment
  22. Signature verification by geometry and image processing
  23. Theoretical and numerical approach for quantifying sensitivity to system parameters of nonlinear systems
  24. Chaotic behaviors, stability, and solitary wave propagations of M-fractional LWE equation in magneto-electro-elastic circular rod
  25. Dynamic analysis and optimization of syphilis spread: Simulations, integrating treatment and public health interventions
  26. Visco-thermoelastic rectangular plate under uniform loading: A study of deflection
  27. Threshold dynamics and optimal control of an epidemiological smoking model
  28. Numerical computational model for an unsteady hybrid nanofluid flow in a porous medium past an MHD rotating sheet
  29. Regression prediction model of fabric brightness based on light and shadow reconstruction of layered images
  30. Dynamics and prevention of gemini virus infection in red chili crops studied with generalized fractional operator: Analysis and modeling
  31. Qualitative analysis on existence and stability of nonlinear fractional dynamic equations on time scales
  32. Fractional-order super-twisting sliding mode active disturbance rejection control for electro-hydraulic position servo systems
  33. Analytical exploration and parametric insights into optical solitons in magneto-optic waveguides: Advances in nonlinear dynamics for applied sciences
  34. Bifurcation dynamics and optical soliton structures in the nonlinear Schrödinger–Bopp–Podolsky system
  35. Review Article
  36. Haar wavelet collocation method for existence and numerical solutions of fourth-order integro-differential equations with bounded coefficients
  37. Special Issue: Nonlinear Analysis and Design of Communication Networks for IoT Applications - Part II
  38. Silicon-based all-optical wavelength converter for on-chip optical interconnection
  39. Research on a path-tracking control system of unmanned rollers based on an optimization algorithm and real-time feedback
  40. Analysis of the sports action recognition model based on the LSTM recurrent neural network
  41. Industrial robot trajectory error compensation based on enhanced transfer convolutional neural networks
  42. Research on IoT network performance prediction model of power grid warehouse based on nonlinear GA-BP neural network
  43. Interactive recommendation of social network communication between cities based on GNN and user preferences
  44. Application of improved P-BEM in time varying channel prediction in 5G high-speed mobile communication system
  45. Construction of a BIM smart building collaborative design model combining the Internet of Things
  46. Optimizing malicious website prediction: An advanced XGBoost-based machine learning model
  47. Economic operation analysis of the power grid combining communication network and distributed optimization algorithm
  48. Sports video temporal action detection technology based on an improved MSST algorithm
  49. Internet of things data security and privacy protection based on improved federated learning
  50. Enterprise power emission reduction technology based on the LSTM–SVM model
  51. Construction of multi-style face models based on artistic image generation algorithms
  52. Research and application of interactive digital twin monitoring system for photovoltaic power station based on global perception
  53. Special Issue: Decision and Control in Nonlinear Systems - Part II
  54. Animation video frame prediction based on ConvGRU fine-grained synthesis flow
  55. Application of GGNN inference propagation model for martial art intensity evaluation
  56. Benefit evaluation of building energy-saving renovation projects based on BWM weighting method
  57. Deep neural network application in real-time economic dispatch and frequency control of microgrids
  58. Real-time force/position control of soft growing robots: A data-driven model predictive approach
  59. Mechanical product design and manufacturing system based on CNN and server optimization algorithm
  60. Application of finite element analysis in the formal analysis of ancient architectural plaque section
  61. Research on territorial spatial planning based on data mining and geographic information visualization
  62. Fault diagnosis of agricultural sprinkler irrigation machinery equipment based on machine vision
  63. Closure technology of large span steel truss arch bridge with temporarily fixed edge supports
  64. Intelligent accounting question-answering robot based on a large language model and knowledge graph
  65. Analysis of manufacturing and retailer blockchain decision based on resource recyclability
  66. Flexible manufacturing workshop mechanical processing and product scheduling algorithm based on MES
  67. Exploration of indoor environment perception and design model based on virtual reality technology
  68. Tennis automatic ball-picking robot based on image object detection and positioning technology
  69. A new CNN deep learning model for computer-intelligent color matching
  70. Design of AR-based general computer technology experiment demonstration platform
  71. Indoor environment monitoring method based on the fusion of audio recognition and video patrol features
  72. Health condition prediction method of the computer numerical control machine tool parts by ensembling digital twins and improved LSTM networks
  73. Establishment of a green degree evaluation model for wall materials based on lifecycle
  74. Quantitative evaluation of college music teaching pronunciation based on nonlinear feature extraction
  75. Multi-index nonlinear robust virtual synchronous generator control method for microgrid inverters
  76. Manufacturing engineering production line scheduling management technology integrating availability constraints and heuristic rules
  77. Analysis of digital intelligent financial audit system based on improved BiLSTM neural network
  78. Attention community discovery model applied to complex network information analysis
  79. A neural collaborative filtering recommendation algorithm based on attention mechanism and contrastive learning
  80. Rehabilitation training method for motor dysfunction based on video stream matching
  81. Research on façade design for cold-region buildings based on artificial neural networks and parametric modeling techniques
  82. Intelligent implementation of muscle strain identification algorithm in Mi health exercise induced waist muscle strain
  83. Optimization design of urban rainwater and flood drainage system based on SWMM
  84. Improved GA for construction progress and cost management in construction projects
  85. Evaluation and prediction of SVM parameters in engineering cost based on random forest hybrid optimization
  86. Museum intelligent warning system based on wireless data module
  87. Optimization design and research of mechatronics based on torque motor control algorithm
  88. Special Issue: Nonlinear Engineering’s significance in Materials Science
  89. Experimental research on the degradation of chemical industrial wastewater by combined hydrodynamic cavitation based on nonlinear dynamic model
  90. Study on low-cycle fatigue life of nickel-based superalloy GH4586 at various temperatures
  91. Some results of solutions to neutral stochastic functional operator-differential equations
  92. Ultrasonic cavitation did not occur in high-pressure CO2 liquid
  93. Research on the performance of a novel type of cemented filler material for coal mine opening and filling
  94. Testing of recycled fine aggregate concrete’s mechanical properties using recycled fine aggregate concrete and research on technology for highway construction
  95. A modified fuzzy TOPSIS approach for the condition assessment of existing bridges
  96. Nonlinear structural and vibration analysis of straddle monorail pantograph under random excitations
  97. Achieving high efficiency and stability in blue OLEDs: Role of wide-gap hosts and emitter interactions
  98. Construction of teaching quality evaluation model of online dance teaching course based on improved PSO-BPNN
  99. Enhanced electrical conductivity and electromagnetic shielding properties of multi-component polymer/graphite nanocomposites prepared by solid-state shear milling
  100. Optimization of thermal characteristics of buried composite phase-change energy storage walls based on nonlinear engineering methods
  101. A higher-performance big data-based movie recommendation system
  102. Nonlinear impact of minimum wage on labor employment in China
  103. Nonlinear comprehensive evaluation method based on information entropy and discrimination optimization
  104. Application of numerical calculation methods in stability analysis of pile foundation under complex foundation conditions
  105. Research on the contribution of shale gas development and utilization in Sichuan Province to carbon peak based on the PSA process
  106. Characteristics of tight oil reservoirs and their impact on seepage flow from a nonlinear engineering perspective
  107. Nonlinear deformation decomposition and mode identification of plane structures via orthogonal theory
  108. Numerical simulation of damage mechanism in rock with cracks impacted by self-excited pulsed jet based on SPH-FEM coupling method: The perspective of nonlinear engineering and materials science
  109. Cross-scale modeling and collaborative optimization of ethanol-catalyzed coupling to produce C4 olefins: Nonlinear modeling and collaborative optimization strategies
  110. Unequal width T-node stress concentration factor analysis of stiffened rectangular steel pipe concrete
  111. Special Issue: Advances in Nonlinear Dynamics and Control
  112. Development of a cognitive blood glucose–insulin control strategy design for a nonlinear diabetic patient model
  113. Big data-based optimized model of building design in the context of rural revitalization
  114. Multi-UAV assisted air-to-ground data collection for ground sensors with unknown positions
  115. Design of urban and rural elderly care public areas integrating person-environment fit theory
  116. Application of lossless signal transmission technology in piano timbre recognition
  117. Application of improved GA in optimizing rural tourism routes
  118. Architectural animation generation system based on AL-GAN algorithm
  119. Advanced sentiment analysis in online shopping: Implementing LSTM models analyzing E-commerce user sentiments
  120. Intelligent recommendation algorithm for piano tracks based on the CNN model
  121. Visualization of large-scale user association feature data based on a nonlinear dimensionality reduction method
  122. Low-carbon economic optimization of microgrid clusters based on an energy interaction operation strategy
  123. Optimization effect of video data extraction and search based on Faster-RCNN hybrid model on intelligent information systems
  124. Construction of image segmentation system combining TC and swarm intelligence algorithm
  125. Particle swarm optimization and fuzzy C-means clustering algorithm for the adhesive layer defect detection
  126. Optimization of student learning status by instructional intervention decision-making techniques incorporating reinforcement learning
  127. Fuzzy model-based stabilization control and state estimation of nonlinear systems
  128. Optimization of distribution network scheduling based on BA and photovoltaic uncertainty
  129. Tai Chi movement segmentation and recognition on the grounds of multi-sensor data fusion and the DBSCAN algorithm
  130. Special Issue: Dynamic Engineering and Control Methods for the Nonlinear Systems - Part III
  131. Generalized numerical RKM method for solving sixth-order fractional partial differential equations
Jetzt anmelden und 20% sparen
Institutioneller Zugang
Wie funktioniert Authentifizierung?
Haben Sie eine Idee, wie wir unsere Website verbessern können?
Bitte schreiben Sie uns.
© 2025 De Gruyter Brill
Heruntergeladen am 14.11.2025 von https://www.degruyterbrill.com/document/doi/10.1515/nleng-2025-0157/html
Button zum nach oben scrollen