Particle swarm optimization and fuzzy C-means clustering algorithm for the adhesive layer defect detection

Lvfen Zhu

doi:10.1515/nleng-2025-0161

Article Open Access

Particle swarm optimization and fuzzy C-means clustering algorithm for the adhesive layer defect detection

Lvfen Zhu

Published/Copyright: September 4, 2025

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Nonlinear Engineering Volume 14 Issue 1

Abstract

To improve the performance of the adhesive layer defect detection (DD) planar array capacitor system, an adhesive layer DD method based on particle swarm optimization and fuzzy C-means (FCM) clustering algorithm is proposed. By classifying erroneous capacitance data, the experiment distinguishes the capacitance values at defect locations from those at defect-free locations. In response to the presence of artifacts in the image reconstruction results, the optimal threshold method is used to post-process the reconstructed images using the mixed regularization method. These experiments confirmed that FCM clustering reduced the mean absolute deviation (MAD) of data by about 6.1%, and the proposed clustering algorithm reduced the MAD of data by about 23.2%. Compared to the Tikhonov method, the mixed regularization method reduced the relative error of reconstructed images by about 13.1% and increased the correlation coefficient of reconstructed images by about 21.6%. Therefore, this research method had significant effects in reducing data fluctuations and errors, effectively improving the image reconstructing quality and the accuracy of DD. This study can effectively improve the accuracy of adhesive layer DD, help reduce production costs, and improve production efficiency.

Keywords: PSO-FCM, adhesive layer; defect detection; image reconstruction; optimal threshold; quality evaluation

1 Introduction

As the modern manufacturing industry develops, defect detection (DD) of the adhesive layer is an urgent problem that needs to be dealt with. The defects in the adhesive layer not only affect the quality of the product but may even lead to serious safety accidents [1]. Therefore, developing an efficient and accurate adhesive layer using the DD method is significant. The initial technology mainly relied on artificial visual inspection, which was not only time-consuming and labor-intensive but also limited by the experience and fatigue of the inspection personnel [2,3]. In addition, existing machine vision-based methods also have some problems, such as dependence on defect types and algorithm complexity [4]. In recent years, the fuzzy C-means (FCM) clustering algorithm has been utilized in data mining and pattern recognition due to its good clustering performance [5]. However, in practical applications, FCM also has some problems, such as sensitivity to the initial cluster center (CC) and susceptibility to local optima. To address these issues, the study introduces particle swarm optimization (PSO) and proposes a PSO-FCM algorithm, aiming to improve the accuracy and efficiency of detection. The study consists of four sections. First, Section 2 provides the summary of research related to PSO, FCM, and DD; second, the DD method is designed and validated in Section 3, and finally, the summary of the entire study is provided.

2 Related works

PSO is a population-based stochastic optimizing technique, in which members of a population continuously change their search patterns through a learning experience. Fan and Wang proposed an average field model for network fake news dissemination based on PSO, assuming that ignorant individuals were more likely to believe and forward fake news spread by similar disseminators. After the analysis, the critical threshold was inversely proportional to the maximum eigenvalue and influenced the coefficient C of the similarity matrix, and the proposed model was effective [6]. Kulkarni and Ghawghawe used a mixed model, combined with the dragonfly algorithm and the PSO, to optimize the configuration of thyristors or controllable series compensators in power systems. These studies validated the effectiveness of this method in optimizing position and parameter settings [7]. Pant and Kumar put forward a new hybrid fuzzy time-series prediction method using PSO and intuitionistic fuzzy sets, which solved the optimal length and uncertainty. These results confirmed that this method reduced the mean square error by 5% [8]. FCM is a clustering algorithm based on fuzzy set theory, which iteratively optimizes the membership function to determine the FCM, thereby achieving fuzzy clustering of datasets. Lin and Chen proposed a centroid self-fusion hierarchical FCM to automatically determine the optimal clusters and solve key problems in existing clustering algorithms. Compared to other methods, this method had simpler hyperparameter adjustment and better clustering performance [9]. Kiruba Nesamalar et al. developed an efficient model that combines FCM with firefly swarm optimization to predict the optimal interaction between genes and ligands. The results showed that the model significantly reduced the binding energy compared to other existing methods among 500 sample instances on the NCBI dataset [10].

DD is a process that utilizes various technical means and methods to identify, locate, and evaluate potential defects in products, materials, or engineering structures. Xiang et al. put forward a new DD method using 3D microtexture surface printing, which utilized directional codes to resist lighting fluctuations and constructed a multi-pair pixel consistency model based on the consistency of pixel pairs. These results confirmed that the DD rate of this method was close to 100% [11]. Cao et al. put forward a means for enhancing aerial images using drones, which effectively detected insulators with self-explosion defects through improved saliency map generation. These results confirmed that the accuracy of this method was 95.1%, which was better than existing solutions [12]. Zhang et al. put forward a fabric DD means using contrastive learning for attention generation adversarial networks, which captured long-range dependencies through contrastive learning and extracted key features through channel attention modules. These results validated that this method achieved 38.25% union intersection values and 51.67% F1 measure values on public datasets [13]. Pan et al. proposed an encoder–decoder architecture using convolutional blocks to improve the efficiency of DD on mobile screen surfaces. These results confirmed that this method had superior DD performance in real industrial scenarios and met the real-time requirements of industrial production [14]. Zhao et al. proposed a frequency domain-based genetic algorithm (GA) variational modulus decomposition reflection coefficient spectrum method for detecting and locating weak defects in cable shielding layers. These results confirmed that this method effectively detected and located weak defects such as single-strand fractures and holes, which accurately identify defected types, providing new ideas for cable shielding layer DD [15]. Nguyen et al. first used traditional clustering methods such as k-means, FCM, and self-organizing mapping to detect defects in finished products. Then, they proposed a new clustering method that combines the sine cosine algorithm and probability FCM (SCA-PFCM) to classify the detected defects into multiple categories and analyze the root cause of the faults. The results showed that the SCA-PFCM algorithm could detect 97% of defects and classify them into four categories [16]. Li et al. proposed an improved Yolov5 algorithm for fabric DD, which improved the model’s ability to detect small defects by introducing a coordinate attention module and a smoother activation function. The proposed algorithm also integrated a particular loss function to address issues of sample imbalance. The experimental results showed that the improved algorithm achieved higher mean average precision metrics and lower parameter computation on the Aliyun TianChi public dataset, meeting the requirements of real-time detection [17]. Tziolas et al. combined deep learning and FCM to fine-tune well-known convolutional neural networks (CNNs) through transfer learning to extract features and used the K-means algorithm for feature clustering. They then defined causal relationships through FCM models to assist decision-making. The experimental results demonstrated that the accuracy of this method in antenna assembly DD tasks reached 80%, which was 3% higher than existing CNN classifiers and still showed high potential in the case of data scarcity [18].

In summary, many researchers have conducted different research and designs on PSO, FCM, and DD. However, existing DD methods suffer from low efficiency when dealing with large amounts of data or complex scenarios. Therefore, a data processing method based on PSO-FCM is proposed for adhesive layer DD, aiming to provide the effect of defect image reconstruction (IR) and improve the performance of DD.

3 Design of DD method for adhesive layer

PSO-FCM is proposed to preprocess capacitance data in planar array capacitance imaging (PACI) systems for adhesive layer DD. Meanwhile, the study adopts the optimal threshold method to post-process the reconstructed images of the mixed regularization method. By reconstructing the regularization matrix, an approximate true distribution of the dielectric constant is obtained, thereby improving the accuracy of reconstructed images.

3.1 Data preprocessing method based on PSO-FCM

The PACI system has been developed for the purpose of detecting defects in the adhesive layer DD. It accomplishes this by providing capacitance distribution information on the surface of the adhesive layer. Figure 1 shows the PACI system, which mainly includes a planar array capacitive sensor, a data acquisition, and an IR module. The sensor module is connected to the data acquisition module through signal lines, and the data acquisition module can obtain 66 capacitance data and import them into the computer. The overall size of the planar array capacitive sensor used in the experiment is 160 mm × 160 mm, with a sensor substrate thickness of 15 mm. The data acquisition module employs the ITS-m3 capacitive acquisition instrument, which has a sensitivity range of 0.01–1 pF and 24 channels. This instrument facilitates single- and double-sided detection.

Figure 1

Structure of the planar array capacitor system.

Noise in capacitive imaging systems typically manifests as irregular fluctuations in data, characterized by randomness, non-structural properties, and independence from useful signals. In the PACI system, noise mainly comes from electronic noise of the measuring equipment, environmental interference, and errors in the signal transmission process. The interference between different noise sources refers to the interaction between them, which may cause noise superposition or cancellation and present non-linear relationships, thereby making the synthesis effect complex. It varies over time and is related to the environmental factors and equipment status of signal acquisition. Noise can also cause poor stability of capacitance data and affect the quality of IR. The PSO-FCM algorithm is proposed to preprocess capacitance data in response to the poor stability of the PACI system’s infrared process and the susceptibility to noise interference, which leads to a decrease in reconstructed image quality. This method classifies erroneous capacitance data, distinguishes the capacitance values at defective and defect-free locations, reduces the error caused by noise interference on capacitance data, and ensures the stability of capacitance data. The dielectric constant’s distribution on the surface of the sensor is represented by the following equation:

(1) G = S T C .

In Eq. (1), G is the distribution of the dielectric constant, S is the sensitivity, and C is the capacitance. The negative gradient of data residuals is represented by the following equation:

(2) ∇ ⋅ 1 2 ∥ S G − C ∥ 2 = S T S G − S T C = S T ( S G − C ) .

In Eq. (2), ∇ ⋅ 1 2 ∥ S G − C ∥ 2 is the negative gradient of data residuals. The iterative formula obtained by using negative gradient as the search direction is represented by the following equation:

(3) G k + 1 = G k − α k S T ( S G k − C ) .

In Eq. (3), G k is the dielectric distribution under error k and α k is the positive parameter. The error is represented by the following equation:

(4) k = C − S G k .

In Eq. (4), S G k is the capacitance value for solving the forward problem. In the DD of PACI systems, capacitance data are affected by the “soft field” characteristics of sensitive fields and the complex properties of materials, resulting in a smaller order of magnitude of data. Meanwhile, due to noise interference from the detection equipment and environment, there is an issue of unstable capacitance data. This unstable capacitance value can cause serious pathological changes when solving the distribution of the dielectric constant, leading to a decrease in the reconstructed images’ quality. Therefore, to obtain high-quality reconstructed images, these capacitance data should be optimized. Using PSO-FCM to perform fuzzy division on capacitance data, the capacitance data at defect locations and at defect-free locations are clearly classified, stabilizing the capacitance data affected by environmental noise. In FCM, the constraint conditions of the membership matrix are represented by the following equation:

(5) ∑ j = 1 c u i j = 1 , ∀ i = 1 , 2 , … , n u i j ∈ [ 0 , 1 ] , i = 1 , 2 , … n , j = 1 , 2 , … , c 0 < ∑ j = 1 n u i j < n , ∀ j = 1 , 2 , … , c .

In Eq. (5), the dataset X has n samples, the quantity of categories is c , the sample is represented as x i , and the membership degree corresponding to class j is u i j . The objective function is represented by the following equation:

(6) J m ( U , V ) = ∑ i = 1 c ∑ j = 1 n u i j m d i j 2 .

In Eq. (6), U is the membership matrix, V is the CC set, m is the fuzzy weighting coefficient, and d i j 2 is the i th sample to the j th CC’s Euclidean distance. Due to the sensitivity of FCM to the selection of initial CCs, it may lead to falling into local optima. Therefore, PSO is introduced to choose the original CC to obtain the global optimal solution. Second, the similarity between the data of the same class is maximized by minimizing the weighted sum of squared errors of classes, while the similarity between the data of different classes is minimized. This process achieves accurate classification of capacitance data.

Figure 2 shows the FCM improvement process. First, the capacitance data are processed using the PACI principle and capacitance detection equipment. The IR method is used for IR. Then, the initial CCs are selected through PSO to avoid FCM falling into local optima. Next, the weighted error square is used as the fitness function to measure the compactness of the classification data to improve the classification performance. The applicability function is represented by the following equation:

(7) Fit = ∑ i = 1 c ∑ j = 1 n u i j m d i j 2 .

Figure 2

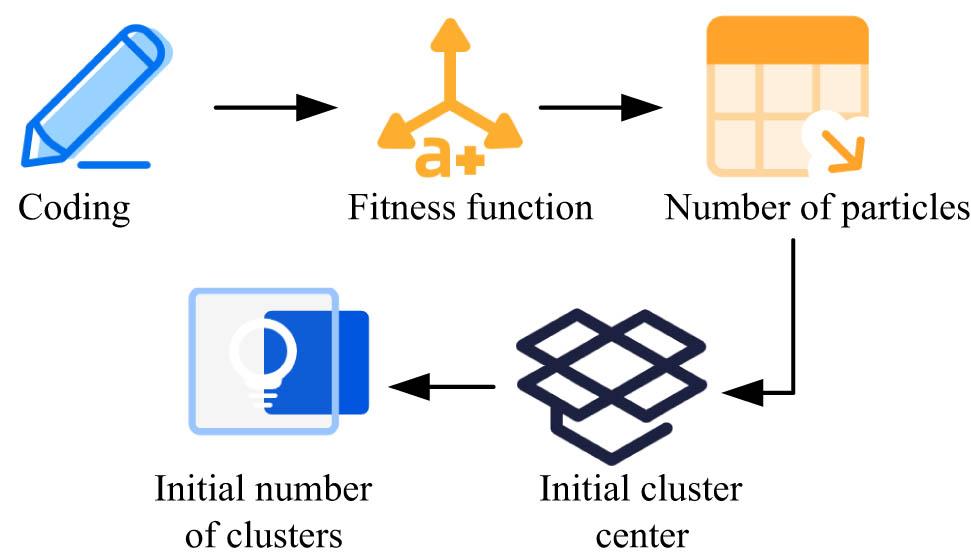
Improvement process of the FCM algorithm.

In Eq. (7), Fit is the fitness function, derived from the objective function in Eq. (6). The particle velocity and position updates are represented by the following equation:

(8) v id ( t + 1 ) = w ⋅ v id ( t ) + c 1 r 1 [ P id ( t ) − x id ( t ) ] + c 2 r 2 [ P gd ( t ) + x id ( t ) ] x id ( t + 1 ) = x id ( t ) + v id ( t + 1 ) .

In Eq. (8), v id and x id are the velocity and position of the i th particle, respectively, w is the weight factor, c 1 and c 2 are the acceleration factors respectively, and r 1 and r 2 are two random numbers, respectively. In PSO, the parameters such as the particle number, initialization speed and position, inertia weight, acceleration factor, and maximum number of iterations are set. Then, through multiple iterations, the optimal particle is found and used as the initial CC for the FCM. Finally, the cluster quantity is initialized, the weighting coefficient and termination threshold are determined, and these optimized stable capacitance data are obtained through continuous iterative clustering for IR. Figure 3 shows the PSO-FCM process.

Figure 3

PSO-FCM algorithm process.

The process of PSO-FCM is as follows. First, various parameters are set, including the initialized cluster quantity. The weighting coefficient, termination threshold, number of clusters, and maximum iteration are determined. CC is initialized. The parameters and their values are usually set as follows: the initial number of clusters is 5, the weighting coefficient is 0.5, the termination threshold is 0.01, the number of clusters is the same as the initial number of clusters, and the maximum number of iterations is 100. These parameters are usually set based on specific problems and experience, and can be adjusted and optimized through experiments to achieve the best clustering effect. Then, the membership degree and CC are updated. When the membership update meets the conditions, the iterative operation stops and the optimized capacitance data are output, and the algorithm ends. The judgment formula for stopping iteration is represented by the following equation:

(9) ∥ Fit ( t + 1 ) − Fit ( t ) ∥ < ε .

In Eq. (9), ε is the termination threshold, and Fit ( t ) and Fit ( t + 1 ) are the fitness values for time t and t + 1 , respectively.

3.2 Design of IR algorithm using the mixed regularization method

The IR results of PACI have issues such as artifacts, which cannot meet the requirements for image quality. Therefore, a new method is needed to improve this situation, namely the hybrid regularization method. The utilization of a mixed regularization method is predicated on its capacity to enhance the quality of the equation, thereby mitigating its ill-conditioned nature. This, in turn, facilitates the identification of an approximate true solution to the inverse problem [19]. This method divides the singular values of the sensitivity matrix into larger and smaller parts by selecting appropriate truncation parameters, with the correction being applied exclusively to the smaller singular values. This not only preserves the estimation of the solution by the smaller singular values but also suppresses the influence of noise on the solution. At the same time, the regularization matrix is reconstructed to obtain an approximate true distribution of dielectric constants, effectively improving the quality of IR. The sensitivity matrix’s singular value decomposing process is represented by the following equation:

(10) S = U S V T = ∑ i = 1 n u i σ i v i T .

In Eq. (10), σ i is the singular value of the sensitivity matrix, v i is the right eigenvector, and u i is the left eigenvector. The ideal state capacitance condition is represented by the following equation:

(11) G L = ∑ i = 1 n u i T C σ i v i = ∑ i = 1 n u i T C L σ i + u i T e σ i v i .

In Eq. (11), G L is the ideal state dielectric constant distribution, C L is the ideal capacitance value, and e is the noise in the observation state. Tikhonov and truncated singular value decomposition (TSVD) regularization methods transform ill-posed equations into well-posed equations by correcting smaller singular values and directly discarding smaller singular values, respectively [20]. However, although Tikhonov corrects smaller singular values, all singular values are corrected, resulting in the obtained solution deviating from the true solution. TSVD not only eliminates small singular value interference but also loses the estimation of the solution by small singular values [21]. Therefore, the mixed regularization method combines the advantages of both and divides the singular values of the sensitivity matrix into larger and smaller parts by truncating the parameters. Then, the Tikhonov method is used to correct only small singular values. Meanwhile, it ensures that larger singular values will not be corrected, thus obtaining stable solutions. To achieve this goal, it is necessary to reconstruct the regularization matrix, which is represented by the following equation:

(12) L H = R V T .

In Eq. (12), L H is the mixed regularization matrix, R is the diagonal matrix, and V T is the sensitivity left singular matrix. The solution of the mixed regularization method is represented by the following equation:

(13) G H = ∑ i = 1 k u i T C σ i v i + ∑ i = k + 1 n σ i 2 ω σ i 2 + ( 1 − ω ) μ 2 u i T C σ i v i .

In Eq. (13), G H is the solution of the mixed regularization method and ω is the parameter used to adjust the filtering coefficients. In a PACI system, regularization parameters are selected to obtain the regularization solution that is closest to the true solution. First, the regularization parameter values need to be determined using the L-curve method. Then, the k value is determined according to certain rules. Finally, the parameter values are determined using the generalized cross-validation method. In this process, the L-curve method is used to find the regularization parameters that balance the solution of the ill-conditioned equation with the regularization matrix. The generalized cross-validation method is used to further determine the parameter ω to obtain the optimal approximate solution.

Figure 4 shows a PACI algorithm using mixed regularization. This algorithm utilizes sensitivity matrix singular decomposition and a regularization matrix for capacitance data IR. By introducing regularization and truncation parameters, the capacitance data are mixed and regularized to avoid overfitting and noise interference. In the reconstructed images of PACI systems, the presence of artifacts leads to blurring of information such as size and shape in the reconstructed images. To solve this challenge and improve the reconstructed images’ accuracy, the optimal threshold method is used for post-processing of the reconstructed images.

Figure 4

A PACI algorithm using mixed regularization.

Figure 5 shows the optimal threshold image post-processing method. First, the grayscale threshold is selected based on the grayscale characteristics of the image. Then, each pixel in the image is compared with the grayscale threshold. After repeatedly calculating the optimal threshold, the image is binarized and segmented. The reconstructed image containing multiple grayscales is transformed into a binary image with only two grayscales. The image G t ( i , j ) after threshold processing is represented by the following equation:

(14) G t ( i , j ) = 1 , G ( i , j ) ≥ T 0 , G ( i , j ) < T .

Figure 5

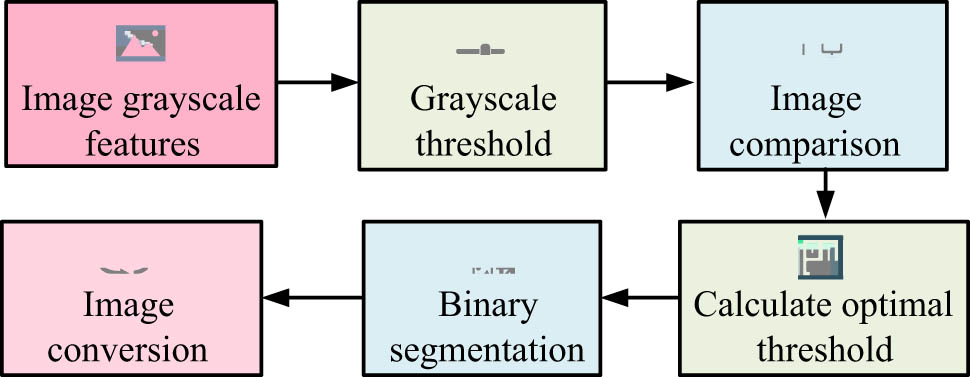
Optimal threshold image post-processing method.

In Eq. (14), G ( i , j ) is the reconstructed image and T is the threshold. After threshold processing of the image, the capacitance value can be calculated by combining the sensitivity matrix. The threshold corresponding to the smallest error is the optimal threshold, and the error of the capacitance value is the smallest at this time, represented by the following equation:

(15) min ∥ C t − C o ∥ 2 2 .

In Eq. (15), C o is the actual capacitance value, and C t is the capacitance value calculated at threshold T . In summary, the mixed regularization method first divides the singular values of the sensitivity matrix into larger and smaller parts, and only corrects the smaller singular values. This effectively suppresses the interference of noise while preserving important information. This method is not only applicable to PACI systems but can also be extended to other fields that require IR, including medical imaging, geophysical exploration, etc. In practical implementation, the hybrid regularization method involves the reconstruction of the regularization matrix and the integration of the L-curve method and the generalized cross-validation method to determine the optimal regularization parameters. This process aims to obtain the regularization solution that is closest to the true solution. In addition, by introducing the optimal threshold method for post-processing the reconstructed image, the clarity and accuracy of the image can be further improved. This method has been demonstrated to reduce artifacts in the reconstructed image, thereby enhancing its resolution and contrast. Consequently, the IR results are rendered more accurate and reliable, making them suitable for situations that demand high image quality.

4 Application analysis of DD methods for adhesive layers

The experiment preprocessed capacitance data using PSO-FCM combined the processed data with sensitivity matrix, and used Tikhonov, TSVD, and mixed regularization methods to perform IR on defect samples to analyze the application effects of different methods.

4.1 Application analysis of data preprocessing methods based on PSO-FCM

The experimental sample is a type of test specimen specifically designed to simulate the performance of the adhesive layer, consisting mainly of the epoxy resin board and ceramic matrix composite material. The size of the epoxy resin board is 160 mm × 160 mm × 2 mm, with good adhesion and mechanical properties, used to simulate the resin part in the bonding layer. The size of the ceramic-based composite material sample is 165 mm × 165 mm × 20 mm, which has high hardness and wear resistance and is used to simulate the ceramic part in the adhesive layer. The source of this experimental sample is specially prepared in industrial production, and its properties are designed to simulate the mechanical, thermal, and chemical properties of the adhesive layer in actual engineering environments. The primary objective of this approach is to evaluate and study the reliability of the adhesive layer. PSO-FCM is used to determine the defects in the adhesive layer. First, in an empty field, sensors collect capacitance data on ceramic matrix composites. Then, under full field conditions, the sensors collect capacitance data on the adhesive layer between the epoxy resin board and the ceramic matrix composite material. By comparing the capacitance data in these two situations, the approximate location of the defect is obtained. The stability of capacitance data is measured by using the mean absolute deviation (MAD). MAD is an indicator that reflects the degree of data fluctuation, which calculates the average of the absolute values of the deviation between data values and the mean. In the experiment, the larger the MAD value, the greater the fluctuation of capacitance data and the larger the error, which affects the accuracy of detection. Relative image error is an important indicator for evaluating the quality of reconstructed images, which compares the differences between the reconstructed image and original image. The smaller the value of the relative image error, the smaller the difference between the reconstructed image and the original image, and the higher the quality of the reconstructed image. The image correlation coefficient is another indicator to measure the quality of reconstructed images, which measures the similarity between the reconstructed image and the original image. The larger the value of the image correlation coefficient, the more similar the reconstructed image is to the original image, and the higher the quality of the reconstructed image. Four different types of defect samples are tested, and the average capacitance data of each group of experiments is calculated. Samples 1 and 2 both have 2 defects, while samples 3 and 4 have 3 to 4 defects. Figure 6 shows the capacitance data processing results of samples 1 and 2.

Figure 6

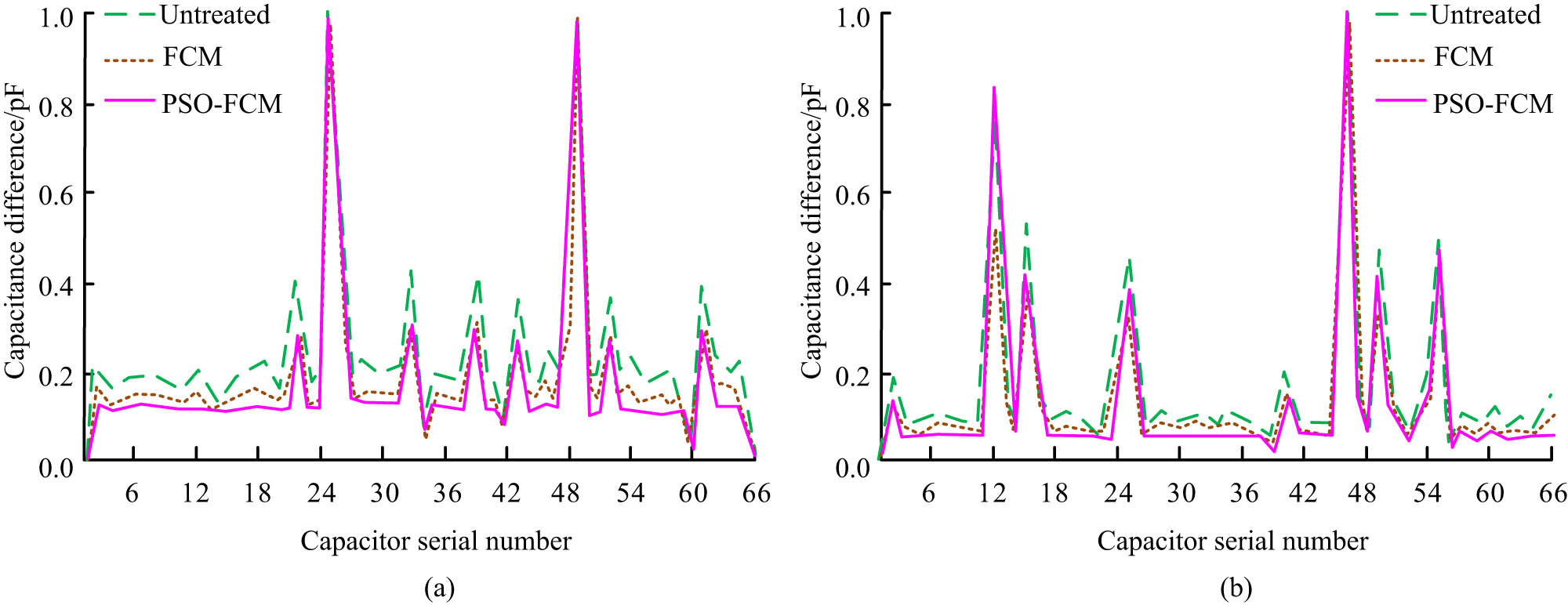
The capacitance data processing results of (a) sample 1 and (b) sample 2.

Figure 6(a) shows the capacitance data processing results of sample 1. The 25th and 49th capacitance data represent the capacitance difference at the defect location. The capacitance differences among 2–21, 27–32, and 53–59 are unstable. This results in low IR quality, which cannot accurately indicate defects’ shape, size, edge and other information, thereby affecting the detection effect of planar array capacitive sensors on adhesive layer defects. However, compared to FCM, after preprocessing the capacitance data using PSO-FCM, the smoothness of the capacitance difference at defect-free positions increases by 56%, improving the data effectiveness and stability. Figure 6(b) shows the capacitance data processing results of sample 2. PSO-FCM not only improves the stability and effectiveness of capacitance data but also makes the capacitance data at the defect location more prominent, enabling more effective detection of defects. Compared to FCM, PSO-FCM has significant advantages in capacitance difference processing. Figure 7 shows the capacitance data processing results of samples 3 and 4.

Figure 7

The capacitance data processing results of (a) sample 3 and (b) sample 4.

Figure 7(a) shows the capacitance data processing results of sample 3. Figure 7(b) shows the capacitance data processing results of sample 4. PSO-FCM not only improves the stability and effectiveness of capacitance data but also effectively highlights the capacitance difference at defect locations, making it easier to detect. Compared to FCM, PSO-FCM has more obvious advantages. It can improve the overall processing efficiency of capacitance data without affecting the stability of the capacitance difference in defect-free positions, providing more reliable data support for DD. Table 1 shows the impact of PSO-FCM on the stability of capacitance data.

Table 1

Impact of the PSO-FCM method on the stability of capacitance data

Sample	Algorithm	Raw data	Optimization data
1	FCM	0.608	0.567
1	PSO-FCM	0.608	0.476
2	FCM	0.621	0.588
2	PSO-FCM	0.621	0.477
3	FCM	0.725	0.681
3	PSO-FCM	0.725	0.549
4	FCM	0.716	0.673
4	PSO-FCM	0.716	0.551

In Table 1, FCM reduces the MAD data by about 6.1%, while PSO-FCM reduces the MAD data by about 23.2%. Compared to traditional FCM, PSO-FCM has significant effects in reducing data fluctuations and errors. PSO-FCM improves the optimized capacitance data stability. These optimized data have a smaller MAD compared to the original data. To further validate the effectiveness of PSO-FCM, the experiment uses local binary pattern (LBP) as the basis for algorithm stacking. Figure 8 shows the quality evaluation results of reconstructed images after stacking different algorithms.

Figure 8

The quality evaluation results of reconstructed images after stacking different algorithms: (a) relative image error and (b) image correlation coefficient.

Figure 8(a) shows the comparison results of relative image errors in reconstructed images, with smaller values indicating higher quality of reconstructed images. Compared to LBP and FCM-LBP, PSO-FCM-LBP reduces the relative error of reconstructed images by approximately 26.2 and 3.2%. Figure 8(b) shows the image correlation coefficients of the reconstructed images, with higher values indicating higher quality of the reconstructed images. Compared to LBP and FCM-LBP, PSO-FCM-LBP increases the image correlation coefficient of reconstructed images by approximately 41.8%. PSO-FCM-LBP has better performance in improving image quality and can be used as an effective data processing method. To verify the advantages of the PSO-FCM algorithm, the experiment compares GA-optimized FCM (GA-FCM), ant colony algorithm (ACO)-optimized FCM (ACO-FCM), and CNN. The performance comparison results of different algorithms are shown in Table 2.

Table 2

Performance comparison results of different algorithms

Algorithm	MAD (%)	Relative image errors	Image correlation coefficients
PSO-FCM	13.6	1.132	0.687
GA-FCM	14.8	1.489	0.579
ACO-FCM	16.7	1.641	0.568
CNN	20.3	1.739	0.521

In Table 2, in terms of indicators, PSO-FCM is 13.6%, while GA-FCM reaches 14.8%. In terms of relative image error, PSO-FCM is 1.132, GA-FCM is 1.489, and CNN is 1.739. In terms of image correlation coefficient, PSO-FCM is 0.687, which is higher than the comparison algorithms. Overall, the PSO-FCM algorithm outperforms other algorithms in all metrics, providing more accurate, less erroneous, and strongly correlated results with the original image.

4.2 Application analysis of the IR algorithm based on the mixed regularization method

This study uses experimental specimens composed of epoxy resin plates and ceramic matrix composites, and four defect settings are followed. By applying PSO-FCM to preprocess capacitance data and combining the processed data with the sensitivity matrix, Tikhonov, TSVD, and mixed regularization methods are used to perform IR on defect samples. Figure 9 shows the IR results of different methods.

Figure 9

IR results using different methods: (a) sample 1 – Tikhonov, (b) sample 1 – TSVD, (c) sample 1 – mix, (d) sample 4 – Tikhonov, (e) sample 4 – TSVD, and (f) sample 4 – mix.

Figure 9(a)–(c) and (d)–(f) shows the reconstructed images of sample 1 and sample 4 obtained through Tikhonov, TSVD, and mixed regularization methods, respectively. Compared to the Tikhonov and TSVD methods, the mixed regularization method had significant advantages in the IR of defective samples. This method improves IR quality, reduces image noise, and more accurately reflects information such as the shape, size, and edges of defects. Therefore, this mixed regularization method is an effective way to improve the quality of IR. Figure 10 shows the reconstructed images’ quality evaluation using different methods.

Figure 10

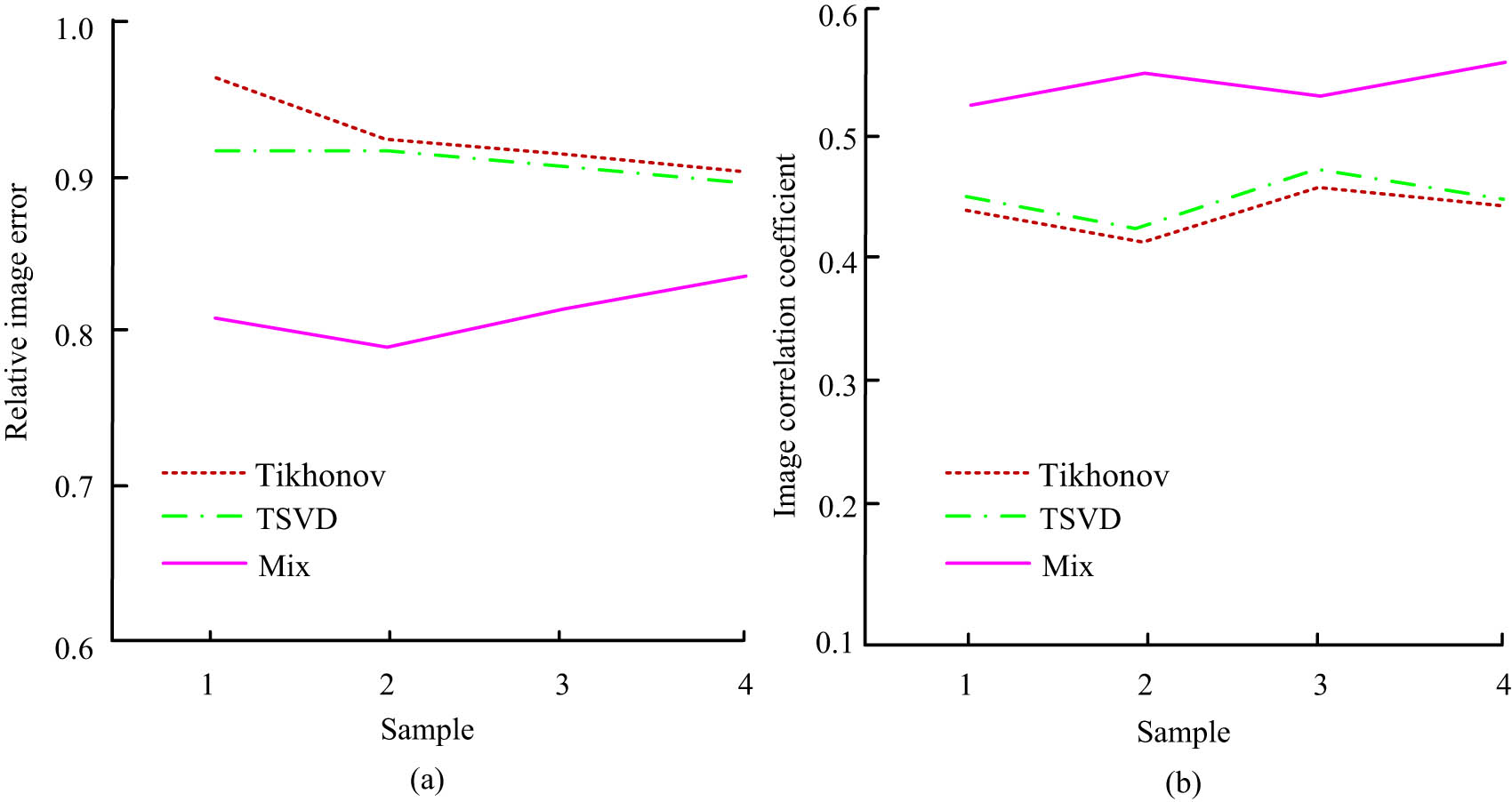
Quality evaluation of reconstructed images: (a) relative image error, and (b) image correlation coefficient.

Figure 10(a) shows the relative image error of the reconstructed images. Compared to the Tikhonov and TSVD methods, the mixed regularization method reduces the relative error of reconstructed images by about 13.1%. Figure 10(b) shows the image correlation coefficients of reconstructed images using different methods. Compared to the Tikhonov and TSVD methods, the mixed regularization method increases the correlation coefficient of reconstructed images by approximately 21.6%. Compared to Tikhonov and TSVD, the mixed regularization method shows higher quality in reducing the relative error of reconstructed images and increasing image correlation coefficients. After the optimal threshold processing, Table 3 shows the quality evaluation and DD accuracy of the reconstructed images.

Table 3

Quality evaluation and DD accuracy of reconstructed images after optimal threshold processing

Project	Algorithm	Sample 1	Sample 2	Sample 3	Sample 4
Relative image error coefficient	Mixed regularization method	0.811	0.794	0.813	0.827
Relative image error coefficient	Optimal threshold method post-processing	0.694	0.683	0.712	0.704
Image correlation	Mixed regularization method	0.512	0.521	0.533	0.534
Image correlation	Optimal threshold method post-processing	0.632	0.624	0.601	0.621
Accuracy	Mixed regularization method	99.3%	99.5%	99.7%	99.8%
Accuracy	Optimal threshold method post-processing	100%	100%	100%	100%

In Table 3, after optimal threshold processing, the relative image error coefficient and image correlation of the reconstructed image are improved, and the DD accuracy reaches 100%. This indicates that the optimal threshold processing method effectively improves the quality of IR and the DD accuracy. To verify the advantages of the DD method, the experiment compares the ultrasonic detection method with X-ray imaging technology. The comparison of DD accuracy of different methods is shown in Table 4.

Table 4

Comparison of DD accuracy using different methods

Method	Sample 1 (%)	Sample 2 (%)	Sample 3 (%)	Sample 4 (%)	Average (%)
Research proposed	100	100	100	100	100
Ultrasonic testing	85.3	81.6	70.3	69.8	76.8
X-ray imaging	98.6	99.2	93.7	94.4	96.5

In Table 4, the accuracy of the proposed method reaches 100%. The average accuracy of the ultrasonic detection method is 76.8%, with the lowest accuracy of 69.8% in Sample 4. The average accuracy of X-ray imaging technology is 96.5%, which is relatively high but still lower than the proposed method. The results indicate that the proposed method has significant advantages in DD, demonstrating its high reliability and effectiveness in practical applications.

5 Conclusion

This PACI system has problems such as poor capacitance data stability and susceptibility to noise interference in the adhesive layer DD. Therefore, a capacitance data preprocessing method based on PSO-FCM was proposed. Meanwhile, the sensitivity matrix and mixed regularization method were combined to perform IR on the defective samples, thereby improving the reconstructed images’ accuracy. These results confirmed that after preprocessing the capacitance data with PSO-FCM, the stationarity of capacitance difference at defect-free positions increased by 56%. FCM reduced the data MAD by about 6.1%, while PSO-FCM reduced the data MAD by about 23.2%. Compared to traditional FCM, PSO-FCM had significant effects in reducing data fluctuations and errors, effectively improving IR quality and DD accuracy. Compared to Tikhonov and TSVD, the mixed regularization method increased the correlation coefficient of reconstructed images by approximately 21.6%. After optimal threshold processing, the relative image error coefficient and image correlation of the reconstructed image were improved, and the DD accuracy reached 100%. The optimal threshold processing method effectively improved the IR quality and DD accuracy. This study provides an effective capacitance data preprocessing method that can improve the accuracy of adhesive layer DD, which has a positive impact on improving production efficiency, reducing production costs, and ensuring product quality and safety. However, there are still certain limitations in this research, as the defects used in this experiment are limited to the adhesive layer. Future research can further explore the impact of research methods on the DD effects of different objects to enhance the generalization ability of this method.

Funding information: Author states no funding involved.
Author contributions: Author has accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: Author states no conflict of interest.
Data availability statement: All data generated or analyzed during this study are included in this published article.

References

[1] Xu JH, Wang LX, Zhang SY, Tan JR. Predictive defect detection for prototype additive manufacturing based on multi-layer susceptibility discrimination. Adv Manuf. 2023;11(3):407–27.10.1007/s40436-023-00446-0Search in Google Scholar

[2] Song XF, Zhang Y, Gong DW, Gao XY. A fast hybrid feature selection based on correlation-guided clustering and particle swarm optimization for high-dimensional data. IEEE Trans Cybern. 2021;52(9):9573–86.10.1109/TCYB.2021.3061152Search in Google Scholar PubMed

[3] Tirumani VHL, Tenneti M, Srikavya KC, Kotamraju SK. Image resolution and contrast enhancement with optimal brightness compensation using wavelet transforms and particle swarm optimization. IET Image Process. 2021;15(12):2833–40.10.1049/ipr2.12268Search in Google Scholar

[4] Minh HL, Khatir S, Wahab MA, Thanh CL. An enhancing particle swarm optimization algorithm (EHVPSO) for damage identification in 3D transmission tower. Eng Struct. 2021;242:112412–34.10.1016/j.engstruct.2021.112412Search in Google Scholar

[5] Wang ZJ, Zhan ZH, Kwong S, Jin H, Zhang J. Adaptive granularity learning distributed particle swarm optimization for large-scale optimization. IEEE Trans Cybern. 2020;51(3):1175–88.10.1109/TCYB.2020.2977956Search in Google Scholar PubMed

[6] Fan D, Wang J. An individual-based mean-field model for fake-news spreading on PSO-based networks. Int J Mod Phys B. 2020;34:2050172–82.10.1142/S0217979220501726Search in Google Scholar

[7] Kulkarni PP, Ghawghawe ND. Hybrid DA-PSO approach for optimal location and parameter settings for TCSC controller in power system. IET Gener Transm Distrib. 2020;14(7):1222–32.10.1049/iet-gtd.2019.0016Search in Google Scholar

[8] Pant M, Kumar S. Particle swarm optimization and intuitionistic fuzzy set-based novel method for fuzzy time series forecasting. Granul Comput. 2022;7(2):285–303.10.1007/s41066-021-00265-3Search in Google Scholar

[9] Lin Y, Chen S. A centroid auto-fused hierarchical fuzzy c-means clustering. IEEE Trans Fuzzy Syst. 2021;29(7):2006–17.10.1109/TFUZZ.2020.2991306Search in Google Scholar

[10] Kiruba Nesamalar E, SatheeshKumar J, Amudha T. Efficient DNA-ligand interaction framework using fuzzy C-means clustering based glowworm swarm optimization (FCMGSO) method. J Biomol Struct Dyn. 2023;41(13):6249–61.10.1080/07391102.2022.2105958Search in Google Scholar PubMed

[11] Xiang S, Liang D, Kaneko S, Asano H. Robust defect detection in 2D images printed on 3D micro-textured surfaces by multiple paired pixel consistency in orientation codes. IET Image Process. 2020;14(7):3373–84.10.1049/iet-ipr.2019.0724Search in Google Scholar

[12] Cao Y, Xu H, Su C, Yang Q. Accurate glass insulators defect detection in power transmission grids using aerial image augmentation. IEEE Trans Power Deliv. 2023;38(2):956–65.10.1109/TPWRD.2022.3202958Search in Google Scholar

[13] Zhang H, Chen X, Lu S, Yao L, Chen X. A contrastive learning-based attention generative adversarial network for defect detection in colour-patterned fabric. Color Technol. 2023;139(3):248–64.10.1111/cote.12642Search in Google Scholar

[14] Pan J, Zeng D, Tan Q, Wu Z, Ren Z. EU-Net: a novel semantic segmentation architecture for surface defect detection of mobile phone screens. IET Image Process. 2022;16(10):2568–76.10.1049/ipr2.12509Search in Google Scholar

[15] Zhao H, Zhang H, Su G, Shi X. Defect diagnosis method of cable shielding layer based on frequency domain reflection coefficient spectrum. IEEE Trans Electromagn Compat. 2023;65(1):114–25.10.1109/TEMC.2022.3213351Search in Google Scholar

[16] Nguyen TPQ, Yang CL, Le MD, Nguyen TT, Luu MT. Enhancing automated defect detection through sequential clustering and classification: an industrial case study using the sine-cosine algorithm, possibilistic fuzzy c-means, and artificial neural network. Adv Prod Eng Manage. 2023;18(2):237–49.10.14743/apem2023.2.470Search in Google Scholar

[17] Li F, Xiao K, Hu Z, Zhang G. Fabric defect detection algorithm based on improved YOLOv5. Vis Comput. 2024;40(4):2309–24.10.1007/s00371-023-02918-7Search in Google Scholar

[18] Tziolas T, Papageorgiou K, Feleki A, Theodosiou T, Rapti K, Papageorgiou E, et al. Deep fuzzy cognitive maps for defect inspection in antenna assembly. Procedia Comput Sci. 2024;232:97–106.10.1016/j.procs.2024.01.010Search in Google Scholar

[19] Zheng S, Zhang S, Luo Y, Xu B, Hao W. Nondestructive analysis of debonding in composite/rubber/rubber structure using ultrasonic pulse-echo method. Nondestruct Test Eval. 2020;36(5):515–27.10.1080/10589759.2020.1825707Search in Google Scholar

[20] Elmoghazy Y, Abuelgasim EMO, Osman SA, Afaneh YRH, Eissa OMA, Safaei B. Effective mechanical properties evaluation of unidirectional and bidirectional composites using virtual domain approach at microscale. Arch Adv Eng Sci. 2023;1(1):27–37.10.47852/bonviewAAES32021723Search in Google Scholar

[21] Nengem SM. Symmetric kernel-based approach for elliptic partial differential equation. J Data Sci Intell Syst. 2023;1(2):99–104.10.47852/bonviewJDSIS3202884Search in Google Scholar

Received: 2024-12-04

Revised: 2024-12-25

Accepted: 2025-05-30

Published Online: 2025-09-04

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/nleng-2025-0161

Keywords for this article

PSO-FCM, adhesive layer; defect detection; image reconstruction; optimal threshold; quality evaluation

Creative Commons

BY 4.0