Exploring bifurcation and chaos control in a discrete-time Lotka–Volterra model framework for COVID-19 modeling

Elhadi E. Elamir; Mahmoud A.M. Abdelaziz; Ibrahim M.E. Abdelsatar; Manal Alqhtani; Mona Alsulami; Hamada F. El-Mekawy; Abdelalim A. Elsadany

doi:10.1515/nleng-2025-0181

Article Open Access

Exploring bifurcation and chaos control in a discrete-time Lotka–Volterra model framework for COVID-19 modeling

Elhadi E. Elamir , Mahmoud A.M. Abdelaziz , Ibrahim M.E. Abdelsatar , Manal Alqhtani , Mona Alsulami , Hamada F. El-Mekawy and Abdelalim A. Elsadany

Published/Copyright: December 29, 2025

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Nonlinear Engineering Volume 14 Issue 1

Abstract

This study investigates the dynamics of a discrete-time epidemic model of COVID-19 formulated on the basis of the Lotka–Volterra framework. The positivity and boundedness of solutions are established to ensure biological feasibility. A stability analysis identifies equilibrium points and reveals critical bifurcations that influence disease transmission. Numerical simulations confirm the occurrence of flip and Neimark–Sacker bifurcations, leading to complex periodic and quasi-periodic oscillations. The analysis of Lyapunov exponents further highlights the transition from stable dynamics to chaotic behavior as key parameters vary. In addition, effective chaos-control strategies are explored to stabilize the system, thereby mitigating unpredictable epidemic oscillations and promoting reliable long-term disease dynamics. These findings underscore the importance of controlling epidemiological factors to prevent irregular epidemic waves and to maintain long-term stability in disease transmission.

Keywords: Lotka–Volterra; discrete-time system; stability; bifurcation; chaos

1 Introduction

Infectious diseases have long posed one of the most serious threats to human survival, with pandemics repeatedly reshaping societies, economies, and public health systems. Classic examples, such as the Black Death of the 14th century and the Spanish flu of 1918 [1], 2], illustrate how rapidly spreading pathogens can devastate populations. Even lesser-known pandemics have had devastating health, social, and economic consequences [3], underscoring the continued vulnerability of human societies to emerging infectious diseases.

The emergence of COVID-19 in late 2019 in Wuhan, China, once again highlighted the global threat of novel pathogens. Within weeks, the virus spread across international borders, prompting the World Health Organization (WHO) to declare a global health emergency in early 2020 [4]. Since then, COVID-19 has caused millions of deaths worldwide and unprecedented disruption to healthcare, economic systems, and daily life. Biologically, the virus primarily targets the respiratory system by binding to angiotensin-converting enzyme 2 receptors on lung epithelial cells [5]. This interaction often leads to severe lung injury, with approximately 10 % of patients experiencing long-term respiratory complications [6], 7]. Disease progression varies widely – from a mild influenza-like illness to acute respiratory distress syndrome, respiratory failure, and death [8].

Despite remarkable advances in vaccination, antiviral therapy, and public health measures, containing pandemics remains a formidable challenge. Interventions such as quarantine, isolation, and vaccination are critical, yet their effectiveness is often limited by biological uncertainties, delayed responses, and ethical or logistical barriers. These limitations underscore the need for complementary approaches that can anticipate epidemic behavior and guide timely interventions.

Mathematical modeling has emerged as one of the most powerful tools for understanding and controlling infectious diseases. By formalizing the interactions between susceptible, infected, and recovered populations, models can predict epidemic trajectories, estimate transmission potential, and evaluate the effectiveness of intervention strategies [9], 10]. Beyond simple forecasting, mathematical models help policymakers quantify outbreak risks and assess the potential impact of measures such as vaccination campaigns, quarantine enforcement, or pharmaceutical treatments [11], 12].

1.1 Contribution

Building on existing modeling frameworks, this study introduces a discrete-time epidemic model of COVID-19 based on the Lotka–Volterra system, designed to capture the interaction dynamics between healthy and infected populations. The analysis establishes the existence, positivity, and boundedness of solutions to guarantee biological feasibility and provides a comprehensive characterization of equilibrium stability. The model further demonstrates rich dynamical behaviors through bifurcations, including flip and Neimark–Sacker types, which generate periodic and quasi-periodic epidemic patterns. The influence of the discretization parameter is examined, highlighting its role in flattening infection curves and shaping epidemic control strategies. In addition, the detection of chaotic oscillations via Lyapunov exponents and their stabilization through chaos-control methods underscores the capacity of the model to address complex epidemic dynamics. Collectively, these contributions advance the theoretical understanding of disease transmission while offering practical insights for effective public health intervention and epidemic management.

Together, these contributions provide both a deeper theoretical understanding of epidemic dynamics and practical tools that may inform effective public health interventions.

2 Lotka–Volterra discrete-time model

Mathematical models of infectious diseases have been widely employed to capture the dynamics of transmission and to evaluate intervention strategies. Among these, Lotka–Volterra (L–V) type formulations have been particularly useful for describing interactions between healthy and infected populations. Wael et al. [13] proposed a COVID-19 model based on the L–V framework, which incorporates the infection rate, recovery rate, migration, and mortality. Their continuous-time formulation takes the form

(2.1) d U t d t = μ U t − β U t V t + r V t , d V t d t = β U t V t − ( r + d − c ) V t ,

where U(t) and V(t) denote the healthy and infected individual population respectively. The parameter β represents the infection rate. The term μU(t) corresponds to the per-capita recruitment of healthy individuals into the system, which can be interpreted as natural births or as external influx, depending on the epidemiological context. The parameter c denotes the migration (or outflow) of infected individuals from the considered population, capturing processes such as relocation, isolation, or emigration rather than recovery or death. The parameter d represents the natural death rate, while r is the recovery rate. In this model, the recovery term rV(t) returns recovered individuals to the healthy class, reflecting the assumption that immunity is temporary and the model therefore has an SIS-type structure.

The model (2.1) admits a trivial equilibrium E ₀ = (0, 0) and a coexistence equilibrium E 1 = r + d − c β , μ r + d − c β d − c . The coexistence equilibrium E ₁ exists provided that d > c.

2.1 Discrete-time approximation

To investigate new dynamical behaviors, the continuous-time system (2.1) is reformulated in discrete time. By applying the Euler discretization method [14], one obtains

(2.2) U n + 1 = U n + h μ U n − β U n V n + r V n , V n + 1 = V n + h β U n V n − ( r + d − c ) V n ,

where h > 0 is the time-step size, with U _n, V _n ≥ 0 for all n ≥ 0.

Theorem 2.1.

If the initial populations satisfy U _n ≥ 0, V _n ≥ 0, then the solution U n , V n n ≥ 0 remains bounded for all n. Specifically, there exists a positive constant M such that U _n + V _n ≤ M, ∀n ≥ 0.

Proof.

Define the total population at step n as

N n = U n + V n .

Summing the two equations of (2.2) gives:

N n + 1 = U n + V n + h μ U n − ( d − c ) V n , = N n + h μ U n − ( d − c ) V n .

Since U _n ≥ 0, V _n ≥ 0, the growth and decay terms can be examined to establish boundedness. If μU _n ≤ (d − c)V _n, then N _n+1 ≤ N _n, meaning the population is non-increasing and hence bounded. Otherwise, if μU _n > (d − c)V _n, then

N n + 1 ≤ N n + h μ U n .

Applying the standard iterative bound:

N n ≤ N 0 e h μ n .

For biologically realistic models, external constraints (such as resource limits or carrying capacity) impose an upper bound M, ensuring that N _n remains finite for all n. Thus, U _n and V _n are bounded.□

To analyze the dynamical behavior of system (2.2), the Jacobian matrix J E * of (2.2) at E * = U * , V * is calculated.

(2.3) J ( E * ) = 1 + h ( μ − β V * ) h ( r − β U * ) h β V * 1 + h ( β U * − ( r + d − c ) ) .

Theorem 2.2.

E ₀ is always unstable.

Proof.

Substituting E 0 = 0,0 into (2.3) gives

J E 0 = 1 + h μ h r 0 1 − h ( r + d − c ) .

The Jacobian matrix J E 0 has two eigenvalues, λ ₁ = 1 + hμ and λ ₂ = 1 − h(r + d − c). Since all parameters are positive, it follows that λ ₁ > 1, and hence the equilibrium E ₀ is unstable.□

To characterize the stability of the coexistence equilibrium E ₁, the eigenvalues of the Jacobian matrix (2.3) are analyzed. The following theorem establishes the stability conditions of the discrete-time system (2.2).

Theorem 2.3.

(i) E ₁ is asymptotically stable (sink) if 0 < h < h ₁ or 0 < h < h ₂, Δ ⩾ 0 , Δ < 0 respectively.

(ii) E ₁ is unstable (source) if h > h ₃ or h > h ₂, Δ ⩾ 0 , Δ < 0 respectively.

(iii) E ₁ is unstable (saddle) if h ₁ < h < h ₃, Δ ⩾ 0.

(iv) Non-hyperbolic if h = h ₁, h = h ₃, Δ ⩾ 0 or h = h ₂, Δ < 0, where h 1 = μ r − 2 Δ μ ( d − c ) ( r + d − c ) , h 2 = r ( d − c ) ( r + d − c ) , h 3 = μ r + 2 Δ μ ( d − c ) ( r + d − c ) and Δ = μ [ − d 3 + ( 3 c − r ) d 2 + ( 2 c r − 3 c 2 ) d + c 3 − c 2 r + μ r 2 4 ] .

Proof.

Substituting E 1 = r + d − c β , μ r + d − c β d − c into (2.3), the Jacobian matrix of E ₁ is derived.

J E 1 = 1 − h μ r d − c − h ( d − c ) h μ 1 + r d − c 1 .

J E 1 has two eigenvalues; λ 1,2 = 1 2 2 − B ± Δ , where A = μ h 2 r + d − c , B = h μ r d − c and Δ = B ² − 4A. Since the eigenvalues λ _1,2 determine the local dynamics of the system, the equilibrium E ₁ is asymptotically stable when both satisfy |λ _i| < 1 (i = 1, 2), which ensures that perturbations from the equilibrium decay over time. If at least one eigenvalue lies on or outside the unit circle, i.e., |λ _i| ≥ 1, the equilibrium becomes unstable. This criterion follows from standard results in discrete-time dynamical systems [15]. Applying this principle yields the stability conditions (i)–(iv).□

Define Φ 1 = h , β , μ , c , d , r : h = h 1 , Δ ≥ 0 , Φ 2 = h , β , μ , c , d , r : h = h 2 , Δ < 0 and Φ 3 = h , β , μ , c , d , r : h = h 3 , Δ ≥ 0 . If Φ₁ or Φ₃ holds then J E 1 has one eigenvalue is −1 and the other is neither 1 nor −1. Thus, it follows that h , β , μ , c , d , r ∈ Φ 1 ∪ Φ 3 . When h changes into the neighborhoods of Φ₁ or Φ₃, the model (2.2) undergoes a flip bifurcation at E ₁. While if Φ₂ holds then J E 1 has a pair of conjugate complex eigenvalues with modulus 1 which means that h , β , μ , c , d , r ∈ Φ 2 . When h changes into the neighborhoods of Φ₂, then N–S bifurcation emerges at E ₁.

3 Bifurcation

In this section, the bifurcation behavior of the system (2.2) at the coexistence point E ₁ is investigated. The analysis follows standard results for discrete-time dynamical systems [16], where bifurcations occur when eigenvalues of the Jacobian cross the unit circle in the complex plane. In particular, we focus on flip (period-doubling) bifurcations, which occur when an eigenvalue passes through −1, and Neimark–Sacker bifurcations, which arise when a complex-conjugate pair of eigenvalues crosses the unit circle [17]. The center manifold theorem [18] is applied to investigate the conditions of flip bifurcation while the normal form method [19] is used to investigate the analysis of N–S bifurcation at E ₁.

3.1 Flip bifurcations

The flip bifurcation analysis associated with E ₁ is introduced in this section when the constant values h , β , μ , c , d , r change in the small vicinity of Φ₁ or Φ₃. Let δ is a disturbance of h, then a disturbance formulation of the system (2.2) given as:

(3.1) U n + 1 = U n + h + δ μ U n − β U n V n + r V n , V n + 1 = V n + h + δ β U n V n − ( r + d − c ) V n .

E 1 U * , V * is translated to the (0,0) by applying the transformations W _n = U _n − U* and Z _n = V _n − V*. Then, (3.1) can be reformulated as follows:

(3.2) W n + 1 Z n + 1 = a 11 W n + a 12 Z n + a 13 W n Z n + b 11 W n + b 12 Z n + b 13 W n Z n δ a 21 W n + a 22 Z n + a 23 W n Z n + b 21 W n + b 22 Z n + b 23 W n Z n δ ,

where,

a 11 = 1 + h μ r + 2 ( d − c ) d − c , a 12 = − d − c h , a 13 = − β h , b 11 = − μ r d − c , b 12 = − d − c , b 13 = − β , a 21 = μ h ( d + r − c ) d − c , a 22 = 1 , a 23 = β h , b 21 = μ ( d + r − c ) d − c , b 22 = 0 , b 23 = β .

Let T 1 = a 11 a 12 a 21 a 22 then, the eigenvector of T ₁ associated with λ ₁ = −1 and λ 2 ≠ 1 are y 1 y 2 = a 12 − 1 − a 11 and y 3 y 4 = a 12 λ 2 − a 11 respectively. Thus, an invertible matrix can be derived as T 2 = a 12 a 12 − 1 − a 11 λ 2 − a 11 . Consider W n Z n = T 2 x n y n . Taking T 2 − 1 on both sides of (3.2), then

x n + 1 y n + 1 = − 1 0 0 λ 2 x n y n + T 2 − 1 f 1 W n , Z n , δ f 2 W n , Z n , δ ,

where,

f 1 U n , V n , δ = a 13 W n Z n + b 11 W n + b 12 Z n + b 13 W n Z n δ f 2 U n , V n , δ = a 23 W n Z n + b 21 W n + b 22 Z n + b 23 W n Z n δ W n = a 12 x n + y n , Z n = − 1 + a 11 x n + λ 2 − a 11 y n .

Then, it follows that

(3.3) x n + 1 y n + 1 = − 1 0 0 λ 2 x n y n + Q 1 x n , y n , δ Q 2 x n , y n , δ ,

where, Q 1 x n , y n , δ = 1 λ 2 + 1 ( λ 2 − a 11 a 12 ) f 1 − f 2 and Q 2 x n , y n , δ = 1 λ 2 + 1 ( 1 + a 11 a 12 ) f 1 + f 2 . Now, the center manifold W c 0,0,0 of (3.3) at 0,0 in a small vicinity of δ = 0 can be created as

W c 0,0,0 = x n , y n , δ ∈ R 3 : x n = g y n , δ , g 0,0 = 0 , D g 0,0 = 0 ,

for x _n, δ sufficiently small such that

x n = g x n , δ = e 2 y n 2 + e 1 δ y n + O y n + δ 3 ,

which must satisfy

(3.4) g − y n + Q 2 y n , g y n , δ , δ = λ 2 g y n , δ + Q 1 y n , g y n , δ , δ .

Solving (3.4), the following result is obtained as

e 2 = ( λ 2 − a 11 ) ∗ ( a 11 a 13 + a 12 a 23 − a 13 λ 2 ) λ 2 2 − 1 , e 1 = a 11 b 13 + a 12 b 23 + b 13 λ 2 − 2 a 11 − 1 1 + a 11 a 11 a 13 + a 12 a 23 + a 13 .

Hence, the function f is defined as

(3.5) f x n = − y n + φ 1 y n δ + φ 2 y n δ 2 + φ 3 y n 2 + φ 4 y n 2 δ + φ 5 y n 3 + O x n + δ 4 ,

where,

φ 1 = 1 a 12 ( λ 2 + 1 ) b 21 a 12 2 − b 12 ( λ 2 − a 11 ) 2 + a 12 × − e 1 2 λ 2 + ( − 2 e 1 − b 11 + b 22 ) λ 2 + ( b 11 − b 22 ) a 11 − e 1 , φ 2 = e 1 a 12 ( λ 2 + 1 ) 2 a 12 2 b 21 − ( b 11 − b 22 ) ( λ 2 − 2 a 11 − 1 ) a 12 + 2 b 12 ( 1 + a 11 ) ( λ 2 − a 11 ) , φ 3 = 1 λ 2 + 1 ( − e 2 − a 13 ) λ 2 2 + ( 2 a 11 a 13 + a 12 a 23 ) λ 2 − a 13 a 11 2 − a 11 a 12 a 23 + e 2 , φ 4 = 1 a 12 ( λ 2 + 1 ) − e 2 b 12 ( 1 + a 11 ) ( λ 2 − a 11 ) + a 12 2 a 11 ( − 3 e 1 a 23 − b 23 ) + ( 2 e 1 a 23 + b 23 ) λ 2 − e 1 a 23 − e 2 b 21 + a 12 a 11 2 ( − 3 e 1 a 13 − b 13 ) + a 11 ( 4 e 1 a 13 + 2 b 13 ) λ 2 + e 2 ( − b 11 + b 22 ) − 2 e 1 a 13 + ( − e 1 a 13 − b 13 ) λ 2 2 + ( − 2 b 22 − b 11 ) e 2 + 2 e 1 a 13 λ 2 − e 2 ( b 22 + 2 b 11 , φ 5 = − e 2 a 13 ( λ 2 − a 11 ) + a 23 a 12 .

The discriminatory quantities χ ₁ and χ ₂ are given by

(3.6) χ 1 = ∂ 2 f ∂ υ n ∂ δ + 1 2 ∂ f ∂ δ ∂ 2 f ∂ υ n 2 0,0 , χ 2 = 1 6 ∂ 3 f ∂ υ n 3 + 1 2 ∂ 2 f ∂ υ n 2 2 0,0 .

Thus, χ ₁ = φ ₁ and χ 2 = φ 5 + φ 3 2 .

Theorem 3.1.

[20] If χ ₂ ≠ 0, and the parameter δ varies within a neighborhood of 0,0 , then the system (3.1) undergoes a flip bifurcation at E ₁. Additionally, the period-2 points emerging from E ₁ are stable when χ ₂ > 0 and unstable when χ ₂ < 0.

3.2 Neimark–Sacker bifurcation

A Neimark–Sacker bifurcation at E ₁ occurs when the parameters h , β , μ , c , d , r vary within a small neighborhood of Φ₂. The perturbed form of the model (2.2) can be expressed as follows:

(3.7) X n + 1 = X n + h + ε μ X n − β X n Y n + r Y n , Y n + 1 = Y n + h + ε β X n Y n − ( r + d − c ) Y n .

where, ε ≪ 1 is a restricted perturbation parameter. Let W _n = U _n − U*, Z _n = V _n − V*, then E 1 U * , V * can be retranslated to 0,0 . The system (3.9) can be written as

(3.8) W n + 1 Z n + 1 = c 11 W n + c 12 Z n + c 13 W n Z n c 21 W n + c 22 Z n + c 23 W n Z n ,

where

c 11 = 1 − μ r d − c h + ε , c 12 = − d − c h + ε , c 13 = − β h + ε , c 21 = μ 1 + r d − c h + ε , c 22 = 1 , c 23 = β h + ε .

The characteristic equation associated with the linearized system of (3.8) at 0,0 is

(3.9) ω 2 + p ε ω + q ε = 0 ,

where, p ε = − 2 − G h + ε , q ε = 1 + G h + ε + H h + ε 2 , G = c 22 − c 11 and H = c ₂₁ c ₁₂ − c ₁₁ c ₂₂. Since, parameters h , β , μ , c , d , r ∈ Φ 2 and ɛ vary in a vicinity of ɛ = 0, and the zeros of (3.9) are a pair of complex conjugate roots ω ₁ and ω ₂ denoted by ω 1,2 = 1 + G h + ε 2 ± i h + ε 2 4 H − G 2 . It follows that ω 1,2 = q ε , d ω 1,2 d ε ε = 0 = − G 2 > 0 . Additionally, when ε = 0 , ω ̄ n , ω n ≠ 1 , n = 1,2,3,4 , which corresponds to p 0 ≠ − 2,0,1,2 . Since p ²(0) − 4q(0) < 0 and q(0) = 1, therefore p ²(0) < 4; then p(0) ≠ ± 2. Now, p(0) ≠ 0, 1, is needed which leads to

(3.10) G 2 ≠ 2 H , 3 H .

Therefore, there are two eigenvalues ω _1,2 at 0,0 of (3.10) do not lie at the intersection of the unit circle with the coordinate axes when ɛ = 0.

Next, the normal form of the system (3.10) when ɛ = 0 is studied. Let θ = Re ω 1,2 , η = Im ω 1,2 and

(3.11) L = c 12 0 θ − c 11 − η = c 11 0 − 1 2 K − 1 2 K 4 K − K 2 .

Consider the translation below

(3.12) W n Z n = L x n y n .

Applying L ⁻¹ on both sides of (3.12) yields

(3.13) x n + 1 y n + 1 = θ − η η θ x n y n + f x n + y n g x n + y n ,

where

f x n + y n = c 13 θ − c 11 x n 2 − η x n y n , g x n + y n = c 13 c 11 − θ + c 12 c 23 × c 11 − θ η x n 2 + x n y n , W n = c 12 x n , Z n = θ − c 11 x n − η y n .

Thus, it follows that

(3.14) ∂ 2 f ∂ x n 2 = 2 c 13 θ − c 11 , ∂ 2 f ∂ x n ∂ y n = − η c 13 , ∂ 2 f ∂ y n 2 = 0 , ∂ 3 f ∂ x n 3 = ∂ 3 f ∂ x n 2 ∂ y n = ∂ 3 f ∂ x n ∂ y n 2 = ∂ 3 f ∂ y n 3 = 0 , ∂ 2 g ∂ x n 2 = 2 c 11 − θ η c 13 c 11 − θ + c 12 c 23 , ∂ 2 g ∂ x n ∂ y n = c 13 c 11 − θ + c 12 c 23 , ∂ 2 g ∂ y n 2 = 0 , ∂ 3 g ∂ x n 3 = ∂ 3 g ∂ x n 2 ∂ y n = ∂ 3 g ∂ x n ∂ y n 2 = ∂ 3 g ∂ y n 3 = 0 .

The quantity ℏ is given as

(3.15) ℏ = − Re 1 − 2 ω ω ̄ 2 1 − ω ξ 11 ξ 20 − 1 2 ξ 11 2 − ξ 02 2 + Re ω ̄ ξ 21 ≠ 0 ,

where

(3.16) ω = θ + i η , ξ 11 = 1 4 ∂ 2 f ∂ x n 2 + ∂ 2 f ∂ y n 2 + i ∂ 2 g ∂ x n 2 − ∂ 2 g ∂ y n 2 x n , y n = 0,0 , ξ 20 = 1 8 ∂ 2 f ∂ x n 2 − ∂ 2 f ∂ y n 2 + 2 ∂ 2 g ∂ x n ∂ y n + i ∂ 2 g ∂ x n 2 − ∂ 2 g ∂ y n 2 − 2 ∂ 2 f ∂ x n ∂ y n x n , y n = 0,0 , ξ 02 = 1 8 ∂ 2 f ∂ x n 2 − ∂ 2 f ∂ y n 2 − 2 ∂ 2 g ∂ x n ∂ y n + i ∂ 2 g ∂ x n 2 − ∂ 2 g ∂ y n 2 + 2 ∂ 2 f ∂ x n ∂ y n x n , y n = 0,0 , ξ 21 = 1 16 ∂ 3 f ∂ x n 3 + ∂ 3 f ∂ x n ∂ y n 2 + ∂ 3 g ∂ x n 2 ∂ y n + ∂ 3 g ∂ y n 3 + i ∂ 3 g ∂ x n 3 + ∂ 3 g ∂ x n ∂ y n 2 − ∂ 3 f ∂ x n 2 ∂ y n − ∂ 3 f ∂ y n 3 x n , y n = 0,0 .

From the above analysis and the N–S bifurcation conditions [21], the following theorem is stated.

Theorem 3.2.

[21] If conditions (3.10) and (3.16) are satisfied, then the model (2.2) undergoes a Neimark–Sacker bifurcation at the equilibrium E ₁ when the parameter ɛ varies within a small neighborhood of h. Moreover, if ℏ < 0 (respectively, ℏ > 0), an attracting, (respectively, repelling) invariant closed curve bifurcates from E ₁ for h > ɛ (respectively, h < ɛ).

4 Numerical simulation

Periodic epidemic patterns can emerge in the system as well. Once h ≥ h ₃, instability occurs at the epidemic interior equilibrium, which results in the continued transmission of the disease across the community. According to the above analysis of local stability and bifurcations at E ₁, the constant values of the system (2.2) will be examined in two case

Case 1. Take μ = β = 0.01, r = 0.98, d = 0.02, c = 0.0001. Then the model (2.2) has an interior point E 1 99.99 , 50.25 with Δ = 0.00008 > 0 and h ₃ = 4.426. According to Theorem 3.1, E ₁ is asymptotically stable when h < h ₃ and loses its stability as h exceeds h ₃.

Varying h in range 4.3 ≤ h ⩽ 5 with initial conditions U 0 , V 0 = 99.9 , 50.2 , when h = h ₃, flip bifurcation emerges from E ₁ with χ ₁ = 0.15 > 0, χ ₂ = 0.007 > 0 and h , β , μ , c , d , r ∈ Φ 3 . Figure 1 illustrates the occurrence of a flip bifurcation. Figure 1 demonstrates that E ₁ remains stable for h < h ₃ but loses its stability via a flip bifurcation when h = h ₃. As the bifurcation parameter crosses the critical threshold h ₃, period-doubling occurs, meaning that the population alternates between two distinct values instead of converging to a single equilibrium. Further increases in the parameter lead to higher-order period-doubling and potentially chaotic dynamics. The appearance of period-doubling implies that infection outbreaks start fluctuating between two (or more) distinct population levels. his behavior suggests that small changes in the epidemic parameters can cause significant variations in infection levels, potentially leading to unpredictable epidemic waves.

Figure 1:

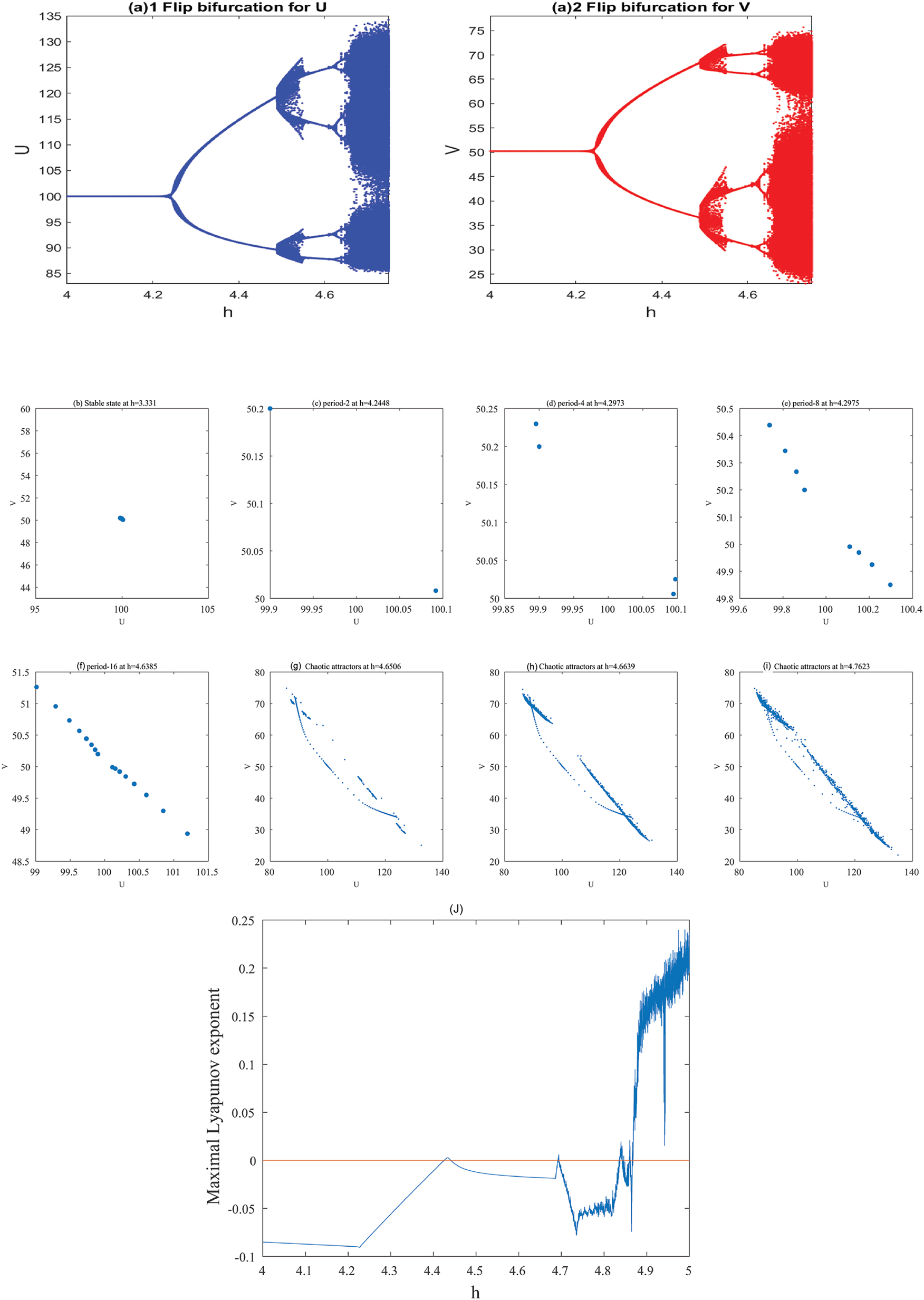
Flip bifurcation behavior of system (2.2) with respect to the step size. (a1) Bifurcation diagram of the state variable; (a2) bifurcation diagram of the state variable; (b–i) phase portraits illustrating the transition from a stable equilibrium to periodic and chaotic dynamics; (j) maximal Lyapunov exponent corresponding to the bifurcation diagram shown in panel (a).

The phase portraits for h ∈ 4,5 are plotted in Figure 1(b–h) to illustrate these observations further. Stable state E ₁ when h < h ₃ is depicted when h = 3.44 in Figure 1(b). Unstable periodic-2 orbits of E ₁ bifurcates when h = h ₃ and forking is initiated when h exceeds the critical flip bifurcation value h ₃. This forking of unstable periodic-2 orbits is shown in Figure 1(c) when h = 4.427. The appearance of period-2, period-4, period-8, and period-16 orbits is observed when h = 4.484, 4.69568, 4.8479 and 4.8682 respectively (see Figure 1(d–f)). Chaotic regions are illustrated in Figure 1(g–i): these phenomena can be observed by phase portraits in Figure 1(g and h) (e.g., when h = 4.8827 and 4.99). The Maximum Lyapunov Exponent serves as a crucial measure for assessing a system’s sensitivity to initial conditions and its tendency to exhibit chaotic behavior. A positive MLE suggests chaotic dynamics, while a negative or zero MLE indicates stability or periodic behavior. MLEs are computed corresponding to Figure 1(a) and plotted in Figure 1(j). It is noted that some LEs are negatives for h < h ₃ and some are positives for h > h ₃. Negative values of the Lyapunov Exponents in Figure 1(j) indicate that the equilibrium point E ₁ remains stable for h < h ₃ while positive values signify the occurrence of a flip bifurcation for h > h ₃.

From an epidemiological viewpoint, it is understood that when s exceeds the critical value h ₃, the disease outbreak persists and becomes pandemic. It is also possible for the system to exhibit periodic outbreaks. For h ≥ h ₃, the epidemic interior equilibrium loses stability, allowing the disease to propagate throughout the population.

The flip bifurcation analysis indicates that in certain parameter regimes, the epidemic model does not settle into a steady state but instead exhibits periodic or chaotic outbreaks. In real-world scenarios, this could correspond to recurrent epidemics where infection levels rise and fall cyclically. Understanding these bifurcations is crucial for epidemic control strategies, as it highlights the conditions under which disease prevalence may become unstable.

Case 2. Varying s in range 6.3 ≤ h ⩽ 6.875 and fixing μ = 0.012, β = 0.01, r = 0.98, d = 0.014, c = 0.0001 with initial conditions U 0 , V 0 = 111,9.6 . Then model (2.2) has the coexistence point E 1 111.99 , 9.606 with Δ = −0.0009 < 0, and h ₂ = 6.6269. According to Theorem 3.2, E ₁ is asymptotically stable when h < h ₂ and unstable when h > h ₂. Based on Theorem 3.2, N–S bifurcation emerges from E ₁ at h = h ₂ with h , β , μ , c , d , r ∈ Φ 2 . The occurrence of N–S bifurcation is illustrated in Figure 2(a and b). It is observed from Figure 2 that E ₁ is stable for h < h ₂ and loses its stability via N–S bifurcation at h = h ₂. As shown in Figure 2, N–S bifurcation leads to the appearance of quasi-periodic oscillations, characteristic of a torus attractor. As h increases further, these periodic orbits break into quasi-periodic oscillations, indicated by the spread of points in the bifurcation diagram. This suggests that the system is evolving towards a more complex dynamic behavior, possibly chaotic in nature.

Figure 2:

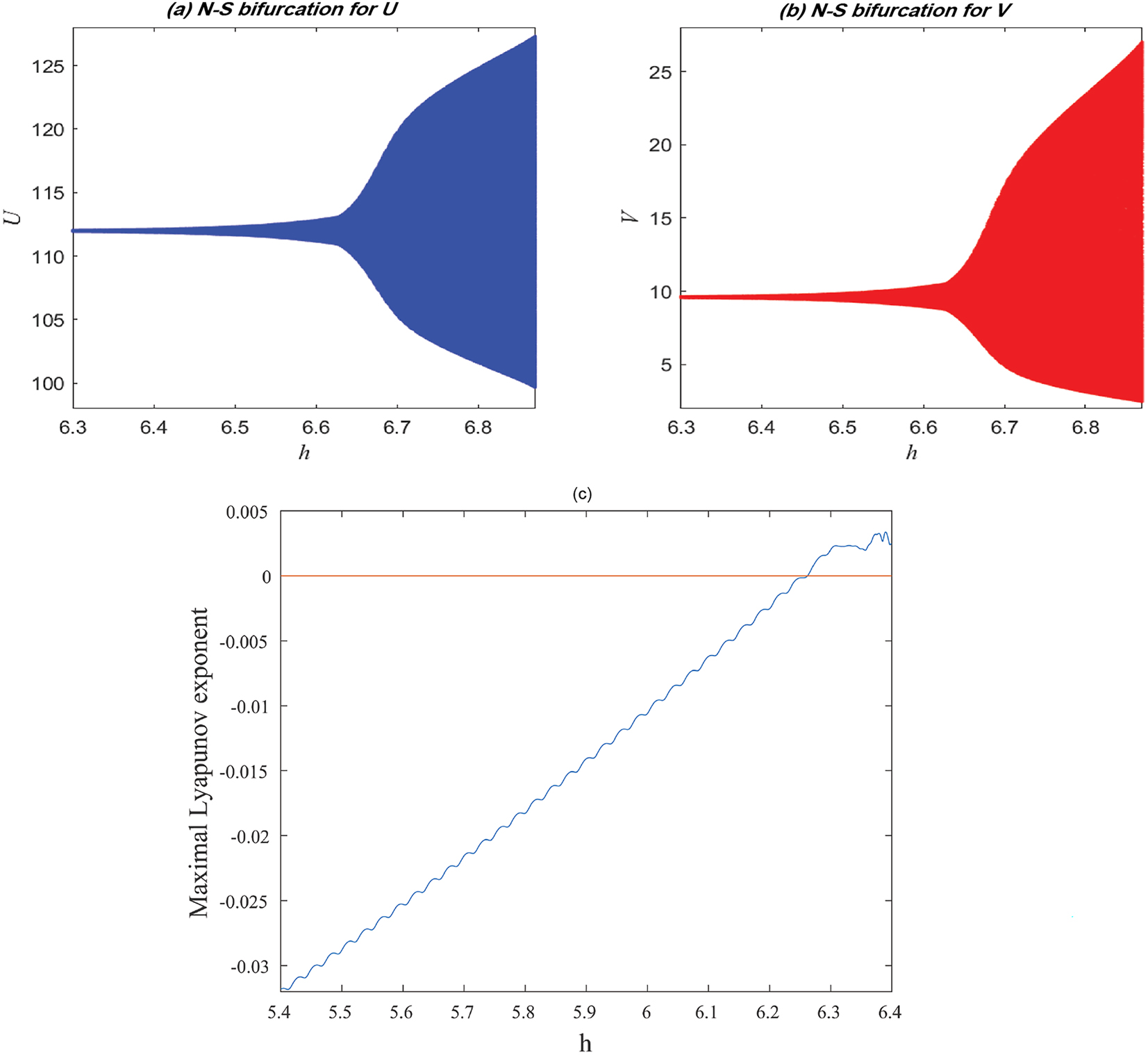
Neimark–Sacker bifurcation of system (2.2) induced by variation of the step size. (a) Bifurcation diagram of the model; (b) bifurcation diagram of the model; (c) maximal Lyapunov exponent confirming the transition from stable to quasi-periodic dynamics.

The phase portraits for various h − values corresponding to Figure 2 are plotted in Figures 3–5 to illustrate these observations. Stable steady state E ₁ is shown when h < h ₂ in Figure 3 at h = 6.6. A closed invariant circle begins to form at a value of h less than the critical value h ₂ (Figure 4). The repelling invariant circle is completely formed at h = h ₂ (Figure 5). An unstable equilibrium point E ₁ bifurcates when h exceeds the critical N–S bifurcation value h ₂. Chaotic region attractors form as h-value increases. The trajectory of system (2.2) converges to an asymptotically stable limit cycle around E ₂. Figure 2(c) presents the computed maximal Lyapunov exponents corresponding to the observations illustrated in Figure 2. It is observed some positive and negative LE values. These observations say that when h > h ₂, the disease is spreading and persist in the population and a pandemic will occur. Measures that are taken by decision-makers to combat epidemics, such as treatment, vaccination, or quarantine, make the epidemic stop spreading sometimes, but this is not necessary to stop the epidemic permanently. That may be interpreted as the oscillating of pandemic observed through the periodic windows which appear within the chaotic regions. When h = h ₂, epidemic equilibrium is unstable and the disease spread in the community. When h < h ₂, epidemic equilibrium is stable and the disease is eradicated.

Figure 3:

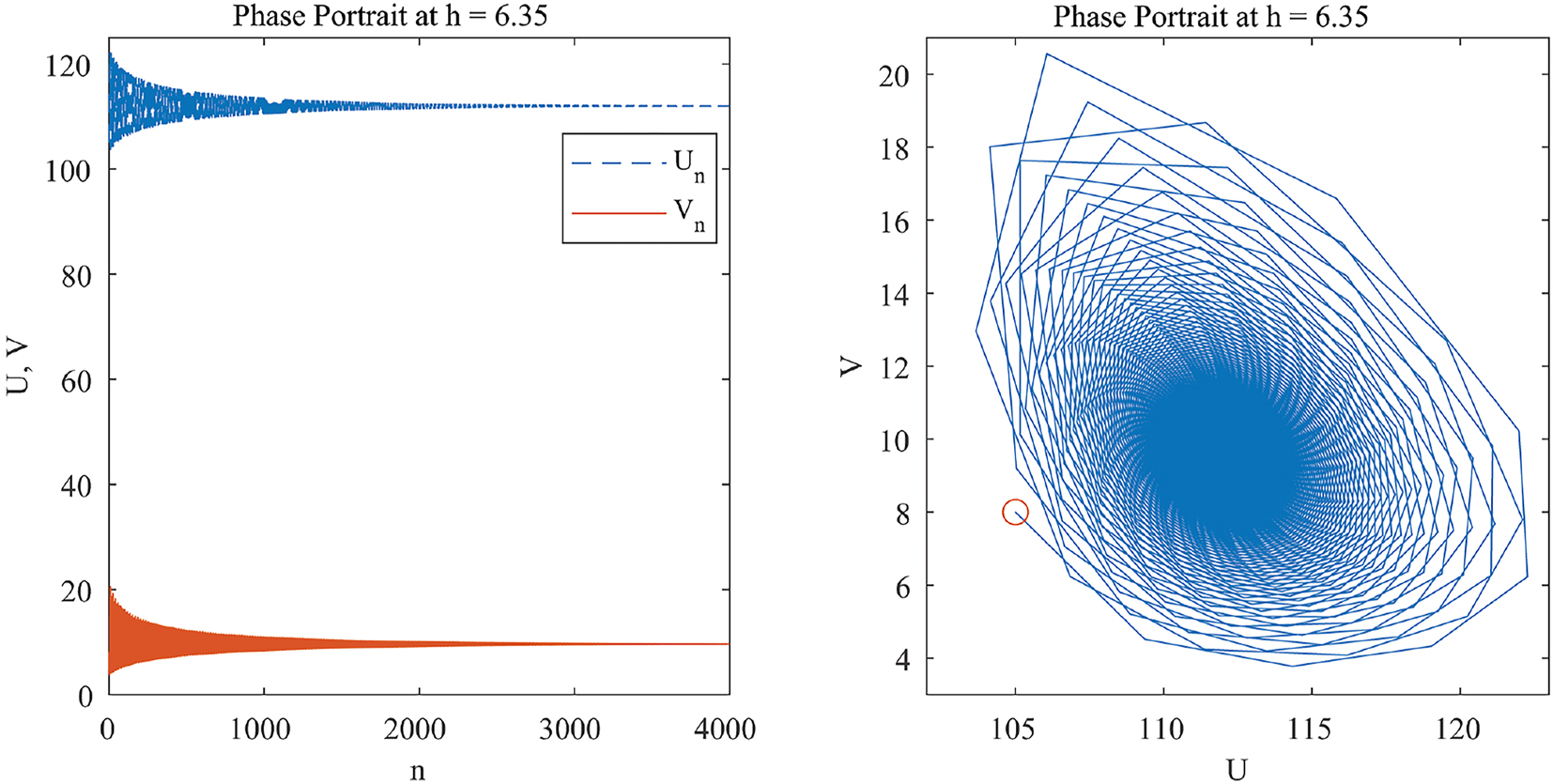
At h = 6.35, the trajectory of system (2.2) converges to E ₁.

Figure 4:

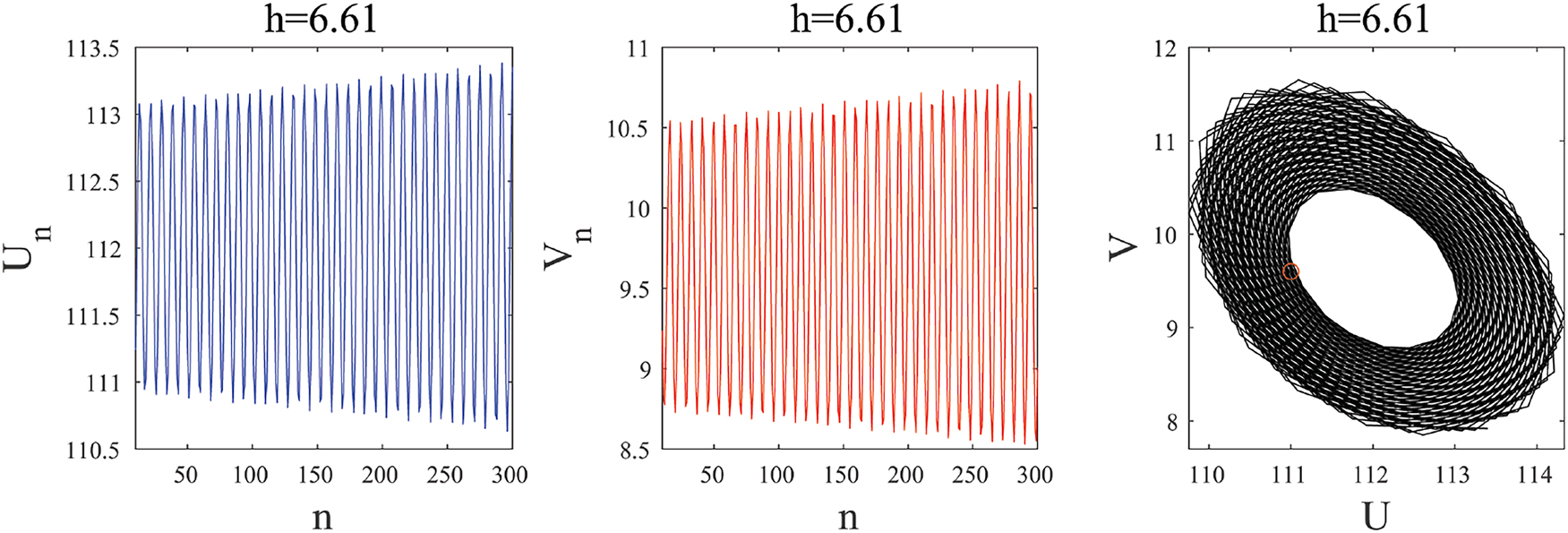
At h = 6.61, the trajectory of system (2.2) converges to an asymptotically stable limit cycle around E ₁.

Figure 5:

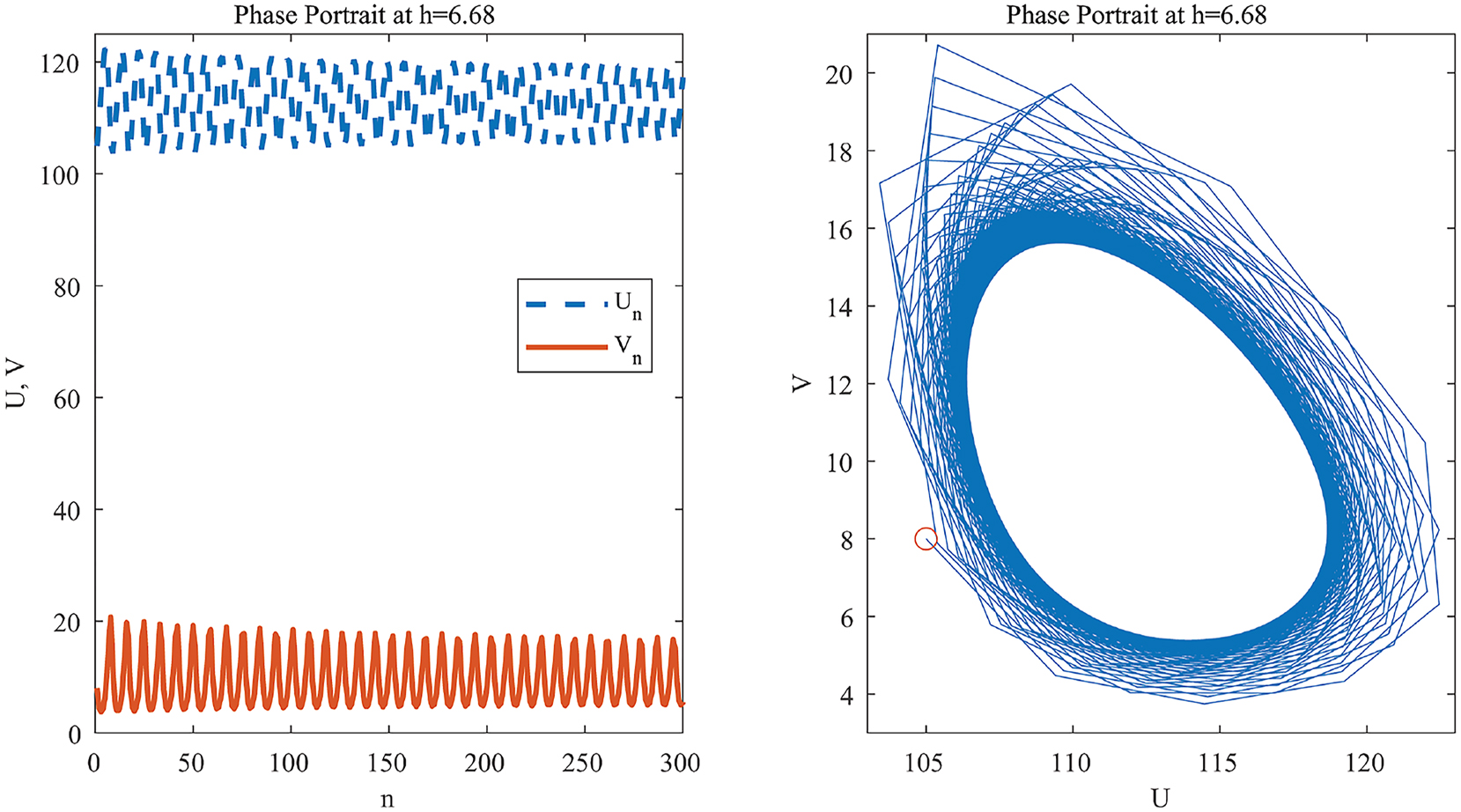
At h = 6.68, the trajectory of system (2.2) converges to an asymptotically stable limit cycle around E ₁.

5 Chaos control

Managing chaos and bifurcation is vital in population models, particularly those related to the biological reproduction of species. Discrete-time models often display more intricate dynamics than their continuous counterparts. To avoid unpredictable outcomes in population dynamics, applying chaos control methods is imperative.

Figure 6:

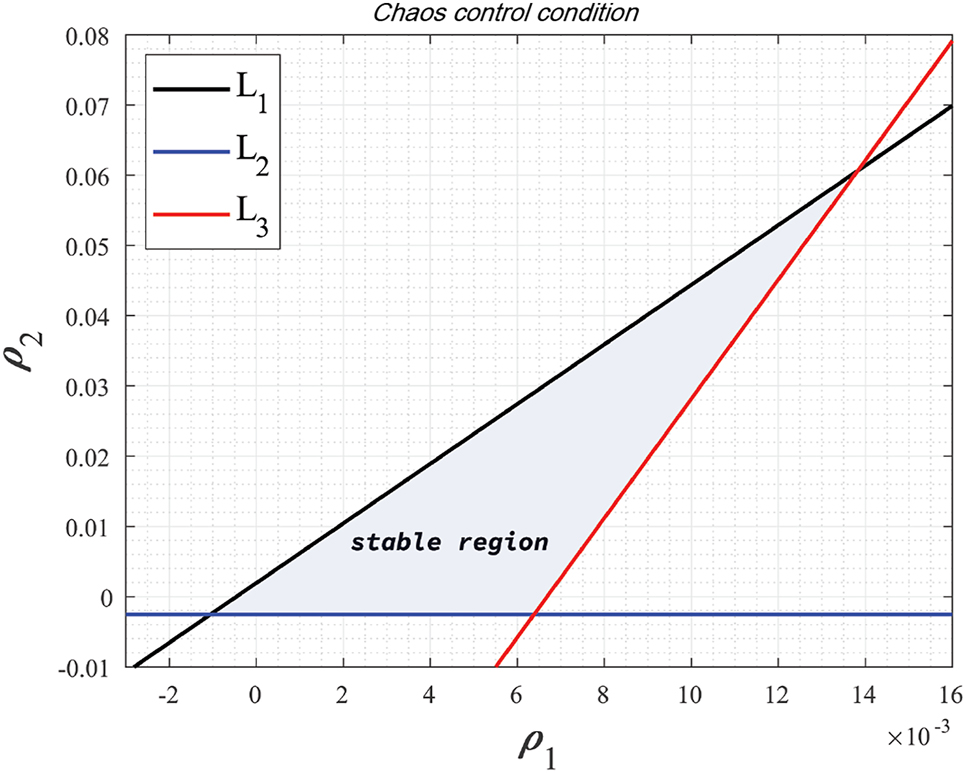
Triangular stability region bounded by L ₁, L ₂ and L ₃ for the controlled system (5.1).

5.1 Pole placement technique

In this subsection, two feedback control strategies are examined, aimed at steering unstable trajectories toward stable ones. As an initial approach, system (2.2) is stabilized by applying the OGY control method [22], with the parameter μ serving as the control parameter. The system in (2.2) can be written in the form

(5.1) U n + 1 = U n + h μ U n − β U n V n + r V n = f U n , V n , μ , V n + 1 = V n + h β U n V n − ( d + r − c ) V n = g U n , V n , μ .

where μ is chosen as the control parameter, enabling the achievement of desired chaos control by applying only minimal perturbations. For this purpose, μ is restricted to lie within a small interval μ ∈ μ 0 − δ , μ 0 + δ with δ > 0 and μ ₀ denotes the nominal value belong to chaotic region. To ensure stability, a feedback control strategy is implemented that directs the system trajectory onto the target orbit. Suppose that E * = U * , V * = r + d − c β , μ r + d − c β ( d − c ) is an unstable equilibrium point of system (2.2) within the chaotic region resulting from either a period-doubling bifurcation or an N–S bifurcation. In that case, system (2.2) can be approximated in the vicinity of this unstable equilibrium point. U * , V * by the following linear map:

(5.2) U n + 1 − U * V n + 1 − V * ≈ J U * , V * , μ 0 U n − U * V n − V * + L μ − μ 0 ,

where

J U * , V * , μ 0 = ∂ f U * , V * , μ 0 ∂ U ∂ f U * , V * , μ 0 ∂ V ∂ g U * , V * , μ 0 ∂ U ∂ g U * , V * , μ 0 ∂ V = 1 + μ 0 r c − d h ( c − d ) h − μ 0 ( d + r − c ) c − d h 1 ,

and

M = ∂ f U * , V * , μ 0 ∂ μ ∂ g U * , V * , μ 0 ∂ μ = ( r + d − c ) β h 0 .

Additionally, system (5.1) is controllable under the condition that the following matrix satisfies:

(5.3) C = M : J M = ( r + d − c ) β h 1 − μ r d − c h r + d − c β h 0 − μ ( r + d − c ) 2 β ( d − c ) h 2 ,

is of rank 2. Moreover, taking μ − μ 0 = − K U n − U * V n − V * , where K = ρ 1 ρ 2 , then system (5.2) can be written as

(5.4) U n + 1 − U * V n + 1 − V * ≈ J − M K U n − U * V n − V * .

In addition, the controlled form associated with system (2.2) can be written as:

(5.5) U n + 1 = U n + h μ 0 − ρ 1 U n − U * − ρ 2 V n − V * U n − β U n V n + r V n , V n + 1 = V n + h β U n V n − ( d + r − c ) V n .

The equilibrium E* attains local asymptotic stability precisely when the eigenvalues of J − M K are located inside the open unit disk. For the controlled system (5.5), the Jacobian matrix J − M K can be formulated as:

J − M K = 1 − h ρ 1 ( r + d − c ) β + μ 0 β r β ( d − c ) − d − c + ρ 2 ( r + d − c ) β h μ 0 ( r + d − c ) d − c h 1 .

The characteristic equation of the Jacobian matrix J − MK is given by

(5.6) P λ = λ 2 − Tr c λ + D e t c = 0 ,

where

(5.7) Tr c = λ c 1 + λ c 2 = 2 − ρ 1 ( r + d − c ) β + μ 0 β r β ( d − c ) h , D e t c = λ c 1 λ c 2 = 1 − ρ 1 ( r + d − c ) β + μ 0 r ( d − c ) h , + μ 0 ρ 2 r − ( β + ρ 2 ) ( d − c ) ( r + d − c ) β ( c − d ) h 2 ,

where Let λ _c1 and λ _c2 are the roots of characteristic equation (5.6).

Consider the case where λ _c1 = ±1 and λ _c1 λ _c2 = 1. Under these constraints, the lines of marginal stability for the controlled system are determined, and λ _c1 together with λ _c2 remain confined within the open unit disk. Under the assumption that λ _c1 λ _c2 = 1, then (5.7) implies the following.

L 1 : ρ 2 = β μ 0 r + ρ 1 ( d − c ) ( r + d − c ) μ 0 h ( c − d − r ) 2 − β ( ( d − c ) 2 + r ( d − c ) ) ( r + d − c ) 2 .

Moreover, it is assumed that λ _c1 = 1, then (5.7) yields that:

L 2 : ρ 2 r + β + ρ 2 d − c = 0 .

Finally by setting λ _c1 = −1, equation (5.7) give the following relation:

L 3 : 4 + 2 ρ 1 ( r + d − c ) β + μ 0 r ( d − c ) h − μ 0 ρ 2 r − ( β + ρ 2 ) ( d − c ) ( r + d − c ) β ( d − c ) h 2 = 0 .

Figure 6 illustrates the stability region in the (ρ ₁, ρ ₂)-plane; specifically, the triangular domain bounded by L ₁, L ₂, L ₃ and corresponds to control gains that place the controlled eigenvalues inside the unit circle. Figures 7 and 8 then show representative trajectories inside and outside this stability region.

Figure 7:

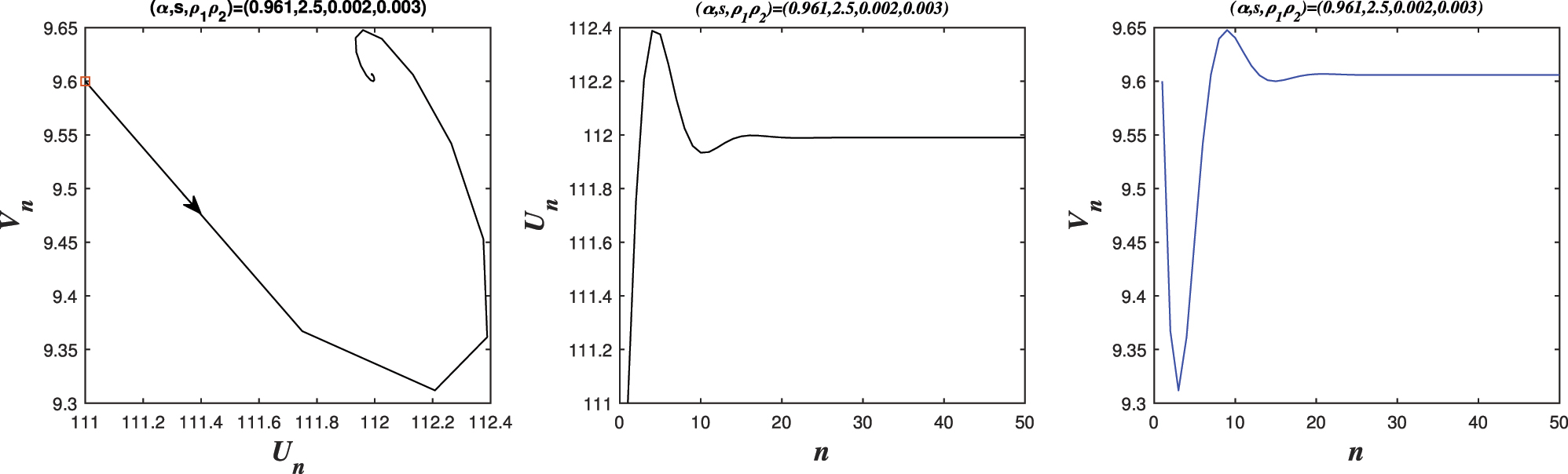
Phase portraits of system (5.1) for parameter values (ρ ₁, ρ ₂) = (0.002, 0.003), corresponding to a point inside the triangular stability region defined by the lines L ₁, L ₂, L ₃. The trajectories converge to the stable equilibrium, confirming that the control parameters lie within the stability domain and successfully suppress chaotic oscillations.

Figure 8:

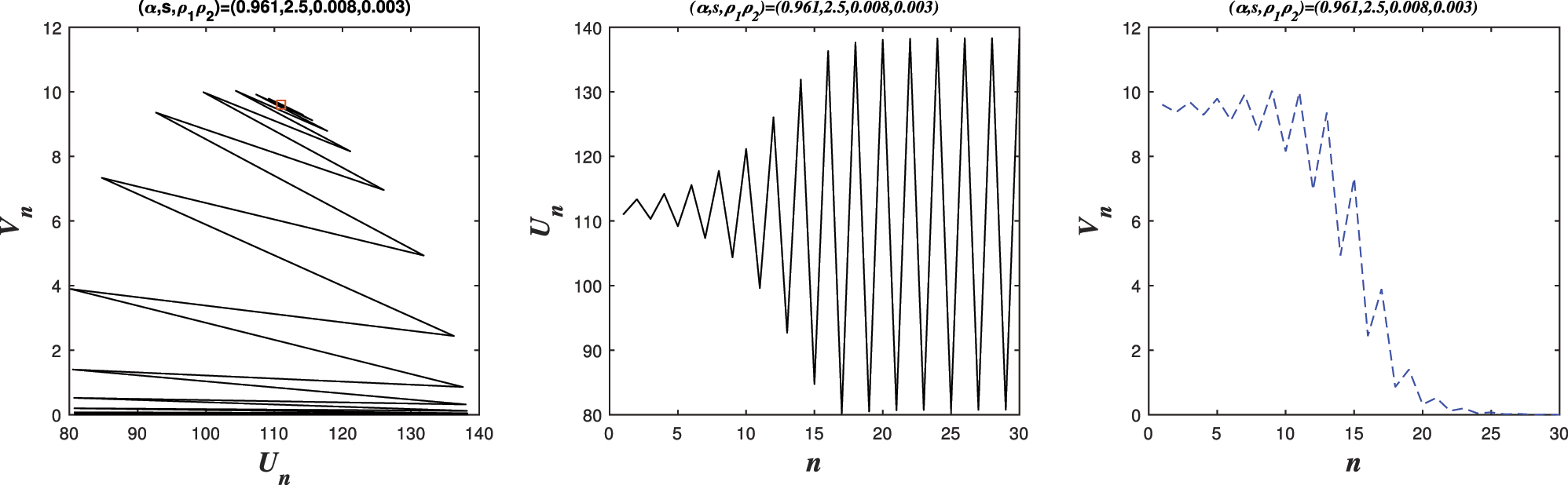
Phase portraits of system (5.1) for parameter values (ρ ₁, ρ ₂) = (0.008, 0.003), corresponding to a point outside the triangular stability region defined by L ₁, L ₂, L ₃. In this case, trajectories diverge or exhibit irregular oscillations, indicating loss of stability when the control parameters are chosen outside the admissible region.

5.2 Hybrid control method

The hybrid control feedback method [23] is employed to address the chaos induced by bifurcation in system (2.2). This technique was initially designed to manage period-doubling bifurcations. In [23], the authors applied the hybrid control feedback approach to control chaos arising from Neimark–Sacker bifurcations. If system (2.2) undergoes bifurcation at the equilibrium point E*, the corresponding controlled system can be formulated as:

(5.8) U n + 1 = ρ U n + h μ U n − β U n V n + r V n + 1 − ρ U n , V n + 1 = ρ V n + h β U n V n − ( r + d − c ) V n + 1 − ρ V n ,

where 0 < ρ < 1. The control strategy in (5.8) combines both parameter perturbation and feedback control. A suitable adjustment of the control parameter ρ makes it possible to advance, postpone, or eliminate the occurrence of period-doubling and Neimark–Sacker bifurcations at the equilibrium E* of the controlled system (5.8). At the positive equilibrium, the Jacobian matrix of the controlled system (5.8) takes the following form:

(5.9) J n s = 1 − r ρ μ d − c h − ρ ( d − c ) h ρ μ ( r + d − c ) d − c h 1 .

It follows that:

(5.10) P n ( λ ) = λ 2 − 2 − μ r ρ d − c h λ + 1 − μ r ρ d − c h + ρ 2 μ r + d − c h 2 = 0 .

For the stability of the system (5.8), P n ( 1 ) > 0 , P n ( − 1 ) > 0 and P n ( 0 ) < 0 . where

(5.11) P n ( 1 ) = 4 + ρ 2 μ ( r + d − c ) h 2 > 0 , P n ( − 1 ) = ρ ( r + d − c ) ( d − c ) h − 2 r > 0 , P n ( 0 ) = 1 − ρ 2 μ ( r + d − c ) h 2 − μ r ρ d − c h < 0 .

The following result provides the conditions for the local asymptotic stability of E ₁ in the controlled system (5.8). Specifically, the coexistence point E ₁ is locally asymptotically stable if the following conditions are satisfied:

(5.12) − ρ 2 μ ( r + d − c ) h 2 < 4 , ρ ( r + d − c ) ( d − c ) h > 2 r , 1 − ρ 2 μ ( r + d − c ) h 2 − μ r ρ d − c h < 0 .

5.3 State feedback control

An efficient way to regulate chaotic dynamics is through state feedback control [24]. In this approach, an optimal controller is applied to reshape the chaotic system into a piecewise linear structure. The procedure lowers the upper bound and, under defined circumstances, guarantees controllability. When an appropriate feedback strategy is implemented, the resulting controlled form of system (2.2) is obtained as:

(5.13) U n + 1 = U n + h μ U n − β U n V n + r V n − X n , V n + 1 = V n + h β U n V n − ( d + r − c ) V n = g U n , V n , μ ,

where

X n = q 1 U n − U * + q 2 V n − V * ,

corresponds to the control force defined by the feedback control law, with q ₁ and q ₂ acting as the respective feedback gains. From the Jacobian matrix of system (5.13), the resulting characteristic equation is obtained as:

(5.14) λ 2 − 2 − q 1 − μ r d − c h λ + μ ( r + d − c ) h 2 + ( ( r + d − c ) q 2 − r ) μ d − c h − q 1 + 1 = 0 .

Let λ _1fd and λ _2fd be two roots of the characteristic equation (5.14) then sum and product of the roots are

(5.15) λ 1 f d + λ 2 f d = 2 − q 1 − μ r d − c h , λ 1 f d λ 2 f d = μ ( r + d − c ) h 2 + ( ( r + d − c ) q 2 − r ) μ d − c h − q 1 + 1 .

Now the conditions for the marginal stability lines are given as

λ 1 f d = ± 1 , λ 1 f d λ 2fd = 1 ,

then for second condition (5.14) gives

(5.16) F C 1 : μ ( r + d − c ) h 2 + ( ( r + d − c ) q 2 − r ) μ d − c h − q 1 = 0 .

Under another stability condition, setting λ _1fd = 1 yields

(5.17) F C 2 : h = − q 2 d − c .

Similarly for λ _1fd = −1, it is obtained

(5.18) F C 3 : 2 − μ ( r + d − c ) h 2 − ( r + d − c ) q 2 μ d − c h = 0 .

Stability requires that every eigenvalue falls within the triangular domain defined by the lines FC ₁, FC ₂, and FC ₃. Accordingly, system (5.13) achieves stability if the associated eigenvalues are confined to the interior of the open unit disk.

6 Conclusions

In this study, the dynamics of a discrete-time epidemic model of COVID-19 based on the Lotka–Volterra model were investigated. To ensure biological feasibility, the positivity and boundedness of solutions are demonstrated, thereby preventing the emergence of negative or unbounded populations within the model. The stability analysis revealed the existence of equilibrium points, and numerical simulations confirmed the occurrence of bifurcations leading to oscillatory and chaotic epidemic dynamics. Our bifurcation analysis highlighted the presence of flip bifurcations, which result in alternating infection levels, and N–S bifurcations, which lead to quasiperiodic epidemic cycles. The Lyapunov exponent analysis provided further evidence of the transition from stable to chaotic dynamics, indicating the loss of predictability in disease spread at critical parameter values. Chaotic dynamics were mitigated and epidemic spread stabilized through the implementation of three chaos-control strategies – Pole Placement Technique, Hybrid Control Method, and State Feedback Control. These approaches proved effective in restoring stable disease dynamics and preventing unpredictable epidemic oscillations. From a biological perspective, these results suggest that disease outbreaks may follow complex, unpredictable oscillations if key parameters-such as infection rates-exceed stability thresholds. This has significant implications for public health interventions, emphasizing the need for controlled policies to prevent instability in disease transmission. Future work could explore optimal control strategies to mitigate chaos in epidemic dynamics and extend the model to incorporate additional real-world factors such as vaccination or spatial heterogeneity.

Corresponding author: Mahmoud A.M. Abdelaziz, Department of Mathematics, Faculty of Science and Arts, Najran University, Najran 66445, Saudi Arabia, E-mail: maabdelaziz@nu.edu.sa

Acknowledgments

The research team thanks the Deanship of Graduate Studies and Scientific Research at Najran University for supporting the research project through the Nama’a program, with the project code NU/GP/SERC/13/590-1.

Funding information: Authors state no funding involved.
Author contributions: Conceptualization, A. A. Elsadany, Mahmoud A. M. Abdelaziz, Mona Alsulami; Methodology, Mahmoud A. M. Abdelaziz, Mona Alsulami, Ibrahim M.E. Abdelsatar, Elhadi E. Elamir; Writing – original draft preparation, Mahmoud A. M. Abdelaziz, Mona Alsulami, Ibrahim M.E. Abdelsatar, Elhadi E. Elamir; Writing – review and editing, Mahmoud A. M. Abdelaziz, Ibrahim M.E. Abdelsatar, Elhadi E. Elamir, A. A. Elsadany, Manal Alqhtani, Hamada F. El-Mekawy. All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: Authors state no conflict of interest.
Data availability statement: All data generated or analysed during this study are included in this published article.

References

1. McNeill, WH. Plagues and peoples. Garden City, NY: Anchor; 1976.Search in Google Scholar

2. Aassve, A, Alfani, G, Gandolfi, F, Le Moglie, M. Epidemics and trust: the case of the Spanish Flu. Health Econ 2021;30:840–57. https://doi.org/10.1002/hec.4218.Search in Google Scholar PubMed PubMed Central

3. Kaur, H, Garg, S, Joshi, H, Ayaz, S, Sharma, S, Bhandari, M. A review: epidemics and pandemics in human history. Int J Pharma Res Health Sci 2020;8:3139–42. https://doi.org/10.21276/ijprhs.2020.02.01.Search in Google Scholar

4. Ciotti, M, Ciccozzi, M, Terrinoni, A, Jiang, WC, Wang, CB, Bernardini, S. The COVID-19 pandemic. Crit Rev Clin Lab Sci 2020;57:365–88. https://doi.org/10.1080/10408363.2020.1783198.Search in Google Scholar PubMed

5. Desai, AD, Lavelle, M, Boursiquot, BC, Wan, EY. Long-term complications of COVID-19. Am J Physiol Cell Physiol 2022;322:C1–11. https://doi.org/10.1152/ajpcell.00375.2021.Search in Google Scholar PubMed PubMed Central

6. Salian, VS, Wright, JA, Vedell, PT, Nair, S, Li, C, Kandimalla, M, et al.. COVID-19 transmission, current treatment, and future therapeutic strategies. Mol Pharm 2021;18:754–71. https://doi.org/10.1021/acs.molpharmaceut.0c00608.Search in Google Scholar PubMed

7. John, AE, Joseph, C, Jenkins, G, Tatler, AL. COVID-19 and pulmonary fibrosis: a potential role for lung epithelial cells and fibroblasts. Immunol Rev 2021;302:228–40. https://doi.org/10.1111/imr.12977.Search in Google Scholar PubMed PubMed Central

8. Li, T, Lu, H, Zhang, W. Clinical observation and management of COVID-19 patients. Emerg Microb Infect 2020;9:687–90. https://doi.org/10.1080/22221751.2020.1741327.Search in Google Scholar PubMed PubMed Central

9. World Health Organization. Coronavirus disease (COVID-19). [Internet]; 2023. Available from: https://www.who.int/.Search in Google Scholar

10. Yuan, LG, Yang, QG. Bifurcation, invariant curve and hybrid control in a discrete-time predator–prey system. Appl Math Model 2015;39:2345–62. https://doi.org/10.1016/j.apm.2014.10.040.Search in Google Scholar

11. Carlson, K. Mathematical modeling of infectious diseases with latency: homogeneous mixing and contact network [Ph.D. thesis]; 2016.Search in Google Scholar

12. Abdelaziz, MA, Ismail, AI, Abdullah, MHM, Mohd, MH. Bifurcations and chaos in a discrete SI epidemic model with fractional order. Adv Differ Equ 2018;2018:44. https://doi.org/10.1186/s13662-018-1481-6.Search in Google Scholar

13. Zakia, AS, Yousef, AM, Rida, SZ, Gouda, YG. On the dynamics of an SIR epidemic model with a saturated incidence rate. J Adv Stud Topol 2017;8:97–110. https://doi.org/10.20454/jast.2017.1333.Search in Google Scholar

14. Brauer, F, Castillo-Chavez, C, Feng, Z. Mathematical models in epidemiology. New York: Springer; 2019, vol 32.10.1007/978-1-4939-9828-9Search in Google Scholar

15. Sahaminejad, F, Nyamoradi, N, Eskandari, Z. Developing a continuous SIR epidemic model and its discrete version using Euler method: analyzing dynamics with analytical and numerical methods. Math Methods Appl Sci 2024;47:1–18. https://doi.org/10.1002/mma.10124.Search in Google Scholar

16. Li, B, Yuan, Z, Eskandari, Z. Dynamics and bifurcations of a discrete-time Moran–Ricker model with a time delay. Mathematics 2023;11:2446. https://doi.org/10.3390/math11112446.Search in Google Scholar

17. Li, X, Shao, X. Flip bifurcation and Neimark–Sacker bifurcation in a discrete predator–prey model with Michaelis–Menten functional response. Electron Res Arch 2023;31:37–57. https://doi.org/10.3934/era.2023003.Search in Google Scholar

18. Du, X, Han, X, Lei, C. Behavior analysis of a class of discrete-time dynamical system with capture rate. Mathematics 2022;10:2410. https://doi.org/10.3390/math10142410.Search in Google Scholar

19. Reja, S, Al Basir, F, Aldawsari, K. A discrete-time mathematical model for mosaic disease dynamics in cassava: Neimark–Sacker bifurcation and sensitivity analysis. AIMS Math 2025;10:18295–320. https://doi.org/10.3934/math.2025817.Search in Google Scholar

20. Abdelaziz, MA, Ismail, AI, Abdullah, FA, Mohd, MH. Codimension one and two bifurcations of a discrete-time fractional-order SEIR measles epidemic model with constant vaccination. Chaos Solitons Fractals 2020;140:110104. https://doi.org/10.1016/j.chaos.2020.110104.Search in Google Scholar

21. Zhou, X, Li, X, Wang, WS. Bifurcations for a deterministic SIR epidemic model in discrete time. Adv Differ Equ 2014;2014:1–16. https://doi.org/10.1186/1687-1847-2014-168.Search in Google Scholar

22. Priyanka, M, Muthukumar, P. Bifurcation patterns and chaos control in discrete-time coral reef model. arXiv preprint 2024. arXiv:2405.07491.Search in Google Scholar

23. Aldosary, SF, Ahmed, R. Stability and bifurcation analysis of a discrete Leslie predator–prey system via piecewise constant argument method. AIMS Math 2024;9:4684–706. https://doi.org/10.3934/math.2024226.Search in Google Scholar

24. Din, Q. Complexity and chaos control in a discrete-time prey–predator model. Commun Nonlinear Sci Numer Simul 2017;49:113–34. https://doi.org/10.1016/j.cnsns.2017.01.025.Search in Google Scholar

Received: 2025-03-09

Accepted: 2025-10-15

Published Online: 2025-12-29

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/nleng-2025-0181

Keywords for this article

Lotka–Volterra; discrete-time system; stability; bifurcation; chaos

Creative Commons

BY 4.0