Perturbation-iteration approach for fractional-order logistic differential equations

Abiodun Ezekiel Owoyemi; Chang Phang; Abdulnasir Isah

doi:10.1515/nleng-2024-0065

Artikel Open Access

Perturbation-iteration approach for fractional-order logistic differential equations

Abiodun Ezekiel Owoyemi , Chang Phang und Abdulnasir Isah

Veröffentlicht/Copyright: 5. März 2025

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen

Aus der Zeitschrift Nonlinear Engineering Band 14 Heft 1

Abstract

In this article, we present an accurate semi-analytical solution for fractional-order logistic equations across a wider domain. We accomplish this by deriving successive approximate solutions using a modified perturbation iteration approach tailored for fractional nonlinear differential equations. This method is also effective in addressing the cubic fractional logistic model and the Allee fractional logistic model. We provide several numerical examples to demonstrate that the perturbation iteration approach not only yields accurate approximations but also performs well across a wider domain.

Keywords: Caputo fractional differential equation; perturbation iteration approach; fractional logistic equation; cubic fractional logistic model; Allee fractional logistic model

MSC 2010: 34A08; 26A18; 65L99

1 Introduction

The logistic equation or fractional-order logistic equation is an important differential equation that has many applications, such as in population growth [1], radar signals [2], electro-analytical chemistry [3], economics [4], food chains [5], and modelling chemical kinetics [6]. Recently, significant efforts have been made to find numerical solutions for the fractional derivative form of the logistic equation as this fractional logistic equation lacks an exact solution. However, many authors present solutions limited to a small time interval from 0 to 1, using methods such as power series solutions [7], Legendre collocation spectral methods [8], first-kind Dickson polynomials spectral Tau method [9], and the homotopy perturbation transform method [10], among others. Therefore, in this article, we aim to provide a simpler approach to obtain an accurate solution for the fractional logistic equation over a wider domain. We achieve this by constructing a successive approximate solution using the perturbation iteration method.

On top of that, several attempts were made to determine the analytical or approximation solution for fractional-order logistic equation [11–14]. However, there are very few approaches based on the iteration method. For example, Bhalekar and Daftardar Gejji [15] obtain the approximation solution for the fractional logistic equation via Daftardar Geiji Jafari iteration, while Sweilam et al. [16] used variational iteration method to solve the fractional logistic equation. Different from these two approaches, we will obtain the approximate solution of the fractional logistic equation via a modified perturbation iteration approach. This method can solve a cubic fractional logistic equation as well as Allee fractional logistic model. Some comparisons with other established methods will be discussed. This perturbation iteration method has successfully solved another kind of fractional calculus problem such as the fractional conformable Boussinesq-like equation [17] and fractional Zakharov–Kuznetsov equation [18].

Here, we define the fractional-order logistic equation as follows:

(1.1) D α u ( t ) = 1 m u ( t ) − u 2 ( t ) k

with the initial condition u ( 0 ) = u 0 , and m , k are positive numbers. The exact solution when α = 1 is known as

(1.2) u ( t ) = u 0 k u 0 + ( k − u 0 ) e − t m .

However, the exact solution for arbitrary order α fractional logistic equation is not available. Hence, we will take u ( t ) as the solution to the perturbed initial value problem. In this article, we use Caputo fractional derivatives as follows:

Definition 1

Let us define the Caputo fractional derivative as follows:

(1.3) D t α u ( t ) = 1 Γ ( 1 − α ) ∫ 0 t u ′ ( x ) ( t − x ) α d x , α ∈ ( 0 , 1 ) ,

where Γ and α represent the function of Gamma and positive alpha, respectively.

The outline of the present article is as follows. In Section 2, we will construct the successive approximate solutions of fractional logistic models via the perturbation iteration approach. Section 3 will discuss the convergence analysis of this perturbation iteration approach. Some numerical examples will be presented in Section 4, while the results and discussion are in Section 5. The conclusion is presented in Section 6.

2 Construction of successive approximate solutions with perturbation-iteration approach

This section builds a corrective measure for the fractional logistic model’s successive approximate solutions via the perturbation iteration formula. The fractional derivative is in terms of α . In this approach, we only utilize one correction term in the perturbation expansion, while ε is the artificially introduced parameter.

For 0 < α < 1 , the fractional logistic equation defined in the Caputo sense can be rewritten as follows:

(2.1) 1 Γ ( 1 − α ) ∫ 0 t u ′ ( x ) ( t − x ) α d x − 1 m u ( t ) − u 2 ( t ) k = 0 ,

where u ( t ) is the desired solution. By introducing the perturbated parameter ε , we assume the fractional logistic equation has the following pattern.

(2.2) F ( u ′ , u , ε ) = 0 .

By using the perturbation iteration approach, we can have the approximate solution u n + 1 at n + 1 iteration steps as follows:

(2.3) u n + 1 = u n + ε ( u c ) n , u n + 1 ′ = u n ′ + ε ( u c ′ ) n ,

where u c and u c ′ are the correction terms in the perturbation expansion.

We expand Eq. (2.2) into Taylor series for only first order derivative as follows:

(2.4) F ( u ′ , u , ε ) ≈ 1 0 ! F ( u ′ , u , ε ) ε = 0 + ε 1 1 ! δ F δ u ′ ( u ′ , u , ε ) ε = 0 + δ F δ u ( u ′ , u , ε ) ε = 0 + δ F δ ε ( u ′ , u , ε ) ε = 0 = 0 .

By using Eq. (2.3), the Eq. (2.4) is equivalent to following,

(2.5) F ( u ′ , u , 0 ) + F u ′ ( u ′ , u , 0 ) ε ( u c ′ ) n + F u ( u ′ , u , 0 ) ε ( u c ) n + F ε ( u ′ , u , 0 ) ε = 0 , F + F u ′ ε ( u c ′ ) n + F u ε ( u c ) n + F ε ε = 0 .

By rearranging Eq. (2.5), we obtain the iteration formula as follows:

(2.6) ( u c ′ ) n + F u F u ′ ( u c ) n = − F ε − F ε F u ′ .

More specifically, imaging that the perturbed initial value fractional logistic model is as Eq. (2.7).

(2.7) D ( α ) u ( t ) = 1 m u ( t ) − u 2 ( t ) k ,

with the initial condition of u ( 0 ) = 1 2 and m , k are positive numbers. By using the definition of Caputo fractional derivative and implementing the small perturbated parameter ε , we have

(2.8) F ( u n ′ , u n , ε ) = ε 1 Γ ( 1 − α ) ∫ 0 t u n ′ ( x ) ( t − x ) α d x − ε 1 m u n ( t ) + ε 1 m k u n 2 ( t ) ,

where u n ′ and u n are the approximate solution at n iteration steps. If we add u n ′ ( t ) and subtract ε u n ′ ( t ) from the equation, and by using the iteration formula, terms in Eq. (2.8) become

(2.9) F ( u n ′ , u n , ε ) = ε 1 Γ ( 1 − α ) ∫ 0 t u n ′ ( x ) ( t − x ) α d x − ε 1 m u n ( t ) + ε 1 m k u n 2 ( t ) + u n ′ ( t ) − ε u n ′ ( t ) .

From Eq. (2.9), we represent the term(s) without ε and with ε as F and F ε , respectively, and we obtain

(2.10) F = u n ′ ( t ) , F u n = 0 , F u n ′ = 1 , F ε = 1 Γ ( 1 − α ) ∫ 0 t u n ′ ( x ) ( t − x ) α d x − 1 m u n ( t ) + 1 m k u n 2 ( t ) − u n ′ ( t ) .

By substituting Eq. (2.10) into Eq. (2.6), we obtain the successive approximate solutions at various points by applying the iteration formula. By applying the initial condition, we integrate Eq. (2.6) (after putting in Eq. (2.10)) to obtain

(2.11) u 1 ( t ) = 1 2 m − 1 4 k t + c .

From Eq. (2.3), we have that c = c 0 = 1 2 , so that

(2.12) u 1 ( t ) = 1 2 m − 1 4 k t + 1 2

and

(2.13) u 1 ′ ( t ) = 1 2 m − 1 4 k .

We repeat the same procedure to obtain the higher iteration. For the sake of simplicity, now, we let A = 1 2 m − 1 4 k , so that

(2.14) u 1 ( t ) = A t + 1 2 and u 1 ′ ( t ) = A .

After repeating the same iteration as in Eq. (2.10), we have

(2.15) u 2 ′ ( t ) = − 1 Γ ( 1 − α ) ∫ 0 t u 1 ′ ( t ) ( t − x ) α d x + 1 m u 1 ( t ) − 1 m k u 1 2 ( t ) + u 1 ′ ( t ) − u 1 ′ ( t ) ε .

By substituting u 1 ( t ) and u 1 ′ ( t ) from Eq. (2.14) into Eq. (2.15), we obtain

(2.16) u 2 ′ ( t ) = − A t 1 − α Γ ( 2 − α ) + 1 m A t + 1 2 − 1 m k A t + 1 2 2 + A − A ε .

By integration, we obtain

(2.17) u 2 ( t ) = − A t 2 − α Γ ( 3 − α ) + 1 m 1 2 t + 1 2 A t 2 − 1 m k 1 4 t + 1 2 A t 2 + 1 3 A 2 t 3 + A t − A t ε + ( u c ) n .

Also, by applying Eq. (2.3), the Eq. (2.17) becomes

(2.18) u 2 ( t ) = 1 2 + A t − A t 2 − α Γ ( 3 − α ) + 1 m 1 2 t + 1 2 A t 2 − 1 m k 1 4 t + 1 2 A t 2 + 1 3 A 2 t 3 + A t − A t ε .

We repeat the same iteration steps to obtain the third iteration as follows:

(2.19) u 3 ( t ) = 1 2 − A t 2 − α Γ ( 3 − α ) + 2 A 2 t 4 − α m k Γ ( 5 − α ) − A ( k − 1 ) t 3 − α m k Γ ( 4 − α ) + ( 8 A k m ε − 4 A k m + 2 k ε − ε ) 4 m k ε t + A ( 3 k ε − k − 3 ε + 1 ) 2 m k ε t 2 − A ( 6 A k m ε − 2 A k m − k 2 ε + 2 k ε − ε ) 6 m 2 k 2 ε t 3 − A 2 ( k − 1 ) 3 m 2 k 2 t 4 − A 2 ( 8 A k m − 3 k 2 + 6 k − 3 ) 60 m 3 k 3 t 5 + A 3 ( k − 1 ) 18 m 3 k 3 t 6 − A 4 63 m 3 k 3 t 7 .

The similar procedure is applied to obtain the higher iteration. Nevertheless, one can follow the same way to obtain the approximation solution for the cubic fractional logistic model, where A = ( μ 4 m − μ 2 m − μ 8 m k + μ 4 m k ) t . Here, we show the first two iterations of the cubic fractional logistic model.

(2.20) u 1 ( t ) = 1 2 + A t , u 2 ( t ) = 1 2 − A t 2 − α Γ ( 3 − α ) + 2 A − μ 4 m + μ 8 m k − A ε t + 3 64 μ A 8 m k t 2 + μ A 2 3 m − μ A 2 6 m k t 3 − μ A 3 4 m k t 4 .

Similarly, we apply the same method to derive the following for the Allee fractional logistic model, where A = ( 1 4 − μ 2 − 1 8 + μ 4 ) t

(2.21) u 1 ( t ) = 1 2 + A t , u 2 ( t ) = 1 2 − A t 2 − α Γ ( 3 − α ) + 2 A + 1 8 − μ 4 − A ε t + A 8 t 2 + − A 2 6 + μ A 2 6 t 3 − A 3 4 t 4 .

3 Convergence analysis

We analyse the method’s level of convergence in this part.

Theorem 1

[19,20] The P I A ( 1 , 1 ) converges at F n ( D α u n , u n , ε , t ) = 0 whenever

(3.1) ∣ u n + 1 − u n ∣ ≤ ε ′ when ε ′ → 0 .

Proof

Assume that F u n + 1 ′ , F u n + 1 , F u n , and F u n ∈ G λ a , where λ ≥ − 1 . Assume that the function F n is a time continuous and differentiable on [ x , y ] . By inserting a = 1 and b = 1 , the general iteration formula of P I A ( a , b ) is changed to P I A ( 1 , 1 ) in the recursive relation. This is given as follows:

(3.2) u n ′ ( t ) + F u n F u n ′ u n ( t ) = − F ε + F ε F u n ′ .

To establish a triangle inequalities connection with respect to u n + 1 ′ ( t ) and u n ( t ) , we need to change n to n + 1 in Eq. (3.2), and by applying norm 2 to both sides of the equation, we obtain

(3.3) ‖ u n ′ ( t ) ‖ ≤ F ε + F ε F u n ′ + F u n F u n ′ . ‖ u n ( t ) ‖ .

(3.4) ‖ u n + 1 ′ ‖ ≤ F ε + F ε F u n + 1 ′ + F u n + 1 F u n + 1 ′ . ‖ u n + 1 ( t ) ‖ .

We are now required to obtain ‖ u n + 1 − u n ‖ from ‖ u n + 1 ′ − u n ′ ‖ . By using the calculus magnitude rules and rewriting inequalities with respect to ‖ u n ‖ and ‖ u n + 1 ‖ , we arrive at,

(3.5) ‖ u n + 1 − u n ‖ ≥ ‖ u n + 1 ‖ − ‖ u n ‖ , ≥ F u n + 1 ′ F u n + 1 ′ . ‖ u n + 1 ′ ‖ − F ε + F ε F u n + 1 ′ − F u n ′ F u n + 1 ′ . ‖ u n ′ ‖ − F ε + F ε F u n ′ .

Therefore, we must find a bound–restriction for ‖ u n + 1 − u n ‖ . To obtain this, we must establish that { u b } is a Cauchy sequence that must converge in the specified space. Except for ‖ u n ′ ‖ and ‖ u n + 1 ′ ‖ , all of the elements of ‖ u n + 1 − u n ‖ in the right-hand side of the inequality are known. As a result, we have,

(3.6) ‖ u n + 1 − u n ‖ ≥ F u n + 1 ′ F u n + 1 ′ . ‖ u n + 1 ′ ‖ − F u n + 1 ′ F u n + 1 ′ . F ε + F ε F u n + 1 ′ − F u n ′ F u n ‖ u n ′ ‖ − F u n ′ F u n . F ε + F ε F u n ′ .

However, with reference to ε , the function F k = F ( u n ′ , u n , ε ) is a chaotic functional, and its overall phase is as follows:

(3.7) F n = F ( u n ′ , u n , ε ) = ε Γ ( 1 − α ) ∫ 0 t u n ′ ( x ) ( s − x ) α d x ± τ 1 ε u n , b ′ ( t ) ± τ 2 ε u n , b ″ ( t ) ± τ 3 ε u n , b ( n ) ( t ) , α [ 0 , 1 ] ,

where τ i for i = 1 , 2 , 3 are constants. As a result, it is possible to write functions for F u n ′ and F u n depending on F n . In addition, we assume that F u n + 1 ′ , F u n + 1 , F u n , and F u n ′ ≠ 0 . Given that F u n + 1 ′ , F u n + 1 , F u n , and F u n ′ ∈ G λ a , λ ≥ − 1 are bounded, we have the following:

(3.8) F u n + 1 ′ F u n + 1 ≤ A 1 , F u n ′ F u n ′ ≤ A 2 .

(3.9) F ε + F ε F u n + 1 ′ ≤ A 1 ′ , F ε + F ε F u n ′ ≤ A 2 ′ .

We obtain

(3.10) ‖ u n + 1 − u n ‖ ≥ A 1 ‖ u n + 1 ′ ‖ − A 1 ⋅ A 2 ′ − M 2 ⋅ ‖ u n ′ ‖ + A 2 ⋅ A 2 ′ .

Furthermore, we look at

(3.11) u n ′ = Λ [ u n ] u n + 1 ′ = Λ [ u n + 1 ] ,

where Λ is a linear operator with the definition of an operator in an infinitely dimensional space, and Λ is defined as Λ = d d * * . Since any linear operator has a finite set of dimensions, we can define

(3.12) ‖ u n ′ ‖ = ‖ Λ [ u n ] ‖ ≤ B 1 , ‖ u n + 1 ′ ‖ = ‖ Λ [ u n + 1 ] ‖ ≤ B 2 ,

such that we can arrive at

(3.13) ‖ u n + 1 − u n ‖ ≥ A 1 B 2 − A 1 B 1 ′ − A 2 B 1 + A 2 A 2 ′ = A 1 ( B 2 − B 1 ′ ) + A 2 ( A 2 ′ − B 1 ) .

So, if ‖ u n + 1 − u n ‖ ⟼ 0 , so that we arrive

(3.14) lim ε ′ ⟶ 0 [ A 1 ( B 2 − B 1 ′ ) + A 2 ( A 2 ′ − B 1 ) ] = 0 .

So, whenever A 1 ( B 2 − B 1 ′ ) = 0 , then we have A 1 = 0 . On the other way round, whenever A 2 ( A 2 ′ − B 1 ) = 0 , then A 2 = 0 or A 2 ′ = B 1 . This therefore end the proof.□

4 Numerical examples

This section presents a few cases to demonstrate the accuracy of the PIA method. The PIA method can obtain high-accuracy results in a larger domain.

Example 1

[21,22] Consider the fractional logistic equation as follows:

(4.1) D α u ( t ) = 1 m u ( t ) − u 2 ( t ) k ,

with the initial condition u ( 0 ) = 1 2 . When α = 1 , (i.e., reduce to integer order logistic equation), the exact solution is known as follows:

(4.2) u ( t ) = u 0 k u 0 + ( k − u 0 ) e − t m .

Solution: When using the iteration formula (2.6), we begin with a base function that is suitable for the boundary condition and calculate coefficients from the boundary condition at each step. From the definition of the Caputo derivative, Eq. (4.1) is recast and confirmed into the Caputo integral equation, giving us the following equation:

(4.3) u ′ ( t ) = − 1 Γ ( 1 − α ) ∫ 0 t u n ′ ( x ) ( t − x ) α d x + 1 m u n ( t ) − 1 m k u n 2 ( t ) + u n ′ ( t ) − u 1 ′ ( t ) ε .

Taking into consideration, α = 1 , k = 1 , m = 4 , ε = 1 , the following sequential approximate solutions are obtained at each stage using the iteration formula.

(4.4) u 1 ( t ) = 1 2 + 1 16 t , u 2 ( t ) = 1 2 + 1 16 t − 1 3072 t 3 , u 3 ( t ) = 1 2 + 1 16 t − 1 3072 t 3 + 1 491520 t 5 − 1 264241152 t 7 , u 4 ( t ) = 1 2 + 1 16 t − 1 3072 t 3 + 1 491520 t 5 − 17 1321205760 t 7 + 19 380507258880 t 9 − 69 446461850419200 t 11 + 1 3376875086807040 t 13 − 1 4189403184617226240 t 15 .

For α = 0.3 , k = 1 , m = 2 , ε = 1 , following sequential approximate solutions are obtained at each stage using the iteration formula.

(4.5) u 1 ( t ) = 1 2 + 1 8 t , u 2 ( t ) = 1 2 + 1 4 t − 1 384 t 3 − 9 80 t 5 ∕ 3 Γ ( 2 ∕ 3 ) , u 3 ( t ) = 1 2 + 3 8 t − 5 384 t 3 + 1 7680 t 5 − 1 2064384 t 7 − 27 80 t 5 ∕ 3 Γ ( 2 ∕ 3 ) + 27 448 3 Γ ( 2 ∕ 3 ) t 7 ∕ 3 π + 513 56320 t 11 ∕ 3 Γ ( 2 ∕ 3 ) − 243 166400 t 13 ∕ 3 ( Γ ( 2 ∕ 3 ) ) 2 − 9 174080 t 17 ∕ 3 Γ ( 2 ∕ 3 ) .

Example 2

We consider a cubic fractional logistic equation taken from Example 6.3 in [23], as follows:

(4.6) D α u ( t ) = μ m u ( t ) 1 − u ( t ) k ( u ( t ) − 1 )

with the initial condition u ( 0 ) = 1 2 . The exact solution is not known.

Solution: Similar to the previous example, when using the iteration formula (2.6), we begin with a base function that is suitable for the boundary condition and calculate coefficients from the boundary condition at each step. From the definition, Eq. (4.6) is recast and confirmed into the Caputo integral equation, giving us as the following equation:

(4.7) u ′ ( t ) = − 1 Γ ( 1 − α ) ∫ 0 t u n ′ ( x ) ( t − x ) α d x − μ m u n ( t ) + μ m u n 2 ( t ) + μ m k u n 2 ( t ) − μ m k u n 3 ( t ) + u n ′ ( t ) − u 1 ′ ( t ) ε .

Taking into consideration, α = 1 , k = 10 , m = 2 , ε = 1 , μ = 1 , the following sequential approximate solutions are obtained at each stage using the iteration formula.

(4.8) u 1 ( t ) = 1 2 − 19 160 t , u 2 ( t ) = 1 2 + 19 160 t − 19 25600 t 2 + 6859 3072000 t 3 + 6859 327680000 t 4 , u 3 ( t ) = 1 2 − 19 160 t − 13699 6144000 t 3 + 48013 983040000 t 4 − 1227761 24576000000 t 5 − 54412447 37748736000000 t 6 + 6794477387 21139292160000000 t 7 + 888919541 53687091200000000 t 8 − 15631612987 57982058496000000000 t 9 − 4994061405793 92771293593600000000000 t 10 − 2573456736581 1814194185830400000000000 t 11 − 322687697779 26388279066624000000000000 t 12 − 322687697779 9147936743096320000000000000 t 13 .

Example 3

We consider an Allee fractional logistic equation taken from a recent works in [14], as follows:

(4.9) D α u ( t ) = u ( t ) ( 1 − u ( t ) ) ( u ( t ) − μ ) ,

with the initial condition u ( 0 ) = 1 2 . The exact solution is not known.

Solution: Taking into consideration, α = 1 , μ = 1 4 , ε = 1 , the iteration is giving as follows:

(4.10) u 1 ( t ) = 1 2 + 1 16 t , u 2 ( t ) = 1 2 + 1 16 t + 1 128 t 2 − 1 3072 t 3 − 1 16384 t 4 , u 3 ( t ) = 1 2 + 1 16 t + 1 128 t 2 + 1 3072 t 3 − 7 49152 t 4 − 11 491520 t 5 − 7 9437184 t 6 + 53 264241152 t 7 + 7 268435456 t 8 + 1 28991029248 t 9 − 37 231928233984 t 10 − 7 1133871366144 t 11 + 1 3298534883328 t 12 + 1 57174604644352 t 13 .

5 Result and discussion

For Example 1, which is the fractional logistic equation, Figure 1 compares perturbation iteration approach, PIA with Legendre-collocation schemes method, which is a previous work by Izadi [8] when α = 1 for u 3 ( t ) and u 8 ( t ) , respectively. Figure 2 displays the comparison result between the exact fractional logistic solution for u 4 ( t ) and u 10 ( t ) , respectively when α = 1 with the approximation using perturbation iteration approach for Example 1. To show the effectiveness when α is not equal to 1, Figure 3 compared the PIA with the Legendre-collocation schemes method, which is a previous work by Izadi [8] when α = 1 3 for u 3 and u 7 , respectively. From the look of things, the PIA method is commendable, satisfactory, and simple. Figure 4 shows the reaction of Example 1 at α = 0.95 , 0.85 , 0.75 . It shows that the value of α ∈ [ 0 , 1 ] has a great influence. When α is approaching 1, the solution will be approaching to the exact solution when α = 1 .

$Figure 1 The comparison of Legendre collocation method [8] with perturbation-iteration approach, PIA for Example 1 at α = 1 \alpha =1 .$

Figure 1

The comparison of Legendre collocation method [8] with perturbation-iteration approach, PIA for Example 1 at α = 1 .

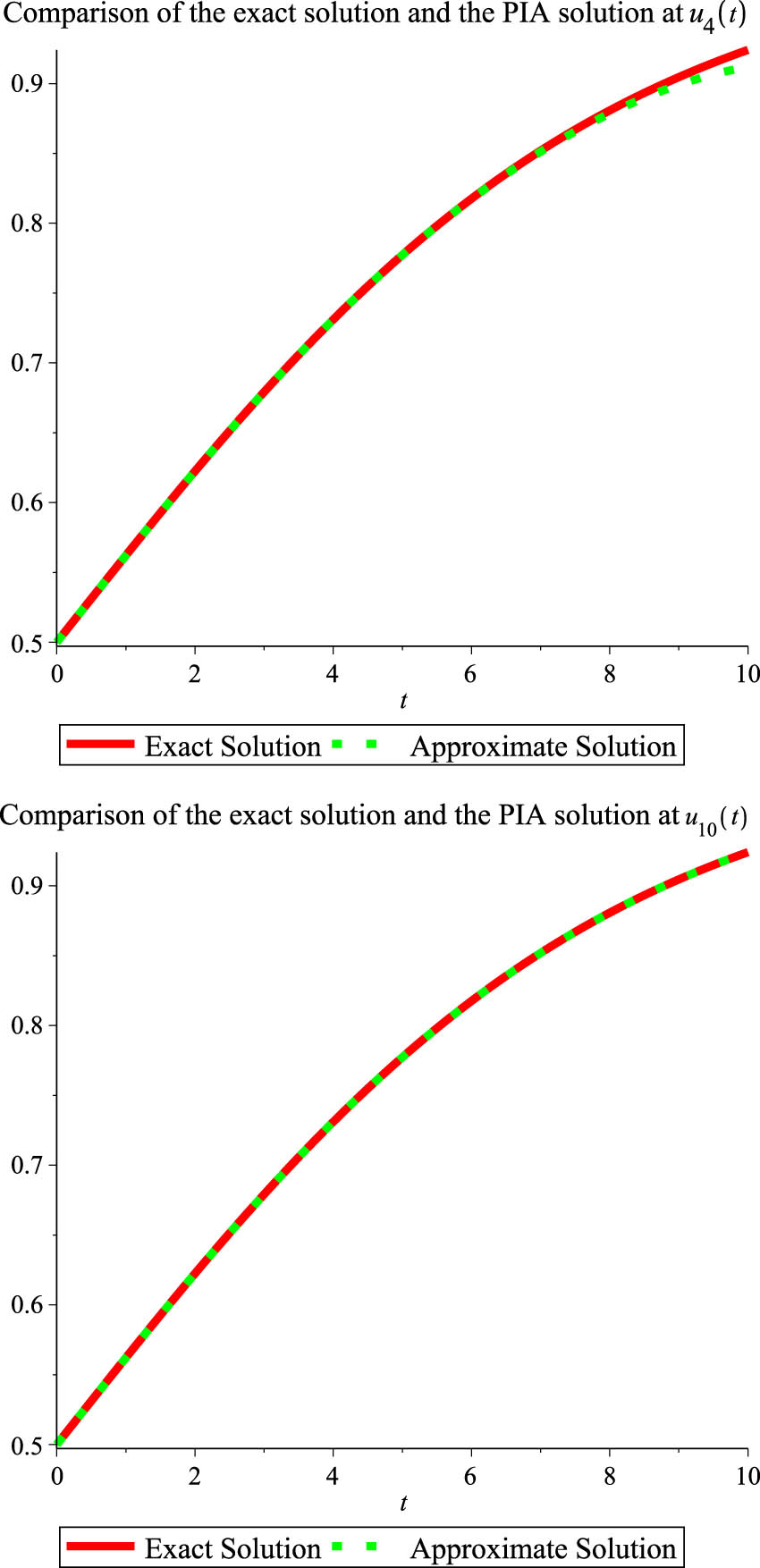
$Figure 2 The comparison result of the exact solution with PIA solutions for Example 1 at α = 1 \alpha =1 .$

Figure 2

The comparison result of the exact solution with PIA solutions for Example 1 at α = 1 .

$Figure 3 The comparison of Legendre-collocation method with perturbation-iteration approach, PIA for Example 1 at α = 1 3 \alpha =\frac{1}{3} with the previous work by Izadi [8].$

Figure 3

The comparison of Legendre-collocation method with perturbation-iteration approach, PIA for Example 1 at α = 1 3 with the previous work by Izadi [8].

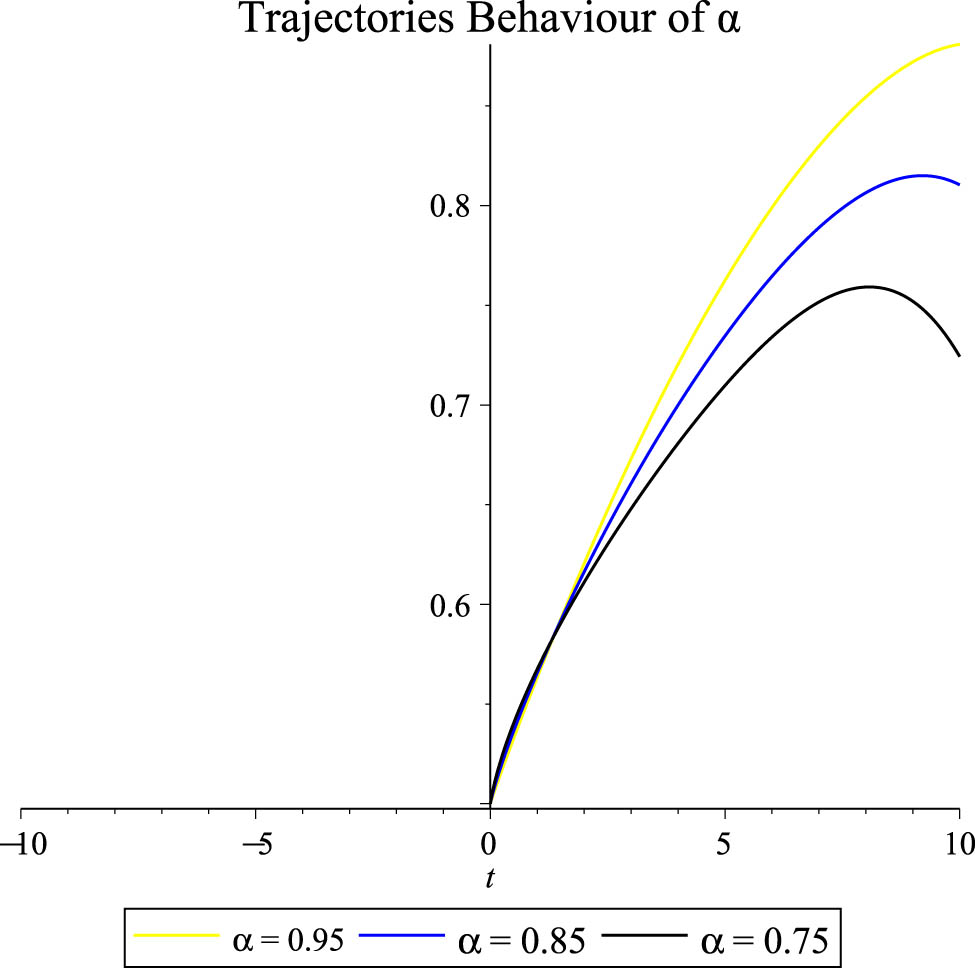
$Figure 4 The trajectories behaviour of Example 1 with respect to different fractional orders α = 0.95 , 0.85 , 0.75 \alpha =0.95,0.85,0.75 .$

Figure 4

The trajectories behaviour of Example 1 with respect to different fractional orders α = 0.95 , 0.85 , 0.75 .

For Example 2, which is the cubic fractional logistic equation, Table 1 displays the comparison between reproducing Kernel method (RKHS) and successive substitution (SS) iterations of Example 6.3 in [23] with the perturbation iteration approach, when α = 1 , k = 10 , m = 2 , ε = 1 , μ = 1 . Figure 5 shows how the cubic logistic solution trajectories for Example 2 change with different values of α = 0.95 , 0.85 , 0.75 . It shows that the value of α ∈ [ 0 , 1 ] has a great influence.

Table 1

Comparison of RKHS and SS solutions of cubic logistic equation with PIA method for Example 2 when α = 1 , k = 10 , m = 2 , ε = 1 , μ = 1

t	SS solution	RKHS solution	PIA solution, u 3 ( t )
0.0	0.500000	0.500000	0.500000
0.1	0.488120	0.488194	0.488120
0.2	0.476238	0.476526	0.476238
0.3	0.464369	0.464997	0.464369
0.4	0.452525	0.453605	0.452525
0.5	0.440720	0.442352	0.440720
0.6	0.428967	0.431237	0.428967
0.7	0.417279	0.420259	0.417280
0.8	0.405670	0.409421	0.405670
0.9	0.394151	0.398720	0.394151
1.0	0.382736	0.388157	0.382736

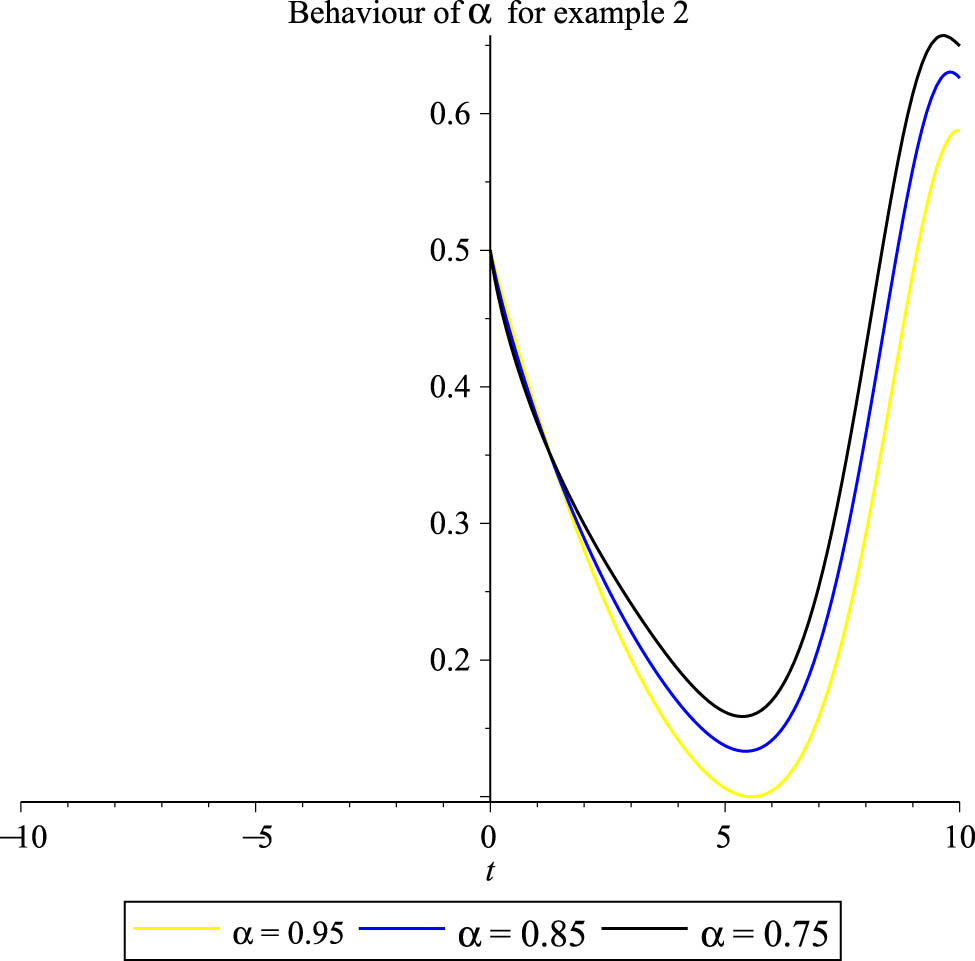
$Figure 5 The reaction of Example 2 solution trajectories with respect to different fractional orders α = 0.95 , 0.85 , 0.75 \alpha =0.95,0.85,0.75 when k = 10 k=10 , m = 2 m=2 , ε = 1 \varepsilon =1 , μ = 1 \mu =1 .$

Figure 5

The reaction of Example 2 solution trajectories with respect to different fractional orders α = 0.95 , 0.85 , 0.75 when k = 10 , m = 2 , ε = 1 , μ = 1 .

For Example 3, which is the Allee fractional logistic equation, the comparison results of PIA method and the results of formal power series (FPS) in a recently published article [14] are presented in Tables 2 and 3, when α = 0.9 . For the fractional order case of this Allee fractional logistic equation, we were able to achieve good results by only using a perturbation-iteration approach as shown in Figure 6 when compare with the FPS solution, taken α = 0.9 , τ = 1 4 , ε = 1 .

Table 2

Comparison of Formal Power Series, FPS solutions of Allee fractional logistic model with PIA method for Example 3 when α = 0.9 , μ = 1 4 , ε = 1

t	FPS solution	PIA solution	∣ FPS – PIA ∣ , u 2 ( t )
0.0	0.500000	0.500000	0.00000 × 10⁰
0.1	0.5083287937	0.5078337718	4.95022 × 1 0 ‒ 4
0.2	0.5157808030	0.5151407652	6.40038 × 1 0 ‒ 4
0.3	0.5230569038	0.5223091041	7.47800 × 1 0 ‒ 4
0.4	0.5302793063	0.5294298050	8.49501 × 1 0 ‒ 4
0.5	0.5375008881	0.5365465320	9.54356 × 1 0 ‒ 4
0.6	0.5447504100	0.5436845974	1.06581 × 1 0 ‒ 3
0.7	0.5520455195	0.5508600884	1.18543 × 1 0 ‒ 3
0.8	0.5593978919	0.5580837277	1.31416 × 1 0 ‒ 3
0.9	0.5668156586	0.5653628047	1.45285 × 1 0 ‒ 3
1.0	0.5743046965	0.5727022505	1.60245 × 1 0 ‒ 3

Table 3

Comparison of Formal Power Series, FPS of Allee fractional logistic equation with PIA method for Example 3 when α = 0.9 , μ = 1 4 , ε = 1

t	FPS solution	PIA solution	∣ FPS – PIA ∣ , u 3 ( t )
0.0	0.500000	0.500000	0.00000E+00
0.1	0.5083298157	0.5082184849	1.11331 × 1 0 ‒ 4
0.2	0.5157874440	0.5156691875	1.18256 × 1 0 ‒ 4
0.3	0.5230767504	0.5229480725	1.28678 × 1 0 ‒ 4
0.4	0.5303224601	0.5301757231	1.46737 × 1 0 ‒ 4
0.5	0.5375797153	0.5374060554	1.73660 × 1 0 ‒ 4
0.6	0.5448793731	0.5446686380	2.10735 × 1 0 ‒ 4
0.7	0.5522410532	0.5519813358	2.59717 × 1 0 ‒ 4
0.8	0.5596783061	0.5593554327	3.22873 × 1 0 ‒ 4
0.9	0.5672010588	0.5667980842	4.02975 × 1 0 ‒ 4
1.0	0.5748169171	0.5743136361	5.03281 × 1 0 ‒ 4

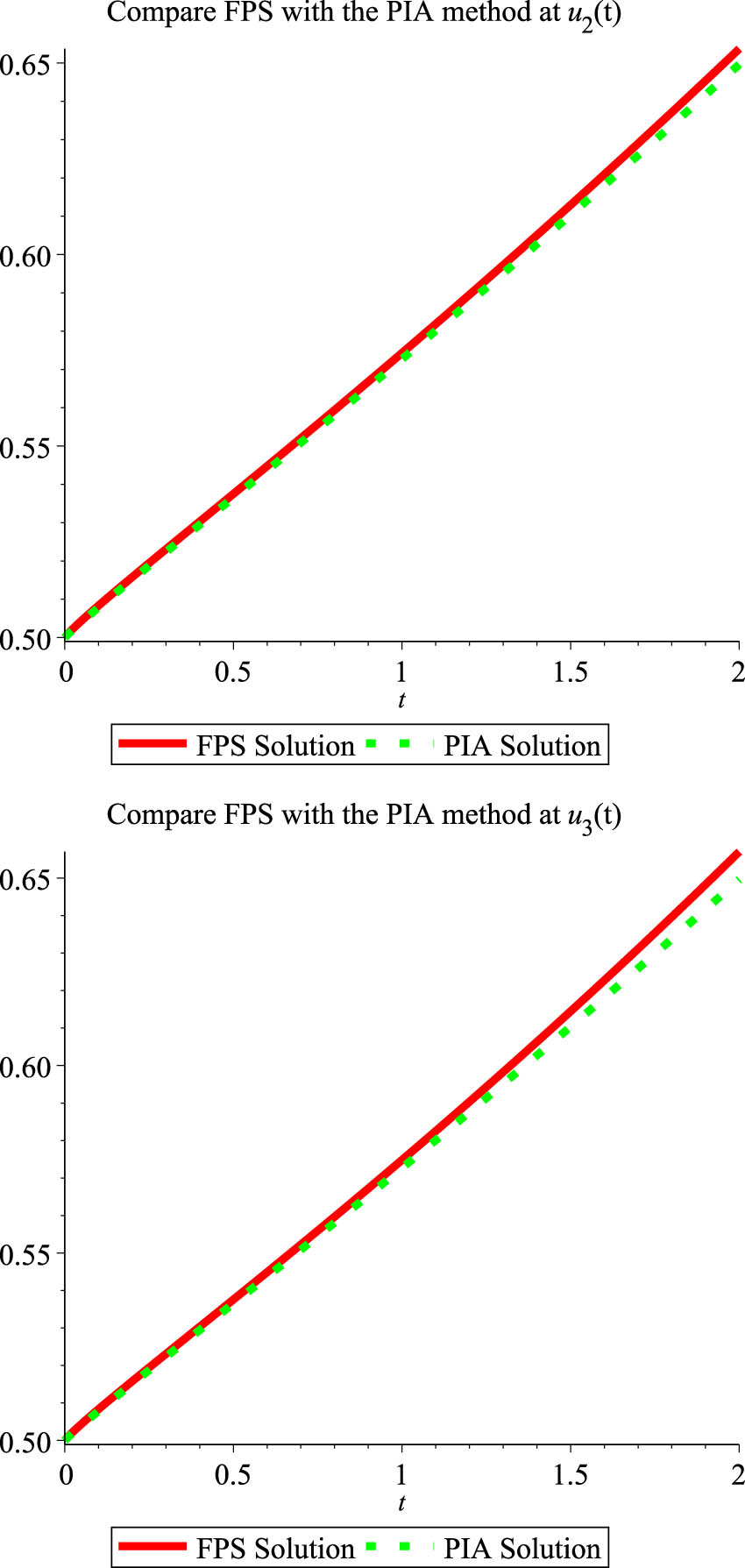
$Figure 6 The comparison result of the FPS with PIA solutions for Example 3 at α = 0.9 \alpha =0.9 .$

Figure 6

The comparison result of the FPS with PIA solutions for Example 3 at α = 0.9 .

6 Conclusion

We present a numerical solution for the fractional logistic equation using a perturbation iteration approach. This method not only yields accurate results for the fractional logistic equation but also extends the solution to a broader domain, overcoming the limitations of many existing studies that confine their results to the interval from 0 to 1. In addition, our approach can effectively tackle the cubic fractional logistic model and the Allee fractional logistic model. We aim to further develop this perturbation iteration technique to address other fractional calculus problems defined by various fractional operators, such as Caputo–Hadamard [24] and tempered fractional differential equations [25]. Furthermore, we aspire to adapt this approach to solve systems of fractional differential equations, as explored in the studies by Jan et al. [26,27].

Acknowledgments

This research was supported by Universiti Tun Hussein Onn Malaysia (UTHM) throughTier 1 (vot Q380).

Funding information: This research was supported by Universiti Tun Hussein Onn Malaysia (UTHM) through Tier 1 (vot Q380).
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: Authors state no conflict of interest.
Data availability statement: All data generated or analysed during this study are included in this published article.

References

[1] Law R, Murrell DJ, Dieckmann U. Population growth in space and time: spatial logistic equations. Ecol. 2003;84(1):252–62. 10.1890/0012-9658(2003)084[0252:PGISAT]2.0.CO;2Suche in Google Scholar

[2] Krishna BT. Binary phase coded sequence generation using fractional order logistic equation. Circ Syst Signal Pr. 2012;31:401–11. 10.1007/s00034-011-9295-8Suche in Google Scholar

[3] Torresi RM, de Torresi SC, Gonzalez ER. On the use of the quadratic logistic differential equation for the interpretation of electrointercalation processes. J Electroanal Chem. 1999;461(1–2):161–6. 10.1016/S0022-0728(98)00069-2Suche in Google Scholar

[4] Tarasov VE, Tarasova VV. Logistic equation with continuously distributed lag and application in economics. Nonlinear Dynam. 2019;97:1313–28. 10.1007/s11071-019-05050-1Suche in Google Scholar

[5] Kooi B, Boer M, Kooijman S. On the use of the logistic equation in models of food chains. B Math Biol. 1998;60(2):231–46. 10.1006/bulm.1997.0016Suche in Google Scholar

[6] Burnham AK. Use and misuse of logistic equations for modeling chemical kinetics. J Therm Anal Calorim. 2017;127(1):1107–16. 10.1007/s10973-015-4879-3Suche in Google Scholar

[7] Area I, Nieto J. Power series solution of the fractional logistic equation. Phys A. 2021;573:125947. 10.1016/j.physa.2021.125947Suche in Google Scholar

[8] Izadi M. A comparative study of two Legendre-collocation schemes applied to fractional logistic equation. Int J Appl Comput Math. 2020;6:1–18. 10.1007/s40819-020-00823-4Suche in Google Scholar

[9] Abd Elaziz El-Sayed A, Boulaaras S, Sweilam N. Numerical solution of the fractional-order logistic equation via the first-kind Dickson polynomials and spectral Tau method. Math Methods Appl Sci. 2023;46(7):8004–17. 10.1002/mma.7345Suche in Google Scholar

[10] Ganie AH, Khan A, Alhamzi G, Saeed AM, et al. A new solution of the nonlinear fractional logistic differential equations utilizing efficient techniques. AIP Adv. 2024;14(3):035134. 10.1063/5.0197704Suche in Google Scholar

[11] Jornet M, Nieto JJ. Power-series solution of the L-fractional logistic equation. Appl Math Lett. 2024;154:109085. 10.1016/j.aml.2024.109085Suche in Google Scholar

[12] Nieto JJ. Fractional Euler numbers and generalized proportional fractional logistic differential equation. Fract Calc Appl Anal. 2022;25(3):876–86. 10.1007/s13540-022-00044-0Suche in Google Scholar PubMed PubMed Central

[13] Kalra P, Malhotra N. Modeling and analysis of fractional order logistic equation incorporating additive Allee effect. Contemp Math. 2024;5:380–401. 10.37256/cm.5120243183Suche in Google Scholar

[14] Area I, Nieto JJ. On the fractional Allee logistic equation in the Caputo sense. Examples Counterexamples. 2023;4:100121. 10.1016/j.exco.2023.100121Suche in Google Scholar

[15] Bhalekar S, Daftardar Gejji V. Solving fractional order logistic equation using a new iterative method. Int J Differ Equ. 2012;2012:975829. 10.1155/2012/975829Suche in Google Scholar

[16] Sweilam NH, Khader M, Mahdy A. Numerical studies for solving fractional-order logistic equation. Int J Pure Appl Math. 2012;78(8):1199–210. 10.1155/2012/764894Suche in Google Scholar

[17] Nisar KS, Akinyemi L, Inc M, Şenol M, Mirzazadeh M, Houwe A, et al. New perturbed conformable Boussinesq-like equation: Soliton and other solutions. Results Phys. 2022;33:105200. 10.1016/j.rinp.2022.105200Suche in Google Scholar

[18] Şenol M, Alquran M, Kasmaei HD. On the comparison of perturbation-iteration algorithm and residual power series method to solve fractional Zakharov-Kuznetsov equation. Results Phys. 2018;9:321–7. 10.1016/j.rinp.2018.02.056Suche in Google Scholar

[19] Şenol M, Dolapci IT. On the Perturbation-Iteration Algorithm for fractional differential equations. J King Saud Univ Sci. 2016;28(1):69–74. 10.1016/j.jksus.2015.09.005Suche in Google Scholar

[20] Şenol M, Kasmaei HD. Perturbation-iteration algorithm for systems of fractional differential equations and convergence analysis. Prog Fract Differ Appl. 2017;4:271–9. 10.18576/pfda/030403Suche in Google Scholar

[21] D’Ovidio M, Loreti P. Solutions of fractional logistic equations by Euler’s numbers. Phys A. 2018;506:1081–92. 10.1016/j.physa.2018.05.030Suche in Google Scholar

[22] Kaharuddin LN, Phang C, Jamaian SS. Solution to the fractional logistic equation by modified Eulerian numbers. Eur Phys J Plus. 2020;135(2):1–11. 10.1140/epjp/s13360-020-00135-ySuche in Google Scholar

[23] Djeddi N, Hasan S, Al-Smadi M, Momani S. Modified analytical approach for generalized quadratic and cubic logistic models with Caputo-Fabrizio fractional derivative. Alex Eng J. 2020;59(6):5111–22. 10.1016/j.aej.2020.09.041Suche in Google Scholar

[24] Toh YT, Phang C, Ng YX. Temporal discretization for Caputo-Hadamard fractional derivative with incomplete Gamma function via Whittaker function. Comput Appl Math. 2021;40:1–19. 10.1007/s40314-021-01673-6Suche in Google Scholar

[25] Owoyemi AE, Phang C, Toh YT. An efficient numerical scheme for solving multiorder tempered fractional differential equations via operational matrix. J Math. 2022;2022:7628592.10.1155/2022/7628592Suche in Google Scholar

[26] Jan R, Boulaaras S, Alnegga M, Abdullah FA. Fractional-calculus analysis of the dynamics of typhoid fever with the effect of vaccination and carriers. Int J Numer Model: Electron Netw Devices Fields. 2024;37(2):e3184. 10.1002/jnm.3184Suche in Google Scholar

[27] Jan R, Razak NNA, Boulaaras S, Rajagopal K, Khan Z, Almalki Y. Fractional perspective evaluation of Chikungunya infection with saturated incidence functions. Alex Eng J. 2023;83:35–42. 10.1016/j.aej.2023.10.036Suche in Google Scholar

Received: 2024-05-30

Revised: 2024-10-01

Accepted: 2024-11-12

Published Online: 2025-03-05

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

https://doi.org/10.1515/nleng-2024-0065

Schlagwörter für diesen Artikel

Caputo fractional differential equation; perturbation iteration approach; fractional logistic equation; cubic fractional logistic model; Allee fractional logistic model

Creative Commons

BY 4.0