A comparative study on residual power series method and differential transform method through the time-fractional telegraph equation

Pratiksha Devshali; Prince Singh

doi:10.1515/nleng-2025-0116

Article Open Access

A comparative study on residual power series method and differential transform method through the time-fractional telegraph equation

Pratiksha Devshali and Prince Singh

Published/Copyright: April 28, 2025

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Nonlinear Engineering Volume 14 Issue 1

Abstract

In the present era of cutting-edge technologies powering electronic devices, energy systems, and modern telecommunication, a mathematical model called the telegraph equation plays a major role. It describes the wave propagation and diffusion processes in a variety of scientific and engineering areas. This work investigates, applies, and compares two semi analytical methods, namely, reduced fractional differential transform method and the Laplace-transformed residual power series method, toward solving the two-dimensional time-fractional telegraph equation. In the recent past, both the methods have been used to solve various linear and non-linear, ordinary, partial, and fractional differential equations. The literature speaks highly about residual power series method being efficient, specially for the non-linear problems. This work puts forth the methodologies and numerical experiments, and it can be observed that both methods result in the same solution for the two-dimensional linear telegraph equation. However, the solutions for the non-linear telegraph equation are better with the differential transform method.

Keywords: fractional telegraph equation; fractional reduced differential transform method; residual power series method; Laplace-transformed residual power series method

1 Introduction

Telegraphy can be understood as transmitting the electric signal over long ranges. In nineteenth century, first evidences of such work was seen. It changed the communication like never before. To analyze the propagation of signals over distances, keeping the effects of resistance, capacitance, and inductance in perspective, there exists a mathematical model known as the “telegraph equation.”

The telegraph equation is a hyperbolic partial differential equation that describes the voltage and current in an electric transmission line. It was first modeled by the British physicist, Lord Kelvin [1], for his work related to signal transition in the cable crossing Atlantic Ocean. Later on, Goldstein, Heaviside, and Poincare provided its interpretation and analytical solution. This equation can model the phenomena such as reaction–diffusion [2,3], signal transition [4], oceanic diffusion [5], population dynamics [6], and random walk [7].

With the advent of fractional calculus, the mathematical models got a different point of view. The integer-order derivatives are replaced with the arbitrary-order derivatives, which can be defined in a number of ways. These derivatives are popular for including the memory effects and for modeling a complex dynamic behavior better than the integer-order derivatives. In some recent investigations, fractional calculus is applied in solving the heat transfer problems [8,9]. Khan et al. [8] used Caputo Fabrizio definition, while in [9], Khan et al. used Caputo’s definition. In previous studies, [10,11], transmission dynamics of infection is studied by the authors incorporating Caputo’s [12] definition. A fractional financial model is discussed in Rehman et al. [13] using the ABC fractional derivative. The cited references can be studied for the details of various types of fractional derivatives.

Kumar et al. [14] have derived one-dimensional hyperbolic second-order telegraph equations. They formulated the space- and time-fractional model of the telegraph equation using a time-fractional derivative and a space-fractional derivative in place of integer-order derivatives. Extending the one-dimensional model into two-dimensional model gives a wider application and acceptability to the model, and at the same time, it is challenging to solve such an endeavor. In case of a two-dimensional fractional differential equation (FDE), the complications arise mainly due to the non-local nature of fractional derivatives. The FDEs hardly have closed-form solutions, which is another analytical challenge. This work is to find an approximate solution of such an FDE using semi analytic techniques.

Consider a general two-dimensional time-fractional telegraph equation (TFTE):

(1) a 1 ∂ 2 ℵ w ∂ t 2 ℵ + a 2 ∂ ℵ w ∂ t ℵ + a 3 w = ∂ 2 w ∂ x 2 + ∂ 2 w ∂ y 2 + ϕ ( x , y , t ) , x ∈ ( − ∞ , ∞ ) , t > 0 , 0 < ℵ ≤ 1 ,

where w ( x , y , t ) denotes the voltage or current or state of the system at point ( x , y ) and at time t ; a 1 , a 2 , and a 3 are the positive constants comprising the parameters such as resistance and inductance of the cable, capacitance, and conductance to the ground etc. The order of the equation is 2 ℵ , where 0 < ℵ ≤ 1 , and the fractional derivatives are of Caputo-type [12]. The continuous function ϕ ( x , y , t ) provides a mechanism for incorporating non-homogeneous or external influences into the model. In the study by Momani [15], the analytical and estimated solution of one-dimensional space, and TFTE has been discussed using the Adomian decomposition method. Boyadjiev and Luchko [16] formulated a neutral telegraph equation and solved that analytically. Numerical methods, such as boundary knot and analog equation [17,18], have also been used to solve this equation. Khan et al. used Laplace–Adomian decomposition method [19] and natural transform decomposition method [20] to solve the fractional telegraph equation. Recently, Hamza et al. [21] used Sumudu transform, and Kapoor et al. [22] gave an analytical approach to solve fractional telegraph equation using Shehu transform. The method of residual power series method (RPSM) [23–30] has gained some popularity recently, and we observed that the fractional telegraph equation is not yet solved by the Laplace-transformed residual power series method (LTRPSM). Our work contributes to the literature related to analysis and solution of the fractional telegraph equation. Moreover, use of two different methods gives a comprehensive evaluation of these approaches to solve FDEs. This comparison is relevant for developing computational and analytic frameworks for fractional calculus.

In this study, we have derived the solution of two-dimensional TFTE using reduced fractional differential transform method (RFDTM) as well as the LTRPSM. Sections 2 and 4 give a brief glimpse of the two methods. Sections 3 and 5 are about the general solution of the TFTE by RFDTM and by LTRPSM, respectively. Section 6 records the solutions of one linear and one non-linear telegraph equation problem. The results are discussed in Section 7, followed by the conclusion in Section 8.

2 RFDTM

The reduced differential transform method [31] was introduced by Keskin et al. as a simplified version of the differential transform method for a function of space and time variables.

The differential transform of a function ω ( x ) is equivalent to finding the κ th differential transform of a function ω ( x ) . Differentiate ω ( x ) , κ times w.r.t. x , find its value at x = x 0 , and divide by κ ! . To obtain the original function back, take the infinite sum on the product of the transformed function Ω ( κ ) with the ( x − x 0 ) κ . Symbolically,

ω ( x ) = ∑ κ = 0 ∞ 1 κ ! d κ ω ( x ) d x κ x = x 0 ( x − x 0 ) κ = ∑ κ = 0 ∞ Ω ( κ ) ( x − x 0 ) κ .

For a function of two variables ω ( x , t ) , DTM can be extended as

ω ( x , t ) = ∑ κ = 0 ∞ ∑ h = 0 ∞ 1 κ ! 1 h ! d κ + h ω ( x , t ) d x κ d t h x 0 , t 0 ( x − x 0 ) κ ( t − t 0 ) h = ∑ κ = 0 ∞ ∑ h = 0 ∞ Ω ( κ , h ) ( x − x 0 ) κ ( t − t 0 ) h .

For a function ω ( x , t ) that can be written as ω 1 ( x ) . ω 2 ( t ) and let x 0 = t 0 = 0 , then

(2) ω ( x , t ) = ∑ i = 0 ∞ ω 1 ( i ) x i ∑ j = 0 ∞ ω 2 ( j ) t j = ∑ i = 0 ∞ ∑ j = 0 ∞ ( Ω ( i , j ) x i ) t j = ∑ κ = 0 ∞ Ω κ ( x ) t κ .

where Ω κ ( x ) is called t -dimensional spectrum function or the reduced differential transform of ω ( x , t ) . Thus the reduced differential transform method reduces the number of variables [32–37].

The fractional analog to the aforementioned definitions lies in taking the fractional derivative of the function and writing the factorial function as gamma function. For a function ω ( x , t ) , continuously differentiable and analytic in the domain of interest, the reduced fractional differential transform (RFDT) is given as

(3) Ω κ ( x ) = 1 Γ ( κ ℵ + 1 ) [ D t κ ℵ ω ( x , t ) ] t = t 0 , κ = 0 , 1 , 2 , …

The inverse RFDT of Ω κ ( x ) is given as

(4) ω ( x , t ) = ∑ κ = 0 ∞ Ω κ ( x ) ( t − t 0 ) κ ℵ .

For a function ω ( x , y , t ) , continuously differentiable and analytic in the domain of interest, the RFDT is given as

(5) Ω κ ( x , y ) = 1 Γ ( κ ℵ + 1 ) [ D t κ ℵ ω ( x , y , t ) ] t = t 0 , κ = 0 , 1 , 2 , . . .

The inverse RFDT of Ω κ ( x , y ) is given as

(6) ω ( x , y , t ) = ∑ κ = 0 ∞ Ω κ ( x , y ) ( t − t 0 ) κ ℵ .

Combining Eqs (5) and (6),

(7) ω ( x , y , t ) = ∑ κ = 0 ∞ 1 Γ ( κ ℵ + 1 ) × [ D t κ ℵ ω ( x , y , t ) ] t = t 0 ( t − t 0 ) κ ℵ .

Out of all the fractional derivatives, the Caputo’s derivative [12] has been explored the most. In this work, Caputo’s definition is used for fractional derivatives. For more details on fractional derivative and Caputo’s definition, refer previous studies [38,39].

3 Methodology of RFDTM

Consider the two-dimensional TFTE (1). We apply the differential transform [40–42] on both sides of the equation and obtain the following expression:

(8) a 1 Γ ( κ ℵ + 2 ℵ + 1 ) Γ ( κ ℵ + 1 ) Ω κ + 2 + a 2 Γ ( κ ℵ + ℵ + 1 ) Γ ( κ ℵ + 1 ) Ω κ + 1 + a 3 Ω κ = ∂ 2 Ω κ ∂ x 2 + ∂ 2 Ω κ ∂ y 2 + Φ κ ( x , y ) .

This can be simplified as

(9) Ω κ + 2 = Γ ( κ ℵ + 1 ) a 1 Γ ( κ ℵ + 2 ℵ + 1 ) ∂ 2 Ω κ ∂ x 2 + ∂ 2 Ω κ ∂ y 2 + Φ κ ( x , y ) − a 2 Γ ( κ ℵ + ℵ + 1 ) Γ ( κ ℵ + 1 ) Ω κ + 1 − a 3 Ω κ .

Now, substituting κ = 0 , we obtain

Ω 2 = Γ ( 1 ) a 1 Γ ( 2 ℵ + 1 ) ∂ 2 Ω 0 ∂ x 2 + ∂ 2 Ω 0 ∂ y 2 + Φ 0 ( x , y ) − a 2 Γ ( ℵ + 1 ) Γ ( 1 ) Ω 1 − a 3 Ω 0 .

By applying the differential transform on the given or assumed preliminary criteria, Ω 0 and Ω 1 are obtained, and hence, Ω 2 is obtained. Then, substituting κ = 1 into Eq. (9), and using Ω 1 and Ω 2 , Ω 3 is obtained. The final approximate solution by inverse differential transform (see Eq. (6)) is given as

(10) ω ( x , y , t ) = Ω 0 + Ω 1 t ℵ + Ω 2 t 2 ℵ + Ω 3 t 3 ℵ + …

Thus, this process is repeated as many times as is the required number of terms in the series solution. The series solution given by RFDTM may be a closed-form solution if the series converges. We have applied this methodology on a linear TFTE and a non-linear TFTE in Section 6. The obtained series solutions are convergent for the non-fractional telegraph equations.

4 RPSM

Linear as well as non-linear differential equations can be analytically solved using the RPSM. It is widely used in mathematical physics and engineering, where it estimates solutions as power series expansions [23,28]. In order to obtain an accurate series solution, the procedure entails building a residual function for the given differential equation and removing the residual error step by step. So for an ordinary differential equation of the type f ( x , y , y ′ ) = g ( x , y ) , the solution is assumed to be a power series, say y ( x ) = ∑ n = 0 ∞ a n ( x − x 0 ) n , where x 0 is the initial value and a n are the coefficients to be determined. For x 0 = 0 , the coefficients can be written as a 0 = y ( 0 ) , a 1 = y ′ ( 0 ) , a 2 = y ″ ( 0 ) 2 ! , a 3 = y ‴ ( 0 ) 3 ! , and so on.

In RPSM, we define the residual function as Res [ y ( x ) ] = f ( x , y , y ′ ) − g ( x , y ) . Ideally, for the solution of the differential equation, the Res [ y ( x ) ] has to be zero. The assumed series solution is then curtailed to k-terms as

y k ( x ) = ∑ n = 0 k a n ( x − x 0 ) n .

The kth residual function is defined as Res [ y k ] = f ( x , y k , y k ′ ) − g ( x , y k ) . Then, the residual function is calculated at different “ k -values” such that Res [ y 1 ( 0 ) ] = 0 , d d x Res [ y 2 ( 0 ) ] = 0 , d 2 d x 2 Res [ y 3 ( 0 ) ] = 0 , and so on. The unknown coefficients are hence evaluated, and the final estimated series solution is obtained. If the series is convergent, then a closed-form solution is obtained.

If the same procedure is applied to the partial differential equations, the aforementioned process may lead to an identity. From the literature, we understood that the mathematical transforms play a crucial role in such cases. Out of many transforms, we choose Laplace transform (LT), as the literature has a good number of papers on the LT of Caputo fractional derivatives.

In LTRPSM, we take the LT of the given differential equation as well as of the assumed solution. Then, the unknown coefficients are calculated using the Laplace-transformed residuals (LTRs). For more details, refer previous studies [14,28–30].

5 Methodology of LTRPSM

In this section, we consider the TFTE of type (1). Taking LT on both sides of (1), we obtain

(11) a 1 [ s 2 ℵ Ω ( x , y , s ) − s 2 ℵ − 1 w ( x , y , 0 ) − s ℵ − 1 ] + a 2 [ s ℵ Ω ( x , y , s ) − s ℵ − 1 w ( x , y , 0 ) ] + a 3 Ω ( x , y , s ) = ∂ 2 Ω ( x , y , s ) ∂ x 2 + ∂ 2 Ω ( x , y , s ) ∂ y 2 + Φ ( x , y , s ) .

Ω ( x , y , s ) = w ( x , y , 0 ) s + w t ( x , y , 0 ) s ℵ + 1 − a 2 a 1 Ω ( x , y , s ) s ℵ − w ( x , y , 0 ) s ℵ + 1 + Φ ( x , y , s ) a 1 s 2 ℵ − a 3 Ω ( x , y , s ) a 1 s 2 ℵ + 1 a 1 s 2 ℵ × ∂ 2 Ω ( x , y , s ) ∂ x 2 + ∂ 2 Ω ( x , y , s ) ∂ y 2 .

The LTR function is defined as

(12) LTRes [ W ] = Ω ( x , y , s ) − w ( x , y , 0 ) s − w t ( x , y , 0 ) s ℵ + 1 + a 2 a 1 Ω ( x , y , s ) s ℵ − w ( x , y , 0 ) s ℵ + 1 − Φ ( x , y , s ) a 1 s 2 ℵ + a 3 Ω ( x , y , s ) a 1 s 2 ℵ − 1 a 1 s 2 ℵ × ∂ 2 Ω ( x , y , s ) ∂ x 2 + ∂ 2 Ω ( x , y , s ) ∂ y 2 .

Let the solution of Eq. (11) be

(13) Ω ( x , y , s ) = ∑ n = 0 ∞ f n ( x , y ) s n + 1 .

The kth curtailed solution of (11) can be written as

Ω k ( x , y , s ) = ∑ n = 0 k f n ( x , y ) s n ℵ + 1

(14) Ω k ( x , y , s ) = f 0 ( x , y ) s + ∑ n = 1 k f n ( x , y ) s n ℵ + 1 .

Clearly, Ω 0 = f 0 ( x , y ) , and Ω 1 is calculated from Eq. (14) and substituted in Eq. (12) for LTR, LTRes [ Ω 1 ] . Then, using lim s → ∞ s ℵ + 1 LTRes [ Ω 1 ] = 0 , the unknown coefficient f 1 is calculated. Then, Ω 2 is written, LTR at Ω 2 is calculated, then by using lim s → ∞ s 2 ℵ + 1 LTRes [ Ω 2 ] = 0 , and the unknown coefficient f 2 is calculated. These steps can be repeated for as many iterations as desired.

The final expression for the third curtailed solution can be written as

(15) Ω ( x , y , s ) = f 0 ( x , y ) s + f 1 ( x , y ) s ℵ + 1 + f 2 ( x , y ) s 2 ℵ + 1 + f 3 ( x , y ) s 3 ℵ + 1 .

Finally, the inverse LT is taken on both sides of the Eq. (15), to obtain the solution of (1).

6 Numerical examples

The examples have been taken from previous studies [17,18] where the ordinary telegraph equation has been solved. We have solved the TFTE and verified the solution for ℵ = 1 .

6.1 Linear TFTE

Consider the two-dimensional linear TFTE

(16) ∂ 2 ℵ w ∂ t 2 ℵ + 2 ∂ ℵ w ∂ t ℵ + w = 1 2 ∂ 2 w ∂ x 2 + ∂ 2 w ∂ y 2

subject to the conditions

(17) w ( x , y , 0 ) = sinh ( x ) sinh ( y ) , w t ( x , y , 0 ) = − 2 sinh ( x ) sinh ( y ) .

6.1.1 Solution by RFDTM

Applying the RFDT [43] on both sides of the given Eq. (16), the following recurrence relation is obtained:

Γ ( κ ℵ + 2 ℵ + 1 ) Ω κ + 2 + 2 Γ ( κ ℵ + ℵ + 1 ) Ω κ + 1 + Γ ( κ ℵ + 1 ) Ω κ = Γ ( κ ℵ + 1 ) 2 ∂ 2 Ω κ ∂ x 2 + ∂ 2 Ω κ ∂ y 2 .

And from this relation Ω i , 1 ≤ i ≤ n can be obtained using the preliminary criteria. Therefore, the series solution obtained from this method is

(18) ω ( x , y , t ) = 1 + ( − 2 ) t ℵ + ( − 2 ) 2 Γ ( ℵ + 1 ) Γ ( 2 ℵ + 1 ) t 2 ℵ + ( − 2 ) 3 Γ ( ℵ + 1 ) Γ ( 3 ℵ + 1 ) t 3 ℵ + … sinh ( x ) sinh ( y ) .

The closed-form solution of this problem for ℵ = 1 is given in the study by Srivastava et al. [18], and the accuracy of this method can be visually verified. The solution is made illustrious with the help of Figures 1, 2, 3, 4, 5, 6, 7.

$Figure 1 Example 1: RFDTM vs LTRPSM: t = 1 , ℵ = 1 t=1,\aleph =1 .$

Figure 1

Example 1: RFDTM vs LTRPSM: t = 1 , ℵ = 1 .

$Figure 2 Example 1: RFDTM vs LTRPSM: t = 1 , ℵ = 0.5 t=1,\aleph =0.5 .$

Figure 2

Example 1: RFDTM vs LTRPSM: t = 1 , ℵ = 0.5 .

$Figure 3 Example 1: RFDTM vs LTRPSM: t = 0.5 , ℵ = 1 t=0.5,\aleph =1 .$

Figure 3

Example 1: RFDTM vs LTRPSM: t = 0.5 , ℵ = 1 .

$Figure 4 Example 1: RFDTM vs LTRPSM: t = 0.5 , ℵ = 0.5 t=0.5,\aleph =0.5 .$

Figure 4

Example 1: RFDTM vs LTRPSM: t = 0.5 , ℵ = 0.5 .

$Figure 5 Example 1: RFDTM vs LTRPSM vs exact solution: t = 1 , ℵ = 1 t=1,\aleph =1 .$

Figure 5

Example 1: RFDTM vs LTRPSM vs exact solution: t = 1 , ℵ = 1 .

$Figure 6 Example 1: RFDTM vs LTRPSM vs exact solution: t = 0.5 , ℵ = 1 t=0.5,\aleph =1 .$

Figure 6

Example 1: RFDTM vs LTRPSM vs exact solution: t = 0.5 , ℵ = 1 .

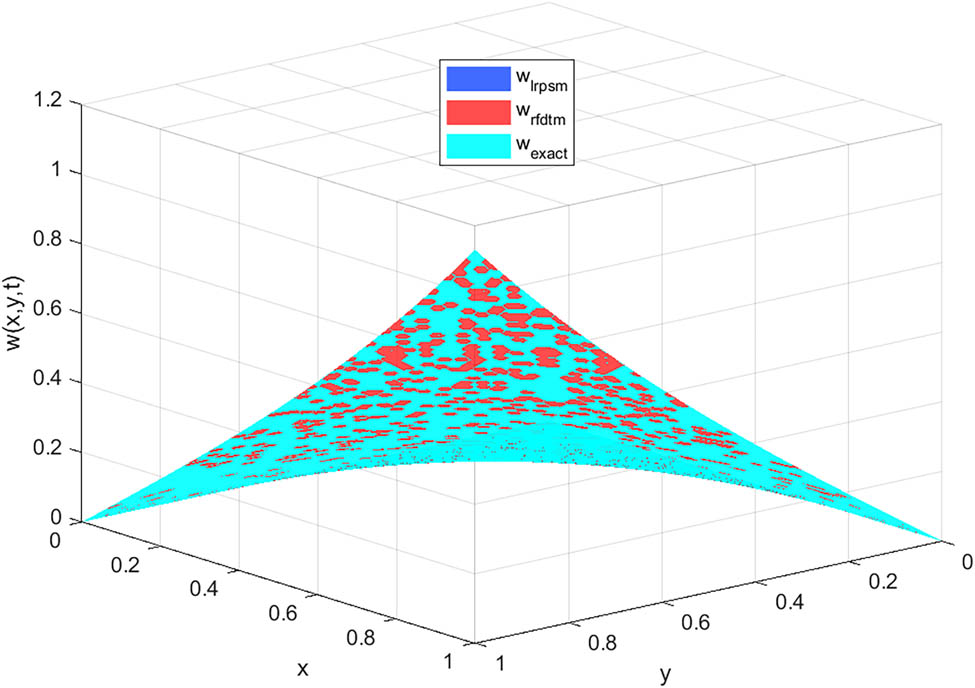
$Figure 7 Example 1: RFDTM vs LTRPSM vs exact solution: t = 0.1 , ℵ = 1 t=0.1,\aleph =1 .$

Figure 7

Example 1: RFDTM vs LTRPSM vs exact solution: t = 0.1 , ℵ = 1 .

6.1.2 Solution by LTRPSM

We solved the same problem with Laplace-transformed power series method. Applying the Laplace transformation on both sides of Eq. (16) and rearranging the terms and using the preliminary criteria, we obtain

(19) Ω ( x , y , s ) = sinh ( x ) sinh ( y ) s − 2 Ω ( x , y , s ) s ℵ − Ω ( x , y , s ) s 2 ℵ + ∇ 2 Ω ( x , y , s ) 2 s 2 ℵ .

The kth LTR function can be defined as

(20) LTRes [ Ω k ] = Ω k ( x , y , s ) − sinh ( x ) sinh ( y ) s + 2 Ω k ( x , y , s ) s ℵ + Ω k ( x , y , s ) s 2 ℵ − ∇ 2 Ω k ( x , y , s ) 2 s 2 ℵ .

Let the kth curtailed solution of (19) be

(21) Ω k = sinh ( x ) sinh ( y ) s + ∑ n = 1 k f n s n ℵ + 1 .

Substituting Ω 1 = sinh ( x ) sinh ( y ) s + f 1 s ℵ + 1 into Eq. (20), we obtain

LTRes [ Ω 1 ] = 2 sinh ( x ) sinh ( y ) s ℵ + 1 + 2 f 1 s 2 ℵ + 1 + f 1 s 3 ℵ + 1 − ∇ 2 f 1 2 s 3 ℵ + 1 + f 1 s ℵ + 1 .

Using

lim s → ∞ s ℵ + 1 LTRes [ Ω 1 ] = 0 ,

we obtain f 1 = − 2 sinh ( x ) sinh ( y ) .

Substituting

Ω 2 = sinh ( x ) sinh ( y ) s + − 2 sinh ( x ) sinh ( y ) s ℵ + 1 + f 2 s 2 ℵ + 1 ,

into Eq. (20), and applying

lim s → ∞ s 2 ℵ + 1 LTRes [ Ω 2 ] = 0 ,

we obtain f 2 = 4 sinh ( x ) sinh ( y ) . Substituting

Ω 3 = sinh ( x ) sinh ( y ) s + − 2 sinh ( x ) sinh ( y ) s ℵ + 1 + 4 sinh ( x ) sinh ( y ) s 2 ℵ + 1 + f 3 s 3 ℵ + 1

in Eq. (20), and applying

lim s → ∞ s 3 ℵ + 1 LTRes [ Ω 3 ] = 0 ,

we obtain f 3 = − 8 sinh ( x ) sinh ( y ) . Thus,

Ω ( x , y , s ) = 1 s + − 2 s ℵ + 1 + 4 s 2 ℵ + 1 + − 8 s 3 ℵ + 1 sinh ( x ) sinh ( y ) .

Taking inverse LT on both sides, we obtain the estimated solution as

(22) ω ( x , y , t ) = 1 − 2 t ℵ Γ ( ℵ + 1 ) + 4 t 2 ℵ Γ ( 2 ℵ + 1 ) − 8 t 3 ℵ Γ ( 3 ℵ + 1 ) sinh ( x ) sinh ( y ) .

6.2 Non-linear TFTE

Consider the two-dimensional non-linear TFTE

(23) ∂ 2 w ∂ x 2 + ∂ 2 w ∂ y 2 = ∂ 2 ℵ w ∂ t 2 ℵ + 2 ∂ ℵ w ∂ t ℵ + w 2 − e 2 ( x + y ) − 4 t + 2 e x + y − 2 t

in compliance with

(24) w ( x , y , 0 ) = e x + y , w t ( x , y , 0 ) = − 2 e x + y .

6.2.1 Solution by RFDTM

Applying the RFDT on both sides of the given Eq. (23), the following recurrence relation is obtained:

Γ ( κ ℵ + 2 ℵ + 1 ) Γ ( κ ℵ + 1 ) Ω κ + 2 + 2 Γ ( κ ℵ + ℵ + 1 ) Γ ( κ ℵ + 1 ) Ω κ + 1 = ∂ 2 Ω κ ∂ x 2 + ∂ 2 Ω κ ∂ y 2 + A ,

where

A = − ∑ r = 0 k Ω r . Ω κ − r + e 2 ( x + y ) ( − 4 ) κ κ ! − 2 e x + y ( − 2 ) κ κ ! .

Using the initial constraints, the estimated solution is obtained as follows:

(25) w ( x , y . t ) = 1 + ( − 2 ) t ℵ + ( − 2 ) 2 Γ ( ℵ + 1 ) Γ ( 2 ℵ + 1 ) t 2 ℵ + ( − 2 ) 3 Γ ( ℵ + 1 ) Γ ( 3 ℵ + 1 ) t 3 ℵ + … e x + y .

The results can be compared for ℵ = 1 with the closed-form solution as shown in Figure 2.

6.2.2 Solution by LTRPSM

Taking the LT on both sides of Eq. (23), using the preliminary criteria and with rearrangement of terms, we can write

(26) Ω ( x , y , s ) = ∇ 2 Ω ( x , y , s ) s 2 ℵ + e x + y s − 2 Ω ( x , y , s ) s ℵ − L ( L − 1 Ω ( x , y , s ) ) 2 s 2 ℵ + e 2 ( x + y ) s 2 ℵ ( s + 4 ) − 2 e x + y s 2 ℵ ( s + 2 ) .

The kth curtailed LTR can be written as

LTRes [ Ω k ] = Ω k ( x , y , s ) − ∇ 2 Ω k ( x , y , s ) s 2 ℵ − e x + y s + 2 Ω k ( x , y , s ) s ℵ + L ( L − 1 Ω k ( x , y , s ) ) 2 s 2 ℵ − e 2 ( x + y ) s 2 ℵ ( s + 4 ) + 2 e x + y s 2 ℵ ( s + 2 ) .

Let the kth curtailed solution of (26) be

(27) Ω k = e x + y s + ∑ n = 1 k f n s n ℵ + 1 .

Substituting Ω 1 = e x + y s + f 1 s ℵ + 1 into the LTR function, we obtain

LTRes [ Ω 1 ] = e x + y s + f 1 s ℵ + 1 − ∇ 2 ( e x + y s + f 1 s ℵ + 1 ) s 2 ℵ − e x + y s − 2 ( e x + y s + f 1 s ℵ + 1 ) s ℵ + L ( L − 1 ( e x + y s + f 1 s ℵ + 1 ) ) 2 s 2 ℵ − e 2 ( x + y ) s 2 ℵ ( s + 4 ) + 2 e x + y s 2 ℵ ( s + 2 ) .

Using

lim s → ∞ s ℵ + 1 LTRes [ Ω 1 ] = 0 ,

we obtain

f 1 = − 2 e x + y .

Substituting Ω 2 = e x + y s + − 2 e x + y s ℵ + 1 + f 2 s 2 ℵ + 1 into the LTR function and after simplification, we obtain

LTRes [ Ω 2 ] = f 2 s 2 ℵ + 1 − 2 e x + y s 2 ℵ + 1 + 4 e x + y s 3 ℵ + 1 − ∇ 2 f 2 s 4 ℵ + 1 − 4 e x + y s 2 ℵ + 1 + 2 f 2 s 3 ℵ + 1 − e 2 x + 2 y s 2 ℵ ( s + 4 ) + 2 e x + y s 2 ℵ ( s + 2 ) + 1 s 2 ℵ e 2 x + 2 y s + 4 e 2 x + 2 y Γ ( 2 ℵ + 1 ) ( Γ ( ℵ + 1 ) ) 2 s 2 ℵ + 1 + f 2 2 Γ ( 4 ℵ + 1 ) ( Γ ( 2 ℵ + 1 ) ) 2 s 4 ℵ + 1 − 4 e 2 x + 2 y s ℵ + 1 − 4 e x + y f 2 Γ ( 3 ℵ + 1 ) Γ ( ℵ + 1 ) Γ ( 2 ℵ + 1 ) s 3 ℵ + 1 + 2 f 2 e x + y s 2 ℵ + 1 .

Then,

(28) lim s → ∞ s 2 ℵ + 1 LTRes [ Ω 2 ] = 0

implies

f 2 = 4 e x + y .

Substituting Ω 3 = e x + y s + − 2 e x + y s ℵ + 1 + 4 e x + y s 2 ℵ + 1 + f 3 s 3 ℵ + 1 into the LTR function and after simplification, we obtain

LTRes [ Ω 3 ] = f 3 s 3 ℵ + 1 − 2 e x + y s 2 ℵ + 1 + 4 e x + y s 3 ℵ + 1 − 8 e x + y s 4 ℵ + 1 − ∇ 2 f 3 s 5 ℵ + 1 + 8 e x + y s 3 ℵ + 1 + 2 f 3 s 4 ℵ + 1 − e 2 x + 2 y s 2 ℵ ( s + 4 ) + 2 e x + y s 2 ℵ ( s + 2 ) + 1 s 2 ℵ e 2 x + 2 y s + 4 e 2 x + 2 y Γ ( 2 ℵ + 1 ) s 2 ℵ + 1 ( Γ ( ℵ + 1 ) ) 2 − 4 e 2 x + 2 y s ℵ + 1 + 16 e 2 x + 2 y Γ ( 4 ℵ + 1 ) Γ ( ℵ + 1 ) Γ ( 2 ℵ + 1 ) s 4 ℵ + 1 + f 3 2 Γ ( 6 ℵ + 1 ) ( Γ ( 3 ℵ + 1 ) ) 2 s 6 ℵ + 1 − 16 e 2 x + 2 y Γ ( 3 ℵ + 1 ) Γ ( ℵ + 1 ) Γ ( 2 ℵ + 1 ) s 3 ℵ + 1 + 8 f 3 e x + y Γ ( 5 ℵ + 1 ) Γ ( 2 ℵ + 1 ) Γ ( 3 ℵ + 1 ) s 5 ℵ + 1 + 8 e 2 x + 2 y s 2 ℵ + 1 − 4 e x + y f 3 Γ ( 4 ℵ + 1 ) Γ ( ℵ + 1 ) Γ ( 3 ℵ + 1 ) s 4 ℵ + 1 + 2 e x + y f 3 s 3 ℵ + 1 .

Then, by

(29) lim s → ∞ s 3 ℵ + 1 LTRes [ Ω 3 ] = 0 ,

and using the Caputo fractional version of the L’Hopital’s rule as described in Kassim and Tatar [44], we obtain

(30) f 3 = 4 ( 1 − Γ ( ℵ + 1 ) ) e 2 x + 2 y − 4 ( 3 − Γ ( ℵ + 1 ) ) e x + y .

Thus, the third curtailed solution becomes

(31) Ω ( x , y , s ) = e x + y s + − 2 e x + y s ℵ + 1 + 4 e x + y s 2 ℵ + 1 + 4 ( 1 − Γ ( ℵ + 1 ) ) e 2 x + 2 y − 4 ( 3 − Γ ( ℵ + 1 ) ) e x + y s 3 ℵ + 1 .

On taking the inverse LT, the solution of the original telegraph Eq. (23) can be given as

(32) ω ( x , y , t ) = e x + y − 2 e x + y t ℵ Γ ( ℵ + 1 ) + 4 e x + y t 2 ℵ Γ ( 2 ℵ + 1 ) + f 3 t 3 ℵ Γ ( 3 ℵ + 1 ) ,

where f 3 is given by Eq. (30).

7 Results and discussion

In this article, we tried calculating an estimated series solution of a linear and a non-linear TFTE by RFDTM (18, 25) and LTRPSM (22, 32).

The two methods can be considered semi analytic in nature and they give a series solution that has to be curtailed. More the term count in the series solution, better is the estimation, but here we restricted our solution for four terms only. Since it is difficult to find the closed-form solution of FDE, we compared the available closed-form solution for ℵ = 1 with the solutions obtained by both the methods at ℵ = 1 .

For the linear TFTE (16), a pictorial comparison is made in the two methods in Figures 1–4. It can be observed that the solutions by the two methods completely overlap for ℵ = 1 . The relative performance of the methods with the exact solution is easy to comprehend from Figures 5–7. It can be observed that the performance of both methods is at par for all the values of t but it is different from exact solution in Figure 5. However, as the value of t is decreased, the solutions by both the methods overlap with the exact solution.

For the non-linear TFTE (23), a pictorial comparison is made in the two methods in Figures 8, 9, 10, 11. It can be observed that the solution by the two methods overlaps only for t = 1 , ℵ = 1 . The solutions by two methods do not coincide for all the values of t as obtained for the linear TFTE. The exact solution and obtained solutions are compared for different values of t in Figures 12–14. It can be observed in Figures 13 and 14 that the solution by RFDTM overlaps with the exact solution as the value of t is decreased.

$Figure 8 Example 2: RFDTM vs LTRPSM: t = 1 , ℵ = 1 t=1,\aleph =1 .$

Figure 8

Example 2: RFDTM vs LTRPSM: t = 1 , ℵ = 1 .

$Figure 9 Example 2: RFDTM vs LTRPSM: t = 1 , ℵ = 0.5 t=1,\aleph =0.5 .$

Figure 9

Example 2: RFDTM vs LTRPSM: t = 1 , ℵ = 0.5 .

$Figure 10 Example 2: RFDTM vs LTRPSM: t = 0.5 , ℵ = 1 t=0.5,\aleph =1 .$

Figure 10

Example 2: RFDTM vs LTRPSM: t = 0.5 , ℵ = 1 .

$Figure 11 Example 2: RFDTM vs LTRPSM: t = 0.5 , ℵ = 0.5 t=0.5,\aleph =0.5 .$

Figure 11

Example 2: RFDTM vs LTRPSM: t = 0.5 , ℵ = 0.5 .

$Figure 12 Example 2: RFDTM vs LTRPSM vs exact solution: t = 1 , ℵ = 1 t=1,\aleph =1 .$

Figure 12

Example 2: RFDTM vs LTRPSM vs exact solution: t = 1 , ℵ = 1 .

$Figure 13 Example 2: RFDTM vs LTRPSM vs exact solution: t = 0.5 , ℵ = 1 t=0.5,\aleph =1 .$

Figure 13

Example 2: RFDTM vs LTRPSM vs exact solution: t = 0.5 , ℵ = 1 .

$Figure 14 Example 2: RFDTM vs LTRPSM vs exact solution: t = 0.1 , ℵ = 1 t=0.1,\aleph =1 .$

Figure 14

Example 2: RFDTM vs LTRPSM vs exact solution: t = 0.1 , ℵ = 1 .

8 Conclusion

To sum up, this work explores the solution of the fractional form of telegraph equation, which is a benchmark model for the physical behaviors exhibiting dual nature (wave propagation + diffusion). We solved the TFTE with two popular methods RFDTM and LTRPSM, which give a series solution. By taking only a small number of terms (here four) in the series solution, the results of both methods are found to be same for ℵ = 1 for linear as well as non-linear cases. We compared these solutions graphically with the available closed-form solution and observed that the solution of the linear TFTE coincided with the closed-form solution, unlike the non-linear TFTE. However, the solution of non-linear TFTE by RFDTM coincided better with the exact solution, as the value of t was reduced, keeping ℵ = 1 .

Thus, we conclude that the RFDTM provides better solutions for linear as well as non-linear TFTE as compared to the LTRPSM. In addition to that, we must admit that the unavailability of the exact solutions of the FDEs is a major limitation for our work; however, it is also the driving force for the researchers to explore and develop analytic, semi-analytic, and numerical methods that may produce best approximate solutions. Another aspect to be worked upon is to understand why the solution of the non-linear system when solved with RFDTM is close to the exact solution for small values of t only.

This work can further be extended by incorporating other definitions of fractional derivatives and by applying other transforms. This work can be extended to solve the space-fractional telegraph equation as well as the space-time-fractional analog of the equation. The methods addressed in this work or their modified versions can be applied to solve propagation and diffusion-related problems in engineering and sciences.

pratiksha.bhavsar@sitpune.edu.in

Acknowledgments

The authors would like to acknowledge the anonymous reviewers for their valuable suggestions.

Funding information: Authors state no funding involved.
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors state no conflict of interest.
Data availability statement: Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.

References

[1] Thomson III W. On the theory of the electric telegraph. Proc R Soc Lond. 1856;31(7):382–99. 10.1098/rspl.1854.0093Search in Google Scholar

[2] Debnath L. Linear partial differential equations. In: Nonlinear partial differential equations for scientists and engineers. Boston: Birkhäuser; 2012. p. 1–47. 10.1007/978-0-8176-8265-1_1Search in Google Scholar

[3] Metaxas AA, Meredith RJ. Industrial microwave heating. United Kingdom: IET; 1983. Search in Google Scholar

[4] Jordan PM, Puri A. Digital signal propagation in dispersive media. J Appl Phys. 1999;85(3):1273–82. 10.1063/1.369258Search in Google Scholar

[5] Ōkubo A. Application of the telegraph equation to oceanic diffusion: another mathematical model. Vol. 71. No. 3. Chesapeake Bay Institute, Johns Hopkins University. 1971; Search in Google Scholar

[6] Holmes EE. Are diffusion models too simple? A comparison with telegraph models of invasion. Am Nat. 1993;142(5):779–95. 10.1086/285572Search in Google Scholar PubMed

[7] Banasiak J, Mika JR. Singularly perturbed telegraph equations with applications in the random walk theory. Int J Stoch Anal. 1998;11:9–28. 10.1155/S1048953398000021Search in Google Scholar

[8] Khan D, Ali G, Kumam P, Almusawa MY, Galal AM. Time fractional model of free convection flow and dusty two-phase couple stress fluid along vertical plates. ZAMM J Appl Math Mech. 2023;103(5):e202200369. 10.1002/zamm.202200369Search in Google Scholar

[9] Khan D, Ali G, Kumam P, Suttiarporn P. A generalized electro-osmotic MHD flow of hybrid ferrofluid through Fourier and Fickas law in inclined microchannel. Numer Heat Transf Part A Appl. 2024;85(18):3091–109. 10.1080/10407782.2023.2232535Search in Google Scholar

[10] Jan R, Razak NNA, Boulaaras S, Rehman ZU, Bahramand S. Mathematical analysis of the transmission dynamics of viral infection with effective control policies via fractional derivative. Nonlinear Eng. 2023;12(1):20220342. 10.1515/nleng-2022-0342Search in Google Scholar

[11] Jan R, Boulaaras S, Alyobi S, Rajagopal K, Jawad M. Fractional dynamics of the transmission phenomena of dengue infection with vaccination. Discrete Contin Dyn Syst- S. 2023;16(8):2096–117. 10.3934/dcdss.2022154Search in Google Scholar

[12] Sikora B. Remarks on the Caputo fractional derivative. Minut. 2023;5:76–84. Search in Google Scholar

[13] Rehman ZU, Boulaaras S, Jan R, Ahmad I, Bahramand S. Computational analysis of financial system through non-integer derivative. J Comput Sci. 2024;75:102204. 10.1016/j.jocs.2023.102204Search in Google Scholar

[14] Kumar D, Singh J, Kumar S. Analytic and approximate solutions of space-time fractional telegraph equations via Laplace transform. Walailak J Sci Technol. 2014;11(8):711–28. Search in Google Scholar

[15] Momani S. Analytic and approximate solutions of the space-and time-fractional telegraph equations. Appl Math Comput. 2005;170(2):1126–34. 10.1016/j.amc.2005.01.009Search in Google Scholar

[16] Boyadjiev L, Luchko Y. The neutral-fractional telegraph equation. Math Model Nat Phenom. 2017;12(6):51–67. 10.1051/mmnp/2017064Search in Google Scholar

[17] Dehghan M, Salehi R. A method based on meshless approach for the numerical solution of the two-space dimensional hyperbolic telegraph equation. Math Methods Appl Sci. 2012;35(10):1220–33. 10.1002/mma.2517Search in Google Scholar

[18] Srivastava VK, Awasthi MK, Chaurasia RK. Reduced differential transform method to solve two and three dimensional second order hyperbolic telegraph equations. J King Saud Univ Eng Sci. 2017;29(2):166–71. 10.1016/j.jksues.2014.04.010Search in Google Scholar

[19] Khan H, Shah R, Kumam P, Baleanu D, Arif M. An efficient analytical technique, for the solution of fractional-order telegraph equations. Mathematics. 2019;7(5):426. 10.3390/math7050426Search in Google Scholar

[20] Khan H, Shah R, Baleanu D, Kumam P, Arif M. Analytical solution of fractional-order hyperbolic telegraph equation, using natural transform decomposition method. Electronics. 2019;8(9):1015. 10.3390/electronics8091015Search in Google Scholar

[21] Hamza AE, Mohamed MZ, Abd Elmohmoud EM, Magzoub M. Conformable Sumudu transform of space-time fractional telegraph equation. Abstr Appl Anal. 2021;2021(1):6682994. 10.1155/2021/6682994Search in Google Scholar

[22] Kapoor M, Shah NA, Saleem S, Weera W. An analytical approach for fractional hyperbolic telegraph equation using Shehu transform in one, two and three dimensions. Mathematics. 2022;10(12):1961. 10.3390/math10121961Search in Google Scholar

[23] Arora G, Pant R, Emadifar H, Khademi M. Numerical solution of fractional relaxation-oscillation equation by using residual power series method. Alex Eng J. 2023;73:249–57. 10.1016/j.aej.2023.04.055Search in Google Scholar

[24] Al-Smadi M. Solving initial value problems by residual power series method. Theor Math Appl. 2013;3(1):199–210. Search in Google Scholar

[25] Zhang J, Wei Z, Li L, Zhou C. Least-squares residual power series method for the time-fractional differential equations. Complexity. 2019;2019(1):6159024. 10.1155/2019/6159024Search in Google Scholar

[26] Dawar A, Khan H, Islam S, Khan W. The improved residual power series method for a system of differential equations: a new semi-numerical method. Int J Model Simul. 2023;1–14. 10.1080/02286203.2023.2270884.Search in Google Scholar

[27] Alquran M. Analytical solutions of fractional foam drainage equation by residual power series method. Math Sci. 2014;8(4):153–60. 10.1007/s40096-015-0141-1Search in Google Scholar

[28] Khresat H, El-Ajou A, Al-Omari S, Alhazmi SE, Oqielat MA. Exact and approximate solutions for linear and non-linear partial differential equations via Laplace residual power series method. Axioms. 2023;12(7):694. 10.3390/axioms12070694Search in Google Scholar

[29] Alaroud M. Application of Laplace residual power series method for approximate solutions of fractional IVP’s. Alex Eng J. 2022;61(2):1585–95. 10.1016/j.aej.2021.06.065Search in Google Scholar

[30] Pant R, Arora G, Singh BK, Emadifar H. Numerical solution of two-dimensional fractional differential equations using Laplace transform with residual power series method. Nonlinear Eng. 2024;13(1):20220347. 10.1515/nleng-2022-0347Search in Google Scholar

[31] Keskin Y, Oturanc G. Reduced differential transform method for partial differential equations. Int J Nonlinear SciNumer Simul. 2009;10(6):741–50. 10.1515/IJNSNS.2009.10.6.741Search in Google Scholar

[32] Wang KL, Wang KJ. A modification of the reduced differential transform method for fractional calculus. Therm Sci. 2018;22(4):1871–5. 10.2298/TSCI1804871WSearch in Google Scholar

[33] Patel HS, Patel T. Applications of fractional reduced differential transform method for solving the generalized fractional-order Fitzhugh-Nagumo equation. Int J Appl Comput Math. 2021;7(5):188. 10.1007/s40819-021-01130-2Search in Google Scholar

[34] Saeed U, Umair M. A modified method for solving non-linear time and space fractional partial differential equations. Eng Comput. 2019;36(7):2162–78. 10.1108/EC-01-2019-0011Search in Google Scholar

[35] Rashid S, Ashraf R, Hammouch Z. New generalized fuzzy transform computations for solving fractional partial differential equations arising in oceanography. J Ocean Eng Sci. 2023;8(1):55–78. 10.1016/j.joes.2021.11.004Search in Google Scholar

[36] Saifullah S, Ali A, Khan A, Shah K, Abdeljawad T. A novel tempered fractional transform: Theory, properties and applications to differential equations. Fractals. 2023;31(10):2340045. 10.1142/S0218348X23400455Search in Google Scholar

[37] Chu YM, Jneid M, Chaouk A, Inc M, Rezazadeh H, Houwe A. Local time fractional reduced differential transform method for solving local time fractional telegraph equations. Fractals. 2024;32(4):2340128. 10.1142/S0218348X2340128XSearch in Google Scholar

[38] Podlubny I. Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. San Diego: Academic Press; 1999. vol. 198. Search in Google Scholar

[39] Miller KS, Ross B. An introduction to the fractional calculus and fractional differential equations. New York: Wiley; 1993. Search in Google Scholar

[40] Arora G, Pratiksha. A cumulative study on differential transform method. Int J Math Eng Manag Sci. 2019;4(1):170. 10.33889/IJMEMS.2019.4.1-015Search in Google Scholar

[41] Srivastava VK, Mishra N, Kumar S, Singh BK, Awasthi MK. Reduced differential transform method for solving (1+n)-Dimensional Burgers’ equation. Egypt J Basic Appl Sci. 2014;1(2):115–9. 10.1016/j.ejbas.2014.05.001Search in Google Scholar

[42] Ünal E, Gökdoğan A. Solution of conformable fractional ordinary differential equations via differential transform method. Optik. 2017;128:264–73. 10.1016/j.ijleo.2016.10.031Search in Google Scholar

[43] Abuasad S, Hashim I, Abdul Karim SA. Modified fractional reduced differential transform method for the solution of multiterm time-fractional diffusion equations. Adv Math Phys. 2019;2019(1):5703916. 10.1155/2019/5703916Search in Google Scholar

[44] Kassim MD, Tatar NE. Asymptotic Behavior for Fractional Systems with Lower-Order Fractional Derivatives. Prog Fract Differ Appl. 2023;9(1):145–66. 10.18576/pfda/090111Search in Google Scholar

Received: 2024-10-17

Revised: 2025-01-05

Accepted: 2025-03-10

Published Online: 2025-04-28

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/nleng-2025-0116

Keywords for this article

fractional telegraph equation; fractional reduced differential transform method; residual power series method; Laplace-transformed residual power series method

Creative Commons

BY 4.0