Unravelling quiescent optical solitons: An exploration of the complex Ginzburg–Landau equation with nonlinear chromatic dispersion and self-phase modulation

Dean Chou; Aamna Amer; Hamood Ur Rehman; Ming-Lung Li

doi:10.1515/nleng-2024-0043

Article Open Access

Unravelling quiescent optical solitons: An exploration of the complex Ginzburg–Landau equation with nonlinear chromatic dispersion and self-phase modulation

Dean Chou , Aamna Amer , Hamood Ur Rehman and Ming-Lung Li

Published/Copyright: March 4, 2025

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Nonlinear Engineering Volume 14 Issue 1

Abstract

In this investigation, we delve into the recovery of quiescent optical solitons amidst the onset of nonlinear chromatic dispersion (CD), employing the complex Ginzburg–Landau equation. Quiescent optical solitons, self-sustaining, locally distributed wave packets, uphold their shape and amplitude over extensive distances through a delicate equilibrium of nonlinearity and dispersion. Our scrutiny extends to four distinct forms of self-phase modulation structures, wherein we adopt the ( 1 ϑ ( ζ ) , ϑ ′ ( ζ ) ϑ ( ζ ) ) method, yielding solutions in hyperbolic function forms. This research meticulously examines the specific parametric constraints influencing the soliton presence, enhancing comprehension of the erratic behaviour by nonlinear waves and dynamic systems. Through vivid graphical representations, we provide insights into solution variations and their characteristics. These findings warn electronics and telecommunication engineers that nonlinear CD could halt global internet connectivity by preventing soliton transmission across borders. Hence, the imperative lies in preserving linear CD during transmission to avert such dire consequences. Furthermore, our study propels future research prospects, as we intend to substitute nonlinear CD with nonlinear cubic–quartic dispersive terms, expecting further discoveries to disseminate subsequently.

Keywords: Ginzburg–Landau equation; solitons; nonlinear chromatic dispersion

1 Introduction

In the realm of telecommunication engineering, the concept of optical solitons emerges as pivotal. Extensive research in this domain primarily centres around optical fibres, metamaterials, metasurfaces, magneto-optic waveguides, fiber Bragg gratings, dense wavelength division multiplexing systems, and other related devices [1,2]. Indeed, the intricate dynamics of solitons constitute a cornerstone of modern technological advancements, without which progress would be unimaginable. This intricate interplay is governed by a variety of models, with diverse types of fibres yielding varying outcomes. Over the years, significant research has been conducted in this area. For instance, Ekici et al. investigated the dispersive optical solitons with Schrödinger–Hirota equation [3], Yasin et al. explored the exact solutions of modified kdv–Zakharov–Kuznetsov equation [4], Ahmad et al. delved into the new wave solutions of nonlinear Landau–Ginzburg–Higgs equation [5,6], and Biswas et al. discovered the stationary solutions of the nonlinear dispersive Schrödinger’s equation [7]. Ekici et al. retrieved nematicons in liquid crystals from its governing equation [8] and stationary optical solitons with nonlinear group velocity dispersion [9]. Owing to their remarkable characteristics, optical solitons traverse vast distances across continents, a feat made possible by the delicate equilibrium between chromatic dispersion (CD) and nonlinearity induced by self-phase modulation (SPM). Over time, various structural forms of SPM have yielded a rich spectrum of outcomes, underscoring the complexity inherent in this phenomenon [10–13].

Among the models employed to explore these dynamics are the nonlinear Schrödinger’s equation and the Sasa–Satsuma equation, each offering unique insights into the intricate interplay between CD and nonlinearity [14–16]. Notably, solitons transit into a quiescent state during trans-oceanic or trans-continental transmission, leading to their temporary cessation [17,18]. In the context of optical fibres, quiescent optical solitons frequently emerge as a result of the intricate interplay between dispersion and nonlinearity. Furthermore, employing software to directly solve reduced ordinary differential equations has yielded a diverse array of results [19–22].

The current study delves into the nuanced exploration of four distinct forms of SPM structures, aimed at generating quiescent solitons within the framework of the complex Ginzburg–Landau equation (CGLE) with nonlinear CD. This endeavour represents a significant step forward in our understanding of soliton dynamics and holds immense promise for future research in this burgeoning field.

The governing model under discussion in this investigation is elucidated by the following equation [23,24]:

(1) ι ℘ t + a ( ∣ ℘ ∣ n ℘ ) x x + H ( ∣ ℘ ∣ 2 ) ℘ = 1 ∣ ℘ ∣ 2 ℘ * { δ 1 ∣ ℘ ∣ 2 ( ∣ ℘ ∣ 2 ) x x − δ 2 { ( ∣ ℘ ∣ 2 ) x } 2 } + γ ℘ ,

where the complex-valued function ℘ = ℘ ( x , t ) signifies the waveform propagating through the fibre, with t and x serving as independent variables denoting time and distance along the fibre, respectively. The first term captures the linear temporal progression, with ι representing the imaginary unit. The coefficient a delineates the nonlinear CD, with n denoting the nonlinearity parameter, falling into the category of linear CD when n = 0 . The function H characterises the nonlinear refractive index structure. Additionally, the real-valued constants δ 1 and δ 2 encapsulate the perturbation effects, while γ embodies the detuning effect.

Various studies have investigated the complex CGLE in diverse contexts. The exploration of quiescent solitons with nonlinear CD was initially introduced in 2006. Systems of coupled real Ginzburg–Landau equations (GLEs) representing patterns in optics, thermal convection, and Bose–Einstein condensates have analytical solutions for domain-wall states [25]. Additionally, the presence, stability, and formation of linearly coupled GLEs with multipulse bound states have been scrutinised [26]. Dissipative solitons’ dynamics are studied within the context of a one-dimensional fractional order CGLE [27]. Various methodologies, including the semi-inverse variational principle and the solitary wave ansatz, have been employed to investigate soliton solutions and their parametric conditions [28,29]. Optical solitons for CGLE with the well-known nonlinearities such as power laws and Kerr have been generated [30]. Multiple types of optical soliton solutions to CGLE have been examined utilising diverse methods [31]. With the perturbed CGLE, six distinct types of nonlinear refractive index structures have been studied [32]. Furthermore, enhanced Kudryashov’s approach has been applied to investigate various soliton types to generate [33,34].

This study focuses on examining CGLE with nonlinear CD, resulting in the formation of quiescent solitons rather than mobile ones. Considering four different types of SPM, the quiescent solitons obtained in this research are produced by combining nonlinear CD with the four proposed SPM types [35,36].

2 Description of ( 1 ϑ ( σ ) , ϑ ′ ( ς ) ϑ ( ς ) ) method

We begin by considering the model equation that is provided below:

(2) ℱ ( V , V x , V t , V x x , V x t , … ) = 0 ,

where the unknown function is V , which depends on variable that are both temporal and spatial, and ℱ is a polynomial function. The primary algorithm of the method presented can be briefly explained as follows:

Consider the transformation as

(3) V ( x , t ) = U ( ς ) , ς = k ( x − ν t ) ,

where ν and k are unknown constants at this stage. Eq. (3) is employed in the context of the CGLE to simplify the problem by focusing on a moving frame of reference where the soliton appears stationary. This reduction in complexity makes it easier to analyze and identify soliton solutions, which are defined by their intrinsic features of being localised and non-dispersive while retaining a consistent form and velocity. Eq. (2) can be rewritten as the evaluation equation by applying transformation (3):

(4) ℱ ( U , − k ν U ′ , k U ′ . k 2 U ″ , … ) = 0 .

The solution to Eq. (4) can be expressed as

(5) U ( ς ) = ω 0 + ∑ τ = 1 ε ω τ + β τ ϑ ′ ( ς ) τ ϑ ( ς ) τ .

Eq. (4) can be evaluated by determining the constants ω 0 , ω τ , and β τ (where τ = 1 , 2 , … , ε ); also, the following evolution equation function is satisfied by the function:

(6) ϑ ′ ( ς ) 2 = ϑ ( ς ) 2 − σ .

The following solution can be obtained by solving Eq. (6):

(7) ϑ ( ς ) = Λ e ς + σ 4 Λ e ς ,

where any constant value can be assigned to a and τ .

The nonlinear term and the highest order derivatives in Eq. (4) are balanced in order to obtain the appropriate value of ε in Eq. (5).

The exact solutions of Eq. (2) can be obtained by using a procedure that includes the substitution of (5), as well as Eq. (6) and its derivatives Eq. (7), into Eq. (4). This leads to the derivation of a polynomial equation in the form of ( 1 ϑ ( ς ) , ϑ ′ ( ς ) ϑ ( ς ) ) , which, by equating the coefficients of the identical powers to zero, allows the creation of an over determined system of algebraic equations. Using mathematical programs such as Maple or Mathematica, we may solve this system of equations and find the constants in (3)–(5).

3 Quiescent solitons of CGLE with nonlinear CD

The existence of nonlinear CD causes stationary solitons [37]. The initial hypothesis for these solitons is as follows:

(8) ℘ ( x , t ) = U ( κ x ) e ι ( ϖ t + λ 0 ) ,

where the wave number is represented by the symbol ϖ , and λ 0 gives rise to phase constant. The following equation is obtained by substituting Eq. (8) into Eq. (1):

(9) a κ 2 ( n + 1 ) U n + 1 U ″ + a κ 2 n ( n + 1 ) U n U ′ 2 + H ( U 2 ) U 2 − 2 δ 1 κ 2 U U ″ − 2 κ 2 ( δ 1 − 2 δ 2 ) U ′ 2 + ( γ − ϖ ) U 2 = 0 .

The subsequent subsections will deal Eq. (1) with different kinds of SPM structures.

3.1 Parabolic law

The parabolic law of nonlinearity can be found in the majority of commercial optical fibres. This law arises as a consequence of Langmuir waves interacting with electrons [38–40]. This law also describes the impact of ponderomotive forces on the nonlinear interaction between high-frequency Langmuir waves and ion-acoustic waves. When the CGLE (1) is incorporated with the parabolic nonlinearity law, it yields

(10) ι ℘ t + a ( ∣ ℘ ∣ n ℘ ) x x + ( b 1 ∣ ℘ ∣ 2 + b 2 ∣ ℘ ∣ 4 ) ℘ = 1 ∣ ℘ ∣ 2 ℘ * { δ 1 ∣ ℘ ∣ 2 ( ∣ ℘ ∣ 2 ) x x − δ 2 { ( ∣ ℘ ∣ 2 ) x } 2 } + γ ℘ .

Eq. (9) thus yields the following expression:

(11) a κ 2 ( n + 1 ) U n + 1 U ″ + a κ 2 n ( n + 1 ) U n U ′ 2 + b 1 U 4 + b 2 U 6 − 2 δ 1 κ 2 U U ″ − 2 κ 2 ( δ 1 − 2 δ 2 ) U ′ 2 + ( γ − ϖ ) U 2 = 0 .

We set n = 2 , for the integrability. So Eq. (11) changes to

(12) 3 a κ 2 U 3 U ″ + 6 a κ 2 U 2 U ′ 2 + b 1 U 4 + b 2 U 6 − 2 δ 1 κ 2 U U ″ − 2 κ 2 ( δ 1 − 2 δ 2 ) U ′ 2 + ( γ − ϖ ) U 2 = 0 .

We obtain ε = 1 in Eq. (5), by balancing U 3 U ″ and U 6 in Eq. (12). Therefore, we obtain

(13) U ( ς ) = ω 0 + ω 1 + β 1 ϑ ′ ( ς ) ϑ ( ς ) .

Substituting Eqs (13) and (6) into Eq. (12) allows us a polynomial equation in the form of 1 ϑ ( ς ) , ϑ ′ ( ς ) ϑ ( ς ) . When the terms in this polynomial with the same powers are grouped together and set to zero, an over-determined system of algebraic equations is created. The following outcomes can be obtained by solving these equations with computer software such as Mathematica or Maple:

Result 1:

(14) ω 0 = 0 , ω 1 = 0 , β 1 = ± 2 − 3 a b 1 − δ 1 b 2 3 a b 2 , δ 2 = δ 1 2 , ϖ = 81 a 2 b 2 γ − 18 a 2 b 1 2 + 6 δ 1 a b 1 b 2 + 4 δ 1 2 b 2 2 81 a 2 b 2 , κ = 3 a b 1 + δ 1 b 2 3 6 a .

By inserting Eq. (14) with the help of Eq. (7) into Eq. (13), we obtain the following solitary wave profile for Eq. (10):

(15) ℘ ( x , t ) = ± 2 − 3 a b 1 − δ 1 b 2 3 a b 2 × 4 Λ 2 exp 3 a b 1 + δ 1 b 2 3 6 a x − σ exp − 3 a b 1 + δ 1 b 2 3 6 a x σ exp − 3 a b 1 + δ 1 b 2 3 6 a x + 4 Λ 2 exp 3 a b 1 + δ 1 b 2 3 6 a x × e ι { 81 a 2 b 2 γ − 18 a 2 b 1 2 + 6 δ 1 a b 1 b 2 + 4 δ 1 2 b 2 2 81 a 2 b 2 } t + λ 0 .

By substituting σ = ± 4 Λ 2 , we obtain the dark and singular quiescent solitons:

(16) ℘ ( x , t ) = ± 2 − 3 a b 1 − δ 1 b 2 3 a b 2 tanh 3 a b 1 + δ 1 b 2 3 6 a x × e ι { 81 a 2 b 2 γ − 18 a 2 b 1 2 + 6 δ 1 a b 1 b 2 + 4 δ 1 2 b 2 2 81 a 2 b 2 } t + λ 0 ,

and

(17) ℘ ( x , t ) = ± 2 − 3 a b 1 − δ 1 b 2 3 a b 2 coth 3 a b 1 + δ 1 b 2 3 6 a x × e ι 81 a 2 b 2 γ − 18 a 2 b 1 2 + 6 δ 1 a b 1 b 2 + 4 δ 1 2 b 2 2 81 a 2 b 2 t + λ 0 .

The results are valid for 3 a b 1 + δ 1 b 2 > 0 .

Result 2:

(18) ω 0 = 0 , ω 1 = 12 a κ 2 σ b 2 , β 1 = 0 , b 1 = − κ 2 ( 6 δ 1 σ + 9 a ω 1 2 − 4 δ 2 σ ) ω 1 2 , ϖ = 4 δ 2 κ 2 + γ − 4 δ 1 κ 2 .

The wave profile of Eq. (10) can be achieved as a consequence of the following:

(19) ℘ ( x , t ) = 2 3 a κ 2 σ b 2 1 σ exp [ − κ x ] + 4 Λ 2 exp [ κ x ] × e ι ( { 4 δ 2 κ 2 + γ − 4 δ 1 κ 2 } t + λ 0 ) .

By substituting σ = ± 4 a 2 , we obtain the quiescent bright and singular solitons:

(20) ℘ ( x , t ) = 2 3 a κ 2 Λ 2 b 2 Λ sech [ κ x ] × e ι ( { 4 δ 2 κ 2 + γ − 4 δ 1 κ 2 } t + λ 0 ) ,

with a κ 2 Λ 2 b 2 > 0 . And

(21) ℘ ( x , t ) = 2 3 − a κ 2 Λ 2 b 2 Λ csch [ κ x ] × e ι ( { 4 δ 2 κ 2 + γ − 4 δ 1 κ 2 } + λ 0 ) .

with a κ 2 Λ 2 b 2 < 0 .

3.2 Generalised quadratic–cubic law

A combination of cubic (self-focusing) and quadratic (self-defocusing) factors makes up this law of nonlinearity. An expression for the generalised quadratic–cubic law, which characterises the nonlinearity in the CGLE, is as follows:

(22) ι ℘ t + a ( ∣ ℘ ∣ n ℘ ) x x + ( b 1 ∣ ℘ ∣ m + b 2 ∣ ℘ ∣ 2 m ) ℘ = 1 ∣ ℘ ∣ 2 ℘ * { δ 1 ∣ ℘ ∣ 2 ( ∣ ℘ ∣ 2 ) x x − δ 2 { ( ∣ ℘ ∣ 2 ) x } 2 } + γ ℘ .

Eq. (9) thus yields the following expression:

(23) a κ 2 ( n + 1 ) U n + 1 U ″ − 2 δ 1 κ 2 U U ″ + a κ 2 n ( n + 1 ) U n U ′ 2 + b 1 U m + 2 + b 2 U 2 m + 2 − 2 κ 2 ( δ 1 − 2 δ 2 ) U ′ 2 + ( γ − ϖ ) U 2 = 0 .

By choosing n = m Eq. (23) changes to

(24) a κ 2 ( m + 1 ) U m + 1 U ″ 2 m ( m + 1 ) U m U ′ 2 − 2 δ 1 κ 2 U U ″ 2 + b 1 U m + 2 + b 2 U 2 m + 2 ( δ 1 − 2 δ 2 ) U ′ 2 + ( γ − ϖ ) U 2 = 0 .

Now, we presume

(25) U = V 2 m .

Eq. (24) thus has the following form:

(26) 2 κ 2 V ′ 2 ( a ( m 2 + 3 m + 2 ) V 2 + 8 δ 2 + 2 δ 1 ( m − 4 ) ) + 2 κ 2 m V V ″ ( a ( m + 1 ) V 2 − 2 δ 1 ) + m 2 V 2 ( b 2 V 4 + b 1 V 2 + γ − ϖ ) = 0 .

Balancing V 6 and V 3 V ″ in Eq. (26), we can obtain ε = 1 . Consequently, we have the following outcome:

(27) V ( ς ) = ω 0 + ω 1 + β 1 ϑ ′ ( ς ) ϑ ( ς ) .

Substituting Eqs (27) and (6) into Eq. (26) allows us a polynomial equation in the form of 1 ϑ ( ς ) , ϑ ′ ( ς ) ϑ ( ς ) . When the terms in this polynomial with the same powers are grouped together and set to zero, an over-determined system of algebraic equations is created. The following outcomes can be obtained by solving these equations with computer software such as Mathematica or Maple:

Result 1:

(28) ω 0 = 0 , ω 1 = 0 , β 1 = ± − a b 1 ( m + 1 ) ( 3 m + 2 ) − 4 δ 1 b 2 m 2 a b 2 ( m + 1 ) 2 , δ 2 = δ 1 − δ 1 m 4 , ϖ = 16 b 2 ( a 2 γ ( m + 1 ) 4 + δ 1 2 b 2 m 2 ) − a 2 b 1 2 ( m + 1 ) 2 ( m + 2 ) ( 3 m + 2 ) + 8 a δ 1 b 1 b 2 ( m + 1 ) m 2 16 a 2 b 2 ( m + 1 ) 4 , κ = − δ 1 m 2 ( a b 1 ( m + 1 ) ( 3 m + 2 ) + 4 δ 1 b 2 m ) a 2 ( m + 1 ) 3 2 2 δ 1 ( 3 m + 2 ) .

The wave profile of Eq. (22) can be achieved as a consequence of the following:

(29) ℘ ( x , t ) = 2 − 2 ∕ m ± 4 Λ 2 exp − δ 1 m 2 ( a b 1 ( m + 1 ) ( 3 m + 2 ) + 4 δ 1 b 2 m ) a 2 ( m + 1 ) 3 2 2 δ 1 ( 3 m + 2 ) x − σ exp δ 1 m 2 ( a b 1 ( m + 1 ) ( 3 m + 2 ) + 4 δ 1 b 2 m ) a 2 ( m + 1 ) 3 2 2 δ 1 ( 3 m + 2 ) x σ exp δ 1 m 2 ( a b 1 ( m + 1 ) ( 3 m + 2 ) + 4 δ 1 b 2 m ) a 2 ( m + 1 ) 3 2 2 δ 1 ( 3 m + 2 ) x + 4 Λ 2 exp − δ 1 m 2 ( a b 1 ( m + 1 ) ( 3 m + 2 ) + 4 δ 1 b 2 m ) a 2 ( m + 1 ) 3 2 2 δ 1 ( 3 m + 2 ) x × − a b 1 ( m + 1 ) ( 3 m + 2 ) − 4 δ 1 b 2 m a b 2 ( m + 1 ) 2 2 ∕ m × e ι { 16 b 2 ( a 2 γ ( m + 1 ) 4 + δ 1 2 b 2 m 2 ) − a 2 b 1 2 ( m + 1 ) 2 ( m + 2 ) ( 3 m + 2 ) + 8 a δ 1 b 1 b 2 ( m + 1 ) m 2 16 a 2 b 2 ( m + 1 ) 4 } t + λ 0 .

By substituting σ = ± 4 Λ 2 , we obtain the dark and singular quiescent solitons:

(30) ℘ ( x , t ) = 2 − 2 ∕ m ± a b 2 ( m + 1 ) 2 − 3 a b 1 m 2 − 5 a b 1 m − 2 a b 1 − 4 δ 1 b 2 m a b 2 ( m + 1 ) 2 × tanh − δ 1 m 2 ( a b 1 ( m + 1 ) ( 3 m + 2 ) + 4 δ 1 b 2 m ) a 2 ( m + 1 ) 3 2 2 δ 1 ( 3 m + 2 ) x 2 ∕ m × e ι { 16 b 2 ( a 2 γ ( m + 1 ) 4 + δ 1 2 b 2 m 2 ) − a 2 b 1 2 ( m + 1 ) 2 ( m + 2 ) ( 3 m + 2 ) + 8 a δ 1 b 1 b 2 ( m + 1 ) m 2 16 a 2 b 2 ( m + 1 ) 4 } t + λ 0 .

and

(31) ℘ ( x , t ) = 2 − 2 ∕ m ± a b 2 ( m + 1 ) 2 − 3 a b 1 m 2 − 5 a b 1 m − 2 a b 1 − 4 δ 1 b 2 m a b 2 ( m + 1 ) 2 × coth − δ 1 m 2 ( a b 1 ( m + 1 ) ( 3 m + 2 ) + 4 δ 1 b 2 m ) a 2 ( m + 1 ) 3 2 2 δ 1 ( 3 m + 2 ) x 2 ∕ m × e ι { 16 b 2 ( a 2 γ ( m + 1 ) 4 + δ 1 2 b 2 m 2 ) − a 2 b 1 2 ( m + 1 ) 2 ( m + 2 ) ( 3 m + 2 ) + 8 a δ 1 b 1 b 2 ( m + 1 ) m 2 16 a 2 b 2 ( m + 1 ) 4 } t + λ 0 .

with δ 1 m 2 ( a b 1 ( m + 1 ) ( 3 m + 2 ) + 4 δ 1 b 2 m ) > 0 , − 3 a b 1 m 2 − 5 a b 1 m − 2 a b 1 − 4 δ 1 b 2 m > 0 and a b 2 > 0 .

Result 2:

(32) ω 0 = 0 , ω 1 = ± − σ ( a b 1 ( m + 1 ) ( 3 m + 2 ) + 2 b 2 ( δ 1 ( m + 4 ) − 4 δ 2 ) ) 2 a b 2 ( m + 1 ) 2 , β 1 = 0 , ϖ = a 2 γ ( 3 m + 2 ) ( m + 1 ) 3 + 4 ( δ 2 − δ 1 ) ( 2 b 2 ( 4 δ 2 − δ 1 ( m + 4 ) ) − a b 1 ( m + 1 ) ( 3 m + 2 ) ) a 2 ( m + 1 ) 3 ( 3 m + 2 ) , κ = − m 2 ( δ 1 ( m + 4 ) − 4 δ 2 ) ( a b 1 ( m + 1 ) ( 3 m + 2 ) + 2 b 2 ( δ 1 ( m + 4 ) − 4 δ 2 ) ) a 2 ( m + 1 ) 3 2 − ( 3 m + 2 ) ( δ 1 ( m + 4 ) − 4 δ 2 ) .

The wave profile of Eq. (22) can be achieved as a consequence of the following:

(33) ℘ ( x , t ) = 2 − 1 ∕ m ± − σ ( a b 1 ( m + 1 ) ( 3 m + 2 ) + 2 b 2 ( δ 1 ( m + 4 ) − 4 δ 2 ) ) a b 2 ( m + 1 ) 2 × 1 σ exp [ κ x ] + 4 Λ 2 exp [ − κ x ] 2 ∕ m × e ι a 2 γ ( 3 m + 2 ) ( m + 1 ) 3 + 4 ( δ 2 − δ 1 ) ( 2 b 2 ( 4 δ 2 − δ 1 ( m + 4 ) ) − a b 1 ( m + 1 ) ( 3 m + 2 ) ) a 2 ( m + 1 ) 3 ( 3 m + 2 ) t + λ 0 .

By substituting σ = ± 4 Λ 2 , we obtain the quiescent bright and singular solitons:

(34) ℘ ( x , t ) = 2 − 1 ∕ m ± a b 2 ( m + 1 ) 2 − 3 a Λ 2 b 1 m 2 − 5 a Λ 2 b 1 m − 2 a Λ 2 b 1 − 8 δ 1 Λ 2 b 2 + 8 Λ 2 b 2 δ 2 − 2 δ 1 Λ 2 b 2 m a 2 b 2 ( m + 1 ) 2 × sech − m 2 ( δ 1 ( m + 4 ) − 4 δ 2 ) ( a b 1 ( m + 1 ) ( 3 m + 2 ) + 2 b 2 ( δ 1 ( m + 4 ) − 4 δ 2 ) ) a 2 ( m + 1 ) 3 2 − ( 3 m + 2 ) ( δ 1 ( m + 4 ) − 4 δ 2 ) x 2 ∕ m e ι { a 2 γ ( 3 m + 2 ) ( m + 1 ) 3 + 4 ( δ 2 − δ 1 ) ( 2 b 2 ( 4 δ 2 − δ 1 ( m + 4 ) ) − a b 1 ( m + 1 ) ( 3 m + 2 ) ) a 2 ( m + 1 ) 3 ( 3 m + 2 ) } t + λ 0 .

and

(35) ℘ ( x , t ) = 2 − 1 ∕ m ± a b 2 ( m + 1 ) 2 3 a Λ 2 b 1 m 2 + 5 a Λ 2 b 1 m + 2 a Λ 2 b 1 + 8 δ 1 Λ 2 b 2 − 8 Λ 2 b 2 δ 2 + 2 δ 1 Λ 2 b 2 m a 2 b 2 ( m + 1 ) 2 × csch − m 2 ( δ 1 ( m + 4 ) − 4 δ 2 ) ( a b 1 ( m + 1 ) ( 3 m + 2 ) + 2 b 2 ( δ 1 ( m + 4 ) − 4 δ 2 ) ) a 2 ( m + 1 ) 3 2 − ( 3 m + 2 ) ( δ 1 ( m + 4 ) − 4 δ 2 ) x 2 ∕ m × e ι { a 2 γ ( 3 m + 2 ) ( m + 1 ) 3 + 4 ( δ 2 − δ 1 ) ( 2 b 2 ( 4 δ 2 − δ 1 ( m + 4 ) ) − a b 1 ( m + 1 ) ( 3 m + 2 ) ) a 2 ( m + 1 ) 3 ( 3 m + 2 ) } t + λ 0 .

with m 2 ( δ 1 ( m + 4 ) − 4 δ 2 ) ( a b 1 ( m + 1 ) ( 3 m + 2 ) + 2 b 2 ( δ 1 ( m + 4 ) − 4 δ 2 ) ) a 2 ( m + 1 ) 3 > 0 and ( 3 m + 2 ) ( δ 1 ( m + 4 ) − 4 δ 2 ) > 0 .

3.3 Generalised cubic–quartic (CQ) law

Physical systems are frequently described using the most basic version of the nonlinearity law, also referred to as cubic nonlinearity. This law is a theoretical model that is suggested and is derived from the combination of quartic and cubic forms. CGLE (1) can be expressed as

(36) ι ℘ t + a ( ∣ ℘ ∣ n ℘ ) x x + ( b 1 ∣ ℘ ∣ 2 m + b 2 ∣ ℘ ∣ 3 m ) ℘ = 1 ∣ ℘ ∣ 2 ℘ * { δ 1 ∣ ℘ ∣ 2 ( ∣ ℘ ∣ 2 ) x x − δ 2 { ( ∣ ℘ ∣ 2 ) x } 2 } + γ ℘ .

Eq. (9) thus yields the following expression:

(37) a κ 2 ( n + 1 ) U n + 1 U ″ + b 1 U 2 m + 2 + b 2 U 3 m + 2 + a κ 2 n ( n + 1 ) U n U ′ 2 − 2 δ 1 κ 2 U U ″ − 2 κ 2 ( δ 1 − 2 δ 2 ) U ′ 2 + ( γ − ϖ ) U 2 = 0 .

By choosing n = 2 m Eq. (37) becomes

(38) a κ 2 ( 2 m + 1 ) 2 m + 1 U ″ 2 m ( 2 m + 1 ) U 2 m U ′ 2 + b 1 U 2 m + 2 + b 2 U 3 m + 2 − 2 δ 1 κ 2 U U ″ 2 ( δ 1 − 2 δ 2 ) U ′ 2 + ( γ − ϖ ) U 2 = 0 .

Now, we presume

(39) U = V 2 m .

Eq. (38) thus has the following form:

(40) 2 κ 2 V ′ 2 ( a ( 6 m 2 + 7 m + 2 ) V 4 + 8 δ 2 + 2 δ 1 ( m − 4 ) ) + 2 κ 2 m V V ″ ( a ( 2 m + 1 ) V 4 − 2 δ 1 ) + m 2 V 2 ( b 2 V 6 + b 1 V 4 + γ − ϖ ) = 0 .

Balancing V 8 and V 5 V ″ into Eq. (40), we can obtain ε = 1 . Consequently, we obtain the following outcome:

(41) V ( ς ) = ω 0 + ω 1 + β 1 ϑ ′ ( ς ) ϑ ( ς ) .

Substituting Eqs (41) and (6) into Eq. (40) allows us a polynomial equation in the form of 1 ϑ ( ς ) , ϑ ′ ( ς ) ϑ ( ς ) . When the terms in this polynomial with the same powers are grouped together and set to zero, an over-determined system of algebraic equations is created. The following outcomes can be obtained by solving these equations with computer software such as Mathematica or Maple:

Result 1:

(42) ω 0 = 0 , ω 1 = 0 , β 1 = ± 2 δ 1 4 m 4 a ( 6 m 2 + 7 m + 2 ) 4 , b 1 = 8 a ( 2 κ m + κ ) 2 m 2 , b 2 = − a κ 2 ( 2 m + 1 ) ( 5 m + 2 ) a ( 6 m 2 + 7 m + 2 ) δ 1 m 5 ∕ 2 , ϖ = γ + 8 δ 1 κ 2 m , δ 2 = δ 1 − δ 1 m 4 .

The wave profile of Eq. (36) can be achieved as a consequence of the following:

(43) ℘ ( x , t ) = 2 1 ∕ m ± δ 1 4 m 4 a ( 6 m 2 + 7 m + 2 ) 4 × 4 Λ 2 exp [ κ x ] − σ exp [ − κ x ] σ exp [ − κ x ] + 4 Λ 2 exp [ κ x ] 2 ∕ m × e ι λ 0 + t { γ + 8 δ 1 k 2 m } .

By substituting σ = ± 4 Λ 2 , we obtain the quiescent dark and singular solitons

(44) ℘ ( x , t ) = 2 1 ∕ m ± δ 1 4 m 4 a ( 6 m 2 + 7 m + 2 ) 4 tanh [ κ x ] 2 ∕ m × e ι λ 0 + t { γ + 8 δ 1 k 2 m } ,

and

(45) ℘ ( x , t ) = 2 1 ∕ m ± δ 1 4 m 4 a ( 6 m 2 + 7 m + 2 ) 4 coth [ κ x ] 2 ∕ m × e ι λ 0 + t { γ + 8 δ 1 k 2 m } .

Here, δ 1 > 0 , m > 0 and a ( 6 m 2 + 7 m + 2 ) > 0 .

Result 2:

(46) ω 0 = 0 , ω 1 = 2 a κ 2 ( 10 m 2 + 9 m + 2 ) σ b 2 m 2 , β 1 = 0 , b 1 = − 4 a κ 2 ( 2 m + 1 ) 2 m 2 , ϖ = 4 δ 1 κ 2 + γ m m , δ 2 = 1 4 δ 1 ( m + 4 ) .

The wave profile of Eq. (36) can be achieved as a consequence of the following:

(47) ℘ ( x , t ) = 2 1 ∕ m a κ 2 ( 10 m 2 + 9 m + 2 ) σ b 2 m 2 × 1 σ exp [ − κ x ] + 4 Λ 2 exp [ κ x ] 2 ∕ m × e ι λ 0 + { 4 δ 1 κ 2 + γ m m } t .

By substituting σ = ± 4 Λ 2 , we obtain the quiescent bright and singular solitons

(48) ℘ ( x , t ) = 2 1 ∕ m a Λ 2 k 2 ( 10 m 2 + 9 m + 2 ) b 2 m 2 Λ sech [ κ x ] 2 ∕ m × e ι λ 0 + { 4 δ 1 κ 2 + γ m m } t ,

with a Λ 2 k 2 ( 10 m 2 + 9 m + 2 ) b 2 m 2 > 0 .

And

(49) ℘ ( x , t ) = 2 1 ∕ m − a Λ 2 k 2 ( 10 m 2 + 9 m + 2 ) b 2 m 2 Λ csch [ κ x ] 2 ∕ m × e ι λ 0 + { 4 δ 1 κ 2 + γ m m } t .

with a Λ 2 k 2 ( 10 m 2 + 9 m + 2 ) b 2 m 2 < 0 .

3.4 Power law

This polynomial nonlinearity includes the septic version of power law. The CGLE Eq. (1) takes the subsequent form

(50) ι ℘ t + a ( ∣ ℘ ∣ n ℘ ) x x + b ∣ ℘ ∣ 2 m ℘ = 1 ∣ ℘ ∣ 2 ℘ * { δ 1 ∣ ℘ ∣ 2 ( ∣ ℘ ∣ 2 ) x x − δ 2 { ( ∣ ℘ ∣ 2 ) x } 2 } + γ ℘ .

Eq. (9) thus yields the following expression:

(51) a κ 2 ( n + 1 ) U n + 1 U ″ − 2 δ 1 κ 2 U U ″ + a κ 2 n ( n + 1 ) U n U ′ 2 + b U 2 m + 2 − 2 κ 2 ( δ 1 − 2 δ 2 ) U ′ 2 + ( γ − ϖ ) U 2 = 0 .

By choosing n = m , Eq. (51) changes to

(52) a κ 2 ( m + 1 ) U m + 1 U ″ − 2 δ 1 κ 2 U U ″ + a κ 2 m ( m + 1 ) U m U ′ 2 + b U 2 m + 2 − 2 κ 2 ( δ 1 − 2 δ 2 ) U ′ 2 + ( γ − ϖ ) U 2 = 0 .

Now, we presume

(53) U = V 2 m .

Eq. (52) thus has the following form:

(54) 2 κ 2 V ′ 2 ( a ( m 2 + 3 m + 2 ) V 2 + 8 δ 2 + 2 δ 1 ( m − 4 ) ) + 2 κ 2 m V V ″ ( a ( m + 1 ) V 2 − 2 δ 1 ) + m 2 V 2 ( b V 4 + γ − ϖ ) = 0 .

Balancing V 6 and V 3 V ″ in Eq. (54), we can obtain ε = 1 . Consequently, we obtain the following outcome:

(55) V ( ς ) = ω 0 + ω 1 + β 1 ϑ ′ ( ς ) ϑ ( ς ) .

Substituting Eqs (55) and Eq. (6) into Eq. (54) allows us a polynomial equation in the form of 1 ϑ ( ς ) , ϑ ′ ( ς ) ϑ ( ς ) . When the terms in this polynomial with the same powers are grouped together and set to zero, an over-determined system of algebraic equations is created. The following outcomes can be obtained by solving these equations with computer software such as Mathematica or Maple:

Result 1:

(56) ω 0 = 0 , ω 1 = 0 , β 1 = ± δ 1 m − a ( m + 1 ) 2 , δ 2 = 1 4 ( 4 δ 1 − δ 1 m ) , ϖ = δ 1 2 b m 2 a 2 ( m + 1 ) 4 + γ , κ = δ 1 b m 3 ∕ 2 a ( m + 1 ) 3 ∕ 2 6 m + 4 .

The wave profile of Eq. (50) can be achieved as a consequence of the following:

(57) ℘ ( x , t ) = ± δ 1 m − a ( m + 1 ) 2 × 4 Λ 2 exp δ 1 b m 3 ∕ 2 a ( m + 1 ) 3 ∕ 2 6 m + 4 x − σ exp − δ 1 b m 3 ∕ 2 a ( m + 1 ) 3 ∕ 2 6 m + 4 x σ exp − δ 1 b m 3 ∕ 2 a ( m + 1 ) 3 ∕ 2 6 m + 4 x + 4 Λ 2 exp δ 1 b m 3 ∕ 2 a ( m + 1 ) 3 ∕ 2 6 m + 4 x 2 ∕ m × e ι { δ 1 2 b m 2 a 2 ( m + 1 ) 4 + γ } t + λ 0 .

By substituting σ = ± 4 Λ 2 , we obtain the quiescent dark and singular solitons:

(58) ℘ ( x , t ) = ± δ 1 m − a ( m + 1 ) 2 tanh δ 1 b m 3 ∕ 2 a ( m + 1 ) 3 ∕ 2 6 m + 4 x 2 ∕ m × e ι { δ 1 2 b m 2 a 2 ( m + 1 ) 4 + γ } t + λ 0

and

(59) ℘ ( x , t ) = ± δ 1 m − a ( m + 1 ) 2 coth δ 1 b m 3 ∕ 2 a ( m + 1 ) 3 ∕ 2 6 m + 4 x 2 ∕ m × e ι { δ 1 2 b m 2 a 2 ( m + 1 ) 4 + γ } t + λ 0 ,

with δ 1 > 0 , m > 0 , b > 0 , and a > 0 .

Result 2:

(60) ω 0 = 0 , ω 1 = ± σ ( 4 δ 2 − δ 1 ( m + 4 ) ) a ( m + 1 ) 2 , β 1 = 0 , ϖ = 8 b ( δ 2 − δ 1 ) ( 4 δ 2 − δ 1 ( m + 4 ) ) a 2 ( m + 1 ) 3 ( 3 m + 2 ) + γ , κ = − b ( δ 1 m ( m + 4 ) − 4 δ 2 m ) 2 a 2 ( m + 1 ) 3 2 − ( 3 m + 2 ) ( δ 1 ( m + 4 ) − 4 δ 2 ) .

The wave profile of Eq. (50) can be achieved as a consequence of the following:

(61) ℘ ( x , t ) = ± σ ( 4 δ 2 − δ 1 ( m + 4 ) ) a ( m + 1 ) 2 × 1 σ exp [ − κ x ] + 4 Λ 2 exp [ κ x ] 2 ∕ m × e ι { 8 b ( δ 2 − δ 1 ) ( 4 δ 2 − δ 1 ( m + 4 ) ) a 2 ( m + 1 ) 3 ( 3 m + 2 ) + γ } t + λ 0 .

By substituting σ = ± 4 Λ 2 , we obtain the quiescent bright and singular solitons:

(62) ℘ ( x , t ) = 2 − 2 ∕ m ± 4 Λ 2 ( 4 δ 2 − δ 1 ( m + 4 ) ) Λ a ( m + 1 ) 2 sech [ κ x ] 2 ∕ m × e ι { 8 b ( δ 2 − δ 1 ) ( 4 δ 2 − δ 1 ( m + 4 ) ) a 2 ( m + 1 ) 3 ( 3 m + 2 ) + γ } t + λ 0 ,

and

(63) ℘ ( x , t ) = 2 − 2 ∕ m ± 4 a 2 ( δ 1 ( m + 4 ) − 4 δ 2 ) Λ a ( m + 1 ) 2 csch [ κ x ] 2 ∕ m × e ι { 8 b ( δ 2 − δ 1 ) ( 4 δ 2 − δ 1 ( m + 4 ) ) a 2 ( m + 1 ) 3 ( 3 m + 2 ) + γ } t + λ 0 ,

with 4 a 2 ( δ 1 ( m + 4 ) − 4 δ 2 ) > 0 , and a ( m + 1 ) 2 > 0 .

4 Results and discussion

In our endeavour to deepen understanding of the solutions at hand, we have meticulously crafted a comprehensive visual representation. By employing both three-dimensional (3D) and two-dimensional (2D) plots, we offer a detailed insight into the absolute part of the solutions, elucidating their interaction and behaviour within our proposed system. The 3D graphs afford a panoramic perspective, capturing the intricate dynamics of soliton propagation, while the 2D graphs delve into a nuanced comparison of soliton profiles across different orders, highlighting variations in amplitude and phase components. These graphical renderings serve as invaluable tools, offering profound insights into the behaviour of the solutions across varying parameters.

Figure 1(a) and (b) presents a vivid portrayal of the quiescent bright soliton profile, corresponding to Eq. (20), across a spectrum of parameters. Moving onwards, Figure 2(a) showcases the 3D plot of Eq. (30), offering a captivating depiction of the dark soliton profile, while Figure 2(b) delves into its 2D representation at various values of m . These illustrations vividly demonstrate the soliton’s propagation, oscillating between forward and backward motion, while undergoing fluctuations in amplitude and phase.

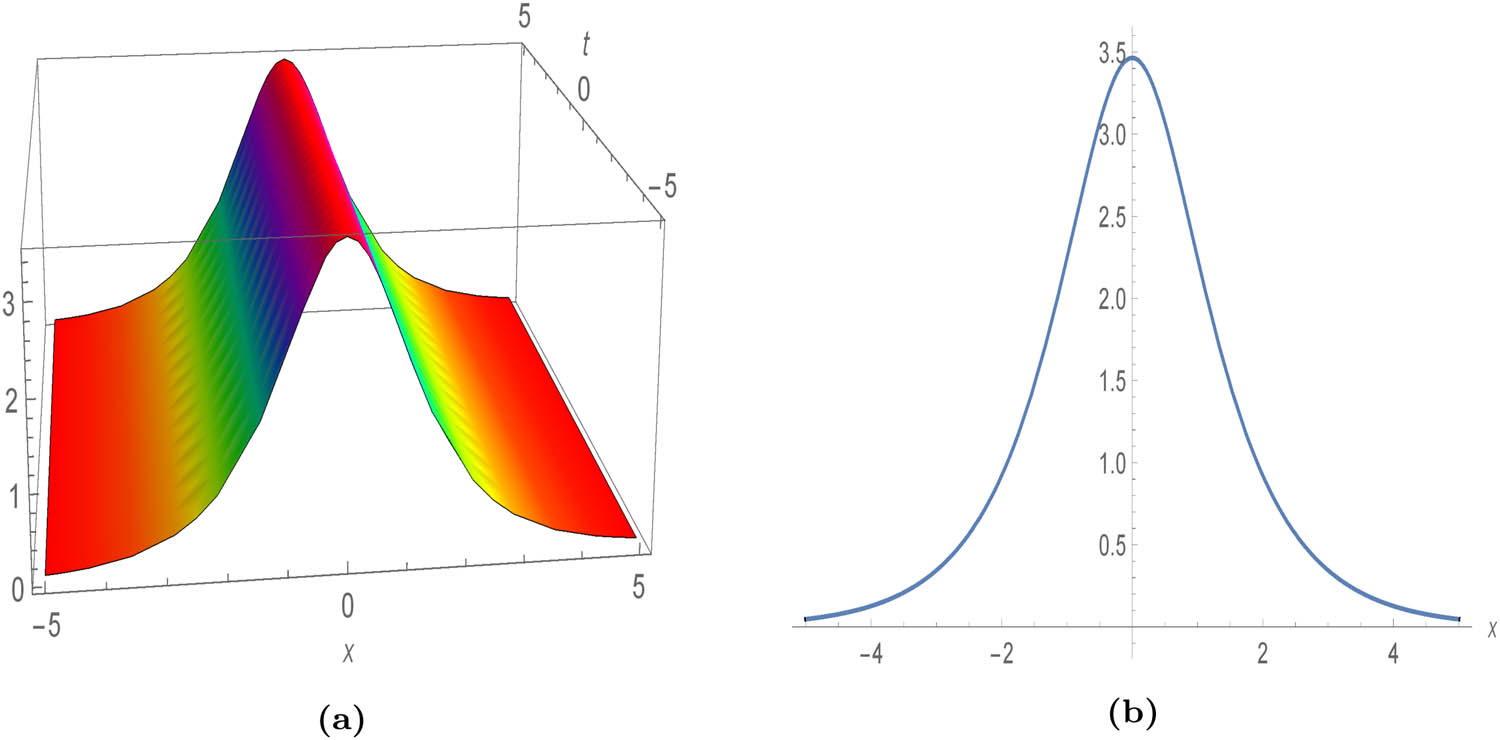
$Figure 1 Profile of a stationary bright soliton of Eq. (20) with δ 1 = a = b 2 = κ = γ = Λ = 1 {\delta }_{1}=a={b}_{2}=\kappa =\gamma =\Lambda =1 , δ 2 = λ 0 = ‒ 1 {\delta }_{2}={\lambda }_{0}=‒1 , and m = 1 m=1 : (a) 3D plot and (b) 2D plot.$

Figure 1

Profile of a stationary bright soliton of Eq. (20) with δ 1 = a = b 2 = κ = γ = Λ = 1 , δ 2 = λ 0 = ‒ 1 , and m = 1 : (a) 3D plot and (b) 2D plot.

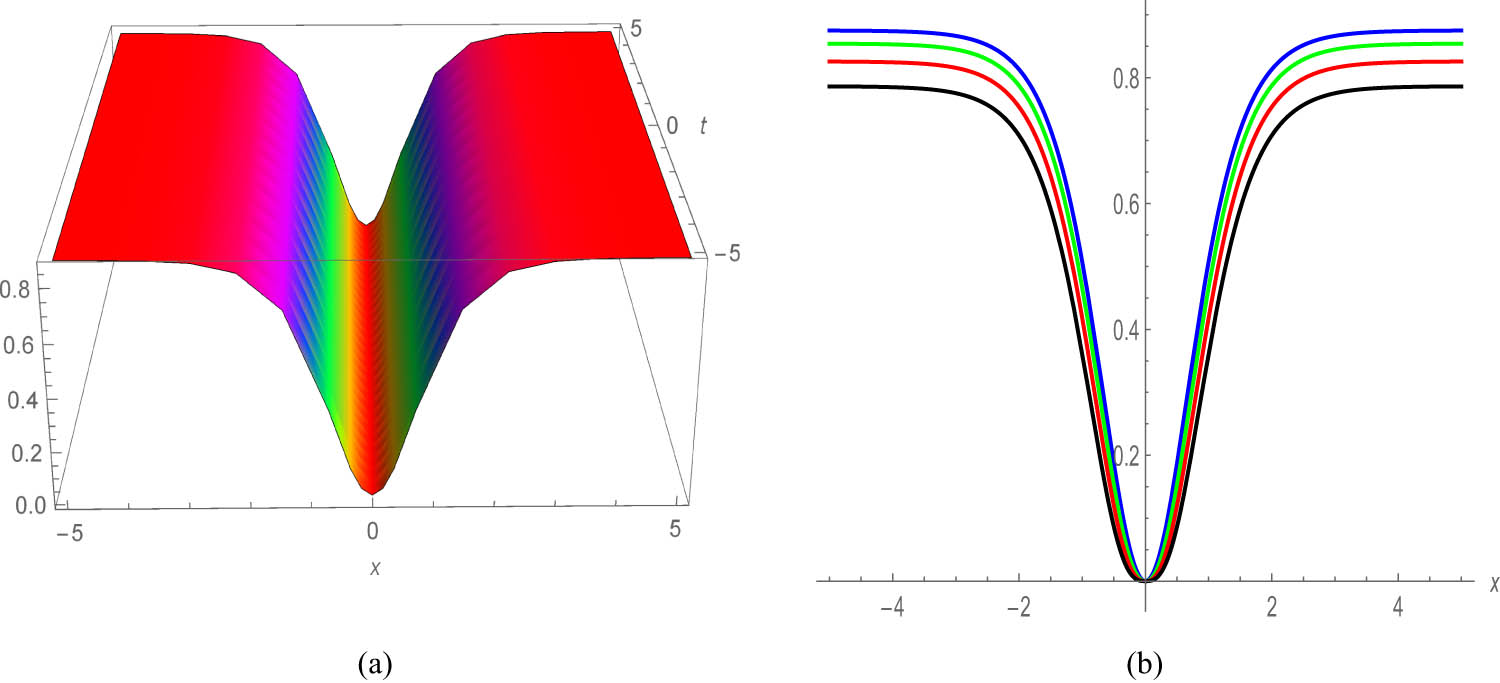
$Figure 2 Profile of a stationary dark soliton of Eq. (30) with δ 1 = 1 {\delta }_{1}=1 , a = 1 a=1 , b 1 = 1 {b}_{1}=1 , b 2 = 1 {b}_{2}=1 , γ = 1 \gamma =1 , λ 0 = ‒ 1 {\lambda }_{0}=‒1 , κ = 1 \kappa =1 : (a) 3D plot with m = 1 m=1 and (b) 2D plot with m = 1 , 0.9 , 0.8 m=1,0.9,0.8 , and 0.7.$

Figure 2

Profile of a stationary dark soliton of Eq. (30) with δ 1 = 1 , a = 1 , b 1 = 1 , b 2 = 1 , γ = 1 , λ 0 = ‒ 1 , κ = 1 : (a) 3D plot with m = 1 and (b) 2D plot with m = 1 , 0.9 , 0.8 , and 0.7.

Transitioning to Figure 3, we unveil the quiescent bright profile of Eq. (34), captured in both 3D and 2D plots, showcasing the dynamic alterations in amplitude and phase as the soliton traverses its path. Figure 4 provides a visual representation of Eq. (44), encapsulating the essence of the dark soliton solution, with the accompanying 2D graphic offering a nuanced exploration of its transmission characteristics at varying m values.

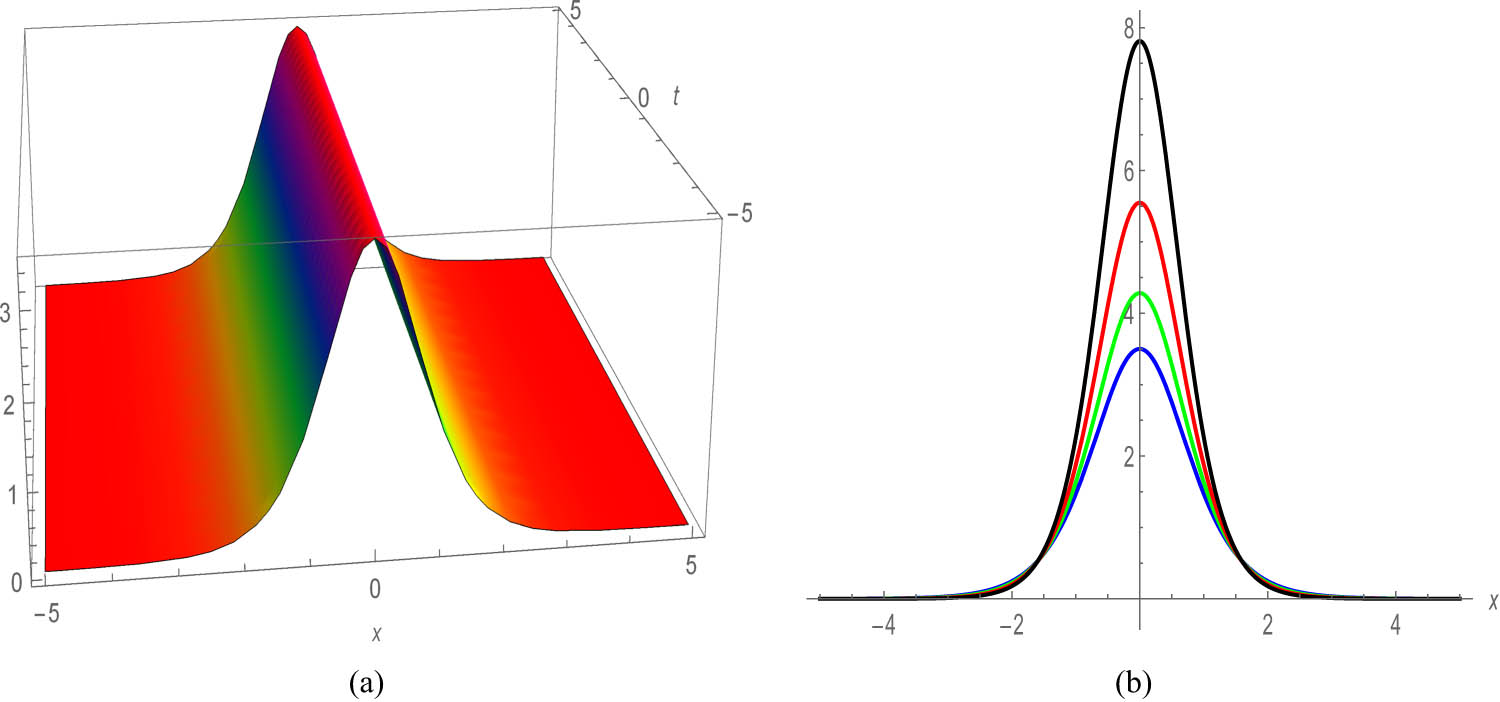
$Figure 3 Profile of a stationary bright soliton of Eq. (34) with Λ = 1 \Lambda =1 , a = 1 a=1 , δ 1 = 1 {\delta }_{1}=1 , b 1 = ‒ 1 {b}_{1}=‒1 , b 2 = ‒ 1 {b}_{2}=‒1 , δ 2 = ‒ 1 {\delta }_{2}=‒1 , γ = 1 \gamma =1 , λ 0 = ‒ 1 {\lambda }_{0}=‒1 , κ = 1 \kappa =1 : (a) 3D plot with m = 1 m=1 , (b) 2D with m = 1 m=1 , 0.9, 0.8, and 0.7.$

Figure 3

Profile of a stationary bright soliton of Eq. (34) with Λ = 1 , a = 1 , δ 1 = 1 , b 1 = ‒ 1 , b 2 = ‒ 1 , δ 2 = ‒ 1 , γ = 1 , λ 0 = ‒ 1 , κ = 1 : (a) 3D plot with m = 1 , (b) 2D with m = 1 , 0.9, 0.8, and 0.7.

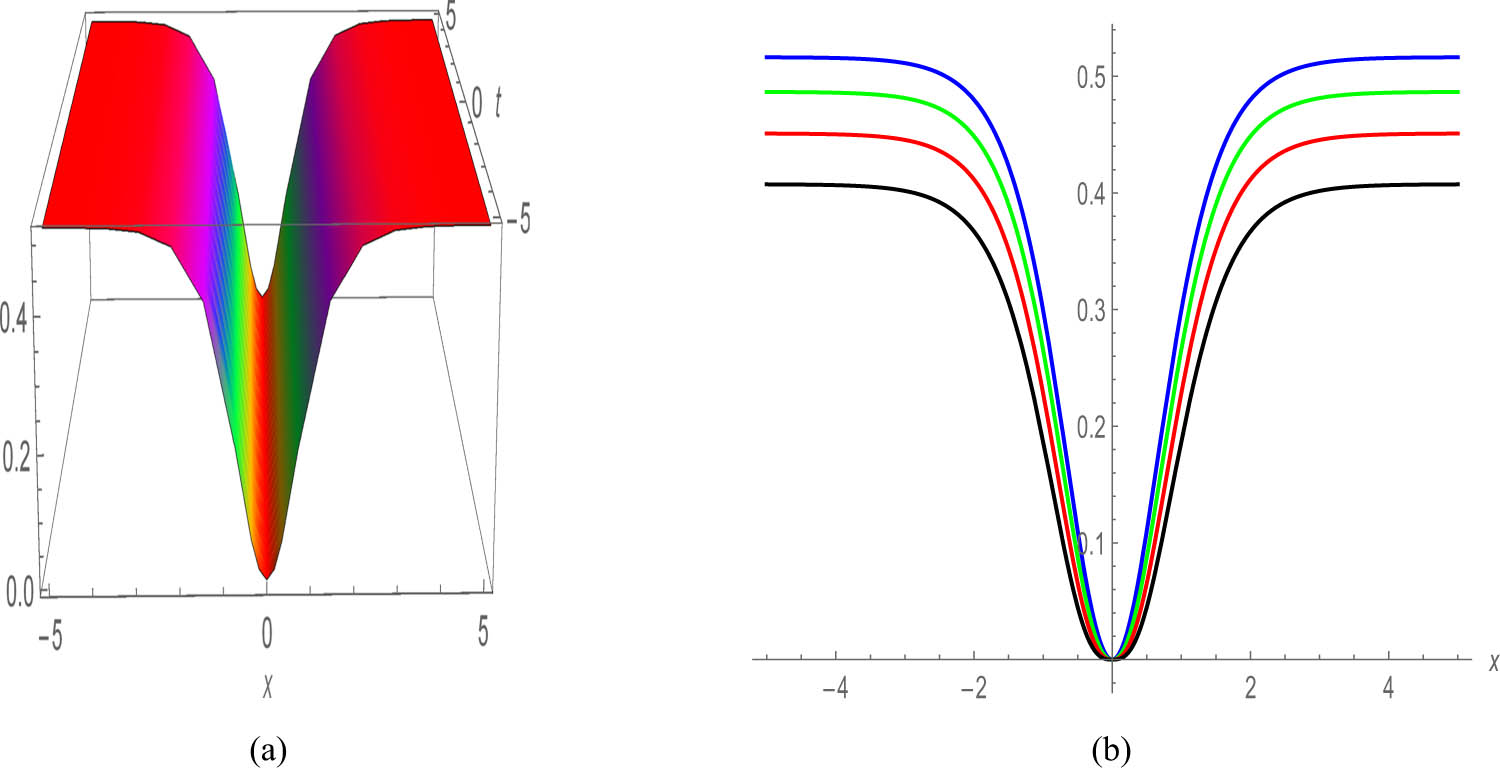
$Figure 4 Profile of a stationary dark soliton of Eq. (44) with a = 1 a=1 , δ 1 = 1 {\delta }_{1}=1 , b 1 = ‒ 1 {b}_{1}=‒1 , b 2 = ‒ 1 {b}_{2}=‒1 , γ = 1 \gamma =1 , λ 0 = ‒ 1 {\lambda }_{0}=‒1 , κ = 1 \kappa =1 : (a) 3D plot with m = 1 m=1 , (b) 2D plot with m = 1 m=1 , 0.9, 0.8, and 0.7.$

Figure 4

Profile of a stationary dark soliton of Eq. (44) with a = 1 , δ 1 = 1 , b 1 = ‒ 1 , b 2 = ‒ 1 , γ = 1 , λ 0 = ‒ 1 , κ = 1 : (a) 3D plot with m = 1 , (b) 2D plot with m = 1 , 0.9, 0.8, and 0.7.

Furthermore, Figure 5 presents the graphical depiction of Eq. (49), capturing the essence of the singular soliton solution. The accompanying 2D plot, across diverse m values, offers a detailed exploration of the soliton’s energy transmission dynamics, shedding light on its phase and amplitude fluctuations.

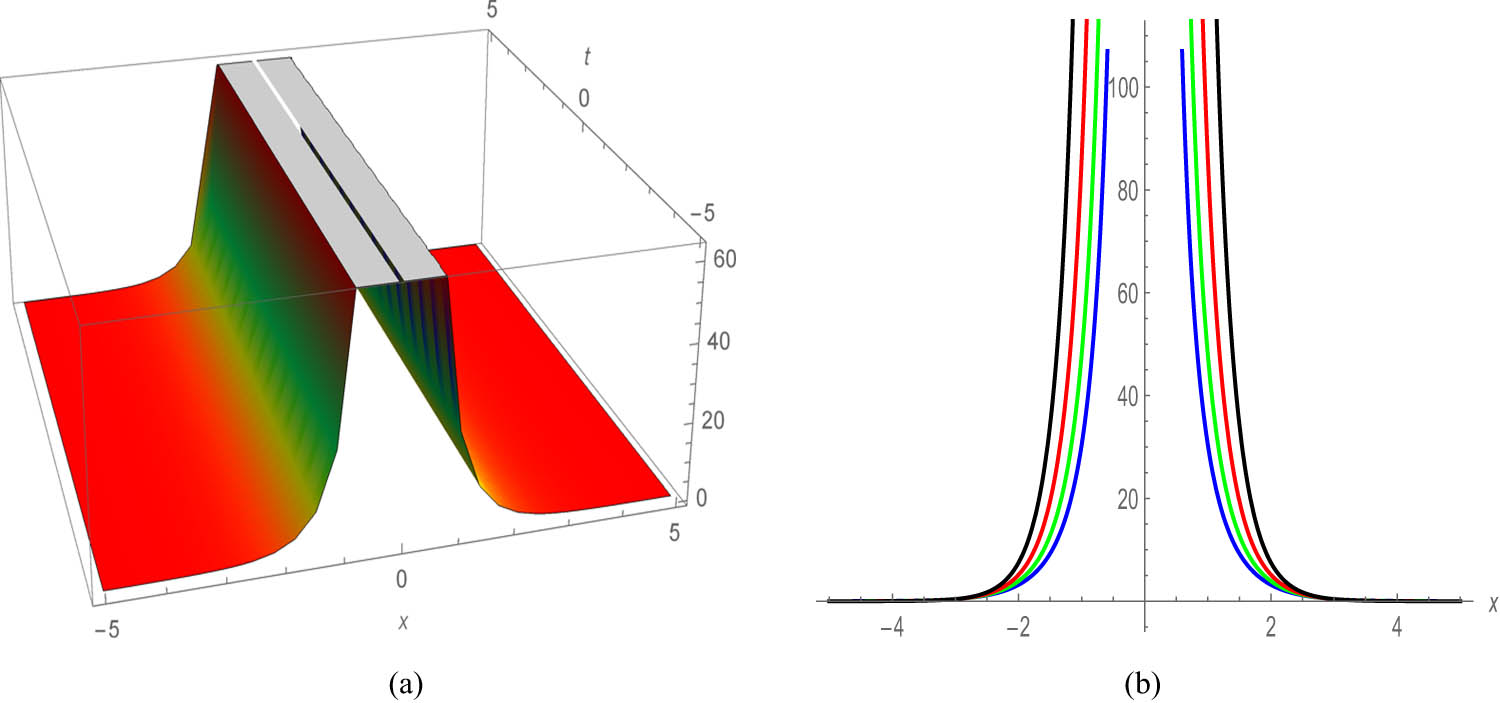
$Figure 5 Profile of a stationary singular soliton of Eq. (49) with Λ = 1 \Lambda =1 , a = 1 a=1 , δ 1 = 1 {\delta }_{1}=1 , b 2 = ‒ 1 {b}_{2}=‒1 , γ = 1 \gamma =1 , λ 0 = ‒ 1 {\lambda }_{0}=‒1 , κ = 1 \kappa =1 : (a) 3D plot with m = 1 m=1 , (b) 2D plot with m = 1 , 0.9 , 0.8 m=1,0.9,0.8 , and 0.7.$

Figure 5

Profile of a stationary singular soliton of Eq. (49) with Λ = 1 , a = 1 , δ 1 = 1 , b 2 = ‒ 1 , γ = 1 , λ 0 = ‒ 1 , κ = 1 : (a) 3D plot with m = 1 , (b) 2D plot with m = 1 , 0.9 , 0.8 , and 0.7.

Figures 6 and 7 round off our visual exploration, presenting the dark and bright soliton profiles of solutions encapsulated in Eqs (54) and (62), respectively. The accompanying 2D graphics offer a nuanced exploration of the soliton’s transmission characteristics across varying amplitudes and phases, providing a comprehensive understanding of their behaviour.

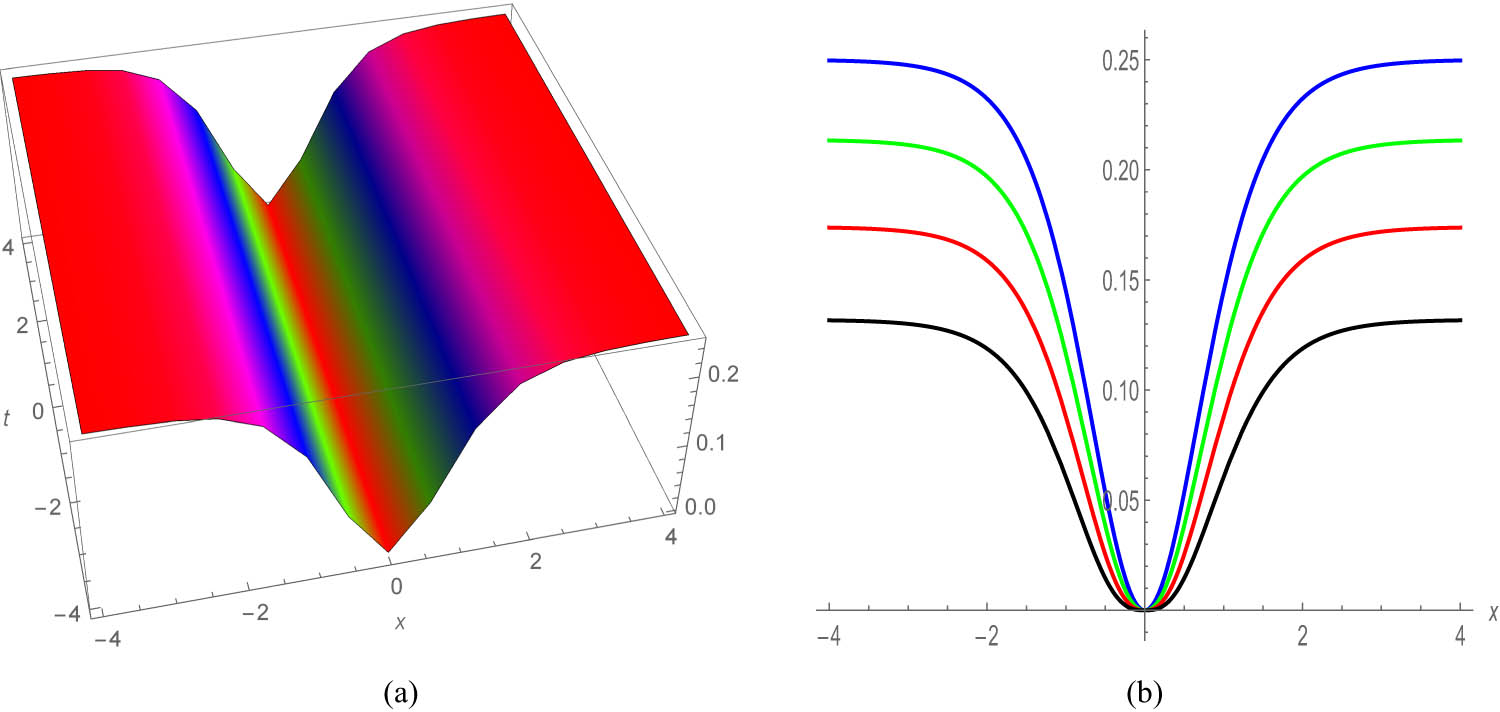
$Figure 6 Profile of a stationary dark soliton of Eq. (58) with a = ‒ 1 a=‒1 , δ 1 = 1 {\delta }_{1}=1 , b = 1 b=1 , γ = ‒ 1 \gamma =‒1 , λ 0 = ‒ 0.1 {\lambda }_{0}=‒0.1 , and κ = 1 \kappa =1 : (a) 3D plot with m = 1 m=1 , (b) 2D plot with m = 1 , 0.9 , 0.8 m=1,0.9,0.8 , and 0.7.$

Figure 6

Profile of a stationary dark soliton of Eq. (58) with a = ‒ 1 , δ 1 = 1 , b = 1 , γ = ‒ 1 , λ 0 = ‒ 0.1 , and κ = 1 : (a) 3D plot with m = 1 , (b) 2D plot with m = 1 , 0.9 , 0.8 , and 0.7.

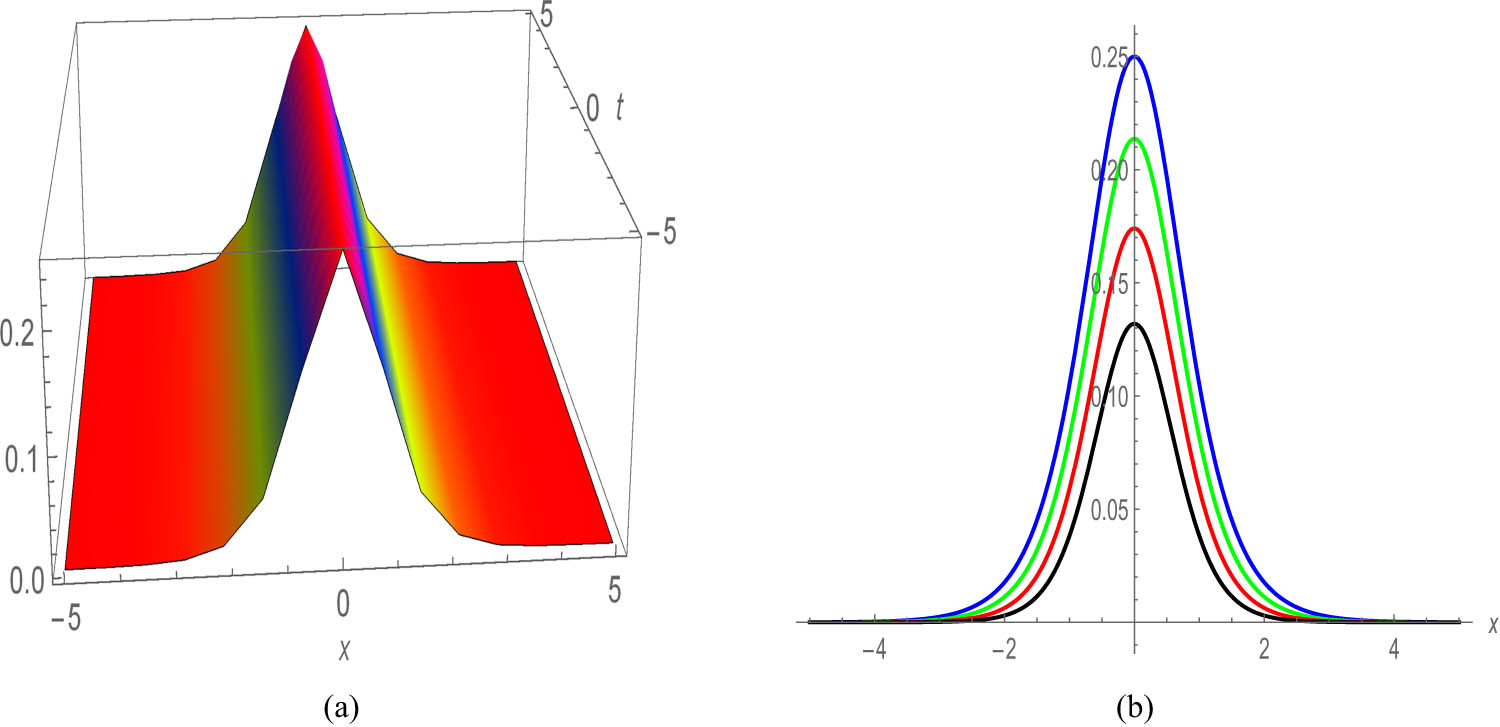
$Figure 7 Profile of a stationary bright soliton of Eq. (62) with Λ = 1 \Lambda =1 , a = 1 a=1 , δ 1 = 1 {\delta }_{1}=1 , b = 1 b=1 , B = 1 B=1 , γ = ‒ 1 \gamma =‒1 , λ 0 = ‒ 0.1 {\lambda }_{0}=‒0.1 , k = 1 k=1 : (a) 3D plot with m = 1 m=1 , (b) 2D plot with m = 1 m=1 , 0.9, 0.8, 0.7.$

Figure 7

Profile of a stationary bright soliton of Eq. (62) with Λ = 1 , a = 1 , δ 1 = 1 , b = 1 , B = 1 , γ = ‒ 1 , λ 0 = ‒ 0.1 , k = 1 : (a) 3D plot with m = 1 , (b) 2D plot with m = 1 , 0.9, 0.8, 0.7.

In summary, our visual representations offer profound insights into the behaviour of solitons under varying conditions, paving the way for a deeper comprehension of their dynamics and implications within the broader context of nonlinear wave phenomena. Various other researches discussed the stationary optical solitons emerge from Lie point symmetry in the CGLE, which possesses nine forms of nonlinear refractive index structures [19]. Six forms of Kudryashov’s nonlinear refractive index structures with nonlinear CD of CGLE are considered to derive bright, dark, and singular solitons [20]. Using the enhanced Kudryashov’s scheme, singular, dark, and bright soliton solutions of CGLE have emerged [24]. Three types of nonlinearity, such as quadratic–cubic, cubic–quintic, and power law nonlinearity, have been studied for CGLE, and dark, singular, and combo soliton solutions have been achieved [29]. However, our findings exhibit dark, bright, and singular soliton solutions for four distinct forms of self-phase modulation structures, resulting in solutions in hyperbolic function forms.

5 Conclusion

In our current endeavour, we have succeeded in elucidating the presence of stationary optical solitons across four distinct types of nonlinear refractive index structures as deduced from the CGLE. Through the adept application of the esteemed 1 ϑ ( ς ) , ϑ ′ ( ς ) ϑ ( ς ) method, we have attained the desired outcomes, marking a notable stride forward in our comprehension of soliton dynamics within optical systems. These seminal findings not only enrich the existing corpus of knowledge but also serve as a resounding admonition to electronics and telecommunication engineers.

Our study underscores the paramount importance of upholding linear CD throughout the transmission of optical signals. The repercussions of introducing nonlinear CD could be calamitous, potentially leading to the cessation of soliton transmission across international borders and precipitating a global upheaval in internet communication. It is incumbent upon us to exercise utmost caution to safeguard against the transformation of CD into a nonlinear state during its transmission, thus averting such dire consequences.

Looking ahead, our findings herald the dawn of further exploration in this realm. Subsequent research endeavours will involve the substitution of nonlinear CD with nonlinear CQ dispersive terms, promising a cornucopia of additional insights into soliton dynamics and their implications for telecommunications systems and technologies. These forthcoming investigations hold the potential to deepen our understanding of nonlinear wave phenomena and herald transformative advancements in the sphere of optical communication.

Acknowledgments

The authors extend their heartfelt appreciation for the invaluable support rendered by the National Science and Technology Council in Taiwan, under Grant Numbers 112-2115-M-006-002 and 112-2321-B-006-020. Their generous assistance has been instrumental in facilitating this research endeavour, and their unwavering commitment to advancing scientific knowledge is deeply acknowledged.

Funding information: The authors state no funding involved.
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors state no conflict of interest.
Data availability statement: All data generated or analysed during this study are included in this published article.

References

[1] Ahmad S, Aldosary SF, Khan MA, ur Rahman M, Alsharif F, Ahmad S. Analyzing optical solitons in the generalized unstable NLSE in dispersive media. Optik. 2024;307:171830. 10.1016/j.ijleo.2024.171830Search in Google Scholar

[2] Khan A, Fahad Aldosary S, Ali Khan M, ur Rahman M, Ahmad S. Modulation instability analysis and optical solitary waves solutions of high-order dispersive parabolic Schrödinger-Hirota equation. Mod Phys Lett B. 2024;39:2450414. 10.1142/S0217984924504141Search in Google Scholar

[3] Ekici M, Mirzazadeh M, Sonmezoglu A, Ullah MZ, Asma M, Zhou Q, et al. Dispersive optical solitons with Schrödinger-Hirota equation by extended trial equation method. Optik. 2017;136:451–61. 10.1016/j.ijleo.2017.02.042Search in Google Scholar

[4] Yasin S, Khan A, Ahmad S, Osman M. New exact solutions of (3+1)-dimensional modified KdV-Zakharov-Kuznetsov equation by Sardar-subequation method. Opt Quantum Electron. 2024;56(1):90. 10.1007/s11082-023-05558-2Search in Google Scholar

[5] Ahmad S, Lou J, Khan MA, ur Rahman M. Analysing the Landau-Ginzburg-Higgs equation in the light of superconductivity and drift cyclotron waves: Bifurcation, chaos and solitons. Phys Scripta. 2023;99(1):015249. 10.1088/1402-4896/ad1735Search in Google Scholar

[6] Ahmad S, Mahmoud EE, Saifullah S, Ullah A, Ahmad S, Akgül A, et al. New waves solutions of a nonlinear Landau-Ginzburg-Higgs equation: The Sardar-subequation and energy balance approaches. Results Phys. 2023;51:106736. 10.1016/j.rinp.2023.106736Search in Google Scholar

[7] Biswas A, Khalique CM. Stationary solutions for nonlinear dispersive Schrödinger’s equation. Nonlinear Dyn. 2011;63:623–6. 10.1007/s11071-010-9824-1Search in Google Scholar

[8] Ekici M, Mirzazadeh M, Sonmezoglu A, Ullah MZ, Zhou Q, Moshokoa SP, et al. Nematicons in liquid crystals by extended trial equation method. J Nonlinear Opt Phys Mater. 2017;26(01):1750005. 10.1142/S0218863517500059Search in Google Scholar

[9] Biswas A, Ekici M, Sonmezoglu A, Belic M. Stationary optical solitons with nonlinear group velocity dispersion by extended trial function scheme. Optik. 2018;171:529–42. 10.1016/j.ijleo.2018.06.067Search in Google Scholar

[10] Kudryashov NA. Solitary waves of model with triple arbitrary power and non-local nonlinearity. Optik. 2022;262:169334. 10.1016/j.ijleo.2022.169334Search in Google Scholar

[11] Arnous AH, Zhou Q, Biswas A, Guggilla P, Khan S, Yıldırım Y, et al. Optical solitons in fibre Bragg gratings with cubic–quartic dispersive reflectivity by enhanced Kudryashov’s approach. Phys Lett A. 2022;422:127797. 10.1016/j.physleta.2021.127797Search in Google Scholar

[12] Arnous AH. Optical solitons to the cubic quartic Bragg gratings with anti-cubic nonlinearity using new approach. Optik. 2022;251:168356. 10.1016/j.ijleo.2021.168356Search in Google Scholar

[13] Arnous AH, Mirzazadeh M, Zhou Q, Moshokoa SP, Biswas A, Belic M. Soliton solutions to resonant nonlinear Schrodinger’s equation with time-dependent coefficients by modified simple equation method. Optik. 2016;127(23):11450–9. 10.1016/j.ijleo.2016.09.055Search in Google Scholar

[14] Adem AR, Ekici M, Biswas A, Asma M, Zayed EM, Alzahrani AK, et al. Stationary optical solitons with nonlinear chromatic dispersion having quadratic–cubic law of refractive index. Phys Lett A. 2020;384(25):126606. 10.1016/j.physleta.2020.126606Search in Google Scholar

[15] Geng Y, Li J. Exact solutions to a nonlinearly dispersive Schrödinger equation. Appl Math Comput. 2008;195(2):420–39. 10.1016/j.amc.2007.04.119Search in Google Scholar

[16] Yan Z. Envelope compactons and solitary patterns. Phys Lett A. 2006;355(3):212–5. 10.1016/j.physleta.2006.02.032Search in Google Scholar

[17] Ekici M. Stationary optical solitons with Kudryashovas quintuple power law nonlinearity by extended Jacobi’s elliptic function expansion. J Nonlinear Opt Phys Mater. 2023;32(01):2350008. 10.1142/S021886352350008XSearch in Google Scholar

[18] Adem AR, Ntsime BP, Biswas A, Khan S, Alzahrani AK, Belic MR. Stationary optical solitons with nonlinear chromatic dispersion for Lakshmanan-Porsezian-Daniel model having Kerr law of nonlinear refractive index. Ukr J Phys Opt. 2021;22(2):83–6. 10.3116/16091833/22/2/83/2021Search in Google Scholar

[19] Adem AR, Ntsime BP, Biswas A, Ekici M, Yildirim Y, Alshehri HM. Implicit quiescent optical solitons with complex Ginzburg–Landau equation having nonlinear chromatic dispersion. J Optoelectron Adv Mater. 2022;24(September–October 2022):450–62. Search in Google Scholar

[20] Ekici M. Stationary optical solitons with complex Ginzburg–Landau equation having nonlinear chromatic dispersion and Kudryashov’s refractive index structures. Phys Lett A. 2022;440:128146. 10.1016/j.physleta.2022.128146Search in Google Scholar

[21] Hong WP. Existence conditions for stable stationary solitons of the cubic–quintic complex Ginzburg–Landau equation with a viscosity term. Z Für Naturforsch A. 2008;63(12):757–62. 10.1515/zna-2008-1203Search in Google Scholar

[22] Kudryashov NA. Stationary solitons of the generalized nonlinear Schrödinger equation with nonlinear dispersion and arbitrary refractive index. Appl Math Lett. 2022;128:107888. 10.1016/j.aml.2021.107888Search in Google Scholar

[23] Han T, Li Z, Li C, Zhao L. Bifurcations, stationary optical solitons and exact solutions for complex Ginzburg–Landau equation with nonlinear chromatic dispersion in non-Kerr law media. J Opt. 2023;52(2):831–44. 10.1007/s12596-022-01041-5Search in Google Scholar

[24] Arnous AH, Biswas A, Yıldırım Y, Moraru L, Moldovanu S, Alghamdi AA. Quiescent optical solitons with complex Ginzburg–Landau equation having a dozen forms of self-phase modulation. Heliyon. 2023;9(5):e15661. 10.1016/j.heliyon.2023.e15661Search in Google Scholar PubMed PubMed Central

[25] Malomed BA. New findings for the old problem: Exact solutions for domain walls in coupled real Ginzburg–Landau equations. Phys Lett A. 2022;422:127802. 10.1016/j.physleta.2021.127802Search in Google Scholar

[26] Atai J, Malomed BA. Bound states of solitary pulses in linearly coupled Ginzburg–Landau equations. Phys Lett A. 1998;244(6):551–6. 10.1016/S0375-9601(98)00308-9Search in Google Scholar

[27] Qiu Y, Malomed BA, Mihalache D, Zhu X, Zhang L, He Y. Soliton dynamics in a fractional complex Ginzburg–Landau model. Chaos Solitons Fractals. 2020;131:109471. 10.1016/j.chaos.2019.109471Search in Google Scholar

[28] Biswas A, Alqahtani RT. Optical soliton perturbation with complex Ginzburg–Landau equation by semi-inverse variational principle. Optik. 2017;147:77–81. 10.1016/j.ijleo.2017.08.018Search in Google Scholar

[29] Arshed S, Biswas A, Mallawi F, Belic MR. Optical solitons with complex Ginzburg–Landau equation having three nonlinear forms. Phys Lett A. 2019;383(36):126026. 10.1016/j.physleta.2019.126026Search in Google Scholar

[30] Arnous AH, Seadawy AR, Alqahtani RT, Biswas A. Optical solitons with complex Ginzburg–Landau equation by modified simple equation method. Optik. 2017;144:475–80. 10.1016/j.ijleo.2017.07.013Search in Google Scholar

[31] Biswas A. Chirp-free bright optical solitons and conservation laws for complex Ginzburg–Landau equation with three nonlinear forms. Optik. 2018;174:207–15. 10.1016/j.ijleo.2018.08.063Search in Google Scholar

[32] Arnous AH, Biswas A, Yıldırım Y, Zhou Q, Liu W, Alshomrani AS, et al. Cubic-quartic optical soliton perturbation with complex Ginzburg–Landau equation by the enhanced Kudryashov’s method. Chaos Solitons Fractals. 2022;155:111748. 10.1016/j.chaos.2021.111748Search in Google Scholar

[33] Kudryashov NA. Mathematical model of propagation pulse in optical fibre with power nonlinearities. Optik. 2020;212:164750. 10.1016/j.ijleo.2020.164750Search in Google Scholar

[34] Kudryashov NA. Method for finding highly dispersive optical solitons of nonlinear differential equations. Optik. 2020;206:163550. 10.1016/j.ijleo.2019.163550Search in Google Scholar

[35] Arnous AH, Nofal TA, Biswas A, Yıldırım Y, Asiri A. Cubic-quartic optical solitons of the complex Ginzburg–Landau equation: A novel approach. Nonlinear Dyn. 2023;111:1–16. 10.1007/s11071-023-08854-4Search in Google Scholar

[36] Rehman HU, Said GS, Amer A, Ashraf H, Tharwat M, Abdel-Aty M, et al. Unraveling the (4+1)-dimensional Davey-Stewartson-Kadomtsev-Petviashvili equation: Exploring soliton solutions via multiple techniques. Alex Eng J. 2024;90:17–23. 10.1016/j.aej.2024.01.058Search in Google Scholar

[37] Ekici M, Sonmezoglu A, Biswas A, Belic M. Sequel to stationary optical solitons with nonlinear group velocity dispersion by extended trial function scheme. Optik. 2018;172:636–50. 10.1016/j.ijleo.2018.07.068Search in Google Scholar

[38] Zayed EM, Shohib RM, Alngar ME. Cubic-quartic nonlinear Schrödinger equation in birefringent fibres with the presence of perturbation terms. Waves Random Complex Media. 2022;32(5):2445–67. 10.1080/17455030.2020.1854490Search in Google Scholar

[39] Debnath A, Tarun J, Khan A. Signature of supersolidity in a driven cubic–quartic nonlinear Schrödinger equation. J Phys B: At Mol Opt Phys. 2022;55(2):025301. 10.1088/1361-6455/ac4c8eSearch in Google Scholar

[40] Zhou Q, Zhu Q. Optical solitons in medium with parabolic law nonlinearity and higher order dispersion. Waves Random Complex Media. 2015;25(1):52–9. 10.1080/17455030.2014.956847Search in Google Scholar

Received: 2024-04-16

Revised: 2024-07-09

Accepted: 2024-10-04

Published Online: 2025-03-04

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/nleng-2024-0043

Keywords for this article

Ginzburg–Landau equation; solitons; nonlinear chromatic dispersion

Creative Commons

BY 4.0