Construction of image segmentation system combining TC and swarm intelligence algorithm

Yongtao Wang

doi:10.1515/nleng-2025-0152

Artikel Open Access

Construction of image segmentation system combining TC and swarm intelligence algorithm

Yongtao Wang

Veröffentlicht/Copyright: 30. August 2025

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen

Aus der Zeitschrift Nonlinear Engineering Band 14 Heft 1

Abstract

Considering the slow convergence speed and local optima in most current swarm intelligence algorithms for image segmentation, this study combines the thresholding clustering with intelligent algorithms. The algorithm is optimized based on the characteristics of image segmentation. First, an improved differential evolution algorithm is applied to enhance the speed of threshold image segmentation. The convergence performance of the algorithm is improved by adjusting the crossover probability and mutation strategy. Second, considering the threshold difference, an improved two-dimensional Otsu threshold segmentation algorithm based on cuckoo algorithm is proposed, and fractional calculus processing and fractional enhancement filtering are introduced to improve the image segmentation quality. The loss value in image feature segmentation was less than 5 × 10², the accuracy exceeded 90% in different types of image segmentation, the running time did not exceed 2 s, and the structural similarity reached 0.912, which was significantly better than other algorithms. Moreover, the pixel accuracy of the image processing algorithm exceeded 90%, with good segmentation details and edge extraction effects. The proposed image segmentation method performs well in segmentation accuracy, edge clarity, and computational efficiency, which can improve the segmentation accuracy and application effect in image processing systems and provide a method for improving the generalization ability of segmentation models in different scenarios.

Keywords: threshold segmentation; differential evolution; cuckoo algorithm; fractional calculus; image segmentation; quality evaluation

1 Introduction

Internet and computer vision technology have greatly increased image data. The dependence of medical imaging, face recognition, biometric security, and other applications on image analysis makes image segmentation results extremely important. The quality of segmentation results will directly affect a series of links in image processing [1]. Image segmentation is to divide the overall informationized image into different modules and regions based on feature differences, which facilitates further image analysis and understanding [2]. Relying on image characteristics, segmentation technique has two categories: edge detection and region detection. Overall, image segmentation problems are complex and difficult [3]. The image threshold segmentation technology mainly divides the set of pixel regions based on the grayscale level of the image. However, due to its excessive dependence on the selected threshold, its segmentation performance has significant differences and limitations. The traditional maximum inter-class variance method (Otsu) is widely used in current threshold segmentation algorithms. It mainly achieves threshold segmentation based on the maximum interclass variance of the image. However, it ignores the pixel information and spatial characteristics of the image during the segmentation process, making its segmentation accuracy difficult to meet practical needs [4]. Therefore, to improve segmentation accuracy and address the shortcomings of the traditional Otsu algorithm, this study combines it with swarm intelligence algorithms with strong optimization capabilities, using improved differential evolution (DE) and cuckoo search (CS) to improve image segmentation accuracy and efficiency. The innovation lies in combining threshold image segmentation characteristics and algorithm performance, which can improve image segmentation performance while ensuring processing accuracy and adaptability for different types of images.

2 Related works

As a fundamental step in image processing and visual analysis, image segmentation is extensively applied in character recognition, medical image analysis, and visual inspection. Traditional segmentation algorithms are significantly affected by factors such as threshold quantity and background noise. Improving the real-time performance of algorithm analysis without affecting search accuracy is a research hotspot. Some scholars have made different attempts. For example, Khrissi et al. used meta-heuristic algorithms to optimize clustering and improve image segmentation quality. The results showed that this method had better image processing performance than other basic methods and required less computation time [5]. Chowdhary et al. designed an intuition-based possibility fuzzy c-means method to improve medical image overlap clustering and data noise problems. The method had good classification performance. The average segmentation accuracy at different noise levels exceeded 85% [6]. Liu et al. considered the limitations of existing image segmentation methods in segmenting small and irregular particles. The morphology was used to segment key regions in images, and deep learning methods were used to achieve image classification. The results showed that the segmentation model could effectively solve the adhesion and overlap problems between adjacent particles. The segmentation performance was good [7]. Zhang et al. optimized the Deeplabv3 + network structure and loss function design for tongue image segmentation. The algorithm effectively reduced image misjudgment and improved the accuracy of tongue edge segmentation [8]. Vadivel and Suguna applied convolutional neural networks to leaf disease image recognition. The results showed that the classification accuracy of this method far exceeded 95% [9]. Stringer et al. proposed a cell segmentation method based on deep learning and trained the dataset using a three-dimensional extension of the cell model. The model did not require parameter adjustment and had good applicability and effectiveness [10].

Threshold segmentation technology is extensively used in image processing due to its high efficiency, accuracy, and precision. Sharma et al. proposed a multi-level threshold segmentation method, which utilized an improved firefly algorithm and the principle of class variance derivation to process images. The method had better structural similarity index measurement and objective function value compared with other meta-heuristic algorithms [11]. Resma and Nair proposed a meta-heuristic Krill flock optimization algorithm for image segmentation. The results showed that this multi-level threshold processing approach exhibited better applicability and lower computational efficiency compared with other algorithms [12]. In response to the limitations of solving and measuring multi-threshold image segmentation techniques, Dhal et al. conducted a literature review and discussion on the application of natural inspired optimization algorithms. The development of multi-threshold image models under this algorithm should consider multiple factors [13]. Wang et al. designed a multi-class segmentation method for aggregated images on the basis of optimized chaotic sparrow search algorithm, which improved processing speed by introducing new parameters. This method had a significant segmentation effect on high-precision images such as aggregates [14]. Nyo et al. used the Otsu thresholding method to achieve image segmentation and used morphological operations to obtain accurate target regions. The results showed that the segmentation accuracy of this method exceeded 95%, and the application effect in medicine was significant [15]. Rawas and El-Zaart designed an image segmentation model based on precise parallel algorithms and combined it with benchmark distribution thresholding techniques to extract and partition segmentation regions. The model had high segmentation accuracy on different benchmark datasets and significantly reduced processing time [16].

In summary, most scholars utilize swarm intelligence algorithms to solve image segmentation processing, but they rarely consider the premature convergence of the algorithm. Image segmentation methods that rely on threshold solving ideas ignore the attention to image pixel information and spatial characteristics, which limits previous research methods. In response to the shortcomings of current image threshold segmentation methods, this study combines threshold algorithms with swarm intelligence algorithms. Then, the fractional calculus processing idea is introduced to improve algorithm performance, enhancing image segmentation accuracy and quality.

3 Construction of image segmentation system combining thresholding clustering (TC) algorithm and swarm intelligence algorithm

The study combines the threshold image segmentation method with swarm intelligence algorithms to design an image segmentation system. First, the traditional TC is adaptively improved using an improved DE algorithm. Considering the complexity of image shapes and differences in target contrast, K-means clustering and subtraction clustering are combined to achieve image threshold segmentation. Subsequently, considering the threshold difference, the Otsu segmentation idea is combined with the improved cuckoo algorithm to improve image segmentation accuracy.

3.1 Threshold segmentation image processing based on improved differential algorithm

Otsu segmentation using the concept of class variance requires threshold traversal within the grayscale range, which can be time-consuming to some extent. Therefore, to improve the speed and accuracy of threshold solution, the DE is used to segment threshold image. The DE has good global search ability, but its traditional idea requires setting relevant parameters and mutation strategies, which is difficult to meet the needs of population evolution and high-dimensional data solving. Therefore, an improved DE based on improved adaptive control parameters is proposed. The improved DE optimizes the convergence performance of the algorithm by adjusting the crossover probability, as expressed mathematically in Eq. (1):

(1) CR i = rand n i × ( μ CR , 0.1 ) ,

where μ CR represents the mean. After each iteration, the control parameters are adaptively updated by introducing a random positive number for solving, as shown in Eq. (2):

(2) μ CR = ( 1 − c ) × μ CR + c × m A × ( S CR ) , μ F = ( 1 − c ) × μ F + c × m L × ( S F )

where S CR represents the set of parameters CR , S F represents a set of parameters F , c is a random positive number, m A is the arithmetic mean, and m L is the Lehmer mean. Figure 1 shows the parameter changes of variation factors.

Figure 1

Changes in parameters of variation factors.

In Figure 1, the amplitude exhibited by excessively large mutation factors is more pronounced, while excessively small factors can cause the population to fall into local optima. Therefore, according to the different stages of the population, an adaptive mutation factor is set to implement parameter adjustment strategies. Eq. (3) is the adaptive mutation factor:

(3) F i = F max − ( F max − F min ) × gen gen total k .

where gen represents the current population algebra, gen total is the total number of iterations, F max signifies the upper bound of the variation factor, F min signifies the lower bound of the variation factor, and k is a random number. Meanwhile, adaptive adjustments are made to the mutation operation. The improved mutation strategy is shown in Eq. (4):

(4) v i g + 1 = x r 1 g + u i × F i × ( x r 2 g − x r 3 g ) + ( 1 − u i ) × F i × ( x best g − x r 4 g ) .

where u i is the disturbance-scale parameter, v i g + 1 is an individual in the population, x best g is the optimal population individual, and x r 2 g is the experimental individual vector. Subsequently, considering the complex shape of the image and its contrast difference with the target, the study combines K-means clustering with subtractive clustering (SC) to achieve image threshold segmentation. The K-means algorithm is an unsupervised clustering algorithm, which often utilizes Euclidean distance to achieve distance partitioning. It can classify images on the basis of the distance between the feature values of image pixels and the cluster center values. Eq. (5) is the minimum cost function of the algorithm:

(5) J = ∑ j = 1 k ∑ i = 1 n dist ( x ij , m j ) ,

where x i j represents the data point, m j signifies the cluster center, dist is the distance, n signifies the data point, and k signifies the clusters. The traditional K-means algorithm is sensitive to the initial clustering center. The processing time of clustering results is related to the number of iterations and image noise points. Therefore, an improved SC algorithm is applied to achieve improvement. The SC algorithm identifies cluster centers by determining the data points with the highest density. To ensure that the obtained cluster centers are more in line with the actual situation, an improved method for cluster center identification based on distance measurement is proposed on the SC algorithm, taking into account the distance between data points and cluster centers. Figure 2 is a schematic diagram of the improved clustering algorithm process.

Figure 2

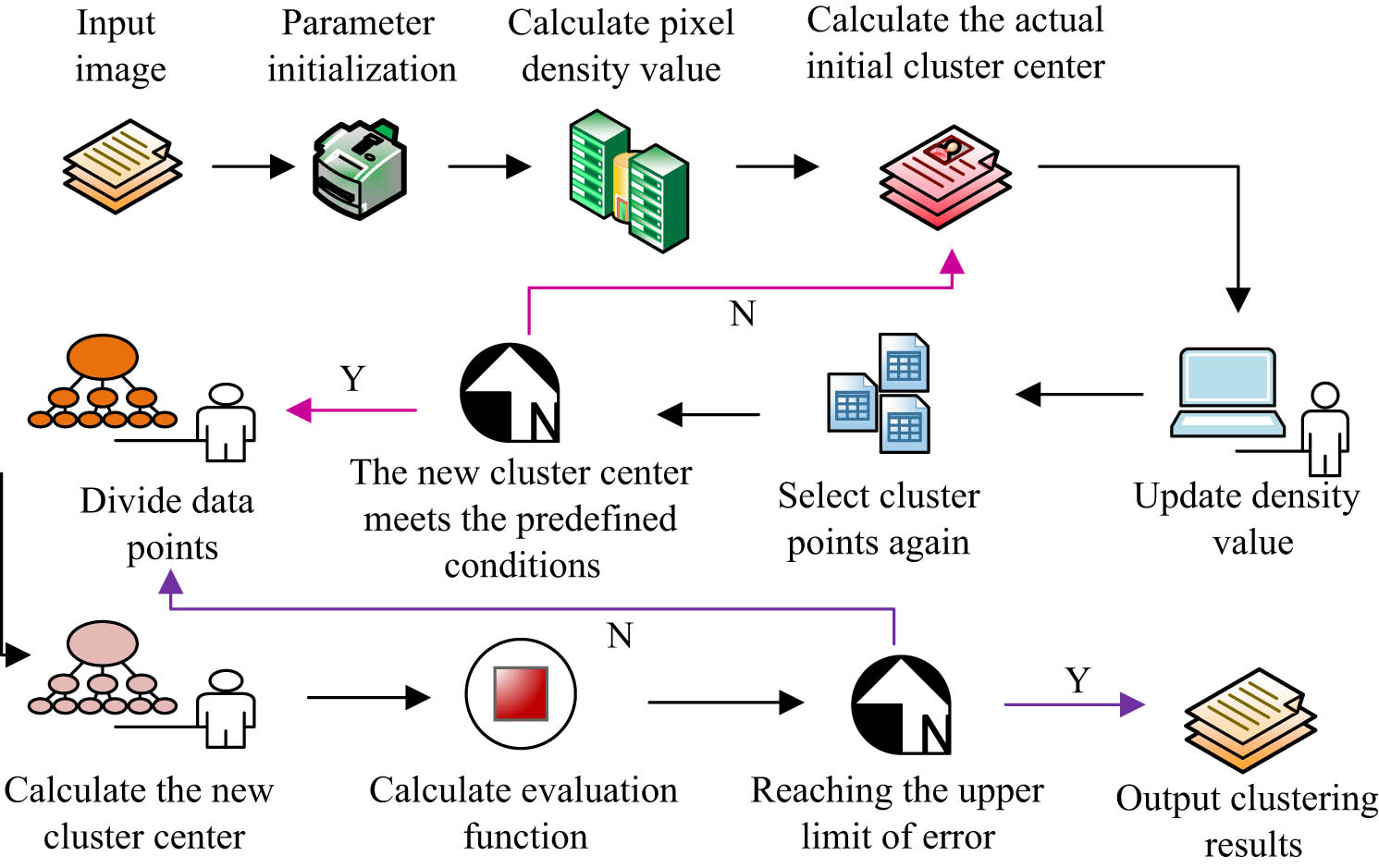
Schematic diagram of the improved clustering algorithm process.

The parameters of the SC algorithm are initialized and improved, including the number of clusters, hypersphere radius, and constraint coefficient. Then, the density values of each pixel are calculated. The density values of data points are updated based on the actual clustering centers to obtain all initial clustering points. The pixel distance of the clustering points is calculated to allocate the clustering centers, calculate the center positions, and end the process when the termination condition is met.

3.2 2D Otsu threshold segmentation algorithm based on the improved CS

Considering the threshold difference, this study introduces the Otsu segmentation for image segmentation. Otsu segmentation uses the maximum value of interclass variance in images to select the optimal threshold. Traditional one-dimensional Otsu thresholds that use grayscale pixels to distinguish between target and background images are inevitably affected by noise interference, leading to prominent excessive or inaccurate image segmentation [17]. Therefore, a two-dimensional Otsu threshold segmentation algorithm is proposed to expand the threshold search space by increasing the grayscale information of adjacent pixels. The probability of image occurrence in the two-dimensional Otsu threshold segmentation algorithm can be explained, as shown in Eq. (6):

(6) p ij = n ij MN ,

where MN signifies the two-dimensional size of the image, i signifies the grayscale, j represents the gradient, and n represents the pixels. Based on segmentation thresholds, images are divided into background and target categories. The occurrence probability can be mathematically represented, thereby reflecting the segmentation quality. Eq. (7) is the dispersion function:

(7) S ( s , t ) = P A × ( μ A − μ ) × ( μ A − μ ) T + P B × ( μ B − μ ) × ( μ B − μ ) T ,

where A is the background image, B is the target image, s is the threshold average grayscale, t is the gradient, μ A is the mean vector of the background image, μ B signifies the mean vector of the target image, μ is the total mean vector of pixels, and T represents the matrix transpose. To further enhance image quality, the study introduces fractional calculus processing and fractional enhancement filtering to improve the information quality of image preprocessing. Fractional calculus is a generalization of classical integer calculus, allowing the order of derivatives and integrals to be any real or complex number. Its definitions include Grunwald–Letnikov (G–L), Riemann–Liouville (R–L), and Caputo [18]. The fractional order is generated by the gamma function, where G–L is defined as transforming the differential order of the gamma function from an integer to a fraction and deriving it from the derivative definition of the integer order. The definition of R–L is to transform the order of calculus from integers to fractions using the Gamma function and then integrate and differentiate them. The definition of Caputo fractional calculus is a transformation defined by R–L, which involves differentiating a function and then integrating it. Eq. (8) is a mathematical expression of three defined forms:

(8) R − L = 1 Γ ( n − α ) d n f d t n ∫ a x f ( τ ) ( t − τ ) α − n + 1 d τ G − L = h − α ∑ k = 0 N ( − 1 ) k Γ ( α + k ) k ! Γ ( α ) f ( t − k h ) Caputo = 1 Γ ( n − α ) ∫ a t ( x − τ ) α − n + 1 f ( n ) ( τ ) d τ

where α represents the fractional order, n represents the order, Γ is the Gamma function, f ( ) is the function to be processed, τ is the integral variable, h is the discretization step size, t is the time, x is the independent variable, k is the summation variable, and N is the total number of discrete points. Fractional-order differentiation and integration are linear operators, where fractional-order derivatives depend on the global information of the function rather than local information, and can describe the memory and historical dependency characteristics of the system. The fractional-order differential filter enhances the high-frequency components of the signal through fractional-order differentiation, while retaining the low-frequency components [19]. The fractional-order integral filter smooths the signal through fractional-order integration and suppresses high-frequency noise. Fractional-order filters convert signals to the frequency domain through Fourier transform, apply fractional-order differentiation or integration operators, and then inverse-transform back to the time domain. The implementation in the time domain is obtained by discretizing fractional-order differentiation and integration. Namely, a two-dimensional Otsu threshold segmentation algorithm based on the improved CS is designed. The CS algorithm is a biomimetic biological intelligent optimization algorithm that effectively solves the optimal problem by simulating the parasitic brooding of cuckoo birds. The transformation and updating of the nest position can achieve the optimal position of the parasitic nest [20]. Eq. (9) is the updated the position of cuckoos.

(9) X k t + 1 = X k t + α 0 ⊗ Levy ( β ) ( X k t − X best ) ( k = 1 , 2 , 3 , . . . , n ) ,

where X k t + 1 represents the candidate solution, X k t represents the current solution, ⊗ represents the point-to-point multiplication, α 0 is the step size control factor, Levy ( β ) represents the Levi’s flight, and X best represents the optimal solution. In the CS algorithm, cuckoo can add new solutions according to the random preference walk strategy. The CS algorithm process is illustrated in Figure 3.

Figure 3

CS algorithm flow diagram.

In Figure 3, after inputting the initial parameters and relevant boundary conditions, the initial value can be solved. The steps of Levy flight and preference random walk can be executed until the global optimal position and optimal value are output. However, the updated cuckoo individuals are more prone to getting stuck in local optima problems. The flight mechanism of the CS algorithm may experience occasional large jumps after multiple gatherings. Therefore, the study improves the CS algorithm through the genetic and memory properties of fractional calculus and applies the fractional differential G–L to the Levy flight mechanism to update the position. Eq. (10) is the updated position:

(10) X k t + 1 − X k t = α 0 Levy ( β ) ( X k t − X best ) ( k = 1 , 2 , 3 , . . . , n ) ,

where X k t + 1 − X k t can be represented as a difference of order 1. G–L can redefine and generalize the order derivatives of functions, expanding the boundaries of calculus. The first four terms defined by G–L are selected to express Levi’s flight, as shown in Eq. (11):

(11) X k t + 1 = α X k t + 1 2 α ( 1 − α ) X k t − 1 + 1 6 α ( 1 − α ) ( 2 − α ) X k t − 2 + 1 24 α ( 1 − α ) ( 2 − α ) ( 3 − α ) X k t − 3 + α 0 Levy ( β ) ( X k t − X best ) .

Meanwhile, the position information of cuckoo birds is used to adaptively adjust the fractional order. The evolutionary factor is introduced to dynamically adjust the algorithm. The factor is displayed in Eq. (12):

(12) f = d g − d min d max − d min ,

where f represents the evolutionary factor, d g signifies the average distance between the global optimal solution and other individuals, and d max and d min signify the maximum and minimum values of the interclass distance. Considering that fractional-order values greater than 0.5 can cause the algorithm to converge too quickly, Eq. (13) is used to constrain the order:

(13) α ( f ) = 0.5 α e − 0.47 ,

where e is the base of the natural logarithm function. The process of image segmentation algorithm is displayed in Figure 4.

Figure 4

Image segmentation algorithm flow.

In Figure 4, the population needs to be initialized. The dispersion and objective function values of the segmented image need to be calculated. Based on the sorting results, the initial optimal solution position and resolution are obtained. Then, the improved Levy flight mechanism is executed, and the position update and resolution are achieved through random walk preference. After the iteration process is completed, the best threshold obtained can be used for image segmentation. The image segmentation process is implemented using the threshold of the individual’s optimal position. The output image ends the process.

4 Analysis of image segmentation results

The experimental environment for the research is Intel(R) Core (TM) i5-8300H CPU @ 2.30 GHz, with 16GB of memory. The system is Windows 10 (64 bit) Professional Edition, and the software is MATLAB R2016a (64 bit). The study selects different types of images from Pascal VOC dataset, USI-SIPI image database of the University of California, and Biomedical Imaging International Symposium Competition database, including people, landscapes, scenes, and medicine. Each image has a resolution of 512 × 512 pixels and a size of 256*256. The study selects indicators such as fitness value, peak signal-to-noise ratio, and structural similarity index to objectively evaluate the quality of image segmentation. The proposed method is compared with lightweight Attention Convolutional Neural Network (ACNN), Multi-Modal Feature Fusion Algorithm (RGB-D Attention, RGB-DA), Fractional Pigeon-Inspired Optimization (FPIO-Otsu), and spatial information Adaptive Fuzzy Clustering (AFC). Composite and mixed functions from the CEC20217 benchmark dataset are selected for testing. Figure 5 displays the fitness results.

Figure 5

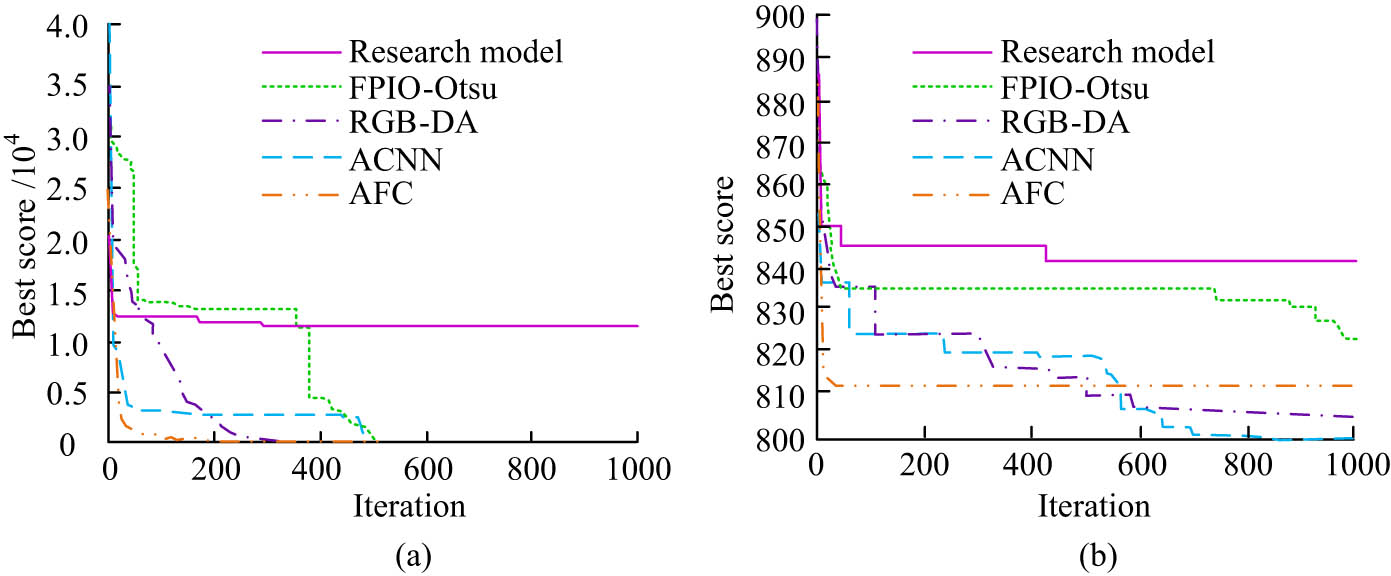
Fitness results of different algorithms: (a) composite function and (b) mixed function.

In Figure 5(a), on the composite function, the proposed algorithm had a slow curve descent rate in finding the optimal value, converging to 1.3 × 10⁴. The fitness curves of other comparison algorithms had different fluctuations, and there was a break in the curve after more than 600 iterations. The optimal values of AFC and ACNN algorithms were less than 0.53 × 10⁴. In Figure 5(b), when the iteration was greater than 200, the curves with good fitness performance were research model > FPIO-Otsu algorithm > RGB-DA algorithm > ACNN algorithm > AFC algorithm. The loss and error during image feature segmentation of the aforementioned algorithms are analyzed. The results are shown in Figure 6.

Figure 6

Data loss and error during image segmentation processing: (a) loss situation and (b) error situation.

In Figure 6(a), the proposed algorithm showed a relatively small loss value on the loss data and remained stable in the later stages of iteration, with a loss value of less than 5 × 10². The number of iterations required for the loss curve of other comparison algorithms to converge was generally greater than 400, with an average loss value greater than 5 × 10². In Figure 6(b), the image feature segmentation error curves of the five algorithms showed a decreasing trend with the increase of iterations. The error value of the proposed algorithm tended to the average value of 0.56 after more than 200 iterations. The FPIO-Otsu algorithm performed second only to the research algorithm, with an error value of less than 0.65. The worst-performing AFC algorithm had an average error value greater than 0.70. The image segmentation accuracy for the aforementioned algorithms is shown in Table 1.

Table 1

Image segmentation accuracy under different algorithm processing

Image type	Model	Accuracy rate (%)	Recall (%)	F1
Character image	Research algorithm	94.33	96.15	97.02
	FPIO-Otsu	92.26	93.22	92.28
	RGB-DA	90.15	89.39	89.61
	ACNN	85.33	88.42	87.11
	AFC	82.25	86.13	83.38
Landscape image	Research algorithm	95.02	97.14	96.65
	FPIO-Otsu	91.15	90.33	91.38
	RGB-DA	87.98	87.22	88.01
	ACNN	80.24	83.26	82.21
	AFC	87.22	88.13	87.34
Scene image	Research algorithm	92.74	90.92	92.11
	FPIO-Otsu	90.78	92.82	91.67
	RGB-DA	86.92	89.74	90.96
	ACNN	82.93	84.87	83.82
	AFC	81.16	85.32	84.53
Medical imaging	Research algorithm	90.25	90.24	90.09
	FPIO-Otsu	84.32	87.16	88.38
	RGB-DA	80.35	82.29	81.24
	ACNN	74.23	75.23	76.23
	AFC	75.23	76.23	77.23

In Table 1, the proposed algorithm demonstrated a feature recognition accuracy of over 90% for all four types of image segmentation, with recall rates of 96.15, 97.14, 90.92, and 90.24%, respectively. The FPIO-Otsu algorithm and RGB-DA algorithm performed better, with an overall accuracy of over 80% for image feature classification and over 85% for segmentation accuracy on character and landscape images, indicating their good processing effect on images with clear features. The AFC algorithm performed the worst in image segmentation accuracy, with segmentation accuracy and recall of 75.23 and 76.23% on medical images, respectively. On character and landscape images, the maximum segmentation accuracy difference among the five algorithms did not exceed 15%, while the difference was obvious on scene and medical images. In comparison algorithms, the single segmentation method is difficult to ensure image details, and the recognition effect is slightly worse than the segmentation algorithms proposed in the research. For example, the FPIO-Otsu algorithm utilizes intelligent algorithm and threshold solving idea for image segmentation. Although it has good segmentation accuracy, its accuracy is less than 90% when processing medical images due to not considering thresholds. The average running time of image segmentation is analyzed, as displayed in Table 2.

Table 2

Average running time (s) of image segmentation using different algorithms

Image type	Model	Number of thresholds
Image type	Model	3	4	5
Character image	Research algorithm	1.62044	1.67633	1.45733
	FPIO-Otsu	1.70022	1.71933	1.56877
	RGB-DA	1.72466	2.53712	1.64712
	ACNN	1.70523	2.60322	1.69912
	AFC	1.72512	2.62071	1.77491
Landscape image	Research algorithm	1.62622	1.70278	1.49922
	FPIO-Otsu	1.74122	1.73422	1.55967
	RGB-DA	1.72678	2.55011	1.66967
	ACNN	1.71933	2.60711	1.73311
	AFC	1.80689	2.62622	1.26822
Scene image	Research algorithm	1.69825	1.70955	1.89922
	FPIO-Otsu	1.73088	1.77333	1.56788
	RGB-DA	1.74444	1.89155	1.99211
	ACNN	1.77444	1.96411	1.88211
	AFC	1.81478	2.05633	1.90055
Medical imaging	Research algorithm	1.52922	1.69933	1.25733
	FPIO-Otsu	2.68855	2.53712	2.56877
	RGB-DA	2.71844	2.67289	2.64712
	ACNN	2.82733	2.70088	2.69912
	AFC	2.85133	2.78522	2.77491

In Table 2, the average running time of the proposed algorithm for image segmentation was lower than other comparison algorithms under the same conditions. Its running time did not exceed 2 s at different threshold numbers, while other algorithms showed more significant changes in running time, with an average running time of over 2s on medical images. The aforementioned results indicate that the proposed algorithm has good processing efficiency. Subsequently, further analysis is conducted on the image segmentation quality, as displayed in Table 3.

Table 3

Evaluation of image segmentation quality under different algorithms

Algorithm	Information entropy	Structural similarity	Mean contrast	Peak signal-to-noise ratio	Brightness relationship factor (%)	Mutual information
AFC	7.658	0.817	1.547	1.352	0.758	6.028
ACNN	7.691	0.824	1.751	1.161	0.804	7.094
RGB-DA	7.805	0.845	1.069	1.341	0.825	6.436
FPIO-Otsu	7.626	0.877	1.495	1.585	0.901	7.385
Research algorithm	7.962	0.912	1.825	2.194	0.934	9.192

In Table 3, the information entropy, structural similarity, contrast mean, peak signal-to-noise ratio, brightness relationship factor, and mutual information of the proposed segmentation algorithm were 7.962, 0.912, 1.825, 2.194, 0.934, and 9.192, respectively. Its overall image segmentation quality was significantly better than other algorithms. The FPIO-Otsu algorithm performed well next. The structural similarity values of the RGB-DA algorithm, ACNN algorithm, and AFC algorithm were 0.845, 0.824, and 0.817, respectively, indicating poor feature extraction performance of the background and target images during image segmentation. Its brightness relationship factor was also less than 0.85, indicating that there may be some information loss. The proposed algorithm exhibits good segmentation accuracy, and the quality evaluation index values are much higher than other algorithms under the same conditions. Table 4 shows the pixel segmentation results of the image.

Table 4

Pixel segmentation results of different algorithms for image segmentation

Algorithm	Pixel accuracy (%)	Average pixel accuracy (%)	Average IoU (%)
AFC	88.32	75.46	62.38
ACNN	89.15	77.39	64.51
RGB-DA	90.06	82.35	71.35
FPIO-Otsu	91.78	85.13	72.33
Research algorithm	94.33	88.76	79.25

Pixel accuracy can reflect the proportion of correctly classified pixels, with a higher value indicating better segmentation performance. Intersection over union (IoU) can reflect the proportion of the segmented area to the real area, with a higher value indicating better model performance. In Table 4, the pixel accuracy, average pixel accuracy, and average IoU of the research algorithm were 94.33, 88.76, and 79.25%, which exceeded other comparison algorithms. The average pixel accuracy and average IoU of the AFC algorithm and the ACNN algorithm were lower than 80 and 65%, respectively, indicating poor segmentation performance. Subsequently, FPIO-Otsu algorithm and RGB-DA algorithm with good performance are selected for image segmentation instance verification and compared with the segmentation algorithm proposed in the study. The results are displayed in Figure 7.

Figure 7

Retinal vascular segmentation results. Original image: (a) research model, (b) FPIO-Otsu, and (c) RGB-DA.

In Figure 7, the proposed algorithm had good segmentation performance. It could capture the details of some blood vessel extensions well. The FPIO-Otsu algorithm utilized the pigeon swarm algorithm and fractional-order thinking to solve problems, but there was oversegmentation in the central part. The continuity in details was insufficient, resulting in slightly lower segmentation accuracy than the research algorithm. The RGB-DA algorithm performed segmentation based on image characteristics, making it difficult to extract vascular edges. Figure 8 shows the segmentation results of indoor and outdoor scene images.

Figure 8

Image segmentation results of indoor and outdoor scenes: (a) indoor scene and (b) outdoor scene.

In Figure 8(a), the proposed model could effectively segment different objects with clear detail processing and distinct feature differentiation. However, the other two algorithms exhibited information loss and target blurring during image segmentation. In Figure 8(b), the other two comparison algorithms had poor segmentation performance for vehicle shape and pedestrian contour, while the proposed model could better reflect the image situation and perform well in segmentation accuracy.

5 Conclusion

To address the shortcomings of traditional swarm intelligence algorithms in image segmentation, a new method combining TC algorithm and swarm intelligence algorithm for image segmentation was designed and tested. From the results, the loss value in image feature segmentation was less than 5 × 10². The error value tended to 0.56 after more than 200 iterations. However, the error curves of other comparison algorithms had fluctuations, with the worst-performing AFC algorithm having an average error value greater than 0.70. The algorithm proposed in the study showed feature recognition accuracy of over 90% in four types of image segmentation: character, landscape, scene, and medical. The FPIO-Otsu algorithm and RGB-DA algorithm performed better, with an overall accuracy of over 80% for image feature classification. The running time of the research algorithm under different threshold numbers did not exceed 2 s, which was much shorter than other comparison algorithms under the same conditions. The information entropy, structural similarity, contrast mean, peak signal-to-noise ratio, brightness relationship factor, and mutual information of the research algorithm reached 7.962, 0.912, 1.825, 2.194, 0.934, and 9.192, respectively. Its overall image segmentation quality was significantly better than other algorithms. The structural similarity values of RGB-DA algorithm, ACNN algorithm, and AFC algorithm were 0.845, 0.824, and 0.817, respectively, indicating poor feature extraction performance of the background and target images during image segmentation. Their brightness relationship factor was also less than 0.85, indicating that there may be some information loss. The pixel accuracy, average pixel accuracy, and average IoU of the research algorithm were 94.33, 88.76, and 79.25%, respectively, which were much higher than other comparison algorithms. Moreover, its segmentation details and edge extraction effects on medical images and scene images were significant. The FPIO-Otsu algorithm and RGB-DA algorithm exhibited information loss and target blurring during image segmentation. The improvement proposed by combining image segmentation with swarm intelligence algorithms can effectively improve segmentation quality and ensure algorithm convergence and solving speed. With the advancement of image processing technology, strengthening the research on segmentation accuracy of multi-target images and dynamic video images is an important focus in the future.

Funding information: The author states no funding involved.
Author contributions: The author has accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The author states no conflict of interest.
Data availability statement: All data generated or analyzed during this study are included in this published article.

References

[1] Minaee S, Boykov Y, Porikli F, Plaza A, Kehtarnavaz N, Terzopoulos D. Image segmentation using deep learning: A survey. IEEE Trans Pattern Anal Mach Intell. 2021;44(7):3523–42.10.1109/TPAMI.2021.3059968Suche in Google Scholar PubMed

[2] Yu Y, Wang C, Fu Q, Kou R, Huang F, Yang B, et al. Techniques and challenges of image segmentation: A review. Electronics. 2023;12(5):1199.10.3390/electronics12051199Suche in Google Scholar

[3] Wang R, Lei T, Cui R, Zhang B, Meng H, Nandi AK. Medical image segmentation using deep learning: A survey. IET Image Process. 2022;16(5):1243–67.10.1049/ipr2.12419Suche in Google Scholar

[4] Pal R, Mukhopadhyay S, Chakraborty D, Suganthan PN. Very high-resolution satellite image segmentation using variable-length multi-objective genetic clustering for multi-class change detection. J King Saud Univ Comput Inf Sci. 2022;34(10):9964–76.10.1016/j.jksuci.2021.12.023Suche in Google Scholar

[5] Khrissi L, El Akkad N, Satori H, Satori K. Clustering method and sine cosine algorithm for image segmentation. Evol Intell. 2022;15(1):669–82.10.1007/s12065-020-00544-zSuche in Google Scholar

[6] Chowdhary CL, Mittal M, Kumaresan P, Pattanaik PA, Marszalek Z. An efficient segmentation and classification system in medical images using intuitionist possibilistic fuzzy C-mean clustering and fuzzy SVM algorithm. Sensors. 2020;20(14):3903.10.3390/s20143903Suche in Google Scholar PubMed PubMed Central

[7] Liu Y, Zhang Z, Liu X, Wang L. Efficient image segmentation based on deep learning for mineral image classification. Adv Powder Technol. 2021;32(10):3885–903.10.1016/j.apt.2021.08.038Suche in Google Scholar

[8] Zhang X, Bian H, Cai Y, Zhang K, Li H. An improved tongue image segmentation algorithm based on Deeplabv3 + framework. IET Image Process. 2022;16(5):1473–85.10.1049/ipr2.12425Suche in Google Scholar

[9] Vadivel T, Suguna R. Retracted Article: Automatic recognition of tomato leaf disease using fast enhanced learning with image processing. Acta Agric Scand B Soil Plant Sci. 2022;72(1):312–24.10.1080/09064710.2021.1976266Suche in Google Scholar

[10] Stringer C, Wang T, Michaelos M, Pachitariu M. Cellpose: A generalist algorithm for cellular segmentation. Nat Methods. 2021;18(1):100–6.10.1038/s41592-020-01018-xSuche in Google Scholar PubMed

[11] Sharma A, Chaturvedi R, Bhargava A. A novel opposition based improved firefly algorithm for multilevel image segmentation. Multimed Tools Appl. 2022;81(11):15521–44.10.1007/s11042-022-12303-6Suche in Google Scholar

[12] Resma KB, Nair MS. Multilevel thresholding for image segmentation using Krill Herd Optimization algorithm. J King Saud Univ Comput Inf Sci. 2021;33(5):528–41.10.1016/j.jksuci.2018.04.007Suche in Google Scholar

[13] Dhal KG, Das A, Ray S, Gálvez J, Das S. Nature-inspired optimization algorithms and their application in multi-thresholding image segmentation. Arch Comput Methods Eng. 2020;27(3):855–88.10.1007/s11831-019-09334-ySuche in Google Scholar

[14] Wang M, Wang W, Feng S, Li L. Adaptive multi-class segmentation model of aggregate image based on improved sparrow search algorithm. KSII Trans Internet Inf Syst. 2023;17(2):391–411.10.3837/tiis.2023.02.006Suche in Google Scholar

[15] Nyo MT, Mebarek-Oudina F, Hlaing SS, Khan NA. Otsu’s thresholding technique for MRI image brain tumor segmentation. Multimed Tools Appl. 2022;81(30):43837–49.10.1007/s11042-022-13215-1Suche in Google Scholar

[16] Rawas S, El-Zaart A. Precise and parallel segmentation model (PPSM) via MCET using hybrid distributions. Appl Comput Inf. 2024;20(3/4):262–78.10.1108/ACI-11-2020-0123Suche in Google Scholar

[17] Mokayed H, Quan TZ, Alkhaled L, Sivakumar V. Real-time human detection and counting system using deep learning computer vision techniques. Artif Intell Appl. 2023;1(4):221–9.10.47852/bonviewAIA2202391Suche in Google Scholar

[18] Huang G, Qin H, Chen Q, Shi Z, Jiang S, Huang C. Research on application of fractional calculus operator in image underlying processing. Fractals. 2024;8(1):37.10.3390/fractalfract8010037Suche in Google Scholar

[19] Arora S, Mathur T, Agarwal S, Tiwari K, Gupta P. Applications of fractional calculus in computer vision: A survey. Neurocomputing. 2022;489:407–28.10.1016/j.neucom.2021.10.122Suche in Google Scholar

[20] Wu J, Wu C, Lin Y, Yoshinaga T, Zhong L, Chen X, et al. Semantic segmentation-based semantic communication system for image transmission. Digit Commun Netw. 2024;10(3):519–27.10.1016/j.dcan.2023.02.006Suche in Google Scholar

Received: 2024-12-13

Revised: 2025-03-31

Accepted: 2025-05-12

Published Online: 2025-08-30

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

https://doi.org/10.1515/nleng-2025-0152

Schlagwörter für diesen Artikel

threshold segmentation; differential evolution; cuckoo algorithm; fractional calculus; image segmentation; quality evaluation

Creative Commons

BY 4.0