Cross-scale modeling and collaborative optimization of ethanol-catalyzed coupling to produce C4 olefins: Nonlinear modeling and collaborative optimization strategies

Jiayang Xiao; Kaijia Luo; Junnan Zhong

doi:10.1515/nleng-2025-0167

Article Open Access

Cross-scale modeling and collaborative optimization of ethanol-catalyzed coupling to produce C₄ olefins: Nonlinear modeling and collaborative optimization strategies

Jiayang Xiao , Kaijia Luo and Junnan Zhong

Published/Copyright: September 23, 2025

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Nonlinear Engineering Volume 14 Issue 1

Abstract

This study uses nonlinear modeling methods to construct a complete modeling framework that integrates univariate quadratic regression, orthogonal experimental design, and multivariate polynomial regression based on 147 sets of multi-catalyst experimental data and dynamic time-series data. This study first revealed the nonlinear influence of temperature on the ethanol conversion rate and C₄ olefin selectivity using a quadratic model. Then, the main effects of factors such as the Co loading, charge ratio, and ethanol concentration were quantified using an orthogonal experimental system. Finally, a standardized multivariate interaction model was constructed to deeply analyze the physical meaning of interaction terms such as temperature, Co loading, and charge ratio. The results show that the root mean square error of the model on the test set is less than 1.14%, and the coefficient of determination (R ²) is higher than 0.937, demonstrating good generalization ability and engineering applicability. This study presents a digital modeling paradigm with explanatory power, predictive power, and scalability based on nonlinear engineering for the mechanism elucidation and industrial processes of complex catalytic reaction systems.

Keywords: ethanol catalytic coupling; C4 olefin; binary quadratic regression

1 Introduction

Driven by the dual carbon strategy, constructing a high-value olefin production pathway using bioethanol as a raw material has become an important development direction for the green chemical industry. As the basic raw material for synthesizing rubber and plastics, the selectivity and yield of olefins are complexly influenced by the microstructure of the catalyst (such as the Co active site density, carrier acidity, and alkalinity) and macroscopic reaction conditions (such as temperature and ethanol concentration). However, most existing studies have limitations, including a focus on the impact of a single reaction factor on the reaction performance, the absence of quantitative interaction models, the complexity of catalyst components, and a disconnect between data-driven and mechanistic approaches. Adamczyk et al. studied alcohol catalytic reductive coupling in green synthesis, investigating monometallic intermediate formation via vanadium aminopyridinate separation and kinetics, aiding reaction optimization and atomic economy [1]. Joshi and Bollini tested ethanol catalytic conversion in a Cu/SiO₂–ZrO₂ segregated bed, focusing on target product selectivity for multi-functional cascades to support efficient low-carbon processes [2]. Tian et al. fitted ethanol selectivity with the Flory–Huggins model (1.6% deviation) but lacked mechanistic explanations, hindering low-carbon catalytic system design and revealing a gap between theory and application [3].

The main contributions of this study include the following: (1) starting from single factor nonlinear modeling (temperature performance relationship), this study gradually expands to multifactor orthogonal experiments and multivariate interaction modeling, forming a cross-scale model system of “data mechanism fusion”; (2) using multiple polynomial regression, standardized regression coefficients, and interaction term analysis, quantitatively reveal the main effects and coupling effects of factors such as temperature, Co loading, and loading ratio; (3) based on the demand for green energy transformation, this study focuses on the nonlinear coupling problem in the ethanol coupling reaction and proposes a high-order modeling scheme that emphasizes both data-driven and mechanism interpretation.

The structure of this article is as follows: Section 1 introduces the background of the research on the ethanol catalytic coupling reaction, elaborates on its importance in the chemical industry, sorts out the research status in the reaction mechanism, catalyst research and development, points out the shortcomings of existing research, and then outlines the research contribution of this article. Section 2 is the methodology, which elaborates on the construction process of the kinetic model for the ethanol catalytic coupling reaction, explains the mechanism of genetic algorithm for parameter optimization, and explains the basis for selecting the neural network structure design and training methods. Section 3 is the experiment, which describes the sources and preprocessing process of 147 sets of multicatalyst experimental data and dynamic time-series data, constructs a univariate quadratic regression model and tests it, uses the controlled variable method to analyze the single-factor influence, an orthogonal experiment to analyze the multifactor coupling effect, and constructs a multivariate polynomial regression model. Section 4 is the results, summarizing the parameter values of the model under different conditions, analyzing the accuracy and reliability of the model, and demonstrating the degree of fitting under typical reaction conditions. Section 5 is the conclusion, summarizing the effectiveness of the constructed model in predicting the distribution of products and reaction rates in ethanol catalytic coupling reactions, and pointing out the limitations of the model. It proposes future research directions, including introducing multiphysics field coupling to extend the model.

2 Materials and methods

The ethanol catalytic coupling reaction is a complex system involving multistep elementary reactions, which include the key step of ethanol dehydrogenation to acetaldehyde under the action of the catalyst active sites. The rate constant k 1 corresponding to this step is significantly affected by factors such as temperature, catalyst type, and activity [4]. Subsequently, the generated acetaldehyde molecules are converted into C 4 olefins through coupling reactions under specific reaction conditions and catalytic environments (rate constant k 2 ). As the reaction progresses, the generated alkenes undergo further deep dehydrogenation reaction (rate constant k 3 ), resulting in the formation of alkynes. According to the classical Arrhenius equation,

(1) k i = A i e − E a , i RT .

There is an exponential relationship between the reaction rate constant and temperature. The above equation not only reveals the quantitative effect of temperature on the reaction rate but also indicates that the reaction rate constant is closely related to the activation energy and pre-exponential factor, providing an important theoretical basis for a deeper understanding of the reaction kinetics of each step in ethanol-catalyzed coupling reactions [5]. At low temperatures where k 2 ≫ k 3 selectivity increases with increasing temperature. At high temperatures, the k 3 growth rate exceeds the k 2 limit, leading to a decrease in selectivity, thus exhibiting a quadratic relationship with temperature. The conversion rate of ethanol is dominated by the total reaction rate, which is the sum of ( k 1 + k 2 + k 3 ) . At high temperatures, the molecular kinetic energy increases, and the conversion rate tends to stabilize, following the convex characteristics of a quadratic curve.

Orthogonal tables L n ( m k ) satisfy orthogonality (uniform distribution of factors at all levels) and representativeness (effective sampling for comprehensive experiments) [6]. For example, each level of L 9 ( 3 4 ) factor appeared three times in nine trials, and any combination of two factors appears once. By calculating the range R 2 and variance values F of each factor, the significance of the factor can be determined:

(2) F = SS factor SS error ⋅ ( n − m ) ( m − 1 ) .

Here, SS factor is the sum of squares of factors and SS error is the sum of squares of errors.

Due to significant differences C _o in the load (wt%), temperature (°C), ethanol concentration (mL/min), and other parameters, standardization is necessary.

(3) x i ⁎ = x i − μ i σ i , y ⁎ = y − μ y σ y .

The standardized regression coefficient β i ⁎ represents the change in the response variable per unit of standard deviation for every 1 standard deviation change in the independent variable, making it easier to directly compare the magnitude of the influence of the factor.

2.1 Dataset source and preprocessing

The dataset in this article is taken from https://www.mcm.edu.cn. A total of 147 samples were collected, covering multiple catalyst combinations and temperatures, covering 21 catalyst combinations and 7 temperature levels (250–450°C). Each set of data contains multiple experimental factors (Co loading, loading ratio, mass, ethanol concentration, etc.) and output indicators (ethanol conversion rate, C 4 olefin selectivity, etc.) for constructing static regression models. Twenty-one combinations were divided into A1–A14 and B1–B7, where A and B represent different loading methods.

The data on the time-resolved reaction performance of a specific catalyst combination (Co 1 wt%, and loading ratio 1:1) at 350°C includes seven time nodes, multiple product selectivity, and conversion rates, which are used to analyze the reaction kinetic characteristics and reactor equilibrium trends. The dataset covers multiple sets of catalysts and multidimensional variable combinations, with good representativeness and structures, providing a solid data foundation for model construction.

Based on the 3σ criterion, outliers were removed, and linear interpolation was implemented to effectively avoid the interference of extreme values on the stability of the model [7]. For the ethanol conversion rate sequence of each catalyst group { α 0 , i } , if a certain point satisfies ∣ α 0 , i − μ ∣ > 3 σ , it is considered an outlier. For the identified abnormal data points, the nearest-neighbor linear interpolation method was used to repair them and maintain the continuity of the data trend. Eight abnormal data points were found and corrected in the static group, while no abnormalities were detected in the dynamic group.

Continuous variables were standardized and unified (temperature, mass, ethanol concentration, etc.) in the dataset using the Z-score. One hot encoding was performed on binary variables (HAP usage, loading method) and then converted them into 0–1 dummy variables [8].

2.2 Construction and testing of a univariate quadratic regression model

There is a correlation between the ethanol conversion rate α 0 and temperature T:

(4) α 0 = β 0 + β 1 T 2 + β 2 T .

Here, β 0 , β 1 , β 2 are unknown parameters, called the regression coefficients or regression parameters, T is the temperature, which is a measurable and controllable variable, called regression factor or predictor variable, and α 0 is the response variable. If there are n observations T i , i = 1 , 2 , … n , then this observation value can be written in the following form:

(5) α 01 = β 0 + β 1 T 1 2 + β 2 T 1 α 02 = β 0 + β 1 T 2 2 + β 2 T 2 ⋯ α 0 n = β 0 + β 1 T n 2 + β 2 T n .

Similarly, a univariate polynomial regression model can be obtained between the selectivity of C 4 olefins and temperature T. That is, it is only necessary to replace the corresponding components α 01 , α 02 , …, α 0 n , in the T model with α 1 , α 11 , α 12 , …, α 1 n , and change the unknown parameters from β 0 , β 1 , and β 2 to γ 0 , γ 1 , and γ 2 .

In summary, a univariate polynomial regression model between the ethanol conversion rate a 0 and temperature T, and a univariate polynomial regression model between the C₄ olefin selectivity a 1 and temperature T were established:

(6) α 0 t = β 0 + β 1 T t 2 + β 2 T t , i = 1 , 2 , … , n α 1 t = γ 0 + γ 1 T t 2 + γ 2 T t , i = 1 , 2 , … , n .

In formula (6), β 0 / γ 0 is the intercept term, β 1 / γ 1 is the linear coefficient, β 2 / γ 2 is the quadratic coefficient, reflecting temperature sensitivity, α 0 i is the ethanol conversion rate at the i-th temperature, α 1 i is the selectivity of C 4 olefins at the ith temperature, β 0 , γ 0 , γ 1 , γ 2 are unknown parameters, and T i is its ith temperature.

Next, model construction was carried out: a univariate quadratic model was established for each of the 21 catalysts to describe α ₀(T) and α ₁(T), and the models were ensured to have physical rationality and statistical stability through grouping, fitting, and parameter significance testing. For solving parameters, Matlab’s Curve Fitting toolbox was used for fitting and performing significance testing and the goodness of fit of the model was evaluated using p-test and R ²:

(7) min β 1 , β 2 , β 3 ∑ i = 1 n ( α 0,1 − ( β 0 + β 1 T i 2 + β 2 T i ) ) 2 .

To perform significance test, the goodness of fit of the model was evaluated using an F-test and R 2 [9].

2.3 Analytical method for reaction performance under multifactor coupling

The grouping design based on the control variable method in the above univariate regression model allows for a clear analysis of the independent effects of each catalyst factor.

The ethanol concentration, Co loading amount, Co/SiO₂ and HAP loading ratio, the sum of the mass of Co/SiO₂ and HAP, the use of quartz sand or HAP catalyst, and the loading method were controlled separately, and then the trends of α 0 and α 1 with T were observed.

2.4 Construction of a multivariate polynomial regression model

Given the interaction between factors in the experimental data (such as the synergistic effect of the Co loading amount and loading ratio), a multivariate quadratic regression model is constructed, which includes seven factors, including the temperature (T), ethanol concentration X 2 , Co loading amount, and pairwise interaction terms:

(8) y = β 0 ⁎ + β 1 ⁎ T ⁎ + β 2 ⁎ X 1 ⁎ + β 3 ⁎ X 3 ⁎ + β 13 ⁎ T ⁎ X 3 ⁎ + ⋯ .

To eliminate dimensional differences, the data were standardized:

(9) x i j ⁎ = x i j − x j ¯ L j j , y i ⁎ = y j − y j ¯ L y y .

Here, L j j = ∑ i = 1 n ( x i j − x j ¯ ) 2 is the sum of squared deviations of the independent variable, and L y y = ∑ i = 1 n ( y i − y j ¯ ) 2 is the sum of squared deviations of the response variable. The standardized model is

(10) y ⁎ = β 0 ⁎ + ∑ j = 1 7 β j ⁎ x j ⁎ + ∑ 1 ≤ i < j ≤ 7 β i j ⁎ x i ⁎ x j ⁎ .

Gradually, the variables were filtered using Matlab functions, insignificant terms were eliminates, and then solved to obtain the optimal model.

3 Results and discussion

3.1 Controlled variable comparative analysis

Using the Curve Fitting toolbox in MATLAB, the univariate polynomial regression equation was solved to obtain the coefficients of the univariate polynomial regression model between the ethanol conversion rate and temperature for 21 catalyst combinations, as well as the coefficients of the univariate polynomial regression model between C₄ olefin selectivity and temperature. Tables 1 and 2 show the regression coefficients for Group A and Group B, with six groups each.

Table 1

Regression model coefficients of the ethanol conversion rate and temperature

No. of catalyst groups	β ₀	β ₁	β ₂	R ²
1	145.3	0.0024	−1.143	0.9832
2	−226.6	−0.0006	1.112	0.9941
3	−133.8	−0.0004	0.6453	0.9838
4	−108.4	0.0004	0.3434	0.9969
5	233.2	0.0034	−1.653	0.9944
6	54.26	0.0016	−0.5812	0.9847
16	190.2	0.0027	−1.312	0.9916
17	107.6	0.0015	−0.774	0.9977
18	154.2	0.0017	−1.122	0.9877
19	184.9	0.0022	−1.373	0.9924
20	191.2	0.0026	−1.443	0.9912
21	226.5	0.0032	−1.712	0.9832

Table 2

Regression model coefficients of C₄ olefin selectivity and temperature

No. of catalyst groups	γ ₀	γ ₁	γ ₂	R ²
1	−192.83	−0.0045	1.4126	0.9864
2	232.78	0.0033	−1.6531	0.9851
3	−172.43	−0.0011	0.9621	0.9881
4	73.63	0.0014	−0.5124	0.9837
5	55.21	0.0013	−0.4953	0.9933
6	173.65	0.0021	−1.4170	0.9874
16	42.53	0.0011	−0.5180	0.9832
17	21.77	0.0007	−0.1813	0.9865
18	81.34	0.0008	−0.5162	0.9937
19	31.90	0.0007	−0.3002	0.9936
20	−12.21	0.0003	−0.0217	0.9824
21	−9.418	0.0005	−0.0610	0.9982

From Tables 1 and 2, it can be seen that the goodness of fit R ² is greater than 0.9824, indicating that regression can reduce the variation of the dependent variable by more than 98.24%. Therefore, from the coefficient of determination, it can be seen that the regression equation is highly significant and the regression effect is good. Four catalyst combinations, A1, A3, A8, and B2, are selected, and their regression function graphs are drawn, as shown in Figures 1 and 2.

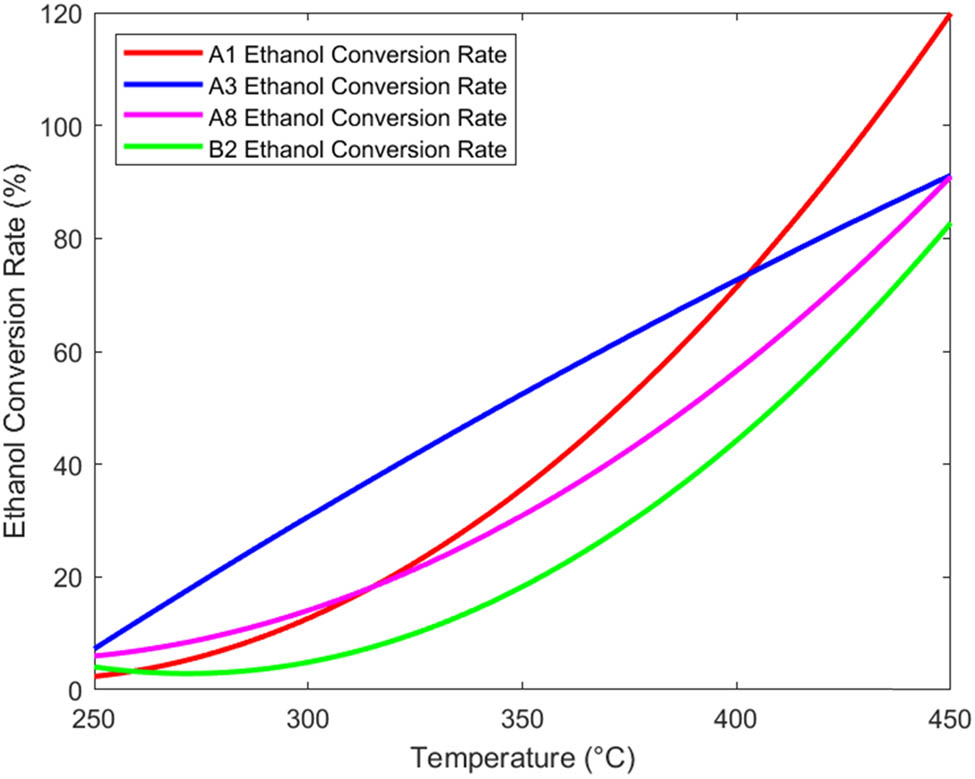
$Figure 1 α 0 − T {\alpha }_{0}-T variation curve.$

Figure 1

α 0 − T variation curve.

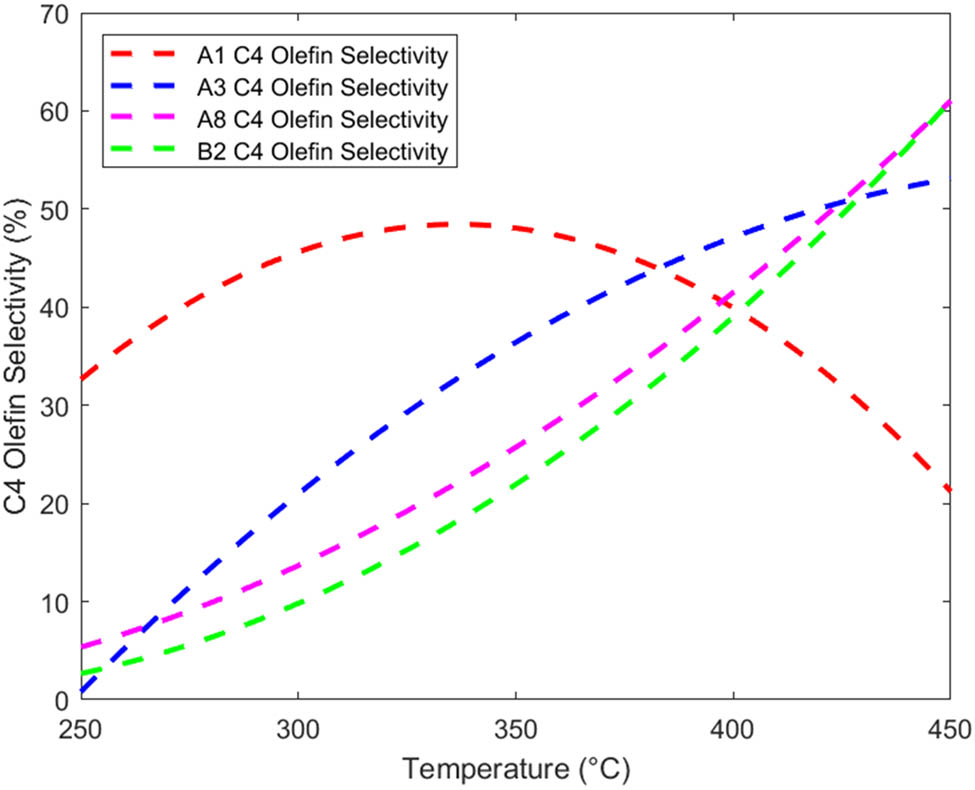
$Figure 2 α 1 − T {\alpha }_{1}-T variation curve.$

Figure 2

α 1 − T variation curve.

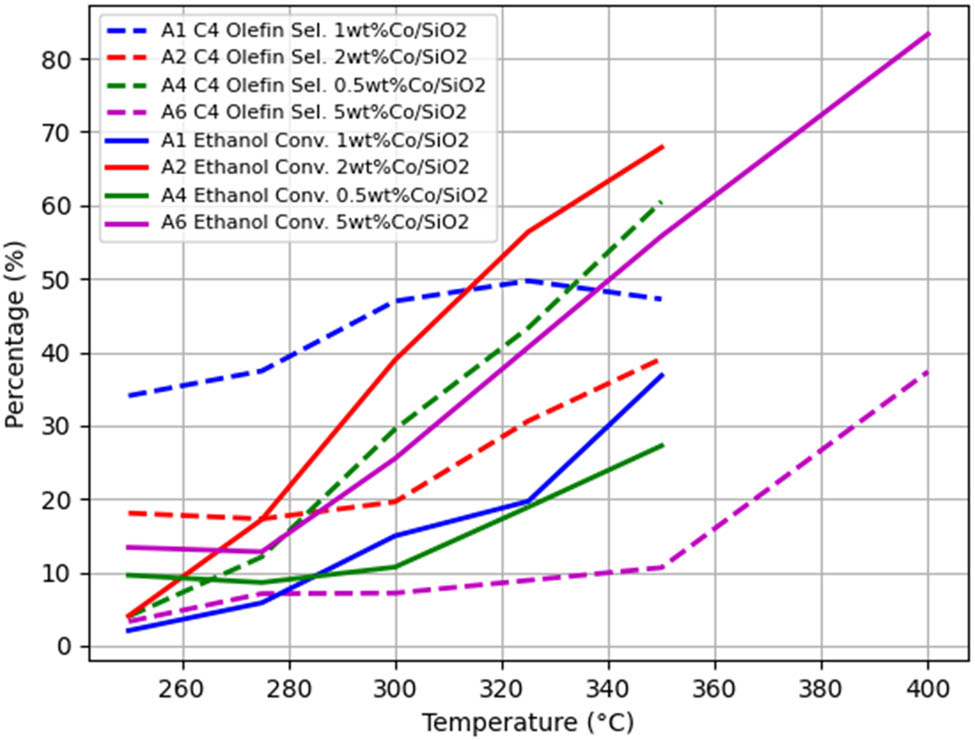
From Figures 1 and 2, within a certain range, the ethanol conversion rate and C₄ olefin selectivity both increase with increasing temperature. However, for the A1 and A3 catalyst combinations, excessive temperature may lead to a decrease in C₄ olefin selectivity [10].

Based on the actual chemical reactions and the data of the reaction, the performance changes with time at 350°C. The calculated C₄ hydrocarbon yield is divided into five categories: C₄ hydrocarbon selectivity, fatty alcohol selectivity (carbons 4–12), acetaldehyde selectivity, and ethanol conversion rate. The specific data of their changes with time are shown in Table 3. The yield of C₄ hydrocarbons is the product of the ethanol conversion rate and C₄ olefin selectivity.

Table 3

Data on a certain catalyst combination at 350°C

Time (min)	Ethanol conversion rate (%)	C₄ olefin selectivity (%)	Selection of fatty alcohols with carbons 4–12 (%)	Ethanol selectivity (%)	C₄ olefin yield (%)
20	43.5	39.9	39.7	5.17	17.37540804
70	37.8	38.55	37.36	5.6	14.56733047
110	36.6	36.72	32.39	6.37	13.42349545
163	32.7	39.53	31.29	7.82	12.93495022
197	31.7	38.96	31.49	8.19	12.35425379
240	29.9	40.32	32.36	8.42	12.03722565
273	29.9	39.04	30.86	8.79	11.67530575

Five types of data shown in Table 3, including C₄ olefin selectivity, fatty alcohol selectivity (carbons 4–12), ethanol conversion rate, acetaldehyde selectivity, and C₄ olefin yield, are plotted onto the same graph, as shown in Figure 3.

Figure 3

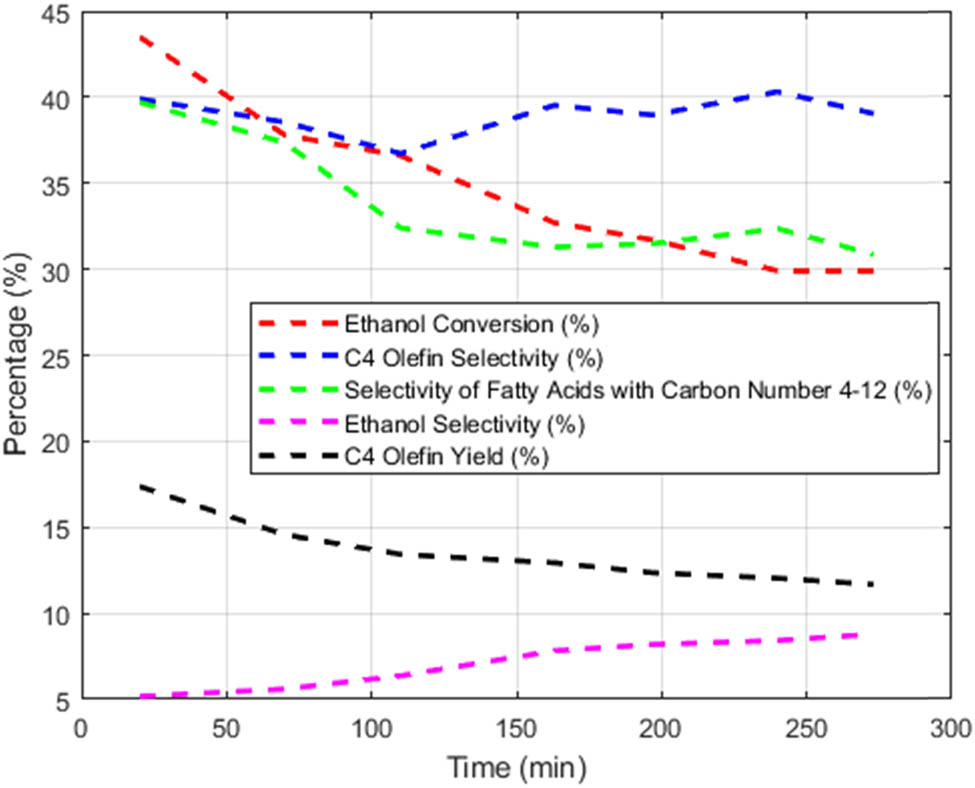
Time-dependent graph of five types of data.

As shown in Figure 3, it can be seen that as time increases, the selectivity of 4–12 fatty alcohols decreases while the selectivity of acetaldehyde increases, indicating that 4–12 fatty alcohols are involved in the generation of acetaldehyde. Ethanol conversion first increases and then gradually decreases. The trend of C₄ olefin selectivity over time is relatively stable, and the value is around 39%. The yield of C₄ olefins decreases continuously with the increase of time. In summary, as the reaction time increases, the selectivity of each product tends to stabilize; that is, the chemical reaction reaches an equilibrium state [11].

When other conditions remain unchanged and only the ethanol concentration is changed, the A1–A3, A2–A5, A7–A8–A9–A12, B1–B5, and B2–B7 groups were used as controls to obtain the temperature-dependent trends of the ethanol conversion rate and C₄ olefin selectivity, as shown in Figures 4–8.

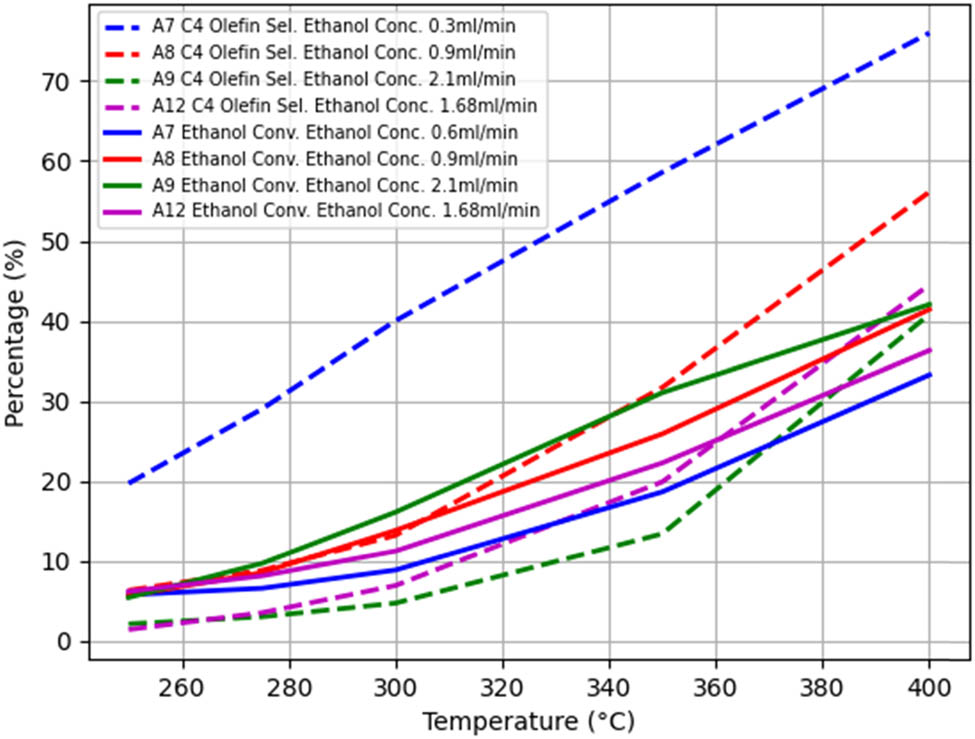
$Figure 4 The trend of changes in α 0 {\alpha }_{0} and α 1 {\alpha }_{1} with T in groups A7–A8–A9–A12 when only changing the ethanol concentration.$

Figure 4

The trend of changes in α 0 and α 1 with T in groups A7–A8–A9–A12 when only changing the ethanol concentration.

$Figure 5 Trends of α 0 {\alpha }_{0} and α 1 {\alpha }_{1} with T in the A1–A2–A4–A6 group when only changing the Co loading amount.$

Figure 5

Trends of α 0 and α 1 with T in the A1–A2–A4–A6 group when only changing the Co loading amount.

$Figure 6 Trends of α 0 {\alpha }_{0} and α 1 {\alpha }_{1} with T in the A12–A13–A14 group when only changing the Co/SiO2 and HAP loading ratios.$

Figure 6

Trends of α 0 and α 1 with T in the A12–A13–A14 group when only changing the Co/SiO₂ and HAP loading ratios.

$Figure 7 Trends of α 0 {\alpha }_{0} and α 1 {\alpha }_{1} variations with T for the A11–A12 groups when using quartz sand or HAP as catalysts.$

Figure 7

Trends of α 0 and α 1 variations with T for the A11–A12 groups when using quartz sand or HAP as catalysts.

$Figure 8 Trends of α 0 {\alpha }_{0} and α 1 {\alpha }_{1} with T in groups A9–B5 when only changing the loading method.$

Figure 8

Trends of α 0 and α 1 with T in groups A9–B5 when only changing the loading method.

Figure 4 shows that in the A7–A8–A9–A12 group, the higher the ethanol concentration, the lower the ethanol conversion rate, and the ethanol conversion rate gradually increases with increasing temperature. At the same temperature, the selectivity of C₄ olefins is highest at an ethanol concentration of 2.1 ml/min and lowest at 0.3 ml/min. As the temperature increases, the selectivity of C₄ olefins gradually increases.

As can be seen from Figure 5, at the same temperature, the ethanol conversion rate is highest when Co loading is 2 wt%, and the ethanol conversion rate gradually increases with the increase of temperature. At the same temperature, the selectivity of C₄ olefins is highest when Co loading is 1 wt%. The selectivity of C₄ hydrocarbons gradually increases with increasing temperature when Co loading is 2, 0.5, and 5 wt%. When Co loading is 1 wt%, the selectivity of C₄ olefins gradually increases at <325°C and shows a decreasing trend at >325°C [12].

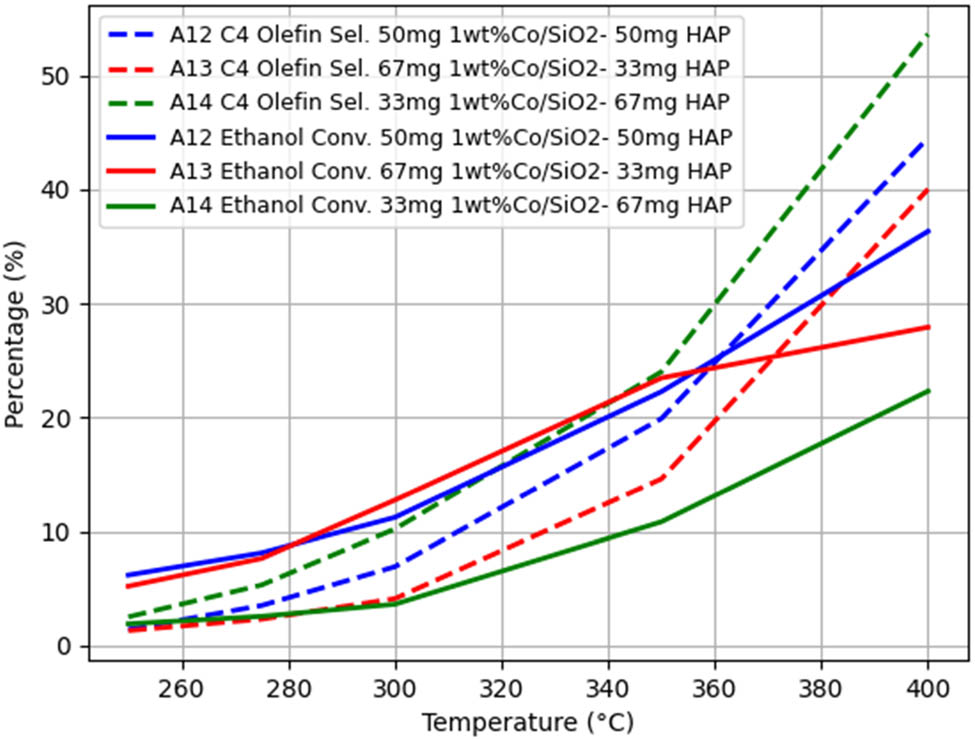
All other conditions being the same, when only changing the Co/SiO₂ and HAP loading ratios, the A12–A13–A14 group experiments were used as controls to obtain the temperature-dependent trends of ethanol conversion rate and C₄ hydrocarbon selectivity, as shown in Figure 6.

As illustrated by the curves in Figure 6, at the same temperature, the smaller the Co/SiO₂ and HAP loading ratios, the higher the ethanol conversion rate, and the ethanol conversion rate gradually increases with the increase of temperature. At the same temperature, the difference in C₄ olefin selectivity between loading ratios of 1 and 2 is not significant and is greater than the selectivity at a loading ratio of 0.5, and the C₄ hydrocarbon selectivity gradually increases with increasing temperature [13].

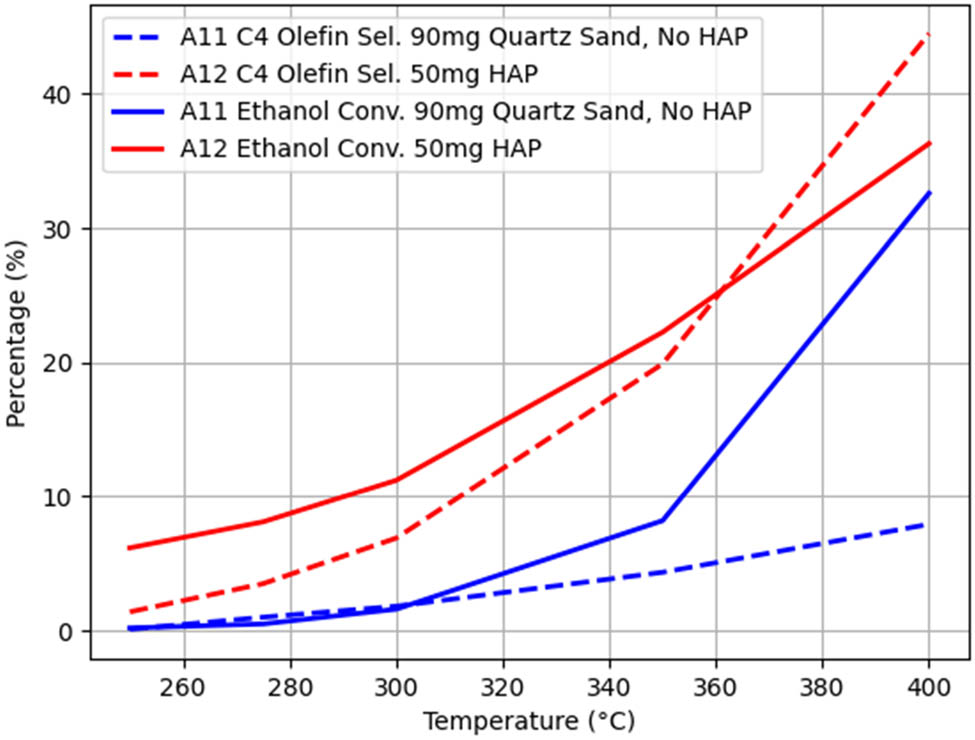
All other conditions being the same, only considering the use of quartz sand or HAP as the chemical agent, the A11–A12 group experiments were used as a control, and the temperature-dependent trends of the ethanol conversion rate and C₄ olefin selectivity are shown in Figure 7.

As depicted in Figure 7, the ethanol conversion rate and C₄ olefin selectivity with HAP are superior to those without HAP, which indicates that the use of HAP exerts a substantial influence on the catalytic performance [14].

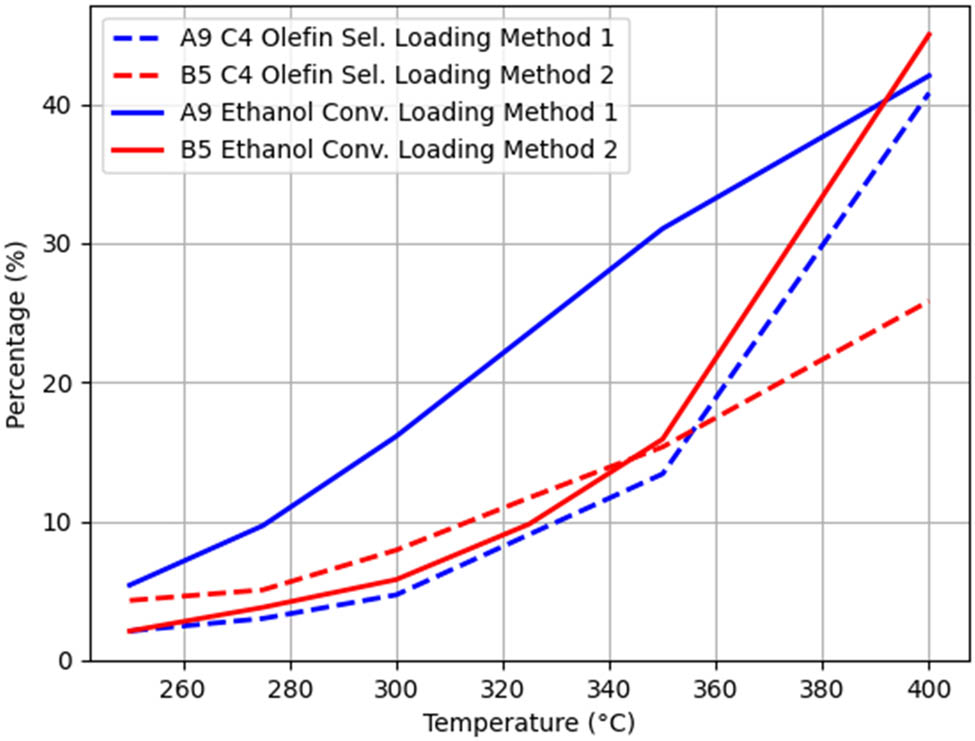
All other conditions being the same, when only the loading method was changed, the A9–B5 group experiment was used as a control, and the trends of ethanol conversion rate and C₄ olefin selectivity with temperature are shown in Figure 8.

From Figure 8, it can be seen that the C₄ hydrocarbon selectivity under loading method I is higher than that under loading method II.

3.2 Optimal multiple quadratic regression equation

Using the stepwise regression function in Matlab, the standard regression coefficient is solved, and the preliminary standard regression equation for the ethanol conversion rate is obtained as follows:

(11) α 0 = − 0.0007 + 0.749 T + 0.345 x 1 − 0.197 x 2 − 0.069 x 3 + 0.128 x 5 + 0.082 x 6 − 1.01 x 7 + 1.023 x 8 + 1.833 x 9 + 1.179 x 11 + 0.723 x 12 .

Due to the presence of multicollinearity among independent variables [15], the significance of the regression equation is low, and the regression effect is poor. Therefore, a stepwise regression was conducted to eliminate some unimportant explanatory variables, and the optimal standard regression equation for the ethanol conversion rate was obtained:

(12) α 0 = − 0.0227 + 0.758 T + 0.464 x 1 − 0.667 x 3 − 0.361 x 4 + 0.0008 x 9 + 0.002 x 10 − 0.002 x 11 + 0.592 x 12 + 0.233 x 13 − 1.125 x 14 .

The regression goodness of fit diagnosis was performed on the obtained model (12), and the results of each indicator are shown in Table 4.

Table 4

Diagnostic indicators for the optimal regression model of the ethanol conversion rate

R	R ²	RMSE	F	P
0.97	0.944	0.0114	36.92	4.28 × 10⁻²⁷

From the relative effect of regression, the complex correlation coefficient R = 0.97 and the determination coefficient R ² = 0.944 indicate that regression can reduce the variation of the dependent variable by 94.4%. Therefore, it can be seen from the determination coefficient that the regression equation is highly significant. From the absolute effect of regression, the root mean square error (RMSE) = 0.0114 is relatively small, indicating that the regression effect is very good. From the perspective of analysis of variance, F = 36.92 and P = 4.28 × 10⁻²⁷. This indicates that the regression equation is highly significant, and the regression coefficients have passed the significance test [16].

Therefore, the interaction among the five factors, the temperature, Co/SiO₂ and HAP mass, ethanol concentration, Co loading, Co/SiO₂ and HAP loading ratio, as well as the four factors other than temperature, has a significant impact on the overall ethanol conversion rate. By comparing the absolute values of the regression coefficients, it can be seen that the Co loading, Co/SiO₂, and HAP loading ratios have the greatest impact on the ethanol conversion rate.

Similarly, the standard regression equation for the optimal selectivity of C₄ olefins can be obtained as follows:

(13) α 1 = − 0.0373 + 0.768 T + 0.358 x 1 + 0.167 x 6 − 0.0008 x 7 + 0.001 x 9 + 0.0002 x 10 − 0.0022 x 11 + 0.191 x 12 − 0.54 x 14 .

The regression goodness of fit diagnosis was performed on the obtained model (13), and the results of each indicator are shown in Table 5.

Table 5

Diagnostic indicators for the optimal regression model of C₄ olefin selectivity

R	R ²	RMSE	F	P
0.96	0.937	0.0085	33.07	1.73 × 10⁻²⁴

From the relative effect of regression, the complex correlation coefficient R = 0.96 and the coefficient of determination R ² = 0.937 indicate that regression can reduce 93.7% of the variation of the dependent variable. Therefore, it can be seen from the coefficient of determination that the regression equation is highly significant. From the absolute effect of regression, RMSE = 0.0085 is relatively small, indicating that the regression effect is very good. From the perspective of analysis of variance, F = 33.07 and P = 1.73 × 10⁻²⁴. This indicates that the regression equation is highly significant, and the regression coefficients have passed the significance test.

Therefore, the six factors, the temperature, Co/SiO₂ and HAP mass, ethanol concentration, Co loading, Co/SiO₂ and HAP loading ratio, and loading method, as well as the interaction between Co/SiO₂ and the HAP mass with ethanol concentration, Co loading, Co/SiO₂ and HAP loading ratio, ethanol concentration with temperature and Co loading, and Co loading with Co/SiO₂ and the HAP loading ratio, have a significant impact on the selectivity of C₄ olefins as a whole. By comparing the absolute values of the regression coefficients, it can be seen that temperature has the greatest impact on the selectivity of C₄ olefins.

4 Conclusions

This study focuses on the cross-scale modeling and collaborative optimization of ethanol-catalyzed coupling to produce C₄ olefins, and constructs a nonlinear modeling framework that integrates univariate quadratic regression, orthogonal experimental design, and multivariate polynomial regression. Using 147 sets of multicatalyst experimental data and dynamic time-series data, the nonlinear effect of temperature on the ethanol conversion rate and C₄ olefin selectivity was revealed. The main effects of factors such as Co loading, feed ratio, and ethanol concentration were quantified, and the physical meaning of the interaction terms of temperature, Co loading, and feed ratio was analyzed in depth. The RMSE of the established model on the test set was less than 1.14%, and R ² was higher than 0.944, demonstrating good generalization ability and engineering applicability. This study provides a nonlinear engineering digital modeling paradigm that combines explanatory power, predictive power, and scalability for the mechanism elucidation and industrial optimization of complex catalytic reaction systems. It provides design references for catalyst formulation optimization and reaction condition regulation in the green production of C₄ olefins. In the future, the model can be expanded by introducing multiphysics field coupling, integrating the catalyst microstructure parameters, and other directions to further enhance its industrial application value.

Funding information: Authors state no funding is involved.
Author contributions: Jiayang Xiao: writing – original draft, writing – review and editing, conceptualization, data curation, formal analysis, and investigation. Kaijia Luo: methodology, resources, validation, and visualization. Junnan Zhong: validation, visualization, writing – review and editing, and supervision. All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: Authors state no conflict of interest.
Data availability statement: All data generated or analyzed during this study are included in this published article.

References

[1] Adamczyk VO, Griffin ES, Fogh AA, Schafer LL. Electronically and sterically varied vanadium aminopyridinate complexes applied to the catalytic reductive coupling of alcohols. Inorg Chem. 2025;64(19):9500–8.10.1021/acs.inorgchem.5c00254Search in Google Scholar PubMed

[2] Joshi VV, Bollini P. Exploiting proximity effects to improve ethyl acetate selectivity in the dehydrogenative coupling of ethanol over supported Cu catalysts. Appl Catal A Gen. 2025;697:120228.10.1016/j.apcata.2025.120228Search in Google Scholar

[3] Tian X, Qiu M, An W, Ren YL. Photocatalytic Hydrogenation of Alkenes Using Water as Both the Reductant and the Proton Source. Adv Sci (Weinheim, Baden-Wurttemberg, Germany). 2024;11(44):e2406046.10.1002/advs.202406046Search in Google Scholar PubMed PubMed Central

[4] Zheng L, Wu H, Zhou Z, Fan X. Distillation-Pervaporation hybrid process for ethanol dehydration: process optimization and economic evaluation. Chem Ing Tech. 2025;97(4):311–23.10.1002/cite.202400126Search in Google Scholar

[5] Doosthosseini M, Talkhoncheh KM, Silberberg LJ, Ghods H. An Arrhenius-based simulation tool for predicting aging of lithium manganese dioxide primary batteries in implantable medical devices. Energies. 2024;17(21):5392.10.3390/en17215392Search in Google Scholar

[6] Li TY, Jin QS, Hu JX, Wang ZJ, Li ZY, Chen L, et al. Examining performance of microchannel cold plate heat sink from its three parts along coolant flow direction and new structure designs based on the new considerations. Appl Therm Eng. 2025;269:125963.10.1016/j.applthermaleng.2025.125963Search in Google Scholar

[7] Reddy SD, Reddy RV, Choi JC. Gaussian distribution on electrical properties of identically fabricated Au/n - GaN Schottky junctions with a Nd2O3 interfacial layer. Mater Sci Semicond Process. 2025;196:109650.10.1016/j.mssp.2025.109650Search in Google Scholar

[8] Gaudet E, Persson F, Saidel M. Z - score - based post - test risk as an alternative risk metric to positive predictive value following positive noninvasive prenatal screening. Am J Obstet Gynecol. 2024;232(4):367–72.10.1016/j.ajog.2024.12.017Search in Google Scholar PubMed

[9] Austin CP, Eekhout I, Buuren VS. Evaluating the median p-value method for assessing the statistical significance of tests when using multiple imputation. J Appl Stat. 2025;52(6):1161–76.10.1080/02664763.2024.2418473Search in Google Scholar PubMed PubMed Central

[10] Liu X, Zhao M, Liu D, Yang J, Han Y, Sultana R, et al. Boosting catalytic oxidation of H2S over activated carbon optimized by the synergistic effect of rich defects and nitrogen sites. Surf Interface. 2025;68:106672.10.1016/j.surfin.2025.106672Search in Google Scholar

[11] Zhao K, Jiao Y, Zhu Z, Varley RJ, Liu W, Niu B, et al. Dual functionalities of inexpensive Mn/TiO2 catalyst to produce oxychar for ammonia capture. J Environ Chem Eng. 2025;13(3):116318.10.1016/j.jece.2025.116318Search in Google Scholar

[12] Fan D, Wen J, Chen P, Tu X, Luo X, Deng Y, et al. Facile synthesis of a single-atom cobalt catalyst to enhance peroxymonosulfate oxidation to degrade emerging contaminants by visibl-light regulation: From radical pathway to synergistic pathway. J Colloid Interface Sci. 2025;693:137626.10.1016/j.jcis.2025.137626Search in Google Scholar PubMed

[13] Fang Y, Li M, Gao Y, Wen Y, Shan B. Static organic p - n junctions in photoelectrodes for solar ammonia production with 86% internal quantum efficiency. Angew Chem. 2024;137(3):e202415729.10.1002/ange.202415729Search in Google Scholar

[14] Li Z, Yang L, Ma W, Lei Y. Eutectic Si - Ti brazing alloy prepared from spent selective catalytic reduction catalyst and diamond - wire sawing silicon waste. Chem Eng J. 2024;496:154053.10.1016/j.cej.2024.154053Search in Google Scholar

[15] Bouka S, Bello PK, Nkiet MG. On estimation and prediction in a spatial semi-functional linear regression model with derivatives. Math Methods Stat. 2024;33(3):310–26.10.3103/S1066530724700169Search in Google Scholar

[16] Hodson TO. Root - mean - square error (RMSE) or mean absolute error (MAE): when to use them or not. Geosci Model Dev. 2022;15(14):5481–7.10.5194/gmd-15-5481-2022Search in Google Scholar

Received: 2025-06-19

Revised: 2025-07-17

Accepted: 2025-07-25

Published Online: 2025-09-23

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/nleng-2025-0167

Keywords for this article

ethanol catalytic coupling; C4 olefin; binary quadratic regression

Creative Commons

BY 4.0