Startseite Technik Nonlinear deformation decomposition and mode identification of plane structures via orthogonal theory
Artikel Open Access

Nonlinear deformation decomposition and mode identification of plane structures via orthogonal theory

  • Na Chen EMAIL logo und Tingting Kang
Veröffentlicht/Copyright: 11. September 2025
Artikel downloaden (PDF)
Veröffentlichen auch Sie bei De Gruyter Brill
Manuskript einreichen Informationen für Autor*innen
Nonlinear Engineering
Aus der Zeitschrift Nonlinear Engineering Band 14 Heft 1

Abstract

This article presents a novel method for nonlinear deformation decomposition and mode identification of plane structures based on orthogonal theory. The plane deformation of a square element is decomposed into rigid body linear displacements, rigid body rotation, tension-compression, bending, and shearing deformations. A complete orthogonal base vector set is constructed for these basic deformation modes, allowing any deformation to be expressed as a linear combination of these vectors. Compared with the traditional finite element method, the proposed approach demonstrates superior accuracy, convergence, and robustness, especially in identifying bending deformation, which is difficult to isolate using conventional techniques. The method also excels in mode identification, effectively revealing coupled modes such as shear-dominated shapes. It outperforms traditional approaches like animation and mass participation ratio methods by offering more accurate, visual, and comprehensive results. A numerical example involving a plane column validates the feasibility and effectiveness of the method, showcasing its potential in analyzing complex nonlinear deformations and identifying modal behavior in plane structures.

Keywords: nonlinear deformation decomposition; mode identification; bending deformation; coupled mode, complete orthogonal base

1 Introduction

Deformation decomposition was first proposed by Bell (1981), considering that rock deformation caused by heterogeneity of the geological structure could be decomposed into progressive shearing deformation and stretching deformation [1]. Since then, the concept that deformation can be decomposed has been widely used in many fields including structural engineering. Veccchio (1986) pointed out that the nonlinear deformation of reinforced concrete columns could be divided into bending and shearing deformation of the plastic zone and bond slippage deformation of longitudinal bars at the column base [2]. Blanchard and Griso (2009) dealt with the introduction of decomposition of the deformations of curved thin beams. A deformation was split into elementary deformation and warping [3]. Nie et al. studied the beam end displacement by decomposing it into a combination of displacements caused by itself, pillar deformation, and deformation of the joint core area [4]. Lee et al. decomposed the deformation of a beam into lateral deflection, bending rotation, and shear deformation and derived the simultaneous differential equations of free vibration of Timoshenko beam [5].

Most of the relevant research studies are concerned with decomposing the structure deformation into a combination of various simple deformations. Williams et al. found that movement and deformation of blocks under certain conditions could be considered as the superposition of rigid body motion and deformation [6]. He and Zheng examined all the possibilities for a given large incompressible deformation to be decomposed into three perpendicular simple shears preceded or followed by a rotation [7]. It is demonstrated that the decomposition of a finite incompressible deformation encompasses, as a particular case, that of an infinitesimal incompressible deformation into three perpendicular simple shears. Zhang et al. (2007, 2014) developed a method to determine the optimal stress fields for the hybrid stress element [8,9]. And the 2D four-node and 3D eight-node hybrid elements are illustrated. Wang et al. identified the eigen-deformation shapes, including axial, bending, and shear deformations by associating the eigenvectors with a node displacement vector [10]. However, normalization and completeness of decomposition variables are always neglected in the existing deformation decomposition methods from a mechanical point of view. Convergence and error analyses are always not taken into account in the literature based on the finite element method.

Han and Feeny used the proper orthogonal decomposition method to extract all of the normal modes contained in the structural responses [11]. Examples based on a homogeneous free–free beam and a non-homogeneous free–free beam were used to verify the applicability. But the method is hardly used on complex structures, due to the reason that modes of the complex structure are difficult to be recognized or identified.

This article constructs a set of complete orthogonal deformation bases and presents a deformation decomposition method of the plane structure. The coupling problem among basic displacement modes is solved. Completeness and orthogonality of the displacement deformation bases are taken into account. Analysis results are compared against those of the finite element method to testify the convergence, robustness, and contribution of the proposed deformation decomposition method. Identifying modes of the structure quantitatively based on the proposed deformation decomposition method is subsequently studied. A numerical example on a plane column is finally applied to demonstrate the feasibility and visualization.

2 Deformation decomposition method and orthogonal complete coordinate base

Based on the strain energy analysis, Cook et al. brought forward that in the case of small deformation, the plane deformation of a four-node square element could be expressed by a combination of eight independent displacement modes [12]. The eight displacement modes included three rigid-body modes, three constant-strain modes, and two bending modes, among which the tension and compression modes were not basic deformation modes. Considering the eight basic deformation modes mentioned in Zhang (2014), the biaxial tension and compression deformation modes in the basic tension-compression deformation in the X direction and the basic tension-compression deformation in the Y direction can be obtained. Using the normalized orthogonal decomposition method, the base vectors of the four-node square element, corresponding to the three rigid-body displacements and five basic deformation modes are constructed (Figure 1), as proposed by Liang et al. [13].

Figure 1 Three rigid body displacement bases and five basic deformation bases of four-node square element. (a) Rigid body displacement base in the X direction. (b) Rigid body displacement base in the Y direction. (c) Rigid body rotation displacement base in the XOY plane. (d) Tension-compression deformation base in the X direction. (e) Tension-compression deformation base in the Y direction. (f) Bending deformation base in the X direction. (g) Bending deformation base in the Y direction. (h) Shearing deformation base in the XOY plane.
Figure 1

Three rigid body displacement bases and five basic deformation bases of four-node square element. (a) Rigid body displacement base in the X direction. (b) Rigid body displacement base in the Y direction. (c) Rigid body rotation displacement base in the XOY plane. (d) Tension-compression deformation base in the X direction. (e) Tension-compression deformation base in the Y direction. (f) Bending deformation base in the X direction. (g) Bending deformation base in the Y direction. (h) Shearing deformation base in the XOY plane.

Moreover, a complete orthogonal base matrix B including all the eight base vectors is introduced as

(1) B = 0.5 0 0.5 0 0.5 0 0.3536 − 0.3536 0 0.5 0 0.5 0 0.5 0.3536 0.3536 0.5 0 − 0.5 0 − 0.5 0 0.3536 − 0.3536 0 0.5 0 0.5 0 − 0.5 − 0.3536 − 0.3536 0.5 0 − 0.5 0 0.5 0 − 0.3536 0.3536 0 0.5 0 − 0.5 0 0.5 − 0.3536 − 0.3536 0.5 0 0.5 0 − 0.5 0 − 0.3536 0.3536 0 0.5 0 − 0.5 0 − 0.5 0.3536 0.3536 ,

where eight columns from left to right successively are rigid body displacement base in the X direction, rigid body displacement base in the Y direction, tension-compression deformation base in the X direction, tension-compression deformation base in the Y direction, bending deformation base in the X direction, bending deformation base in the Y direction, shearing deformation base in the XOY plane, and rigid body rotation displacement base, respectively.

The complete orthogonal base matrix B is of 8 × 8 with the completeness and satisfies

(2) B B T = E ,

where E is the identity matrix of 8 × 8 .

Assume the nodal deformation vector is

(3) d e = u 1 v 1 u 2 v 2 u 3 v 3 u 4 v 4 T .

Then, d e can be expressed as

(4) d e = B · d ,

where

(5) d = d 1 d 2 d 3 d 4 d 5 d 6 d 7 d 8 T .

Here, d i denotes the projection coefficient of the i th displacement or deformation mode to the element deformation. Eqs. (4) and (5) indicate that any nodal displacement or deformation vector can be expressed by the linear combination of the eight displacement and deformation base vectors.

Furthermore, Eq. (4) can be transformed as

(6) d = B − 1 d e = B T d e .

Hence, when the nodal displacement vector is given, the projection coefficient vector can be calculated using Eq. (6).

Example: The nodal displacement vector of an element in the finite element analysis of the beam bending problem is assumed as

d e = 0 . 7 0 81 − 2 . 6779 0 . 73 0 9 − 2 . 7766 0 . 8267 − 2 . 781 0 0 . 8 0 63 − 2 . 682 0 T .

Using Eq. (6), the projection coefficient vector can be calculated as

d = 1 . 536 0 − 5 . 4588 − 0.0 216 0.00 42 − 0.00 12 − 0.000 2 0.00 13 0 . 1385 T .

Carry out normalization processing of vector d , namely

(7) d i ′ = ∣ d i ∣ ∑ 1 8 ∣ d i ∣ .

Then, the contributing coefficient vector d ′ can be derived as

d ′ = 0 .2145 0 .7622 0.00 3 0 0.000 6 0.000 2 0 0.000 2 0 .0193 T .

Hence, the deformation decomposition results according to vector d ′ are expressed in Table 1.

Table 1

Deformation decomposition results of the example problem

Displacement or deformation mode Proportion of displacement mode (%) Proportion of deformation mode (%)
Rigid body displacement in the X direction 21.45
Rigid body displacement in the Y direction 76.22
Tension-compression deformation in the X direction 0.30
Tension-compression deformation in the Y direction 0.06
Bending deformation in the X direction 0.02
Bending deformation in the Y direction 0.00
Shearing deformation base in the XOY plane 0.02
Rigid body rotation displacement 1.93

Because the rigid body linear displacement and the rigid body rotation displacement do not produce stress and strain, rigid body displacements including the rigid body displacement in the X direction, the rigid body displacement in the Y direction, and the rigid body rotation displacement are not taken into account. Comparing the absolute values of contributing coefficients of other deformation modes, the deformation mode with maximum value indicates the main deformation of the element. The deformation mode with the second largest value suggests the secondary deformation of the element. In the same way, detailed deformation conditions can be derived. Besides, for the tension-compression deformation in X and Y directions, positive contributing coefficient value means the tension deformation; negative contributing coefficient value means the compression deformation.

3 Comparison and verification

Example: Consider a cantilever column of 400 mm width and 800 mm height, denoted as column A, and a cantilever column of 200 mm width and 800 mm height, denoted as column B. In both columns, one end is fixed and the other end is free. Top of the column is under a horizontal load.

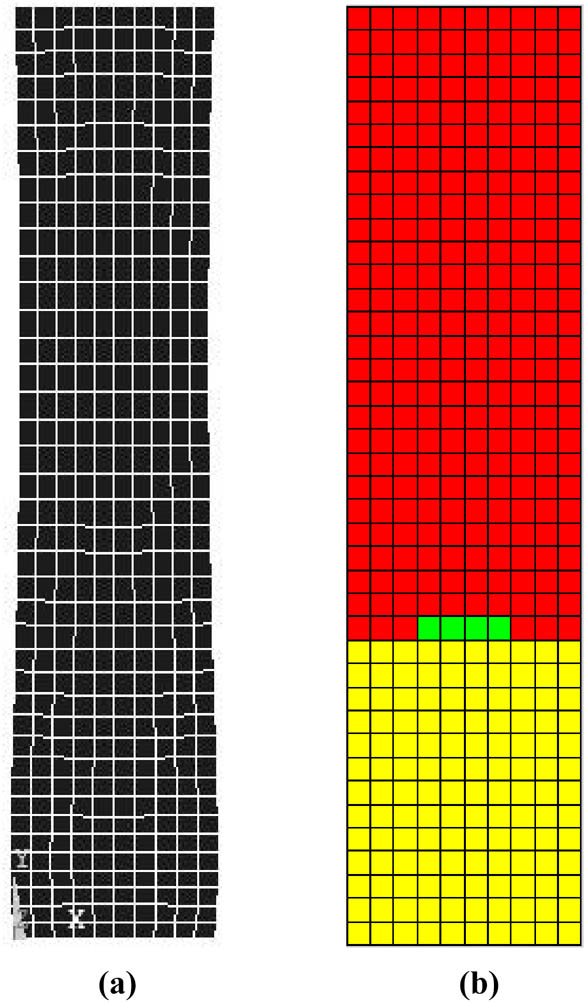
Through the finite element method using a commercial code (ANSYS), the deformation graph can be obtained, which is shown in Figure 2. The deformation decomposition graph of column A can be obtained using the proposed deformation decomposition method, which is shown in Figure 3. The stress nephogram of column A is shown in Figure 4. Likewise, the deformation graph, the deformation decomposition graph, and the stress nephogram of column B are obtained, which are shown in Figures 5–7, respectively. Black denotes that main deformation of the element is the compression deformation mode in the X direction; white denotes that main deformation of the element is the tension deformation mode in the X direction; red denotes that main deformation of the element is the tension deformation mode in the Y direction; yellow denotes that main deformation of the element is the compression deformation mode in the X direction; green denotes that main deformation of the element is the bending deformation mode in the X direction; gray denotes that main deformation of the element is the bending deformation in the Y direction; blue denotes that main deformation of the element is the shear deformation.

Figure 2 Deformation graph using the finite element method. The height–width ratio of column A is 2.
Figure 2

Deformation graph using the finite element method. The height–width ratio of column A is 2.

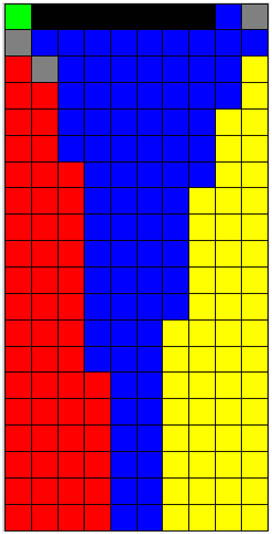
Figure 3 Deformation decomposition graph using the proposed method. The height–width ratio of column A is 2.
Figure 3

Deformation decomposition graph using the proposed method. The height–width ratio of column A is 2.

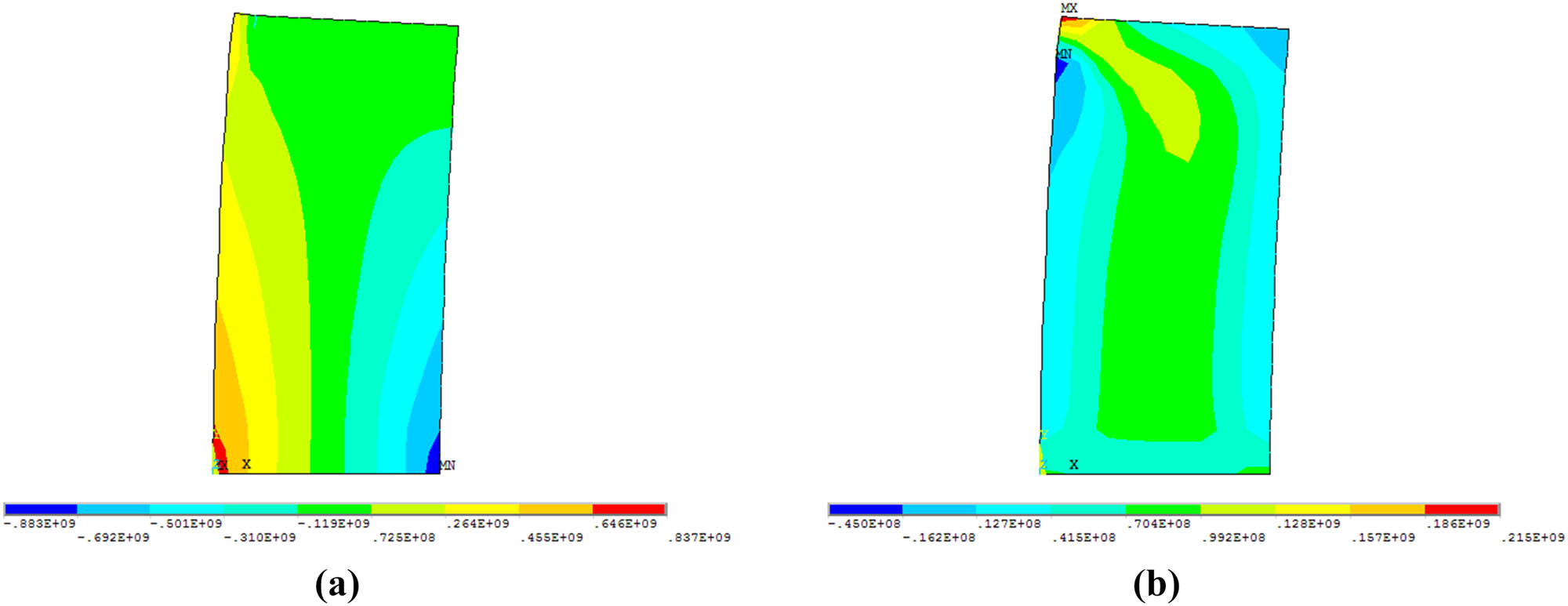
Figure 4 Stress nephograms of column A. (a) Stress nephogram of tension in the Y direction (the height–width ratio of column A is 2). (b) Stress nephogram of shearing in the XOY plane (the height–width ratio of column A is 2).
Figure 4

Stress nephograms of column A. (a) Stress nephogram of tension in the Y direction (the height–width ratio of column A is 2). (b) Stress nephogram of shearing in the XOY plane (the height–width ratio of column A is 2).

Figure 5 Deformation graph using the finite element method. The height–width ratio of column A is 4.
Figure 5

Deformation graph using the finite element method. The height–width ratio of column A is 4.

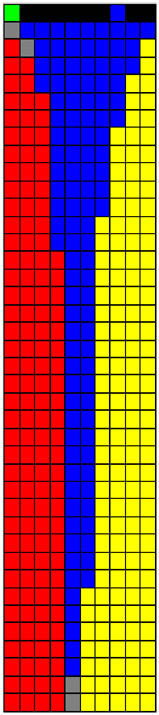
Figure 6 Deformation decomposition graph using the proposed method. The height–width ratio of column A is 4.
Figure 6

Deformation decomposition graph using the proposed method. The height–width ratio of column A is 4.

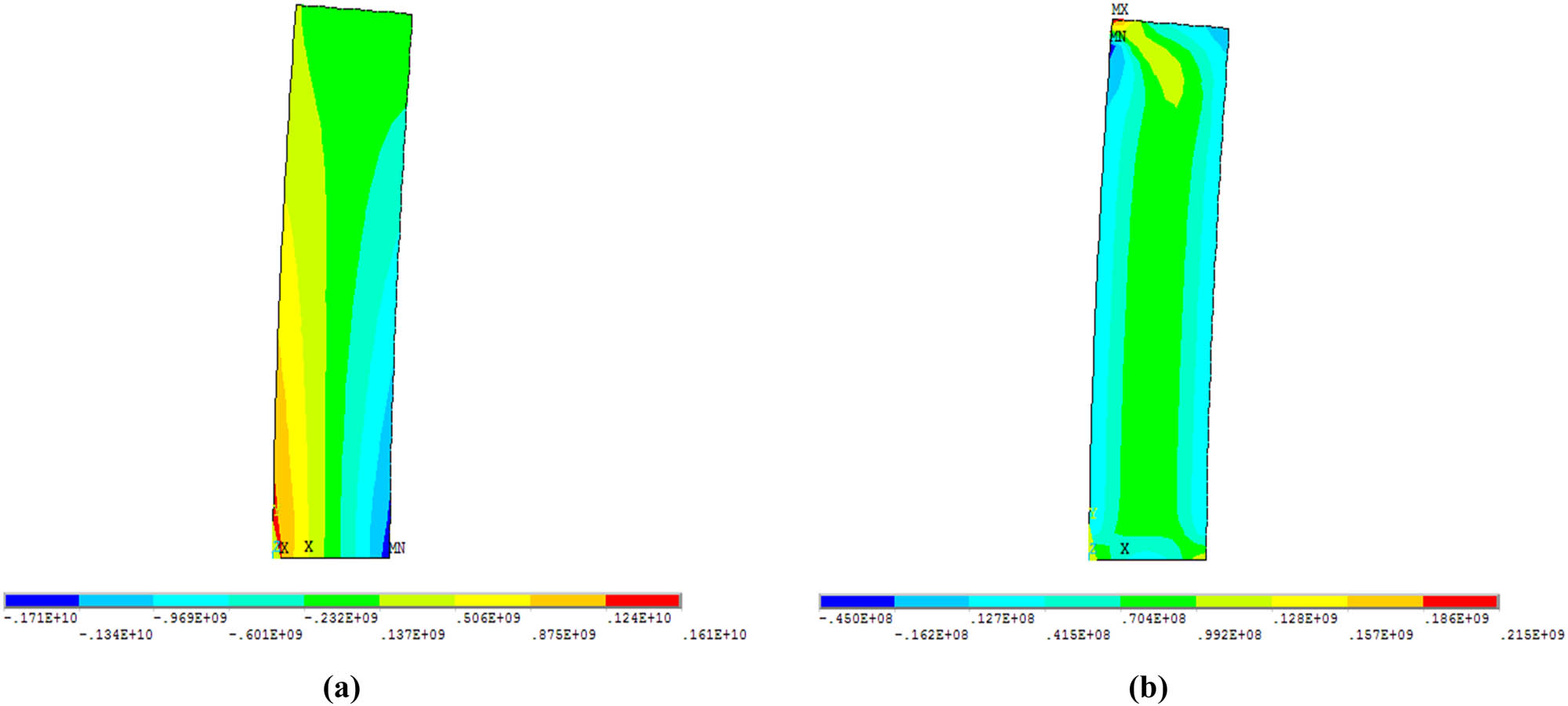
Figure 7 Stress nephograms of column B. (a) Stress nephogram of tension in the Y direction (the height–width ratio of column A is 4). (b) Stress nephogram of shearing in the XOY plane (the height–width ratio of column A is 4).
Figure 7

Stress nephograms of column B. (a) Stress nephogram of tension in the Y direction (the height–width ratio of column A is 4). (b) Stress nephogram of shearing in the XOY plane (the height–width ratio of column A is 4).

From Figure 3, it can be observed that under a horizontal load, main deformation in left half part of column A is tension deformation in the Y direction, while main deformation in right half part of column A is compression deformation in the Y direction. Main deformation of the upper part is shearing deformation, and main deformation of the lower end is bending deformation. Figure 4a indicates that left half of column A is subject to tensile stress in the Y direction, while the right half is subject to compressive stress in the Y direction. Figure 4b shows that the upper part of column A is at shear stress.

From Figure 6, under a horizontal load, main deformation in the left half part of column B is tension deformation in the Y direction, while main deformation in right half part of column B is compression deformation in the Y direction. Main deformation of the upper part is shearing deformation, and main deformation of the middle part and lower end is bending deformation. Figure 7a indicates that left half of column B is subject to tensile stress in the Y direction, while the right half is subject to compressive stress in the Y direction. Figure 7b shows that the middle part and upper part in the XOY plane of column B is under shear stress.

From the above example, we can find that it is easy to get the maximum stress zone using the finite element method, while it is easier for the deformation decomposition method to obtain the zone with main deformation. As shown in Table 2, two graphs are needed for the finite element method, while only one graph is needed for the deformation decomposition method. Comparing the deformation decomposition results of column A and column B, it is noted that the zone in column A with main deformation of shearing deformation is larger than that in column B. Column A is more likely to be influenced by shear failure. Hence, the deformation decomposition method could provide more information and is more visual than the finite element method.

Table 2

Deformation decomposition results of columns A and B

Tension deformation in the Y direction Compression deformation in the Y direction Shearing deformation
Column A 27.5% 27.5% 39.5%
Column B 34% 35% 27.25%

4 Numerical example and application in mode identification

Mode identification is often determined according to the animation of the finite element analysis software (e.g., ANSYS) in engineering practice. However, this method is often influenced by the perspective and subjective factors of the observer, leading to the error of observation. In order to overcome the problem, Wilson brought forward the modal participating mass ratio method to conduct mode identification (Clough and Penzien, 1995) [14]. But Wilson’s method cannot identify the shearing mode of a structure. And the main mode type cannot be identified for the coupled mode, too.

4.1 Plane cantilever column

The proposed deformation decomposition method in the article can be directly used for mode identification. Using the constructed complete orthogonal base matrix B , it is convenient to carry out orthogonal decomposition of the modal shape of each order. Consider a plane column of 400 mm width and 1,600 mm height. One end is fixed and the other end is free. Using the modal analysis procedure of the finite element method, modal shape of each order can be obtained. Meanwhile, based on the proposed deformation decomposition method, deformation decomposition graphs corresponding to modal shapes of all orders can be obtained, as shown in Figures 8–15.

Figure 8 First-order modal shape and its corresponding orthogonal decomposition graph. (a) Modal shape. (b) Orthogonal decomposition graph.
Figure 8

First-order modal shape and its corresponding orthogonal decomposition graph. (a) Modal shape. (b) Orthogonal decomposition graph.

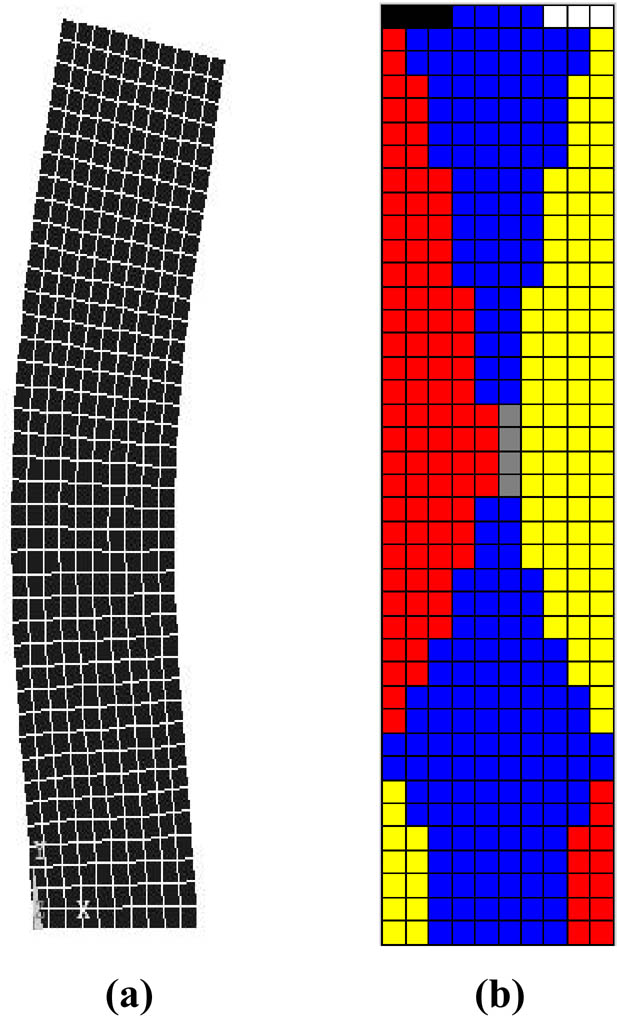
Figure 9 Second-order modal shape and its corresponding orthogonal decomposition graph. (a) Modal shape. (b) Orthogonal decomposition graph.
Figure 9

Second-order modal shape and its corresponding orthogonal decomposition graph. (a) Modal shape. (b) Orthogonal decomposition graph.

Figure 10 Third-order modal shape and its corresponding orthogonal decomposition graph. (a) Modal shape. (b) Orthogonal decomposition graph.
Figure 10

Third-order modal shape and its corresponding orthogonal decomposition graph. (a) Modal shape. (b) Orthogonal decomposition graph.

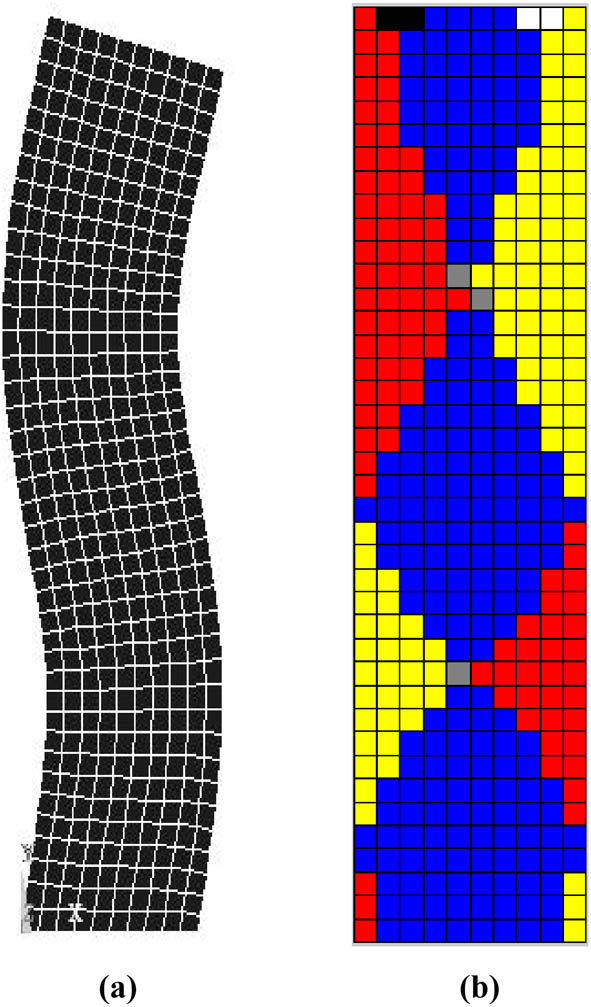
Figure 11 Fourth-order modal shape and its corresponding orthogonal decomposition graph. (a) Modal shape. (b) Orthogonal decomposition graph.
Figure 11

Fourth-order modal shape and its corresponding orthogonal decomposition graph. (a) Modal shape. (b) Orthogonal decomposition graph.

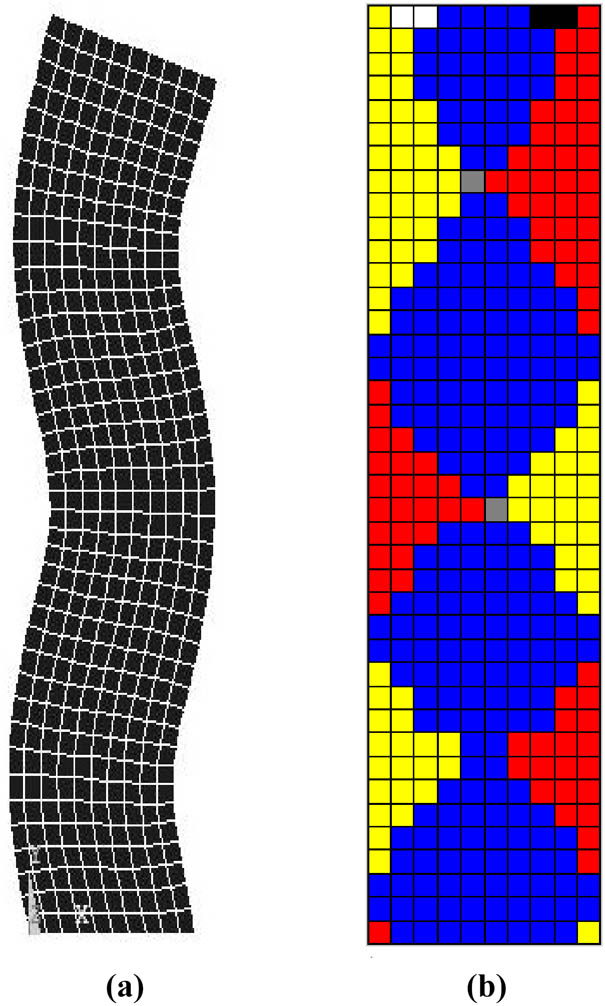
Figure 12 Fifth-order modal shape and its corresponding orthogonal decomposition graph. (a) Modal shape. (b) Orthogonal decomposition graph of the fifth-order modal shape.
Figure 12

Fifth-order modal shape and its corresponding orthogonal decomposition graph. (a) Modal shape. (b) Orthogonal decomposition graph of the fifth-order modal shape.

Figure 13 Sixth-order modal shape and its corresponding orthogonal decomposition graph. (a) Modal shape. (b) Orthogonal decomposition graph of the sixth-order modal shape.
Figure 13

Sixth-order modal shape and its corresponding orthogonal decomposition graph. (a) Modal shape. (b) Orthogonal decomposition graph of the sixth-order modal shape.

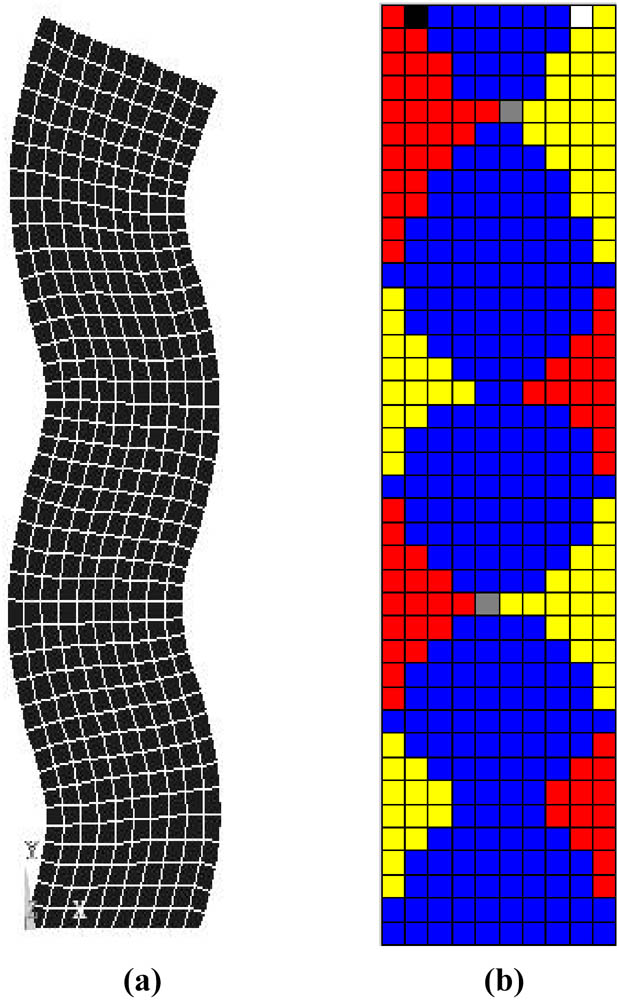
Figure 14 Seventh-order modal shape and its corresponding orthogonal decomposition graph. (a) Modal shape. (b) Orthogonal decomposition graph.
Figure 14

Seventh-order modal shape and its corresponding orthogonal decomposition graph. (a) Modal shape. (b) Orthogonal decomposition graph.

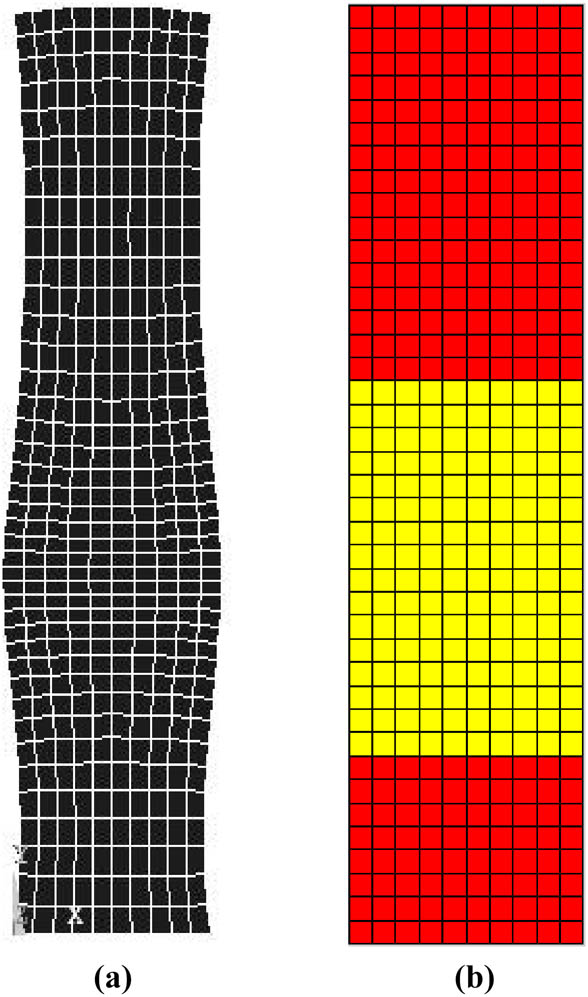
Figure 15 Eighth-order modal shape and its corresponding orthogonal decomposition graph. (a) Modal shape. (b) Orthogonal decomposition graph.
Figure 15

Eighth-order modal shape and its corresponding orthogonal decomposition graph. (a) Modal shape. (b) Orthogonal decomposition graph.

It can be found that the first-order modal shape of the column is a first-order horizontal bending mode; the second-order modal shape is a second-order horizontal bending mode; the third-order modal shape is a first-order tension-compression mode in the Y direction; the fourth-order modal shape is a third order horizontal bending mode; the fifth-order modal shape is a fourth-order horizontal bending mode; the sixth-order modal shape is a second-order tension-compression mode in the Y direction; the seventh-order modal shape is a fifth-order horizontal bending mode; and the eighth-order modal shape is a third-order tension-compression mode in the Y direction.

Table 3 indicates that in the first and second-order modal shape, proportions of the shearing dominated zone are both less than 50%. One side of the shearing dominated zone is tension in the Y direction dominated zone, while the other side is compression in the Y direction dominated zone. Hence, the first-order modal shape of the column is a first-order bending-shearing mode. Hence, the second-order modal shape of the column is a second-order bending-shearing mode. For the fourth-, fifth-, and seventh-order modal shape, proportions of the shearing dominated zone are all more than 50%. In the zone between the shearing dominated zones, the bending mode is dominant. One side of the bending dominated zone is tension in the Y direction dominated zone, and the other side is compression in the Y direction dominated zone. Namely, the fourth modal shape of the column is a third order shearing-bending mode, the fifth modal shape of the column is a fourth-order shearing-bending mode; the seventh modal shape of the column is a fifth-order shearing-bending mode. As shown in Figure 10b, the proportion of tension in the Y direction dominated zone is 100%. In Figure 13b, the proportion of compression in the Y direction dominated zone is 66% in the upper part, and the proportion of compression in the Y direction dominated zone is 33% in the lower part. As Figure 15b suggests, for the proportion of compression in the Y direction dominated zone in the upper part and the proportion of compression in the Y direction dominated zone in the lower part, the total value is 60%. The proportion of tension in the Y direction dominated zone in the middle part is 40%. Hence, the third modal shape of the column is first tension-compression in the Y direction mode. The sixth modal shape of the column is second tension-compression in the Y direction mode. The eighth modal shape of the column is third tension-compression in the Y direction mode. Mode identification analysis based on the proposed deformation decomposition method is a feasible and convenient means to determine the shearing modal shape and modes of the coupled modal shape.

Table 3

Proportion of the shearing dominated zone in the first- to eighth-order modal shape

Order of modal shape First Second Third Fourth Fifth Sixth Seventh Eighth
Proportion (%) 37.0 46.5 0 52.5 58.5 0 62.5 0

Note: Proportion is the ratio of the area of shearing dominated zone to the total area of the column.

Furthermore, analysis results of the modal participating mass ratio method and the mode identification based on the proposed deformation decomposition method are compared, as shown in Table 4. The results of the two methods are consistent, testifying the feasibility and applicability of the mode identification analysis method.

Table 4

Comparison between results of the modal participating mass ratio method and the proposed mode identification method

Mode order Frequency (Hz) Modal participating mass ratio method Proposed method
X Y RZ Mode description Proportion of shearing dominated zone (%) Mode description
1 91.1882 0.6174 0 0.9307 First-order bending mode 37.0 First-order bending-shearing mode
2 468.275 0.2096 0 0.0221 Second-order bending mode 46.5 Second-order shearing-bending mode
3 589.570 0 0.8159 0.0357 First tension-compression in Y direction mode 0 First tension-compression in Y direction mode
4 1083.81 0.0707 0 0.0022 Third-order bending mode 52.5 Third-order shearing-bending mode
5 1761.48 0.0348 0 0.0003 Fourth-order bending mode 58.5 Fourth-order shearing-bending mode
6 1765.87 0 0.0904 0.0040 Second tension-compression in Y direction mode 0 Second tension-compression in Y direction mode
7 2468.67 0.0188 0 0 Fifth-order bending mode 62.5 Fifth-order shearing-bending mode
8 2926.45 0 0.0320 0.0014 Third tension-compression in Y direction mode 0 Third tension-compression in Y direction mode

4.2 Plane framed column

The plane framed column is analyzed based on the proposed orthogonal decomposition method. The height–width ratio of the plane framed column is 10.0. Orthogonal decomposition is performed on the first 15 modes of the moderate column to analyze their variation patterns. The longitudinal tension-compression mode is not considered due to the absence of adverse deformations such as shear deformation. The deformation decomposition graphs corresponding to modal shapes of the first four orders can be obtained, as shown in Figures 16–19.

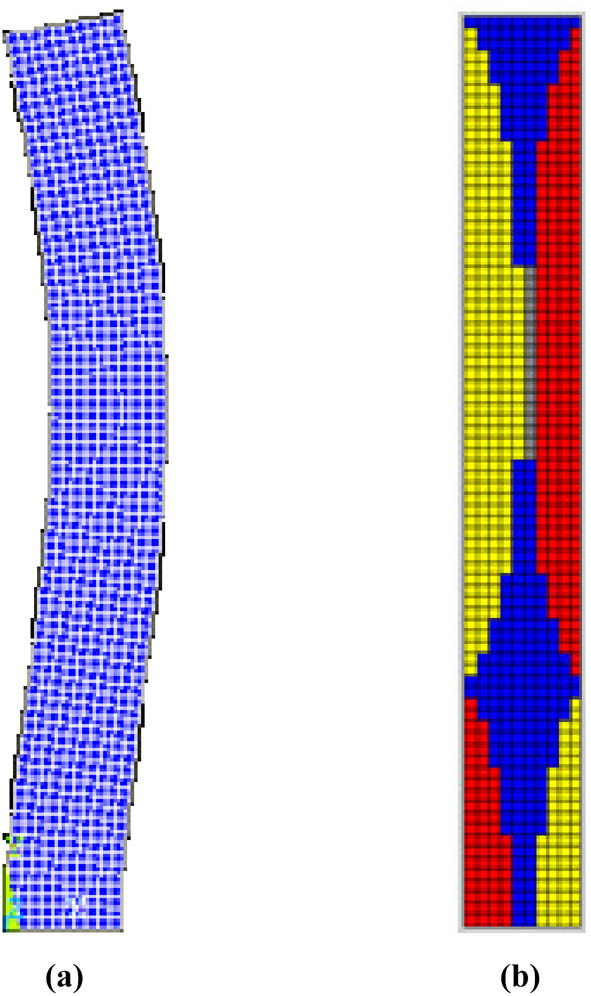
Figure 16 First-order mode of the plane framed column. (a) Modal shape. (b) Orthogonal decomposition graph.
Figure 16

First-order mode of the plane framed column. (a) Modal shape. (b) Orthogonal decomposition graph.

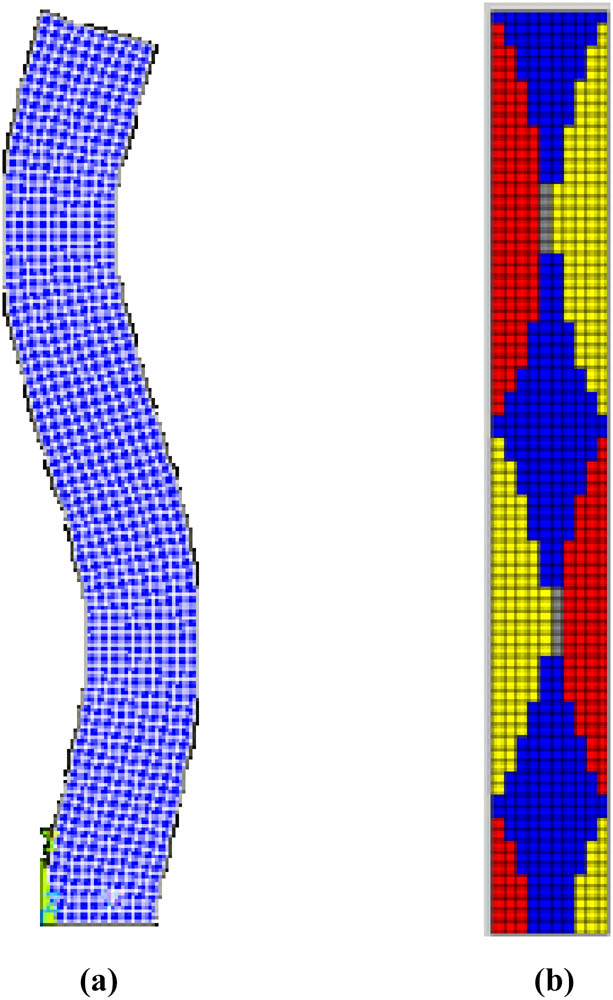
Figure 17 Second-order mode of the plane framed column. (a) Modal shape. (b) Orthogonal decomposition graph.
Figure 17

Second-order mode of the plane framed column. (a) Modal shape. (b) Orthogonal decomposition graph.

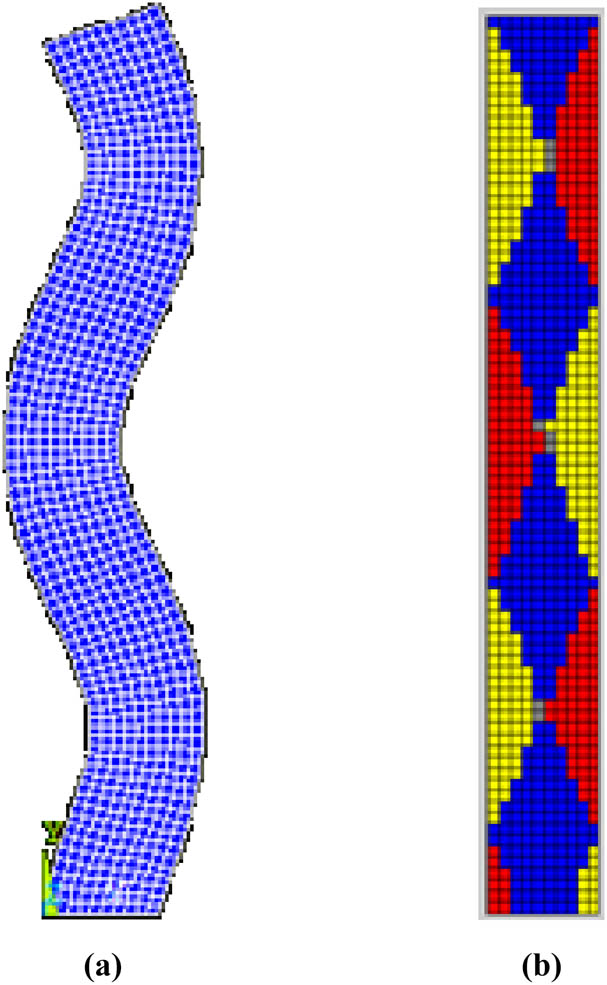
Figure 18 Third-order mode of the plane framed column. (a) Modal shape. (b) Orthogonal decomposition graph.
Figure 18

Third-order mode of the plane framed column. (a) Modal shape. (b) Orthogonal decomposition graph.

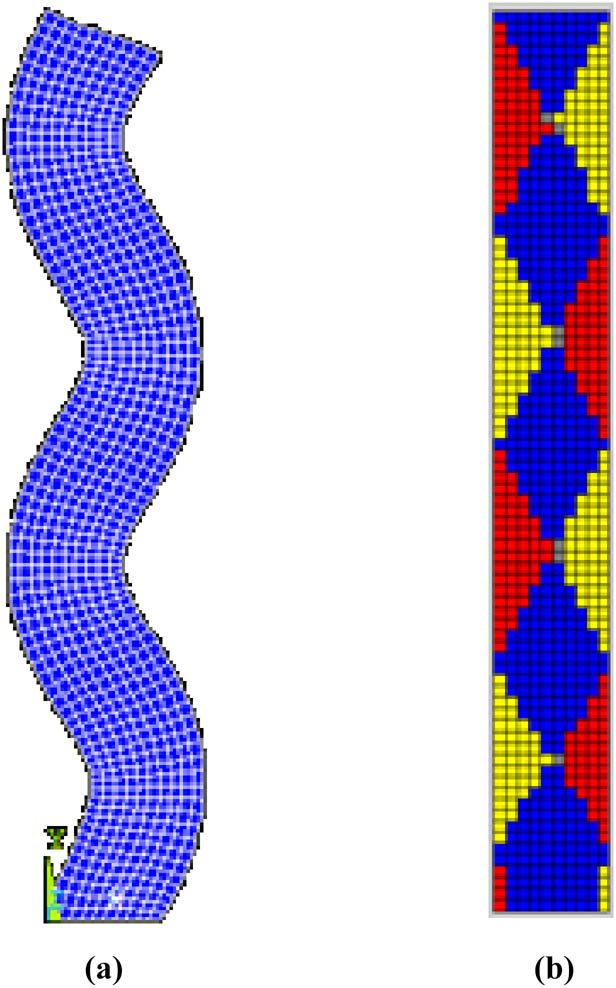
Figure 19 Fourth-order mode of the plane framed column. (a) Modal shape. (b) Orthogonal decomposition graph.
Figure 19

Fourth-order mode of the plane framed column. (a) Modal shape. (b) Orthogonal decomposition graph.

As shown in Figure 20, with the increase of the mode order, the proportion of the moderate column shear mode region gradually increases. As shown in Figure 21, with the increase of the order of vibration modes, the column end gradually becomes dominated by shear vibration mode, with the column end taking 200 mm. Under static action, the structural deformation is mainly manifested in the form of first-order vibration mode, but under dynamic action, higher-order vibration modes will become the main participants in the deformation base, especially at the column end where shear deformation is the main form of failure. Therefore, under seismic loads, even moderate columns may experience shear failure at the ends of frame columns.

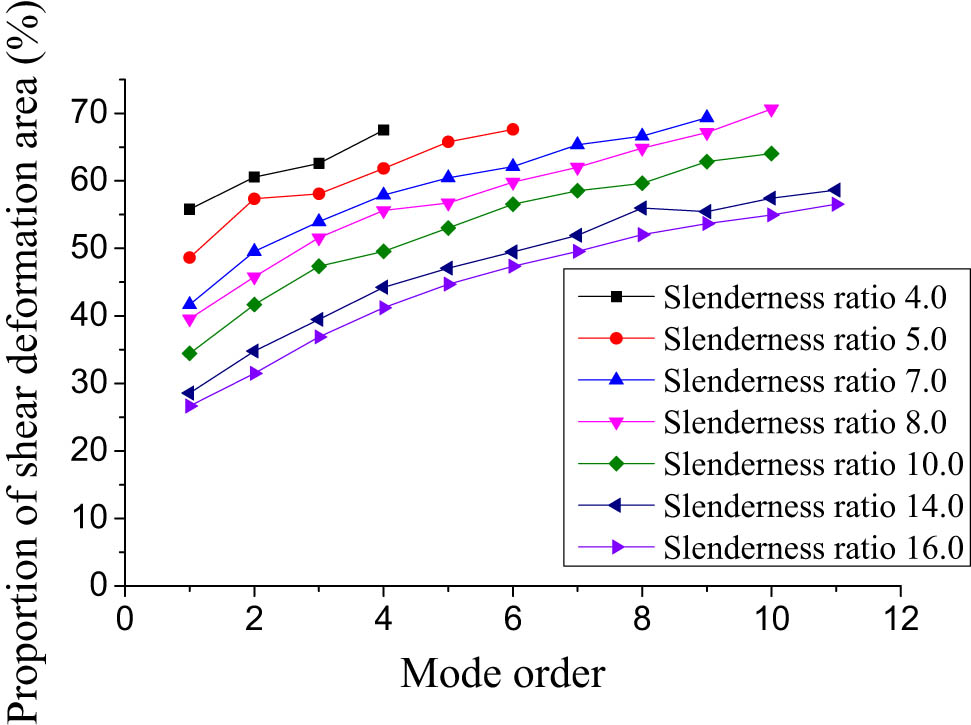
Figure 20 The proportion of shear deformation area in the transverse bending vibration mode of frame columns.
Figure 20

The proportion of shear deformation area in the transverse bending vibration mode of frame columns.

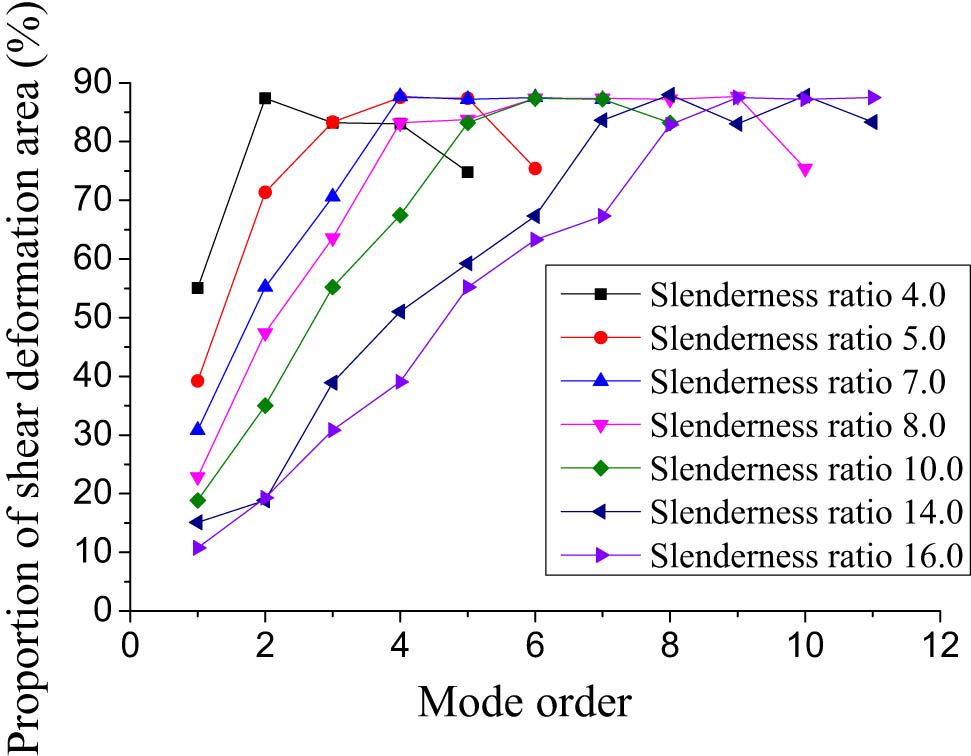
Figure 21 The proportion of shear deformation area at the column end in the transverse bending vibration mode of the frame column.
Figure 21

The proportion of shear deformation area at the column end in the transverse bending vibration mode of the frame column.

5 Conclusions

Deformation decomposition and mode identification are of significance for structure analysis and conceptual design. This study investigated the deformation decomposition method through constructing a set of complete orthogonal bases. Application of the proposed method in mode identification field was studied. Based on the numerical results, the following conclusions can be drawn:

  1. The deformation decomposition method based on the complete orthogonal base shows good accuracy, convergence, and robustness. It demonstrates a high similarity degree in the analysis results, compared with the existing finite element method. Moreover, the proposed method can identify the bending deformation of plane structures efficiently, which make the analysis results more consistent with the engineering practices.

  2. Compared with the animation identification of the finite element method and Wilson’s modal participating mass ratio method, the mode identification method based on the proposed deformation decomposition method is more visual and complete. It has advantages in quantitatively identifying the shearing dominated mode and the coupled mode of the plane structure.

  3. As the order of vibration modes increases, the proportion of shear deformation area gradually increases for plane columns. Especially at the end of the column, the proportion of shear deformation area is relatively large, and failure mainly caused by shear deformation may occur.

Acknowledgments

This research was funded by the project (No. 50978232) supported by the National Natural Science Foundation of China.

  1. Funding information: The authors state no funding was involved.

  2. Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.

  3. Conflict of interest: The authors state no conflict of interest.

  4. Data availability statement: The datasets used and analyzed during the current study are available from the corresponding author on reasonable request.

References

[1] Bell TH. Foliation development: The contribution, geometry and significance of progressive bulk inhomogeneous shortening. Tectonophysics. 1981;75(3–4):273–96.10.1016/0040-1951(81)90278-XSuche in Google Scholar

[2] Vecchio F, Collins MP. The modified compression-field theory for reinforced concrete elements subjected to shear. ACI Struct J. 1986;83(2):219–31.10.14359/10416Suche in Google Scholar

[3] Blanchard D, Griso G. Decomposition of deformations of thin roads: application to nonlinear elasticity. Anal Appl. 2009;7(1):21–71.10.1142/S021953050900130XSuche in Google Scholar

[4] Nie J, Tang L, Cai CS. Performance of steel-concrete composite beams under combined bending and torsion. J Struct Eng. 2009;135(9):1048–57.10.1061/(ASCE)ST.1943-541X.0000042Suche in Google Scholar

[5] Lee BK, Oh SJ, Lee TE. Free vibration of tapered Timoshenko beams by deformation decomposition. Int J Struct Stab Dyn. 2013;13(2):1250057.10.1142/S0219455412500575Suche in Google Scholar

[6] Williams JR, Hocking G, Mustoe GGW. The theoretical basis of the discrete element method. In Proceedings of the International Conference on Numerical Methods in Engineering: Theory and Applications; 1985.Suche in Google Scholar

[7] He QC, Zheng QS. Decomposition of large incompressible deformations. J Elast. 2006;85(3):175–87.10.1007/s10659-006-9080-2Suche in Google Scholar

[8] Zhang CH, Wang DD, Zhang JL, Feng W, Huang Q. On the equivalence of various hybrid finite elements and a new orthogonalization method for explicit element stiffness formulation. Finite Elem Anal Des. 2007;43(4):321–32.10.1016/j.finel.2006.11.002Suche in Google Scholar

[9] Zhang C, Hoa SV. A systematic and quantitative method to determine the optimal assumed stress fields for hybrid stress finite elements. Finite Elem Anal Des. 2014;80:41–62.10.1016/j.finel.2013.10.008Suche in Google Scholar

[10] Wang JM, Yuan LL, Law SS. Deformation decomposition based on the elemental eigen-deformation shapes. In Earth and Space 2010: Engineering, science, construction, and operations in challenging environments. Reston, VA: ASCE; 2010. p. 2336–42.10.1061/41096(366)216Suche in Google Scholar

[11] Han S, Feeny B. Application of proper orthogonal decomposition to structural vibration analysis. Mech Syst Signal Process. 2003;17(5):989–1001.10.1006/mssp.2002.1570Suche in Google Scholar

[12] Cook RD, Malkus DS, Plesha ME, Witt RJ. Concepts and applications of finite element analysis. Hoboken, NJ: John Wiley & Sons Inc; 2001.Suche in Google Scholar

[13] Liang KX, Sun PX, Wang DW, Yan Y. A complete orthogonal decomposition method for the comprehensive deformation energy of discrete elastomers. Acta Mech Sin. 2024;40(11):22–36.10.1007/s10409-024-23181-xSuche in Google Scholar

[14] Clough R, Penzien J. Dynamics of structures. Berkeley, CA: Computers & Structures Inc; 1995.Suche in Google Scholar
Received: 2025-06-06
Revised: 2025-07-18
Accepted: 2025-07-25
Published Online: 2025-09-11

© 2025 the author(s), published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

  1. Research Articles
  2. Generalized (ψ,φ)-contraction to investigate Volterra integral inclusions and fractal fractional PDEs in super-metric space with numerical experiments
  3. Solitons in ultrasound imaging: Exploring applications and enhancements via the Westervelt equation
  4. Stochastic improved Simpson for solving nonlinear fractional-order systems using product integration rules
  5. Exploring dynamical features like bifurcation assessment, sensitivity visualization, and solitary wave solutions of the integrable Akbota equation
  6. Research on surface defect detection method and optimization of paper-plastic composite bag based on improved combined segmentation algorithm
  7. Impact the sulphur content in Iraqi crude oil on the mechanical properties and corrosion behaviour of carbon steel in various types of API 5L pipelines and ASTM 106 grade B
  8. Unravelling quiescent optical solitons: An exploration of the complex Ginzburg–Landau equation with nonlinear chromatic dispersion and self-phase modulation
  9. Perturbation-iteration approach for fractional-order logistic differential equations
  10. Variational formulations for the Euler and Navier–Stokes systems in fluid mechanics and related models
  11. Rotor response to unbalanced load and system performance considering variable bearing profile
  12. DeepFowl: Disease prediction from chicken excreta images using deep learning
  13. Channel flow of Ellis fluid due to cilia motion
  14. A case study of fractional-order varicella virus model to nonlinear dynamics strategy for control and prevalence
  15. Multi-point estimation weldment recognition and estimation of pose with data-driven robotics design
  16. Analysis of Hall current and nonuniform heating effects on magneto-convection between vertically aligned plates under the influence of electric and magnetic fields
  17. A comparative study on residual power series method and differential transform method through the time-fractional telegraph equation
  18. Insights from the nonlinear Schrödinger–Hirota equation with chromatic dispersion: Dynamics in fiber–optic communication
  19. Mathematical analysis of Jeffrey ferrofluid on stretching surface with the Darcy–Forchheimer model
  20. Exploring the interaction between lump, stripe and double-stripe, and periodic wave solutions of the Konopelchenko–Dubrovsky–Kaup–Kupershmidt system
  21. Computational investigation of tuberculosis and HIV/AIDS co-infection in fuzzy environment
  22. Signature verification by geometry and image processing
  23. Theoretical and numerical approach for quantifying sensitivity to system parameters of nonlinear systems
  24. Chaotic behaviors, stability, and solitary wave propagations of M-fractional LWE equation in magneto-electro-elastic circular rod
  25. Dynamic analysis and optimization of syphilis spread: Simulations, integrating treatment and public health interventions
  26. Visco-thermoelastic rectangular plate under uniform loading: A study of deflection
  27. Threshold dynamics and optimal control of an epidemiological smoking model
  28. Numerical computational model for an unsteady hybrid nanofluid flow in a porous medium past an MHD rotating sheet
  29. Regression prediction model of fabric brightness based on light and shadow reconstruction of layered images
  30. Dynamics and prevention of gemini virus infection in red chili crops studied with generalized fractional operator: Analysis and modeling
  31. Qualitative analysis on existence and stability of nonlinear fractional dynamic equations on time scales
  32. Fractional-order super-twisting sliding mode active disturbance rejection control for electro-hydraulic position servo systems
  33. Analytical exploration and parametric insights into optical solitons in magneto-optic waveguides: Advances in nonlinear dynamics for applied sciences
  34. Bifurcation dynamics and optical soliton structures in the nonlinear Schrödinger–Bopp–Podolsky system
  35. User profiling in university libraries by combining multi-perspective clustering algorithm and reader behavior analysis
  36. Exploring bifurcation and chaos control in a discrete-time Lotka–Volterra model framework for COVID-19 modeling
  37. Review Article
  38. Haar wavelet collocation method for existence and numerical solutions of fourth-order integro-differential equations with bounded coefficients
  39. Special Issue: Nonlinear Analysis and Design of Communication Networks for IoT Applications - Part II
  40. Silicon-based all-optical wavelength converter for on-chip optical interconnection
  41. Research on a path-tracking control system of unmanned rollers based on an optimization algorithm and real-time feedback
  42. Analysis of the sports action recognition model based on the LSTM recurrent neural network
  43. Industrial robot trajectory error compensation based on enhanced transfer convolutional neural networks
  44. Research on IoT network performance prediction model of power grid warehouse based on nonlinear GA-BP neural network
  45. Interactive recommendation of social network communication between cities based on GNN and user preferences
  46. Application of improved P-BEM in time varying channel prediction in 5G high-speed mobile communication system
  47. Construction of a BIM smart building collaborative design model combining the Internet of Things
  48. Optimizing malicious website prediction: An advanced XGBoost-based machine learning model
  49. Economic operation analysis of the power grid combining communication network and distributed optimization algorithm
  50. Sports video temporal action detection technology based on an improved MSST algorithm
  51. Internet of things data security and privacy protection based on improved federated learning
  52. Enterprise power emission reduction technology based on the LSTM–SVM model
  53. Construction of multi-style face models based on artistic image generation algorithms
  54. Research and application of interactive digital twin monitoring system for photovoltaic power station based on global perception
  55. Special Issue: Decision and Control in Nonlinear Systems - Part II
  56. Animation video frame prediction based on ConvGRU fine-grained synthesis flow
  57. Application of GGNN inference propagation model for martial art intensity evaluation
  58. Benefit evaluation of building energy-saving renovation projects based on BWM weighting method
  59. Deep neural network application in real-time economic dispatch and frequency control of microgrids
  60. Real-time force/position control of soft growing robots: A data-driven model predictive approach
  61. Mechanical product design and manufacturing system based on CNN and server optimization algorithm
  62. Application of finite element analysis in the formal analysis of ancient architectural plaque section
  63. Research on territorial spatial planning based on data mining and geographic information visualization
  64. Fault diagnosis of agricultural sprinkler irrigation machinery equipment based on machine vision
  65. Closure technology of large span steel truss arch bridge with temporarily fixed edge supports
  66. Intelligent accounting question-answering robot based on a large language model and knowledge graph
  67. Analysis of manufacturing and retailer blockchain decision based on resource recyclability
  68. Flexible manufacturing workshop mechanical processing and product scheduling algorithm based on MES
  69. Exploration of indoor environment perception and design model based on virtual reality technology
  70. Tennis automatic ball-picking robot based on image object detection and positioning technology
  71. A new CNN deep learning model for computer-intelligent color matching
  72. Design of AR-based general computer technology experiment demonstration platform
  73. Indoor environment monitoring method based on the fusion of audio recognition and video patrol features
  74. Health condition prediction method of the computer numerical control machine tool parts by ensembling digital twins and improved LSTM networks
  75. Establishment of a green degree evaluation model for wall materials based on lifecycle
  76. Quantitative evaluation of college music teaching pronunciation based on nonlinear feature extraction
  77. Multi-index nonlinear robust virtual synchronous generator control method for microgrid inverters
  78. Manufacturing engineering production line scheduling management technology integrating availability constraints and heuristic rules
  79. Analysis of digital intelligent financial audit system based on improved BiLSTM neural network
  80. Attention community discovery model applied to complex network information analysis
  81. A neural collaborative filtering recommendation algorithm based on attention mechanism and contrastive learning
  82. Rehabilitation training method for motor dysfunction based on video stream matching
  83. Research on façade design for cold-region buildings based on artificial neural networks and parametric modeling techniques
  84. Intelligent implementation of muscle strain identification algorithm in Mi health exercise induced waist muscle strain
  85. Optimization design of urban rainwater and flood drainage system based on SWMM
  86. Improved GA for construction progress and cost management in construction projects
  87. Evaluation and prediction of SVM parameters in engineering cost based on random forest hybrid optimization
  88. Museum intelligent warning system based on wireless data module
  89. Optimization design and research of mechatronics based on torque motor control algorithm
  90. Special Issue: Nonlinear Engineering’s significance in Materials Science
  91. Experimental research on the degradation of chemical industrial wastewater by combined hydrodynamic cavitation based on nonlinear dynamic model
  92. Study on low-cycle fatigue life of nickel-based superalloy GH4586 at various temperatures
  93. Some results of solutions to neutral stochastic functional operator-differential equations
  94. Ultrasonic cavitation did not occur in high-pressure CO2 liquid
  95. Research on the performance of a novel type of cemented filler material for coal mine opening and filling
  96. Testing of recycled fine aggregate concrete’s mechanical properties using recycled fine aggregate concrete and research on technology for highway construction
  97. A modified fuzzy TOPSIS approach for the condition assessment of existing bridges
  98. Nonlinear structural and vibration analysis of straddle monorail pantograph under random excitations
  99. Achieving high efficiency and stability in blue OLEDs: Role of wide-gap hosts and emitter interactions
  100. Construction of teaching quality evaluation model of online dance teaching course based on improved PSO-BPNN
  101. Enhanced electrical conductivity and electromagnetic shielding properties of multi-component polymer/graphite nanocomposites prepared by solid-state shear milling
  102. Optimization of thermal characteristics of buried composite phase-change energy storage walls based on nonlinear engineering methods
  103. A higher-performance big data-based movie recommendation system
  104. Nonlinear impact of minimum wage on labor employment in China
  105. Nonlinear comprehensive evaluation method based on information entropy and discrimination optimization
  106. Application of numerical calculation methods in stability analysis of pile foundation under complex foundation conditions
  107. Research on the contribution of shale gas development and utilization in Sichuan Province to carbon peak based on the PSA process
  108. Characteristics of tight oil reservoirs and their impact on seepage flow from a nonlinear engineering perspective
  109. Nonlinear deformation decomposition and mode identification of plane structures via orthogonal theory
  110. Numerical simulation of damage mechanism in rock with cracks impacted by self-excited pulsed jet based on SPH-FEM coupling method: The perspective of nonlinear engineering and materials science
  111. Cross-scale modeling and collaborative optimization of ethanol-catalyzed coupling to produce C4 olefins: Nonlinear modeling and collaborative optimization strategies
  112. Unequal width T-node stress concentration factor analysis of stiffened rectangular steel pipe concrete
  113. Special Issue: Advances in Nonlinear Dynamics and Control
  114. Development of a cognitive blood glucose–insulin control strategy design for a nonlinear diabetic patient model
  115. Big data-based optimized model of building design in the context of rural revitalization
  116. Multi-UAV assisted air-to-ground data collection for ground sensors with unknown positions
  117. Design of urban and rural elderly care public areas integrating person-environment fit theory
  118. Application of lossless signal transmission technology in piano timbre recognition
  119. Application of improved GA in optimizing rural tourism routes
  120. Architectural animation generation system based on AL-GAN algorithm
  121. Advanced sentiment analysis in online shopping: Implementing LSTM models analyzing E-commerce user sentiments
  122. Intelligent recommendation algorithm for piano tracks based on the CNN model
  123. Visualization of large-scale user association feature data based on a nonlinear dimensionality reduction method
  124. Low-carbon economic optimization of microgrid clusters based on an energy interaction operation strategy
  125. Optimization effect of video data extraction and search based on Faster-RCNN hybrid model on intelligent information systems
  126. Construction of image segmentation system combining TC and swarm intelligence algorithm
  127. Particle swarm optimization and fuzzy C-means clustering algorithm for the adhesive layer defect detection
  128. Optimization of student learning status by instructional intervention decision-making techniques incorporating reinforcement learning
  129. Fuzzy model-based stabilization control and state estimation of nonlinear systems
  130. Optimization of distribution network scheduling based on BA and photovoltaic uncertainty
  131. Tai Chi movement segmentation and recognition on the grounds of multi-sensor data fusion and the DBSCAN algorithm
  132. Special Issue: Dynamic Engineering and Control Methods for the Nonlinear Systems - Part III
  133. Generalized numerical RKM method for solving sixth-order fractional partial differential equations
https://doi.org/10.1515/nleng-2025-0168
Schlagwörter für diesen Artikel
nonlinear deformation decomposition; mode identification; bending deformation; coupled mode, complete orthogonal base
Creative Commons
BY 4.0

Artikel in diesem Heft

  1. Research Articles
  2. Generalized (ψ,φ)-contraction to investigate Volterra integral inclusions and fractal fractional PDEs in super-metric space with numerical experiments
  3. Solitons in ultrasound imaging: Exploring applications and enhancements via the Westervelt equation
  4. Stochastic improved Simpson for solving nonlinear fractional-order systems using product integration rules
  5. Exploring dynamical features like bifurcation assessment, sensitivity visualization, and solitary wave solutions of the integrable Akbota equation
  6. Research on surface defect detection method and optimization of paper-plastic composite bag based on improved combined segmentation algorithm
  7. Impact the sulphur content in Iraqi crude oil on the mechanical properties and corrosion behaviour of carbon steel in various types of API 5L pipelines and ASTM 106 grade B
  8. Unravelling quiescent optical solitons: An exploration of the complex Ginzburg–Landau equation with nonlinear chromatic dispersion and self-phase modulation
  9. Perturbation-iteration approach for fractional-order logistic differential equations
  10. Variational formulations for the Euler and Navier–Stokes systems in fluid mechanics and related models
  11. Rotor response to unbalanced load and system performance considering variable bearing profile
  12. DeepFowl: Disease prediction from chicken excreta images using deep learning
  13. Channel flow of Ellis fluid due to cilia motion
  14. A case study of fractional-order varicella virus model to nonlinear dynamics strategy for control and prevalence
  15. Multi-point estimation weldment recognition and estimation of pose with data-driven robotics design
  16. Analysis of Hall current and nonuniform heating effects on magneto-convection between vertically aligned plates under the influence of electric and magnetic fields
  17. A comparative study on residual power series method and differential transform method through the time-fractional telegraph equation
  18. Insights from the nonlinear Schrödinger–Hirota equation with chromatic dispersion: Dynamics in fiber–optic communication
  19. Mathematical analysis of Jeffrey ferrofluid on stretching surface with the Darcy–Forchheimer model
  20. Exploring the interaction between lump, stripe and double-stripe, and periodic wave solutions of the Konopelchenko–Dubrovsky–Kaup–Kupershmidt system
  21. Computational investigation of tuberculosis and HIV/AIDS co-infection in fuzzy environment
  22. Signature verification by geometry and image processing
  23. Theoretical and numerical approach for quantifying sensitivity to system parameters of nonlinear systems
  24. Chaotic behaviors, stability, and solitary wave propagations of M-fractional LWE equation in magneto-electro-elastic circular rod
  25. Dynamic analysis and optimization of syphilis spread: Simulations, integrating treatment and public health interventions
  26. Visco-thermoelastic rectangular plate under uniform loading: A study of deflection
  27. Threshold dynamics and optimal control of an epidemiological smoking model
  28. Numerical computational model for an unsteady hybrid nanofluid flow in a porous medium past an MHD rotating sheet
  29. Regression prediction model of fabric brightness based on light and shadow reconstruction of layered images
  30. Dynamics and prevention of gemini virus infection in red chili crops studied with generalized fractional operator: Analysis and modeling
  31. Qualitative analysis on existence and stability of nonlinear fractional dynamic equations on time scales
  32. Fractional-order super-twisting sliding mode active disturbance rejection control for electro-hydraulic position servo systems
  33. Analytical exploration and parametric insights into optical solitons in magneto-optic waveguides: Advances in nonlinear dynamics for applied sciences
  34. Bifurcation dynamics and optical soliton structures in the nonlinear Schrödinger–Bopp–Podolsky system
  35. User profiling in university libraries by combining multi-perspective clustering algorithm and reader behavior analysis
  36. Exploring bifurcation and chaos control in a discrete-time Lotka–Volterra model framework for COVID-19 modeling
  37. Review Article
  38. Haar wavelet collocation method for existence and numerical solutions of fourth-order integro-differential equations with bounded coefficients
  39. Special Issue: Nonlinear Analysis and Design of Communication Networks for IoT Applications - Part II
  40. Silicon-based all-optical wavelength converter for on-chip optical interconnection
  41. Research on a path-tracking control system of unmanned rollers based on an optimization algorithm and real-time feedback
  42. Analysis of the sports action recognition model based on the LSTM recurrent neural network
  43. Industrial robot trajectory error compensation based on enhanced transfer convolutional neural networks
  44. Research on IoT network performance prediction model of power grid warehouse based on nonlinear GA-BP neural network
  45. Interactive recommendation of social network communication between cities based on GNN and user preferences
  46. Application of improved P-BEM in time varying channel prediction in 5G high-speed mobile communication system
  47. Construction of a BIM smart building collaborative design model combining the Internet of Things
  48. Optimizing malicious website prediction: An advanced XGBoost-based machine learning model
  49. Economic operation analysis of the power grid combining communication network and distributed optimization algorithm
  50. Sports video temporal action detection technology based on an improved MSST algorithm
  51. Internet of things data security and privacy protection based on improved federated learning
  52. Enterprise power emission reduction technology based on the LSTM–SVM model
  53. Construction of multi-style face models based on artistic image generation algorithms
  54. Research and application of interactive digital twin monitoring system for photovoltaic power station based on global perception
  55. Special Issue: Decision and Control in Nonlinear Systems - Part II
  56. Animation video frame prediction based on ConvGRU fine-grained synthesis flow
  57. Application of GGNN inference propagation model for martial art intensity evaluation
  58. Benefit evaluation of building energy-saving renovation projects based on BWM weighting method
  59. Deep neural network application in real-time economic dispatch and frequency control of microgrids
  60. Real-time force/position control of soft growing robots: A data-driven model predictive approach
  61. Mechanical product design and manufacturing system based on CNN and server optimization algorithm
  62. Application of finite element analysis in the formal analysis of ancient architectural plaque section
  63. Research on territorial spatial planning based on data mining and geographic information visualization
  64. Fault diagnosis of agricultural sprinkler irrigation machinery equipment based on machine vision
  65. Closure technology of large span steel truss arch bridge with temporarily fixed edge supports
  66. Intelligent accounting question-answering robot based on a large language model and knowledge graph
  67. Analysis of manufacturing and retailer blockchain decision based on resource recyclability
  68. Flexible manufacturing workshop mechanical processing and product scheduling algorithm based on MES
  69. Exploration of indoor environment perception and design model based on virtual reality technology
  70. Tennis automatic ball-picking robot based on image object detection and positioning technology
  71. A new CNN deep learning model for computer-intelligent color matching
  72. Design of AR-based general computer technology experiment demonstration platform
  73. Indoor environment monitoring method based on the fusion of audio recognition and video patrol features
  74. Health condition prediction method of the computer numerical control machine tool parts by ensembling digital twins and improved LSTM networks
  75. Establishment of a green degree evaluation model for wall materials based on lifecycle
  76. Quantitative evaluation of college music teaching pronunciation based on nonlinear feature extraction
  77. Multi-index nonlinear robust virtual synchronous generator control method for microgrid inverters
  78. Manufacturing engineering production line scheduling management technology integrating availability constraints and heuristic rules
  79. Analysis of digital intelligent financial audit system based on improved BiLSTM neural network
  80. Attention community discovery model applied to complex network information analysis
  81. A neural collaborative filtering recommendation algorithm based on attention mechanism and contrastive learning
  82. Rehabilitation training method for motor dysfunction based on video stream matching
  83. Research on façade design for cold-region buildings based on artificial neural networks and parametric modeling techniques
  84. Intelligent implementation of muscle strain identification algorithm in Mi health exercise induced waist muscle strain
  85. Optimization design of urban rainwater and flood drainage system based on SWMM
  86. Improved GA for construction progress and cost management in construction projects
  87. Evaluation and prediction of SVM parameters in engineering cost based on random forest hybrid optimization
  88. Museum intelligent warning system based on wireless data module
  89. Optimization design and research of mechatronics based on torque motor control algorithm
  90. Special Issue: Nonlinear Engineering’s significance in Materials Science
  91. Experimental research on the degradation of chemical industrial wastewater by combined hydrodynamic cavitation based on nonlinear dynamic model
  92. Study on low-cycle fatigue life of nickel-based superalloy GH4586 at various temperatures
  93. Some results of solutions to neutral stochastic functional operator-differential equations
  94. Ultrasonic cavitation did not occur in high-pressure CO2 liquid
  95. Research on the performance of a novel type of cemented filler material for coal mine opening and filling
  96. Testing of recycled fine aggregate concrete’s mechanical properties using recycled fine aggregate concrete and research on technology for highway construction
  97. A modified fuzzy TOPSIS approach for the condition assessment of existing bridges
  98. Nonlinear structural and vibration analysis of straddle monorail pantograph under random excitations
  99. Achieving high efficiency and stability in blue OLEDs: Role of wide-gap hosts and emitter interactions
  100. Construction of teaching quality evaluation model of online dance teaching course based on improved PSO-BPNN
  101. Enhanced electrical conductivity and electromagnetic shielding properties of multi-component polymer/graphite nanocomposites prepared by solid-state shear milling
  102. Optimization of thermal characteristics of buried composite phase-change energy storage walls based on nonlinear engineering methods
  103. A higher-performance big data-based movie recommendation system
  104. Nonlinear impact of minimum wage on labor employment in China
  105. Nonlinear comprehensive evaluation method based on information entropy and discrimination optimization
  106. Application of numerical calculation methods in stability analysis of pile foundation under complex foundation conditions
  107. Research on the contribution of shale gas development and utilization in Sichuan Province to carbon peak based on the PSA process
  108. Characteristics of tight oil reservoirs and their impact on seepage flow from a nonlinear engineering perspective
  109. Nonlinear deformation decomposition and mode identification of plane structures via orthogonal theory
  110. Numerical simulation of damage mechanism in rock with cracks impacted by self-excited pulsed jet based on SPH-FEM coupling method: The perspective of nonlinear engineering and materials science
  111. Cross-scale modeling and collaborative optimization of ethanol-catalyzed coupling to produce C4 olefins: Nonlinear modeling and collaborative optimization strategies
  112. Unequal width T-node stress concentration factor analysis of stiffened rectangular steel pipe concrete
  113. Special Issue: Advances in Nonlinear Dynamics and Control
  114. Development of a cognitive blood glucose–insulin control strategy design for a nonlinear diabetic patient model
  115. Big data-based optimized model of building design in the context of rural revitalization
  116. Multi-UAV assisted air-to-ground data collection for ground sensors with unknown positions
  117. Design of urban and rural elderly care public areas integrating person-environment fit theory
  118. Application of lossless signal transmission technology in piano timbre recognition
  119. Application of improved GA in optimizing rural tourism routes
  120. Architectural animation generation system based on AL-GAN algorithm
  121. Advanced sentiment analysis in online shopping: Implementing LSTM models analyzing E-commerce user sentiments
  122. Intelligent recommendation algorithm for piano tracks based on the CNN model
  123. Visualization of large-scale user association feature data based on a nonlinear dimensionality reduction method
  124. Low-carbon economic optimization of microgrid clusters based on an energy interaction operation strategy
  125. Optimization effect of video data extraction and search based on Faster-RCNN hybrid model on intelligent information systems
  126. Construction of image segmentation system combining TC and swarm intelligence algorithm
  127. Particle swarm optimization and fuzzy C-means clustering algorithm for the adhesive layer defect detection
  128. Optimization of student learning status by instructional intervention decision-making techniques incorporating reinforcement learning
  129. Fuzzy model-based stabilization control and state estimation of nonlinear systems
  130. Optimization of distribution network scheduling based on BA and photovoltaic uncertainty
  131. Tai Chi movement segmentation and recognition on the grounds of multi-sensor data fusion and the DBSCAN algorithm
  132. Special Issue: Dynamic Engineering and Control Methods for the Nonlinear Systems - Part III
  133. Generalized numerical RKM method for solving sixth-order fractional partial differential equations
Jetzt anmelden und 20% sparen
Institutioneller Zugang
Wie funktioniert Authentifizierung?
Haben Sie eine Idee, wie wir unsere Website verbessern können?
Bitte schreiben Sie uns.
© 2025 De Gruyter Brill
Heruntergeladen am 30.12.2025 von https://www.degruyterbrill.com/document/doi/10.1515/nleng-2025-0168/html
Button zum nach oben scrollen