Tennis automatic ball-picking robot based on image object detection and positioning technology

2.1 Construction of an automatic tennis ball-picking robot model based on RFID technology

In the last few years, with the quick advancement of science and technology, robots have been widely used in various fields of social life [18]. Among them, intelligent ball-collecting robots are applied in indoor table tennis and tennis courts. They detect the ball based on images, locate the position of the ball, and achieve the goal of collecting the ball [19]. However, traditional image detection and positioning technologies often suffer from low accuracy, so research plans to use RFID systems to optimize the positioning accuracy of ball-picking robots. In the optimization process, it is necessary to establish a model, as denoted in Figure 1, for the tennis automatic ball-picking robot model.

Figure 1

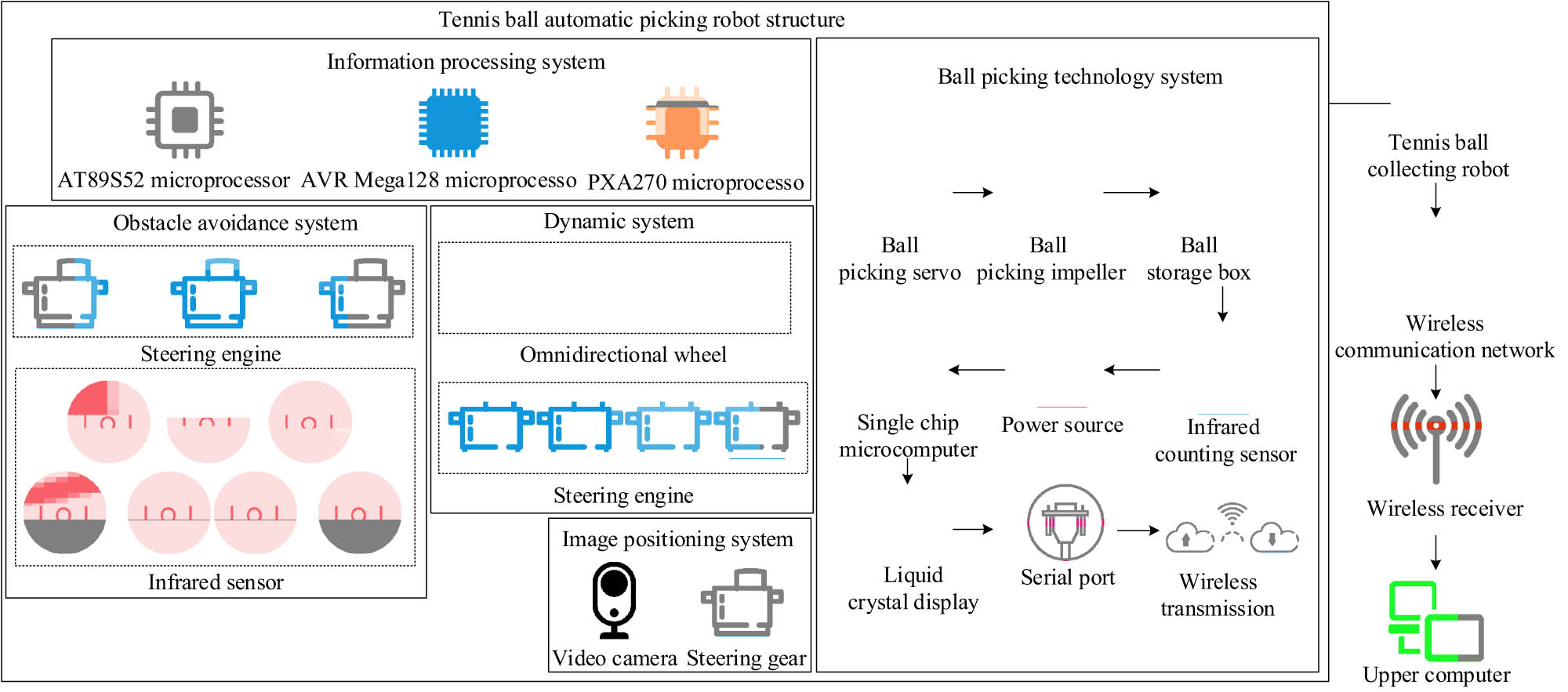
Tennis automatic ball-picking robot model.

As shown in Figure 1, the model consists of four parts: an automatic tennis ball-picking robot, a wireless communication network, a wireless network receiver, and an upper computer. Among them, the tennis automatic ball-picking robot consists of an information processing system, an image target detection and positioning system, an obstacle avoidance system, a power system, and a ball-picking technology system. The image object detection and positioning system includes a camera and a servo. The servo controls the camera to locate the sphere that needs to be collected at various angles. When the target sphere meets the image detection conditions, the robot adjusts its position to collect the sphere after calculating the position information and distance. The obstacle avoidance system consists of servo and infrared sensors, and four infrared sensors are selected to be arranged at the corners of the tennis ball-picking robot in each of the four directions. Three servos and three infrared sensors are selected and combined into a sensor with an angle and the ability to swing freely. When the sensor detects an obstacle, the robot automatically avoids it. The power system consists of four servos and four omnidirectional wheels. The servos are responsible for controlling the omnidirectional wheels and forming an angle with the front of the robot. The ball collection technology system includes a servo and wireless communication transmitter. The servo controls the impeller to collect the ball into the ball storage box while triggering a counting infrared sensor. The infrared counting sensor sends the recorded quantity to the microcontroller, which then displays the number of balls received through the LCD screen. The LCD screen sends data to the wireless communication transmitter through a serial port, and then the wireless communication receiver receives the data and sends it to the upper computer. The upper computer displays the acquired data to the operator, thereby achieving real-time monitoring and monitoring purposes. The information processing system consists of three microprocessors, which are responsible for controlling the counting and action operations during the robot’s ball collection process.

The process of an automatic tennis ball-picking robot is as follows. First, the infrared sensor and camera are used to locate the tennis ball to be collected at three different angles of 0°, 45°, and 90° in front of the robot. Second, the external features of the tennis ball, such as images and shapes, are collected and processed. Then, based on the processing results of the collected features, it determines whether it is the tennis ball that needs to be collected. If so, proceed with the collection. If not, proceed to the next step. After completing this series of actions, the robot switches its angle and moves forward 2 m, repeating the previous action in a loop until the end of one cycle. However, the positioning and picking cycle of the tennis ball-picking robot is within a range of 6 m², which poses a problem of long search time. Finding a method to improve the search efficiency of robots is of great significance. RFID technology has advantages such as fast recognition speed, high stability, and strong adaptability, and is widely used in fields such as intelligent robots and integrated circuits [20]. The structure of RFID technology is shown in Figure 2 [21].

Figure 2

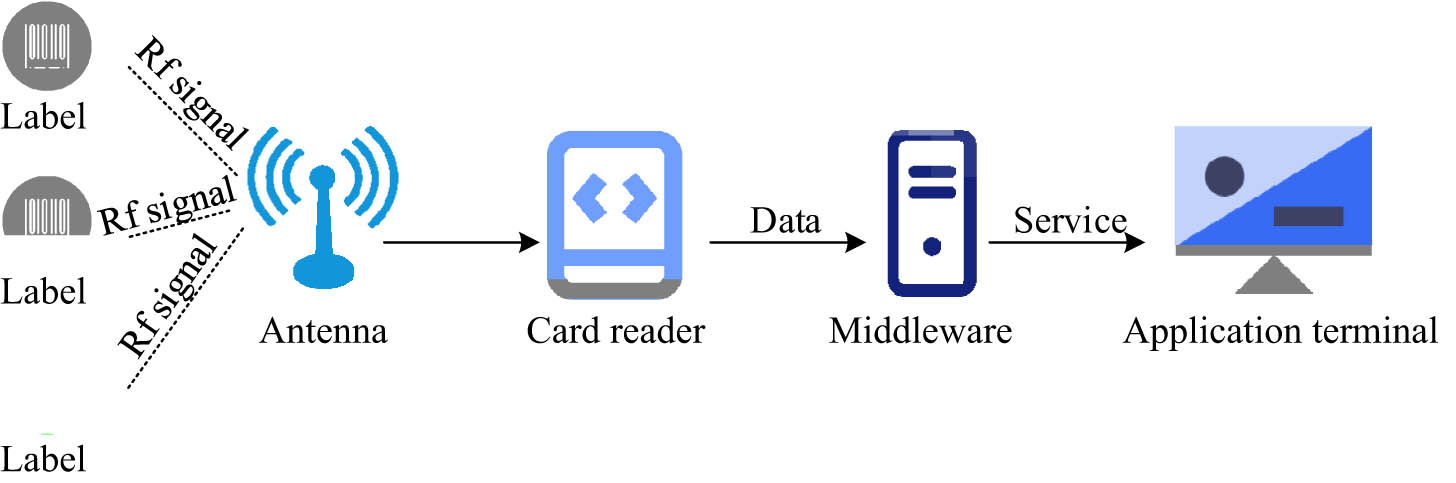
The RFID system structure diagram.

As shown in Figure 2, RFID mainly consists of antennas, card readers, electronic tags, terminals, and middleware. The RFID operation process consists of three steps. First, the antenna transmits electronic tag position information and other data to the card reader. Second, the received information is transmitted to the middleware through the card reader, and the positioning algorithm in the middleware is used to calculate this information, thereby locating the radio frequency tag with this information and obtaining its position information. Finally, the middleware will transmit the obtained radio frequency tag position to the terminal, and the terminal will display the positioning result of this tag on the display. In addition, the terminal is also responsible for storing the historical data information of each label. Due to the indoor environment and numerous obstacles in tennis, the calculation of RFID signal path loss adopts an attenuation factor propagation model, and the basic formula is shown in Eq. (1):

In Eq. (1), λ 0 is the reference distance, α is the attenuation constant, λ is the distance between the transmitter and receiver, φ η θ is the index value, and ϖ ς ϖ is the attenuation factor. Second, the logarithmic reference model is used to describe the transmission distance of the signal, and its calculation formula is shown in Eq. (2):

In Eq. (2) ∂ 0 represents the reference distance, EP ∂ and EP ∂ 0 represent the RSSI values when the distance between the transmitter and receiver is ∂ and ∂ 0 , respectively, ℓ represents the loss coefficient, ϑ τ represents the standard deviation of Gaussian noise as τ , and the mean is 0. Based on the above content, the RFID system is applied to the automatic ball collection robot for tennis, and a model of the automatic ball-picking robot for tennis based on RFID is constructed. Its structure is shown in Figure 3.

Figure 3

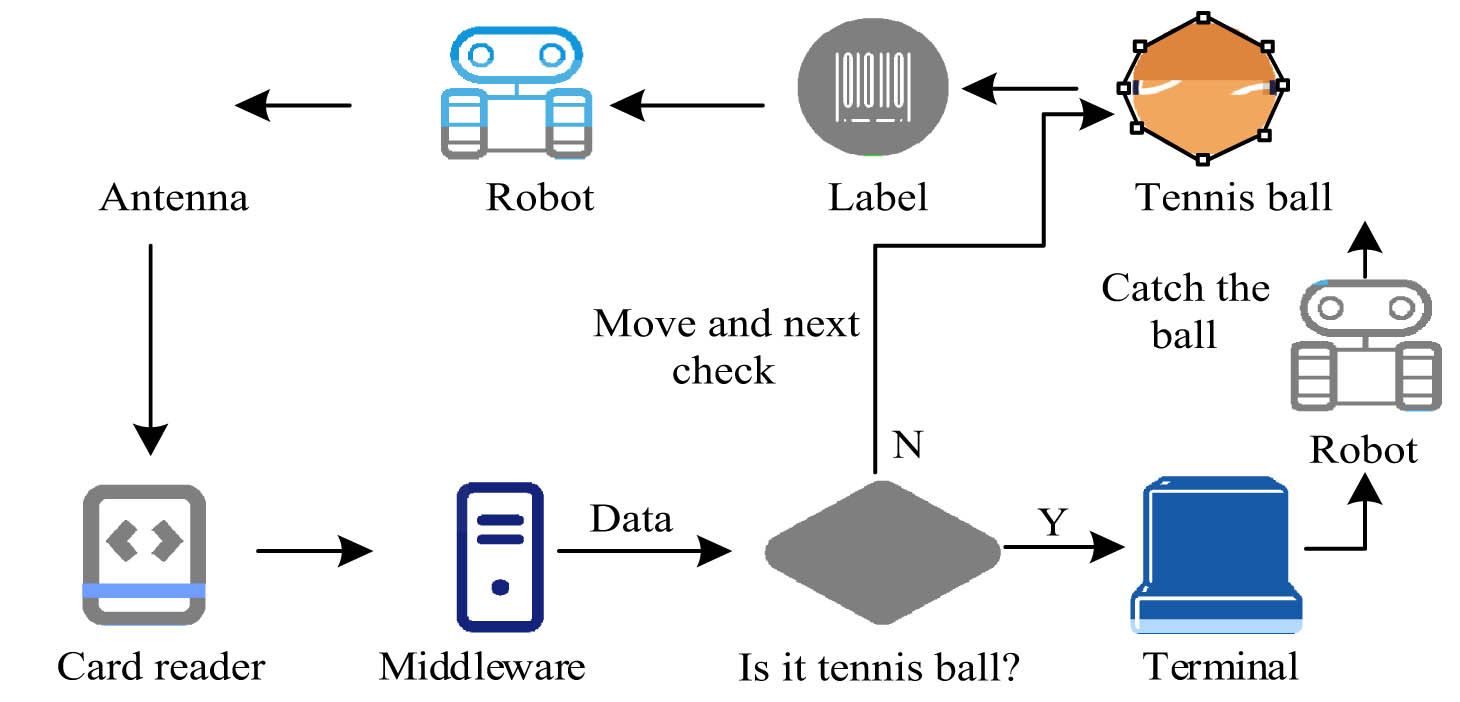
RFID-based tennis ball-picking robot model.

As shown in Figure 3, the specific operation process of the model is as follows. First, the robot obtains tennis ball images and other information through sensors and cameras and then transmits them to the card reader through antennas. Then, the card reader sends the information to the middleware, which processes the image information through algorithms and makes judgments on the processed image information. If the image information matches the set tennis ball information, the information will be transmitted to the terminal, and the ball-picking situation will be counted and stored. The terminal will issue a ball-picking command to the robot, and the robot will receive the ball. After picking it, the robot will continue with the next ball-picking operation. Otherwise, the robot will move forward to the next picking range to receive the ball until the end.

2.2 Design of a tennis automatic ball-picking robot model incorporating an improved LANDMARC algorithm

Due to the complex indoor environment, it is difficult for RFID systems to accurately locate the position of the sphere, resulting in a decrease in the accuracy of robot positioning when picking the ball. Therefore, finding an effective indoor positioning algorithm is of great significance for robots to accurately locate the position of the sphere. The LANDMARC algorithm is a positioning algorithm that uses computer vision and machine learning techniques to establish a visual map of indoor landmarks and determine the position of objects based on the map. It has the advantages of adaptive environmental changes and real-time acquisition of RSSIs and is widely utilized in the field of indoor positioning. The LANDMARC algorithm process is shown in Figure 1.

As shown in Figure 4, the process of the LANDMARC algorithm consists of three steps. First, the position of the RL and the strength of the received signal are obtained, and then the strength of the received signal of the tag to be located is obtained. Second, it calculates the Euclidean distance between the target label (TL) and the RL. Then, it obtains k neighboring RLs, which are the RLs with the shortest Euclidean distance and calculates the weights of the k RLs. Finally, it calculates the position of the label to be located based on the RL position and ends the calculation after completion. The calculation steps of the LANDMARC algorithm are as follows: first is to set a total of U readers to exist in the environment. The number of RLs in this environment is represented by M , and the number of positioning labels is represented by N . In addition, other settings in this environment include R h m = ( R h 1 m , R h 2 m , … , R h U m ) representing the vector of the electromagnetic strength of the received signal from the reference tag on each reader, where R h m represents the RSSI of the RL on the reader, R g t = ( R g 1 t , R g 2 t , … , R g U t ) represents the vector of the electromagnetic strength of the received signal from the tag to be located on each reader, and the RSSI value of the tag to be located on the reader is R g n . Second, the Euclidean distance calculation formula for the field strength of the TL and the RL can be obtained from the first step, as shown in Eq. (3):

Figure 4

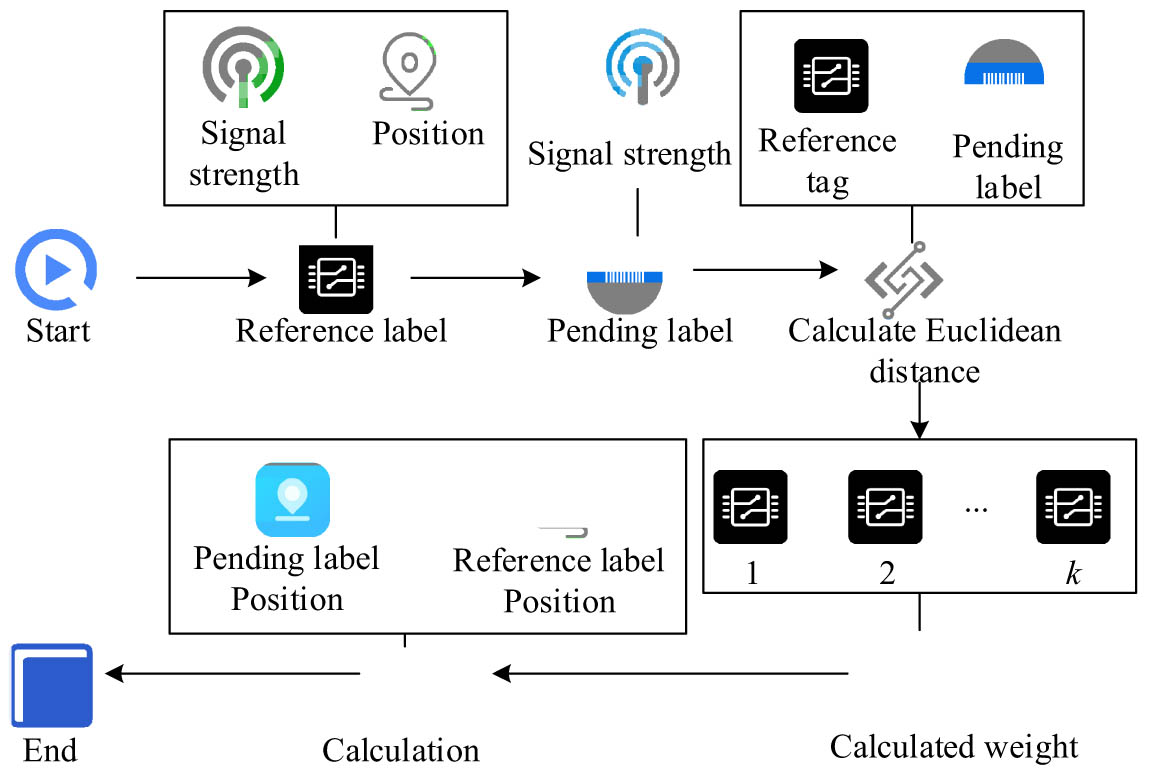
Flowchart of the LANDMARC algorithm.

In Eq. (3), u represents the card reader, n represents the tag to be located and n ∈ ( 1 , N ) , m represents the reference tag and m ∈ ( 1 , M ) , and S g h n m represents the Euclidean distance of the electric field strength between n and m . Then, by calculating the field strength Euclidean distance between the TL and RL, adjacent RLs are obtained, and the calculation formula is shown in Eq. (4):

In Eq. (4), S g h n represents the Euclidean distance vector of the electric field strength of n and its corresponding m , SK g h n represents the vector composed of the smallest k elements in S g h n , arranged in ascending order, and k represents the number of adjacent RLs. Next, it calculates the weight and coordinate values of the RL during the calculation process and assigns values and empirical formulas based on the size of the vector composed of the k smallest elements obtained. The formula for calculating the coordinate values is shown in Eq. (5):

In Eq. (5), ( x n ′ , y n ′ ) represents the estimated coordinates of the tag to be located, ( x j , y j ) represents the coordinates of the j th neighboring reference tag, which are known, and w j represents the weight of the j th neighboring RL. The formula for calculating weights is shown in Eq. (6):

The calculation formula for the final system error estimation of j ∈ ( 1 , k ) in Eq. (6) is shown in Eq. (7):

In Eq. (7), ( x n , y n ) represents the actual coordinates of the undetermined label. From the above content, the LANDMARC algorithm can collect information and achieve localization in complex indoor environments by placing RLs. However, this method is only limited to selecting fewer RLs in a small-scale positioning environment. When more RLs are needed to assist in positioning in a larger space, certain problems may arise. The error variation of the LANDMARC algorithm under different numbers of adjacent RLs is shown in Figure 5.

Figure 5

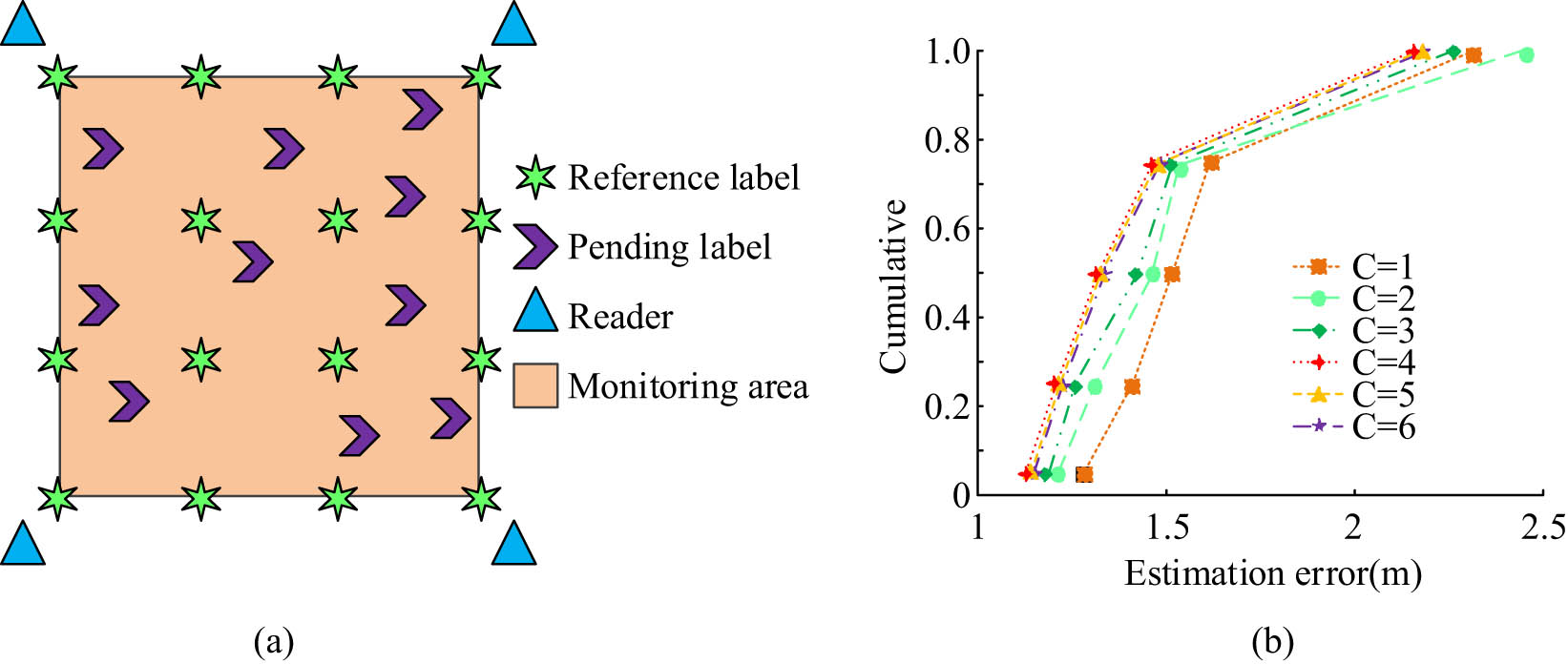
Error variation of LANDMARC algorithm under different numbers of adjacent RLs. (a) 6 × 6 Positioning system block diagram. (b) Different numbers of RL errors in the environment.

Figure 5(a) shows the specific layout structure of the LANDMARC positioning system is uniformly distributed by RLs in a 6 × 6 manner, with four readers distributed in four corners and positioning labels irregularly arranged in the monitoring area. Figure 5(b) shows that the error value of the LANDMARC algorithm increases with the increase of neighboring labels C in this environment. After the number of neighboring labels exceeds 4, there is no significant change in accuracy, but the computational load still increases. Finding a method to improve the LANDMARC algorithm’s ability to compute more neighboring labels is of great significance for improving the accuracy of positioning systems. The weighted factor refers to the number or coefficient assigned to each variable’s relative importance or influence [22]. The mechanism of weighted factor is a coefficient that assigns different importance or weights to different data points in statistical analysis or data processing. The weighted factor is used to adjust the importance of the data so that some data have more influence in the calculation than others. By using weighted factors to assign weights to neighboring RLs and correcting coefficients, smaller weight values are assigned to neighboring RLs that are further away from the Euclidean distance of the RL and TL, thereby achieving the effect of increasing the number of RLs without increasing the error [23]. The role of the introduction of a weighted factor is that with the increase in the range area of RFID positioning, the number of tags will also increase, but the increase in the number of tags will cause a large number of interference signals, and the positioning accuracy will be greatly reduced. The introduction of a weighted factor can increase the number of RLs in a wide range of positioning, but the allocation of a weighted factor to label weights will not increase the system error, and the positioning effect will be increased. Therefore, by introducing a weighted factor in weight allocation, the calculation process of the weights of neighboring labels after being improved by the weighted factor is as follows: first, the weights are improved, and the calculation formula is indicated in Eq. (8):

W j ⁎ is the improved weighted factor in Eq. (8), where j ∈ ( 1 , k ) and u represents the path loss index. Second, the formula for calculating the estimated coordinates of the tag to be located is shown in Eq. (9):

In Eq. (9), ( x n ⁎ , y n ⁎ ) represents the estimated coordinate position of the improved label to be located. Next, the formula for calculating the system estimation error is shown in Eq. (10):

In Eq. (10), e ⁎ represents the estimation error of the improved system. Finally, the formula for calculating the variation in the strength of the received signal emitted by the label during indoor propagation is shown in Eq. (11):

In Eq. (11), X δ represents the standard deviation, q represents the value of the signal received by the card reader, d represents the Euclidean distance value, and the d 0 table represents the reference point. However, although if there are more RLs, the higher is the positioning accuracy and precision, it is not allowed to place a large number of RLs in the actual environment [24]. In the RFID system, when there are a large number of reference tags in the recognition range of the reader, the data accuracy may be reduced and the system efficiency is reduced to avoid the problem of too many RLs. The virtual RL has the same characteristics as the real RL, but there is no real signal interference when the field strength is calculated by the multichannel stiffness loss model, so the signal interference can be reduced by reducing the real RL. The method of collaboration with factor weighting analysis is to process both virtual RLs and actual RLs as virtual RLs. After the virtual RLs are introduced, the field strength Euclidean distance between the virtual RLs and the pending labels is calculated to obtain the adjacent virtual RLs. Finally, the estimated coordinates of the pending labels are obtained according to the weight assignment. Virtual RLs are introduced into the LANDMARC algorithm. By arranging virtual RLs in the LANDMARC algorithm and calculating the position information, useful virtual RLs are retained, and excess virtual RL coordinate information is discarded, thereby improving the accuracy of localization [25]. The algorithm process is to set a certain number of card readers, actual RLs, and TLs in a certain environment under certain conditions, represented by A , D , and F , respectively. Moreover, it locates the card reader, actual RL, and TL to obtain the relationship between the actual RL and TL. The calculation formula is shown in Eq. (12):

In Eq. (12), V represents the number of adjacent labels. D 1 f to D v f are arranged in ascending order based on the Euclidean distance from the undetermined label to the adjacent RL. The formula for calculating the number of virtual RLs is shown in Eq. (13):

In Eq. (13), XF f represents the number of virtual RLs. ( X max f , Y max f ) and ( X min f , Y min f ) , respectively, represent the coordinates of the maximum and minimum Euclidean distances of the actual RLs corresponding to the virtual RLs. The calculation formula for the abscissa of the virtual RL is shown in Eq. (14):

In Eq. (14), X XF i f represents the horizontal axis of the virtual RL. The vertical coordinate calculation formula for virtual RLs is shown in Eq. (15):

In Eqs. (14) and (15), ( X XD i d , Y XD i d ) represents the i th virtual label, and i ∈ ( 1 , XD d ) . Based on the above content, this study constructs an improved LANDMARC algorithm, and its calculation process is shown in Figure 6.

Figure 6

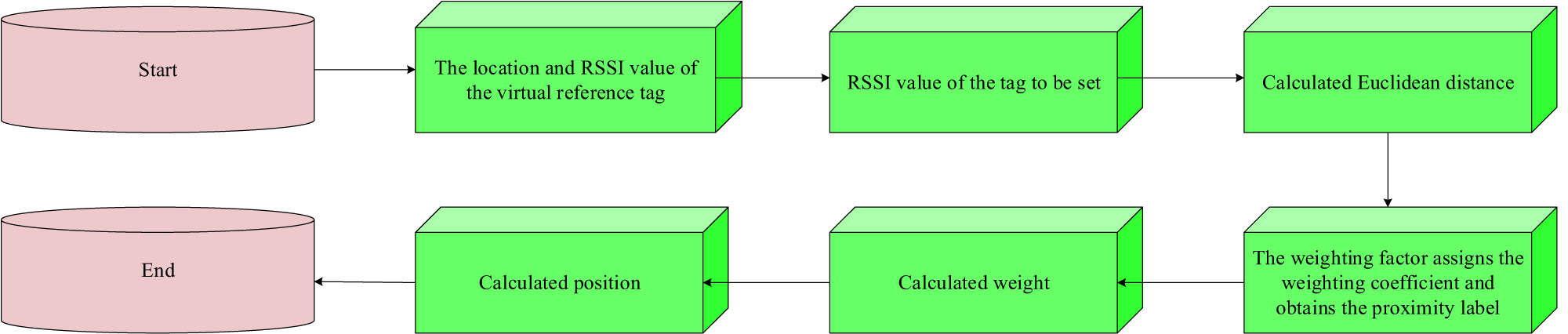
The flow chart of the improved LANDMARC algorithm.

As shown in Figure 6, the calculation process of this algorithm first treats both the RL and virtual RL as virtual RLs, and obtains their RSSI values and coordinate positions. Second, it obtains the RSSI value of the label to be located and calculates the Euclidean distance between the label to be located and the virtual RL. Then, a weighted factor is taken to assign weight correction coefficients to each virtual RL, and neighboring labels are obtained by calculating the weight of the virtual RL. Finally, the position of the label to be located is calculated based on the position of the virtual RL. Finally, this study introduces the improved LANDMARC algorithm into the RFID system and applies the system to the tennis automatic ball-picking robot model. A tennis automatic ball-picking robot model based on the improved LANDMARC algorithm and RFID technology is constructed, and its structure is denoted in Figure 7.

Figure 7

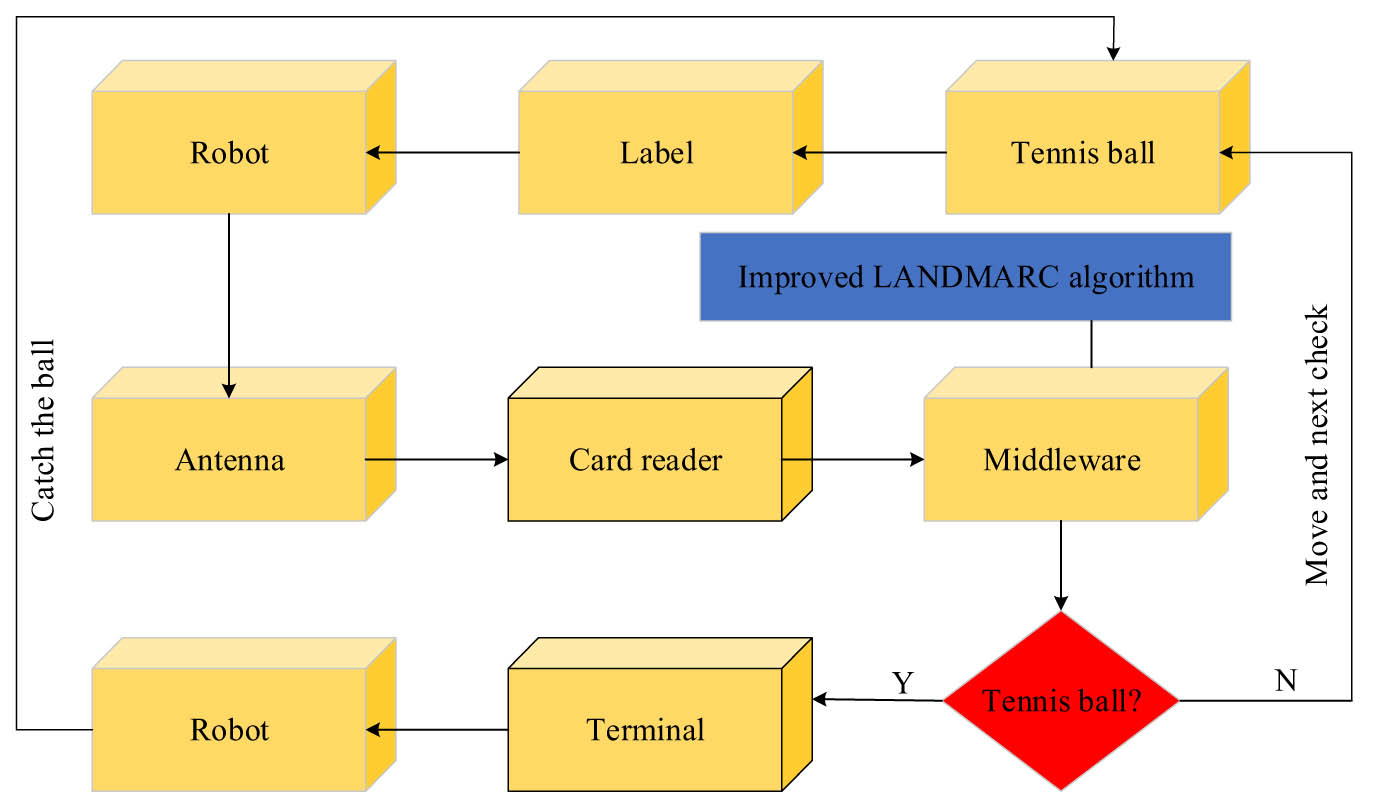
A tennis ball-picking robot model based on improved LANDMARC algorithm and RFID technology.

From Figure 7, the specific process of the model is as follows. First, the robot performs image detection on the labeled tennis balls and transmits the detection information to the card reader through an antenna. Then, it writes the improved LANDMARC algorithm middleware for calculation, determines whether the image is a tennis ball after calculation, and if so, it will send the information to the terminal for counting while the robot collects the ball. If it is not a tennis ball, the robot will move to the next range to continue the first step. In this study, to improve RFID, the coefficient is first introduced by the factor-weighted method, and the weight allocation of the LANDMARC algorithm is improved. Second, virtual RLs are introduced into the LANDMARC algorithm to reduce the number of real labels and improve positioning accuracy and efficiency. Then, the LANDMARC algorithm, which has been improved twice, is introduced into RFID middleware. Finally, when RFID uses tags for positioning, the positioning is improved through middleware calculation and processing. The effective frequency and interface of the RFID tag reader are 308 MHz and 802.11b interfaces, respectively, and have eight measurable power energy levels. The electronic tag is an active electronic tag with an average transmission interval of 7.5 s and a 7-bit ID. The maximum read and write distance of the label is about 45.71 m, and the reading range of the card reader can be expanded to 304.7 m by the antenna. In an indoor environment with an area of 6 m × 6 m, the layout density unit positioning grid is divided into four RLs, and the virtual RLs are evenly arranged in a 4 × 4 network structure.

3.1 Performance comparison testing of the improved LANDMARC algorithm

To prove the superiority of the improved LANDMARC algorithm (Algorithm 1) proposed in the study, it was experimentally compared with the improved PSO (Algorithm 2), BP-LANDMARC (Algorithm 3), and Harris-SIFT algorithm (Algorithm 4) in Matlab simulation software. The improved PSO algorithm overcomes the defects of premature convergence and improves the computational efficiency and convergence speed of the algorithm, but it still has the disadvantages of high computational cost and cannot guarantee optimal conditions in all cases. The advantage of the BP-LANDMARC algorithm is to realize the region adaptive positioning function of pending labels, reduce the introduction of interference RLs, and improve the accuracy of pending labels. Its disadvantages are low training efficiency and slow convergence speed. Although the Harris-SIFT algorithm has the advantages of simple computation and insensitive viewpoint transformation, it still has some shortcomings, such as the slow computation speed. The experimental environment was set as the number of adjacent virtual RLs was 4, the number of unpositioned labels was 10, the number of robots was 4, and the experimental area was a monitoring area of 6 m × 6 m. The experimental indicators included error value, accuracy, and running time. The specific experimental environment for this study is shown in Table 1.

In the above environment, first, comparative experiments were conducted on the error values and accuracy of the four algorithms under different neighboring label densities. The error values and accuracy results of each algorithm are shown in Figure 8.

Figure 8

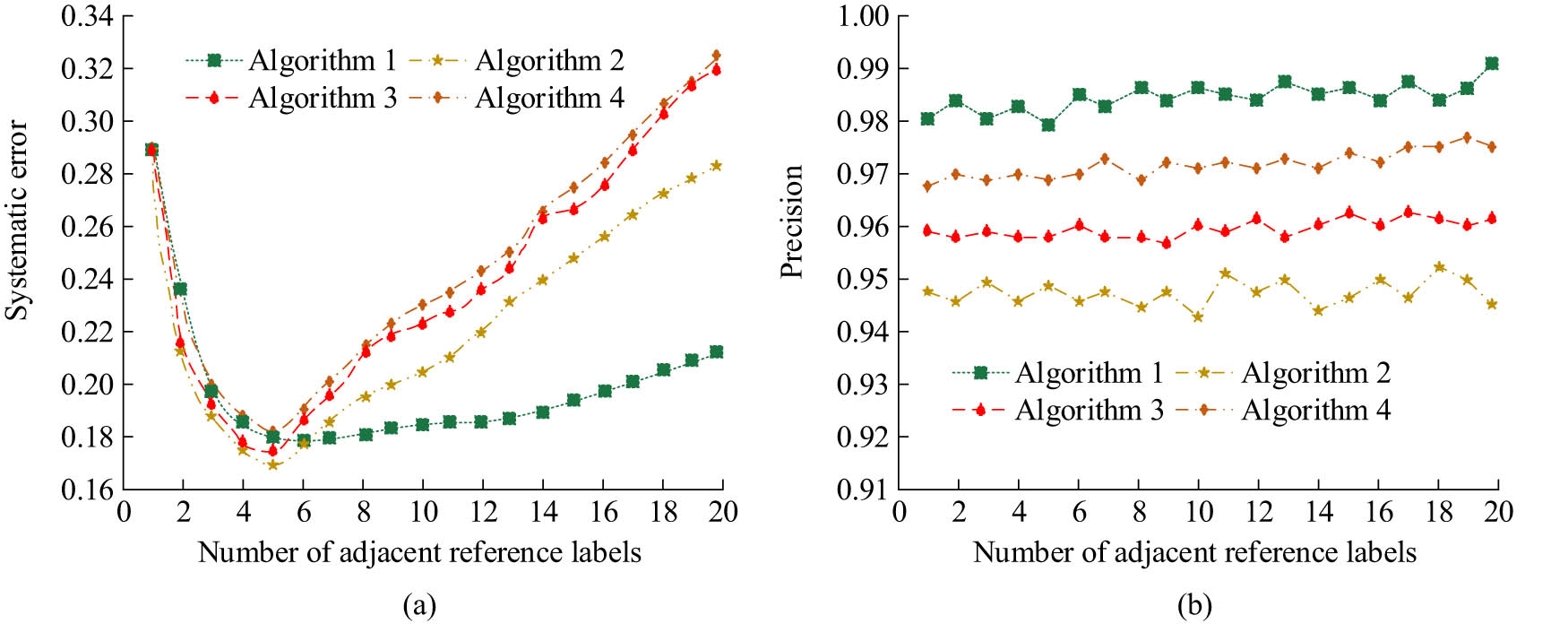
Comparison results of error values and precision of each algorithm under different neighboring tag densities. (a) The error value of each algorithm with a different number of neighboring RLs. (b) The precision of each algorithm with a different number of neighboring RLs.

As shown in Figure 8(a), the error value curve of Algorithm 1 was at its lowest point when the number of adjacent RLs was 8 and was in the range of 0.18–0.21. When the number of adjacent RLs was 20, the error value was 0.21. The error value curve of Algorithm 2 had the lowest number of adjacent RLs in the range of 0–5 and then rapidly increased higher than Algorithm 2. Moreover, when the number of adjacent RLs was 20, the error value was 0.21. Algorithm 3 had an error value of 0.31 when the number of adjacent RLs was 20. Algorithm 4 had an error value of 0.32 when the number of adjacent RLs was 20. From Figure 8(b), the average precision of Algorithm 1 was 0.983, which was significantly higher than the other algorithms. The average precision of Algorithm 2 was 0.947, Algorithm 3 was 0.958, and Algorithm 4 was 0.959. The above results indicate that from the dimensions of precision and error value, Algorithm 1 proposed in the study performs better than the comparison algorithm. The comparison results of the running time and accuracy of each algorithm are shown in Figure 9.

Figure 9

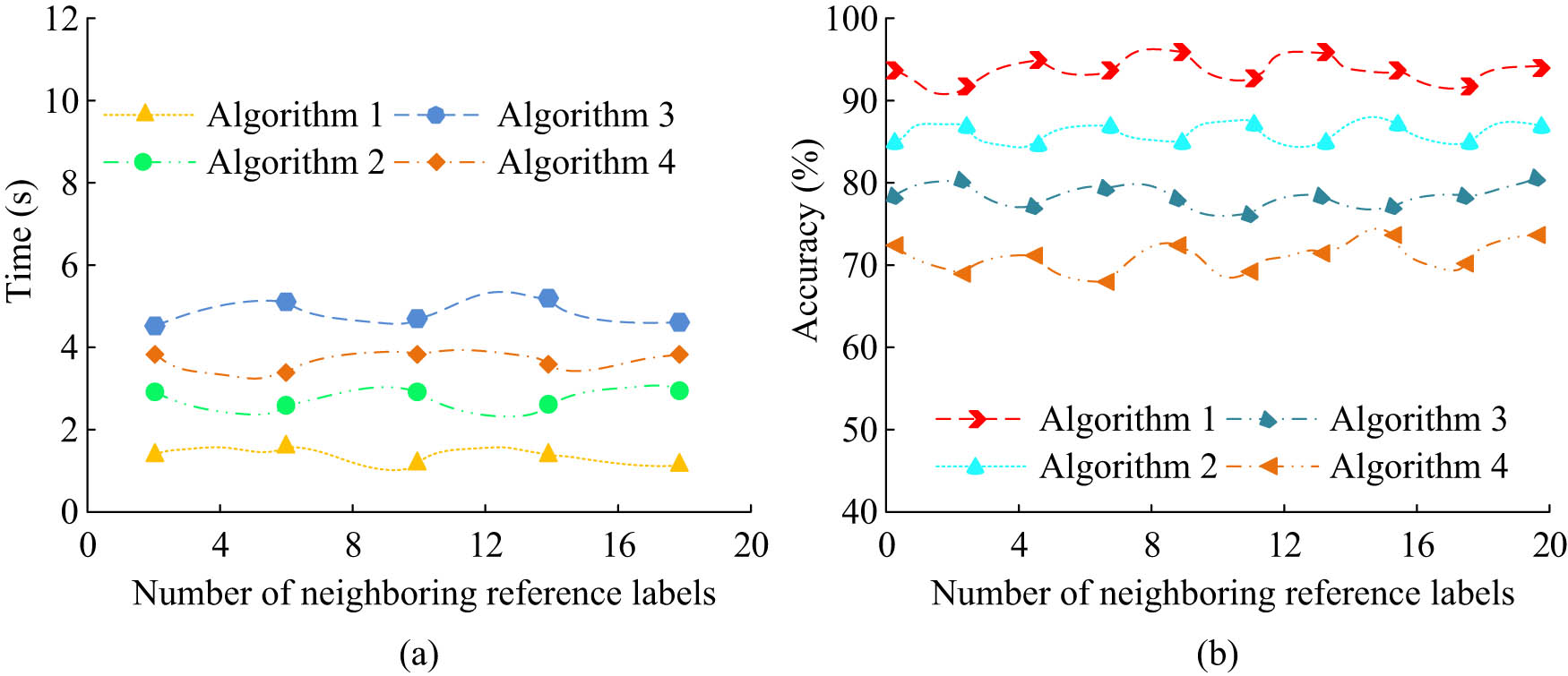
Comparison results of the running time and accuracy of each algorithm. (a) Each algorithm detects the running time. (b) Comparison result of prediction accuracy of each algorithm.

From Figure 9(a), the average running time of Algorithm 1 was 1.36 s, which was lower than 2.97 s of Algorithm 2, 4.74 s of Algorithm 3, and 3.89 s of Algorithm 4. In Figure 9(b), the average accuracy of Algorithm 1 was 94.6%, which was higher than 86.7% of Algorithm 2, 79.6% of Algorithm 3, and 72.8% of Algorithm 4. The above results indicated that from the dimensions of runtime and accuracy, the proposed Algorithm 1 performs better than other algorithms. The comparison results of the mean square error (MSE) and root mean square error (RMSE) of each algorithm are shown in Figure 10.

Figure 10

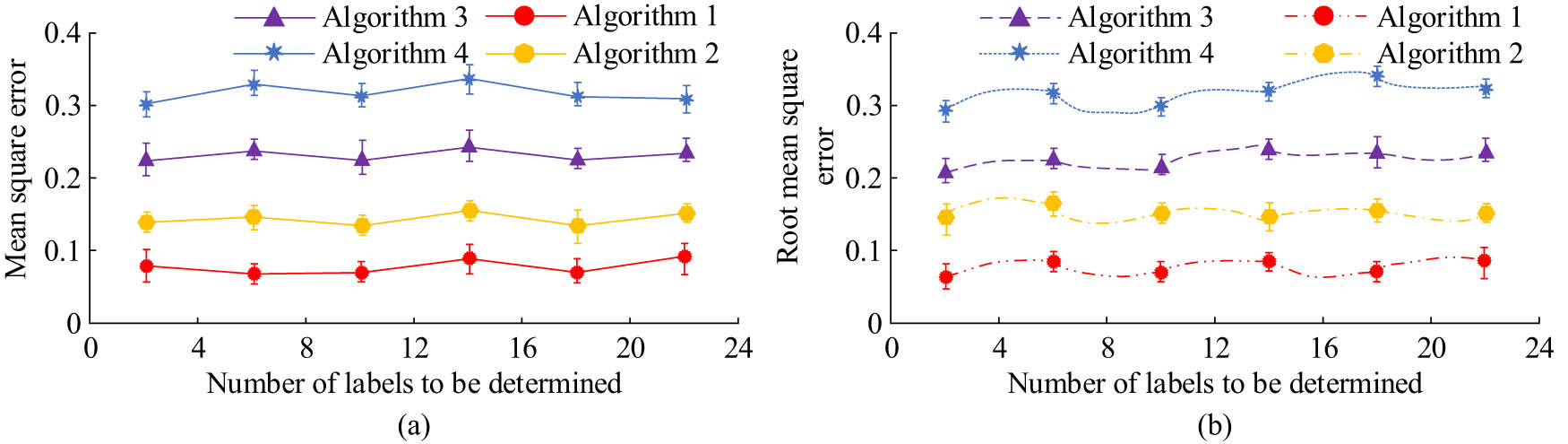
Comparison results of MSE and RMSE of each algorithm. (a) Positioning error of each algorithm. (b) Each algorithm locates the error root.

From Figure 10(a), the MSE of Algorithm 1 was 0.083, Algorithm 2 was 0.142, Algorithm 3 was 0.226, and Algorithm 4 was 0.309. Among them, Algorithm 1 had the lowest MSE. From Figure 10(b), the RMSE values of Algorithms 1, 2, 3, and 4 were 0.798, 0.136, 0.216, and 0.306, respectively. Among them, Algorithm 1 had the lowest RMSE. In addition, to further verify the superiority of the proposed algorithms, a comparison experiment on response time, computational complexity, and energy consumption was also carried out for each algorithm. The index was the comparison results of response time, time complexity, and CUP usage, and the specific results are shown in Table 2.

From Table 2, the response time, time complexity, and CUP usage of Algorithm 1 proposed in this study were 0.14 s, O(1), and 7.26%, respectively, which were superior to those of the comparison algorithms. The above results showed that the performance of the proposed algorithm was significantly better than that of the comparison algorithms in terms of response time, time complexity, and CUP usage. The above results indicated that from the dimensions of MSE and RMSE, the proposed Algorithm 1 had significantly better positioning accuracy than comparison algorithms. In summary, from the dimensions of MSE, RMSE, running time, accuracy, and precision, the algorithm proposed in the study performs better than the comparative algorithms, indicating its effectiveness.

3.2 Analysis of the application effect of the tennis automatic ball-picking robot model

To verify the performance superiority of the proposed tennis automatic ball-picking robot model (Model 1), comparative experiments were conducted with the improved PSO-based tennis automatic ball-picking robot model (Model 2), the BP-LANDMARC-based tennis automatic ball-picking robot model (Model 3), and the Harris-SIFT-based tennis automatic ball-picking robot model (Model 4). The robot collected the ball by targeting the nearest sphere detected within its field of view. To verify its stability and detection accuracy, a study was conducted by placing four tennis balls in different positions, allowing four model robots to collect the ball from the starting point, and conducting a comparative experiment on the trajectory of the ball collection action. The comparison results of the picking trajectory of each model robot are shown in Figure 11.

Figure 11

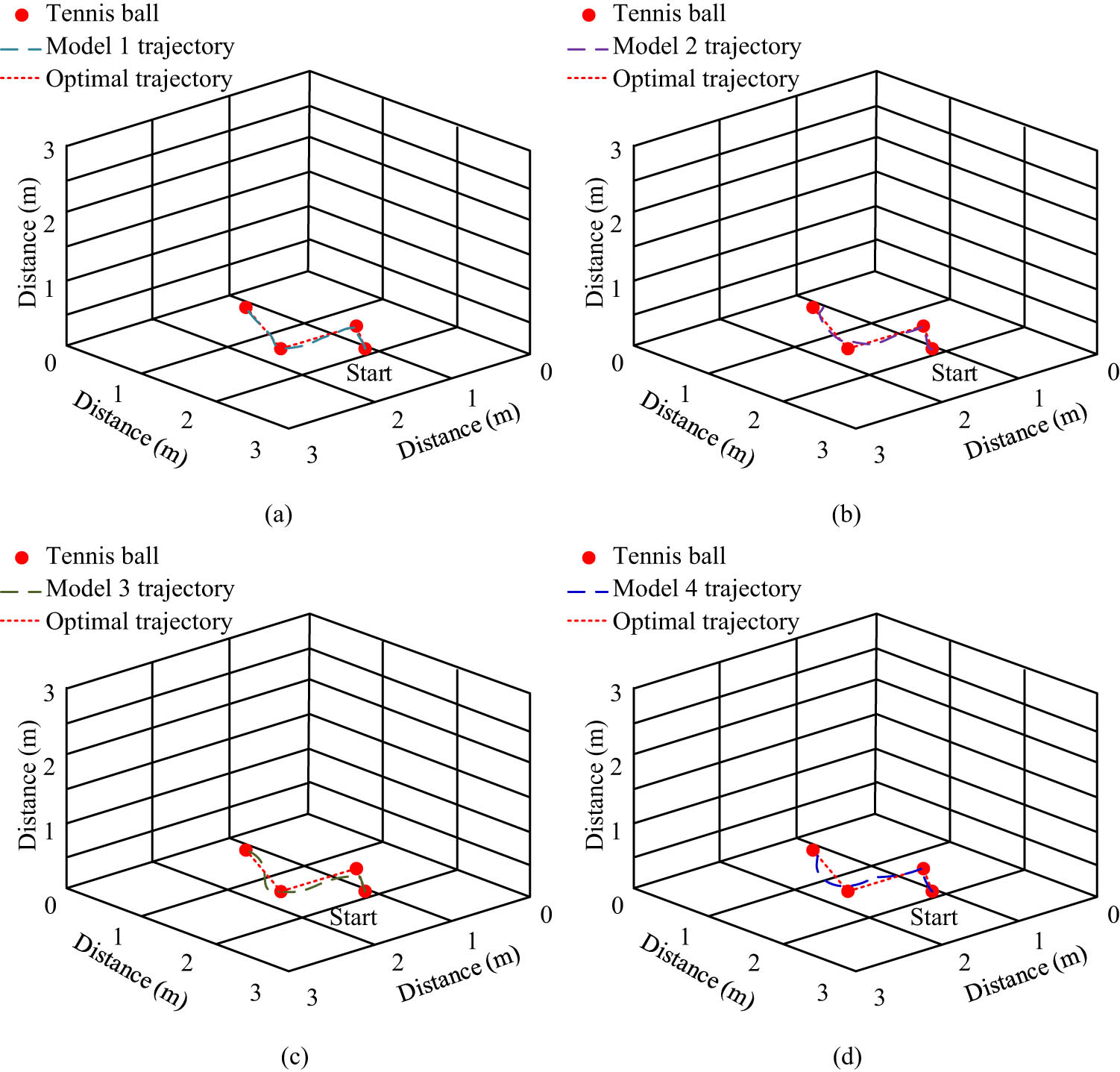
Comparison results of ball collecting action trajectories of each model robot: (a) Model 1, (b) Model 2, (c) Model 3, and (d) Model 4.

From Figure 11(a), the Model 1 robot’s ball-picking action trajectory and optimal trajectory fitted best; the walking path was close to the optimal path, the straight-line curvature was the lowest, and the target detection and positioning were the most stable. From Figure 11(b), the motion trajectory of Model 2 fitted well with the optimal trajectory, but there was a slight curvature in the latter half, and there was a deviation in the positioning of the last ball, resulting in poor motion stability. From Figure 11(c), the action trajectory of Model 3 fitted well with the optimal trajectory in the first segment, with some deviation in the second and third segments and a deviation in the positioning of the second ball, resulting in poor stability of its action. From Figure 11(d), Model 4 had the worst action trajectory in the second and third segments, and there was a significant deviation in the positioning of the third ball. The above results indicate that during the process of the robot detecting and locating the sphere, moving forward, and finally picking the sphere, the signal reception strength is interfered with, resulting in positioning deviation during the journey. Model 1 robot performed better than the comparison model robot, and it had good performance in object detection and positioning. At the same time and in the same environment, the comparison results of the tennis recognition rate and ball-picking speed of each model robot are shown in Figure 12.

Figure 12

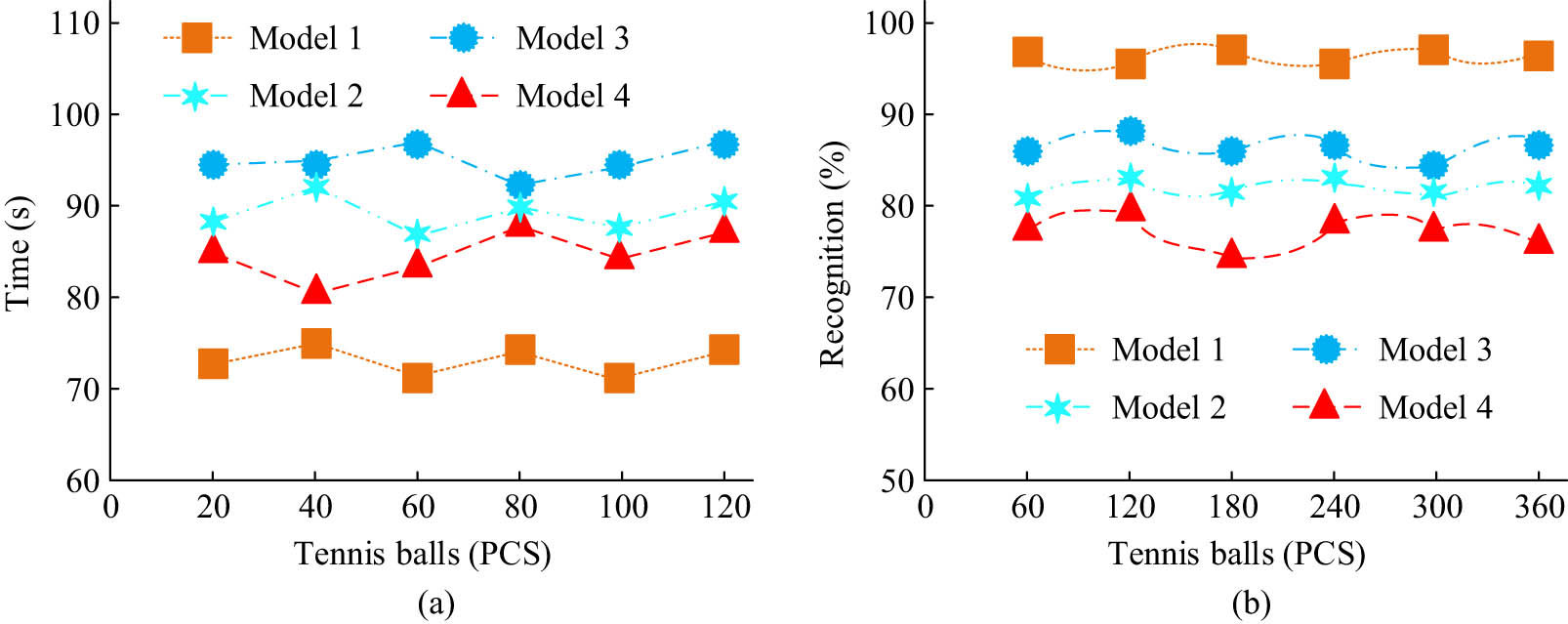
Comparison of accuracy rate and picking speed of each model robot. (a) Ball receiving speed of each model robot. (b) Each model robot recognizes tennis ball accuracy.

As shown in Figure 12(a), Model 1 received the most balls at the same time, with an average picking speed of 3.72 s per ball, Model 2 had an average picking speed of 4.62 s per ball, Model 3 had an average picking speed of 4.71 s per ball, and Model 4 had an average picking speed of 4.03 s per ball. As shown in Figure 12(b), the average recognition rate of tennis balls in Model 1 was 99.7%, the average recognition rate of robot tennis balls in Model 2 was 89.9%, the average recognition rate of tennis balls in Model 3 was 81.7%, and the average recognition rate of tennis balls in Model 4 was 78.9%. Among them, the average recognition rate of tennis balls in Model 1 was the highest. The above results indicate that, from the dimensions of ball-picking speed and tennis recognition rate, the performance of Model 1 proposed in the study is significantly better than that of the comparative model. A monitoring area of 6 m × 6 m was selected, RLs were arranged in a 5 × 5 grid shape and it randomly distributed ten labels to be located. At the same time, the positioning accuracy of four model robots was analyzed, with four adjacent RLs. The positioning results of each model are shown in Figure 13.

Figure 13

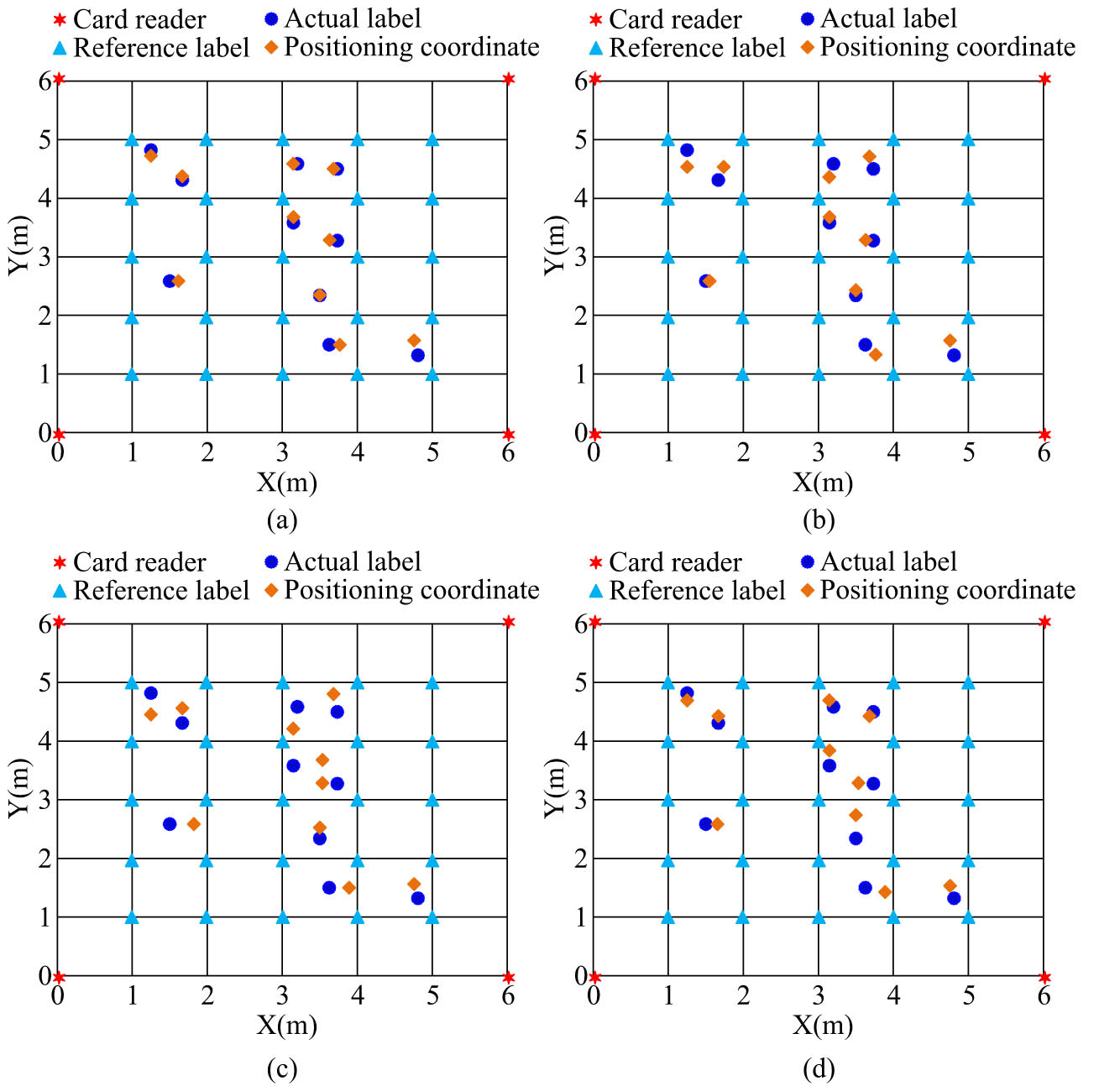
Positioning results of each model: (a) Model 1, (b) Model 2, (c) Model 3, and (d) Model 4.

As shown in Figure 13(a), the positioning coordinates of Model 1 were mostly close to the actual coordinates, with the smallest position error and the most accurate positioning. The positioning coordinates of Model 2 had three significant errors compared to the actual coordinates, but overall, the positioning was more accurate. The overall error between the positioning coordinates of Model 3 and the actual coordinates was the largest, and the positioning effect was the worst. There were four significant errors between the positioning coordinates of Model 4 and the actual coordinates, and its positioning accuracy was average. The above results indicate that under the same number of RLs and adjacent labels, the proposed Model 1 has the most accurate localization and practicality. There are many obstacles in indoor tennis, and the automatic ball-picking robot will inevitably encounter obstacles during the ball-picking process. It was compared with other models for obstacle avoidance experiments. The comparative experimental results of obstacle avoidance for each model are shown in Figure 14.

Figure 14

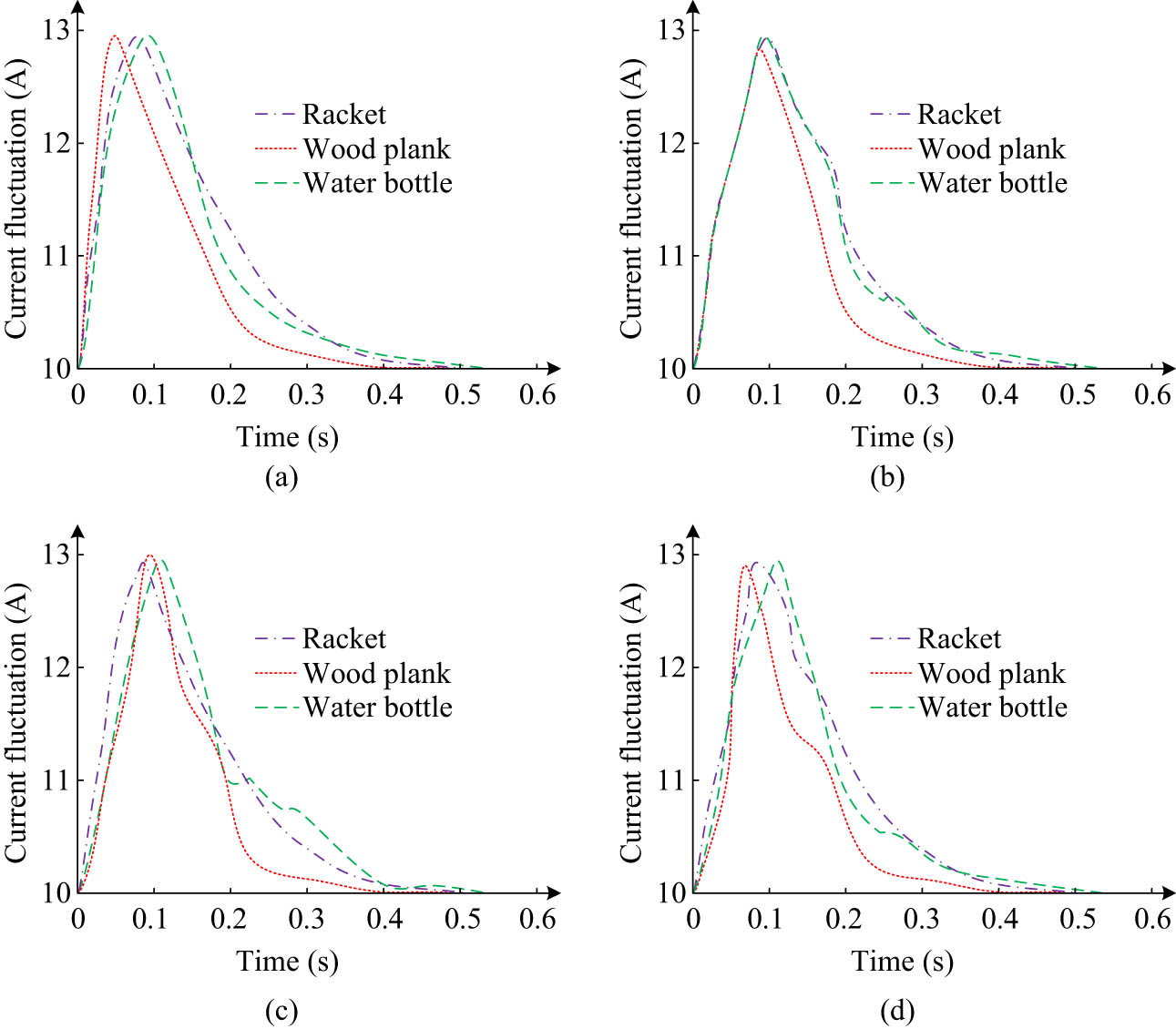
Experimental results of obstacle avoidance comparison among different models: (a) Model 1, (b) Model 2, (c) Model 3, and (d) Model 4.

As shown in Figure 14(a), Model 1 took 0.33, 0.28, and 0.19 s to avoid the racket, wooden board, and water bottle, respectively, and quickly resumed normal walking. As shown in Figure 14(b), Model 2 took 0.41, 0.35, and 0.23 s to avoid the racket, wooden board, and water bottle, respectively, and resumed normal walking speed slightly slower. As shown in Figure 14(c), Model 3 took 0.51, 0.36, and 0.29 s, respectively, to avoid the racket, wooden board, and water bottle, and the recovery of normal walking speed was relatively slow. The above results indicate that from the perspective of obstacle avoidance, Model 1 proposed in the study performs better than the comparative model. In summary, from the dimensions of obstacle avoidance, ball collection trajectory, coordinate positioning, etc., the performance of Model 1 proposed in the study is superior to the comparative model, indicating that the model is effective and practical. The comparison results of ball collection and real-time rate of each model are shown in Figure 15.

Figure 15

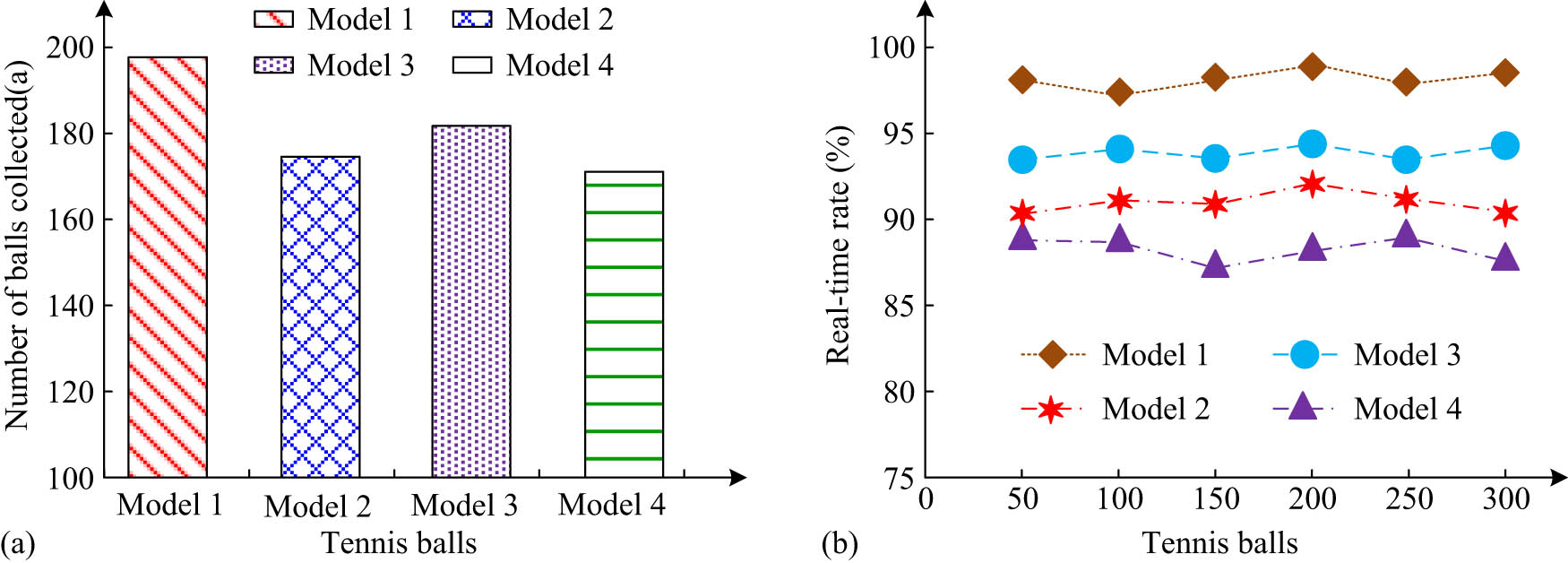
Comparison results of balls collected and real-time rates for each model. (a) Comparison of the number of balls collected by each model. (b) Real-time rate comparison results of each model.

As shown in Figure 15(a), among the 200 balls, Model 1 had the highest number of balls (198), Model 2 had 176, Model 3 had 183, and Model 4 had 175. As shown in Figure 15(b), the real-time ball collection rates of Model l, Model 2, Model 3, and Model 4 were 96.9, 90.4, 94.8, and 89.9%, respectively, among which Model 1 proposed in the study had the highest real-time ball collection rate. From the above results, the performance of the proposed Model 1 was superior to the comparison model in terms of the number of successful ball collections and real-time ball collection rate. In addition, to ensure the effectiveness and credibility of the experiment, statistical analysis was made on each algorithm according to each experimental index. The significance of the performance difference among the comparison algorithms was represented by the P-value. When the P-value was less than 0.05, the performance difference between the algorithms was significant, as shown in Table 3.

From Table 3, there were significant differences in statistical analysis among algorithms during comparison experiments, indicating that the experiment of this study is credible.