Construction of teaching quality evaluation model of online dance teaching course based on improved PSO-BPNN

3.1 Construction of online dance TQ evaluation index

With the continuous popularization of network information technology, dance teaching is no longer limited to traditional classroom teaching. Combining online education and building an interactive dance teaching model between online and offline education has become a new development demand. The online dance teaching course has changed the traditional dance learning mode. Students have more opportunities to have access to higher quality dance teaching as they break the time and geographical restrictions in dance learning [19]. The quality evaluation system of online dance teaching course is to better adapt to the reform and progress of teaching mode in the information age. However, the teaching effect evaluation of this learning mode is not perfect. There are many components of formative and summative evaluation, which can affect the teaching effect [20]. Therefore, the construction of this evaluation quality index needs to follow the principles of orientation, dynamics, and validity to ensure the rationality and objectivity. The study constructs the evaluation index of online dance TQ relying on consulting opinions of relevant online course experts and considering the individual differences and needs of students. The specific index system composition is illustrated in Table 1.

The index system consists of 4 primary indicators and 16 secondary indicators together. For the above index system, a questionnaire is developed to score the evaluation indicators. The reliability of the scoring results is analyzed through the Kendall’s harmony coefficient (Kendall W). It is applied to evaluate the correlation degree of multi-level variable indicators, which can be used to test whether expert opinions are consistent. The coefficient is generally between 0 and 1. A higher value indicates a higher consensus of opinions, as shown in Eq. (1).

where W indicates the Kendall. N indicates the number of evaluation indicators. K indicates the number of experts. T represents the number of evaluated objects. S indicates the squared difference of the sum of ratings. The Kendall’s concordance coefficient reaches 0.273, indicating that the opinions of the consulting experts are relatively consistent. After determining the reliability of the scoring opinions, the weight coefficients of the indicators are calculated using the mean normalization method, as illustrated in Eq. (2).

where R denotes the indicator weight. V denotes the average of the indicator importance scores.

3.2 Construction of a quality evaluation model for online dance teaching based on IPSO-BPNN

Based on the above constructed network dance TQ evaluation index system, this study uses BPNN to establish an intelligent evaluation model for online dance TQ. BPNN belongs to multi-layer feed-forward neural network, whose forward propagation signal is sequentially transmitted to the input layer, hidden layer, and output layer. If the output does not match the expected value, the back-propagation is continued [21]. The back-propagation is to pass the error signal obtained in the forward propagation process to the hidden layer in the reverse form. The error criterion function for a single sample P is shown in Eq. (3).

where y k stands for the output of the k in the output. T k stands for the expected output of the k in the output. The total error function of sample S is shown in Eq. (4).

Figure 1 illustrates the implementation process based on the BPNN.

Figure 1

Process of BPNN.

However, the dance TQ evaluation model based on BPNN has a major drawback. Its performance heavily depends on the selection of initial parameters. To address this problem, the PSO is applied to optimize BPNN and obtain the best initial parameters to improve the availability and evaluation accuracy of the dance teaching evaluation model [22]. Particle swarm algorithm finds the optimal solution by simulating birds foraging. As a simple and effective population optimization algorithm, it can better optimize various models. Compared with GA and ant colony optimization, the core idea of PSO is more intuitive, and the algorithm steps are relatively simple. Specifically, PSO can maintain a certain degree of diversity during the search process, is less likely to fall into local optima, and has stronger global search capabilities. Therefore, taking PSO as an optimization algorithm can better achieve performance optimization. In the PSO, each individual is a particle, and its initial position and flight direction are in a random state. Figure 2 illustrates the search protocol of the PSO in two-dimensional space.

Figure 2

Schematic diagram of two-dimensional space particle search.

In a D -dimensional space, Eq. (5) illustrates the population.

The i -particle is a D -dimensional vector, denoted as X i = [ x i 1 , x i 2 , … , x i D ] , which is the position of i in D search space. Eq. (6) illustrates the velocity of i .

The best point of the individual is P i = [ P i 1 , P i 2 , … , P i D ] . The best point of the global is P g = [ P g 1 , P g 2 , … , P g D ] . During each iteration, particles update their speed through individual and global optimal points, as shown in Eq. (7).

where ω denotes the inertia weight. k denotes the iteration. c 1 and c 2 are both non-negative constants. r 1 and r 2 both denote random numbers between [0, 1]. The position update is shown in Eq. (8).

Based on the above calculation results, the fitness function values of particles are recalculated. The individual extremes and population extremes of particles are updated. If the desired error has been reached or the iteration has reached, the iteration is ended. Otherwise, the new fitness value continues to be calculated. Therefore, the implementation flow of the PSO is illustrated in Figure 3.

Figure 3

PSO algorithm process.

The obtained optimal values are the initial weights and thresholds (WAT) of the BPNN. PSO has a simple structure, which is easy to implement. However, it is difficult to achieve a balanced state between global optimization and local optimization. In addition, it is prone to premature aging. Therefore, the study introduces an improved method to optimize it. On the basis of the standard PSO, the inertia weight of the PSO is improved, and the crossover operator is introduced [23]. In the standard PSO described above, the initial inertia weight is a fixed-value constant, which affects the search range and convergence of the algorithm to some extent. Therefore, a nonlinear decreasing weight change is selected instead of the initial fixed-value, as shown in Eq. (9).

where w max and w min are maximum and minimum of the inertia weight. t max stands for the maximum number of iterations. t stands for the current iteration. In the earlier stage of PSO iteration, the nonlinear descent strategy ensures that particles can search for the largest possible spatial range. As the iteration increases, the inertia weight nonlinearly decreases and the search space gradually shrinks. When the maximum number of iterations is obtained, the inertia weight is determined as w min . This strategy can effectively accelerate the speed of particle change and improve convergence accuracy. In addition, the PSO is prone to premature aging. The study improves it by referring to the idea of hybridization in GA. In each iteration, a certain particle is placed in the hybridization pool. The particles in the pool are randomly combined to produce the same next-generation particles s . Then, the child particles replace the parent particles f to increase the particle diversity. The child positions are obtained by crossing the parent positions. The crossover is calculated, as shown in Eq. (10).

where f x denotes the parent particle’s position. s x denotes the child particle’s position. i is a random constant located in [ 0 , 1 ] . The update rate of the child particles is shown in Eq. (11).

where fv denotes the parent particle’s position. sv denotes the child particle’s position. PSO improves BPNN by optimizing the WAT. When constructing the online dance TQ evaluation model based on IPSO-BPNN, the two methods are combined. The WAT of BP is the position of particles in the PSO. The total WAT is the dimension of the particle swarm. The objective function is the fitness function of particles, as shown in Eq. (12).

where m denotes the output vector dimension. S stands for the total samples. T k s stands for the expected output of the s -th sample. y k s stands for the actual output of the s -th sample. The PSO is applied to improve the WAT of BPNN, which can effectively solve the slow convergence and local optimum of BPNN. In the search process of particles, the minimum fitness value is demonstrated in Eq. (13).

where N denotes the total number of sample training sets. M stands for the neuron nodes in the output. W i , j d stands for the expected value of the i -th sample at the j -th in the output. W i , j stands for the actual value of the i -th sample at the j -th in the output. The structural flow of the optimized BPNN based on the IPSO is shown in Figure 4. In the IPSO-BPNN model, first, the raw data are processed and initial parameters are set, including the size of the particle swarm, the number of iterations, the learning factor and inertia weight, as well as the weight and threshold of the BPNN. Next the fitness function is determined to evaluate the quality of particles. Based on the evaluation results of the fitness function, the position and velocity vectors of each particle are updated and the optimization process is iterated until the maximum number of iterations is reached.

Figure 4

IPSO-BPNN algorithm process.

4.1 Analysis of online dance TQ evaluation index

The study pre-processes the collected sample data by first handling missing values, deleting missing sample data, and removing abnormal data. For missing data, if the missing data are small, it will be deleted directly. On the contrary, based on the characteristics and sources of the collected data, relevant data should be collected again to fill in the gaps. For abnormal data, the reasons for the occurrence of outliers are analyzed. If the outliers are generated by random factors and have little impact on the analysis, they will be directly deleted. If the abnormal data are generated by other mechanisms and has a direct impact on subsequent analysis, the average value is used to replace the abnormal data. Next data are standardized to eliminate the impact of variable dimensions. Then, methods such as scatter plots are used to analyze the distribution characteristics of the data. Finally, according to the experimental needs, Relevant feature datasets are selected to validate the performance of the model. Students' personal information data are relatively private. Therefore, this study strictly adheres to data protection principles, clearly informs users of the purpose of collecting and using data, and obtains the consent of the research subjects. The research constructs the online dance TQ evaluation index system for analysis, with 4 primary indicators, and 16 secondary indicators to develop the corresponding questionnaire. Relevant students are invited to rate. The processed data are input according to the experimental steps. The weights of the quality evaluation indexes of the online dance teaching course are obtained, as shown in Table 2. The weight value of this online dance TQ evaluation index reflects the importance degree of this index in the whole evaluation system. The highest weight of 0.1 was given to the dance presentation, which showed that the presentation was the key to the overall TQ. In addition, the weight of skill mastery was 0.09. Therefore, to improve the online dance TQ, it is necessary to continuously improve dance learning skills, gain experience in teaching, adopt appropriate teaching methods, improve teaching level, and comprehensively enhance the TQ.

4.2 Analysis of online dance teaching quality evaluation model based on IPSO-BPNN

To investigate the TQ of online dance teaching courses, the study intends to evaluate the teaching effectiveness of this teaching model. An evaluation model based on IPSO-BPNN is constructed. The evaluation indicators include Error, F1 value, accuracy, and root mean square error (RMSE). Error represents the average square difference between the predicted and actual values. The smaller the indicator, the better the predictive performance of the model. The F1 value, RMSE, and recall of the BPNN are used to comprehensively evaluate the performance of the model. F1 considers both precision and recall, providing a balanced evaluation for these two indicators. When F1 is high, it indicates that the model has achieved a good balance between precision and recall, and the model performance is better. The accuracy of the model represents the proportion of correctly predicted samples to the total number of samples, indicating the model's predictive ability for positive samples. RMSE is the square root of mean square error. The smaller the metric, the better the predictive performance of the model. The experimental data used in the study come from the relevant course statistics of an online dance teaching course in a university. After pre-processing the data, 3,000 data are used for training. The remaining 1,000 data are used for testing the samples. To better validate the performance of the IPSO-BPNN TQ evaluation model, Table 3 illustrates the experimental parameters of the BPNN and PSO models.

To ensure the superiority of BPNN in the TQ evaluation, the study compares the TQ obtained from IPSO-BPNN model and BPNN trained with the actual results. The outcomes are indicated in Figure 5. In Figure 5(a), the linear trend of the training results and the real values were basically the same. There was a high degree of overlap between the training results and the real values. In Figure 5(b), there was a significant error in the training results and the actual results. The overlap of the linear trend was significantly below the BPNN. The same indicators were used to check and evaluate the performance of the model. The maximum positive and negative error of the BPNN were 24.68 and −15.41. The positive and negative cumulative error were 7.16 and −3.78. The maximum positive and negative error of the IPSO-BPNN model were 12.15 and −15.33. The positive and negative cumulative error were 3.14 and −1.62. This indicates that the improved online dance TQ evaluation model has higher accuracy.

Figure 5

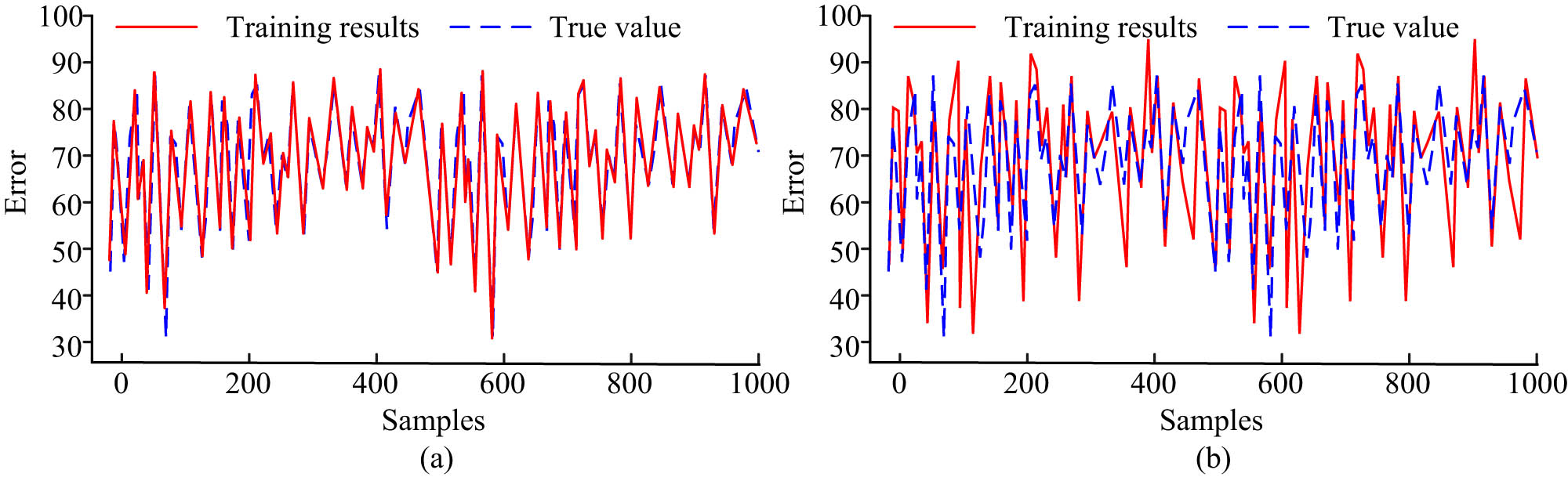
Comparison of training results and actual results between IPSO-BPNN and BPNN. (a) Teaching quality evaluation results based on IPSO-BPNN. (b) Teaching quality evaluation results based on BPNN.

To verify the IPSO-BPNN, the evaluation errors of the method are compared. Figure 6 illustrates the results. A negative error displays that the evaluation results are lower than normal. A positive error value indicates that the evaluation error exceeds normal. From Figure 6, the error of the BPNN online dance TQ evaluation model before improvement was significantly higher than that of the IPSO-BPNN model. In the whole dataset, multiple maximum and minimum values appeared. The error fluctuated greatly, and the maximum error was −0.028. The error of the IPSO-BPNN basically remained at 0.005. There is no significant increase or decrease in the error value, and the overall was relatively stable.

Figure 6

Comparison of evaluation errors between IPSO-BPNN and BPNN.

To further scientifically validate the performance of IPSO-BPNN dance TQ rating model, the study compares the BPNN model before improvement and obtains the precision and F1 training results of different models, as illustrated in Figure 7. From Figure 7, the precision and F1 were the highest, reaching 97.62 and 95.41%, respectively, and the curve fluctuation was small. The precision and F1 of the BPNN model were lower, at 92.06 and 90.53%, respectively, and the curve fluctuation was large. It demonstrates that the performance of the BPNN is unstable. The IPSO-BPNN has higher precision and model performance.

Figure 7

Precision and F1 value results of (a) IPSO-BPNN and (b) BPNN.

For the intelligent evaluation of the data, the commonly used K-means-based optimized Radial basis function (K-RBF)neural network, support vector machine (SVM) model, and GA-based optimized BPNN (GA-BPNN) are compared with IPSO-BPNN model. Figure 8 displays the accuracy on the training and testing sets. In Figure 8(a), on the training set, the accuracy of IPSO-BPNN model was 94.86%. The accuracy of GA-BPNN, K-RBF, and SVM models were 93.67, 93.04, and 92.78%, which were 1.09, 1.82, and 2.08% higher than that of GA-BPNN model and SVM, respectively. In Figure 8(b), on the testing set, the IPSO-BPNN achieved an accuracy of 97.25%, which was 1.56, 1.94, and 2.85% higher than that of the GA-BPNN model and SVM, respectively.

Figure 8

Accuracy comparison of commonly used evaluation models. (a) Training set. (b) Testing set.

To further evaluate the positioning performance of the four methods, the study analyzes the actual application effects based on the TQ evaluation results of dance teaching and training institutions in two different places. This study uses average running time, precision, recall, and F1 score as reference indicators. The results are shown in Table 4. In location A, the average running time, precision, recall, and F1 values of IPSO-BPNN were 2.43s, 92.54, 94.62, and 91.86, respectively. A P-value less than 0.05 indicated that the differences between the models were statistically significant, with a confidence range of 1.98–2.14. In location B, the average running time, precision, recall, and F1 values of IPSO-BPNN were 4.02s, 86.37, 88.35, and 89.64, respectively. The results from this location also showed a P-value less than 0.05, indicating that the differences between the models were statistically significant, with a confidence range of 2.91–3.46. The performance differences between different methods were significant. The proposed method demonstrates better performance optimization.

To further analyze the performance of the proposed method, different datasets are used for analysis. The dataset includes a student practice dataset from a certain training institution, which includes exercise videos and action data in dance courses. It is usually used to evaluate their learning progress and provide teaching suggestions. Dance teaching dataset is a teaching dataset that includes basic skills for Chinese dance from level 1 to level 10, detailing the movements and skills that should be learned at each level. The accuracy of the research method obtained from different datasets is shown in Table 5. According to Table 5, the accuracy of the proposed method in the three datasets was 94.76, 95.21, and 94.38%, respectively. Because there are certain differences in data characteristics among different datasets, there are differences in accuracy between different datasets. However, within the same dataset, the performance of the research method is relatively better.

The study uses RMSE and Root Mean Square Logarithmic Error (RMSLE) to measure the online dance TQ evaluation model. A functional evaluation questionnaire is also constructed to investigate the satisfaction of students using the evaluation model. 600 students are randomly invited to rate the model. The comparative analysis and the satisfaction results are illustrated in Figure 9. From Figure 9, in the RMSE comparison, the RMSE value of SVM, GA-BPNN, K-RBF, and IPSO-BPNN was 24.591, 23.106, 22.212, and 20.793. The designed IPSO-BPNN had the lowest RMSE value. In the comparison of RMLSE metrics, the RMSE of SVM, GA-BPNN, K-RBF, and IPSO-BPNN was 0.153, 0.145, 0.142, and 0.122. The designed method had the lowest RMSE value. This shows that the fusion model has higher performance. In terms of satisfaction scores, satisfaction score 1 was 0, satisfaction score 2 was 40, satisfaction score 3 was 100, satisfaction score 4 was 240, and satisfaction score 5 was 220. 76.7% of the students were satisfied with the evaluation model, which showed that most of the students were satisfied with the effectiveness of the model.

Figure 9

Comparative analysis results and satisfaction results. (a) RMSE. (b) RMLSE. (c) Evaluation score.

To further evaluate the real-time performance of the research method, the real-time data processing capabilities of different methods are compared. The results are shown in Figure 10. As shown in the Figure 10, K-RBF, SVM, and GA-BPNN all had high data packet loss rates. The research method showed slight packet loss before 25 frames/s. However, it quickly recovered and stabilized, with a final packet loss rate of 2.3%, significantly better than the compared methods. The research method has stronger real-time data processing performance, which can provide real-time feedback and adjustments during the teaching process.

Figure 10

Real time data processing performance of different methods.

To further verify the long-term impact of this method on academic performance, the comprehensive academic performance of 5 students from a certain university during their freshman to senior years is randomly selected for analysis. 1–8 represent 8 different semesters in 4 years. The vertical axis represents the changes in dance basic abilities of the students in the student ranking (where 1, 2, and 3 were not evaluated using this method, and 4 and 5 were based on the research method), as shown in Figure 11. As shown in Figure 11, the closer the curve is to the bottom, the higher the ranking of students. The rankings of students 4 and 5 have significantly improved over the past 4 years. Students 1, 2, and 3 have fluctuated significantly, and the overall ranking has declined. By analyzing the comprehensive abilities of students, it is possible to clearly and intuitively analyze the changes in their abilities during the long-term learning process, which verifies the long-term effectiveness of the model.

Figure 11

Changes in long-term academic performance of students.

To analyze the performance advantages of the research method more clearly, the performance indicators of this method are summarized, as shown in Table 6. According to Table 6, the performance of the research method was analyzed from multiple indicators and different testing scenarios. The results all showed that the various indicators of the research method exhibited good performance advantages in different scenarios.