Curves in multiplicative equiaffine plane

Meltem Ogrenmis; Alper Osman Ogrenmis; Emad E. Mahmoud

doi:10.1515/phys-2025-0212

Artikel Open Access

Curves in multiplicative equiaffine plane

Meltem Ogrenmis , Alper Osman Ogrenmis und Emad E. Mahmoud

Veröffentlicht/Copyright: 15. Oktober 2025

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen Erkunden Sie dieses Fachgebiet

Aus der Zeitschrift Open Physics Band 23 Heft 1

Abstract

In this study, we deal with multiplicative equiaffine plane curves. First, the concepts of multiplicative equiaffine arc length and multiplicative curvature are introduced. Multiplicative equiaffine Frenet formulas and an analog of the fundamental theorem are established. Finally, multiplicative equiaffine plane curves with constant multiplicative equiaffine curvature are classified.

Keywords: Affine plane; equiaffine plane curves; multiplicative derivative; multiplicative integral

1 Introduction

The foundational framework of classical analysis, which is extensively used in modern mathematical theory, was first developed by Leibniz and Newton toward the end of the seventeenth century, focusing on differential and integral calculus notations. Classical analysis builds upon core topics in trigonometry, algebra, and analytic geometry, encompassing key ideas such as limits, differentiation, integration, and series expansions. These operations are often viewed as basic and fundamental, akin to addition and subtraction, which is why classical analysis is sometimes referred to as summational analysis. Its applications are extensive, spanning a wide range of disciplines where precise mathematical modeling and the pursuit of optimal solutions are of great importance.

However, when dealing with phenomena governed by proportional change, scale invariance, or multiplicative growth and decay, the additive framework of classical analysis may not be the most natural or effective choice. This creates a gap in geometric modeling where multiplicative structures could provide a more accurate representation.

Despite its broad utility, classical analysis has limitations in certain mathematical contexts. Consequently, alternative frameworks have been developed that are founded on various arithmetic operations while maintaining classical analysis as a foundation. For example, during 1887, Volterra and Hostinsky introduced a novel analytical approach termed Volterra-type or multiplicative analysis, which is grounded in multiplication rather than addition as the primary operation [1]. In this framework, the operations of multiplication and division replace the roles traditionally assigned to addition and subtraction in classical analysis, offering a novel approach to mathematical modeling. This shift represents a fundamental rethinking of conventional analysis, where the relationships between variables are governed by multiplicative rather than additive structures. Between 1972 and 1983, Grossman and Katz expanded upon Volterra’s earlier contributions by formulating what became known as non-Newtonian analysis. This new analytical framework introduced innovative definitions and concepts, redefining how mathematical operations could be applied across various domains [2,3]. Collectively, these methodologies are known as geometric, bigeometric, and anageometric analysis, each offering unique perspectives and tools for addressing problems where classical approaches prove inadequate.

Multiplicative analysis, presented as a counterpart to classical analysis, has garnered increasing interest in the mathematical community, spurring further research and development. These alternative methods have shown potential in addressing a range of mathematical problems by exploring new structural frameworks. Consequently, they have enriched the scope of mathematical analysis and found applications in various fields.

In particular, the need to extend classical geometric frameworks – such as equiaffine differential geometry – into the multiplicative setting is motivated by the lack of a comprehensive theory that unifies multiplicative operations with affine invariance. Existing studies address either multiplicative analysis in general or classical equiaffine curves separately, but there is no systematic development of multiplicative equiaffine Frenet formulas, arc length, and curvature theory.

The recent surge of interest in multiplicative analysis is reflected in numerous mathematical studies. While a comprehensive listing is beyond the scope of this discussion, previous studies [4–8] have provided substantial contributions to the field. More recently, differential geometry has also incorporated multiplicative analysis. Notably, Georgiev advanced the study of multiplicative analysis with the publication of three key works [9–11]. These publications, particularly [10], are regarded as foundational texts in multiplicative geometry. They provide novel definitions and theorems that connect fundamental geometric structures with the principles of multiplicative analysis. In addition, these works highlight the relationships between multiplicative geometry and other mathematical fields, thereby providing valuable insights for researchers working in various areas of mathematics.

Furthering the development of geometric analysis, Nurkan and collaborators made significant advancements by applying geometric calculus to the derivation of Gram-Schmidt vectors [12]. In a related study, [13], spherical indicatrices and helices in non-Newtonian (multiplicative) Euclidean spaces are analyzed, offering new characterizations and examples. On the other hand, Aydın et al. provided a classification and visualization of rectifying curves within multiplicative Euclidean space, employing multiplicative spherical curves to illustrate their findings [14]. The study by Ceyhan et al. [15] extends these ideas to investigate tube surfaces using the algebra of multiplicative quaternions.

Other recent studies continue to apply non-Newtonian analysis to various branches of geometry. For instance, Has et al.’s work explores geometric approaches in the Lorentz-Minkowski space L * 3 using non-Newtonian techniques [16]. Meanwhile, Özdemir and Ceyhan examined the use of multiplicative hyperbolic split quaternions and their role in generating geometric hyperbolic rotation matrices [17]. In another study, Has and Yılmaz studied non-Newtonian conics through the lens of multiplicative analytic geometry [18]. Es [19] focused on the use of homothetic multiplicative calculus to derive new kinematic expressions in the study of plane kinematics. Later, the research conducted by Has and Yılmaz [20] examined the behavior of magnetic curves in multiplicative Riemannian manifolds using non-Newtonian analysis. Finally, Aydin defined [21] multiplicative rectifying submanifolds of multiplicative Euclidean space. Broscăţeanu et al. [22] analyzed the infinitesimal bending of rectifying curves, Burlacu and Mihai [23] investigated applications of curve theory in road design, and Jianu et al. [24] explored a surface associated with the Catalan triangle.

On the topic of affine geometry, extensive research has been conducted on affine spaces and their properties. For an in-depth exploration of both fundamental and advanced topics within this domain, readers may refer to works such as [25–28], which offer detailed discussions of classical and modern perspectives on affine geometry.

Besides differential geometry, there are applications of multiplicative calculus in dynamical systems [29,30], in eco-nomics [31,32], and in image analysis [33,34].

In addition to its intrinsic mathematical elegance, equiaffine differential geometry holds significant relevance in various physical contexts. The equiaffine framework, which preserves volume under affine transformations, naturally aligns with the modeling of physical systems where volume preservation or density invariance is critical. For instance, in fluid mechanics, the behavior of incompressible flows can be more accurately described using equiaffine invariants. Similarly, in continuum mechanics, equiaffine structures provide a geometric interpretation of stress and strain in materials that undergo deformation without volume change. Moreover, affine-invariant quantities appear in general relativity and gauge theories, where they are associated with affine connections and energy-momentum distributions. These examples illustrate that equiaffine geometry is not merely an abstract mathematical construct but also a powerful analytical tool with substantial applicability in theoretical and applied physics.

The aim of this study is to bridge the gap between multiplicative analysis and equiaffine geometry by developing a complete multiplicative equiaffine framework for plane curves. The main contributions can be summarized as follows: (1) defining multiplicative equiaffine arc length and curvature, (2) deriving multiplicative equiaffine Frenet formulas and an analogue of the fundamental theorem, and (3) classifying plane curves with constant multiplicative equiaffine curvature. Such a framework is expected to have applications in modeling scale-invariant geometric phenomena in physics, continuum mechanics, and data science.

This study is organized as follows: first, the foundational concepts of multiplicative calculus are introduced. Next, essential aspects of equiaffine geometry relevant to the analysis are presented. Finally, the curvature of a multiplicative plane curve is computed, and curves with constant curvature are characterized.

The novelty of this study lies in the systematic development of a full-fledged differential geometry framework within a multiplicative equiaffine setting. Unlike prior studies, we provide explicit Frenet equations, arc-length formulations, and curvature characterizations based on multiplicative operations. This presents a foundational shift that invites new geometric intuition and theoretical development.

2 Preliminaries

In this section, we introduce two essential topics. The first subsection presents the basics of equiaffine plane curves, focusing on the determinant in the affine plane and the equi-affine arc-length. The second subsection introduces the concept of multiplicative analysis. We explore multiplicative operations and structures, including multiplicative addition, multiplication, and derivatives. Additionally, we define the multiplicative determinant as a logarithmic analogue of the classical determinant.

2.1 Basics of equiaffine plane curves

In this section, we will briefly discuss the fundamental concepts of equiaffine plane curves without going into detailed explanations.

Let R 2 be the affine plane with the determinant

(2.1) ∣ u v ∣ = u 1 u 2 v 1 v 2 = u 1 v 2 − u 2 v 1 ,

where u = ( u 1 , u 2 ) and v = ( v 1 , v 2 ) ∈ R 2 .

Let c : I → R 2 represent a regular curve in the plane. Typically, for equi-affine regular curves, the condition of nondegeneracy det ( c ˙ ( t ) , c ¨ ( t ) ) ≠ 0 for every t ∈ I is assumed, where c ˙ ( t ) = d c d t ( t ) and c ¨ ( t ) = d 2 c d t 2 ( t ) . Given this, the equi-affine arc-length of c , measured from c ( t 0 ) ( t 0 ∈ I ), is given as follows:

(2.2) s ( t ) = ∫ t 0 t det ( c ˙ ( t ) , c ¨ ( t ) ) 1 3 d t .

The arc-length parameter s is chosen so that det ( c ′ ( s ) , c ″ ( s ) ) = 1 , where c ′ ( s ) = d c d s ( s ) and c ″ ( s ) = d 2 c d s 2 ( s ) . A regular curve c is parameterized by the equi-affine arc-length if it satisfies det ( c ′ ( s ) , c ″ ( s ) ) = 1 for all s . We denote t ( s ) = c ′ ( s ) and n ( s ) = c ″ ( s ) . Then, ( t ( s ) , n ( s ) ) ∈ S L ( 2 , R ) , and the following Frenet-type relation is obtained:

(2.3) t ′ ( s ) n ′ ( s ) = 0 1 − κ ( s ) 0 t ( s ) n ( s ) ,

where κ ( s ) = det ( c ″ ( s ) , c ‴ ( s ) ) . The function κ is referred to as the equi-affine curvature of the curve c .

According to the fundamental theorem of equiaffine plane curves, a smooth function κ ( σ ) , for σ ∈ I , defines a unique equiaffine plane curve y , up to an equiaffine transformation of R 2 . This curve is parametrized by σ as the equiaffine arc-length and κ as the equiaffine curvature. Moreover, if κ is constant, then y corresponds to either a parabola ( κ = 0 ) , an ellipse ( κ > 0 ) , or a hyperbola ( κ < 0 ) . These curves are represented by the equations y = 1 2 x 2 for the parabola and κ x 2 + ( κ y ) 2 = 1 for the ellipse or hyperbola [28].

2.2 Multiplicative analysis

In this section, we outline fundamental definitions and principles concerning multiplicative analysis, drawing insights from Georgiev’s works [9–11]. Following this, we will discuss multiplicative equiaffine plane curves.

Let R * = ( 0 , ∞ ) . In R * , we define multiplicative addition, multiplication, subtraction, and division as follows:

(2.4) Operation Logarithmic expression Result x + * y e log x + log y x ⋅ y x ⋅ * y e log x log y x log y x − * y e log x − log y x y x ∕ * y e log x log y x 1 log y , y ≠ 1 .

These operations form a multiplicative structure denoted by ( R * , + * , − * ) . Each x * in R * is termed a multiplicative number, where x * = exp ( x ) .

The multiplicative zero and unit in R * are

(2.5) Multiplicative value Result 0 * 1 1 * e .

For k ∈ N , the power k * of a multiplicative number x is defined as follows:

(2.6) Operation Expression Result Multiplicative Power x k * = x ⋅ * x ⋯ ⋅ * x ( k times ) ( e log x ) k .

The multiplicative sine ( sin * ) and cosine ( cos * ) functions are defined as follows:

(2.7) Function Result sin * x e sin ( log x ) cos * x e cos ( log x ) .

Similarly, multiplicative hyperbolic functions are given by

(2.8) Function Result sinh * x e sinh ( log x ) cosh * x e cosh ( log x ) .

Let A ∈ R * and f be a first-order continuously differentiable function. The first-order multiplicative derivative of f , denoted by f * ( x ) , is defined as follows:

(2.9) Operation Expression Result Multiplicative derivative f * ( x ) = f ( x + * h ) − * f ( x ) ∕ * h e x f ′ ( x ) f ( x ) ,

where f ′ is the classical derivative of f .

For a , b ∈ R * and f : R * → R * , the multiplicative indefinite integral and the multiplicative Cauchy integral are defined by

(2.10) Integral type Multiplicative operations Result MII ∫ * f ( x ) ⋅ * d * x e ∫ 1 x log f ( x ) d x MCIl ∫ * a b f ( x ) ⋅ * d * x e ∫ a b 1 x log f ( x ) d x .

Moreover, for two vectors x = ( x 1 , x 2 ) and y = ( y 1 , y 2 ) , the *multiplicative determinant* is defined as follows:

(2.11) Operation Multiplicative operations Result det * ( x , y ) x 1 ⋅ * y 2 − * x 2 ⋅ * y 1 e log x 1 ⋅ log y 2 − log x 2 ⋅ log y 1 .

This represents a multiplicative analogue of the classical determinant and is defined in the space R * 2 using logarithmic operations.

3 Multiplicative equiaffine plane curves

In this section, we develop the theory of multiplicative equiaffine plane curves by defining the multiplicative affine plane and the multiplicative determinant, which generalizes area calculations. We also introduce key concepts like multiplicative linear independence, the multiplicative equiaffine group, and the multiplicative arc length. Furthermore, we present the multiplicative Frenet apparatus and the corresponding Frenet equations, which describe the curvature and frame transformations of these curves.

Definition 3.1

The multiplicative affine plane R * 2 is a two-dimensional affine space equipped with a multiplicative structure, rather than the usual additive structure. In this context, the space retains a constant area form det * ( ⋅ , ⋅ ) , which serves as a generalized determinant for calculating the “area” between two vectors. This area form is defined multiplicatively as follows:

(3.1) det * ( x , y ) = x 1 ⋅ * y 2 − * x 2 ⋅ * y 1 = e log x 1 ⋅ log y 2 − log x 2 ⋅ log y 1 ,

where x = ( x 1 , x 2 ) and y = ( y 1 , y 2 ) are vectors in R * 2 .

Proposition 3.2

For vector fields x = ( x 1 , x 2 ) and y = ( y 1 , y 2 ) , the following equality

(3.2) ( det * ( x , y ) ) * = det * ( x * , y ) + * det * ( x , y * ) ,

is satisfied.

Proof

Let’s assume x = ( x 1 , x 2 ) and y = ( y 1 , y 2 ) are two vector fields. Now, consider x and y as 2 × 2 matrices with the vectors as rows

(3.3) x = x 1 x 2 , y = y 1 y 2 .

Then, the determinant of the matrix formed by x and y , denoted as det ( x , y ) , is given by:

(3.4) det * ( x , y ) = det * x 1 x 2 y 1 y 2 = x 1 ⋅ * y 2 − * x 2 ⋅ * y 1 = e log x 1 ⋅ log y 2 − log x 2 ⋅ log y 1 .

Now, let’s multiplicative differentiate this expression, then

(3.5) ( det * ( x , y ) ) * = ( e log x 1 ⋅ log y 2 − log x 2 ⋅ log y 1 ) * .

is obtained. By using multiplicative derivative rule, we have

(3.6) ( det * ( x , y ) ) * = e x ( ( log x 1 ) * ⋅ log y 2 − ( log x 2 ) * ⋅ log y 1 ) . e x ( log x 1 ⋅ ( log y 2 ) * − log x 2 ⋅ ( log y 1 ) * ) .

The right side of this expression is written as follows:

(3.7) e x ( ( log x 1 ) * ⋅ log y 2 − ( log x 2 ) * ⋅ log y 1 ) + * e x ( log x 1 ⋅ ( log y 2 ) * − log x 2 ⋅ ( log y 1 ) * )

(3.8) det * ( x * , y ) + * det * ( x , y * ) .

Therefore, we have proved the result.□

Definition 3.3

A pair { x , y } of vectors in R * 2 is said to be multiplicatively linearly independent if the equation

(3.9) λ 1 ⋅ * x + * λ 2 ⋅ * y = 0 * = 1

holds only when λ 1 = λ 2 = 1 . Otherwise, if there exist λ 1 , λ 2 ∈ R * , not both equal to 1, such that Eq. (3.9) holds, then x and y are said to be multiplicatively linearly dependent.

Definition 3.4

A multiplicative nondegenerate smooth parametric curve in R * 2 , c = c ( t ) = ( c 1 ( t ) , c 2 ( t ) ) , t ∈ I ⊂ R * is defined by

(3.10) det * ( c * , c * * ) ≠ 0 * = 1 ,

for any t .

Definition 3.5

The multiplicative equiaffine arc length function ρ for the curve c is defined as follows:

(3.11) ρ ( t ) = ∫ * t 0 t [ det * ( c * , c * * ) ] 1 3 * ⋅ * d * u = e ∫ t 0 t 1 u [ log det * ( c * , c * * ) ] 1 3 d u ,

where det * ( c * , c * * ) is the multiplicative determinant of the first and second multiplicative derivatives of the curve c .

Proposition 3.6

The multiplicative equiaffine curvature κ of c at ρ is given by

(3.12) κ = det * ( v 2 , v 2 * ) .

Proof

Consider v 1 = c * ( ρ ) and v 2 = c * * ( ρ ) . Then, it follows that

(3.13) det * ( v 1 , v 2 ) = 1 * = e ,

for all ρ . Here, ρ represents the parameter defining the multiplicative equiaffine arc length. The vector fields v 1 and v 2 are the multiplicative tangent vector and multiplicative Blaschke normal vector of c , respectively.

If we differentiate Eq. (3.13) with respect to ρ , we obtain

(3.14) det * ( v 1 , v 2 * ) = 0 * = 1 ,

which implies that v 1 and v 2 * are multiplicatively linearly dependent. Consequently, there exists a function κ ( ρ ) such that

(3.15) v 2 * + * κ ⋅ * v 1 = 0 * = 1 .

Therefore, we conclude the proof.□

Definition 3.7

Let c be a multiplicative nondegenerate smooth curve in R * 2 parameterized by the multiplicative equiaffine arc length ρ . Then, the set { v 1 , v 2 , κ } is called the multiplicative equiaffine Frenet apparatus of c .

The multiplicative Frenet equations in the equiaffine sense are as follows:

(3.16) c * v 1 * v 2 * = 0 * 1 * 0 * 0 * 0 * 1 * 0 * − * κ 0 * c v 1 v 2 .

It is obvious that the following occurs

(3.17) v 2 * + * κ ⋅ * v 1 = 0 * .

The relations between the multiplicative equiaffine frames of c can be presented as follows. Let ℬ * = v 1 * v 2 * and ℬ = v 1 v 2 for ℬ * , ℬ ∈ S O * ( e 2 ) . Thus, we have

(3.18) ℬ * = 0 * 1 * − * κ 0 * ℬ .

4 Plane curves of constant multiplicative equiaffine curvature

In this section, we classify the plane curves with constant multiplicative equiaffine curvature. Let c = c ( s ) be a multiplicative nondegenerate smooth curve in R * 2 parameterized by the multiplicative equiaffine arc length parameter, and let { v 1 * , v 2 * , κ } denote the multiplicative equiaffine Frenet apparatus.

We seek to construct a curve c in R * 2 with constant multiplicative equiaffine curvature κ = λ , where λ ∈ R * . Thus, the following vector ordinary differential equation results:

(4.1) v 2 * + * λ ⋅ * v 1 = 0 * = 1 .

Substituting v 1 = w into Eq. (4.1), we obtain:

(4.2) w * * + * λ ⋅ * w = 0 * = 1 .

To solve Eq. (4.2), we examine different cases:

(i) λ = 0 * = 1 .

The relation Eq. (4.2) give

(4.3) w ( s ) = m ⋅ * s + * n ,

for constant vectors m , n ∈ R * 2 such that det * ( m , n ) = e . Considering that v 1 = c *

(4.4) c * ( s ) = m ⋅ * s + * n

is obtained. The following relation is given by integrating Eq. (4.4)

(4.5) c ( s ) = m ⋅ * ( s 2 * ∕ * 2 ) + * n ⋅ * s + * l ,

for a constant vector l ∈ R * 2 . With respect to a convenient coordinate system, one can choose

(4.6) m = ( 0 * , 1 * ) = ( 1 , e ) , n = ( 1 * , 0 * ) = ( e , 1 ) , l = ( 0 * , 0 * ) = ( 1 , 1 ) ,

and hence, Eq. (4.5) is

(4.7) c ( s ) = s , e ( log s ) 2 log 2 .

(ii) λ > 0 * = 1 .

The relation Eq. (4.2) give

(4.8) w ( s ) = m ⋅ * cos * ( λ * ⋅ * s ) + * n ⋅ * sin * ( λ * ⋅ * s ) ,

where w ( π * ∕ * 2 ⋅ * λ * ) = n and w * ( π * ∕ * 2 ⋅ * λ * ) = − * λ * m and then det * ( m , n ) = − * 1 ∕ * λ * . Considering that v 1 = c *

(4.9) c * ( s ) = m ⋅ * cos * ( λ * ⋅ * s ) + * n ⋅ * sin * ( λ * ⋅ * s ) .

is obtained. Integrating Eq. (4.9), one obtains

(4.10) c ( s ) = m ⋅ * ( sin * ( λ * ⋅ * s ) ) ∕ * λ * + * n ⋅ * ( − * cos * ( λ * ⋅ * s ) ) ∕ * λ * + * l ,

for a constant vector l ∈ R * 2 . According to a suitable coordinate system, one can choose

(4.11) m = ( 1 * , 0 * ) = ( e , 1 ) , n = ( 0 * , − * 1 ∕ * λ * ) = ( 1 , e − 1 log λ ) , l = ( 0 * , 0 * ) = ( 1 , 1 ) ,

and Eq. (4.10) is

(4.12) c ( s ) = 1 log λ e sin ( log λ log s ) , − 1 log λ e cos ( log λ log s ) .

(iii) λ < 0 * = 1 .

By Eq. (4.2),

(4.13) w ( s ) = m ⋅ * cosh * ( − * λ * ⋅ * s ) + * n ⋅ * sinh * ( − * λ * ⋅ * s ) .

Analogously by similar approach with the previous case, we obtain

(4.14) c ( s ) = 1 − log λ e sinh ( − log λ log s ) , − 1 − log λ e cosh ( − log λ log s ) .

Thus, we have briefly proven following theorem.

Theorem 4.1

Let y be a parameterized curve by α -equiaffine arc length parameter. If y has constant α -equiaffine curvature, then it is given by one of those indicated by Eqs (4.7), (4.12), and (4.14).

Then, the graphs of Eqs (4.7) and (4.12) are shown in Figures 1 and 2.

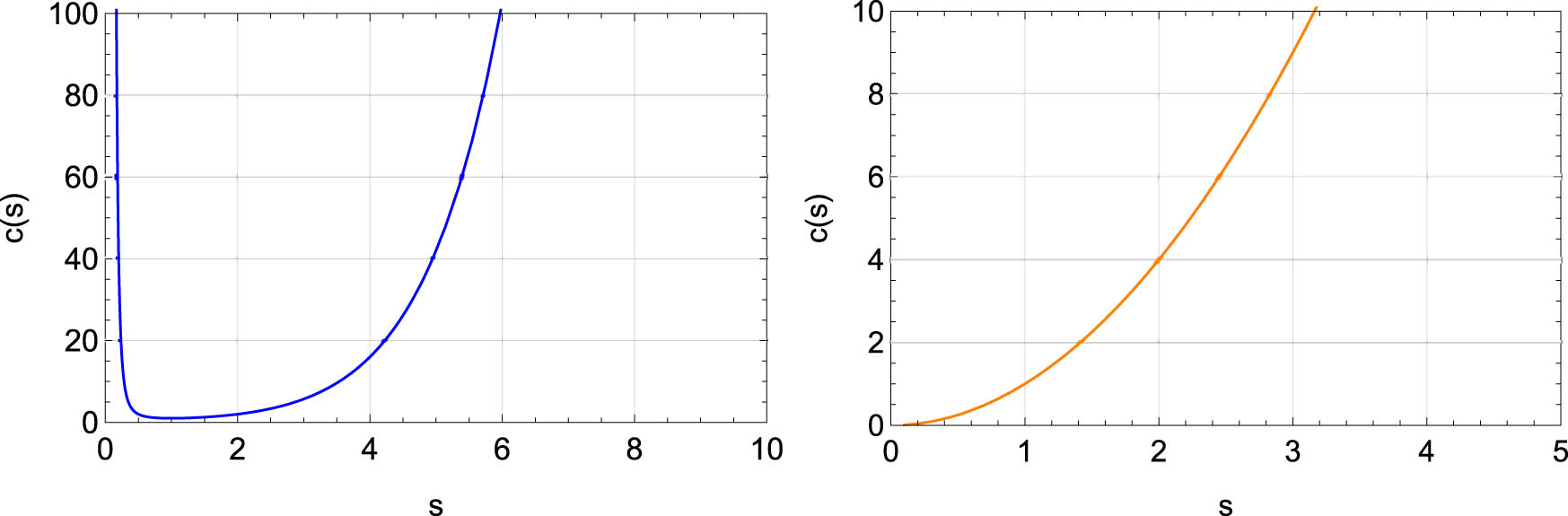
$Figure 1 The curve describes a multiplicative parabola arising from the condition λ = 0 * = 1 \lambda ={0}_{* }=1 , exhibiting quadratic behavior in the multiplicative sense.$

Figure 1

The curve describes a multiplicative parabola arising from the condition λ = 0 * = 1 , exhibiting quadratic behavior in the multiplicative sense.

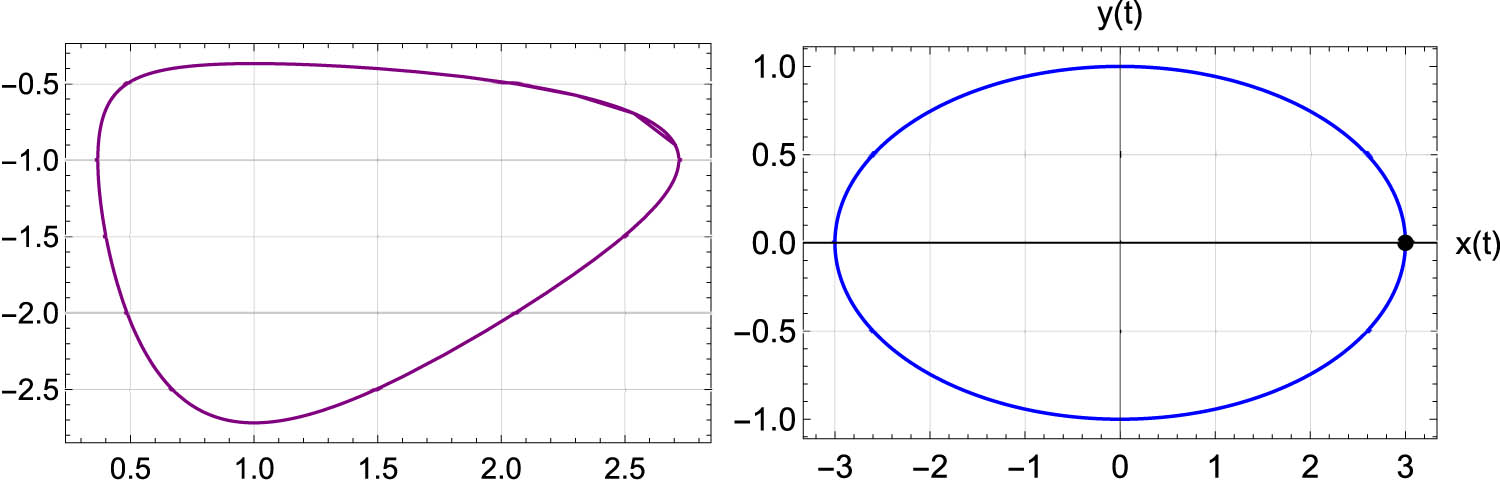
$Figure 2 A multiplicative ellipse corresponding to constant multiplicative equiaffine curvature λ > 0 * = 1 \lambda \gt {0}_{* }=1 , based on multiplicative trigonometric functions.$

Figure 2

A multiplicative ellipse corresponding to constant multiplicative equiaffine curvature λ > 0 * = 1 , based on multiplicative trigonometric functions.

5 Multiplicative equiaffine curvature of plane curves with an arbitrary parameter

In the preceding section, plane curves parameterized by arc length were considered. Here, we generalize the setting and compute the multiplicative equiaffine curvature for plane curves equipped with an arbitrary parameter. A proposition is provided to facilitate the computation, and illustrative examples are given to clarify the method.

Proposition 5.1

Let c be a multiplicative plane curve given with an arbitrary parameter t. Let ρ be the arc-length parameter defined by Eq. (3.11). Then, the multiplicative curvature κ of c with respect to ρ is given by

(5.1) κ ( ρ ) = e − 5 9 ⋅ * [ det * ( d * , d * * ) ] − 8 3 * ⋅ * [ det * ( d * , d * * * ) ] 2 + * e 4 3 ⋅ * [ det * ( d * , d * * ) ] − 5 3 * ⋅ * [ det * ( d * * , d * * * ) ] + * e 1 3 ⋅ * [ det * ( d * , d * * ) ] − 5 3 * ⋅ * [ det * ( d * , d * * * * ) ] ,

where d ( t ) = c ( ρ ) .

Proof

Let ρ be the arc-length parameter defined by Eq. (3.11). If d ( t ) = c ( ρ ) is taken, then

(5.2) d * ( ρ ) ⋅ * ρ * ( t ) = d * ( t )

is obtained. Here, det * ( d * , d * * ) ≠ 0 * holds. From Eq. (3.11), we have

(5.3) ρ * ( t ) = [ det * ( d * , d * * ) ] 1 3 * .

Thus,

(5.4) d * ( t ) = [ det * ( d * , d * * ) ] − 1 3 * ⋅ * d * ( ρ )

is obtained. That is, d * ( t ) = c * ( ρ ) .

Now, let us compute the multiplicative curvature κ ( ρ ) of the curve c , namely,

(5.5) κ ( ρ ) = det * ( d * * , d * * * ) .

From Eq. (5.4), that is, from

(5.6) d * ( t ) = [ det * ( d * , d * * ) ] − 1 3 * ⋅ * d * ( ρ ) ,

taking the multiplicative derivative once more yields

(5.7) d * * ( t ) = e − 1 3 ⋅ * [ det * ( d * , d * * ) ] − 5 3 * ⋅ * [ det * ( d * , d * * * ) ] ⋅ * d * + * [ det * ( d * , d * * ) ] − 2 3 * ⋅ * d * *

is obtained. Taking the multiplicative derivative once again gives

(5.8) d * * * ( t ) = e 5 9 ⋅ * [ det * ( d * , d * * ) ] − 3 * ⋅ * [ det * ( d * , d * * * ) ] 2 ⋅ * d * − * e 1 3 ⋅ * [ det * ( d * , d * * ) ] − 2 * ⋅ * [ det * ( d * * , d * * * ) + * det * ( d * , d * * * * ) ] ⋅ * d * + * e − 1 3 * ⋅ * [ det * ( d * , d * * ) ] − 2 * ⋅ * [ det * ( d * , d * * ) ] ⋅ * d * * + * e − 2 3 * ⋅ * [ det * ( d * , d * * ) ] − 2 * ⋅ * [ det * ( d * , d * * * ) ] ⋅ * d * * + * [ det * ( d * , d * * ) ] − 1 * ⋅ * d * * *

is obtained. Substituting Eqs (5.7) and (5.8) into Eq. (5.5) yields Eq. (5.1), and thus, the proposition is proved.□

Example 1

Let c ( t , e ( log t ) 3 ) be a multiplicative plane curve with an arbitrary parameter. Considering Eq. (5.1), the multiplicative curvature κ of c is given by

(5.9) κ ( t ) = ( 20 ) * ⋅ * e ( log ( e 6 ⋅ * t ) ) − 8 3 .

The graph of this curve is shown in Figure 3.

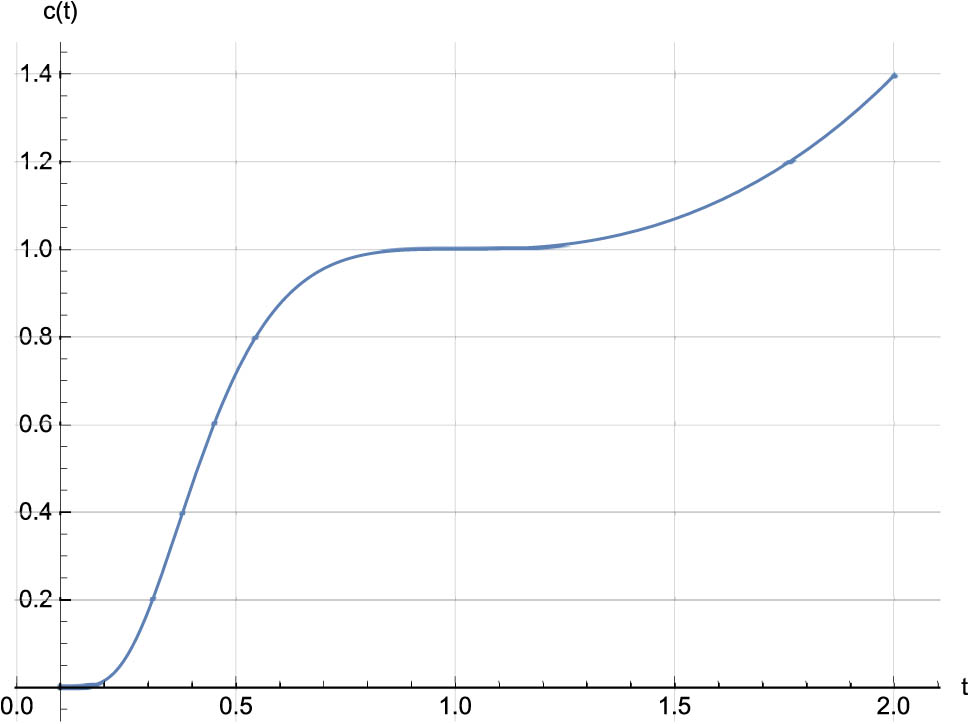
$Figure 3 The curve c ( t , e ( log t ) 3 ) {\bf{c}}\left(t,{e}^{{\left(\log t)}^{3}}) represents a multiplicative plane curve with an arbitrary parameter.$

Figure 3

The curve c ( t , e ( log t ) 3 ) represents a multiplicative plane curve with an arbitrary parameter.

Example 2

Let c ( e t log cos t , e t log sin t ) be a multiplicative plane curve with an arbitrary parameter. Considering Eq. (5.1), the multiplicative curvature κ of c is given by

(5.10) κ ( t ) = e 40 9 ⋅ * e 2 − 8 3 ⋅ * e − 4 t 3 .

The graph of this curve is shown in Figure 4.

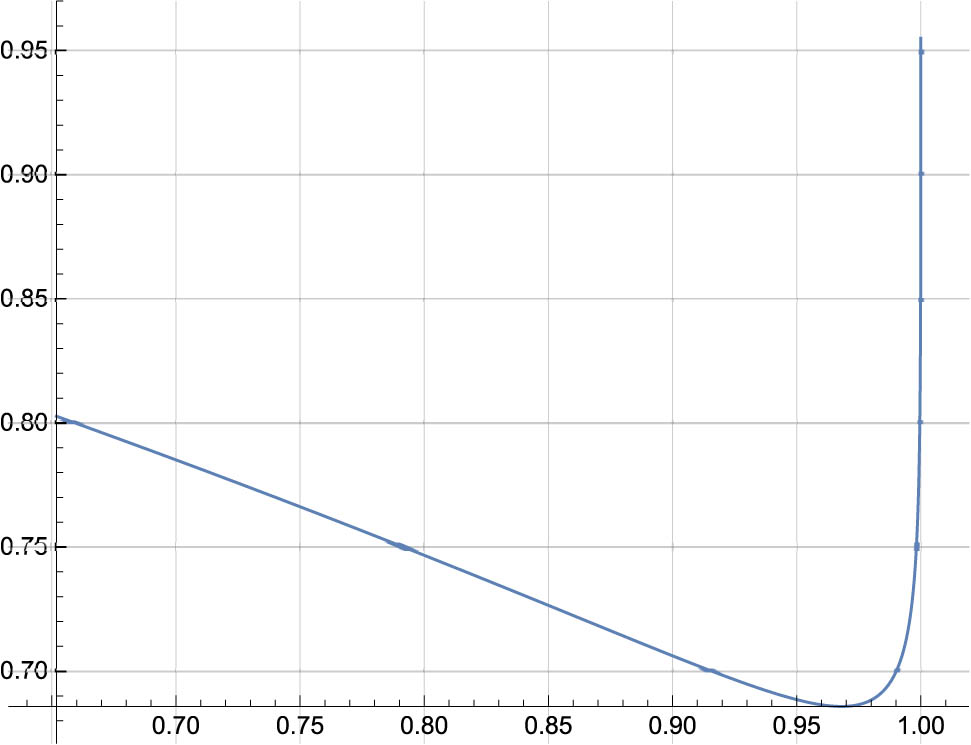
$Figure 4 The curve c ( e t log cos t , e t log sin t ) {\bf{c}}\left({e}^{t\log \cos t},{e}^{t\log \sin t}) represents a multiplicative plane curve with an arbitrary parameter.$

Figure 4

The curve c ( e t log cos t , e t log sin t ) represents a multiplicative plane curve with an arbitrary parameter.

Example 3

Let c ( e 1 3 ( log t ) 3 , ( ln t ) − 1 3 ) be a multiplicative plane curve with an arbitrary parameter. Considering Eq. (5.1), the multiplicative curvature κ of c is given by

(5.11) κ ( t ) = − * e 2 ⋅ * e ( log t ) − 2 .

The graph of this curve is shown in Figure 5.

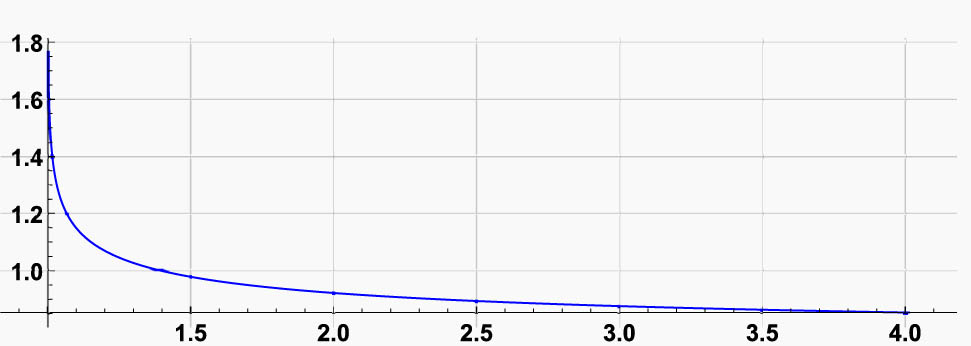
$Figure 5 The curve c ( e 1 3 ( log t ) 3 , ( ln t ) − 1 3 ) {\bf{c}}\left({e}^{\tfrac{1}{3}{\left(\log t)}^{3}},{\left(\mathrm{ln}t)}^{-\tfrac{1}{3}}) represents a multiplicative plane curve with an arbitrary parameter.$

Figure 5

The curve c ( e 1 3 ( log t ) 3 , ( ln t ) − 1 3 ) represents a multiplicative plane curve with an arbitrary parameter.

Example 4

Let c ( e 2 3 ( log t ) 3 2 , e − 4 9 ( log t ) 3 2 . ( ln t ) 2 3 ( log t ) 3 2 ) be a multiplicative plane curve with an arbitrary parameter. Considering Eq. (5.1), the multiplicative curvature κ of c is given by

(5.12) κ ( t ) = − * e 1 4 ⋅ * e ( log t ) − 2 .

The graph of this curve is shown in Figure 6.

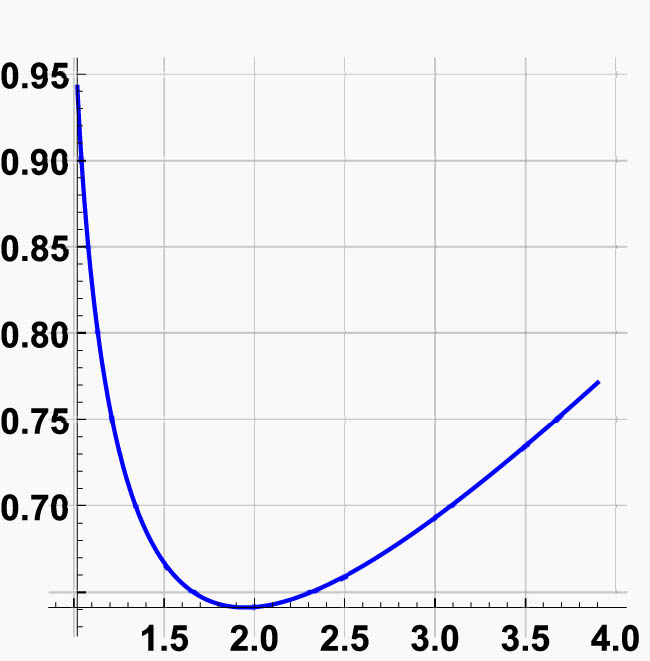
$Figure 6 The curve c ( e 2 3 ( log t ) 3 2 , e − 4 9 ( log t ) 3 2 . ( ln t ) 2 3 ( log t ) 3 2 ) {\bf{c}}\left({e}^{\tfrac{2}{3}{\left(\log t)}^{\frac{3}{2}}},{e}^{-\tfrac{4}{9}{\left(\log t)}^{\frac{3}{2}}}.{\left(\mathrm{ln}t)}^{\tfrac{2}{3}{\left(\log t)}^{\frac{3}{2}}}) represents a multiplicative plane curve with an arbitrary parameter.$

Figure 6

The curve c ( e 2 3 ( log t ) 3 2 , e − 4 9 ( log t ) 3 2 . ( ln t ) 2 3 ( log t ) 3 2 ) represents a multiplicative plane curve with an arbitrary parameter.

6 Discussion

Although this work is formulated in a purely mathematical framework, the use of multiplicative structures aligns with modeling approaches in physics, particularly in scale-invariant systems, exponential decay/growth models, and systems governed by proportional change. Such frameworks may appear in thermodynamics, population dynamics, or quantum models involving exponential operators. Potential applications of the proposed geometric model include areas where traditional additive calculus fails to provide natural descriptions – such as biological growth, economic systems under compounding interest, or dynamical systems characterized by proportional (rather than incremental) evolution. In addition, the structure can be useful in data science contexts involving multiplicative noise. Compared to classical equiaffine differential geometry, where additive operations govern the frame evolution, the proposed multiplicative approach replaces these operations with their exponential-logarithmic analogues. For instance, the multiplicative curvature is derived from logarithmic determinants, which offer a different perspective on area preservation and invariance under the multiplicative group SL * ( 2 , R ) . These distinctions introduce new phenomena not captured by traditional affine curvature theory.

Acknowledgments

The authors extend their appreciation to Fırat University. This work was supported by Taif University, Saudi Arabia, through project number (TU-DSPP-2024-94).

Funding information: This research was funded by Fırat University and supported by Taif University, Saudi Arabia, Project No. (TU-DSPP-2024-94).
Author contributions: Meltem Ogrenmis: conceptualization; methodology; writing-original draft; visualization; investigation; Alper Osman Ogrenmis: formal analysis; literature review; writing-review and editing; manuscript revision; Emad E. Mahmoud: supervision; project administration; writing-review and editing. All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors state no conflict of interest.
Data availability statement: All data generated or analyzed during this study are included in this manuscript.

References

[1] Volterra V, Hostinsky B. Operations infinitesimales lineares. Paris: Herman; 1938. Suche in Google Scholar

[2] Grossman M, Katz R. Non-Newtonian calculus. 1st ed. Pigeon Cove, Massachusetts: Lee Press; 1972. Suche in Google Scholar

[3] Grossman M. Bigeometric calculus: A system with a scale-free derivative. Massachusetts: Archimedes Foundation; 1983. Suche in Google Scholar

[4] Stanley D. A multiplicative calculus. Primus. 1999;9(4):310–26. 10.1080/10511979908965937Suche in Google Scholar

[5] Bashirov A, Riza M. On complex multiplicative differentiation. TWMS J Appl Eng Math. 2011;1(1):75–85. Suche in Google Scholar

[6] Yazici M, Selvitopi H. Numerical methods for the multiplicative partial differential equations. Open Math. 2017;15:1344–50. 10.1515/math-2017-0113Suche in Google Scholar

[7] Yalçín N, Celik E. Solution of multiplicative homogeneous linear differential equations with constant exponentials. New Trends Math Sci. 2018;6(2):58–67. 10.20852/ntmsci.2018.270Suche in Google Scholar

[8] Goktas S, Kemaloglu H, Yilmaz E. Multiplicative conformable fractional Dirac system. Turkish J Math. 2022;46:973–90. 10.55730/1300-0098.3136Suche in Google Scholar

[9] Georgiev SG, Zennir K. Multiplicative differential calculus. 1st ed. New York: Chapman and Hall/CRC; 2022. 10.1201/9781003299080-1Suche in Google Scholar

[10] Georgiev SG. Multiplicative differential geometry. 1st ed. New York: Chapman and Hall/CRC; 2022. 10.1201/9781003299844-1Suche in Google Scholar

[11] Georgiev SG, Zennir K, Boukarou A. Multiplicative analytic geometry. 1st ed. New York: Chapman and Hall/CRC; 2022. 10.1201/9781003325284-1Suche in Google Scholar

[12] Nurkan SK, Gurgil I, Karacan MK. Vector properties of geometric calculus. Math Meth Appl Sci. 2023;46:17672–91. 10.1002/mma.9525Suche in Google Scholar

[13] Has A, Yílmaz B. On non-Newtonian helices in multiplicative Euclidean space. Fund Contemp Math Sci. 2025;6(2):196–217. 10.54974/fcmathsci.1644427Suche in Google Scholar

[14] Aydin ME, Has A, Yílmaz B. A non-Newtonian approach in differential geometry of curves: multiplicative rectifying curves, Bullet Korean Math Soc. 2024;61(3):849–66. Suche in Google Scholar

[15] Ceyhan H, Özdemir Z, Gök İ. Multiplicative generalized tube surfaces with multiplicative quaternions algebra. Math Meth Appl Sci. 2024;47:9157–68. 10.1002/mma.10065Suche in Google Scholar

[16] Has A, Yílmaz B, Yíldírím H. A non-Newtonian perspective on multiplicative Lorentz-Minkowski space L*3. Math Meth Appl Sci. 2024;47:13875–888. 10.1002/mma.10243Suche in Google Scholar

[17] Özdemir Z, Ceyhan H. Multiplicative hyperbolic split quaternions and generating geometric hyperbolical rotation matrices. Appl Math Comput. 2024;479:128862. 10.1016/j.amc.2024.128862Suche in Google Scholar

[18] Has A, Yílmaz B. A non-Newtonian conics in multiplicative analytic geometry. Turkish J Math. 2024;48(5):976–94. 10.55730/1300-0098.3554Suche in Google Scholar

[19] Es H. Plane kinematics in homothetic multiplicative calculus. J Univ Math. 2024;7(1):37–47. 10.33773/jum.1408506Suche in Google Scholar

[20] Has A, Yílmaz B. A non-Newtonian magnetic curves in multiplicative Riemann manifolds. Phys Scr. 2024;99(4):045238. 10.1088/1402-4896/ad32b7Suche in Google Scholar

[21] Aydin ME, Has A, Yílmaz B. Multiplicative rectifying submanifolds of multiplicative Euclidean space. Math Meth Appl Sci. 2025;48:329–39. 10.1002/mma.10329Suche in Google Scholar

[22] Broscateanu SC, Mihai A, Olteanu A. A note on the infinitesimal bending of a rectifying curve. Symmetry. 2024;16(10):1361. 10.3390/sym16101361. Suche in Google Scholar

[23] Burlacu A, Mihai A. Applications of differential geometry of curves in roads design. Rom J Trans Infrastruct. 2023;12(2):1–13, 10.2478/rjti-2023-0010. Suche in Google Scholar

[24] Jianu M, Achimescu S, Dăauş L, Mierluş-Mazilu I, Mihai A, Tudor D. On a surface associated to the catalan triangle. Axioms. 2022;11(12):685. 10.3390/axioms11120685Suche in Google Scholar

[25] Aydin ME, Mihai A, Yokus A. Applications of fractional calculus in equiaffine geometry: plane curves with fractional order. Math Meth Appl Sci. 2021;44:13659–69. 10.1002/mma.7649Suche in Google Scholar

[26] Davis D. Generic affine differential geometry of curves in Rn. Proc R Soc Edinburgh A. 2006;136:1195–205. 10.1017/S0308210500004947Suche in Google Scholar

[27] Guggenheimer HW. Differential geometry. New York: McGraw-Hill; 1963. Suche in Google Scholar

[28] Nomizu K, Sasaki T. Affine differential geometry: Geometry of affine immersions. Cambridge Tracts in Mathematics. Cambridge: Cambridge University Press; 1994. Suche in Google Scholar

[29] Aniszewska D, Rybaczuk M. Analysis of the multiplicative Lorenz system. Chaos Solitons Fract. 2005;25(1):79–90. 10.1016/j.chaos.2004.09.060Suche in Google Scholar

[30] Aniszewska D, Rybaczuk M. Lyapunov type stability and Lyapunov exponent for exemplary multiplicative dynamical systems. Nonlinear Dyn. 2008;54:345–54. 10.1007/s11071-008-9333-7Suche in Google Scholar

[31] Cordova-Lepe F. The multiplicative derivative as a measure of elasticity in economics. TEMAT-Theaeteto Atheniensi Math. 2006;2(3):7. Suche in Google Scholar

[32] Filip DA, Piatecki C. A non-newtonian examination of the theory of exogenous economic growth. Math. Aeterna. 2014;4:101–17. Suche in Google Scholar

[33] Florack L, Van Assen H. Multiplicative calculus in biomedical image analysis. J. Math. Imaging. Vis. 2012;42:64–75. 10.1007/s10851-011-0275-1Suche in Google Scholar

[34] Mora M, Cordova-Lepe F, Del-Valle R. A non-Newtonian gradient for contour detection in images with multiplicative noise. Pattern Recogn Lett. 2012;33(10):1245–56. 10.1016/j.patrec.2012.02.012Suche in Google Scholar

Received: 2025-03-23

Revised: 2025-08-13

Accepted: 2025-09-09

Published Online: 2025-10-15

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

https://doi.org/10.1515/phys-2025-0212

Schlagwörter für diesen Artikel

Affine plane; equiaffine plane curves; multiplicative derivative; multiplicative integral

Creative Commons

BY 4.0