Threshold dynamics and optimal control of an epidemiological smoking model

Jianglin Zhao; Lirong Ma

doi:10.1515/nleng-2025-0153

40% Rabatt

auf Fachbücher bei De Gruyter Brill *

Artikel Open Access

Threshold dynamics and optimal control of an epidemiological smoking model

Jianglin Zhao und Lirong Ma

Veröffentlicht/Copyright: 7. Juli 2025

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen

Aus der Zeitschrift Nonlinear Engineering Band 14 Heft 1

Abstract

This article proposes a potential-light-smoker-quit smoker smoking model by incorporating the infection and quitting behavior of occasional smokers. Theoretical analysis shows that the reproduction number R 0 serves as a threshold parameter: smoking is eradicated when R 0 ≤ 1 , but becomes endemic when R 0 > 1 . Numerical simulations confirm these findings. The impact of parameters on R 0 implies that effective control measures require a reduction in transmission and conversion rates, as well as an increase in quit rates. Sensitivity analysis further demonstrates that decreasing transmission and conversion rates significantly reduce the peak of smokers, whereas increasing quit rates delay the onset of this peak. Optimal control strategies identify three key interventions: creating smoke-free environments, conducting smoking hazard education campaigns, and offering treatment for chain smokers, which can effectively curb the prevalence level of smoking behavior.

Keywords: smoking epidemic model; stability results; sensitivity analysis; optimal control

1 Introduction

In 2019, an estimated 1.14 billion individuals worldwide were smokers, with China leading the list with approximately 306 million smokers, making it the country with the largest smoking population globally [1]. It is noted that all types of tobacco use are damaging and that no safe level of tobacco exposure exists. Tobacco is responsible for more than 8 million deaths each year, of which over 7 million are a direct result of tobacco use and about 1.3 million result from secondhand smoke exposure [2]. In addition, tobacco use contributes to poverty by diverting household expenditures from essential supplies to cigarette consumption [3]. Since smoking behavior can spread through social contact, it has become one of the most severe challenges to global public health [4]. Thus, it is imperative to implement measures to mitigate the tobacco epidemic and foster the establishment of smoke-free communities. A deeper understanding of the smoking transmission is therefore essential for determining the optimal control strategies and preventing its spread.

Nowadays, researchers in epidemiology extensively employ mathematical modeling, with the aim of reducing transmission and effectively controlling infectious diseases [5–19]. To better understand the propagation of smoking behavior in a population, numerous mathematical models have been constructed. These models often analyze the transmission dynamics of smoking behavior by treating it as an infectious disease that can be transmitted through social interactions [3,20–24]. Zaman [25] divided the total population into four classes: (i) potential smokers, who do not currently smoke but may do so in the future; (ii) occasional smokers, who do not smoke every day; (iii) smokers, who smoke every day; and (iv) quit smokers, who have permanently stopped smoking. On the basis of these classifications, Zeb et al. studied the square-root dynamics [26]. Furthermore, Rahman et al. considered the harmonic mean type incidence rate of potential and occasional smokers [27]. They presented a threshold for determining the prevalence of smoking behavior. Notably, although most models classify smokers into occasional and chain smokers, many studies only consider that contact with chain smokers influences potential smokers to start smoking, while ignoring the transmission role of occasional smokers [3,20–27]. In fact, the smoking behavior of occasional smokers can influence potential smokers to start smoking, especially among teenagers, because adolescents are more vulnerable to peer influence and tend to imitate the behaviors they observe in their social circles [1]. On the other hand, the number of smokers can be significantly decreased as the quit rate rises [20,21]. However, most smoking models solely consider chain smokers’ quitting and overlook the quitting behavior of occasional smokers, despite the fact that occasional smokers tend to have a higher success rate in quitting. While some models have considered occasional smokers as a source of infection and some have considered the quitting behavior of occasional smokers [28,29], few studies have considered both the infection and quitting behavior of occasional smokers. Therefore, to achieve a more comprehensive comprehension of smoking behavior, it would be more realistic to include both the influence of occasional smokers on potential smokers and the quitting behavior of occasional smokers in the smoking model.

Motivated by the aforementioned consideration, we presented a smoking model by incorporating the infection and quitting behavior of occasional smokers. The purpose of this article is to propose feasible and effective measures to successfully create a smoke-free community by analyzing the dynamical behavior of the smoking population. The rest of the article is structured as follows. Section 2 describes the model formulation and the invariant set of solutions. Section 3 presents the basic reproduction number and the stability of equilibria. Section 4 performs numerical simulations to validate analytical results and studies the sensitivity of parameters. Finally, a brief conclusion and discussion are given in Section 5.

2 Model formulation

On the basis of previous studies [25–27], we classify the whole population ( N ) into four subclasses: potential smokers ( P ) , occasional smokers ( L ) , chain smokers ( S ) , and quitters ( Q ) . Potential smokers refer to individuals who do not currently use tobacco but may do so in the future. Occasional smokers are individuals who smoke less frequently than daily smokers. Chain smokers, also known as heavy smokers, are individuals who smoke cigarettes with great frequency, often continuously and throughout the day. Quitters, also referred to as ex-smokers or former smokers, are individuals who have previously smoked but have successfully stopped the habit of smoking. The transition between these subpopulations is illustrated in Figure 1. Potential smokers grow at a constant rate Λ . Potential smokers can become occasional smokers through exposure to occasional and chain smokers. This transmission is denoted by β P ( L + S ) , where β represents the transmission rate of potential smokers in contact with occasional and chain smokers. The transitions between L , S , and Q are dominated by terms that are proportional to the size of these subpopulations. Occasional smokers may manage themselves to stop tobacco use with the quit rate γ . The conversion rate of occasional smokers to chain smokers is σ . The quit rate of chain smokers is δ . The natural death rate is μ for all classes. Therefore, the mathematical model for the spread of smoking behavior is as follows:

(1) P ˙ = Λ − β P ( L + S ) − μ P , L ˙ = β P ( L + S ) − ( σ + γ + μ ) L , S ˙ = σ L − ( δ + μ ) S , Q ˙ = γ L + δ S − μ Q .

Figure 1

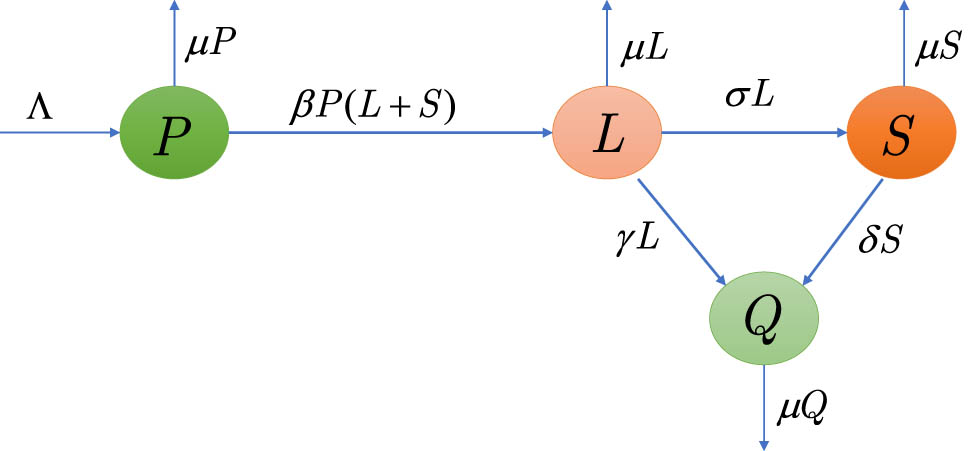
Flowchart of system (1).

Let N = P + L + S + Q . It follows from (1) that d N ∕ d t = Λ − μ N , which implies that lim t → ∞ N ( t ) = Λ ∕ μ . Therefore, the feasible region Ω = ( P , L , S , Q ) ∈ R + 4 : N ( t ) ⩽ Λ μ is positively invariant. Furthermore, in the region Ω , the existence, uniqueness, and continuation of solutions hold for system (1). Hence, the system (1) is biologically meaningful and mathematically well-posed, and all solutions of (1) starting with initial value ( P ( 0 ) , L ( 0 ) , S ( 0 ) , Q ( 0 ) ) ∈ Ω will remain in Ω for all t > 0 .

3 Threshold dynamics

3.1 Equilibria and basic reproduction number

The smoking-free equilibrium of system (1) is E 0 ( P 0 , 0 , 0 , 0 ) = ( Λ μ , 0 , 0 , 0 ) . The next-generation matrix method is to be utilized to find the basic reproduction number R 0 of system (1). The new infection matrix F and the transition matrix V are determined as follows:

F = β P ( L + S ) 0 , V = ( σ + γ + μ ) L − σ L + ( δ + μ ) S .

By evaluating the Jacobian matrix of F and V at E 0 , we have

F = β Λ μ β Λ μ 0 0 , V = σ + γ + μ 0 − σ δ + μ .

Thus, the next-generation matrix is

FV − 1 = Λ μ β σ + γ + μ 1 + σ δ + μ β Λ μ ( δ + μ ) 0 0 .

Hence, the basic reproduction number of system (1) is given by

(2) R 0 = Λ μ β σ + γ + μ 1 + σ δ + μ = Λ μ β σ + γ + μ + Λ μ β σ + γ + μ σ δ + μ ,

where Λ μ β σ + γ + μ and Λ μ β σ + γ + μ σ δ + μ represent the contribution of occasional and chain smokers to the basic reproduction number, respectively.

Let E * ( P * , L * , S * , Q * ) be the smoking-present equilibrium of system (1). By taking the right-hand side of the system (1) to zero, one obtains

(3) P * = ( σ + γ + μ ) ( δ + μ ) β ( σ + δ + μ ) , L * = 1 σ + γ + μ [ Λ − μ P * ] , S * = σ δ + μ L * , Q * = γ μ + δ σ μ ( δ + μ ) L * .

According to (2) and (3), we have L * = Λ σ + γ + μ 1 − 1 R 0 . Therefore, there exists a unique smoking-present equilibrium E * ( P * , L * , S * , Q * ) if and only if R 0 > 1 .

3.2 Stability of the equilibria

Theorem 1

The smoking-free equilibrium E 0 is locally asymptotically stable if R 0 < 1 and unstable if R 0 > 1 .

Proof

The Jacobian matrix of system (1) at E 0 is

J ( E 0 ) = − μ − β Λ μ − β Λ μ 0 0 β Λ μ − ( σ + γ + μ ) β Λ μ 0 0 σ − ( δ + μ ) 0 0 γ δ − μ .

The characteristic equation of J ( E 0 ) is given by

( λ + μ ) 2 ( λ 2 + a 1 λ + a 0 ) = 0 ,

where a 0 = ( δ + μ ) ( σ + γ + μ ) ( 1 − R 0 ) and a 1 = − β Λ μ + ( σ + γ + μ ) + ( δ + μ ) . One of the eigenvalues of J ( E 0 ) is − μ (a double root). The other two eigenvalues of J ( E 0 ) is the characteristic roots of the equation:

(4) λ 2 + a 1 λ + a 0 = 0 .

If R 0 < 1 , then a 0 > 0 . According to the (2), when R 0 < 1 , we have β Λ μ < ( σ + γ + μ ) δ + μ σ + δ + μ < σ + γ + μ , which implies that a 1 > 0 . By Routh–Hurwitz criterion, the roots of (4) have negative real parts. Thus, the smoking-free equilibrium E 0 is locally asymptotically stable when R 0 < 1 . If R 0 > 1 , then a 0 < 0 . In this case, there exists a positive root of (4), which implies that the smoking-free equilibrium E 0 is unstable.□

Theorem 2

The smoking-present equilibrium E * is locally asymptotically stable if R 0 > 1 .

Proof

The Jacobian matrix of system (1) at E * is

J ( E * ) = − β ( L * + S * ) − μ − β P * − β P * 0 β ( L * + S * ) β P * − ( σ + γ + μ ) β P * 0 0 σ − ( δ + μ ) 0 0 γ δ − μ .

The characteristic equation of J ( E * ) is given by

( λ + μ ) ( λ 3 + a 2 λ 2 + a 1 λ + a 0 ) = 0 ,

where

a 0 = β Λ ( σ + δ + μ ) 1 − 1 R 0 , a 1 = β Λ ( σ + δ + μ ) δ + μ + β Λ ( σ + δ + μ ) σ + γ + μ − μ ( δ + μ ) ( σ + γ + μ ) σ + δ + μ > β Λ − μ ( δ + μ ) ( σ + γ + μ ) σ + δ + μ = β Λ 1 − 1 R 0 , a 2 = β Λ ( σ + δ + μ ) ( δ + μ ) ( σ + γ + μ ) + ( σ + γ + μ ) + ( δ + μ ) − ( δ + μ ) ( σ + γ + μ ) σ + δ + μ > ( σ + γ + μ ) − ( σ + γ + μ ) δ + μ σ + δ + μ > 0 .

Furthermore,

a 1 a 2 − a 0 > ( δ + μ ) β Λ ( σ + δ + μ ) δ + μ − μ ( δ + μ ) ( σ + γ + μ ) σ + δ + μ − [ β Λ ( σ + δ + μ ) − μ ( δ + μ ) ( σ + γ + μ ) ] = μ ( δ + μ ) ( σ + γ + μ ) 1 − δ + μ σ + δ + μ > 0 .

If R 0 > 1 , then a 0 > 0 and a 1 > 0 . According to Routh–Hurwitz criterion, the smoking-present equilibrium E * is locally asymptotically stable if R 0 > 1 .□

Theorem 3

The smoking-free equilibrium E 0 is globally asymptotically stable if R 0 ⩽ 1 .

Proof

Consider the following Lyapunov function:

(5) V = P − P 0 − P 0 ln P P 0 + L + β P 0 δ + μ S .

The derivative of V along any solution of system (1) is given by

d V d t = 1 − P 0 P P ˙ + L ˙ + β P 0 δ + μ S ˙ = P − P 0 P [ Λ − β P ( L + S ) − μ P ] + [ β P ( L + S ) − ( σ + γ + μ ) L ] + β P 0 δ + μ [ σ L − ( δ + μ ) S ] = P − P 0 P [ μ P 0 − β P ( L + S ) − μ P ] + [ β P ( L + S ) − ( σ + γ + μ ) L ] + β P 0 δ + μ [ σ L − ( δ + μ ) S ] = − μ ( P − P 0 ) 2 P − ( σ + γ + μ ) − β P 0 − β P 0 σ δ + μ L = − μ ( P − P 0 ) 2 P − ( σ + γ + μ ) ( 1 − R 0 ) L .

Then V ˙ ⩽ 0 if R 0 < 1 , and V ˙ = 0 when P = P 0 , L = 0 and S = 0 . Hence, the only invariant set satisfying V ˙ = 0 is the singleton { E 0 } . By LaSalle’s Invariance Principle, every solution of system (1) approaches E 0 as t → ∞ . Therefore, the smoking-free equilibrium E 0 is globally asymptotically stable if R 0 ⩽ 1 .□

Theorem 4

The smoking-present equilibrium E * is globally asymptotically stable If R 0 > 1 .

Proof

Consider a Lyapunov function of the following form:

(6) W = P − P * − P * ln P P * + L − L * − L * ln L L * + β P * S * σ L * S − S * − S * ln S S * .

By calculating the derivative of W along any solution of system (1), we obtain

d W d t = 1 − P * P P ˙ + 1 − L * L L ˙ + β P * S * σ L * 1 − S * S S ˙ = μ P * 2 − P P * − P * P + β P * L * − P L − P * P P * L * + P * L + β P * S * − P S − P * P P * S * + P * S + β P L + P S − P * L − P * S * L L * − P L * − P S L * L + P * L * + P * S * + β P * S * L L * − P * S − P * S * S * L S L * + P * S * = ( μ P * + β P * L * ) 2 − P P * − P * P + β P * S * 3 − P * P − S * L S L * − P S L * P * S * L .

By using the fact that the geometric mean is less than or equal to the arithmetic mean, it can be deduced that 2 − P P * − P * P ⩽ 0 and 3 − P * P − S * L S L * − P S L * P * S * L ⩽ 0 . Therefore, W ˙ ⩽ 0 and W ˙ = 0 if and only if P = P * and L * L = S * S . Hence, the largest invariant set satisfying W ˙ = 0 in the positively invariant set Ω is the singleton { E * } . By LaSalle’s invariance principle, the smoking-present equilibrium E * is globally asymptotically stable when R 0 > 1 .□

4 Numerical simulations and sensitivity analysis

4.1 Verification of theoretical results

This subsection aims to perform some numerical simulations to verify the dynamical behavior of system (1). Given an average lifespan of 70 years, the natural death rate is μ = 1 70 ≈ 0.0143 per year. Let the transmission rate β be 0.02 per year [30]. Suppose that it takes an average of 5 years for occasional smokers to become chain smokers. Thus, the conversion rate is set as σ = 0.2 per year. The average duration of smoking for occasional smokers is assumed to be 2 years. Consequently, the quit rate for occasional smokers is γ = 1 2 = 0.5 per year. For chain smokers, the average duration of smoking is estimated to be 10 years. Thus, the quit rate for chain smokers is δ = 1 10 = 0.1 per year. The initial value of system (1) is set as ( P ( 0 ) , L ( 0 ) , S ( 0 ) , Q ( 0 ) ) = (20, 12, 8, 2). In the following numerical simulations, we assume that the specified values remain unchanged.

First, let Λ = 0.1 per year. Then, R 0 is 0.5384, which is less than unity. Thus, according to Theorem 3, the smoking-free equilibrium is globally asymptotically stable. Figure 2(a) shows that the number of potential smokers tends to P 0 = 6.993 , and the number of occasional and chain smokers tends to zero, while the number of quit smokers finally converges to zero. This implies that smoking behavior has been eliminated.

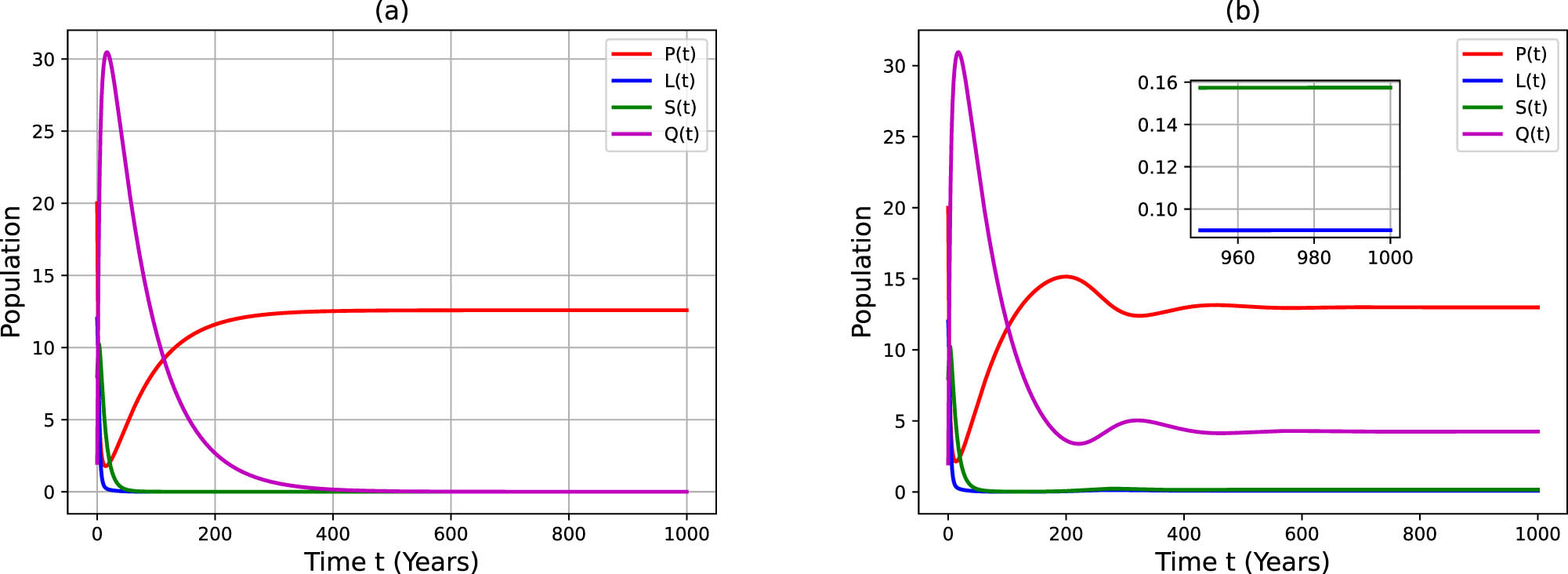
$Figure 2 The plot shows the dynamical behavior of all classes for (a) R 0 < 1 {{\mathscr{R}}}_{0}\lt 1 and (b) R 0 > 1 {{\mathscr{R}}}_{0}\gt 1 .$

Figure 2

The plot shows the dynamical behavior of all classes for (a) R 0 < 1 and (b) R 0 > 1 .

Then, let Λ = 0.25 per year. Then, R 0 is 1.3460, which is greater than unity. Theorem 4 indicates that the smoking-present equilibrium is globally asymptotically stable. In Figure 2(b), it can be observed that the number of potential, occasional, chain, and quit smokers tend to stable values, namely, P * = 12.9883 , L * = 0.08997 , S * = 0.1574 , and Q * = 4.2468 . This implies that smoking behavior has been endemic.

4.2 Sensitivity analysis

4.2.1 Impact of parameters on R 0

Understanding the transmission dynamics of smoking behavior in populations is crucial for controlling this public health epidemic. To design effective strategies for reducing smoking prevalence, we will use sensitivity analysis to assess how model parameters influence the basic reproduction number. It will reveal the key drivers of smoking’s persistence and transmission in communities.

The sensitivity index of R 0 with respect to p is defined as follows:

(7) Γ p R 0 = ∂ R 0 ∂ p × p R 0 .

According to (2), the sensitivity indices of R 0 for model parameters are listed in Table 1. Table 1 shows that the basic reproduction number R 0 is most sensitive to the natural death rate μ . However, this parameter is unrealistic to manipulate in practice. The sensitivity indices of R 0 for both Λ and β are 1, indicating that a 100% increase (decrease) in the recruitment rate or the transmission rate would lead to a corresponding 100% increase (decrease) in the value of R 0 . As presented in Table 1, a 100% increase in the conversion rate ( σ ) raises R 0 by 36%. Positive sensitivity indices of Λ , β , and σ imply that higher values of these parameters increase R 0 , thereby promoting smoking spread. Conversely, μ , γ , and δ have negative indices, meaning higher values reduce R 0 and suppress smoking spread. Table 1 shows that a 100% increase in the quit rate ( γ ) reduces R 0 by 70%, while a 100% increase in δ reduces it by 56% .

Table 1

Sensitivity indices of R 0 corresponding to all parameters in system (1)

Parameter	Sensitivity index	Parameter	Sensitivity index
Λ	1	β	1
μ	− 1.099631029	σ	0.3563403119
γ	− 0.6999860005	δ	− 0.5567232827

Therefore, the basic reproduction number R 0 can be decreased by (i) reducing the recruitment rate Λ , lowering the transmission rate β , and decreasing the conversion rate σ ; and (ii) increasing the quit rates γ and δ . In real-world situations, the recruitment rate Λ of potential smokers is typically fixed. To effectively curb the spread of smoking behavior, we should focus on controlling the four parameters: the transmission rate β , the conversion rate σ , and the quit rates γ and δ .

Furthermore, the contour plots of R 0 as a function of σ and β , δ , and γ are shown in Figure 3. Figure 3(a) shows that R 0 can be reduced to less than 1 when the transmission rate β and the conversion rate σ are low enough, implying that the smoking transmission behavior is controlled. Figure 3(b) shows that when the quit smoking rates γ and δ are high enough, R 0 can drop below 1, indicating that smoking behavior would eventually be eliminated from the population.

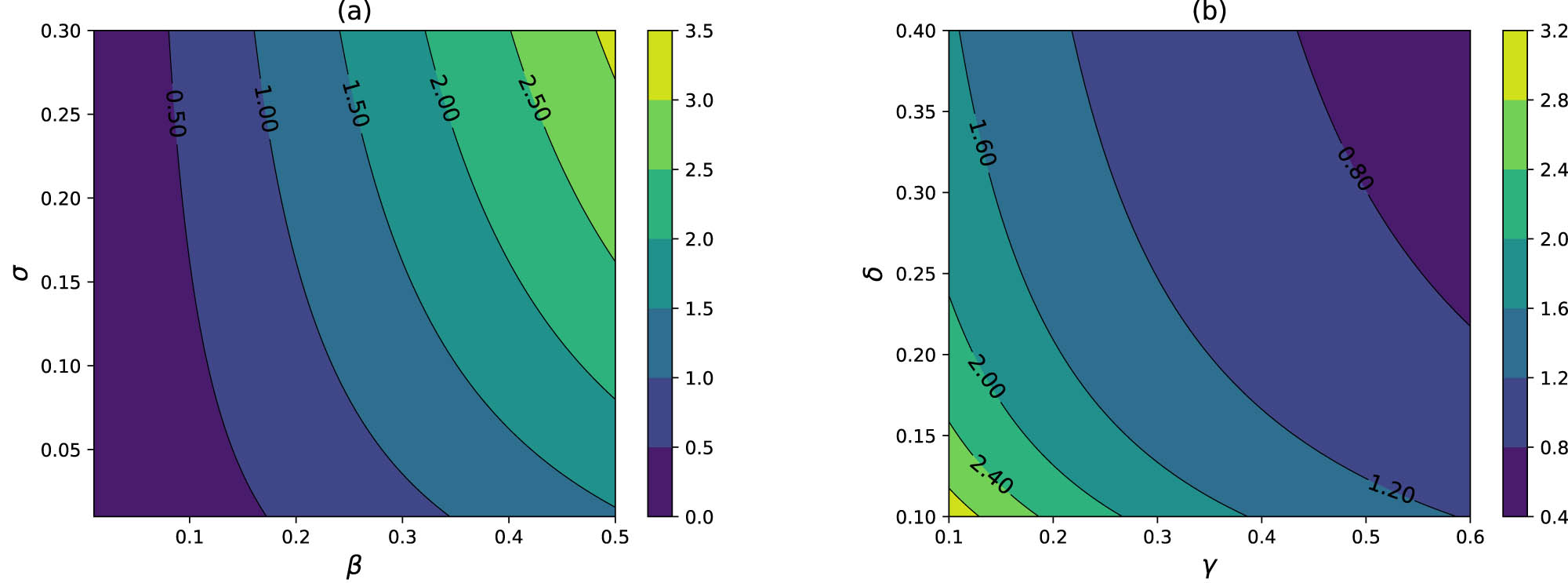
$Figure 3 Contour plots of R 0 {{\mathscr{R}}}_{0} for different parameters: (a) σ \sigma and β \beta and (b) δ \delta and γ \gamma .$

Figure 3

Contour plots of R 0 for different parameters: (a) σ and β and (b) δ and γ .

4.2.2 Impact of parameters on the level of occasional and chain smokers

To further investigate the effect of parameters on the number of occasional and chain smokers, Λ is set as 0.05. Figure 4 illustrates the effect of the transmission and conversion rates on the population of occasional and chain smokers when R 0 < 1 . From Figure 4(a), it can be observed that a reduction in β can diminish the peak of occasional smokers, but the peak arrival time is not influenced. When β is sufficiently small, the peak of occasional smokers does not occur at all, leading to a monotonic decline toward extinction. Figure 4(b) indicates that as β decreases, the peak of chain smokers is reduced and the peak arrival time remains almost unchanged. Figure 4(c) reveals that when σ is small enough, occasional smokers do not show a peak but rather monotonically decrease toward zero. As shown in Figure 4(d), a decrease in σ reduces the peak of chain smokers but does not change the peak arrival time. As shown in Figure 4, the smaller the transmission and conversion rates, the fewer smokers there are.

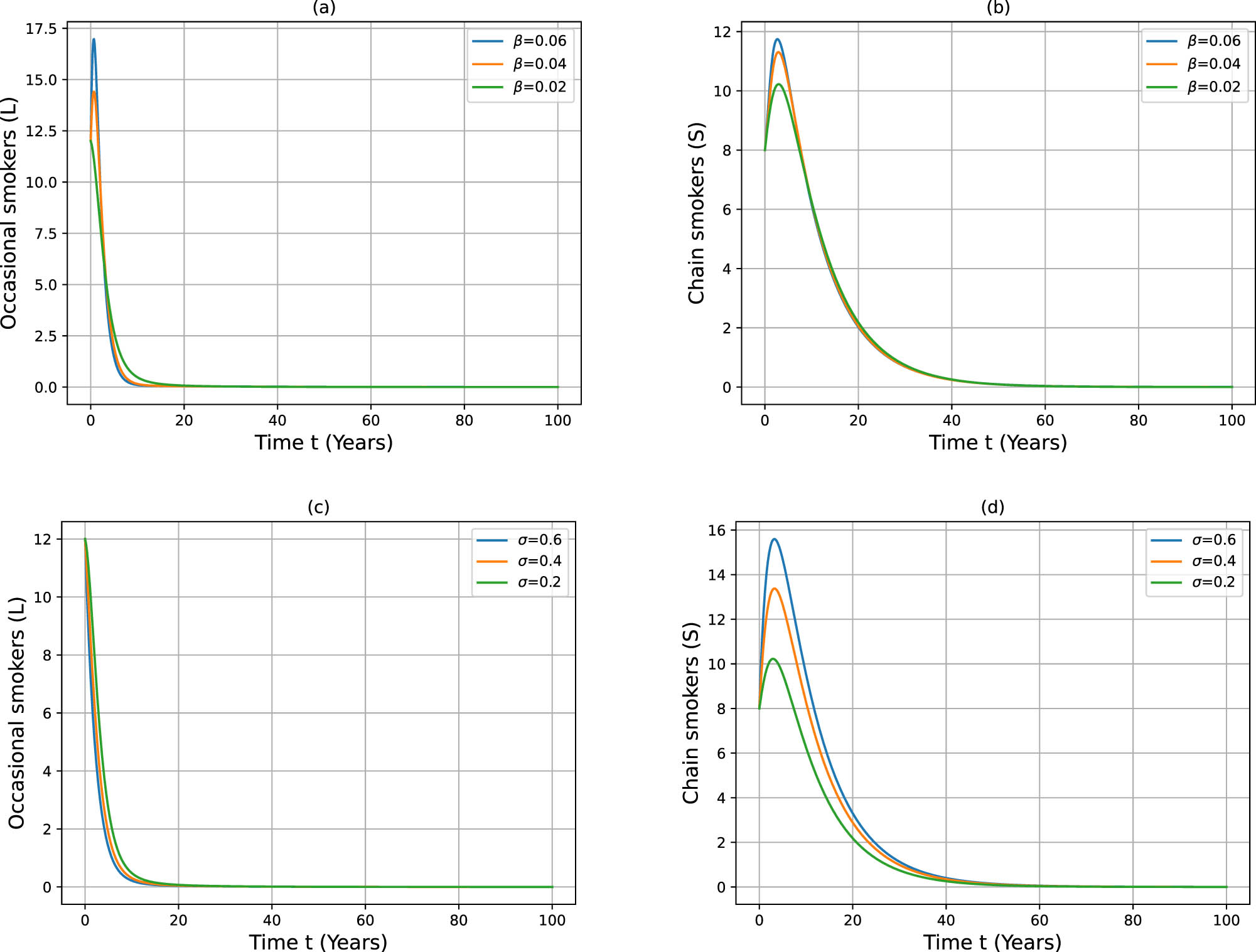
$Figure 4 Impact of changes in β \beta and σ \sigma on the number of occasional and chain smokers at R 0 < 1 {{\mathscr{R}}}_{0}\lt 1 .$

Figure 4

Impact of changes in β and σ on the number of occasional and chain smokers at R 0 < 1 .

Figure 5 presents the influence of the quit rates γ and δ on the population size of occasional and chain smokers when R 0 < 1 . Figure 5(a) and (c) indicate that when γ and δ are high enough, occasional smokers do not exhibit a peak but rather a monotonically decreasing tendency to zero. Figure 5(b) and (d) show that when γ and δ are increased, the peak of chain smokers is reduced and the peak arrival time is advanced. As shown in Figure 5, the higher the quit rates, the lower the prevalence level of smokers.

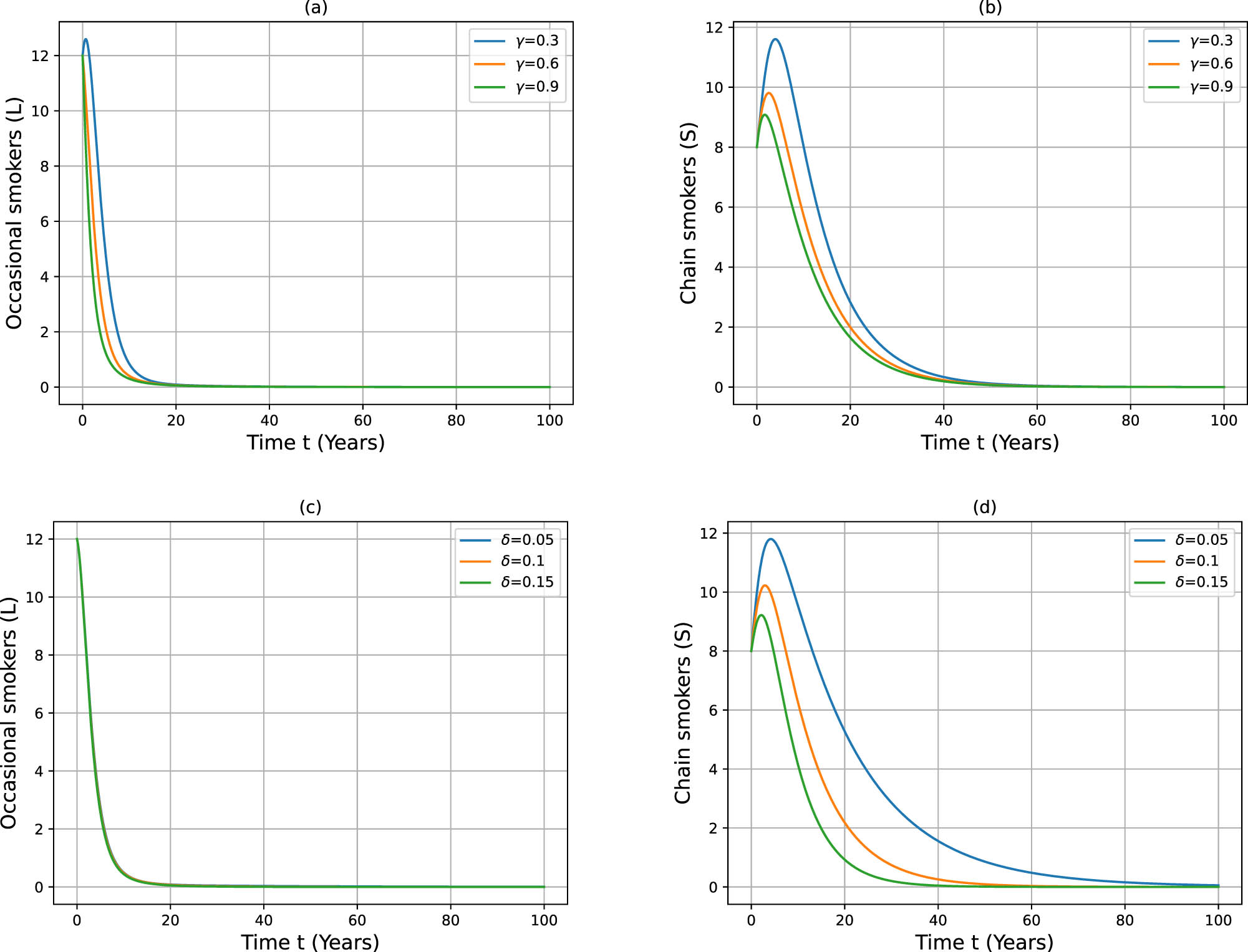
$Figure 5 Impact of changes in γ \gamma and δ \delta on the number of occasional and chain smokers at R 0 < 1 {{\mathscr{R}}}_{0}\lt 1 .$

Figure 5

Impact of changes in γ and δ on the number of occasional and chain smokers at R 0 < 1 .

When smoking behavior can be eliminated, i.e., R 0 < 1 , there is a significant interest in the peak size and the peak time of smokers. As shown in Figures 4 and 5, a lower transmission rate can reduce the peak of occasional and chain smokers. When either the transmission rate or the conversion rate is small enough, or the quit rates ( γ or δ ) are large enough, the number of occasional smokers does not show a peak. However, a reduction in β and σ does not significantly change the peak time of chain smokers. In contrast, an increase in the quit rates γ and δ can cause the peak to occur earlier.

Completely banning smoking in large areas is unrealistic. Thus, when R 0 > 1 , assessing how changes in parameters affect the prevalence of occasional and chain smokers is meaningful. Let Λ be 0.25. Furthermore, we will discuss the prevalence level of occasional and chain smokers. Figure 6 demonstrates transmission rate ( β ) and conversion rate ( σ ) affect occasional and chain smokers. As shown in Figure 6(a), a reduction in β can reduce the peak of occasional smokers. When β is small enough, occasional smokers do not show a peak. Notably, reducing β does not delay or advance the peak arrival time of occasional smokers. Furthermore, lowering β can contribute to a decrease in the endemic level of occasional smokers. From Figure 6(b), it can be observed that a decrease in β reduces the peak and final endemic level of chain smokers. However, the peak arrival time of chain smokers remains almost unchanged. Figure 6(c) shows that a reduction in the conversion rate σ can mitigate the prevalence level of occasional smokers. Moreover, when σ is small enough, there is no peak in the prevalence of occasional smokers. Figure 6(d) illustrates that a reduction in σ leads to a decrease in both the peak and prevalence level of chain smokers. It is noteworthy, however, that the decrease in σ does not delay or advance the peak arrival time of chain smokers. As shown in Figure 6, smaller transmission and conversion rates result in a lower prevalence level of smokers.

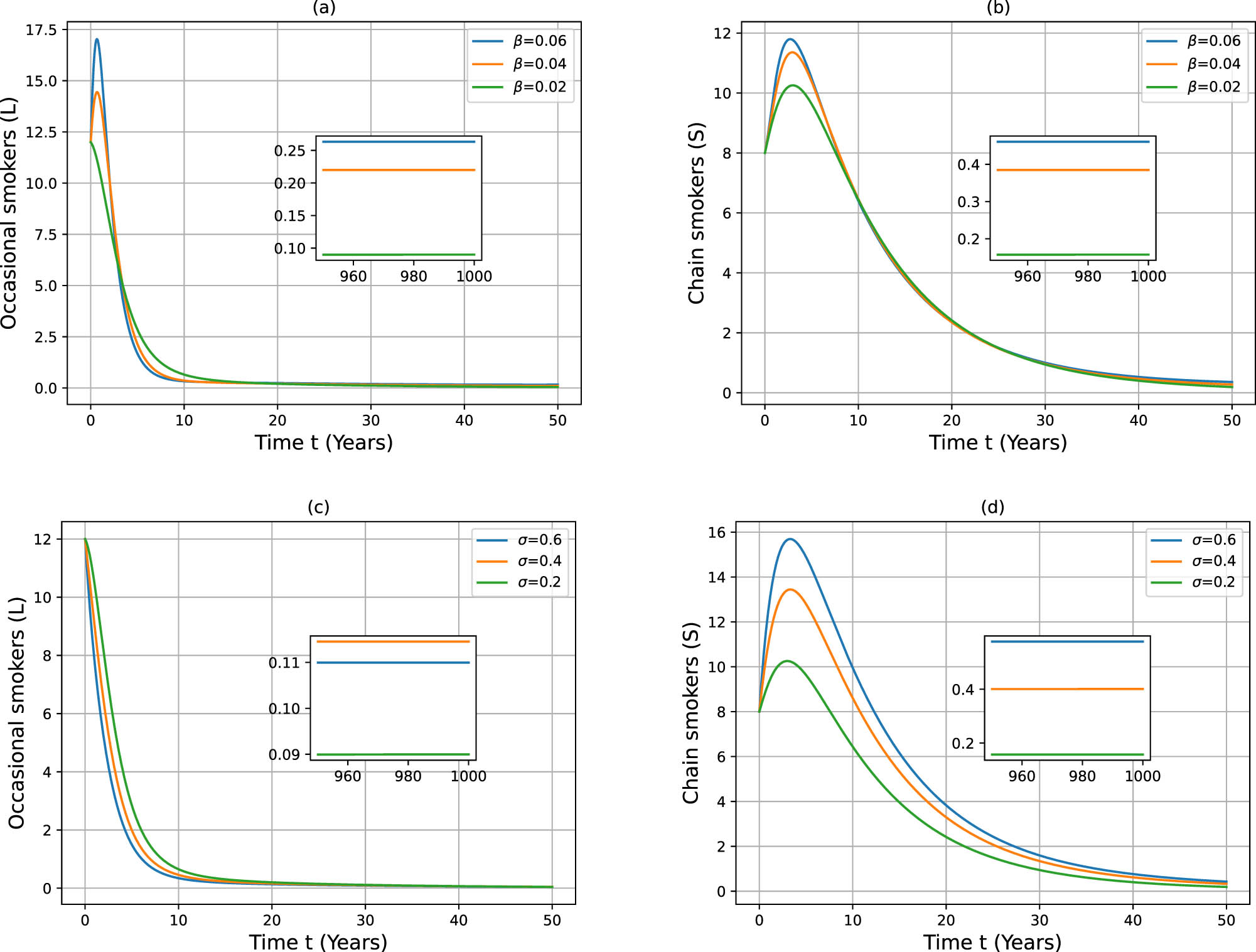
$Figure 6 Impact of changes in β \beta and σ \sigma on the number of occasional and chain smokers at R 0 > 1 {{\mathscr{R}}}_{0}\gt 1 .$

Figure 6

Impact of changes in β and σ on the number of occasional and chain smokers at R 0 > 1 .

Figure 7 demonstrates how quit rates ( γ and δ ) influence the prevalence level of smokers. From Figure 7(a), it can be seen that an increase in γ causes a decline in the prevalence of occasional smokers. In addition, when γ is sufficiently high, occasional smokers do not exhibit a peak but instead display a monotonically decreasing trend towards the endemic level. Figure 7(b) shows that an increase in β results in an earlier peak arrival time and a lower peak for chain smokers. Furthermore, the increase in γ leads to suppression in the prevalence of chain smokers. Figure 7(c) indicates that as δ increases, the prevalence level of occasional smokers is reduced. Figure 7(d) illustrates that as δ increases, the peak of chain smokers is reduced, the peak arrival time is advanced, and the final size is decreased. As shown in Figure 7, larger quit rates result in lower prevalence level among smokers.

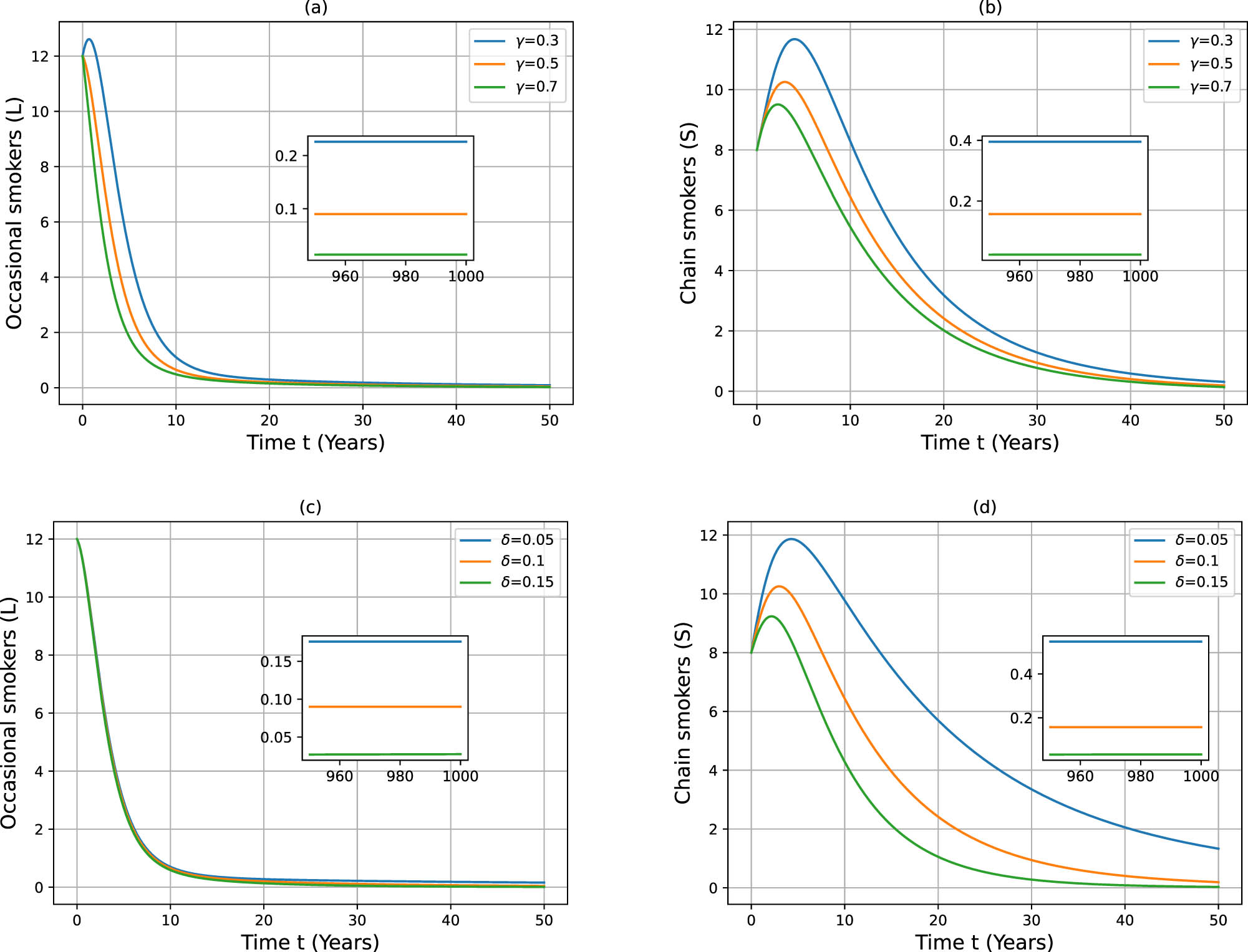
$Figure 7 Impact of changes in γ \gamma and δ \delta on the number of occasional and chain smokers at R 0 > 1 {{\mathscr{R}}}_{0}\gt 1 .$

Figure 7

Impact of changes in γ and δ on the number of occasional and chain smokers at R 0 > 1 .

As shown in Figures 6 and 7, a decrease in the transmission rate ( β ) or conversion rate ( σ ), or an increase in quit rate ( γ or δ ) can reduce the endemic prevalence level of occasional and chain smokers. In addition, reducing the transmission rate can decrease the peak of occasional smokers. When the transmission rate or conversion rate is extremely low, or the quit rate is very high, occasional smokers will not show a peak in their population dynamics. It should be emphasized that a decrease in the transmission or conversion rate has little effect on the peak time of chain smokers, but a rise in the quit rate ( γ or δ ) advances the peak time.

5 Optimal control strategy

This section is dedicated to exploring the optimal control strategy of system (1). Sensitivity analysis has shown that the key to controlling smoking prevalence lies in the parameters β , γ , and δ . By incorporating three control variables, model (1) is augmented as follows:

(8) P ˙ = Λ − β ( 1 − u 1 ) P ( L + S ) − μ P , L ˙ = β ( 1 − u 1 ) P ( L + S ) − ( σ + γ + μ ) L − u 2 L , S ˙ = σ L − ( δ + μ ) S − u 3 S , Q ˙ = γ L + δ S + u 2 L + u 3 S − μ Q .

u 1 ( t ) represents the ratio of the non-smoking area to the total community area. This ratio can be used to measure the degree of implementation of no-smoking policies in a community and the size of the smoke-free environment provided for residents. A larger u 1 ( t ) implies stronger smoking prohibition measures, thereby reducing the contact between smokers and susceptible individuals. u 2 ( t ) denotes the intensity of educational campaigns implemented to control smoking within a community. u 3 ( t ) represents the success rate of chain smokers quitting smoking, which is enhanced by smoking cessation treatment. To obtain the optimal control strategies, an objective functional is given by

(9) J ( u 1 , u 2 , u 3 ) = ∫ 0 t f A 1 L + A 2 S + 1 2 ( B 1 u 1 2 + B 2 u 2 2 + B 3 u 3 2 ) d t ,

where t f is the final time, and the coefficients A 1 , A 2 , B 1 , B 2 , and B 3 are positive weights. The objective of optimal control is to determine a control set that minimizes the number of smokers while simultaneously minimizing the control costs. Let the measurable control set be

U = { ( u 1 , u 2 , u 3 ) : 0 ⩽ u 1 ( t ) ⩽ 1,0 ⩽ u 2 ( t ) ⩽ u 2 max < M , 0 ⩽ u 3 ( t ) ⩽ u 3 max < N , t ∈ [ 0 , t f ] } ,

where M and N are fixed nonnegative constants. Subsequently, it is necessary to identify the optimal controls u 1 * , u 2 * , and u 3 * that satisfy

(10) J ( u 1 * , u 2 * , u 3 * ) = min { J ( u 1 , u 2 , u 3 ) : ( u 1 , u 2 , u 3 ) ∈ U } .

Pontryagin’s maximum principle [31] is employed to deduce the necessary conditions for determining the optimal controls u 1 * , u 2 * , and u 3 * . This principle transforms the optimal control problem into minimizing the Hamiltonian function, which represents

(11) H = A 1 L + A 2 S + 1 2 ( B 1 u 1 2 + B 2 u 2 2 + B 3 u 3 2 ) + λ 1 P ˙ + λ 2 L ˙ + λ 3 S ˙ + λ 4 Q ˙ ,

where λ i , i = 1 , 2, 3, 4 are the adjoint variables that satisfy the following co-state system:

(12) λ ˙ 1 = − ∂ H ∂ P = λ 1 [ β ( 1 − u 1 ) ( L + S ) + μ ] − λ 2 β ( 1 − u 1 ) ( L + S ) , λ ˙ 2 = − ∂ H ∂ L = − A 1 + λ 1 β ( 1 − u 1 ) P − λ 2 [ β ( 1 − u 1 ) P − ( σ + γ + μ ) − u 2 ] − λ 3 σ − λ 4 ( γ + u 2 ) , λ ˙ 3 = − ∂ H ∂ S = − A 2 + λ 1 β ( 1 − u 1 ) P − λ 2 β ( 1 − u 1 ) P + λ 3 [ ( δ + μ ) + u 3 ] − λ 4 ( δ + u 3 ) , λ ˙ 4 = − ∂ H ∂ Q = λ 4 μ ,

with boundary conditions λ i ( t f ) = 0 , i = 1 , 2, 3, 4. In addition, the optimality conditions ∂ H ∂ u i = 0 , i = 1 , 2, 3 yield the optimal controls:

(13) u 1 * = min 1 , max 0 , β P ( L + S ) ( λ 2 − λ 1 ) B 1 , u 2 * = min u 2 max , max 0 , L ( λ 2 − λ 4 ) B 2 , u 3 * = min u 3 max , max 0 , S ( λ 3 − λ 4 ) B 3 .

Now, the optimal control system (8–9) will be solved numerically. The weight constants are taken as A 1 = 1 , A 2 = 3 , B 1 = 3 , B 2 = 4 , and B 3 = 6 . Let Λ be 0.25. Then, smoking behavior is endemic in the community. Consequently, three control measures are put into effect with the anticipation of diminishing the number of smokers and thereby controlling the prevalence of smoking. Suppose the implementation period of the three control measures is 20 years. As shown in from Figure 8(c and d), the number of occasional and chain smokers decreases rapidly. Figure 8(b) illustrates that while the number of potential smokers is indeed on the decline, the rate of this decrease is less significant compared to the scenario without control measures in place. It is worth noting that Figure 8(e) indicates that when control measures are implemented, the number of quitters first increases and then remains essentially unchanged, with the number of quitters being less than without control measures. Furthermore, Figure 8(b–e) illustrates that the implementation of control measures gives rise to a reduction in the number of smokers. Consequently, this leads to a decline in the number of those who quit smoking. Nevertheless, the number of potential smokers has increased. The control profile is depicted in Figure 8(a). This profile reveals that the implementation of three control measures is capable of substantially reducing the number of smokers within a 4-year period, thereby attaining the objective of smoking control.

Figure 8

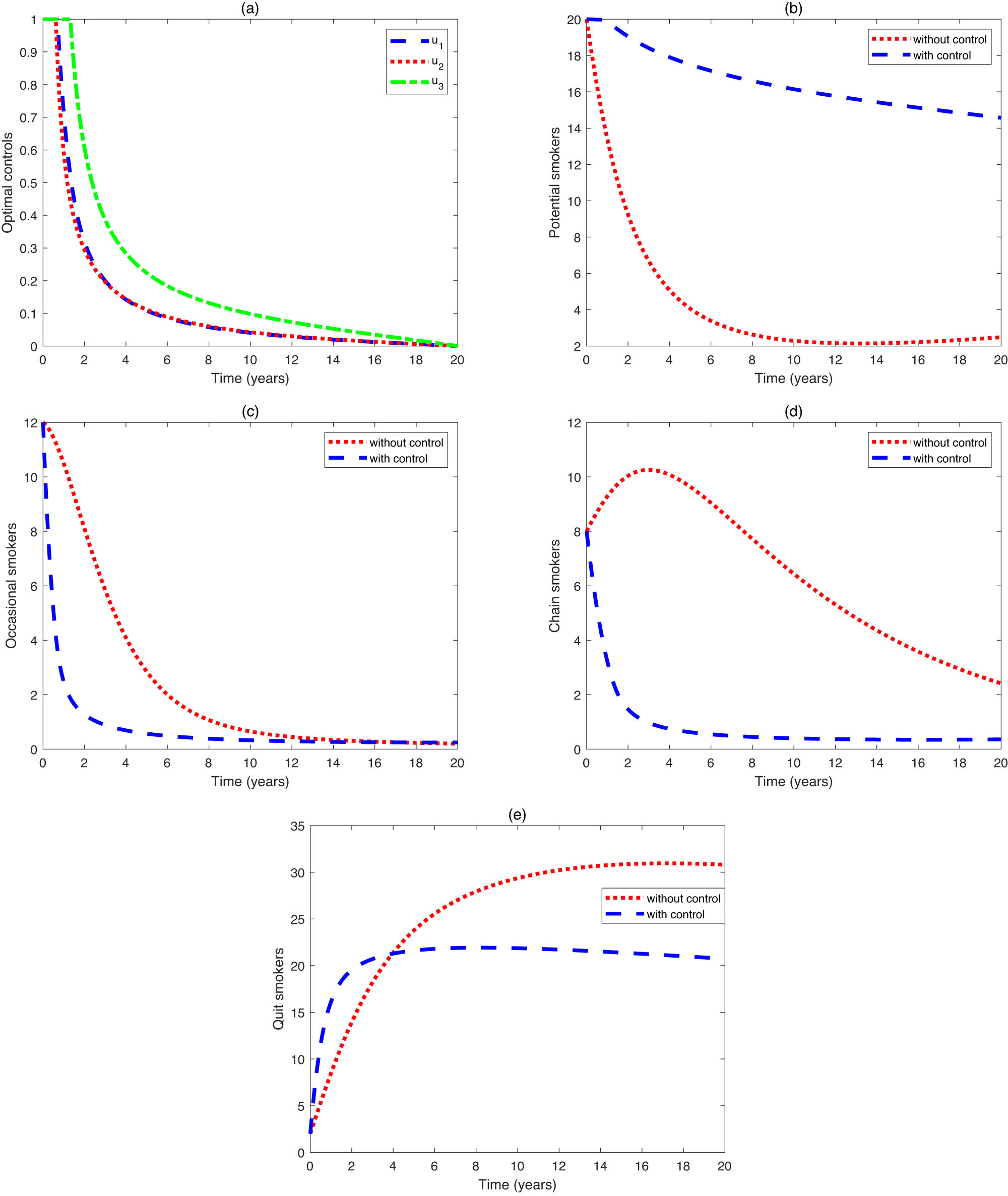
Controls applied to the population.

6 Conclusion

This article develops a potential-light-smoker-quit smoker smoking transmission model by incorporating the infection and quitting behaviors of occasional smokers. On the basis of the expression of R 0 , we find that the basic reproduction number is larger in the smoking model when the spread of occasional smokers is taken into account than when it is ignored. This suggests that they play an important role in the transmission of smoking behavior. By constructing a Lyapunov function, the smoking-free equilibrium E 0 is globally asymptotically stable when R 0 ⩽ 1 , which implies the extinction of smoking behavior and the establishment of a smoke-free environment. For R 0 > 1 , the smoking-present equilibrium E * uniquely exists and is globally asymptotically stable. This result indicates that smoking behavior will be prevalent in the community. Numerical simulations confirm the stabilities of the equilibria. By conducting sensitivity analysis, R 0 is most sensitive to the transmission rate β , followed by the quit rate γ of occasional smokers, then the quit rate δ of chain smokers, and finally the conversion rate σ . Furthermore, the smaller transmission and conversion rates can significantly reduce the prevalence level of smoking behavior. And the higher rates can also markedly decrease the prevalence level of smoking behavior. Finally, on the basis of sensitivity analysis, we present three intervention strategies for controlling the prevalence of smoking behavior. The implementation of three control measures can significantly reduce the number of smokers and achieve the tobacco control goals within 4 years.

7 Discussion

Because neither the potential smoker recruitment rate nor the natural death rate can be practically adjusted, smoking control efforts must target the transmission, conversion, and quit rates. Therefore, to create smoke-free communities, policymakers should primarily focus on measures that impact the transmission rate and the quit rates of of smokers. Moreover, Figure 3 shows that the prevalence of smoking behavior can be efficiently controlled when the transmission rate β and the conversion rate σ are sufficiently small, or when the quit rates ( γ and δ ) are high enough. It is worth noting that the smaller transmission and conversion rates reduce the peak of smokers without advancing the peak arrival time. Conversely, the higher quit rates not only reduce the peak of chain smokers but also advance the peak arrival time.

To control smoking prevalence, we propose three interventions: (i) creating smoke-free zones, (ii) implementing public health education about smoking risks, and (iii) providing treatment for nicotine dependence. These measures aim to reduce the number of smokers and ultimately eliminate smoking behavior. Figure 8 shows that the three control measures can achieve good results in tobacco control within 4 years. However, the number of potential smokers still exists and is increasing compared to the situation without control measures. Therefore, to prevent the resurgence of smoking, policymakers should also pay attention to how to reduce the number of potential smokers, such as by implementing periodic smoking hazard education campaigns.

Although this study is based on hypothetical data or values used in published articles, the same principles can be applied to communities where real data are available. Actually, relapse often occurs in ex-smokers due to stress, socialization, lack of will, etc. It is noticeable that in the smoking model (1), we do not take into account the relapse of quitters. We will consider this situation in future studies.

Funding information This work was supported by Sichuan Minzu College (No. XYZB2302ZA).
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission. Jianglin Zhao conceptualized, formulated, and analyzed the model. Lirong Ma reviewed the work.
Conflict of interest: The authors state no conflict of interest.
Data availability statement: All data generated or analysed during this study are included in this published article.

References

[1] Lin B, Liu X, Lu W, Wu X, Li Y, Zhang Z, et al. Prevalence and associated factors of smoking among chinese adolescents: a school-based cross-sectional study. BMC Public Health 2023;23:669. 10.1186/s12889-023-15565-3Suche in Google Scholar PubMed PubMed Central

[2] World Health Organization. Tobacco 2023. https://www.who.int/news-room/fact-sheets/detail/tobacco (accessed October 5, 2023). Suche in Google Scholar

[3] Zhang S, Meng Y, Chakraborty AK, Wang H. Controlling smoking: A smoking epidemic model with different smoking degrees in deterministic and stochastic environments. Math Biosci. 2024;368:109132. 10.1016/j.mbs.2023.109132Suche in Google Scholar PubMed

[4] Tan Y, Li X, Yang J, Cheke RA. Global stability of an age-structured model of smoking and its treatment. Int J Biomath 2023;16:2250063. 10.1142/S1793524522500632Suche in Google Scholar

[5] Naik PA, Yeolekar BM, Qureshi S, Manhas N, Ghoreishi M, Yeolekar M, et al. Global analysis of a fractional-order hepatitis B virus model under immune response in the presence of cytokines. Adv Theor Simul. 2024;7:2400726. 10.1002/adts.202400726Suche in Google Scholar

[6] Farman M, Hincal E, Naik PA, Hasan A, Sambas A, Nisar KS. A sustainable method for analyzing and studying the fractional-order panic spreading caused by the COVID-19 pandemic. Partial Differ Equ Appl Math. 2025;13:101047. 10.1016/j.padiff.2024.101047Suche in Google Scholar

[7] Naik PA, Farman M, Jamil K, Nisar KS, Hashmi MA, Huang Z. Modeling and analysis using piecewise hybrid fractional operator in time scale measure for ebola virus epidemics under Mittag-Leffler kernel. Sci Rep. 2024;14:24963. 10.1038/s41598-024-75644-2Suche in Google Scholar PubMed PubMed Central

[8] Naik PA, Yavuz M, Qureshi S, Naik M, Owolabi KM, Soomro A, et al. Memory impacts in hepatitis C: A global analysis of a fractional-order model with an effective treatment. Comput Methods Programs Biomed. 2024;254:108306. 10.1016/j.cmpb.2024.108306Suche in Google Scholar PubMed

[9] Naik PA, Yeolekar BM, Qureshi S, Yeolekar M, Madzvamuse A. Modeling and analysis of the fractional-order epidemic model to investigate mutual influence in HIV/HCV co-infection. Nonlinear Dyn. 2024;112:11679–710. 10.1007/s11071-024-09653-1Suche in Google Scholar

[10] Saleem MU, Farman M, Sarwar R, Naik PA, Abbass P, Hincal E, et al. Modeling and analysis of a carbon capturing system in forest plantations engineering with mittag-leffler positive invariant and global Mittag-Leffler properties. Model Earth Syst Environ. 2024;11:38. 10.1007/s40808-024-02181-2Suche in Google Scholar

[11] Jan R, Xiao Y. Effect of pulse vaccination on dynamics of dengue with periodic transmission functions. Adv Contin Discrete Models. 2019;2019:368. 10.1186/s13662-019-2314-ySuche in Google Scholar

[12] Jan R, Jan A. MSGDTM for solution of frictional order dengue disease model. Int J Sci Res. 2015;6:1139–44. Suche in Google Scholar

[13] Jan R, Boulaaras S, Alnegga M, Abdullah FA. Fractional-calculus analysis of the dynamics of typhoid fever with the effect of vaccination and carriers. Int J Numer Model El. 2024;37:e3184. 10.1002/jnm.3184Suche in Google Scholar

[14] Jan R, Razak NNA, Boulaaras S, Rehman ZU, Bahramand S. Mathematical analysis of the transmission dynamics of viral infection with effective control policies via fractional derivative. Nonlinear Eng Model. 2023;12:20220342. 10.1515/nleng-2022-0342Suche in Google Scholar

[15] Alshehri A, Shah Z, Jan R. Mathematical study of the dynamics of lymphatic filariasis infection via fractional-calculus. Eur Phys J Plus. 2023;138:280. 10.1140/epjp/s13360-023-03881-xSuche in Google Scholar PubMed PubMed Central

[16] Jan R, Hinçal E, Hosseini K, Razak NNA, Abdeljawad T, Osman MS. Fractional view analysis of the impact of vaccination on the dynamics of a viral infection. Alex Eng J. 2024;102:36–48. 10.1016/j.aej.2024.05.080Suche in Google Scholar

[17] Bahi MC, Bahramand S, Jan R, Boulaaras S, Ahmad H, Guefaifia R. Fractional view analysis of sexual transmitted human papilloma virus infection for public health. Sci Rep. 2024;14(1):3048. 10.1038/s41598-024-53696-8Suche in Google Scholar PubMed PubMed Central

[18] Deebani W, Jan R, Shah Z, Vrinceanu N, Racheriu M. Modeling the transmission phenomena of water-borne disease with non-singular and non-local kernel. Comput Methods Biomech Biomed Engin. 2023;26:1294–307. 10.1080/10255842.2022.2114793Suche in Google Scholar PubMed

[19] Jan R, Boulaaras S, Alyobi, Rajagopal K, Jawad M. Fractional dynamics of the transmission phenomena of dengue infection with vaccination. Discrete Cont Dyn-S. 2023;16(8):2096–117. 10.3934/dcdss.2022154Suche in Google Scholar

[20] Hussain T, Awan AU, Abro KA, Ozair M, Manzoor M. A mathematical and parametric study of epidemiological smoking model: a deterministic stability and optimality for solutions. Eur Phys J Plus. 2021;136:11. 10.1140/epjp/s13360-020-00979-4Suche in Google Scholar

[21] Harvim P, Zhang H, Georgescu P, Zhang L. Cigarette smoking on college campuses: an epidemical modelling approach. J Appl Math Comput. 2021;65:515–40. 10.1007/s12190-020-01402-ySuche in Google Scholar

[22] Khan H, Alzabut J, Gómez-Aguilar JF, Alkhazan A. Essential criteria for existence of solution of a modified-ABC fractional order smoking model. Ain Shams Eng J. 2024;15(5):102646. 10.1016/j.asej.2024.102646Suche in Google Scholar

[23] Madhusudanan V, Srinivas MN, Murthy BSN, Ansari KJ, Zeb A, Althobaiti A, et al. The influence of time delay and Gaussian white noise on the dynamics of tobacco smoking model. Chaos Soliton Fract. 2023;173:113616. 10.1016/j.chaos.2023.113616Suche in Google Scholar

[24] Rahman G, Agarwal RP, Liu L, Khan A. Threshold dynamics and optimal control of an age-structured giving up smoking model. Nonlinear Anal-Real. 2018;43:96–120. 10.1016/j.nonrwa.2018.02.006Suche in Google Scholar

[25] Zaman G. Qualitative behavior of giving up smoking model. B Malays Math Sci So. 2009;34:403–15. Suche in Google Scholar

[26] Zeb A, Zaman G, Momani S. Square-root dynamics of a giving up smoking model. Appl Math Model. 2013;37(7):5326–34. 10.1016/j.apm.2012.10.005Suche in Google Scholar

[27] Rahman G, Agarwal RP, Din Q. Mathematical analysis of giving up smoking model via harmonic mean type incidence rate. Appl Math Comput. 2019;354:128–48. 10.1016/j.amc.2019.01.053Suche in Google Scholar

[28] Sharomi O, Gumel AB. Curtailing smoking dynamics: A mathematical modeling approach. Appl Math Comput. 2008;195(2):475–99. 10.1016/j.amc.2007.05.012Suche in Google Scholar

[29] Guerrero F, Santonja F, Villanueva R. Analysing the Spanish smoke-free legislation of 2006: A new method to quantify its impact using a dynamic model. Int J Drug Policy. 2011;22(4):247–51. 10.1016/j.drugpo.2011.05.003Suche in Google Scholar PubMed

[30] Zhang Z, Ur Rahman G, Agarwal RP. Harmonic mean type dynamics of a delayed giving up smoking model and optimal control strategy via legislation. J Franklin Inst. 2020;357(15):10669–90. 10.1016/j.jfranklin.2020.09.002Suche in Google Scholar

[31] Lenhart S, Workman JT. Optimal control applied to biological models. 1st ed. New York: Chapman and Hall/CRC; 2007. 10.1201/9781420011418Suche in Google Scholar

Received: 2025-03-07

Revised: 2025-04-30

Accepted: 2025-05-19

Published Online: 2025-07-07

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

https://doi.org/10.1515/nleng-2025-0153

Schlagwörter für diesen Artikel

smoking epidemic model; stability results; sensitivity analysis; optimal control

Creative Commons

BY 4.0