Home Physical Sciences Re-examination of nonlinear vibration and nonlinear bending of porous sandwich cylindrical panels reinforced by graphene platelets
Article Open Access

Re-examination of nonlinear vibration and nonlinear bending of porous sandwich cylindrical panels reinforced by graphene platelets

  • Hui-Shen Shen EMAIL logo and Chong Li
Published/Copyright: April 18, 2023
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
Nanotechnology Reviews
From the journal Nanotechnology Reviews Volume 12 Issue 1

Abstract

This article re-examines the nonlinear vibration and nonlinear bending responses of porous sandwich cylindrical panels reinforced by graphene platelets resting on elastic foundations in thermal environments. The graphene platelet-reinforced composite (GPLRC) core is assumed to be of multilayers, and each layer may have different porosity coefficient values to achieve a piece-wise functionally graded pattern. By introducing an inhomogeneous model instead of the equivalent isotropic model (EIM), the Young’s moduli along with the shear modulus of the porous GPLRC core are predicted through a generic Halpin–Tsai model in which the porosity is included. The thermomechanical properties of metal face sheets and the porous GPLRC core are assumed to be temperature-dependent. Governing equations of motion for sandwich cylindrical panels with porous GPLRC core are formulated based on Reddy’s third-order shear deformation theory coupled with von Kármán nonlinear strain–displacement relationships. In the modeling, the panel–foundation interaction and the thermal effects are also considered. The analytical solutions for the nonlinear vibration and nonlinear bending problems are obtained by applying a two-step perturbation approach. Numerical studies are performed to compare the results obtained from the present model and the EIM. The results confirm that the EIM is not suitable for linear free vibration analysis of sandwich cylindrical panels with the porous GPLRC core, but the EIM may be valid for the cases of nonlinear vibration and nonlinear bending analyses of the same panel resting on Pasternak elastic foundations.

Graphical abstract

Keywords: porous material; graphene platelets; sandwich cylindrical panel; functionally graded; temperature-dependent

1 Introduction

Porous materials are realized as a new class of advanced engineering materials characterized by low density, electrical conductivity, great energy absorption capability, and thermal resistance [1,2,3,4]. However, the presence of porosities in the metal matrix will lead to a significant reduction in terms of structural stiffness [5,6,7,8]. With the development of nanotechnology and additive manufacturing technology [9,10], nanofillers such as carbon nanotubes (CNTs) [11] or graphene platelets (GPLs) [12] can be added into porous metal foams to increase the stiffness of porous metal materials while maintaining the lightweight nature of foams. GPL can be regarded as an isotropic solid, which consists of a large number of stacked monolayer graphene. GPL-reinforced porous metal foams may be created as particle-reinforced composites where GPLs are uniformly or randomly dispersed in the porous metal foams. The mechanical performance of the porous metal materials reinforced by GPLs may be enhanced substantially while maintaining the lightweight advantage of the porous metal materials.

Many studies have been carried out on the static and dynamic analyses of porous GPL-reinforced composite (GPLRC) flat panels without or with face sheets [13,14,15,16,17,18,19,20,21,22,23,24]. However, relatively few studies have been done on the static and dynamic analyses of porous GPLRC cylindrical panels. In order to enhance the mechanical performance of porous metal panels, it is an effective approach to incorporate the functionally graded (FG) material concept [25] into the design of the porous metal panel. Zhou et al. [26] investigated vibration and flutter characteristics of porous FG-GPLRC cylindrical panels subjected to supersonic flow based on Reddy’s third-order shear deformation theory (TSDT) and by applying the standard Lagrange procedure. Similar to the flat panels, the porous GPLRC cylindrical panels cannot be used as structural components directly in engineering practice. It is a better way to add two face sheets on the outer and inner surfaces of the porous GPLRC layer to create a sandwich panel where the porous GPLRC layer is treated as a hard core, and in that case the Reddy’s TSDT is still valid. Twinkle and Pitchaimani [27,28] studied the effects of grading, porosity, and non-uniform edge loads on the natural frequency and buckling load of porous FG-GPLRC cylindrical panels and sandwich cylindrical panels with the porous FG-GPLRC core based on the higher-order shear deformation theory (HSDT) and by applying the Galerkin method. Sun et al. [29] calculated free vibration frequencies of sandwich cylindrical panels with the porous FG-GPLRC core based on the Love shell theory and by applying the Ritz method. In the aforementioned works, the equivalent isotropic model (EIM) was adopted to determine the equivalent Young’s modulus of the GPLRC layer through a modified Halpin–Tsai model and the shear modulus is assumed to be related to the Young’s modulus by a well-known formula of isotropic material.

It has been reported that, even for the GPLRC flat panel without porosity, the shear modulus will be underestimated by using the EIM [30]. Shen and his co-authors [31,32] proposed an inhomogeneous model instead of the EIM and re-examined the linear and nonlinear vibration and the nonlinear bending along with the buckling and postbuckling responses of porous sandwich plates reinforced by GPLs. They found that the shear modulus is overestimated when the porosity coefficient is less than 0.2, while underestimated when the porosity coefficient is greater than 0.25 by using the EIM. Their results reveal that, owing to the shear modulus effect, for most cases, the difference in the natural frequencies between the two models is over 30%. The nonlinear free vibration frequency–amplitude curves, the nonlinear bending load–deflection curves, and the thermal postbuckling load–deflection curves are always underestimated, while the compressive postbuckling equilibrium paths of the porous sandwich plates are always overestimated by using the EIM. Only in the case of porous sandwich plates resting on Pasternak elastic foundations with sufficiently large foundation stiffnesses, the difference between the two models may be negligible, and the EIM may be valid in the analysis.

The purpose of this article is to evaluate the appropriateness of applying the EIM in vibration and bending analyses of porous GPLRC cylindrical panels. We re-examine the nonlinear vibration and the nonlinear bending of sandwich cylindrical panels with metal face sheets and porous GPLRC core resting on elastic foundations in thermal environments. We choose two kinds of porous GPLRC core in the present study, i.e., uniformly distributed (UD) and piece-wise FG patterns. The material properties of both metal face sheets and porous GPLRC core are assumed to be temperature-dependent. The novelty of this study is that an inhomogeneous model is introduced instead of the EIM for the porous GPLRC core, where the Young’s moduli along with the shear modulus are predicted through a generic Halpin–Tsai model in which the porosity is included. Governing equations of motion for porous sandwich cylindrical panels are formulated based on Reddy’s TSDT coupled with the von Kármán nonlinear strain–displacement relationships. In the modeling, the panel–foundation interaction and thermal effect are also considered. By applying a two-step perturbation approach to solve these equations, the analytical solutions for the two cases of nonlinear vibration and nonlinear bending problems of porous sandwich cylindrical panels are obtained. Numerical comparisons are performed to show the differences between the current model and the EIM.

2 Modeling of porous sandwich cylindrical panels

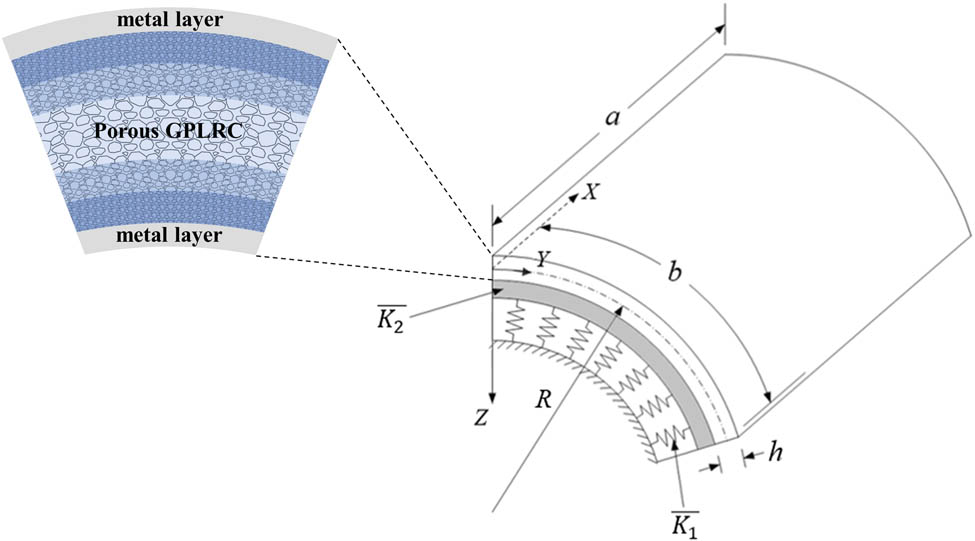
Consider a porous sandwich cylindrical panel with outer and inner face sheets made of titanium alloy and a core made of aluminum foams reinforced by GPLs. The GPLRC core consists of six layers. Each layer of the porous GPLRC core may have different porosity values and, therefore, the piece-wise FG distribution patterns of porosities across the panel thickness can be achieved. Consider a coordinate system (X, Y, Z) with its origin located at one corner of the panel on the mid-plane, where X and Y are placed in the axial and circumferential directions, and Z is pointed inward and placed in the panel thickness direction (Figure 1). The panel is of length a in the X direction, length b in the Y direction, the radius of curvature R, and total thickness h. The thickness of the GPLRC core is h c, while the thickness of each metal face sheet is h f. The panel is resting on an elastic foundation that is idealized as a Pasternak-type model with two stiffnesses, where K ¯ 1 is the vertical spring stiffness and K ¯ 2 is the shearing layer stiffness.

Figure 1 Geometry and the coordinate system of a porous cylindrical panel resting on a Pasternak elastic foundation.
Figure 1

Geometry and the coordinate system of a porous cylindrical panel resting on a Pasternak elastic foundation.

The key issue for analyzing the mechanical response of the GPLRC structures successfully is to determine the material properties of the GPLRC layer accurately and effectively. Since the porous metal foam is slightly anisotropic [33,34], in particular, the shear modulus does not obey the well-known formula of an isotropic material, we introduce an inhomogeneous model instead of the EIM for the porous GPLRC core, where the Young’s moduli E 11 and E 22 along with the shear modulus G 12 of the porous GPLRC layer are determined by a generic Halpin–Tsai model [35]:

(1a) E 11 = 1 + 2 ( a GPL / h GPL ) γ 11 GPL V GPL 1 − γ 11 GPL V GPL E m ,

(1b) E 22 = 1 + ( 2 b GPL / h GPL ) γ 22 GPL V GPL 1 − γ 22 GPL V GPL E m ,

(1c) G 12 = 1 1 − γ 12 GPL V GPL G m ,

where a GPL is the length, b GPL is the width, and h GPL is the thickness of the GPL; in addition, γ 11 GPL , γ 22 GPL , and γ 12 GPL are defined by

(2a) γ 11 GPL = E 11 GPL / E m − 1 E 11 GPL / E m + 2 a GPL / h GPL ,

(2b) γ 22 GPL = E 22 GPL / E m − 1 E 22 GPL / E m + 2 b GPL / h GPL ,

(2c) γ 12 GPL = G GPL / G m − 1 G GPL / G m ,

in which E GPL and G GPL are the Young’s and shear moduli of the GPL, and E m and G m are the Young’s and shear moduli of the porous metal matrix.

The mass density and Poisson’s ratio of each porous GPLRC layer may be predicted by the rule of the mixture model:

(3) ν 12 ρ = ν GPL ν m ρ GPL ρ m V GPL V m ,

where ρ and ν are the mass density and Poisson’s ratio, and V GPL and V m represent the volume fractions of the GPL and metal matrix, respectively.

For a GPLRC layer without porosity, the volume fraction relationship V GPL + V m = 1 is valid, whereas the relationship V GPL + V m = 1 is invalid for porous metal foams, as reported in Shen and Li [36]. For this reason, we remove the relationship V GPL + V m = 1 for the porous GPLRC layer, and assume that

(4) V m + V GPL = 1 − α ⁎ ,

where α ⁎ represents the porosity coefficient and is given by

(5) α ⁎ = 1 − ρ m ρ M ,

with ρ M and ρ m being the mass densities of the metal matrix without or with porosity.

For a porous GPLRC layer, the weight fractions still follow the relationship w GPL + w m = 1. Hence, the relationships between the weight fractions (w GPL, w m) and the volume fractions (V GPL, V m) for a porous GPLRC layer can be written as

(6a) w GPL = V GPL V GPL + ρ m ρ GPL ( 1 − α ⁎ − V GPL ) ,

(6b) w m = V m V m + ρ GPL ρ m ( 1 − α ⁎ − V m ) .

In the previous studies [13,14,15,16,17,18,19,20,21,22,23,24,26,27,28,29], the Young’s modulus E m of the porous matrix is assumed to obey the Gibson–Ashby model [37], and Poisson’s ratio ν m is assumed to obey the Roberts–Garboczi model [38]:

(7a) E m = E M [ 1 – ( α ⁎ ) ] 2 ,

(7b) ν m = 0.221 ( α ⁎ ) + ν M [ 1 − 1.21 ( α ⁎ ) + 0.342 ( α ⁎ ) 2 ] .

The main difference between the present model compared with the EIM is that the Young’s modulus E m, the shear modulus G m, and Poisson’s ratio ν m of the porous matrix in equations (1a) and (1b)–(3) are all functions of the porosity coefficient. Mondal et al. [39] reported that the experimental data of the Young’s modulus, the shear modulus, and Poisson’s ratio for closed-cell porous aluminum foams decreased as the porosity coefficient increased, from which the polynomial fit curves for E m, G m, and ν m are obtained as follows:

(8a) E m = E M [ 1.0 − 3.27933 ( α ⁎ ) + 4.68868 ( α ⁎ ) 2 − 3.78983 ( α ⁎ ) 3 + 1.43045 ( α ⁎ ) 4 ] ,

(8b) G m = G M [ 1.0 − 1.34119 ( α ⁎ ) − 1.99118 ( α ⁎ ) 2 + 6.5494 ( α ⁎ ) 3 − 4.55079 ( α ⁎ ) 4 ] ,

(8c) ν m = ν M [ 1.0 − 0.33684 ( α ⁎ ) + 0.12968 ( α ⁎ ) 2 ] ,

in which E M is the Young’s modulus, G M is the shear modulus, and ν M is the Poisson’s ratio of the matrix without porosity.

The panel is subjected to a transverse dynamic load q(X, Y, t ¯ ) on the outer surface and is located in an elevated temperature environment. The governing equations of motion for porous sandwich cylindrical panels are established based on Reddy’s TSDT [40] coupled with the von Kármán nonlinear strain–displacement relationships. These equations can be expressed as

(9a) L ˜ 11 ( W ¯ ) − L ˜ 12 ( Ψ ¯ x ) − L ˜ 13 ( Ψ ¯ y ) + L ˜ 14 ( F ¯ ) − L ˜ 15 ( N ¯ T ) − L ˜ 16 ( M ¯ T ) − 1 R ∂ 2 F ¯ ∂ X 2 + K ¯ 1 W ¯ − K ¯ 2 ∇ 2 W ¯ = L ˜ ( W ¯ , F ¯ ) + L ˜ 17 ( W ¯ ̈ ) − I ˜ 5 ∂ Ψ ¯ ̈ x ∂ X + I ˜ 5 ' ∂ Ψ ¯ ̈ y ∂ Y + q ,

(9b) L ˜ 21 ( F ¯ ) + L ˜ 22 ( Ψ ¯ x ) + L ˜ 23 ( Ψ ¯ y ) − L ˜ 24 ( W ¯ ) − L ˜ 25 ( N ¯ T ) + 1 R ∂ 2 W ¯ ∂ X 2 = − 1 2 L ˜ ( W ¯ , W ¯ ) ,

(9c) L ˜ 31 ( W ¯ ) + L ˜ 32 ( Ψ ¯ x ) − L ˜ 33 ( Ψ ¯ y ) + L ˜ 34 ( F ¯ ) − L ˜ 35 ( N ¯ T ) − L ˜ 36 ( S ¯ T ) = I ˆ 5 ∂ W ¯ ̈ ∂ X − I ˆ 3 Ψ ¯ ̈ x ,

(9d) L ˜ 41 ( W ¯ ) − L ˜ 42 ( Ψ ¯ x ) + L ˜ 43 ( Ψ ¯ y ) + L ˜ 44 ( F ¯ ) − L ˜ 45 ( N ¯ T ) − L ˜ 46 ( S ¯ T ) = I ˆ 5 ' ∂ W ¯ ̈ ∂ Y − I ˆ 3 ' Ψ ¯ ̈ y ,

where W ¯ is the panel displacement in the Z direction; F ¯ is the stress function defined by N ¯ x = ∂ 2 F ¯ / ∂ Y 2 , N ¯ y = ∂ 2 F ¯ / ∂ X 2 , and N ¯ x y = − ∂ 2 F ¯ / ∂ X ∂ Y ; and Ψ ¯ x and Ψ ¯ y are the rotations of the normal to the middle surface with respect to the Y- and X-axis. L ˜ ( ) represents the nonlinear operator related to the geometric nonlinearity in the von Kármán sense and can be defined as

(10) L ˜ ( ) = ∂ 2 ( ) ∂ X 2 ∂ 2 ( ) ∂ Y 2 − 2 ∂ 2 ( ) ∂ X ∂ Y ∂ 2 ( ) ∂ X ∂ Y + ∂ 2 ( ) ∂ Y 2 ∂ 2 ( ) ∂ X 2

and other linear operators L ˜ i j ( ) in equations (9a)–(9d) are defined in Shen and Xiang [41].

In equation (9a)–(9d), the superposed dots indicate differentiation with respect to time, and the inertias I ˆ 3 , I ˆ 5 , etc., are given in detail in equation (23). The panel–foundation interaction, defined by K ¯ 1 W ¯ − K ¯ 2 ∇ 2 W ¯ and the temperature variation are included, where the thermal forces N ¯ T , the thermal moments M ¯ T , and the higher-order moments P ¯ T caused by elevated temperature are defined by

(11a) N ¯ x T N ¯ y T N ¯ x y T M ¯ x T M ¯ y T M ¯ x y T P ¯ x T P ¯ y T P ¯ x y T = ∑ k = 1 ∫ h k − 1 h k A x A y A x y k ( 1 , Z , Z 3 ) Δ T d Z ,

and S ¯ T is defined by

(11b) S ¯ x T S ¯ y T S ¯ x y T = M ¯ x T M ¯ y T M ¯ x y T − 4 3 h 2 P ¯ x T P ¯ y T P ¯ x y T ,

where Δ T = T − T 0 is the temperature change from the reference temperature T 0 at which they are free of thermal strains, and

(12) A x A y A x y = − Q ¯ 11 Q ¯ 12 Q ¯ 16 Q ¯ 12 Q ¯ 22 Q ¯ 26 Q ¯ 16 Q ¯ 26 Q ¯ 66 1 0 0 1 0 0 α 11 α 22 ,

in which α 11 and α 22 are the thermal expansion coefficients for the kth ply, and can be expressed as [42]

(13a) α 11 = V GPL E GPL α GPL + V m E m α M V GPL E GPL + V m E m ,

(13b) α 22 = ( 1 + ν GPL ) V GPL α GPL + ( 1 + ν m ) V m α M − ν 12 α 11

in which α GPL and α M are the thermal expansion coefficients of the GPL and metal matrix without porosity. In equation (12), Q ¯ i j are the transformed elastic constants, as defined in Reddy and Liu [40]. For a porous GPLRC layer, Q ¯ i j = Q i j in which

(14) Q 11 = E 11 1 − ν 12 ν 21 , Q 22 = E 22 1 − ν 12 ν 21 , Q 12 = ν 21 E 11 1 − ν 12 ν 21 , Q 44 = G 23 , Q 55 = G 13 , Q 66 = G 12 , Q 16 = Q 26 = 0 ,

where E 11, E 22, G 12, ν 12 , and ν 21 are the Young’s and shear moduli and Poisson’s ratios for the kth layer.

We assume that the four edges of a porous sandwich cylindrical panel are simply supported without or with in-plane displacements, referred to as ‘immovable’ or ‘movable’ edges, respectively. The associated boundary conditions are given by

(15a) W ¯ = Ψ ¯ y = M ¯ x = P ¯ x = 0 ( at X = 0 , a ) ,

(15b) W ¯ = Ψ ¯ x = M ¯ y = P ¯ y = 0 ( at Y = 0 , b ) ,

in which M ¯ x and M ¯ y are the bending moments and P ¯ x and P ¯ y are the higher-order moments, as defined in Reddy and Liu [40]. It is noted that, when the temperature increases, M ¯ x and M ¯ y contain M ¯ x T and M ¯ y T , respectively, and in that case M ¯ x = 0 and M ¯ y = 0 become the non-homogeneous boundary conditions.

Meanwhile, the in-plane boundary conditions on the X = (0, a) edges are

(16a) U ¯ = 0 ( immovable ) ,

(16b) ∫ 0 b N ¯ x d Y = 0 ( movable ) ,

and the in-plane boundary conditions on the Y = (0, b) edges are

(17a) V ¯ = 0 ( immovable ) ,

(17b) ∫ 0 a N ¯ y d X = 0 ( movable ) ,

in which U ¯ and V ¯ are the panel displacements in the X and Y directions.

The immovability conditions of equations (16a) and (17a) may be fulfilled in the average sense as

(18) ∫ 0 b ∫ 0 a ∂ U ¯ ∂ X d X d Y = 0 , ∫ 0 a ∫ 0 b ∂ V ¯ ∂ Y d Y d X = 0 ,

or

(19a) ∫ 0 b ∫ 0 a A 11 ⁎ ∂ 2 F ¯ ∂ Y 2 + A 12 ⁎ ∂ 2 F ¯ ∂ X 2 + ( B 11 ⁎ − 4 3 h 2 E 11 ⁎ ) ∂ Ψ ¯ x ∂ X + ( B 12 ⁎ − 4 3 h 2 E 12 ⁎ ) ∂ Ψ ¯ y ∂ Y − 4 3 h 2 E 11 ⁎ ∂ 2 W ¯ ∂ X 2 + E 12 ⁎ ∂ 2 W ¯ ∂ Y 2 − 1 2 ∂ W ¯ ∂ X 2 − ( A 11 ⁎ N ¯ x T + A 12 ⁎ N ¯ y T ) d X d Y = 0 ,

(19b) ∫ 0 a ∫ 0 b A 22 ⁎ ∂ 2 F ¯ ∂ X 2 + A 12 ⁎ ∂ 2 F ¯ ∂ Y 2 + ( B 21 ⁎ − 4 3 h 2 E 21 ⁎ ) ∂ Ψ ¯ x ∂ X + ( B 22 ⁎ − 4 3 h 2 E 22 ⁎ ) ∂ Ψ ¯ y ∂ Y − 4 3 h 2 E 21 ⁎ ∂ 2 W ¯ ∂ X 2 + E 22 ⁎ ∂ 2 W ¯ ∂ Y 2 + W ¯ R − 1 2 ∂ W ¯ ∂ Y 2 − ( A 12 ⁎ N ¯ x T + A 22 ⁎ N ¯ y T ) d Y d X = 0 .

In the above equations, the reduced stiffness matrices, such as [ A i j ∗ ] , [ B i j ∗ ] , [ D i j ∗ ] , [ E i j ⁎ ] , [ F i j ⁎ ] , and [ H i j ⁎ ] , are defined as [43]

(20) A ⁎ = A − 1 , B ⁎ = - A − 1 B , D ⁎ = D – B A − 1 B , E ⁎ = − A − 1 E , F ⁎ = F – E A − 1 B , H ⁎ = H – E A − 1 E ,

where the panel stiffnesses A ij , B ij ,… are given by

(21a) ( A i j , B i j , D i j , E i j , F i j , H i j ) = ∑ k = 1 ∫ h k − 1 h k ( Q ¯ i j ) k ( 1 , Z , Z 2 , Z 3 , Z 4 , Z 6 ) d Z , ( i , j = 1 , 2 , 6 ) ,

(21b) ( A i j , D i j , F i j ) = ∑ k = 1 ∫ h k − 1 h k ( Q ¯ i j ) k ( 1 , Z 2 , Z 4 ) d Z , ( i , j = 4 , 5 ) ,

and the inertias I i ( i = 1 , 2 , 3 , 4 , 5 , 7 ) are defined by

(22) ( I 1 , I 2 , I 3 , I 4 , I 5 , I 7 ) = ∑ k = 1 ∫ h k − 1 h k ρ k ( 1 , Z , Z 2 , Z 3 , Z 4 , Z 6 ) d Z ,

where ρ k is the mass density of the kth layer, and

(23) I ¯ 1 = I 1 , I ¯ 2 = I 2 − c 1 I 4 , I ¯ 3 = c 1 I 4 , I ¯ 4 = I ¯ 4 ′ = I 3 − 2 c 1 I 5 + c 1 2 I 7 , I ¯ 5 = I ¯ 5 ' = c 1 I 5 − c 1 2 I 7 , I ¯ 1 ' = I 1 + 2 R I 2 , I ¯ 2 ' = I 2 + 1 R I 3 − c 1 I 4 − c 1 R I 5 , I ¯ 3 ' = c 1 I 4 + c 1 R I 5 , I ˆ 3 = I ¯ 4 − I ¯ 2 I ¯ 2 I ¯ 1 , I ˆ 5 = I ¯ 5 − I ¯ 2 I ¯ 3 I ¯ 1 , I ˆ 7 = I ¯ 3 I ¯ 3 I ¯ 1 − c 1 2 I 7 , I ˆ 3 ' = I ¯ 4 ' − I ¯ 2 ' I ¯ 2 ' I ¯ 1 ' , I ˆ 5 ' = I ¯ 5 ' − I ¯ 2 ' I ¯ 3 ' I ¯ 1 ' , I ˆ 7 ' = I ¯ 3 ' I ¯ 3 ' I ¯ 1 ' − c 1 2 I 7 , I ˜ 5 = I ˆ 3 + I ˆ 5 , I ˜ 5 ' = I ˆ 3 ' + I ˆ 5 ' , I ˜ 7 = I ˆ 7 − I ˆ 5 , I ˜ 7 ' = I ˆ 7 ' − I ˆ 5 ' ,

where c 1 = 4/(3h 2).

3 Solution procedure

A two-step perturbation method was developed in Shen [43]. This approach is successfully employed to solve various nonlinear boundary-value problems of curved panels [44,45,46,47,48,49,50,51,52]. To apply this two-step perturbation approach to solve nonlinear vibration and nonlinear bending problems of porous sandwich cylindrical panels, the motion equations (9a)–(9d) are first re-written in the non-dimensional forms as

(24a) L 11 ( W ) − L 12 ( Ψ x ) − L 13 ( Ψ y ) + γ 14 L 14 ( F ) − L 16 ( M T ) − η − 1 γ 14 ∂ 2 F ∂ x 2 + K 1 W − K 2 ∇ 2 W = γ 14 β 2 L ( W , F ) + L 17 ( W ̈ ) + γ 81 ∂ Ψ ̈ x ∂ x + γ 82 β ∂ Ψ ̈ y ∂ y + λ q ,

(24b) L ( F ) 21 + γ 24 L 22 ( Ψ x ) + γ 24 L 23 ( Ψ y ) − γ 24 L 24 ( W ) + η − 1 γ 24 ∂ 2 W ∂ x 2 = − 1 2 γ 24 β 2 L ( W , W ) ,

(24c) L 31 ( W ) + L 32 ( Ψ x ) − L 33 ( Ψ y ) + γ 14 L 34 ( F ) − L 36 ( S T ) = γ 83 ∂ W ̈ ∂ x + γ 91 Ψ ̈ x ,

(24d) L 41 ( W ) − L 42 ( Ψ x ) + L 43 ( Ψ y ) + γ 14 L 44 ( F ) − L 46 ( S T ) = γ 84 β ∂ W ̈ ∂ y + γ 92 Ψ ̈ y ,

where

(25) L 17 ( ) = γ 170 + γ 171 ∂ 2 ∂ x 2 + γ 172 β 2 ∂ 2 ∂ y 2 ,

and the other non-dimensional L ij ( ) and L( ) are given in Shen and Xiang [41]. In these equations, the non-dimensional parameters are given by

(26) x = π X a , y = π Y b , β = a b , η = π 2 R a 2 [ D 11 ⁎ D 22 ⁎ A 11 ⁎ A 22 ⁎ ] 1 / 4 , W = W ¯ [ D 11 ⁎ D 22 ⁎ A 11 ⁎ A 22 ⁎ ] 1 / 4 , F = F ¯ [ D 11 ⁎ D 22 ⁎ ] 1 / 2 , ( Ψ x , Ψ y ) = a π ( Ψ ¯ x , Ψ ¯ y ) [ D 11 ⁎ D 22 ⁎ A 11 ⁎ A 22 ⁎ ] 1 / 4 , γ 14 = D 22 ⁎ D 11 ⁎ 1 / 2 , γ 24 = A 11 ⁎ A 22 ⁎ 1 / 2 , γ 5 = − A 12 ⁎ A 22 ⁎ , ( γ T 1 , γ T 2 ) = ( A x T , A y T ) R A 11 ⁎ A 22 ⁎ D 11 ⁎ D 22 ⁎ 1 / 4 , ( γ T 4 , γ T 5 , γ T 7 , γ T 8 ) = a 2 π 2 h D 11 ⁎ ( D x T , D y T , 4 3 h 2 F x T , 4 3 h 2 F y T ) , ( M x , P x ) = a 2 π 2 1 D 11 ⁎ [ D 11 ⁎ D 22 ⁎ A 11 ⁎ A 22 ⁎ ] 1 / 4 M ¯ x , 4 3 h 2 P ¯ x , ( K 1 , k 1 ) = K ¯ 1 a 4 π 4 D 11 ⁎ , b 4 E 0 h 3 , ( K 2 , k 2 ) = K ¯ 2 a 2 π 2 D 11 ⁎ , b 2 E 0 h 3 , ω L = Ω L a π ρ 0 E 0 , t = π t ¯ a E 0 ρ 0 , γ 170 = − I 1 E 0 a 2 π 2 ρ 0 D 11 ⁎ , ( γ 91 , γ 92 , γ 81 , γ 82 , γ 83 , γ 84 , γ 171 , γ 172 ) = ( − I ˆ 3 , − I ˆ 3 ' , − I ˜ 5 , − I ˜ 5 ' , I ˆ 5 , I ˆ 5 ' , − I ˜ 7 , − I ˜ 7 ' ) E 0 ρ 0 D 11 ⁎ , λ q = q a 4 π 4 D 11 ⁎ [ D 11 ⁎ D 22 ⁎ A 11 ⁎ A 22 ⁎ ] 1 / 4 ,

in which ρ 0 and E 0 are the reference values of ρ M and E M, respectively, for the metal matrix at room temperature; k 1 and k 2 are the non-dimensional forms of foundation stiffnesses used in the numerical examples; and A x T , A y T , D x T , D y T , F x T , and F y T are defined by

(27) A x T A y T D x T D y T F x T F y T Δ T = − ∑ k = 1 ∫ h k − 1 h k A x A y ( 1 , Z , Z 3 ) Δ T d Z .

The simply supported boundary conditions of equations (15a) and (15b) can be re-written in non-dimensional forms as

(28a) W = Ψ y = M x = P x = 0 ( at x = 0 , π ) ,

(28b) W = Ψ x = M y = P y = 0 ( at y = 0 , π ) ,

and the in-plane boundary conditions on the x = (0, π) edges become

(29a) 1 π ∫ 0 π β 2 ∂ 2 F ∂ y 2 d y = 0 ( movable ) ,

(29b) ∫ 0 π ∫ 0 π γ 24 2 β 2 ∂ 2 F ∂ y 2 − γ 5 ∂ 2 F ∂ x 2 + γ 24 γ 511 ∂ Ψ x ∂ x + γ 233 β ∂ Ψ y ∂ y − γ 24 γ 611 ∂ 2 W ∂ x 2 + γ 244 β 2 ∂ 2 W ∂ y 2 − 1 2 γ 24 ∂ W ∂ x 2 + η − 1 ( γ 24 2 γ T 1 − γ 5 γ T 2 ) Δ T ] d x d y = 0 ( immovable ) ,

and the in-plane boundary conditions on the y = (0, π) edges become

(30a) ∫ 0 π ∂ 2 F ∂ x 2 d x = 0   ( movable ) ,

(30b) ∫ 0 π ∫ 0 π ∂ 2 F ∂ x 2 − γ 5 β 2 ∂ 2 F ∂ y 2 + γ 24 γ 220 ∂ Ψ x ∂ x + γ 522 β ∂ Ψ y ∂ y − γ 24 γ 240 ∂ 2 W ∂ x 2 + γ 622 β 2 ∂ 2 W ∂ y 2 + η − 1 γ 24 W − 1 2 γ 24 β 2 ∂ W ∂ y 2 + η − 1 ( γ T 2 − γ 5 γ T 1 ) Δ T ] d y d x = 0 , ( immovable ) .

3.1 Nonlinear vibration solutions for porous sandwich cylindrical panels

To explore the nonlinear vibration problem, we need to determine the relationship between the frequency and vibration amplitude of the porous sandwich cylindrical panel. By applying the two-step perturbation approach, the asymptotic solutions of equations (24a)–(24d) satisfying boundary conditions (equations (28a) and (28b)–(30a) and (30b)) are obtained as

(31) W ( x , y , t ) = ε A 11 ( 1 ) ( t ) sin m x sin n y + ( ε A 11 ( 1 ) ( t ) ) 3 [ a 313 sin m x sin 3 n y + a 331 sin 3 m x sin n y ] + O ( ε 4 ) ,

(32) Ψ x ( x , y , t ) = [ ( ε A 11 ( 1 ) ( t ) ) c 111 + ( ε A ̈ 11 ( 1 ) ( t ) ) c 311 ] cos m x sin n y + ( ε A 11 ( 1 ) ( t ) ) 3 [ c 313 cos m x sin 3 n y + c 331 cos 3 m x sin n y ] + O ( ε 4 ) ,

(33) Ψ y ( x , y , t ) = [ ( ε A 11 ( 1 ) ( t ) ) d 111 + ( ε A ̈ 11 ( 1 ) ( t ) ) d 311 ] sin m x cos n y + ( ε A 11 ( 1 ) ( t ) ) 3 [ d 313 sin m x cos 3 n y + d 331 sin 3 m x cos n y ] + O ( ε 4 ) ,

(34) F ( x , y , t ) = − B 00 ( 0 ) y 2 / 2 − b 00 ( 0 ) x 2 / 2 + [ ( ε A 11 ( 1 ) ( t ) ) b 111 + ( ε A ̈ 11 ( 1 ) ( t ) ) b 311 ] sin m x sin n y + ( ε A 11 ( 1 ) ( t ) ) 2 [ − B 00 ( 2 ) y 2 / 2 − b 00 ( 2 ) x 2 / 2 + b 220 cos 2 m x + b 202 cos 2 n y ] + ( ε A 11 ( 1 ) ( t ) ) 3 [ b 313 sin m x sin 3 n y + b 331 sin 3 m x sin n y ] + O ( ε 4 ) ,

(35) λ q ( x , y , t ) = [ ( ε A ̈ 11 ( 1 ) ( t ) ) g 30 + ( ε A 11 ( 1 ) ( t ) ) g 31 ] sin m x sin n y + ( ε A 11 ( 1 ) ( t ) ) 2 [ g 220 cos 2 m x + g 202 cos 2 n y ] + ( ε A 11 ( 1 ) ( t ) ) 3 [ g 33 sin m x sin n y ] + …

It is worth noting that in equations (31)–(35), ε has no specific physical meaning but is definitely a small perturbation parameter in the first step.

For the free vibration problem of the panel, the dynamic load vanishes and we have λ q = 0 . Employing the Galerkin procedure to equation (35), one has

(36) g 30 d 2 ( ε A 11 ( 1 ) ) d t 2 + g 31 ( ε A 11 ( 1 ) ) + g 32 ( ε A 11 ( 1 ) ) 2 + g 33 ( ε A 11 ( 1 ) ) 3 = 0 .

In the second step, we take ( ε A 11 ( 1 ) ) as the second perturbation parameter, which relates to the non-dimensional maximum amplitude W max. Hence, the solution of equation (36) can be written as

(37) ω NL = ω L 1 + 9 g 31 g 33 − 10 g 32 2 12 g 31 2 A 2 1 / 2 ,

where ω L = [ g 31 / g 30 ] 1 / 2 is the non-dimensional linear frequency and A = W max = W ¯ max / [ D 11 ⁎ D 22 ⁎ A 11 ⁎ A 22 ⁎ ] 1 / 4 is the non-dimensional amplitude of the panel. In equation (36), g 30 to g 33 are all functions of the porosity coefficient for the porous sandwich cylindrical panel, and details may be found in Appendix A.

3.2 Nonlinear bending solutions for porous sandwich cylindrical panels

For the nonlinear bending problem, we need to determine the relationship between the applied pressure and central deflection of the porous sandwich cylindrical panel. In the present case, the applied pressure is static and uniform and is taken to be q ( x , y , t ) = q 0 . Hence, the solutions are independent of time and the terms with respect to the time in equations (24a)–(24d) are vanished. Equation (35) can be re-written as

(38) λ q = A q ( 0 ) + A q ( 1 ) ( A 11 ( 1 ) ε ) + A q ( 2 ) ( A 11 ( 1 ) ε ) 2 + A q ( 3 ) ( A 11 ( 1 ) ε ) 3 + .. .

in which ( A 11 ( 1 ) ε ) is treated as the second perturbation parameter. From equation (31), one has

(39) A 11 ( 1 ) ε = W m + Θ 3 ( W m ) 3 ⋯

Substituting equation (39) into equation (38), the load–central deflection relationship can be obtained. In equation (38), A q ( j ) (j = 0–3) are all functions of the porosity coefficient for the porous sandwich cylindrical panel, and details are given in Appendix B.

4 Numerical results and discussion

In this section, the evaluation is made through the free vibration natural frequencies, the nonlinear-to-linear frequency ratio curves, and the nonlinear bending load–deflection curves. The free vibration natural frequencies and the nonlinear-to-linear frequency ratio curves are obtained from equation (37), while the nonlinear bending load–deflection curves are obtained from equations (38) and (39). The reliability and accuracy of the present solution method have been validated by many comparison studies with other research teams using different methods [41,53,54,55]. In the current research, numerical studies are performed to compare the results obtained from the present model and the EIM, where the equivalent Young’s modulus is predicted by a modified Halpin–Tsai model [22].

(40) E eff = 3 8 E 11 + 5 8 E 22 ,

in which E 11 and E 22 have the same forms of equation (1a) and (1b), and the shear modulus is expressed by

(41) G eff = E eff 2 ( 1 + ν eff ) ,

in which

(42) ν eff = V GPL ν GPL + V m ν m ,

where V m = 1 − V GPL and E m and ν m have the same forms of equations (8a) and (8c). It is noted that in the present model, we use a generic Halpin–Tsai model of equations (1a)–(1c) instead of equation (40), and we remove equation (41) and the relationship V GPL + V m = 1.

The thermomechanical properties of the metal face sheets and the porous GPLRC core have to be determined first. We select titanium alloy (referred to as Ti–6Al–4V) for the metal face sheets, and the temperature-dependent material properties of Ti–6Al–4V are as follows [25]: E Ti = 122.56 × (1.0 − 4.586 × 10−4 T) GPa, ν Ti = 0.29, ρ Ti = 4,429 kg/m3, and α Ti = 7.5788 × (1.0 + 6.638 × 10−4 T − 3.147 × 10−6 T 2) × 10−6/K, where T = T 0 + ΔT and T 0 is set at room temperature.

For the porous GPLRC core, the dimension of the GPL is set as a GPL = 2.5 μm, b GPL = 1.5 μm, and h GPL = 1.5 nm. Through a literature survey study, we found that the linear fitting formulae E GPL = (1.112 − 0.00034T) TPa, α GPL = (23.5 + 0.004ΔT) × 10−6/K [56] and E GPL = (1087.8 − 0.261T) GPa, α GPL = (13.92 − 0.0299T) × 10−6/K [57] were utilized for GPLs. These equations came from the first author’s previous works [58,59] and were only suitable for the monolayer graphene but were invalid for GPLs. Owing to the lack of the experiment data and/or the molecular dynamics (MD) simulation results, the material properties of GPLs are set as follows [60,61,62]: E GPL = 1,010 GPa, ρ GPL = 1062.5 kg/m 3 , ν GPL = 0.186, and α GPL = 2.35 × 10−5/K. The temperature-dependent material properties of the aluminum matrix are set as follows [63]: E M = 69.0 × (1.0 − 0.00053ΔT) GPa, ν M = 0.29658, ρ M = 26 0 1 kg/m 3 , and α M = 23.0 × (1 + 0.00072ΔT) × 10−6/oC, where ΔT = T −T 0 and T 0 = 20oC.

In the present study, the GPL weight fraction w GPL is set to be 1–3%. From equations (6a) and (6b), the volume fractions (V GPL, V m) of porous GPLRC layers with different porosity coefficient values are obtained and listed in Table 1. The results confirm that the volume fraction relationship must be V GPL + V m < 1 for the porous GPLRC layers [31].

Table 1

Volume fractions of the porous GPLRC layer with different porosity coefficients

w GPL (V GPL, V m)
α ⁎ = 0.2 α ⁎ = 0.4 α ⁎ = 0.6 α ⁎ = 0.8
0.01 (0.0155, 0.7845) (0.0088, 0.5912) (0.0039, 0.3961) (0.001, 0.199)
0.02 (0.0307, 0.7693) (0.0175, 0.5825) (0.0078, 0.3922) (0.002, 0.198)
0.03 (0.0457, 0.7543) (0.0261, 0.5739) (0.0118, 0.3882) (0.003, 0.197)

In the current study, the sandwich cylindrical panel has a total thickness h = 0.05 m, while the thickness of the face sheet is 1 mm. The porous GPLRC core consists of six layers and the thickness of each layer is equal to 8 mm. To conduct a six-layer porous GPLRC core with a piece-wise FG pattern, the porosity coefficient in each layer is selected as α ⁎ = 0.2, 0.4, or 0.6. Two FG patterns, referred to as FG-X and FG-O, are considered, i.e., the FG-X pattern with [0.2/0.4/0.6]S and the FG-O pattern with [0.6/0.4/0.2]S (Figure 2). For comparison purposes, a UD pattern core with six layers having an identical porosity coefficient of 0.4 is also considered.

Figure 2 A porous GPLRC core: (a) UD, (b) FG-O, and (c) FG-X.
Figure 2

A porous GPLRC core: (a) UD, (b) FG-O, and (c) FG-X.

4.1 Vibration characteristics of porous sandwich cylindrical panels

We next focus on the linear and nonlinear vibrations of sandwich cylindrical panels with a porous GPLRC core resting on elastic foundations in thermal environments. The in-plane boundary conditions are set as “immovable.” The sandwich panels have a/b = 1, b/h = 20, and a/R = 0.2, 0.5, and 0.8. Typical results are shown in Tables 2–4 and Figures 3–6, in which the non-dimensional frequency is defined by Ω ˜ = Ω ( b 2 / h ) ρ 0 / E 0 , where ρ 0 and E 0 are the reference values of ρ M and E M, respectively, for the aluminum matrix at Δ T = 0 .

Table 2

Natural frequency Ω ˜ = Ω ( b 2 / h ) ρ 0 / E 0 of porous sandwich cylindrical panels reinforced by GPLs (h = 50 mm, a/b = 1, b/h = 20, a/R = 0.5, Δ T = 0)

w GPL Ω ˜ 11 Ω ˜ 12 Ω ˜ 21 Ω ˜ 22 Ω ˜ 13 Ω ˜ 31
0.01 UD Present model 8.2011 15.8791 17.6890 25.5357 30.7112 31.9889
EIMa 6.4727 12.7184 14.1066 20.2790 24.6440 25.6230
Differenceb 21.08% 19.90% 20.25% 20.59% 19.76% 19.90%
FG-O Present model 7.6483 13.8134 15.9581 22.6151 26.6173 28.1634
EIM 6.1225 11.2003 12.9311 18.0503 21.8444 23.0738
Difference 19.95% 18.92% 18.97% 20.18% 17.93% 18.07%
FG-X Present model 8.9972 18.1325 19.8045 28.7035 34.9736 36.1468
EIM 7.4225 15.0236 16.3520 23.6690 28.6817 29.6270
Difference 17.50% 17.15% 17.43% 17.54% 17.99% 18.04%
0.02 UD Present model 8.6836 17.0489 19.0376 27.0124 33.2275 34.6933
EIM 7.2340 14.0798 15.6978 22.4806 27.3054 28.4472
Difference 16.69% 17.42% 17.54% 16.78% 17.82% 18.00%
FG-O Present model 8.0365 14.6577 17.0214 23.6886 28.4762 30.2547
EIM 6.7926 12.2208 14.2416 19.7256 23.8308 25.2705
Difference 15.48% 16.63% 16.33% 16.73% 16.31% 16.47%
FG-X Present model 9.5731 19.5847 21.3979 30.5573 37.9584 39.2849
EIM 8.2944 16.7188 18.2450 26.3835 31.9832 33.0676
Difference 13.36% 14.63% 14.73% 13.66% 15.74% 15.83%
0.03 UD Present model 9.1050 18.1279 20.2431 28.3839 35.5124 37.1270
EIM 7.9194 15.3131 17.1339 24.4711 29.7111 30.9968
Difference 13.02% 15.53% 15.36% 13.79% 16.34% 16.51%
FG-O Present model 8.3729 15.4525 17.9767 24.7030 30.2102 32.1753
EIM 7.4007 13.1625 15.4393 21.2679 25.6619 27.2876
Difference 11.61% 14.82% 14.11% 13.91% 15.06% 15.19%
FG-X Present model 10.0828 20.9029 22.8166 32.2517 40.6130 42.0622
EIM 9.0760 18.2391 19.9410 28.8130 34.9349 36.1432
Difference 9.99% 12.74% 12.60% 10.66% 13.98% 14.07%

aEIM = equivalent isotropic model.

bDifference = 100%[ Ω ˜ i j (present model) − Ω ˜ i j (EIM)]/ Ω ˜ i j (present model).

Table 3

Natural frequency Ω ˜ = Ω ( b 2 / h ) ρ 0 / E 0 of porous sandwich cylindrical panels reinforced by GPLs in thermal environments (h = 50 mm, a/b = 1, b/h = 20, a/R = 0.8, w GPL = 0.03)

Δ T (K) Ω ˜ 11 Ω ˜ 12 Ω ˜ 21 Ω ˜ 22 Ω ˜ 13 Ω ˜ 31
0 UD Present model 11.4800 18.3571 23.3051 29.2218 35.5434 39.4425
EIMa 10.0678 15.5124 19.7960 25.2393 29.7367 32.9255
Differenceb 12.30% 15.50% 15.06% 13.63% 16.34% 16.52%
FG-O Present model 10.9894 15.7311 21.4879 25.6980 30.2481 34.9283
EIM 9.8658 13.4173 18.6208 22.2358 25.6946 29.6745
Difference 10.22% 14.71% 13.34% 13.47% 15.05% 15.04%
FG-X Present model 12.3373 21.1087 25.6613 33.0151 40.6411 44.1897
EIM 11.1753 18.4235 22.4892 29.5329 34.9589 37.9736
Difference 9.42% 12.72% 12.36% 10.55% 13.98% 14.07%
100 UD Present model 10.0044 16.3137 21.2590 26.7716 33.2817 36.8454
EIM 8.6848 13.2599 17.9844 22.9536 27.2794 30.6460
Difference 13.19% 18.72% 15.40% 14.26% 18.03% 16.83%
FG-O Present model 9.2473 12.9703 19.0883 22.6668 27.3175 31.8615
EIM 8.2881 10.4680 16.4978 19.3914 22.5982 26.9371
Difference 10.37% 19.29% 13.57% 14.45% 17.28% 15.46%
FG-X Present model 10.7738 18.9980 23.5754 30.5029 38.2357 41.5578
EIM 9.7800 16.2971 20.6841 27.3112 32.5731 35.7134
Difference 9.22% 14.22% 12.26% 10.46% 14.81% 14.06%
200 UD Present model 8.2206 13.8587 18.9734 24.0079 30.7349 34.0399
EIM 7.0334 10.5339 15.9664 20.4111 24.5747 28.1799
Difference 14.44% 23.99% 15.85% 14.98% 20.04% 17.22%
FG-O Present model 7.0132 9.2216 16.2986 19.0527 23.8479 28.4350
EIM 6.3247 6.2468 14.0533 16.0442 18.9971 23.8822
Difference 9.82% 32.26% 13.78% 15.79% 20.34% 16.01%
FG-X Present model 8.8810 16.5016 21.2537 27.6882 35.5424 38.7218
EIM 8.1464 13.8440 18.7023 24.8881 29.9938 33.2960
Difference 8.27% 16.11% 12.00% 10.11% 15.61% 14.01%

aEIM = equivalent isotropic model.

bDifference = 100% [ Ω ˜ i j (present model) − Ω ˜ i j (EIM)]/ Ω ˜ i j (present model).

Table 4

Natural frequency Ω ˜ = Ω ( b 2 / h ) ρ 0 / E 0 of porous sandwich cylindrical panels reinforced by GPLs resting on elastic foundations (h = 50 mm, a/b = 1, b/h = 20, a/R = 0.2, w GPL = 0.01, Δ T = 0)

(k 1 ,k 2) Ω ˜ 11 Ω ˜ 12 Ω ˜ 21 Ω ˜ 22 Ω ˜ 13 Ω ˜ 31
(0, 0) UD Present model 6.7422 15.7720 16.0868 25.1109 30.6978 30.9303
EIMa 5.3650 12.6362 12.8698 19.9569 24.6335 24.7928
Differenceb 20.43% 19.88% 20.00% 20.52% 19.75% 19.84%
FG-O Present model 5.9774 13.6839 14.0636 22.1112 26.6010 26.8847
EIM 4.7734 11.0954 11.3925 17.6428 21.8311 22.0325
Difference 20.14% 18.92% 18.99% 20.21% 17.93% 18.05%
FG-X Present model 7.6313 18.0346 18.3204 28.3112 34.9612 35.1679
EIM 6.3570 14.9457 15.1672 23.3604 28.6716 28.8250
Difference 16.70% 17.13% 17.21% 17.95% 17.99% 18.04%
(100, 0) UD Present model 16.9385 22.1031 22.3287 29.4760 34.3465 34.5545
EIM 13.5547 17.7108 17.8782 23.4826 27.5581 27.7006
Difference 17.85% 19.87% 19.93% 20.33% 19.76% 19.84%
FG-O Present model 16.2420 20.3500 20.6072 26.7330 30.5389 30.7864
EIM 13.3432 16.6588 16.8582 21.5611 25.0940 25.2694
Difference 17.85% 18.14% 18.19% 19.35% 17.83% 17.92%
FG-X Present model 16.9045 23.4719 23.6922 32.0252 38.0189 38.2091
EIM 13.9814 19.4282 19.5991 26.4384 31.2232 31.3641
Difference 17.29% 17.23% 17.28% 17.45% 17.87% 17.91%
(100, 10) UD Present model 27.6321 40.8883 41.0108 52.4422 59.3463 59.4671
EIM 22.1265 32.7663 32.8571 41.9605 47.6020 47.6846
Difference 19.92% 19.86% 19.88% 19.99% 19.79% 19.81%
FG-O Present model 26.7209 39.1624 39.2967 49.9709 56.1555 56.2906
EIM 22.0114 32.2411 32.3446 40.9605 46.2691 46.3645
Difference 17.62% 17.67% 17.69% 18.03% 17.61% 17.63%
FG-X Present model 27.1087 40.7999 40.9271 52.8673 60.3975 60.5175
EIM 22.3958 33.7316 33.8303 43.6948 49.8321 49.9205
Difference 17.39% 17.32% 17.34% 17.35% 17.49% 17.51%

aEIM = equivalent isotropic model.

bDifference = 100% [ Ω ˜ i j (present model) − Ω ˜ i j (EIM)]/ Ω ˜ i j (present model).

Figure 3 Effect of the porosity distribution pattern on the frequency–amplitude curves of porous sandwich cylindrical panels reinforced by GPLs.
Figure 3

Effect of the porosity distribution pattern on the frequency–amplitude curves of porous sandwich cylindrical panels reinforced by GPLs.

Figure 4 Effect of the GPL weight fraction on the frequency–amplitude curves of porous sandwich cylindrical panels reinforced by GPLs.
Figure 4

Effect of the GPL weight fraction on the frequency–amplitude curves of porous sandwich cylindrical panels reinforced by GPLs.

Figure 5 Effect of foundation stiffnesses on the frequency–amplitude curves of porous sandwich cylindrical panels reinforced by GPLs resting on elastic foundations.
Figure 5

Effect of foundation stiffnesses on the frequency–amplitude curves of porous sandwich cylindrical panels reinforced by GPLs resting on elastic foundations.

Figure 6 Effect of temperature variation on the frequency–amplitude curves of porous sandwich cylindrical panels reinforced by GPLs in thermal environments.
Figure 6

Effect of temperature variation on the frequency–amplitude curves of porous sandwich cylindrical panels reinforced by GPLs in thermal environments.

Table 2 shows the effects of the weight fraction of GPL and the FG patterns of core porosity on the natural frequency of porous sandwich cylindrical panels with a/R = 0.5 at Δ T = 0 . Three GPL weight fractions 1, 2, and 3% are considered. It can be seen that the natural frequencies are increased as the weight fraction w GPL increases. The difference between the two models is about 10% or more, and the maximum difference between the two models is 21.08% for the panel with a porous UD core at w GPL = 1%.

Table 3 shows the effects of the temperature variation and the FG patterns of core porosity on the natural frequency of porous sandwich cylindrical panels with a/R = 0.8. The GPL weight fraction w GPL = 3%, and the thermal environmental conditions are set as Δ T = 0, 100, and 200 K. Note that the thermal expansion coefficient is taken as α = α 11 = α 22 by using the EIM. Like the conventional observation [53], the natural frequencies decrease when the temperature increases. This is due to the fact that the increase of temperature reduces the panel stiffness which in turn decreases the linear frequencies of the panel. The difference between the two models is about 8% or more, and the maximum difference between the two models is 32.26% for the panel with a porous FG-O core at Δ T = 200 K.

Table 4 shows the effects of the foundation stiffnesses and the FG patterns of core porosity on the natural frequency of porous sandwich cylindrical panels with a/R = 0.2 at Δ T = 0. The GPL weight fraction w GPL = 1%. The corresponding foundation stiffnesses are (k 1, k 2) = (100, 10) for the Pasternak foundation, (k 1, k 2) = (100, 0) for the Winkler foundation, and (k 1, k 2) = (0, 0) for the sandwich cylindrical panel without any elastic foundation. Like the conventional observation [53], the natural frequencies are increased as foundation stiffnesses increase. The difference between the two models is about 16% or more, and the maximum difference between the two models is 20.52% for the foundationless panel with a porous UD core.

From Tables 2–4, we observe that the panel with the porous FG-X core has the highest natural frequencies, while the panel with the porous FG-O core has the lowest among the three. Comparing the results obtained from the present model with those obtained from the EIM, it is found that, for most cases, the difference is over 10%, in particular for the case w GPL = 1%.

For nonlinear vibration analysis, the porous sandwich cylindrical panels have a/R = 0.5 and the GPL weight fraction w GPL = 3%, except in Figure 4. The effect of the porosity distribution pattern on the nonlinear-to-linear frequency ratio curves of porous sandwich cylindrical panels at Δ T = 0 is shown in Figure 3. Contrary to Tables 2–4, where the panel with the porous FG-X core has the highest natural frequencies, while the panel with the porous FG-O core has the lowest, in Figure 3, the panel with the porous FG-X core has the lowest frequency–amplitude curves, while the panel with the porous FG-O core has the highest among the three. It is observed that the maximum difference between the two models is 2.6% for the panel with the porous FG-O core when the non-dimensional panel deflection W ¯ / h reaches 1.0. Note that this difference will increase as the panel deflection increases.

Figure 4 shows the effect of the GPL weight fraction on the nonlinear-to-linear frequency ratio curves of sandwich cylindrical panels with the porous FG-X core at Δ T = 0 . Three GPL weight fractions w GPL = 1, 2, and 3% are considered. We observe that the frequency–amplitude curve becomes higher when the GPL weight fraction is increased. It can also be seen that the frequency–amplitude curves with w GPL = 2 and 3% obtained from the present model are higher than those obtained based on the EIM, while for the case of w GPL = 1%, the results are inversed. In this example, the maximum difference between the two models is only 1.9% for the porous panel with w GPL = 3% when W ¯ / h reaches 1.0.

Figure 5 shows the effect of foundation stiffnesses on the nonlinear-to-linear frequency ratio curves of sandwich cylindrical panels with the porous FG-X core resting on elastic foundations at Δ T = 0 . Two foundation models are considered where (k 1, k 2) = (50, 5) for the Pasternak foundation and (k 1, k 2) = (50, 0) for the Winkler foundation. Contrary to the results in Table 4, where the natural frequencies are increased with an increase in foundation stiffnesses, in Figure 5, the frequency–amplitude curves are reduced with an increase in foundation stiffnesses. In this example, the maximum difference between the two models is only 1.9% for the foundationless panel when W ¯ / h reaches 1.0, and the difference may be neglected when the panel rests on a Pasternak foundation with (k 1, k 2) = (50, 5).

Figure 6 shows the effect of temperature variation on the nonlinear-to-linear frequency ratio curves of sandwich cylindrical panels with the porous FG-X core in thermal environments. The thermal environmental conditions are taken as Δ T = 0, 50, and 100 K. Contrary to the results in Table 3, where the natural frequencies are decreased with an increase in the temperature, in Figure 6, the frequency–amplitude curves are increased with an increase in the temperature. In this example, we observe that the maximum difference between the two models is 3% for the porous panel at Δ T = 100 K when W ¯ / h reaches 1.0.

4.2 Nonlinear bending responses of porous sandwich cylindrical panels

Then, we turn our attention to the nonlinear bending of sandwich cylindrical panels with the porous GPLRC core resting on elastic foundations in thermal environments. The sandwich panels have a/b = 1.5, b/h = 20, and a/R = 0.5. The GPL weight fraction w GPL = 3%, except in Figure 8.

Figure 7 shows the effect of the porosity distribution pattern on the nonlinear bending load–deflection curves of porous sandwich cylindrical panels at Δ T = 0 . Like the conventional observation [54], the panel with the porous FG-X core has the lowest nonlinear bending load–deflection curves, while the panel with the porous FG-O core has the highest among the three when the non-dimensional panel deflection W ¯ / h ≤ 1.0 . Unlike the conventional observation [54], the bending load–deflection curve of the panel with porous UD core becomes the highest among the three when the panel deflection W ¯ / h > 1.0 . In this example, we observe that the maximum difference between the two models is 5.1% for the panel with the porous UD core when W ¯ / h reaches 2.0.

Figure 7 Effect of porosity distribution pattern on the nonlinear bending load–deflection curves of porous sandwich cylindrical panels reinforced by GPLs.
Figure 7

Effect of porosity distribution pattern on the nonlinear bending load–deflection curves of porous sandwich cylindrical panels reinforced by GPLs.

Figure 8 shows the effect of the GPL weight fraction on the nonlinear bending load–deflection curves of sandwich cylindrical panels with the porous FG-X core at Δ T = 0 . Three GPL weight fractions 1, 2, and 3% are considered. It is observed that the nonlinear bending load–deflection curves are reduced with an increase in the GPL weight fraction. In this example, we observe that the maximum difference between the two models is 6.1% for the panel with w GPL = 1% when W ¯ / h reaches 2.0.

Figure 8 Effect of the GPL weight fraction on the nonlinear bending load–deflection curves of porous sandwich cylindrical panels reinforced by GPLs.
Figure 8

Effect of the GPL weight fraction on the nonlinear bending load–deflection curves of porous sandwich cylindrical panels reinforced by GPLs.

Figure 9 shows the effect of foundation stiffnesses on the nonlinear bending load–deflection curves of sandwich cylindrical panels with the porous FG-X core resting on elastic foundations at Δ T = 0 . The same two foundation models are adopted as in Figure 5. It is observed that the nonlinear bending load–deflection curves are reduced as the foundation stiffnesses increase. In this example, we observe that the maximum difference between the two models is 4.7% for the foundationless panel when W ¯ / h reaches 2.0. The difference between the two models may be neglected when the foundation stiffness is sufficiently large.

Figure 9 Effect of foundation stiffnesses on the nonlinear bending load–deflection curves of porous sandwich cylindrical panels reinforced by GPLs resting on elastic foundations.
Figure 9

Effect of foundation stiffnesses on the nonlinear bending load–deflection curves of porous sandwich cylindrical panels reinforced by GPLs resting on elastic foundations.

Figure 10 shows the effect of temperature variation on the nonlinear bending load–deflection curves of sandwich cylindrical panels with the porous FG-X core in thermal environments. The thermal environmental conditions are set as Δ T = 0, 100, and 200 K. Like the conventional observation [54], the nonlinear bending load–deflection curve becomes higher when the temperature increases. Unlike the conventional observation [54], the small initial deflection can be observed at Δ T = 100 and 200 K. In this example, we observe that the maximum difference between the two models is 4.7% for the panel at Δ T = 0 when W ¯ / h reaches 2.0.

Figure 10 Effect of temperature variation on the nonlinear bending load–deflection curves of porous sandwich cylindrical panels reinforced by GPLs in thermal environments.
Figure 10

Effect of temperature variation on the nonlinear bending load–deflection curves of porous sandwich cylindrical panels reinforced by GPLs in thermal environments.

5 Conclusions

The quantitative evaluation for the nonlinear vibration and nonlinear bending of sandwich cylindrical panels with the porous metal core reinforced by GPLs has been presented. The FG material concept is incorporated into the design of the porous GPLRC layer. By introducing an inhomogeneous model, the Young’s moduli along with the shear modulus for the porous GPLRC layer are predicted through a generic Halpin–Tsai model containing a porosity coefficient. Comparison investigations between the present model and the EIM have been presented for the sandwich cylindrical panels with the porous UD, FG-O, or FG-X GPLRC core. The numerical results reveal that, in most cases, the natural frequencies, the frequency–amplitude curves, and the bending load–deflection curves of the porous sandwich cylindrical panels are underestimated by using the EIM. In contrast, for some special cases, the frequency–amplitude curves of sandwich cylindrical panels with the porous FG-X core under w GPL = 1% at Δ T = 0 K, and/or the bending load–deflection curves of the sandwich cylindrical panels with the porous FG-X core under w GPL = 3% at Δ T = 200 K are overestimated by using the EIM. In most cases, the difference between the two models is over 10% for the natural frequencies and the maximum difference between the two models may reach 32.26%. The difference between the two models is relatively small for the frequency–amplitude curves and the bending load–deflection curves of the sandwich cylindrical panels with the porous GPLRC core. Only in the case when the panel rests on a Pasternak elastic foundation with sufficiently large foundation stiffnesses, the difference between the two models may be negligible, and the EIM may be valid.

  1. Funding information: The authors state that no funding was involved.

  2. Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.

  3. Conflict of interest: The authors state that there is no conflict of interest.

Appendix

Appendix A

In equation (36).

(A.1) g 30 = − [ γ 170 − ( γ 171 m 2 + γ 172 n 2 β 2 ) ] − γ 81 m 2 g 04 + γ 82 n 2 β 2 g 03 g 00 + γ 14 γ 24 g 05 ⁎ g 06 γ 81 m 2 g 02 + γ 82 n 2 β 2 g 01 g 00 − g 08 ⁎ − γ 14 γ 24 g 07 ⁎ g 05 ⁎ ⁎ g 06 , g 31 = Q 11 − D 02 , g 33 = 1 16 γ 14 γ 24 m 4 γ 7 + n 4 β 4 γ 6 − D 22 , g 32 = − 2 3 π 2 m n γ 14 γ 24 m 2 n 2 β 2 γ 8 γ 6 + γ 9 γ 7 + 1 4 m 2 η γ 6 + 4 g 05 ⁎ g 06 ( 1 − cos m π ) ( 1 − cos n π ) , + 2 g 33 Φ ( T )

in the above equations (other symbols are defined as in ref. [41])

(A.2) Q 11 = g 08 + γ 14 γ 24 g 05 ⁎ g 07 ⁎ g 06 + [ K 1 + K 2 ( m 2 + n 2 β 2 ) ] , D 02 = γ 14 ( B 000 m 2 + b 000 n 2 β 2 ) , D 22 = γ 14 ( B 200 m 2 + b 200 n 2 β 2 ) ,

and

(A.3) Φ ( T ) = λ + Θ 2 ( λ ) 2 + Θ 3 ( λ ) 3 + ⋯ ,

where (with m = n = 1)

(A.4) λ = 16 π 2 G 08 ( γ T 4 m 2 + γ T 5 n 2 β 2 ) − ( γ T 4 − γ T 7 ) m 2 g 102 + ( γ T 5 − γ T 8 ) n 2 β 2 g 101 g 00 Δ T × h [ D 11 ⁎ D 22 ⁎ A 11 ⁎ A 22 ⁎ ] 1 / 4 , Θ 2 = 8 3 π 2 G 08 γ 14 γ 24 m 2 n 2 β 2 γ 8 γ 6 + γ 9 γ 7 + 1 4 m 2 η γ 6 + 4 g 05 ⁎ g 06 , Θ 3 = 2 Θ 2 2 − g 33 G 08 , G 08 = Q 11 − D 02 ,

and for the case of “movable” edges,

(A.5) B 000 = B 200 = b 000 = b 200 = 0 ,

and for the case of “immovable” edges,

(A.6) B 000 = η − 1 γ T 1 Δ T , B 200 = − 1 8 γ 24 m 2 + γ 5 n 2 β 2 γ 24 2 − γ 5 2 , b 000 = η − 1 γ T 2 Δ T , b 200 = − 1 8 γ 24 γ 5 m 2 + γ 24 2 n 2 β 2 γ 24 2 − γ 5 2

Appendix B

In equations (38) and (39).

(B.1) A q ( 0 ) = − 1 m n ( γ T 4 m 2 + γ T 5 n 2 β 2 ) − γ 14 γ 24 g 07 ⁎ g 01 ⁎ g 06 − g 02 ⁎ 16 π 2 Δ T h [ D 11 ⁎ D 22 ⁎ A 11 ⁎ A 22 ⁎ ] 1 / 4 , A q ( 1 ) = C 11 G 08 , A q ( 2 ) = − C 11 8 3 π 2 γ 14 γ 24 m 2 n 2 β 2 γ 8 γ 6 + γ 9 γ 7 + 4 g 05 ⁎ g 06 + 1 4 m 2 γ 6 η , A q ( 3 ) = C 11 1 16 γ 14 γ 24 m 4 γ 7 + n 4 β 4 γ 6 − γ 14 ( m 2 B 200 + n 2 β 2 b 200 ) ,

in which (other symbols are defined as in ref. [41])

(B.2) C 11 = π 2 16 m n , Θ 3 = α 313 + α 331 , α 313 = 1 16 γ 14 γ 24 m 4 γ 7 G 138 , α 331 = 1 16 γ 14 γ 24 n 4 β 4 γ 6 G 318 , G 08 = g 08 + γ 14 γ 24 g 07 ⁎ g 05 ⁎ g 06 + [ K 1 + K 2 ( m 2 + n 2 β 2 ) ] − γ 14 ( m 2 B 000 + n 2 β 2 b 000 ) − 32 3 π 2 γ 14 γ 24 m 2 n 2 β 2 g 01 ⁎ g 06 16 π 2 Δ T h [ D 11 ⁎ D 22 ⁎ A 11 ⁎ A 22 ⁎ ] 1 / 4 , G 138 = g 138 + γ 14 γ 24 g 137 ⁎ g 135 ⁎ g 136 + [ K 1 + K 2 ( m 2 + 9 n 2 β 2 ) ] − γ 14 ( m 2 B 000 + 9 n 2 β 2 b 000 ) , G 318 = g 318 + γ 14 γ 24 g 317 ⁎ g 315 ⁎ g 316 + [ K 1 + K 2 ( 9 m 2 + n 2 β 2 ) ] − γ 14 ( 9 m 2 B 000 + n 2 β 2 b 000 ) ,

in the above equations, B 000, b 000, B 200, and b 200 are the same as defined in equations (A.5) and (A.6).

References

[1] Lu G, Lu GQ, Xiao ZM. Mechanical properties of porous materials. J Porous Mater. 1999;6:359–68.10.1023/A:1009669730778Search in Google Scholar

[2] Banhart J. Manufacture, characterisation and application of cellular metals and metal foams. Prog Mater Sci. 2001;46:559–632.10.1016/S0079-6425(00)00002-5Search in Google Scholar

[3] Lefebvre L-P, Banhart J, Dunand D. Porous metals and metallic foams: Current status and recent developments. Adv Eng Mater. 2008;10:775–87.10.1002/adem.200800241Search in Google Scholar

[4] Babaei1 M, Kiarasi1 F, Asemi K, Hosseini M. Functionally graded saturated porous structures: A review. J Comput Appl Mech. 2022;53:297–308.Search in Google Scholar

[5] Kalpakoglou T, Yiatros S. Metal foams: A review for mechanical properties under tensile and shear stress. Front Mater. 2022;9:998673.10.3389/fmats.2022.998673Search in Google Scholar

[6] Kiarasi1 F, Babaei1 M, Asemi K, Dimitri R, Tornabene F. Three-dimensional buckling analysis of functionally graded saturated porous rectangular plates under combined loading conditions. Appl Sci. 2021;11:10434.10.3390/app112110434Search in Google Scholar

[7] Babaei1 M, Hajmohammad MH, Asemi K. Natural frequency and dynamic analyses of functionally graded saturated porous annular sector plate and cylindrical panel based on 3D elasticity. Aerosp Sci Technol. 2020;96:105524.10.1016/j.ast.2019.105524Search in Google Scholar

[8] Babaei1 M, Asemi K, Kiarasi1 F. Static response and free-vibration analysis of a functionally graded annular elliptical sector plate made of saturated porous material based on 3D finite element method. Mech Based Des Struct Mach. 2023;51:1272–96.10.1080/15397734.2020.1864401Search in Google Scholar

[9] Barbaros I, Yang Y, Safaei B, Yang Z, Qin Z, Asmael M. State-of-the-art review of fabrication, application, and mechanical properties of functionally graded porous nanocomposite materials. Nanotechnol Rev. 2022;11:321–71.10.1515/ntrev-2022-0017Search in Google Scholar

[10] You X, Zhang Q, Yang J, Dong S. Review on 3D-printed graphene-reinforced composites for structural applications. Compos Part A-Appl Sci Manufact. 2023;167:107420.10.1016/j.compositesa.2022.107420Search in Google Scholar

[11] Duarte I, Ventura E, Olhero S, Ferreira JM. An effective approach to reinforced closed-cell Al-alloy foams with multiwalled carbon nanotubes. Carbon. 2015;95:589–600.10.1016/j.carbon.2015.08.065Search in Google Scholar

[12] Li M, Gao H, Liang J, Gu S, You W, Shu D, et al. Microstructure evolution and properties of graphene nanoplatelets reinforced aluminum matrix composites. Mater Character. 2018;140:172–8.10.1016/j.matchar.2018.04.007Search in Google Scholar

[13] Li K, Wu D, Chen X, Cheng J, Liu Z, Gao W, et al. Isogeometric analysis of functionally graded porous plates reinforced by graphene platelets. Compos Struct. 2018;204:114–30.10.1016/j.compstruct.2018.07.059Search in Google Scholar

[14] Phan DH. Isogeometric analysis of functionally-graded graphene platelets reinforced porous nanocomposite plates using a refined plate theory. Int J Struct Stabil Dyn. 2020;20:2050076.10.1142/S0219455420500765Search in Google Scholar

[15] Nguyen NV, Nguyen-Xuan H, Lee D, Lee J. A novel computational approach to functionally graded porous plates with graphene platelets reinforcement. Thin-Walled Struct. 2020;150:106684.10.1016/j.tws.2020.106684Search in Google Scholar

[16] Nguyen NV, Nguyen-Xuan H, Lee J. A quasi-three-dimensional isogeometric model for porous sandwich functionally graded plates reinforced with graphene nanoplatelets. J Sandw Struct Mater. 2022;24:825–59.10.1177/10996362211020451Search in Google Scholar

[17] Fan X, Wang A, Jiang P, Wu S, Sun Y. Nonlinear bending of sandwich plates with graphene nanoplatelets reinforced porous composite core under various loads and boundary conditions. Mathematics. 2022;10:3396.10.3390/math10183396Search in Google Scholar

[18] Gao K, Gao W, Chen D, Yang J. Nonlinear free vibration of functionally graded graphene platelets reinforced porous nanocomposite plates resting on elastic foundation. Compos Struct. 2018;204:831–46.10.1016/j.compstruct.2018.08.013Search in Google Scholar

[19] Pan H-G, Wu Y-S, Zhou J-N, Fu Y-M, Liang X, Zhao T-Y. Free vibration analysis of a graphene-reinforced porous composite plate with different boundary conditions. Materials. 2021;14:3879.10.3390/ma14143879Search in Google Scholar PubMed PubMed Central

[20] Teng MW, Wang YQ. Nonlinear forced vibration of simply supported functionally graded porous nanocomposite thin plates reinforced with graphene platelets. Thin-Walled Struct. 2021;164:107799.10.1016/j.tws.2021.107799Search in Google Scholar

[21] Huang X, Wang C, Wang J, Wei N. Nonlinear vibration analysis of functionally graded porous plates reinforced by graphene platelets on nonlinear elastic foundations. Strojniski Vestnik-J Mech Eng. 2022;68:571–82.10.5545/sv-jme.2022.274Search in Google Scholar

[22] Yang J, Chen D, Kitipornchai S. Buckling and free vibration analyses of functionally graded graphene reinforced porous nanocomposite plates based on Chebyshev-Ritz method. Compos Struct. 2018;193:281–94.10.1016/j.compstruct.2018.03.090Search in Google Scholar

[23] Saidia AR, Bahaadinia R, Majidi-Mozafari K. On vibration and stability analysis of porous plates reinforced by graphene platelets under aerodynamical loading. Compos Part B- Eng. 2019;164:778–99.10.1016/j.compositesb.2019.01.074Search in Google Scholar

[24] Safarpour M, Rahimi A, Alibeigloo A, Bisheh H, Forooghi A. Parametric study of three-dimensional bending and frequency of FG-GPLRC porous circular and annular plates on different boundary conditions. Mech Based Des Struct Mach. 2021;49:707–37.10.1080/15397734.2019.1701491Search in Google Scholar

[25] Shen H-S. Functionally graded materials nonlinear analysis of plates and shells. Boca Raton: CRC Press; 2009.Search in Google Scholar

[26] Zhou X, Wang Y, Zhang W. Vibration and flutter characteristics of GPL-reinforced functionally graded porous cylindrical panels subjected to supersonic flow. Acta Astron. 2021;183:89–100.10.1016/j.actaastro.2021.03.003Search in Google Scholar

[27] Twinkle CM, Pitchaimani J. Free vibration and stability of graphene platelet reinforced porous nano-composite cylindrical panel: Influence of grading, porosity and non-uniform edge loads. Eng Struct. 2021;230:111670.10.1016/j.engstruct.2020.111670Search in Google Scholar

[28] Twinkle CM, Pitchaimani J. Static stability and vibration behavior of graphene platelets reinforced porous sandwich cylindrical panel under non-uniform edge loads using semi-analytical approach. Compos Struct. 2022;280:114837.10.1016/j.compstruct.2021.114837Search in Google Scholar

[29] Sun X, Chi W, Luo J. Free vibration analysis of a graphene-platelet-reinforced, porous, two-cylindrical-panel system. Materials. 2022;15:6158.10.3390/ma15176158Search in Google Scholar PubMed PubMed Central

[30] Moradi-Dastjerdi R, Radhi A, Behdinan K. Damped dynamic behavior of an advanced piezoelectric sandwich plate. Compos Struct. 2020;243:112243.10.1016/j.compstruct.2020.112243Search in Google Scholar

[31] Shen H-S, Li C. Modeling and re-examination of nonlinear vibration and nonlinear bending of sandwich plates with porous FG-GPLRC core. Adv Eng Mater. 2023. 10.1002/adem.202300299.Search in Google Scholar

[32] Chen XH, Shen H-S, Xiang Y. Re-examination of thermo-mechanical buckling and postbuckling responses of sandwich plates with porous FG-GPLRC core. Thin-Walled Struct. 2023;187:110735.10.1016/j.tws.2023.110735Search in Google Scholar

[33] Simone AE, Gibson LJ. Effects of solid distribution on the stiffness and strength of metallic foams. Acta Mater. 1998;46:2139–50.10.1016/S1359-6454(97)00421-7Search in Google Scholar

[34] Roberts AP, Garboczi EJ. Elastic moduli of model random three dimensional closed-cell cellular solids. Acta Mater. 2001;49:189–97.10.1016/S1359-6454(00)00314-1Search in Google Scholar

[35] Halpin JC, Kardos JL. The Halpin-Tsai equations: A review. Polym Eng Sci. 1976;16:344–52.10.1002/pen.760160512Search in Google Scholar

[36] Shen H-S, Li C. Modeling and evaluation for large amplitude vibration and nonlinear bending of perovskite solar cell. Compos Struct. 2023;303:116235.10.1016/j.compstruct.2022.116235Search in Google Scholar

[37] Gibson LJ, Ashby MF. The mechanics of three-dimensional cellular materials. Proc R Soc Lond A. 1982;382:43–59.10.1098/rspa.1982.0088Search in Google Scholar

[38] Roberts A, Garboczi EJ. Computation of the linear elastic properties of random porous materials with a wide variety of microstructure. Proc R Soc Lond A. 2002;458:1033–54.10.1098/rspa.2001.0900Search in Google Scholar

[39] Mondal DP, Ramakrishnan N, Suresh KS, Das S. On the moduli of closed-cell aluminum foam. Scr Mater. 2007;57:929–32.10.1016/j.scriptamat.2007.07.021Search in Google Scholar

[40] Reddy JN, Liu CF. A higher-order shear deformation theory of laminated elastic shells. Int J Eng Sci. 1985;23:319–30.10.1016/0020-7225(85)90051-5Search in Google Scholar

[41] Shen H-S, Xiang Y. Nonlinear vibration of nanotube-reinforced composite cylindrical panels resting on elastic foundations in thermal environments. Compos Struct. 2014;111:291–300.10.1016/j.compstruct.2014.01.010Search in Google Scholar

[42] Schapery RA. Thermal expansion coefficients of composite materials based on energy principles. J Compos Mater. 1968;2:380–404.10.1177/002199836800200308Search in Google Scholar

[43] Shen H-S. A two-step perturbation method in nonlinear analysis of beams, plates and shells. Germany: John Wiley & Sons Inc; 2013.10.1002/9781118649893Search in Google Scholar

[44] Li Z-M, Zhao Y-X, Chen X-D. Non-linear buckling and postbuckling behavior of 3d braided cylindrical panels under axial compression in thermal environments. Mech Adv Mater Struct. 2014;21:490–504.10.1080/15376494.2012.699590Search in Google Scholar

[45] Sahmani S, Fattahi AM. Imperfection sensitivity of the size-dependent nonlinear instability of axially loaded FGM nanopanels in thermal environments. Acta Mech. 2017;228:3789–810.10.1007/s00707-017-1912-6Search in Google Scholar

[46] Zhao Y-X, Liu T, Li Z-M. Nonlinear bending analysis of a 3D braided composite cylindrical panel subjected to transverse loads in thermal environments. Chin J Aeron. 2018;31:1716–27.10.1016/j.cja.2018.03.022Search in Google Scholar

[47] Bayat MR, Mashhadi MM. Low-velocity impact response of sandwich cylindrical panels with nanotube-reinforced and metal face sheet in thermal environment. Aeronaut J. 2018;122:1943–66.10.1017/aer.2018.104Search in Google Scholar

[48] Babaei H, Kiani Y, Eslami MR. Application of two-steps perturbation technique to geometrically nonlinear analysis of long FGM cylindrical panels on elastic foundation under thermal load. J Therm Stress. 2018;41:847–65.10.1080/01495739.2017.1421054Search in Google Scholar

[49] Babaei H, Kiani Y, Eslami MR. Large amplitude free vibrations of long FGM cylindrical panels on nonlinear elastic foundation based on physical neutral surface. Compos Struct. 2019;220:888–98.10.1016/j.compstruct.2019.03.064Search in Google Scholar

[50] Ma W, Yang C, Ma D, Zhong JL. Low-velocity impact response of nanotube-reinforced composite sandwich curved panels. SADHANA-Acad Proc Eng Sci. 2019;44:227.10.1007/s12046-019-1214-xSearch in Google Scholar

[51] Babaei H, Eslami MR. Nonlinear analysis of thermal-mechanical coupling bending of FGP infinite length cylindrical panels based on PNS and NSGT. Appl Math Model. 2021;91:1061–80.10.1016/j.apm.2020.10.004Search in Google Scholar

[52] Babaei H. Thermomechanical analysis of snap-buckling phenomenon in long FG-CNTRC cylindrical panels resting on nonlinear elastic foundation. Compos Struct. 2022;286:115199.10.1016/j.compstruct.2022.115199Search in Google Scholar

[53] Shen H-S, Xiang Y, Fan Y, Hui D. Nonlinear vibration of functionally graded graphene-reinforced composite laminated cylindrical panels resting on elastic foundations in thermal environments. Compos Part B-Eng. 2018;136:177–86.10.1016/j.compositesb.2017.10.032Search in Google Scholar

[54] Shen H-S, Xiang Y, Fan Y, Hui D. Nonlinear bending analysis of FG-GRC laminated cylindrical panels on elastic foundations in thermal environments. Compos Part B-Eng. 2018;141:148–57.10.1016/j.compositesb.2017.12.048Search in Google Scholar

[55] Shen H-S, Xiang Y, Fan Y. Large amplitude vibration of doubly curved FG-GRC laminated panels in thermal environments. Nanotechnol Rev. 2019;8:467–83.10.1515/ntrev-2019-0042Search in Google Scholar

[56] Li X, Chen XC, Jiang WT. Dynamic stability of graded graphene reinforced truncated conical shells under both periodic spinning speeds and axial loads considering thermal effects. Eng Struct. 2022;256:113963.10.1016/j.engstruct.2022.113963Search in Google Scholar

[57] Xu Z, Huang Q. Vibro-acoustic analysis of functionally graded graphene-reinforced nanocomposite laminated plates under thermal-mechanical loads. Eng Struct. 2019;186:345–55.10.1016/j.engstruct.2019.01.137Search in Google Scholar

[58] Lin F, Xiang Y, Shen H-S. Temperature dependent mechanical properties of graphene reinforced polymer nanocomposites – A molecular dynamics simulation. Compos B-Eng. 2017;111:261–9.10.1016/j.compositesb.2016.12.004Search in Google Scholar

[59] Shen H-S, Xiang Y, Lin F. Nonlinear vibration of functionally graded graphene- reinforced composite laminated plates in thermal environments. Comput Methods Appl Mech Eng. 2017;319:175–93.10.1016/j.cma.2017.02.029Search in Google Scholar

[60] Rafiee MA, Rafiee J, Wang Z, Song H, Yu Z-Z, Koratkar N. Enhanced mechanical properties of nanocomposites at low graphene content. ACS Nano. 2009;3:3884–90.10.1021/nn9010472Search in Google Scholar PubMed

[61] Liu F, Ming P, Li J. Ab initio calculation of ideal strength and phonon instability of graphene under tension. Phys Rev B. 2007;76:064120.10.1103/PhysRevB.76.064120Search in Google Scholar

[62] Wu H, Drzal LT. Effect of graphene nanoplatelets on coefficient of thermal expansion of polyetherimide composite. Mater Chem Phys. 2014;146:26–36.10.1016/j.matchemphys.2014.02.038Search in Google Scholar

[63] Shen H-S, Wang H. Thermal postbuckling of functionally graded fiber reinforced composite cylindrical shells surrounded by an elastic medium. Compos Struct. 2013;102:250–60.10.1016/j.compstruct.2013.03.011Search in Google Scholar
Received: 2023-02-07
Revised: 2023-03-28
Accepted: 2023-04-04
Published Online: 2023-04-18

© 2023 the author(s), published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Research Articles
  2. Preparation of CdS–Ag2S nanocomposites by ultrasound-assisted UV photolysis treatment and its visible light photocatalysis activity
  3. Significance of nanoparticle radius and inter-particle spacing toward the radiative water-based alumina nanofluid flow over a rotating disk
  4. Aptamer-based detection of serotonin based on the rapid in situ synthesis of colorimetric gold nanoparticles
  5. Investigation of the nucleation and growth behavior of Ti2AlC and Ti3AlC nano-precipitates in TiAl alloys
  6. Dynamic recrystallization behavior and nucleation mechanism of dual-scale SiCp/A356 composites processed by P/M method
  7. High mechanical performance of 3-aminopropyl triethoxy silane/epoxy cured in a sandwich construction of 3D carbon felts foam and woven basalt fibers
  8. Applying solution of spray polyurea elastomer in asphalt binder: Feasibility analysis and DSR study based on the MSCR and LAS tests
  9. Study on the chronic toxicity and carcinogenicity of iron-based bioabsorbable stents
  10. Influence of microalloying with B on the microstructure and properties of brazed joints with Ag–Cu–Zn–Sn filler metal
  11. Thermohydraulic performance of thermal system integrated with twisted turbulator inserts using ternary hybrid nanofluids
  12. Study of mechanical properties of epoxy/graphene and epoxy/halloysite nanocomposites
  13. Effects of CaO addition on the CuW composite containing micro- and nano-sized tungsten particles synthesized via aluminothermic coupling with silicothermic reduction
  14. Cu and Al2O3-based hybrid nanofluid flow through a porous cavity
  15. Design of functional vancomycin-embedded bio-derived extracellular matrix hydrogels for repairing infectious bone defects
  16. Study on nanocrystalline coating prepared by electro-spraying 316L metal wire and its corrosion performance
  17. Axial compression performance of CFST columns reinforced by ultra-high-performance nano-concrete under long-term loading
  18. Tungsten trioxide nanocomposite for conventional soliton and noise-like pulse generation in anomalous dispersion laser cavity
  19. Microstructure and electrical contact behavior of the nano-yttria-modified Cu-Al2O3/30Mo/3SiC composite
  20. Melting rheology in thermally stratified graphene-mineral oil reservoir (third-grade nanofluid) with slip condition
  21. Re-examination of nonlinear vibration and nonlinear bending of porous sandwich cylindrical panels reinforced by graphene platelets
  22. Parametric simulation of hybrid nanofluid flow consisting of cobalt ferrite nanoparticles with second-order slip and variable viscosity over an extending surface
  23. Chitosan-capped silver nanoparticles with potent and selective intrinsic activity against the breast cancer cells
  24. Multi-core/shell SiO2@Al2O3 nanostructures deposited on Ti3AlC2 to enhance high-temperature stability and microwave absorption properties
  25. Solution-processed Bi2S3/BiVO4/TiO2 ternary heterojunction photoanode with enhanced photoelectrochemical performance
  26. Electroporation effect of ZnO nanoarrays under low voltage for water disinfection
  27. NIR-II window absorbing graphene oxide-coated gold nanorods and graphene quantum dot-coupled gold nanorods for photothermal cancer therapy
  28. Nonlinear three-dimensional stability characteristics of geometrically imperfect nanoshells under axial compression and surface residual stress
  29. Investigation of different nanoparticles properties on the thermal conductivity and viscosity of nanofluids by molecular dynamics simulation
  30. Optimized Cu2O-{100} facet for generation of different reactive oxidative species via peroxymonosulfate activation at specific pH values to efficient acetaminophen removal
  31. Brownian and thermal diffusivity impact due to the Maxwell nanofluid (graphene/engine oil) flow with motile microorganisms and Joule heating
  32. Appraising the dielectric properties and the effectiveness of electromagnetic shielding of graphene reinforced silicone rubber nanocomposite
  33. Synthesis of Ag and Cu nanoparticles by plasma discharge in inorganic salt solutions
  34. Low-cost and large-scale preparation of ultrafine TiO2@C hybrids for high-performance degradation of methyl orange and formaldehyde under visible light
  35. Utilization of waste glass with natural pozzolan in the production of self-glazed glass-ceramic materials
  36. Mechanical performance of date palm fiber-reinforced concrete modified with nano-activated carbon
  37. Melting point of dried gold nanoparticles prepared with ultrasonic spray pyrolysis and lyophilisation
  38. Graphene nanofibers: A modern approach towards tailored gypsum composites
  39. Role of localized magnetic field in vortex generation in tri-hybrid nanofluid flow: A numerical approach
  40. Intelligent computing for the double-diffusive peristaltic rheology of magneto couple stress nanomaterials
  41. Bioconvection transport of upper convected Maxwell nanoliquid with gyrotactic microorganism, nonlinear thermal radiation, and chemical reaction
  42. 3D printing of porous Ti6Al4V bone tissue engineering scaffold and surface anodization preparation of nanotubes to enhance its biological property
  43. Bioinspired ferromagnetic CoFe2O4 nanoparticles: Potential pharmaceutical and medical applications
  44. Significance of gyrotactic microorganisms on the MHD tangent hyperbolic nanofluid flow across an elastic slender surface: Numerical analysis
  45. Performance of polycarboxylate superplasticisers in seawater-blended cement: Effect from chemical structure and nano modification
  46. Entropy minimization of GO–Ag/KO cross-hybrid nanofluid over a convectively heated surface
  47. Oxygen plasma assisted room temperature bonding for manufacturing SU-8 polymer micro/nanoscale nozzle
  48. Performance and mechanism of CO2 reduction by DBD-coupled mesoporous SiO2
  49. Polyarylene ether nitrile dielectric films modified by HNTs@PDA hybrids for high-temperature resistant organic electronics field
  50. Exploration of generalized two-phase free convection magnetohydrodynamic flow of dusty tetra-hybrid Casson nanofluid between parallel microplates
  51. Hygrothermal bending analysis of sandwich nanoplates with FG porous core and piezomagnetic faces via nonlocal strain gradient theory
  52. Design and optimization of a TiO2/RGO-supported epoxy multilayer microwave absorber by the modified local best particle swarm optimization algorithm
  53. Mechanical properties and frost resistance of recycled brick aggregate concrete modified by nano-SiO2
  54. Self-template synthesis of hollow flower-like NiCo2O4 nanoparticles as an efficient bifunctional catalyst for oxygen reduction and oxygen evolution in alkaline media
  55. High-performance wearable flexible strain sensors based on an AgNWs/rGO/TPU electrospun nanofiber film for monitoring human activities
  56. High-performance lithium–selenium batteries enabled by nitrogen-doped porous carbon from peanut meal
  57. Investigating effects of Lorentz forces and convective heating on ternary hybrid nanofluid flow over a curved surface using homotopy analysis method
  58. Exploring the potential of biogenic magnesium oxide nanoparticles for cytotoxicity: In vitro and in silico studies on HCT116 and HT29 cells and DPPH radical scavenging
  59. Enhanced visible-light-driven photocatalytic degradation of azo dyes by heteroatom-doped nickel tungstate nanoparticles
  60. A facile method to synthesize nZVI-doped polypyrrole-based carbon nanotube for Ag(i) removal
  61. Improved osseointegration of dental titanium implants by TiO2 nanotube arrays with self-assembled recombinant IGF-1 in type 2 diabetes mellitus rat model
  62. Functionalized SWCNTs@Ag–TiO2 nanocomposites induce ROS-mediated apoptosis and autophagy in liver cancer cells
  63. Triboelectric nanogenerator based on a water droplet spring with a concave spherical surface for harvesting wave energy and detecting pressure
  64. A mathematical approach for modeling the blood flow containing nanoparticles by employing the Buongiorno’s model
  65. Molecular dynamics study on dynamic interlayer friction of graphene and its strain effect
  66. Induction of apoptosis and autophagy via regulation of AKT and JNK mitogen-activated protein kinase pathways in breast cancer cell lines exposed to gold nanoparticles loaded with TNF-α and combined with doxorubicin
  67. Effect of PVA fibers on durability of nano-SiO2-reinforced cement-based composites subjected to wet-thermal and chloride salt-coupled environment
  68. Effect of polyvinyl alcohol fibers on mechanical properties of nano-SiO2-reinforced geopolymer composites under a complex environment
  69. In vitro studies of titanium dioxide nanoparticles modified with glutathione as a potential drug delivery system
  70. Comparative investigations of Ag/H2O nanofluid and Ag-CuO/H2O hybrid nanofluid with Darcy-Forchheimer flow over a curved surface
  71. Study on deformation characteristics of multi-pass continuous drawing of micro copper wire based on crystal plasticity finite element method
  72. Properties of ultra-high-performance self-compacting fiber-reinforced concrete modified with nanomaterials
  73. Prediction of lap shear strength of GNP and TiO2/epoxy nanocomposite adhesives
  74. A novel exploration of how localized magnetic field affects vortex generation of trihybrid nanofluids
  75. Fabrication and physicochemical characterization of copper oxide–pyrrhotite nanocomposites for the cytotoxic effects on HepG2 cells and the mechanism
  76. Thermal radiative flow of cross nanofluid due to a stretched cylinder containing microorganisms
  77. In vitro study of the biphasic calcium phosphate/chitosan hybrid biomaterial scaffold fabricated via solvent casting and evaporation technique for bone regeneration
  78. Insights into the thermal characteristics and dynamics of stagnant blood conveying titanium oxide, alumina, and silver nanoparticles subject to Lorentz force and internal heating over a curved surface
  79. Effects of nano-SiO2 additives on carbon fiber-reinforced fly ash–slag geopolymer composites performance: Workability, mechanical properties, and microstructure
  80. Energy bandgap and thermal characteristics of non-Darcian MHD rotating hybridity nanofluid thin film flow: Nanotechnology application
  81. Green synthesis and characterization of ginger-extract-based oxali-palladium nanoparticles for colorectal cancer: Downregulation of REG4 and apoptosis induction
  82. Abnormal evolution of resistivity and microstructure of annealed Ag nanoparticles/Ag–Mo films
  83. Preparation of water-based dextran-coated Fe3O4 magnetic fluid for magnetic hyperthermia
  84. Statistical investigations and morphological aspects of cross-rheological material suspended in transportation of alumina, silica, titanium, and ethylene glycol via the Galerkin algorithm
  85. Effect of CNT film interleaves on the flexural properties and strength after impact of CFRP composites
  86. Self-assembled nanoscale entities: Preparative process optimization, payload release, and enhanced bioavailability of thymoquinone natural product
  87. Structure–mechanical property relationships of 3D-printed porous polydimethylsiloxane films
  88. Nonlinear thermal radiation and the slip effect on a 3D bioconvection flow of the Casson nanofluid in a rotating frame via a homotopy analysis mechanism
  89. Residual mechanical properties of concrete incorporated with nano supplementary cementitious materials exposed to elevated temperature
  90. Time-independent three-dimensional flow of a water-based hybrid nanofluid past a Riga plate with slips and convective conditions: A homotopic solution
  91. Lightweight and high-strength polyarylene ether nitrile-based composites for efficient electromagnetic interference shielding
  92. Review Articles
  93. Recycling waste sources into nanocomposites of graphene materials: Overview from an energy-focused perspective
  94. Hybrid nanofiller reinforcement in thermoset and biothermoset applications: A review
  95. Current state-of-the-art review of nanotechnology-based therapeutics for viral pandemics: Special attention to COVID-19
  96. Solid lipid nanoparticles for targeted natural and synthetic drugs delivery in high-incidence cancers, and other diseases: Roles of preparation methods, lipid composition, transitional stability, and release profiles in nanocarriers’ development
  97. Critical review on experimental and theoretical studies of elastic properties of wurtzite-structured ZnO nanowires
  98. Polyurea micro-/nano-capsule applications in construction industry: A review
  99. A comprehensive review and clinical guide to molecular and serological diagnostic tests and future development: In vitro diagnostic testing for COVID-19
  100. Recent advances in electrocatalytic oxidation of 5-hydroxymethylfurfural to 2,5-furandicarboxylic acid: Mechanism, catalyst, coupling system
  101. Research progress and prospect of silica-based polymer nanofluids in enhanced oil recovery
  102. Review of the pharmacokinetics of nanodrugs
  103. Engineered nanoflowers, nanotrees, nanostars, nanodendrites, and nanoleaves for biomedical applications
  104. Research progress of biopolymers combined with stem cells in the repair of intrauterine adhesions
  105. Progress in FEM modeling on mechanical and electromechanical properties of carbon nanotube cement-based composites
  106. Antifouling induced by surface wettability of poly(dimethyl siloxane) and its nanocomposites
  107. TiO2 aerogel composite high-efficiency photocatalysts for environmental treatment and hydrogen energy production
  108. Structural properties of alumina surfaces and their roles in the synthesis of environmentally persistent free radicals (EPFRs)
  109. Nanoparticles for the potential treatment of Alzheimer’s disease: A physiopathological approach
  110. Current status of synthesis and consolidation strategies for thermo-resistant nanoalloys and their general applications
  111. Recent research progress on the stimuli-responsive smart membrane: A review
  112. Dispersion of carbon nanotubes in aqueous cementitious materials: A review
  113. Applications of DNA tetrahedron nanostructure in cancer diagnosis and anticancer drugs delivery
  114. Magnetic nanoparticles in 3D-printed scaffolds for biomedical applications
  115. An overview of the synthesis of silicon carbide–boron carbide composite powders
  116. Organolead halide perovskites: Synthetic routes, structural features, and their potential in the development of photovoltaic
  117. Recent advancements in nanotechnology application on wood and bamboo materials: A review
  118. Application of aptamer-functionalized nanomaterials in molecular imaging of tumors
  119. Recent progress on corrosion mechanisms of graphene-reinforced metal matrix composites
  120. Research progress on preparation, modification, and application of phenolic aerogel
  121. Application of nanomaterials in early diagnosis of cancer
  122. Plant mediated-green synthesis of zinc oxide nanoparticles: An insight into biomedical applications
  123. Recent developments in terahertz quantum cascade lasers for practical applications
  124. Recent progress in dielectric/metal/dielectric electrodes for foldable light-emitting devices
  125. Nanocoatings for ballistic applications: A review
  126. A mini-review on MoS2 membrane for water desalination: Recent development and challenges
  127. Recent updates in nanotechnological advances for wound healing: A narrative review
  128. Recent advances in DNA nanomaterials for cancer diagnosis and treatment
  129. Electrochemical micro- and nanobiosensors for in vivo reactive oxygen/nitrogen species measurement in the brain
  130. Advances in organic–inorganic nanocomposites for cancer imaging and therapy
  131. Advancements in aluminum matrix composites reinforced with carbides and graphene: A comprehensive review
  132. Modification effects of nanosilica on asphalt binders: A review
  133. Decellularized extracellular matrix as a promising biomaterial for musculoskeletal tissue regeneration
  134. Review of the sol–gel method in preparing nano TiO2 for advanced oxidation process
  135. Micro/nano manufacturing aircraft surface with anti-icing and deicing performances: An overview
  136. Cell type-targeting nanoparticles in treating central nervous system diseases: Challenges and hopes
  137. An overview of hydrogen production from Al-based materials
  138. A review of application, modification, and prospect of melamine foam
  139. A review of the performance of fibre-reinforced composite laminates with carbon nanotubes
  140. Research on AFM tip-related nanofabrication of two-dimensional materials
  141. Advances in phase change building materials: An overview
  142. Development of graphene and graphene quantum dots toward biomedical engineering applications: A review
  143. Nanoremediation approaches for the mitigation of heavy metal contamination in vegetables: An overview
  144. Photodynamic therapy empowered by nanotechnology for oral and dental science: Progress and perspectives
  145. Biosynthesis of metal nanoparticles: Bioreduction and biomineralization
  146. Current diagnostic and therapeutic approaches for severe acute respiratory syndrome coronavirus-2 (SARS-COV-2) and the role of nanomaterial-based theragnosis in combating the pandemic
  147. Application of two-dimensional black phosphorus material in wound healing
  148. Special Issue on Advanced Nanomaterials and Composites for Energy Conversion and Storage - Part I
  149. Helical fluorinated carbon nanotubes/iron(iii) fluoride hybrid with multilevel transportation channels and rich active sites for lithium/fluorinated carbon primary battery
  150. The progress of cathode materials in aqueous zinc-ion batteries
  151. Special Issue on Advanced Nanomaterials for Carbon Capture, Environment and Utilization for Energy Sustainability - Part I
  152. Effect of polypropylene fiber and nano-silica on the compressive strength and frost resistance of recycled brick aggregate concrete
  153. Mechanochemical design of nanomaterials for catalytic applications with a benign-by-design focus
https://doi.org/10.1515/ntrev-2022-0544
Keywords for this article
porous material; graphene platelets; sandwich cylindrical panel; functionally graded; temperature-dependent
Creative Commons
BY 4.0

Articles in the same Issue

  1. Research Articles
  2. Preparation of CdS–Ag2S nanocomposites by ultrasound-assisted UV photolysis treatment and its visible light photocatalysis activity
  3. Significance of nanoparticle radius and inter-particle spacing toward the radiative water-based alumina nanofluid flow over a rotating disk
  4. Aptamer-based detection of serotonin based on the rapid in situ synthesis of colorimetric gold nanoparticles
  5. Investigation of the nucleation and growth behavior of Ti2AlC and Ti3AlC nano-precipitates in TiAl alloys
  6. Dynamic recrystallization behavior and nucleation mechanism of dual-scale SiCp/A356 composites processed by P/M method
  7. High mechanical performance of 3-aminopropyl triethoxy silane/epoxy cured in a sandwich construction of 3D carbon felts foam and woven basalt fibers
  8. Applying solution of spray polyurea elastomer in asphalt binder: Feasibility analysis and DSR study based on the MSCR and LAS tests
  9. Study on the chronic toxicity and carcinogenicity of iron-based bioabsorbable stents
  10. Influence of microalloying with B on the microstructure and properties of brazed joints with Ag–Cu–Zn–Sn filler metal
  11. Thermohydraulic performance of thermal system integrated with twisted turbulator inserts using ternary hybrid nanofluids
  12. Study of mechanical properties of epoxy/graphene and epoxy/halloysite nanocomposites
  13. Effects of CaO addition on the CuW composite containing micro- and nano-sized tungsten particles synthesized via aluminothermic coupling with silicothermic reduction
  14. Cu and Al2O3-based hybrid nanofluid flow through a porous cavity
  15. Design of functional vancomycin-embedded bio-derived extracellular matrix hydrogels for repairing infectious bone defects
  16. Study on nanocrystalline coating prepared by electro-spraying 316L metal wire and its corrosion performance
  17. Axial compression performance of CFST columns reinforced by ultra-high-performance nano-concrete under long-term loading
  18. Tungsten trioxide nanocomposite for conventional soliton and noise-like pulse generation in anomalous dispersion laser cavity
  19. Microstructure and electrical contact behavior of the nano-yttria-modified Cu-Al2O3/30Mo/3SiC composite
  20. Melting rheology in thermally stratified graphene-mineral oil reservoir (third-grade nanofluid) with slip condition
  21. Re-examination of nonlinear vibration and nonlinear bending of porous sandwich cylindrical panels reinforced by graphene platelets
  22. Parametric simulation of hybrid nanofluid flow consisting of cobalt ferrite nanoparticles with second-order slip and variable viscosity over an extending surface
  23. Chitosan-capped silver nanoparticles with potent and selective intrinsic activity against the breast cancer cells
  24. Multi-core/shell SiO2@Al2O3 nanostructures deposited on Ti3AlC2 to enhance high-temperature stability and microwave absorption properties
  25. Solution-processed Bi2S3/BiVO4/TiO2 ternary heterojunction photoanode with enhanced photoelectrochemical performance
  26. Electroporation effect of ZnO nanoarrays under low voltage for water disinfection
  27. NIR-II window absorbing graphene oxide-coated gold nanorods and graphene quantum dot-coupled gold nanorods for photothermal cancer therapy
  28. Nonlinear three-dimensional stability characteristics of geometrically imperfect nanoshells under axial compression and surface residual stress
  29. Investigation of different nanoparticles properties on the thermal conductivity and viscosity of nanofluids by molecular dynamics simulation
  30. Optimized Cu2O-{100} facet for generation of different reactive oxidative species via peroxymonosulfate activation at specific pH values to efficient acetaminophen removal
  31. Brownian and thermal diffusivity impact due to the Maxwell nanofluid (graphene/engine oil) flow with motile microorganisms and Joule heating
  32. Appraising the dielectric properties and the effectiveness of electromagnetic shielding of graphene reinforced silicone rubber nanocomposite
  33. Synthesis of Ag and Cu nanoparticles by plasma discharge in inorganic salt solutions
  34. Low-cost and large-scale preparation of ultrafine TiO2@C hybrids for high-performance degradation of methyl orange and formaldehyde under visible light
  35. Utilization of waste glass with natural pozzolan in the production of self-glazed glass-ceramic materials
  36. Mechanical performance of date palm fiber-reinforced concrete modified with nano-activated carbon
  37. Melting point of dried gold nanoparticles prepared with ultrasonic spray pyrolysis and lyophilisation
  38. Graphene nanofibers: A modern approach towards tailored gypsum composites
  39. Role of localized magnetic field in vortex generation in tri-hybrid nanofluid flow: A numerical approach
  40. Intelligent computing for the double-diffusive peristaltic rheology of magneto couple stress nanomaterials
  41. Bioconvection transport of upper convected Maxwell nanoliquid with gyrotactic microorganism, nonlinear thermal radiation, and chemical reaction
  42. 3D printing of porous Ti6Al4V bone tissue engineering scaffold and surface anodization preparation of nanotubes to enhance its biological property
  43. Bioinspired ferromagnetic CoFe2O4 nanoparticles: Potential pharmaceutical and medical applications
  44. Significance of gyrotactic microorganisms on the MHD tangent hyperbolic nanofluid flow across an elastic slender surface: Numerical analysis
  45. Performance of polycarboxylate superplasticisers in seawater-blended cement: Effect from chemical structure and nano modification
  46. Entropy minimization of GO–Ag/KO cross-hybrid nanofluid over a convectively heated surface
  47. Oxygen plasma assisted room temperature bonding for manufacturing SU-8 polymer micro/nanoscale nozzle
  48. Performance and mechanism of CO2 reduction by DBD-coupled mesoporous SiO2
  49. Polyarylene ether nitrile dielectric films modified by HNTs@PDA hybrids for high-temperature resistant organic electronics field
  50. Exploration of generalized two-phase free convection magnetohydrodynamic flow of dusty tetra-hybrid Casson nanofluid between parallel microplates
  51. Hygrothermal bending analysis of sandwich nanoplates with FG porous core and piezomagnetic faces via nonlocal strain gradient theory
  52. Design and optimization of a TiO2/RGO-supported epoxy multilayer microwave absorber by the modified local best particle swarm optimization algorithm
  53. Mechanical properties and frost resistance of recycled brick aggregate concrete modified by nano-SiO2
  54. Self-template synthesis of hollow flower-like NiCo2O4 nanoparticles as an efficient bifunctional catalyst for oxygen reduction and oxygen evolution in alkaline media
  55. High-performance wearable flexible strain sensors based on an AgNWs/rGO/TPU electrospun nanofiber film for monitoring human activities
  56. High-performance lithium–selenium batteries enabled by nitrogen-doped porous carbon from peanut meal
  57. Investigating effects of Lorentz forces and convective heating on ternary hybrid nanofluid flow over a curved surface using homotopy analysis method
  58. Exploring the potential of biogenic magnesium oxide nanoparticles for cytotoxicity: In vitro and in silico studies on HCT116 and HT29 cells and DPPH radical scavenging
  59. Enhanced visible-light-driven photocatalytic degradation of azo dyes by heteroatom-doped nickel tungstate nanoparticles
  60. A facile method to synthesize nZVI-doped polypyrrole-based carbon nanotube for Ag(i) removal
  61. Improved osseointegration of dental titanium implants by TiO2 nanotube arrays with self-assembled recombinant IGF-1 in type 2 diabetes mellitus rat model
  62. Functionalized SWCNTs@Ag–TiO2 nanocomposites induce ROS-mediated apoptosis and autophagy in liver cancer cells
  63. Triboelectric nanogenerator based on a water droplet spring with a concave spherical surface for harvesting wave energy and detecting pressure
  64. A mathematical approach for modeling the blood flow containing nanoparticles by employing the Buongiorno’s model
  65. Molecular dynamics study on dynamic interlayer friction of graphene and its strain effect
  66. Induction of apoptosis and autophagy via regulation of AKT and JNK mitogen-activated protein kinase pathways in breast cancer cell lines exposed to gold nanoparticles loaded with TNF-α and combined with doxorubicin
  67. Effect of PVA fibers on durability of nano-SiO2-reinforced cement-based composites subjected to wet-thermal and chloride salt-coupled environment
  68. Effect of polyvinyl alcohol fibers on mechanical properties of nano-SiO2-reinforced geopolymer composites under a complex environment
  69. In vitro studies of titanium dioxide nanoparticles modified with glutathione as a potential drug delivery system
  70. Comparative investigations of Ag/H2O nanofluid and Ag-CuO/H2O hybrid nanofluid with Darcy-Forchheimer flow over a curved surface
  71. Study on deformation characteristics of multi-pass continuous drawing of micro copper wire based on crystal plasticity finite element method
  72. Properties of ultra-high-performance self-compacting fiber-reinforced concrete modified with nanomaterials
  73. Prediction of lap shear strength of GNP and TiO2/epoxy nanocomposite adhesives
  74. A novel exploration of how localized magnetic field affects vortex generation of trihybrid nanofluids
  75. Fabrication and physicochemical characterization of copper oxide–pyrrhotite nanocomposites for the cytotoxic effects on HepG2 cells and the mechanism
  76. Thermal radiative flow of cross nanofluid due to a stretched cylinder containing microorganisms
  77. In vitro study of the biphasic calcium phosphate/chitosan hybrid biomaterial scaffold fabricated via solvent casting and evaporation technique for bone regeneration
  78. Insights into the thermal characteristics and dynamics of stagnant blood conveying titanium oxide, alumina, and silver nanoparticles subject to Lorentz force and internal heating over a curved surface
  79. Effects of nano-SiO2 additives on carbon fiber-reinforced fly ash–slag geopolymer composites performance: Workability, mechanical properties, and microstructure
  80. Energy bandgap and thermal characteristics of non-Darcian MHD rotating hybridity nanofluid thin film flow: Nanotechnology application
  81. Green synthesis and characterization of ginger-extract-based oxali-palladium nanoparticles for colorectal cancer: Downregulation of REG4 and apoptosis induction
  82. Abnormal evolution of resistivity and microstructure of annealed Ag nanoparticles/Ag–Mo films
  83. Preparation of water-based dextran-coated Fe3O4 magnetic fluid for magnetic hyperthermia
  84. Statistical investigations and morphological aspects of cross-rheological material suspended in transportation of alumina, silica, titanium, and ethylene glycol via the Galerkin algorithm
  85. Effect of CNT film interleaves on the flexural properties and strength after impact of CFRP composites
  86. Self-assembled nanoscale entities: Preparative process optimization, payload release, and enhanced bioavailability of thymoquinone natural product
  87. Structure–mechanical property relationships of 3D-printed porous polydimethylsiloxane films
  88. Nonlinear thermal radiation and the slip effect on a 3D bioconvection flow of the Casson nanofluid in a rotating frame via a homotopy analysis mechanism
  89. Residual mechanical properties of concrete incorporated with nano supplementary cementitious materials exposed to elevated temperature
  90. Time-independent three-dimensional flow of a water-based hybrid nanofluid past a Riga plate with slips and convective conditions: A homotopic solution
  91. Lightweight and high-strength polyarylene ether nitrile-based composites for efficient electromagnetic interference shielding
  92. Review Articles
  93. Recycling waste sources into nanocomposites of graphene materials: Overview from an energy-focused perspective
  94. Hybrid nanofiller reinforcement in thermoset and biothermoset applications: A review
  95. Current state-of-the-art review of nanotechnology-based therapeutics for viral pandemics: Special attention to COVID-19
  96. Solid lipid nanoparticles for targeted natural and synthetic drugs delivery in high-incidence cancers, and other diseases: Roles of preparation methods, lipid composition, transitional stability, and release profiles in nanocarriers’ development
  97. Critical review on experimental and theoretical studies of elastic properties of wurtzite-structured ZnO nanowires
  98. Polyurea micro-/nano-capsule applications in construction industry: A review
  99. A comprehensive review and clinical guide to molecular and serological diagnostic tests and future development: In vitro diagnostic testing for COVID-19
  100. Recent advances in electrocatalytic oxidation of 5-hydroxymethylfurfural to 2,5-furandicarboxylic acid: Mechanism, catalyst, coupling system
  101. Research progress and prospect of silica-based polymer nanofluids in enhanced oil recovery
  102. Review of the pharmacokinetics of nanodrugs
  103. Engineered nanoflowers, nanotrees, nanostars, nanodendrites, and nanoleaves for biomedical applications
  104. Research progress of biopolymers combined with stem cells in the repair of intrauterine adhesions
  105. Progress in FEM modeling on mechanical and electromechanical properties of carbon nanotube cement-based composites
  106. Antifouling induced by surface wettability of poly(dimethyl siloxane) and its nanocomposites
  107. TiO2 aerogel composite high-efficiency photocatalysts for environmental treatment and hydrogen energy production
  108. Structural properties of alumina surfaces and their roles in the synthesis of environmentally persistent free radicals (EPFRs)
  109. Nanoparticles for the potential treatment of Alzheimer’s disease: A physiopathological approach
  110. Current status of synthesis and consolidation strategies for thermo-resistant nanoalloys and their general applications
  111. Recent research progress on the stimuli-responsive smart membrane: A review
  112. Dispersion of carbon nanotubes in aqueous cementitious materials: A review
  113. Applications of DNA tetrahedron nanostructure in cancer diagnosis and anticancer drugs delivery
  114. Magnetic nanoparticles in 3D-printed scaffolds for biomedical applications
  115. An overview of the synthesis of silicon carbide–boron carbide composite powders
  116. Organolead halide perovskites: Synthetic routes, structural features, and their potential in the development of photovoltaic
  117. Recent advancements in nanotechnology application on wood and bamboo materials: A review
  118. Application of aptamer-functionalized nanomaterials in molecular imaging of tumors
  119. Recent progress on corrosion mechanisms of graphene-reinforced metal matrix composites
  120. Research progress on preparation, modification, and application of phenolic aerogel
  121. Application of nanomaterials in early diagnosis of cancer
  122. Plant mediated-green synthesis of zinc oxide nanoparticles: An insight into biomedical applications
  123. Recent developments in terahertz quantum cascade lasers for practical applications
  124. Recent progress in dielectric/metal/dielectric electrodes for foldable light-emitting devices
  125. Nanocoatings for ballistic applications: A review
  126. A mini-review on MoS2 membrane for water desalination: Recent development and challenges
  127. Recent updates in nanotechnological advances for wound healing: A narrative review
  128. Recent advances in DNA nanomaterials for cancer diagnosis and treatment
  129. Electrochemical micro- and nanobiosensors for in vivo reactive oxygen/nitrogen species measurement in the brain
  130. Advances in organic–inorganic nanocomposites for cancer imaging and therapy
  131. Advancements in aluminum matrix composites reinforced with carbides and graphene: A comprehensive review
  132. Modification effects of nanosilica on asphalt binders: A review
  133. Decellularized extracellular matrix as a promising biomaterial for musculoskeletal tissue regeneration
  134. Review of the sol–gel method in preparing nano TiO2 for advanced oxidation process
  135. Micro/nano manufacturing aircraft surface with anti-icing and deicing performances: An overview
  136. Cell type-targeting nanoparticles in treating central nervous system diseases: Challenges and hopes
  137. An overview of hydrogen production from Al-based materials
  138. A review of application, modification, and prospect of melamine foam
  139. A review of the performance of fibre-reinforced composite laminates with carbon nanotubes
  140. Research on AFM tip-related nanofabrication of two-dimensional materials
  141. Advances in phase change building materials: An overview
  142. Development of graphene and graphene quantum dots toward biomedical engineering applications: A review
  143. Nanoremediation approaches for the mitigation of heavy metal contamination in vegetables: An overview
  144. Photodynamic therapy empowered by nanotechnology for oral and dental science: Progress and perspectives
  145. Biosynthesis of metal nanoparticles: Bioreduction and biomineralization
  146. Current diagnostic and therapeutic approaches for severe acute respiratory syndrome coronavirus-2 (SARS-COV-2) and the role of nanomaterial-based theragnosis in combating the pandemic
  147. Application of two-dimensional black phosphorus material in wound healing
  148. Special Issue on Advanced Nanomaterials and Composites for Energy Conversion and Storage - Part I
  149. Helical fluorinated carbon nanotubes/iron(iii) fluoride hybrid with multilevel transportation channels and rich active sites for lithium/fluorinated carbon primary battery
  150. The progress of cathode materials in aqueous zinc-ion batteries
  151. Special Issue on Advanced Nanomaterials for Carbon Capture, Environment and Utilization for Energy Sustainability - Part I
  152. Effect of polypropylene fiber and nano-silica on the compressive strength and frost resistance of recycled brick aggregate concrete
  153. Mechanochemical design of nanomaterials for catalytic applications with a benign-by-design focus
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 27.12.2025 from https://www.degruyterbrill.com/document/doi/10.1515/ntrev-2022-0544/html
Scroll to top button