Optimization design and research of mechatronics based on torque motor control algorithm

Jun Ma

doi:10.1515/nleng-2025-0160

Artikel Open Access

Optimization design and research of mechatronics based on torque motor control algorithm

Jun Ma

Veröffentlicht/Copyright: 3. November 2025

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen

Aus der Zeitschrift Nonlinear Engineering Band 14 Heft 1

Abstract

The study proposes a torque motor control method based on the improved model predictive control algorithm, aiming to solve the core problems such as insufficient dynamic adaptability, weak anti-interference ability, and difficulty in multi-objective collaborative optimization in the traditional mechatronics optimization technology. Through the improved model predictive control algorithm in the torque motor control algorithm, the load is reasonably distributed and the status of mechatronics integration is monitored in real-time, thereby optimizing mechatronics integration. The results showed that the improved control algorithm performed significantly better than the other two algorithms in optimizing mechatronics technology. Under different external interference conditions, the improved algorithm had strong anti-interference ability and could optimize mechatronics technology without being affected by external interference factors. The optimization accuracy was always maintained within the range of 1.00–1.05. At 1.0032 min, the accuracy curve of the algorithm for optimizing mechatronics technology has already flattened. When comparing the optimization effects of the three algorithms, the improved algorithm maintained an optimization error value within the range of 0.00–0.01%, significantly lower than the optimization error values of other algorithms. Overall, the algorithm achieves high-precision real-time control and multi-objective collaborative optimization through rolling time-domain optimization and dynamic load allocation, providing theoretical support and technical paths for the efficient and stable operation of complex electromechanical systems.

Keywords: torque motor control algorithm; MPC algorithm; improved MPC algorithm; mechatronics integration; optimize accuracy

1 Introduction

The development of science and technology has promoted the integration of different engineering fields and propelled technological innovation and development [1,2]. Mechatronics technology, as a combination of mechanical technology and electronic information technology, integrates the advantages of both technologies and compensates for the shortcomings of two different technologies, making them high-tech [3]. This technology is a high-tech product built upon information processing technology, detection and sensing technology, and other advanced technologies. The emergence of mechatronics integration has made traditional single machinery and electronics as powerful as gods and has applied rapidly developing computers in the fields of machinery and electronics, improving work efficiency and greatly reducing application costs. In recent years, the optimization research of mechatronics technology has shown a diversified development trend. For instance, Kavianipour proposed a global optimization scheme, but its control strategy had insufficient adaptability to dynamic load changes [4]. Qu et al. designed an electromechanical-cyber-physical system based on the meta-modeling method. Although it could achieve a multi-disciplinary collaborative design, the real-time control accuracy was limited by the simplification error of the model [5]. Higgins et al. pointed out that the performance improvement of traditional electromechanical control algorithms was constrained by Moore’s Law, and it was urgent to combine the new predictive control framework to break through the optimization bottleneck under hardware limitations [6]. It was worth noting that most of the existing studies focused on a single performance index. Although Zhou et al. verified the feasibility of the electromechanical coupling behavior in the design of piezoelectric energy harvesters, they did not solve the stability problem in a strong interference environment [7]. The above research indicates that mechatronics technology has made progress in multiple fields, but its optimization methods still face challenges such as insufficient dynamic adaptability, difficulty in multi-objective coordination, and limited anti-interference ability. With the continuous progress of society, there is a higher demand for mechatronics technology. Although traditional methods can optimize mechatronics technology, they cannot achieve maximum optimization. To address this issue and improve the intelligence of mechatronics technology, this study introduces the Model predictive control (MPC) algorithm from the Torque motor control algorithm (TMCA) to optimize mechatronics technology and improve the MPC algorithm to enhance its performance advantages. Compared with traditional optimization algorithms, the application scope of mechatronics technology optimized by the MPC algorithm is wider, which can effectively improve the optimization effect and achieve the optimization of mechatronics technology.

The contribution of this study lies in the use of real-time monitoring technology, which not only optimizes the control accuracy of mechatronics systems but also improves the system’s responsiveness. Second, the improved MPC algorithm has stronger anti-interference ability, can operate stably under external interference, and the optimization accuracy is not affected. The error range is always kept within a very small range. Finally, by introducing an improved MPC algorithm, this study not only improves the accuracy and stability of mechatronics technology but also expands its application fields.

2 Related work

With the widespread use of mechatronics technology, the optimization of mechatronics has received extensive attention from many scholars. Yang et al. proposed a Mechatronics electro-hydraulic coupling system to improve the dynamic performance of vehicles during frequent start-stop cycles. They also established a rule-based dynamic management strategy for officials to control the dynamic switching of energy allocation and work modes. The use of this method could effectively improve the dynamic performance of vehicles during frequent starting and stopping, and enhance the overall efficiency of the motor operating point [8]. Zhong proposed a multi-sensor information fusion-based mechatronics technology to address the problem of insufficient noise reduction capability in fusion methods in mechatronics technology. This method performed fusion processing on the actual measured data of the sensor to eliminate duplicate information in the sliding window, which not only enhanced the noise reduction ability but also reduced the value of the error sequence [9]. Zhang et al. proposed a motor control system with a Proportional-Integral-Derivative (PID) controller algorithm as the core to improve the intelligent control system of mechatronics technology and realize the intelligent control application of mechatronics technology. This method had good anti-interference ability, good control effect and accuracy, and could effectively control the intelligent control system of motor integration technology [10]. Vazquez-Santacruz et al. proposed an integrated design method for mechatronic design problems. During the process, the model-driven systems engineering field is integrated into a three-dimensional cube model. Experiments showed that the proposed method could effectively manage multi-level information [11]. Wang et al. proposed a new type of rigid-flexible hybrid exoskeleton for the design of knee joint exoskeletons in mechatronics. By designing the walking intervention strategy and conducting experiments, the application effect of the exoskeleton in gait intervention was verified [12]. Brusa et al. proposed a configuration of a circular frame supporting a radial dual-die piezoelectric beam for the design problem of industrial piezoelectric vibration energy harvesters in mechatronics. The energy storage efficiency was evaluated through the integrated model of the electrical and mechanical systems, proving its feasibility in practical industrial applications [13]. Luo et al. proposed a manipulator for the design problem of cable-driven super-redundant manipulators in mechatronics. The proposed method improved the motion accuracy and the ability to adapt to complex environments. The experimental results verified its excellent flexibility and operability [14]. Hernando et al. proposed a fully integrated gesture robot hand ManoPla for the design problem of gesture communication robot hands in mechatronics. Elastic components were used in the design to achieve the flexibility of the joint, and the color gradient method was adopted to feedback the joint position. The Cutkosky grasping classification method was successfully reproduced, verifying its excellent flexibility and applicability [15].

The MPC algorithm in TMCA is increasingly being applied in various fields. Therefore, how to conduct deeper research on the MPC algorithm in TMCA has become a widely concerned research hotspot among industry scholars. Schwenzer et al. proposed the MPC algorithm to physically eliminate controlled obstacles to address the problem of optimization constraints that arise when predicting controlled systems. This method mainly solved the problem of constrained optimization by adjusting the controller [16]. Drgoňa et al. proposed the MPC algorithm to address the instability in building climate control environments to reduce energy use and mitigate greenhouse gas emissions. This method could effectively alleviate uncertainty [17]. Hewing et al. proposed the MPC algorithm to enhance the concept of learning-based controllers. This algorithm provided important opportunities for a large amount of data through constraint control, which could enhance the concept of learning controller while bringing the best closed-loop effect [18]. Guo et al. proposed a real-time Nonlinear model predictive control (NMPC) strategy to address the issue of inequality constraints that traditional algorithms cannot directly solve. The NMPC strategy transformed inequality constraint problems into equivalent constraint problems to verify the existence and uniqueness of the algorithm, which could ensure vehicle stability performance and solve inequality constraint problems [19]. Köhler et al. proposed a nonlinear robust MPC framework for general disturbances to ensure robust constraint satisfaction and practical asymptotic stability. This method mainly tightened nominal constraints by using an online constructed tube, which could efficiently ensure actual stability [20]. Luis et al. proposed a distributed MPC algorithm to avoid multiple robots colliding with obstacles during operation. This method could calculate non-collision trajectories during excessive tasks and could identify an average of 50% of obstacles that the robot encounters during motion [21].

Although existing studies have proposed a variety of algorithms and control strategies in the field of mechatronics optimization, different practical norms still have significant limitations. For example, although the integrated design method can achieve multi-level information management, its computational complexity is relatively high and it is difficult to meet the requirements of real-time monitoring and dynamic optimization. In addition, existing MPC algorithms have advantages in constraint handling and prediction capabilities. However, the inherent defect of the terminal error term in its optimization function leads to insufficient accuracy and a significant decrease in stability in strong interference environments. It is worth noting that the current research in the field of mechatronics optimization mostly focuses on a single performance index, lacking systematic solutions for multi-objective collaborative optimization. The above limitations indicate an urgent need for a control algorithm that balances high precision and strong anti-interference ability to solve the optimization challenges of mechatronics integration in complex dynamic environments.

3 TMCA optimization for mechatronics integration

3.1 TMCA based on improved MPC

Mechatronics technology has been widely applied in various fields. However, due to the inability of traditional algorithms to achieve high-precision control of mechatronics and their low performance in mechatronics control, this study introduces the MPC algorithm from TMCA to improve mechatronics technology. The MPC algorithm has the advantages of handling multiple variables, handling constraint conditions, and predicting system behavior, which can be used to improve the accuracy and performance of electromechanical control. The MPC algorithm mainly predicts the motor state over a period of time by using the dynamic mathematical model of the motor for prediction and improves the performance of motor control based on the calculated optimal control signal [22,23]. Figure 1 shows the structure of the MPC algorithm.

Figure 1

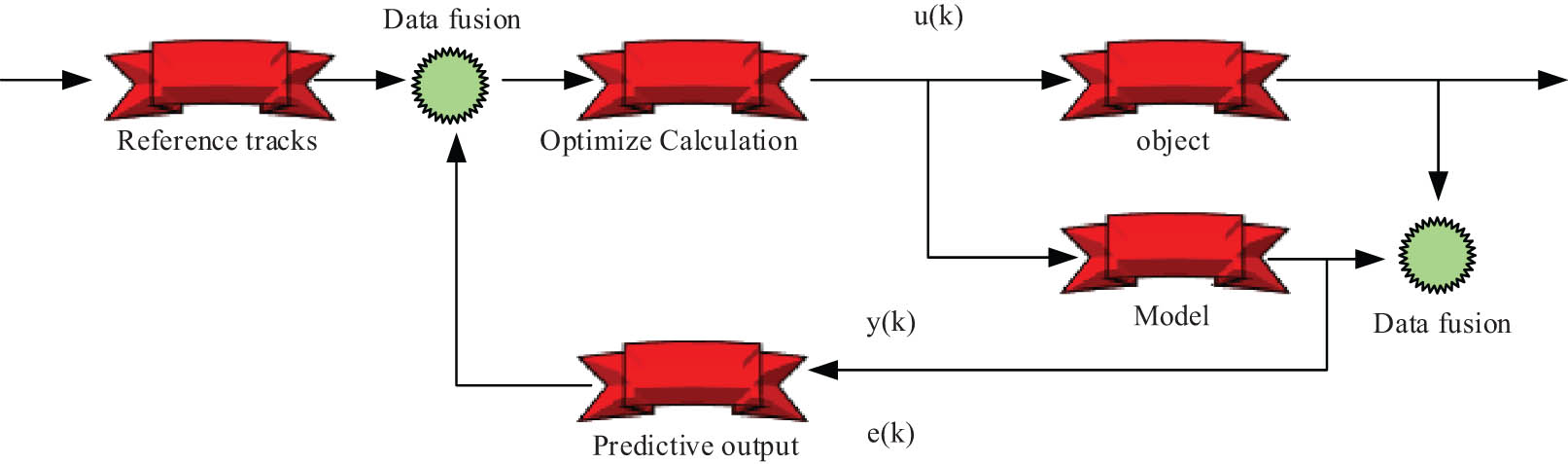
MPC algorithm structure for mechatronics integration optimization.

In Figure 1, the structure of the MPC algorithm primarily consists of three key elements: model prediction, rolling optimization, and feedback correction. By integrating these elements, a complete control loop is formed. u ( k ) represents the control quantity. e ( k ) represents the error quantity. y ( k ) represents the model feedback quantity. The model predicts future system behavior to improve mechatronics integration, with the state equation derived through linear control methods. The system uses this predictive framework to iteratively optimize control actions, ensuring optimal performance despite changing conditions. The model predicts an improvement to mechatronics integration, and the state equation is obtained using linear control method, as shown in Eq. (1).

(1) X ̇ = A X + B ( u ⌢ − K p X ⌢ − K i z ) ,

where both K i and K p represent sub-matrixes of matrix K . The process of discretizing the state equation in Eq. (1) is detailed in Eq. (2).

(2) x k + 1 = A x k + Bu k y k = C x k .

After discretizing the state equation, an optimization function is constructed based on the state space at time k + 1, as shown in Eq. (3).

(3) min J = E ( k + N ∣ k ) T F E ( k + N ∣ k ) + ∑ i = 0 N − 1 [ E ( K + i ∣ k ) T Q E ( k + N ∣ k ) + u ( k + N ∣ k ) T Ru ( k + N ∣ k ) ] ,

where E is the error between the reference values. ( K + i ∣ k ) is the step size at K . The goal of Eq. (3) is to minimize a function that includes errors and control costs. In short, it optimizes the control input by calculating the error between the reference value and the current state, as well as the penalty on the system control signal. In this process, the control strategy is iteratively updated to get closer to the optimal control signal, so that the system can be controlled optimally in the future. The specific expression for converting the optimization problem in Eq. (3) into a quadratic programming problem is shown in Eq. (4).

(4) min 1 2 Z T Q Z + C T Z .

By gradually calculating the discrete state equation at each step of the prediction, the state variables at time K are obtained, as shown in Eq. (5).

(5) x ( k + N ∣ k ) = A N x k + A N − 1 Bu ( k ∣ k ) + ⋯ + Bu ( k + N − 1 ∣ k ) ,

where N is the prediction step size at time K . If the state variables at all times are placed in the same matrix, then the matrix is shown in Eq. (6).

(6) X k = I A A 2 ⋮ A N x k + 0 0 ⋯ 0 B 0 ⋯ 0 A B B ⋯ 0 ⋮ ⋮ ⋮ ⋮ A N − 1 B A N − 2 B ⋯ B u ( k ∣ k ) u ( k + 1 ∣ k ) ⋮ u ( k + N − 1 ∣ k ) ,

where X k is the synthesis matrix and U k is the control quantity matrix. The comprehensive matrix is introduced into the optimization function to obtain a new coefficient matrix, which is shown in Eq. (7).

(7) M = C I C A C A 2 ⋮ C A N , G _ = 0 0 ⋯ 0 C B 0 ⋯ 0 C A B C B ⋯ 0 ⋮ ⋮ ⋮ ⋮ C A N − 1 B C A N − 2 B ⋯ C B ,

where M and G are new coefficient matrices. When only the control variables are retained in the coefficient matrix, a new optimization function will be obtained, as shown in Eq. (8).

(8) min J = ( M x k − Y k + G U k ) T Q ( M x k − Y k + G U k ) + U k T R U k = 2 ( M x k − Y k ) T T U k + U k T H U k .

Eq. (8) aims to optimize electromechanical technology by minimizing errors and energy consumption in control systems. The coefficient matrix of the control system reflects the dynamic characteristics and control variables of the system. By adjusting the parameters in these matrices, the performance of the system can be optimized, especially in the control algorithms of electromechanical systems. By comparing the optimization effects of the above two optimization functions on mechatronics technology, the optimization ability of the MPC algorithm controller for mechatronics technology is analyzed, and the optimization of the algorithm for mechatronics technology is achieved. Figure 2 shows the process of optimizing mechatronics technology using the MPC algorithm.

Figure 2

Structure diagram of MPC algorithm optimization for mechatronics integration technology.

Figure 2 shows the optimized process structure of mechatronics technology based on the MPC algorithm. The core contribution of this diagram lies in systematically integrating the rolling optimization and feedback correction mechanism of MPC into the entire process of mechatronics optimization, which is specifically divided into four key stages. Parameter optimization and path planning: Through the condition controller and control object of mechatronics technology, the system parameters are dynamically adjusted and the optimized path is planned based on the real-time status. This step ensures the dynamic matching of the initial parameters with the target task, providing a foundation for the subsequent model construction. The construction of the optimization model establishes a multi-objective optimization model of mechatronics technology based on the planned path, covering indicators such as dynamic response, energy consumption efficiency, and anti-interference ability. The optimization model is combined with the MPC algorithm to form a closed-loop control framework. The process design highlights the core advantages of the MPC algorithm in mechatronics technology: through the dynamic collaboration of model prediction and real-time feedback, it provides a theoretical framework for the subsequent improvement of the MPC algorithm. The above optimization of mechatronics technology using the MPC method has a terminal position error term and low optimization accuracy in its optimization function. To reduce errors and improve the optimization accuracy of mechatronics technology, this study improves the MPC algorithm by first establishing a new optimization function. The expression of this function is shown in Eq. (9).

(9) min J = ∑ i = 0 i = N − 1 u ( k + i ∣ k ) T Ru ( k + i ∣ k ) + E ( K + N ∣ k ) T F E ( k + N ∣ k ) .

Then, Eq. (9) is transformed to obtain Eq. (10).

(10) M = C A N G = [ C A N − 1 B , C A N − 2 B , ⋯ , C B ] .

Eq. (10) is the transformed coefficient matrix. Eq. (10) represents the optimization of the control process by transforming the original coefficient matrix of the system. In this process, the matrix is restructured so that MPC can be performed more efficiently. The purpose is to obtain more appropriate control parameters through optimization calculation, so that the behavior of the system is more stable and accurate. After improving the optimization function, a new coefficient matrix is obtained, as shown in Eq. (11).

(11) Q I = F , R I = R 0 0 0 0 R 0 0 0 0 ⋱ 0 0 0 0 R ,

where Q I and R I are the improved optimization functions, which are transformed into a new coefficient matrix.

When the optimization function optimizes mechatronics, it is necessary to constrain the control variables, and the constraint formula is shown in Eq. (12).

(12) { δ ≤ k ⋅ δ stall ,

where δ represents the actual control input quantity. k represents the proportional coefficient of thrust to stall speed. δ stall represents the theoretical thrust value corresponding to the stall speed. After optimizing the functions of the MPC algorithm as described above, an improved MPC algorithm is obtained, and its structure is shown in Figure 3.

Figure 3

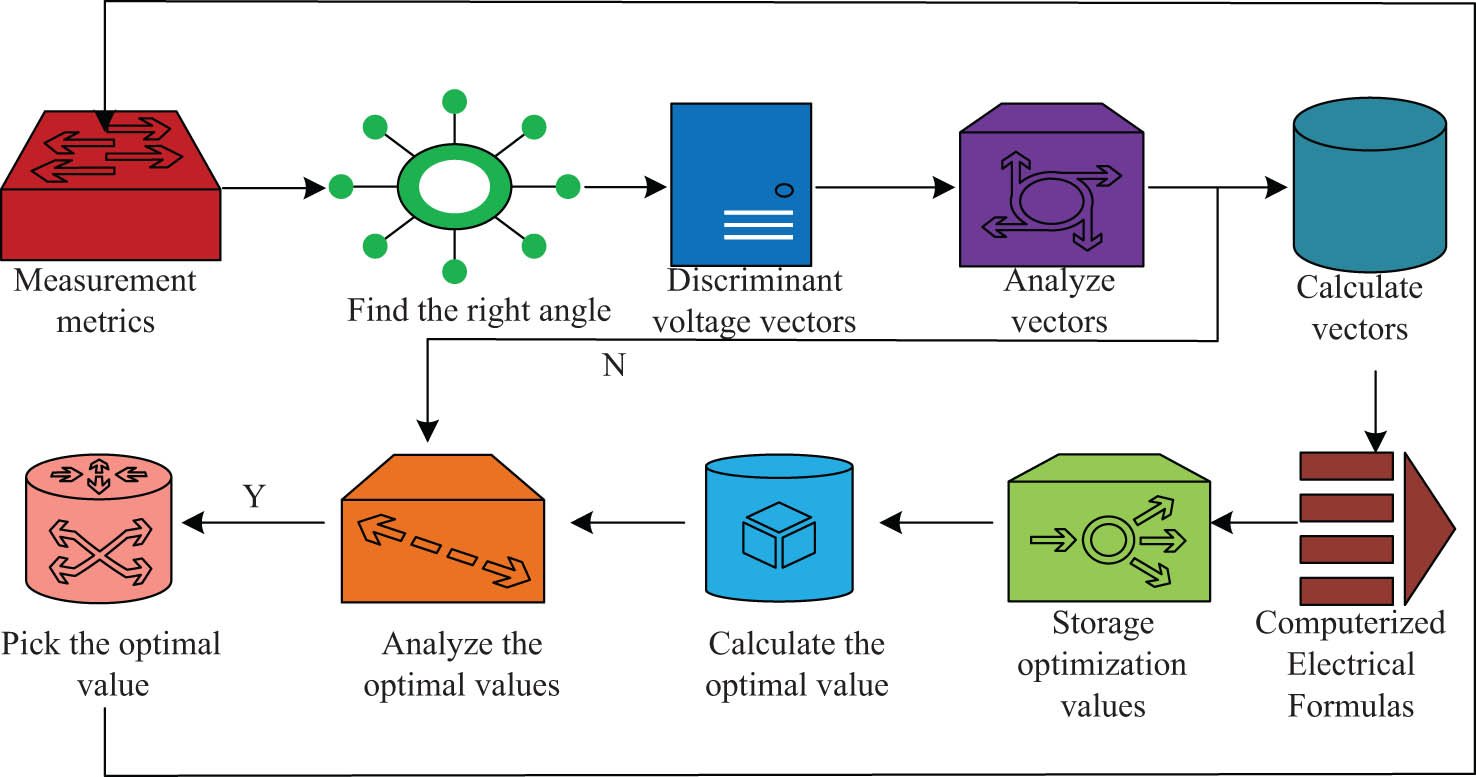
Structure of the improved MPC algorithm.

In Figure 3, the improved MPC algorithm first measures the vector of mechatronics technology through a measuring device, obtains the formula for vector angle, and determines whether the obtained voltage vector corresponds to the vector value of mechatronics technology. If it is not the corresponding vector value, it will be eliminated. If it is the corresponding vector value, the vector value will be analyzed. The analyzed vector value is considered as the optimal storage quality, and the optimized value obtained from the calculation is analyzed. The final step is to select the optimal value that best fits the mechatronics technology.

3.2 Implementing mechatronics integration based on improved MPC algorithm

Mechatronics technology is mainly a technology that combines mechanics and microelectronics by processing information and controlling mechanical devices. This study utilizes an improved MPC algorithm to optimize the technology. The basic system composition of mechatronics technology is shown in Figure 4.

Figure 4

Mechatronics AC torque motor system structure diagram.

In Figure 4, the structure is mainly composed of regulators, and the feedback element in the structure is used as a tension sensor. The main function of tension sensors is a key component in the application and implementation of mechatronics technology. In the process of improving mechatronics technology, the MPC algorithm in TMCA is mainly used to monitor the real-time status of mechatronics and optimize load distribution. The improved MPC algorithm in TMCA mainly achieves real-time monitoring of the state of mechatronics integration through the linearity between the actual output and input quantities [24,25]. To reflect the degree of linearity, the first step is to calculate the linearity, as shown in Eq. (13).

(13) F k = ∣ k c ∣ r f × 100% ,

where k c is the maximum difference and r f is the output signal quantity. Next step is to calculate the sensitivity change in the sensor using Eq. (14).

(14) l ( x ) = Δ y Δ x ,

where l ( x ) is the change amount, Δ y is the output change amount, and Δ x is the input change amount. Then, the hysteresis degree of the sensor is calculated based on the input signal obtained, and the formula is shown in Eq. (15).

(15) F h = Δ h max r f × 100 % ,

where Δ h max is the maximum value of hysteresis and F h is the degree of hysteresis. Finally, to ensure the accuracy of the monitoring data, the degree of repetition between the output and input curves is calculated, as shown in Eq. (16).

(16) F R = ∣ R ∣ r f × 100 % ,

where R is the oscillation monitoring measurement and F R is the degree of repetition. Real-time monitoring of mechatronics technology through the above operations can achieve optimization of mechatronics technology. To reduce the excessive consumption of energy and load in the process of optimizing mechatronics technology, this study optimizes load distribution to achieve reasonable load distribution. First, load allocation conditions are set and the objective function for allocation optimization is constructed, as shown in Eq. (17).

(17) f ( β , s ) = 1 γ ( β , s ) ,

where β is the load rate, s is the total negative charge rate, and γ ( ⋅ ) is the weighted efficiency function. In Eq. (17), the goal of load distribution is to rationally distribute the load in the system to optimize the working efficiency of mechatronic technology. By setting the load rate, the total load change rate of the load and the weighted efficiency function, the formula evaluates how to distribute the load efficiently to ensure the optimization of the whole system. The extremum of the weighted efficiency function is solved by the second derivative method, and the optimal load distribution scheme is determined. This process helps reduce energy consumption and improve the overall performance of the system. Then, the second derivative of the weighted function is solved using the extremum points in the objective function. The specific calculation process is shown in Eq. (18).

(18) r ( θ ) = v 1 θ + v 2 θ 2 ≥ 0 θ ≥ 0 v 1 θ + v 2 θ ≥ 0 ,

where θ is the load quantity. v 1 and v 2 are the second derivatives. Finally, the maximum and minimum values of the weighting function are solved using the second derivative, as shown in Eq. (19).

(19) max γ ˜ t = γ s n min P ˜ t = λ n 1 γ s ,

where λ is the ideal power in mechatronics technology. The maximum and minimum values of the weighting function obtained through a second-order function achieve the rational allocation of load. Combined with the improved MPC algorithm in TMCA for real-time monitoring of mechatronics technology, the optimization of mechatronics technology is ultimately achieved. The specific process of optimizing mechatronics integration using the improved MPC algorithm in TMCA is shown in Figure 5.

Figure 5

The optimization process of the improved MPC algorithm for mechatronics technology.

In Figure 5, the improved MPC algorithm first constructs an initial search graph (where each edge can be explored by sensors), and then initializes the search graph. Then, the initialized target area is explored through sensors to determine whether it meets the requirements of the task point. If it is not met, return to the third step. If it is met, the sensor’s next roadmap is planned based on the detection results. The sensor continues to explore according to the roadmap, determining whether a target has been found. If a target has been found, the feasibility of the target is analyzed. Finally, the algorithm is used to find the target position and optimize the mechatronics integration. If the target is not found, return to step three to continue searching for the target location.

4 Performance analysis of improved algorithms and effect analysis of mechatronics technology

4.1 Performance analysis of improved MPC algorithm

To verify that the improved MPC algorithm in TMCA can effectively optimize mechatronics technology, this study will analyze the performance advantages of the improved MPC algorithm. By introducing two commonly used algorithms for optimizing mechatronics technology, the optimization advantages of the three algorithms on mechatronics technology are compared under different conditions to demonstrate the effectiveness of the improved MPC algorithm in TMCA.

To verify the application effect of the improved MPC algorithm in mechatronics optimization, this study conducts simulation experiments using MATLAB R2023a. The mechatronic system model used in the experiment is based on an AC torque motor, with the following model parameters: motor inertia of 0.01 kg m², motor constant of 0.5 N m/A, and damping coefficient of 0.02 N m s. The control system’s sampling time is set to 0.01 s, with a prediction horizon of 30 steps and an optimization horizon of 10 steps. The selection of experimental parameters in the research is based on the analysis of the dynamic characteristics of the electromechanical system and the practical verification in the existing literature. Specifically, the setting of the motor’s inertia and damping coefficient refers to the nominal parameter range of a typical AC torque motor. The sampling time of the control system is determined by the Nyquist sampling theorem to ensure the effective capture of the motor speed while taking into account the requirements of real-time computing. The selection of the prediction step size and the optimization step size is based on the stability criterion of the model’s predictive control, aiming to balance the computational complexity and prediction accuracy. In addition, the monitoring range of key parameters such as load current and temperature is based on the definition of safety thresholds for electromechanical systems in IEEE standards to avoid overload risks. Experimental data are collected using virtual sensors that simulate key parameters such as motor speed, load current, and temperature. All experimental data are filtered using MATLAB’s Signal Processing Toolbox to eliminate high-frequency noise. To evaluate the algorithm’s performance, the experimental data include motor speed response, optimization error, and energy consumption. The data are collected under various interference conditions and repeated multiple times to ensure reliability and stability. To better highlight the improved MPC algorithm’s ability to enhance the efficiency of mechatronics technology, this study compares and analyzes the performance of three algorithms in optimizing mechatronics technology. Figure 6 shows the performance analysis results of three algorithms.

Figure 6

Comparison of the performance of different algorithms in optimizing mechatronics. (a) SVM algorithm, (b) PID algorithm, and (c) improved MPC algorithm.

In Figure 6(a), the Support vector machine (SVM) algorithm shows a large fluctuation in current when optimizing the motor, and the maximum current value exceeds 0.2 A, indicating poor performance of the algorithm. In Figure 6(b), during motor optimization, although the fluctuation amplitude of the PID algorithm’s current is slightly smoother than that of the SVM algorithm, its amplitude is far less than that of the MPC algorithm’s fluctuation amplitude, and the current value is in the range of −0.1 to 0.2 A. In Figure 6(c), the improved MPC algorithm did not show significant fluctuations in the current value during motor optimization, and the current value remained below 0.1 A, with the maximum current value not exceeding 0.1 A. The significant advantage of the improved MPC algorithm in current control stems from its core mechanism of model prediction and rolling optimization. The improved MPC dynamically updates the system model and introduces multi-step prediction, which can more accurately predict the impact of load fluctuations and external disturbances. Hence, anti-interference control strategies can be generated in advance to suppress instantaneous fluctuations in current.

To have a more comprehensive and accurate understanding of the optimization effects of the three algorithms on mechatronics integration, the study compares the errors that occurred during the optimization process of the three algorithms. The error variation results are shown in Figure 7.

Figure 7

Error results of the three algorithms in optimizing the motor.

In Figure 7, the improved MPC algorithm has a small fluctuation in error value during the optimization process, and the maximum error value is only 0.09%. This indicates that the algorithm does not show significant deviations in optimizing electromechanical systems, and the optimization effect is positive. The SVM algorithm and PID algorithm exhibit the maximum error value in the 0–2 s interval during the optimization process, and their average error values are significantly higher than that of the MPC algorithm during the optimization process. The fluctuation amplitude of the errors in both algorithms is relatively large. The improved MPC algorithm has significantly lower error values than the other two algorithms in optimizing mechatronics technology, verifying its excellent optimization performance. Afterwards, to verify the effectiveness of the improved MPC algorithm, this study will analyze the effect of changing the three parameters of time t, predicted time domain ph, and optimized time domain ch in the improved MPC algorithm on the optimization of mechatronics integration. Figure 8 shows a comparison of optimization effects.

Figure 8

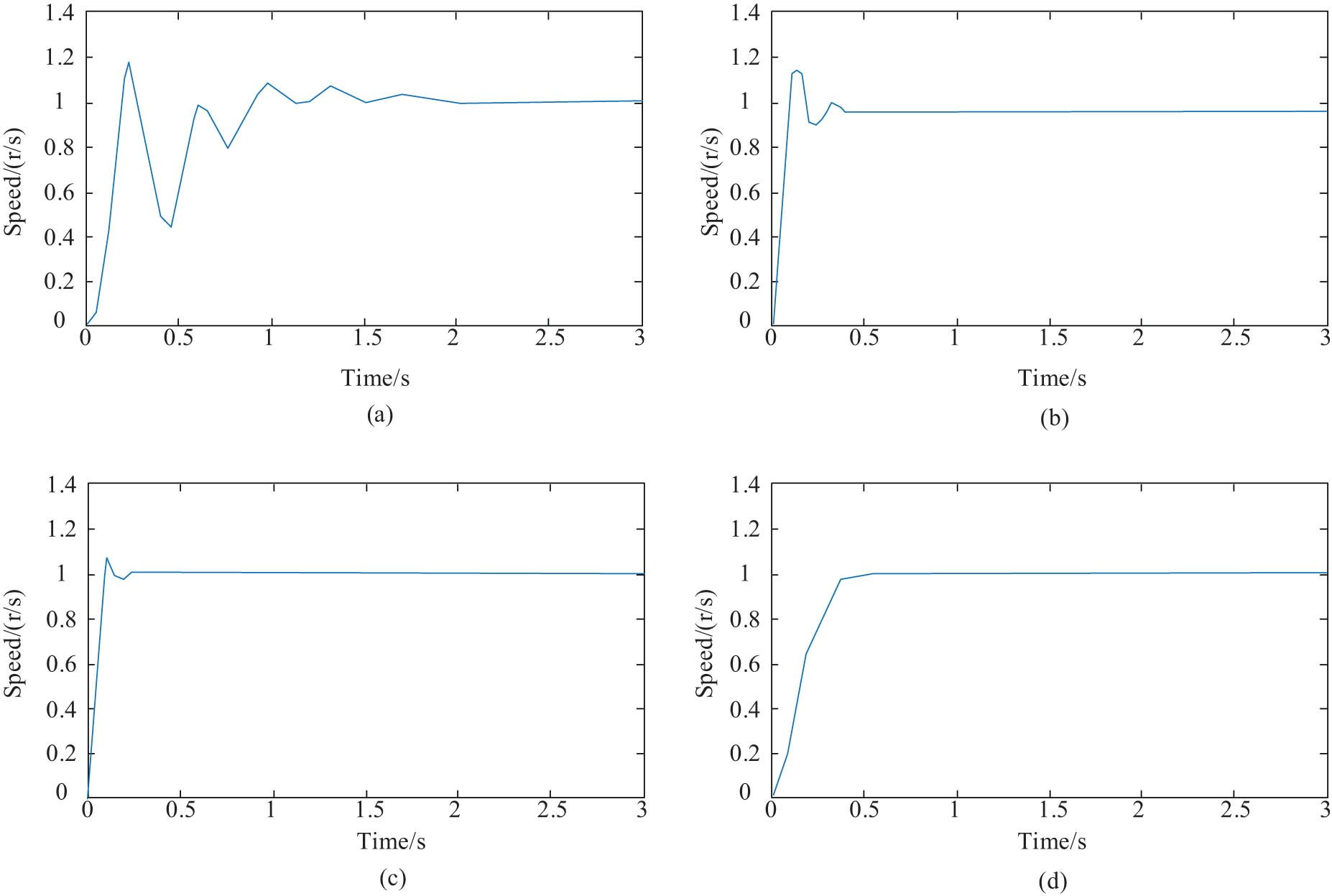
Results of the improved MPC algorithm for optimizing the mechatronics technology when the parameters change. (a) Optimized curve when t = 0.2, ph = 60, and ch = 2; (b) optimized curve when t = 0.0002, ph = 15, and ch = 2; (c) optimized curve when t = 0.006, ph = 60, and ch = 13; and (d) optimized curve when t = 0.003, ph = 60, and ch = 2.

In Figure 8(a), when t = 0.2, ph = 60, and ch = 2, there is a slight fluctuation in the optimization speed of the improved MPC algorithm. In Figure 8(b), when t = 0.0002, ph = 15, and ch = 2, the fluctuation amplitude of the optimization speed is relatively gentle. In Figure 8(d), when t = 0.003, ph = 60, and ch = 2, the fluctuation amplitude of the optimization speed is relatively smooth. In Figure 8(c), when t = 0.006, ph = 60, and ch = 13, the search speed is fast and there is no significant fluctuation. The improved MPC algorithm has better optimization effects on mechatronics technology in (a), (b), and (d), and is optimal in the numerical value of (c). In summary, the improved MPC algorithm does not show significant fluctuations in the optimization effect of mechatronics technology under constantly changing parameters, and the effectiveness of the algorithm is verified.

4.2 Analysis of the application effect of mechatronics technology based on improved MPC algorithm

To verify the application effect of the mechatronics technology based on the improved MPC algorithm, this study adopts the kappa statistical value to measure the practical application effect of this technology. The integral of the statistics corresponding to the shaded area within the time interval [0,45] minutes is shown in Figure 9.

Figure 9

Optimization capability test results.

In Figure 9, with the continuous increase in time, the kappa value curve of this technology shows a rapid upward trend and then shows a slow growth trend after reaching a certain value. When the optimization time is within the interval of 0–4 min, the kappa value curve always tends to rise linearly, with a maximum value of 0.6. After 4.1 min, the value curve shows a slow growth trend. The future output numerical satisfaction of the optimized mechatronics technology is high, and it can effectively improve the application effect. This study introduces two commonly used algorithms for optimizing mechatronics technology and compares the application effects of the three algorithms on the optimized mechatronics technology under two conditions: without external interference and with external interference. The application effect is shown in Figure 10.

Figure 10

Comparison of the stability of the three algorithms under different conditions. (a) There is no interference conditions and (b) with interference conditions.

In Figure 10(a), under the condition of not receiving external interference, when using the SVM algorithm to optimize mechatronics, the curve fluctuation amplitude of its application effect is relatively large, indicating that the stability characteristics of this method are poor. When using the improved MPC algorithm to optimize the motor, the fluctuation amplitude of its application effect curve is relatively small, and it tends to flatten out at 1.0032 min. The other two algorithms both tend to flatten out at 1.0057 min. This indicates that using the improved MPC algorithm to optimize mechatronics technology has a better application effect, and the application effect is significantly higher than the other two algorithms. In Figure 10(b), when the improved MPC algorithm is used to optimize the motor under external interference, the application effect curve of this technology tends to be a smooth straight line without significant fluctuations. Its fluctuation amplitude always remains within the range of 1.00∼1.05. When using other algorithms for optimization, the curve fluctuates within the range of 0.94–1.25. The fluctuation amplitude of the improved MPC algorithm is significantly lower than the other two algorithms, indicating that the use of the MPC algorithm can effectively improve the stability of motor applications.

To demonstrate that the improved MPC algorithm has shown good application results in optimizing mechatronics technology under different conditions, this study sets the click start time to be the same and compares the application effects of different algorithm optimized mechatronics technology. The result changes are shown in Figure 11.

Figure 11

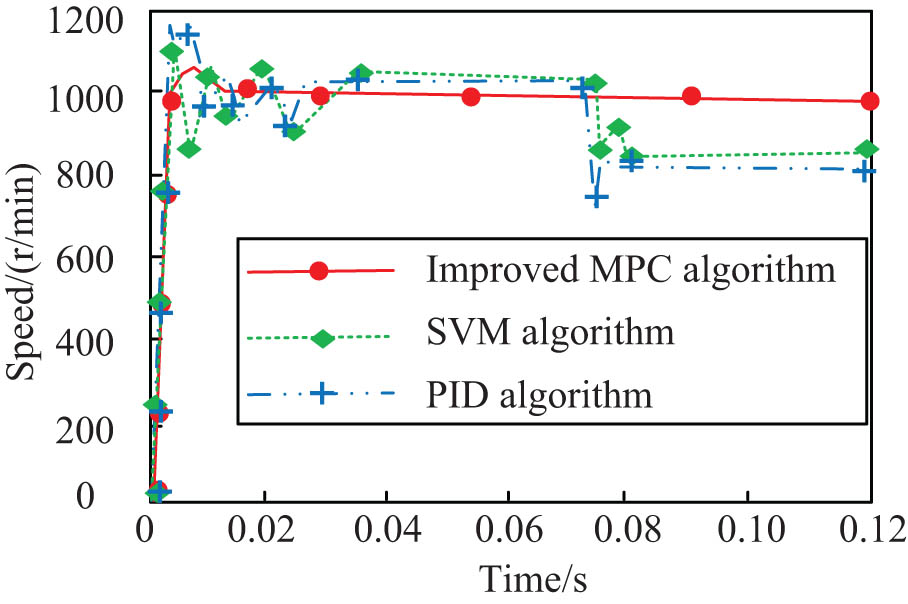
Motor speed curves of the three algorithms.

In Figure 11, when the starting time of the motor is the same, the improved MPC algorithm optimizes the motor at the fastest speed to seek the optimal point, and finds the optimal point of the motor in a shorter time. The motor speed begins to flatten out at 0.01 s without significant fluctuations. SVM and PID both exhibit significant fluctuations when seeking the optimal point of the motor, and both tend to flatten out in the range of 0.06–0.08 s, which is significantly longer than the time for the improved MPC to flatten out. This indicates that the application effect of the two algorithms in optimizing motors is poor. The results indicate that the improved MPC can quickly find the optimal point in the motor optimization process. Moreover, the stability of this algorithm is significantly better than other algorithms, which verifies that using this algorithm can achieve better results. Under the same starting time of the motor, the torque fluctuation of the mechatronics technology optimized by three algorithms is shown in Figure 12.

Figure 12

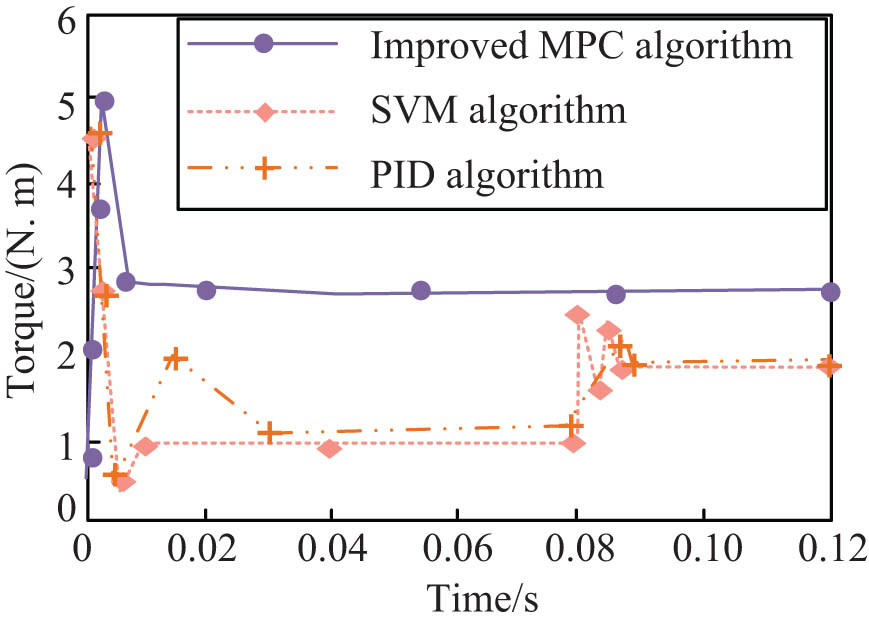
The variation results of the torque curves of the three algorithms.

In Figure 12, SVM and PID show significant torque fluctuations after optimizing the motor, and both stabilize at 0.09 s. After optimizing the motor, the improved MPC algorithm has a smaller torque fluctuation amplitude, which tends to stabilize at 0.01 s and reaches the highest torque value. Overall, after optimizing the mechatronics technology using the improved MPC algorithm, the practicality of this technology is significantly better than SVM and PID algorithms. Test the research method in a dynamic environment, as shown in Table 1.

Table 1

Dynamic environment test

Metric	Improved MPC algorithm	SVM algorithm	PID algorithm	Specification limit
Startup response time (s)	0.01	0.08	0.06	≤0.05
Braking response time (s)	0.01	0.07	0.06	≤0.05
Load change response (s)	0.02	0.12	0.09	≤0.10
Maximum current fluctuation (A)	0.1	0.2	0.18	≤0.15
Error fluctuation (%)	0.09	0.3	0.25	≤0.20
Optimization stability	High (within 1.00–1.05 range)	Medium (0.94–1.25 range)	Medium (0.95–1.20 range)	1.00 ± 0.10
Energy consumption (J)	0.5	0.7	0.65	≤0.60

Note: The limit values of the specification refer to the definitions of the dynamic performance and safety thresholds of the electromechanical system in the IEEE 1451.2-2022 standard. Among them, indicators such as the start-up response time and braking response time need to meet the requirements of real-time control.

As shown in Table 1, the improved MPC algorithm significantly outperforms the traditional SVM and PID algorithms in terms of response time, stability, energy consumption, and error fluctuations during dynamic processes such as startup, braking, and load changes. These results highlight the algorithm’s superior ability to optimize mechatronics systems under varying conditions, making it the optimal choice for high-performance control in dynamic environments. The research introduces the advanced integrated design method and 3D topology optimization in recent years for comparison [26,27]. The comparison results of advanced algorithms are shown in Table 2.

Table 2

Comparison of advanced algorithms

Metric	Improved MPC algorithm	Integrated design method	3D topology optimization	Specification limit
Maximum current fluctuation (A)	0.10	0.20	0.18	≤0.15
Error fluctuation (%)	0.09	0.30	0.25	≤0.20
Optimization time (s)	0.01	0.06	0.05	≤0.05
Maximum power demand (W)	0.20	0.25	0.22	≤0.25
Stability rating	High (stable fluctuation range: 1.00–1.05)	Medium (fluctuation range: 0.94–1.25)	Medium (fluctuation range: 0.95–1.20)	1.00 ± 0.10

Note: The limit values of the specification refer to the index requirements regarding the stability and energy efficiency of electromechanical systems in the ISO 13849-2015 standard.

As shown in Table 2, the improved MPC algorithm maintains a much smaller current fluctuation (maximum 0.1 A), indicating higher stability during dynamic control. In comparison, the Integrated Design Method and 3D Topology Optimization Method show larger current fluctuations, with values of 0.2 and 0.18 A, respectively. The power demand is similar among all three methods, but the improved MPC algorithm shows a slight advantage with a maximum power demand of 0.2 W, suggesting it is more efficient in energy consumption. The results indicate that the algorithm can predict load disturbances in advance and generate optimal control sequences through multi-step state prediction and rolling time-domain quadratic programming. With respect to energy efficiency, the maximum power demand of the enhanced MPC demonstrates marginal superiority over alternative approaches, thereby signifying its capacity for multi-objective collaborative optimization. By dynamically balancing the control accuracy and energy consumption, the algorithm reduces redundant control actions on the premise of ensuring stability, while the integrated design method makes it difficult to achieve dynamic energy efficiency optimization due to its reliance on static models. In addition, improving the rapid convergence characteristic of MPC shortens the transition time of the system from the transient state to the steady state, further reducing ineffective energy consumption. This has significant economic value for industrial scenarios with high-frequency start-stop, such as servo drives and automated production lines. From the perspective of engineering application, improving the stability and energy efficiency advantages of MPC can directly translate into enhanced reliability of electromechanical systems and reduced operation and maintenance costs. For example, in precision machine tools, a current fluctuation of 0.1 A means lower electromagnetic interference and mechanical vibration, which can extend tool life and improve processing accuracy. The optimization of power demand at 0.2 W helps to reduce the power consumption during long-term operation. This makes the improved MPC algorithm particularly attractive for real-world applications, especially in complex dynamic control systems.

5 Conclusion

This study introduced an improved MPC algorithm from TMCA to solve the problem of poor optimization performance of traditional algorithms in optimizing mechatronics technology. This study introduced two commonly used algorithms SVM and PID for optimizing mechatronics technology, analyzed the performance advantages and disadvantages of the three algorithms, and compared the optimization effects of mechatronics technology under different conditions. The innovation of this study lay in the deep integration of an improved MPC algorithm with TMCA, which for the first time proposed a real-time control framework that combined dynamic constraints and multi-objective collaborative optimization. It has broken through the bottleneck of insufficient stability of traditional algorithms in a strong interference environment. Furthermore, the closed-loop mechanism of load distribution and status monitoring has been demonstrated to achieve high-precision adaptive optimization of the mechatronic system under complex working conditions. In the experimental analysis, the algorithm used for optimizing mechatronics technology maintained a current value fluctuation within 0.1 A, and the fluctuation amplitude of the current value was relatively small. This indicated that the algorithm had good performance advantages in optimizing mechatronics technology. Under different interference conditions, the optimization effect of research algorithms on mechatronics integration was always better than other algorithms, and the fluctuation amplitude of optimization accuracy was relatively small. At 1.0032 min, the fluctuation curve of the optimized accuracy has already become flat. When comparing the optimization effects of the three algorithms, the variation in error values of the research algorithms was relatively small, and the average error value was 0.01%, significantly lower than other algorithms. Research has shown that using the improved MPC algorithm in TMCA can effectively optimize mechatronics technology. However, the limitation of the research lies in the fact that more advanced control strategies have not been compatible or integrated at present. Future work will attempt to develop a lightweight computing framework to reduce algorithm complexity and expand its application validation in fields such as intelligent manufacturing and new energy equipment, exploring its scalability in large-scale systems.

Funding information: Author states no funding involved.
Author contributions: Jun Ma: writing – original draft preparation; methodology, writing – review and editing. Author has accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: Author states no conflict of interest.
Data availability statement: All data generated or analyzed during this study are included in this published article.

References

[1] Steinbuch M, Oomen T, Vermeulen H. Motion control, mechatronics design, and Moore’s law. IEEJ J Ind Appl. 2022;11(2):245–55.10.1541/ieejjia.21006010Suche in Google Scholar

[2] Panchenko A, Voloshina A, Titova O. Design of hydraulic mechatronic systems with specified output characteristics. Design, simulation, manufacturing: The innovation exchange. Vol. 7, No. 3, Cham: Springer International Publishing; 2020. p. 42–51.10.1007/978-3-030-50491-5_5Suche in Google Scholar

[3] Aliu J, Oke AE, Oni SB. Evaluating strategies to promote mechatronics deployment in AECO projects: a Nigerian construction practitioners’ perspective. Int J Constr Manag. 2024;24(14):1540–9.10.1080/15623599.2023.2266630Suche in Google Scholar

[4] Kavianipour O. Energy regeneration effects on the vehicle suspension system performance considering non-idealities. J Vib Eng Technol. 2023;11(7):3081–92.10.1007/s42417-022-00732-4Suche in Google Scholar

[5] Qu PF, Zhang LM, Zhu QZ. Meta‐modeling of fractional constitutive relationships for rocks based on physics‐induced machine learning. Int J Numer Anal Methods Geomech. 2023;47(6):1000–21.10.1002/nag.3502Suche in Google Scholar

[6] Higgins O, Short BL, Chalup SK, Wilson RL. Artificial intelligence (AI) and machine learning (ML) based decision support systems in mental health: An integrative review. Int J Ment Health Nurs. 2023;32(4):966–78.10.1111/inm.13114Suche in Google Scholar PubMed

[7] Zhou L, Wang Y, Chai Y. Mechanic-electro coupling overlapping finite element method for piezoelectric structures. Arch Appl Mech. 2024;94(11):3429–54.10.1007/s00419-024-02677-4Suche in Google Scholar

[8] Yang J, Zhang T, Hong J. Research on driving control strategy and Fuzzy logic optimization of a novel mechatronics-electro-hydraulic power coupling electric vehicle. Energy. 2021;233(6):126–35.10.1016/j.energy.2021.121221Suche in Google Scholar

[9] Zhong L. Design of mechatronics system based on multi-sensor information fusion. Mod Electron Technol. 2021;44(12):6–10.Suche in Google Scholar

[10] Zhang Y, Zhou WT, Wang X. Application of digital intelligent control in mechatronics system modeling technology. Autom Instrum. 2023;34(1):100–10.Suche in Google Scholar

[11] Vazquez-Santacruz JA, Portillo-Velez R, Torres-Figueroa J, Marin-Urias LF, Portilla-Flores E. Towards an integrated design methodology for mechatronic systems. Res Eng Des. 2023;34(4):497–512.Suche in Google Scholar

[12] Wang Z, Zhou Z, Ruan L, Duan X, Wang Q. Mechatronic design and control of a rigid-soft hybrid knee exoskeleton for gait intervention. IEEE/ASME Trans Mechatron. 2023;28(5):2553–64.10.1109/TMECH.2023.3245810Suche in Google Scholar

[13] Brusa E, Carrera A, Delprete C. Integrated mechatronic design of an industrial piezoelectric vibration energy harvester. Mech Adv Mater Struct. 2024;31(27):8966–80.10.1080/15376494.2023.2264047Suche in Google Scholar

[14] Luo M, Li E, Zhang A, Tan M, Liang Z. A bioinspired coiled cable-driven manipulator: Mechatronic design and kinematics planning with multiconstraints. IEEE/ASME Trans Mechatron. 2023;28(6):3155–66.10.1109/TMECH.2023.3257481Suche in Google Scholar

[15] Hernando M, Morillo C, Guffanti D, Brunete A. Mechatronic design of a self-contained dexterous robotic hand for gestural communication. Int J Soc Robot. 2023;15(2):221–31.10.1007/s12369-022-00963-1Suche in Google Scholar

[16] Schwenzer M, Ay M, Bergs T. Review on model predictive control: An engineering perspective. Int J Adv Manuf Technol. 2021;117(5):1327–49.10.1007/s00170-021-07682-3Suche in Google Scholar

[17] Drgoňa J, Arroyo J, Figueroa IC. All you need to know about model predictive control for buildings. Annu Rev Control. 2020;50(7):190–232.10.1016/j.arcontrol.2020.09.001Suche in Google Scholar

[18] Hewing L, Wabersich KP, Menner M. Learning-based model predictive control: Toward safe learning in control. Ann Rev Control, Robot, Auton Syst. 2020;3(1):269–96.10.1146/annurev-control-090419-075625Suche in Google Scholar

[19] Guo N, Lenzo B, Zhang X. A real-time nonlinear model predictive controller for yaw motion optimization of distributed drive electric vehicles. IEEE Trans Veh Technol. 2020;69(5):4935–46.10.1109/TVT.2020.2980169Suche in Google Scholar

[20] Köhler J, Soloperto R, Müller MA. A computationally efficient robust model predictive control framework for uncertain nonlinear systems. IEEE Trans Autom Control. 2020;66(2):794–801.10.1109/TAC.2020.2982585Suche in Google Scholar

[21] Luis CE, Vukosavljev M, Schoellig AP. Online trajectory generation with distributed model predictive control for multi-robot motion planning. IEEE Robot Autom Lett. 2020;5(2):604–11.10.1109/LRA.2020.2964159Suche in Google Scholar

[22] Lin Y, McPhee J, Azad NL. Comparison of deep reinforcement learning and model predictive control for adaptive cruise control. IEEE Trans Intell Veh. 2020;6(2):221–31.10.1109/TIV.2020.3012947Suche in Google Scholar

[23] Berberich J, Köhler J, Müller MA. Data-driven model predictive control with stability and robustness guarantees. IEEE Trans Autom Control. 2020;66(4):1702–17.10.1109/TAC.2020.3000182Suche in Google Scholar

[24] Abdel-Rahim O, Wang H. A new high gain DC-DC converter with model-predictive-control based MPPT technique for photovoltaic systems. CPSS Trans Power ElectrAppl. 2020;5(2):191–200.10.24295/CPSSTPEA.2020.00016Suche in Google Scholar

[25] Rodriguez J, Garcia C, Mora A. Latest advances of model predictive control in electrical drives—Part I: Basic concepts and advanced strategies. IEEE Trans Power Electron. 2021;37(4):3927–42.10.1109/TPEL.2021.3121532Suche in Google Scholar

[26] Vazquez-Santacruz JA, Portillo-Velez R, Torres-Figueroa J, Marin-Urias LF, Portilla-Flores E. Towards an integrated design methodology for mechatronic systems. Res Eng Des. 2023;34(4):497–512.10.1007/s00163-023-00416-4Suche in Google Scholar

[27] Sun Y, Lueth TC Enhancing torsional stiffness of continuum robots using 3-D topology optimized flexure joints. IEEE/ASME Trans Mechatron, 2023, 28(4): 1844–52.10.1109/TMECH.2023.3266873Suche in Google Scholar

Received: 2024-11-22

Revised: 2025-05-16

Accepted: 2025-05-30

Published Online: 2025-11-03

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

https://doi.org/10.1515/nleng-2025-0160

Schlagwörter für diesen Artikel

torque motor control algorithm; MPC algorithm; improved MPC algorithm; mechatronics integration; optimize accuracy

Creative Commons

BY 4.0