Visco-thermoelastic rectangular plate under uniform loading: A study of deflection

Deepti Chopra; Prince Singh

doi:10.1515/nleng-2025-0148

40% Rabatt

auf Fachbücher bei De Gruyter Brill *

Artikel Open Access

Visco-thermoelastic rectangular plate under uniform loading: A study of deflection

Deepti Chopra und Prince Singh

Veröffentlicht/Copyright: 2. Juli 2025

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen

Aus der Zeitschrift Nonlinear Engineering Band 14 Heft 1

Abstract

Examining the deflection properties while designing and analyzing structural elements offers important information about working of visco-thermoelastic plates in microelectromechanical systems, sensors, and flexible electronic systems. The aim of the current study is to increase the stability and durability in heat-sensitive situations. This study focuses on the transverse deflection in a homogeneous, isotropic, visco-thermoelastic rectangular plate under the influence of uniform loading. The edges of plate are considered at different boundary conditions. Boundary conditions can either involve all edges being simply supported or keeping them simply supported and clamped alternatively. The deflection analysis utilizes the Laplace transform and Finite Fourier sine transform. Inverse Laplace transform is resolved using residue method. MATLAB software aids numerical computation of deflection expression post-Inverse Laplace Transform. Graphical analysis explores the diverse boundary conditions across different modes. The variation in deflection has been studied in the plate under varied circumstances. The findings provide useful insights for engineering applications involving thermal and mechanical stability and advance theoretical and computational understanding of deflection dynamics in visco-thermoelastic rectangular plates under uniform loads.

Keywords: visco-thermoelastic; uniform loading; method of residues; simply supported; clamped

1 Introduction

The applications of visco-thermoelastic rectangular plate resonators in precision engineering, microelectromechanical systems (MEMS), and nanoelectromechanical systems (NEMS) have drawn a lot of attention to their study. The combined effects of viscosity, thermal relaxation, and elastic deformation cause these resonators to behave complexly under external loading. The deflection response, damping properties, and stability of these structures are influenced by the interplay of mechanical vibrations, thermal conduction, and material viscosity.

Lord and Shulman [1] developed a comprehensive theory of thermoelasticity that integrated the interplay between temperature and strain rate, leading to the emergence of finite-speed propagation for heat waves. Bauchau and Craig [2] developed the theory of analysis of plates having one dimension much smaller than the other two and derived the expressions for all strain, stress, displacement components, bending moments, and transverse forces. Sharma and Grover [3] studied thermoelastic damping in MEMS/NEMS thin plates with voids to derive the expressions for deflection, frequency shift, under different boundary conditions. Grover [4] explored the impact of viscosity, thermal relaxation, and geometric variation on damping characteristics. The author investigated the influence of material properties and geometric parameters on deflection, frequency shift, and stability. Li et al. [5] presented an analytical model for the thermoelastic damping in the fully clamped and simply supported rectangular and circular microplates and derived the expression for quality factor using the energy dissipated over the volume of microplate per cycle of vibration. Lal and Kumar [6] studied the free transverse vibration of thin rectangular plates of linearly varying thickness using two-dimensional characteristic orthogonal polynomial. Lal and Saini [7] analyzed the transverse vibration in thin rectangular plates of linearly varying thickness using generalized differential quadrature method. Rana and Robin [8] analyzed the effect on damping due to non-homogeneity in a rectangular plate of parabolically varying thickness resting on elastic foundation. Grover [9] studied the effect of fixed aspect ratio, fixed radius, and fixed thickness on thermoelastic damping of out of plane vibrations in visco-thermoelastic circular plate resonator. Partap and Chugh [10] investigated the expressions for thermoelastic damping temperature distribution, deflection in micro-scale microstretch, micropolar, generalized thermoelastic thin plate. Grover and Seth [11] analyzed the effect of time delay and mechanical relaxation time on thermoelastic damping using generalized dual-phase-lagging model. Liu et al. [12] studied the effect of size and shape on thermoelastic damping and out-of-plane vibration of the laminated rectangular plate. Zuo et al. [13] derived the expressions for thermoelastic damping in trilayered microplate under the boundary conditions of fully clamped. The authors discussed the magnitude of fluctuate temperature, thermoelastic damping and energy dissipation among the three layers. Khan et al. [14] analyzed the dusty viscoelastic fluids under shear stress and heat absorption by considering inclined vertical plates. The study was mainly concerned with fluid flow, but it also demonstrated the wider applicability of boundary-driven thermal effects, which theoretically facilitate the modeling of heat-influenced deflection in visco-thermoelastic solids. Chopra and Singh [15] investigated the transverse deflection in a visco-thermoelastic beam under harmonic loading for different boundary conditions. Gohar et al. [16] examined the effect of periodic magnetic fields and thermal radiation between parallel plates in viscoelastic fluids with dusty nanoparticles. The study provided a better understanding of thermomechanical coupling under detailed boundary conditions. The study played significant role in understanding the study of deflection behavior in visco-thermoelastic plates, where structural response is greatly influenced by heat transfer and external field effects.

Several researchers have previously examined the bending and transverse vibrations in rectangular plates using thermoelasticity theories. Nevertheless, few studies have combined thermal and viscoelastic effects to analyze deflection behavior under external loading. A more realistic framework for comprehending heat conduction and its effect on mechanical deformation is offered by the Lord–Shulman (LS) thermoelastic model, which incorporates thermal relaxation time. Previous research has examined the transverse vibrations of thermoelastic rectangular plates, both with and without external loading. The present study focuses on determining deflection in visco-thermoelastic rectangular plate under uniform loading.

The LS model serves as the basis for the formulation of the governing equations, which include viscoelastic damping and thermal relaxation effects. The governing equations for rectangular plate under the specified initial circumstances are solved using the Laplace transform with respect to time domain. Under the specified clamped-simply supported plate (CSCS) and simply supported plate (SSSS) boundary conditions, a partial differential equation (PDE) that was produced by applying the Finite Fourier sine transform (FFST) with respect to the space domain has been resolved. Further time-domain solutions are extracted by computing the inverse Laplace transform using the method of residues. A thorough foundation for comprehending the dynamic behavior of visco-thermoelastic beam resonators under recurring external excitations is offered by the suggested methodology. The effects of viscosity and boundary conditions on plate deflection are investigated through a variety of graphical investigations. Numerical simulations using MATLAB are performed to validate the theoretical model and illustrate the deflection patterns over time.

2 Primary equations

The present problem considers a homogeneous, isotropic, thermally conductive visco-thermoelastic rectangular plate, which is initially undeformed and at temperature T 0 . The basic equation of motion has been considered in cartesian coordinate system from the study by Grover [4].

(1) σ i j = λ * δ i j e k k + 2 μ * e i j − β * T δ i j .

In view of the Lord and Shulman [1] model of generalized thermoelasticity, the equation of heat conduction along with the constitutive relations, in the absence of heat sources and body forces, which govern the displacement vector u = ( u 1 , u 2 , u 3 ) and temperature change T ( x , y , z , t ) at time t , are given as

(2) ( λ * + 2 μ * ) ∇ ( ∇ ⋅ u ) − μ * ∇ × ( ∇ × u ) − β 1 * ∇ T = ρ ∂ 2 u ∂ t 2 ,

(3) K ∇ 2 T = ρ C e ∂ T ∂ t + t 0 ∂ 2 T ∂ t 2 + β 1 * T 0 ∂ ∂ t + t 0 ∂ 2 ∂ t 2 ∇ ⋅ u ,

where

λ * = λ 1 + α 0 ∂ ∂ t μ * = μ 1 + α 1 ∂ ∂ t ,

β * = β 1 + β 0 ∂ ∂ t β 0 = ( 3 λ α 0 + 2 μ α 1 ) α T β .

Symbols used in the study are defined in Table 1.

LS model derivation The fundamental heat equation, based on Fourier’s law and energy conservation, is

ρ C e ∂ T ∂ t = K ∇ 2 T + Q 0 .

To account for thermal relaxation, we can modify Fourier’s law by introducing a relaxation time τ

q + τ ∂ q ∂ t = − K ∇ T ,

where q is the heat flux vector. Combining this with the energy conservation equation leads to the Cattaneo–Vernotte equation, which includes a second-order time derivative of temperature:

ρ C e ∂ T ∂ t + τ ∂ 2 T ∂ t 2 = K ∇ 2 T + Q 0 .

In thermoelasticity, temperature changes can induce strains, and conversely, strains can affect the temperature field. This coupling is often represented by a term proportional to the divergence of the displacement or velocity field ∇ ⋅ u .

Considering further generalization of the Cattaneo–Vernotte equation, including characteristic time, coupling parameter of temperature and velocity field and also, introducing a heat source term ( Q 0 ) that is dependent on the velocity field

Q 0 = − β T 0 ∂ ∂ t + t 0 ∂ 2 ∂ t 2 ( ∇ ⋅ u ) .

This form suggests that the heat source is not only influenced by the rate of deformation ∂ ∂ t but also by its acceleration ∂ 2 ∂ t 2 , possibly reflecting inertial effects in the material’s response. Substituting this expression for Q into the Cattaneo–Vernotte equation and replacing τ with t 0

ρ C e ∂ T ∂ t + t 0 ∂ 2 T ∂ t 2 = K ∇ 2 T − β T 0 ∂ ∂ t + t 0 ∂ 2 ∂ t 2 ( ∇ ⋅ u ) .

Table 1

Nomenclature

σ i j	Components of stress tensor
e i j	Components of strain tensor
λ and μ	Lames parameters
ρ	Density of medium
α 0 and α 1	Viscoelastic relaxation times
t 0	Thermal relaxation time
α T	Linear thermal expansion coefficient
C e	Specific heat
δ i j	Kronecker delta function
K	Thermal conductivity
Q 0	Heat source term
β	Coupling coefficient linking the temperature field to the velocity field

3 Modeling of rectangular plate structure

A homogeneous isotropic, visco-thermoelastic rectangular plate with dimensions as length L ( 0 ≤ x ≤ L ) , width b − b 2 ≤ y ≤ b 2 , and thickness h − h 2 ≤ z ≤ h 2 is considered for studying the transverse deflection induced due to loading. In equilibrium, the plate is at stable temperature T 0 , is under no stress, and unstrained. In accordance with Kirchhoff–Love plate theory assumptions [2], normal material line remains straight and normal to the mid plane of the plate after deformation. The displacement vector u and temperature function T are given as

u 1 = − z ∂ w ∂ x , u 2 = − z ∂ w ∂ y , u 3 = w ( x , y , t ) .

Figure 1

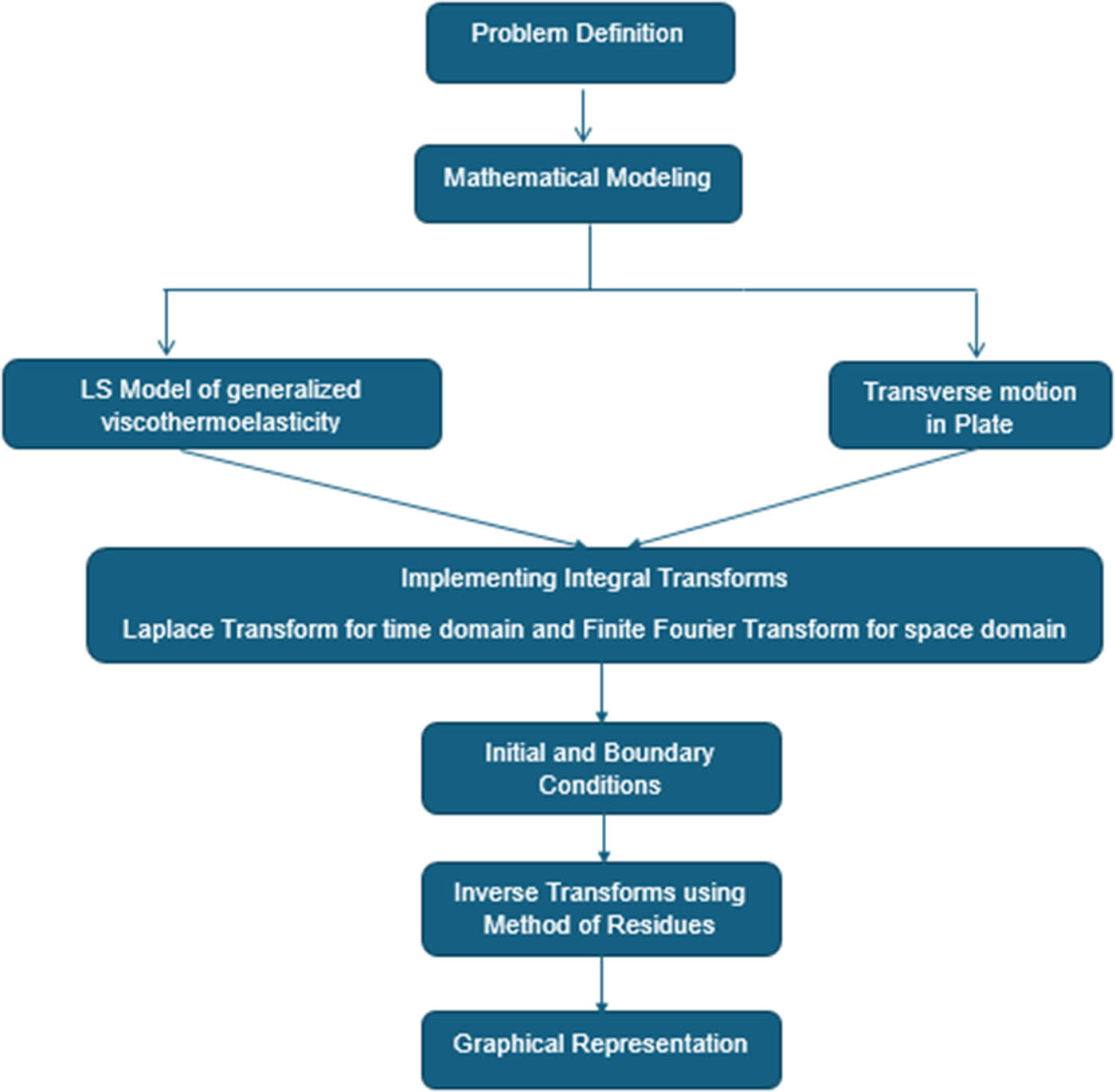
Flowchart for the modeling of the visco-thermoelastic rectangular plate.

Using the above displacement vector values, Eqs (1)–(3) reduce to

(4) σ x x = ( λ + 2 μ ) − z ∂ 2 w ∂ x 2 + λ − z ∂ 2 w ∂ y 2 + ( λ α 0 + 2 μ α 1 ) − z ∂ 3 w ∂ t ∂ x 2 + λ α 0 − z ∂ 3 w ∂ t ∂ y 2 − β T + β 0 ∂ T ∂ t . σ y y = ( λ + 2 μ ) − z ∂ 2 w ∂ y 2 + λ − z ∂ 2 w ∂ x 2 + ( λ α 0 + 2 μ α 1 ) − z ∂ 3 w ∂ t ∂ y 2 + λ α 0 − z ∂ 3 w ∂ t ∂ x 2 − β T + β 0 ∂ T ∂ t , σ x y = − 2 μ z ∂ 2 w ∂ x ∂ y + α 1 ∂ 3 w ∂ t ∂ x ∂ y ,

(5) − z ( λ + 2 μ ) ∂ 3 w ∂ x 3 + ∂ 3 w ∂ x ∂ y 2 − z ( λ α 0 + 2 μ α 1 ) ∂ 4 w ∂ t ∂ x 3 + ∂ 4 w ∂ t ∂ x ∂ y 2 − β ∂ T ∂ x + β 0 ∂ 2 T ∂ x ∂ t = − ρ z ∂ 3 w ∂ x ∂ t 2 , − z ( λ + 2 μ ) ∂ 3 w ∂ y 3 + ∂ 3 w ∂ y ∂ x 2 − z ( λ α 0 + 2 μ α 1 ) ∂ 4 w ∂ t ∂ y ∂ x 2 + ∂ 4 w ∂ t ∂ y 3 − β ∂ T ∂ y + β 0 ∂ 2 T ∂ y ∂ t = − ρ z ∂ 3 w ∂ y ∂ t 2 , − λ ∂ 2 w ∂ x 2 + ∂ 2 w ∂ y 2 − λ α 0 ∂ 3 w ∂ t ∂ x 2 + ∂ 3 w ∂ t ∂ y 2 − β ∂ T ∂ z + β 0 ∂ 2 T ∂ z ∂ t = ρ ∂ 2 w ∂ t 2 ,

(6) K ∇ 2 T = ρ C e ∂ T ∂ t + t 0 ∂ 2 T ∂ t 2 − β z T 0 1 + β 0 ∂ ∂ t ∂ ∂ t + t 0 ∂ 2 ∂ t 2 ∇ 1 2 w ,

where ∇ 2 = ∂ 2 ∂ x 2 + ∂ 2 ∂ y 2 + ∂ 2 ∂ z 2 and ∇ 1 2 = ∂ 2 ∂ x 2 + ∂ 2 ∂ y 2 .

The bending moments per unit length M x x , M y y are induced in visco-thermoelastic plate due to normal stresses σ x x , σ y y and the twisting moment per unit length M x y is induced due to the shearing stresses σ x y , σ y x , which are given as

M x x = ∫ − h ∕ 2 h ∕ 2 σ x x z d z , M y y = ∫ − h ∕ 2 h ∕ 2 σ y y z d z , M x y = ∫ − h ∕ 2 h ∕ 2 σ x y z d z .

Using the stress components from (4), we obtain

(7) M x x = − h 3 12 ( λ + 2 μ ) ∂ 2 w ∂ x 2 + λ ∂ 2 w ∂ y 2 + ( λ α 0 + 2 μ α 1 ) ∂ 3 w ∂ t ∂ x 2 + λ α 0 ∂ 3 w ∂ t ∂ y 2 − β M T + β 0 ∂ M T ∂ t , M y y = − h 3 12 ( λ + 2 μ ) ∂ 2 w ∂ y 2 + λ ∂ 2 w ∂ x 2 + ( λ α 0 + 2 μ α 1 ) ∂ 3 w ∂ t ∂ y 2 + λ α 0 ∂ 3 w ∂ t ∂ x 2 − β M T + β 0 ∂ M T ∂ t , M x y = − 2 μ h 3 12 ∂ 2 w ∂ x ∂ y + α 1 ∂ 3 w ∂ t ∂ x ∂ y ,

where M T = ∫ − h ∕ 2 h ∕ 2 T z d z represents moment of plate due to thermal effects.

Now, taking up the equation of transverse motion in plate (Figure 1)

(8) ∂ 2 M x x ∂ x 2 + 2 ∂ 2 M x y ∂ x ∂ y + ∂ 2 M y y ∂ y 2 = − q ( x , y , t ) + ρ h ∂ 2 w ∂ t 2 ,

where q ( x , y , t ) represents loading on plate.

Taking uniform loading under consideration, i.e., q ( x , y , t ) = − q 0 .

Using Eq. (7) in (8), we obtain

(9) − h 3 12 ( λ + 2 μ ) ∇ 1 2 ( ∇ 1 2 w ) + ( λ α 0 + 2 μ α 1 ) ∂ ∂ t ∇ 1 2 ( ∇ 1 2 w ) − β ∇ 1 2 M T + β 0 ∂ M T ∂ t = q 0 + ρ h ∂ 2 w ∂ t 2 .

Considering non-dimensional quantities

x ′ = x L , y ′ = y L , w ′ = w h , z ′ = z h , t ′ = c 1 L t , t 0 ′ = c 1 L t 0 , T ′ = T − T 0 T 0 .

Using the non-dimensional quantities in Eqs (6) and (9), we obtain

(10) 1 12 A R 2 ( λ + 2 μ ) ∇ 1 2 ( ∇ 1 2 w ) + ( λ α 0 + 2 μ α 1 ) c 1 L ∂ ∂ t ∇ 1 2 ( ∇ 1 2 w ) + β T 0 ∇ 1 2 M T + c 1 β 0 L ∂ M T ∂ t + ρ c 1 2 ∂ 2 w ∂ t 2 = − q 0 A R 2 . ∂ 2 T ∂ x 2 + ∂ 2 T ∂ y 2 + A R 2 ∂ 2 T ∂ z 2 = ρ C e c 1 L K ∂ T ∂ t + t 0 ∂ 2 T ∂ t 2 − c 1 β z h 2 K L 1 + β 0 c 1 L ∂ ∂ t ∂ ∂ t + t 0 ∂ 2 ∂ t 2 ∇ 1 2 w ,

where M T = ∫ − 1 ∕ 2 1 ∕ 2 T z d z .

(Ignoring the primes for the sake of convenience.)

4 Initial and boundary conditions

A rectangular plate, whose either all the edges are subjected to simply supported conditions (SSSS) or horizontal edges are subjected to simply supported and vertical edges as clamped (CSCS), is considered. The initial conditions in rectangular plate [3] are considered as:

(11) w ( x , y , 0 ) = ∂ w ∂ t t = 0 = ∂ 2 w ∂ t 2 t = 0 = 0 , T ( x , y , z , 0 ) = ∂ T ∂ t t = 0 = 0 .

The first condition on the deflection ensures that the plate is in undeformed position initially and the other two conditions signify that no external momentum or force is acting initially. The first condition on T ( x , y , z , t ) means that change in temperature from initial temperature T 0 is zero in the beginning. The other condition states that temperature gradient is zero initially. and the following boundary conditions [17] are taken into account.

Case I: For SSSS

(12) w ( 0 , y , t ) = w ( 1 , y , t ) = 0 and w ( x , 0 , t ) = w ( x , b ˆ , t ) = 0 . ∂ 2 w ∂ x 2 x = 0 = ∂ 2 w ∂ x 2 x = 1 = 0 and ∂ 2 w ∂ y 2 y = 0 = ∂ 2 w ∂ y 2 y = b ˆ = 0 .

Case II: For CSCS

(13) w ( 0 , y , t ) = w ( 1 , y , t ) = 0 and w ( x , 0 , t ) = w ( x , b ˆ , t ) = 0 . ∂ w ∂ x x = 0 = ∂ w ∂ x x = 1 = 0 and ∂ 2 w ∂ y 2 y = 0 = ∂ 2 w ∂ y 2 y = b ˆ = 0 .

With all the edges under simply supported conditions, state that the plate is rigid at the edges and is not allowing the vertical movement but is free to rotate with zero resistance to bending at the boundaries when an external load is applied, while the boundary conditions of CSCS signify that all the edges are restricting the vertical movement, but rotation is restricted only at vertical edges.

Also, there is no flow of heat through the lower and upper surface of visco-thermoelastic rectangular plate, i.e., ∂ T ∂ z = 0 at z = ± 1 2 .

5 Solution along thickness direction

5.1 Laplace transfrom technique

The differential equations given in (10) are analyzed using the Laplace transform technique. Laplace transform converts time-domain problems into complex frequency-domain. The transform converts the time derivatives into algebraic equations, which makes it easier to solve. We apply Laplace transform to the equations w.r.t the time domain, defined as

ℒ ( w ( x , y , t ) ) = w ¯ ( x , y , s ) = ∫ 0 ∞ e − s t w ( x , y , t ) d t and ℒ ( T ( x , y , z , t ) ) = Θ ( x , y , z , s ) = ∫ 0 ∞ e − s t T ( x , y , z , t ) d t .

On applying Laplace transform, under the initial conditions given by (11), we obtain

ℒ ∂ w ∂ t = s w ¯ , ℒ ∂ 2 w ∂ t 2 = s 2 w ¯ ℒ ∂ T ∂ t = s Θ .

Using the above expressions, the set of equations in (10) reduce to

(14) 1 12 A R 2 ( λ + 2 μ ) ∇ 1 2 ( ∇ 1 2 w ¯ ) + ( λ α 0 + 2 μ α 1 ) c 1 s L ∇ 1 2 ( ∇ 1 2 w ¯ ) + β T 0 1 + c 1 β 0 s L ∇ 1 2 M Θ + ρ c 1 2 s 2 w ¯ = − q 0 A R 2 s ,

(15) ∂ 2 Θ ∂ x 2 + ∂ 2 Θ ∂ y 2 + A R 2 ∂ 2 Θ ∂ z 2 = ρ C e c 1 L s γ 0 Θ K − c 1 β z h 2 K L s γ 0 γ 1 ∇ 1 2 w ¯ ,

where 1 + s t 0 = γ 0 , 1 + s c 1 β 0 L = γ 1 , and

(16) M Θ = ∫ − 1 ∕ 2 1 ∕ 2 Θ z d z .

Under the conditions that no heat flows through upper and lower surfaces of rectangular plate and considerig the fact that thermal gradients are much larger along thickness direction than in the plane of cross section, i.e., ∇ 1 2 Θ ≪ ∂ 2 Θ ∂ z 2 , so the solution of Eq. (15) is obtained as follows:

(17) Θ ( x , y , z , s ) = β γ 1 ρ C e A R 2 z − sin p z p cos ( p ∕ 2 ) ∇ 1 2 w ¯ where p 2 = − ρ C e s γ 0 γ 1 K .

Using Eq. (16) to find M Θ , we obtain

(18) ∇ 1 2 M Θ = β γ 1 12 ρ C e A R 2 1 + 24 p 3 p 2 − tan p 2 ∇ 1 2 ( ∇ 1 2 w ¯ ) .

Using the above expression, Eq. (14) reduces to

(19) 1 12 A R 2 [ 1 + ε 0 s + ε 1 γ 1 2 ( 1 + f ( p ) ) ] ∇ 1 2 ( ∇ 1 2 w ¯ ) + s 2 w ¯ = − q 0 A R 2 ρ c 1 2 s ,

where ε 0 = ( λ α 0 + 2 μ α 1 ) c 1 ( λ + 2 μ ) L , ε 1 = β 2 T 0 ρ 2 C e c 1 2 , ( λ + 2 μ ) = ρ c 1 2 .

Re-writing the above expression, we obtain

G s ∇ 1 2 ( ∇ 1 2 w ¯ ) + s 2 w ¯ = − Q s .

(20) ∇ 1 2 ( ∇ 1 2 w ¯ ) − η 4 w ¯ = − Q s G s ,

where Q = q 0 A R 2 ρ c 1 2 and

(21) G s = 1 12 A R 2 [ 1 + ε 0 s + ε 1 γ 1 2 ( 1 + f ( p ) ) ] , η 4 = − s 2 G s .

5.2 Fourier transform technique

The FFST method is used to investigate the differential equations mentioned in (20). In general, the Fourier transform makes it easier to analyze wave-like behavior by converting functions from the spatial domain to the wavenumber domain. In particular, PDE can be simplified by converting them into ordinary differential equations using the FFST. This transformation is especially helpful when the function is zero at the domain boundaries and fulfills homogeneous Dirichlet boundary constraints. The FFST greatly reduces computer complexity by breaking down the differential equation into a sequence of sine components by eliminating spatial derivatives. This method is useful for studying wave propagation, thermal conduction, and structural vibrations since it also sheds light on the system’s inherent frequencies and mode shapes.

We apply FFST to the equation w.r.t y , defined as

W ( x , n , s ) = ℱ ( w ¯ ( x , y , s ) ) = ∫ 0 b ˆ w ¯ ( x , y , s ) sin n π y b ˆ d y .

Using the boundary conditions from Eqs (12) and (13) along y , we obtain

(22) ℱ ∂ 2 w ¯ ∂ y 2 = − n 2 π 2 b ˆ 2 W , ℱ ∂ 4 w ¯ ∂ y 4 = n 4 π 4 b ˆ 4 W .

Using the above expressions, Eq. (20) reduces to non-homogeneous differential equation with constant coefficients as follows:

(23) D 2 − n 2 π 2 b ˆ 2 2 − η 4 W = − Q b ˆ ( 1 − cos n π ) s G s n π ,

where D ≡ ∂ ∂ x .

Solving the above differential equation, we obtain

(24) W = A cosh m 1 x + B sinh m 1 x + C cos m 2 x + D sin m 2 x − 1 n 4 π 4 b ˆ 4 − η 4 . Q b ˆ ( 1 − cos n π ) s G s n π ,

where m 1 = η 2 + n 2 π 2 b ˆ 2 , m 2 = η 2 − n 2 π 2 b ˆ 2 .

Using the boundary conditions along x from (12), (13), solution of (24) is obtained as follows:

Case I: For SSSS

(25) W = A 1 ( m 1 , m 2 ) cosh m 1 x + B 1 ( m 1 , m 2 ) sinh m 1 x + C 1 ( m 1 , m 2 ) cos m 2 x + D 1 ( m 1 , m 2 ) sin m 2 x H 1 ( m 1 , m 2 ) − 1 × Q b ˆ ( 1 − cos n π ) n π s s 2 + n 4 π 4 b ˆ 4 G s .

Case II: For CSCS

(26) W = A 2 ( m 1 , m 2 ) cosh m 1 x + B 2 ( m 1 , m 2 ) sinh m 1 x + C 2 ( m 1 , m 2 ) cos m 2 x + D 2 ( m 1 , m 2 ) sin m 2 x H 2 ( m 1 , m 2 ) − 1 × Q b ˆ ( 1 − cos n π ) n π s s 2 + n 4 π 4 b ˆ 4 G s ,

where A 1 ( m 1 , m 2 ) = m 2 2 sinh m 1 sin m 2 , B 1 ( m 1 , m 2 ) = m 2 2 ( 1 − cosh m 1 ) sin m 2 , C 1 ( m 1 , m 2 ) = m 1 2 sin m 2 sinh m 1 .

D 1 ( m 1 , m 2 ) = m 1 2 ( 1 − cos m 2 ) sinh m 1 , H 1 ( m 1 , m 2 ) = 2 η 2 sinh m 1 sin m 2 .

A 2 ( m 1 , m 2 ) = m 1 m 2 ( 1 − cos m 2 ) ( cosh m 1 + 1 ) − m 2 2 sinh m 1 sin m 2 .

B 2 ( m 1 , m 2 ) = m 2 2 sin m 2 ( cosh m 1 − 1 ) − m 1 m 2 sinh m 1 ( 1 − cos m 2 ) .

C 2 ( m 1 , m 2 ) = m 1 2 sinh m 1 sin m 2 − m 1 m 2 ( 1 + cos m 2 ) ( cosh m 1 − 1 ) .

D 2 ( m 1 , m 2 ) = m 1 2 sinh m 1 ( 1 − cos m 2 ) − m 1 m 2 sin m 2 ( cosh m 1 − 1 ) .

H 2 ( m 1 , m 2 ) = 2 m 1 m 2 ( 1 − cosh m 1 cos m 2 ) + ( m 1 2 − m 2 2 ) sinh m 1 sin m 2 .

Taking inverse FFST of (25) and (26) w.r.t. y

w ¯ = 2 b ˆ ∑ n = 1 ∞ W ( x , n , s ) sin n π y b ˆ .

Using method of residues for finding inverse Laplace transform defined as

(27) ℒ − 1 ( w ¯ ( x , y , s ) ) = w ( x , y , t ) = Σ Residues of e s t w ¯ ( x , y , s ) .

Case I: For SSSS

s = 0 is pole of order 2 and residue is 0.

s = ± ι n 2 π 2 b ˆ 2 G s = ± ι s 1 are simple poles.

Residue at s = ± ι s 1 is

− Q b ˆ e ± ι s 1 t ( 1 − cos n π ) 2 n π s 1 2 A 1 ( m 11 , m 12 ) cosh m 11 x + B 1 ( m 11 , m 12 ) sinh m 11 x + C 1 ( m 11 , m 12 ) cos m 12 x + D 1 ( m 11 , m 12 ) sin m 12 x H 1 ( m 11 , m 12 ) − 1 .

Singularities w.r.t H 1 ( m 1 , m 2 ) = 0 , i.e., the auxilliary roots are given by Rao [17] as m 1 = ι k π = m 1 k , m 2 = k π = m 2 k ; k = 1 , 2 , 3 , … are simple poles.

Using m 1 k 2 = η 1 k 2 + n 2 π 2 b ˆ 2 , m 2 k 2 = η 2 k 2 − n 2 π 2 b ˆ 2 , s 1 k = ± ι η 1 k 2 G s , s 2 k = ± ι η 2 k 2 G s .

Residue at s = s 1 k is

Q b ˆ e s 1 k t ( 1 − cos n π ) n π s 1 k n 4 π 4 b ˆ 4 G s + s 1 k 2 A 1 ( m 1 , m 2 ) cosh m 1 x + B 1 ( m 1 , m 2 ) sinh m 1 x + C 1 ( m 1 , m 2 ) cos m 2 x + D 1 ( m 1 , m 2 ) sin m 2 x 2 η 1 k 2 d H 1 d s m 1 = m 1 k .

Residue at s = s 2 k is

Q b ˆ e s 2 k t ( 1 − cos n π ) n π s 2 k n 4 π 4 b ˆ 4 G s + s 2 k 2 A 1 ( m 1 , m 2 ) cosh m 1 x + B 1 ( m 1 , m 2 ) sinh m 1 x + C 1 ( m 1 , m 2 ) cos m 2 x + D 1 ( m 1 , m 2 ) sin m 2 x 2 η 2 k 2 d H 1 d s m 2 = m 2 k .

Case II: For CSCS

s = 0 is pole of order 2 and residue is 0.

s = ± ι n 2 π 2 b ˆ 2 G s = ± ι s 1 are simple poles.

Residue at s = ± ι s 1 is

− Q b ˆ e ± ι s 1 t ( 1 − cos n π ) 2 n π s 1 2 A 2 ( m 11 , m 12 ) cosh m 11 x + B 2 ( m 11 , m 12 ) sinh m 11 x + C 2 ( m 11 , m 12 ) cos m 12 x + D 2 ( m 11 , m 12 ) sin m 12 x H 2 ( m 11 , m 12 ) − 1

Singularities w.r.t H 2 ( m 1 , m 2 ) = 0 , i.e., the auxilliary roots are given by Rao [17] as m 1 = ι k + 1 2 π = m 1 k , m 2 = k + 1 2 π = m 2 k ; k = 1,2,3 , … are simple poles. Using m 1 k 2 = η 1 k 2 + n 2 π 2 b ˆ 2 , m 2 k 2 = η 2 k 2 − n 2 π 2 b ˆ 2 , s 1 k = ± ι η 1 k 2 G s , s 2 k = ± ι η 2 k 2 G s .

Residue at s = s 1 k is

Q b ˆ e s 1 k t ( 1 − cos n π ) n π s 1 k n 4 π 4 b ˆ 4 G s + s 1 k 2 A 2 ( m 1 , m 2 ) cosh m 1 x + B 2 ( m 1 , m 2 ) sinh m 1 x + C 2 ( m 1 , m 2 ) cos m 2 x + D 2 ( m 1 , m 2 ) sin m 2 x 2 η 1 k 2 d H 2 d s m 1 = m 1 k .

Residue at s = s 2 k is

Q b ˆ e s 2 k t ( 1 − cos n π ) n π s 2 k n 4 π 4 b ˆ 4 G s + s 2 k 2 A 2 ( m 1 , m 2 ) cosh m 1 x + B 2 ( m 1 , m 2 ) sinh m 1 x + C 2 ( m 1 , m 2 ) cos m 2 x + D 2 ( m 1 , m 2 ) sin m 2 x 2 η 2 k 2 d H 2 d s m 2 = m 2 k ,

where s 1 = s 0 1 + ε 0 s 0 2 + β 2 γ 0 2 T 0 2 ρ 2 c 1 2 C e ( 1 + f p 0 ) , s 0 = 1 2 3 A R n 2 π 2 b ˆ 2 , γ 0 = 1 + s 0 β 0 c 1 L , P 0 2 = ρ C e c 1 L s 0 ( 1 + s 0 t 0 ) K A R 2 , f p 0 = − 12 P 0 2 + 24 P 0 3 tanh P 0 2 , γ 1 = 1 ± ι s 1 β 0 c 1 L , P 1 2 = ± ι s 1 ρ C e c 1 L ( 1 ± ι s 1 t 0 ) K A R 2 , f p 1 = − 12 P 1 2 + 24 P 1 3 tanh P 1 2 , η 1 2 = 2 3 A R s 1 1 ∓ ι ε 0 s 1 2 − ε 1 γ 1 2 2 ( 1 + f p 1 ) , m 11 = η 1 2 + n 2 π 2 b ˆ 2 , m 12 = η 1 2 − n 2 π 2 b ˆ 2 .

6 Numerical results and graphical discussion

Consider visco-thermoelastic solid-like magnesium with the physical specifications by Sharma and Grover [3] as given below:

λ = 9.4 × 1 0 10 N ∕ m 2 , μ = 4.0 × 1 0 10 N ∕ m 2 , ρ = 1.74 × 1 0 3 kg ∕ m 3 , C e = 1.04 × 1 0 3 J kg − 1 deg − 1 , T 0 = 29 8 ∘ K , α 0 = α 1 = 0.779 × 1 0 − 9 , K = 1.7 × 1 0 6 W m − 1 deg − 1 , q 0 = 2 × 1 0 − 7 .

Dimensions of the rectangular plate are taken as: L = 500 μ m , h = 50 μ m and b = 100 μ m .

Non-dimensional deflection has been computed for different modes in view of Eq. (27). Figures 2, 3, 4, 5, 6, 7, 8, 9 represent variation in deflection along the dimensions of plate for different modes (1, 1), (1, 2), (2, 1), and (2, 2) for SSSS and CSCS plate under the uniform load. Numerical simulations utilizing MATLAB software programming were conducted for a material analogous to magnesium. Graphical representations of the computer-simulated outcomes were provided, depicting diverse boundary conditions.

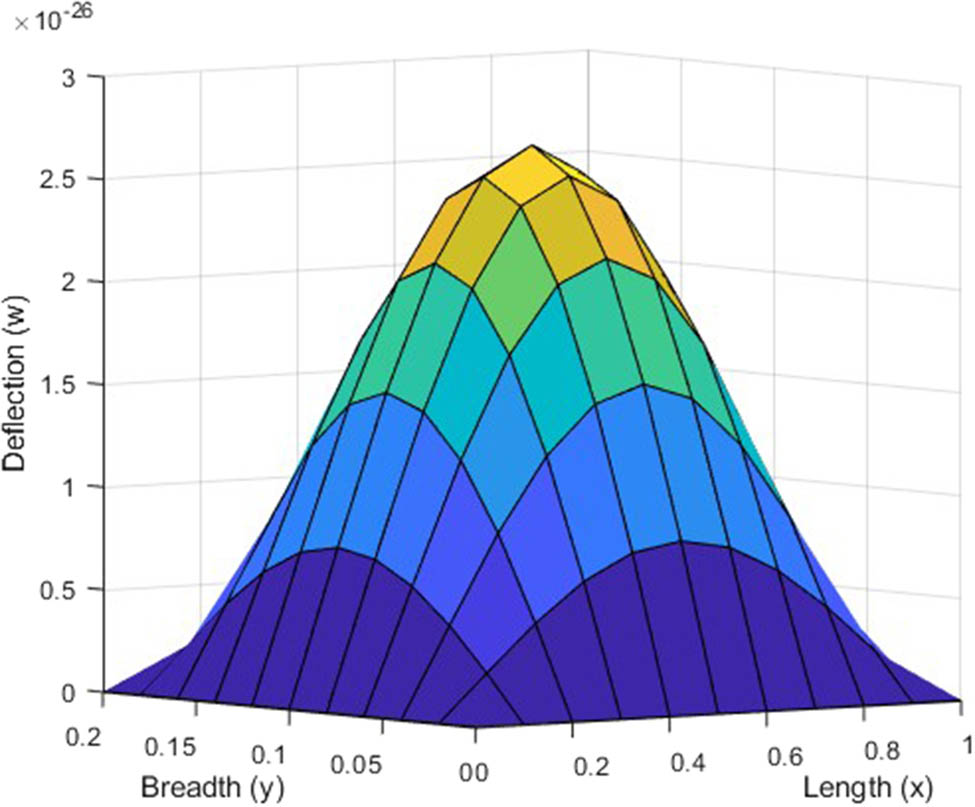
$Figure 2 Variation in deflection for (1,1) mode in visco-thermoelastic SSSS plate under uniform load along the ( x , y ) \left(x,y) dimensions at t = 30 t=30 .$

Figure 2

Variation in deflection for (1,1) mode in visco-thermoelastic SSSS plate under uniform load along the ( x , y ) dimensions at t = 30 .

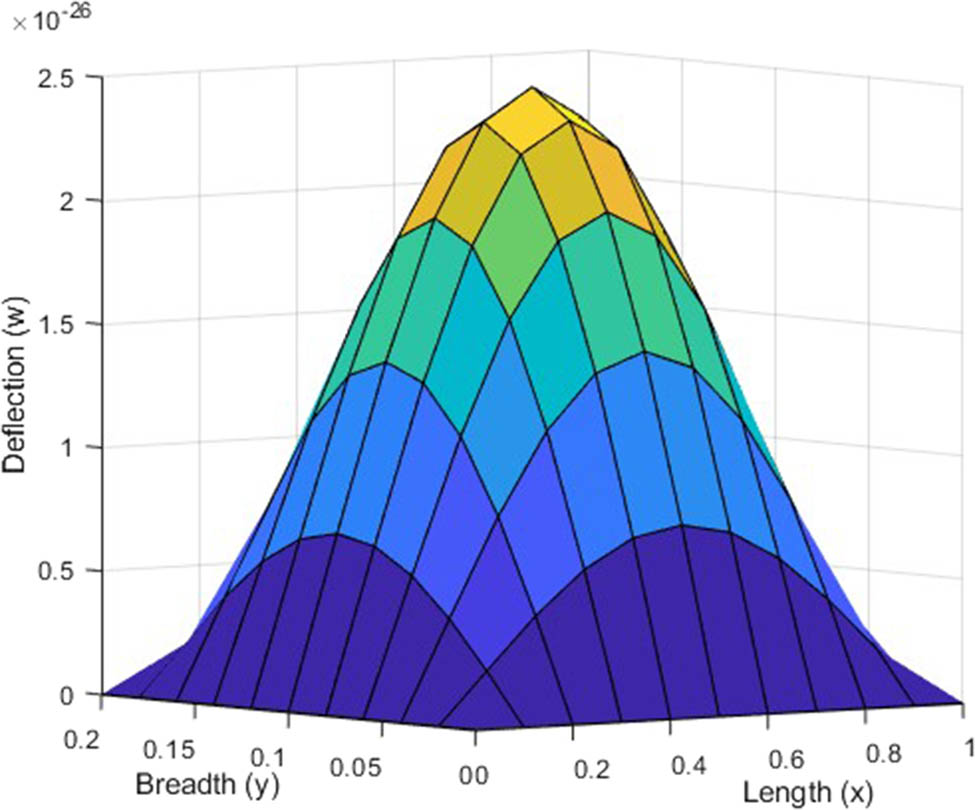
$Figure 3 Variation in deflection for (1,2) mode in visco-thermoelastic SSSS plate under uniform load along the ( x , y ) \left(x,y) dimensions at t = 30 t=30 .$

Figure 3

Variation in deflection for (1,2) mode in visco-thermoelastic SSSS plate under uniform load along the ( x , y ) dimensions at t = 30 .

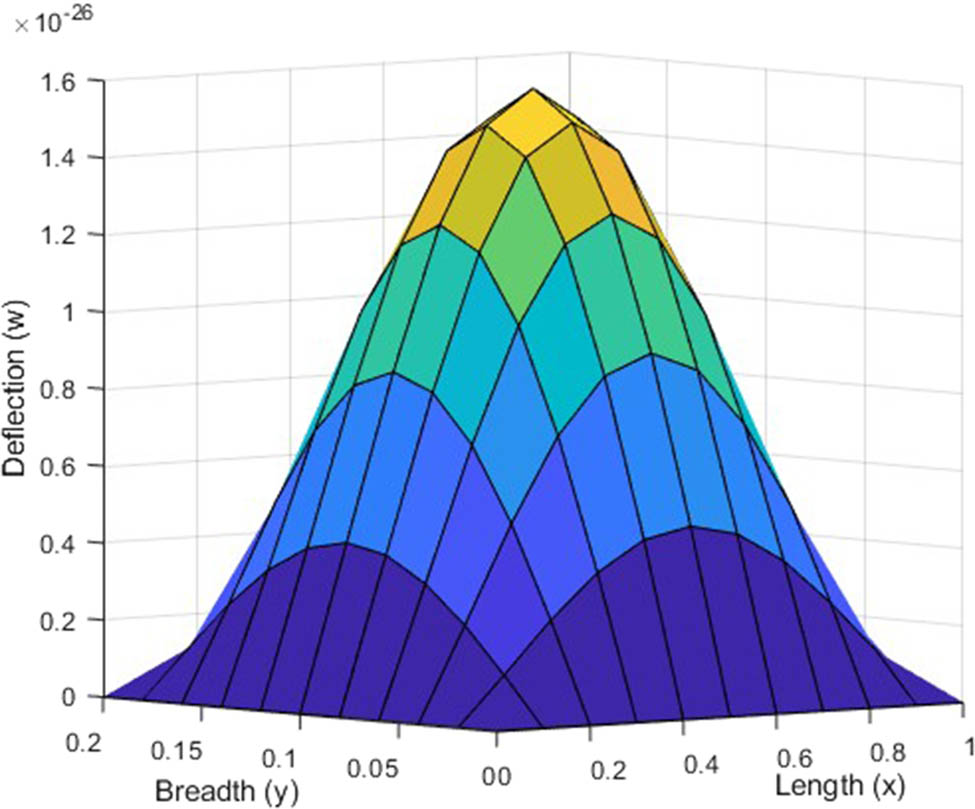
$Figure 4 Variation in deflection for (2,1) mode in visco-thermoelastic SSSS plate under uniform load along the ( x , y ) \left(x,y) dimensions at t = 30 t=30 .$

Figure 4

Variation in deflection for (2,1) mode in visco-thermoelastic SSSS plate under uniform load along the ( x , y ) dimensions at t = 30 .

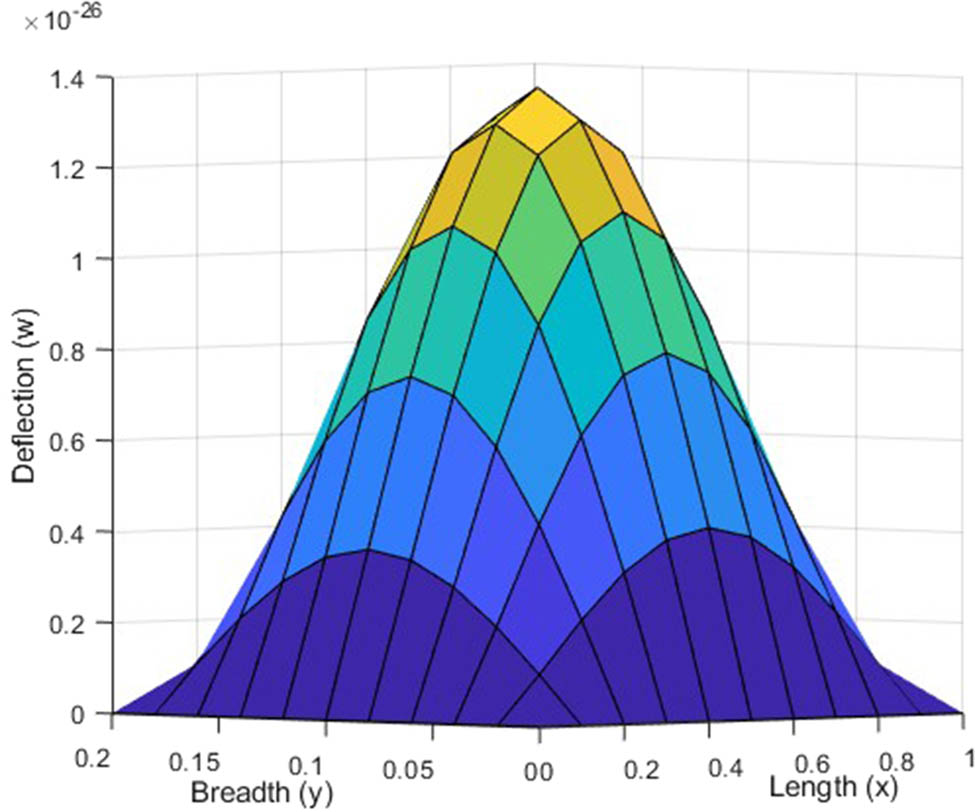
$Figure 5 Variation in deflection for (2,2) mode in visco-thermoelastic SSSS plate under uniform load along the ( x , y ) \left(x,y) dimensions at t = 30 t=30 .$

Figure 5

Variation in deflection for (2,2) mode in visco-thermoelastic SSSS plate under uniform load along the ( x , y ) dimensions at t = 30 .

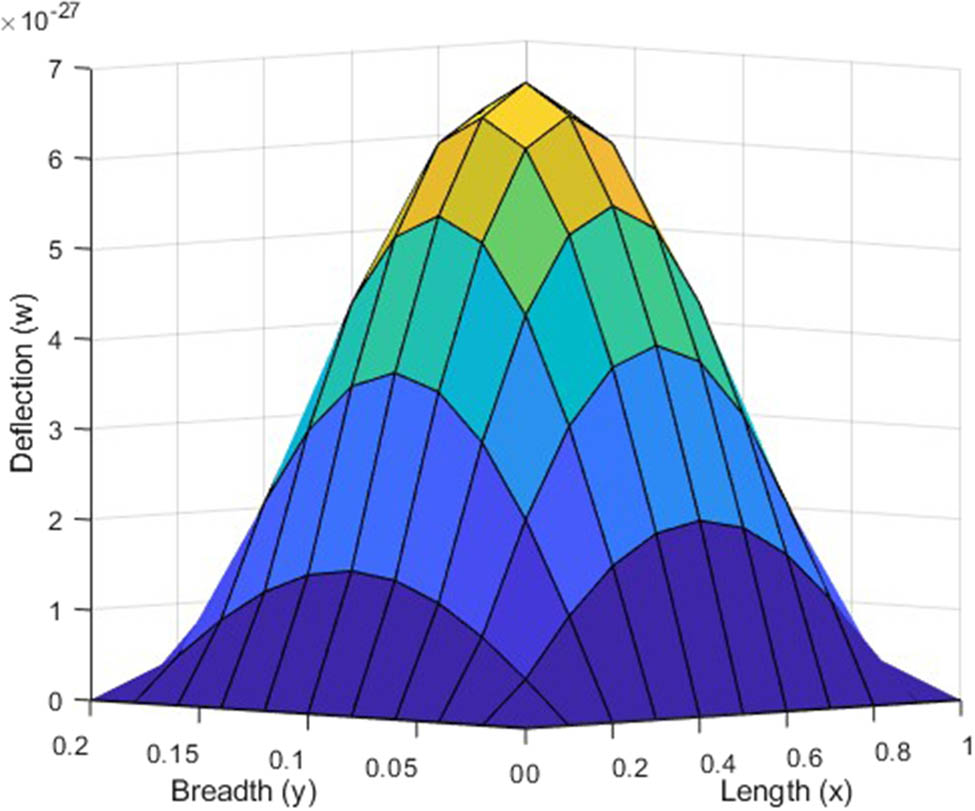
$Figure 6 Variation in deflection for (1,1) mode in visco-thermoelastic CSCS plate under uniform load along the ( x , y ) \left(x,y) dimensions at t = 30 t=30 .$

Figure 6

Variation in deflection for (1,1) mode in visco-thermoelastic CSCS plate under uniform load along the ( x , y ) dimensions at t = 30 .

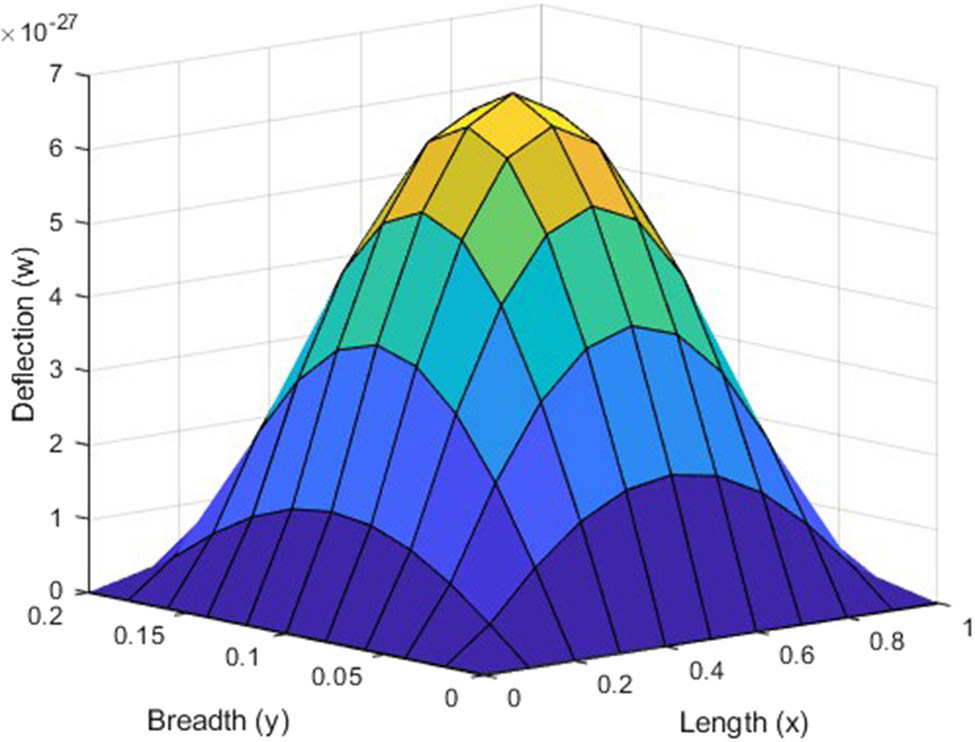
$Figure 7 Variation in deflection for (1,2) mode in visco-thermoelastic CSCS plate under uniform load along the ( x , y ) \left(x,y) dimensions at t = 30 t=30 .$

Figure 7

Variation in deflection for (1,2) mode in visco-thermoelastic CSCS plate under uniform load along the ( x , y ) dimensions at t = 30 .

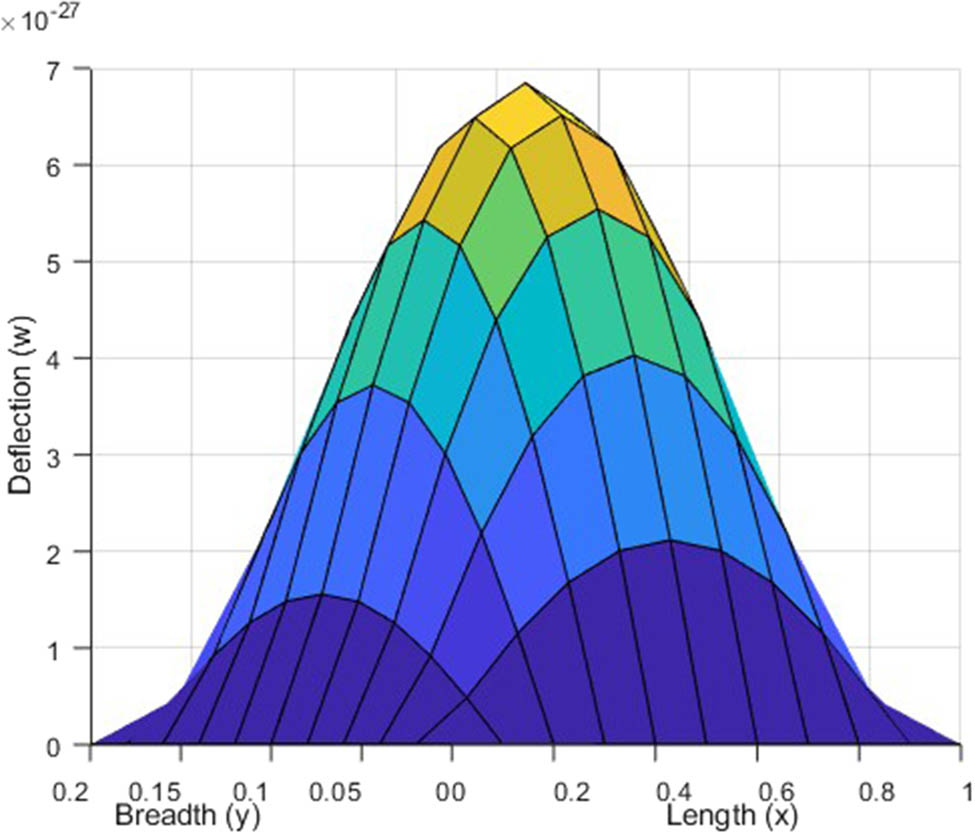
$Figure 8 Variation in deflection for (2,1) mode in visco-thermoelastic CSCS plate under uniform load along the ( x , y ) \left(x,y) dimensions at t = 30 t=30 .$

Figure 8

Variation in deflection for (2,1) mode in visco-thermoelastic CSCS plate under uniform load along the ( x , y ) dimensions at t = 30 .

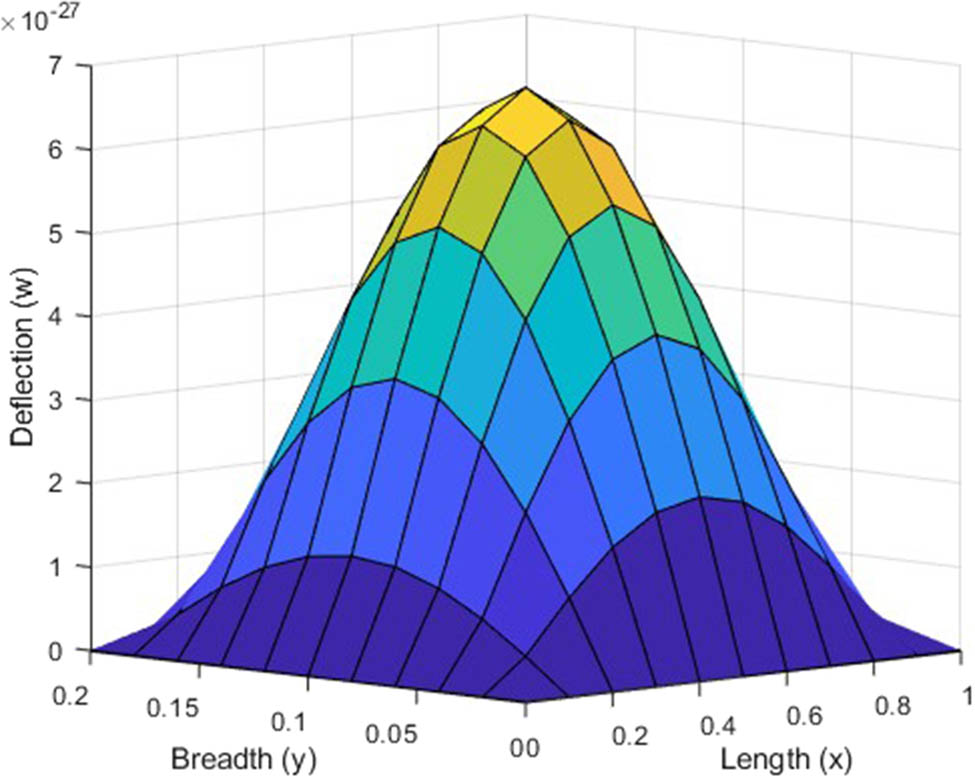
$Figure 9 Variation in deflection for (2,2) mode in visco-thermoelastic CSCS plate under uniform load along the ( x , y ) \left(x,y) dimensions at t = 30 t=30 .$

Figure 9

Variation in deflection for (2,2) mode in visco-thermoelastic CSCS plate under uniform load along the ( x , y ) dimensions at t = 30 .

The deflection plot clearly signifies the zero deflection at all the four edges. In case of Figures 6–9, the clamped edges are observed to be flat, which signifies that rotation is restricted around these edges. While, in case of Figures 2–5, the absence of flatness in simply supported edges signify that bending of edges is allowed here. It has been remarked that the magnitude of deflection is maximum at the center of the plate and it decreases as we deviate from center in either direction. The symmetric deflection profile depicts the uniform loading on the plate.

Also, it is observed that w 11 < w 12 < w 21 < w 22 in case of SSSS plate, but the values are in different order in case of CSCS plate w 12 < w 22 < w 11 < w 21 . The change in deflection due to different mode is found to be more forceful in SSSS plate than CSCS plate. The deflection is observed to be high in magnitude in SSSS as compared to CSCS.

7 Conclusion

An investigation was conducted into the dynamic, behavior of a uniform, isotropic visco-thermoelastic rectangular plate subjected to uniform loading. The Laplace transform FFST has been used w.r.t. time and space domain, respectively. It is infered that

The magnitude of deflection is more in SSSS as compared to CSCS.
The deflection curve is symmetrical about the center of plate. The deflection is found to be more symmetrical along both the dimensions in case of SSSS as compared to CSCS.
Maxima of deflection occurs at the center of plate and its magnitude diminishes progressively as it moves further away in either direction.
The change in deflection due to different modes is found to be more pronounced in SSSS plate than CSCS plate.

8 Future Work

The present study provides a comprehensive analysis of the deflection behavior of a rectangular plate under uniform loading. However, several aspects remain open for further exploration. Future research can focus on extending the analysis of deflection on circular plate resonators. Additionally, the impact of loading can be studied by incorporating anisotropic properties and variable thickness to better represent real-world materials.

Funding information: The authors state no funding involved.
Author contributions: Deepti Chopra: writing – original draft and visualization; Prince Singh: writing – review and editing, and supervision.
Conflict of interest: The authors state no conflict of interest.
Data availability statement: Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.

References

[1] Lord HW, Shulman Y. A generalized dynamical theory of thermoelasticity. J Mech Phys Solids. 1967;15(5):299–309. 10.1016/0022-5096(67)90024-5Suche in Google Scholar

[2] Bauchau O, Craig J. Kirchhoff plate theory. In: Structural analysis. Dordrecht: Springer Netherlands; 2009. p. 819–914. 10.1007/978-90-481-2516-6_16Suche in Google Scholar

[3] Sharma J, Grover D. Thermoelastic vibration analysis of MEMS/NEMS plate resonators with voids. Acta Mech. 2012;223(1):167–87. 10.1007/s00707-011-0557-0Suche in Google Scholar

[4] Grover D. Viscothermoelastic vibrations in micro-scale beam resonators with linearly varying thickness. Can J Phys. 2012;90(5):487–96. 10.1139/p2012-044Suche in Google Scholar

[5] Li P, Fang Y, Hu R. Thermoelastic damping in rectangular and circular microplate resonators. J Sound Vibrat. 2012;331(3):721–33. 10.1016/j.jsv.2011.10.005Suche in Google Scholar

[6] Lal R, Kumar Y. Transverse vibrations of nonhomogeneous rectangular plates with variable thickness. Mech Adv Mater Struct. 2013;20(4):264–75. 10.1080/15376494.2011.584273Suche in Google Scholar

[7] Lal R, Saini R. Transverse vibrations of nonhomogeneous rectangular Kirchhoff plates of variable thickness. In: Mathematical analysis and its applications: Roorkee, India, December 2014. New Delhi: Springer India; 2015. p. 609–18. 10.1007/978-81-322-2485-3_50Suche in Google Scholar

[8] Rana U, Robin R. Study of damped vibration of non homogeneous rectangular plate of variable thickness. Int J Eng Appl Sci. 3(8):257605. Suche in Google Scholar

[9] Grover D. Damping in thin circular visco-thermoelastic plate resonators. Can J Phys. 2015;93(12):1597–605. 10.1139/cjp-2014-0575Suche in Google Scholar

[10] Partap G, Chugh N. Thermoelastic damping in microstretch thermoelastic rectangular plate. Microsyst Tech. 2017;23:5875–86. 10.1007/s00542-017-3350-8Suche in Google Scholar

[11] Grover D, Seth R. Generalized visco-thermoelasticity theory of dual-phase-lagging model for damping analysis in circular micro-plate resonators. Mech Time-Dependent Materials. 2019;23:119–32. 10.1007/s11043-018-9388-xSuche in Google Scholar

[12] Liu S, Ma J, Yang X, Sun Y, Yang J, Wang X. Theoretical 3D model of thermoelastic damping in laminated rectangular plate resonators. Int J Struct Stability Dyn. 2018;18(12):1850158. 10.1142/S0219455418501584Suche in Google Scholar

[13] Zuo W, Li P, Du J, Huang J. Thermoelastic damping in trilayered microplate resonators. Int J Mech Sci. 2019;151:595–608. 10.1016/j.ijmecsci.2018.12.015Suche in Google Scholar

[14] Khan D, Ali G, Kumam P, ur Rahman A. A scientific outcome of wall shear stress on dusty viscoelastic fluid along heat absorbing in an inclined channel. Case Stud Thermal Eng. 2022;30:101764. 10.1016/j.csite.2022.101764Suche in Google Scholar

[15] Chopra D, Singh P. Analysis of deflection in visco-thermoelastic beam resonators subjected to harmonic loading. Int J Appl Mech Eng. 2022;27(2):35–52. 10.2478/ijame-2022-0018Suche in Google Scholar

[16] Ali G, Mahariq I, Abdelmohimen MA, Ahammad NA, Ali MR, Khan D. Enhanced heat transfer in viscoelastic fluids with periodic magnetic fields and dusty nanoparticles between two parallel plates under thermal radiation. Case Stud Thermal Eng. 2024;60:104686. 10.1016/j.csite.2024.104686Suche in Google Scholar

[17] Rao SS. Vibration of continuous systems. Hoboken, NJ: John Wiley & Sons; 2019. Suche in Google Scholar

Received: 2024-05-25

Revised: 2025-04-07

Accepted: 2025-05-05

Published Online: 2025-07-02

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

https://doi.org/10.1515/nleng-2025-0148

Schlagwörter für diesen Artikel

visco-thermoelastic; uniform loading; method of residues; simply supported; clamped

Creative Commons

BY 4.0