Abstract
Introduction
In order to improve the effect of intelligent recommendation of piano repertoire, this article combines the convolutional neural network (CNN) model to perform intelligent analysis of piano repertoire and combines personal preference for piano repertoire recommendation.
Objectives
Moreover, this article conducts research on the identification of piano waveform features in the process of piano practice by piano practitioners in complex situations.
Methods
In addition, this article conducts waveform extraction through hardware design, which provides a basis for piano preference identification, and theoretically analyzes the design of sealed resonant windows and the design of concentrated electric field strength resonant gaps.
Results
About 92.72% of the samples have a maximum ratio of more than 0.9, and the maximum ratio of the samples is greater than 0.5. That is to say, most of the errors still come from prediction and classification errors, and a small part of them are data errors. Finally, this article constructs an intelligent recommendation model for piano repertoire based on the CNN model after introducing the resonance element into the piano waveform characteristic factor limiter.
Conclusion
The proposed CNN-based recommendation algorithm demonstrates high accuracy and effectively enhances piano repertoire recommendations.
1 Introduction
The frequency domain is a description of the frequency characteristics of the signal. The frequency domain coordinate system takes the frequency value as the abscissa and the ordinate as the statistical quantity of each frequency value. Frequency domain analysis is an important part of signal analysis, mainly used in electronics, acoustic signals, and other fields. Nowadays, piano music in the network generally stores digital audio information, which is generated by sampling analog audio data. The higher the sampling frequency, the larger the amount of digital audio data, and the better the fidelity effect of digital audio. As a form of sound wave signal, digital audio can also be analyzed in the frequency domain and decomposed into tonal components of different frequencies [1].
Some studies use piano frequency domain research to extract piano audio signals, thereby improving the efficiency of piano audio data processing. The frequency domain is composed of many sine functions (or cosine functions, or a combination of the two), and these sine functions have different amplitudes and phases, representing that the audio has rich information in the frequency domain [2]. The digital audio information stored in piano music is directly expanded to the energy amplitude trend that changes with time, which is called the time domain characteristic of the audio signal and is the most intuitive representation of the signal. Time domain analysis and frequency domain analysis consider signal characteristics from two perspectives. For digital audio, the amount of data in the time domain is very large. The higher the sampling frequency, the larger the amount of data, which often leads to a large amount of calculation [3]. Compared with time domain analysis, the data volume of frequency domain analysis is smaller, and frequency domain analysis can better reflect some substantial characteristics. Therefore, frequency domain analysis has gradually become the mainstream of signal analysis. The frequency domain feature is the feature result obtained by the frequency domain analysis and is the basic feature for describing the audio signal. Using the frequency domain feature to represent music is not only easy to implement, but also reduces the amount of data and facilitates data processing [4].
In the process of decomposing piano signal features, it is necessary to extract the rapid changes of piano signals through reliable algorithms, in order to accurately improve the extraction of piano signal features. There are many ways to decompose the signal; the more commonly used method is to use several sine and cosine functions to fit complex signal changes. Compared with other methods, the sine and cosine functions have many advantages: the combination of several sine and cosine functions can fit complex waveforms; the function parameters are few, the input and output change little, only the phase and amplitude are changed [5]. The integral form of the function is still a sine–cosine function, which is convenient when integrating time-domain data. Fourier transform (FT) is one of the important basic algorithms of frequency domain analysis. Initially, the computational load of FT was still very large, and many subsequent algorithms have been greatly improved on this basis, such as fast Fourier transform (FFT), which greatly saves computation time while maintaining frequency domain accuracy [6].
Digital processing captures the player’s pitch, rhythm, strength, and other parameters through sensors and audio analysis technology, forming a multi-dimensional performance data file. These data provide an objective quantitative basis for the subsequent track recommendation. The system can record the user’s practice frequency, error types, and improvement tracks and analyze its technical weaknesses and advantages in combination with the artificial intelligence algorithm, so as to match the track library suitable for improving specific skills. Through the “digital portrait” generated by the intelligent system based on the analysis of user’s performance data, the system can recommend tracks consistent with its technical level and style preference. For example, rhythmic etudes are recommended first for those with weak rhythm control, and the real-time feedback mechanism enables the recommendation system to have the ability to dynamic update.
At present, the recommendation of piano curved surface mostly focuses on the interests of users and does not focus on capturing the player’s pitch, rhythm, strength, and other parameters through digital processing and sensor and audio analysis technology. Therefore, it is necessary to combine digital technology to improve the capture effect of pitch, rhythm, strength, and other parameters, so as to recommend more appropriate piano tracks for users.
Based on the feature extraction technology of piano waveform in various complex environments, this article combines digital processing technology with piano hardware structure to design a resonant element suitable for piano signal extraction. Based on the extraction of the piano waveform, combined with the convolutional neural network (CNN) model, the intelligent recommendation model of piano repertoire is constructed. Combined with digital technology, the capture effect of pitch, rhythm, strength, and other parameters is improved, and a more suitable piano repertoire is recommended for users.
2 Related work
In the piano area recommendation, it is necessary to collect piano music preferences and classify them, and based on this, recommend piano pieces that are suitable for personal taste according to the customer’s personalized characteristics. Dean [7] concluded that the preference for piano music is positively correlated with extroversion, and the degree of preference for popular piano music and Western classical piano music is negatively correlated with introversion and extroversion, but there are correlations between different piano music types and personality traits. Not significantly. Mahanta et al. [8] took non-piano music majors as the research object and found that traditional piano music was negatively correlated with spirituality, and popular and trendy piano music was positively correlated with introversion, which was just the opposite of Guo Na’s previous research results. Hong et al. [9] found that students with neutral personality, emotional anxiety, emotional centeredness, and mental loneliness prefer popular piano music; students with an extroverted personality and emotional stability prefer traditional piano music much more than other groups of students. Bando and Tanaka [10] selected subjects with a larger age span and added the variable of different contexts. The results showed that if subjects were placed in different life situations, the correlation between personality characteristics and piano music preference would be weakened, but the findings that rigor and agreeableness are positively related to traditional piano music are still consistent with previous findings. Another part of the research used the Big Five Personality Scale to measure personality traits. Jiam and Limb [11] show that agreeableness is negatively correlated with traditional piano music and classical piano music; openness is positively correlated with popular piano music, classical piano music, and piano musicals, and there is a certain difference with foreign-related studies. Foley and Schutz [12] divide piano music types into four piano music preference dimensions through factor analysis and then analyze the relationship between different piano music preference dimensions and personality variables. The results in the dimension of classical piano music are completely opposite to popularization and positively correlated with agreeableness.
Research on piano surface preferences is often conducted from a psychological perspective, providing a certain basis for intelligent recommendation of pianos. Piano music preference is the expression of the individual’s preference for specific piano music objects, and it is an individual’s tendency to choose piano music objects, which is expressed as the pleasure of acceptance and the degree of liking. Chari et al. [13] pointed out that piano music preference is an individual’s choice of the preferred piano music in various situations. The piano music preference model is an interactive hierarchical model that assumes several levels of interacting factors that influence individual piano music preferences. The model includes variables related to piano music and cultural characteristics (friends, family, teachers), some of which are related to listeners (gender, personality traits, piano musical ability, etc.). Dissegna et al. [14] show that piano music preference is a decision based on an individual’s liking or continuing interest in piano music. Pamies [15] believes that piano music preference is a subjective preference choice made by the appreciator in two or more piano music works or elements that is immediate and does not involve cognitive or aesthetic judgments. Piano music preference is the simplest form of emotional response to piano music, which is the result of a combination of factors. The choice of piano music preference is affected by many factors such as age class, gender characteristics, educational level, personality traits, piano music elements, and listening environment.
Some experts and scholars analyze the positive impact of piano music on users from a psychological perspective. The Mozart effect in psychological research is a phenomenon that can significantly improve the cognitive performance of test subjects by listening to piano music similar to Mozart for a certain period of time. In the proposed piano training method, the learner’s rest time is determined by collecting the learner’s EEG data, and combined with the learner’s piano music preference, the piano music with the Mozart effect is played for a certain period of time to help the trainer eliminate fatigue faster. At the same time, this training method can significantly improve the learning efficiency of learners by combining physiological data and psychological laws [16]. In the piano music preference test part, after the tester wears the brain–computer acquisition device, the piano music of different genres is played, and the brainwave data of the tester listening to the piano music of different genres are collected, respectively, and sent to the centralized processing platform to calculate the test. Based on the tester’s brain relaxation degree in different musical styles, combined with the tester’s historical piano music data, the recommendation algorithm is used to obtain the tester’s preferred piano music genre library, and the tester’s piano music preference repertoire is generated [17]. The rest time determination part collects the trainer’s brainwave data through the brain–computer device when the trainer is playing the piano and sends it to the data central processing platform to calculate the trainer’s concentration and brain volume in this time period. When the trainer’s concentration is lower than the given threshold, the trainer will be prompted to rest, and the piano music in the trainer’s personal preferred piano music library will be automatically played. By combining the physiological data and psychological laws of trainers, the training time and rest time with the best training efficiency are determined, and the most effective piano music is provided for trainers to relax, helping them to effectively eliminate fatigue, which significantly improves the learning efficiency of trainers per unit time, thus helping trainers to better master skills [18].
In the era of big data, recommendation methods for massive music data are facing new challenges and opportunities. On the one hand, the processing of massive data has become complex and needs to be combined with personalized user needs, requiring corresponding upgrades to existing recommendation algorithms. On the other hand, the problems existing in the original recommendation algorithms also urgently need to be solved, such as the “cold start” problem of collaborative filtering (CF) recommendation [19]. In contrast, new computer technologies such as big data processing and deep learning are constantly emerging, which will help design new recommendation algorithms with stronger processing capabilities and higher recommendation accuracy [20].
This article conducts research on the identification of piano waveform features in the process of piano practice by piano practitioners in complex situations. In addition, this article conducts waveform extraction through hardware design, which provides a basis for piano preference identification, and theoretically analyzes the design of sealed resonant windows and the design of concentrated electric field strength resonant gaps. Finally, this article constructs an intelligent recommendation model for piano repertoire based on the CNN model after introducing the resonance element into the piano waveform characteristic factor limiter.
This article combines the CNN model to carry out the intelligent analysis of the piano repertoire and combines the personal preference to recommend the piano repertoire, which will help to improve personal personality development.
3 Feature extraction of piano waveforms in a complex environment
This article combines the piano practitioners in complex situations to carry out the piano waveform feature recognition in the process of piano practice and conducts waveform extraction through hardware design, which provides a basis for piano preference recognition and provides a reliable piano repertoire for piano practitioners.
The model in this article mainly consists of two parts, as shown in Figure 1. The first part is the piano waveform feature extraction part, and the second part is the CNN piano surface recommendation module. The piano feature extraction module mainly extracts and analyzes piano signal features through various complex environment piano waveform feature factor limiters and resonant elements. The obtained information is transmitted to the CNN model-based piano track intelligent recommendation system as the user feature basis, recommending more accurate tracks for users.
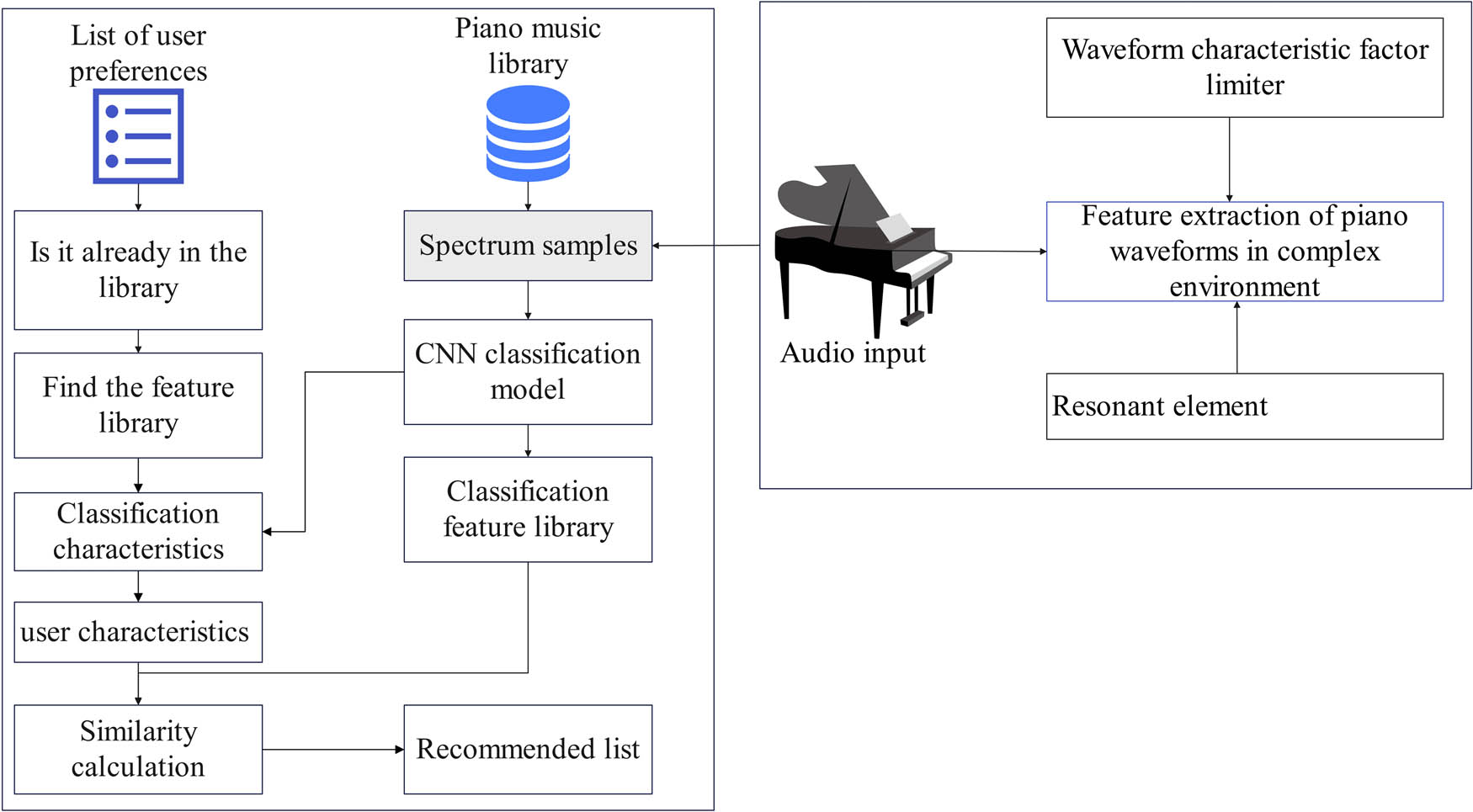
Piano feature extraction algorithm model and piano surface recommendation model.
3.1 Design of a limiter for piano waveform characteristic factors in various complex environments
The frequency of the piano waveform eigenfactor is a very important parameter of the piano waveform eigenfactor, and the piano structure density is n 0. We can assume that there is a small displacement Δx between the electrons and the relatively stationary ions, so there is an excess of electrons on the side where the characteristic factor of the slab piano waveform appears. However, there is a phenomenon of excess ions on the other side of the characteristic factor of the slab piano waveform. We can think of these two charge regions as thin enough surfaces with a surface charge density of n 0 e, and the resulting electrostatic field is
where
This electric field has a tendency to pull the electrons back to their original positions, which is called the restoring force. In the absence of an external magnetic field and the thermal motion of charged particles is negligible, the equation of motion for a single electron is
Among them, the electron mass is
where
Among them,
is called the electronic piano waveform characteristic factor frequency. By substituting each constant and combining formula (4) and
where
Similarly, electrostatic oscillations of ions can be discussed. We can assume that electrons are more active than other particles, and the electrons form a uniform distribution in space during the entire oscillation period, which mainly depends on the thermal motion of the electrons themselves. The ion oscillates in the electron background, where the electron background is uniformly distributed, and the ion oscillation frequency is
Among them,
Due to the fact that the mass of particles is much greater than that of electrons, there exists a situation where
In general, the oscillation frequency of the characteristic factor of the piano waveform can be written as the following formula, which also considers the movement of electrons and ions under the action of the electric field
3.2 Design of resonant elements
The structure of the resonance window can be considered as a metal diaphragm with a sealed solid medium. Typically, the sealing medium is low-loss glass or ceramic. Because the window is a vacuum-sealed element, the tightness of the medium and the metal should also be considered.
Figure 2 is a schematic diagram of a commonly used resonant window structure. The 10 and 3 cm bands are commonly used.
Schematic diagram of the structure of the resonance window.
The resonant window is a resonant element. In the waveguide piano waveform characteristic factor limiter, its equivalent circuit and frequency response curve are shown in Figure 3.
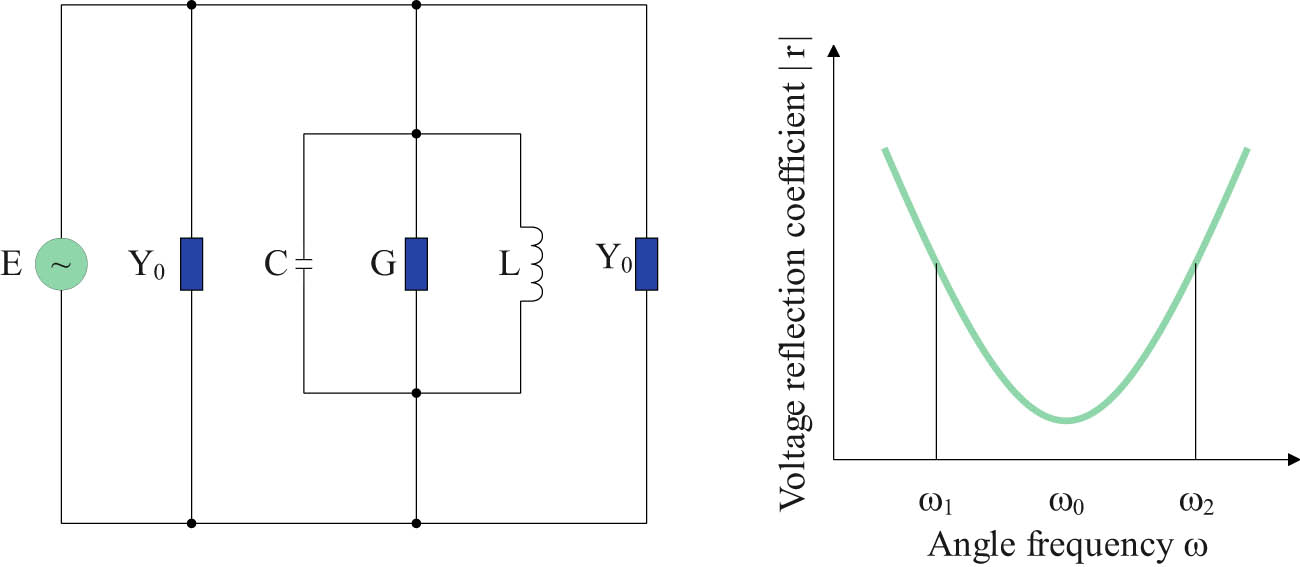
Response diagram of resonant tank and frequency.
The susceptance B of the equivalent circuit is
The angular frequency at
Because there is a relationship between the resonant frequency and the resonant angular frequency
In the formula, C is considered the equivalent capacitance of the resonant window, L is considered the equivalent inductance of the resonant window, G is considered the equivalent conductance of the resonant window, and
The on-load quality factor of the resonant window is defined as
In the formula,
When
By combining formulas (13) and (14), the calculation formula for
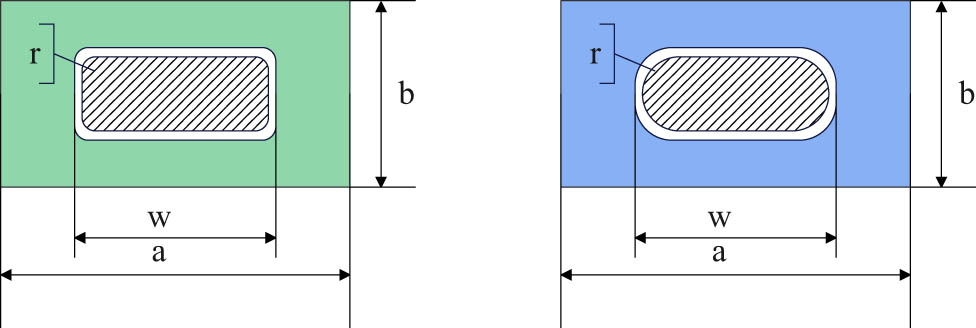
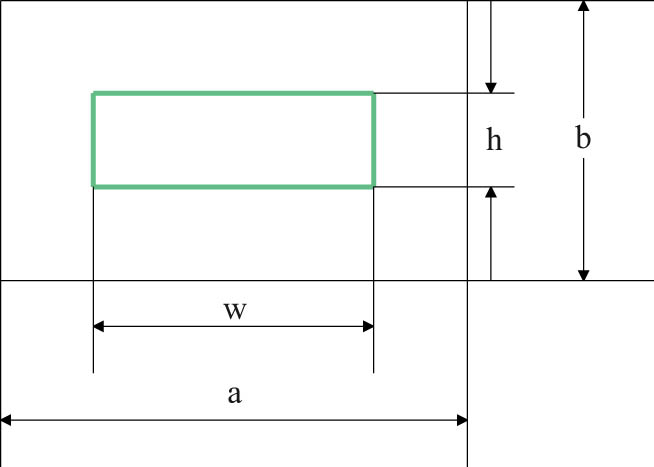
The calculation of the air medium rectangular window is the basis for the design of the rounded window. The structural form of the rectangular window is shown in Figure 4.
Schematic diagram of the structure of the resonant window.
The rectangular window can be regarded as a small rectangular waveguide, and the characteristic impedance of the small waveguide is equal to that of the main waveguide, so the resonant wavelength of the rectangular window can be calculated
Therefore, it can be obtained
Among them, the broad side of the inner section of the main waveguide is denoted as a, the narrow side of the inner section of the waveguide is denoted as a, the broad side of the rectangular window is denoted as w, h is the narrow side of the rectangular window, and
However, the resonant windows used in practice are not right-angled. In order to avoid the local stress of the glass sealing, the right angle is usually changed to a small rounded corner or a semicircle. In order to calculate the rounded window, the rounded window can still be regarded as a rounded rectangular waveguide, so that the characteristic impedance of the rounded rectangular waveguide is equal to that of the main waveguide, and the resonance wavelength of the rounded window can be obtained. However, the characteristic impedance of the rounded rectangular waveguide is difficult to calculate precisely, and we have only approximate methods. The rounded rectangular waveguide can be equivalent to a right-angled rectangular waveguide under the condition that the cross-sectional area and height are equal, and the characteristics of the two are the same. According to this principle, after the rounded rectangular waveguide is equivalent to the right-angled rectangular waveguide, we can obtain the broadside dimension
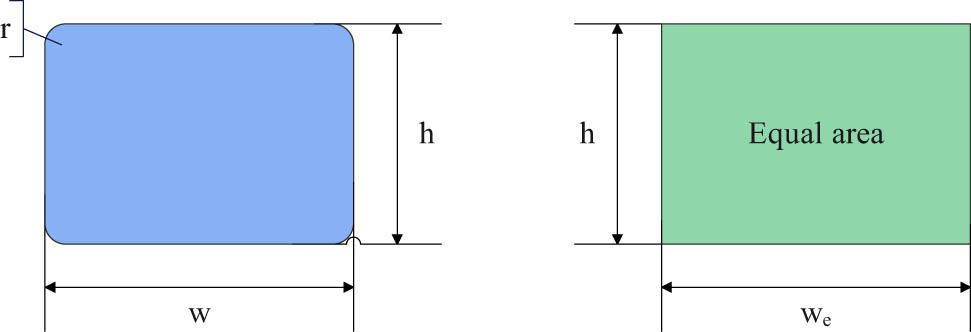
Rounded rectangular waveguide is equivalent to a right-angled rectangular waveguide.
According to the condition of equal area, it can be seen from the figure:
Therefore,
By making the characteristic impedance of the equivalent right-angle rectangular waveguide equal to the characteristic impedance of the rectangular waveguide of the main waveguide, the resonant frequency of the rounded window can be obtained
The resonant frequency of the rounded window is obtained as
When
After sealing the resonant window with a solid dielectric, the equivalent capacitance of the window increases, and the resonant frequency decreases. At this time, the resonance wavelength formula of the rectangular resonant window becomes
In the formula,
Comparing the two equations, it can be seen that after the resonant window is sealed with a solid medium, it is equivalent to changing the width
The above formula only considers the influence of the dielectric constant of the medium on the resonance wavelength and does not consider the relationship between the thickness of the medium and the resonance wavelength. In fact, the change of dielectric thickness is very sensitive to the influence of the resonance frequency. For an X-band resonant window, an increase of 0.05 mm in 7070 glass thickness reduces the resonant frequency by about 150–200 MHz. Therefore, when calculating the resonant frequency of solid dielectric windows, the effect of dielectric thickness must be considered. Therefore, it can be modified as
Therefore, it can be obtained
In this formula,
According to the design requirements, the resonant gap and the resonant window should be tuned to the same frequency, but the value of the loaded quality factor
Usually, 23 resonant gaps are used in the wave-guiding piano waveform characteristic factor limiter, but there are also cases where one resonant gap is used, and two resonant gaps are used in this article. The structure of the resonant gap is shown in Figure 6, in which the pheasant, the electrode, is the enemy of the concentrated electric field. Changing its size can change its equivalent capacitance C, and changing the width of the diaphragm can change its equivalent inductance L.
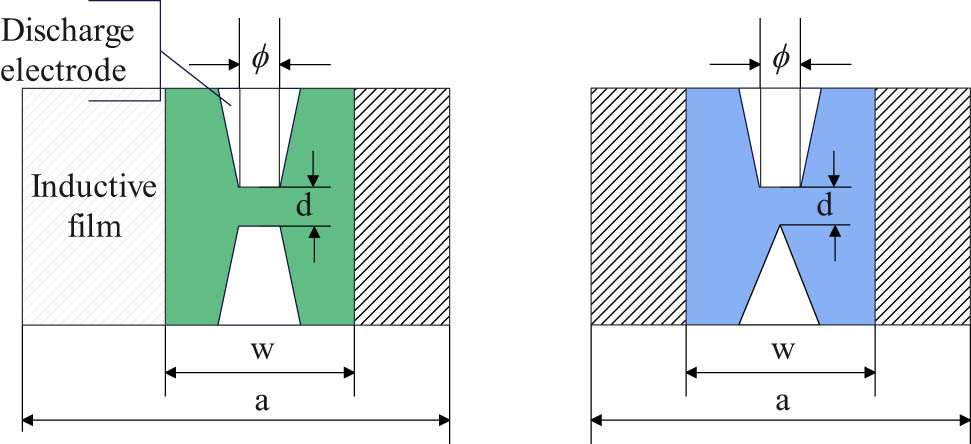
Structure of the resonance gap.
There are two parameters that characterize the resonant gap, namely the resonant frequency
The planned inductive admittance of the symmetrical inductive diaphragm in the eigenfactor limiter of the waveguide piano waveform is approximated as
Among them, a is the width of the inner section of the waveguide, λ go is the wavelength of the resonant waveguide, and w is the slit width of the diaphragm.
We set
The curve given in Figure 7 shows the relationship between the susceptance parameter K and the normalized slit width w/a of the resonant gap diaphragm. According to the given f 0 (or ω 0) and Q L2, the susceptance parameter −K is calculated by the formula. The value of w/a can be found out using the curve in Figure 6 [21,22], so that the slit width dimension w of the resonant gap diaphragm can be calculated.
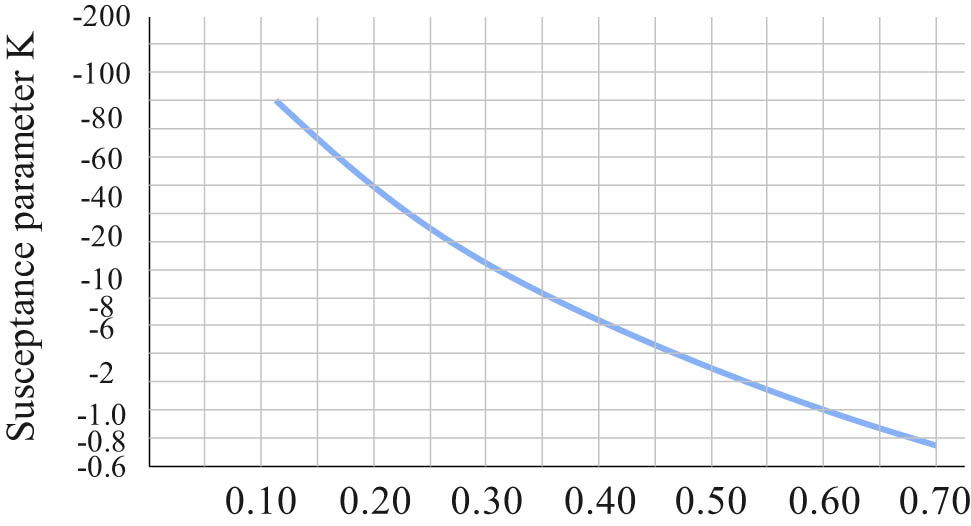
Relationship curve between the susceptance parameter and the normalized slit width of the resonant gap diaphragm.
In the parallel resonant circuit composed of the equivalent inductance of the metal diaphragm and the gap capacitance of the discharge electrode, the slit width w of the diaphragm determines the size of the equivalent inductance L. The inductance L increases with the increase of the slit width w. The size of the equivalent capacitance of the resonance gap is determined by the distance d between the cones. The larger the gap distance d, the larger the capacitance C. In fact, in the design process of the resonance gap, there is no need to calculate the size of d, only d is required to be less than a certain minimum value d min. One of the empirical formulas is as follows:
In the formula, p is the pressure of the gas filled in the limiter of the waveform characteristic factor of the waveguide piano, and
3.3 Intelligent recommendation of piano repertoire based on the CNN model
Combined with the algorithm in the second part, the intelligent recognition of piano music features is carried out. This part uses the CNN model to intelligently recommend piano pieces. The CNN model in this article is shown in Figure 8.
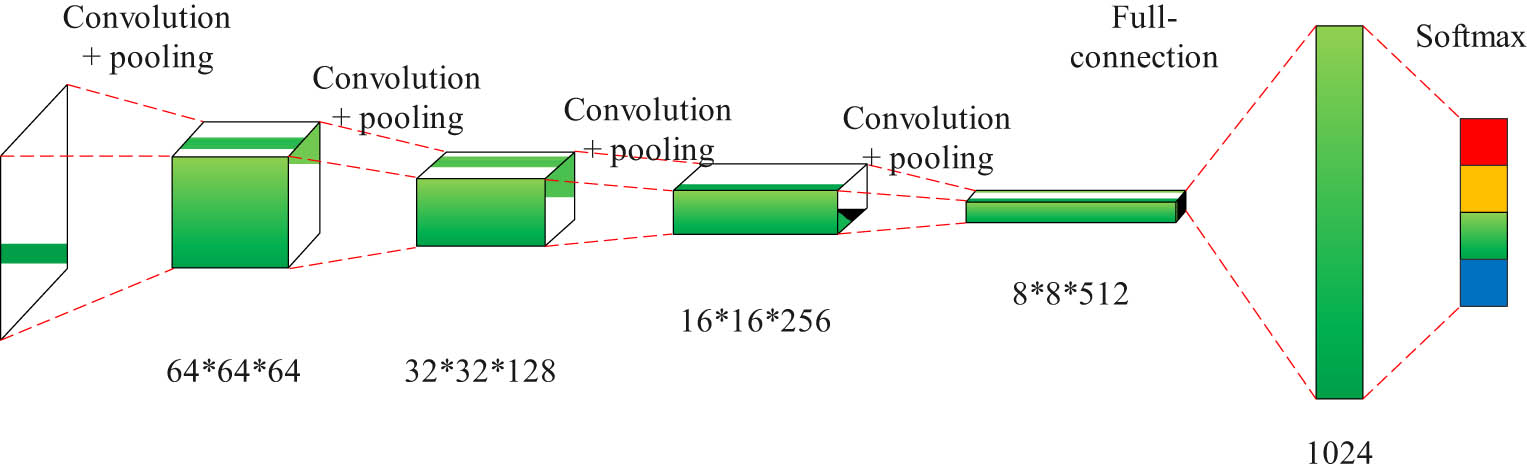
CNN model.
On the basis of statistics and analysis, this article further processes the classification results, optimizes the classification results, and obtains the classification features of piano music. The intelligent recommendation model for piano pieces based on the CNN model constructed in this article is shown in Figure 9.
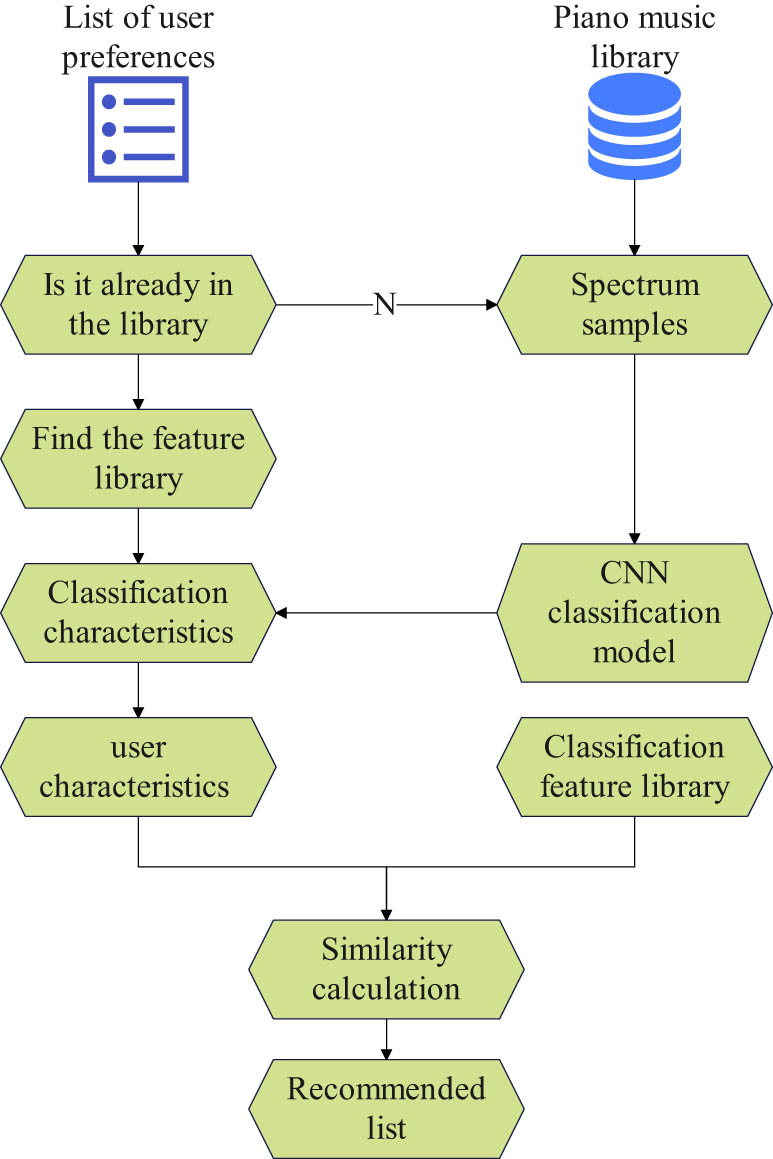
System model.
The core of the model is based on the feature extraction ability of CNN, combined with user features and piano track features, to achieve accurate personalized recommendations. The input items include the user’s age, gender, music preferences, historical playback history, etc. These features are encoded as numerical vectors, which serve as one of the inputs to the model. The characteristics of the qin melody can be extracted from multiple dimensions, such as rhythm, melody, harmony, style, etc. These features are also encoded as numerical vectors as another input to the model. Use CNN for feature extraction of user features and piano repertoire features. CNN can automatically learn and extract advanced features useful for recommendation tasks through multi-layer convolution and pooling operations. Merge the extracted results of user features and piano track features. This can be achieved through concatenation, weighted summation, and other methods to combine the features of users and tracks, providing comprehensive information for subsequent recommendation tasks. After feature fusion, calculate the similarity between user features and each piano piece feature. This can be achieved through measurement methods such as cosine similarity and Euclidean distance. The higher the similarity, the more the track matches the user’s preferences. Sort piano pieces based on similarity calculation results and generate a recommended list. The songs in the recommended list are arranged in descending order of similarity, and users can choose based on the songs in the list.
A trained CNN can predict and classify the frequency spectrum of piano music and obtain classification feature vectors. User feature calculation is based on the relationship between piano music and classification features, combined with the relationship between piano music and users, to obtain the relationship between users and classification features, and then match piano tracks according to users’ personalized needs, and obtain highly accurate matching results, thereby providing users with more reliable recommendation results.
4 Test
4.1 Test method
To verify the effectiveness of the proposed piano repertoire recommendation model (hereinafter referred to as the wave CNN model), a control experiment was designed to compare the model with existing models.
The main source of the dataset for this article is GiantMIDI Piano, MAESTRO Dataset, PianoMotion10M.
Each track contains the original audio waveform (sampling rate 44.1 kHz), manually annotated difficulty levels (1–10 levels), technical labels (arpeggios/chords/rhythms, etc.), and user interaction data.
About 1,000 users of different skill levels (beginner/intermediate/advanced) are simulated, and their historical performance data (pitch errors, rhythm stability, etc.) are recorded. The traditional CF, LSTM-based sequence recommendation model, and ResNet-18 audio classification recommendation model are selected as baseline models and compared with the wave CNN model. At the same time, accuracy, robustness, cold start performance, and computational efficiency are selected as comparison parameters.
4.2 Results
The performance comparison test results are shown in Table 1.
Performance comparison test results
| Model | Precision | Recall | MRR | Cold start accuracy | Response time (ms) |
|---|---|---|---|---|---|
| Wave-CNN | 0.85 | 0.78 | 0.70 | 0.64 | 123.60 |
| ResNet-18 | 0.73 | 0.67 | 0.61 | 0.49 | 97.85 |
| LSTM | 0.68 | 0.60 | 0.53 | 0.42 | 206.00 |
| CF | 0.57 | 0.50 | 0.44 | 0.22 | 51.50 |
The robustness test is conducted on the basis of the performance test. After adding the ambient noise (snr = 5 dB), the performance decline of each model is shown in Table 2.
Robustness test results
| Model | Noiseless environment | Noise environment (5 dB) | Degree of decline (%) |
|---|---|---|---|
| Wave-CNN | 0.85 | 0.78 | 8.23 |
| ResNet-18 | 0.73 | 0.58 | 20.35 |
| LSTM | 0.68 | 0.47 | 31.25 |
| CF | 0.57 | 0.38 | 33.32 |
This article makes the following statistical analysis on the CNN classification results, as shown in Figure 10.
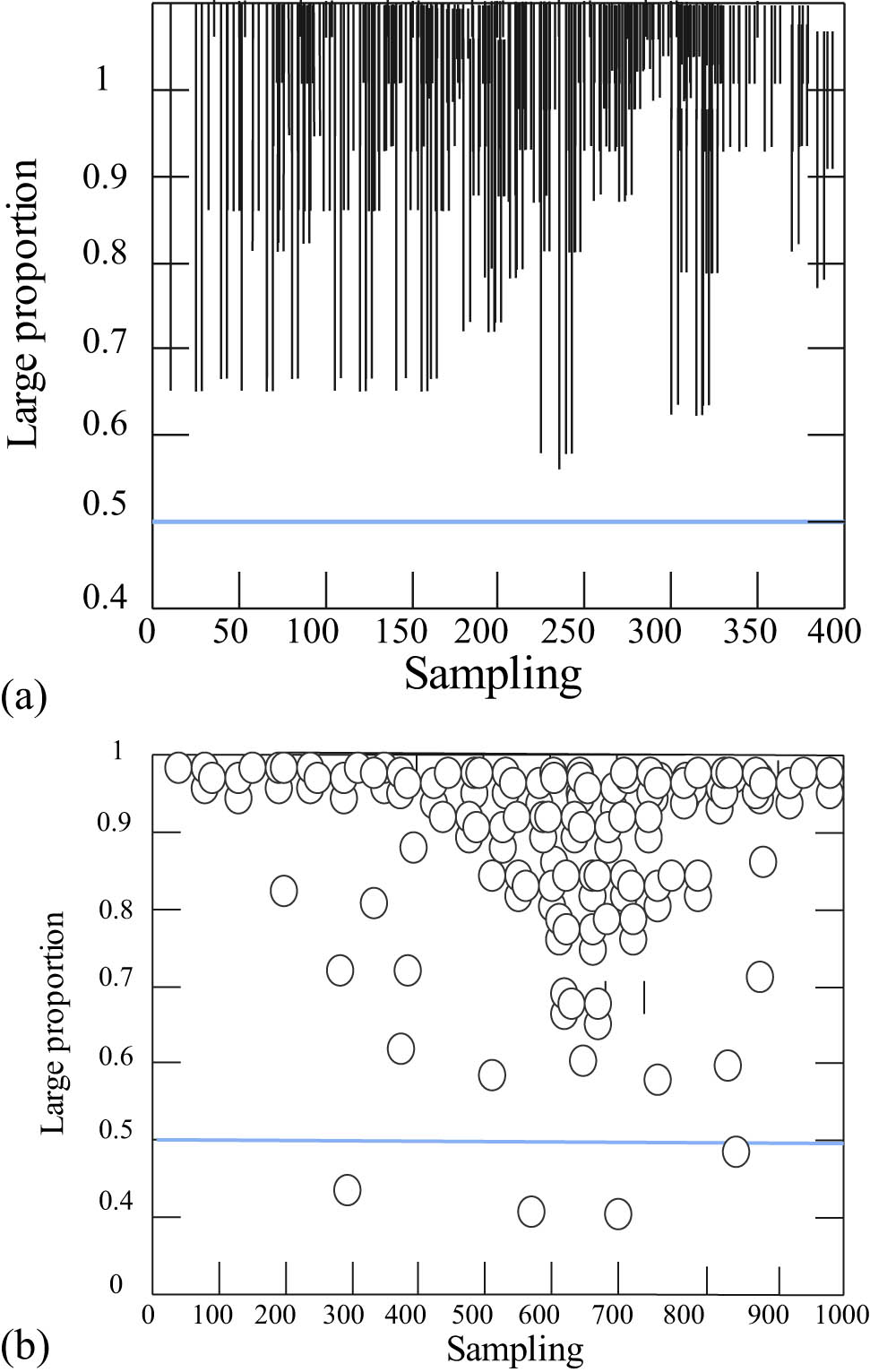
Test of recommended sample effect. The distribution of the maximum proportion of (a) the predicted classification for the test sample and (b) music test sample components.
4.3 Analysis and discussion
In Table 1, the precision of wave CNN is 0.85, recall is 0.78, which is significantly higher than other models. The precision and recall of the traditional CF model are 0.57 and 0.5, respectively, which perform the worst among these models. The precision and recall of resnet-18, which performs better in the traditional model, are 0.73 and 0.67, respectively, and have some disadvantages compared with wave CNN. The advantage of wave CNN comes from the physical modeling ability of its piano waveform feature extraction module, the cascade structure of limiter resonant elements, and accurately capturing the transient response and harmonic distribution of keystroke by simulating the acoustic characteristics of the real piano resonance plate, so as to improve the fidelity of features. The joint spectrum time domain analysis effectively integrates the harmonic energy distribution and performance dynamic characteristics of piano timbre and overcomes the problem of high-frequency overtone loss caused by traditional spectrum diagram methods (such as resnet-18).
In terms of cold start accuracy, compared with 0.22 of the CF model, Wave CNN achieved a leap in cold start performance through real-time performance feature analysis. Wave CNN uses the collected data to generate user technical portraits, which can match tracks without historical interaction records. Reasonable utilization of the matching mechanism driven by physical characteristics directly relates the user’s performance ability and tracks technical requirements through the fundamental harmonic relationship based on piano timbre in the actual recommendation.
In terms of the corresponding time, the corresponding time of Wave CNN is 123.6 ms, which is better than 97.85 ms of resnet-18 and 51.50 ms of CF, and is better than 206 ms of LSTM. In terms of the overall actual demand, the response time of these models is milliseconds, so they can meet the daily needs of users.
In Table 2, the performance degradation of wave CNN is the lowest in the noisy environment, with a decline of only 8.23%. Resnet-18 performs best in the traditional model, but the accuracy rate also decreases by 20.35%. The adaptive signal processing module of wave CNN uses a dynamic limiter to suppress the amplitude mutation caused by environmental noise and retain the core harmonic components. The frequency selectivity of the resonant element strengthens the characteristic frequency band of the piano and filters the irrelevant noise energy, so as to ensure that the performance in the noise environment is not greatly affected.
In Figure 10, 92.72% of the samples have a maximum ratio of more than 0.9, and the maximum ratio of the samples is greater than 0.5. That is to say, most of the errors still come from prediction and classification errors, and a small part of them are data errors.
Wave CNN relies on the cascade structure of limiter resonant elements to simulate the resonance characteristics of the piano, but the acoustic response of the real piano is affected by environmental temperature and humidity, nonlinear keystroke force, and other factors. The change of string tension leads to the fundamental frequency offset, and the nonlinear relationship between the actual keystroke force and timbre has not been fully modeled. In general, the error of wave CNN mainly comes from the idealized assumption of physical modeling, the instantaneous noise of user behavior, and the implicit deviation driven by data. Through dynamic parameter calibration, multi-session feature fusion, de bias loss function design, and other improvements, the robustness of the model can be significantly improved. In the future, it is necessary to further explore the cross-instrument generalization ability and real-time adaptive learning mechanism to achieve more universal intelligent music teaching support.
It can be seen from the research that the intelligent piano repertoire recommendation algorithm based on the CNN model proposed in this article has a high accuracy in piano repertoire recommendation and can effectively improve the recommendation effect of piano repertoire.
5 Conclusion
Modern piano music is positively correlated with extroversion and openness. Popular piano music is positively correlated with agreeableness, extroversion, and openness. In addition, neuroticism is not associated with any dimension of piano music preference. By sorting out the correlation studies between the above different personality trait measures and piano music preference, it can be concluded that there is a significant correlation between piano music preference and personality traits. However, due to the individual differences of the research subjects cannot be ignored, and it is difficult to accurately control. Moreover, the cultural backgrounds of the subjects growing up from small to large in different regions are also different, resulting in certain differences in the research results. This article combines the CNN model to perform intelligent analysis of piano repertoires and combines personal preferences to recommend piano repertoires. It can be seen from the research that the intelligent piano repertoire recommendation algorithm based on the CNN model proposed in this article has a high accuracy in piano repertoire recommendation, and can effectively improve the recommendation effect of piano repertoire. This model can also be applied to other piano-like playing instruments to improve the performance of song recommendations and enhance practice efficiency.
Although wave CNN performs well, its response time (123.6 ms) is still higher than that of CF model (51.5 ms), which is mainly limited by the parallel computing load of resonant elements. Therefore, in the future, it can be further optimized through lightweight resonant network (such as a mobilenet Architecture).
-
Funding information: 2022 Guangxi Vocational Education Teaching Reform Research Project “Research and Practice of Ideological and Political Education in Piano Curriculum for Vocational College Students Based on Traditional Jingyun Culture” (No.: GXGZJG2022B057).
-
Author contributions: Author has accepted responsibility for the entire content of this manuscript and approved its submission.
-
Conflict of interest: Author states no conflict of interest.
-
Data availability statement: The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
References
[1] Wang X. Research on the improved method of fundamental frequency extraction for music automatic recognition of piano music. J Intell Fuzzy Syst. 2018;35(3):2777–83.10.3233/JIFS-169630Suche in Google Scholar
[2] Lampe R, Turova V, Alves-Pinto A. Piano jacket for perceiving and playing music for patients with cerebral palsy. Disabil Rehabil Assist Technol. 2019;14(3):221–5.10.1080/17483107.2017.1419384Suche in Google Scholar PubMed
[3] Johnson D, Damian D, Tzanetakis G. Detecting hand posture in piano playing using depth data. Comput Music J. 2020;43(1):59–78.10.1162/comj_a_00500Suche in Google Scholar
[4] Gruhn W, Ristm R, Schneider P, D’Souza A, Kiilu K. How stable is pitch labeling accuracy in absolute pitch possessors. Empir Musicol Rev. 2018;13(3–4):110–23.10.18061/emr.v13i3-4.6637Suche in Google Scholar
[5] Schutz M, Gillard J. On the generalization of tones: a detailed exploration of non-speech auditory perception stimuli. Sci Rep. 2020;10(1):1–14.10.1038/s41598-020-63132-2Suche in Google Scholar PubMed PubMed Central
[6] Nan Y, Liu L, Geiser E, Shu H, Gong CC, Dong Q, et al. Piano training enhances the neural processing of pitch and improves speech perception in Mandarin-speaking children. Proc Natl Acad Sci U S A. 2018;115(28):E6630–9.10.1073/pnas.1808412115Suche in Google Scholar PubMed PubMed Central
[7] Dean RT. The multi-tuned piano: Keyboard music without a tuning system. Leonardo. 2022;55(2):166–9.10.1162/leon_a_02066Suche in Google Scholar
[8] Mahanta SK, Khilji AFUR, Pakray P. Deep neural network for musical instrument recognition using MFCCs. Comput Sist. 2021;25(2):351–60.10.13053/cys-25-2-3946Suche in Google Scholar
[9] Hong Y, Chau CJ, Horner A. How often and why mode fails to predict mood in low-arousal classical piano music. J N Music Res. 2018;47(5):462–75.10.1080/09298215.2018.1478428Suche in Google Scholar
[10] Bando Y, Tanaka M. A chord recognition method of guitar sound using its constituent tone information. IEEJ Trans Electr Electron Eng. 2022;17(1):103–9.10.1002/tee.23492Suche in Google Scholar
[11] Jiam NT, Limb CJ. Music perception and training for pediatric cochlear implant users. Expert Rev Med Devices. 2020;17(11):1193–206.10.1080/17434440.2020.1841628Suche in Google Scholar PubMed
[12] Foley L, Schutz M. High time for temporal variation: improving sonic interaction with auditory interfaces. IEEE Instrum Meas Mag. 2021;24(7):4–9.10.1109/MIM.2021.9549230Suche in Google Scholar
[13] Chari DA, Barrett KC, Patel AD, Colgrove TR, Jiradejvong P, Jacobs LY, et al. Impact of auditory-motor musical training on melodic pattern recognition in cochlear implant users. Otol Neurotol. 2020;41(4):e422–31.10.1097/MAO.0000000000002525Suche in Google Scholar PubMed
[14] Dissegna D, Sponza M, Falleti E, Fabris C, Vit A, Angeli P, et al. Morbidity and mortality after transjugular intrahepatic portosystemic shunt placement in patients with cirrhosis. Eur J Gastroenterol Hepatol. 2019;31(5):626–32.10.1097/MEG.0000000000001342Suche in Google Scholar PubMed
[15] Pamies S. Deconstructing modal jazz piano techniques: The relation between Debussy’s piano works and the innovations of post-bop pianists. Jazz Educ Res Pract. 2021;2(1):76–105.10.2979/jazzeducrese.2.1.06Suche in Google Scholar
[16] Miyazaki KI, Rakowski A, Makomaska S, Jiang C, Tsuzaki M, Oxenham AJ, et al. Absolute pitch and relative pitch in music students in the East and the West: implications for aural-skills education. Music Percept. 2018;36(2):135–55.10.1525/mp.2018.36.2.135Suche in Google Scholar
[17] Donchev R, Pescara E, Beigl M. Investigating retention in passive haptic learning of piano songs. Proc ACM Interact Mob Wearable Ubiquitous Technol. 2021;5(2):1–14.10.1145/3463513Suche in Google Scholar
[18] Xi C, Qin S. The design and construction based on the ASEAN piano music library and display platform. J Intell Fuzzy Syst. 2018;35(3):2861–6.10.3233/JIFS-169640Suche in Google Scholar
[19] Wanga F, Ahmad I, Ahmad H, Alsulami MD, Alimgeer KS, Cesarano C, et al. Meshless method based on RBFs for solving three-dimensional multiterm time-fractional PDEs arising in engineering phenomenons. J King Saud Univ Sci. 2021;33:1–7.10.1016/j.jksus.2021.101604Suche in Google Scholar
[20] Crisanti F, Cesarano C, Ishkhanyan A. The Grad-Shafranov equation in cap-cyclide coordinates: the Heun function solution. Mathematics. 2023;11:1–13.10.3390/math11092087Suche in Google Scholar
[21] Honari MM, Sarabandi K, Mousavi P. Design and analysis of corrugated antennas based on surface susceptance of a single cell of corrugation. IEEE Trans Antennas Propag. 2020;68(7):5218–27.10.1109/TAP.2020.2979278Suche in Google Scholar
[22] Xu Y. The importance of true random number to network communication security. Appl Comput Lett. 2023;7(1):39–51.Suche in Google Scholar
© 2025 the author(s), published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Artikel in diesem Heft
- Research Articles
- Generalized (ψ,φ)-contraction to investigate Volterra integral inclusions and fractal fractional PDEs in super-metric space with numerical experiments
- Solitons in ultrasound imaging: Exploring applications and enhancements via the Westervelt equation
- Stochastic improved Simpson for solving nonlinear fractional-order systems using product integration rules
- Exploring dynamical features like bifurcation assessment, sensitivity visualization, and solitary wave solutions of the integrable Akbota equation
- Research on surface defect detection method and optimization of paper-plastic composite bag based on improved combined segmentation algorithm
- Impact the sulphur content in Iraqi crude oil on the mechanical properties and corrosion behaviour of carbon steel in various types of API 5L pipelines and ASTM 106 grade B
- Unravelling quiescent optical solitons: An exploration of the complex Ginzburg–Landau equation with nonlinear chromatic dispersion and self-phase modulation
- Perturbation-iteration approach for fractional-order logistic differential equations
- Variational formulations for the Euler and Navier–Stokes systems in fluid mechanics and related models
- Rotor response to unbalanced load and system performance considering variable bearing profile
- DeepFowl: Disease prediction from chicken excreta images using deep learning
- Channel flow of Ellis fluid due to cilia motion
- A case study of fractional-order varicella virus model to nonlinear dynamics strategy for control and prevalence
- Multi-point estimation weldment recognition and estimation of pose with data-driven robotics design
- Analysis of Hall current and nonuniform heating effects on magneto-convection between vertically aligned plates under the influence of electric and magnetic fields
- A comparative study on residual power series method and differential transform method through the time-fractional telegraph equation
- Insights from the nonlinear Schrödinger–Hirota equation with chromatic dispersion: Dynamics in fiber–optic communication
- Mathematical analysis of Jeffrey ferrofluid on stretching surface with the Darcy–Forchheimer model
- Exploring the interaction between lump, stripe and double-stripe, and periodic wave solutions of the Konopelchenko–Dubrovsky–Kaup–Kupershmidt system
- Computational investigation of tuberculosis and HIV/AIDS co-infection in fuzzy environment
- Signature verification by geometry and image processing
- Theoretical and numerical approach for quantifying sensitivity to system parameters of nonlinear systems
- Chaotic behaviors, stability, and solitary wave propagations of M-fractional LWE equation in magneto-electro-elastic circular rod
- Dynamic analysis and optimization of syphilis spread: Simulations, integrating treatment and public health interventions
- Visco-thermoelastic rectangular plate under uniform loading: A study of deflection
- Threshold dynamics and optimal control of an epidemiological smoking model
- Numerical computational model for an unsteady hybrid nanofluid flow in a porous medium past an MHD rotating sheet
- Regression prediction model of fabric brightness based on light and shadow reconstruction of layered images
- Dynamics and prevention of gemini virus infection in red chili crops studied with generalized fractional operator: Analysis and modeling
- Qualitative analysis on existence and stability of nonlinear fractional dynamic equations on time scales
- Fractional-order super-twisting sliding mode active disturbance rejection control for electro-hydraulic position servo systems
- Analytical exploration and parametric insights into optical solitons in magneto-optic waveguides: Advances in nonlinear dynamics for applied sciences
- Bifurcation dynamics and optical soliton structures in the nonlinear Schrödinger–Bopp–Podolsky system
- Review Article
- Haar wavelet collocation method for existence and numerical solutions of fourth-order integro-differential equations with bounded coefficients
- Special Issue: Nonlinear Analysis and Design of Communication Networks for IoT Applications - Part II
- Silicon-based all-optical wavelength converter for on-chip optical interconnection
- Research on a path-tracking control system of unmanned rollers based on an optimization algorithm and real-time feedback
- Analysis of the sports action recognition model based on the LSTM recurrent neural network
- Industrial robot trajectory error compensation based on enhanced transfer convolutional neural networks
- Research on IoT network performance prediction model of power grid warehouse based on nonlinear GA-BP neural network
- Interactive recommendation of social network communication between cities based on GNN and user preferences
- Application of improved P-BEM in time varying channel prediction in 5G high-speed mobile communication system
- Construction of a BIM smart building collaborative design model combining the Internet of Things
- Optimizing malicious website prediction: An advanced XGBoost-based machine learning model
- Economic operation analysis of the power grid combining communication network and distributed optimization algorithm
- Sports video temporal action detection technology based on an improved MSST algorithm
- Internet of things data security and privacy protection based on improved federated learning
- Enterprise power emission reduction technology based on the LSTM–SVM model
- Construction of multi-style face models based on artistic image generation algorithms
- Research and application of interactive digital twin monitoring system for photovoltaic power station based on global perception
- Special Issue: Decision and Control in Nonlinear Systems - Part II
- Animation video frame prediction based on ConvGRU fine-grained synthesis flow
- Application of GGNN inference propagation model for martial art intensity evaluation
- Benefit evaluation of building energy-saving renovation projects based on BWM weighting method
- Deep neural network application in real-time economic dispatch and frequency control of microgrids
- Real-time force/position control of soft growing robots: A data-driven model predictive approach
- Mechanical product design and manufacturing system based on CNN and server optimization algorithm
- Application of finite element analysis in the formal analysis of ancient architectural plaque section
- Research on territorial spatial planning based on data mining and geographic information visualization
- Fault diagnosis of agricultural sprinkler irrigation machinery equipment based on machine vision
- Closure technology of large span steel truss arch bridge with temporarily fixed edge supports
- Intelligent accounting question-answering robot based on a large language model and knowledge graph
- Analysis of manufacturing and retailer blockchain decision based on resource recyclability
- Flexible manufacturing workshop mechanical processing and product scheduling algorithm based on MES
- Exploration of indoor environment perception and design model based on virtual reality technology
- Tennis automatic ball-picking robot based on image object detection and positioning technology
- A new CNN deep learning model for computer-intelligent color matching
- Design of AR-based general computer technology experiment demonstration platform
- Indoor environment monitoring method based on the fusion of audio recognition and video patrol features
- Health condition prediction method of the computer numerical control machine tool parts by ensembling digital twins and improved LSTM networks
- Establishment of a green degree evaluation model for wall materials based on lifecycle
- Quantitative evaluation of college music teaching pronunciation based on nonlinear feature extraction
- Multi-index nonlinear robust virtual synchronous generator control method for microgrid inverters
- Manufacturing engineering production line scheduling management technology integrating availability constraints and heuristic rules
- Analysis of digital intelligent financial audit system based on improved BiLSTM neural network
- Attention community discovery model applied to complex network information analysis
- A neural collaborative filtering recommendation algorithm based on attention mechanism and contrastive learning
- Rehabilitation training method for motor dysfunction based on video stream matching
- Research on façade design for cold-region buildings based on artificial neural networks and parametric modeling techniques
- Intelligent implementation of muscle strain identification algorithm in Mi health exercise induced waist muscle strain
- Optimization design of urban rainwater and flood drainage system based on SWMM
- Improved GA for construction progress and cost management in construction projects
- Evaluation and prediction of SVM parameters in engineering cost based on random forest hybrid optimization
- Museum intelligent warning system based on wireless data module
- Optimization design and research of mechatronics based on torque motor control algorithm
- Special Issue: Nonlinear Engineering’s significance in Materials Science
- Experimental research on the degradation of chemical industrial wastewater by combined hydrodynamic cavitation based on nonlinear dynamic model
- Study on low-cycle fatigue life of nickel-based superalloy GH4586 at various temperatures
- Some results of solutions to neutral stochastic functional operator-differential equations
- Ultrasonic cavitation did not occur in high-pressure CO2 liquid
- Research on the performance of a novel type of cemented filler material for coal mine opening and filling
- Testing of recycled fine aggregate concrete’s mechanical properties using recycled fine aggregate concrete and research on technology for highway construction
- A modified fuzzy TOPSIS approach for the condition assessment of existing bridges
- Nonlinear structural and vibration analysis of straddle monorail pantograph under random excitations
- Achieving high efficiency and stability in blue OLEDs: Role of wide-gap hosts and emitter interactions
- Construction of teaching quality evaluation model of online dance teaching course based on improved PSO-BPNN
- Enhanced electrical conductivity and electromagnetic shielding properties of multi-component polymer/graphite nanocomposites prepared by solid-state shear milling
- Optimization of thermal characteristics of buried composite phase-change energy storage walls based on nonlinear engineering methods
- A higher-performance big data-based movie recommendation system
- Nonlinear impact of minimum wage on labor employment in China
- Nonlinear comprehensive evaluation method based on information entropy and discrimination optimization
- Application of numerical calculation methods in stability analysis of pile foundation under complex foundation conditions
- Research on the contribution of shale gas development and utilization in Sichuan Province to carbon peak based on the PSA process
- Characteristics of tight oil reservoirs and their impact on seepage flow from a nonlinear engineering perspective
- Nonlinear deformation decomposition and mode identification of plane structures via orthogonal theory
- Numerical simulation of damage mechanism in rock with cracks impacted by self-excited pulsed jet based on SPH-FEM coupling method: The perspective of nonlinear engineering and materials science
- Cross-scale modeling and collaborative optimization of ethanol-catalyzed coupling to produce C4 olefins: Nonlinear modeling and collaborative optimization strategies
- Unequal width T-node stress concentration factor analysis of stiffened rectangular steel pipe concrete
- Special Issue: Advances in Nonlinear Dynamics and Control
- Development of a cognitive blood glucose–insulin control strategy design for a nonlinear diabetic patient model
- Big data-based optimized model of building design in the context of rural revitalization
- Multi-UAV assisted air-to-ground data collection for ground sensors with unknown positions
- Design of urban and rural elderly care public areas integrating person-environment fit theory
- Application of lossless signal transmission technology in piano timbre recognition
- Application of improved GA in optimizing rural tourism routes
- Architectural animation generation system based on AL-GAN algorithm
- Advanced sentiment analysis in online shopping: Implementing LSTM models analyzing E-commerce user sentiments
- Intelligent recommendation algorithm for piano tracks based on the CNN model
- Visualization of large-scale user association feature data based on a nonlinear dimensionality reduction method
- Low-carbon economic optimization of microgrid clusters based on an energy interaction operation strategy
- Optimization effect of video data extraction and search based on Faster-RCNN hybrid model on intelligent information systems
- Construction of image segmentation system combining TC and swarm intelligence algorithm
- Particle swarm optimization and fuzzy C-means clustering algorithm for the adhesive layer defect detection
- Optimization of student learning status by instructional intervention decision-making techniques incorporating reinforcement learning
- Fuzzy model-based stabilization control and state estimation of nonlinear systems
- Optimization of distribution network scheduling based on BA and photovoltaic uncertainty
- Tai Chi movement segmentation and recognition on the grounds of multi-sensor data fusion and the DBSCAN algorithm
- Special Issue: Dynamic Engineering and Control Methods for the Nonlinear Systems - Part III
- Generalized numerical RKM method for solving sixth-order fractional partial differential equations
Artikel in diesem Heft
- Research Articles
- Generalized (ψ,φ)-contraction to investigate Volterra integral inclusions and fractal fractional PDEs in super-metric space with numerical experiments
- Solitons in ultrasound imaging: Exploring applications and enhancements via the Westervelt equation
- Stochastic improved Simpson for solving nonlinear fractional-order systems using product integration rules
- Exploring dynamical features like bifurcation assessment, sensitivity visualization, and solitary wave solutions of the integrable Akbota equation
- Research on surface defect detection method and optimization of paper-plastic composite bag based on improved combined segmentation algorithm
- Impact the sulphur content in Iraqi crude oil on the mechanical properties and corrosion behaviour of carbon steel in various types of API 5L pipelines and ASTM 106 grade B
- Unravelling quiescent optical solitons: An exploration of the complex Ginzburg–Landau equation with nonlinear chromatic dispersion and self-phase modulation
- Perturbation-iteration approach for fractional-order logistic differential equations
- Variational formulations for the Euler and Navier–Stokes systems in fluid mechanics and related models
- Rotor response to unbalanced load and system performance considering variable bearing profile
- DeepFowl: Disease prediction from chicken excreta images using deep learning
- Channel flow of Ellis fluid due to cilia motion
- A case study of fractional-order varicella virus model to nonlinear dynamics strategy for control and prevalence
- Multi-point estimation weldment recognition and estimation of pose with data-driven robotics design
- Analysis of Hall current and nonuniform heating effects on magneto-convection between vertically aligned plates under the influence of electric and magnetic fields
- A comparative study on residual power series method and differential transform method through the time-fractional telegraph equation
- Insights from the nonlinear Schrödinger–Hirota equation with chromatic dispersion: Dynamics in fiber–optic communication
- Mathematical analysis of Jeffrey ferrofluid on stretching surface with the Darcy–Forchheimer model
- Exploring the interaction between lump, stripe and double-stripe, and periodic wave solutions of the Konopelchenko–Dubrovsky–Kaup–Kupershmidt system
- Computational investigation of tuberculosis and HIV/AIDS co-infection in fuzzy environment
- Signature verification by geometry and image processing
- Theoretical and numerical approach for quantifying sensitivity to system parameters of nonlinear systems
- Chaotic behaviors, stability, and solitary wave propagations of M-fractional LWE equation in magneto-electro-elastic circular rod
- Dynamic analysis and optimization of syphilis spread: Simulations, integrating treatment and public health interventions
- Visco-thermoelastic rectangular plate under uniform loading: A study of deflection
- Threshold dynamics and optimal control of an epidemiological smoking model
- Numerical computational model for an unsteady hybrid nanofluid flow in a porous medium past an MHD rotating sheet
- Regression prediction model of fabric brightness based on light and shadow reconstruction of layered images
- Dynamics and prevention of gemini virus infection in red chili crops studied with generalized fractional operator: Analysis and modeling
- Qualitative analysis on existence and stability of nonlinear fractional dynamic equations on time scales
- Fractional-order super-twisting sliding mode active disturbance rejection control for electro-hydraulic position servo systems
- Analytical exploration and parametric insights into optical solitons in magneto-optic waveguides: Advances in nonlinear dynamics for applied sciences
- Bifurcation dynamics and optical soliton structures in the nonlinear Schrödinger–Bopp–Podolsky system
- Review Article
- Haar wavelet collocation method for existence and numerical solutions of fourth-order integro-differential equations with bounded coefficients
- Special Issue: Nonlinear Analysis and Design of Communication Networks for IoT Applications - Part II
- Silicon-based all-optical wavelength converter for on-chip optical interconnection
- Research on a path-tracking control system of unmanned rollers based on an optimization algorithm and real-time feedback
- Analysis of the sports action recognition model based on the LSTM recurrent neural network
- Industrial robot trajectory error compensation based on enhanced transfer convolutional neural networks
- Research on IoT network performance prediction model of power grid warehouse based on nonlinear GA-BP neural network
- Interactive recommendation of social network communication between cities based on GNN and user preferences
- Application of improved P-BEM in time varying channel prediction in 5G high-speed mobile communication system
- Construction of a BIM smart building collaborative design model combining the Internet of Things
- Optimizing malicious website prediction: An advanced XGBoost-based machine learning model
- Economic operation analysis of the power grid combining communication network and distributed optimization algorithm
- Sports video temporal action detection technology based on an improved MSST algorithm
- Internet of things data security and privacy protection based on improved federated learning
- Enterprise power emission reduction technology based on the LSTM–SVM model
- Construction of multi-style face models based on artistic image generation algorithms
- Research and application of interactive digital twin monitoring system for photovoltaic power station based on global perception
- Special Issue: Decision and Control in Nonlinear Systems - Part II
- Animation video frame prediction based on ConvGRU fine-grained synthesis flow
- Application of GGNN inference propagation model for martial art intensity evaluation
- Benefit evaluation of building energy-saving renovation projects based on BWM weighting method
- Deep neural network application in real-time economic dispatch and frequency control of microgrids
- Real-time force/position control of soft growing robots: A data-driven model predictive approach
- Mechanical product design and manufacturing system based on CNN and server optimization algorithm
- Application of finite element analysis in the formal analysis of ancient architectural plaque section
- Research on territorial spatial planning based on data mining and geographic information visualization
- Fault diagnosis of agricultural sprinkler irrigation machinery equipment based on machine vision
- Closure technology of large span steel truss arch bridge with temporarily fixed edge supports
- Intelligent accounting question-answering robot based on a large language model and knowledge graph
- Analysis of manufacturing and retailer blockchain decision based on resource recyclability
- Flexible manufacturing workshop mechanical processing and product scheduling algorithm based on MES
- Exploration of indoor environment perception and design model based on virtual reality technology
- Tennis automatic ball-picking robot based on image object detection and positioning technology
- A new CNN deep learning model for computer-intelligent color matching
- Design of AR-based general computer technology experiment demonstration platform
- Indoor environment monitoring method based on the fusion of audio recognition and video patrol features
- Health condition prediction method of the computer numerical control machine tool parts by ensembling digital twins and improved LSTM networks
- Establishment of a green degree evaluation model for wall materials based on lifecycle
- Quantitative evaluation of college music teaching pronunciation based on nonlinear feature extraction
- Multi-index nonlinear robust virtual synchronous generator control method for microgrid inverters
- Manufacturing engineering production line scheduling management technology integrating availability constraints and heuristic rules
- Analysis of digital intelligent financial audit system based on improved BiLSTM neural network
- Attention community discovery model applied to complex network information analysis
- A neural collaborative filtering recommendation algorithm based on attention mechanism and contrastive learning
- Rehabilitation training method for motor dysfunction based on video stream matching
- Research on façade design for cold-region buildings based on artificial neural networks and parametric modeling techniques
- Intelligent implementation of muscle strain identification algorithm in Mi health exercise induced waist muscle strain
- Optimization design of urban rainwater and flood drainage system based on SWMM
- Improved GA for construction progress and cost management in construction projects
- Evaluation and prediction of SVM parameters in engineering cost based on random forest hybrid optimization
- Museum intelligent warning system based on wireless data module
- Optimization design and research of mechatronics based on torque motor control algorithm
- Special Issue: Nonlinear Engineering’s significance in Materials Science
- Experimental research on the degradation of chemical industrial wastewater by combined hydrodynamic cavitation based on nonlinear dynamic model
- Study on low-cycle fatigue life of nickel-based superalloy GH4586 at various temperatures
- Some results of solutions to neutral stochastic functional operator-differential equations
- Ultrasonic cavitation did not occur in high-pressure CO2 liquid
- Research on the performance of a novel type of cemented filler material for coal mine opening and filling
- Testing of recycled fine aggregate concrete’s mechanical properties using recycled fine aggregate concrete and research on technology for highway construction
- A modified fuzzy TOPSIS approach for the condition assessment of existing bridges
- Nonlinear structural and vibration analysis of straddle monorail pantograph under random excitations
- Achieving high efficiency and stability in blue OLEDs: Role of wide-gap hosts and emitter interactions
- Construction of teaching quality evaluation model of online dance teaching course based on improved PSO-BPNN
- Enhanced electrical conductivity and electromagnetic shielding properties of multi-component polymer/graphite nanocomposites prepared by solid-state shear milling
- Optimization of thermal characteristics of buried composite phase-change energy storage walls based on nonlinear engineering methods
- A higher-performance big data-based movie recommendation system
- Nonlinear impact of minimum wage on labor employment in China
- Nonlinear comprehensive evaluation method based on information entropy and discrimination optimization
- Application of numerical calculation methods in stability analysis of pile foundation under complex foundation conditions
- Research on the contribution of shale gas development and utilization in Sichuan Province to carbon peak based on the PSA process
- Characteristics of tight oil reservoirs and their impact on seepage flow from a nonlinear engineering perspective
- Nonlinear deformation decomposition and mode identification of plane structures via orthogonal theory
- Numerical simulation of damage mechanism in rock with cracks impacted by self-excited pulsed jet based on SPH-FEM coupling method: The perspective of nonlinear engineering and materials science
- Cross-scale modeling and collaborative optimization of ethanol-catalyzed coupling to produce C4 olefins: Nonlinear modeling and collaborative optimization strategies
- Unequal width T-node stress concentration factor analysis of stiffened rectangular steel pipe concrete
- Special Issue: Advances in Nonlinear Dynamics and Control
- Development of a cognitive blood glucose–insulin control strategy design for a nonlinear diabetic patient model
- Big data-based optimized model of building design in the context of rural revitalization
- Multi-UAV assisted air-to-ground data collection for ground sensors with unknown positions
- Design of urban and rural elderly care public areas integrating person-environment fit theory
- Application of lossless signal transmission technology in piano timbre recognition
- Application of improved GA in optimizing rural tourism routes
- Architectural animation generation system based on AL-GAN algorithm
- Advanced sentiment analysis in online shopping: Implementing LSTM models analyzing E-commerce user sentiments
- Intelligent recommendation algorithm for piano tracks based on the CNN model
- Visualization of large-scale user association feature data based on a nonlinear dimensionality reduction method
- Low-carbon economic optimization of microgrid clusters based on an energy interaction operation strategy
- Optimization effect of video data extraction and search based on Faster-RCNN hybrid model on intelligent information systems
- Construction of image segmentation system combining TC and swarm intelligence algorithm
- Particle swarm optimization and fuzzy C-means clustering algorithm for the adhesive layer defect detection
- Optimization of student learning status by instructional intervention decision-making techniques incorporating reinforcement learning
- Fuzzy model-based stabilization control and state estimation of nonlinear systems
- Optimization of distribution network scheduling based on BA and photovoltaic uncertainty
- Tai Chi movement segmentation and recognition on the grounds of multi-sensor data fusion and the DBSCAN algorithm
- Special Issue: Dynamic Engineering and Control Methods for the Nonlinear Systems - Part III
- Generalized numerical RKM method for solving sixth-order fractional partial differential equations


