Application of numerical calculation methods in stability analysis of pile foundation under complex foundation conditions

Huimin Wang; Kaiqing Ma; Jing Zhang; Kai Zhang

doi:10.1515/nleng-2025-0162

Artikel Open Access

Application of numerical calculation methods in stability analysis of pile foundation under complex foundation conditions

Huimin Wang , Kaiqing Ma , Jing Zhang und Kai Zhang

Veröffentlicht/Copyright: 2. Juli 2025

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen

Aus der Zeitschrift Nonlinear Engineering Band 14 Heft 1

Abstract

Pile foundation has been widely applied in modern civil engineering due to its excellent performance under complex foundation conditions. However, when subjected to dynamic loads such as waves, tides, and earthquakes, the long-term stability of pile foundations becomes a significant concern. Traditional stability analysis methods are predominantly based on static loading assumptions, which neglect the nonlinear behavior of soils and the time-varying characteristics of dynamic loads. This leads to reduced prediction accuracy and limited applicability under real-world, complex working conditions. To address these challenges, this study proposes an innovative numerical calculation method based on a two-parameter model, which integrates dynamic load effects – such as wave and tidal actions – into the pile-soil interaction framework. Compared with the conventional Winkler model, the two-parameter model incorporates both the stiffness of the subgrade and the shear interaction between adjacent soil springs, thereby capturing the nonlinear and spatially correlated behavior of foundation soils more accurately. The core innovations of this study lie in two aspects. First, it introduces a more refined numerical model by incorporating key parameters such as pile water entry depth, lateral soil resistance coefficient, and pile stiffness, offering a more realistic simulation of complex marine foundation conditions. Second, it performs a comprehensive stability analysis under dynamic loading environments, systematically investigating the influence of various factors including soil properties, pile length, and pile diameter on the critical frequency and overall structural stability. The research findings show that the proposed two-parameter model significantly improves the precision of stability analysis and effectively reveals the nonlinear dynamic responses of pile foundations. This contributes to both the theoretical development of pile-soil interaction modeling and practical engineering applications in marine and offshore structures.

Keywords: pile foundation; stability analysis; numerical calculation method; two-parameter model; dynamic loading; complex foundation conditions; carbon peak strategy

1 Introduction

As a key form of deep foundation, pile foundation has been widely used in the engineering fields of buildings, bridges, wharves, and marine structures [1]. With the expansion of the project scale and the increasing complexity of the construction environment, the design and stability analysis of pile foundations are facing many challenges, especially in the marine and water environment, pile foundations need to withstand complex loads such as waves, tides, and earthquakes for a long period of time, so its stability has become one of the hotspots in civil engineering research [2,3].

The stability of pile foundation is mainly affected by soil–pile interaction, and this factor is crucial in the design process. The traditional static analysis method has some applicability under simple foundation conditions, but its prediction accuracy and safety are limited when facing complex geological environment and dynamic loading [4]. The non-uniformity and anisotropy of foundation soil and the dynamic interaction between pile and soil will affect the stability of pile foundation, so how to accurately assess the stability of pile foundation under complex foundation conditions has become the core issue of current research [5,6].

As computer technology and numerical calculation techniques advance, more and more studies are using numerical simulation tools to analyze the stability of pile foundations. The mechanical analysis of pile foundations has made extensive use of the finite element method (FEM), boundary element method, and discrete element method, which can simulate the pile force and take into account the pile–soil interaction to some degree [7,8]. However, when dealing with large-scale complex foundation problems, these methods still face challenges in computational accuracy and efficiency, which become the key difficulties in research.

At present, pile foundation stability analysis mostly focuses on static loading conditions, such as static analysis methods [9]. Although there are studies to explore the influence of dynamic loads such as wave load and earthquake load, most of them adopt simplified soil model, failing to fully consider the nonlinear and time-varying characteristics of the soil and the complex interactions between the pile and soil, which is difficult to comprehensively reflect the behavioral characteristics of the pile foundation under the actual working conditions, thus affecting its reliability and value of engineering applications [10].

This study addresses these limitations by proposing a numerical computation method based on a two-parameter model to thoroughly examine the effects of dynamic stresses – such as wave loads – on pile foundation stability [11]. Compared to the conventional Winkler model, the two-parameter model more effectively captures the nonlinear behavior of soil-pile interaction, thus enhancing the accuracy of the stability analysis [12]. The influence of key parameters, including pile water depth, lateral soil resistance coefficient, and pile stiffness, is systematically analyzed. An optimized analysis scheme that aligns more closely with actual engineering conditions is presented.

The main contributions of this study are twofold: first, it introduces an innovative methodology by replacing the traditional Winkler model with a two-parameter model, thereby improving the accuracy of stability prediction; second, it conducts an in-depth analysis of pile foundation stability under dynamic environmental conditions such as wave and tidal loads, offering valuable theoretical support for the design of offshore and deep-water pile foundations. The proposed method is validated through numerical and experimental comparisons, demonstrating promising application potential for enhancing the safety and reliability of pile foundation designs.

The structure of this study is organized as follows: Chapter 2 reviews relevant literature on pile foundation stability analysis. Chapter 3 introduces the theoretical background and modeling approach of the two-parameter method. Chapter 4 presents the numerical modeling and parameter sensitivity studies. Chapter 5 discusses the results and compares them with experimental data. Finally, Chapter 6 summarizes the main findings and suggests future research directions.

2 Analysis of pile skidding effect based on bending damage

Pile foundations not only bear vertical loads but also need to resist horizontal loads in complex geological environments, especially in the context of geologic hazards such as landslides and slope instability, and their anti-slip effect is crucial [13]. When subjected to horizontal loads, the pile body may undergo bending damage, and this damage mode has a direct impact on the slip resistance of the pile foundation. Therefore, it is of great significance to study the anti-slip effect of pile body based on bending damage to improve the stability and safety of pile foundation design.

2.1 Formation mechanism of pile bending damage

When the pile is subjected to horizontal loading, the soil–pile interaction leads to bending moments in the pile body and bending damage at specific parts of the pile. The damage is mainly affected by the following factors.

Different types of soil layers (e.g., soft soil, sandy soil, clay, etc.) have different lateral restraining effects on the pile body, which affects the bending pattern and damage mode of the pile body; static horizontal load, ground vibration load, wave load, etc., will induce different degrees of pile bending damage; Pile material and cross-section stiffness determine its bending resistance. Piles with lower stiffness are more likely to be bent when subjected to larger horizontal loads; the shear strength and compactness of the soil around the pile affect the deformation and bending damage of the pile.

2.2 Analysis of pile skid resistance effect

The anti-slip capacity of pile foundation mainly depends on the restraining effect of pile body in the direction of slip, and its anti-slip effect can be analyzed by the following aspects.

Stress distribution of pile body: In the process of slip resistance, the distribution of bending moment and shear force at different depths of pile body determines its slip resistance. Usually, the stress is concentrated at the top of the pile and the bending of the pile body, which is prone to plastic deformation or even damage; The soil body provides lateral support force to the pile body, which affects the slip resistance of the pile body. When the landslide force increases, the change in pile–soil interaction force determines whether the pile body can effectively prevent the landslide from occurring. In group pile structure, the interaction between adjacent piles enhances the overall skid resistance, but it may also lead to increased bending of the pile body due to the local damage of the soil between the piles; by adjusting the parameters of pile length, pile diameter, stiffness, and burial depth, the anti-slip performance of the pile body can be optimized to improve its bearing capacity and durability.

2.3 Numerical simulation and experimental validation

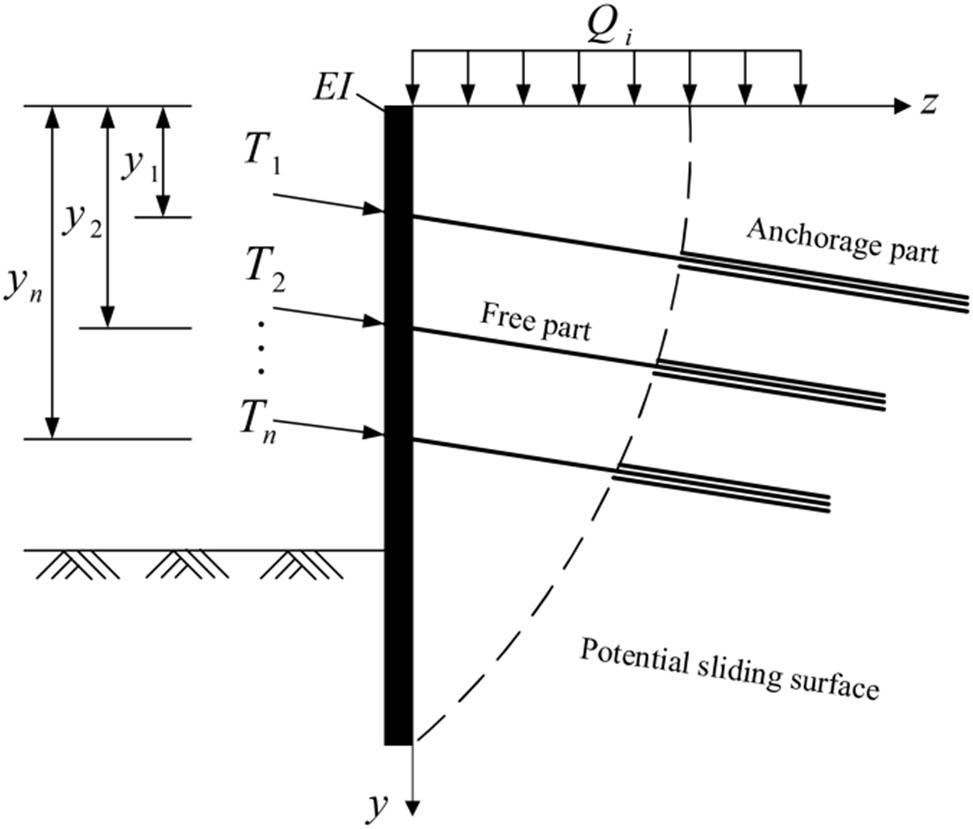
This study uses the FEM to create a model of the pile–soil interaction and simulate the deformation, stress distribution, and skidding resistance of the pile body under various operating conditions in order to thoroughly examine the skidding effect of the pile body under bending damage [14]. In order to examine the real skid resistance performance of the pile body and investigate the impact of various soil conditions, pile diameters, and load variations on the skid resistance effect, the numerical calculation results are simultaneously validated through physical model testing. Figure 1 displays the pile skid resistance analytical model.

Figure 1

Analytical model of pile skid resistance effect.

The pile sliding moment M R P i within the potential slip surface can be expressed as:

(1) M R P i = ∫ z 1 z 2 p ( z ) ⋅ ( z − z 0 ) d z ,

where p ( z ) is the lateral earth pressure distribution of the pile along the depth direction (kN/m²); z is the coordinates of the pile depth (m); z 0 is the depth of slip surface location (m); and z 1 and z 2 are the starting depth and ending depth of the pile in the range of potential slip surface (m), respectively.

The formula indicates that the slip-resisting moment of the pile body in the range of slip surface is determined by the integral of lateral earth pressure and force arm, which can be further modeled by specific earth pressure [15].

The mechanical equilibrium relationship for the skidding section of a pile subjected to horizontal net thrust (thrust minus resistance), vertical axial force, and bedding tension binding force can be expressed as follows:

(2) ∑ F x = P h − R h + T x = 0 ,

where P h is the horizontal thrust acting on the pile body (kN); R h is the horizontal resistance force generated by the pile body (kN); and T x is the horizontal restraining force of the mat reinforcement (kN).

Vertical force balance equation:

(3) ∑ F z = N − W + T z = 0 ,

where N is the vertical axial force on the pile body (kN); W is the self-weight of pile body and additional load (kN); and T z is the vertical restraining force of the bedding reinforcement (kN).

Moment balance equation (around a reference point O):

(4) ∑ M O = M R P + P h ⋅ h p − R h ⋅ h r + T x ⋅ h t = 0 ,

where M R P is the pile sliding moment (kN-m); and h p , h r , and h t are the force arms of the horizontal thrust, resistance, and tension points relative to the reference point, respectively (m).

2.4 Pile bearing moment and ultimate net horizontal thrust

In cement fly-ash gravel (CFG) pile or concrete pile composite foundation, the pile body will produce bending moment when subjected to horizontal load, and the resulting tensile stress in the cross-section is often preceded by the compressive stress or shear strength to reach the limit, so that the bending damage is the dominant damage mode [16]. Bending damage not only affects the stability of single pile but also reduces the bearing capacity of the whole composite foundation system.

The bending damage of CFG piles is affected by several factors, including

CFG piles have a somewhat lower bending strength than conventional concrete piles and are often composed of a mixture of cement, fly ash, sand, and gravel. The pile body is vulnerable to bending damage when the tensile stress is above the limit when the bending moment is very great; piles with a smaller cross-section have a lower bending capacity and are more vulnerable to bending damage. The bending stiffness of the pile body is comparatively improved when the vertical load is large; however, if the load is too large, it may result in pile-soil contact surface slippage, which in turn affects the overall stability. This can be achieved by increasing the pile diameter or by optimizing the pile design. In the design of composite foundation, it is necessary to reasonably allocate the bearing proportion of pile and soil, in order to avoid local stress concentration leading to bending damage.

The stiffness and resistance of different soil layers affect the pile stress state. Weak soil layer may lead to insufficient pile lateral support, which increases the bending moment value and raises the risk of bending damage. In the composite foundation under embankment, the bending damage of CFG piles is mainly caused by the combined effect of the horizontal net thrust generated by the lateral slip of the foundation, the vertical axial force shared by the embankment load, and the binding force of the bedding reinforcement. Since the compressive strength of CFG piles is much larger than the tensile strength, its damage mode usually manifests itself as bending-tension damage, i.e., the bending and tensile stresses of the pile cross-section reach the limit [17].

In the force analysis, the maximum bending and tensile stresses σ _t and the maximum bending and compressive stresses σ _c in the pile cross-section under the joint action of the pile bearing moment M i and the axial force N i can be expressed as follows:

(5) σ t = M i W + N i A σ c = M i W − N i A .

When σ _t exceeds the tensile strength of the CFG pile, the pile body undergoes bending and tensile damage, a phenomenon that is particularly significant under soft ground or foundation conditions where lateral slip exists. Therefore, in the engineering design, it is necessary to optimize the cross-section size of the pile, reasonably distribute the load, and take measures to reduce the influence of the horizontal thrust on the pile in order to reduce the risk of bending damage.

When the pile slip section force is treated as a cantilever beam, the side-slip deformation of the composite foundation caused by the embankment filling causes the pile slip section to be subjected to the joint action of the horizontal net thrust of the soil between the piles, P _h and the binding force of the bedding reinforcement on the top of the pile, T. In this case, the bending moment of the pile section at the potential slip surface, M _s, can be expressed as

(6) M s = P h ⋅ h s − T ⋅ h t .

The formula shows that the horizontal thrust of soil between piles P _h is mainly generated by the combination of lateral pressure of fill and lateral slip force of foundation, and its moment increases with the increase in the slip surface depth h _s. The binding force of bedding reinforcement T at the top of pile produces negative bending moment on pile body.

The binding force of the top bedding reinforcement T produces a negative bending moment on the pile body, and its effect depends on the height of the action point h _t and the strength of the reinforcement. The magnitude of bending moment determines whether the pile body undergoes bending damage or not. If M _s is too large, it may lead to bending cracking or overall instability of the pile body near the slip surface.

When the bending moment M i and axial force N i are combined, the bending and tensile stresses in the pile cross-section reach the tensile strength f _t of the pile material, then the pile body undergoes bending and tensile damage. According to the aforementioned stress calculation formula,

(7) σ t = M i W + N i A = f t ,

(8) M i = f t W − N i A W .

Since the ultimate bending moment M _i of the pile body at the potential slip surface is generated by the net horizontal thrust P h , ult action, i.e.,

(9) M i = P h , ult ⋅ h s − T ⋅ h t .

Combining the above equations gives the ultimate net horizontal thrust that the CFG pile can withstand

(10) P h , ult = f t W − N i A W + T h t h s .

2.5 Pile-soil load sharing and pile bearing vertical axial force

In engineering practice, the pile body is not only subjected to horizontal thrust, but also to vertical load at the same time. Through the force analysis of the anti-slip section of the pile body, it can be seen that the compressive stress caused by the vertical load can partially offset the bending and tensile stress generated by the horizontal net thrust at the potential slip surface, thus improving the bending capacity and horizontal bearing capacity of the pile body, and enhancing the restraining effect of the pile body on the side-slip of the foundation.

Under the premise of ensuring the vertical bearing capacity of single pile, Hewlett’s method [18] is usually adopted to calculate the load N t transferred to the top of the pile by the soil arch effect. According to the limit equilibrium condition of the soil unit between the top of the pile and the top of the arch, the corresponding state of the pile load-sharing ratios of ν 1 and ν 2 can be obtained.

(11) ν 1 = 1 − e − k 1 ⋅ S / D 1 + k 2 ⋅ S / D ν 2 = 1 1 + k 3 ⋅ ( S / D ) 2 ,

where ν 1 , ν 2 are the pile bearing load sharing ratio (dimensionless); S is the pile spacing (m); D is the pile diameter (m); k 1 , k 2 , k 3 are the Hewlett’s empirical coefficients, related to the soil arch effect and pile–soil interaction characteristics.

The load sharing ratio ν 1 and ν 2 characterize the proportion of the load borne by the pile body. Usually as the pile spacing increases, the pile-bearing load sharing ratio decreases and more of the load is borne by the soil body. The increase in vertical load helps to reduce the effect of horizontal thrust and improve the stability of pile body. The soil arch effect is the key mechanism of load transfer. It is necessary to reasonably control the pile spacing S and pile diameter D to optimize the pile-soil sharing characteristics during design.

In actual engineering application, the parameters should be adjusted according to specific foundation conditions and load distribution to ensure the safety and stability of the pile foundation system.

2.6 Horizontal binding force on pile top by bedding reinforcement

In a composite foundation system, bedding reinforcement (e.g., geogrids or reinforcing mesh) is able to provide additional horizontal restraining force by interacting with the fill, thereby enhancing the stability of the pile tops and limiting the lateral deformation of the foundation. The role of bedding reinforcement is mainly reflected in the following aspects.

Through its own tension action, the bedding tension bar shares the horizontal load with the embankment fill to reduce the horizontal deformation at the top of individual piles. The presence of tension bars spreads the horizontal thrust over a wider area and reduces the local stress concentration.

The bedding reinforcement is equivalent to applying a certain horizontal binding force T on the top of the pile, which is mainly affected by the tensile rigidity of the reinforcement E t A t and its laying method. The following formula can be used to calculate the restraint contribution of the tension bar to the top of the pile, which increases to a smooth value T _c at the slip surface (Figure 2):

(12) T = E t A t L t ⋅ Δ u ,

where T is the horizontal restraining force provided by the bedding reinforcement to the top of the pile (kN); E t is the modulus of elasticity of the tension bar material (MPa); A t is the effective force area of the tension bar (m²); L t is the effective acting length of the tension bar (m); Δ u is the horizontal displacement of pile top (m).

Figure 2

Distribution of bedding tendon strip tension extension.

Under the action of horizontal thrust, the binding force of the pile top reinforcement can effectively reduce the bending moment response of the pile body and improve the bending bearing capacity of the pile foundation system. When the role of the reinforcement is stronger, it can reduce the risk of bending and tension damage of the pile body and prolong the service life of the structure.

3 Stabilization factor for composite foundations

Under the action of flexible embankment fill load, the stress situation of CFG pile composite foundation is more complicated, and there is a significant asynchrony in the pile destruction process. At the outer edge of the foundation reinforcement area, the CFG piles in this area are the first to break due to ultimate bending damage because of the large lateral slip of the soil around the piles. The load of the damaged pile is then transferred to the neighboring piles, which triggers chain damage and may eventually lead to the overall instability of the whole foundation.

The circular arc strip division approach is used to do the overall stability study based on the approximate circular slip pattern of the composite foundation beneath the embankment. Because the slip surface’s undercut depth is greatest close to the circle’s center, the pile body there experiences a higher side-slide force. Damage from bending and tensile cracking will happen when the pile body’s cross-sectional bending and tensile stresses at the point tangent to the slip surface reach their maximum strength. Based on this, the pile body with the longest slip-resistant section of the composite foundation can be defined as the critical pile, i.e., the pile body with the first bending damage near the foot of the embankment slope, and accordingly, the determination criteria of two limit states can be established.

The bending and tensile stress of the key pile reaches the ultimate bending strength. The embankment as a whole is destabilized. Due to the asynchronous nature of pile failure, even if the critical piles reach the ultimate tensile strength, the piles at other locations may not be fully subjected to the ultimate bending moment.

In the foot of the slope area, the critical piles are subjected to a more special situation. Due to the small fill load in this area, the horizontal net pressure on the soil in the slip-resistant section of the pile is distributed in a triangular shape. The net horizontal pressure of the soil on the key pile at the slip surface is p k , and the combined force is the ultimate net horizontal thrust F hk on the key pile.

The simulation analysis results show that the horizontal displacement of the composite foundation near the toe of the slope significantly increases compared to the symmetric location of the center of the roadbed and gradually increases from the center of the roadbed to the toe of the slope area. Therefore, it can be approximated to assume that the horizontal displacement of the foundation is zero at the center of the roadbed and grows along a linear trend to reach a maximum at the foot of the slope. Similarly, based on the numerical simulation analysis [19], the distribution characteristics of pile body shear force along the depth can be obtained, and the deduced horizontal net pressure p i of the pile body can be obtained by shear force differentiation, and its lateral distribution also shows a linear trend after normalization (Figure 3).

Figure 3

Horizontal thrust calculation model for the pile anti-slip portion.

When the CFG pile composite foundation under the embankment is in a critical state, the key pile near the foot of the slope undergoes bending and tensile damage near the potential slip surface. Based on Eq. (13), the ultimate horizontal net thrust F hk of the critical pile can be calculated.

In order to characterize the asynchrony of the bending and pulling damage process of the pile in the composite foundation, the ratio of the pile-bearing horizontal net thrust F hi of each pile’s anti-slip section to the ultimate horizontal net thrust F hk of the key pile is defined as the coefficient of the pile-bearing horizontal net thrust β i , which is calculated by the following formula:

(13) β i = F hi F hk .

This coefficient is used to characterize the relative differences in the slip resistance of different piles during the stressing process, reflecting their asynchrony in the bending and tension damage process.

4 Experiments

4.1 Calculation of unsteady loads

When analyzing the unsteady load of the pile under harmonic loading, the corresponding formula can be derived by adjusting the amplitude. Therefore, in this paper, under the ideal assumption of Case 3, the unsteady load formula is converted by splitting the formula, and the weld is split based on the same constraints in the other three cases to ensure the accuracy of the corresponding unsteady load calculation.

Accurately capturing the dynamic reaction of the pile body under various weights is crucial for modifying the equations under various working situations. We can guarantee that the calculation of the unstable load has a high degree of accuracy and practicability by equitably allocating the effects and transformations of the loads. Additionally, the load fluctuations under various situations must be assessed through appropriate modeling and analysis, taking into account the material attributes and structural complexity.

In this context, the calculation of unsteady loads involves the variation in amplitude with the conversion of loads under different operating conditions. In order to simplify the expression, a sample equation is given below to show the basic framework of unstable load calculation. It is assumed that the unstable load F instable is related to the amplitude A, the effect of the weld, and the load conversion factor for different operating conditions

(14) F instable = C 1 ⋅ A ⋅ 1 + C 2 C 3 ⋅ e − k 1 ⋅ t ,

where F instable is the instability load; A is the amplitude; C 1 , C 2 , C 3 are the constant coefficients, depending on material properties, structure type, etc.; k 1 is the time-dependent decay factor; and t is the time or number of loadings.

Adjustment formula for weld impact:

(15) F weld = C 4 ⋅ F instable ⋅ 1 − C 5 C 6 ⋅ e − k 2 ⋅ t ,

where F weld is the weld-adjusted instability load; C 4 , C 5 , C 6 are the constants related to the welded joint; and k 2 is the time-dependent weld attenuation factor.

With the above equations, the amplitude variation, weld influence, and other factors can be combined for the calculation of unstable loads.

4.2 Analysis of destabilizing loads in relation to key parameters

Figure 4 shows the relationship between the instability load N tcr and the vertical static load p 0 . It can be observed that the instability load N tcr decreases slightly with the increase in p 0 . When p 0 increases to a certain critical value, the curve changes abruptly, resulting in an instantaneous decrease in the instability load to close to 0. Further analysis shows that the abrupt change mainly originates from the parameter resonance, i.e., the pile enters into the unstable region when the loading frequency is equal to the critical frequency, showing the abrupt change phenomenon region, which exhibits the sudden change phenomenon. In this state, even if a very small external force is applied, the pile may be destabilized, which constitutes a serious impact on the structural safety. In addition, it is found that the critical frequency tends to decrease with the increase in p 0 , which is different from the conventional resonance phenomenon. The change in critical frequency is not only affected by pile parameters, but also constrained by other environmental factors. In order to further clarify the influence mechanism, the parametric analysis will be developed in the subsequent sections.

Figure 4

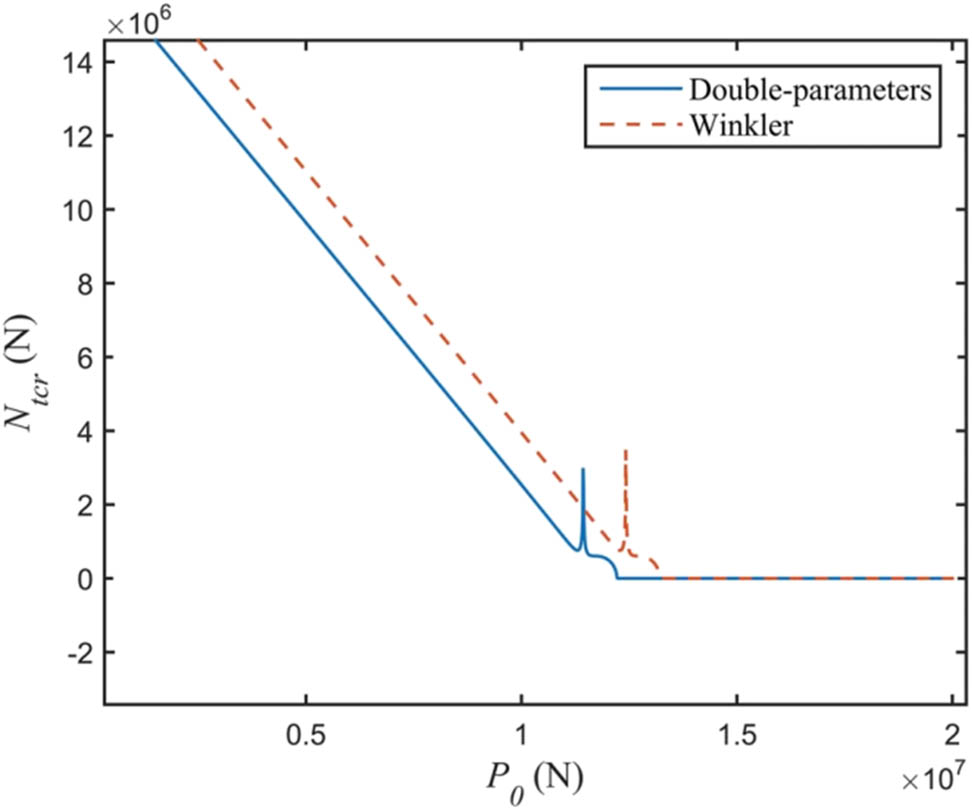
The effect of static load P ₀ at the top of the pile on the destabilizing load.

Furthermore, the instability loads determined by the Winkler model and the two-parameter model are contrasted in Figure 5. The findings demonstrate that the instability load determined by the two-parameter model is comparatively lower. This suggests that the shear impact weakens the soil constraint surrounding the pile and decreases soil stiffness, which in turn affects the instability load calculation. This fact suggests that in real-world engineering applications, the two-parameter model is safer and more dependable.

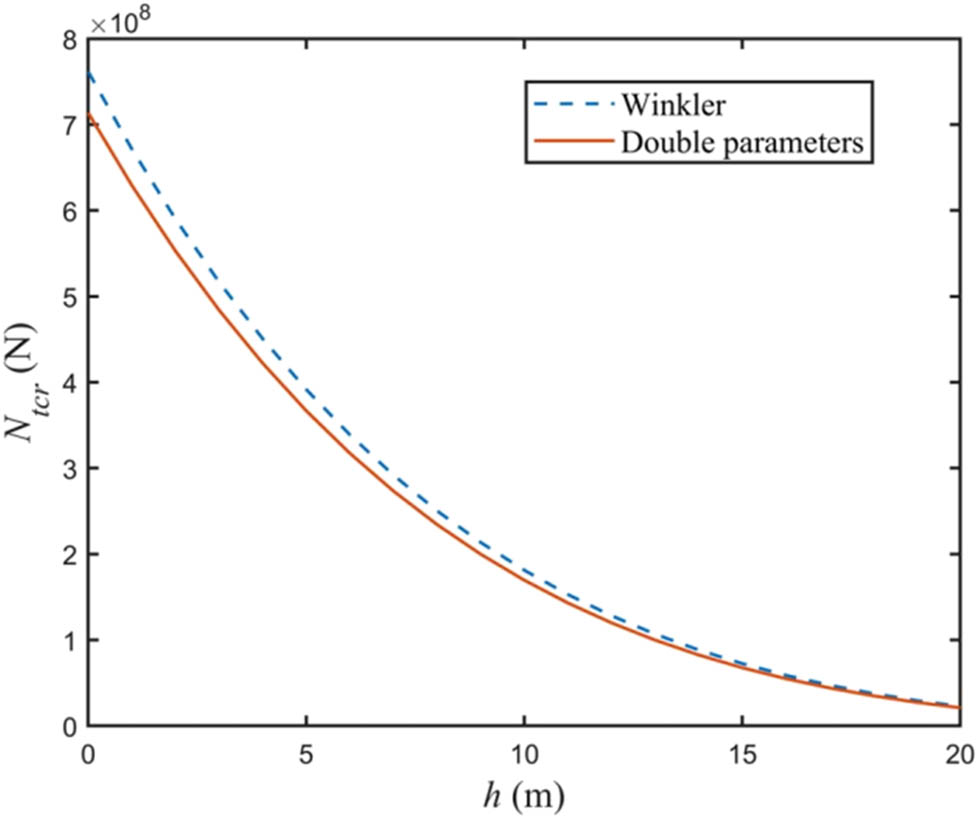
$Figure 5 Impact of pile stiffness capacity load N tcr {N}_{\text{tcr}} on pile water entry depth h.$

Figure 5

Impact of pile stiffness capacity load N tcr on pile water entry depth h.

4.3 Connection between destabilizing load and pile depth

The impact of pile depth h on the destabilizing load is seen in Figure 6. The destabilizing load exhibits a sharp declining trend as h increases, followed by a steady slowdown and eventual stabilization of the lowering rate. Actually, the impact of wave scour on the foundation is reflected in the variation in pile depth. Continuous wave action causes the soil on the pile side to gradually disappear under conditions of constant water depth. This weakens the lateral constraint force and increases the pile body’s free length, which in turn causes the instability load to diminish. The two-parameter model’s rationality and practical relevance are further confirmed by the fact that, when comparing the two models’ findings, the instability loads it produced were lower than those of the Winkler model.

Figure 6

Lateral coefficient k of foundation soil on unstable situation urban load.

Figure 6 illustrates the relationship between pile depth h and the corresponding destabilizing load under dynamic conditions. As shown in the figure, the destabilizing load decreases significantly with increasing pile depth at the initial stage, indicating a high sensitivity of pile stability to wave-induced scour effects. This rapid reduction reflects the substantial weakening of lateral soil support as scour increases the effective free length of the pile.

As the depth h continues to increase, the declining trend in destabilizing load slows and eventually tends toward stabilization. This implies that beyond a certain point, further scour has a diminishing effect on the reduction in pile stability, likely because the soil-pile interaction reaches a critical lower bound where lateral resistance becomes minimal.

The comparison between the two-parameter model and the traditional Winkler model in this figure highlights a key finding: the instability loads predicted by the two-parameter model are consistently lower. This suggests that the two-parameter model more accurately captures the degradation of lateral resistance and pile–soil interaction under scour conditions, thereby offering a more conservative and realistic estimate of pile performance under dynamic marine environments.

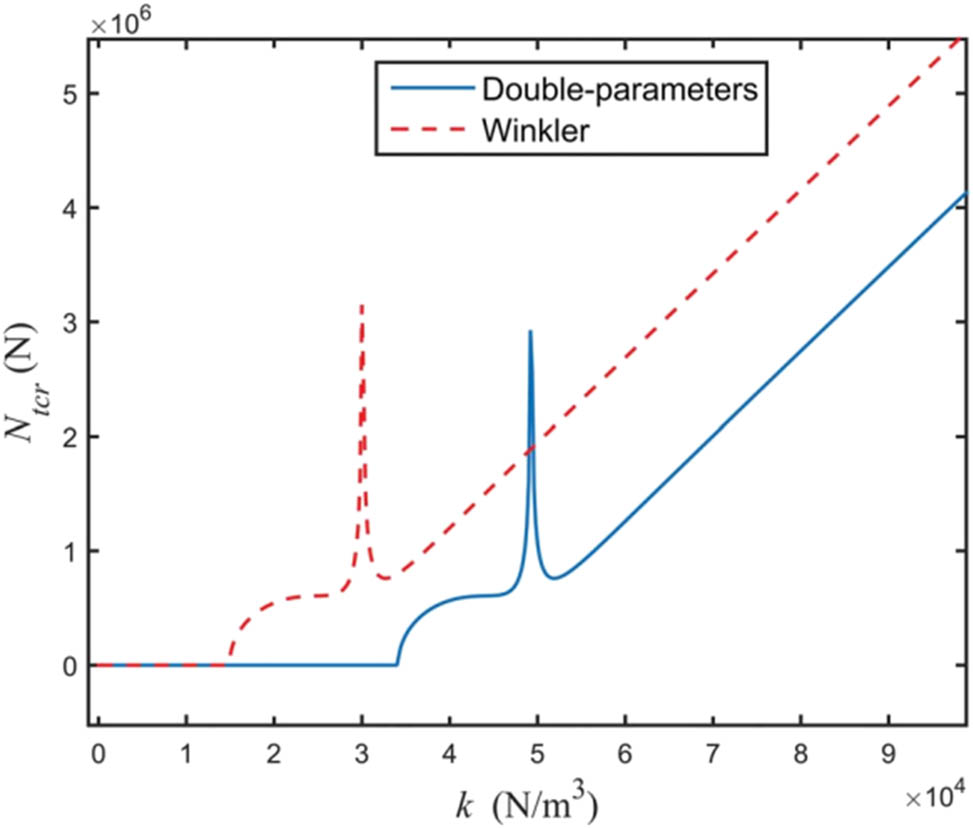
4.4 Impact of the pile-side horizontal resistance coefficient kk on destabilizing loads

Figure 7 shows the trend of destabilizing loads with different horizontal resistance coefficients k on the pile side. When k is small, N tcr is about 0, which indicates that the pile is weakly restrained, and although the vertical harmonic load has not been applied yet, the pile is already in an unstable state under the combined effect of wave load and static load. With the increase in k, the destabilizing load curve shows a sudden change, and then N tcr rises gradually and shows a linear growth trend. This phenomenon indicates that the parameter resonance frequency increases when the pile side constraint increases. When the resonance frequency is equal to the load frequency, the pile body enters into the unstable region, resulting in a sharp decrease in the destabilizing load; when the resonance frequency exceeds the load frequency, the destabilizing load increases linearly with the increase in k, and the stability of the pile body gradually improves.

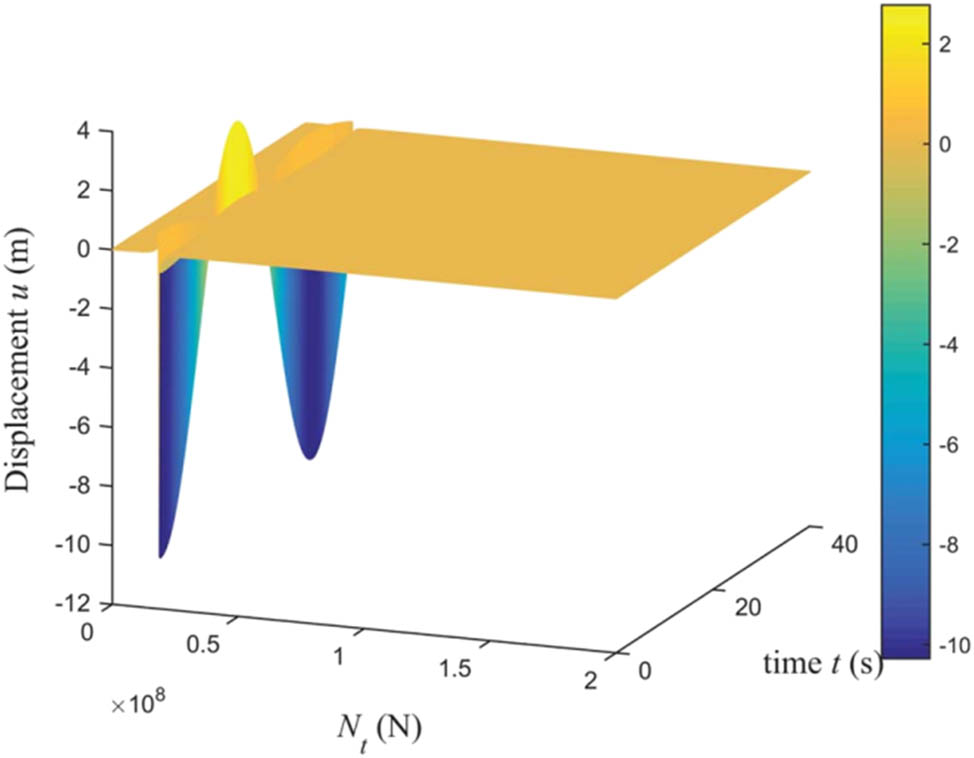
$Figure 7 3-D image of displacement vs N t {N}_{t} and time t.$

Figure 7

3-D image of displacement vs N t and time t.

4.5 Relationship between pile displacement u and instability load N t

From the figure, it can be seen that the displacement curve has a sudden change in some areas, and the corresponding N t value is the destabilizing load. In other cases, the change in N t is relatively smooth, which indicates that the pile is in normal working condition. This result shows that the displacement analysis can effectively identify the destabilization points and provide a basis for the stability assessment of engineering structures.

The critical load frequency of the system is Ω, according to the analysis of frequency impacting factors. First, we examine how the Winkler model and the two-parameter model affect the crucial frequency computation. The graph showing how the load frequency change affects the amplitude in Case 3 is shown in Figure 8. It is evident from the graph that when the load frequency rises, the amplitude changes significantly. The parametric resonant frequency of the system is the equivalent load frequency when the amplitude reaches its maximum value.

Figure 8

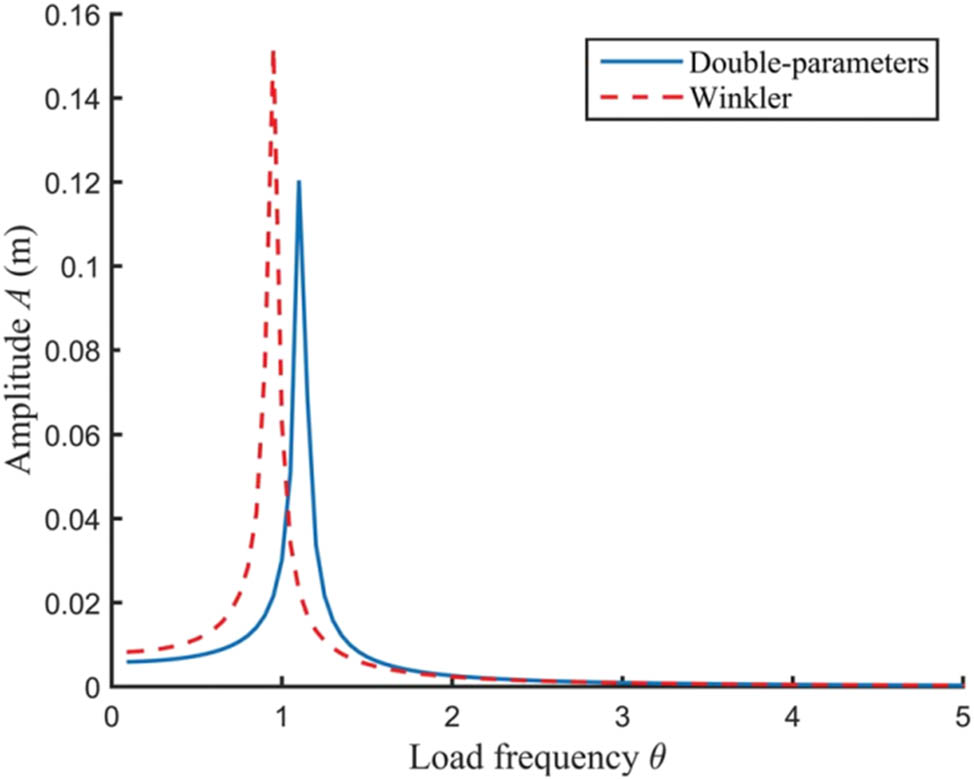
Critical frequency comparison between two-parameter.

The damping effect causes the amplitude to fluctuate sharply in the range near the parametric resonance frequency rather than tending to infinity when the load frequency is near that frequency. The amplitude’s sharp rise and fall trend in the parametric resonance frequency range close to |δ|, the unstable zone of pile vibration, is shown in Figure 8. The critical frequency derived from the two-parameter model is less than the Winkler model’s computed value, according to a comparison of the two curves’ computation results.

In addition, Figure 9 demonstrates the characteristics of the system’s displacement with time and frequency in three dimensions, allowing for a more intuitive distribution of the unstable region. This figure further validates the difference in critical frequency under different models and provides a deeper understanding of the dynamic response characteristics of the system.

Figure 9

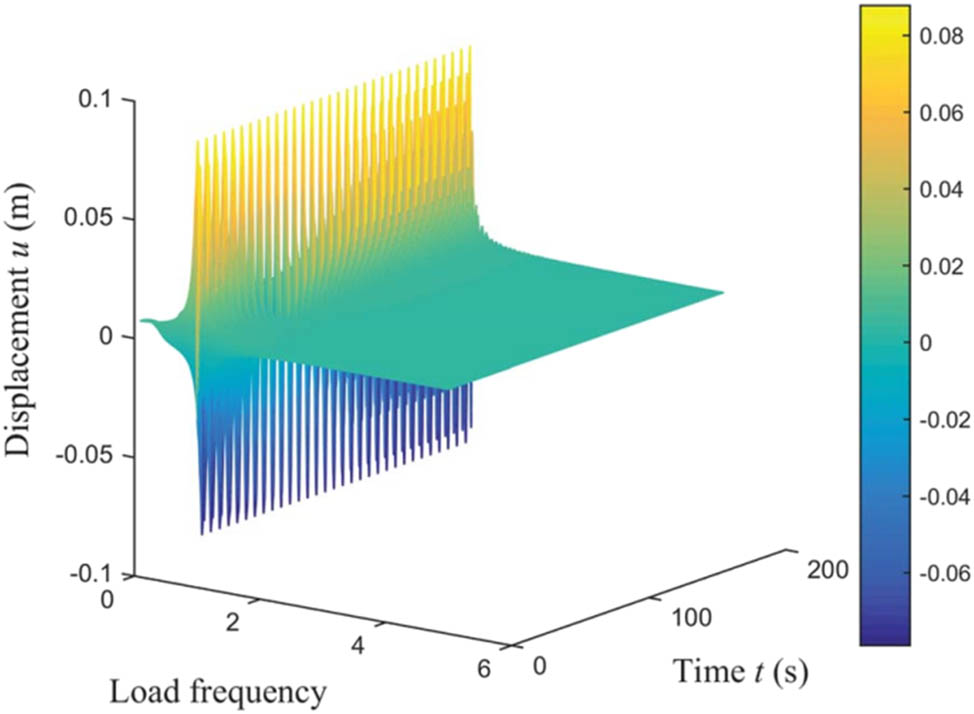
Displacement u as a function of time t and load frequency.

Figure 9 shows the displacement response of the system under different loading frequencies and times in a three-dimensional way, which visually depicts the dynamic response characteristics of the pile foundation under cyclic dynamic loading. In the figure, it is obvious that the displacement response amplitude of certain frequency regions increases significantly, forming “peak zone” or “high response zone,” which are the frequency ranges where the system may be destabilized.

4.6 Impact of shear stiffness and soil coefficient k on the pile’s side

The impact of shear stiffness G and coefficient k on the pile lateral soil and its mechanism on the critical frequency are the main topics of this section. We discovered in the previous load instability analysis that the critical frequency is significantly impacted by the pile lateral soil’s resistance coefficient, k. In order to identify its action mechanism, we further examine its influence pattern in this part.

The curve in Figure 10 illustrates that the impact of mass mm on the critical frequency is opposite to that of k. In particular, the crucial frequency progressively rises as k increases, although the increase tends to diminish. Furthermore, Figure 10 shows a curve interval close to zero. According to the research, this is because the soil constraint is weak when k is small, which causes the pile to become unstable under wave and vertical loads and causes the curve to exhibit an interval of zero close to horizontal. The soil constraint on the pile side rises as kk increases further, raising the critical frequency. It is important to note that the figure’s comparison of the two curves confirms the two-parameter method’s superiority in this particular case.

Figure 10

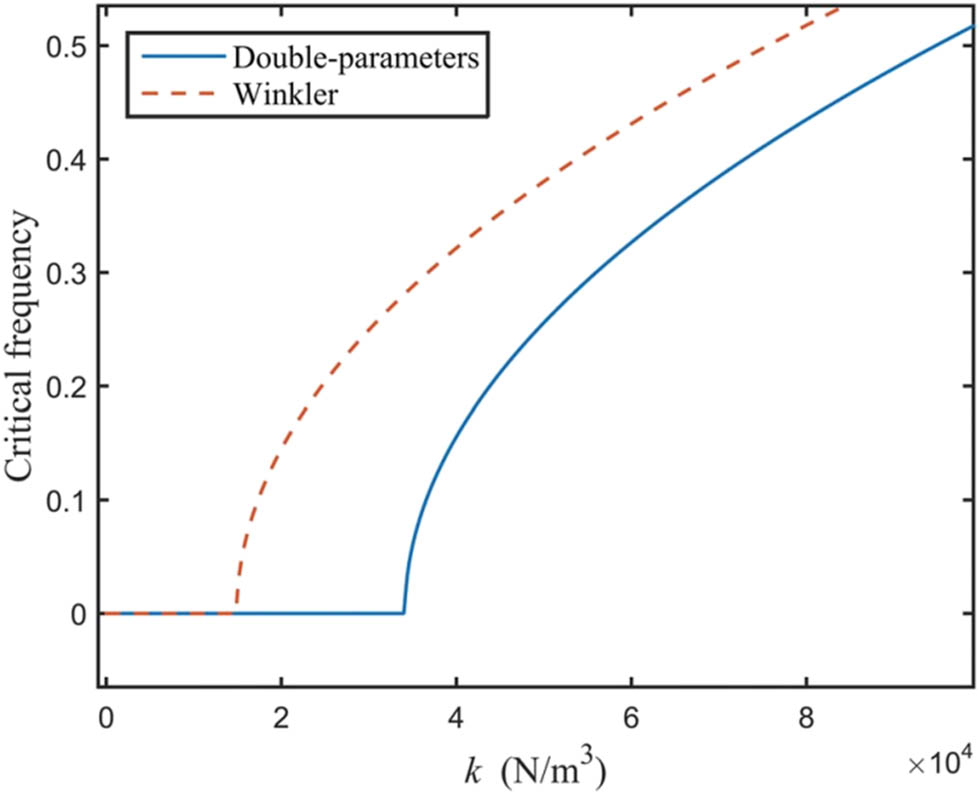
Effect of soil parameter k on the critical frequency.

Figure 11 shows how shear stiffness G affects the critical frequency. According to the chart, the crucial frequency decreases as G increases. It is clear from comparing Figures 10 and 11 that, in the same conditions, the soil resistance coefficient k has a greater effect on the critical frequency than does shear stiffness G. This suggests that dirt on the pile’s side is necessary to increase its stability since it may effectively boost the critical frequency and lessen the instability caused by the loading in addition to helping the pile’s lateral restraining ability. Practical engineering applications must consider the effect of surrounding soil on pile stability and put effective measures in place to prevent erosion and soil loosening on the pile’s side due to wave loading in order to ensure the long-term stability of the pile foundation structure.

Figure 11

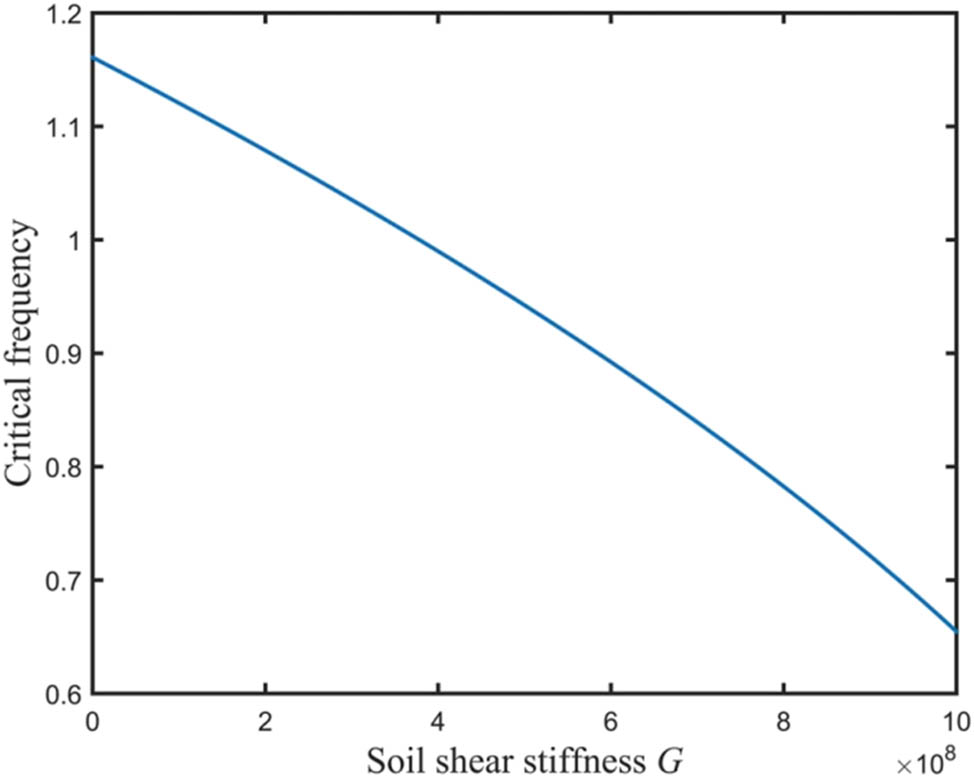
The relationship between critical frequency and soil stiffness G.

In the previous part of the study, we have demonstrated the effect of pile-side soil on pile stability. Since the pile foundation in the marine environment is subjected to wave loading for a long time, part of the soil around it is susceptible to erosion and scouring, leading to the gradual loss of soil on the pile side. With the loss of soil, the free length of the pile increases, which makes the restraining effect of the soil on the pile side weaken, thus affecting its critical frequency.

Specifically, the trend of critical frequency is shown in Figure 12. The figure shows that the critical frequency decreases nonlinearly with the increase in the h/l ratio (the ratio of the free length of the pile to the total length) and falls below 0.5 when the h/l exceeds a certain threshold. In this state, the critical frequency is close to the frequency of wave loading, which increases the possibility of parametric resonance. This resonance effect may cause fatigue damage to the pile body and even lead to structural instability, thus significantly reducing the long-term service performance of the pile foundation.

Figure 12

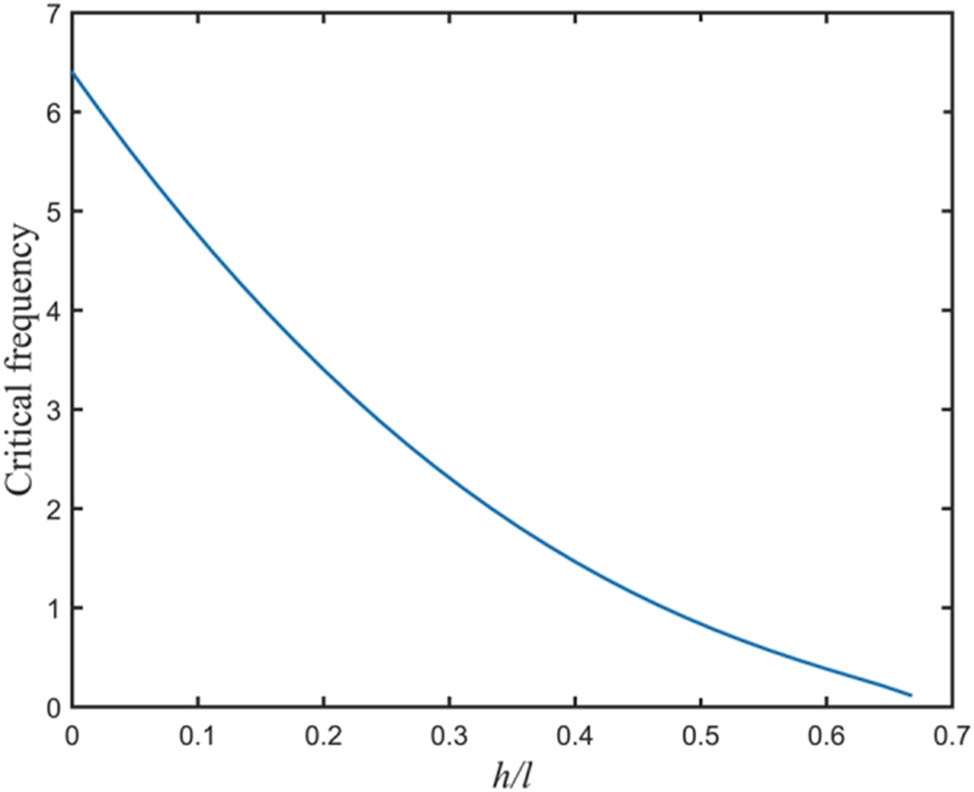
The impact of the ratio of pile length h to pile body length h in water length of critical frequency pile l.

In order to slow down soil loss and improve the restraining ability of the soil on the pile’s side, practical engineering applications must implement effective protective measures. These measures include optimizing the soil protection structure around the pile, increasing the scour prevention device, or adopting high-strength composite materials. This will improve the resonance resistance of the pile foundation structure, reduce the decrease in the critical frequency, and improve the structure’s long-term stability and safety in the marine environment.

4.7 How pile diameter (d) and length (l) affect critical frequency

The impact of increasing pile length on critical frequency is the main topic of this section. While the free length of the pile exposed to the earth stays the same, the increase in pile length in this instance relates to the depth of the pile foundation submerged in the seabed. An intriguing phenomenon is revealed by Figure 14, which shows how pile length l affects the critical frequency. Unlike what was initially thought, the critical frequency does not decrease steadily as pile length increases; rather, it begins to increase as pile length increases beyond a certain point.

The study demonstrates that the alteration of the soil constraint effect is directly linked to the phenomenon’s cause. The crucial frequency gradually drops when the pile length is minimal because the buried soil layer is shallow and the soil’s restraining impact on the pile is weak. At this point, though, it is easier to see how increasing pile length reduces the critical frequency. The constraint of the soil on the pile side increases as the pile moves deeper into the soil layer. When the pile length reaches a certain equilibrium point, the restriction of the soil to the pile tends to stabilize and the critical frequency no longer drops significantly. The crucial frequency rises as the pile length increases because the soil’s restraining impact keeps growing.

Moreover, Figure 15 illustrates how pile dimension dd affects the critical frequency. In the first half of the curve, a larger pile diameter is linked to a higher critical frequency, whereas in the second half, a smaller pile diameter is linked to a lower critical frequency. As demonstrated by the earlier study, an increase in mass significantly reduces the critical frequency for the same pile length, which is why a greater pile diameter denotes a larger mass. Therefore, pile length and pile diameter must be carefully determined in the pile foundation design in order to control the critical frequency away from the loading frequency and avoid the instability risk caused by parametric resonance.

The critical frequency may decrease to zero as the pile length increases when the pile diameter d is small, indicating that the pile has entered the unstable state. This phenomenon suggests that if the pile’s length to diameter ratio is too high, the pile may become unstable from its own weight. In order to guarantee structural stability, the length-to-diameter ratio of the pile should be suitably optimized in the actual project based on the particular working conditions. Appropriate steps should also be taken to increase the pile foundation’s resonance resistance in order to improve overall durability and safety.

Figure 12 shows the influence of the ratio of the depth of pile entry to the total length of the pile on the critical frequency.

The figure demonstrates that under the condition of constant free length of pile body, the critical frequency decreases and then increases with the increase in total length of pile body. It shows that the effect of pile length on the critical frequency is closely related to the soil constraint, when the pile is buried at a shallow depth, the constraint is weak and the critical frequency decreases, while when the pile is deepened to a certain depth, the soil constraint is strengthened and the critical frequency rises instead.

Figure 13 shows the joint effect of pile diameter d and pile length l on critical frequency. The figure shows that the critical frequency may drop to zero with the increase in pile length when the pile diameter is small, suggesting that the pile may be destabilized due to self-weight, and a reasonable length-to-diameter ratio needs to be controlled; whereas, when the pile diameter is large, the critical frequency rises and then decreases in spite of the increase in the mass, and the mass needs to be balanced with the stability.

Figure 13

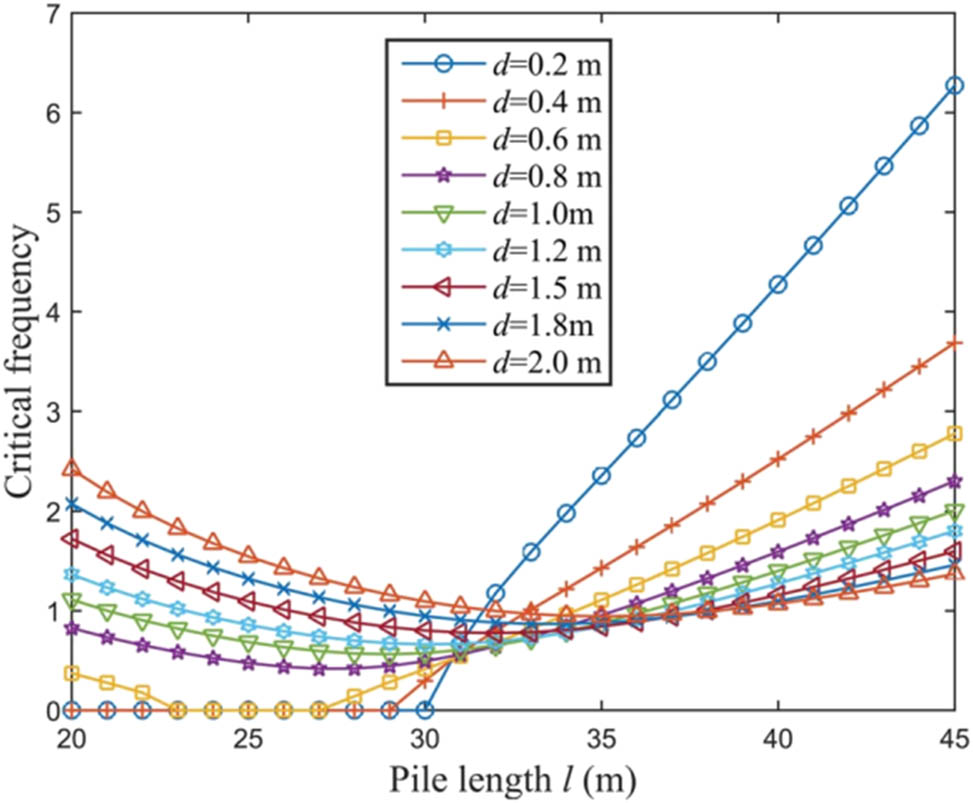
The impact of pile diameter (d) and length (l) on the critical value.

Figure 14 shows the effect of pile-soil stiffness ratio on amplitude, which illustrates that an increase in the pile-soil stiffness ratio decreases the vibration response amplitude, implying that an increase in the soil confinement capacity or pile stiffness helps to improve the vibration resistance of the structure and enhances the resistance of the system to dynamic loading.

Figure 14

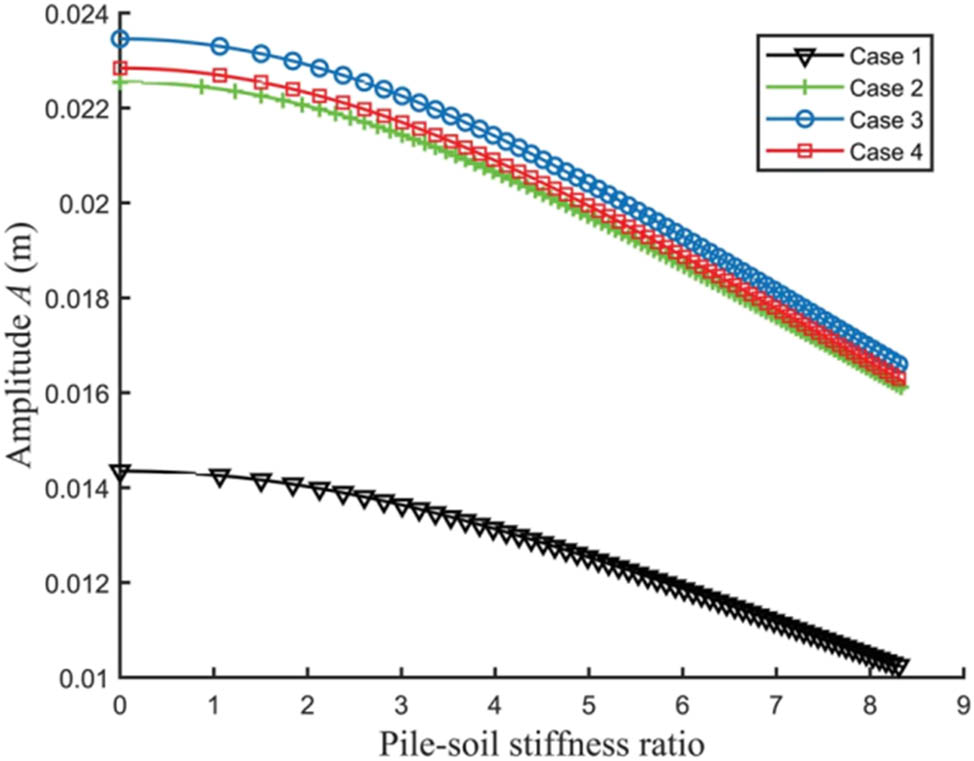
Effect of pile-soil stiffness ratio on amplitude.

Figure 15 demonstrates that the amplitude varies nonlinearly with the pile diameter. In the initial stage, as the pile diameter increases, the amplitude decreases, indicating improved vibration resistance. However, beyond a certain point, further increases in pile diameter lead to a rise in amplitude. This suggests that the self-weight of the pile has a significant impact on its vibration characteristics. Therefore, in structural design, it is essential to balance the benefits of increased stiffness with the adverse effects of added self-weight.

Figure 15

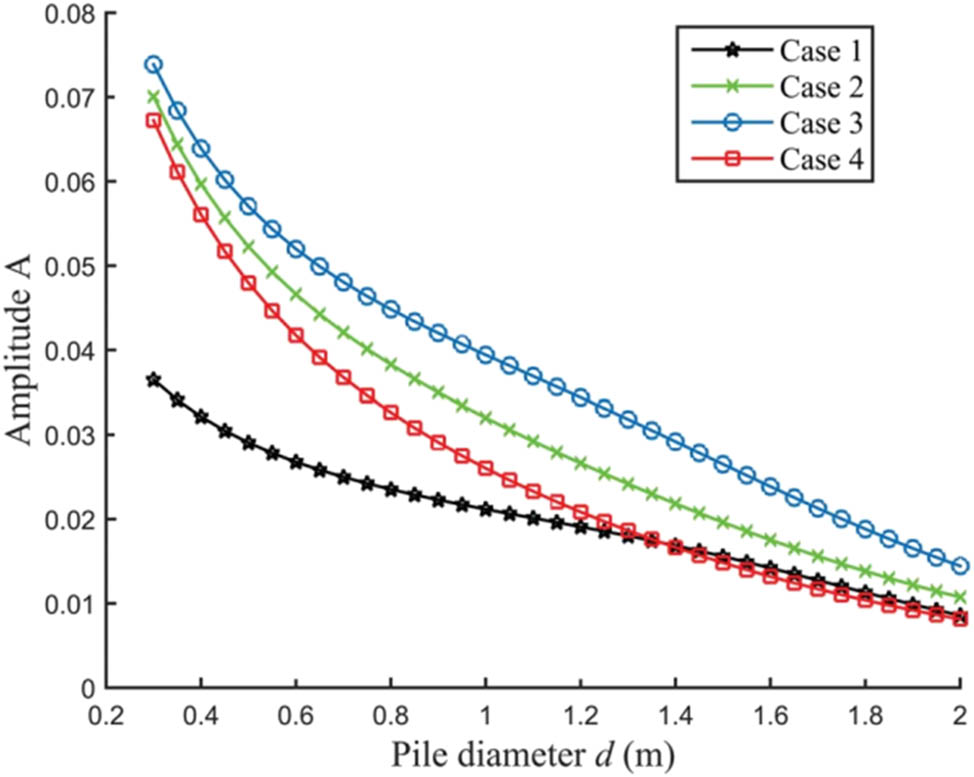
Amplitude as a function of pile diameter d.

5 Conclusion

This work proposes a numerical calculation method based on a two-parameter model for analyzing the stability of pile foundations under complex foundation conditions. By considering dynamic loads and soil nonlinearity, the model accurately reflects the influence of key parameters such as pile water entry depth, soil resistance, and pile stiffness. Compared with the traditional Winkler model, the two-parameter model demonstrates higher precision in predicting critical and destabilizing loads, especially under dynamic loading.

However, further validation is needed to assess its effectiveness in real engineering applications, particularly under extreme conditions. Future studies may incorporate more complex soil behaviors and loading types to enhance the model’s generality and engineering applicability.

Funding information: This study is supported by Natural Science Research Project of Colleges and Universities of Jiangsu Province (22KJD560007). Jiangsu Province Industry-university-research Cooperation Project: (BY20231049, BY20231095).
Author contributions: The authors confirm contribution to the article as follows: study conception and design: Huimin Wang and Jing Zhang; data collection: Kai Zhang; analysis and interpretation of results: Jing Zhang and Kaiqing Ma; draft manuscript preparation: Huimin Wang and Kaiqing Ma. All authors reviewed the results and approved the final version of the manuscript. All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: Authors state no conflict of interest.
Data availability statement: The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

References

[1] Yin X, Ni H. Displacement analysis and numerical simulation of pile-anchor retaining structure in deep foundation pit. J Meas Eng. 2024;12(1):124–37.10.21595/jme.2023.23635Suche in Google Scholar

[2] Li D, Yi F, Li X, Chen S, Hu Z, Liu J. Excavation effects on reinforced concrete pile foundations: a numerical analysis. Buildings. 2024;14(4):995.10.3390/buildings14040995Suche in Google Scholar

[3] Han M, Jia J, Li Z, Zhu Z, Tu B, Liu L. Improved analytical method for stabilizing piles in loess slope considering nonlinear pile–soil interactions. Int J Geomech. 2024;24(3):04024002.10.1061/IJGNAI.GMENG-8796Suche in Google Scholar

[4] Sheng M, Lu F, Jiang N, Guo P, Li X, An R, et al. Bearing behavior of pile foundation in karst region: Physical model test and finite element analysis. Appl Rheol. 2024;34(1):20230115.10.1515/arh-2023-0115Suche in Google Scholar

[5] Xu Q, Xie J, Lu L, Wang Y, Wu C, Meng Q. Numerical and theoretical analysis on soil arching effect of prefabricated piles as deep foundation pit supports. Undergr Space. 2024;16:314–30.10.1016/j.undsp.2023.09.011Suche in Google Scholar

[6] Xie B, Sun H, Liu T, Tan H. Investigation of the local scour depth of a pile foundation on the migrating sand waves seabed in the western South China Sea. Front Earth Sci. 2024;12:1404430.10.3389/feart.2024.1404430Suche in Google Scholar

[7] Cao MM, Ma SJ, Zhang JW. Numerical analysis study on the influence of shield cutting pile on the settlement of pile–soil composite foundation. Adv Civ Eng. 2024;2024(1):5345820.10.1155/2024/5345820Suche in Google Scholar

[8] Wen Z, Xu W, Yuan B, Zhang L, Liang Z. Numerical analysis of anti-slide pile reinforcement for slope stability under rainfall conditions. Buildings. 2025;15(4):638.10.3390/buildings15040638Suche in Google Scholar

[9] Shen K, Zhang H, Liu J, Zhao X, Zhang Y. Study of cement-soil mixed piles reinforcement method for offshore wind turbine pile foundation. Ocean Eng. 2024;313:119423.10.1016/j.oceaneng.2024.119423Suche in Google Scholar

[10] Liu T, Liu Z, Ma C, Xu Z, Yu L, Zhang X, et al. A numerical analysis of the role of pile foundations in shaft sinking using the vertical shaft sinking machine (VSM). Buildings (2075-5309). 2024;14(11):3383.10.3390/buildings14113383Suche in Google Scholar

[11] Li J, Hou H, Li Z, Lin G. A novel hybrid framework based on modified continued-fraction for pile-soil dynamic interaction of large-scale nuclear power structures. Comput Geotech. 2024;173:106571.10.1016/j.compgeo.2024.106571Suche in Google Scholar

[12] Xu Q, Zhou X, Liu X, Yang G, Xu B, Tu Y. Mechanism of structural defects in cut-and-cover tunnels within high-fill regions and gradient pile foundation reinforcement technology. Tunn Undergr Space Technol. 2024;154:106123.10.1016/j.tust.2024.106123Suche in Google Scholar

[13] Hasan MM, Hore S, Al Alim M, Hore R, Ansary MA. Numerical modeling of seismic soil-pile-structure interaction (SSPSI) effects on tall buildings with pile mat foundation. Arab J Geosci. 2025;18(1):1–14.10.1007/s12517-024-12155-4Suche in Google Scholar

[14] Qu Z, Han Z, Tang H, Xu J, Wang H, Liu Y. Study on numerical simulation of arch mechanism of bridge pile foundation. Buildings. 2024;14(1):146.10.3390/buildings14010146Suche in Google Scholar

[15] Zhao Z, Zhang H, Shiau J, Du W, Ke L, Wu F, et al. Failure envelopes of rigid tripod pile foundation under combined vertical-horizontal-moment loadings in clay. Appl Ocean Res. 2024;150:104131.10.1016/j.apor.2024.104131Suche in Google Scholar

[16] Li X, Zhang X, Zhang F, Huang J, Tang S, Liu Z. A case study for stability analysis of a toppling bank slope with fault fracture zones developed under the action of bridge loads and reservoir water. Water. 2024;16(3):494.10.3390/w16030494Suche in Google Scholar

[17] Gao Y, Zhang Y, Xie Q, Liu Q, Liu T, You T, et al. A study on the influence of anchor rods’ layout on the uplift resistance characteristics of inclined anchor short-pile foundations based on FEA. Buildings. 2024;14(8):2580.10.3390/buildings14082580Suche in Google Scholar

[18] Wu R, Jiang Y, Zhao S, Chen M, Shang S, Lang X. Application and comparative analysis of intelligent monitoring technology for grouted pile construction based on Abaqus. Sci Rep. 2024;14(1):9253.10.1038/s41598-024-59653-9Suche in Google Scholar PubMed PubMed Central

[19] Sun M, Shan Z, Wang W, Xu S, Liu X, Zhang H, et al. Numerical investigation into the stability of offshore wind power piles subjected to lateral loads in extreme environments. J Mar Sci Eng. 2024;12(6):915.10.3390/jmse12060915Suche in Google Scholar

Received: 2025-03-02

Revised: 2025-04-29

Accepted: 2025-05-23

Published Online: 2025-07-02

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

https://doi.org/10.1515/nleng-2025-0162

Schlagwörter für diesen Artikel

pile foundation; stability analysis; numerical calculation method; two-parameter model; dynamic loading; complex foundation conditions; carbon peak strategy

Creative Commons

BY 4.0