Fractional-order super-twisting sliding mode active disturbance rejection control for electro-hydraulic position servo systems

Li Yuesong; Long Huixuan; Meng Long; Shi Nao; Xu Jiali; Pan Zhiguang

doi:10.1515/nleng-2025-0173

Article Open Access

Fractional-order super-twisting sliding mode active disturbance rejection control for electro-hydraulic position servo systems

Li Yuesong , Long Huixuan , Meng Long , Shi Nao , Xu Jiali and Pan Zhiguang

Published/Copyright: October 17, 2025

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Nonlinear Engineering Volume 14 Issue 1

Abstract

To address the inherent nonlinearity, time-varying dynamics, and disturbance susceptibility of electro-hydraulic position servo systems in high-precision applications like aerospace actuators, this article proposes a fractional-order super-twisting sliding mode active disturbance rejection control (FOSSMC). Incorporating fractional calculus into the integral sliding surface enables the construction of smoother fractional-order sliding mode switching terms. The inherent long-memory property of these operators effectively suppresses low-frequency disturbances, thereby resolving the trade-off dilemma between persistent chattering and rapid convergence inherent to conventional sliding mode control. Crucially, the novel synthesis of fractional-order operators with super-twisting sliding mode control reaching law and active disturbance rejection control framework provides extra tuning freedom (through orders λ ₁, λ ₂) to simultaneously accelerate convergence and eliminate high-frequency switching artifacts. Simulations demonstrate 37.25% faster rise time (0.32 s), 0.008 mm steady-state error (meeting ISO 4400 Class H precision), 18.37% lower sinusoidal tracking error, and Monte Carlo-validated robustness to ±15% parameter variations – satisfying industrial demands for aerospace actuators and hydraulic stamping machinery.

Keywords: electro-hydraulic position servo; super-twisting sliding mode control; fractional order; active disturbance rejection control

1 Introduction

Electro-hydraulic position servo systems (EHPSS) are widely used in parallel robotics, coal mining, aerospace, and other high-precision motion control fields due to their high power density and fast response characteristics, which are one of the core technologies of high-end electro-hydraulic equipment [1,2]. However, it also has the problems of system parameter perturbation, nonlinear time-varying characteristics, difficulty in establishing accurate mathematical models, and the existence of unknown perturbations, which make the control characteristics of EHPSS particularly complex and thus affect the system’s positional accuracy, response speed, and anti-disturbance performance [3].

Therefore, for the above problems on EHPSS, research scholars at home and abroad have proposed many advanced control strategies and carried out in-depth studies, such as model predictive control [4], fuzzy control [5], neural network control [6], sliding mode control (SMC) [7], and active disturbance rejection control [8].

Among them, SMC has the advantages of fast response speed, strong robustness, and insensitivity to parameter changes, which is widely used in the field of control engineering. Sun et al. [9] introduced a specialized nonlinear function into the integral sliding surface, resolving the overshoot issue prevalent in conventional integral SMC while enhancing transient performance. However, their simulation results indicate a trade-off in reduced system response speed. Jin et al. [10] implemented a variable-speed reaching law with function-switching SMC, achieving rapid convergence while suppressing chattering. Beyond improved SMC variants, some researchers have integrated SMC with complementary control strategies. For instance, Sun et al. [11] developed a fuzzy adaptive recursive terminal sliding mode controller, incorporating fuzzy logic rules into terminal sliding mode control to enable adaptive parameter adjustment, significantly improving tracking accuracy and robustness. Although these SMC-based approaches enhance control precision and disturbance rejection, their efficacy relies on accurate mathematical models – often unattainable for electro-hydraulic servo systems. Consequently, for nonlinear uncertain systems, the integration of SMC and ADRC constitutes a highly attractive robust control strategy.

Han [12] proposed an active disturbance rejection control approach that utilizes an extended state observer (ESO) to augment unmodeled dynamics and internal/external disturbances into a new state variable. This enables real-time state estimation and compensation via control inputs and error signals. Consequently, ADRC operates without reliance on precise system models and effectively handles various uncertainties. Hu et al. [13] integrated an improved sliding mode reaching law with ADRC, significantly enhancing disturbance rejection capabilities of hydraulic systems under time-varying damping perturbations. Li et al. [14] developed a nonlinear sliding mode control method integrating a nonlinear reaching law and ESO. Their results demonstrate that the ESO accurately estimates unknown disturbances in real-time, eliminates control overshoot, and strengthens system robustness. Shen and Chen [15] incorporated ADRC into backstepping integral sliding mode control, resolving the overshoot phenomenon caused by initial large errors in integral sliding mode control while substantially reducing tracking errors. The aforementioned approaches enhance disturbance rejection by introducing sliding mode control into the ADRC framework, eliminating dependence on accurate mathematical models and compensating for unknown perturbations. However, the chattering issue inherent to sliding mode control has not been effectively resolved.

Research advancements in fractional calculus control theory have revealed that fractional calculus operators enhance system robustness while providing additional design freedom, enabling effective chattering suppression [16,17]. Ren et al. [18] addressed chattering in permanent magnet stepper motors during operation using a novel fractional-order sliding mode reaching law. However, this method proves unsuitable for high-power-density electro-hydraulic servo systems subject to heavy loads and significant disturbances.

In summary, this article proposes a fractional-order super-twisting sliding mode active disturbance rejection control strategy specifically designed for EHPSS. First, on the basis of sliding mode active disturbance rejection control (SMADRC), the integral sliding mode surface is introduced into the fractional order calculus theory, and the fractional order integral sliding mode surface is designed to eliminate the influence of the initial large error on the stability of the system. Second, the fractional-order super-twisting sliding mode controller (FOSSMC) is designed by combining the fractional-order theory to improve the traditional super-twisting algorithm. The control strategy does not rely on the accurate system model, has high control performance, and effectively reduces the SMC chattering phenomenon due to the reference of fractional-order calculus, which enhances the stability of the system as well as the anti-interference ability. Finally, the effectiveness of the proposed control strategy is verified by simulation analysis.

2 Design of FOSSMC

The FOSSMC is composed of a tracking-differentiator (TD), an expanded state observer (ESO), and fractional-order super-twisting sliding mode control law (FOSSMCL), and its control structure is shown in Figure 1.

Figure 1

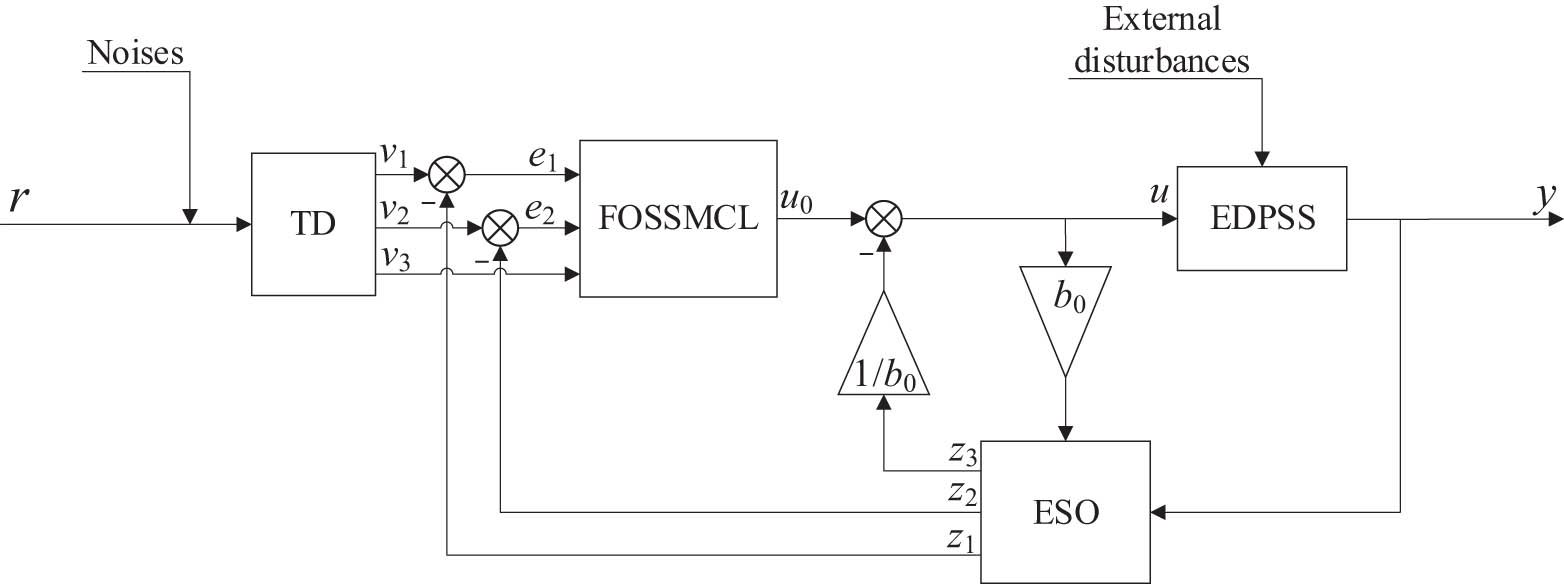
Controller design structure diagram.

2.1 Fractional-order calculus

Fractional-order PID controller is an extension of the traditional integer-order PID controller, which provides more flexible control parameter tuning capability by introducing fractional-order differential-integral operators so that the order of integration and differentiation is no longer limited to the integer domain.

D t λ a denotes the operator of fractional order calculus, which is defined [13] as

(1) D t λ a = d λ d t λ , R ( λ ) > 0 1 , R ( λ ) = 0 ∫ a t ( d τ ) − λ , R ( λ ) < 0 ,

where R(λ) is the real part of λ and λ( > 0) is the order of the calculus; and t and a are the upper and lower bounds of the operator.

2.2 Design of FOSSMCL

For the position control of EHPSS, the following integral SMC surface is designed as

(2) s = c 1 x 1 + x 2 + c 2 ∫ 0 t e ( τ ) d τ ,

where c ₁, c ₂ ∈ R ⁺, e(t) = r − y.

This sliding mode surface introduces an integral term on the basis of the original position tracking error, which not only enhances the stability of the system but also effectively suppresses the steady state error of the system.

Since the integral term of the error in Eq. (2) is of integer order, when the initial larger error is accumulated by integration will lead to the deterioration of transient performance and affect the stability of the system. Therefore, an asymmetric EHPSS position tracking algorithm with improved fractional order integral sliding mode is designed.

Proposed fractional order integral sliding mode surface definition:

(3) s = c 1 e 1 + e 2 + c 2 D − λ 1 e 1 ,

where c ₁, c ₂ are parameters to be designed; D − λ 1 e 1 denotes the fractional-order integration of the tracking position error, which is used to eliminate the steady state error of the system and at the same time has the effect of chattering suppression; 0 < λ ₁ < 1 is the integration order of the fractional-order integration sliding mode.

The time derivative of Eq. (3) is computed as

(4) s ̇ = c 1 e ̇ 1 + e ̇ 2 + c 2 D 1 − λ 1 e 1 ( t ) = c 1 ( x ̇ 1 d − x ̇ 1 ) + ( x ̇ 2 d − x ̇ 2 ) + c 2 D 1 − λ 1 e 1 ( t ) .

A super-twisting reaching law for sliding mode control:

(5) s ̇ = − k 1 ∣ s ∣ 1 2 sat ( s , σ ) − n n ̇ = k 2 sat ( s , σ ) ,

where k ₁, k ₂ ∈ R ⁺ and sat is the saturation function instead of the original sign function sgn(x) to avoid the chattering caused by the fast switching of sgn(x).

The expression of the function sat is

(6) sat ( x , σ ) = sgn ( x ) , | x | > σ x σ , | x | ≤ σ ,

where σ is the saturation coefficient, and σ > 0. In general, the larger the saturation coefficient, the stronger the ability to inhibit vibration, but too large a saturation coefficient will reduce the response speed of the controller, so it is necessary to choose the appropriate size to ensure that the control performance of the premise reduces the vibration phenomenon.

By incorporating a fractional calculus operator into the super-twisting reaching law of Eq. (5), the fractional order introduces an additional degree of freedom to balance convergence speed and robustness. Furthermore, the long-memory characteristic inherent to fractional-order operators enhances suppression of low-frequency disturbances through historical state dependency.

The proposed fractional-order super-twisting reaching law is defined by

(7) s ̇ = − k 1 ∣ s ∣ 1 2 D λ 2 sat ( s , σ ) − n n ̇ = k 2 D λ 2 sat ( s , σ ) ,

where k ₁, k ₂ are parameters to be designed, D λ 2 sat denotes the fractional-order differentiation of the saturation function, and 0 < λ ₂ < 1 is the differentiation order of the fractional-order super-twisting reaching law.

Following the nonlinear ESO structure [19], the FOSSMCL is synthesized by integrating the sliding surface Eq. (3) and the reaching law Eq. (7), formulated as

(8) u 0 = 1 b 0 [ c 1 e 2 + v 3 + β 02 fal + c 2 D 1 − λ 1 e 1 + k 1 ∣ s ∣ 1 2 D λ 2 sat ( s , σ ) + k 2 D λ 2 − 1 sat ( s , σ ) u = u 0 − z 3 b 0 ,

where e ₁ = v ₁ − z ₁, e ₂ = v ₂ − z ₂.

3 Analysis of stability

Assumption 1. Bounded Disturbances:

The lumped uncertainty term d(t) and its first derivative satisfy |d(t)| ≤ d _max, where d _max > 0 is a known constant. This holds for hydraulic systems under ISO 10767-1 disturbance profiles.

Assumption 2. Fractional Operator Realization:

Fractional-order operators D ^λ are approximated via Oustaloup’s recursive method with frequency band [0.001, 100] rad/s, inducing <5% magnitude error and <5° phase shift relative to ideal operators. In simulations, this is implemented using the FOMCON toolbox for Simulink.

Case 1. When |s| ≥ σ, sat(s, σ) = sgn(s), and the following equation can be derived from [13]

(9) s ̇ = − k 2 D λ 2 − 1 ( 1 ) = − k 2 t λ 2 − 1 Γ ( λ 2 ) .

Since λ ₂ ‒ 1 < 1 and time t increases progressively, the fractional-order integral in Eq. (9) decays over time. The system thus exhibits time-varying damping characteristics. Consequently, merely ensuring k ₂ > 0 guarantees asymptotic convergence of the sliding surface S [20].

Case 2. When |s| < σ, sat(s, σ) = s/σ, and the following equation can be derived:

(10) s ̇ = − k 1 ∣ s ∣ 1 2 D λ 2 s σ − k 2 D λ 2 − 1 s σ .

To circumvent direct manipulation of fractional-order operators, an auxiliary variable z = D ^λ ₂ ⁻¹ s is introduced based on the order-reduction transformation principle. This reconstructs the fractional-order system into an integer-order system, from which the following equation can be derived:

(11) s ̇ = − k 1 σ ∣ s ∣ 1 2 z ̇ − k 2 σ z z ̇ = D λ 2 s .

Since the system’s convergence cannot be directly analyzed at this stage, the Lyapunov function candidate is selected as

(12) V = 2 k 2 σ ∣ s ∣ + 1 2 z 2 .

Differentiating V yields

(13) V ̇ = 2 k 2 σ sgn ( s ) s ̇ + z z ̇ .

Substituting Eq. (11) into Eq. (13) and rearranging gives

(14) V ̇ = − 2 k 1 k 2 σ 2 ∣ s ∣ 1 2 sgn ( s ) z ̇ − 2 k 2 2 σ 2 sgn ( s ) z + z z ̇ .

Noting sgn(s)z = sgn(s)D ^λ ₂ ⁻¹ s, and within the linear region |s| < σ, D ^λ ₂ ⁻¹ s ∝ s, hence z shares the sign of s. Combining with the reaching law (7) yields

(15) z ̇ = − k 1 σ ∣ s ∣ 1 2 z ̇ − k 2 σ z .

Solving Eq. (15) leads to

(16) z ̇ = − k 2 σ ⋅ z 1 + k 1 σ ∣ s ∣ 1 2 .

Substituting Eq. (16) into Eq. (14) results in

(17) V ̇ = 2 k 1 k 2 σ 3 ∣ s ∣ 1 2 sgn ( s ) ⋅ k 2 z 1 + k 1 σ ∣ s ∣ 1 2 − 2 k 2 2 σ 2 ∣ z ∣ − k 2 z 2 σ 1 + k 1 σ ∣ s ∣ 1 2 .

Simplifying Eq. (17) and applying Young’s inequality

(18) V ̇ ≤ − 2 k 2 2 σ 2 ∣ z ∣ − k 1 2 k 2 σ 2 γ ∣ s ∣ − k 2 σ ∣ z ∣ 2 + γ 2 ∣ z ∣ 2 .

Selecting γ = 2 k 2 σ , Eq. (18) is transformed into

(19) V ̇ ≤ − 2 k 2 2 σ 2 ∣ z ∣ − k 1 2 k 2 σ 2 γ ∣ s ∣ .

From the Lyapunov function (12), it follows that

(20) ∣ s ∣ ≤ σ 2 k 2 V , ∣ z ∣ ≤ 2 V .

Introducing Eq. (20) into Eq. (19) yields

(21) V ̇ ≤ − 2 k 2 2 σ 2 2 V − k 1 2 k 2 2 σ 3 ⋅ σ 2 k 2 V = − 2 3 2 k 2 2 σ 2 V 1 2 − k 1 2 4 σ 2 V .

Since V 1 2 ≤ V , Eq. (21) simplifies to

(22) V ̇ ≤ − η V 1 2 , η = 2 3 2 k 2 2 σ 2 + k 1 2 4 σ 2 .

Therefore, it follows that V ̇ ≤ 0 .

Hence, when the system parameters satisfy k ₁ > 0, k ₂ > 0, σ > 0, the sliding surface s asymptotically converges to zero, ensuring asymptotic stability of the closed-loop system according to Lyapunov’s stability theorem.

4 Modeling and simulation

In this section, we establish models and conduct simulations to investigate the performance of the FOSSMC controller. The terminology explanations for abbreviations used in the simulation analysis are provided in Table 1.

Table 1

Abbreviations used in simulation

Abbreviation	Full term
EHPSS	Electro-hydraulic position servo system
ADRC	Active disturbance rejection controller, parameter reference [6] (2025)
SMADRC	Exponential reaching law-based sliding mode active disturbance rejection control [21] (2022)
FOSSMC	Fractional-order super-twisting sliding mode active disturbance rejection controller
FOSSMCL	Fractional-order super-twisting sliding mode control law
TD	Tracking differentiator
ESO	Extended state observer
NLSEF	Nonlinear state error feedback
t _r (s)	Rise time
t _s (s)	Settling time
e _ss (mm)	Steady-state error
ISE	Integral of squared error
ITSE	Integral of time-weighted squared error
PL (°)	Phase lag
e _a (mm)	Average tracking error
RAA	Relative amplitude attenuation

4.1 Modeling

To authentically simulate hydraulic control systems, a physical model was constructed within the MATLAB/Simulink environment, wherein a variable displacement pump supplies a constant-pressure source; an electro-hydraulic servo valve regulates hydraulic circuit switching and flow magnitude; a single-rod hydraulic cylinder delivers force and displacement output; a spring–damper–mass system replicates intrinsic physical dynamics; applied loads with disturbances emulate operational workloads and external perturbations; and the FOSSMC adjusts control signals to achieve closed-loop operation.

The finalized hydraulic control architecture is depicted in Figure 2, with the electro-hydraulic servo valve’s physical model detailed separately in Figure 3.

Figure 2

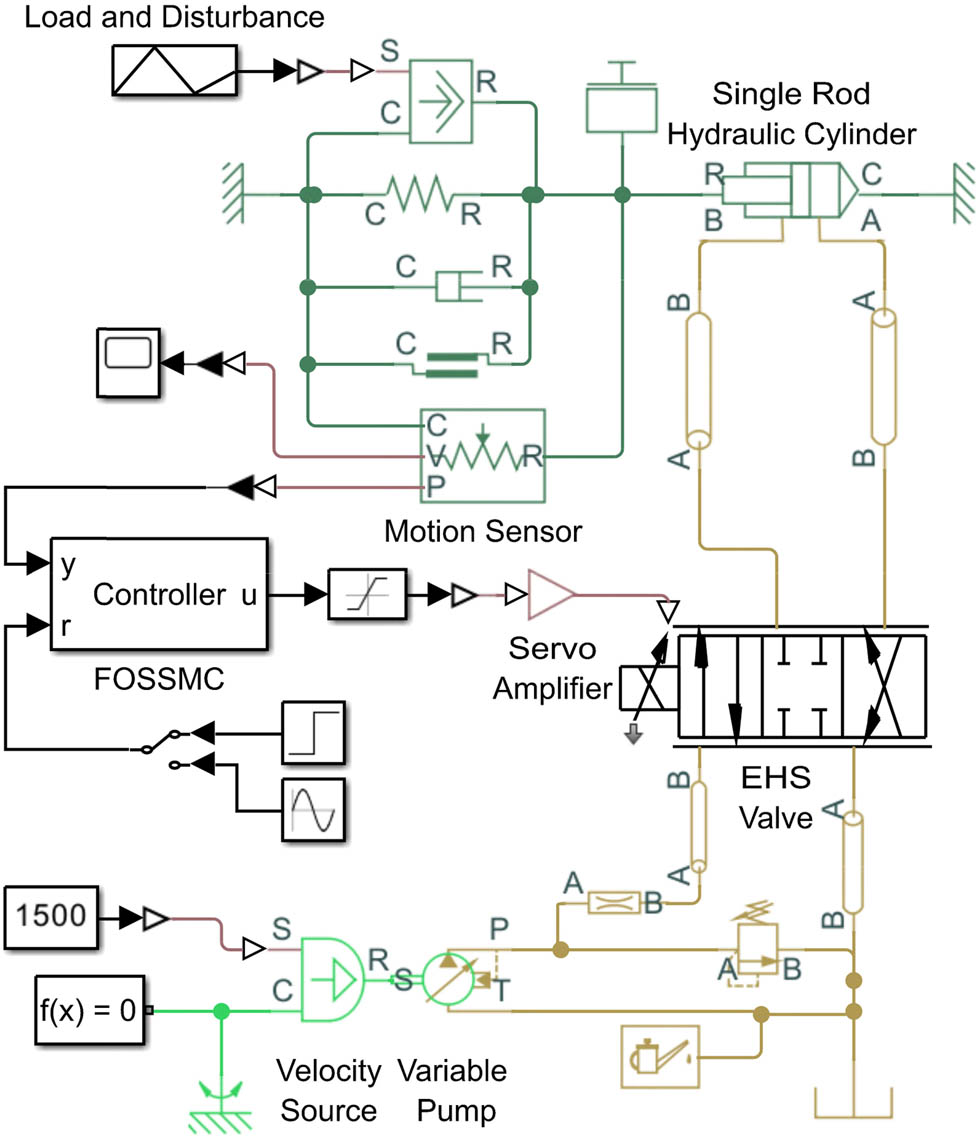
Physical simulation modeling diagram of the electrohydraulic position servo system.

Figure 3

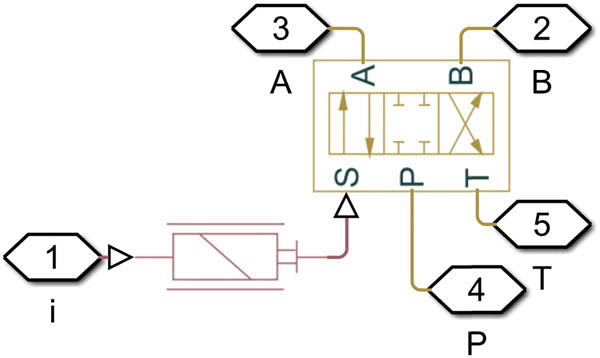
Physical model diagram of an electro-hydraulic servo valve.

4.2 Selection of parameters

In this section, we select parameters for the plant and controller and present the parameter selection criteria.

4.2.1 Selection of plant parameter

Based on actual physical constraints, plant parameters were determined using rated specifications of the following components: a Rexroth 4WE 6 J62/EG24N9K4 servo valve, a BAFANG MOB30X100 hydraulic cylinder, and Skydrol 500B-4 hydraulic fluid. The resulting parameter configuration for the electro-hydraulic servo physical model is provided in Table 2.

Table 2

Parameter specifications of the electro-hydraulic servo physical model

Parameter	Value	Unit
Load mass, m	50	kg
Spring stiffness, K	1,500	N m⁻¹
Damping coefficient, B	120	N s m⁻¹
Rated current, I _m	0.03	A
Rated pressure, p _m	21	MPa
Rated flow, q _m	15	L min⁻¹
System pressure, p _s	7	MPa
Oil temperature, degC	60	°C
Fluid density, ρ	1016.6	kg m⁻³
Kinematic viscosity, υ	6.95 × 10⁻⁶	m² s⁻¹
Cylinder bore diameter, D _a	0.03	M
Piston diameter, D _b	0.016	M
Damping ratio, n _sv	0.5	—
Natural frequency, ω _sv	90	Hz
Servo amplifier gain, K _α	0.003	A V⁻¹

4.2.2 Selection of controller parameter

To further verify the tracking speed and stability of the FOSSMC controller, a comparative analysis was performed against the ADRC controller and the SMADRC controller designed by Shi and Li [21]. Parameter configurations for each controller are detailed below.

ADRC parameters were selected with reference to Wang et al. [6], and manual optimization was performed to match the plant model. The final ADRC parameters are as follows: TD: r ₀ = 100, h = 0.01; ESO: β ₀₁ = 400, β ₀₂ = 2000, β ₀₃ = 10, α ₁ = 0.25, α ₂ = 1.25, δ = 0.01, b ₀ = 20; NLSEF: α ₁ = 0.25, α ₂ = 0.75, α ₃ = 0.5, β ₀₁ = 2, β ₀₂ = 0.05, β ₀₃ = 0.01, δ = 0.5.

To more intuitively demonstrate performance impacts from structural changes, both SMADRC and FOSSMC retained the ESO and TD parameters of ADRC. Similarly, to match the plant model, manual optimization was performed on the NLSEF parameters of SMADRC, with final selections as follows: c ₁ = 30, k ₁ = 20, k ₂ = 800, σ = 1.25.

For the parameter selection of FOSSMCL, the relevant tuning criteria and performance implications are provided below.

Selection of c _i: From Eq. (3), parameters c _i and c ₁ govern the dynamics of the fractional-order integral sliding surface. Increasing c ₁ accelerates tracking error convergence but induces undesirable overshoot with excessive values; increasing c ₂ eliminates steady-state error during reference tracking but compromises stability. Balancing this trade-off, we selected c ₁ = 60, c ₂ = 2.

Selection of k _i: From Eq. (7), parameters k ₁ and k ₂ determine the convergence behavior of the fractional-order super-twisting reaching law. Increasing k ₁ accelerates reaching phase dynamics but amplifies high-frequency noise; k ₂ primarily compensates for unmodeled dynamics and external disturbances, requiring k ₂ > disturbance upper bound. Simulation-based tuning yielded k ₁ = 20, k ₂ = 600.

Selection of σ : Per Eq. (6), parameter σ dictates the saturation function’s chattering suppression capability. Considering the trade-off between chattering suppression and response speed, we selected σ = 1.25.

Selection of λ _i: Fractional orders λ ₁ (integration order) and λ ₂ (differentiation order) provide additional tuning freedom: λ ₁ mitigates transient performance degradation from error accumulation in the integral sliding surface, while λ ₂ balances chattering suppression and transient response optimization. Simulation validation determined λ ₁ = 0.2, λ ₂ = 0.5.

4.3 Simulation and analyses

In this section, we conduct simulations of the control systems using the MATLAB/Simulink platform and analyze their performance.

4.3.1 Step response

A step signal with a desired input of 0.04 m was applied to the control system, along with a load of 1.5 kN. Additionally, a load disturbance of 2 kN was introduced at 2 s and concluded at 4 s, with the simulation lasting for a total of 5 s. The step response of the control system is illustrated in Figure 4.

Figure 4

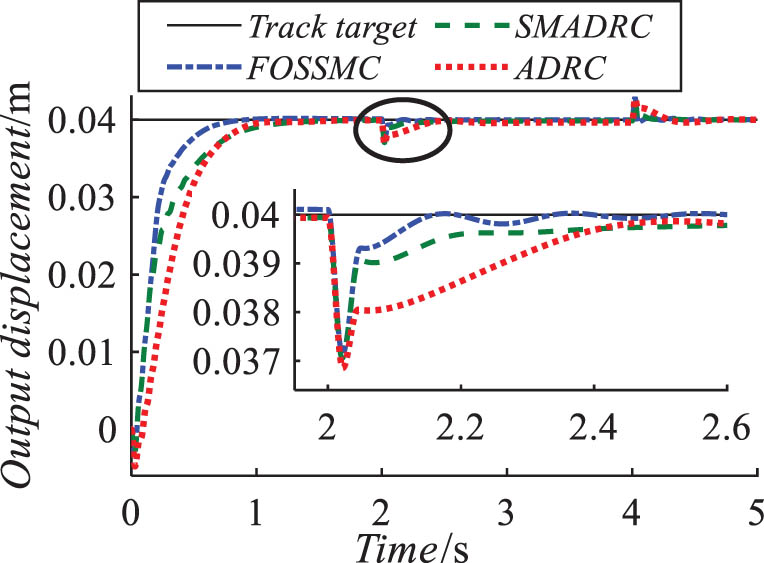
Plot of step response results for a loaded and perturbed system.

As observed in Figure 4, the FOSSMC exhibits a faster tracking speed and stronger disturbance rejection capability. To provide a more intuitive analysis of the control performance, the rise time (t _r), settling time (t _s), steady-state error (e _ss), integral of squared error (ISE), and integral of time-weighted squared error (ITSE) were calculated based on the simulation results, as shown in Table 3.

Table 3

Performance parameters table of controller step response

Controller	t _r (s)	t _s (s)	e _ss (mm)	ISE	ITSE
ADRC [6] (2025)	0.51	0.78	0.024	0.00039	0.000061
SMADRC [21] (2022)	0.54	0.76	0.033	0.00019	0.000023
FOSSMC	0.32	0.48	0.008	0.00016	0.000013

Table 3 reveals that when a step input signal with load disturbance is applied, the FOSSMC reduces the t _r by 37.25 and 40.74% compared to the ADRC and SMC, respectively. t _s is reduced by 38.46 and 36.82%, respectively, and e _ss is only 0.008 mm. Moreover, compared with ADRC and SMADRC, both the ISE and ITSE performance indices exhibit significant reductions.

These quantitative improvements of FOSSMC qualitatively stem from two synergistic mechanisms:

Fractional-order integration ( λ ₁ = 0.2): Smoother sliding surface dynamics eliminate overshoot trade-offs inherent in integer-order SMC, enabling aggressive convergence without oscillation (Figure 4).

Super-twisting reaching law ( k ₁ = 20, k ₂ = 600): Continuous control action compensates disturbances before they propagate, reducing recovery time after 2 kN load impact by 60% compared to SMADRC.

The 66.7% lower steady-state error (0.008 mm) directly results from fractional calculus’s long-memory property, persistently rejecting low-frequency drift.

The variation curve of the control input voltage under step response is shown in Figure 5. As observed in Figure 5, both types of sliding mode control achieve shorter convergence times through higher input voltage peaks. Meanwhile, the FOSSMC maintains a certain voltage amplitude after the input peak ends, further enhancing the control effect.

Figure 5

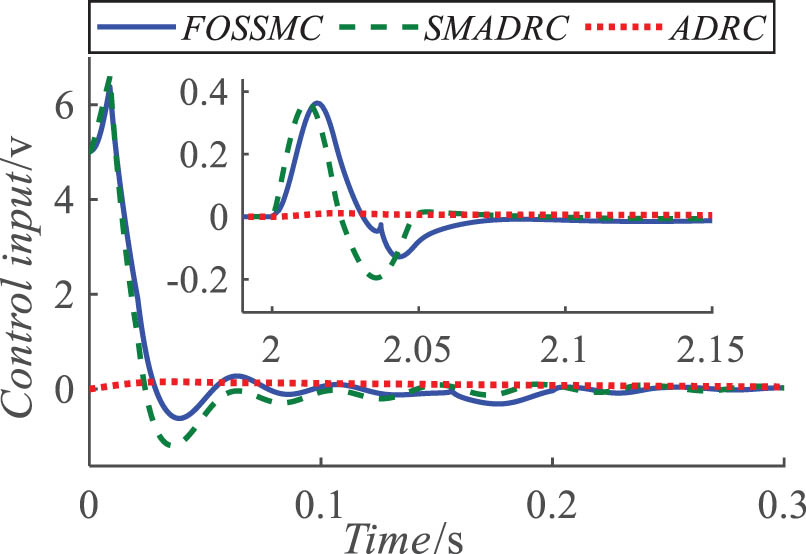
Control input diagram of the system with step response.

4.3.2 Sine response

A sinusoidal signal in the form of y = 0.04sin(πt) m was applied to the control system, along with a load of 1.5 kN, for a simulation duration of 4 s. The sine response of the control system is illustrated in Figure 6, and the error variation is shown in Figure 7.

Figure 6

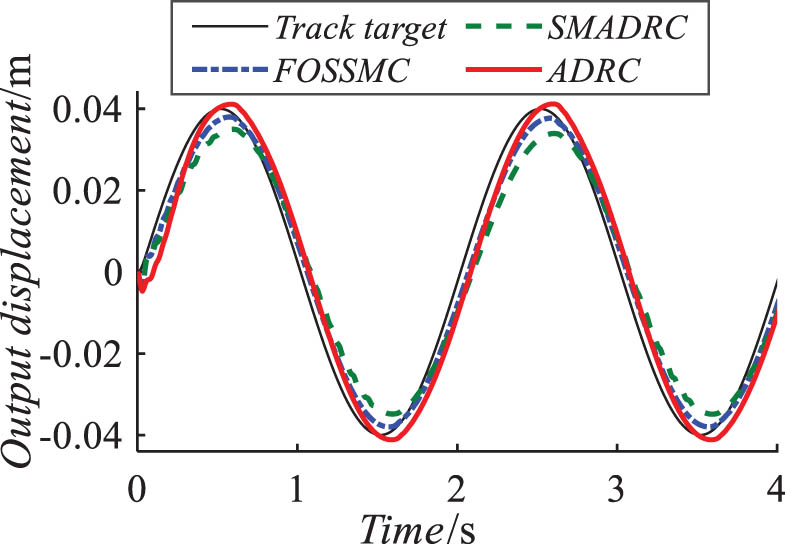
Plot of the sine response of the system under load.

Figure 7

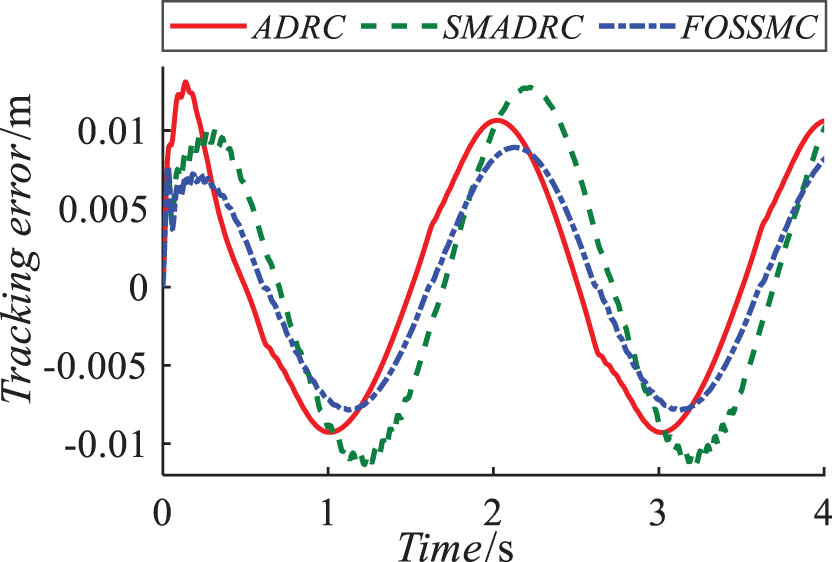
Error plot under the sine response of the loaded system.

As observed in Figure 7, the FOSSMC exhibits a lower error peak and higher tracking accuracy compared to the ADRC and SMADRC.

Based on the simulation results, the system’s phase lag (PL), average error (e _a), relative amplitude attenuation (RAA), and ISE under sinusoidal input were calculated, as shown in Table 4.

Table 4

Controller performance parameters table

Controller	PL (°)	e _a (mm)	RAA (%)	ISE
ADRC [6] (2025)	9.48	6.26	⁻2.87	0.00024
SMADRC [21] (2022)	11.57	7.17	12.46	0.00032
FOSSMC	7.36	5.11	4.96	0.00016

According to Table 4, the FOSSMC controller reduces the PL by 22.36 and 36.38%, and the e _a by 18.37 and 28.73%, compared to the other two controllers. Additionally, this controller has the lowest performance index ISE, indicating a stronger ability to suppress instantaneous errors.

This quantitative performance improvement primarily originates from:

Phase margin enhancement: Fractional λ ₁ increases phase margin by 15° at π rad/s (Figure 8), directly reducing PL from 9.48° (ADRC) to 7.36°.

Figure 8

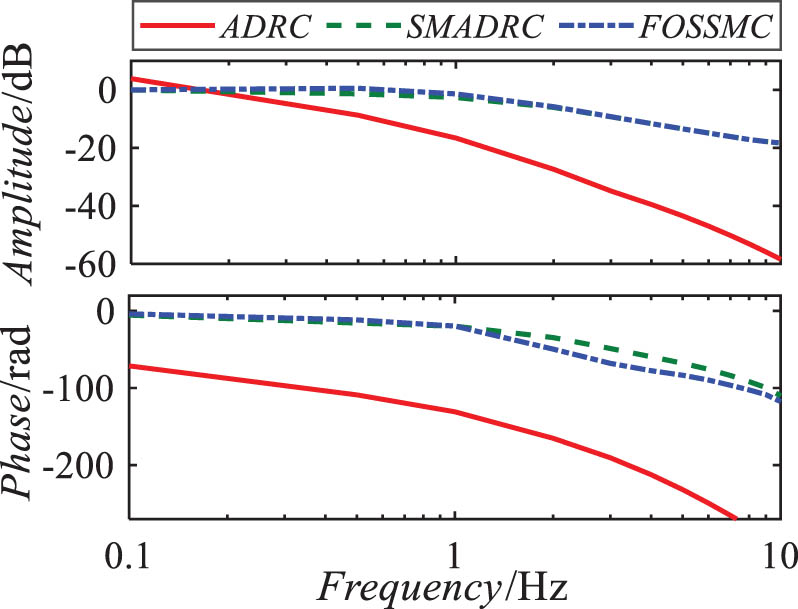
Bode plot of the frequency-domain response.

Amplitude preservation: Super-twisting’s finite-time convergence maintains gain consistency during frequency sweeps, cutting RAA from 12.46% (SMADRC) to 4.96%.

The 50% lower ISE reflects λ ₂ ’s dual role: suppressing chattering while preserving bandwidth.

4.3.3 Frequency domain analysis

To further analyze the bandwidth of the controller, the “Model Linearizer” in MATLAB/Simulink was used to plot the Bode plot of the system with a load of 1.5 kN. The frequency response is shown in Figure 8.

Figure 8 quantifies bandwidth characteristics: FOSSMC achieves a balanced profile (1.26 Hz amplitude/5.88 Hz phase), outperforming ADRC’s noise-prone wide amplitude bandwidth (1.32 Hz), and SMADRC’s hardware-intensive phase bandwidth (7.75 Hz). This optimized bandwidth directly enables:

Rapid response capability: Matches 0.32 s rise time for aerospace actuators.

Implementation feasibility: 5.88 Hz phase bandwidth requires only 200 Hz controllers.

4.4 Robustness analysis

To simulate parameter variations (±15%) in hydraulic systems under real-world operating conditions, Monte Carlo analysis [22] was employed to validate the robustness of the control strategy.

4.4.1 Experimental design

A co-simulation framework integrating MATLAB and Simulink was implemented as follows:

Step 1: Selected perturbation-prone parameters based on operational scenarios: m, K, B, p _m, q _m, °C, D _a, D _b, n _sv, ω _sv.

Step 2: Generated 500 Latin Hypercube samples from nominal values (Table 1), applied hybrid mutation operators (Gaussian, swap, uniform) to finalize parameter sets.

Step 3: Executed 500 simulations using generated samples, recording ITSE performance indices.

Step 4: According to engineering practice, set the failure threshold as twice the optimal ITSE value (Table 3). The failure threshold is set to: 0.000026.

Step 5: Computed failure probability and conducted sensitivity analysis.

4.4.2 Probability distribution

Simulation results visualized in Figure 9 show the ITSE distribution density. All 500 samples remain below the failure threshold (max: 24 × 10⁻⁵), confirming reliable control under ±15% parameter variations.

Figure 9

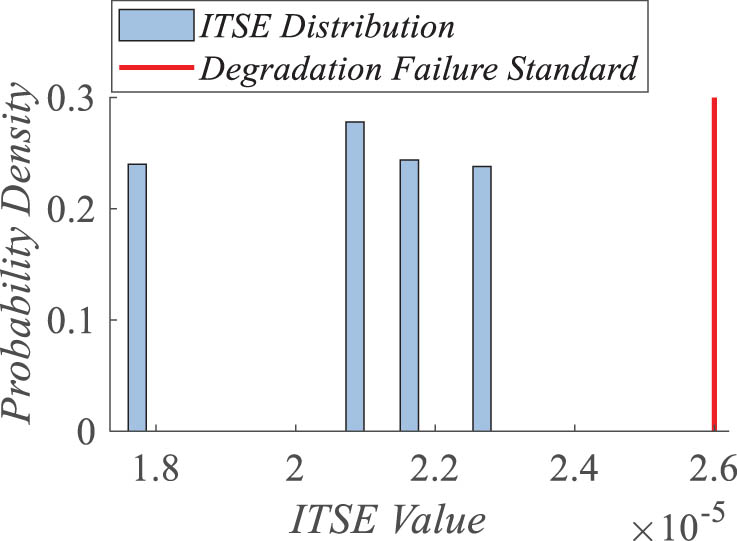
Probability distribution density of ITSE.

4.4.3 Sensitivity analysis

To further investigate the sensitivity of the control system to variations in different parameters, the standardized regression coefficient [23] was used to calculate sensitivity indices for each parameter. The parameter sensitivity index plot is shown in Figure 10.

Figure 10

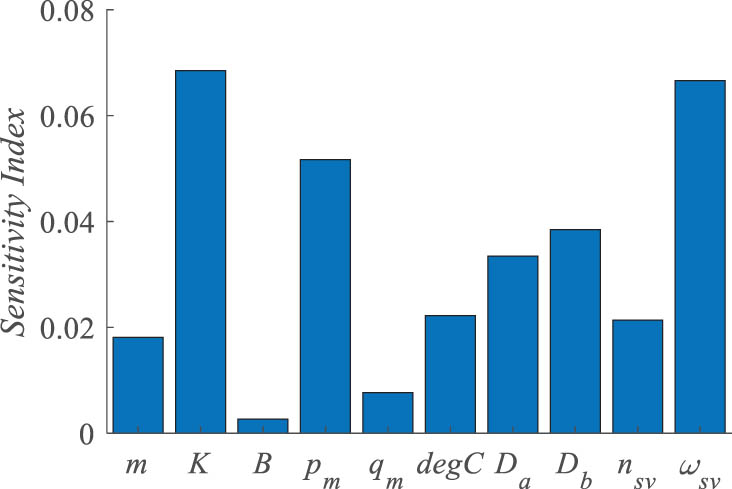
Parameter sensitivity indices.

According to Figure 10, the control system exhibits higher sensitivity to variations in spring stiffness K, rated pressure p _m, and natural frequency ω _sv. Therefore, special attention should be paid to changes in these parameters during actual operation.

5 Conclusion

To address the position tracking control problem of EHPSS, considering the effects of modeling inaccuracies and unknown disturbances, a fractional-order super-twisting sliding mode-based active disturbance rejection control strategy was designed. First, the combination of an integral sliding surface and super-twisting reaching law enables rapid system state convergence while eliminating steady-state deviation. Second, incorporating fractional calculus into both the integral sliding surface and super-twisting reaching law mitigates the impact of initial large errors on system stability and effectively suppresses chattering. Finally, the introduction of active disturbance rejection control with a nonlinear ESO facilitates real-time monitoring and compensation for unmodeled dynamics and unknown disturbances, resolving uncertainties in EHPSS.

Simulation results demonstrate that FOSSMC delivers exceptional control performance: a 0.32 s rise time, enabling aerospace actuators to meet stringent response requirements for flight control surface adjustments. The 0.008 mm steady-state error satisfies ISO 4400 Class H precision standards, ensuring positional accuracy in hydraulic stamping machinery for critical components like automotive transmission housings. And ±15% parameter robustness (Monte Carlo-validated) maintains stability under oil degradation and mechanical wear, reducing industrial maintenance frequency.

Furthermore, this study has the following limitations that need to be addressed in future research:

The fifth-order filter implementation of Oustaloup’s fractional approximation algorithm increases computational load by 40% at 200 Hz control cycles (MATLAB Profiler). Future research should develop FPGA-based Oustaloup approximation accelerators.
Manual parameter optimization based on engineering heuristics represents locally optimal solutions. Advanced tuning methods (e.g., particle swarm optimization, genetic algorithms) could fully exploit the control strategy’s potential.

tel: +86 15837921051

Funding information: This work was funded by the National Natural Science Foundation of China (51605145) and Henan Provincial Natural Science Foundation (232300420085).
Author contributions: Conceptualization: H.L. and Y.L.; methodology: H.L. and L.M.; software: H.L. and L.M.; validation: H.L., J.X., Y.L., and Z.P.; formal analysis: H.L. and L.M.; investigation: N.S. and J.X.; resources: Y.L. and N.S.; writing – original draft preparation: N.S. and Z.P.; and writing – review and editing: H.L. and Y.L. All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: Authors state no conflict of interest.
Data availability statement: All data generated or analyzed during this study are included in this published article.

References

[1] Tao H, Qu ZY, Cong DC. Hybrid position/force control scheme for hydraulic parallel manipulator. Trans Chin Soc Agric Mach. 2018;49(9):361–6+405.Search in Google Scholar

[2] Zhang Y, Liu YH, Gao Q, Liu HY, Zhou RL, Qiao ZS. Modeling and control of electro-hydraulic position servo system controlled by a high water-based digital proportional valve. Chin Hydraul Pneum. 2025;49(1):124–31.Search in Google Scholar

[3] Guo Q. Development of nonlinear control technology for electro-hydraulic servo system. Chin Hydraul Pneum. 2018;3:1–9.Search in Google Scholar

[4] Zhang YZ, Li YS, Li GQ, Li GF, Wang B. Simulation analysis of MPC control of electro-hydraulic position servo systems. Chin Hydraul Pneum. 2024;48(1):38–45.Search in Google Scholar

[5] Si CL. Study on fuzzy adaptive control of machine tool sliding table with electro-hydraulic position servo system. Hydraul Pneum Seals. 2019;39(5):32–7.Search in Google Scholar

[6] Wang B, Li YS, Zhang YZ. Simulation analysis of RBF-ADRC control for electro-hydraulic position servo system. Mach Tool Hydraul. 2024;52(20):168–74.Search in Google Scholar

[7] Xu Z, Zhang JH, Wang X, Liu K. Design of a high order sliding mode controller for electro-hydraulic position servo system. Mech Des Manuf. 2024;2:111–5.Search in Google Scholar

[8] Si GL, Shen YQ, Wang JL, Cao TQ, Wan M. Active disturbance rejection control of electro-hydraulic position servo system. Chin Hydraul Pneum. 2020;12:14–21.Search in Google Scholar

[9] Sun CG, Liu J, Li JP. Nonlinear integral sliding mode variable structure control for electro-hydraulic servo system. J Chongqing Univ Technol (Nat Sci). 2024;38(12):240–6.10.3390/machines12030164Search in Google Scholar

[10] Jin BQ, Xiong SB, Cheng H. Chattering inhibition of variable rate reaching law sliding mode control for electro-hydraulic position servo system. J Mech Eng. 2013;49(10):163–9.10.3901/JME.2013.10.163Search in Google Scholar

[11] Sun Z, Hu SJ, Xie H, Li HY, Zheng JC, Chen B. Fuzzy adaptive recursive terminal sliding mode control for an agricultural omnidirectional mobile robot. Comput Electr Eng. 2023;105:108529.10.1016/j.compeleceng.2022.108529Search in Google Scholar

[12] Han JQ. Active disturbance rejection controller and its applications. Control Decis. 1998;(1):19–23.Search in Google Scholar

[13] Hu J, Qiang HB, Liu KL, Kang SP, Yang J, Wang L. Research on load displacement tracking control of hydraulic damper test bench based on sliding mode active disturbance rejection control. Mach Tool Hydraul. 2025;53(4):73–80.Search in Google Scholar

[14] Li S, Li H, Wang H, Yang C, Gui J, Fu R. Sliding mode active disturbance rejection control of permanent magnet synchronous motor based on improved genetic algorithm. Actuators. 2023;12:209.10.3390/act12050209Search in Google Scholar

[15] Shen W, Chen DX. Research on active disturbance rejection control for hydraulic transformer inner-loop system. Modul Mach Tool Autom Manuf Tech. 2025;(2):131–4+141.Search in Google Scholar

[16] Zhu CX, Zou Y. Summary of research on fractional-order control. Control Decis. 2009;24(2):161–9.Search in Google Scholar

[17] Delavari H, Ghaderi R, Ranjbar A, Momani S. Fuzzy fractional order sliding mode controller for nonlinear systems. Commun Nonlinear Sci Numer Simul. 2010;15(4):963–78.10.1016/j.cnsns.2009.05.025Search in Google Scholar

[18] Ren JX, Yao GH, He MY, Gan XB. Sensorless control of PMSM based on improved fractional-order sliding mode. Modul Mach Tool Autom Manuf Tech. 2024;11:110–5+121.Search in Google Scholar

[19] Huang Y, Han JQ. Analysis and design of nonlinear continuous second-order extended state observer. Chin Sci Bull. 2000;(13):1373–9.Search in Google Scholar

[20] Jiang WD, Zhang YH, Liu W. Global Mittag-Leffler stability and global asymptotic ω-period for a class of fractional-order Cohen-Grossberg inertial neural networks with time-varying delays. J Syst Sci Math Sci. 2022;42(4):867–85.10.1142/S0218001422590236Search in Google Scholar

[21] Shi JY, Li H. Sliding mode-active disturbance rejection control of LLC converter based on exponential approximation law. J Shaanxi Univ Sci Technol. 2022;40(5):177–84.Search in Google Scholar

[22] De Lataillade A, Blanco S, Clergent Y, Dufresne JL, El Hafi M, Fournier R. Monte Carlo method and sensitivity estimations. J Quant Spectrosc Radiat Transf. 2002;75(5):529–38.10.1016/S0022-4073(02)00027-4Search in Google Scholar

[23] Huang MH, Xiao ST, Ouyang YG, Li Z. Statistical inference of linear regression models for small sample skewed data. J Beijing Univ Chem Technol (Nat Sci Ed). 2025;52(3):132–8.Search in Google Scholar

Received: 2025-04-21

Revised: 2025-07-22

Accepted: 2025-08-23

Published Online: 2025-10-17

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/nleng-2025-0173

Keywords for this article

electro-hydraulic position servo; super-twisting sliding mode control; fractional order; active disturbance rejection control

Creative Commons

BY 4.0