Startseite Tension buckling and postbuckling of nanocomposite laminated plates with in-plane negative Poisson’s ratio
Artikel Open Access

Tension buckling and postbuckling of nanocomposite laminated plates with in-plane negative Poisson’s ratio

  • Hui-Shen Shen EMAIL logo , Yin Fan EMAIL logo und Yeqing Wang
Veröffentlicht/Copyright: 12. Januar 2024
Artikel downloaden (PDF)
Veröffentlichen auch Sie bei De Gruyter Brill
Manuskript einreichen Informationen für Autor*innen
Nanotechnology Reviews
Aus der Zeitschrift Nanotechnology Reviews Band 13 Heft 1

Abstract

Mechanical metamaterials with negative Poisson’s ratio (NPR) have emerged as a novel class of engineering material, and have attracted increasing attention in various engineering sectors. Most studies available on the buckling problem of laminated plates with positive or NPR are those under uniaxial compression. Here, we report that the buckling phenomenon may occur for auxetic nanocomposite laminated plates under uniaxial tension when the unloaded edges of the plates are immovable. Two types of nanocomposites are considered, including graphene/Cu and carbon nanotube/Cu composites. Governing equations of the auxetic nanocomposite laminated plates are formulated based on the framework of Reddy’s higher-order shear deformation theory. In modeling, the von Kármán nonlinear strain–displacement relationship, temperature-dependent material properties, thermal effects, and the plate–substrate interaction are considered. The explicit analytical solutions for postbuckling of auxetic nanocomposite laminated plates subjected to uniaxial tension are obtained for the first time by employing a two-step perturbation approach. Numerical investigations are performed for tension buckling and postbuckling behaviors of auxetic nanocomposite laminated rectangular plates with in-plane NPR rested on an elastic substrate under temperature environments.

Graphical abstract

Keywords: nanocomposites; auxetic laminates; tension buckling; rectangular plate; elastic substrate; temperature-dependent

1 Introduction

Buckling is an important problem for the thin plates subjected to uniaxial or biaxial compression [1]. Under tensile loads, thin plates usually do not experience buckling. However, according to the literature survey, there are two special cases, in which buckling can occur under tensile loads, namely “tension buckling,” for the thin plates/sheets. One case is if a plate contains a hole [2,3,4] or a crack [5,6,7], the compressive stresses arise locally near the hole or the crack under a uniaxial tensile load, where these compressive stresses may cause local buckling. Another case is wrinkling (i.e., local short-wavelength buckling), which is commonly observed in stretched-thin sheets [8,9,10,11,12] and single-layer graphene sheets [13,14,15,16] due to the variation of Poisson’s effect. For nanocomposite structures, which are generally considered as the next-generation composite structures, although much research has been done on the buckling and postbuckling analyses of nanocomposite plates under uniaxial or biaxial compression, no attention is paid to the buckling of nanocomposite plates when they are subjected to a tensile load. The buckling of nanocomposite plates under tensile load represents a unique and crucial failure mode in the design of these structures, which has not been reported in the literature. To guide the design and optimization of nanocomposites for future engineering applications, it is of great significance to establish a scientific and theoretical tool to predict the critical tension buckling load, and hence, the factor of safety under this unique buckling failure mode.

Auxetic laminated composites with negative Poisson’s ratio (NPR) are one class of mechanical metamaterials. With the development of nanotechnology and additive manufacturing technology [17,18], nanofillers such as graphene sheets [19] or carbon nanotubes (CNTs) [20] can be embedded in a single-crystal copper matrix to achieve auxetic nanocomposite laminates [21,22]. Owing to their special properties and characteristics, auxetic nanocomposite materials have shown better performance in certain aspects than those of conventional materials and are expected to have a wide range of technological applications [23,24].

Recently, Shen et al. [25] combined the functionally graded (FG) concept with the auxetic concept to design the FG-GRMMC (graphene-reinforced metal-matrix composite) laminates. Considering the auxetic effect of GRMMCs, Shen and his co-authors [25,26] investigated the impact of in-plane NPR on the compressive postbuckling behaviors of FG-GRMMC laminated and sandwich plates subjected to uniaxial compression. Unlike fiber-reinforced composite (FRC), graphene-reinforced composite (GRC) and carbon nanotube-reinforced composite (CNTRC) laminated plates with positive Poisson’s ratios [27,28,29] where the buckling loads and initial postbuckling load–deflection curves for the plate with unloaded edges that are movable (i.e., displacement is unconstrained in the in-plane direction) are higher than those of the same plate with unloaded edges that are immovable (i.e., displacement is constrained in the direction perpendicular to the loaded edges), the auxetic GRMMC laminated plates showed the opposite behavior. Specifically, for auxetic laminated plates, the buckling loads and postbuckling load–deflection curves with unloaded edges that are movable in the in-plane direction are lower than those of the same plate under immovable unloaded edges. This indicates that the unique lateral contraction of the auxetic laminates under uniaxial compressive load locally enhanced the buckling strength. Such an exceptional behavior leads us to believe that auxetic laminated plates with unloaded edges that are immovable may buckle under a uniaxial tensile load as compressive reaction force will be produced on unloaded edges to restrict the lateral expansion of the auxetic plates under uniaxial tension. This provides the motivation for the present investigation.

The present research is to investigate the buckling and postbuckling behavior of auxetic nanocomposite laminated plates with unloaded edges that are immovable and subjected to the uniaxial tensile load under thermal environmental conditions. In the current study, we chose two types of auxetic nanocomposite laminates. One is a graphene/Cu laminated plate with in-plane NPR and the other is a CNT/Cu laminated plate with in-plane NPR. The material properties of both graphene/Cu and CNT/Cu composites are temperature-dependent. The governing equations of the auxetic nanocomposite laminated plates are established based on the framework of Reddy’s higher-order shear deformation theory (HSDT). In modeling, the von Kármán nonlinear strain–displacement relationship, the effect of temperature, the interaction between the plate and substrate, and the effect of the plate's initial geometric imperfection are also taken into consideration. The explicit analytical solutions for buckling and postbuckling of auxetic nanocomposite laminated plates subjected to uniaxial tension are obtained for the first time by employing a two-step perturbation approach. The impacts of the plate aspect ratio, the plate width-to-thickness ratio, temperature variation, and foundation stiffness on tension buckling and postbuckling behavior of auxetic nanocomposite laminated plates are discussed in the numerical investigation.

2 Modeling

Consider an N-ply laminated rectangular plate, where each ply is made of nanocomposites having an in-plane NPR. As shown in Figure 1, a is the length, b is the width, and h is the total thickness of the plate. The coordinate system (X, Y, Z) is located on the middle surface of the plate with its origin placed at one corner of the plate, where the X and Y axes are set along the length and the width directions, respectively, while the Z-axis is set along the thickness direction pointing downward. The plate is rested on an elastic substrate that is idealized as a Pasternak-type foundation model with two stiffnesses, where K ¯ 1 denotes the vertical spring stiffness and K ¯ 2 denotes the shearing layer stiffness.

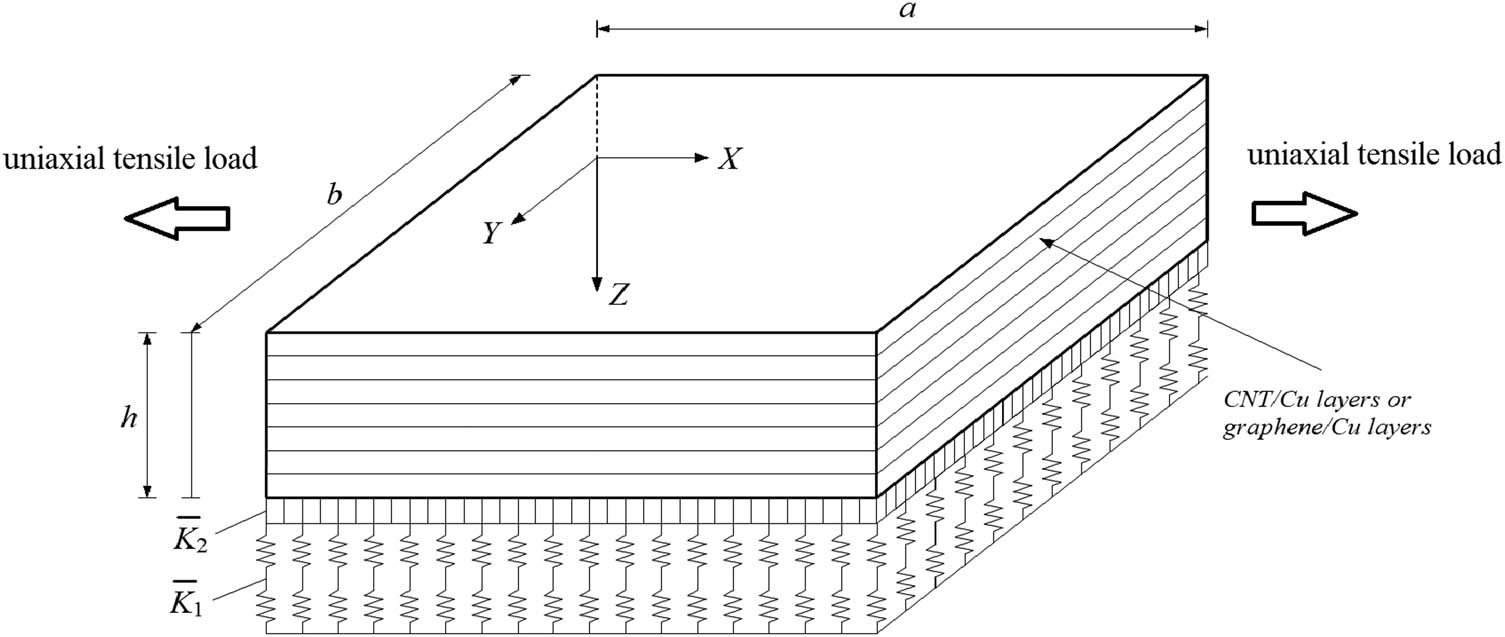
Figure 1 Auxetic nanocomposite laminated rectangular plate rests on an elastic substrate under uniaxial tensile load.
Figure 1

Auxetic nanocomposite laminated rectangular plate rests on an elastic substrate under uniaxial tensile load.

The plate is exposed to elevated temperature and is subjected to uniaxial tensile load. Based on the framework of HSDT of Reddy [30] and that coupled with the von Kármán nonlinear strain–displacement relationships, the governing equations for the postbuckling of the nanocomposite laminated plate with in-plane NPR are given by Shen [1]

(1a) L ˜ 11 ( W ¯ ) − L ˜ 12 ( Ψ ¯ x ) − L ˜ 13 ( Ψ ¯ y ) + L ˜ 14 ( F ¯ ) − L ˜ 15 ( N ¯ T ) − L ˜ 16 ( M ¯ T ) + K ¯ 1 W ¯ − K ¯ 2 ∇ 2 W ¯ = L ˜ ( W ¯ + W ¯ ⁎ , F ¯ ) ,

(1b) L ˜ 21 ( F ¯ ) + L ˜ 22 ( Ψ ¯ x ) + L ˜ 23 ( Ψ ¯ y ) − L ˜ 24 ( W ¯ ) − L ˜ 25 ( N ¯ T ) = − 1 2 L ˜ ( W ¯ + 2 W ¯ ⁎ , W ¯ ) ,

(1c) L ˜ 31 ( W ¯ ) + L ˜ 32 ( Ψ ¯ x ) + L ˜ 33 ( Ψ ¯ y ) + L ˜ 34 ( F ¯ ) − L ˜ 35 ( N ¯ T ) − L ˜ 36 ( S ¯ T ) = 0 ,

(1d) L ˜ 41 ( W ¯ ) + L ˜ 42 ( Ψ ¯ x ) + L ˜ 43 ( Ψ ¯ y ) + L ˜ 44 ( F ¯ ) − L ˜ 45 ( N ¯ T ) − L ˜ 46 ( S ¯ T ) = 0 ,

where W ¯ is the plate displacement in the Z direction, W ¯ ⁎ is the initial geometric imperfection, F ¯ is the stress function defined by N ¯ x = ∂ 2 F ¯ / ∂ Y 2 , N ¯ y = ∂ 2 F ¯ / ∂ X 2 , and N ¯ x y = − ∂ 2 F ¯ / ∂ X ∂ Y , and Ψ ¯ x and Ψ ¯ y are two rotations with respect to the Y and X axes. L ˜ i j ( ) represent the linear operators [1], and L ˜ ( ) representing the nonlinear operator involving geometric nonlinearity in the von Kármán sense is expressed by

(2) L ˜ ( ) = ∂ 2 ( ) ∂ Y 2 ∂ 2 ( ) ∂ X 2 − 2 ∂ 2 ( ) ∂ X ∂ Y ∂ 2 ( ) ∂ Y ∂ X + ∂ 2 ( ) ∂ X 2 ∂ 2 ( ) ∂ Y 2 .

Meanwhile, the interaction of the plate foundation defined by K ¯ 1 W ¯ − K ¯ 2 ∇ 2 W ¯ along with the thermal effect is included in equations (1a)–(1d). The thermal forces, the thermal moments, and the higher-order thermal moments ( N ¯ T , M ¯ T , P ¯ T ) due to elevated temperature are given by

(3a) N ¯ x T N ¯ y T N ¯ x y T M ¯ x T M ¯ y T M ¯ x y T P ¯ x T P ¯ y T P ¯ x y T = ∑ k = 1 ∫ h k − 1 h k A x A y A x y k ( 1 , Z , Z 3 ) Δ T d Z ,

and S ¯ T in equations (1c) and (1d) are given by

(3b) S ¯ x T S ¯ y T S ¯ x y T = M ¯ x T M ¯ y T M ¯ x y T − 4 3 h 2 P ¯ x T P ¯ y T P ¯ x y T ,

In equation (3a), Δ T = T − T 0 denotes the temperature increase with reference to temperature T 0, and

(4) A x A y A x y = − Q ¯ 11 Q ¯ 12 Q ¯ 16 Q ¯ 12 Q ¯ 22 Q ¯ 26 Q ¯ 16 Q ¯ 26 Q ¯ 66 c 2 s 2 s 2 c 2 2 c s − 2 c s α 11 α 22 ,

where α 11 and α 22 are the thermal expansion coefficients in the longitudinal and transverse directions of the kth ply, respectively, and Q ¯ i j represent the transformed elastic constants, defined by

(5a) Q ¯ 11 Q ¯ 12 Q ¯ 22 Q ¯ 16 Q ¯ 26 Q ¯ 66 = c 4 c 2 s 2 s 4 2 c 2 s 2 c 4 + s 4 2 c 2 s 2 s 4 c 2 s 2 c 4 4 c 2 s 2 − 4 c 2 s 2 4 c 2 s 2 c 3 s c s 3 c 2 s 2 c s 3 − c 3 s c 3 s − c s 3 − 2 c 2 s 2 − c s 3 − c 3 s c 2 s 2 − 2 c s ( c 2 − s 2 ) 2 c s ( c 2 − s 2 ) ( c 2 − s 2 ) 2 Q 11 Q 12 Q 22 Q 66 ,

(5b) Q ¯ 44 Q ¯ 45 Q ¯ 55 = c 2 s 2 − c s c s s 2 c 2 Q 44 Q 55 ,

where

(5c) ( Q 11 , Q 12 , Q 22 ) = 1 ( 1 − ν 12 ν 21 ) ( E 11 , ν 21 E 11 , E 22 ) , ( Q 44 , Q 55 , Q 66 ) = ( G 23 , G 13 , G 12 ) ,

where E 11, E 22, G 12, G 13, G 23, ν 12 , and ν 21 are Young’s moduli, shear moduli, and Poisson’s ratios for the kth ply, and c = cos θ and s = sin θ ( θ is the lamination angle with respect to the plate X-axis).

Besides the governing equations (1a)–(1d), for the boundary-value problem, we require the boundary conditions for the auxetic laminated plate. In order to derive the theoretical solution, the four edges of the auxetic laminated plate are assumed to be SSSS (i.e., simply supported on all four edges). Specifically, on the X = 0 and X = a edges,

(6a) W ¯ = Ψ ¯ y = 0 , M ¯ x = P ¯ x = 0 ,

and on the Y = 0 and Y = b edges,

(6b) W ¯ = Ψ ¯ x = 0 , M ¯ y = P ¯ y = 0 ,

where M ¯ x and M ¯ y are the bending moments, and P ¯ x and P ¯ y are the higher-order moments, as given in the study of Reddy [30].

The tensile loads are applied on the X = 0 and X = a edges and the two loaded edges are freely movable (i.e., the displacement can move in the X-direction), while the other two unloaded edges are immovable (i.e., the displacement is constrained in the Y-direction). The in-plane boundary condition on the Y = 0 and Y = b edges is

(7) V ¯ = 0 ,

where V ¯ is the displacement of the plate in the Y direction, and equation (7) can be expressed in an average sense as

(8a) ∫ 0 a ∫ 0 b ∂ V ¯ ∂ Y d Y d X = 0 ,

or

(8b) ∫ 0 a ∫ 0 b A 22 ⁎ ∂ 2 F ¯ ∂ X 2 + A 12 ⁎ ∂ 2 F ¯ ∂ Y 2 + B 26 ⁎ − 4 3 h 2 E 26 ⁎ ∂ Ψ ¯ x ∂ Y + ∂ Ψ ¯ y ∂ X − 8 3 h 2 E 26 ⁎ ∂ 2 W ¯ ∂ X ∂ Y − 1 2 ∂ W ¯ ∂ Y 2 − ∂ W ¯ ∂ Y ∂ W ¯ ⁎ ∂ Y − ( A 12 ⁎ N ¯ x T + A 22 ⁎ N ¯ y T ) d Y d X = 0 .

Although the governing equations (1a)–(1d) have the same forms for the compressive buckling and tension buckling problems, unlike the compressive buckling problem [25,26], in the current study, the equilibrium of force in the X-direction is expressed as

(9) ∫ 0 b N ¯ x d Y − σ x b h = 0 ,

where σ x denotes the average tensile stress at X = 0 and X = a edges.

In equation (8b), the reduced stiffness coefficients are contained in the reduced stiffness matrices, including [ A i j ∗ ], [ B i j ∗ ], [ D i j ∗ ], [ E i j ⁎ ], [ F i j ⁎ ], and [ H i j ⁎ ]. They can be obtained by [1]

(10) A ⁎ = A − 1 , E ⁎ = − A − 1 E , B ⁎ = − A − 1 B , F ⁎ = F – E A − 1 B , D ⁎ = D – B A − 1 B , H ⁎ = H – E A − 1 E ,

where the plate stiffness coefficients A ij , B ij , etc., are expressed as

(11a) ( A i j , B i j , D i j , E i j , F i j , H i j ) = ∑ k = 1 ∫ h k − 1 h k ( Q ¯ i j ) k ( 1 , Z , Z 2 , Z 3 , Z 4 , Z 6 ) d Z , ( i , j = 1 , 2 , 6 ) ,

(11b) ( A i j , D i j , F i j ) = ∑ k = 1 ∫ h k − 1 h k ( Q ¯ i j ) k ( 1 , Z 2 , Z 4 ) d Z , ( i , j = 4 , 5 ) .

3 Solution procedure

In order to solve the buckling and postbuckling problems of nanocomposite structures analytically, the Ritz and Galerkin methods are usually employed [31,32,33,34,35,36,37,38]. The accuracy of applying the Ritz and Galerkin methods depends strongly on the chosen modal shape functions. Shen [39] developed a two-step perturbation approach that gives explicit analytical expressions of all the variables in the large deflection region. The advantage of this method is that it is unnecessary to guess the form of the modal shape function, which can be obtained step by step, and such solutions satisfy both the governing equations and the boundary conditions accurately in the asymptotic sense. This approach has been applied to successfully solve various plate nonlinear boundary-value problems by other research teams [40,41,42,43,44,45,46,47,48,49,50]. To employ this approach for solving the postbuckling problem of auxetic laminated plates with in-plane NPR, the governing equations (1a)–(1d) are first converted into the non-dimensional forms as

(12a) L 11 ( W ) − L 12 ( Ψ x ) − L 13 ( Ψ y ) + γ 14 L 14 ( F ) − L 16 ( M T ) + K 1 W − K 2 ∇ 2 W = γ 14 β 2 L ( W + W ⁎ , F ) ,

(12b) L ( F ) 21 + γ 24 L 22 ( Ψ x ) + γ 24 L 23 ( Ψ y ) − γ 24 L 24 ( W ) = − 1 2 γ 24 β 2 L ( W + 2 W ⁎ , W ) ,

(12c) L 31 ( W ) + L 32 ( Ψ x ) − L 33 ( Ψ y ) + γ 14 L 34 ( F ) − L 36 ( S T ) = 0 ,

(12d) L 41 ( W ) − L 42 ( Ψ x ) + L 43 ( Ψ y ) + γ 14 L 44 ( F ) − L 46 ( S T ) = 0 ,

where the non-dimensional operators L ij ( ) and L( ) are given in the study of Shen [1]. Note that the operators L 15( ), L 25( ), L 35( ), and L 45( ) vanish due to the uniform temperature field. The dimensionless parameters are defined by

x = π X a , y = π Y b , β = a b , ( W , W ⁎ ) = ( W ¯ , W ¯ ⁎ ) [ D 11 ⁎ D 22 ⁎ A 11 ⁎ A 22 ⁎ ] 1 / 4 ,

F = F ¯ [ D 11 ⁎ D 22 ⁎ ] 1 / 2 , ( Ψ x , Ψ y ) = a π ( Ψ ¯ x , Ψ ¯ y ) [ D 11 ⁎ D 22 ⁎ A 11 ⁎ A 22 ⁎ ] 1 / 4 ,

γ 14 = D 22 ⁎ D 11 ⁎ 1 / 2 , γ 24 = A 11 ⁎ A 22 ⁎ 1 / 2 ,

γ 5 = − A 12 ⁎ A 22 ⁎ , ( γ T 1 , γ T 2 ) = a 2 π 2 ( A x T , A y T ) [ D 11 ⁎ D 22 ⁎ ] 1 / 2 ,

( K 1 , k 1 ) = K ¯ 1 a 4 π 4 D 11 ⁎ , b 4 E 0 h 3 , ( K 2 , k 2 ) = K ¯ 2 a 2 π 2 D 11 ⁎ , b 2 E 0 h 3 ,

( M x , M y , P x , P y ) = a 2 π 2 1 D 11 ⁎ [ D 11 ⁎ D 22 ⁎ A 11 ⁎ A 22 ⁎ ] 1 / 4 M ¯ x , M ¯ y , 4 3 h 2 P ¯ x , 4 3 h 2 P ¯ y ,

(13) ( λ x , λ y ) = ( σ x b 2 h , σ y a 2 h ) 4 π 2 [ D 11 ⁎ D 22 ⁎ ] 1 / 2 ,

where k 1 and k 2 are only utilized for numerical examples in Section 4, E 0 is the reference value of Young’s modulus for the single-crystal copper matrix at T = 300 K, and is set to be E 0 = 101.14 GPa [22]. A x T , D x T , F x T , etc., are given by

(14) A x T D x T F x T A y T D y T F y T = − ∑ k = 1 ∫ h k − 1 h k A x A y k ( 1 , Z , Z 3 ) d Z .

Accordingly, the plate boundary conditions on the x = 0 and x = π edges can be nondimensionalized as

(15a) W = Ψ y = 0 , M x = P x = 0 ,

and those on the y = 0 and y = π edges can be nondimensionalized as

(15b) W = Ψ x = 0 , M y = P y = 0 .

And, hence, the in-plane boundary condition for the plate becomes

∫ 0 π ∫ 0 π ∂ 2 F ∂ x 2 − γ 5 β 2 ∂ 2 F ∂ y 2 + γ 24 γ 230 β ∂ Ψ x ∂ y + ∂ Ψ y ∂ x

− 2 γ 24 γ 526 β ∂ 2 W ∂ x ∂ y − 1 2 γ 24 β 2 ∂ W ∂ y 2 − γ 24 β 2 ∂ W ∂ y ∂ W ⁎ ∂ y

(16) + ( γ T 2 − γ 5 γ T 1 ) Δ T } d y d x = 0 ,

where γ 230 and γ 526 are defined in the study of Shen [1].

For the auxetic laminated plate subjected to uniaxial tension, equation (9) becomes

(17) 1 π ∫ 0 π β 2 ∂ 2 F ∂ y 2 d y − 4 λ x β 2 = 0 .

The initial geometric imperfection of the auxetic laminated plate in the dimensionless form is given by

(18) W ⁎ ( x , y , ε ) = ε μ A 11 ( 1 ) ( sin m x sin n y ) ,

where ε is the small perturbation parameter and μ is the imperfection parameter.

By employing the two-step perturbation approach, the asymptotic solutions of equations (12a)–(12d) along with the boundary conditions (15a) and (15b) are obtained as follows:

(19) W = ε [ A 11 ( 1 ) sin m x sin n y ] + ε 3 [ A 13 ( 3 ) sin m x sin 3 n y + A 31 ( 3 ) sin 3 m x sin n y ] + ε 4 [ A 22 ( 4 ) sin 2 m x sin 2 n y + A 24 ( 4 ) sin 2 m x sin 4 n y + A 42 ( 4 ) sin 4 m x sin 2 n y ] + O ( ε 5 ) ,

(20) Ψ x = ε [ C 11 ( 1 ) cos m x sin n y ] + ε 2 [ C 02 ( 2 ) sin 2 n y ] + ε 3 [ C 13 ( 3 ) cos m x sin 3 n y + C 31 ( 3 ) cos 3 m x sin n y ] + ε 4 [ C 02 ( 4 ) sin 2 n y + C 04 ( 4 ) sin 4 n y + C 22 ( 4 ) cos 2 m x sin 2 n y + C 24 ( 4 ) cos 2 m x sin 4 n y + C 42 ( 4 ) cos 4 m x sin 2 n y ] + O ( ε 5 ) ,

(21) Ψ y = ε [ D 11 ( 1 ) sin m x cos n y ] + ε 2 [ D 20 ( 2 ) sin 2 m x ] + ε 3 [ D 13 ( 3 ) sin m x cos 3 n y + D 31 ( 3 ) sin 3 m x cos n y ] + ε 4 [ D 20 ( 4 ) sin 2 m x + D 40 ( 4 ) sin 4 m x + D 22 ( 4 ) sin 2 m x cos 2 n y + D 24 ( 4 ) sin 2 m x cos 4 n y + D 42 ( 4 ) sin 4 m x cos 2 n y ] + O ( ε 5 ) .

Note that to restrict the lateral expansion of the auxetic laminated plate subjected to uniaxial tensile loads, compressive stresses are produced in two unloaded edges that are immovable, so that

(22) F = − b 00 ( 0 ) x 2 2 + B 00 ( 0 ) y 2 2 + ε [ B 11 ( 1 ) cos m x cos n y ] + ε 2 [ − b 00 ( 2 ) x 2 2 + B 00 ( 2 ) y 2 2 + B 20 ( 2 ) cos 2 m x + B 02 ( 2 ) cos 2 n y ] + ε 3 [ B 13 ( 3 ) cos m x cos 3 n y + B 31 ( 3 ) cos 3 m x cos n y ] + ε 4 [ − b 00 ( 4 ) x 2 2 + B 00 ( 4 ) y 2 2 + B 20 ( 4 ) cos 2 m x + B 02 ( 4 ) cos 2 n y + B 22 ( 4 ) cos 2 m x cos 2 n y + B 40 ( 4 ) cos 4 m x + B 04 ( 4 ) cos 4 n y + B 24 ( 4 ) cos 2 m x cos 4 n y + B 42 ( 4 ) cos 4 m x cos 2 n y ] + O ( ε 5 ) .

It is worth noting that solution (22) is different from that obtained for the compressive postbuckling problem, as reported in the study of Shen et al. [25]. Thereafter, by substituting equation (22) into equation (17), one has

(23) λ x = 1 4 β 2 ( β 2 B 00 ( 0 ) + ε 2 β 2 B 00 ( 2 ) + ε 4 β 2 B 00 ( 4 ) + ⋯ ) .

Similarly, we have

(24) λ y = ( b 00 ( 0 ) + ε 2 b 00 ( 2 ) + ε 4 b 00 ( 4 ) + ⋯ ) .

From perturbation procedure, we can obtain the expressions for ( − m 2 β 2 B 00 ( j ) + n 2 β 2 b 00 ( j ) ) , ( j = 0, 2, 4,…) step by step, and adding them yields

γ 14 [ − m 2 ( β 2 B 00 ( 0 ) + ε 2 β 2 B 00 ( 2 ) + ε 4 β 2 B 00 ( 4 ) + ⋯ ) + n 2 β 2 ( b 00 ( 0 ) + ε 2 b 00 ( 2 ) + ε 4 b 00 ( 4 ) + ⋯ ) ]

(25) = Q 11 ( 1 + μ ) + 1 16 γ 14 γ 24 Θ 2 ( 1 + 2 μ ) ( A 11 ( 1 ) ε ) 2 − 1 256 γ 14 2 γ 24 2 Θ 44 ( 1 + μ ) ( 1 + 2 μ ) ( A 11 ( 1 ) ε ) 4 + ⋯ ,

and substituting W, Ψ x , Ψ y , and F into equation (16) yields

− ( b 00 ( 0 ) + ε 2 b 00 ( 2 ) + ε 4 b 00 ( 4 ) + … ) − γ 5 ( β 2 B 00 ( 0 ) + ε 2 β 2 B 00 ( 2 ) + ε 4 β 2 B 00 ( 4 ) + ⋯ )

(26) − 1 8 γ 24 n 2 β 2 ( 1 + 2 μ ) ( A 11 ( 1 ) ε ) 2 + ( γ T 2 − γ 5 γ T 1 ) Δ T = 0 .

From equations (25) and (26), we obtain

(27) λ y = γ 5 γ 14 ( m 2 + γ 5 n 2 β 2 ) Q 11 ( 1 + μ ) − S 0 T + 1 16 γ 14 γ 24 Θ 2 − 2 m 2 n 2 β 2 γ 5 ( 1 + 2 μ ) ( A 11 ( 1 ) ε ) 2 − 1 256 γ 14 2 γ 24 2 Θ 44 ( 1 + μ ) ( 1 + 2 μ ) ( A 11 ( 1 ) ε ) 4 + ⋯ ] ,

where ( A 11 ( 1 ) ε ) is treated as the second perturbation parameter and is related to the non-dimensional plate deflection W m . From equation (19), one has

(28) A 11 ( 1 ) ε = W m + Θ 3 ( W m ) 3 ⋯ .

In the current study, buckling is caused by compressed stress on the unloaded edges. By minimizing the compressive stress in equation (27) with respect to m and n, the buckling load of a perfect plate can readily be numerically obtained by setting μ = 0 (or W ¯ ⁎ / h = 0), while taking W m = 0 (or W ¯ / h = 0). The corresponding buckling mode (m, n) is obtained simultaneously, which determines the number of half-waves in the X and Y directions, respectively.

After the buckling mode (m, n) and buckling loads are determined, the postbuckling tensile load–deflection curve can be obtained as

(29) λ x = − 1 4 γ 5 β 2 λ y + 1 8 γ 24 n 2 β 2 ( 1 + 2 μ ) ( A 11 ( 1 ) ε ) 2 + … .

All symbols used in equations (27)–(29) are explained in Appendix.

4 Numerical results

In this section, we will present numerical studies for tension buckling and postbuckling behavior of perfect and imperfect auxetic nanocomposite laminated plates with in-plane NPR that are rested on elastic foundations. Two types of nanocomposite materials are selected for each ply of the laminated plate. One is the graphene/Cu composite with the graphene weight fraction w G = 3%, while another is the CNT/Cu composite with the CNT weight fraction w CNT = 3%. The material properties of the two composites are both temperature-dependent and are taken from the molecular dynamics simulation results of Fan et al. [21] and Zhang et al. [22], respectively, which are listed in Tables 1 and 2, respectively.

Table 1

Temperature-dependent properties of graphene/Cu composites (w G = 3%) [21]

T = 300 K T = 500 K T = 700 K
E 11 (GPa) 207.55 193.15 180.50
E 22 (GPa) 196.69 183.94 171.58
E 33 (GPa) 61.454 55.773 47.192
G 12 (GPa) 66.389 62.092 58.314
G 13 (GPa) 33.617 31.536 28.928
G 23 (GPa) 32.327 31.009 28.200
ν 12 −0.0649 −0.0721 −0.0751
ν 13 0.6297 0.6298 0.6826
ν 23 0.6512 0.6617 0.6742
α 11 (×10−6 K−1) 1.4224 1.5037 1.6222
α 22 (×10−6 K−1) 1.4194 1.5006 1.6278
Table 2

Temperature-dependent properties of CNT/Cu composites (w CNT = 3%) [22]

T = 300 K T = 500 K T = 700 K
E 11 (GPa) 226.24 216.70 209.84
E 22 (GPa) 96.918 89.186 81.311
E 33 (GPa) 68.336 63.629 59.185
G 12 (GPa) 15.496 14.090 12.584
G 13 (GPa) 48.932 45.508 42.145
G 23 (GPa) 49.838 46.357 43.688
ν 12 −0.1537 −0.1637 −0.1762
ν 13 0.7508 0.7677 0.7833
ν 23 0.8121 0.8215 0.8316
α 11 (×10−6 K−1) 8.3366 8.3227 8.3089
α 22 (×10−6 K−1) 12.649 13.000 13.349

In the current research, symmetric (0/90/0)S and anti-symmetric (10/−10)3T laminated rectangular plates are considered. The thickness of each ply is identical and the total thickness of the plate is h = 1.2 mm. The plate aspect ratios are selected as a/b = 2, 3, 4, and 5. To avoid cases where stresses increase beyond the elastic range, the plate width-to-thickness ratio is set as b/h = 50, 100, and 200. The in-plane effective Poisson’s ratio (EPR) ν 1 2 e of these nanocomposite laminated plates are determined by employing the method as reported in the study of Shen et al. [51], and listed in Table 3. From Table 3, it can be seen that the absolute value of NPR of (0/90/0)S CNT/Cu laminated plate is the largest, whereas that of the (10/−10)3T graphene/Cu laminated plate is the smallest at all three temperature levels considered.

Table 3

Effective Poisson’s ratios ν 1 2 e for nanocomposite laminates

T (K) CNT/Cu laminates Graphene/Cu laminates
(0/90/0)S (0/90/0)S (10/−10)3T
300 −0.111 −0.064 −0.040
500 −0.115 −0.071 −0.047
700 −0.120 −0.074 −0.050

The buckling load is of practical concern of the nanocomposite laminated plates and, therefore, we need to determine the buckling tensile load and the corresponding buckling mode for the auxetic nanocomposite laminated plates first. Since the tension buckling of the auxetic laminated plates is investigated for the first time, no experimental data are currently available for model validation. In order to validate the accuracy and reliability of the present solution method, the finite element analysis is performed and the results are depicted in Figure 2. The buckling load associated with the buckling mode agrees well in each case, which clearly shows the validity and accuracy of the current solution for the tension buckling analysis of auxetic laminated plates.

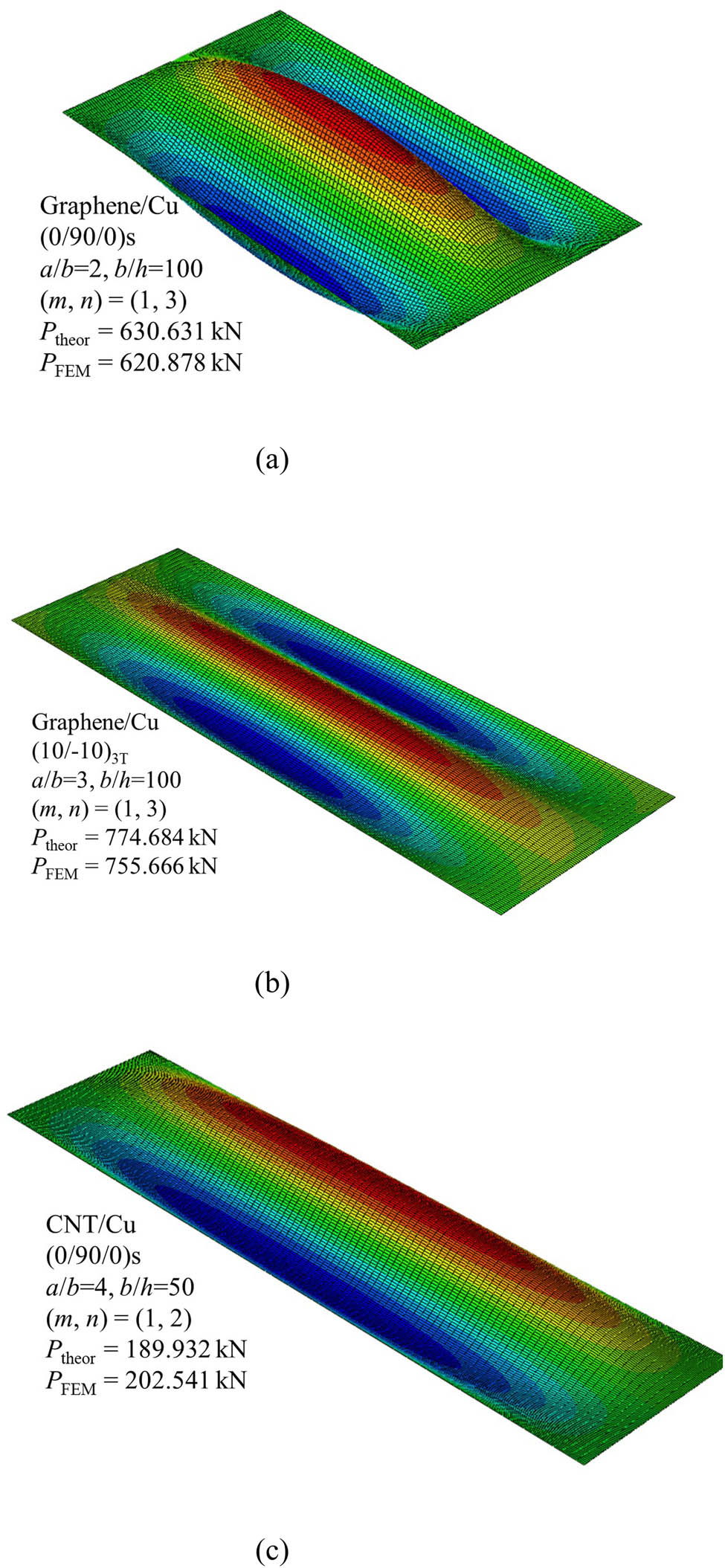
Figure 2 Comparisons of buckling loads of nanocomposite laminated plates under uniaxial tension: (a) a/b = 2, (m, n) = (1,3); (b) a/b = 3, (m, n) = (1,3); and (c) a/b = 4, (m, n) = (1,2).
Figure 2

Comparisons of buckling loads of nanocomposite laminated plates under uniaxial tension: (a) a/b = 2, (m, n) = (1,3); (b) a/b = 3, (m, n) = (1,3); and (c) a/b = 4, (m, n) = (1,2).

Buckling tensile loads P cr (kN) of the (0/90/0)S and (10/−10)3T graphene/Cu laminated plates and (0/90/0)S CNT/Cu laminated plates, with different values of plate aspect ratios (a/b = 2, 3, and 4) rested on the elastic foundations under temperature conditions are presented in Tables 4–6. The thermal environments are set as T = 300, 500, and 700 K. Two foundation models with (k 1, k 2) = (10, 0) for the Winkler foundation and (k 1, k 2) = (10, 1) for the Pasternak foundation are considered. Owing to the NPR effect, the applied tensile load acting in the longitudinal direction produces a compressive reaction force and, hence, compressive stress, when the transverse displacement is constrained. Buckling occurs when the compressive stress reaches a critical value. As can be observed, the buckling tensile loads for the (10/−10)3T graphene/Cu laminated plates are larger than those of the (0/90/0)S graphene/Cu laminated plates, whereas the buckling tensile loads of the (0/90/0)S CNT/Cu laminated plates are lower than those of the (0/90/0)S graphene/Cu laminated plates, even if the (0/90/0)S CNT/Cu laminated plate is relatively thicker (i.e., lower b/h) than the (0/90/0)S graphene/Cu laminated plate. This is because the (10/−10)3T graphene/Cu laminated plate has the lowest negative EPR, while the (0/90/0)S CNT/Cu laminated plate has the highest negative EPR among the three. In other words, a higher negative EPR will exacerbate the compressive stress caused by the reaction force, and hence, make the composites more prone to buckle. We also observe that the buckling mode (m, n) changes from (1, 3) to (1, 2) for the (0/90/0)S CNT/Cu and graphene/Cu laminated plates, whereas the buckling mode (m, n) changes from (1, 4) to (1, 2) for the (10/−10)3T graphene/Cu laminated plates when the plate aspect ratio a/b changes from 2 to 4. The changes in the buckling mode can also be observed when the temperature increases from 300 to 700 K. These simulation results indicate that changing the aspect ratio of the plates and applying the temperature condition significantly affect the distribution of the compressive stress along the unloaded edges, thereby resulting in shifts in the buckling mode. Additionally, similar to cases of compressive buckling [25], the buckling tensile loads decrease when the temperature increases and increase when the foundation stiffnesses are increased.

Table 4

Buckling tensile loads P cr (kN) of (0/90/0)S laminated plates made of graphene/Cu with unloaded edges that are immovable [h = 1.2 mm, b/h = 100]

T (K) a/b = 2 a/b = 3 a/b = 4
( k 1 , k 2 ) = (0, 0)
300 630.6308 (1, 3)a 281.1347 (1, 2) 205.3563 (1, 2)
500 199.6882 (1, 2) 209.9876 (1, 3) 189.8835 (1, 3)
700 62.7413 (1, 3) 40.8513 (1, 3) 35.6539 (1, 3)
( k 1 , k 2 ) = (10, 0)
300 635.3398 (1, 3) 291.7302 (1, 2) 213.2104 (1, 2)
500 250.4258 (1, 2) 212.8428 (1, 3) 192.4932 (1, 3)
700 66.4007 (1, 3) 43.5732 (1, 3) 38.1518 (1, 6)
( k 1 , k 2 ) = (10, 1)
300 678.3310 (1, 3) 334.7214 (1, 2) 244.7016 (1, 2)
500 335.6300 (1, 3) 238.5179 (1, 3) 215.8357 (1, 3)
700 99.8081 (1, 3) 68.0491 (1, 3) 60.4938 (1, 3)

  1. aBuckling mode (m, n).

Table 5

Buckling tensile loads P cr (kN) of (±10)3T laminated plates made of graphene/Cu with unloaded edges that are immovable [h = 1.2 mm, b/h = 100]

T (K) a/b = 2 a/b = 3 a/b = 4
( k 1 , k 2 ) = (0, 0)
300 1569.6150 (1, 4)a 774.6838 (1, 3) 395.1861 (1, 2)
500 658.9609 (1, 3) 345.4806 (1, 3) 294.1510 (1, 3)
700 131.6798 (1, 3) 65.4747 (1, 3) 53.8327 (1, 3)
( k 1 , k 2 ) = (10, 0)
300 1573.5280 (1, 4) 780.7916 (1, 3) 410.8407 (1, 2)
500 667.8953 (1, 3) 350.3338 (1, 3) 298.3353 (1, 3)
700 139.4096 (1, 3) 69.9492 (1, 3) 57.7324 (1, 3)
( k 1 , k 2 ) = (10, 1)
300 1636.2960 (1, 4) 835.7136 (1, 3) 473.6080 (1, 2)
500 749.4606 (1, 3) 393.9758 (1, 3) 335.7609 (1, 3)
700 209.9779 (1, 3) 110.1851 (1, 3) 92.6123 (1, 3)

aBuckling mode (m, n).

Table 6

Buckling tensile loads P cr (kN) of (0/90/0)S laminated plates made of CNT/Cu with unloaded edges that are immovable [h = 1.2 mm, b/h = 50]

T (K) a/b = 2 a/b = 3 a/b = 4
( k 1 , k 2 ) = (0, 0)
300 523.3330 (1, 3)a 233.8883 (1, 2) 189.9320 (1, 2)
500 118.3289 (1, 3) 91.2130 (1, 3) 84.3524 (1, 3)
700 86.4904 (1, 4) 75.9266 (1, 4) 72.7877 (1, 4)
( k 1 , k 2 ) = (10, 0)
300 529.4551 (1, 3) 247.6630 (1, 2) 201.1594 (1, 2)
500 176.8505 (1, 3) 95.8015 (1, 3) 88.6184 (1, 3)
700 89.1192 (1, 4) 78.2660 (1, 4) 75.0403 (1, 4)
( k 1 , k 2 ) = (10, 1)
300 585.3463 (1, 3) 303.5543 (1, 2) 246.1761 (1, 2)
500 230.2771 (1, 3) 137.0625 (1, 3) 126.7755 (1, 3)
700 131.2807 (1, 4) 115.4652 (1, 4) 110.7512 (1, 4)

aBuckling mode (m, n).

Figure 3 shows the effect of plate aspect ratio a/b ( = 3, 4 and 5) on the postbuckling behavior of (0/90/0)S and ( ± 10)3T graphene/Cu and (0/90/0)S CNT/Cu laminated plates under tension at T = 300 K. The depicted curves in Figure 3 indicate that increasing the plate aspect ratio significantly reduces the critical tension buckling load as well as the peak of the postbuckling load–deflection curves. These simulation results suggest that in the postbuckling range, the increase of the amplitude of the plate deflection will counteract the lateral expansion displacement of the auxetic plate. The stress on the unloaded edges changes from compressive stress to tensile stress when the amplitude of the plate deflection reaches a certain value, which leads the tensile load–deflection curve to switch from rising to falling at the peak point. The postbuckling curves of tensile load vs deflection for the imperfect auxetic laminated plates are also plotted in Figure 3, where W ¯ ⁎ / h = 0.1 (or 0.05) denotes the non-dimensional maximum initial geometric imperfection of the auxetic laminated plates.

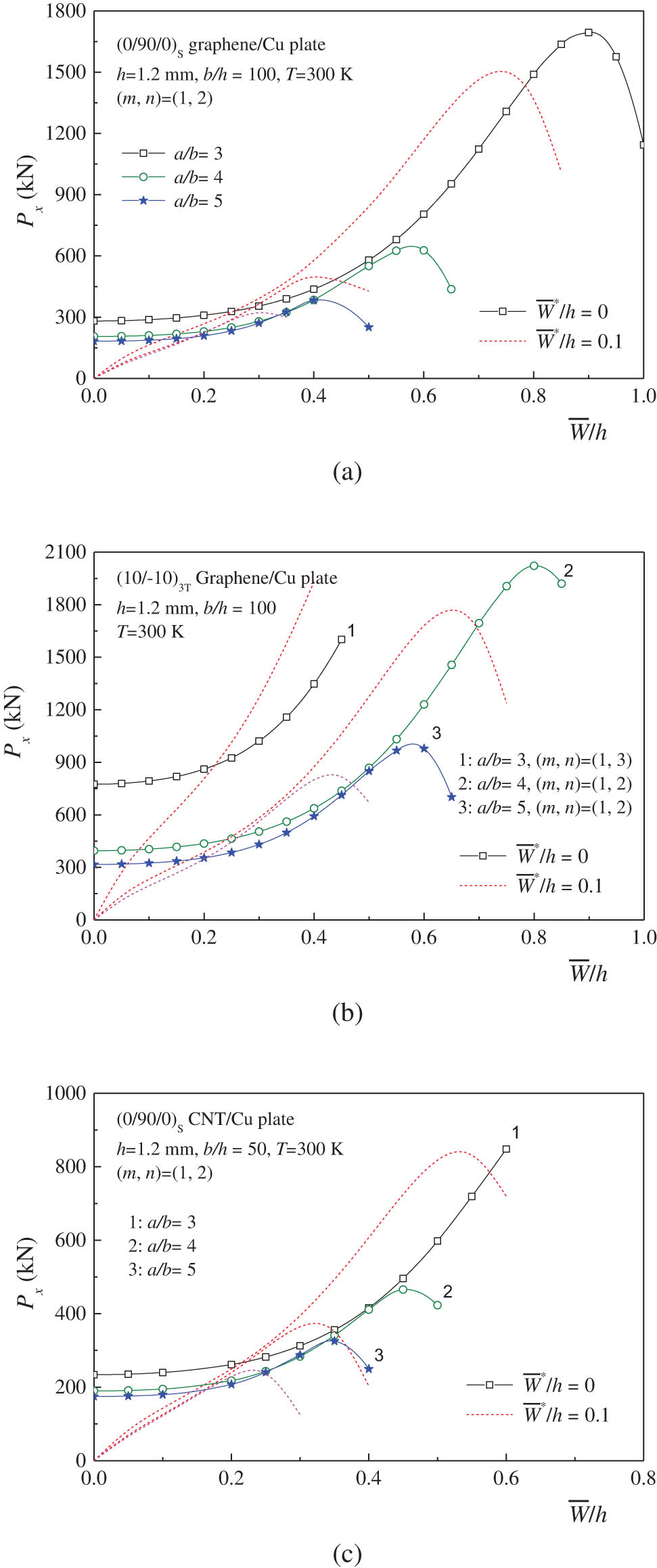
Figure 3 Effect of the plate aspect ratio on the postbuckling behavior of auxetic laminated plates under tension: (a) (0/90/0)S graphene/Cu plate; (b) (10/−10)3T graphene/Cu plate; and (c) (0/90/0)S CNT/Cu plate.
Figure 3

Effect of the plate aspect ratio on the postbuckling behavior of auxetic laminated plates under tension: (a) (0/90/0)S graphene/Cu plate; (b) (10/−10)3T graphene/Cu plate; and (c) (0/90/0)S CNT/Cu plate.

The effect of plate width-to-thickness ratio on the postbuckling behavior of the three configurations of auxetic laminated plates with a/b = 3 under tension at 300 K is illustrated in Figure 4. Three cases of b/h = 50, 100, and 200 are chosen for the (0/90/0)S CNT/Cu and graphene/Cu laminated plates, while b/h is set as 100, 150, and 200 for the (10/−10)3T graphene/Cu laminated plates. Such choices of the b/h ratios for the two types of laminates have ensured that the compressive or tensile stresses stay within the elastic range. As a result, no peak can be observed on the postbuckling tensile load–deflection curves for b/h = 50 for the (0/90/0)S laminated plates and b/h = 100 for the (10/−10)3T laminated plates. It is found that the postbuckling tensile load–deflection curves are reduced when the plate becomes thinner.

Figure 4 Effect of the plate width-to-thickness ratio on the postbuckling behavior of auxetic laminated plates under tension: (a) (0/90/0)S graphene/Cu plate; (b) (10/−10)3T graphene/Cu plate; and (c) (0/90/0)S CNT/Cu plate.
Figure 4

Effect of the plate width-to-thickness ratio on the postbuckling behavior of auxetic laminated plates under tension: (a) (0/90/0)S graphene/Cu plate; (b) (10/−10)3T graphene/Cu plate; and (c) (0/90/0)S CNT/Cu plate.

The effect of temperature change on the postbuckling behavior of three configurations of auxetic laminated plates with a/b = 3 is depicted in Figure 5. Three thermal environmental conditions, T = 300, 500, and 700 K, are considered. The temperature effect is included in the simulations by using the temperature-dependent material properties of both graphene/Cu and CNT/Cu composites. As the temperature increases, the elastic moduli reduce and the strength degrades for nanocomposites. As a result, the postbuckling tensile load–deflection curves are decreased as the temperature increases. Note that the initial geometric imperfection is set as W ¯ ⁎ / h = 0.05 in this example. Our results show that the (10/−10)3T graphene/Cu laminated plate has no buckling mode change. Additionally, the postbuckling tensile load–deflection curve becomes extremely low at T = 700 K compared to the case at T = 300 K.

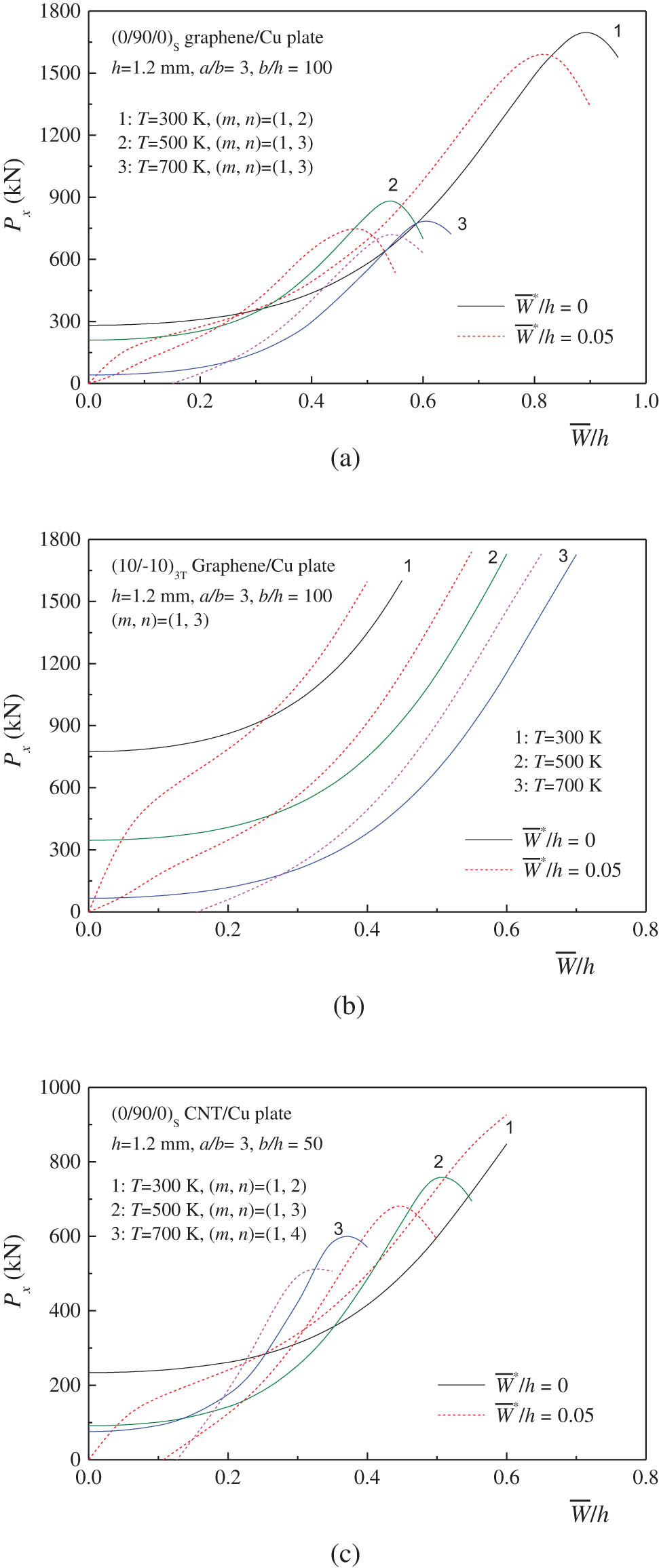
Figure 5 Effect of temperature variation on the postbuckling behavior of auxetic laminated plates under tension: (a) (0/90/0)S graphene/Cu plate; (b) (10/−10)3T graphene/Cu plate; and (c) (0/90/0)S CNT/Cu plate.
Figure 5

Effect of temperature variation on the postbuckling behavior of auxetic laminated plates under tension: (a) (0/90/0)S graphene/Cu plate; (b) (10/−10)3T graphene/Cu plate; and (c) (0/90/0)S CNT/Cu plate.

Figure 6 illustrates the effect of foundation stiffnesses on the postbuckling behavior of three configurations of auxetic laminated plates with a/b = 3 rested on elastic foundations at T = 300 K. In this example, two foundation models with (k 1, k 2) = (50, 0) for the Winkler foundation and (k 1, k 2) = (50, 5) for the Pasternak foundation are considered. Similar to conventional observations in laminated plates [25], the postbuckling curves of tensile load vs deflection increase with higher foundation stiffnesses. This implies that the tensile buckling could be mitigated by using a stiffer foundation as a substrate. Furthermore, no change in the buckling mode is observed when the auxetic laminated plate is supported by either the Winkler foundation or the Pasternak foundation.

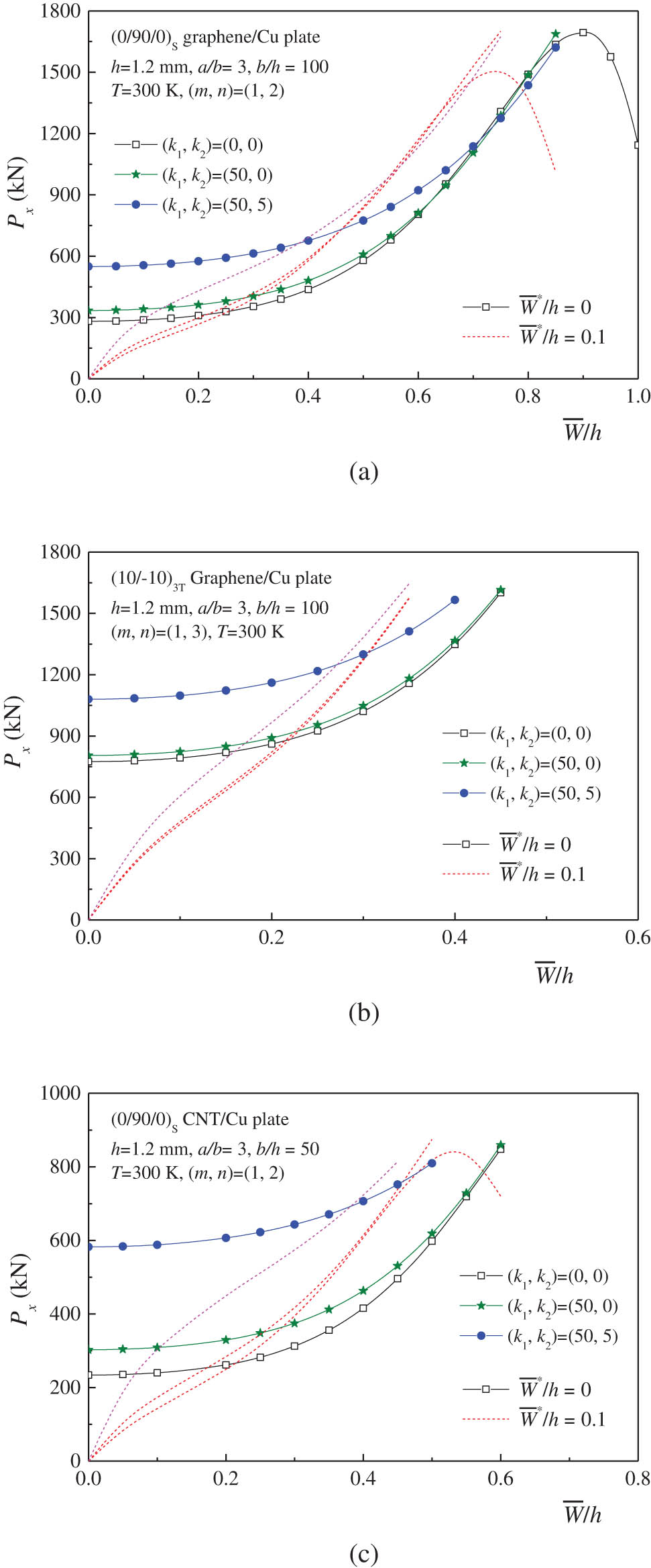
Figure 6 Effect of substrate stiffnesses on the postbuckling behavior of auxetic laminated plates under tension: (a) (0/90/0)S graphene/Cu plate; (b) (10/−10)3T graphene/Cu plate; and (c) (0/90/0)S CNT/Cu plate.
Figure 6

Effect of substrate stiffnesses on the postbuckling behavior of auxetic laminated plates under tension: (a) (0/90/0)S graphene/Cu plate; (b) (10/−10)3T graphene/Cu plate; and (c) (0/90/0)S CNT/Cu plate.

5 Conclusion

Tension buckling and postbuckling phenomena of auxetic nanocomposite laminated plates with immovable unloaded edges are presented. The material properties of the two nanocomposites considered in this study, CNT/Cu and graphene/Cu composites, are both dependent on temperature. Based on the two-step perturbation method, the explicit analytical solutions are obtained for the first time. The numerical studies have been presented for three configurations of laminated plates, including (0/90/0)S and (10/−10)3T graphene/Cu laminated plates and (0/90/0)S CNT/Cu laminated plates, with or without an elastic substrate under temperature environments. The buckling tensile loads and associated buckling modes have been verified by FE simulation. The results presented explore for the first time the important issue of auxetic nanocomposite laminated plates, and thus are greatly useful in the engineering design of the novel nanocomposite structures. The findings are summarized as follows:

  1. Due to the impact of in-plane NPR, the buckling tensile loads exist for the auxetic laminated rectangular plates with unloaded edges that are “immovable” under uniaxial tension. The tensile loads on “movable” ends lead to compressive stress on “immovable” ends, which is exactly the origin of tension buckling and postbuckling.

  2. Unlike the traditional compressive postbuckling case where the postbuckling load–deflection curve rises slowly, in the tension postbuckling case, the postbuckling tensile load–deflection curve rises rapidly, in particular for cases when the temperature variation is under consideration.

  3. In the postbuckling range, the increase of the amplitude of the plate deflection will counteract the lateral expansion displacement of the auxetic plate. The stress on the unloaded edges may shift from compressive stress to tensile stress when the amplitude of the plate deflection reaches a certain value. In most cases, a peak point exists on the postbuckling tensile load–deflection curves.

Funding information

Y. Fan would like to acknowledge financial support from the National Natural Science Foundation of China (NSFC) under Grant No. 12102255. Y. Wang would like to acknowledge financial support provided by the National Science Foundation under Award No. CMMI-2202737.

  1. Funding information: Y. Fan would like to acknowledge financial support from the National Natural Science Foundation of China (NSFC) under Grant No. 12102255. Y. Wang would like to acknowledge financial support provided by the National Science Foundation under Award No. CMMI-2202737.

  2. Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.

  3. Conflict of interest: The authors state no conflict of interest.

Appendix

In equations (27) and (29),

S 0 T = γ 14 n 2 β 2 ( γ T 2 − γ 5 γ T 1 ) Δ T ,

Q 11 = Θ 11 + K 1 + K 2 ( m 2 + n 2 β 2 ) , Θ 22 = m 4 γ 7 + n 4 β 4 γ 6 ,

Θ 3 = 1 16 γ 14 γ 24 ( m 2 + γ 5 n 2 β 2 ) m 4 J 13 γ 7 + n 4 β 4 J 31 γ 6 ( 1 + μ ) 2 ( 1 + 2 μ ) ,

(A1) Θ 44 = ( m 2 + γ 5 n 2 β 2 ) m 8 J 13 + γ 24 4 n 8 β 8 J 31 [ 2 ( 1 + μ ) 2 + ( 1 + 2 μ ) ] ,

where (with other symbols being defined as in the study of Shen [1])

J 13 = Q 13 C 11 ( 1 + μ ) − Q 11 C 13 − J 13 T , J 31 = Q 31 C 11 ( 1 + μ ) − Q 11 C 31 − J 31 T ,

C 11 = m 2 + γ 5 n 2 β 2 , C 13 = m 2 + 9 γ 5 n 2 β 2 , C 31 = 9 m 2 + γ 5 n 2 β 2 ,

Q 13 = Θ 13 + [ K 1 + K 2 ( m 2 + 9 n 2 β 2 ) ] , Q 31 = Θ 31 + [ K 1 + K 2 ( 9 m 2 + n 2 β 2 ) ] ,

J 31 T = − J 13 T = 8 γ 14 m 2 n 2 β 2 ( 1 + μ ) ( γ T 2 − γ 5 γ T 1 ) Δ T ,

Θ 11 = ( m 4 + 2 γ 12 m 2 n 2 β 2 + γ 14 2 n 4 β 4 ) + γ 14 γ 24 m 2 n 2 β 2 ( γ 141 m 2 + γ 143 n 2 β 2 ) 2 m 4 + 2 γ 22 m 2 n 2 β 2 + γ 24 2 n 4 β 4 ,

Θ 13 = ( m 4 + 18 γ 12 m 2 n 2 β 2 + 81 γ 14 2 n 4 β 4 ) + γ 14 γ 24 9 m 2 n 2 β 2 ( γ 141 m 2 + 9 γ 143 n 2 β 2 ) 2 m 4 + 18 γ 22 m 2 n 2 β 2 + 81 γ 24 2 n 4 β 4 ,

Θ 31 = ( 81 m 4 + 18 γ 12 m 2 n 2 β 2 + γ 14 2 n 4 β 4 ) + γ 14 γ 24 9 m 2 n 2 β 2 ( 9 γ 141 m 2 + γ 143 n 2 β 2 ) 2 81 m 4 + 18 γ 22 m 2 n 2 β 2 + γ 24 2 n 4 β 4 ,

(A2) γ 6 = 1 + γ 14 γ 24 γ 230 2 4 m 2 γ 42 + γ 322 4 m 2 , γ 7 = γ 24 2 + γ 14 γ 24 γ 223 2 4 n 2 β 2 γ 31 + γ 322 4 n 2 β 2 .

References

[1] Shen H-S. Postbuckling Behavior of Plates and Shells. Singapore: World Scientific Publishing Co. Pte. Ltd; 2017.10.1142/10208Suche in Google Scholar

[2] Shimizu S, Yoshida S, Enomoto N. Buckling of plates with a hole under tension. Thin-Walled Struct. 1991;12:35–49.10.1016/0263-8231(91)90025-ESuche in Google Scholar

[3] Shimizu S. Tension buckling of plate having a hole. Thin-Walled Struct. 2007;45:827–33.10.1016/j.tws.2007.08.033Suche in Google Scholar

[4] Kremer T, Schurmann H. Buckling of tension-loaded thin-walled composite plates with cut-outs. Compos Sci Technol. 2008;68:90–7.10.1016/j.compscitech.2007.05.035Suche in Google Scholar

[5] Fujimoto T, Sumi S. Postbuckling behavior of centrally cracked plates under tension. JSME Int J. 1987;30:1714–23.10.1299/jsme1987.30.1714Suche in Google Scholar

[6] Shaw D, Huang YH. Buckling behavior of a central cracked thin plate under tension. Eng Fract Mech. 1990;35:1019–27.10.1016/0013-7944(90)90129-5Suche in Google Scholar

[7] Biks E, Bankin CC, Brogan FA. The buckling behavior of a central crack in a plate under tension. Eng Fract Mech. 1992;43:529–48.10.1016/0013-7944(92)90197-MSuche in Google Scholar

[8] Segedin RH, Collins IF, Segedin CM. The elastic wrinkling of rectangular sheets. Int J Mech Sci. 1988;30:719–32.10.1016/0020-7403(88)90037-9Suche in Google Scholar

[9] Cerda E, Ravi-Chandar K, Mahadevan L. Wrinkling of an elastic sheet under tension. Nature. 2002;419:579–80.10.1038/419579bSuche in Google Scholar PubMed

[10] Nayyar V, Ravi-Chandar K, Huang R. Stretch-induced stress patterns and wrinkles in hyperelastic thin sheets. Int J Solids Struct. 2011;48:3471–83.10.1016/j.ijsolstr.2011.09.004Suche in Google Scholar

[11] Puntel E, Deseri L, Fried E. Wrinkling of a stretched thin sheet. J Elast. 2011;105:137–70.10.1007/s10659-010-9290-5Suche in Google Scholar

[12] Silvestre N. Wrinkling of stretched thin sheets: Is restrained Poisson’s effect the sole cause? Eng Struct. 2016;106:195–208.10.1016/j.engstruct.2015.09.035Suche in Google Scholar

[13] Shen H-S, Xu Y-M, Zhang C-L. Graphene: why buckling occurs? Appl Phys Lett. 2013;102:131905.10.1063/1.4799673Suche in Google Scholar

[14] Xiang Y, Shen H-S. Tension buckling of graphene: a new phenotype. Solid State Commun. 2014;192:20–3.10.1016/j.ssc.2014.04.021Suche in Google Scholar

[15] Wang C, Lan L, Tan H. The physics of wrinkling in graphene membranes under local tension. Phys Chem Chem Phys. 2013;15:2764–73.10.1039/c2cp44033dSuche in Google Scholar PubMed

[16] Huang J, Han Q. Wrinkling in graphene subjected to gradient tension. Nano. 2015;10:53–61.10.1142/S179329201550037XSuche in Google Scholar

[17] Dahiya M, Bansal SA. Graphene-reinforced nanocomposites: synthesis, micromechanics models, analysis and applications – a review. Proc IMechE Part C-J Mech Eng Sci. 2022;236:9218–40.10.1177/09544062221091773Suche in Google Scholar

[18] Soni SK, Thomas B, Kar VR. A comprehensive review on CNTs and CNT-reinforced composites: syntheses, characteristics and applications. Mater Today Commun. 2020;25:101546.10.1016/j.mtcomm.2020.101546Suche in Google Scholar

[19] Fan Y, Xiang Y, Shen H-S. Temperature-dependent negative Poisson’s ratio of monolayer graphene: Prediction from molecular dynamics simulations. Nanotechnol Rev. 2019;8:415–21.10.1515/ntrev-2019-0037Suche in Google Scholar

[20] Zhang H-N, Fan Y, Shen H-S. Chirality-dependent and intrinsic auxeticity for single-walled carbon nanotubes. Materials. 2022;15:8720.10.3390/ma15248720Suche in Google Scholar PubMed PubMed Central

[21] Fan Y, Xiang Y, Shen H-S. Temperature-dependent mechanical properties of graphene/Cu nanocomposites with in-plane negative Poisson’s ratios. Research. 2020;2020:5618021.10.34133/2020/5618021Suche in Google Scholar PubMed PubMed Central

[22] Zhang H-N, Fan Y, Shen H-S. Prediction of temperature-dependent mechanical properties for SWCNT/Cu nanocomposite metamaterials: A molecular dynamics study. Nanomaterials. 2023;13:1885.10.3390/nano13121885Suche in Google Scholar PubMed PubMed Central

[23] Ren X, Das R, Tran P, Ngo TD, Xie YM. Auxetic metamaterials and structures: a review. Smart Mater Struct. 2018;27:023001.10.1088/1361-665X/aaa61cSuche in Google Scholar

[24] Fan Y, Wang Y. The effect of negative Poisson’s ratio on the low-velocity impact response of an auxetic nanocomposite laminate beam. Int J Mech Mater Des. 2021;17:153–69.10.1007/s10999-020-09521-xSuche in Google Scholar

[25] Shen H-S, Xiang Y, Reddy JN. Effect of negative Poisson’s ratio on the post-buckling behavior of FG-GRMMC laminated plates in thermal environments. Compos Struct. 2020;253:112731.10.1016/j.compstruct.2020.112731Suche in Google Scholar

[26] Chen XH, Shen H-S, Huang X-H. Thermo-mechanical postbuckling analysis of sandwich plates with functionally graded auxetic GRMMC core on elastic foundations. Compos Struct. 2022;279:114796.10.1016/j.compstruct.2021.114796Suche in Google Scholar

[27] Librescu L, Stein M. A geometrically nonlinear theory of transversely isotropic laminated composite plates and its use in the post-buckling analysis. Thin-Walled Struct. 1991;11:177–201.10.1016/0263-8231(91)90016-CSuche in Google Scholar

[28] Shen H-S, Xiang Y, Lin F, Hui D. Buckling and postbuckling of functionally graded graphene-reinforced composite laminated plates in thermal environments. Compos Part B-Eng. 2017;119:67–78.10.1016/j.compositesb.2017.03.020Suche in Google Scholar

[29] Shen H-S, Zhu ZH. Buckling and postbuckling behavior of functionally graded nanotube-reinforced composite plates in thermal environments. CMC-Comput Mater Continua. 2010;18:155–82.Suche in Google Scholar

[30] Reddy JN. A refined nonlinear theory of plates with transverse shear deformation. Int J Solids Struct. 1984;20:881–96.10.1016/0020-7683(84)90056-8Suche in Google Scholar

[31] Sofiyev AH, Tornabene F, Dimitri R, Kuruoglu N. Buckling behavior of FG-CNT reinforced composite conical shells subjected to a combined loading. Nanomaterials. 2020;10:419.10.3390/nano10030419Suche in Google Scholar PubMed PubMed Central

[32] Sofiyev AH, Fantuzzi N. Stability analysis of shear deformable inhomogeneous nanocomposite cylindrical shells under hydrostatic pressure in thermal environment. Materials. 2023;16:4887.10.3390/ma16134887Suche in Google Scholar PubMed PubMed Central

[33] Mirzaei M, Kiani Y. Thermal buckling of temperature dependent FG-CNT reinforced composite plates. Meccanica. 2016;51:2185–201.10.1007/s11012-015-0348-0Suche in Google Scholar

[34] Kiani Y. Thermal post-buckling of FG-CNT reinforced composite plates. Compos Struct. 2017;159:299–306.10.1016/j.compstruct.2016.09.084Suche in Google Scholar

[35] Kiani Y. Shear buckling of FG-CNT reinforced composite plates using Chebyshev-Ritz method. Compos Part B-Eng. 2016;105:176–87.10.1016/j.compositesb.2016.09.001Suche in Google Scholar

[36] Zeverdejani MK, Beni YT, Kiani Y. Multi-scale buckling and post-buckling analysis of functionally graded laminated composite plates reinforced by defective graphene sheets. Int J Struct Stab Dyn. 2020;20:2050001.10.1142/S0219455420500017Suche in Google Scholar

[37] Abbaspour F, Arvin H, Kiani Y. Mechanical buckling analysis of functionally graded composite laminated plates reinforced with temperature dependent graphene sheets resting on elastic foundation. ZAMM. 2022;102:e202100097.10.1002/zamm.202100097Suche in Google Scholar

[38] Guo H, Zur KK, Ouyang X. New insights into the nonlinear stability of nanocomposite cylindrical panels under aero-thermal loads. Compos Struct. 2023;303:116231.10.1016/j.compstruct.2022.116231Suche in Google Scholar

[39] Shen H-S. A two-step perturbation method in nonlinear analysis of beams. Plates and Shells. Singapore: John Wiley & Sons Inc; 2013.10.1002/9781118649893Suche in Google Scholar

[40] Li ZM. Thermal postbuckling behavior of 3D braided rectangular plates. J Therm Stresses. 2011;34:626–49.10.1080/01495739.2011.581050Suche in Google Scholar

[41] Wang Z-X, Xu J, Qiao P. Nonlinear low-velocity impact analysis of temperature-dependent nanotube-reinforced composite plates. Compos Struct. 2014;108:423–34.10.1016/j.compstruct.2013.09.024Suche in Google Scholar

[42] Fu Y, Zhong J, Shao X, Tao C. Analysis of nonlinear dynamic stability for carbon nanotube-reinforced composite plates resting on elastic foundations. Mech Adv Mater Struct. 2016;23:1284–9.10.1080/15376494.2015.1068404Suche in Google Scholar

[43] Fallah F, Nosier A, Sharifi M, Ghezelbash F. On perturbation method in mechanical, thermal and thermo-mechanical loadings of plates: cylindrical bending of FG plates. ZAMM. 2016;96:217–32.10.1002/zamm.201400136Suche in Google Scholar

[44] Najafi F, Shojaeefard MH, Googarchin HS. Nonlinear low-velocity impact response of functionally graded plate with nonlinear three-parameter elastic foundation in thermal field. Compos Part B-Eng. 2016;107:123–40.10.1016/j.compositesb.2016.09.070Suche in Google Scholar

[45] Fan Y, Wang H. Thermal postbuckling and vibration of postbuckled matrix cracked hybrid laminated plates containing carbon nanotube reinforced composite layers on elastic foundation. Compos Struct. 2016;157:386–97.10.1016/j.compstruct.2016.08.040Suche in Google Scholar

[46] Fan Y, Wang H. Nonlinear dynamics of matrix-cracked hybrid laminated plates containing carbon nanotube-reinforced composite layers resting on elastic foundations. Nonlinear Dyn. 2016;84:1181–99.10.1007/s11071-015-2562-7Suche in Google Scholar

[47] Fan Y, Wang H. Nonlinear low-velocity impact analysis of matrix cracked hybrid laminated plates containing CNTRC layers resting on visco-Pasternak foundation. Compos Part B-Eng. 2017;117:9–19.10.1016/j.compositesb.2017.02.010Suche in Google Scholar

[48] Huang X-H, Yang J, Azim I, Ren X, Wang X. Static and dynamic analyses of auxetic hybrid FRC/CNTRC laminated plates. Nanotechnol Rev. 2020;9:1625–42.10.1515/ntrev-2020-0106Suche in Google Scholar

[49] Huang X-H, Yang J, Wang X, Azim I. Combined analytical and numerical approach for auxetic FG-CNTRC plate subjected to a sudden load. Eng Comput. 2022;38:S55–70.10.1007/s00366-020-01106-8Suche in Google Scholar

[50] Huang X-H, Yu N-T, Azim I, Zhu J, Wu M-J. A comparative analysis of thermos-mechanical behavior of CNT-reinforced composite plates: Capturing the effects of thermal shrinkage. Case Stud Therm Eng. 2022;38:102347.10.1016/j.csite.2022.102347Suche in Google Scholar

[51] Shen H-S, Li C, Huang X-H. Assessment of negative Poisson’s ratio effect on the postbuckling of pressure-loaded FG-CNTRC laminated cylindrical shells. Mech Based Des Struct Mach. 2023;51:1856–80.10.1080/15397734.2021.1880934Suche in Google Scholar
Received: 2023-09-07
Revised: 2023-10-12
Accepted: 2023-11-28
Published Online: 2024-01-12

© 2024 the author(s), published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

  1. Research Articles
  2. Tension buckling and postbuckling of nanocomposite laminated plates with in-plane negative Poisson’s ratio
  3. Polyvinylpyrrolidone-stabilised gold nanoparticle coatings inhibit blood protein adsorption
  4. Energy and mass transmission through hybrid nanofluid flow passing over a spinning sphere with magnetic effect and heat source/sink
  5. Surface treatment with nano-silica and magnesium potassium phosphate cement co-action for enhancing recycled aggregate concrete
  6. Numerical investigation of thermal radiation with entropy generation effects in hybrid nanofluid flow over a shrinking/stretching sheet
  7. Enhancing the performance of thermal energy storage by adding nano-particles with paraffin phase change materials
  8. Using nano-CaCO3 and ceramic tile waste to design low-carbon ultra high performance concrete
  9. Numerical analysis of thermophoretic particle deposition in a magneto-Marangoni convective dusty tangent hyperbolic nanofluid flow – Thermal and magnetic features
  10. Dual numerical solutions of Casson SA–hybrid nanofluid toward a stagnation point flow over stretching/shrinking cylinder
  11. Single flake homo p–n diode of MoTe2 enabled by oxygen plasma doping
  12. Electrostatic self-assembly effect of Fe3O4 nanoparticles on performance of carbon nanotubes in cement-based materials
  13. Multi-scale alignment to buried atom-scale devices using Kelvin probe force microscopy
  14. Antibacterial, mechanical, and dielectric properties of hydroxyapatite cordierite/zirconia porous nanocomposites for use in bone tissue engineering applications
  15. Time-dependent Darcy–Forchheimer flow of Casson hybrid nanofluid comprising the CNTs through a Riga plate with nonlinear thermal radiation and viscous dissipation
  16. Durability prediction of geopolymer mortar reinforced with nanoparticles and PVA fiber using particle swarm optimized BP neural network
  17. Utilization of zein nano-based system for promoting antibiofilm and anti-virulence activities of curcumin against Pseudomonas aeruginosa
  18. Antibacterial effect of novel dental resin composites containing rod-like zinc oxide
  19. An extended model to assess Jeffery–Hamel blood flow through arteries with iron-oxide (Fe2O3) nanoparticles and melting effects: Entropy optimization analysis
  20. Comparative study of copper nanoparticles over radially stretching sheet with water and silicone oil
  21. Cementitious composites modified by nanocarbon fillers with cooperation effect possessing excellent self-sensing properties
  22. Confinement size effect on dielectric properties, antimicrobial activity, and recycling of TiO2 quantum dots via photodegradation processes of Congo red dye and real industrial textile wastewater
  23. Biogenic silver nanoparticles of Moringa oleifera leaf extract: Characterization and photocatalytic application
  24. Novel integrated structure and function of Mg–Gd neutron shielding materials
  25. Impact of multiple slips on thermally radiative peristaltic transport of Sisko nanofluid with double diffusion convection, viscous dissipation, and induced magnetic field
  26. Magnetized water-based hybrid nanofluid flow over an exponentially stretching sheet with thermal convective and mass flux conditions: HAM solution
  27. A numerical investigation of the two-dimensional magnetohydrodynamic water-based hybrid nanofluid flow composed of Fe3O4 and Au nanoparticles over a heated surface
  28. Development and modeling of an ultra-robust TPU-MWCNT foam with high flexibility and compressibility
  29. Effects of nanofillers on the physical, mechanical, and tribological behavior of carbon/kenaf fiber–reinforced phenolic composites
  30. Polymer nanocomposite for protecting photovoltaic cells from solar ultraviolet in space
  31. Study on the mechanical properties and microstructure of recycled concrete reinforced with basalt fibers and nano-silica in early low-temperature environments
  32. Synergistic effect of carbon nanotubes and polyvinyl alcohol on the mechanical performance and microstructure of cement mortar
  33. CFD analysis of paraffin-based hybrid (Co–Au) and trihybrid (Co–Au–ZrO2) nanofluid flow through a porous medium
  34. Forced convective tangent hyperbolic nanofluid flow subject to heat source/sink and Lorentz force over a permeable wedge: Numerical exploration
  35. Physiochemical and electrical activities of nano copper oxides synthesised via hydrothermal method utilising natural reduction agents for solar cell application
  36. A homotopic analysis of the blood-based bioconvection Carreau–Yasuda hybrid nanofluid flow over a stretching sheet with convective conditions
  37. In situ synthesis of reduced graphene oxide/SnIn4S8 nanocomposites with enhanced photocatalytic performance for pollutant degradation
  38. A coarse-grained Poisson–Nernst–Planck model for polyelectrolyte-modified nanofluidic diodes
  39. A numerical investigation of the magnetized water-based hybrid nanofluid flow over an extending sheet with a convective condition: Active and passive controls of nanoparticles
  40. The LyP-1 cyclic peptide modified mesoporous polydopamine nanospheres for targeted delivery of triptolide regulate the macrophage repolarization in atherosclerosis
  41. Synergistic effect of hydroxyapatite-magnetite nanocomposites in magnetic hyperthermia for bone cancer treatment
  42. The significance of quadratic thermal radiative scrutinization of a nanofluid flow across a microchannel with thermophoretic particle deposition effects
  43. Ferromagnetic effect on Casson nanofluid flow and transport phenomena across a bi-directional Riga sensor device: Darcy–Forchheimer model
  44. Performance of carbon nanomaterials incorporated with concrete exposed to high temperature
  45. Multicriteria-based optimization of roller compacted concrete pavement containing crumb rubber and nano-silica
  46. Revisiting hydrotalcite synthesis: Efficient combined mechanochemical/coprecipitation synthesis to design advanced tunable basic catalysts
  47. Exploration of irreversibility process and thermal energy of a tetra hybrid radiative binary nanofluid focusing on solar implementations
  48. Effect of graphene oxide on the properties of ternary limestone clay cement paste
  49. Improved mechanical properties of graphene-modified basalt fibre–epoxy composites
  50. Sodium titanate nanostructured modified by green synthesis of iron oxide for highly efficient photodegradation of dye contaminants
  51. Green synthesis of Vitis vinifera extract-appended magnesium oxide NPs for biomedical applications
  52. Differential study on the thermal–physical properties of metal and its oxide nanoparticle-formed nanofluids: Molecular dynamics simulation investigation of argon-based nanofluids
  53. Heat convection and irreversibility of magneto-micropolar hybrid nanofluids within a porous hexagonal-shaped enclosure having heated obstacle
  54. Numerical simulation and optimization of biological nanocomposite system for enhanced oil recovery
  55. Laser ablation and chemical vapor deposition to prepare a nanostructured PPy layer on the Ti surface
  56. Cilostazol niosomes-loaded transdermal gels: An in vitro and in vivo anti-aggregant and skin permeation activity investigations towards preparing an efficient nanoscale formulation
  57. Linear and nonlinear optical studies on successfully mixed vanadium oxide and zinc oxide nanoparticles synthesized by sol–gel technique
  58. Analytical investigation of convective phenomena with nonlinearity characteristics in nanostratified liquid film above an inclined extended sheet
  59. Optimization method for low-velocity impact identification in nanocomposite using genetic algorithm
  60. Analyzing the 3D-MHD flow of a sodium alginate-based nanofluid flow containing alumina nanoparticles over a bi-directional extending sheet using variable porous medium and slip conditions
  61. A comprehensive study of laser irradiated hydrothermally synthesized 2D layered heterostructure V2O5(1−x)MoS2(x) (X = 1–5%) nanocomposites for photocatalytic application
  62. Computational analysis of water-based silver, copper, and alumina hybrid nanoparticles over a stretchable sheet embedded in a porous medium with thermophoretic particle deposition effects
  63. A deep dive into AI integration and advanced nanobiosensor technologies for enhanced bacterial infection monitoring
  64. Effects of normal strain on pyramidal I and II 〈c + a〉 screw dislocation mobility and structure in single-crystal magnesium
  65. Computational study of cross-flow in entropy-optimized nanofluids
  66. Significance of nanoparticle aggregation for thermal transport over magnetized sensor surface
  67. A green and facile synthesis route of nanosize cupric oxide at room temperature
  68. Effect of annealing time on bending performance and microstructure of C19400 alloy strip
  69. Chitosan-based Mupirocin and Alkanna tinctoria extract nanoparticles for the management of burn wound: In vitro and in vivo characterization
  70. Electrospinning of MNZ/PLGA/SF nanofibers for periodontitis
  71. Photocatalytic degradation of methylene blue by Nd-doped titanium dioxide thin films
  72. Shell-core-structured electrospinning film with sequential anti-inflammatory and pro-neurogenic effects for peripheral nerve repairment
  73. Flow and heat transfer insights into a chemically reactive micropolar Williamson ternary hybrid nanofluid with cross-diffusion theory
  74. One-pot fabrication of open-spherical shapes based on the decoration of copper sulfide/poly-O-amino benzenethiol on copper oxide as a promising photocathode for hydrogen generation from the natural source of Red Sea water
  75. A penta-hybrid approach for modeling the nanofluid flow in a spatially dependent magnetic field
  76. Advancing sustainable agriculture: Metal-doped urea–hydroxyapatite hybrid nanofertilizer for agro-industry
  77. Utilizing Ziziphus spina-christi for eco-friendly synthesis of silver nanoparticles: Antimicrobial activity and promising application in wound healing
  78. Plant-mediated synthesis, characterization, and evaluation of a copper oxide/silicon dioxide nanocomposite by an antimicrobial study
  79. Effects of PVA fibers and nano-SiO2 on rheological properties of geopolymer mortar
  80. Investigating silver and alumina nanoparticles’ impact on fluid behavior over porous stretching surface
  81. Potential pharmaceutical applications and molecular docking study for green fabricated ZnO nanoparticles mediated Raphanus sativus: In vitro and in vivo study
  82. Effect of temperature and nanoparticle size on the interfacial layer thickness of TiO2–water nanofluids using molecular dynamics
  83. Characteristics of induced magnetic field on the time-dependent MHD nanofluid flow through parallel plates
  84. Flexural and vibration behaviours of novel covered CFRP composite joints with an MWCNT-modified adhesive
  85. Experimental research on mechanically and thermally activation of nano-kaolin to improve the properties of ultra-high-performance fiber-reinforced concrete
  86. Analysis of variable fluid properties for three-dimensional flow of ternary hybrid nanofluid on a stretching sheet with MHD effects
  87. Biodegradability of corn starch films containing nanocellulose fiber and thymol
  88. Toxicity assessment of copper oxide nanoparticles: In vivo study
  89. Some measures to enhance the energy output performances of triboelectric nanogenerators
  90. Reinforcement of graphene nanoplatelets on water uptake and thermomechanical behaviour of epoxy adhesive subjected to water ageing conditions
  91. Optimization of preparation parameters and testing verification of carbon nanotube suspensions used in concrete
  92. Max-phase Ti3SiC2 and diverse nanoparticle reinforcements for enhancement of the mechanical, dynamic, and microstructural properties of AA5083 aluminum alloy via FSP
  93. Advancing drug delivery: Neural network perspectives on nanoparticle-mediated treatments for cancerous tissues
  94. PEG-PLGA core–shell nanoparticles for the controlled delivery of picoplatin–hydroxypropyl β-cyclodextrin inclusion complex in triple-negative breast cancer: In vitro and in vivo study
  95. Conduction transportation from graphene to an insulative polymer medium: A novel approach for the conductivity of nanocomposites
  96. Review Articles
  97. Developments of terahertz metasurface biosensors: A literature review
  98. Overview of amorphous carbon memristor device, modeling, and applications for neuromorphic computing
  99. Advances in the synthesis of gold nanoclusters (AuNCs) of proteins extracted from nature
  100. A review of ternary polymer nanocomposites containing clay and calcium carbonate and their biomedical applications
  101. Recent advancements in polyoxometalate-functionalized fiber materials: A review
  102. Special contribution of atomic force microscopy in cell death research
  103. A comprehensive review of oral chitosan drug delivery systems: Applications for oral insulin delivery
  104. Cellular senescence and nanoparticle-based therapies: Current developments and perspectives
  105. Cyclodextrins-block copolymer drug delivery systems: From design and development to preclinical studies
  106. Micelle-based nanoparticles with stimuli-responsive properties for drug delivery
  107. Critical assessment of the thermal stability and degradation of chemically functionalized nanocellulose-based polymer nanocomposites
  108. Research progress in preparation technology of micro and nano titanium alloy powder
  109. Nanoformulations for lysozyme-based additives in animal feed: An alternative to fight antibiotic resistance spread
  110. Incorporation of organic photochromic molecules in mesoporous silica materials: Synthesis and applications
  111. A review on modeling of graphene and associated nanostructures reinforced concrete
  112. A review on strengthening mechanisms of carbon quantum dots-reinforced Cu-matrix nanocomposites
  113. Review on nanocellulose composites and CNFs assembled microfiber toward automotive applications
  114. Nanomaterial coating for layered lithium rich transition metal oxide cathode for lithium-ion battery
  115. Application of AgNPs in biomedicine: An overview and current trends
  116. Nanobiotechnology and microbial influence on cold adaptation in plants
  117. Hepatotoxicity of nanomaterials: From mechanism to therapeutic strategy
  118. Applications of micro-nanobubble and its influence on concrete properties: An in-depth review
  119. A comprehensive systematic literature review of ML in nanotechnology for sustainable development
  120. Exploiting the nanotechnological approaches for traditional Chinese medicine in childhood rhinitis: A review of future perspectives
  121. Twisto-photonics in two-dimensional materials: A comprehensive review
  122. Current advances of anticancer drugs based on solubilization technology
  123. Recent process of using nanoparticles in the T cell-based immunometabolic therapy
  124. Future prospects of gold nanoclusters in hydrogen storage systems and sustainable environmental treatment applications
  125. Preparation, types, and applications of one- and two-dimensional nanochannels and their transport properties for water and ions
  126. Microstructural, mechanical, and corrosion characteristics of Mg–Gd–x systems: A review of recent advancements
  127. Functionalized nanostructures and targeted delivery systems with a focus on plant-derived natural agents for COVID-19 therapy: A review and outlook
  128. Mapping evolution and trends of cell membrane-coated nanoparticles: A bibliometric analysis and scoping review
  129. Nanoparticles and their application in the diagnosis of hepatocellular carcinoma
  130. In situ growth of carbon nanotubes on fly ash substrates
  131. Structural performance of boards through nanoparticle reinforcement: An advance review
  132. Reinforcing mechanisms review of the graphene oxide on cement composites
  133. Seed regeneration aided by nanomaterials in a climate change scenario: A comprehensive review
  134. Surface-engineered quantum dot nanocomposites for neurodegenerative disorder remediation and avenue for neuroimaging
  135. Graphitic carbon nitride hybrid thin films for energy conversion: A mini-review on defect activation with different materials
  136. Nanoparticles and the treatment of hepatocellular carcinoma
  137. Special Issue on Advanced Nanomaterials and Composites for Energy Conversion and Storage - Part II
  138. Highly safe lithium vanadium oxide anode for fast-charging dendrite-free lithium-ion batteries
  139. Recent progress in nanomaterials of battery energy storage: A patent landscape analysis, technology updates, and future prospects
  140. Special Issue on Advanced Nanomaterials for Carbon Capture, Environment and Utilization for Energy Sustainability - Part II
  141. Calcium-, magnesium-, and yttrium-doped lithium nickel phosphate nanomaterials as high-performance catalysts for electrochemical water oxidation reaction
  142. Low alkaline vegetation concrete with silica fume and nano-fly ash composites to improve the planting properties and soil ecology
  143. Mesoporous silica-grafted deep eutectic solvent-based mixed matrix membranes for wastewater treatment: Synthesis and emerging pollutant removal performance
  144. Electrochemically prepared ultrathin two-dimensional graphitic nanosheets as cathodes for advanced Zn-based energy storage devices
  145. Enhanced catalytic degradation of amoxicillin by phyto-mediated synthesised ZnO NPs and ZnO-rGO hybrid nanocomposite: Assessment of antioxidant activity, adsorption, and thermodynamic analysis
  146. Incorporating GO in PI matrix to advance nanocomposite coating: An enhancing strategy to prevent corrosion
  147. Synthesis, characterization, thermal stability, and application of microporous hyper cross-linked polyphosphazenes with naphthylamine group for CO2 uptake
  148. Engineering in ceramic albite morphology by the addition of additives: Carbon nanotubes and graphene oxide for energy applications
  149. Nanoscale synergy: Optimizing energy storage with SnO2 quantum dots on ZnO hexagonal prisms for advanced supercapacitors
  150. Aging assessment of silicone rubber materials under corona discharge accompanied by humidity and UV radiation
  151. Tuning structural and electrical properties of Co-precipitated and Cu-incorporated nickel ferrite for energy applications
  152. Sodium alginate-supported AgSr nanoparticles for catalytic degradation of malachite green and methyl orange in aqueous medium
  153. An environmentally greener and reusability approach for bioenergy production using Mallotus philippensis (Kamala) seed oil feedstock via phytonanotechnology
  154. Micro-/nano-alumina trihydrate and -magnesium hydroxide fillers in RTV-SR composites under electrical and environmental stresses
  155. Mechanism exploration of ion-implanted epoxy on surface trap distribution: An approach to augment the vacuum flashover voltages
  156. Nanoscale engineering of semiconductor photocatalysts boosting charge separation for solar-driven H2 production: Recent advances and future perspective
  157. Excellent catalytic performance over reduced graphene-boosted novel nanoparticles for oxidative desulfurization of fuel oil
  158. Special Issue on Advances in Nanotechnology for Agriculture
  159. Deciphering the synergistic potential of mycogenic zinc oxide nanoparticles and bio-slurry formulation on phenology and physiology of Vigna radiata
  160. Nanomaterials: Cross-disciplinary applications in ornamental plants
  161. Special Issue on Catechol Based Nano and Microstructures
  162. Polydopamine films: Versatile but interface-dependent coatings
  163. In vitro anticancer activity of melanin-like nanoparticles for multimodal therapy of glioblastoma
  164. Poly-3,4-dihydroxybenzylidenhydrazine, a different analogue of polydopamine
  165. Chirality and self-assembly of structures derived from optically active 1,2-diaminocyclohexane and catecholamines
  166. Advancing resource sustainability with green photothermal materials: Insights from organic waste-derived and bioderived sources
  167. Bioinspired neuromelanin-like Pt(iv) polymeric nanoparticles for cancer treatment
  168. Special Issue on Implementing Nanotechnology for Smart Healthcare System
  169. Intelligent explainable optical sensing on Internet of nanorobots for disease detection
  170. Special Issue on Green Mono, Bi and Tri Metallic Nanoparticles for Biological and Environmental Applications
  171. Tracking success of interaction of green-synthesized Carbopol nanoemulgel (neomycin-decorated Ag/ZnO nanocomposite) with wound-based MDR bacteria
  172. Green synthesis of copper oxide nanoparticles using genus Inula and evaluation of biological therapeutics and environmental applications
  173. Biogenic fabrication and multifunctional therapeutic applications of silver nanoparticles synthesized from rose petal extract
  174. Metal oxides on the frontlines: Antimicrobial activity in plant-derived biometallic nanoparticles
  175. Controlling pore size during the synthesis of hydroxyapatite nanoparticles using CTAB by the sol–gel hydrothermal method and their biological activities
  176. Special Issue on State-of-Art Advanced Nanotechnology for Healthcare
  177. Applications of nanomedicine-integrated phototherapeutic agents in cancer theranostics: A comprehensive review of the current state of research
  178. Smart bionanomaterials for treatment and diagnosis of inflammatory bowel disease
  179. Beyond conventional therapy: Synthesis of multifunctional nanoparticles for rheumatoid arthritis therapy
https://doi.org/10.1515/ntrev-2023-0173
Schlagwörter für diesen Artikel
nanocomposites; auxetic laminates; tension buckling; rectangular plate; elastic substrate; temperature-dependent
Creative Commons
BY 4.0

Artikel in diesem Heft

  1. Research Articles
  2. Tension buckling and postbuckling of nanocomposite laminated plates with in-plane negative Poisson’s ratio
  3. Polyvinylpyrrolidone-stabilised gold nanoparticle coatings inhibit blood protein adsorption
  4. Energy and mass transmission through hybrid nanofluid flow passing over a spinning sphere with magnetic effect and heat source/sink
  5. Surface treatment with nano-silica and magnesium potassium phosphate cement co-action for enhancing recycled aggregate concrete
  6. Numerical investigation of thermal radiation with entropy generation effects in hybrid nanofluid flow over a shrinking/stretching sheet
  7. Enhancing the performance of thermal energy storage by adding nano-particles with paraffin phase change materials
  8. Using nano-CaCO3 and ceramic tile waste to design low-carbon ultra high performance concrete
  9. Numerical analysis of thermophoretic particle deposition in a magneto-Marangoni convective dusty tangent hyperbolic nanofluid flow – Thermal and magnetic features
  10. Dual numerical solutions of Casson SA–hybrid nanofluid toward a stagnation point flow over stretching/shrinking cylinder
  11. Single flake homo p–n diode of MoTe2 enabled by oxygen plasma doping
  12. Electrostatic self-assembly effect of Fe3O4 nanoparticles on performance of carbon nanotubes in cement-based materials
  13. Multi-scale alignment to buried atom-scale devices using Kelvin probe force microscopy
  14. Antibacterial, mechanical, and dielectric properties of hydroxyapatite cordierite/zirconia porous nanocomposites for use in bone tissue engineering applications
  15. Time-dependent Darcy–Forchheimer flow of Casson hybrid nanofluid comprising the CNTs through a Riga plate with nonlinear thermal radiation and viscous dissipation
  16. Durability prediction of geopolymer mortar reinforced with nanoparticles and PVA fiber using particle swarm optimized BP neural network
  17. Utilization of zein nano-based system for promoting antibiofilm and anti-virulence activities of curcumin against Pseudomonas aeruginosa
  18. Antibacterial effect of novel dental resin composites containing rod-like zinc oxide
  19. An extended model to assess Jeffery–Hamel blood flow through arteries with iron-oxide (Fe2O3) nanoparticles and melting effects: Entropy optimization analysis
  20. Comparative study of copper nanoparticles over radially stretching sheet with water and silicone oil
  21. Cementitious composites modified by nanocarbon fillers with cooperation effect possessing excellent self-sensing properties
  22. Confinement size effect on dielectric properties, antimicrobial activity, and recycling of TiO2 quantum dots via photodegradation processes of Congo red dye and real industrial textile wastewater
  23. Biogenic silver nanoparticles of Moringa oleifera leaf extract: Characterization and photocatalytic application
  24. Novel integrated structure and function of Mg–Gd neutron shielding materials
  25. Impact of multiple slips on thermally radiative peristaltic transport of Sisko nanofluid with double diffusion convection, viscous dissipation, and induced magnetic field
  26. Magnetized water-based hybrid nanofluid flow over an exponentially stretching sheet with thermal convective and mass flux conditions: HAM solution
  27. A numerical investigation of the two-dimensional magnetohydrodynamic water-based hybrid nanofluid flow composed of Fe3O4 and Au nanoparticles over a heated surface
  28. Development and modeling of an ultra-robust TPU-MWCNT foam with high flexibility and compressibility
  29. Effects of nanofillers on the physical, mechanical, and tribological behavior of carbon/kenaf fiber–reinforced phenolic composites
  30. Polymer nanocomposite for protecting photovoltaic cells from solar ultraviolet in space
  31. Study on the mechanical properties and microstructure of recycled concrete reinforced with basalt fibers and nano-silica in early low-temperature environments
  32. Synergistic effect of carbon nanotubes and polyvinyl alcohol on the mechanical performance and microstructure of cement mortar
  33. CFD analysis of paraffin-based hybrid (Co–Au) and trihybrid (Co–Au–ZrO2) nanofluid flow through a porous medium
  34. Forced convective tangent hyperbolic nanofluid flow subject to heat source/sink and Lorentz force over a permeable wedge: Numerical exploration
  35. Physiochemical and electrical activities of nano copper oxides synthesised via hydrothermal method utilising natural reduction agents for solar cell application
  36. A homotopic analysis of the blood-based bioconvection Carreau–Yasuda hybrid nanofluid flow over a stretching sheet with convective conditions
  37. In situ synthesis of reduced graphene oxide/SnIn4S8 nanocomposites with enhanced photocatalytic performance for pollutant degradation
  38. A coarse-grained Poisson–Nernst–Planck model for polyelectrolyte-modified nanofluidic diodes
  39. A numerical investigation of the magnetized water-based hybrid nanofluid flow over an extending sheet with a convective condition: Active and passive controls of nanoparticles
  40. The LyP-1 cyclic peptide modified mesoporous polydopamine nanospheres for targeted delivery of triptolide regulate the macrophage repolarization in atherosclerosis
  41. Synergistic effect of hydroxyapatite-magnetite nanocomposites in magnetic hyperthermia for bone cancer treatment
  42. The significance of quadratic thermal radiative scrutinization of a nanofluid flow across a microchannel with thermophoretic particle deposition effects
  43. Ferromagnetic effect on Casson nanofluid flow and transport phenomena across a bi-directional Riga sensor device: Darcy–Forchheimer model
  44. Performance of carbon nanomaterials incorporated with concrete exposed to high temperature
  45. Multicriteria-based optimization of roller compacted concrete pavement containing crumb rubber and nano-silica
  46. Revisiting hydrotalcite synthesis: Efficient combined mechanochemical/coprecipitation synthesis to design advanced tunable basic catalysts
  47. Exploration of irreversibility process and thermal energy of a tetra hybrid radiative binary nanofluid focusing on solar implementations
  48. Effect of graphene oxide on the properties of ternary limestone clay cement paste
  49. Improved mechanical properties of graphene-modified basalt fibre–epoxy composites
  50. Sodium titanate nanostructured modified by green synthesis of iron oxide for highly efficient photodegradation of dye contaminants
  51. Green synthesis of Vitis vinifera extract-appended magnesium oxide NPs for biomedical applications
  52. Differential study on the thermal–physical properties of metal and its oxide nanoparticle-formed nanofluids: Molecular dynamics simulation investigation of argon-based nanofluids
  53. Heat convection and irreversibility of magneto-micropolar hybrid nanofluids within a porous hexagonal-shaped enclosure having heated obstacle
  54. Numerical simulation and optimization of biological nanocomposite system for enhanced oil recovery
  55. Laser ablation and chemical vapor deposition to prepare a nanostructured PPy layer on the Ti surface
  56. Cilostazol niosomes-loaded transdermal gels: An in vitro and in vivo anti-aggregant and skin permeation activity investigations towards preparing an efficient nanoscale formulation
  57. Linear and nonlinear optical studies on successfully mixed vanadium oxide and zinc oxide nanoparticles synthesized by sol–gel technique
  58. Analytical investigation of convective phenomena with nonlinearity characteristics in nanostratified liquid film above an inclined extended sheet
  59. Optimization method for low-velocity impact identification in nanocomposite using genetic algorithm
  60. Analyzing the 3D-MHD flow of a sodium alginate-based nanofluid flow containing alumina nanoparticles over a bi-directional extending sheet using variable porous medium and slip conditions
  61. A comprehensive study of laser irradiated hydrothermally synthesized 2D layered heterostructure V2O5(1−x)MoS2(x) (X = 1–5%) nanocomposites for photocatalytic application
  62. Computational analysis of water-based silver, copper, and alumina hybrid nanoparticles over a stretchable sheet embedded in a porous medium with thermophoretic particle deposition effects
  63. A deep dive into AI integration and advanced nanobiosensor technologies for enhanced bacterial infection monitoring
  64. Effects of normal strain on pyramidal I and II 〈c + a〉 screw dislocation mobility and structure in single-crystal magnesium
  65. Computational study of cross-flow in entropy-optimized nanofluids
  66. Significance of nanoparticle aggregation for thermal transport over magnetized sensor surface
  67. A green and facile synthesis route of nanosize cupric oxide at room temperature
  68. Effect of annealing time on bending performance and microstructure of C19400 alloy strip
  69. Chitosan-based Mupirocin and Alkanna tinctoria extract nanoparticles for the management of burn wound: In vitro and in vivo characterization
  70. Electrospinning of MNZ/PLGA/SF nanofibers for periodontitis
  71. Photocatalytic degradation of methylene blue by Nd-doped titanium dioxide thin films
  72. Shell-core-structured electrospinning film with sequential anti-inflammatory and pro-neurogenic effects for peripheral nerve repairment
  73. Flow and heat transfer insights into a chemically reactive micropolar Williamson ternary hybrid nanofluid with cross-diffusion theory
  74. One-pot fabrication of open-spherical shapes based on the decoration of copper sulfide/poly-O-amino benzenethiol on copper oxide as a promising photocathode for hydrogen generation from the natural source of Red Sea water
  75. A penta-hybrid approach for modeling the nanofluid flow in a spatially dependent magnetic field
  76. Advancing sustainable agriculture: Metal-doped urea–hydroxyapatite hybrid nanofertilizer for agro-industry
  77. Utilizing Ziziphus spina-christi for eco-friendly synthesis of silver nanoparticles: Antimicrobial activity and promising application in wound healing
  78. Plant-mediated synthesis, characterization, and evaluation of a copper oxide/silicon dioxide nanocomposite by an antimicrobial study
  79. Effects of PVA fibers and nano-SiO2 on rheological properties of geopolymer mortar
  80. Investigating silver and alumina nanoparticles’ impact on fluid behavior over porous stretching surface
  81. Potential pharmaceutical applications and molecular docking study for green fabricated ZnO nanoparticles mediated Raphanus sativus: In vitro and in vivo study
  82. Effect of temperature and nanoparticle size on the interfacial layer thickness of TiO2–water nanofluids using molecular dynamics
  83. Characteristics of induced magnetic field on the time-dependent MHD nanofluid flow through parallel plates
  84. Flexural and vibration behaviours of novel covered CFRP composite joints with an MWCNT-modified adhesive
  85. Experimental research on mechanically and thermally activation of nano-kaolin to improve the properties of ultra-high-performance fiber-reinforced concrete
  86. Analysis of variable fluid properties for three-dimensional flow of ternary hybrid nanofluid on a stretching sheet with MHD effects
  87. Biodegradability of corn starch films containing nanocellulose fiber and thymol
  88. Toxicity assessment of copper oxide nanoparticles: In vivo study
  89. Some measures to enhance the energy output performances of triboelectric nanogenerators
  90. Reinforcement of graphene nanoplatelets on water uptake and thermomechanical behaviour of epoxy adhesive subjected to water ageing conditions
  91. Optimization of preparation parameters and testing verification of carbon nanotube suspensions used in concrete
  92. Max-phase Ti3SiC2 and diverse nanoparticle reinforcements for enhancement of the mechanical, dynamic, and microstructural properties of AA5083 aluminum alloy via FSP
  93. Advancing drug delivery: Neural network perspectives on nanoparticle-mediated treatments for cancerous tissues
  94. PEG-PLGA core–shell nanoparticles for the controlled delivery of picoplatin–hydroxypropyl β-cyclodextrin inclusion complex in triple-negative breast cancer: In vitro and in vivo study
  95. Conduction transportation from graphene to an insulative polymer medium: A novel approach for the conductivity of nanocomposites
  96. Review Articles
  97. Developments of terahertz metasurface biosensors: A literature review
  98. Overview of amorphous carbon memristor device, modeling, and applications for neuromorphic computing
  99. Advances in the synthesis of gold nanoclusters (AuNCs) of proteins extracted from nature
  100. A review of ternary polymer nanocomposites containing clay and calcium carbonate and their biomedical applications
  101. Recent advancements in polyoxometalate-functionalized fiber materials: A review
  102. Special contribution of atomic force microscopy in cell death research
  103. A comprehensive review of oral chitosan drug delivery systems: Applications for oral insulin delivery
  104. Cellular senescence and nanoparticle-based therapies: Current developments and perspectives
  105. Cyclodextrins-block copolymer drug delivery systems: From design and development to preclinical studies
  106. Micelle-based nanoparticles with stimuli-responsive properties for drug delivery
  107. Critical assessment of the thermal stability and degradation of chemically functionalized nanocellulose-based polymer nanocomposites
  108. Research progress in preparation technology of micro and nano titanium alloy powder
  109. Nanoformulations for lysozyme-based additives in animal feed: An alternative to fight antibiotic resistance spread
  110. Incorporation of organic photochromic molecules in mesoporous silica materials: Synthesis and applications
  111. A review on modeling of graphene and associated nanostructures reinforced concrete
  112. A review on strengthening mechanisms of carbon quantum dots-reinforced Cu-matrix nanocomposites
  113. Review on nanocellulose composites and CNFs assembled microfiber toward automotive applications
  114. Nanomaterial coating for layered lithium rich transition metal oxide cathode for lithium-ion battery
  115. Application of AgNPs in biomedicine: An overview and current trends
  116. Nanobiotechnology and microbial influence on cold adaptation in plants
  117. Hepatotoxicity of nanomaterials: From mechanism to therapeutic strategy
  118. Applications of micro-nanobubble and its influence on concrete properties: An in-depth review
  119. A comprehensive systematic literature review of ML in nanotechnology for sustainable development
  120. Exploiting the nanotechnological approaches for traditional Chinese medicine in childhood rhinitis: A review of future perspectives
  121. Twisto-photonics in two-dimensional materials: A comprehensive review
  122. Current advances of anticancer drugs based on solubilization technology
  123. Recent process of using nanoparticles in the T cell-based immunometabolic therapy
  124. Future prospects of gold nanoclusters in hydrogen storage systems and sustainable environmental treatment applications
  125. Preparation, types, and applications of one- and two-dimensional nanochannels and their transport properties for water and ions
  126. Microstructural, mechanical, and corrosion characteristics of Mg–Gd–x systems: A review of recent advancements
  127. Functionalized nanostructures and targeted delivery systems with a focus on plant-derived natural agents for COVID-19 therapy: A review and outlook
  128. Mapping evolution and trends of cell membrane-coated nanoparticles: A bibliometric analysis and scoping review
  129. Nanoparticles and their application in the diagnosis of hepatocellular carcinoma
  130. In situ growth of carbon nanotubes on fly ash substrates
  131. Structural performance of boards through nanoparticle reinforcement: An advance review
  132. Reinforcing mechanisms review of the graphene oxide on cement composites
  133. Seed regeneration aided by nanomaterials in a climate change scenario: A comprehensive review
  134. Surface-engineered quantum dot nanocomposites for neurodegenerative disorder remediation and avenue for neuroimaging
  135. Graphitic carbon nitride hybrid thin films for energy conversion: A mini-review on defect activation with different materials
  136. Nanoparticles and the treatment of hepatocellular carcinoma
  137. Special Issue on Advanced Nanomaterials and Composites for Energy Conversion and Storage - Part II
  138. Highly safe lithium vanadium oxide anode for fast-charging dendrite-free lithium-ion batteries
  139. Recent progress in nanomaterials of battery energy storage: A patent landscape analysis, technology updates, and future prospects
  140. Special Issue on Advanced Nanomaterials for Carbon Capture, Environment and Utilization for Energy Sustainability - Part II
  141. Calcium-, magnesium-, and yttrium-doped lithium nickel phosphate nanomaterials as high-performance catalysts for electrochemical water oxidation reaction
  142. Low alkaline vegetation concrete with silica fume and nano-fly ash composites to improve the planting properties and soil ecology
  143. Mesoporous silica-grafted deep eutectic solvent-based mixed matrix membranes for wastewater treatment: Synthesis and emerging pollutant removal performance
  144. Electrochemically prepared ultrathin two-dimensional graphitic nanosheets as cathodes for advanced Zn-based energy storage devices
  145. Enhanced catalytic degradation of amoxicillin by phyto-mediated synthesised ZnO NPs and ZnO-rGO hybrid nanocomposite: Assessment of antioxidant activity, adsorption, and thermodynamic analysis
  146. Incorporating GO in PI matrix to advance nanocomposite coating: An enhancing strategy to prevent corrosion
  147. Synthesis, characterization, thermal stability, and application of microporous hyper cross-linked polyphosphazenes with naphthylamine group for CO2 uptake
  148. Engineering in ceramic albite morphology by the addition of additives: Carbon nanotubes and graphene oxide for energy applications
  149. Nanoscale synergy: Optimizing energy storage with SnO2 quantum dots on ZnO hexagonal prisms for advanced supercapacitors
  150. Aging assessment of silicone rubber materials under corona discharge accompanied by humidity and UV radiation
  151. Tuning structural and electrical properties of Co-precipitated and Cu-incorporated nickel ferrite for energy applications
  152. Sodium alginate-supported AgSr nanoparticles for catalytic degradation of malachite green and methyl orange in aqueous medium
  153. An environmentally greener and reusability approach for bioenergy production using Mallotus philippensis (Kamala) seed oil feedstock via phytonanotechnology
  154. Micro-/nano-alumina trihydrate and -magnesium hydroxide fillers in RTV-SR composites under electrical and environmental stresses
  155. Mechanism exploration of ion-implanted epoxy on surface trap distribution: An approach to augment the vacuum flashover voltages
  156. Nanoscale engineering of semiconductor photocatalysts boosting charge separation for solar-driven H2 production: Recent advances and future perspective
  157. Excellent catalytic performance over reduced graphene-boosted novel nanoparticles for oxidative desulfurization of fuel oil
  158. Special Issue on Advances in Nanotechnology for Agriculture
  159. Deciphering the synergistic potential of mycogenic zinc oxide nanoparticles and bio-slurry formulation on phenology and physiology of Vigna radiata
  160. Nanomaterials: Cross-disciplinary applications in ornamental plants
  161. Special Issue on Catechol Based Nano and Microstructures
  162. Polydopamine films: Versatile but interface-dependent coatings
  163. In vitro anticancer activity of melanin-like nanoparticles for multimodal therapy of glioblastoma
  164. Poly-3,4-dihydroxybenzylidenhydrazine, a different analogue of polydopamine
  165. Chirality and self-assembly of structures derived from optically active 1,2-diaminocyclohexane and catecholamines
  166. Advancing resource sustainability with green photothermal materials: Insights from organic waste-derived and bioderived sources
  167. Bioinspired neuromelanin-like Pt(iv) polymeric nanoparticles for cancer treatment
  168. Special Issue on Implementing Nanotechnology for Smart Healthcare System
  169. Intelligent explainable optical sensing on Internet of nanorobots for disease detection
  170. Special Issue on Green Mono, Bi and Tri Metallic Nanoparticles for Biological and Environmental Applications
  171. Tracking success of interaction of green-synthesized Carbopol nanoemulgel (neomycin-decorated Ag/ZnO nanocomposite) with wound-based MDR bacteria
  172. Green synthesis of copper oxide nanoparticles using genus Inula and evaluation of biological therapeutics and environmental applications
  173. Biogenic fabrication and multifunctional therapeutic applications of silver nanoparticles synthesized from rose petal extract
  174. Metal oxides on the frontlines: Antimicrobial activity in plant-derived biometallic nanoparticles
  175. Controlling pore size during the synthesis of hydroxyapatite nanoparticles using CTAB by the sol–gel hydrothermal method and their biological activities
  176. Special Issue on State-of-Art Advanced Nanotechnology for Healthcare
  177. Applications of nanomedicine-integrated phototherapeutic agents in cancer theranostics: A comprehensive review of the current state of research
  178. Smart bionanomaterials for treatment and diagnosis of inflammatory bowel disease
  179. Beyond conventional therapy: Synthesis of multifunctional nanoparticles for rheumatoid arthritis therapy
Jetzt anmelden und 20% sparen
Institutioneller Zugang
Wie funktioniert Authentifizierung?
Haben Sie eine Idee, wie wir unsere Website verbessern können?
Bitte schreiben Sie uns.
© 2025 De Gruyter Brill
Heruntergeladen am 6.9.2025 von https://www.degruyterbrill.com/document/doi/10.1515/ntrev-2023-0173/html
Button zum nach oben scrollen