Time-dependent Darcy–Forchheimer flow of Casson hybrid nanofluid comprising the CNTs through a Riga plate with nonlinear thermal radiation and viscous dissipation

Karuppiah Senthilvadivu; Sheniyappan Eswaramoorthi; Karuppusamy Loganathan; Mohamed Abbas

doi:10.1515/ntrev-2023-0202

Article Open Access

Time-dependent Darcy–Forchheimer flow of Casson hybrid nanofluid comprising the CNTs through a Riga plate with nonlinear thermal radiation and viscous dissipation

Karuppiah Senthilvadivu , Sheniyappan Eswaramoorthi , Karuppusamy Loganathan and Mohamed Abbas

Published/Copyright: March 4, 2024

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Nanotechnology Reviews Volume 13 Issue 1

Abstract

Carbon nanotubes (CNTs) are gaining popularity due to their expanding uses in industrial and technical processes, such as geothermal reservoirs, water and air filters, coatings, solar collection, ceramic material reinforcement, electrostatic dissipation, etc. In addition, the CNTs have superior electrical conductivity and biocompatibility. Based on the aforementioned applications, the current work examines the time-dependent and Darcy–Forchheimer flow of water/glycerin-based Casson hybrid nanofluid formed by single-walled CNTs and multi-walled CNTs over a Riga plate under velocity slip. The energy expression is modeled through nonlinear thermal radiation and viscous dissipation impacts. The incorporation of convective boundary condition into the current model improves its realism. By employing suitable variables, the governing models are re-framed into ordinary differential equations. The bvp4c and the homotopy analysis method are used to find the computational results of the re-framed equations and boundary conditions. The novel characteristics of a variety of physical parameters on velocity, temperature, skin friction coefficient (SFC), and local Nusselt number (LNN) are discussed via graphs, charts, and tables. It is found that the fluid velocity decays when enriching the Forchheimer number, unsteady and porosity parameters. The radiation parameter plays an opposite role in convective heating and cooling cases. The modified Hartmann number enhances the surface drag force, and the Forchheimer number declines the SFC. The unsteady parameter develops the heat transfer rate, and the Forchheimer number suppresses the LNN. The simulated flow problem has many applications in engineering sectors, including ceramic manufacture, heating and cooling systems, energy storage units, thermodynamic processes, and other fields.

Keywords: carbon nanotubes; Darcy–Forchheimer flow; Casson hybrid nanofluid; HAM; Riga plate

Nomenclature

a , a 1	positive constants
C p	capacity of specific heat
c b	drag force coefficient
k 1 *	permeability of the porous medium
Ec	Eckert number
σ *	Stefan–Boltzmann constant
h c	heat transfer coefficient
C ℱ Re	skin friction coefficient
N u Re	local Nusselt number
Bi	Biot number
K 1	slip parameter
ρ C p	heat capacity
J 0	current density applied to the electrodes
k *	thermal conductivity
M 0	magnetic property of the permanent magnets
	that are organized on top of the plate surface
ν	kinematic viscosity
℧	dimensionless variable
Q	heat generation or absorption coefficient
ρ	density
T	temperature of the fluid
T w	surface temperature
T ∞	ambient temperature
ℋ	non-dimensional temperature
u , v	velocity factors
x , y	space coordinates
A	unsteady parameter
λ	porosity parameter
Λ	temperature ratio parameter
Fr	Forchheimer number
β	Casson parameter
β R	dimensionless parameter
Ha	modified Hartmann number
Pr	Prandtl number
R	radiation parameter
Re	Reynolds number
Hg	heat consumption/generation parameter

1 Introduction

Many scientists have been interested in nanofluids in recent decades because of their significant heat transfer properties. The heat transmission characteristics of diverse fluids have a significant influence on the performance of many equipment, including air conditioning, the food industry, power generation, transportation, microelectronics, and the thinning and annealing of copper wires. The heat transfer capabilities in many of these applications have been constrained by the use of standard heat transit fluids such as water, ethylene glycol, mineral oils, and they have poor thermal characteristics. Scientists from a variety of disciplines are working to address this shortcoming in several ways. One of the easiest ways to address this shortcoming is by adding solid nanometer-scaled particles like metals ( Ag, Au, Al, Cu, Fe ) , metallic oxides ( CuO , TiO 2 , Al 2 O 3 , Fe 3 O 4 ), carbide ceramics ( SiC, TiC ) , nitride ceramics ( AlN, SiN ) , CNTs (SWCNT, MWCNT) and this new fluid is called “nanofluid,” see the study of Choi [1]. The heat transfer features of Al 2 O 3 water-based nanofluid over an SS (stretching surface) with viscous dissipation were analyzed by Ali et al. [2]. They acknowledged that the greater the presence of NPVF (nanoparticle volume fraction), better the thermal profile. Iqbal and Abbas [3] addressed the thermal behavior of ethylene glycol-based Cu nanofluid flow past an SS. They achieved that the platelet-shaped nanoparticles have a high heat transfer rate compared to the other-shaped nanoparticles. The thermal consequence of the time-dependent flow of nanofluid on a plate was portrayed by Fakour et al. [4]. They proved that the water–alumina nanofluid has better heat transfer than copper, silver, and titanium. Sadiq [5] inspected the water-based Cu , Al 2 O 3 , and TiO 2 nanofluid flow over an SS. He uncovered that the TBL (thermal boundary layer) improves when strengthening the NPVF quantity.

Carbon nanotubes (CNTs) are cylinder-shaped materials made of coils of graphite. The CNTs are measured in micrometers and have a diameter of approximately 0.4–2.0 nm. Based on their carbon molecular count, CNTs are divided into two distinct types: SWCNTs (single-walled carbon nanotubes) and MWCNTs (multi-walled carbon nanotubes). The dusty liquid’s thermal and flow characteristics past an SS (stretching sheet) with viscous dissipation immersed by SWCNTs were investigated by Srilatha et al. [6]. They used methanol as a base fluid. Also, they found that the heat transmission rate in the dust phase improves more quickly than in the fluid phase when the Eckert number rises. The flow of ethylene glycol-based CNTs on a stretchable rotating disk with CCHF (Cattaneo–Christov heat flux) theory was mathematically modeled by Tulu and Ibrahim [7]. Their results clearly show that the MWCNTs have higher radial velocity than the SWCNTs when varying the NPVF values. Khan et al. [8] made an effort that addresses the influence of 3D DFF (Darcy–Forchheimer flow) of micropolar nanofluid suspended with CNTs in H 2 O . They have seen that the velocity profile exhibits dual conduct as the nanofluid volume fraction rises. Alsagri et al. [9] presented the attributes of heat transportation in human blood-based CNTs over a cylinder. It is noteworthy to note that rising levels of NPVF develop the fluid velocity profile. Wang et al. [10] looked at the flow of CNTs in a porous region with Newtonian heating. They have seen that the rising temperature shift in blood-SWCNTs is more significant than in blood-MWCNTs. The DFF feature of micropoler CNT nanofluid flow in a rotating frame was examined by Alzahrani et al. [11]. They detected that the larger quantity of NPVF leads to a higher thermal profile.

Due to its applicability in several technical and physical processes, the study of nonlinear thermal radiative flow over a plate is an area of prospective interest for scientists and engineers. Some areas that might benefit from such techniques include atomic power, space technology, combustion, furnace design, photochemical reactors, propulsion devices, etc. Jawad et al. [12] employed a homotopy analysis method (HAM) approach to address a 3D CNT flow in a permeable medium with nonlinear thermal radiation. It should be noted that larger radiation values improve the heat transfer rate. The nonlinear thermal radiation impact of 3D Jeffrey nanofluid with viscous dissipation and Joule heating was inspected by Kumar et al. [13]. They deduced that the temperature ratio parameter minimizes the mass transport rate. Some of the rheological aspects of the flow of CNTs in ethylene glycol with nonlinear thermal radiation were looked at by Ramzan et al. [14]. Their results clearly show that the SWCNTs have a higher heat transfer rate compared to the MWCNTs for changing the radiation values. The mathematical model of nonlinear radiative flow of hybrid nanofluid on a wedge was developed by Rana et al. [15]. They made the discovery that the rate of heat transfer for nonlinear thermal radiation is larger in comparison to linear thermal radiation. Mahabaleshwar et al. [16] looked into the radiative characteristics of CNT flow subject to the heat source/sink past a stretching/shrinking sheet. They achieved that the water-SWCNTs have a momentum profile that is noticeably greater than that of the water-MWCNTs. The nonlinear radiative flow of Casson nanofluid past an SS was investigated by Satya Narayana et al. [17]. Mabood et al. [18] investigated how the motion of a water-based hybrid nanofluid (WBHNF) ( Cu + Al 2 O 3 ) that flows over a stretched surface is affected by the motion of MHD flow and the transfer of heat inside a boundary layer flow. They noted that the larger radiation parameter creates a thicker thermal layer. The non-linear radiative flow of Casson HNF past a rotating disk was examined by Mohanty et al. [19]. They uncovered that the temperature ratio parameter develops the heat transfer rate. Nayak et al. [20] scrutinized the flow of HNF with nonlinear radiation. They saw that a higher Bejan number was observed in HNF than in the nanofluid.

The study of boundary layer flow with convective heating plays a necessary role in many industrial processes, such as heat exchangers, drying metal, atomic power, etc. The EMHD flow of nanofluid via a heated Riga plate according to the passive control approach was theoretically explored by Rasool et al. [21]. The authors observed that a large improvement in the wall heat transit rate may be effectively obtained by modifying the convective heating process appropriately. Shah et al. [22] look at how thermophoresis particle deposition affects the flow characteristics of a second-grade fluid with a convective boundary condition. The consequences of MHD NFF past a heated spinning disc were explored by Wakif and Shah [23]. They declared that the convective heating accelerates the thermophoresis process. Dawar et al. [24] performed the theoretical analysis of the 3D MHD flow of Jeffrey nanofluid on a dual SS with velocity slip circumstances. The authors found that the Biot number leads to the development of the thermal profile. The hydrothermal features of non-Darcian flow of water-based alumina nanofluid past a Riga plate were quantitatively assessed by Rasool et al. [25]. Their results clearly explain that the loading of nanoparticles and convection heating speed up the rate of surface heat transfer. Rashid et al. [26] looked into the thermal energy transfer of a WBHNF flow on a heated SS with activation energy. They also mentioned that the fluid temperature enhances when increasing the Biot number.

Prior to conducting the aforementioned literature research, the authors are confident that no study of a WBHNF containing SWCNTs and MWCNTs across a Riga plate under convective condition has been conducted. Therefore, the authors have looked into the nonlinear radiative DFF of a WBHNF containing both SWCNTs and MWCNTs past the heated Riga plate. The combination of two nanoparticles with a base fluid is referred to as a hybrid nanofluid. The exceptional efficiency in transferring heat and the enhanced ability to transmit thermal energy of these fluids have attracted several researchers in the area of nanotechnology. Hybrid nanofluids are a modern kind of nanofluid that have a wide range of uses in heat transfer in several sectors, including vehicle radiators, cooling electronic devices, energy generation, drug delivery, and biomedicine. Also, the DFF plays an important role in tissue transformation, thermal insulation, geothermal reservoirs, and petroleum reservoirs, see Chamkha [27,28].

After we have finished our investigation, we provide the responses to the following inquiries for further research:

What are the impacts of embedded variables on flow profile such as modified Hartmann–Forchheimer numbers, Casson, porosity, unsteady, and slip parameters?
Which of the two base fluids (water and glycerin) forecasts a higher temperature and a lower temperature?
How does convective heating affect the temperature of CNTs flowing over a Riga plate?
Which of the two fluids (viscous and Casson) predicts a greater and smaller skin friction coefficient (SFC), and heat transfer gradient (HTG)?

2 Mathematical formulation

Consider the time-varying DFF of hybrid CNTs (HCNTs) through a Riga plate. The notations u and v stand for the x- and y-component velocity factors, respectively. The nonlinear radiation in the context of the energy expression is obtained by using the nonlinear Rosseland approximation theory. Additionally, T ∞ and T w are used to represent the free stream temperature and plate temperature, respectively. The bottom of the plate is heated with a hot fluid of temperature T f and this creates a heat transfer coefficient h c (Figure 1). The mathematical modeling of continuity, momentum, and energy expressions is described in the following form (see Hayat et al. [29] and Jamshed et al. [30]):

(1) ∂ u ∂ x + ∂ v ∂ y = 0 ,

(2) ∂ u ∂ t + u ∂ u ∂ x + v ∂ u ∂ y = μ h n f ρ h n f 1 + 1 β ∂ 2 u ∂ y 2 − μ h n f ρ h n f k 1 * u − c b x k 1 * u 2 + π J 0 M 0 8 ρ h n f Exp − π a 1 y ,

(3) ∂ T ∂ t + u ∂ T ∂ x + v ∂ T ∂ y = k h n f ( ρ C p ) h n f ∂ 2 T ∂ y 2 + 16 σ * 3 k * ( ρ C p ) h n f ∂ ∂ y × T 3 ∂ T ∂ y + Q ( ρ C p ) h n f ( T − T ∞ ) + 1 + 1 β μ h n f ( ρ C p ) h n f ∂ u ∂ y 2 .

Figure 1

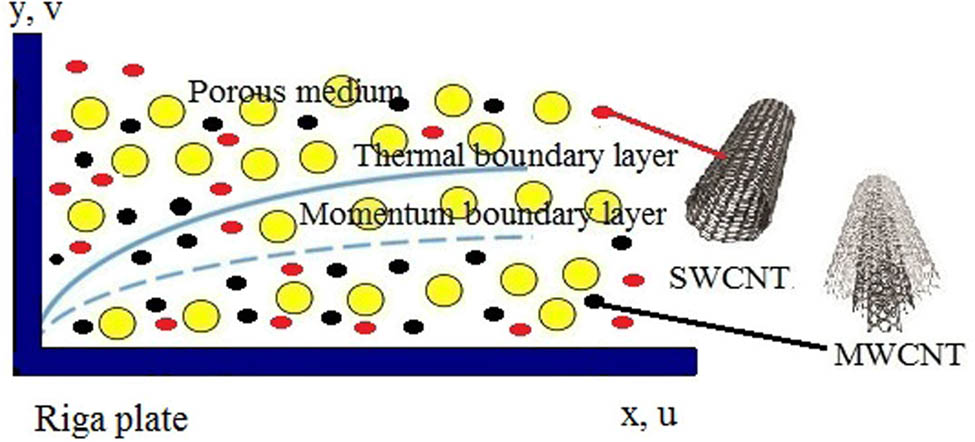
Physical sketch of the model.

The boundary conditions are as follows:

(4) u = a x 1 − ε t + μ h n f L 1 + 1 β ∂ u ∂ y ; v = 0 − k h n f ∂ T ∂ y = h c [ T f − T ] at y = 0 ,

(5) u → 0 , v → 0 , T → T ∞ as y → ∞ .

Define, see Mahmood et al. [31] and Madhu et al. [32],

(6) ℧ = a ν f ( 1 − ε t ) y ; u = a x 1 − ε t ℱ ′ ( ℧ ) ; v = a ν f ( 1 − ε t ) ℱ ( ℧ ) ; ℋ = T − T ∞ T f − T ∞ .

The Equations (2)–(3) becomes

(7) A 1 A 2 1 + 1 β ℱ ‴ ( ℧ ) + ℱ ( ℧ ) ℱ ″ ( ℧ ) − ℱ ′ 2 ( ℧ ) − A ℱ ′ ( ℧ ) + ℧ 2 ℱ ″ ( ℧ ) − A 1 A 2 λ ℱ ′ ( ℧ ) − Fr ℱ ′ 2 ( ℧ ) + A 2 Ha Exp ( − β R ℧ ) = 0 ,

(8) A 3 A 4 Pr ℋ ″ ( ℧ ) + ℱ ( ℧ ) ℋ ′ ( ℧ ) − ℋ ( ℧ ) ℱ ′ ( ℧ ) − A ℋ ( ℧ ) + ℧ 2 ℋ ′ ( ℧ ) + A 1 A 2 E c 1 + 1 β ℱ ″ 2 ( ℧ ) + A 4 Pr 4 R 3 [ ( Λ − 1 ) 3 [ 3 ℋ 2 ( ℧ ) ℋ ′ 2 ( ℧ ) + ℋ 3 ( ℧ ) ℋ ″ ( ℧ ) ] + ( Λ − 1 ) 2 [ 6 ℋ ( ℧ ) ℋ ′ 2 ( ℧ ) + 3 ℋ 2 ( ℧ ) ℋ ″ ( ℧ ) ] + ( Λ − 1 ) [ 3 ℋ ′ 2 ( ℧ ) + 3 ℋ ( ℧ ) ℋ ″ ( ℧ ) ] + ℋ ″ ( ℧ ) ] + A 4 H g ℋ ( ℧ ) = 0 .

Boundary condition are as follows:

(9) ℱ ( 0 ) = 0 , ℱ ′ ( 0 ) = 1 + A 1 1 + 1 β K 1 ℱ ″ ( 0 ) , ℱ ′ ( ∞ ) = 0 , ℋ ′ ( 0 ) = − Bi A 3 ( 1 − ℋ ( 0 ) ) , ℋ ( ∞ ) = 0 .

Here

A 1 = μ h n f μ f , where μ h n f μ f = 1 ( 1 − ϕ 1 ) 2.5 ( 1 − ϕ 2 ) 2.5 , A 2 = ρ f ρ h n f , where ρ h n f ρ f = ( 1 − ϕ 2 ) ( 1 − ϕ 1 ) + ϕ 1 ρ MWCNTs ρ f + ϕ 2 ρ SWCNTs ρ f , A 3 = k h n f k f , where k h n f k n f = ( 1 − ϕ 2 ) + 2 ϕ 2 k SWCNTs k SWCNTs − k n f In k SWCNTs + k n f 2 k n f ( 1 − ϕ 2 ) + 2 ϕ 2 k n f k SWCNTs − k n f In k SWCNTs + k n f 2 k n f , and k n f k f = ( 1 − ϕ 1 ) + 2 ϕ 1 k MWCNTs k MWCNTs − k f In k MWCNTs + k f 2 k f ( 1 − ϕ 1 ) + 2 ϕ 1 k f k MWCNTs − k f In k MWCNTs + k f 2 k f , A 4 = ( ρ C p ) f ( ρ C p ) h n f , where ( ρ C p ) h n f ( ρ C p ) f = ( 1 − ϕ 2 ) ( 1 − ϕ 1 ) + ϕ 1 ( ρ C p ) MWCNTs ( ρ C p ) f + ϕ 2 ( ρ C p ) SWCNTs ( ρ C p ) f .

3 Quantities of physical interest

3.1 Skin friction coefficient (SFC)

The mathematical expression of skin friction can be defined as

C ℱ = τ x y ρ h n f U w 2 .

The wall shear stress ( τ x y ) is written as

τ x y = μ h n f 1 + 1 β ∂ u ∂ y y=0 .

The dimensionless form of SFC is defined as

C ℱ Re = A 1 1 + 1 β ℱ ″ ( 0 ) .

3.2 Local Nusselt number (LNN)

The mathematical expression of the LNN can be defined as

Nu = x q w k h n f ( T f − T ∞ ) .

The wall heat flux q w is defined as

q w = − k h n f ∂ T ∂ y + 16 σ * 3 k * ( ρ C p ) h n f ∂ ∂ y T 3 ∂ T ∂ y y = 0 .

The dimensionless form of LNN is defined as

Nu Re = − A 3 + 4 3 R { 1 + ( Λ − 1 ) ℋ ( 0 ) } 3 ℋ ′ ( 0 ) .

4 Methodology

4.1 Analytical method

The analytical computation of the reduced mathematical expressions (7)–(8) and their boundary constraints (9) is made by using the HAM scheme. This method is a semi-analytical one, and it is a quite helpful tool for effectively solving nonlinear ordinary differential equations (ODEs) and partial differential equations. The technique provides a considerable deal of freedom in the representation of series-form solutions in terms of a wide variety of base functions and linear operators for the purpose of constructing solutions, see Loganathan et al. [33].

Initial approximations:

ℱ 0 ( ℧ ) = 1 + 1 β 1 1 + K 1 A 1 1 − 1 Exp ( ℧ ) ; ℋ 0 ( ℧ ) = Bi ( A 3 + B i ) Exp ( ℧ ) .

Linear operators:

L ℱ = ℱ ‴ − ℱ ′ ; L ℋ = ℋ ″ − ℋ .

Linear properties:

L ℱ ψ 1 + ψ 2 Exp ( ℧ ) + ψ 3 1 Exp ( ℧ ) = 0 = L ℋ ψ 4 Exp ( ℧ ) + ψ 5 1 Exp ( ℧ ) ,

where ψ i ; i = 1 , 2 , … , 5 are constants.

Zeroth-order deformation problems:

( 1 − q ) L ℱ [ ℱ ( ℧ , q ) − ℱ 0 ( ℧ ) ] = q h ℱ R 1 [ ℱ ( ℧ , q ) ] , ( 1 − q ) L ℋ [ ℋ ( ℧ , q ) − ℋ 0 ( ℧ ) ] = p h ℋ R 2 [ ℱ ( ℧ , q ) , ℋ ( ℧ , q ) ] .

Here q ∈ [ 0 , 1 ] is an embedding parameter and R 1 and R 2 are non-linear operators.

The n th order problems:

ℱ n ( ℧ ) = ℱ n * ( ℧ ) + ψ 1 + ψ 2 Exp ( ℧ ) + ψ 3 1 Exp ( ℧ ) ; ℋ n ( ℧ ) = ℋ n * ( ℧ ) + ψ 4 Exp ( ℧ ) + ψ 5 1 Exp ( ℧ ) .

Here ℱ n * ( ℧ ) and ℋ n * ( ℧ ) are the particular solutions.

The HAM parameters ( h ℱ and h ℋ ) are the responsible parameters for the solution’s convergency, see Prabakaran et al. [34] and Naresh Kumar et al. [35]. The ambit of h ℱ is [ − 0.75 , − 0.35 ] (Water), [ − 0.75 , − 0.2 ] (Glycerin), and h ℋ is [ − 2.2 , − 0.4 ] (Water), [ − 2.3 , − 0.4 ] (Glycerin) (Figure 2(a) and (b)).

$Figure 2 h h -curves of (a) ℱ ″ ( 0 ) {{\mathcal{ {\mathcal F} }}}^{^{\prime\prime} }\left(0) and (b) ℋ ′ ( 0 ) {\mathcal{ {\mathcal H} }}^{\prime} \left(0) for both base fluids.$

Figure 2

h -curves of (a) ℱ ″ ( 0 ) and (b) ℋ ′ ( 0 ) for both base fluids.

4.2 Numerical method

The numerical computation of transferred nonlinear ODEs (7)–(8) with boundary restrictions (9) is made possible by using the MATLAB bvp4c solution technique. In the current situation, the first thing that we do is transform the system of higher ODEs into a system of first-order differential equations, see Eswaramoorthi et al. [36] and see Sahu et al. [37]. The convergence criteria were decided to be a difference of 1 0 − 5 .

Let us take

ℱ = s 1 , ℱ ′ = s 2 , ℱ ″ = s 3 , ℱ ′ ′ ′ = s 3 ′ , ℋ = s 4 , ℋ ′ = s 5 , ℋ ″ = s 5 ′ .

s 1 ′ = s 2 , s 2 ′ = s 3 , s 3 ′ = s 2 2 − s 1 s 3 + A [ s 2 + ℧ 2 s 3 ] + λ A 1 A 2 s 2 + Fr ( s 2 ) 2 − A 2 Ha Exp ( − β R ℧ ) A 1 A 2 ( 1 + 1 β ) , s 4 ′ = s 5 , s 5 ′ = D 1 D 2 , where D 1 = − s 1 s 5 + s 2 s 4 + A s 4 + ℧ 2 s 5 − A 1 A 2 Ec 1 + 1 β ( s 3 ) 2 − A 4 Pr 4 R 3 [ [ Λ − 1 ] 3 ( 3 s 4 2 s 5 2 ) + [ Λ − 1 ] 2 6 s 4 s 5 2 + [ Λ − 1 ] ( 3 s 5 2 ) ] − A 4 H g s 4 and D 2 = A 3 A 4 Pr + A 4 Pr 4 R 3 [ [ Λ − 1 ] 3 ( s 4 ) 3 + [ Λ − 1 ] 2 3 ( s 4 ) 2 + [ Λ − 1 ] ( 3 s 4 ) + 1 ] .

with the conditions

s 1 ( 0 ) = 0 , s 2 ( 0 ) = 1 + K 1 A 1 1 + 1 β s 3 ( 0 ) , s 2 ( ∞ ) = 0 , s 5 ( 0 ) = − B i A 3 [ 1 − s 4 ( 0 ) ] , s 4 ( ∞ ) = 0 .

5 Result and discussions

This section illustrates the physical interference of results after the problem is successfully computed using an analytical and numerical approaches. The physical characteristics of SWCNTs, MWCNTs, glycerin, and water are provided in Table 1. Table 2 gives the HAM order of approximations and numerical solution. It is clear from this table that 15th order is enough for all computations, and it is also seen that our HAM and numerical solution are almost the same. Comparison of − ℱ ″ ( 0 ) with A = Fr = ϕ 1 = ϕ 2 = Ha = K 1 = 0 , and β = ∞ for various values of λ to Akbara et al. [38] is tabulated in Table 3, and it is concluded that our computational results are almost the same as Akbara et al. [38].

Table 1

Physical properties

Physical characteristics	SWCNTs	MWCNTs	Glycerin	Water
k (W/m K)	6,600	3,000	0.286	0.613
ρ ( kg/m 3 )	2,600	1,600	1259.9	997.1
C p (J/kg K)	425	796	2,427	4,179
Pr	—	—	6.78	6.2

Table 2

HAM order of approximations and numerical solution

	W-CHCNTs		G-CHCNTs		W-VHCNTs		G-VHCNTs
Order	‒ ℱ ″ ( 0 )	‒ ℋ ′ ( 0 )	‒ ℱ ″ ( 0 )	‒ ℋ ′ ( 0 )	‒ ℱ ″ ( 0 )	‒ ℋ ′ ( 0 )	‒ ℱ ″ ( 0 )	‒ ℋ ′ ( 0 )
HAM
1	0.304376	0.235875	0.312055	0.227445	0.552727	0.241729	0.555362	0.232897
5	0.293273	0.241622	0.291654	0.233159	0.527721	0.242044	0.524919	0.233406
10	0.293201	0.241823	0.291830	0.233258	0.527796	0.242058	0.524718	0.233437
15	0.293203	0.241823	0.291827	0.233259	0.527795	0.242058	0.524722	0.233437
20	0.293203	0.241823	0.291827	0.233259	0.527795	0.242058	0.524722	0.233437
25	0.293203	0.241823	0.291827	0.233259	0.527795	0.242058	0.524722	0.233437
30	0.293203	0.241823	0.291827	0.233259	0.527795	0.242058	0.524722	0.233437
Numerical solution
—	0.293202	0.241823	0.291826	0.233259	0.527794	0.242058	0.524721	0.233438

Table 3

Comparison of ‒ ℱ ″ ( 0 ) with A = Fr = ϕ 1 = ϕ 2 = Ha = K 1 = 0 , and β = ∞ for various values of λ to Akbara et al. [38]

λ	Present study	Ref. [38]
0	1.000000	1.0000
1	1.414214	1.4132
5	2.449490	2.4485
10	3.316625	3.3165
100	10.049876	10.0498
500	22.383029	22.3831
1,000	31.638584	31.6385

Figure 3(a)–(d) is constructed to analyze the consequences of A (a), Fr (b), Ha (c), and λ (d) on velocity profile for water (solid line) and glycerin (dashed line)-based HCNTs. These graphs show that the fluid velocity elevates when mounting the size of modified Hartmann number, and it slumps for a larger quantity of the unsteady parameter, the Forchheimer number, and the porosity parameter. Physically, a larger porosity property results in greater friction and more particle interactions, which slows the flow of fluid. The modified Hartann number creates more external electric field and helps enrich the fluid speed. The behavioral change of thermal profile for different amounts of R (a,b) and Ec (c,d) with convective heating (a,c) and cooling (b,d) for water (solid line) and glycerin (dashed line)-based HCNTs is interrogated in Figure 4(a)–(d). It is noteworthy to note that the thermal profile escalates when heightening the radiation parameter in the heating case, and the cooling case behaves in the opposite direction. The rate of heat energy transfer to the fluid accelerates by enhancing the radiation parameter and thereby increasing the fluid temperature. Also, it seems that a higher assessment of the Eckert number is responsible for the TBL thickening in both cases. Figure 5(a)–(d) reports the behavior of NPVF in the thermal profile for convective heating and cooling in water (solid line) and glycerin (dashed line)-based HCNTs. It is noted from these figures that the fluid warmness depresses near the plate and improves away from the plate when varying the size of NPVF in the heating case. Also, it is seen that the mono CNTs have a higher thermal profile near the plate, and away from the plate, they have a lesser thermal profile. The quite opposite trend is attained in the cooling case.

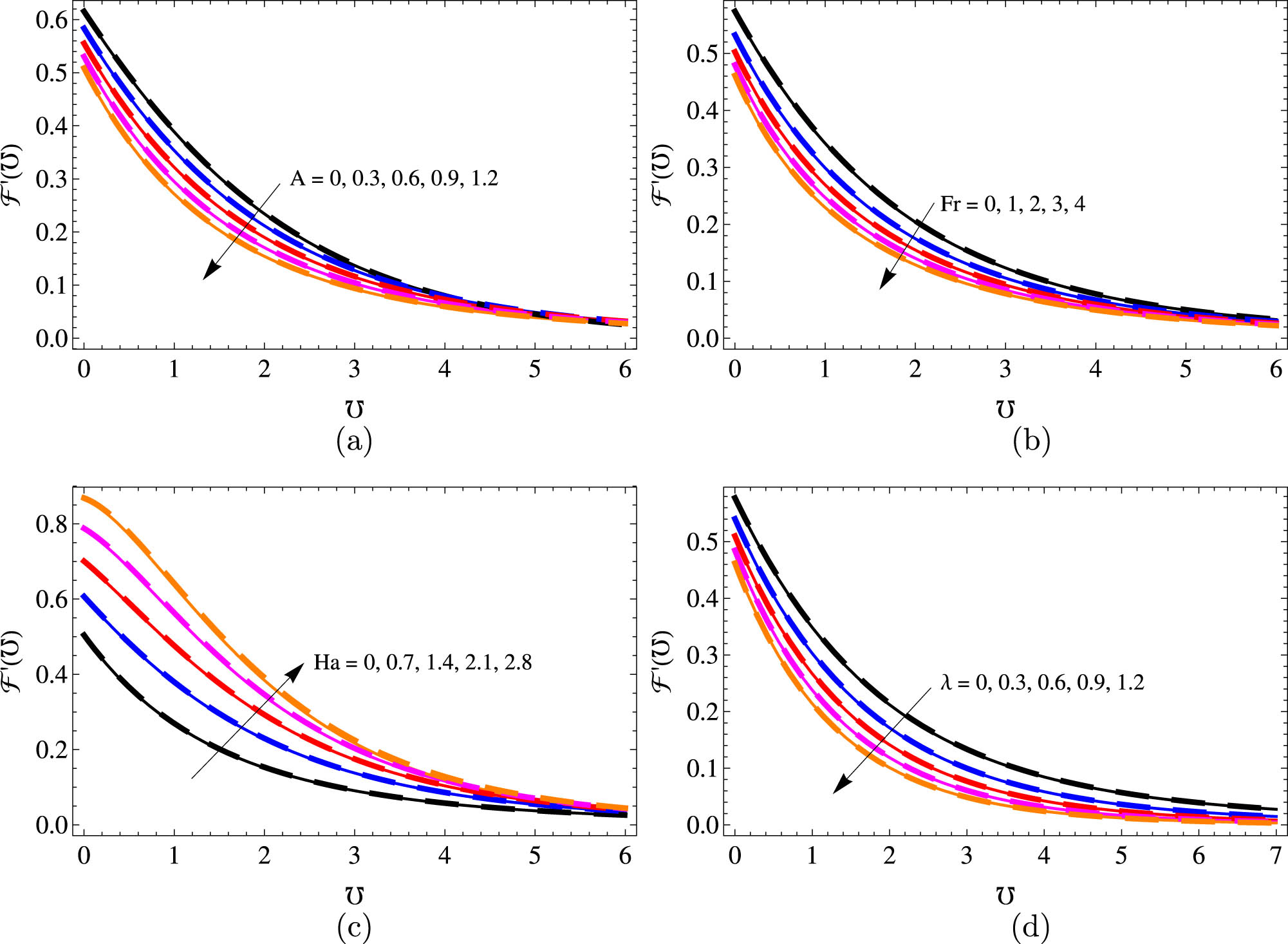
$Figure 3 The velocity profile for distinct quantities of A \hspace{0.1em}\text{A}\hspace{0.1em} (a), Fr \hspace{0.1em}\text{Fr}\hspace{0.1em} (b), Ha \hspace{0.1em}\text{Ha}\hspace{0.1em} (c), and λ \lambda (d) for water (solid line) and glycerin (dashed line)-based HCNTs.$

Figure 3

The velocity profile for distinct quantities of A (a), Fr (b), Ha (c), and λ (d) for water (solid line) and glycerin (dashed line)-based HCNTs.

$Figure 4 The thermal profile for distinct quantities of R R (a and b) and Ec \hspace{0.1em}\text{Ec}\hspace{0.1em} (c and d) with convective heating (a and c) and cooling (b and d) for water (solid line) and glycerin (dashed line)-based HCNTs.$

Figure 4

The thermal profile for distinct quantities of R (a and b) and Ec (c and d) with convective heating (a and c) and cooling (b and d) for water (solid line) and glycerin (dashed line)-based HCNTs.

$Figure 5 The thermal profile for distinct quantities of ϕ 1 {\phi }_{1} (a,b) and ϕ 2 {\phi }_{2} (c,d) with convective heating (a,c) and cooling (b,d) for water (solid line) and glycerin (dashed line)-based HCNTs.$

Figure 5

The thermal profile for distinct quantities of ϕ 1 (a,b) and ϕ 2 (c,d) with convective heating (a,c) and cooling (b,d) for water (solid line) and glycerin (dashed line)-based HCNTs.

The thermal profile for distinct quantities of Hg for water-based HCNTs (a,c) and glycerin-based HCNTs (b,d) with convective heating (a,b) and cooling was displayed in Figure 6(a)–(d) via contour graphs. Figure 7(a) and (b) clearly show the changes of SFC for distinct quantities of ( A and λ ) (a), ( Fr and Ha ) (b), ( λ and Fr ) (c), and ( A and Ha ) (d) for water (solid line) and glycerin (dashed line) based HCNTs. It is important to note that higher sizes of Ha cause improved surface shear stress, while A , λ , and Fr decay the surface shear stress. The variations of LNN for distinct quantities of ( A and λ ) (a), ( λ and Fr ) (b), ( A and Ha ) (c), and ( Λ and Hg ) for water (solid line) and glycerin (dashed line)-based HCNTs are illustrated in Figure 8(a)–(d). It is important to note that the higher HTG (heat transfer gradient) is caused by higher values of A , Ha , and Λ . The LNN decays when heightening the size of λ , Fr , and Hg . Figure 9(a)–(d) explains the changes of LNN for distinct quantities of ( Hg and R ) in water-based HCNTs (a) and glycerin-based HCNTs (b) and ( R and Λ ) in water-based HCNTs (c) and glycerin-based HCNTs (d) via contour graphs.

$Figure 6 The thermal profile for distinct quantities of Hg \hspace{0.1em}\text{Hg}\hspace{0.1em} for water-based HCNTs (a and c) and glycerin-based HCNTs (b and d) with convective heating (a and b) and cooling (c and d) cases.$

Figure 6

The thermal profile for distinct quantities of Hg for water-based HCNTs (a and c) and glycerin-based HCNTs (b and d) with convective heating (a and b) and cooling (c and d) cases.

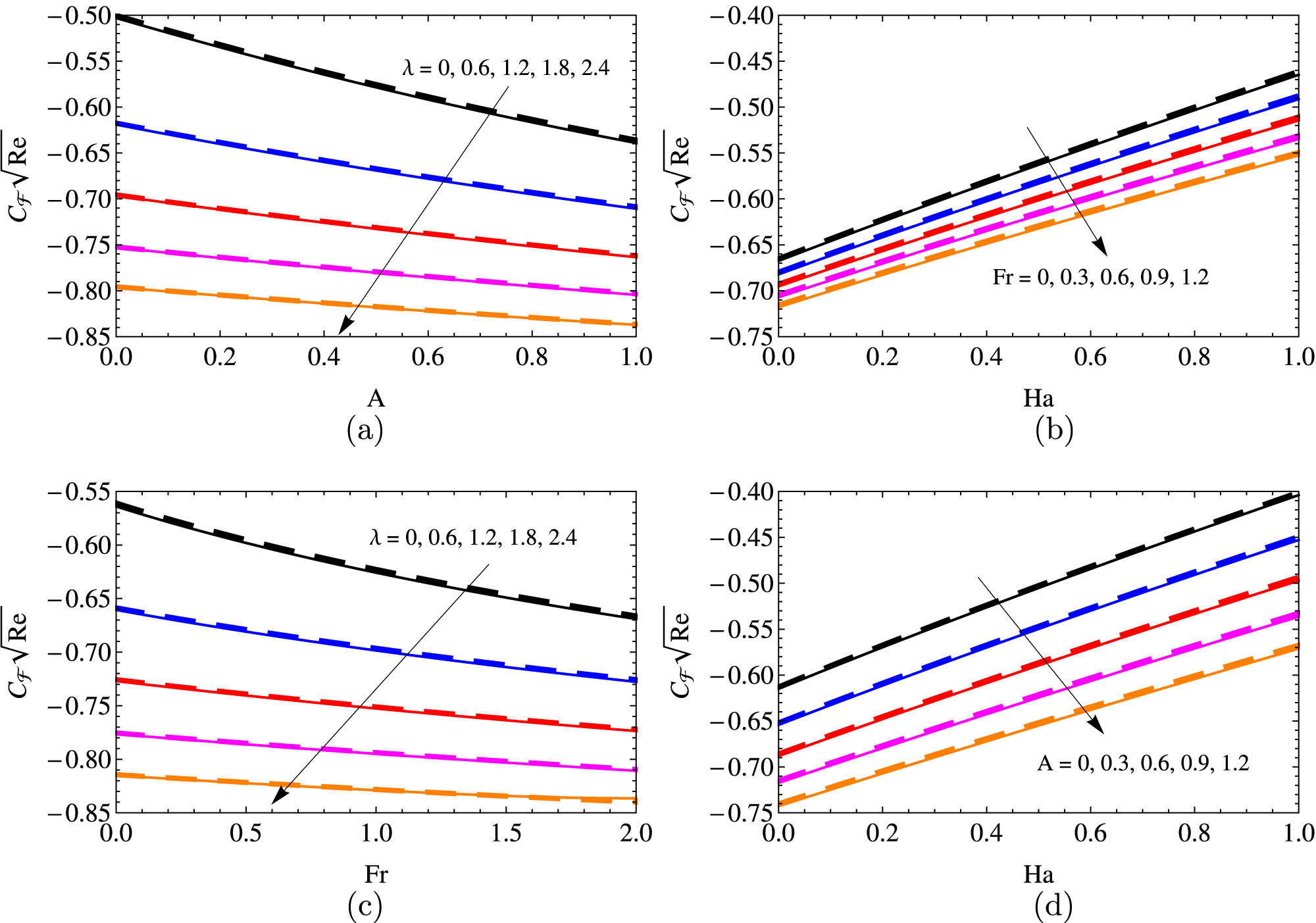
$Figure 7 The SFC for distinct quantities of (A and λ \lambda ) (a), (Fr and Ha) (b), ( λ \lambda and Fr) (c), and (A and Ha) (d) for water (solid line) and glycerin (dashed line) based HCNTs.$

Figure 7

The SFC for distinct quantities of (A and λ ) (a), (Fr and Ha) (b), ( λ and Fr) (c), and (A and Ha) (d) for water (solid line) and glycerin (dashed line) based HCNTs.

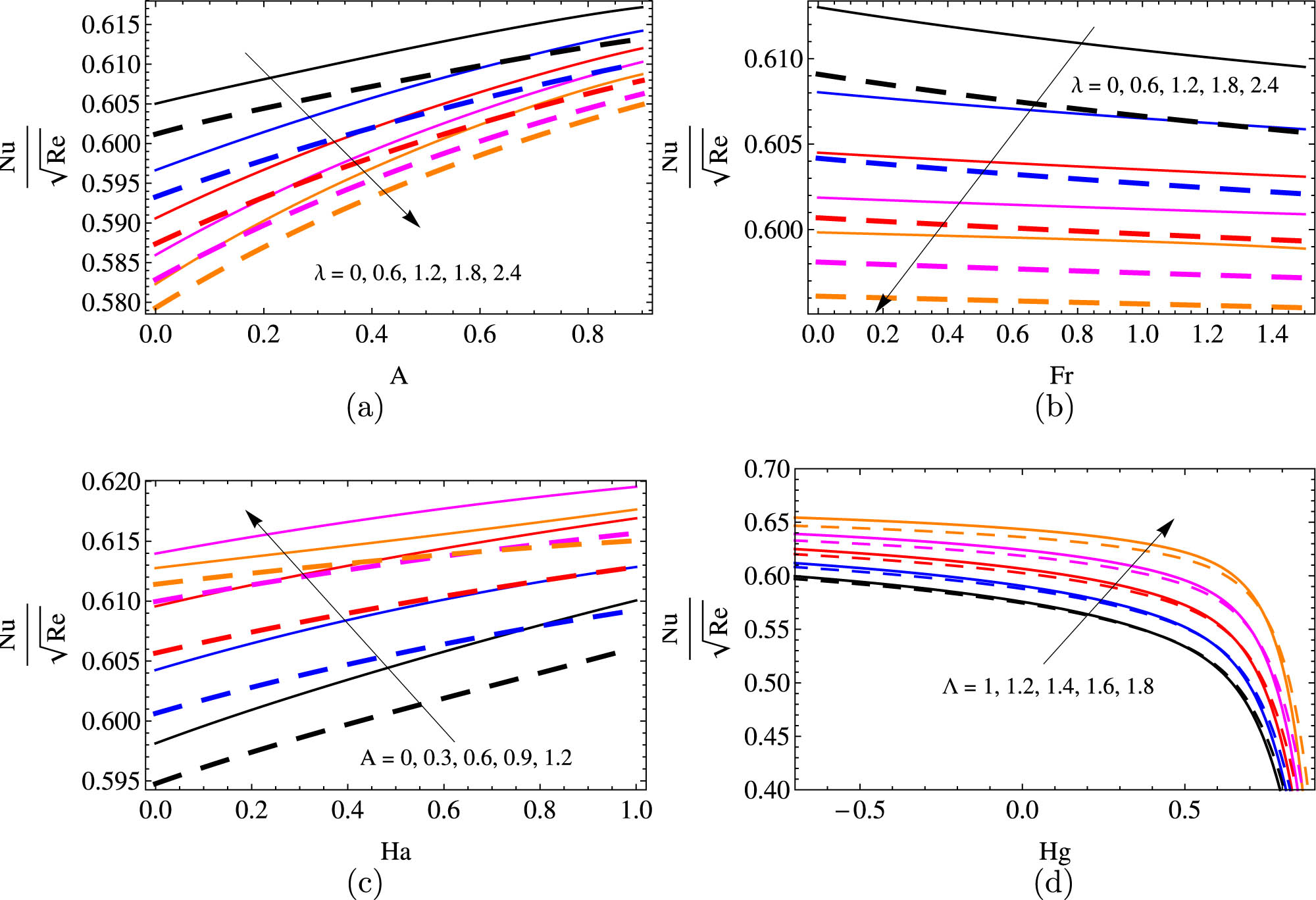
$Figure 8 The LNN for distinct quantities of (A and λ \lambda ) (a), ( λ \lambda and Fr) (b), (A and Ha) (c), and ( Λ \Lambda and Hg) (d) for water (solid line) and glycerin (dashed line) based HCNTs.$

Figure 8

The LNN for distinct quantities of (A and λ ) (a), ( λ and Fr) (b), (A and Ha) (c), and ( Λ and Hg) (d) for water (solid line) and glycerin (dashed line) based HCNTs.

$Figure 9 The LNN for distinct quantities of (Hg and R) in water-based HCNTs (a), and glycerin-based HCNTs (b), and (R and Λ \Lambda ) in water-based HCNTs (c), and glycerin-based HCNTs (d).$

Figure 9

The LNN for distinct quantities of (Hg and R) in water-based HCNTs (a), and glycerin-based HCNTs (b), and (R and Λ ) in water-based HCNTs (c), and glycerin-based HCNTs (d).

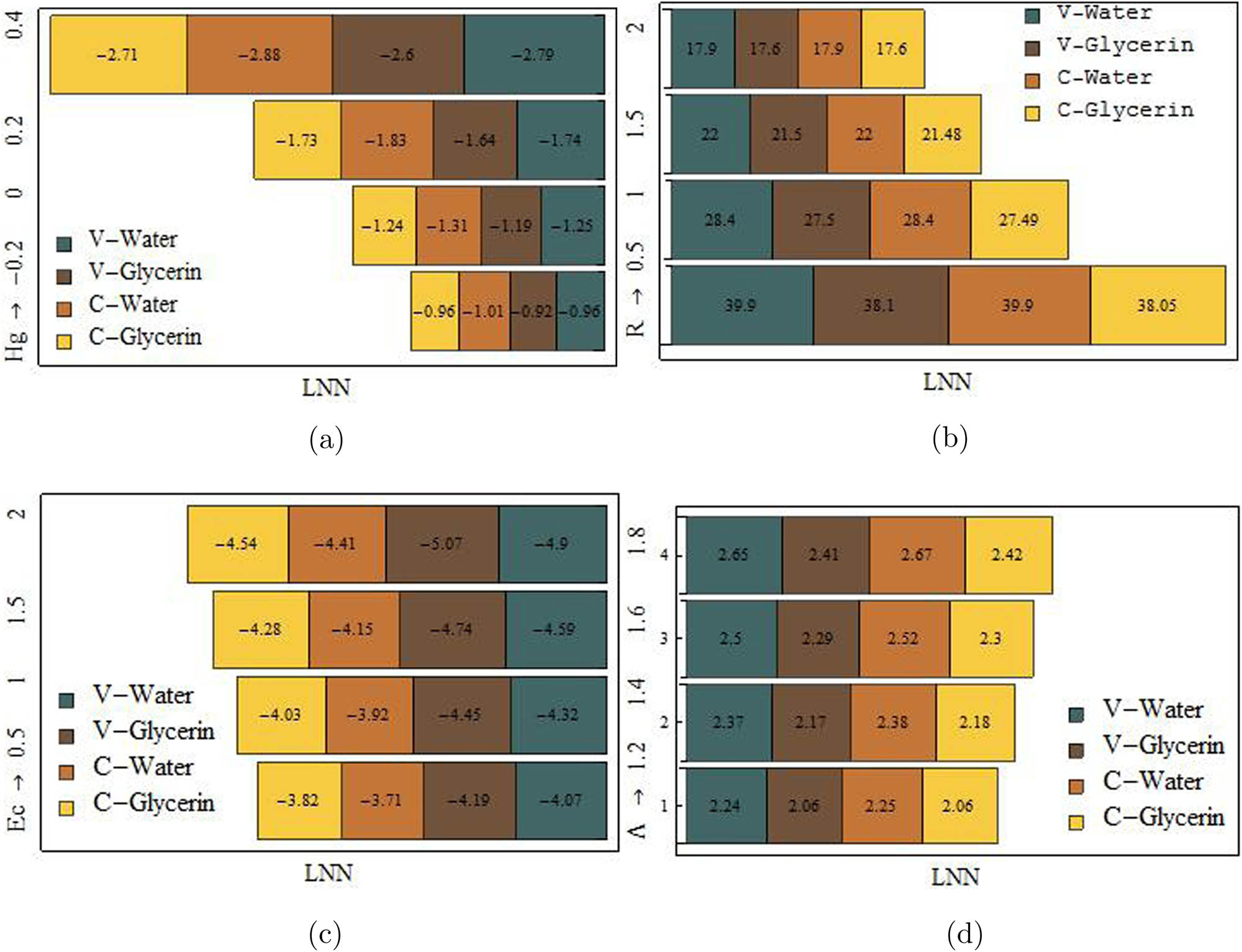
Figure 10(a)–(d) is taken to analyze the fluctuating percentage of λ , Fr , Ha , and K 1 for water/glycerin-based viscous HCNTs and Casson HCNTs. For λ variations in water-based viscous HCNTs, the least downturn percentage (5.7) is found when λ goes from 1.5 to 2, and the greater downturn percentage (15.5) is found when λ goes from 0 to 0.5. In glycerin-based viscous HCNTs, the least downturn percentage (5.8) is found when λ goes from 1.5 to 2, and the greater downturn percentage (15.8) is found when λ goes from 0 to 0.5. In water-based Casson HCNTs, the least downturn percentage (4.7) is found when λ goes from 1.5 to 2, and the greater downturn percentage (13.4) is found when λ goes from 0 to 0.5. In glycerin-based Casson HCNTs, the least downturn percentage (4.8) is found when λ goes from 1.5 to 2, and the greater downturn percentage (13.7) is found when λ goes from 0 to 0.5. For Fr variations in water-based viscous HCNTs, the least downturn percentage (3.6) is found when Fr goes from 1.5 to 2, and the greater downturn percentage (7) is found when Fr goes from 0 to 0.5. In glycerin-based viscous HCNTs, the least downturn percentage (3.7) is found when Fr goes from 1.5 to 2, and the greater downturn percentage (7.1) is found when Fr goes from 0 to 0.5. In water-based Casson HCNTs, the least downturn percentage (2) is found when Fr goes from 1.5 to 2, and the greater downturn percentage (5.3) is found when Fr goes from 0 to 0.5. In glycerin-based Casson HCNTs, the least downturn percentage (2.8) is found when Fr goes from 1.5 to 2, and the greater downturn percentage (5.3) is found when Fr goes from 0 to 0.5. For Ha variations in water-based viscous HCNTs, the least ascent percentage (17.6) is found when Ha goes from 0 to 0.5 and the greater ascent percentage (29), which is found when Ha goes from 1.5 to 2. In glycerin-based viscous HCNTs, the least ascent percentage (17.8) is found when Ha goes from 0 to 0.5, and the greater ascent percentage (29.6) is found when Ha goes from 1.5 to 2. In water-based Casson HCNTs, the least ascent percentage (14.9) is found when Ha goes from 0 to 0.5, and the greater ascent percentage (21.4) is found when Ha goes from 1.5 to 2. In glycerin-based Casson HCNTs, the least ascent percentage (15) is found when Ha goes from 0 to 0.5, and the greater ascent percentage (21.7) is found when Ha goes from 1.5 to 2. For K 1 variations in water-based viscous HCNTs, the least ascent percentage (18.4) is found when K 1 goes from 1.5 to 2, and the greater ascent percentage (46.4) is found when K 1 goes from 0 to 0.5. In glycerin-based viscous HCNTs, the least ascent percentage (18.4) is found when K 1 goes from 1.5 to 2, and the greater ascent percentage (46.2) is found when K 1 goes from 0 to 0.5. In water-based Casson HCNTs, the least ascent percentage (19.9) is found when K 1 goes from 1.5 to 2, and the greater ascent percentage (54.9) is found when K 1 goes from 0 to 0.5. In glycerin-based Casson HCNTs, the least ascent percentage (19.9) is found when K 1 goes from 1.5 to 2, and the greater ascent percentage (55.7) is found when K 1 goes from 0 to 0.5.

$Figure 10 The increment/decrement percentage of SFC for variations of λ \lambda (a), Fr (b), Ha (c), and K 1 {K}_{1} (d) for viscous HCNTs and Casson HCNTs.$

Figure 10

The increment/decrement percentage of SFC for variations of λ (a), Fr (b), Ha (c), and K 1 (d) for viscous HCNTs and Casson HCNTs.

The fluctuating percentage of LNN for various values of λ , Fr , Ha , and A for water/glycerin-based viscous HCNTs and Casson HCNTs is shown in Figure 11(a)–(d). For λ variations in water-based viscous HCNTs, the least downturn percentage (0.37) is found when λ goes from 1.5 to 2, and the greater downturn percentage (0.71) is found when λ goes from 0 to 0.5. In glycerin-based viscous HCNTs, the least downturn percentage (0.37) is found when λ goes from 1.5 to 2, and the greater downturn percentage (0.71) is found when λ goes from 0 to 0.5. In water-based Casson HCNTs, the least downturn percentage (0.31) is found when λ goes from 1.5 to 2, and the greater downturn percentage (0.65) is found when λ goes from 0 to 0.5. In glycerin-based Casson HCNTs, the least downturn percentage (0.31) is found when λ goes from 1.5 to 2, and the greater downturn percentage (0.65) is found when λ goes from 0 to 0.5. For Fr variations in water-based viscous HCNTs, the least downturn percentage (0.15) is found when Fr goes from 1.5 to 2, and the greater downturn percentage (0.24) is found when Fr goes from 0 to 0.5. In glycerin-based viscous HCNTs, the least downturn percentage (0.15) is found when Fr goes from 1.5 to 2, and the greater downturn percentage (0.24) is found when Fr goes from 0 to 0.5. In water-based Casson HCNTs, the least downturn percentage (0.13) is found when Fr goes from 1.5 to 2, and the greater downturn percentage (0.2) is found when Fr goes from 0 to 0.5. In glycerin-based Casson HCNTs, the least downturn percentage (0.12) is found when Fr goes from 1.5 to 2, and the greater downturn percentage (0.2) is found when Fr goes from 0 to 0.5. For Ha variations in water-based viscous HCNTs, the least ascent percentage (0.4) is found when Ha goes from 1.5 to 2, and the greater ascent percentage (0.95) is found when Ha goes from 0 to 0.5. In glycerin-based viscous HCNTs, the least ascent percentage (0.39) is found when Ha goes from 1.5 to 2, and the greater ascent percentage (0.94) is found when Ha goes from 0 to 0.5. In water-based Casson HCNTs, the least ascent percentage (0.34) is found when Ha goes from 1.5 to 2, and the greater ascent percentage (0.72) is found when Ha goes from 0 to 0.5. In glycerin-based Casson HCNTs, the least ascent percentage (0.33) is found when Ha goes from 1.5 to 2, and the greater ascent percentage (0.71) is found when Ha goes from 0 to 0.5. For A variations in water-based viscous HCNTs, the least ascent percentage (0.69) is found when A goes from 1.5 to 2, and the greater ascent percentage (1.24) is found when A goes from 0 to 0.5. In glycerin-based viscous HCNTs, the least ascent percentage (0.65) is found when A goes from 1.5 to 2, and the greater ascent percentage (1.18) is found when A goes from 0 to 0.5. In water-based Casson HCNTs, the least ascent percentage (0.73) is found when A goes from 1.5 to 2, and the greater ascent percentage (1.37) is found when A goes from 0 to 0.5. In glycerin-based Casson HCNTs, the least ascent percentage (0.69) is found when A goes from 1.5 to 2, and the greater ascent percentage (1.3) is found when A goes from 0 to 0.5. Figure 12(a)–(d) are taken to analyze the fluctuating percentages of Hg , R , Ec , and Λ for water/glycerin-based viscous HCNTs and Casson HCNTs. For Hg variations in water-based viscous HCNTs, the least downturn percentage (0.96) is found when Hg goes from − 0.4 to − 0.2 , and the greater downturn percentage (2.79) is found when Hg goes from 0.2 to 0.4. In glycerin-based viscous HCNTs, the least downturn percentage (0.92) is found when Hg goes from − 0.4 to − 0.2 , and the greater downturn percentage (2.6) is found when Hg goes from 0.2 to 0.4. In water-based Casson HCNTs, the least downturn percentage (1.01) is found when Hg goes from − 0.4 to − 0.2 , and the greater downturn percentage (2.88) is found when Hg goes from 0.2 to 0.4. In glycerin-based Casson HCNTs, the least downturn percentage (0.96) is found when Hg goes from − 0.4 to − 0.2 , and the greater downturn percentage (2.71) is found when Hg goes from 0.2 to 0.4. In water-based viscous HCNTs, the least ascent percentage (17.9) is found when R goes from 1.5 to 2, and the greater ascent percentage (39.9) is found when R goes from 0 to 0.5. In glycerin-based viscous HCNTs,the least ascent percentage (17.6) is found when R goes from 1.5 to 2, and the greater ascent percentage (38.1) is found when R goes from 0 to 0.5. In water-based Casson HCNTs, the least ascent percentage (17.9) is found when R goes from 1.5 to 2, and the greater ascent percentage (39.9) is found when R goes from 0 to 0.5. In glycerin-based Casson HCNTs, the least ascent percentage (17.6) is found when R goes from 1.5 to 2, and the greater ascent percentage (38.05) is found when R goes from 0 to 0.5. In water-based viscous HCNTs, the least downturn percentage (4.07) is found when Ec goes from 0 to 0.5, and the greater downturn percentage (4.9) is found when Ec goes from 1.5 to 2. In glycerin-based viscous HCNTs, the least downturn percentage (4.19) is found when Ec goes from 0 to 0.5, and the greater downturn percentage (5.07) is found when Ec goes from 1.5 to 2. In water-based Casson HCNTs, the least downturn percentage (3.71) is found when Ec goes from 0 to 0.5, and the greater downturn percentage (4.41) is found when Ec goes from 1.5 to 2. In glycerin-based Casson HCNTs, the least downturn percentage (3.82) is found when Ec goes from 0 to 0.5, and the greater downturn percentage (4.54) is found when Ec goes from 1.5 to 2. In water-based viscous HCNTs, the least ascent percentage (2.24) is found when Λ goes from 1 to 1.2, and the greater ascent percentage (2.65) is found when Λ goes from 1.6 to 1.8. In glycerin-based viscous HCNTs, the least ascent percentage (2.06) is found when Λ goes from 1 to 1.2, and the greater ascent percentage (2.41) is found when Λ goes from 1.6 to 1.8. In water-based Casson HCNTs, the least ascent percentage (2.25) is found when Λ goes from 1 to 1.2, and the greater ascent percentage (2.67) is found when Λ goes from 1.6 to 1.8. In glycerin-based Casson HCNTs, the least ascent percentage (2.06) is found when Λ goes from 1 to 1.2, and the greater ascent percentage (2.42) is found when Λ goes from 1.6 to 1.8.

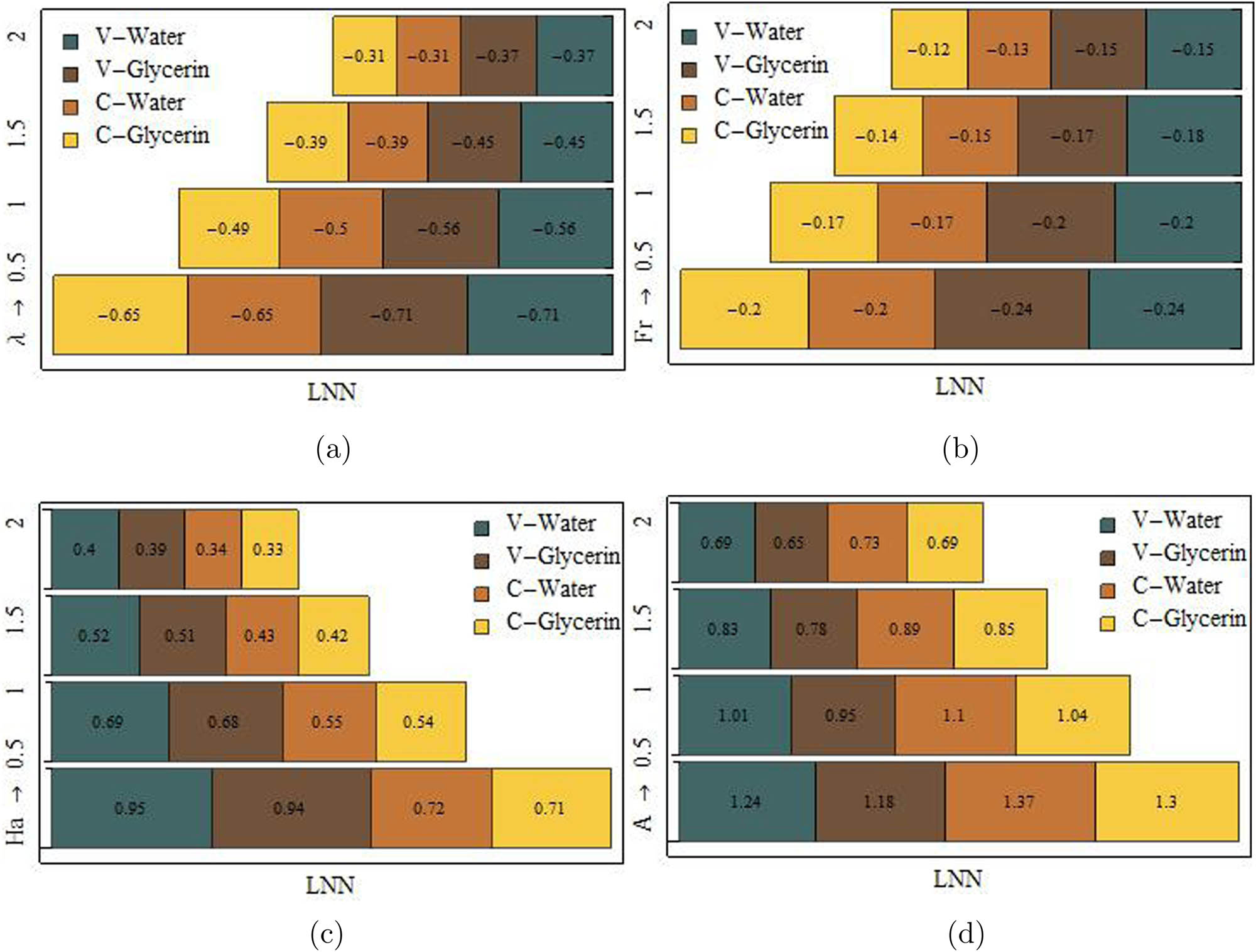
$Figure 11 The increment/decrement percentage of LNN for variations of λ \lambda (a), Fr (b), Ha (c), and A (d) for viscous HCNTs and Casson HCNTs.$

Figure 11

The increment/decrement percentage of LNN for variations of λ (a), Fr (b), Ha (c), and A (d) for viscous HCNTs and Casson HCNTs.

$Figure 12 The increment/decrement percentage of LNN for variations of Hg (a), R (b), Ec (c), and Λ \Lambda (d) for viscous HCNTs and Casson HCNTs.$

Figure 12

The increment/decrement percentage of LNN for variations of Hg (a), R (b), Ec (c), and Λ (d) for viscous HCNTs and Casson HCNTs.

6 Conclusions

The current endeavor focuses on the time-dependent and DFF of Casson hybrid nanofluids made of SWCNTs and MWCNTs running over a heated Riga plate with a velocity slip condition. By implementing the necessary transformations, the controlling equations are converted into ODEs. The bvp4c technique is applied to determine the numerical results of the converted equations and boundary conditions. The current flow model has applications in engineering and industrial areas, such as ceramic manufacture, the food industry, energy storage units, power generation, etc. Our findings are stated as follows:

The fluid velocity diminished when enhancing the size of the unsteady and porosity parameters.
Convective heating and cooling exhibit the opposite nature when changing the radiation parameter.
The thermal profile grows when intensifying the Eckert number.
The least decrement percent of SFC is obtained in water-based Casson HCNTs when the Forchheimer number goes from 1.5 to 2, and the largest decrement percent of SFC is obtained in glycerin-based viscous HCNTs when the porosity parameter goes from 0 to 0.5.
The least ascent percentage of LNN obtained in glycerin-based viscous HCNTs occurs when the unsteady parameter goes from 1.5 to 2, and the largest ascent percentage of LNN occurs in water-based viscous HCNTs when the radiation parameter goes from 0 to 0.5.
In the future, it is anticipated that a number of scientific and practical applications will be based on the dynamics of the stream throughout a Riga plate. The outcomes of the current study might be applied to a variety of model investigations. In many areas of science and technology, including microchips, electronic cooling systems, heat exchangers, etc., the findings of the current issue are also highly exciting. Also, we will extend our work with ion slip and Hall effect in the future.

Acknowledgments

The authors extend their appreciation to the Ministry of Education in KSA for funding this research work through the project number KKU- IFP2-DA-6.

Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors state no conflict of interest.
Data availability statement: The datasets generated and/or analysed during the current study are available from the corresponding author on reasonable request.

References

[1] Choi SUS. Enhancing thermal conductivity of fluids with nanoparticles. Proc ASME Int Mech Eng Congress Expo. 1995;66:99–105. Search in Google Scholar

[2] Ali R, Shahzad A, Saher KU, Elahi Z, Abbas T. The thin film flow of Al2O3 nanofluid particle over an unsteady stretching surface. Case Stud Therm Eng. 2022;29:101695:13pages. 10.1016/j.csite.2021.101695Search in Google Scholar

[3] Iqbal A, Abbas T. A study on heat transfer enhancement of Copper (Cu)-Ethylene glycol based nanoparticle on radial stretching sheet. Alex Eng J. 2023;71:13–20. 10.1016/j.aej.2023.03.025Search in Google Scholar

[4] Fakour M, Rahbari A, Khodabandeh E, Ganji DD. Nanofluid thin film flow and heat transfer over an unsteady stretching elastic sheet by LSM. J Mech Sci Technol. 2018;32(1):177–83. 10.1007/s12206-017-1219-5Search in Google Scholar

[5] Sadiq MA. Heat transfer of a nanoliquid thin film over a stretching sheet with surface temperature and internal heat generation. J Therm Anal Calorim. 2021;143(3):2075–83. 10.1007/s10973-020-09614-xSearch in Google Scholar

[6] Srilatha P, Gamaoun F, Marouani H, Kumar R, Prasanna Rani S, Yogeesha KM, et al. Melting phenomenon in the flow of dusty nanofluid over a stretching sheet in the presence of single walled carbon nanotubes. Case Stud Therm Eng. 2022;40:102585:10pages. 10.1016/j.csite.2022.102585Search in Google Scholar

[7] Tulu A, Ibrahim W. MHD slip flow of CNT-ethylene glycol nanofluid due to a stretchable rotating disk with Cattaneo–Christov heat flux model. Math Probl Eng. 2020;1374658:13pages. 10.1155/2020/1374658Search in Google Scholar

[8] Khan A, Shah Z, Islam S, Dawar A, Bonyah E, Ullah H, et al. Darcy–Forchheimer flow of MHD CNTs nanofluid radiative thermal behaviour and convective non uniform heat source/sink in the rotating frame with microstructure and inertial characteristics. AIP Adv. 2018;28(12):125024:18pages. 10.1063/1.5066223Search in Google Scholar

[9] Alsagri AS, Nasir S, Gul T, Islam S, Nisar KS, Shah Z, et al. MHD thin film flow and thermal analysis of blood with CNTs nanofluid. Coat. 2019;9(3):175:16pages. 10.3390/coatings9030175Search in Google Scholar

[10] Wang Y, Mansir IB, Al-Khaled K, Raza A, Khan SU, Khan MI, et al. Thermal outcomes for blood-based carbon nanotubes (SWCNTs and MWCNTs) with Newtonian heating by using new Prabhakar fractional derivative simulations. Case Stud Therm Eng. 2022;32:101904:10pages. 10.1016/j.csite.2022.101904Search in Google Scholar

[11] Alzahrani EO, Shah Z, Alghamdi W, Ullah MZ. Darcy–Forchheimer radiative flow of micropoler CNT nanofluid in rotating frame with convective heat generation/consumption. Processes. 2019;7(10):16pages. 10.3390/pr7100666Search in Google Scholar

[12] Jawad M, Shah Z, Islam S, Majdoubi J, Tlili I, Khan W, et al. Impact of nonlinear thermal radiation and the viscous dissipation effect on the unsteady three-dimensional rotating flow of single-wall carbon nanotubes with aqueous suspensions. Symmetry. 2019;11(12):207:18pages. 10.3390/sym11020207Search in Google Scholar

[13] Kumar KG, Rudraswamy NG, Gireesha BJ, Krishnamurthy MR. Influence of nonlinear thermal radiation and viscous dissipation on three-dimensional flow of Jeffrey nanofluid over a stretching sheet in the presence of Joule heating. Nonlinear Eng. 2017;6:207–19. 10.1515/nleng-2017-0014Search in Google Scholar

[14] Ramzan M, Riasat S, Shah Z, Kumam P, Thounthong P. Unsteady MHD carbon nanotubes suspended nanofluid flow with thermal stratification and nonlinear thermal radiation. Alex Eng J. 2020;59(3):1557–66. 10.1016/j.aej.2020.04.004Search in Google Scholar

[15] Rana P, Gupta S, Gupta G, FEM computations and Taguchi optimization in nonlinear radiative MHD MWCNT-MgO/EG hybrid nanoliquid flow and heat transfer over a 3D wedge surface. Case Stud Therm Eng. 2023;41:102639:15pages. 10.1016/j.csite.2022.102639Search in Google Scholar

[16] Mahabaleshwar US, Sneha KN, Chan A, Zeidan D. An effect of MHD fluid flow heat transfer using CNTs with thermal radiation and heat source/sink across a stretching/shrinking sheet. Int Commun Heat Mass Transf. 2022;135:106080. 10.1016/j.icheatmasstransfer.2022.106080Search in Google Scholar

[17] Satya Narayana PV, Tarakaramu N, Sarojamma G, Animasaun IL, Numerical simulation of nonlinear thermal radiation on the 3D flow of a couple stress Casson nanofluid due to a stretching sheet. J Therm Sci Eng Appl. 2021;13(2):021028:10pages. 10.1115/1.4049425Search in Google Scholar

[18] Mabood F, Yusuf TA, Khan WA. Cu−Al2O3−H2O hybrid nanofluid flow with melting heat transfer, irreversibility analysis and nonlinear thermal radiation. J Therm Anal Calorim. 2021;143(2):973–84. 10.1007/s10973-020-09720-wSearch in Google Scholar

[19] Mohanty D, Mahanta G, Shaw S. Analysis of irreversibility for 3-D MHD convective Darcy–Forchheimer Casson hybrid nanofluid flow due to a rotating disk with Cattaneo–Christov heat flux, Joule heating, and nonlinear thermal radiation. Numer Heat Transf B Fund. 2023;84(2):115–42. 10.1080/10407790.2023.2189644Search in Google Scholar

[20] Nayak MK, Mahanta G, Das M, Shaw S. Entropy analysis of a 3D nonlinear radiative hybrid nanofluid flow between two parallel stretching permeable sheets with slip velocities. Int J Ambient Energy. 2022;43(1):8710–21. 10.1080/01430750.2022.2101523Search in Google Scholar

[21] Rasool G, Shah NA, El-Zahar ER, Wakif A. Numerical investigation of EMHD nanofluid flows over a convectively heated Riga pattern positioned horizontally in a Darcy–Forchheimer porous medium: Application of passive control strategy and generalized transfer laws. Waves Random Complex Media. 2022:1–20. 10.1080/17455030.2022.2074571. Search in Google Scholar

[22] Shah NA, Yook SJ, Tosin O. Analytic simulation of thermophoretic second grade fluid flow past a vertical surface with variable fluid characteristics and convective heating. Sci Rep. 2022;12:5445:17pages. 10.1038/s41598-022-09301-xSearch in Google Scholar PubMed PubMed Central

[23] Wakif A, Shah NA. Hydrothermal and mass impacts of azimuthal and transverse components of Lorentz forces on reacting Von Kármán nanofluid flows considering zero mass flux and convective heating conditions. Waves Random Complex Media. 2022:1–22. 10.1080/17455030.2022.2136413. Search in Google Scholar

[24] Dawar A, Wakif A, Saeed A, Shah Z, Muhammad T, Kumam P. Significance of Lorentz forces on Jeffrey nanofluid flows over a convectively heated flat surface featured by multiple velocity slips and dual stretching constraint: a homotopy analysis approach. J Comput Des Eng. 2022;9:564–82. 10.1093/jcde/qwac019Search in Google Scholar

[25] Rasool G, Wakif A, Wang X, Shafiq A, Chamkha Ali J. Numerical passive control of alumina nanoparticles in purely aquatic medium featuring EMHD driven non-Darcian nanofluid flow over convective Riga surface. Alex Eng J. 2023;68:747–62. 10.1016/j.aej.2022.12.032Search in Google Scholar

[26] Rashid A, Ayaz M, Islam S, Saeed A, Kumam P, Suttiarporn P. Theoretical analysis of the MHD flow of a tangent hyperbolic hybrid nanofluid over a stretching sheet with convective conditions: A nonlinear thermal radiation case. S Afr J Chem Eng. 2022;42:255–69. 10.1016/j.sajce.2022.09.005Search in Google Scholar

[27] Chamkha Ali J. Non-Darcy hydromagnetic free convection from a cone and a wedge in porous media. Int Comm Heat Mass Transf. 1996;23(6):875–87. 10.1016/0735-1933(96)00070-XSearch in Google Scholar

[28] Chamkha Ali J. Non-Darcy fully developed mixed convection in a porous medium channel with heat generation/absorption and hydromagnetic effects. Numer Heat Transf A. 1997;32:653–75. 10.1080/10407789708913911Search in Google Scholar

[29] Hayat T, Khan MI, Khan TA, Khan MI, Ahmad S, Alsaedi A. Entropy generation in Darcy–Forchheimer bidirectional flow of water-based carbon nanotubes with convective boundary conditions. J Mol Liq. 2018;265:629–38. 10.1016/j.molliq.2018.06.017Search in Google Scholar

[30] Jamshed W, Suriya Uma Devi S, Goodarzi M, Prakash M, Nisar KS, Zakarya M, et al. Evaluating the unsteady Casson nanofluid over a stretching sheet with solar thermal radiation: An optimal case study. Case Stud Therm Eng. 2021;26:101160:15pages. 10.1016/j.csite.2021.101160Search in Google Scholar

[31] Mahmood A, Jamshed W, Aziz A. Entropy and heat transfer analysis using Cattaneo–Christov heat flux model for a boundary layer flow of Casson nanofluid. Results Phys. 2018;10:640–9. 10.1016/j.rinp.2018.07.005Search in Google Scholar

[32] Madhu M, Kishana N, Chamkha Ali J. Unsteady flow of a Maxwell nanofluid over a stretching surface in the presence of magnetohydrodynamic and thermal radiation effects. Propuls Power Res. 2017;6(1):31–40. 10.1016/j.jppr.2017.01.002Search in Google Scholar

[33] Loganathan K, Eswaramoorthi S, Chinnasamy P, Jain R, Sivasakthivel R, Ali R, et al. Heat and mass transport in Casson nanofluid flow over a 3-D Riga plate with Cattaneo–Christov double flux: A computational modeling through analytical method. Symmetry. 2023;15:725:15pages. 10.3390/sym15030725Search in Google Scholar

[34] Prabakaran R, Eswaramoorthi S, Loganathan K, Sarris IE. Investigation on thermally radiative mixed convective flow of carbon nanotubes/Al2O3 nanofluid in water past a stretching plate with Joule heating and viscous dissipation. Micromachines. 2022;13:1424:19pages. 10.3390/mi13091424Search in Google Scholar PubMed PubMed Central

[35] Naresh Kumar N, Sastry DRVSRK, Shaw S. Irreversibility analysis of an unsteady micropolar CNT-blood nanofluid flow through a squeezing channel with activation energy-Application in drug delivery. Comput Methods Programs Biomed. 2022;226:107156. 10.1016/j.cmpb.2022.107156Search in Google Scholar PubMed

[36] Eswaramoorthi S, Alessa N, Sangeethavaanee M, Kayikci S, Namgyel N. Mixed convection and thermally radiative flow of MHD Williamson nanofluid with Arrhenius activation energy and Cattaneo–Christov heat-mass flux. J Math. 2021;2021:16. 10.1155/2021/2490524Search in Google Scholar

[37] Sahu SK, Rout S, Shaw S, Dash N, Thatoi DN, Nayak MK. Hydrothermal stagnation point flow of Carreau nanofluid over a moving thin needle with non-linear Navier’s slip and cubic autocatalytic chemical reactions in Darcy–Forchheimer medium. J Indian Chem Soc. 2002;99(11):100741. 10.1016/j.jics.2022.100741. Search in Google Scholar

[38] Akbara NS, Tripathib D, Khanc ZH. Numerical investigation of Cattanneo-Christov heat flux in CNT suspended nanofluid flow over a stretching porous surface with suction and injection. Discrete Contin Dyn Syst S. 2018;11(4):1–12. 10.3934/dcdss.2018033Search in Google Scholar

Received: 2023-09-08

Revised: 2024-01-04

Accepted: 2024-01-19

Published Online: 2024-03-04

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/ntrev-2023-0202

Keywords for this article

carbon nanotubes; Darcy–Forchheimer flow; Casson hybrid nanofluid; HAM; Riga plate

Creative Commons

BY 4.0