Home Physical Sciences A comparative study of the elasto-plastic properties for ceramic nanocomposites filled by graphene or graphene oxide nanoplates
Article Open Access

A comparative study of the elasto-plastic properties for ceramic nanocomposites filled by graphene or graphene oxide nanoplates

  • Lian-Hua Ma EMAIL logo , Kun Zhang , Xiao-Dong Pan and Wei Zhou EMAIL logo
Published/Copyright: July 4, 2022
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
Nanotechnology Reviews
From the journal Nanotechnology Reviews Volume 11 Issue 1

Abstract

As nanoscale reinforcements, the graphene and graphene oxide nanoplates exhibit distinct mechanical and physical properties. The determination of the effective elasto-plastic behavior of nanoplate/ceramic nanocomposites and the different filling effects of graphene and graphene oxide nanoplate deserve systematic investigation. In this work, we intend to uncover how the graphene and graphene oxide nanoplates affect the macroscopic elasto-plastic characteristics of ceramic matrix nanocomposites and what differences in both nanoplates enhancements. A homogenization model is first utilized for determining the effective elastic parameters of nanoplate/ceramic composite with a perfect interface. Then the slightly weakened interface model is introduced to characterize the sliding effects of nanoplates in a ceramic matrix, and the effective elastic parameters of such nanoplates filled composites incorporating the interfacial sliding effects are explicitly formulated. Furthermore, a nonlinear micromechanics model is developed to investigate the macroscopic elastoplasticity and the yield behavior of graphene and graphene oxide nanoplate-filled ceramic nanocomposites subjected to confining pressure. The filling effects of the two kinds of nanoplates on the mechanical properties of such nanocomposite are comparatively examined. The calculated results demonstrate that types of the nanoplates and the imperfect interfaces between nanoplates and ceramic matrix have significant influences on the effective elasto-plastic behaviors of the nanoplate composites.

Keywords: ceramic matrix composite; nanoplate; elasto-plastic properties; micromechanics

1 Introduction

Graphene nanoplates (GNPs) and graphene oxide nanoplates (GONPs) are quasi-two-dimensional (2D) platelet-shaped nanoparticles, which are usually used in composites as fillers [1,2,3]. Due to their unique mechanical properties, GNPs and GONPs are widely applied in various fields, including electronics [4], aerospace [5,6], and construction [7,8]. In recent years, the applications of GNPs and GONPs in ceramic matrix composites are gradually emerging. The ceramic matrix composites filled with graphene-family nanoplates [9,10] have attracted broad research interest, as reviewed in refs. [11–15]. Sun et al. [16] studied the reinforcing mechanisms of graphene and nano-TiC in Al2O3-based ceramic tool materials. In their work, the effects of graphene and nano-TiC on the microstructure and mechanical properties were examined. GNPs and GONPs have been the striking nanofillers applied in ceramics due to their unique structures together with exceptional mechanical and physical properties [17,18]. Li et al. [19] fabricated the multilayer graphene (MLG)-reinforced Al2O3/TiC ceramics and presented the reinforcing effect of MLG on the microstructure and mechanical properties of such composites by experiments and simulation approaches. Their results showed that the composite added with 0.2 wt% MLG had excellent flexural strength and high fracture toughness. Wang et al. [20] investigated the microstructure, mechanical properties, and toughening mechanisms of the graphene-reinforced Al2O3–WC–TiC composite ceramic tool materials. The results showed that the more refined and denser composite microstructures were obtained with the introduction of graphene. Liu et al. [21] characterized the mechanical properties and microstructure of reaction sintering SiC ceramics reinforced with graphene‑based fillers by using X-ray diffraction and scanning electron microscopy. Furthermore, the relation between phase content and mechanical properties was examined. Cano-Crespo et al. [22] comparatively investigated the mechanical properties of the graphene oxide-reinforced alumina composites and the carbon nanofiber-reinforced alumina ones. It was confirmed that the possibility of combining remarkable electrical conductivities together with an enhancement of mechanical properties motivated the research in graphene-family nanoplates filled ceramic composites.

In practical engineering applications, ceramic materials are widely used as proppants in the process of hydraulic fracturing to increase oil and gas production. In hydraulic fracturing treatment, ceramic proppants are transported in fracking fluid with high pressure to fill an induced fracture in rocks to keep the fracture open. As typical brittle materials, ceramic proppants are prone to breakage in the hydraulic fracturing process. To toughen the ceramics, as nanofillers, GNPs or GONPs can be added in ceramics to form nanocomposites, which are potential fracture-resistant proppants in hydraulic fracturing engineering. Although ceramic usually behaves elastic deformation and brittle failure, it could exhibit elasto-plastic behavior under high confining pressure conditions [23], e.g., hydraulic fracturing by fluid with great pressures. It is essential to investigate comparatively the effects of GNPs and GONPs on the effective elasto-plastic properties of ceramic matrix composites under high confining pressure circumstances. The previous research work mainly focused on the experimental characterizations of the GNP- or GONP-filled ceramic matrix composites. However, theoretical investigations of the effective mechanical properties of ceramic matrix composites filled with GNP or GONP have not attracted sufficient attention, and more thorough and systematic analytical investigations are required [11].

Micromechanics-based theoretical approaches, such as the Halpin–Tsai model [24], the Nielsen model [25,26], the Mori–Tanaka model [27,28,29], and the Eshelby’s model [30], can be efficiently used to predict the effective mechanical properties of the composite. Sadeghpour et al. [29] presented a novel modified Mori–Tanaka (M–T) approach to estimate the stress–strain response of graphene nanocomposites subjected to large deformation and conducted the quasi-static tensile loading and unloading tests on polyvinyl alcohol–graphene oxide nanocomposite samples. Their theoretical results compared well with experimental stress–strain data for both loading and unloading. Dimitrijevic et al. [31] developed a micromechanical model for the fiber-reinforced ceramic matrix composites and used the finite element method to simulate the mechanical behaviors of such materials. As mentioned earlier, the ceramic matrix composite exhibits elasto-plastic behavior under high confining pressure. To date, the micromechanics-based theoretical evaluation and comparative investigations on the elasto-plasticity of GNP- and GONP-filled ceramics are seldom reported, although some micromechanics models have been proposed to estimate the mechanical properties of nanocomposites.

In this study, a micromechanics-based model is proposed to predict the macroscopic elasto-plastic mechanical properties of the ceramic nanocomposites filled with GNPs or GONPs by taking into account the effects of the imperfect interface. The comparisons of the effects of GNP and GONP additions on the effective elastic properties of the ceramic nanocomposite are made. In addition, the uniaxial equivalent stress–strain response and initial yield surface of such nanocomposite filled with GNPs and GONPs are comparatively analyzed based on the second-order stress moment micromechanical model. The outcome will be a protocol for predicting the elasto-plastic behaviors of ceramic nanocomposites based on the types and properties of nanoplates.

2 Effective elastic properties of nanoplate/ceramic composite

2.1 Effective elasticity of the nanoplate composite with perfect interface

GNPs or GONPs are typical platelet-shaped nanomaterials whose thickness is much smaller than the plane size. The graphene-family nanoplates are usually used as nanofillers, which are added in the ceramic matrix and the nanoplate-filled composites are formed. For the micromechanics model, in this work, nanoplates can be assumed as penny-shaped inclusion with average diameter and thickness. GNPs or GONPs are supposed to be uniformly and randomly dispersed in the ceramic matrix with no agglomerations. To investigate the effective elastic properties of the nanocomposites, a representative volume element (RVE) containing GNPs or GONPs with random orientations is selected, as shown in Figure 1.

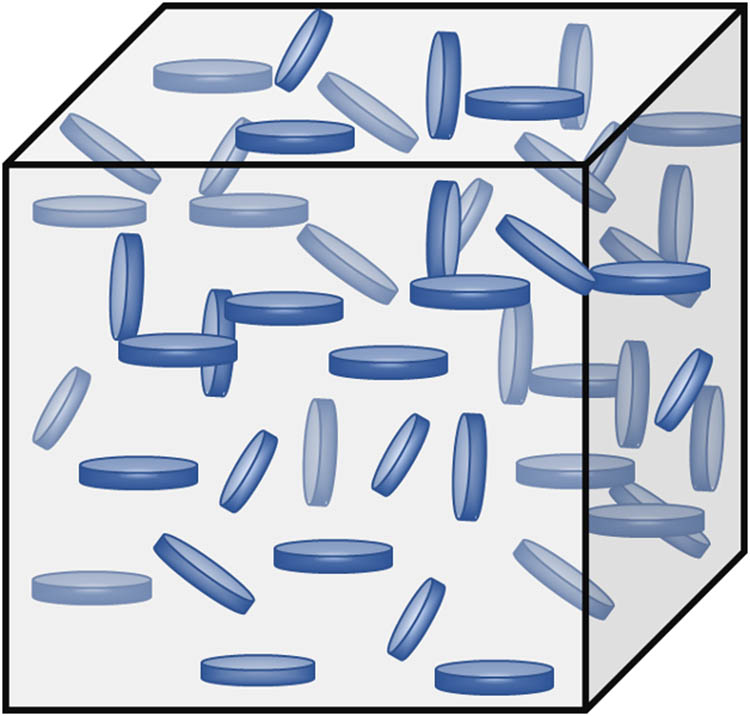
Figure 1 A schematic diagram of a microscale RVE of the ceramic matrix nanocomposite with randomly distributed GNPs or GONPs.
Figure 1

A schematic diagram of a microscale RVE of the ceramic matrix nanocomposite with randomly distributed GNPs or GONPs.

Due to the unique 2D structure, GNPs or GONPs exhibit obvious transversely isotropic mechanical properties [32], and the in-plane stiffness of the nanoplates is substantially higher than that in the thickness direction. The nanoplates are assumed to deform only elastically in the nanocomposite.

From a micromechanical point of view, the nanoplate phase can be treated as spheroidal inclusion whose shape and size can be defined by introducing the spheroid aspect ratio X = c a , where c and a are, respectively, the semi-principal axes of length along e 1 and e 2 (and e 3) direction, as sketched in Figure 2. It is readily observed that the case where X < 1 is associated with oblate spheroid, and it can be further mapped to the penny-shaped platelet specifically considered in this work by the asymptotic definition of the aspect ratio X approaching zero (X → 0). Taking e 1 to be the normal direction and plane e 2–e 3 isotropic, the adopted elastic constants of typical GNPs and GONPs are presented in Table 1.

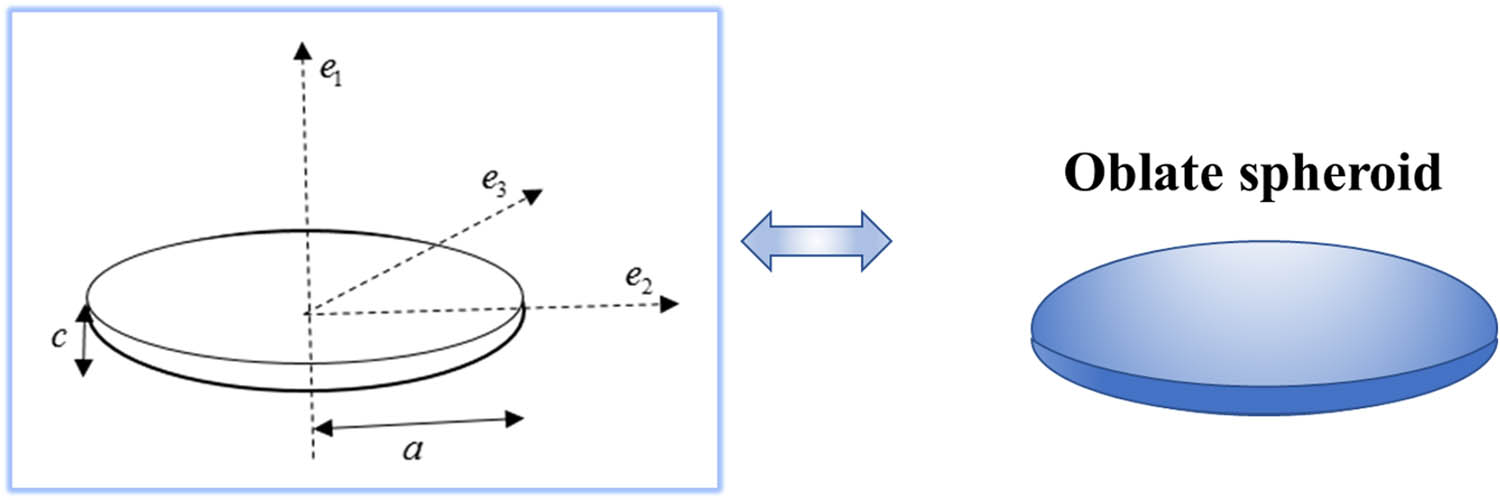
Figure 2 Sketch of the nanosized inclusion and local coordinate system.
Figure 2

Sketch of the nanosized inclusion and local coordinate system.

Table 1

The adopted elastic constants of typical GNPs and GONPs

Typical nanoplates c 11 c 22 c 44 c 23 c 12 c 66
GNPs (GPa) 36.5 1,060 5.05 180 7.9 440
GONPs (GPa) 123 268 17 45.5 27 111.25

The nanoplates are assumed to have the same geometry and size, and the overall aspect ratio of the nanoplate is defined as follows:

(1) α = t D ,

where D and t represent the diameter and thickness of the nanoplate, respectively.

According to Hill’s notation [33] for the constitutive equation of a transversely isotropic material, the elastic tensor for the nanoplates can be written in terms of five independent constants:

(2) L 1 = ( 2 k 1 , l 1 , n 1 , 2 m 1 , 2 p 1 ) ,

where k 1, l 1, n 1, m 1, and p 1 are the plane-strain bulk modulus, cross modulus, through-the-thickness modulus, in-plane shear modulus, and transverse shear modulus, respectively. According to this method, the stress–strain relationship of the nanoplates can be expressed as follows:

(3) σ 11 σ 22 σ 33 σ 12 σ 31 σ 23 = n 1 l 1 l 1 0 0 0 l 1 k 1 + m 1 k 1 − m 1 0 0 0 l 1 k 1 − m 1 k 1 + m 1 0 0 0 0 0 0 2 p 1 0 0 0 0 0 0 2 p 1 0 0 0 0 0 0 2 m 1 ε 11 ε 22 ε 33 ε 12 ε 31 ε 23 .

Based on the elastic stiffness coefficients of the typical GNPs and GONPs given in Table 1, their five elastic constants are given by k 1 = (c 22 + c 23)/2, l 1 = c 12, m 1 = c 66/2, n 1 = c 11, and p 1 = c 44/2, respectively.

The effective elastic stress–strain (σ̅ − ε̅) relationship of the nanoplate composite can be written as follows:

(4) σ ¯ = L ¯ ε ¯ ,

where L̅ represents the effective elastic tensor. Due to the random distribution of the nanoplates in the ceramic matrix, the nanocomposite can be envisioned to be isotropic in a statistical sense. The macroscopic elastic stiffness of the composite can be expressed as follows:

(5) L ¯ = ( 3 K ¯ , 2 G ¯ ) ,

where K̅ and G̅ represent the effective bulk and shear moduli of the nanocomposites, respectively.

According to the Mori–Tanaka model for a heterogeneous medium with random microstructure, the effective stiffness tensor of the nanoplate composite with perfect interface can be given by

(6) L ¯ = ( f 1 〈 L 1 A 〉 + f 0 L 0 ) ( f 1 〈 A 〉 + f 0 I ) − 1 ,

where A = [I + SL 0 (L 1 − L 0 )]−1. In the aforementioned equation, f 0 and f 1 are the volume concentration of the matrix and the nanoplates, respectively. L 0 and I are the elastic stiffness tensor of the matrix and the fourth-rank identity tensor, and 〈·〉 in equation (6) represents the orientational average. S represents the Eshelby tensor, which is related to the Poisson’s ratio, v 0, of the matrix and aspect ratio (α) of the nanoplates.

In accordance with the expression of the elastic stiffness of the transversely isotropic nanoplate in Hill’s notation, the elastic stiffness of the ceramic matrix, L 0 , can also be decomposed into five components, with

(7) L 0 = ( 2 k 0 , l 0 , n 0 , 2 m 0 , 2 p 0 ) ,

where k 0, l 0, m 0, n 0, and p 0 are the elastic constants of the matrix corresponding to the five elastic constants of the nanoplates, and their relationships with the bulk modulus, κ 0, and shear modulus, μ 0, are as follows:

k 0 = κ 0 + μ 0 / 3 , l 0 = κ 0 − 2 μ 0 / 3 , n 0 = κ 0 + 4 μ 0 / 3 , m 0 = p 0 = μ 0 .

The Mori–Tanaka model could provide a sufficiently accurate estimate result when the volume fraction of the inclusion is not significantly high, as is the case for the considered nanoplate composite. Upon substitution of L 1 and L 0 from equations (2) and (7) into equation (6), the macroscopic bulk and shear moduli of the nanocomposite can be explicitly calculated as follows:

(8) K ¯ = f 0 κ 0 + f 1 ξ 1 f 0 + 3 f 1 ξ 2 , G ¯ = f 0 μ 0 + f 1 ζ 1 f 0 + 2 f 1 ζ 2 ,

where K̅ and G̅ are the macroscopic bulk modulus and shear modulus of the nanocomposite, respectively. The explicit forms of ξ 1, ξ 2, ξ 1, and ξ 2 given by ref. [34]

ξ 1 = [ 4 ( k 1 d − l 1 g ) + 2 ( l 1 d − n 1 g + l 1 b − 2 k 1 h ) + ( n 1 b − 2 l 1 h ) ] / 9 ( b d − 2 g h ) , ξ 2 = [ 2 d − 2 ( g + h ) + b ] / 9 ( b d − 2 g h ) , ζ 1 = [ ( k 1 d − l 1 g ) − ( l 1 d − n 1 g + l 1 b − 2 k 1 h ) + ( n 1 b − 2 l 1 h ) ] / 15 ( b d − 2 g h ) + 2 m / 5 e + 2 p / 5 f , ζ 2 = [ d + 2 ( g − h ) + 2 b ] / 30 ( b d − 2 g h ) + 1 / 5 e + 1 / 5 f ,

where the six constants of b, d, e, f, g, and h are related to the elastic constants of the ceramic matrix, the nanoplates, and the Eshelby tensor components, and they are respectively given by

b = 1 + 2 ( k 1 − k 0 ) [ ( 1 − ν 0 ) ( S 2222 + S 2233 ) − 2 ν 0 S 2211 ] + 2 ( l 1 − l 0 ) [ ( 1 − ν 0 ) S 1122 − ν 0 S 1111 ] / E 0 ,

d = 1 + { ( n 1 − n 0 ) [ S 1111 − 2 ν 0 S 1122 ] + 2 ( l 1 − l 0 ) [ ( 1 − ν 0 ) S 1122 − ν 0 S 1111 ] } / E 0 ,

e = 1 + 2 ( m 1 − m 0 ) S 2323 / E 0 ,

f = 1 + 2 ( p 1 − p 0 ) S 1212 / p 0 ,

g = 2 ( k 1 − k 0 ) [ ( 1 − ν 0 ) S 1122 − ν 0 S 1111 ] + ( l 1 − l 0 ) [ S 1111 − 2 ν 0 S 1122 ] / E 0 ,

h = { ( n 1 − n 0 ) [ S 2211 − ν 0 ( S 2222 − S 2233 ) ] + ( l 1 − l 0 ) [ ( 1 − ν 0 ) ( S 2222 + S 2233 ) − 2 ν 0 S 2211 ] } / E 0 ,

where E 0 denotes Young’s modulus of the matrix, which is expressed by E 0 = 2μ 0(1 + ν 0).

As mentioned earlier, we complete the formulation for determining the effective bulk and shear modulus of the nanoplate nanocomposites with the perfect interface.

2.2 The imperfect interface effect

The assumption of the perfect interface is made, without considering the discontinuity of the stress or displacement between the nanoplates and the adjacent matrix. In reality, however, the nanoplates do not bond perfectly with the ceramic matrix. To consider the discontinuity of the interfaces, the slightly weakened interface model proposed by Qu [35] is employed to reexamine the effective elastic properties of such nanocomposite.

Following the works of Qu et al. [35,36,37,38], the traction continuity conditions are explicitly given by

(9) Δ σ i j n j = [ σ i j ( x ) ] n j = 0 .

According to the linear spring-layer model [39], the displacement jump condition is presented as follows:

(10) Δ u i = [ u i ( x ) ] = λ i j σ j k n k ,

where [·] represents the jump of the said quantity at the interface with an outward normal, n i , from nanoplate filler to the matrix, and λ i j represents the compliance of the interface layer. This interface parameter could be expressed by

(11) λ i j = γ δ i j + ( β − γ ) n i n j ,

when β is 0, the interface is allowed to slide without normal separation or interpenetration, which is the case in nanoplate composites considered here. It is assumed that only sliding is allowed in the following analysis. The effects of sliding parameter γ on the effective elastic properties of such composites will be investigated. It is well accepted that, when γ → 0 , it corresponds to a perfectly bonded interface, and when γ → ∞ , the interface is completely unbonded. Taking into account the imperfect interface effects, the traditional Eshelby tensor S can be modified as S M by introducing the sliding parameter γ, and the components of the modified tensor S M can be expressed by

(12) S i j k l M = S i j k l + ( I i j k l − S i j p q ) H p q r s L 0 r s m n ( I m n l k − S m n k l ) .

The components of the introduced imperfection compliance tensor H ijkl can be found in the study by Qu et al. [35], that is,

(13) H i j k l = γ ( P i j k l − Q i j k l ) ,

where

P i j k l = 3 16 π ∫ 0 π ∫ 0 2 π ( δ i k n ′ j n ′ l + δ j k n ′ i n ′ l + δ i l n ′ k n ′ j + δ j l n ′ k n ′ i ) n − 1 d θ sin ϕ d ϕ ,

Q i j k l = 3 4 π ∫ 0 π ∫ 0 2 π ( n ′ i n ′ j n ′ l n ′ k l ) n − 3 d θ sin ϕ d ϕ ,

n ' i = ( cos ϕ , α sin ϕ cos θ , α sin ϕ sin θ ) / D ,

n = n ′ i n ′ i .

The nonzero components of tensors P and Q are calculated using the aforementioned formula as follows:

P 1111 = 3 2 t 1 ( 1 − α 2 ) 1 − α 2 1 − α 2 sinh − 1 1 − α 2 α ,

P 2222 = 3 4 t α 2 ( 1 − α 2 ) 2 − α 2 1 − α 2 sinh − 1 1 − α 2 α − 1 ,

P 1212 = 3 8 t α 2 1 − α 2 sinh − 1 1 − α 2 α − 2 − α 2 2 ( 1 − α 2 ) α 2 1 − α 2 sinh − 1 1 − α 2 α − 1 ,

P 3333 = P 2222 ,

P 2323 = P 2222 / 2 ,

P 1313 = P 1212 ,

Q 1111 = 3 2 t 2 α 2 + 1 ( 1 − α 2 ) 2 − 3 α 2 ( 1 − α 2 ) 5 / 2 sinh − 1 1 − α 2 α ,

Q 2222 = 9 8 t α 2 + α 4 ( 5 − 2 α 2 ) 2 ( 1 − α 2 ) 2 − α 4 ( 4 − α 2 ) 2 ( 1 − α 2 ) 5 / 2 sinh − 1 1 − α 2 α ,

Q 1212 = 3 4 t α 2 ( α 2 + 2 ) ( 1 − α 2 ) 5 / 2 sinh − 1 1 − α 2 α − α 2 ( 4 − α 2 ) ( 1 − α 2 ) 2 ,

Q 3333 = Q 2222 ,

Q 1212 = Q 1133 = Q 1313 = Q 1122 ,

Q 1313 = Q 1212 ,

Q 2233 = Q 2323 = Q 2222 / 3 .

Substituting the modified Eshelby tensor S M into equation (6) by replacing the Eshelby tensor S, the effective bulk modulus K ¯ and shear modulus G ¯ of the nanocomposite with imperfect interfacial effects can be obtained as follows:

(14) K ¯ = f 0 κ 0 + f 1 ξ 1 f 0 + 3 f 1 ( ξ 2 + ξ H ) , G ¯ = f 0 μ 0 + f 1 ζ 1 f 0 + 2 f 1 ( ζ 2 + ζ H ) ,

where ξ 1, ξ 2, ζ 1, and ζ 2 have the same expressions as mentioned earlier. The parameters reflecting the effect of imperfect interfaces are contained in the tensor H. Compared with the case of perfect interfaces, the two additional parameters, ξ H and ζ H , introduced in equation (14), denote the hydrostatic and deviatoric components of the isotropic tensor 〈 H L 1 [ I + S L 0 ( L 1 − L 0 ) ] − 1 〉 , respectively. The parameters ξ H and ζ H can be easily obtained after calling upon Walpole’s mathematical scheme for evaluating the relevant orientational average [40]. It is noted that the effects of the imperfect interfaces are incorporated into the derived effective moduli by introducing an interfacial sliding parameter. However, the interfacial damage and fracture of the nanoplate composites cannot be directly considered in the micromechanics model. To understand how the interfaces slide and fracture, it may be necessary to resort to numerical approach, which is beyond the scope of this study.

3 Effective elasto-plastic behavior of nanoplate/ceramic composite

In Section 2, we formulate the explicit expressions of the effective elastic properties of the nanoplate/ceramic composite with perfect/imperfect interfaces. In this section, through consideration of the elasto-plastic behaviors of such composite subjected to high confining pressure, we intend to establish the nonlinear elastoplastic micromechanics model using the concept of linear comparison material [41] and the field fluctuation method [42].

For the nanoplate composite modeled as a linear comparison material, its nonlinear mechanical properties are characterized by the instantaneous secant modulus dependent on strain. It is well accepted that the stress or strain field is heterogeneous in a composite, indicating that the secant moduli are also heterogeneous. To simplify the analysis, we assume that the secant modulus of the nonlinear phase is uniform.

According to Hill’s lemma for the composite, we have

(15) σ ¯ : M : σ ¯ = 〈 σ : m : σ 〉 ,

where σ̅ and σ denote the macroscopic and local stress in the composite, respectively. M and m represent the macroscopic compliance tensor of the composite and the local compliance tensor, respectively.

Following the procedures of the field fluctuation method [43], we let the local compliance tensor m undergo a small variation δ m, when the constant stress boundary condition is prescribed. This will result in a perturbation of the local stress field, δ σ. Thus, we obtain

(16) σ ¯ : δ M : σ ¯ = 〈 σ : δ m : σ 〉 + 2 〈 δ σ : m : σ 〉 .

Recalling the constantly applied stress condition, the volume average of the local stress perturbation vanishes, and the second term on the right-hand side of equation (16) vanishes. The ceramic matrix is taken as an isotropic elastoplastic solid. For a small perturbation of the shear modulus µ 0 of the matrix, equation (16) is reformulated as follows:

(17) σ ¯ : δ M : σ ¯ = f 0 δ 1 2 μ 0 〈 σ ′ : σ ′ 〉 V 0 ,

where σ′ is the local deviatoric stress of the matrix. By utilizing the equivalent stress of the matrix [43], σ ¯ e 0 2 = 3 2 〈 σ ′ : σ ′ 〉 V 0 , we could rearrange equation (17) as follows:

(18) − 3 μ 0 2 σ ¯ : δ M δ μ 0 : σ ¯ = f 0 σ ¯ e 0 2 .

As can be observed in equation (18), the macroscopic stress, σ̅, is correlated with the averaged equivalent stress of the matrix, σ ¯ e 0 . For the macroscopically isotropic composite, the deformation can be decomposed into volume and shape deformation, and equation (18) can be rewritten as follows:

(19) 3 μ 0 2 σ ¯ m 2 K ¯ 2 δ K ¯ δ μ 0 + 1 3 σ ¯ e 2 G ¯ 2 δ G ¯ δ μ 0 = f 0 σ ¯ e 0 2 .

We introduce a dimensionless quantity, λ = σ ¯ m σ ¯ e , the aforementioned equation becomes

(20) 3 λ 2 K ¯ 2 δ K ¯ δ μ 0 + 1 G ¯ 2 δ G ¯ δ μ 0 σ ¯ e 2 = f 0 σ ¯ e 0 2 μ 0 2 .

Here, λ = 1/3 corresponds to uniaxial tension deformation, and λ = −1/3 corresponds to uniaxial compression deformation.

In the case of high confining pressure, the ceramic matrix would produce a plastic deformation before fracture under the external loads. In the calculations presented subsequently, the employed strain-hardening power law for the ceramic could be expressed as follows [17]:

(21) σ e = σ y 2 1 + ε e p l ε Y M ,

where σ y is the yield strength, ε Y denotes the plastic strain at which σ e = σ y , ε e p l represents the equivalent plastic strain, and M is the strain hardening exponent. Table 2 lists the adopted material parameters of alumina ceramic matrix [23].

Table 2

The material parameters of alumina ceramic matrix [23]

G 0 (GPa) v 0 σ y (GPa) ε Y M
146 0.2 4 0.002 0.1

The secant elastic modulus of ceramic matrix at a given plastic state could be given by

(22) E 0 s = 1 1 E 0 + ε e p l σ y 2 1 + ε e p l ε Y M .

According to the isotropic relationship and plastic incompressibility of the matrix material, the secant bulk, κ 0s , and shear moduli, µ 0s , and the secant Poisson’s ratio, v 0s , are respectively expressed as follows:

(23) κ 0 s = κ 0 = E 0 3 ( 1 − 2 v 0 ) , μ 0 s = 3 κ 0 E 0 s 9 κ 0 − E 0 s , v 0 s = 3 κ 0 − 2 μ 0 s 2 ( 3 κ 0 + μ 0 s ) .

It is noted that when the ceramic matrix undergoes plastic deformation, the moduli of the composite and matrix phase in equation (20) should be replaced by their corresponding instantaneous secant moduli, which are in terms of the averaged equivalent plastic strain of the matrix.

According to the solution procedure in ref. [43], we can treat the average equivalent stress of the matrix ( σ ¯ e 0 ) as a known quantity to determine the macroscopic stress ( σ ¯ ) using equations (20), (14), and (23). With the established nonlinear micromechanics model, the overall stress–strain relationships and the initial yield surfaces of the nanocomposite with different inclusion concentrations and interfacial parameters can be estimated analytically. In what follows, the elasto-plastic behavior of the ceramic nanocomposites filled by GNPs or GONPs will be comparatively studied. The filling effects of two kinds of nanoplates and the effect of weakened interface on the elasto-plastic mechanical properties will be analyzed.

4 Results and discussion

4.1 Effective elastic properties

As an illustrative application of the micromechanics model, we comparatively analyze the filling effects of the GNPs and GONPs on the effective elastic properties of the ceramic matrix composites that account for the slightly weakened interface effects. Figure 3 shows the relationship between the macroscopic bulk modulus of the composites with different volume fractions and interface sliding parameters. It can be observed that the bulk modulus of the ceramic composite decreases with the increase of the volume fraction with the same interface sliding parameters, and the macroscopic bulk modulus decreases with the increase of the interface sliding parameters. It is shown that the interface sliding weakens the macroscopic bulk modulus of the materials. However, the bulk modulus of the GONP-filled composite is larger than that of the GNP-filled composite with the same volume fraction. It demonstrates that the GONPs have better enhancement effects than the GNPs to resist the volumetric deformation of the nanoplate composite.

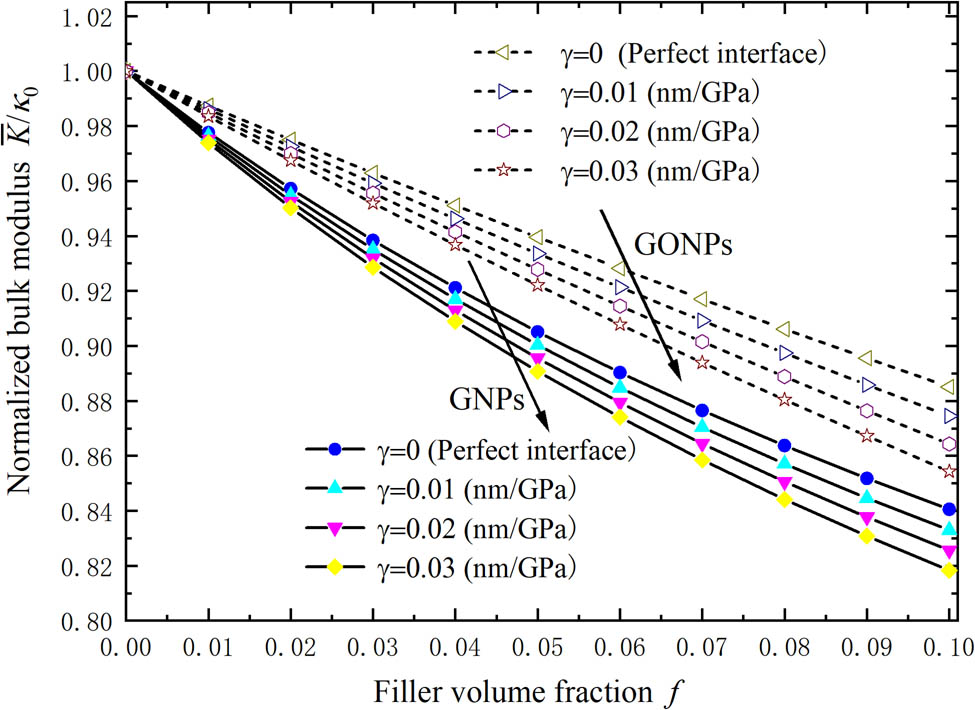
Figure 3 The relationship between the normalized bulk modulus of the nanoplate composites with the volume fractions and interface sliding parameters.
Figure 3

The relationship between the normalized bulk modulus of the nanoplate composites with the volume fractions and interface sliding parameters.

The relationship between the normalized shear modulus and elastic modulus of the ceramic matrix composites with the filler volume fractions and interface sliding parameters is shown in Figure 4. For the case of identical interface sliding parameters, the prediction of our model is nearly consistent with Iftikhar’s results [44]. It is shown that the shear modulus and elastic modulus of composites decrease with the increasing interfacial sliding parameters at a certain filler volume fraction. This implies that the interfacial sliding effects reduce the macroscopic shear modulus and elastic modulus of composites.

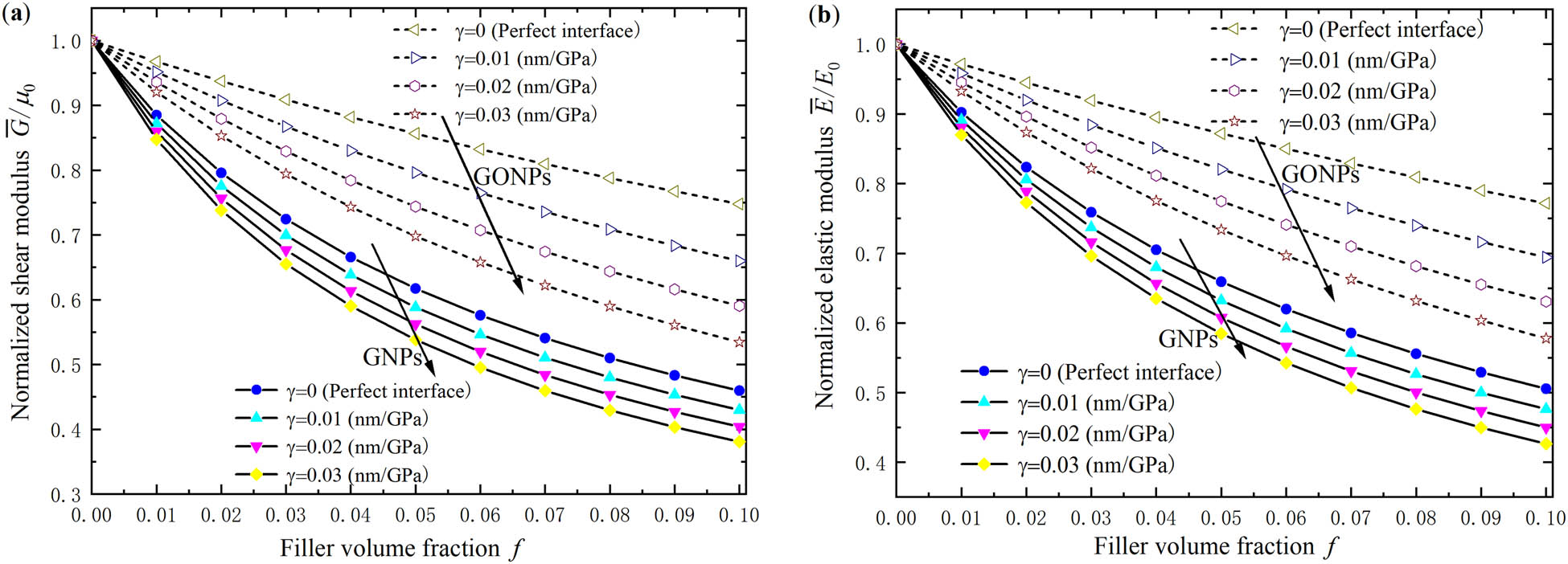
Figure 4 The relationship between the normalized shear modulus (a) and elastic modulus (b) of the nanoplate composite with the filler volume fractions and interface sliding parameters.
Figure 4

The relationship between the normalized shear modulus (a) and elastic modulus (b) of the nanoplate composite with the filler volume fractions and interface sliding parameters.

The relationship between the macroscopic Poisson’s ratio and interface sliding parameters of the ceramic matrix composites is shown in Figure 5. It is readily seen that with the identical interface sliding parameter, the macroscopic Poisson’s ratio increases with the increasing filler concentrations, which exhibits the opposite tendency when compared to the macroscopic bulk, shear, and elastic moduli. In addition, the Poisson’s ratio of the GONP composite is lower than that of the GNP composite. The macroscopic Poisson’s ratio increases accordingly as the increasing interfacial sliding parameter, indicating that the weakened interface effects improve the Poisson’s ratio of the materials. We also find that the interface sliding of the GONP-filled composite has a greater influence on the macroscopic Poisson’s ratio than that of the GNP-filled composite.

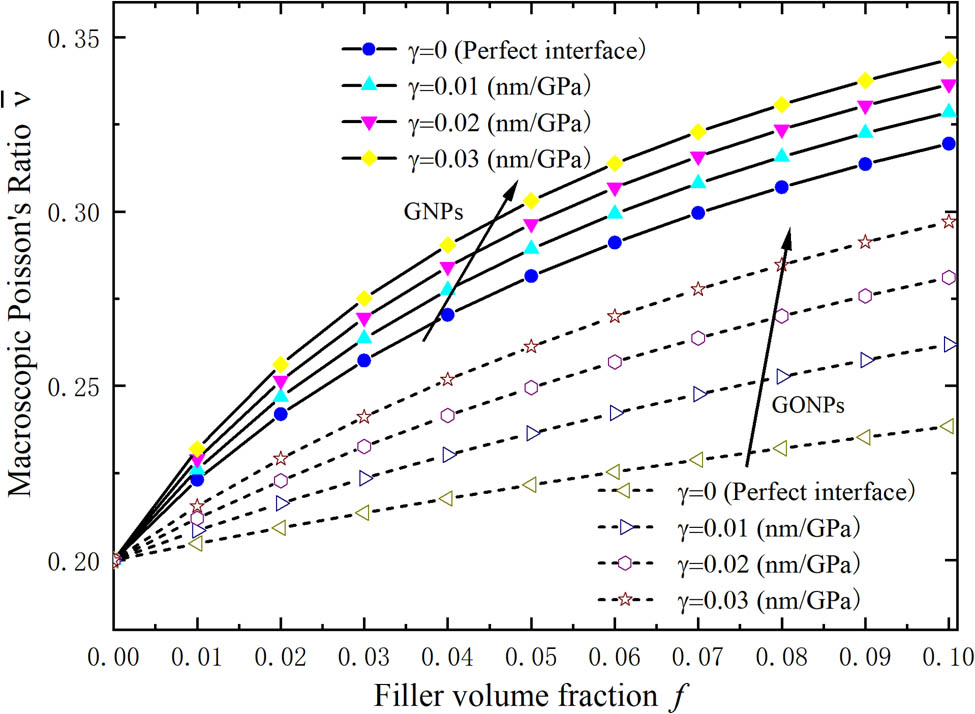
Figure 5 The relationship between the macroscopic Poisson’s ratio of the nanoplate composite with the filler volume fractions and interface sliding parameters.
Figure 5

The relationship between the macroscopic Poisson’s ratio of the nanoplate composite with the filler volume fractions and interface sliding parameters.

4.2 Effective elasto-plastic properties

The uniaxial equivalent stress–strain responses and the initial yield surfaces of the ceramic matrix composites with the two types of nanoplates are comparatively examined based on the nonlinear micromechanics model. The normalized equivalent stress–strain curves of the ceramic matrix composites with the different filler volume fractions are plotted in Figure 6. It could be seen that the GONPs produce the higher elastic modulus of such composite than the GNPs in the elastic stage, which is consistent with the aforementioned results. For the plastic deformation, slightly higher yield strength and more remarkable strain hardening effects can be found for the GNPs composite, Furthermore, the additions of the nanoplates into the ceramic can decrease its elastic stiffness and increase the flow stress of the plastic stage.

Figure 6 The normalized equivalent stress–strain curves of the nanoplate composite with the filler volume fractions.
Figure 6

The normalized equivalent stress–strain curves of the nanoplate composite with the filler volume fractions.

To investigate the effects of the weakened interfaces, the normalized uniaxial equivalent stress–strain curves of the composite with various interface sliding parameters are plotted in Figure 7. It is readily observed that the increasing interfacial parameters decrease the effective elastic modulus and the yield strength of the composite. Compared with the GONPs, GNPs produce a more evident strain hardening tendency. Besides, the effects of the sliding parameters on the flow stress of the composite are negligible when the plastic strain is sufficiently loaded.

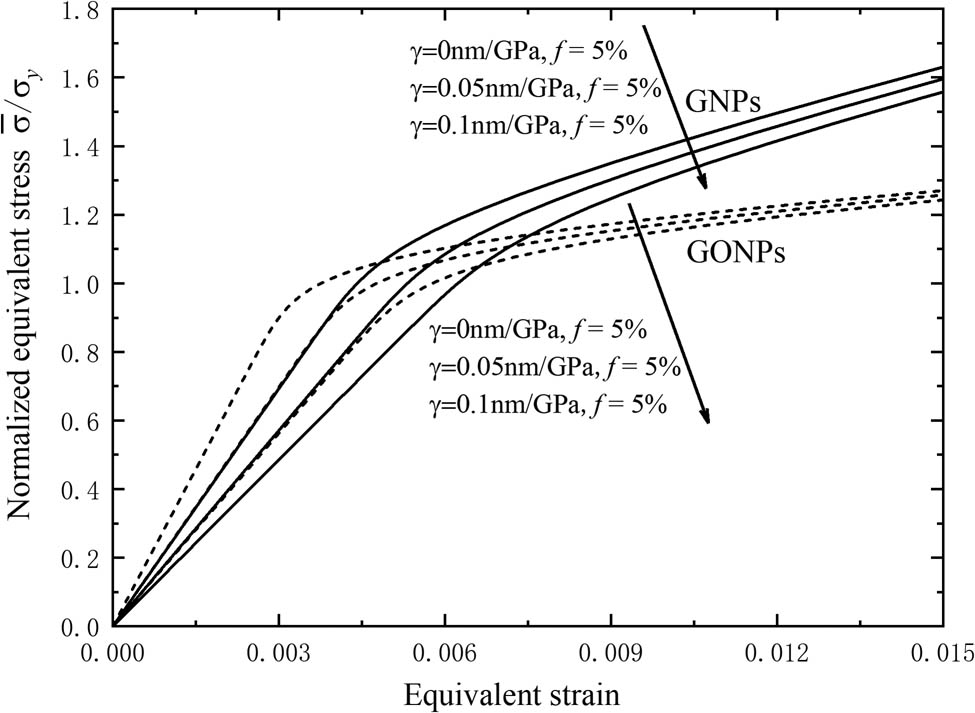
Figure 7 The normalized equivalent stress–strain curves of the nanoplate composite with the different sliding parameters under the same filler concentration of 5%.
Figure 7

The normalized equivalent stress–strain curves of the nanoplate composite with the different sliding parameters under the same filler concentration of 5%.

The normalized uniaxial equivalent stress–strain curves of the ceramic matrix composites with the different nanoplate thicknesses are shown in Figure 8. It is easy to observe that the elastic modulus and the yield strength of the composite are improved with the increasing nanoplate thickness with the same filler concentration and interfacial sliding conditions. Also, the effects of the nanoplate thickness on the flow stress are negligible for the nanocomposite subjected to the relatively large plastic strain.

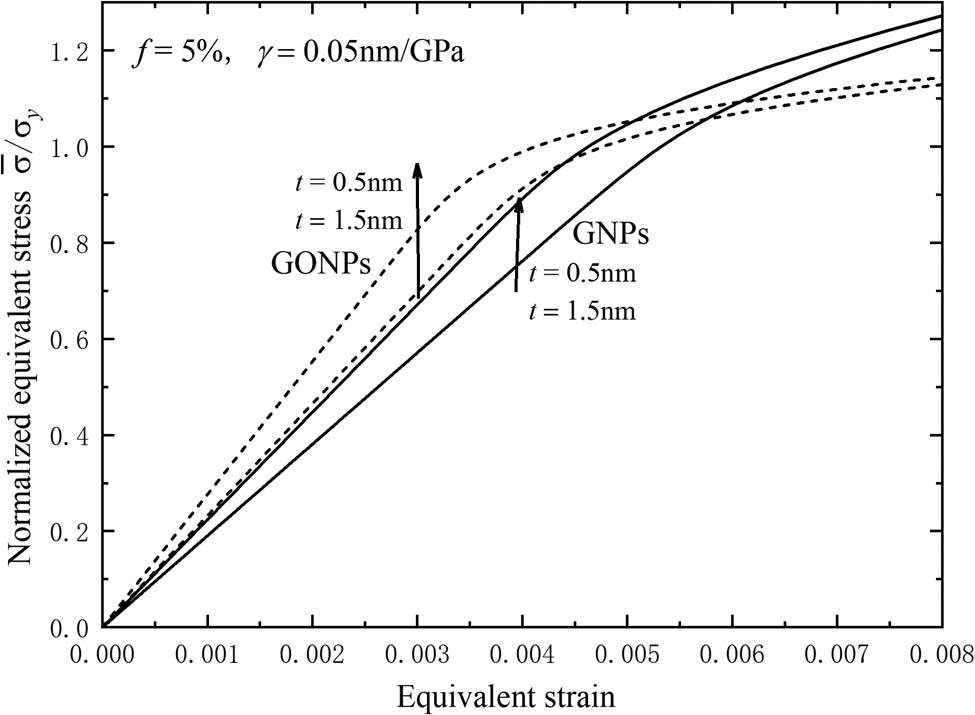
Figure 8 The normalized equivalent stress–strain curves of the nanoplate composite with the different nanoplate thickness under the same filler concentration and the sliding parameter.
Figure 8

The normalized equivalent stress–strain curves of the nanoplate composite with the different nanoplate thickness under the same filler concentration and the sliding parameter.

Under certain macroscopic stress states, the matrix yielding of the nanoplate composite initiates, and the material is said to have become plastic. The evolution of the yield surface, which is described in stress space where the loading produces elastic strains only, is one of the important characteristics of the plastic behavior of the nanocomposite. Figure 9 depicts the variations of the yield surface curves in the normalized hydrostatic stress–equivalent stress space of the nanocomposite with different filler concentrations and interfacial sliding parameters. From Figure 9, the yield surfaces of the nanocomposites continue to shrink when the volume fraction of both the nanoplate fillers varies from 1 to 5%. In other words, the higher filler concentration results in the smaller yield surface. As shown in Figure 9a, GONPs have more prominent effects than the GNPs on the yield surface of the composite when the filler concentration varies. It can be observed in Figure 9b, the increasing interfacial sliding parameter leads to the narrowing yield surface of the composite with a certain filler concentration, indicating the composite with the weaker interfacial bonding is more prone to yield. Likewise, GONPs exhibit more apparent effects than GNPs when the interfacial sliding parameter varies. Overall, the yield surface of the GNP composite is much smaller than that of the GONP composite in most stress spaces.

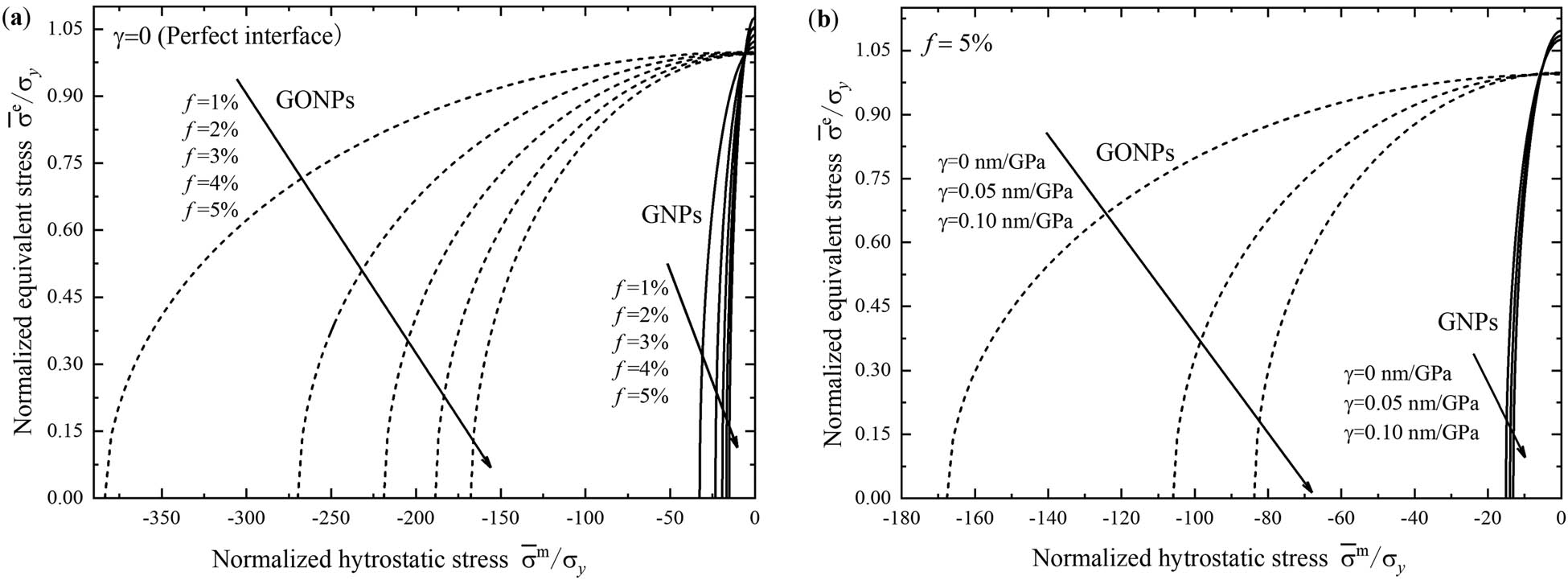
Figure 9 Variations of the normalized yield surface curves of the nanoplate composite with the different filler concentrations (a) and the different interfacial sliding parameters (b).
Figure 9

Variations of the normalized yield surface curves of the nanoplate composite with the different filler concentrations (a) and the different interfacial sliding parameters (b).

5 Conclusions

In this study, a micromechanics model is developed to predict the effective elastic and plastic mechanical properties of the ceramic nanocomposites filled by GNPs or GONPs. The explicit expressions for the effective elastic parameters of the nanoplate composite are presented that account for the effects of the imperfect interface between the nanoplates and the ceramic matrix. Furthermore, the influences of the types of nanoplate and the imperfect interface on the macroscopic elastic properties of the ceramic composites are analyzed. The results show that the nanoplate additions decrease the effective moduli and increase the effective Poisson’s ratio, and the GONPs fillers cause the higher effective moduli and the lower effective Poisson’s ratio of the composite than GNPs. The increasing interfacial sliding parameters decrease the effective moduli and improve the effective Poisson’s ratio.

On the other hand, the macroscopic elasto-plastic behaviors of the nanoplate composite are comparatively investigated by the developed nonlinear micromechanics model based on the field fluctuation method. The influences of the types of nanoplates and interface sliding parameters on the effective elasto-plastic stress–strain curves and yield surface of such composite are examined. The addition of both the nanoplates increases the plastic flow stress and shrinks the yield surface of the ceramic matrix composite. The weakened interface has a significant effect to reduce the yield strength and narrow the yield surface of such composite. The GNP-filled composites exhibit more apparent strain hardening effects and smaller yield surface than the GONP-filled composite under the same conditions.

The present micromechanics model can help to find out how the types of the graphene-family nanoplates and the imperfect interface dominate quantitatively the overall elastoplastic properties of the ceramic matrix composites. It is expected that the micromechanics model and the theoretical findings provide useful references for the microstructural design and the mechanical property evaluation of the nanoplate composite.

  1. Funding information: The authors gratefully acknowledge the financial supports of the National Natural Science Foundation of China (Grant no. 11572109) and Science Foundation for Returned Scholars of Hebei Province of China (Grant no. C20190318).

  2. Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.

  3. Conflict of interest: The authors state no conflict of interest.

References

[1] Wang Q. Simulations of the bending rigidity of graphene. Phys Lett A. 2010;374(9):1180–3.10.1016/j.physleta.2009.12.063Search in Google Scholar

[2] Zhang YY, Pei QX, He XQ, Mai YW. A molecular dynamics simulation study on thermal conductivity of functionalized bilayer graphene sheet. Chem Phys Lett. 2015;622:104–8.10.1016/j.cplett.2015.01.034Search in Google Scholar

[3] Saji VS. Carbon nanostructure-based superhydrophobic surfaces and coatings. Nanotechnol Rev. 2021;10(1):518–71.10.1515/ntrev-2021-0039Search in Google Scholar

[4] Marra F, Lecini J, Tamburrano A, Pisu L, Sarto MS. Electromagnetic wave absorption and structural properties of wide-band absorber made of graphene-printed glass-fibre composite. Sci Rep. 2018;8(1):12029.10.1038/s41598-018-30498-3Search in Google Scholar PubMed PubMed Central

[5] Das DK, Sarkar J. Graphene–magnesium nanocomposite: An advanced material for aerospace application. Mod Phys Lett B. 2018;32(06):1850075.10.1142/S0217984918500756Search in Google Scholar

[6] Kausar A, Rafique I, Muhammad B. Aerospace application of polymer nanocomposite with carbon nanotube, graphite, graphene oxide and nanoclay. Polym Plast Technol Eng. 2017;56:56–1456.10.1080/03602559.2016.1276594Search in Google Scholar

[7] Krystek M, Ciesielski A, Samori P. Graphene-based cementitious composites: toward next-generation construction technologies. Adv Funct Mater. 2021;31:27.10.1002/adfm.202101887Search in Google Scholar

[8] Wang ZY, Jia ZM, Feng XP, Zou Y. Graphene nanoplatelets/epoxy composites with excellent shear properties for construction adhesives. Compos B Eng. 2018;152:311–5.10.1016/j.compositesb.2018.08.113Search in Google Scholar

[9] Zhang X, An Y, Han J, Han W, Zhao G, Jin X. Graphene nanosheet reinforced ZrB2–SiC ceramic composite by thermal reduction of graphene oxide. RSC Adv. 2015;5(58):47060–5.10.1039/C5RA05922DSearch in Google Scholar

[10] Shuai C, Gao C, Feng P, Peng S. Graphene-reinforced mechanical properties of calcium silicate scaffolds by laser sintering. RSC Adv. 2014;4(25):12782–8.10.1039/C3RA47862ASearch in Google Scholar

[11] Ahmad I, Yazdani B, Zhu Y. Recent advances on carbon nanotubes and graphene reinforced ceramics nanocomposites. Nanomaterials (Basel). 2015;5:90–114.10.3390/nano5010090Search in Google Scholar PubMed PubMed Central

[12] Zhou B-Y, Fan S-J, Fan Y-C, Zheng Q, Zhang X, Jiang W, et al. Recent progress in ceramic matrix composites reinforced with graphene nanoplatelets. Rare Met. 2019;39(5):513–28.10.1007/s12598-019-01306-2Search in Google Scholar

[13] Chen F, Yan K, Sun J, Hong J, Zhu Y, Huang Z. From the research state of the thermal properties of graphene reinforced ceramics to the future of computer simulation. Ceram Int. 2020;46(11):18428–45.10.1016/j.ceramint.2020.04.265Search in Google Scholar

[14] Porwal H, Grasso S, Reece MJ. Review of graphene–ceramic matrix composites. Adv Appl Ceram. 2014;112(8):443–54.10.1179/174367613X13764308970581Search in Google Scholar

[15] Kośla K, Olejnik M, Olszewska K. Preparation and properties of composite materials containing graphene structures and their applicability in personal protective equipment: A Review. Rev Adv Mater Sci. 2020;59(1):215–42.10.1515/rams-2020-0025Search in Google Scholar

[16] Sun Z, Zhao J, Wang X, Cui E, Yu H. Reinforcing mechanisms of graphene and nano-TiC in Al2O3-based ceramic-tool materials. Nanomaterials (Basel). 2020;10:9.10.3390/nano10091815Search in Google Scholar PubMed PubMed Central

[17] Zhao W, Sun J, Huang Z. Three-dimensional graphene-carbon nanotube reinforced ceramics and computer simulation. Ceram Int. 2021;47(24):33941–55.10.1016/j.ceramint.2021.08.304Search in Google Scholar

[18] Ramirez C, Osendi MI. Toughening in ceramics containing graphene fillers. Ceram Int. 2014;40(7):11187–92.10.1016/j.ceramint.2014.03.150Search in Google Scholar

[19] Li Z-l, Zhao J, Sun J-l, Gong F, Ni X-y. Reinforcing effect of graphene on the mechanical properties of Al2O3/TiC ceramics. Int J Min Met Mater. 2017;24(12):1403–11.10.1007/s12613-017-1533-zSearch in Google Scholar

[20] Wang X, Zhao J, Cui E, Song S, Liu H, Song W. Microstructure, mechanical properties and toughening mechanisms of graphene reinforced Al2O3–WC–TiC composite ceramic tool material. Ceram Int. 2019;45(8):10321–9.10.1016/j.ceramint.2019.02.087Search in Google Scholar

[21] Liu F, Wang M, Chen Y, Gao J, Ma T. Mechanical properties and microstructure of reaction sintering SiC ceramics reinforced with graphene-based fillers. Appl Phys A. 2019;125:10.10.1007/s00339-019-2975-0Search in Google Scholar

[22] Cano-Crespo R, Moshtaghioun BM, Gómez-García D, Domínguez-Rodríguez A, Moreno R. Carbon nanofibers replacing graphene oxide in ceramic composites as a reinforcing-phase: Is it feasible? J Eur Ceram Soc. 2017;37(12):3791–6.10.1016/j.jeurceramsoc.2017.03.027Search in Google Scholar

[23] Deshpande VS, Evans AG. Inelastic deformation and energy dissipation in ceramics: A mechanism-based constitutive model. J Mech Phys Solids. 2008;56(10):3077–100.10.1016/j.jmps.2008.05.002Search in Google Scholar

[24] Aminipour H, Janghorban M, Civalek O. Analysis of functionally graded doubly-curved shells with different materials via higher order shear deformation theory. Compos Struct. 2020;251:251.10.1016/j.compstruct.2020.112645Search in Google Scholar

[25] Cao Y, Zhang D, Yang Y, Lin B, Lv J, Yang X, et al. Dispersed-monolayer graphene-doped polymer/silica hybrid Mach-Zehnder interferometer (MZI) thermal optical switch with low-power consumption and fast response. Polymers (Basel). 2019;11:11.10.3390/polym11111898Search in Google Scholar

[26] Ozbas B, O’Neill CD, Register RA, Aksay IA, Prud’homme RK, Adamson DH. Multifunctional elastomer nanocomposites with functionalized graphene single sheets. J Polym Sci B Polym Phys. 2012;50(13):910–6.10.1002/polb.23080Search in Google Scholar

[27] Seidel G, Lagoudas D. Micromechanical analysis of the effective elastic properties of carbon nanotube reinforced composites. Mech Mater. 2006;38:884–907.10.1016/j.mechmat.2005.06.029Search in Google Scholar

[28] Domínguez-Rodríguez G, Tapia A, Seidel GD, Avilés F. Influence of structural defects on the electrical properties of carbon nanotubes and their polymer composites. Adv Eng Mater. 2016;18(11):1897–905.10.1002/adem.201600116Search in Google Scholar

[29] Sadeghpour E, Guo Y, Chua D, Shim VPW. A modified Mori–Tanaka approach incorporating filler-matrix interface failure to model graphene/polymer nanocomposites. Int J Mech Sci. 2020;180:180.10.1016/j.ijmecsci.2020.105699Search in Google Scholar

[30] Bayard O, Plé O. Fracture mechanics of reactive powder concrete: material modelling and experimental investigations. Eng Fract Mech. 2003;70(7):839–51.10.1016/S0013-7944(02)00153-4Search in Google Scholar

[31] Dimitrijevic MM, Tomic N, Medjo B, Jancic-Heinemann R, Rakin M, Volkov-Husovic T. Modeling of the mechanical behavior of fiber-reinforced ceramic composites using finite element method (FEM). Sci Sinter. 2014;46(3):385–90.10.2298/SOS1403385DSearch in Google Scholar

[32] Jiménez Riobóo R, Climent-Pascual E, Díez-Betriu X, Jimenez-Villacorta F, Prieto C, Andres A. Elastic constants of graphene oxide few-layer films: Correlations with interlayer stacking and bonding. J Mater Chem C. 2015;3:3–4875.10.1039/C4TC02883JSearch in Google Scholar

[33] Hill R. Theory of mechanical properties of fibre-strengthened materials: I. Elastic behaviour. J Mech Phys Solids. 1964;12(4):199–212.10.1016/0022-5096(64)90019-5Search in Google Scholar

[34] Sun Y, Hu Y, Liu M. Elasto-plastic behavior of graphene reinforced nanocomposites with hard/soft interface effects. Mater Des. 2021;202:199.10.1016/j.matdes.2020.109421Search in Google Scholar

[35] Qu J. The effect of slightly weakened interfaces on the overall elastic properties of composite materials. Mech Mater. 1993;14(4):269–81.10.1016/0167-6636(93)90082-3Search in Google Scholar

[36] Liu DY, Chen WQ. Thermal stresses in bilayer systems with weak interface. Mech Res Commun. 2010;37(6):520–4.10.1016/j.mechrescom.2010.07.005Search in Google Scholar

[37] Perelmuter M. Analysis of interaction of bridged cracks and weak interfaces. Int J Mech Sci. 2018;149:349–60.10.1016/j.ijmecsci.2018.10.011Search in Google Scholar

[38] Li Yd, Bin J, Nan Z, Tang Lq, Yao D. Dynamic stress intensity factor of the weak/micro-discontinuous interface crack of a FGM coating. Int J Solids Struct. 2006;43(16):4795–809.10.1016/j.ijsolstr.2005.07.030Search in Google Scholar

[39] Zhu QZ, Gu ST, Yvonnet J, Shao JF, He QC. Three-dimensional numerical modelling by XFEM of spring-layer imperfect curved interfaces with applications to linearly elastic composite materials. Int J Numer Methods Eng. 2011;88(4):307–28.10.1002/nme.3175Search in Google Scholar

[40] Hashemi R. On the overall viscoelastic behavior of graphene/polymer nanocomposites with imperfect interface. Int J Eng Sci. 2016;105:38–55.10.1016/j.ijengsci.2016.04.006Search in Google Scholar

[41] Castañeda PP. The effective mechanical properties of nonlinear isotropic composites. J Mech Phys Solids. 1991;39(1):45–71.10.1016/0022-5096(91)90030-RSearch in Google Scholar

[42] Ma L-H, Yang Q-S, Yan X-H, Qin Q-H. Elastoplastic mechanics of porous materials with varied inner pressures. Mech Mater. 2014;73:58–75.10.1016/j.mechmat.2014.02.005Search in Google Scholar

[43] Qiu YP, Weng GJ. A theory of plasticity for porous materials and particle-reinforced composites. J Appl Mech-T ASME. 1992;59:(Copyright 1992, IEE) 261–8.10.1115/1.2899515Search in Google Scholar

[44] Ahmad I, Islam M, Abdo HS, Subhani T, Khalil KA, Almajid AA, et al. Toughening mechanisms and mechanical properties of graphene nanosheet-reinforced alumina. Mater Des. 2015;88:1234–43.10.1016/j.matdes.2015.09.125Search in Google Scholar
Received: 2021-12-31
Revised: 2022-05-07
Accepted: 2022-05-24
Published Online: 2022-07-04

© 2022 Lian-Hua Ma et al., published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Research Articles
  2. Theoretical and experimental investigation of MWCNT dispersion effect on the elastic modulus of flexible PDMS/MWCNT nanocomposites
  3. Mechanical, morphological, and fracture-deformation behavior of MWCNTs-reinforced (Al–Cu–Mg–T351) alloy cast nanocomposites fabricated by optimized mechanical milling and powder metallurgy techniques
  4. Flammability and physical stability of sugar palm crystalline nanocellulose reinforced thermoplastic sugar palm starch/poly(lactic acid) blend bionanocomposites
  5. Glutathione-loaded non-ionic surfactant niosomes: A new approach to improve oral bioavailability and hepatoprotective efficacy of glutathione
  6. Relationship between mechano-bactericidal activity and nanoblades density on chemically strengthened glass
  7. In situ regulation of microstructure and microwave-absorbing properties of FeSiAl through HNO3 oxidation
  8. Research on a mechanical model of magnetorheological fluid different diameter particles
  9. Nanomechanical and dynamic mechanical properties of rubber–wood–plastic composites
  10. Investigative properties of CeO2 doped with niobium: A combined characterization and DFT studies
  11. Miniaturized peptidomimetics and nano-vesiculation in endothelin types through probable nano-disk formation and structure property relationships of endothelins’ fragments
  12. N/S co-doped CoSe/C nanocubes as anode materials for Li-ion batteries
  13. Synergistic effects of halloysite nanotubes with metal and phosphorus additives on the optimal design of eco-friendly sandwich panels with maximum flame resistance and minimum weight
  14. Octreotide-conjugated silver nanoparticles for active targeting of somatostatin receptors and their application in a nebulized rat model
  15. Controllable morphology of Bi2S3 nanostructures formed via hydrothermal vulcanization of Bi2O3 thin-film layer and their photoelectrocatalytic performances
  16. Development of (−)-epigallocatechin-3-gallate-loaded folate receptor-targeted nanoparticles for prostate cancer treatment
  17. Enhancement of the mechanical properties of HDPE mineral nanocomposites by filler particles modulation of the matrix plastic/elastic behavior
  18. Effect of plasticizers on the properties of sugar palm nanocellulose/cinnamon essential oil reinforced starch bionanocomposite films
  19. Optimization of nano coating to reduce the thermal deformation of ball screws
  20. Preparation of efficient piezoelectric PVDF–HFP/Ni composite films by high electric field poling
  21. MHD dissipative Casson nanofluid liquid film flow due to an unsteady stretching sheet with radiation influence and slip velocity phenomenon
  22. Effects of nano-SiO2 modification on rubberised mortar and concrete with recycled coarse aggregates
  23. Mechanical and microscopic properties of fiber-reinforced coal gangue-based geopolymer concrete
  24. Effect of morphology and size on the thermodynamic stability of cerium oxide nanoparticles: Experiment and molecular dynamics calculation
  25. Mechanical performance of a CFRP composite reinforced via gelatin-CNTs: A study on fiber interfacial enhancement and matrix enhancement
  26. A practical review over surface modification, nanopatterns, emerging materials, drug delivery systems, and their biophysiochemical properties for dental implants: Recent progresses and advances
  27. HTR: An ultra-high speed algorithm for cage recognition of clathrate hydrates
  28. Effects of microalloying elements added by in situ synthesis on the microstructure of WCu composites
  29. A highly sensitive nanobiosensor based on aptamer-conjugated graphene-decorated rhodium nanoparticles for detection of HER2-positive circulating tumor cells
  30. Progressive collapse performance of shear strengthened RC frames by nano CFRP
  31. Core–shell heterostructured composites of carbon nanotubes and imine-linked hyperbranched polymers as metal-free Li-ion anodes
  32. A Galerkin strategy for tri-hybridized mixture in ethylene glycol comprising variable diffusion and thermal conductivity using non-Fourier’s theory
  33. Simple models for tensile modulus of shape memory polymer nanocomposites at ambient temperature
  34. Preparation and morphological studies of tin sulfide nanoparticles and use as efficient photocatalysts for the degradation of rhodamine B and phenol
  35. Polyethyleneimine-impregnated activated carbon nanofiber composited graphene-derived rice husk char for efficient post-combustion CO2 capture
  36. Electrospun nanofibers of Co3O4 nanocrystals encapsulated in cyclized-polyacrylonitrile for lithium storage
  37. Pitting corrosion induced on high-strength high carbon steel wire in high alkaline deaerated chloride electrolyte
  38. Formulation of polymeric nanoparticles loaded sorafenib; evaluation of cytotoxicity, molecular evaluation, and gene expression studies in lung and breast cancer cell lines
  39. Engineered nanocomposites in asphalt binders
  40. Influence of loading voltage, domain ratio, and additional load on the actuation of dielectric elastomer
  41. Thermally induced hex-graphene transitions in 2D carbon crystals
  42. The surface modification effect on the interfacial properties of glass fiber-reinforced epoxy: A molecular dynamics study
  43. Molecular dynamics study of deformation mechanism of interfacial microzone of Cu/Al2Cu/Al composites under tension
  44. Nanocolloid simulators of luminescent solar concentrator photovoltaic windows
  45. Compressive strength and anti-chloride ion penetration assessment of geopolymer mortar merging PVA fiber and nano-SiO2 using RBF–BP composite neural network
  46. Effect of 3-mercapto-1-propane sulfonate sulfonic acid and polyvinylpyrrolidone on the growth of cobalt pillar by electrodeposition
  47. Dynamics of convective slippery constraints on hybrid radiative Sutterby nanofluid flow by Galerkin finite element simulation
  48. Preparation of vanadium by the magnesiothermic self-propagating reduction and process control
  49. Microstructure-dependent photoelectrocatalytic activity of heterogeneous ZnO–ZnS nanosheets
  50. Cytotoxic and pro-inflammatory effects of molybdenum and tungsten disulphide on human bronchial cells
  51. Improving recycled aggregate concrete by compression casting and nano-silica
  52. Chemically reactive Maxwell nanoliquid flow by a stretching surface in the frames of Newtonian heating, nonlinear convection and radiative flux: Nanopolymer flow processing simulation
  53. Nonlinear dynamic and crack behaviors of carbon nanotubes-reinforced composites with various geometries
  54. Biosynthesis of copper oxide nanoparticles and its therapeutic efficacy against colon cancer
  55. Synthesis and characterization of smart stimuli-responsive herbal drug-encapsulated nanoniosome particles for efficient treatment of breast cancer
  56. Homotopic simulation for heat transport phenomenon of the Burgers nanofluids flow over a stretching cylinder with thermal convective and zero mass flux conditions
  57. Incorporation of copper and strontium ions in TiO2 nanotubes via dopamine to enhance hemocompatibility and cytocompatibility
  58. Mechanical, thermal, and barrier properties of starch films incorporated with chitosan nanoparticles
  59. Mechanical properties and microstructure of nano-strengthened recycled aggregate concrete
  60. Glucose-responsive nanogels efficiently maintain the stability and activity of therapeutic enzymes
  61. Tunning matrix rheology and mechanical performance of ultra-high performance concrete using cellulose nanofibers
  62. Flexible MXene/copper/cellulose nanofiber heat spreader films with enhanced thermal conductivity
  63. Promoted charge separation and specific surface area via interlacing of N-doped titanium dioxide nanotubes on carbon nitride nanosheets for photocatalytic degradation of Rhodamine B
  64. Elucidating the role of silicon dioxide and titanium dioxide nanoparticles in mitigating the disease of the eggplant caused by Phomopsis vexans, Ralstonia solanacearum, and root-knot nematode Meloidogyne incognita
  65. An implication of magnetic dipole in Carreau Yasuda liquid influenced by engine oil using ternary hybrid nanomaterial
  66. Robust synthesis of a composite phase of copper vanadium oxide with enhanced performance for durable aqueous Zn-ion batteries
  67. Tunning self-assembled phases of bovine serum albumin via hydrothermal process to synthesize novel functional hydrogel for skin protection against UVB
  68. A comparative experimental study on damping properties of epoxy nanocomposite beams reinforced with carbon nanotubes and graphene nanoplatelets
  69. Lightweight and hydrophobic Ni/GO/PVA composite aerogels for ultrahigh performance electromagnetic interference shielding
  70. Research on the auxetic behavior and mechanical properties of periodically rotating graphene nanostructures
  71. Repairing performances of novel cement mortar modified with graphene oxide and polyacrylate polymer
  72. Closed-loop recycling and fabrication of hydrophilic CNT films with high performance
  73. Design of thin-film configuration of SnO2–Ag2O composites for NO2 gas-sensing applications
  74. Study on stress distribution of SiC/Al composites based on microstructure models with microns and nanoparticles
  75. PVDF green nanofibers as potential carriers for improving self-healing and mechanical properties of carbon fiber/epoxy prepregs
  76. Osteogenesis capability of three-dimensionally printed poly(lactic acid)-halloysite nanotube scaffolds containing strontium ranelate
  77. Silver nanoparticles induce mitochondria-dependent apoptosis and late non-canonical autophagy in HT-29 colon cancer cells
  78. Preparation and bonding mechanisms of polymer/metal hybrid composite by nano molding technology
  79. Damage self-sensing and strain monitoring of glass-reinforced epoxy composite impregnated with graphene nanoplatelet and multiwalled carbon nanotubes
  80. Thermal analysis characterisation of solar-powered ship using Oldroyd hybrid nanofluids in parabolic trough solar collector: An optimal thermal application
  81. Pyrene-functionalized halloysite nanotubes for simultaneously detecting and separating Hg(ii) in aqueous media: A comprehensive comparison on interparticle and intraparticle excimers
  82. Fabrication of self-assembly CNT flexible film and its piezoresistive sensing behaviors
  83. Thermal valuation and entropy inspection of second-grade nanoscale fluid flow over a stretching surface by applying Koo–Kleinstreuer–Li relation
  84. Mechanical properties and microstructure of nano-SiO2 and basalt-fiber-reinforced recycled aggregate concrete
  85. Characterization and tribology performance of polyaniline-coated nanodiamond lubricant additives
  86. Combined impact of Marangoni convection and thermophoretic particle deposition on chemically reactive transport of nanofluid flow over a stretching surface
  87. Spark plasma extrusion of binder free hydroxyapatite powder
  88. An investigation on thermo-mechanical performance of graphene-oxide-reinforced shape memory polymer
  89. Effect of nanoadditives on the novel leather fiber/recycled poly(ethylene-vinyl-acetate) polymer composites for multifunctional applications: Fabrication, characterizations, and multiobjective optimization using central composite design
  90. Design selection for a hemispherical dimple core sandwich panel using hybrid multi-criteria decision-making methods
  91. Improving tensile strength and impact toughness of plasticized poly(lactic acid) biocomposites by incorporating nanofibrillated cellulose
  92. Green synthesis of spinel copper ferrite (CuFe2O4) nanoparticles and their toxicity
  93. The effect of TaC and NbC hybrid and mono-nanoparticles on AA2024 nanocomposites: Microstructure, strengthening, and artificial aging
  94. Excited-state geometry relaxation of pyrene-modified cellulose nanocrystals under UV-light excitation for detecting Fe3+
  95. Effect of CNTs and MEA on the creep of face-slab concrete at an early age
  96. Effect of deformation conditions on compression phase transformation of AZ31
  97. Application of MXene as a new generation of highly conductive coating materials for electromembrane-surrounded solid-phase microextraction
  98. A comparative study of the elasto-plastic properties for ceramic nanocomposites filled by graphene or graphene oxide nanoplates
  99. Encapsulation strategies for improving the biological behavior of CdS@ZIF-8 nanocomposites
  100. Biosynthesis of ZnO NPs from pumpkin seeds’ extract and elucidation of its anticancer potential against breast cancer
  101. Preliminary trials of the gold nanoparticles conjugated chrysin: An assessment of anti-oxidant, anti-microbial, and in vitro cytotoxic activities of a nanoformulated flavonoid
  102. Effect of micron-scale pores increased by nano-SiO2 sol modification on the strength of cement mortar
  103. Fractional simulations for thermal flow of hybrid nanofluid with aluminum oxide and titanium oxide nanoparticles with water and blood base fluids
  104. The effect of graphene nano-powder on the viscosity of water: An experimental study and artificial neural network modeling
  105. Development of a novel heat- and shear-resistant nano-silica gelling agent
  106. Characterization, biocompatibility and in vivo of nominal MnO2-containing wollastonite glass-ceramic
  107. Entropy production simulation of second-grade magnetic nanomaterials flowing across an expanding surface with viscidness dissipative flux
  108. Enhancement in structural, morphological, and optical properties of copper oxide for optoelectronic device applications
  109. Aptamer-functionalized chitosan-coated gold nanoparticle complex as a suitable targeted drug carrier for improved breast cancer treatment
  110. Performance and overall evaluation of nano-alumina-modified asphalt mixture
  111. Analysis of pure nanofluid (GO/engine oil) and hybrid nanofluid (GO–Fe3O4/engine oil): Novel thermal and magnetic features
  112. Synthesis of Ag@AgCl modified anatase/rutile/brookite mixed phase TiO2 and their photocatalytic property
  113. Mechanisms and influential variables on the abrasion resistance hydraulic concrete
  114. Synergistic reinforcement mechanism of basalt fiber/cellulose nanocrystals/polypropylene composites
  115. Achieving excellent oxidation resistance and mechanical properties of TiB2–B4C/carbon aerogel composites by quick-gelation and mechanical mixing
  116. Microwave-assisted sol–gel template-free synthesis and characterization of silica nanoparticles obtained from South African coal fly ash
  117. Pulsed laser-assisted synthesis of nano nickel(ii) oxide-anchored graphitic carbon nitride: Characterizations and their potential antibacterial/anti-biofilm applications
  118. Effects of nano-ZrSi2 on thermal stability of phenolic resin and thermal reusability of quartz–phenolic composites
  119. Benzaldehyde derivatives on tin electroplating as corrosion resistance for fabricating copper circuit
  120. Mechanical and heat transfer properties of 4D-printed shape memory graphene oxide/epoxy acrylate composites
  121. Coupling the vanadium-induced amorphous/crystalline NiFe2O4 with phosphide heterojunction toward active oxygen evolution reaction catalysts
  122. Graphene-oxide-reinforced cement composites mechanical and microstructural characteristics at elevated temperatures
  123. Gray correlation analysis of factors influencing compressive strength and durability of nano-SiO2 and PVA fiber reinforced geopolymer mortar
  124. Preparation of layered gradient Cu–Cr–Ti alloy with excellent mechanical properties, thermal stability, and electrical conductivity
  125. Recovery of Cr from chrome-containing leather wastes to develop aluminum-based composite material along with Al2O3 ceramic particles: An ingenious approach
  126. Mechanisms of the improved stiffness of flexible polymers under impact loading
  127. Anticancer potential of gold nanoparticles (AuNPs) using a battery of in vitro tests
  128. Review Articles
  129. Proposed approaches for coronaviruses elimination from wastewater: Membrane techniques and nanotechnology solutions
  130. Application of Pickering emulsion in oil drilling and production
  131. The contribution of microfluidics to the fight against tuberculosis
  132. Graphene-based biosensors for disease theranostics: Development, applications, and recent advancements
  133. Synthesis and encapsulation of iron oxide nanorods for application in magnetic hyperthermia and photothermal therapy
  134. Contemporary nano-architectured drugs and leads for ανβ3 integrin-based chemotherapy: Rationale and retrospect
  135. State-of-the-art review of fabrication, application, and mechanical properties of functionally graded porous nanocomposite materials
  136. Insights on magnetic spinel ferrites for targeted drug delivery and hyperthermia applications
  137. A review on heterogeneous oxidation of acetaminophen based on micro and nanoparticles catalyzed by different activators
  138. Early diagnosis of lung cancer using magnetic nanoparticles-integrated systems
  139. Advances in ZnO: Manipulation of defects for enhancing their technological potentials
  140. Efficacious nanomedicine track toward combating COVID-19
  141. A review of the design, processes, and properties of Mg-based composites
  142. Green synthesis of nanoparticles for varied applications: Green renewable resources and energy-efficient synthetic routes
  143. Two-dimensional nanomaterial-based polymer composites: Fundamentals and applications
  144. Recent progress and challenges in plasmonic nanomaterials
  145. Apoptotic cell-derived micro/nanosized extracellular vesicles in tissue regeneration
  146. Electronic noses based on metal oxide nanowires: A review
  147. Framework materials for supercapacitors
  148. An overview on the reproductive toxicity of graphene derivatives: Highlighting the importance
  149. Antibacterial nanomaterials: Upcoming hope to overcome antibiotic resistance crisis
  150. Research progress of carbon materials in the field of three-dimensional printing polymer nanocomposites
  151. A review of atomic layer deposition modelling and simulation methodologies: Density functional theory and molecular dynamics
  152. Recent advances in the preparation of PVDF-based piezoelectric materials
  153. Recent developments in tensile properties of friction welding of carbon fiber-reinforced composite: A review
  154. Comprehensive review of the properties of fly ash-based geopolymer with additive of nano-SiO2
  155. Perspectives in biopolymer/graphene-based composite application: Advances, challenges, and recommendations
  156. Graphene-based nanocomposite using new modeling molecular dynamic simulations for proposed neutralizing mechanism and real-time sensing of COVID-19
  157. Nanotechnology application on bamboo materials: A review
  158. Recent developments and future perspectives of biorenewable nanocomposites for advanced applications
  159. Nanostructured lipid carrier system: A compendium of their formulation development approaches, optimization strategies by quality by design, and recent applications in drug delivery
  160. 3D printing customized design of human bone tissue implant and its application
  161. Design, preparation, and functionalization of nanobiomaterials for enhanced efficacy in current and future biomedical applications
  162. A brief review of nanoparticles-doped PEDOT:PSS nanocomposite for OLED and OPV
  163. Nanotechnology interventions as a putative tool for the treatment of dental afflictions
  164. Recent advancements in metal–organic frameworks integrating quantum dots (QDs@MOF) and their potential applications
  165. A focused review of short electrospun nanofiber preparation techniques for composite reinforcement
  166. Microstructural characteristics and nano-modification of interfacial transition zone in concrete: A review
  167. Latest developments in the upconversion nanotechnology for the rapid detection of food safety: A review
  168. Strategic applications of nano-fertilizers for sustainable agriculture: Benefits and bottlenecks
  169. Molecular dynamics application of cocrystal energetic materials: A review
  170. Synthesis and application of nanometer hydroxyapatite in biomedicine
  171. Cutting-edge development in waste-recycled nanomaterials for energy storage and conversion applications
  172. Biological applications of ternary quantum dots: A review
  173. Nanotherapeutics for hydrogen sulfide-involved treatment: An emerging approach for cancer therapy
  174. Application of antibacterial nanoparticles in orthodontic materials
  175. Effect of natural-based biological hydrogels combined with growth factors on skin wound healing
  176. Nanozymes – A route to overcome microbial resistance: A viewpoint
  177. Recent developments and applications of smart nanoparticles in biomedicine
  178. Contemporary review on carbon nanotube (CNT) composites and their impact on multifarious applications
  179. Interfacial interactions and reinforcing mechanisms of cellulose and chitin nanomaterials and starch derivatives for cement and concrete strength and durability enhancement: A review
  180. Diamond-like carbon films for tribological modification of rubber
  181. Layered double hydroxides (LDHs) modified cement-based materials: A systematic review
  182. Recent research progress and advanced applications of silica/polymer nanocomposites
  183. Modeling of supramolecular biopolymers: Leading the in silico revolution of tissue engineering and nanomedicine
  184. Recent advances in perovskites-based optoelectronics
  185. Biogenic synthesis of palladium nanoparticles: New production methods and applications
  186. A comprehensive review of nanofluids with fractional derivatives: Modeling and application
  187. Electrospinning of marine polysaccharides: Processing and chemical aspects, challenges, and future prospects
  188. Electrohydrodynamic printing for demanding devices: A review of processing and applications
  189. Rapid Communications
  190. Structural material with designed thermal twist for a simple actuation
  191. Recent advances in photothermal materials for solar-driven crude oil adsorption
https://doi.org/10.1515/ntrev-2022-0150
Keywords for this article
ceramic matrix composite; nanoplate; elasto-plastic properties; micromechanics
Creative Commons
BY 4.0

Articles in the same Issue

  1. Research Articles
  2. Theoretical and experimental investigation of MWCNT dispersion effect on the elastic modulus of flexible PDMS/MWCNT nanocomposites
  3. Mechanical, morphological, and fracture-deformation behavior of MWCNTs-reinforced (Al–Cu–Mg–T351) alloy cast nanocomposites fabricated by optimized mechanical milling and powder metallurgy techniques
  4. Flammability and physical stability of sugar palm crystalline nanocellulose reinforced thermoplastic sugar palm starch/poly(lactic acid) blend bionanocomposites
  5. Glutathione-loaded non-ionic surfactant niosomes: A new approach to improve oral bioavailability and hepatoprotective efficacy of glutathione
  6. Relationship between mechano-bactericidal activity and nanoblades density on chemically strengthened glass
  7. In situ regulation of microstructure and microwave-absorbing properties of FeSiAl through HNO3 oxidation
  8. Research on a mechanical model of magnetorheological fluid different diameter particles
  9. Nanomechanical and dynamic mechanical properties of rubber–wood–plastic composites
  10. Investigative properties of CeO2 doped with niobium: A combined characterization and DFT studies
  11. Miniaturized peptidomimetics and nano-vesiculation in endothelin types through probable nano-disk formation and structure property relationships of endothelins’ fragments
  12. N/S co-doped CoSe/C nanocubes as anode materials for Li-ion batteries
  13. Synergistic effects of halloysite nanotubes with metal and phosphorus additives on the optimal design of eco-friendly sandwich panels with maximum flame resistance and minimum weight
  14. Octreotide-conjugated silver nanoparticles for active targeting of somatostatin receptors and their application in a nebulized rat model
  15. Controllable morphology of Bi2S3 nanostructures formed via hydrothermal vulcanization of Bi2O3 thin-film layer and their photoelectrocatalytic performances
  16. Development of (−)-epigallocatechin-3-gallate-loaded folate receptor-targeted nanoparticles for prostate cancer treatment
  17. Enhancement of the mechanical properties of HDPE mineral nanocomposites by filler particles modulation of the matrix plastic/elastic behavior
  18. Effect of plasticizers on the properties of sugar palm nanocellulose/cinnamon essential oil reinforced starch bionanocomposite films
  19. Optimization of nano coating to reduce the thermal deformation of ball screws
  20. Preparation of efficient piezoelectric PVDF–HFP/Ni composite films by high electric field poling
  21. MHD dissipative Casson nanofluid liquid film flow due to an unsteady stretching sheet with radiation influence and slip velocity phenomenon
  22. Effects of nano-SiO2 modification on rubberised mortar and concrete with recycled coarse aggregates
  23. Mechanical and microscopic properties of fiber-reinforced coal gangue-based geopolymer concrete
  24. Effect of morphology and size on the thermodynamic stability of cerium oxide nanoparticles: Experiment and molecular dynamics calculation
  25. Mechanical performance of a CFRP composite reinforced via gelatin-CNTs: A study on fiber interfacial enhancement and matrix enhancement
  26. A practical review over surface modification, nanopatterns, emerging materials, drug delivery systems, and their biophysiochemical properties for dental implants: Recent progresses and advances
  27. HTR: An ultra-high speed algorithm for cage recognition of clathrate hydrates
  28. Effects of microalloying elements added by in situ synthesis on the microstructure of WCu composites
  29. A highly sensitive nanobiosensor based on aptamer-conjugated graphene-decorated rhodium nanoparticles for detection of HER2-positive circulating tumor cells
  30. Progressive collapse performance of shear strengthened RC frames by nano CFRP
  31. Core–shell heterostructured composites of carbon nanotubes and imine-linked hyperbranched polymers as metal-free Li-ion anodes
  32. A Galerkin strategy for tri-hybridized mixture in ethylene glycol comprising variable diffusion and thermal conductivity using non-Fourier’s theory
  33. Simple models for tensile modulus of shape memory polymer nanocomposites at ambient temperature
  34. Preparation and morphological studies of tin sulfide nanoparticles and use as efficient photocatalysts for the degradation of rhodamine B and phenol
  35. Polyethyleneimine-impregnated activated carbon nanofiber composited graphene-derived rice husk char for efficient post-combustion CO2 capture
  36. Electrospun nanofibers of Co3O4 nanocrystals encapsulated in cyclized-polyacrylonitrile for lithium storage
  37. Pitting corrosion induced on high-strength high carbon steel wire in high alkaline deaerated chloride electrolyte
  38. Formulation of polymeric nanoparticles loaded sorafenib; evaluation of cytotoxicity, molecular evaluation, and gene expression studies in lung and breast cancer cell lines
  39. Engineered nanocomposites in asphalt binders
  40. Influence of loading voltage, domain ratio, and additional load on the actuation of dielectric elastomer
  41. Thermally induced hex-graphene transitions in 2D carbon crystals
  42. The surface modification effect on the interfacial properties of glass fiber-reinforced epoxy: A molecular dynamics study
  43. Molecular dynamics study of deformation mechanism of interfacial microzone of Cu/Al2Cu/Al composites under tension
  44. Nanocolloid simulators of luminescent solar concentrator photovoltaic windows
  45. Compressive strength and anti-chloride ion penetration assessment of geopolymer mortar merging PVA fiber and nano-SiO2 using RBF–BP composite neural network
  46. Effect of 3-mercapto-1-propane sulfonate sulfonic acid and polyvinylpyrrolidone on the growth of cobalt pillar by electrodeposition
  47. Dynamics of convective slippery constraints on hybrid radiative Sutterby nanofluid flow by Galerkin finite element simulation
  48. Preparation of vanadium by the magnesiothermic self-propagating reduction and process control
  49. Microstructure-dependent photoelectrocatalytic activity of heterogeneous ZnO–ZnS nanosheets
  50. Cytotoxic and pro-inflammatory effects of molybdenum and tungsten disulphide on human bronchial cells
  51. Improving recycled aggregate concrete by compression casting and nano-silica
  52. Chemically reactive Maxwell nanoliquid flow by a stretching surface in the frames of Newtonian heating, nonlinear convection and radiative flux: Nanopolymer flow processing simulation
  53. Nonlinear dynamic and crack behaviors of carbon nanotubes-reinforced composites with various geometries
  54. Biosynthesis of copper oxide nanoparticles and its therapeutic efficacy against colon cancer
  55. Synthesis and characterization of smart stimuli-responsive herbal drug-encapsulated nanoniosome particles for efficient treatment of breast cancer
  56. Homotopic simulation for heat transport phenomenon of the Burgers nanofluids flow over a stretching cylinder with thermal convective and zero mass flux conditions
  57. Incorporation of copper and strontium ions in TiO2 nanotubes via dopamine to enhance hemocompatibility and cytocompatibility
  58. Mechanical, thermal, and barrier properties of starch films incorporated with chitosan nanoparticles
  59. Mechanical properties and microstructure of nano-strengthened recycled aggregate concrete
  60. Glucose-responsive nanogels efficiently maintain the stability and activity of therapeutic enzymes
  61. Tunning matrix rheology and mechanical performance of ultra-high performance concrete using cellulose nanofibers
  62. Flexible MXene/copper/cellulose nanofiber heat spreader films with enhanced thermal conductivity
  63. Promoted charge separation and specific surface area via interlacing of N-doped titanium dioxide nanotubes on carbon nitride nanosheets for photocatalytic degradation of Rhodamine B
  64. Elucidating the role of silicon dioxide and titanium dioxide nanoparticles in mitigating the disease of the eggplant caused by Phomopsis vexans, Ralstonia solanacearum, and root-knot nematode Meloidogyne incognita
  65. An implication of magnetic dipole in Carreau Yasuda liquid influenced by engine oil using ternary hybrid nanomaterial
  66. Robust synthesis of a composite phase of copper vanadium oxide with enhanced performance for durable aqueous Zn-ion batteries
  67. Tunning self-assembled phases of bovine serum albumin via hydrothermal process to synthesize novel functional hydrogel for skin protection against UVB
  68. A comparative experimental study on damping properties of epoxy nanocomposite beams reinforced with carbon nanotubes and graphene nanoplatelets
  69. Lightweight and hydrophobic Ni/GO/PVA composite aerogels for ultrahigh performance electromagnetic interference shielding
  70. Research on the auxetic behavior and mechanical properties of periodically rotating graphene nanostructures
  71. Repairing performances of novel cement mortar modified with graphene oxide and polyacrylate polymer
  72. Closed-loop recycling and fabrication of hydrophilic CNT films with high performance
  73. Design of thin-film configuration of SnO2–Ag2O composites for NO2 gas-sensing applications
  74. Study on stress distribution of SiC/Al composites based on microstructure models with microns and nanoparticles
  75. PVDF green nanofibers as potential carriers for improving self-healing and mechanical properties of carbon fiber/epoxy prepregs
  76. Osteogenesis capability of three-dimensionally printed poly(lactic acid)-halloysite nanotube scaffolds containing strontium ranelate
  77. Silver nanoparticles induce mitochondria-dependent apoptosis and late non-canonical autophagy in HT-29 colon cancer cells
  78. Preparation and bonding mechanisms of polymer/metal hybrid composite by nano molding technology
  79. Damage self-sensing and strain monitoring of glass-reinforced epoxy composite impregnated with graphene nanoplatelet and multiwalled carbon nanotubes
  80. Thermal analysis characterisation of solar-powered ship using Oldroyd hybrid nanofluids in parabolic trough solar collector: An optimal thermal application
  81. Pyrene-functionalized halloysite nanotubes for simultaneously detecting and separating Hg(ii) in aqueous media: A comprehensive comparison on interparticle and intraparticle excimers
  82. Fabrication of self-assembly CNT flexible film and its piezoresistive sensing behaviors
  83. Thermal valuation and entropy inspection of second-grade nanoscale fluid flow over a stretching surface by applying Koo–Kleinstreuer–Li relation
  84. Mechanical properties and microstructure of nano-SiO2 and basalt-fiber-reinforced recycled aggregate concrete
  85. Characterization and tribology performance of polyaniline-coated nanodiamond lubricant additives
  86. Combined impact of Marangoni convection and thermophoretic particle deposition on chemically reactive transport of nanofluid flow over a stretching surface
  87. Spark plasma extrusion of binder free hydroxyapatite powder
  88. An investigation on thermo-mechanical performance of graphene-oxide-reinforced shape memory polymer
  89. Effect of nanoadditives on the novel leather fiber/recycled poly(ethylene-vinyl-acetate) polymer composites for multifunctional applications: Fabrication, characterizations, and multiobjective optimization using central composite design
  90. Design selection for a hemispherical dimple core sandwich panel using hybrid multi-criteria decision-making methods
  91. Improving tensile strength and impact toughness of plasticized poly(lactic acid) biocomposites by incorporating nanofibrillated cellulose
  92. Green synthesis of spinel copper ferrite (CuFe2O4) nanoparticles and their toxicity
  93. The effect of TaC and NbC hybrid and mono-nanoparticles on AA2024 nanocomposites: Microstructure, strengthening, and artificial aging
  94. Excited-state geometry relaxation of pyrene-modified cellulose nanocrystals under UV-light excitation for detecting Fe3+
  95. Effect of CNTs and MEA on the creep of face-slab concrete at an early age
  96. Effect of deformation conditions on compression phase transformation of AZ31
  97. Application of MXene as a new generation of highly conductive coating materials for electromembrane-surrounded solid-phase microextraction
  98. A comparative study of the elasto-plastic properties for ceramic nanocomposites filled by graphene or graphene oxide nanoplates
  99. Encapsulation strategies for improving the biological behavior of CdS@ZIF-8 nanocomposites
  100. Biosynthesis of ZnO NPs from pumpkin seeds’ extract and elucidation of its anticancer potential against breast cancer
  101. Preliminary trials of the gold nanoparticles conjugated chrysin: An assessment of anti-oxidant, anti-microbial, and in vitro cytotoxic activities of a nanoformulated flavonoid
  102. Effect of micron-scale pores increased by nano-SiO2 sol modification on the strength of cement mortar
  103. Fractional simulations for thermal flow of hybrid nanofluid with aluminum oxide and titanium oxide nanoparticles with water and blood base fluids
  104. The effect of graphene nano-powder on the viscosity of water: An experimental study and artificial neural network modeling
  105. Development of a novel heat- and shear-resistant nano-silica gelling agent
  106. Characterization, biocompatibility and in vivo of nominal MnO2-containing wollastonite glass-ceramic
  107. Entropy production simulation of second-grade magnetic nanomaterials flowing across an expanding surface with viscidness dissipative flux
  108. Enhancement in structural, morphological, and optical properties of copper oxide for optoelectronic device applications
  109. Aptamer-functionalized chitosan-coated gold nanoparticle complex as a suitable targeted drug carrier for improved breast cancer treatment
  110. Performance and overall evaluation of nano-alumina-modified asphalt mixture
  111. Analysis of pure nanofluid (GO/engine oil) and hybrid nanofluid (GO–Fe3O4/engine oil): Novel thermal and magnetic features
  112. Synthesis of Ag@AgCl modified anatase/rutile/brookite mixed phase TiO2 and their photocatalytic property
  113. Mechanisms and influential variables on the abrasion resistance hydraulic concrete
  114. Synergistic reinforcement mechanism of basalt fiber/cellulose nanocrystals/polypropylene composites
  115. Achieving excellent oxidation resistance and mechanical properties of TiB2–B4C/carbon aerogel composites by quick-gelation and mechanical mixing
  116. Microwave-assisted sol–gel template-free synthesis and characterization of silica nanoparticles obtained from South African coal fly ash
  117. Pulsed laser-assisted synthesis of nano nickel(ii) oxide-anchored graphitic carbon nitride: Characterizations and their potential antibacterial/anti-biofilm applications
  118. Effects of nano-ZrSi2 on thermal stability of phenolic resin and thermal reusability of quartz–phenolic composites
  119. Benzaldehyde derivatives on tin electroplating as corrosion resistance for fabricating copper circuit
  120. Mechanical and heat transfer properties of 4D-printed shape memory graphene oxide/epoxy acrylate composites
  121. Coupling the vanadium-induced amorphous/crystalline NiFe2O4 with phosphide heterojunction toward active oxygen evolution reaction catalysts
  122. Graphene-oxide-reinforced cement composites mechanical and microstructural characteristics at elevated temperatures
  123. Gray correlation analysis of factors influencing compressive strength and durability of nano-SiO2 and PVA fiber reinforced geopolymer mortar
  124. Preparation of layered gradient Cu–Cr–Ti alloy with excellent mechanical properties, thermal stability, and electrical conductivity
  125. Recovery of Cr from chrome-containing leather wastes to develop aluminum-based composite material along with Al2O3 ceramic particles: An ingenious approach
  126. Mechanisms of the improved stiffness of flexible polymers under impact loading
  127. Anticancer potential of gold nanoparticles (AuNPs) using a battery of in vitro tests
  128. Review Articles
  129. Proposed approaches for coronaviruses elimination from wastewater: Membrane techniques and nanotechnology solutions
  130. Application of Pickering emulsion in oil drilling and production
  131. The contribution of microfluidics to the fight against tuberculosis
  132. Graphene-based biosensors for disease theranostics: Development, applications, and recent advancements
  133. Synthesis and encapsulation of iron oxide nanorods for application in magnetic hyperthermia and photothermal therapy
  134. Contemporary nano-architectured drugs and leads for ανβ3 integrin-based chemotherapy: Rationale and retrospect
  135. State-of-the-art review of fabrication, application, and mechanical properties of functionally graded porous nanocomposite materials
  136. Insights on magnetic spinel ferrites for targeted drug delivery and hyperthermia applications
  137. A review on heterogeneous oxidation of acetaminophen based on micro and nanoparticles catalyzed by different activators
  138. Early diagnosis of lung cancer using magnetic nanoparticles-integrated systems
  139. Advances in ZnO: Manipulation of defects for enhancing their technological potentials
  140. Efficacious nanomedicine track toward combating COVID-19
  141. A review of the design, processes, and properties of Mg-based composites
  142. Green synthesis of nanoparticles for varied applications: Green renewable resources and energy-efficient synthetic routes
  143. Two-dimensional nanomaterial-based polymer composites: Fundamentals and applications
  144. Recent progress and challenges in plasmonic nanomaterials
  145. Apoptotic cell-derived micro/nanosized extracellular vesicles in tissue regeneration
  146. Electronic noses based on metal oxide nanowires: A review
  147. Framework materials for supercapacitors
  148. An overview on the reproductive toxicity of graphene derivatives: Highlighting the importance
  149. Antibacterial nanomaterials: Upcoming hope to overcome antibiotic resistance crisis
  150. Research progress of carbon materials in the field of three-dimensional printing polymer nanocomposites
  151. A review of atomic layer deposition modelling and simulation methodologies: Density functional theory and molecular dynamics
  152. Recent advances in the preparation of PVDF-based piezoelectric materials
  153. Recent developments in tensile properties of friction welding of carbon fiber-reinforced composite: A review
  154. Comprehensive review of the properties of fly ash-based geopolymer with additive of nano-SiO2
  155. Perspectives in biopolymer/graphene-based composite application: Advances, challenges, and recommendations
  156. Graphene-based nanocomposite using new modeling molecular dynamic simulations for proposed neutralizing mechanism and real-time sensing of COVID-19
  157. Nanotechnology application on bamboo materials: A review
  158. Recent developments and future perspectives of biorenewable nanocomposites for advanced applications
  159. Nanostructured lipid carrier system: A compendium of their formulation development approaches, optimization strategies by quality by design, and recent applications in drug delivery
  160. 3D printing customized design of human bone tissue implant and its application
  161. Design, preparation, and functionalization of nanobiomaterials for enhanced efficacy in current and future biomedical applications
  162. A brief review of nanoparticles-doped PEDOT:PSS nanocomposite for OLED and OPV
  163. Nanotechnology interventions as a putative tool for the treatment of dental afflictions
  164. Recent advancements in metal–organic frameworks integrating quantum dots (QDs@MOF) and their potential applications
  165. A focused review of short electrospun nanofiber preparation techniques for composite reinforcement
  166. Microstructural characteristics and nano-modification of interfacial transition zone in concrete: A review
  167. Latest developments in the upconversion nanotechnology for the rapid detection of food safety: A review
  168. Strategic applications of nano-fertilizers for sustainable agriculture: Benefits and bottlenecks
  169. Molecular dynamics application of cocrystal energetic materials: A review
  170. Synthesis and application of nanometer hydroxyapatite in biomedicine
  171. Cutting-edge development in waste-recycled nanomaterials for energy storage and conversion applications
  172. Biological applications of ternary quantum dots: A review
  173. Nanotherapeutics for hydrogen sulfide-involved treatment: An emerging approach for cancer therapy
  174. Application of antibacterial nanoparticles in orthodontic materials
  175. Effect of natural-based biological hydrogels combined with growth factors on skin wound healing
  176. Nanozymes – A route to overcome microbial resistance: A viewpoint
  177. Recent developments and applications of smart nanoparticles in biomedicine
  178. Contemporary review on carbon nanotube (CNT) composites and their impact on multifarious applications
  179. Interfacial interactions and reinforcing mechanisms of cellulose and chitin nanomaterials and starch derivatives for cement and concrete strength and durability enhancement: A review
  180. Diamond-like carbon films for tribological modification of rubber
  181. Layered double hydroxides (LDHs) modified cement-based materials: A systematic review
  182. Recent research progress and advanced applications of silica/polymer nanocomposites
  183. Modeling of supramolecular biopolymers: Leading the in silico revolution of tissue engineering and nanomedicine
  184. Recent advances in perovskites-based optoelectronics
  185. Biogenic synthesis of palladium nanoparticles: New production methods and applications
  186. A comprehensive review of nanofluids with fractional derivatives: Modeling and application
  187. Electrospinning of marine polysaccharides: Processing and chemical aspects, challenges, and future prospects
  188. Electrohydrodynamic printing for demanding devices: A review of processing and applications
  189. Rapid Communications
  190. Structural material with designed thermal twist for a simple actuation
  191. Recent advances in photothermal materials for solar-driven crude oil adsorption
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 28.12.2025 from https://www.degruyterbrill.com/document/doi/10.1515/ntrev-2022-0150/html?lang=en
Scroll to top button