Nonlinear dynamic and crack behaviors of carbon nanotubes-reinforced composites with various geometries

Ashish Maharjan; Piljo Yu; Sang-Youl Lee

doi:10.1515/ntrev-2022-0079

Article Open Access

Nonlinear dynamic and crack behaviors of carbon nanotubes-reinforced composites with various geometries

Ashish Maharjan , Piljo Yu and Sang-Youl Lee

Published/Copyright: March 22, 2022

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Nanotechnology Reviews Volume 11 Issue 1

Abstract

This study carried out finite element dynamic analyses of carbon nanotubes/fiber/polymer composites (CNTFPC) with various geometries. In the first application, the effects of CNTs on the nonlinear transient responses of doubly curved shells for various cutout sizes and curvatures are studied. The numerical results obtained are in good agreement with those reported by other investigators. For the practical application, the focus of this study is to evaluate various performances of concrete structures reinforced with a rebar-type CNTFPC. The new results reported in this article show the interactions between CNT weight ratios and crack sizes in CNTFPC-reinforced concrete structures. Key observation points are discussed and a brief design guideline is given.

Keywords: CNTFPC cylindrical shell; CNTFPC-reinforced concrete beam; multi-scale analysis; nonlinear dynamics; crack analysis

1 Introduction

CNT has received wide attention from the researchers as it is well known for its unparalleled lightness and mechanical properties exceeding those of any existing materials. Carbon nanotube-reinforced composites (CNTRCs) may expand its application in major areas like automobiles, submarine, aerospace structures, sports, etc. Therefore, conducting research helps in understanding the mechanical properties of CNTRCs in detail.

Structural behavior of CNTRC members has been studied previously by a host of investigators using a variety of approaches. Zhang et al. [1] presented the nonlinear analysis of CNTRC cylindrical panels. Dynamic stability analysis of CNTRC cylindrical panels under static and periodic axial force using the element-free kp-Ritz method was examined by Lei et al. [2]. Mirzaei and Kiani [3] studied the free vibration characteristics of composite plates reinforced with single-walled CNT (SWCNT). Zhang and Xiao [4] employed element-free IMLS-Ritz method for the mechanical behavior of laminated SWCNT-reinforced composite skew plates subjected to a dynamic loading. Besides, various mechanical behaviors of Functional grade (FG)-CNT-reinforced composites were investigated (Kiani [5]; Kiani [6]; Kiani and Mirzaeib [7]).

As the cost of CNT is still high today, it is not feasible to use it as two-phase reinforcing materials such as CNTRC or FG-CNT composites, especially for civil structures. Therefore, synthesizing CNT in the polymer and further reinforcing with fibers result in a three-phase carbon nanotube fiber polymer composite (CNTFPC) which is desirable from a practical point of view (Rafiee et al. [8]). A few researchers have carried out multi-scale analyses of composite structures with the three-phase CNTFPC. Lee [9] dealt with the dynamic instability assessment of CNTFPC skew plates with delamination. Lee and Hwang [10] studied the finite element nonlinear transient modeling of CNTFPC spherical shells with a central cutout. Ahmadi et al. [11] performed linear free and forced vibration analysis of rectangular, circular, and annular plates made of CNTFPC, which is used carbon fibers. Based on stochastic finite element method, fracture behaviors of the CNT/carbon fiber/polymer multi-scale L-shape composites under bending test were investigated [12]. This study was extended to study free vibrations of micro-beam and plate type models [13,14,15]. For complicated structures with a curvature, Lee [16] presented nonlinear transient behaviors of CNTFPC flat and cylindrical panels without a cutout. However, the cutout size could play a dominant role in determining the dynamic characteristics for a composite laminate. Thus, the study is further extended in this investigation to take into account effects of cutout sizes and curvatures of doubly-curved shells.

In more practical application for civil structures, this study uses a concrete beam model reinforced with a CNTFPC rebar-type. Chaallal and Benmokrane [17] reported a laboratory investigation for concrete structures reinforced by the glass-fiber-reinforced polymer (GFRP) rebar. Ductility characteristics of concrete beams reinforced with FRP rebars are presented by Wang and Belarbi [18]. Inman et al. [19] performed a mechanical and environmental assessment and comparison of basalt-fiber-reinforced polymer (BFRP) rebar and steel rebar in concrete beams. Duic et al. [20] evaluated the performance of concrete beams reinforced with BFRP rebars in shear and flexure.

All these works are limited in that they do not consider the CNT effects on frequency or crack behaviors of the reinforced concrete structures. To the authors’ knowledge, a CNTFPC rebar-reinforced concrete model presented in the article is the first attempt. An intuitive prediction of the nonlinear dynamic or crack behaviors of structures made of CNTFPC is difficult because of their complexity due to the combined effect of anisotropy and geometry. In this study, high-performance GFRP rebars are further reinforced based on the concept of CNTFPC. Optimizing the performance of concrete beams reinforced with CNTFPC rebars is studied by carrying out rebar tensile test, frequency, linear static, and crack analyses.

2 Multi-scale formulation

In this study, the Halpin–Tsai model and micro-mechanical approaches are used to perform the multi-scale analysis of the three-phase composites (CNTFPC). Figure 1 illustrates the concept of laminated CNTs/fiber/polymer multi-phase composites. It is assumed that the three-phase CNTs/fiber/polymer multi-scale laminated composite host is made from a mixture of isotropic matrix (epoxy resin), CNTs, and fibers (E-glass) with different alignments for each lamina through the thickness. The CNT composites are regarded as isotropic, as the CNTs are assumed to be uniformly distributed and randomly oriented through the matrix. It is also assumed that the CNTs matrix bonding and dispersion in the matrix are perfect, such that each CNT has the same mechanical properties and aspect ratio, all CNTs are straight, there is no void in the matrix, and the fiber–matrix bonding is also perfect [8,9].

Figure 1

Symmetric cross-ply laminated CNT/fiber/polymer multi-phase composite [9].

First, the effective Young’s modulus of CNTRC is determined by the Halpin–Tsai equation as (ref. [21]):

(1) E cnr = E re 8 3 1 + 2 ( l cnt / d cnt ) γ dl V cnt 1 − γ dl V cnt + 5 1 + 2 γ dd V cnt 1 − γ dd V cnt ,

where

γ dd = ( E 11 cnt / E re ) − ( d cnt / 4 t cnt ) ( E 11 cnt / E re ) + ( d cnt / 2 t cnt ) , γ dl = ( E 11 cnt / E re ) − ( d cnt / 4 t cnt ) ( E 11 cnt / E re ) + ( l cnt / 2 t cnt ) ,

where E cnr , E re , and E 11 cnt are Young’s moduli of CNTRC, matrix, and CNT, while l cnt , d cnt , and t cnt are the length, diameter, and thickness of the CNT, respectively. The volume fraction of CNT ( V cnt ) can be determined as:

(2) V cnt = w cnt w cnt + ( ρ cnt / ρ re ) − ( ρ cnt / ρ re ) w cnt ,

where w cnt is the weight ratio of CNT, and ρ cnt and ρ re are the mass densities of CNT and matrix. The CNTRC is further reinforced with fibers forming CNTFPC. The effective longitudinal Young’s modulus ( E 11 ) can be determined as

(3) E 11 = E f V f + E cnr ( 1 − V f ) ,

where E f and V f are Young’s modulus and volume fraction of the fiber, respectively. The transverse Young’s modulus ( E 22 ) of CNTFPC can be determined from the Halpin–Tsai model as:

(4) E 22 = E cnr 1 + χ 1 η 1 V f 1 − η 1 V f , η 1 = ( E f / E cnr ) − 1 ( E f / E cnr ) + χ 1 .

Similarly, the shear modulus ( G 12 ) can be obtained as:

(5) G 12 = G cnr 1 + χ 2 η 2 V f 1 − η 2 V f , η 2 = ( G f / G cnr ) − 1 ( G f / G cnr ) + χ 2 ,

where G f , G re , and G cnr are the shear moduli of the fiber, matrix, and CNTRC. For the volume fraction of fiber ( V f ) higher than 0.5 in the CNTFPC, the Halpin–Tsai equation gives a result lower than the actual. So, the equation from Hewitt and Malherbe [22], derived from the experimental results, is used to determine χ 1 and χ 2 :

(6) χ 1 = 2.0 + 40 ( V f ) 10 , χ 2 = 1.0 + 40 ( V f ) 10 ,

The tensile strength of CNTFPC can be determined from the rule of mixture as

(7) S 11 = S f V f + S cnr ( 1 − V f ) ,

where S 11 , S f , and S cnr are the tensile strengths of CNTFPC, fiber, and CNTRC.

3 Finite element nonlinear dynamic procedure

For completeness, the shear deformation theory and the relevant formulas in the finite element analysis of shells are reviewed below. From the macro-mechanical point of view, the first-order shear deformation theory (FSDT) reviewed in this study is derived from the first-order laminate formulation of Reddy [23]. Figure 2 shows the geometry and cross-section of a doubly-curved shell containing central cutout. The equivalent displacement field for the FSDT now can be expressed as

(8) u 1 = u ( λ 1 , λ 2 , λ , t ) = u 0 + λ ϕ 1 , u 2 = v ( λ 1 , λ 2 , λ , t ) = v 0 + λ ϕ 2 , u 3 = w ( λ 1 , λ 2 , λ , t ) = w 0 .

where u, v, and w are the displacements along the orthogonal curvilinear coordinates, u 0 , v 0 , and w 0 are the mid-plane displacements in the Cartesian coordinate system ( x 1 , x 2 , x 3 ), and ϕ 1 and ϕ 2 are the rotations at λ = 0 , respectively.

Figure 2

Laminated composite cylindrical panel with a central cutout [16].

Using Hamilton’s principle, the equation of motion of the simplified theory in the Cartesian coordinate are obtained as

(9) N x 1 x 1 , x 1 + N x 1 x 2 , x 2 + Q x 1 ξ 1 = I 0 u ̈ 0 + I 1 ϕ ̈ 1 , N x 1 x 2 , x 1 + N x 2 x 2 , x 2 + Q x 2 ξ 2 = I 0 v ̈ 0 + I 1 ϕ ̈ 2 , Q x 1 , x 1 + Q x 2 , x 2 − N x 1 x 1 ξ 1 − N x 2 x 2 ξ 2 − q = I 0 w ̈ 0 , M x 1 x 1 , x 1 + M x 1 x 2 , x 2 − Q x 1 = I 1 u ̈ 0 + I 2 ϕ ̈ 1 , M x 1 x 2 , x 1 + M x 2 x 2 , x 2 − Q x 2 = I 1 v ̈ 0 + I 2 ϕ ̈ 2 ,

where

I i = ∑ k = 1 N ∫ λ k λ k + 1 ρ ( k ) ( λ ) i d λ ,

In equation (9), q is the transverse load on the upper surface of the shell, ( N α β , M α β , Q α ) are the stress resultants, and ρ is the mass density. The resultants are related to the strain by the relationships:

(10) { N } { M } { Q } = [ A ] [ B ] 0 [ B ] [ D ] 0 0 0 [ A ] { ε ( 0 ) } { ε ( 1 ) } { γ ( 0 ) } ,

where {N}, {M}, and {Q} denote the in-plane force, moment, and transverse force resultants using material properties obtained from the multi-scale formation in Section 2, and the related nonlinear strains are:

(11) ε 1 0 = u 0 , x 1 + w 0 ξ 1 + 1 2 ( w 0 , x 1 ) 2 , ε 2 0 = v 0 , y + w 0 ξ 2 + 1 2 ( w 0 , x 2 ) 2 , ε 6 0 = v 0 , x + u 0 , y + w 0 , x 1 w 0 , x 2 , ε 1 1 = ϕ 1 , x 1 , ε 2 1 = ϕ 2 , x 2 , ε 6 1 = ϕ 2 , x 1 + ϕ 1 , x 2 , γ 4 0 = ϕ 2 + w 0 , x 2 − v 0 ξ 2 , γ 5 0 = ϕ 1 + w 0 , x 1 − u 0 ξ 1 .

In the finite element formulation, a nonconforming element for doubly-curved shells has five degrees-of-freedom, namely, u ˜ , v ˜ , w ˜ , ϕ λ 1 , ϕ λ 2 . The notations ( u ˜ , v ˜ , w ˜ ) and ( ϕ λ 1 , ϕ λ 2 ) are the mid-plane displacements in the λ 1 , λ 2 , and λ -directions, the respective derivatives and the rotations transverse normal about λ 2 - and λ 1 -axes, respectively. The generalized displacements can be approximated by the following expressions:

(12) u ˜ v ˜ w ˜ ϕ λ 1 ϕ λ 2 = ∑ ς = 1 4 Ψ ς [ I 5 ] u ˜ ς v ˜ ς w ˜ ς ϕ λ 1 ς ϕ λ 1 ς ,

where [ I 4 ] is a 5 × 5 identity matrix, and Ψ ς is the Lagrange interpolation function. By substituting equation (12) in equation (11), equation (9) yields the finite element model. It can be rewritten in compact form as:

(13) 0 = ∑ β = 1 5 ∑ j = 1 n ( K i j α β Δ j β + M i j α β Δ ̈ j β ) − F i α ≡ R i α , i = 1 , 2 , … , n ,

for α = 1,2,…,5, where Δ j β denotes the nodal values, in the order ( u ˜ , v ˜ , w ˜ , ϕ λ 1 , ϕ λ 2 ), at the ith node of the element, and K i j α β is the stiffness coefficient, and M i j α β is the mass coefficient. Equation (13), when generalized to include structural damping, has the form

(14) [ M ] { Δ ̈ } + [ C ] { Δ ̇ } + [ K ] { Δ } = { F } .

The fully discretized equations are

(15) [ K ˆ ( { Δ } s + 1 ) ] { Δ } s + 1 = { F ˆ } s , s + 1 ,

where

(16) [ K ˆ ( { Δ } s + 1 ) ] = [ K ( { Δ } s + 1 ) ] + b 3 [ M ] s + 1 + b 6 [ C ] s + 1 , { F ˆ } s , s + 1 = { F } s + 1 + [ M ] s + 1 { E } s + [ C ] s + 1 { G } s , { E } s = b 3 { Δ } s + b 4 { Δ ̇ } s + b 5 { Δ ̈ } s , { G } s = b 6 { Δ } s + b 7 { Δ ̇ } s + b 8 { Δ ̈ } s ,

where b i is the integration constant. At the end of time step, the new velocity vector { Δ ̇ } s + 1 and acceleration vector { Δ ̈ } s + 1 are determined using the following equations:

(17) { Δ ̈ } s + 1 = b 3 ( { Δ } s + 1 − { Δ } s ) − b 4 { Δ ̇ } − b 5 { Δ ̈ } s ,

(18) { Δ ̇ } s + 1 = { Δ ̇ } s + b 2 { Δ ̈ } s + b 1 { Δ ̈ } s + 1 .

In the finite element nonlinear dynamic solution, equation (15) by the Newton–Raphson method results in the following linearized equations for the incremental solution at the ( r + 1 ) st iteration

(19) { δ Δ } = − [ K ˆ T ( { Δ } s + 1 r ) ] − 1 { R } s + 1 r ,

(20) [ K ˆ T ( { Δ } s + 1 r ) ] ≡ ∂ { R } ∂ { Δ } s + 1 r , { R } s + 1 r = [ K ˆ T ( { Δ } s + 1 r ) ] { Δ } s + 1 r − { F ˆ } s , s + 1 .

The total solution is obtained from

(21) { Δ } s + 1 r + 1 = { Δ } s + 1 r + { ∂ Δ } .

The tangent stiffness matrix is evaluated using the latest known solution, while the residual vector contains contributions from the latest knsown solution in computing [ K ˆ T ( { Δ } s + 1 r ) ] { Δ } s + 1 r and previous time step solution in computing { F ˆ } s , s + 1 . The velocity and acceleration vectors are updated using equations (17) and (18) only after convergence is reached for a given time step.

4 Parametric studies

The multi-scale formulation of CNTFPC has been implemented for four purposes: To determine (1) natural frequency of a panel, (2) linear dynamic behaviors, (3) nonlinear dynamic behaviors, and (4) cracks of a concrete beam reinforced with CNTFPC rebars in the more complicated and practical applications. It also includes analyses of CNTFPC panels with/without central cutout for different curvatures, central cutout sizes, CNT weight ratios, and layup angle sequences.

In the numerical models, the following three types of boundary conditions are used.

(22) N x x = 0 , v 0 = 0 , w 0 = 0 , M x x = 0 : Simply supported (S) ,

(23) u 0 = 0 , v 0 = 0 , w 0 = 0 , ∂ w 0 ∂ x = 0 : Clamped ( C ) ,

(24) N x x = 0 , N x y = 0 , ∂ M x x ∂ x + 2 ∂ M x x ∂ x = 0 , M x x = 0 : Simply supported ( F ) .

The detailed loading as well as other parameters used for panels (Figure 2) is tabulated in Table 1. The panels are clamped on one side and free on the other three sides (CFFF). Figure 3 shows the diagram of a dimensioned concrete beam reinforced with CNTFPC rebars for frequency, linear static, and crack analyses. CNT weight ratios of 0.00, 0.005, 0.01, 0.015, 0.02, 0.03, and 0.04 are considered in the rebars for the comparison of the structural performance of the beam. To validate the procedures, the present results from the program are compared with those published by other investigators.

Table 1

Details used for the three different analyses of CNTFPC panel

Analysis	Frequency	Linear dynamic		Nonlinear dynamic
Cases	All	R/a ratio	c/a ratio	CNT wt ratio	Layup sequence
Loading point	—	J (100 kN)	I (1 kN)	J (100 kN)
Displacement measuring point	—	K	I	K
Load distribution	—	Concentrated
Model shape	Cylindrical
Boundary condition	CFFF

Figure 3

Schematic drawing of the beam.

4.1 Verification

Verifications are done for the frequency and nonlinear transient analyses using isotropic and orthotropic materials, while linear dynamic and linear static analyses using CNTRC materials are compared with previous studies. The convergence study has been carried out for the fundamental frequencies of vibration of isotropic cylindrical panel clamped on all edges (CCCC) with central square cutout of size ratios c/a = 0 and 0.5. The results shown in Table 2 are compared with the results reported by Sahu and Datta [24] and Rao et al. [25], which indicate good agreement. Figure 4 shows the vibration of center transverse deflection with respect to time for different load magnitudes q, 5q, and 10q. The effect of load magnitude on nonlinear response is seen. The present results show that it agrees well with the previous study. Table 3 shows the comparison of the non-dimensional central deflection of a square laminated CNTRC plate subjected to a uniform transverse load q _o = 0.1 MPa under different boundary conditions. The present results agree well with the previous study.

Table 2

Comparison of frequencies in Hz for the CCCC cylindrical curved panel with and without cutout

R/a	Mode no.	c/a = 0.0			c/a = 0.5
R/a	Mode no.	Ref. [24]	Ref. [25]	Present	Ref. [24]	Ref. [25]	Present
Plate	1	69.76	69.2	69.799	126.73	125.7	126.7
	2	142.27	140.9	142.57	147.92	147.3	147.82
	3	142.27	140.9	142.57	147.92	147.3	147.82
	4	209.79	206.9	210.13	199.04	199.2	198.93
4	1	215.23	213.9	215.4	184.73	185.3	183.16
	2	245.23	243.2	245.32	187.52	188.2	186
	3	328.34	326.1	328.76	295.68	295.9	294.6
	4	336.83	333.3	337.13	310.3	309.7	309.36

Figure 4

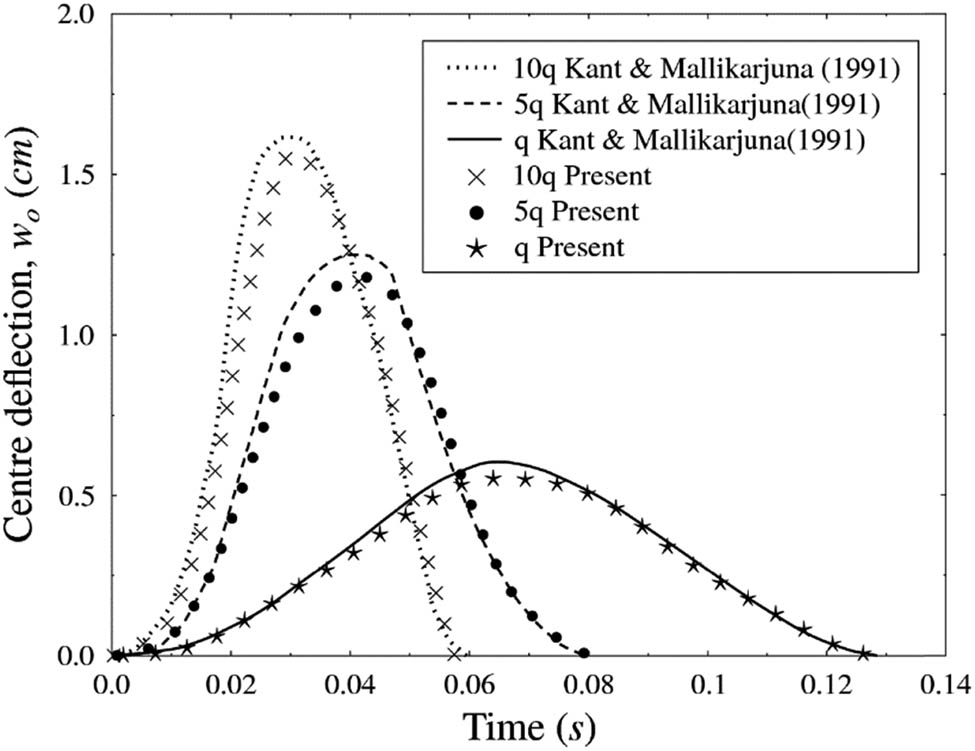
Comparison of nonlinear transient responses of isotropic square plates under suddenly applied uniformly distributed pulse loading.

Table 3

Comparison of non-dimensional central deflection w̄ = wE _m t ³ × 10³/(qb ⁴) for cross-ply [0°/90°/0°/90°/0°] square laminated CNTRC plates with different values of CNT volume fraction

V _cnt	Boundary conditions
	SSSS		CCCC		CFFF
	Ref. [26]	Present	Ref. [26]	Present	Ref. [26]	Present
0.11	7.3234	7.575	3.8306	3.725	28.6211	28.375
0.14	6.3455	6.475	3.506	3.4	24.8896	24.175
0.17	4.7024	4.875	2.4289	2.365	18.3666	18.3

Figure 5 shows the comparison of time histories of the square laminate with Reddy [23], Mallikarjun and Kant [27], and Zhang and Xiao [4]. It can be observed from the plot that the curve from the present result agrees well with the previous studies.

Figure 5

Comparison of linear dynamic responses of square laminated [0°/90°/0°] clamped plate.

4.2 CNTFPC panel

A square shell structure with sides 1 m and a thickness of 10 mm is used for the analyses. Table 4 shows the detailed mechanical properties of the CNT, resin, and fibers used for the numerical examples. A multi-scale analysis is performed for the effective material properties of the CNTFPC tabulated in Table 5 assuming volume fraction of fiber as 0.8.

Table 4

Mechanical and geometrical properties of the materials used for CNTFPC panel

Material	Source	Symbol	Value	Definition
Epoxy resin	Kim et al. [28]	E ^re	2.72 GPa	Young’s modulus of epoxy resin
		ρ ^re	1,200 kg/m³	Mass density of epoxy resin
		ν ^re	0.33	Poisson’s ratio of epoxy resin
SWCNT	Han and Elliott [29]	E 11 cnt	640 GPa	Young’s modulus of SWCNT
		E 22 cnt	10 GPa	Young’s modulus of SWCNT
		G 12 cnt	17.2 GPa	Shear modulus of SWCNT
		ρ ^cnt	1,350 kg/m³	Mass density of SWCNT
		ν ^cnt	0.33	Poisson’s ratio of SWCNT
		t ^cnt	0.34 nm	Thickness of SWCNT
		d ^cnt	1.4 nm	Diameter of SWCNT
		l ^cnt	25 μm	Length of SWCNT
E-glass fiber	Kim et al. (2009)	E ^f	69 GPa	Young’s modulus of E-glass fiber
		ρ ^f	1,200 kg/m³	Mass density of E-glass fiber
		ν ^f	0.2	Poisson’s ratio of E-glass fiber

Table 5

Mechanical properties of CNTFPC panels for increased CNT weight ratios using multi-scale analysis

CNT weight ratio	ρ (kg/m³)	E ₁₁ (GPa)	E ₂₂ (GPa)	G (GPa)
0.00	1,224	55.8	34.5	12.8
0.01	1,225	56.3	42.4	16.3
0.02	1,227	56.7	46.8	18.2
0.03	1,228	57.2	49.6	19.5
0.04	1,229	57.7	51.7	20.5
0.05	1,231	58.1	53.2	21.2
0.06	1,232	58.6	54.5	21.8
0.07	1,233	59.1	55.6	22.3
0.08	1,235	59.5	56.6	22.7

Theoretical and experimental results of SWCNT have shown the Young’s modulus to be up to 600 GPa and tensile strength of 50–200 GPa [29]. It has longitudinal Young’s modulus of approximately 300 times larger than that of epoxy resin, and approximately 10 times larger than that of glass fiber as shown in Table 4. For this reason, properties of CNTFPC panels are improved for increased CNT weight ratios as shown in Table 5. The effect of the CNT weight ratio is studied from 0.00 to 0.08 at an interval of 0.01. Panels with R/a ratios of ∞ (flat plate), 0.8, 0.55, 0.4, and 0.32 are considered. Layup sequences in the same thickness of 10 mm considered are [0°/90°], [0°/90°/90°/0°], [0°/90°/0°/90°], [45°/−45°], [45°/−45°/45°/−45°], and [45°/−45°/−45°/45°]. Figure 6 shows the central cutout sizes of c/a = 0.1, 0.2, 0.4, and 0.6 considered in the study.

Figure 6

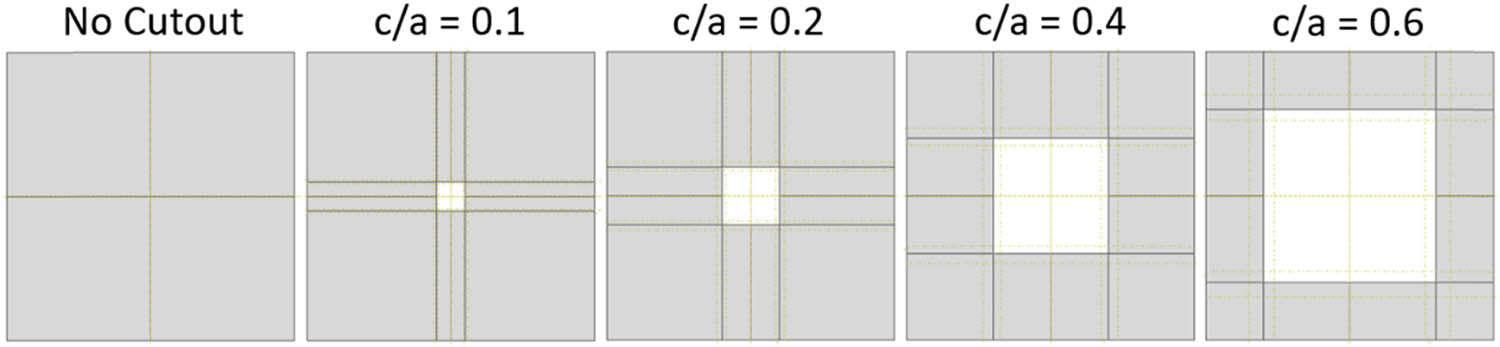
Panels with and without central cutout.

In frequency analysis, the following effects are considered: CNT weight ratio, R/a ratio, layup sequence, size of the cutout, and mode shapes. Figure 7 represents the variation in fundamental frequency due to different R/a ratios of the panel [0°/90°] under different CNT weight ratios. As the R/a ratio of the panel decreases, the frequency increases significantly. This is possibly due to the membrane force which increases with the decrease in R/a ratio. Besides, it is also observed that for all geometric shapes, as the CNT weight ratio increases, the frequency also increases. It shows that the panel’s stiffness increases when the CNT weight ratio is higher. It can also be seen that the increase in frequency is not linear and the rate decreases as the CNT weight ratio increases for all the geometric shapes. As CNT is still very expensive, adding more CNT is not beneficial. To investigate the change in frequency due to CNT weight ratio from 0.00 to 0.08 for R/a = 0.32, the percentage increase in the frequencies is 6.38, 2.95, 1.82, 1.28, 0.95, 0.81, 0.69, and 0.57%, respectively, showing that the addition of CNT weight ratio less than 0.02 would be better considering the cost.

Figure 7

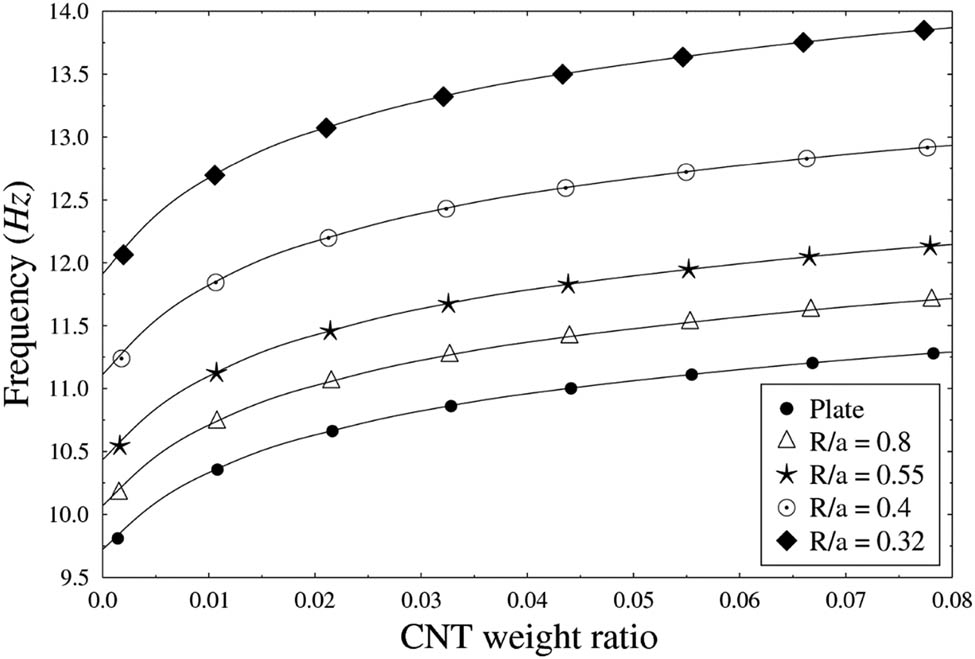
Induced natural frequencies of CNTFPC cylindrical panels for different SWCNT weight ratios and R/a ratios.

Figure 8 illustrates the effect of different layup sequences on the frequency of the flat panel with different CNT weight ratios. It can be observed that different layup sequences exhibit different frequencies. The layup sequence [0°/90°/90°/0°] exhibits the highest frequency among the six different layup sequences that are assumed. The results indicate that the effect of the layup sequence is significant on the stiffness of the panel. Table 6 lists the frequencies of flat panel [0°/90°] with different c/a ratios and CNT weight ratios. It is observed that the frequency decreases with the increase in c/a ratio and the frequency lost due to the cutout can be recovered by the addition of CNT. For example, the frequency of the panel with cutout size ratio c/a = 0.4 with no CNT is 8.9472 Hz. With the addition of CNT weight ratio 0.02, the frequency is increased to 9.7978 Hz which is close to the frequency of the panel with no cutout and no CNT. It shows that the effect of the CNT weight ratio is significant to recover the frequency lost from a cutout in laminated composite plates [30]. Figure 9 shows the mode shapes of a [0°/90°] composite square plate without and with 1% CNT weight ratio. It can be observed that the mode shapes of the plate are significantly different with different cutout sizes in both the figures. However, no significant changes are seen in the mode shapes when CNT is added to the plate.

Figure 8

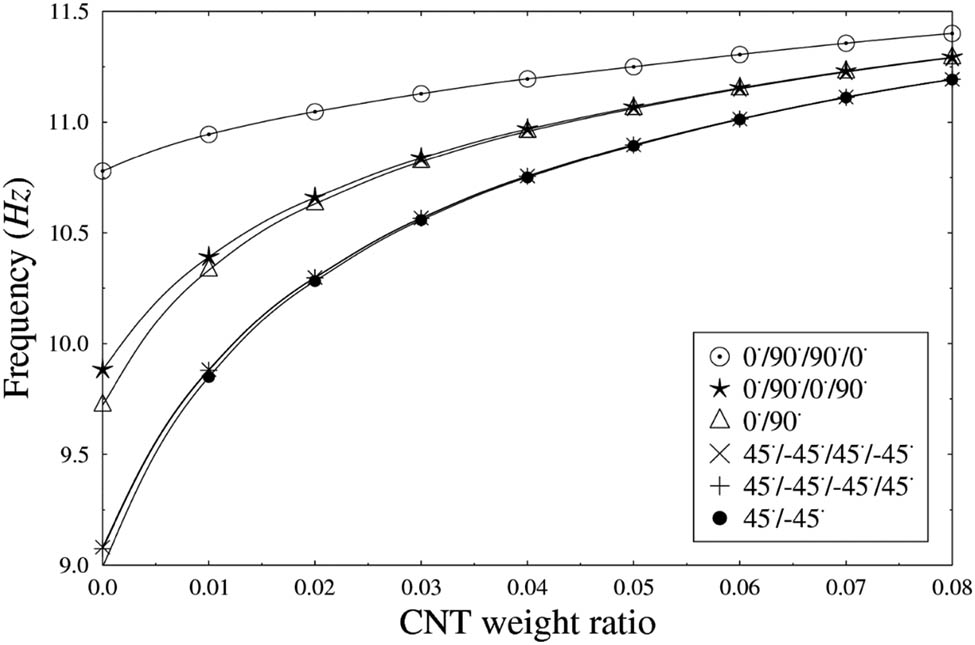
Induced natural frequencies of CNTFPC flat panels for different SWCNT weight ratios and layup sequences.

Table 6

Natural frequencies of CNTFPC flat panels with and without cutout for increased SWCNT weight ratios

CNT weight ratio	No cutout	c/a = 0.1	c/a = 0.2	c/a = 0.4	c/a = 0.6
0.00	9.7224	9.6964	9.5924	8.9472	7.7300
0.01	10.332	10.304	10.195	9.5177	8.2271
0.02	10.631	10.603	10.491	9.7978	8.4713
0.03	10.822	10.793	10.68	9.9766	8.6271
0.04	10.959	10.930	10.816	10.105	8.7389
0.05	11.062	11.033	10.917	10.201	8.8226
0.06	11.151	11.122	11.005	10.284	8.8946
0.07	11.227	11.198	11.081	10.355	8.9568
0.08	11.291	11.262	11.144	10.415	9.0082

Figure 9

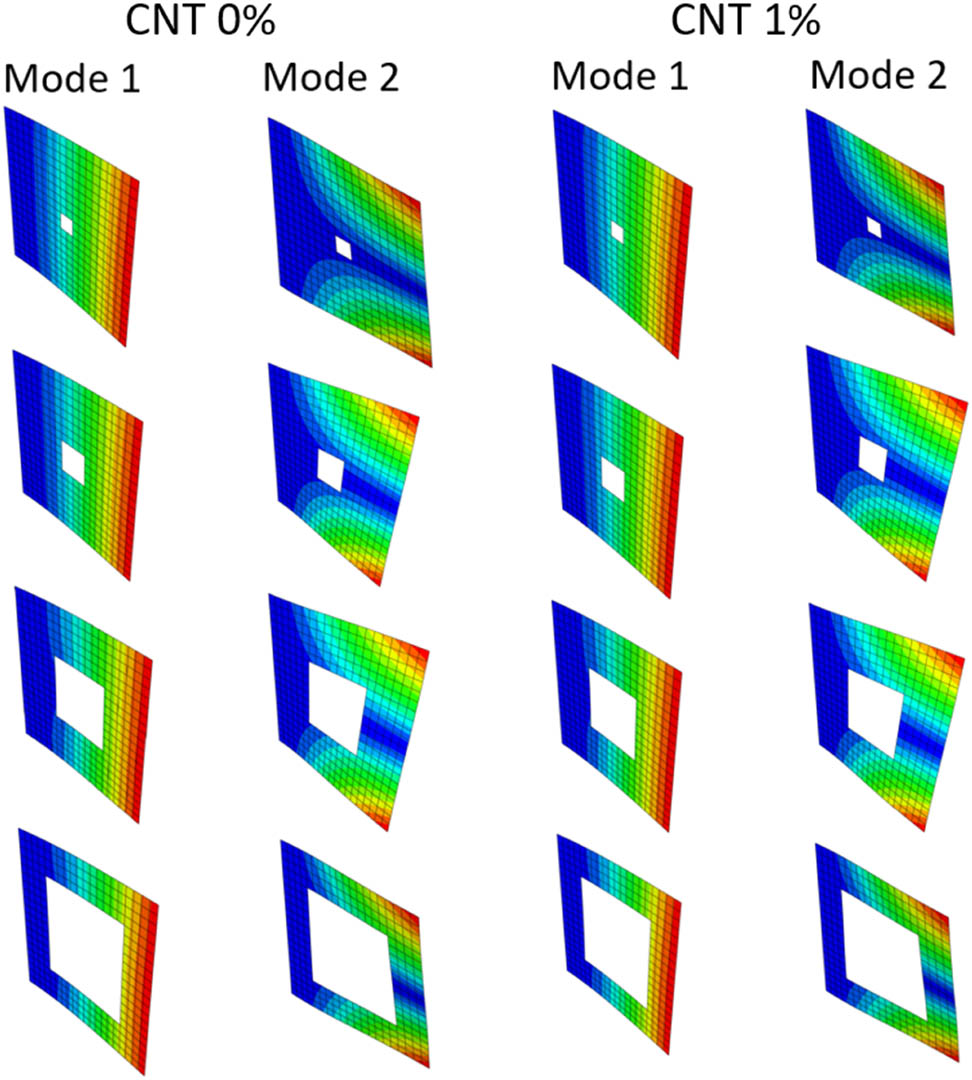
Mode shapes of CNTFPC flat panels with different cutout sizes for SWCNT 0% and 1%.

In the linear dynamic analysis, the following effects of CNTFPC cylindrical panel are investigated: R/a ratios and sizes of the cutout. Figure 10 shows the time histories of the panel [0°/90°] with no CNT for different R/a ratios. It can be observed that the deflection decreases with the decrease in R/a ratio. The reason for this is membrane force which increases with the decrease in the ratio. It can be concluded that stiffness increases with the increase in curvature resulting in lower deflection. Figure 11 depicts the effect of the central cutout sizes in the dynamic response of the composite plate [0°/90°] with no CNT. It is observed that the deflections till c/a = 0.2 are almost the same and increases when c/a ratio is beyond 0.2. When cutouts are introduced to a structure, mass as well as stiffness of the structure change simultaneously. This is the reason for no significant change till c/a = 0.2. It can be concluded that c/a ratio greater than 0.2 is not desirable for use due to higher deflection with the parameters considered in the study.

Figure 10

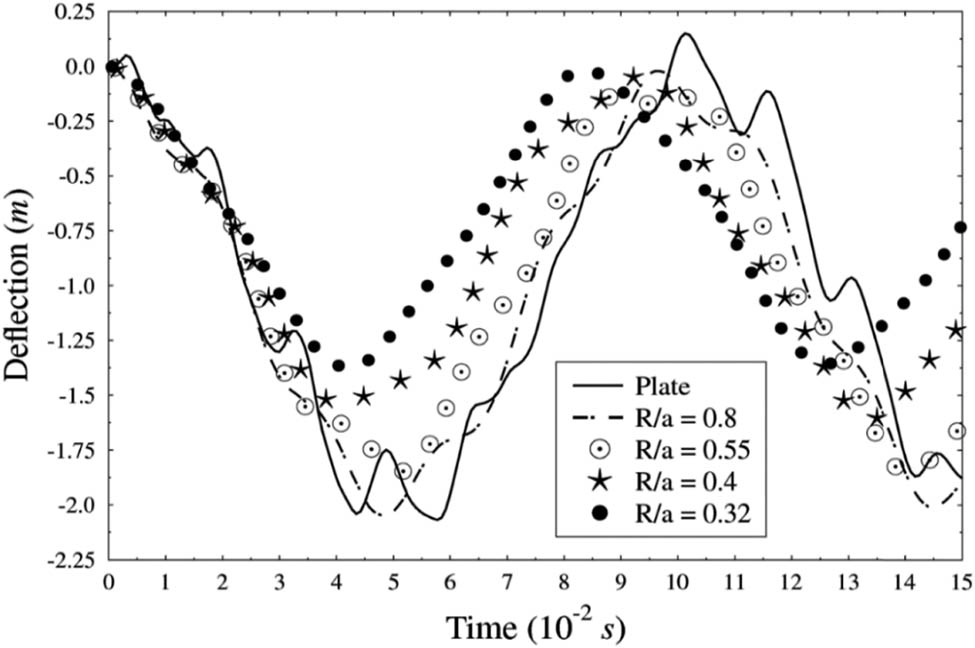
Linear dynamic time histories of CNTFPC cylindrical panels for different R/a ratios.

Figure 11

Linear dynamic time histories of CNTFPC flat panels for different central cutout sizes.

In the nonlinear dynamic analysis, the following effects of CNTFPC cylindrical panel are investigated: CNT weight ratio and layup angle sequence. Also, load–deflection curves using linear and nonlinear dynamic analyses are compared. Figure 12 shows the deflections of CNTFPC cylindrical panels [0°/90°] with R/a = 0.32 for different SWCNT weight ratios. It can be observed that the deflection decreases with the increase in CNT weight ratio showing that the panel gets stiffer with the increase in CNT weight ratio. Besides, it is also observed that the rate of decrease in deflection decreases with the increase in CNT weight ratio. Therefore, it is concluded that the addition of CNT weight ratio of more than 2% is not beneficial considering the cost. Figure 13 depicts the time histories for different layup sequences of the panel with R/a ratio 0.32 and no CNT. It can be seen that different layup sequences exhibit different deflections showing that the effect of the layup sequence is significant on the stiffness of the panel. It is found that the panel with layup sequence of [0°/90°/90°/0°] is the stiffest exhibiting the least deflection among the six layup sequences considered in the study.

Figure 12

Nonlinear dynamic time histories of CNTFPC cylindrical panels for different SWCNT weight ratios.

Figure 13

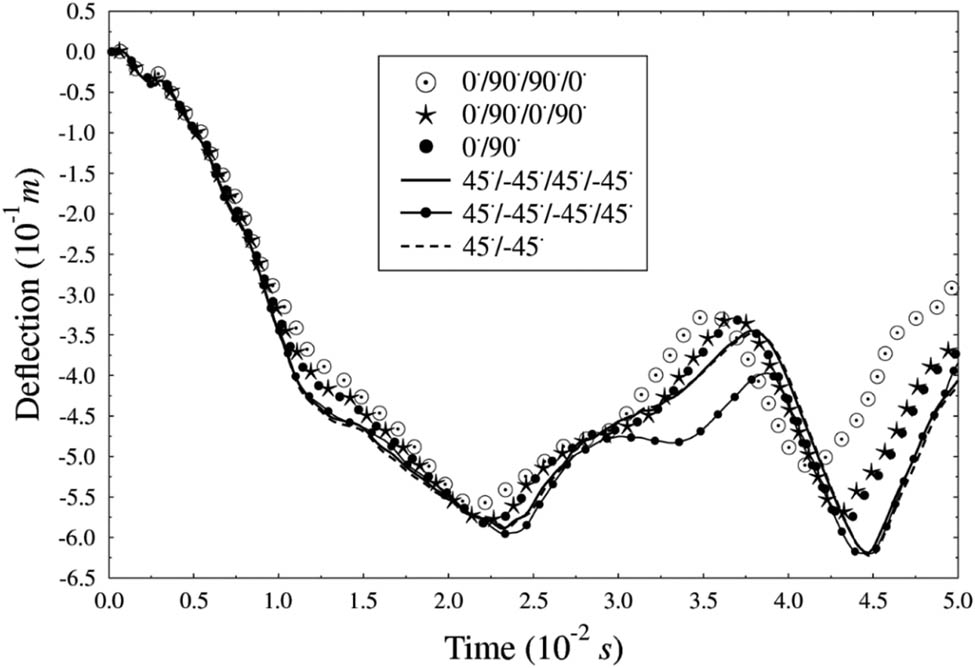
Nonlinear dynamic time histories of CNTFPC cylindrical panels for different layup angle sequences.

The load–deflection curves using linear and nonlinear dynamic analyses for a CNTFPC flat panel [0°/90°] with CNT weight ratio 1% is depicted in Figure 14. In linear dynamic analysis, there is a linear relationship between applied loads and deflections as it is assumed that the stresses remain in the linear elastic range of the used material, while in nonlinear dynamic analysis, there is a nonlinear relation as nonlinear effects can originate from geometrical nonlinearity (i.e., large deformations), material nonlinearity (i.e., elasto-plastic material), and contact. In this case, the nonlinear effect is related to geometrical nonlinearity. While linear dynamic analysis is simple, reduces time, and effort, it does not consider the nonlinearities concluding that nonlinear dynamic analysis is an accurate estimation technique.

Figure 14

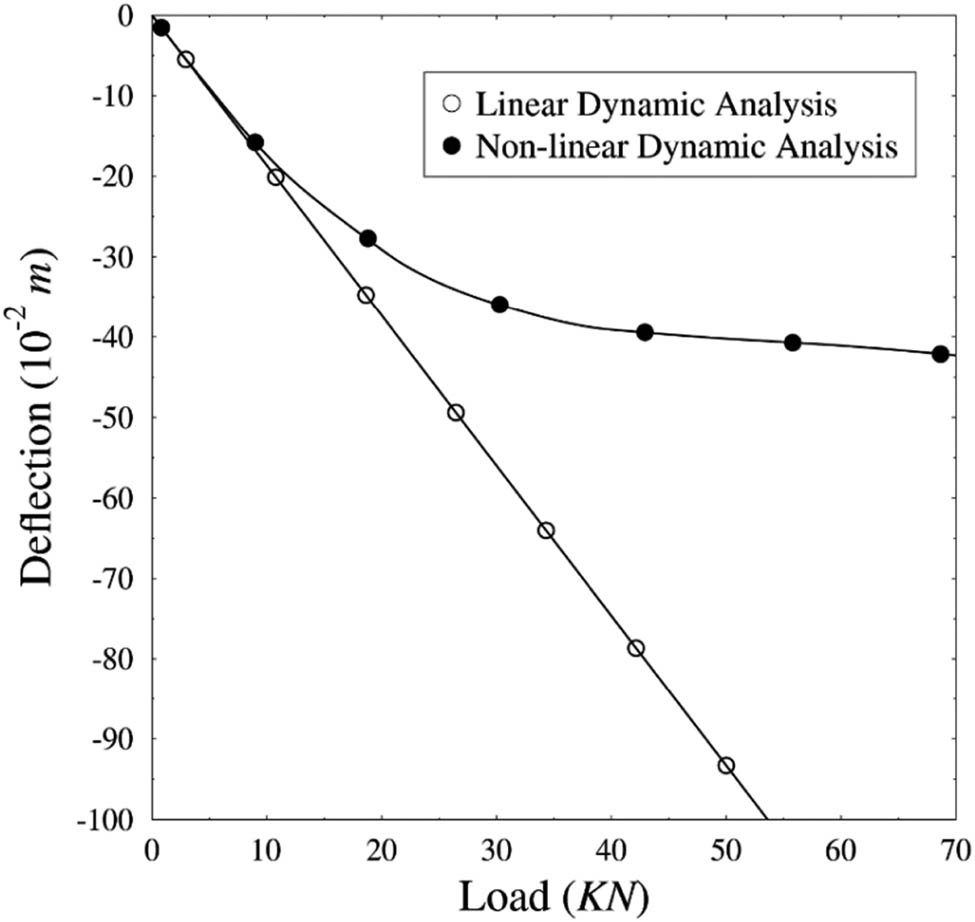
Load–deflection curves of CNTFPC flat panels using linear and nonlinear dynamic analyses.

4.3 Concrete beam reinforced with CNTFPC rebars

In order to validate the procedure for more complex and practical conditions, we apply the method to a concrete beam reinforced with CNTFPC rebars. The reinforced concrete beam of length (L) 5,500 mm, breadth 300 mm, and height 600 mm is modeled. Longitudinal rebars of diameter 19 mm and stirrups of diameter 8.0 mm are used. Three top and four bottom longitudinal bars are provided. The spacing of stirrups for L/3 length at the sides is 100 mm c/c and the spacing at the middle is 150 mm c/c. The details of the arrangement of the rebars are shown in Figure 15. The experimental mechanical properties of MWNTs/phenolic composites (CNTRC) from a study by Yeh et al. [31] are shown in Table 7. The mechanical properties of electrical/chemical resistance (ECR) – glass fiber are shown in Table 8. In the restricted scope of our study, our research focuses on the nonlinear dynamic and crack behaviors of curved panels with a cutout or CNTFPC-rebar type reinforced concrete beams.

Figure 15

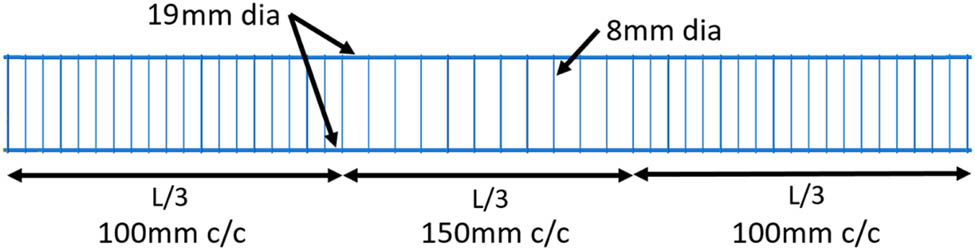
Details of the rebars in concrete beam.

Table 7

Experimental mechanical properties of MWNTs/phenolic composites (CNTRC) from ref. [29] used for CNTFPC rebar

CNT weight ratio (%)	0	0.5	1.0	1.5	2.0	3.0	4.0
Young’s modulus (GPa)	5.13	5.65	6.4	6.88	6.96	7.25	7.53
Tensile strength (MPa)	42.32	50.29	60.15	59.89	63.03	64.30	69.66

Table 8

Mechanical properties of E-glass fiber used for CNTFPC rebar

Material	Value	Unit	Definition
Advantex® ECR glass	81	GPa	Young’s modulus of ECR glass
	2,620	kg/m³	Mass density of ECR glass
	0.2		Poisson’s ratio of ECR glass
	3,751	MPa	Tensile strength of ECR glass

The multi-scale analysis is used to calculate the effective mechanical properties of the CNTFPC rebars tabulated in Table 9 for different CNT weight ratios assuming volume fraction of fiber as 0.55. It can be observed that the enhancement of the mechanical properties due to CNT is low. Concrete properties used in this study are tabulated in Table 10. The boundary condition is simply supported in all cases. Tensile tests of the rebars of 240 mm length with different CNT weight ratios are carried out. The rebars are fixed at one end and the load is applied on the other end. Table 11 shows the maximum elongations and loads necessary for the failure of the rebars. It can be observed that the maximum elongation of the rebar decreases, while the maximum load increases as the CNT weight ratios increases. The elongation is decreased by 1.67% and the applied load is increased by 0.6% when a 4% CNT weight ratio is added to the rebar. Therefore, it is concluded that CNT contributes to the stiffness of the rebar, hence, enhancing its performance.

Table 9

Mechanical properties of CNTFPC rebar for different CNT weight ratios using multi-scale analysis

CNT wt(%)	E ₁₁ (MPa)	E ₂₂ (MPa)	G (MPa)	ρ (tons/mm³)	ν ₁₂	Tensile strength (MPa)
0	46858.5	18394.211	5789.121	1.905 × 10⁻⁹	0.2585	2082.09
0.5	47092.5	19769.673	6276.844	1.905 × 10⁻⁹	0.2585	2085.68
1	47,430	21645.323	6954.827	1.905 × 10⁻⁹	0.2585	2090.12
1.5	47,646	22784.369	7373.835	1.906 × 10⁻⁹	0.2585	2090.00
2	47,682	22969.848	7442.586	1.906 × 10⁻⁹	0.2585	2091.41
3	47812.5	23632.183	7689.282	1.907 × 10⁻⁹	0.2585	2091.99
4	47938.5	24257.223	7923.791	1.908 × 10⁻⁹	0.2585	2094.40

Table 10

Material properties of concrete used in this study

Properties	Definition	Value	Unit
Density	Mass density	2,500	kg/m³
Elastic properties	Young’s modulus	29,000	MPa
	Poisson’s ratio	0.18
	Strain at compressive strength	0.002
Compressive behavior	Yield stress	20	MPa
	Inelastic strain	0
	Uniaxial compressive strength (%)	37	MPa
Tensile behavior	Yield stress	1.8	MPa
	Crack strain	0
	Tensile strength	3.7	MPa
	Strain at end of yield plateau	0.0002

Table 11

Results of the tensile test of rebars

CNT (wt%)	Maximum elongation (mm)	Difference (%)	Maximum load (N)	Difference (%)
0	10.664	−0.33	590,333.5	0.17
0.5	10.629	−0.50	591,350.4	0.21
1	10.576	−0.46	592,608.4	−0.01
1.5	10.528	−0.01	592,575.2	0.07
2	10.527	−0.25	592,975.8	0.03
3	10.501	−0.15	593,137.9	0.12
4	10.485		593,821.7

Table 12 shows the natural frequencies of the five modes of the beam which is reinforced by rebars with the CNT weight ratios of 0, 0.5, 1, 1.5, 2, 3, and 4%. It is observed that the natural frequencies increase with the increase in the CNT weight ratio. This is because the rebars get stiffer with the increase in the CNT weight ratio. While there is an increase in the frequency of the beam, the change is insignificant as the enhancement of the mechanical properties of CNTFPC rebars due to CNT is low. Table 13 shows the maximum deflection of the beam reinforced with different CNT weight ratio rebars using linear static analysis. A uniformly distributed static load of magnitude 0.13 MPa is applied and the beam is not conditioned to crack. It can be observed that the deflection decreases with the increase in the CNT weight ratio which is due to the stiffness effect of the CNT on the CNTFPC rebars. However, the change in deflection of the beam is very low as the enhancement of mechanical properties of CNTFPC due to CNT is low and concrete must crack before the rebar can take up most of the tensile stresses.

Table 12

Natural frequencies of the beam with different CNT weight ratio rebars

Mode (Hz)	CNT weight ratio
Mode (Hz)	0	0.005	0.01	0.015	0.02	0.03	0.04
1	16.092	16.093	16.096	16.097	16.097	16.098	16.099
2	28.627	28.63	28.635	28.638	28.638	28.64	28.641
3	53.001	53.009	53.022	53.029	53.031	53.035	53.039
4	57.109	57.114	57.122	57.127	57.127	57.13	57.133
5	78.073	78.091	78.116	78.131	78.134	78.143	78.152

Table 13

Maximum deflection of the beam with different CNT weight ratio rebars under static loading

CNT weight ratio (%)	Maximum deflection (mm)	Difference (%)
0	15.886	−0.74
0.5	15.768	−0.22
1	15.733	−0.36
1.5	15.677	−0.06
2	15.667	−0.59
3	15.575	−0.21
4	15.543

As concrete must crack before the rebar can take up most of the tensile stresses, crack analysis is done for the beam reinforced with different CNT weight ratio rebars. Inelastic properties are included for the concrete while only elastic properties are used for the rebars to show an average difference in the deflection of the beam. The spacing of the stirrups is doubled and CNT weight ratios considered are 0.00, 0.01, 0.02, and 0.04. Figure 16 presents the load–deflection curve of the beam after the beam cracks. It is apparent that for any load applied on the beam, the deflection decreases with the increase in the CNT weight ratio. This is because the stiffness of the CNTFPC rebars increases when the CNT weight ratio rises. Besides, the deflection of the beam at load 2,700 kN is tabulated in Table 14. It can be seen from the table that when the CNT weight ratios are increased from 0 to 1%, 1 to 2%, and 2 to 4%, there is an approximate reduction in the deflection of the beam by 2.62, 1.89, and 4.91%, respectively. This result indicates that the effect of the CNT weight ratio in the rebars is significant for the reduction in beam deflection.

Figure 16

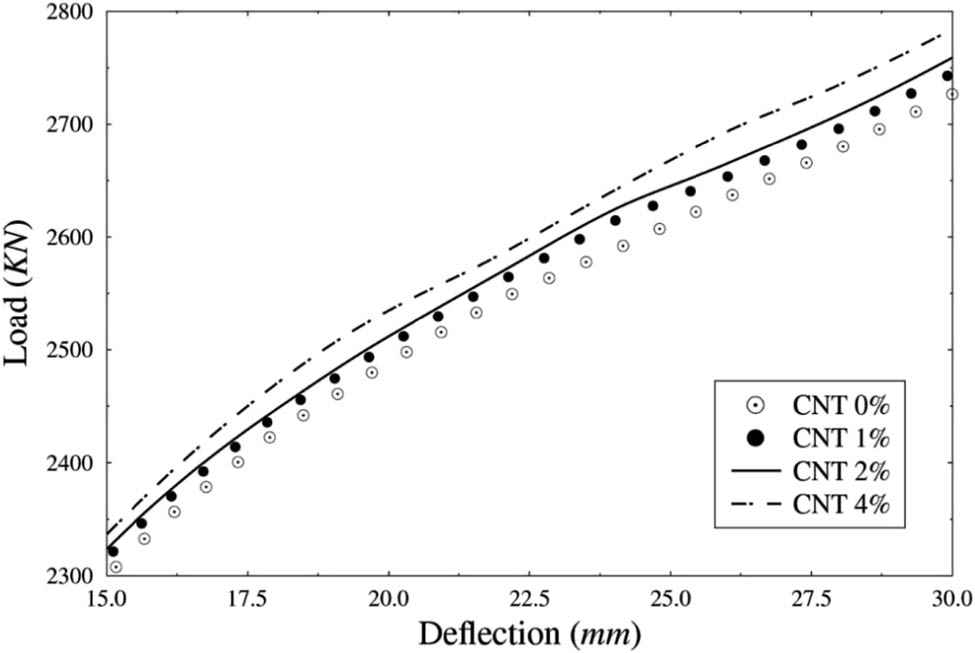
Load–deflection curve of the beam with different CNT weight ratio rebars after the beam cracks.

Table 14

Deflection of the beam at load 2,700kN

CNT weight ratio %	Deflection (mm)	Difference (%)
0	28.9032	−2.62
1	28.1452	−1.89
2	27.6129	−4.91
4	26.2581

Figure 17 shows the severity of cracks in the entire beam for different CNT weight ratios in the rebars. Inelastic properties are considered for both the concrete as well as rebars. The spacing of stirrups is doubled. It can be observed that the width of the cracks in the beam decreases when the CNT weight ratio increases. Also, Table 15 shows the maximum crack width at the bottom center of the beam when a load of 1,150 kN is applied. It can be seen from the table that the crack width decreases by 4.26, 0.89, and 0.69% in the linear region, while in the nonlinear region, the crack width increases by 2.41% at first and later decreases by 3.46 and 7.53% when CNT weight ratios are increased from 0 to 1%, 1 to 2%, and 2 to 4%, respectively. Although the enhancement of the mechanical properties of the rebar due to CNT is low, the increment in Young’s modulus and tensile strength contributes to the reduction in the crack width of the overall beam. It can be concluded from the results that CNT plays an important role in reducing the crack width of the overall beam.

Figure 17

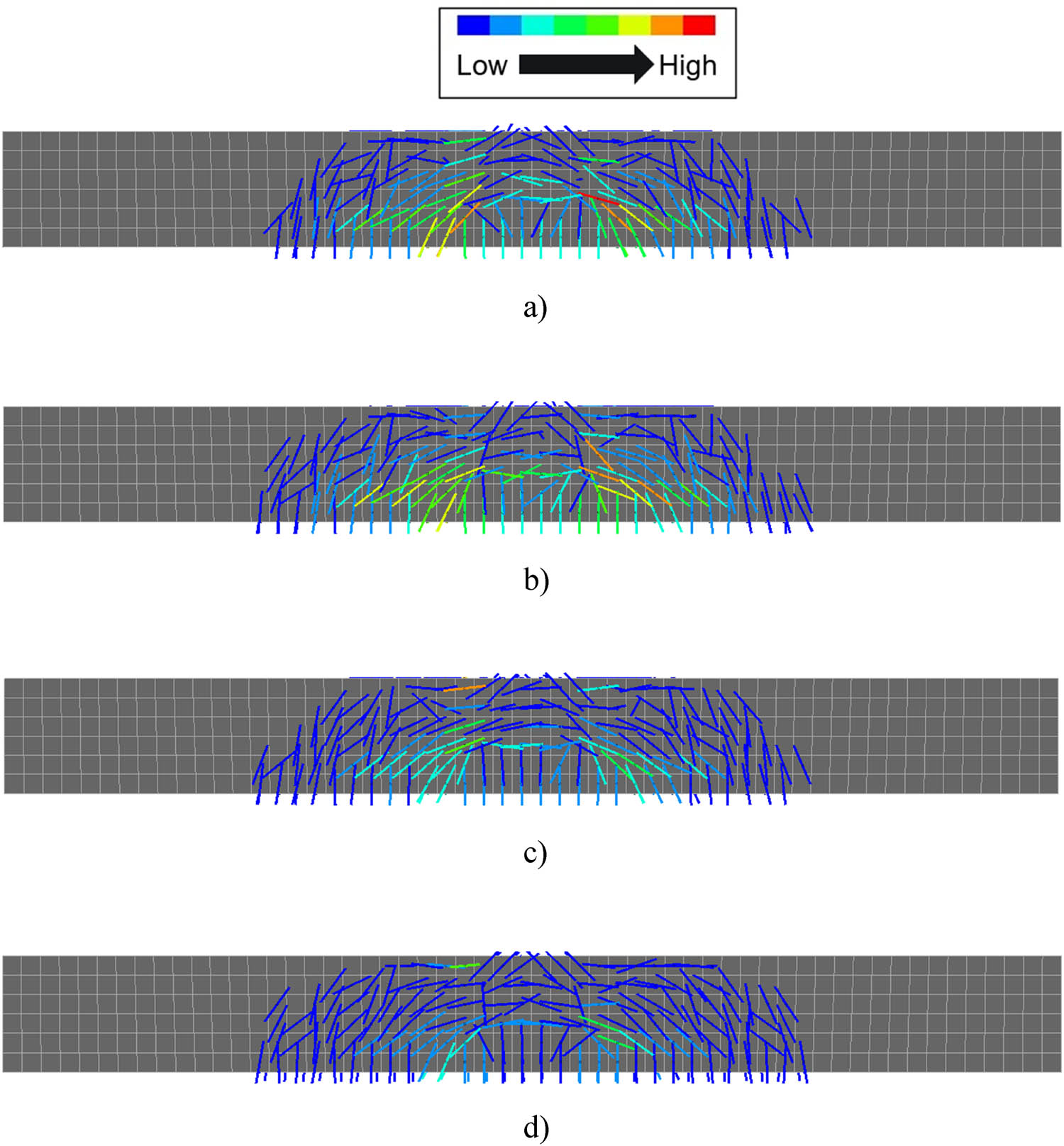
Crack images of beam reinforced with CNTFPC rebars. (a) CNT weight ratio of 0.00, (b) CNT weight ratio of 0.01, (c) CNT weight ratio of 0.02, and (d) CNT weight ratio of 0.04.

Table 15

Crack width at the bottom center of the beam (load = 1,150 kN)

CNT wt%	Crack at linear region (mm)	Difference (%)	Crack at nonlinear region (mm)	Difference (%)
0	0.379	−4.26	1.1387	2.41
1	0.3629	−0.89	1.1661	−3.46
2	0.3597	−0.69	1.1258	−7.53
4	0.3572		1.0411

5 Summary and conclusion

In this study, we applied the modified Halpin–Tsai model to estimate the effective material properties of CNTFPC reinforced structures for various geometries. An intuitive prediction of the nonlinear dynamic behavior of composite structures reinforced by CNTFPC is difficult because of their complexity due to the combined effect of anisotropy and geometry. The effects of the CNT are shown by performing the natural frequency, linear dynamic, and nonlinear dynamic analyses of CNTFPC panels, and linear static and crack analyses of CNTFPC rebar reinforced concrete beams. We find the following key observations in designing structures reinforced by CNTFPC:

The tensile test for examining the performance of the CNTFPC rebars with different CNT weight ratios showed that the elongation of the rebar decreases and the load necessary for the failure of rebar increases with the increase in the CNT weight ratio. The elongation decreased by 1.67% and applied load increased by 0.6% when a 4% CNT weight ratio is added in the rebars. Thus, CNT increases the stiffness of the rebar resulting in enhancement of its performance.
In frequency analysis, the change in frequencies of all the five modes of the beam for different CNT weight ratios in the rebars is low. The same trend can be seen for linear static analysis where the change in deflection of the beam is low. The mechanical enhancements due to CNT in the rebars are low to bring significant change in these cases. It should be noted that the reinforcements used in the study are passive and resist most of the loads only after the concrete starts cracking. As the concrete is not conditioned to crack in both the analyses, the change in the results is low.
The crack analysis with inelastic concrete and elastic rebar properties showed the average reduction in the deflections of the beam to be 2.6, 1.8, and 4.9% when the CNT weight ratio in the rebar is increased from 0 to 1%, 1 to 2%, and 2 to 4%, respectively, which shows that higher CNT content in the rebar is better for lowering the deflection of the beam.
In the case of the crack width of the overall beam, a significant reduction in the crack width is seen as the CNT weight ratio increases in the rebars. Moreover, the crack width at the bottom center of the beam at a load of 1,150 kN is lowered by approximately 5.7% in the linear region and 8.5% in the nonlinear region when a 4% CNT weight ratio is added to the rebar. Although the enhancement of the mechanical properties of the rebar due to CNT is low, the increment in Young’s modulus and tensile strength contributes to the reduction in the crack width of the beam. CNT shows significant results for tensile tests, deflection of the beam after the concrete cracks, and reduction in crack width of the overall beam.

In conclusion, this study analyzed the effect of CNT on composite material and compared the structural performance of the beam reinforced with the CNTFPC rebars for different CNT weight ratios through finite element analysis. However, the results of this study are limited because the analyses are performed through finite element analysis with limited cases. It will be necessary to prove the mechanism of action of CNT and fiber from further experimental studies such as SEM images, FTIR or Raman, and XRD analyses.

tel: +82 54 820 5847; fax: +82 54 820 6255

Funding information: This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIP) (no. 2018R1D1A1B07050080).
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors state no conflict of interest.

References

[1] Zhang LW, Lei ZX, Liew KM, Yu JL. Large deflection geometrically nonlinear analysis of carbon nanotube-reinforced functionally graded cylindrical panels. Comput Methods Appl Mech Eng. 2014;273:1–18. 10.1016/j.cma.2014.01.024.Search in Google Scholar

[2] Lei ZX, Zhang LW, Liew KM, Yu JL. Dynamic stability analysis of carbon nanotube-reinforced functionally graded cylindrical panels using the element-free kp-Ritz method. Composite Struct. 2014;113:328–38. 10.1016/j.compstruct.2014.03.035.Search in Google Scholar

[3] Mirzaei M, Kiani Y. Free vibration of functionally graded carbon nanotube reinforced composite cylindrical panels. Composite Struct. 2016;142:45–56. 10.1016/j.compstruct.2015.12.071.Search in Google Scholar

[4] Zhang LW, Xiao LN. Mechanical behavior of laminated CNT-reinforced composite skew plates subjected to dynamic loading. Compos Part B: Eng. 2017;122:219–30. 10.1016/j.compositesb.2017.03.041.Search in Google Scholar

[5] Kiani Y. Analysis of FG-CNT reinforced composite conical panel subjected to moving load using Ritz method. J Therm Stresses. 2017a;40:1442–60. 10.1080/01495739.2017.1336742.Search in Google Scholar

[6] Kiani Y. Thermal buckling of temperature-dependent FG-CNT-reinforced composite skew plates. Thin-Walled Struct. 2017b;119:47–57. 10.1016/j.tws.2017.05.03.Search in Google Scholar

[7] Kiani Y, Mirzaeib M. Rectangular and skew shear buckling of FG-CNT reinforced composite skew plates using Ritz method. Aerosp Sci Technol. 2018;77:388–98. 10.1016/j.ast.2018.03.022.Search in Google Scholar

[8] Rafiee M, Liu XF, He XQ, Kitipornchai S. Geometrically nonlinear free vibration of shear deformable piezoelectric carbon nanotube/fiber/polymer multiscale laminated composite plates. J Sound Vib. 2014;333(14):3236–51. 10.1016/j.jsv.2014.02.033.Search in Google Scholar

[9] Lee SY. Dynamic instability assessment of carbon nanotube/fiber/polymer multiscale composite skew plates with delamination based on HSDT. Composite Struct. 2018;200:757–70. 10.1016/j.compstruct.2018.05.121.Search in Google Scholar

[10] Lee S, Hwang J. Finite element nonlinear transient modelling of carbon nanotubes reinforced fiber/polymer composite spherical shells with a cutout. Nanotechnol Rev. 2019;8(1):444–51. 10.1515/ntrev-2019-0039.Search in Google Scholar

[11] Ahmadi M, Ansari R, Rouhi H. Free and forced vibration analysis of rectangular-circular-annular plates made of carbon fiber-carbon nanotube-polymer hybrid composites. Sci Eng Compos Mater. 2019a;2019:70–6. 10.1515/secm-2017-0279.Search in Google Scholar

[12] Ahmadi M, Ansari R, Rouhi H. Fracture behavior of the carbon nanotube/carbon fiber/polymer multiscale composites under bending test – A stochastic finite element method. Mech Adv Mater Struct. 2019b;26:1169–77. 10.1080/15376494.2018.1432790.Search in Google Scholar

[13] Ahmadi M, Ansari R, Rouhi H. On the free vibrations of piezoelectric carbon nanotube-reinforced microbeams: a multiscale finite element approach. Iran J Sci Technol Trans Mech Eng. 2019c;43:285–94. 10.1007/S40997-018-0157-X.Search in Google Scholar

[14] Ahmadi M, Ansari R, Rouhi H. Free vibration analysis of carbon fiber-carbon nanotube-polymer matrix composite plates by a finite element-based multi-scale modeling approach. J Multiscale Model. 2018;9:1850002. 10.1142/S1756973718500026.Search in Google Scholar

[15] Ahmadi M, Ansari R, Rouhi H. Multi-scale bending, buckling and vibration analyses of carbon fiber/carbon nanotube-reinforced polymer nanocomposite plates with various shapes. Phys E Low-Dimensional Syst Nanostructures Multiscale Model. 2017;93:17–25. 10.1016/j.physe.2017.05.009.Search in Google Scholar

[16] Lee S. Dynamic stability and nonlinear transient behaviors of CNT-reinforced fiber/polymer composite cylindrical panels with delamination around a cutout. Nonlinear Dyn. 2020;99:2551–69. 10.1007/s11071-020-05477-x.Search in Google Scholar

[17] Chaallal O, Benmokrane B. Fiber-reinforced plastic rebars for concrete applications. Compos Part B Eng. 1996;27(3–4):245–52. 10.1016/1359-8368(95)00023-2.Search in Google Scholar

[18] Wang H, Belarbi A. Ductility characteristics of fiber-reinforced-concrete beams reinforced with FRP rebars. Constr Build Mater. 2011;25(5):2391–401. 10.1016/j.conbuildmat.2010.11.040.Search in Google Scholar

[19] Inman M, Thorhallsson ER, Azrague K. A mechanical and environmental assessment and comparison of basalt fibre reinforced polymer (BFRP) rebar and steel rebar in concrete beams. Energy Procedia. 2017;111:31–40. 10.1016/j.egypro.2017.03.005.Search in Google Scholar

[20] Duic J, Kenno S, Das S. Performance of concrete beams reinforced with basalt fibre composite rebar. Constr Build Mater. 2018;176:470–81. 10.1016/j.conbuildmat.2018.04.208.Search in Google Scholar

[21] Gojny FH, Wichmann MHG, Köpke U, Fiedler B, Schulte K. Carbon nanotube-reinforced epoxy-composites enhanced stiffness and fracture toughness at low nanotube content. Compos Sci Technol. 2004;64(15):2363–71. 10.1016/j.compscitech.2004.04.002.Search in Google Scholar

[22] Hewitt RL, Malherbe MC. An approximation for the longitudinal shear modulus of continuous fiber composites. J Composite Mater. 1970;4(2):280–2. 10.1177/002199837000400214.Search in Google Scholar

[23] Reddy JN. Dynamic (transient) analysis of layered anisotropic composite material plates. Int J Numer Methods Eng. 1983;19(2):237–55. 10.1002/nme.1620190206.Search in Google Scholar

[24] Sahu SK, Datta PK. Dynamic stability of curved panels with cutouts. J Sound Vib. 2002;251(4):683–96. 10.1006/jsvi.2001.3961.Search in Google Scholar

[25] Sivasubramonian B, Rao GV, Krishnan A. Free vibration of longitudinally stiffened curved panels with cutout. J Sound Vib. 1999;226(1):41–55. 10.1006/jsvi.1999.2281.Search in Google Scholar

[26] Lei ZX, Zhang LW, Liew KM. Analysis of laminated CNT reinforced functionally graded plates using the element-free kp-Ritz method. Compos Part B: Eng. 2016;84:211–21. 10.1016/j.compositesb.2015.08.081.Search in Google Scholar

[27] Mallikarjuna, Kant T. Dynamics of laminated composite plates with a higher order theory and finite element discretization. J Sound Vib. 1988;126(3):463–75. 10.1016/0022-460X(88)90224-6.Search in Google Scholar

[28] Han Y, Elliott J. Molecular dynamics simulations of the elastic properties of polymer/carbon nanotube composites. Comput Mater Sci. 2007;39(2):315–23. 10.1016/j.commatsci.2006.06.011.Search in Google Scholar

[29] Kim M, Park YB, Okoli OI, Zhang C. Processing, characterization, and modeling of carbon nanotube-reinforced multiscale composites. Compos Sci Technol. 2009;69(3–4):335–42. 10.1016/j.compscitech.2008.10.019.Search in Google Scholar

[30] Lee SY, Park T. Free vibration of laminated composite skew plates with central cutouts. Struct Eng Mech. 2009;31(5):587–603. 10.12989/sem.2009.31.5.587.Search in Google Scholar

[31] Yeh MK, Tai NH, Liu JH. Mechanical behavior of phenolic-based composites reinforced with multi-walled carbon nanotubes. Carbon. 2006;44(1):1–9. 10.1016/j.carbon.2005.07.005.Search in Google Scholar

Received: 2021-09-04

Revised: 2022-01-12

Accepted: 2022-03-02

Published Online: 2022-03-22

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/ntrev-2022-0079

Keywords for this article

CNTFPC cylindrical shell; CNTFPC-reinforced concrete beam; multi-scale analysis; nonlinear dynamics; crack analysis

Creative Commons

BY 4.0