Home Effect of deformation conditions on compression phase transformation of AZ31
Article Open Access

Effect of deformation conditions on compression phase transformation of AZ31

  • Qianhua Yang , Bowen Yang , Zhibing Chu EMAIL logo , Chun Xue , Yugui Li , Leifeng Tuo and Hong Gao
Published/Copyright: July 5, 2022
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
Nanotechnology Reviews
From the journal Nanotechnology Reviews Volume 11 Issue 1

Abstract

In this article, the compression simulation of AZ31 magnesium alloy is simulated by the molecular dynamics method. The effects of loading mode, temperature, and strain rate on the compression behavior are analyzed. The lattice distortion, mechanical behavior, structural evolution, and dislocation evolution in the compression process are deeply analyzed, and the results of different loading modes are obtained. The hexagonal close-packed (HCP) → face-centered cubic (FCC) phase transformation mechanism of AZ31 magnesium alloy during compression at temperature and strain rate, which is related to the mechanical behavior, has been studied completely. This article perfects the research on the compression behavior of magnesium alloys, excavates the application potential of magnesium alloys, and provides a new idea for improving the processing technology and developing high-performance magnesium alloys.

Keywords: plane strain compression; uniaxial compression; temperature; strain rate; phase transformation

1 Introduction

Magnesium and magnesium alloys have excellent physical and mechanical properties, high specific strength, good thermal conductivity, and some more properties. They are important and excellent materials for automotive and aerospace industry structures [1,2,3,4,5,6,7,8,9]. Mg–Al–Zn magnesium alloy is currently one of the most widely used magnesium alloy series [10], of which the most representative is AZ31 wrought magnesium alloy. However, the large-scale commercial application of mg-based alloys still faces some obstacles [11,12,13]. To further improve the strength of magnesium alloy, it is necessary to fully understand the influence of microstructure and dislocation evolution on the strength [14]. Magnesium alloys have a hexagonal closely packed structure [15], and its deformation mechanism is closely related to stress/strain state, temperature, and strain rate. Plastic deformation still plays a key role in the strengthening of the hexagonal close-packed (HCP) phase [16,17]. Grain refinement of magnesium alloys, especially magnesium–aluminum (Mg–Al) alloys, is the most effective method to improve strength [18].

Integrated computational material engineering has become a reliable tool to establish the relationship between structure, process, and properties, which will promote the development and the application of new magnesium alloys to a great extent [19,20,21]. Among them, molecular dynamics (MD) simulation, as an important method in the study of plastic deformation mechanism at micro- and nano-scale in metal materials [22,23,24,25], can predict the effects of grain size, grain boundaries, stacking faults, and dislocations on the deformation behavior of materials at the atomic level [26,27,28,29,30,31,32,33,34,35,36,37]. MD simulations show that grain boundaries are the origin of dislocations in nanomaterials [38]. The nucleation and diffusion of some Shockley dislocations are caused by grain boundary (GB) deformation, that is, the position migration under the action of atomic phase transformation and stress [39,40]. Therefore, the study of dislocation evolution mechanism and phase transformation mechanism is of great significance to the total plastic deformation [41].

Rajput and Paul [42] studied the effect of uniaxial and plane strain tensile deformation on the mechanical behavior of nanocrystalline copper and found that the yield of the material begins with the nucleation of Shockley partial dislocations, and the subsequent deformation leads to the increase of dislocation line length in the material. The nucleation and diffusion of dislocations and stacking faults jointly control the strain hardening behavior of materials. The uneven distribution of atomic strain and dislocation was observed in uniaxial and plane strain tensile deformation. Higher GB migration was observed during uniaxial tensile deformation. Vlasova [43] investigated the deformation characteristics of nanocrystalline magnesium under high-speed deformation by MD simulation. Uniaxial compression and plane strain compression (PSC) of [0001]-nanocrystalline magnesium were carried out, and the effects of loading methods on the deformation and strength properties of [0001]-nanocrystalline magnesium were investigated. Paul et al. [44] studied the deformation mechanism and pore nucleation of nanocrystalline aluminum under uniaxial and plane strain loading. Compared with uniaxial loading, nanocavities nucleate earlier under plane strain loading. Zhang et al. [45] studied the micro-mechanical behavior of Cu/Ti laminated composites during uniaxial tension and PSC by the MD method and revealed the microdeformation mechanism of closely packed hexagonal metal laminated composites.

To sum up, the compression simulation of AZ31 magnesium alloy is simulated by the MD method, the effects of loading mode, temperature, and strain rate on the compression behavior are analyzed, the lattice distortion, mechanical behavior, structural evolution, and dislocation evolution in the compression process are deeply analyzed, and different loading modes are obtained. The HCP → face-centered cubic (FCC) phase transformation mechanism of AZ31 magnesium alloy during compression at temperature and strain rate, which is related to the mechanical behavior, has been studied completely. This article studies the compression behavior of magnesium alloys, excavates the application potential of magnesium alloys, and provides a new idea for improving the processing technology and developing high-performance magnesium alloys.

2 Simulation method

The potential function is a mathematical function that describes the total energy E and particle coordinates (r) of the model particles in the study of MD [46,47,48,49]. The modified embedded atomic method potential function can be used to calculate the pairwise interactions of various materials, which is more suitable for the calculation of metals and alloys with FCC, body-centered cubic (BCC), HCP, and diamond structures [50,51,52,53,54,55,56]. Eq. (1) for modified embedded atom method is given as follows:

(1) E = ∑ i F i ( ρ ¯ i ) + 1 2 ∑ i ≠ j ϕ ij ( γ ij ) .

In Eq. (1), E is the total energy of atom i, F is the embedded energy and is the function of atomic electron density ρ, ρ is the atomic electron density, γ and ϕ is a pair of potential interactions, and α and β is the element type of atoms i and j.

The model of AZ31 magnesium alloy was established by Atomsk [57], and the X-axis, Y-axis, and Z-axis were set to correspond to [1̅21̅0], [1̅010], and [0001], respectively. The model is imported into large-scale atomic/molecular massively parallel simulator (LAMMPS) [58] for MD simulation. The potential function developed by Stukowski [59] can be used to study the deformation and recrystallization characteristics of Mg–Al–Zn alloy in the whole processing temperature range, and so this potential function is used for calculation. X, Y, and Z are all periodic boundary conditions, constant-pressure, constant-temperature (NPT) ensemble is adopted, and the time step is 0.001 ps. The NPT ensemble and the nose-hoover thermostat maintain the stability of the entire system at constant pressure and temperature. The conjugate gradient algorithm is used to minimize the model energy to obtain the equilibrium structure at a given temperature in the NPT ensemble. Therefore, the model is first relaxed 10 ps under constant temperature and pressure, and then different deformation conditions are imposed, the deformation time is 20 ps, and the final deformation of magnesium alloy reaches 20%. The deformation Eq. (2) is expressed as follows:

(2) ε = L 1 − L 2 L 1 × 100 % .

In Eq. (2), ε is strain; L 1 is the initial length of the model in [0001] crystal direction; and L 2 is the length of the model compressed along the [0001] crystal direction.

The results are imported into the visualization software OVITO for analysis. Common neighbor analysis (CNA) can observe the face-centered cubic, body-centered cubic, closely packed hexagonal (HCP) structure, and other structure (GB atoms) in the metal. DXA (dislocation analysis) can determine the Burgers vector of each dislocation and identify the dislocation junction. Grain segmentation can observe the grain changes in the simulation process. Construct surface mesh can identify the cavity and calculate the cavity area [60,61,62,63,64,65].

3 Results and analysis

3.1 Influence of compression mode on phase transition

The model of AZ31 magnesium alloy with a size of 192.6 Å × 222.395 Å × 208.4 Å is established, in which 96% are Mg atoms, 3% are Al atoms, and 1% are Zn atoms. The model contains 20 grains, and the X-axis, Y-axis, and Z-axis are set to correspond to the crystal directions of [1̅21̅0], [1̅010], and [0001], respectively. Import the model into LAMMPS and then assign the potential function developed by Hyo-Sun Jang to the model. X, Y, and Z are all periodic boundary conditions, and the time step is 0.001 ps. The model energy is minimized and 10 ps is relaxed at 300 K. The temperature change in the relaxation process is shown in Figure 1a. The model is uniformly compressed 20 ps along the Z-axis ([0001] direction) at 300 K with the strain rate of 0.01 ps−1, and the uniaxial compression simulation (UC) is realized. The process diagram is shown in Figure 1b.

Figure 1 Uniaxial compression: (a) the change of temperature during relaxation and (b) process diagram.
Figure 1

Uniaxial compression: (a) the change of temperature during relaxation and (b) process diagram.

The model of AZ31 magnesium alloy with a size of 200 Å × 200 Å × 200 Å is established, in which 96% are Mg atoms, 3% are Al atoms, and 1% are Zn atoms. The model contains 20 grains, and the X-axis, Y-axis, and Z-axis are set to correspond to the crystal directions of [1̅21̅0], [1̅010], and [0001], respectively. The MD simulation is carried out by LAMMPS, and the potential function developed by Jang is assigned to the model. X, Y, and Z are all periodic boundary conditions, the time step is 0.001 ps, and the 10 ps is relaxed at 300 K. The change of temperature during the relaxation process is shown in Figure 2a. Keeping the size of the Y-axis model unchanged, the model is uniformly compressed 20 ps along the Z-axis ([0001] direction) at the strain rate of 0.01 ps−1 at 300 K, and the PSC simulation is realized. The process diagram is shown in Figure 2b.

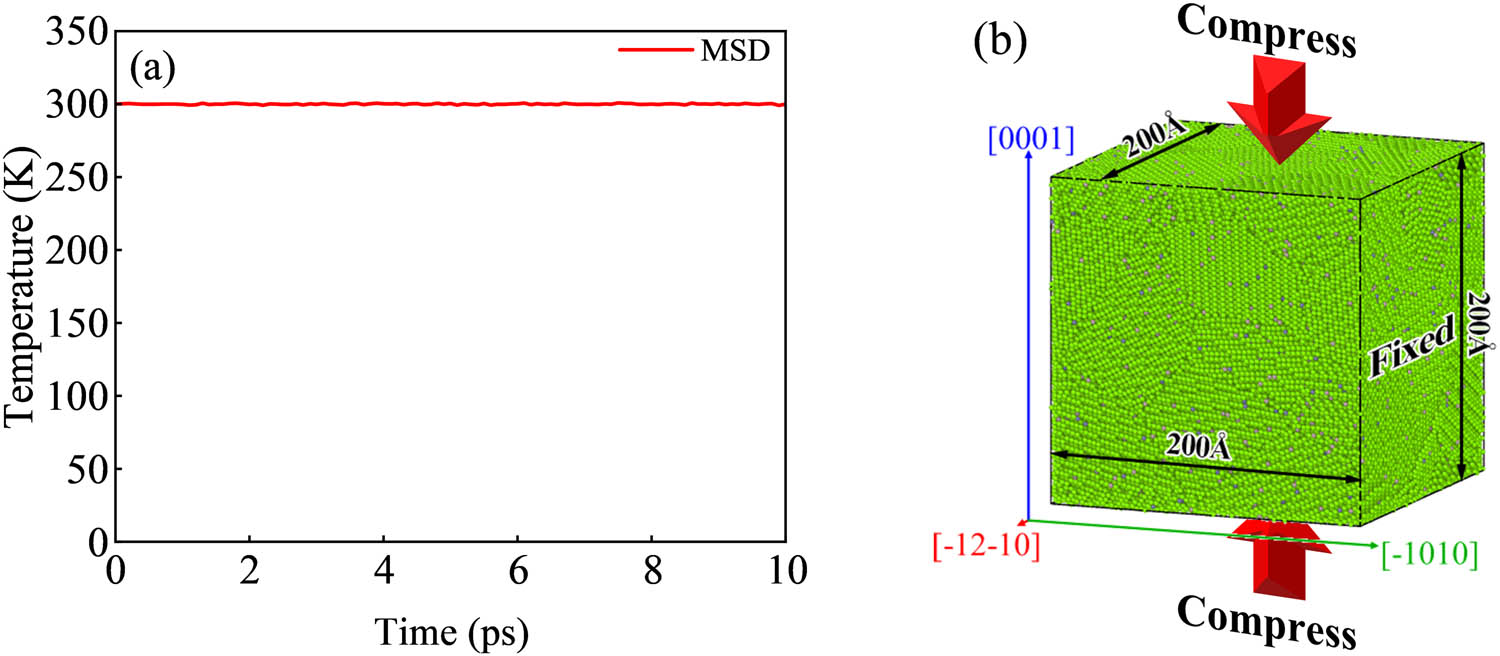
Figure 2 Plane strain compression: (a) the change of temperature during relaxation and (b) process diagram.
Figure 2

Plane strain compression: (a) the change of temperature during relaxation and (b) process diagram.

Figure 3 shows the grain change, Figure 3a shows the grain number curve, Figure 3b shows the grains at different strains under PSC, and Figure 3c shows the grains at different strains under UC. It can be seen that under PSC, the grain number is more, the grain volume is smaller, the grain refinement is more obvious, and the grain refinement occurs earlier.

Figure 3 Grain change: (a) grain number curve, (b) grain change under PSC, and (c) grain change under UC.
Figure 3

Grain change: (a) grain number curve, (b) grain change under PSC, and (c) grain change under UC.

Figure 4 shows parameter changes during compression. Figure 4a shows the stress–strain curve. The yield stress under PSC is 2.85 GPa, and the yield stress under UC is 1.92 GPa, which increases by 48.43%. The yield strain under PSC is 10.2%, and the yield strain under UC is 9.6%, with an increase of 6.25%. The elastic modulus of PSC is larger, which means that PSC can improve the plasticity of AZ31 magnesium alloy. Figure 4b shows the dislocation density curve. The dislocation occurs earlier, and the dislocation density is higher in AZ31 magnesium alloy under PSC.

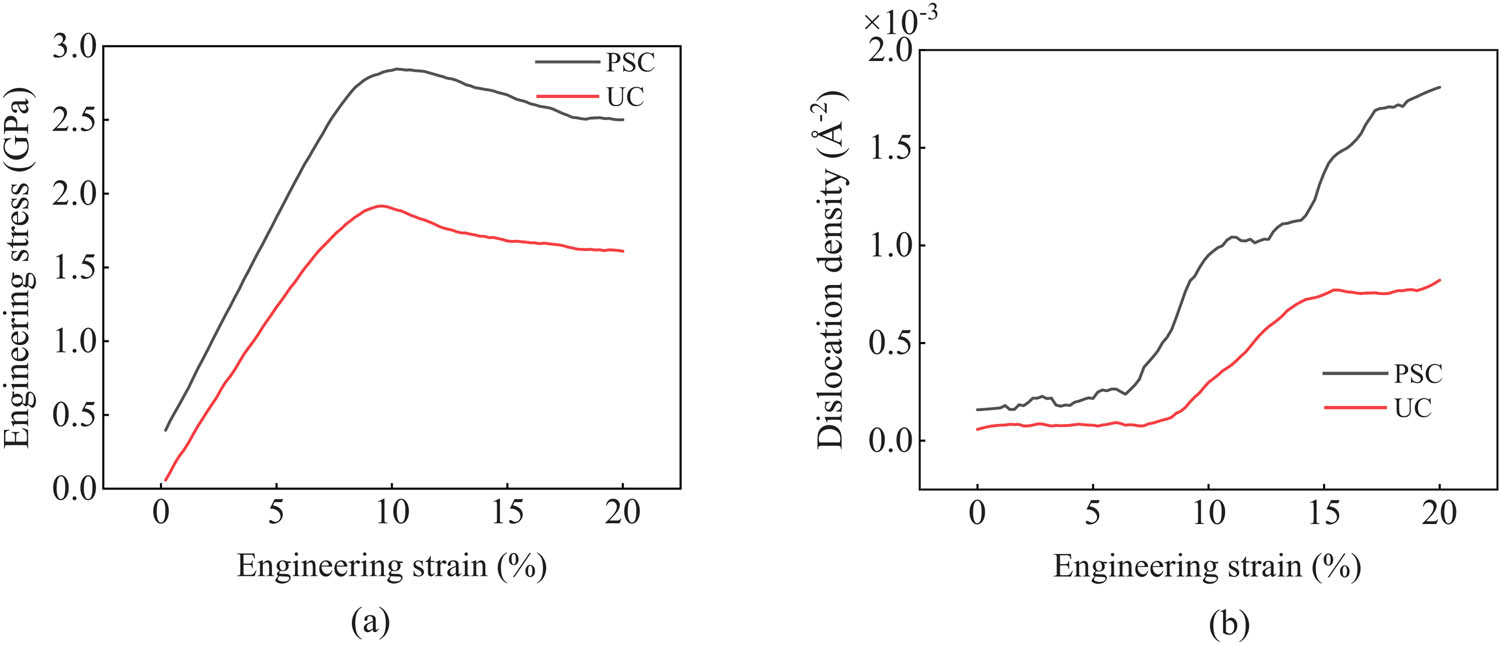
Figure 4 Parameter changes during compression: (a) stress–strain curve and (b) dislocation density curve.
Figure 4

Parameter changes during compression: (a) stress–strain curve and (b) dislocation density curve.

Figure 5 shows cavity evolution. Figure 5a shows the curve of the cavity area, Figure 5b shows the evolution of the cavity under PSC, and Figure 5c shows the evolution of the cavity under UC. It can be found that cavity appears earlier in magnesium alloys under PSC, the time of cavity appearing is almost consistent with the time of dislocation increase, and the cavty area formed under PSC is larger. Therefore, in the PSC process, because the Y direction is fixed, the atomic position changes faster, forming dislocations and cavity, and at the same time, the yield stress of magnesium alloy increases.

Figure 5 Cavity evolution: (a) cavity area curve, (b) cavity evolution under PSC, and (c) cavity evolution under UC.
Figure 5

Cavity evolution: (a) cavity area curve, (b) cavity evolution under PSC, and (c) cavity evolution under UC.

Figure 6 shows GB evolution. Figure 6a shows the atomic fraction curve within the grain, and Figure 6b shows the atomic fraction curve of the GB. The GB diffusion of magnesium alloy occurs earlier under PSC, and the rate and degree of diffusion are higher than that of UC. Figure 6c and d are CNA diagrams of PSC and UC, respectively, in which the red atom is the HCP structure, the green atom is FCC structure, and the white atom is GB atom. It is obvious that with the increase in compression, the number of atoms in the GB increases, the GB diffuses, and the atoms of the FCC structure increase gradually, and the FCC stacking faults increase. The FCC stacking fault first forms at the GB and then expands into the grain. The formation principle is as follows: due to the compression, the position of the HCP structure atom changes and becomes the GB atom. With the increase in the squeezing amount, the GB atom forms an FCC stacking fault.

Figure 6 Grain boundary evolution: (a) fraction curve of GI atoms, (b) fraction curve of GB atoms (c) figure of CNA under PSC and (d) figure of CNA in UC.
Figure 6

Grain boundary evolution: (a) fraction curve of GI atoms, (b) fraction curve of GB atoms (c) figure of CNA under PSC and (d) figure of CNA in UC.

Figure 7 shows structural evolution. Figure 7a–c shows the fractional curve of HCP, FCC, and BCC structure, respectively. It can be seen that the change of grain internal (GI) atoms curve is mainly caused by HCP structure and FCC structure, while the proportion of the BCC structure is very small. The structural change of PSC is earlier than that of UC, and the number of BCC atoms in PSC is slightly more than that of UC. The changes of HCP structure and FCC structure are earlier than the occurrence of plastic deformation. In the process of compression, the atoms of the HCP structure first become GB atoms. With the increase in the amount of compression, the position of GB atoms continues to change, and some atoms form FCC stacking faults. Figure 7d–f shows the evolution diagram of each structure under PSC, and Figure 7g–i shows the evolution diagram of each structure under UC. It can be seen that under PSC, the occurrence of FCC stacking fault is earlier than that of UC and the occurrence of the BCC structure is earlier than that of UC. The FCC stacking fault occurs between the HCP structure and the GB, so that the phase structure transformation of HCP → GB → FCC occurs during compression.

Figure 7 Structural evolution: (a) HCP structure fraction curve, (b) FCC structure fraction curve, (c) BCC structure fraction curve, (d)–(f) structural evolution diagram under PSC, and (g)–(i) structural evolution diagram under UC.
Figure 7

Structural evolution: (a) HCP structure fraction curve, (b) FCC structure fraction curve, (c) BCC structure fraction curve, (d)–(f) structural evolution diagram under PSC, and (g)–(i) structural evolution diagram under UC.

Figure 8 shows dislocation evolution. Figure 8a and b shows the dislocation evolution diagrams under PSC and UC, respectively. With the increase in the amount of squeezing, the atomic position changes, and the dislocation density increases. Figure 8c and d shows the dislocation density curves under PSC and UC, respectively. It is found that the dislocations in the model are mainly other dislocations and 1 3 〈 1 ¯ 100 〉 dislocations. Under PSC, the dislocation density in magnesium alloy is significantly higher than that in UC. This is because the Y-axis is fixed, and the atom can only move to the X-axis, resulting in more 1 3 〈 1 ¯ 100 〉 dislocations and other dislocations, resulting in more FCC stacking faults. The change of other dislocation density is almost the same as that of GB atom, and the change of 1 3 〈 1 ¯ 100 〉 dislocation is almost the same as that of FCC stacking fault. Table 1 presents the Bergson markings of common dislocations in closely packed hexagonal crystals. Among them, A B → 1 3 〈 11 2 ¯ 0 〉 is the basal complete dislocation, T S → ( [ 0001 ] ) is the cylindrical complete dislocation, S A → / T B → 1 3 〈 11 2 ¯ 3 〉 is the incomplete dislocation, and A σ → ( A σ → 1 3 〈 1 ¯ 100 〉 ) is the Shockley incomplete dislocation [66]. The strain corresponding to the increase of dislocation density is consistent with that when the atomic fraction of FCC structure begins to increase, so that there is a positive correlation between Shockley partial dislocations and FCC stacking faults.

Figure 8 Dislocation evolution: (a) dislocation evolution diagram under PSC, (b) dislocation evolution diagram under UC, (c) dislocation density curve under PSC, and (d) dislocation density curve under UC.
Figure 8

Dislocation evolution: (a) dislocation evolution diagram under PSC, (b) dislocation evolution diagram under UC, (c) dislocation density curve under PSC, and (d) dislocation density curve under UC.

Table 1

Bergson marks of common dislocations in hexagonal close packed crystals [67]

Mark A B → T S → S A → / T B → A σ → σ S → A S →
b 1 3 〈 11 2 ¯ 0 〉 [ 0001 ] 1 3 〈 11 2 ¯ 3 〉 1 3 〈 1 ¯ 100 〉 1 2 [ 0001 ] 1 6 〈 2 ¯ 203 〉

3.2 Effect of temperature on phase transition under PSC

The AZ31 magnesium alloy model with a size of 200 Å × 200 Å × 200 Å is imported into LAMMPS, then the potential function is assigned to the model, X, Y, and Z are all set as periodic boundary conditions, NPT ensemble is adopted, the time step is 0.001 ps, and the 10 ps is relaxed under 300–700 K, respectively. The change of temperature during the relaxation process is shown in Figure 9. Then, keeping the size of the Y-axis model unchanged, the PSC is realized by uniformly compressing 20 ps along the Z-axis ([0001] direction) at the strain rate of 0.01 ps−1.

Figure 9 Temperature change during relaxation.
Figure 9

Temperature change during relaxation.

Figure 10 shows the grain evolution, Figure 10(a) shows the grain diagram, and Figure 10(b) shows the grain curve. It can be seen that the change in the number of grains is not very obvious with the change of temperature, and the number of grains at different temperatures is roughly the same. Therefore, it is speculated that temperature has little effect on grain refinement.

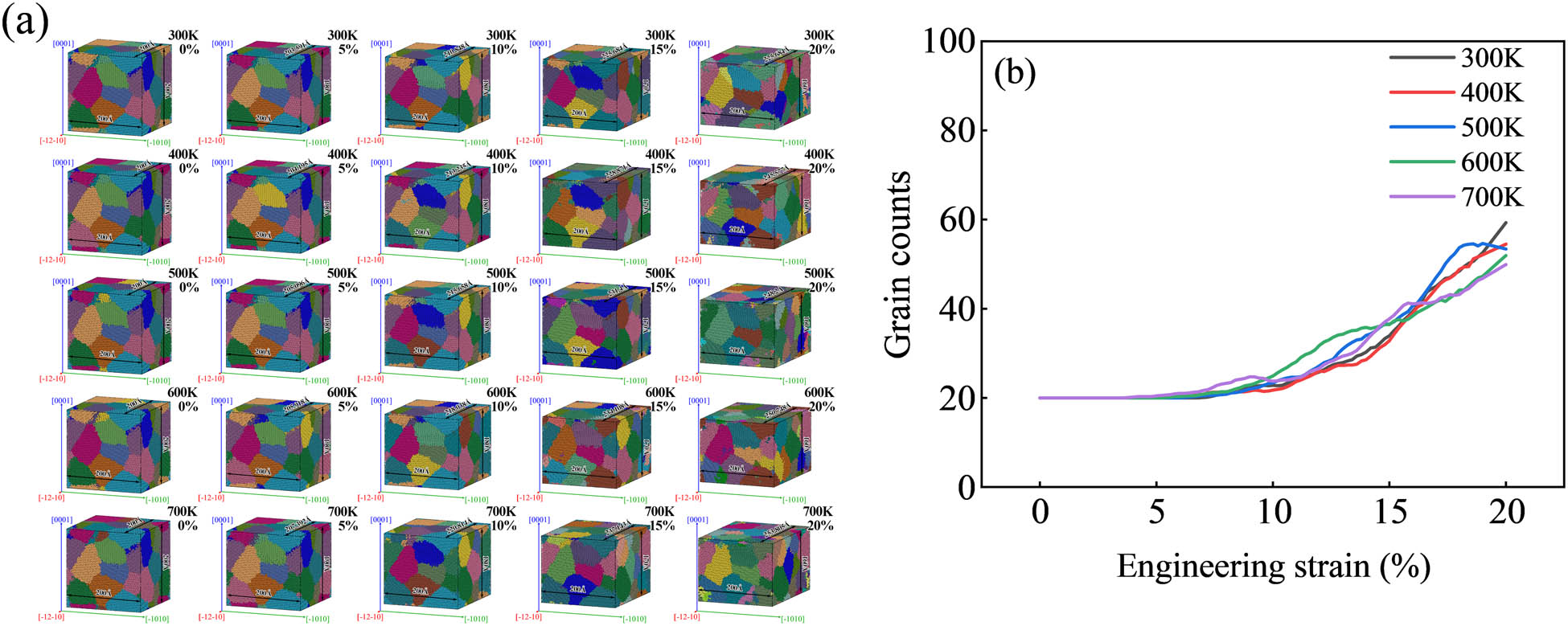
Figure 10 Grain evolution: (a) grain diagram and (b) grain number curve.
Figure 10

Grain evolution: (a) grain diagram and (b) grain number curve.

Figure 11 shows the force–energy parameter curve under PSC, and Figure 11a shows the stress–strain curve. With the increase in temperature, the initial stress increases, the yield stress decreases, and the elastic modulus decreases. In the PSC process, with the increase in temperature, the potential energy of AZ31 magnesium alloy increases and plastic deformation occurs more easily, so the yield stress and yield strain decrease with the increase in temperature. Figure 11b shows the potential energy curve. The higher the temperature is, the more energy is obtained and the greater the potential energy is. Figure 11c is a volume curve. With the increase in the amount of compression, the elastic deformation first occurs and the volume decreases. When the strain reaches the yield strain, the volume begins to increase when the strain reaches the plastic stage. The higher the temperature is, the shorter the elastic stage is and the smaller the volume change is. Figure 11d shows the total dislocation density curve. With the increase in the amount of compression, the atomic position changes, and the total dislocation density increases.

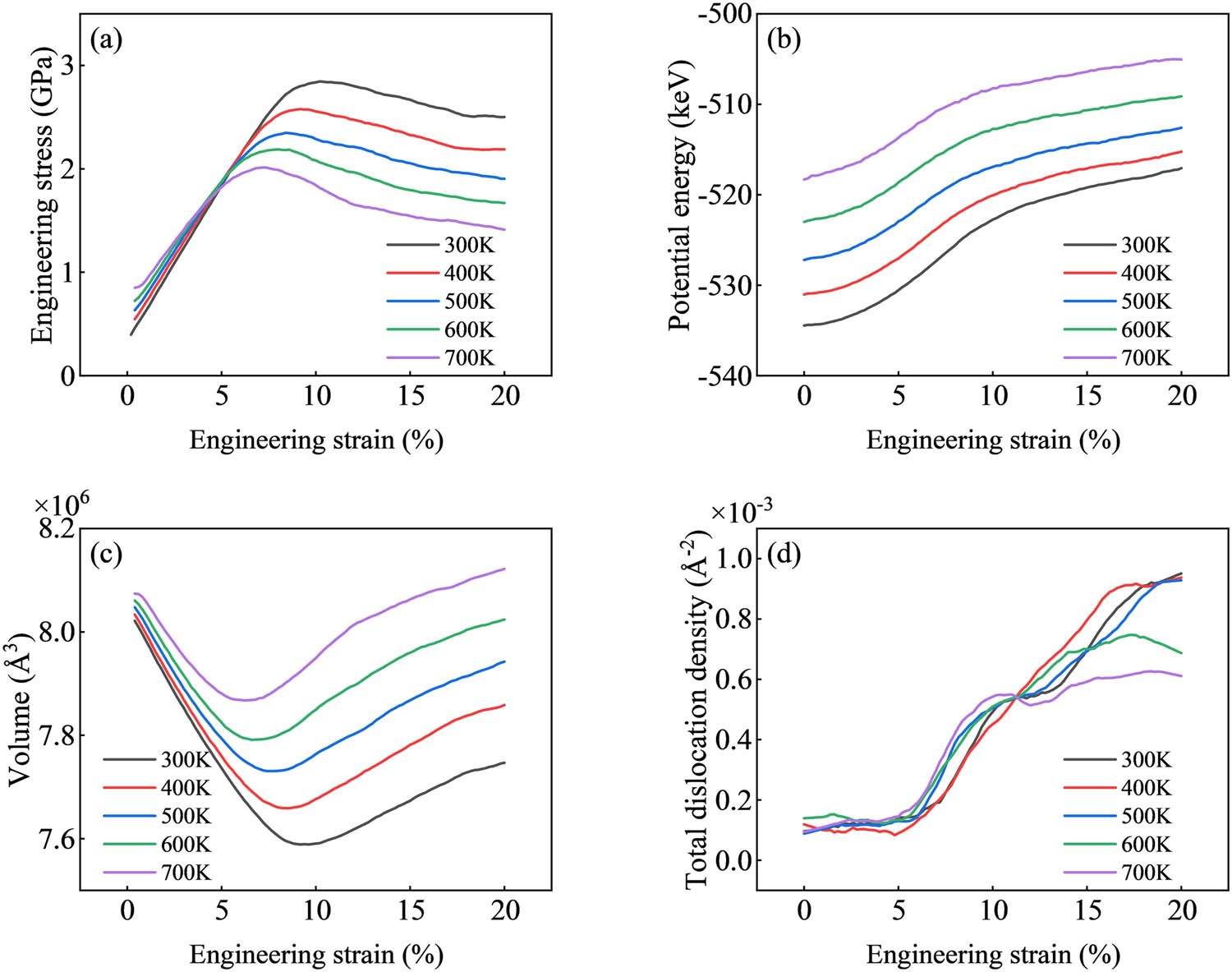
Figure 11 Force energy parameter curve: (a) stress–strain curve, (b) potential energy curve, (c) volume curve, and (d) total dislocation density curve.
Figure 11

Force energy parameter curve: (a) stress–strain curve, (b) potential energy curve, (c) volume curve, and (d) total dislocation density curve.

Figure 12 shows the evolution of the cavity, Figure 12a shows the cavity, and Figure 12b shows the cavity curve. It can be seen that cavityies appear at the same time as the yield time of magnesium alloy; so in the process of compression, cavities are generated with the change of atomic position, and at the end of elastic deformation, magnesium alloys begin to yield and enter the plastic stage, the number of cavity increases, and the area increases, increasing the overall volume of magnesium alloys.

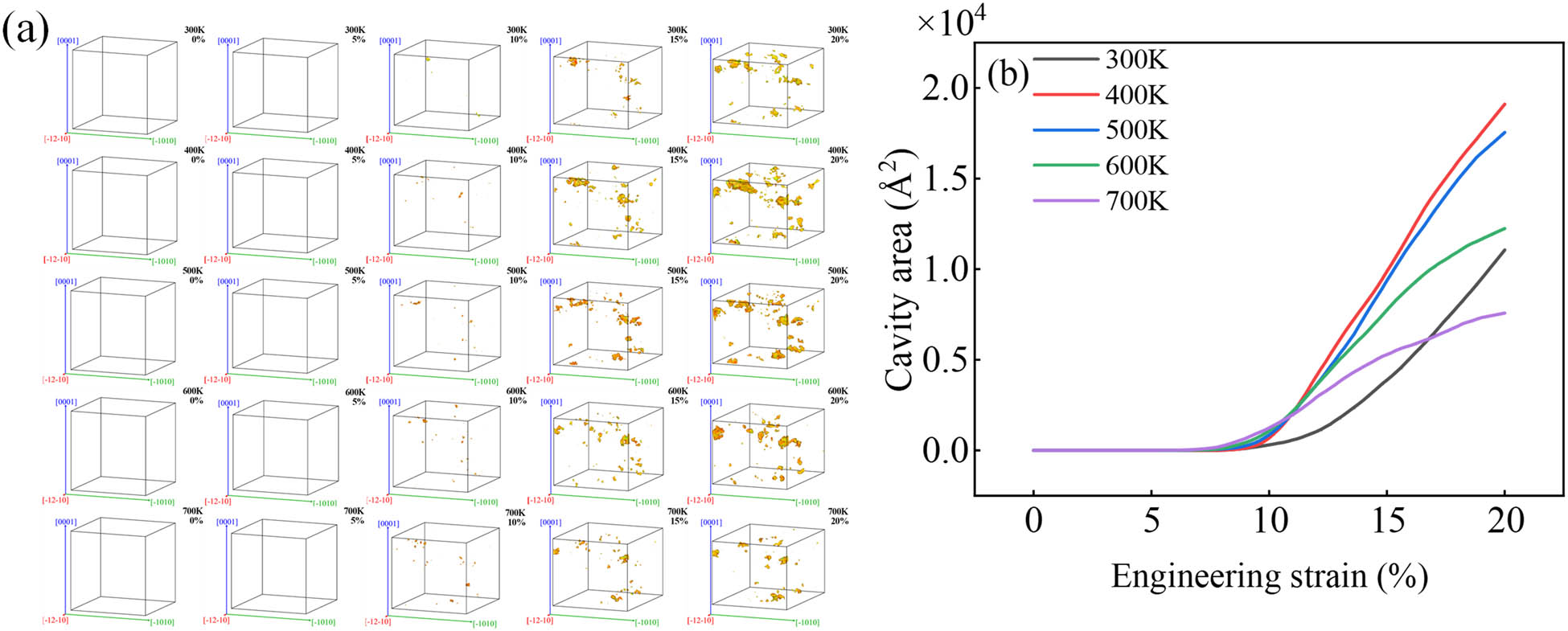
Figure 12 Cavity evolution: (a) cavity diagram and (b) cavity curve.
Figure 12

Cavity evolution: (a) cavity diagram and (b) cavity curve.

Figure 13 shows the evolution of grain boundaries under PSC, and Figure 13a shows the diagram of CNA. It is obvious that with the increase in compression, the number of atoms in the FCC structure increases, and the number of atoms in grain boundaries increases. When ε = 10 % , a large number of FCC stacking faults have occurred in the model. Figure 13b shows the GI atomic curve, and Figure 13c shows the GB atomic curve. It can be seen that the atomic fraction of GB decreases with the increase in compression, and the higher the temperature is, the higher the atomic fraction of GB is. When the atomic fraction of GB increases, the strain is about 4.5% smaller than the yield strain, so the phase transformation of magnesium alloy is earlier than plastic deformation.

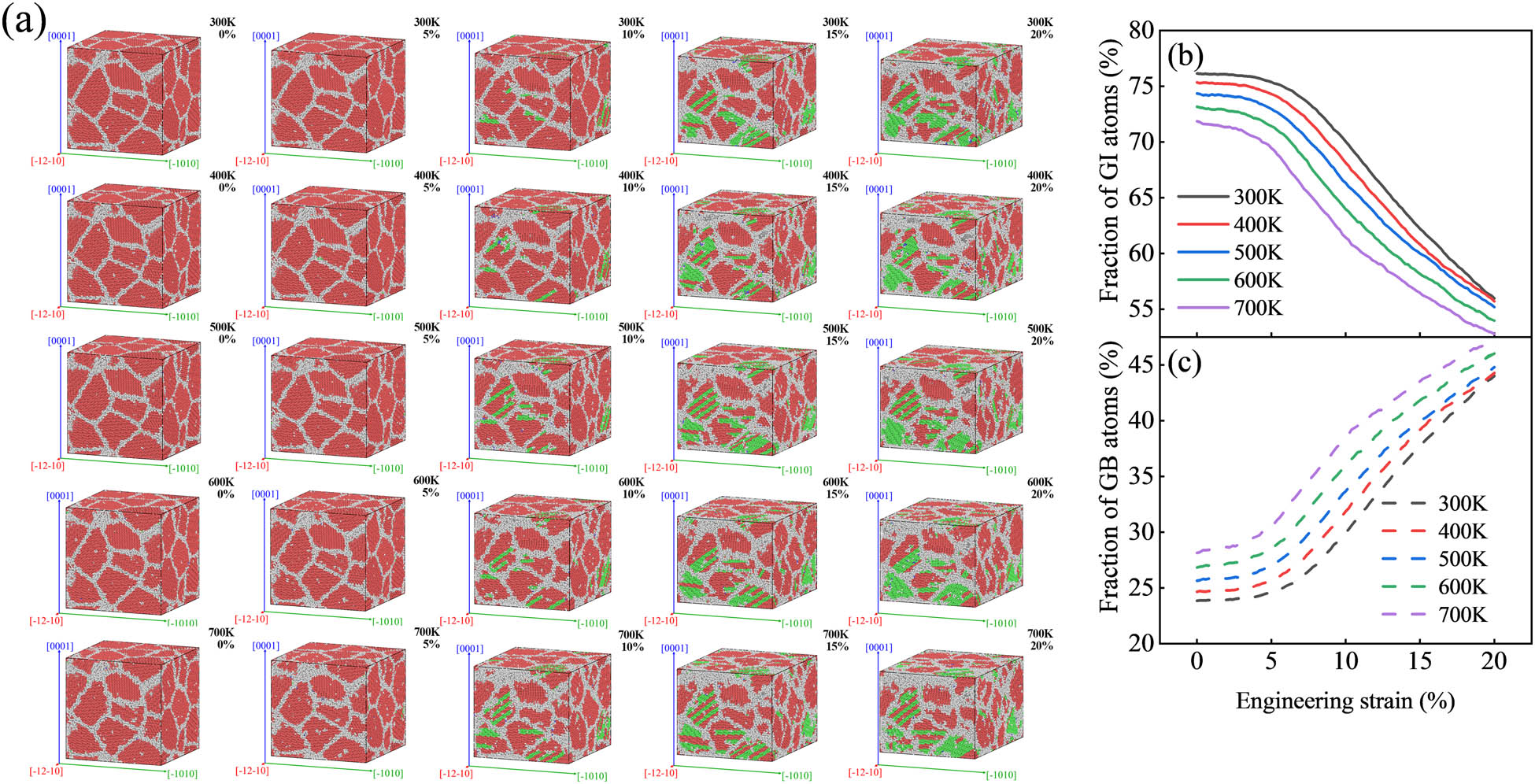
Figure 13 Grain boundary evolution under PSC: (a) CNA diagram, (b) GI atomic curve, and (c) GB atomic curve.
Figure 13

Grain boundary evolution under PSC: (a) CNA diagram, (b) GI atomic curve, and (c) GB atomic curve.

Figure 14 shows the structure evolution, Figure 14a shows the CNA diagram of HCP structure, Figure 14b shows the CNA diagram of the FCC structure, Figure 14c shows the CNA diagram of the BCC structure, Figure 14d shows the atomic curve of the HCP structure, Figure 14e shows the atomic curve of FCC structure, and Figure 14f shows the atomic curve of the BCC structure. It can be seen that the higher the temperature is, the earlier the atomic fraction of HCP begins to change, and the smaller the atomic fraction of the BCC structure is. When ε = 20 % , the atomic fraction curve of the FCC structure tends to be smooth. The higher the temperature is, the greater the potential energy of magnesium alloy is, the more active the atom is, and the position of magnesium alloy is easier to change. The earlier the HCP structure decreases, so the higher the temperature is, the smaller the yield strength is.

Figure 14 Structural evolution: (a) CNA diagram of HCP structure, (b) CNA diagram of FCC structure, (c) CNA diagram of BCC structure, (d) atomic curve of HCP structure, (e) atomic curve of FCC structure, and (f) atomic curve of BCC structure.
Figure 14

Structural evolution: (a) CNA diagram of HCP structure, (b) CNA diagram of FCC structure, (c) CNA diagram of BCC structure, (d) atomic curve of HCP structure, (e) atomic curve of FCC structure, and (f) atomic curve of BCC structure.

Figure 15 shows the evolution of dislocations, Figure 15a shows the dislocation lines, and Figure 15b–f shows the dislocation density curves at different temperatures. With the increase in compression, the number of dislocation lines increases, the dislocation lines become longer, and the dislocation density increases. Among them, the dislocations with the highest dislocation densities are 1 3 〈 1 ¯ 100 〉 dislocations (Shockley partial dislocations) and other dislocations. With the increase in temperature, the densities of 1 3 〈 1 ¯ 100 〉 dislocations (Shockley partial dislocations) and other dislocations decrease. The strain corresponding to the increase of 1 3 1 ¯ 100 dislocation density is consistent with that when the atomic fraction of the FCC structure begins to increase, so that there is a positive correlation between Shockley partial dislocations and FCC stacking faults.

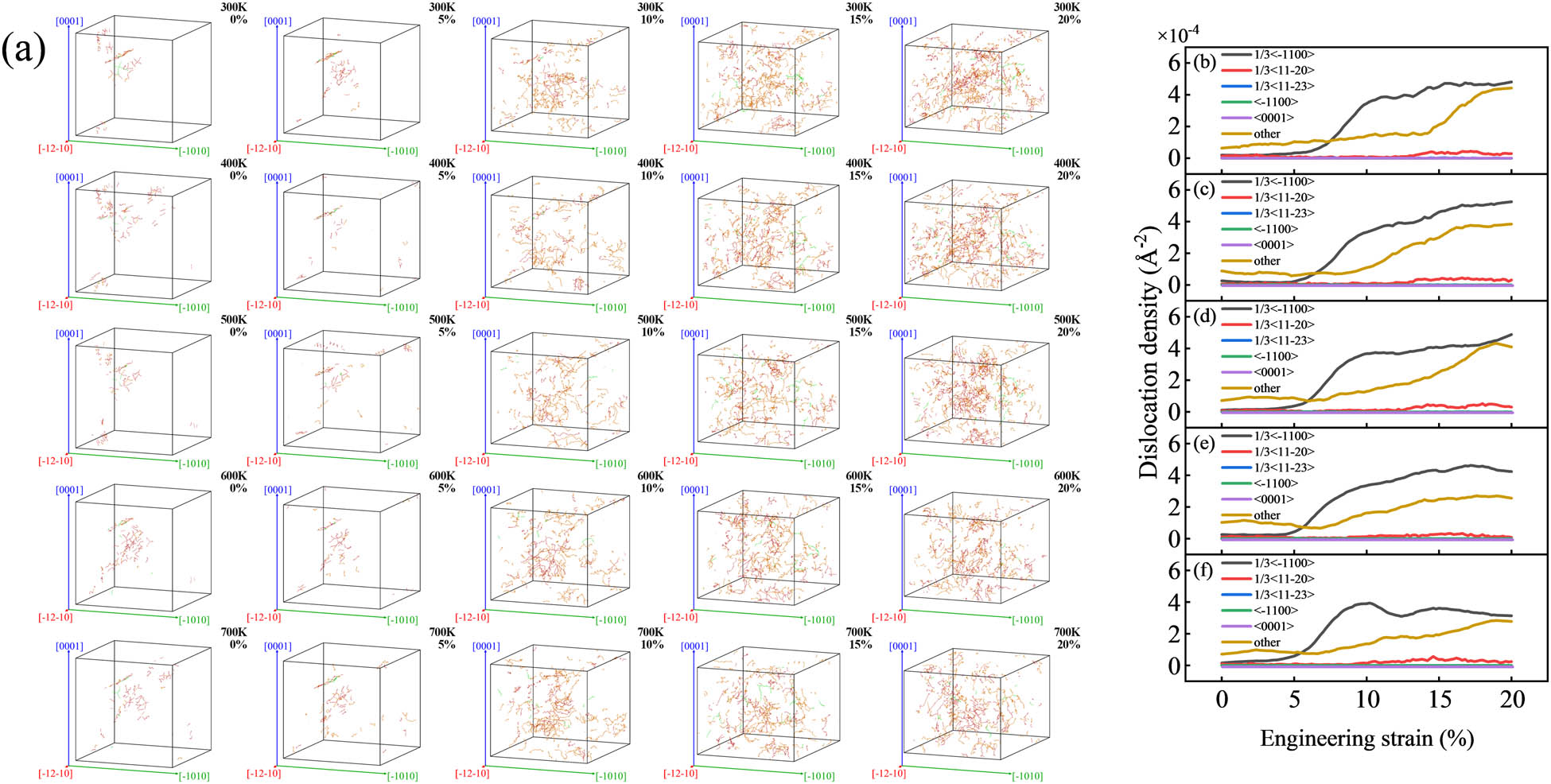
Figure 15 Dislocation evolution: (a) dislocation line diagram and (b)–(f) dislocation density curve.
Figure 15

Dislocation evolution: (a) dislocation line diagram and (b)–(f) dislocation density curve.

3.3 Effect of strain rate on phase transformation under PSC

The AZ31 magnesium alloy model with a size of 200 Å × 200 Å × 200 Å is imported into LAMMPS, and the potential function is assigned to the model. X, Y, and Z are all periodic boundary conditions, using NPT ensemble, the time step is 0.001 ps, and the 10 ps is relaxed at 300 K. The change of temperature during the relaxation process is shown in Figure 16. Keeping the size of the Y-axis model unchanged, the model was uniformly compressed 20 ps along the Z-axis ([0001] direction) at 300 K at the strain rate of 0.001–0.1 ps−1 to achieve PSC.

Figure 16 Temperature change during relaxation.
Figure 16

Temperature change during relaxation.

Figure 17 shows the grain evolution, Figure 17a shows the grain diagram, and Figure 17b presents the grain curve. It can be seen that there is no obvious rule in the number of grains at different strain rates, so it is inferred that the strain rate has no significant effect on the grain refinement of magnesium alloys.

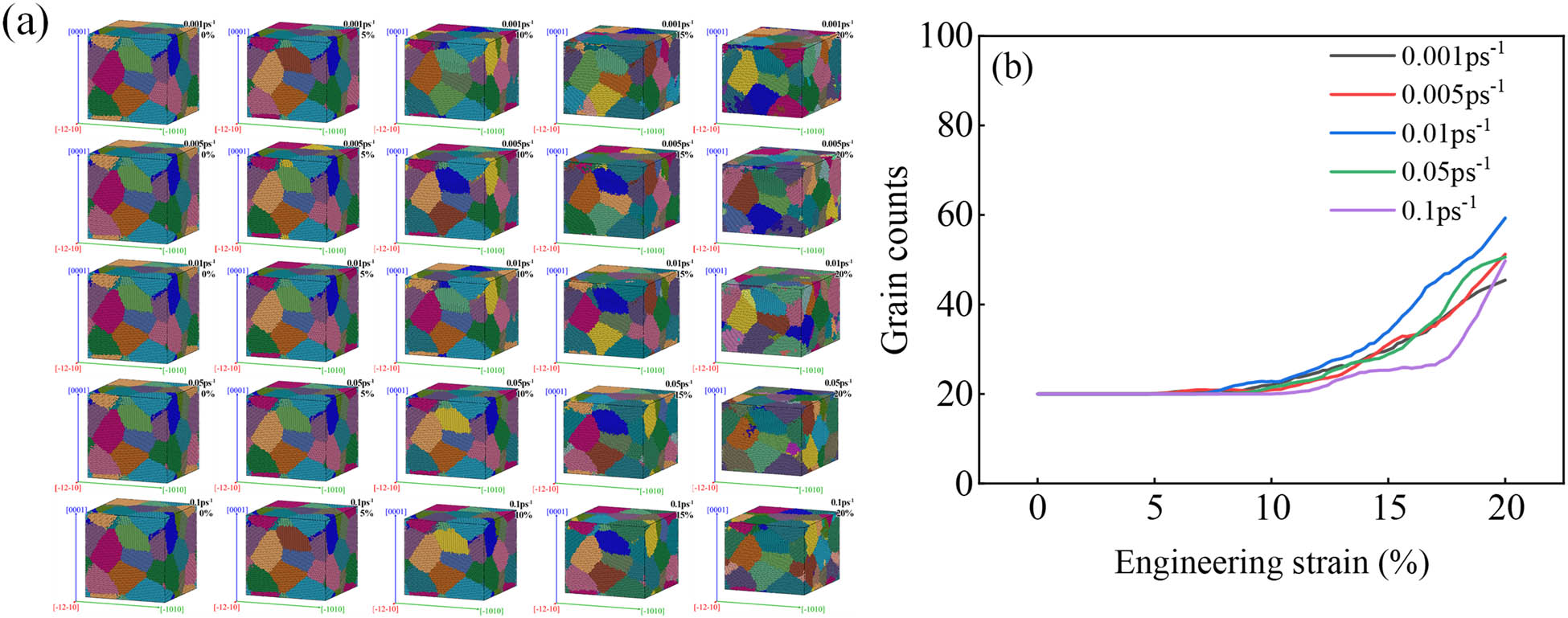
Figure 17 Grain evolution: (a) grain diagram and (b) grain curve.
Figure 17

Grain evolution: (a) grain diagram and (b) grain curve.

Figure 18 shows the force–energy parameter curve under PSC, and Figure 18a shows the stress–strain curve. When ε ̇ ≤ 0.01 ps − 1 , the yield stress and elastic modulus increase gradually with the increase in the strain rate. When ε ̇ > 0.01 ps − 1 , the magnesium alloy no longer yielded. Figure 18b shows a potential energy curve. The higher the strain rate is, the greater the potential energy of magnesium alloy is, and the greater the rate of potential energy increase is. Figure 18c shows a volume curve. When ε ̇ ≤ 0.01 ps − 1 , as the number of compression increases, the elastic deformation first occurs and the volume decreases, and the larger the strain rate is, the greater the rate of volume reduction is. When the strain reaches yield strain, the volume begins to increase when the strain reaches the plastic stage. When ε ̇ > 0.01 ps − 1 , the volume decreases all the time and the decreasing rate increases with the increase in the strain rate. Figure 18d shows the curve of total dislocation density, which increases with the increase in compression. However, the change of total dislocation density of ε ̇ > 0.01 ps − 1 is different from that of ε ̇ ≤ 0.01 ps − 1 .

Figure 18 Force energy parameter curve: (a) stress–strain curve, (b) potential energy curve, (c) volume curve, and (d) total dislocation density curve.
Figure 18

Force energy parameter curve: (a) stress–strain curve, (b) potential energy curve, (c) volume curve, and (d) total dislocation density curve.

Figure 19 shows the evolution of cavitys, Figure 19a shows cavities, and Figure 19b shows cavitys curve. It can be seen that the time of appearance of the cavity is the same as the yield time of magnesium alloy, and so in the process of compression, with the change of atomic position, cavity is produced, at the end of elastic deformation, magnesium alloys begin to yield and enter the plastic stage, the number of cavity increases, and the volume increases, increasing the overall volume of magnesium alloys. With the increase in the strain rate, the cavity area decreases, and when ε ̇ = 0.1 ps − 1 , there will be no more cavity in the model.

Figure 19 Cavity evolution: (a) cavity diagram and (b) cavity curve.
Figure 19

Cavity evolution: (a) cavity diagram and (b) cavity curve.

Figure 20 shows the evolution of the GB, and Figure 20a shows the CNA diagram. It is obvious that with the increase in the amount of compression, the number of atoms in the FCC structure increases, and the number of atoms in the GB increases. With the increase in the strain rate, the FCC stacking fault occurs later. Figure 20b shows the GI atomic curve, and Figure 20c shows the GB atomic curve. It can be seen that the fraction of GB atoms increases with the increase in compression. The higher the strain rate, the later the growth of GB atoms and the greater the growth rate, so the strain rate affects the time and degree of phase transformation. The higher the rate is, the later the phase transformation is, and the greater the degree of phase transformation is.

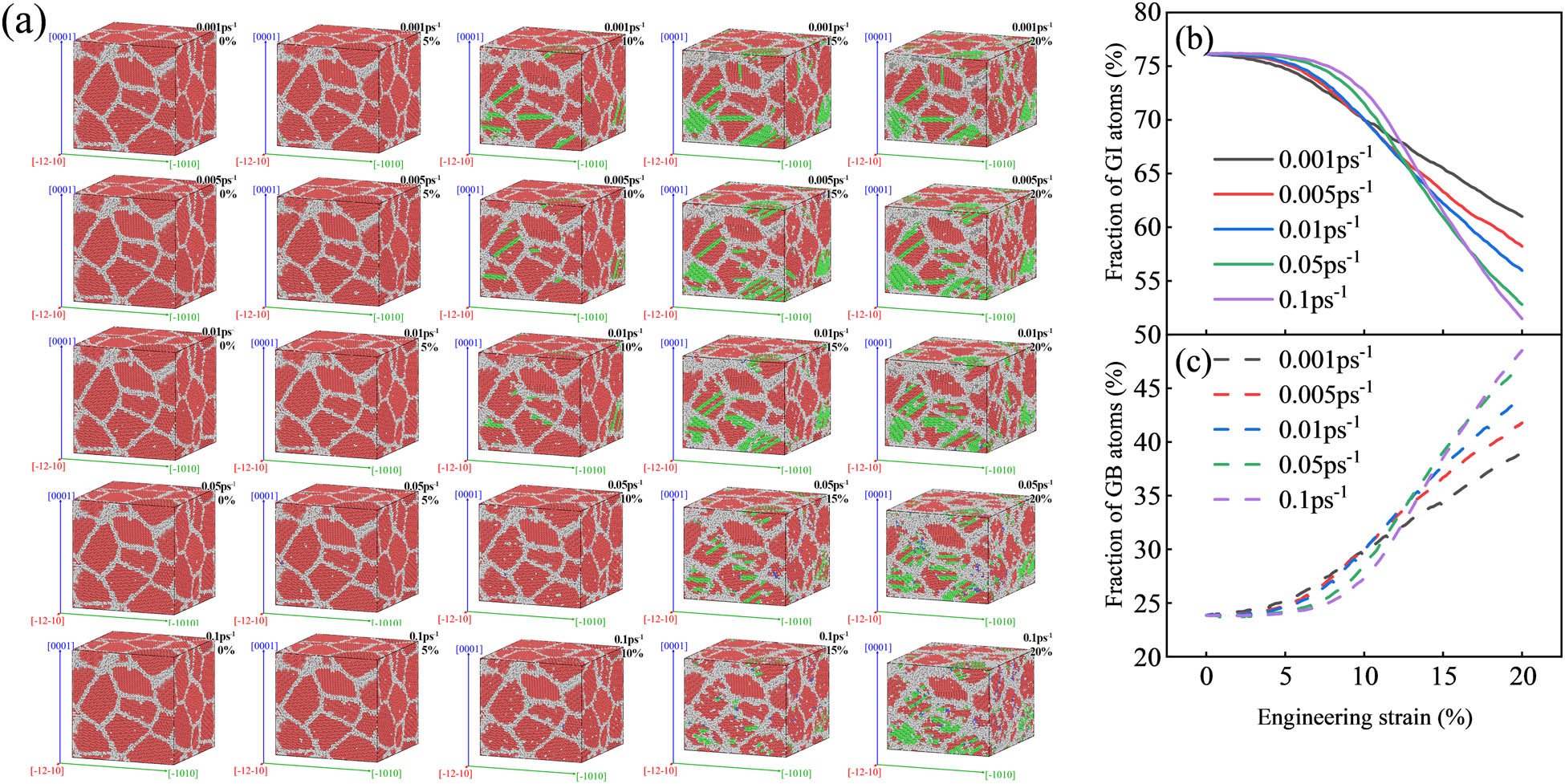
Figure 20 Grain boundary evolution: (a) CNA diagram, (b) GI atomic curve, and (c) GB atomic curve.
Figure 20

Grain boundary evolution: (a) CNA diagram, (b) GI atomic curve, and (c) GB atomic curve.

Figure 21 is the structure evolution under PSC, Figure 21a shows the CNA diagram of the HCP structure, Figure 21b shows the CNA diagram of the FCC structure, Figure 21c shows the CNA diagram of the BCC structure, Figure 21d shows the atomic curve of the HCP structure, Figure 21e shows the atomic curve of the FCC structure, and Figure 21f shows the atomic curve of the BCC structure. It can be seen that the higher the strain rate is, the later the atomic fraction of HCP begins to change. This is because the larger the strain rate is, the smaller the potential energy is, the less the atom is, and the position of the atom is not easy to change. The smaller the pore area is, the higher the strain rate is, the greater the yield strain is, and the greater the yield strength is. With the increase in the strain rate, the atomic fraction curves of the HCP structure and the FCC structure change later, while the strain phase of the BCC structure changes. The atomic fraction of the BCC structure increases with the increase in the strain rate. Therefore, the strain rate mainly affects the phase transition time and the degree of phase transformation.

Figure 21 Structural evolution: (a) CNA diagram of HCP structure, (b) CNA diagram of FCC structure, (c) CNA diagram of BCC structure, (d) atomic curve of HCP structure, (e) atomic curve of FCC structure, and (f) atomic curve of BCC structure.
Figure 21

Structural evolution: (a) CNA diagram of HCP structure, (b) CNA diagram of FCC structure, (c) CNA diagram of BCC structure, (d) atomic curve of HCP structure, (e) atomic curve of FCC structure, and (f) atomic curve of BCC structure.

Figure 22 shows the evolution of dislocations, Figure 22a shows the dislocation lines, and Figure 22b–f shows the dislocation density curves at different temperatures. It can be seen that the dislocation densities at all strain rates increase with the increase in compression. In the process of compression, the dislocations with the highest dislocation density are still 1 3 〈 1 ¯ 100 〉 dislocations (Shockley partial dislocations) and other dislocations. The strain corresponding to the increase of 1 3 〈 1 ¯ 100 〉 dislocation density is still the same as that when the atomic fraction of the FCC structure begins to increase, so there is still a strong correlation between HCP transition FCC phase transition and Shockley partial dislocations.

Figure 22 Dislocation evolution: (a) dislocation line diagram and (b)–(f) dislocation density curve.
Figure 22

Dislocation evolution: (a) dislocation line diagram and (b)–(f) dislocation density curve.

4 Conclusion

In this article, the compression simulation of AZ31 magnesium alloy is simulated by the MD method. The effects of loading mode, temperature, and strain rate on the compression behavior are analyzed. The lattice distortion, mechanical behavior, structural evolution, and dislocation evolution in the compression process are deeply analyzed, and the results of different loading modes are obtained. The HCP → FCC phase transformation mechanism of AZ31 magnesium alloy during compression at temperature and strain rate, which is related to the mechanical behavior, has been studied completely. The main results are as follows:

  1. PSC can improve the plasticity of AZ31 magnesium alloy and produce more severe grain refinement, GB diffusion, and phase transformation earlier, and the dislocation density is significantly higher than that of UC.

  2. The plastic deformation mechanism of magnesium alloy changes into GB diffusion due to the increase of temperature, which has no obvious effect on grain refinement and dislocation evolution. With the increase in temperature, the potential energy of magnesium alloy increases and plastic deformation occurs more easily, so the yield stress and yield strain decrease.

  3. The strain rate affects the time and degree of phase transformation. The higher the strain rate is, the later the phase transformation is, and the greater the degree of phase transformation is, the greater the yield strength and yield strain are.

  4. The phase transformation of HCP → GB → FCC occurs in AZ31 magnesium alloy during compression. With the increase in compression amount, the number of atoms in GB increases, the number of atoms in GB diffuses, the number of atoms in the FCC structure increases gradually, and the number of FCC stacking faults increases. Due to the compression, the position of the HCP structure atom changes and becomes the GB atom, resulting in Shockley partial dislocations. As the squeezing continues to increase, the GB atom becomes an FCC stacking fault.

  5. The phase transformation is before the specific plastic deformation in the compression process of magnesium alloy, and the yield occurs during the formation of the cavity. With the increase in the amount of compression, the elastic deformation of magnesium alloy occurs at first, the volume decreases, the atomic position changes gradually, and the phase transformation occurs. When a cavity occurs in the magnesium alloy, it begins to yield and enters the plastic stage, and the volume begins to increase.

  6. There is a strong correlation between Shockley partial dislocations and FCC stacking faults. The corresponding strain when the density of Shockley partial dislocations increases is consistent with that when the atomic fraction of FCC structure begins to increase.

Acknowledgments

This work was supported by the National Key Research and Development Project (2018YFB1307902), Shanxi Province Joint Student Training Base Talent Training Project (No. 2018JD33), Shanxi young top talent project, Shanxi Province Science Foundation for Youths (201901D211312), Excellent young academic leaders in Shanxi colleges and universities (No. 2019045), Excellent Achievements Cultivation Project of Shanxi Higher Education Institutions (No. 2019KJ028), Shanxi Province emerging industry leader talent project, Shanxi Graduate Education Innovation Project (No. 2019SY482).

  1. Funding information: This work was supported by the National Key Research and Development Project (2018YFB1307902), Shanxi Province Joint Student Training Base Talent Training Project (No. 2018JD33), Shanxi young top talent project, Shanxi Province Science Foundation for Youths (201901D211312), Excellent young academic leaders in Shanxi colleges and universities (No. 2019045), Excellent Achievements Cultivation Project of Shanxi Higher Education Institutions (No. 2019KJ028), Shanxi Province emerging industry leader talent project, Shanxi Graduate Education Innovation Project (No. 2019SY482).

  2. Author contributions: Q.H. Yang ideated, designed the study and analyzed the results. Q.H. Yang carried out the MC/MD structure evolution analysis, dislocation visualization analysis and making the figures. Z.B. Chu contributed to the overall guidance for the work and provided financial support. C. Xue, B.W. Yang, Y.G. Li, L.F. Tuo and H. Gao provided ideas. All authors have accepted responsibility for the entire content of this manuscript and approved its submission.

  3. Conflict of interest: The authors declare that they have no conflict of interest.

  4. Data availability statement: The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

References

[1] Luo Q, Guo Y, Liu B, Feng Y, Zhang J, Li Q, et al. Thermodynamics and kinetics of phase transformation in rare earth-magnesium alloys: A critical review. J Mater Sci Technol. 2020;44:171–90.10.1016/j.jmst.2020.01.022Search in Google Scholar

[2] Wu Z, Wang J, Wang H, Ma S, Huang S, Li S, et al. Enhanced damping capacities of Mg–Ce alloy by the special microstructure with parallel second phase. J Mater Sci Technol. 2017;33:941–6.10.1016/j.jmst.2016.06.027Search in Google Scholar

[3] Wang J, Gao S, Song P, Huang X, Shi Z, Pan F. Effects of phase composition on the mechanical properties and damping capacities of as-extruded Mg-Zn-Y-Zr alloys. J Alloy Compd. 2011;509:8567–72.10.1016/j.jallcom.2011.06.017Search in Google Scholar

[4] Qin D, Wang J, Chen Y, Lu R, Pan F. Effect of long period stacking ordered structure on the damping capacities of Mg-Ni-Y alloys. Mater Sci Eng A. 2015;624:9–13.10.1016/j.msea.2014.11.011Search in Google Scholar

[5] Liu L, Chen X, Pan F, Tang A, Wang X, Liu J, et al. Microstructure, texture, mechanical properties and electromagnetic shielding effectiveness of Mg-Zn-Zr-Ce alloys. Mater Sci Eng A. 2016;669:259–68.10.1016/j.msea.2016.05.098Search in Google Scholar

[6] Song JM, Wen TX, Wang JY. Vibration fracture properties of a lightweight Mg-Li-Zn alloy. Scr Mater. 2007;56:529–32.10.1016/j.scriptamat.2006.11.017Search in Google Scholar

[7] Pan H, Pan F, Yang R, Peng J, Zhao C, She J, et al. Thermal and electrical conductivity of binary magnesium alloys. J Mater Sci. 2014;49:3107–24.10.1007/s10853-013-8012-3Search in Google Scholar

[8] Zhu WF, Luo Q, Zhang JY, Li Q. Phase equilibria of Mg-La-Zr system and thermal conductivity of selected alloys. J Alloy Compd. 2018;731:784–95.10.1016/j.jallcom.2017.10.013Search in Google Scholar

[9] Zha M, Zhang H, Yu Z, Zhang X, Meng X, Wang H, et al. Bimodal microstructure – A feasible strategy for high-strength and ductile metallic materials. J Mater Sci Technol. 2018;34:257–64.10.1016/j.jmst.2017.11.018Search in Google Scholar

[10] Zhang H. Analysis of phase transformation and solidification structure of AZ magnesium alloy. Chongqing University; 2007.Search in Google Scholar

[11] Itoi T, Ichikawa R, Hirohashi M. Deformation behavior of Mg-Ni-Y alloy with long period stacking ordered phase. Mater Sci Forum. 2012;706–709:1176–80.10.4028/www.scientific.net/MSF.706-709.1176Search in Google Scholar

[12] Cui X, Yu Z, Liu F, Du Z, Bai P. Influence of secondary phases on crack initiation and propagation during fracture process of as-cast Mg–Al–Zn-Nd alloy. Mater Sci Eng A. 2019;759:708–14.10.1016/j.msea.2019.05.062Search in Google Scholar

[13] Song G, Bowles AL, StJohn DH. Corrosion resistance of aged die cast magnesium alloy AZ91D. Mater Sci Eng A. 2004;366:74–86.10.1016/j.msea.2003.08.060Search in Google Scholar

[14] Nie JF. Precipitation and hardening in magnesium alloys. Metall Mater Trans A. 2012;43:3891–939.10.1007/s11661-012-1217-2Search in Google Scholar

[15] Fischer J, Becker G. In: Kainer KU, editor. Magnesium – Eigenschaften, Anwendungen, potenziale. VCH Wiley Weinheim; 2000. p. 99–110.Search in Google Scholar

[16] Allavikutty R, Gupta P, Santr TS, Rengaswamy J. Additive manufacturing of Mg alloys for biomedical applications: Current status and challenges. Curr OpBiomed Eng. 2021;18:100276.10.1016/j.cobme.2021.100276Search in Google Scholar

[17] Wu G, Wang C, Sun M, Ding W. Recent developments and applications on high-performance cast magnesium rare-earth alloys. J Magnes Alloy. 2021;9:1–20.10.1016/j.jma.2020.06.021Search in Google Scholar

[18] Alia Y, Qiu D, Jiang B, Pan F, Zhang MX. Current research progress in grain refinement of cast magnesium alloys: A review article. J Alloy Compd. 2015;619:639–51.10.1016/j.jallcom.2014.09.061Search in Google Scholar

[19] Nie KB, Wang XJ, Deng KK, Hu XS, Wu K. Magnesium matrix composite reinforced by nanoparticles-A review. J Magnes Alloy. 2021;1:57–77.10.1016/j.jma.2020.08.018Search in Google Scholar

[20] Song J, She J, Chen D, Pan F. Latest research advances on magnesium and magnesium alloys worldwide. J Magnes Alloy. 2020;1:1–41.10.1016/j.jma.2020.02.003Search in Google Scholar

[21] Wang XJ, Xu DK, Wu RZ, Chen XB, Peng QM, Jin L, et al. What is going on in magnesium alloys. J Mater Sci Technol. 2018;2:245–7.10.1016/j.jmst.2017.07.019Search in Google Scholar

[22] Liu P, Han X, Sun D, Wang Q. Research progress of molecular dynamics simulation of friction and wear of materials. Mater Sci Technol. 2017;3:26–34.Search in Google Scholar

[23] Srivastava I, Kotia A, Ghosh SK, Ali MKA. Recent advances of molecular dynamics simulations in nanotribology. J Mol Liq. 2021;335:116154.10.1016/j.molliq.2021.116154Search in Google Scholar

[24] Yan SR, Toghraie D, Hekmatifar M, Miansari M, Rostami S. Molecular dynamics simulation of Water-Copper nanofluid flow in a three-dimensional nanochannel with different types of surface roughness geometry for energy economic management. J Mol Liq. 2020;311:113222.10.1016/j.molliq.2020.113222Search in Google Scholar

[25] Kedharnath A, Kapoor R, Sarkar A. Classical molecular dynamics simulations of the deformation of metals under uniaxial monotonic loading: A review. Computers & Struct. 2021;254:106614.10.1016/j.compstruc.2021.106614Search in Google Scholar

[26] Yang B, Peng Y, Pan F, Shi B. Research progress on plastic deformation mechanism of magnesium alloys based on molecular dynamics. Mater Eng. 2019;47:40–8.Search in Google Scholar

[27] Wang Y, Tang A, Pan R, Pan F. Application of molecular dynamics in micro plastic deformation of magnesium and magnesium alloys. Mater Rep. 2019;19:3290–7.Search in Google Scholar

[28] Mollahosseini A, Abdelrasoul A. Molecular dynamics simulation for membrane separation and porous materials: A current state of art review. J Mol Graph Model. 2021;107:107947.10.1016/j.jmgm.2021.107947Search in Google Scholar PubMed

[29] Dong L, Li Y, Devanathan R, Gao F. Molecular dynamics simulation of the structural, elastic, and thermal properties of pyrochlores. RSC Adv. 2016;6(47):41410–9.10.1039/C6RA04779CSearch in Google Scholar

[30] Wolf D, Yamakov V, Phillpot SR, Mukherjee A, Gleiter H. Deformation of nanocrystalline materials by molecular-dynamics simulation: relationship to experiments. Acta Mater. 2005;53:1–40.10.1016/j.actamat.2004.08.045Search in Google Scholar

[31] Tsuruta K, Uchida A, Totsuji C, Totsuji H. Molecular dynamics simulation of nanostructured materials. Mater Sci Forum. 2007;539–543:2804–9.10.4028/www.scientific.net/MSF.539-543.2804Search in Google Scholar

[32] Rida A, Micoulaut M, Rouhaud E, Makke A. Understanding the strain rate sensitivity of nanocrystalline copper using molecular dynamics simulations. Comp Mater Sci. 2020;172:109294.10.1016/j.commatsci.2019.109294Search in Google Scholar

[33] Rupert TJ. Strain localization in a nanocrystalline metal: atomic mechanisms and the effect of testing conditions. J Appl Phys. 2013;114(3):033527.10.1063/1.4815965Search in Google Scholar

[34] Zhang Y, Tucker GJ, Trelewicz JR. Stress-assisted grain growth in nanocrystalline metals: grain boundary mediated mechanisms and stabilization through alloying. Acta Mater. 2017;131:39–47.10.1016/j.actamat.2017.03.060Search in Google Scholar

[35] Kobler A, Brandl C, Hahn H, Kübel C. In situ observation of deformation processes in nanocrystalline face-centered cubic metals. Beilstein J Nanotechnol. 2016;7:572–80.10.3762/bjnano.7.50Search in Google Scholar PubMed PubMed Central

[36] Tucker GJ, Foiles SM. Quantifying the influence of twin boundaries on the deformation of nanocrystalline copper using atomistic simulations. Int J Plast. 2015;65:191–205.10.1016/j.ijplas.2014.09.006Search in Google Scholar

[37] Rida A, Rouhaud E, Makke A, Micoulaut M, Mantisi B. Study of the effects of grain size on the mechanical properties of nanocrystalline copper using molecular dynamics simulation with initial realistic samples. Phil Mag. 2017;97(27):2387–405.10.1080/14786435.2017.1334136Search in Google Scholar

[38] Dupraz M, Sun Z, Brandl C, Van Swygenhoven H. Dislocation interactions at reduced strain rates in atomistic simulations of nanocrystalline Al. Acta Mater. 2018;144:68–79.10.1016/j.actamat.2017.10.043Search in Google Scholar

[39] Van Swygenhoven H, Derlet P, Frøseth A. Nucleation and propagation of dislocations in nanocrystalline fcc metals. Acta Mater. 2006;54(7):1975–83.10.1016/j.actamat.2005.12.026Search in Google Scholar

[40] Frøseth A, Derlet P, Van Swygenhoven H. Dislocations emitted from nanocrystalline grain boundaries: nucleation and splitting distance. Acta Mater. 2004;52(20):5863–70.10.1016/j.actamat.2004.09.001Search in Google Scholar

[41] Vo N, Averback R, Bellon P, Odunuga S, Caro A. Quantitative description of plastic deformation in nanocrystalline Cu: dislocation glide versus grain boundary sliding. Phys Rev B. 2008;77(13):134108.10.1103/PhysRevB.77.134108Search in Google Scholar

[42] Rajput A, Paul SK. Effect of different tensile loading modes on deformation behavior of nanocrystalline copper: atomistic simulations. Results Mater. 2019;4:100042.10.1016/j.rinma.2019.100042Search in Google Scholar

[43] Vlasova AM. Hardening of [0001]-magnesium nanocrystals: molecular dynamics simulation. AIP Conf Proc. 2019;2167:020385.10.1063/1.5132252Search in Google Scholar

[44] Paul SK, Kumar S, Tarafder S. Effect of loading conditions on nucleation of nano Cavity and failure of nanocrystalline aluminum: an atomistic investigation. Eng Fract Mech. 2017;176:257–62.10.1016/j.engfracmech.2017.03.010Search in Google Scholar

[45] Zhang H, Yan H, Jia N, Jin J, Zhao X. Exploring plastic deformation mechanism of multilayered Cu/Ti composites by using molecular dynamics modeling. Acta Metal Sin. 2018;54(9):1333–42.Search in Google Scholar

[46] Caro A, Crowson DA, Caro M. Classical many-body potential for concentrated alloys and the inversion of order in iron-chromium alloys. Phys Rev Lett. 2005;95:075702.10.1103/PhysRevLett.95.075702Search in Google Scholar PubMed

[47] Stukowski A, Sadigh B, Erhart P, Caro A. Efficient implementation of the concentration-dependent embedded atom method for molecular-dynamics and Monte-Carlo simulations. Model Simul Mater Sci Eng. 2009;17:075005.10.1088/0965-0393/17/7/075005Search in Google Scholar

[48] Zhou XW, Johnson RA, Wadley HNG. Misfit-energy-increasing dislocations in vapor-deposited CoFe/NiFe multilayers. Phys Rev B. 2004;69:144113.10.1103/PhysRevB.69.144113Search in Google Scholar

[49] Baskes MI. Modified embedded-atom potentials for cubic materials and impurities. Phys Rev B. 1992;46:2727–42.10.1103/PhysRevB.46.2727Search in Google Scholar PubMed

[50] Fang H, Michael GP, Alexander S, Horstemeyer Mark F, Baskes Michael I, John WG, et al. Numerical tools for atomistic simulations. United States; 2004.10.2172/918395Search in Google Scholar

[51] Lee B-J, Baskes MI. Second nearest-neighbor modified embedded-atom-method potential. Phys Rev B. 2000;62:8564–7.10.1103/PhysRevB.62.8564Search in Google Scholar

[52] Lee B-J, Baskes MI, Kim H, Cho YK. Second nearest-neighbor modified embedded atom method potentials for bcc transition metals. Phys Rev B. 2001;64:184102.10.1103/PhysRevB.64.184102Search in Google Scholar

[53] Valone SM, Baskes MI, Martin RL. Atomistic model of helium bubbles in gallium-stabilized plutonium alloys. Phys Rev B. 2006;73:214209.10.1103/PhysRevB.73.214209Search in Google Scholar

[54] Wang GF, Van Hove MA, Ross PN, Baskes MI. Monte Carlo simulations of segregation in Pt-Re catalyst nanoparticles. J Chem Phys. 2004;121:5410–22.10.1063/1.1781151Search in Google Scholar PubMed

[55] Ziegler JF, Biersack JP. The stopping and range of ions in matter. In: Bromley DA, editors. Treatise on heavy-ion science. Boston, MA: Springer; 1985.10.1007/978-1-4615-8103-1_3Search in Google Scholar

[56] Hirel P. Atomsk: A tool for manipulating and converting atomic data files. Computer Phys Commun. 2015;197:212–9.10.1016/j.cpc.2015.07.012Search in Google Scholar

[57] Plimpton S. Fast parallel algorithms for short-range molecular dynamics. J Comput Phys. 1995;117:1–19.10.2172/10176421Search in Google Scholar

[58] Jang H-S, Seol D, Lee B-J. Modified embedded-atom method interatomic potentials for Mg-Al-Ca and Mg–Al–Zn ternary systems. J Magnes Alloy. 2021;9:317–35.10.1016/j.jma.2020.09.006Search in Google Scholar

[59] Stukowski A. Visualization and analysis of atomistic simulation data with OVITO–the open visualization tool. Model Simul Mater Sci Eng. 2009;18:015012.10.1088/0965-0393/18/1/015012Search in Google Scholar

[60] Larsen PM, Schmidt S, Schiøtz J. Robust structural identification via polyhedral template matching. Model Simul Mater Sci Eng. 2016;24:055007.10.1088/0965-0393/24/5/055007Search in Google Scholar

[61] Bonald T, Charpentier B, Galland A, Hollocou A. Hierarchical graph clustering using node pair samplin. arXiv. 1806 01664[cs.SI].Search in Google Scholar

[62] Panzarino JF, Rupert TJ. Tracking microstructure of crystalline materials: a post-processing algorithm for atomistic simulations. JOM. 2014;66:417–28.10.1007/s11837-013-0831-9Search in Google Scholar

[63] Stukowski A, Bulatov VV, Arsenlis A. Automated identification and indexing of dislocations in crystal interfaces. Model Simul Mater Sci Eng. 2012;20:085007.10.1088/0965-0393/20/8/085007Search in Google Scholar

[64] Honeycutt JD, Andersen HC. Molecular dynamics study of melting and freezing of small Lennard-Jones clusters. J Phys Chem A. 1987;91:4950–63.10.1021/j100303a014Search in Google Scholar

[65] Stukowski A. Computational analysis methods in atomistic modeling of crystals. JOM. 2014;66(3):399–407.10.1007/s11837-013-0827-5Search in Google Scholar

[66] Berghezan A, Fourdeux A, Amelinckx S. Transmission electron microscopy studies of dislocations and stacking faults in a hexagonal metal: Zinc Etudes par microscopie electronique par transmission des dislocations et des fautes d’empilement dans un metal hexagonal: Zinc Untersuchungen von Versetzungen in stapelfehlern mit elektronenmikroskopischer Durchstrahlung in einem hexagonalen metal: Zink. Acta Mater. 1961;9:464.10.1016/0001-6160(61)90142-0Search in Google Scholar

[67] Yanan W, Shujiang C, Xichun D. Dislocation theory and its application. Metallurgical Industry Press; 2007.Search in Google Scholar
Received: 2021-09-15
Revised: 2021-11-03
Accepted: 2022-02-17
Published Online: 2022-07-05

© 2022 Qianhua Yang et al., published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Research Articles
  2. Theoretical and experimental investigation of MWCNT dispersion effect on the elastic modulus of flexible PDMS/MWCNT nanocomposites
  3. Mechanical, morphological, and fracture-deformation behavior of MWCNTs-reinforced (Al–Cu–Mg–T351) alloy cast nanocomposites fabricated by optimized mechanical milling and powder metallurgy techniques
  4. Flammability and physical stability of sugar palm crystalline nanocellulose reinforced thermoplastic sugar palm starch/poly(lactic acid) blend bionanocomposites
  5. Glutathione-loaded non-ionic surfactant niosomes: A new approach to improve oral bioavailability and hepatoprotective efficacy of glutathione
  6. Relationship between mechano-bactericidal activity and nanoblades density on chemically strengthened glass
  7. In situ regulation of microstructure and microwave-absorbing properties of FeSiAl through HNO3 oxidation
  8. Research on a mechanical model of magnetorheological fluid different diameter particles
  9. Nanomechanical and dynamic mechanical properties of rubber–wood–plastic composites
  10. Investigative properties of CeO2 doped with niobium: A combined characterization and DFT studies
  11. Miniaturized peptidomimetics and nano-vesiculation in endothelin types through probable nano-disk formation and structure property relationships of endothelins’ fragments
  12. N/S co-doped CoSe/C nanocubes as anode materials for Li-ion batteries
  13. Synergistic effects of halloysite nanotubes with metal and phosphorus additives on the optimal design of eco-friendly sandwich panels with maximum flame resistance and minimum weight
  14. Octreotide-conjugated silver nanoparticles for active targeting of somatostatin receptors and their application in a nebulized rat model
  15. Controllable morphology of Bi2S3 nanostructures formed via hydrothermal vulcanization of Bi2O3 thin-film layer and their photoelectrocatalytic performances
  16. Development of (−)-epigallocatechin-3-gallate-loaded folate receptor-targeted nanoparticles for prostate cancer treatment
  17. Enhancement of the mechanical properties of HDPE mineral nanocomposites by filler particles modulation of the matrix plastic/elastic behavior
  18. Effect of plasticizers on the properties of sugar palm nanocellulose/cinnamon essential oil reinforced starch bionanocomposite films
  19. Optimization of nano coating to reduce the thermal deformation of ball screws
  20. Preparation of efficient piezoelectric PVDF–HFP/Ni composite films by high electric field poling
  21. MHD dissipative Casson nanofluid liquid film flow due to an unsteady stretching sheet with radiation influence and slip velocity phenomenon
  22. Effects of nano-SiO2 modification on rubberised mortar and concrete with recycled coarse aggregates
  23. Mechanical and microscopic properties of fiber-reinforced coal gangue-based geopolymer concrete
  24. Effect of morphology and size on the thermodynamic stability of cerium oxide nanoparticles: Experiment and molecular dynamics calculation
  25. Mechanical performance of a CFRP composite reinforced via gelatin-CNTs: A study on fiber interfacial enhancement and matrix enhancement
  26. A practical review over surface modification, nanopatterns, emerging materials, drug delivery systems, and their biophysiochemical properties for dental implants: Recent progresses and advances
  27. HTR: An ultra-high speed algorithm for cage recognition of clathrate hydrates
  28. Effects of microalloying elements added by in situ synthesis on the microstructure of WCu composites
  29. A highly sensitive nanobiosensor based on aptamer-conjugated graphene-decorated rhodium nanoparticles for detection of HER2-positive circulating tumor cells
  30. Progressive collapse performance of shear strengthened RC frames by nano CFRP
  31. Core–shell heterostructured composites of carbon nanotubes and imine-linked hyperbranched polymers as metal-free Li-ion anodes
  32. A Galerkin strategy for tri-hybridized mixture in ethylene glycol comprising variable diffusion and thermal conductivity using non-Fourier’s theory
  33. Simple models for tensile modulus of shape memory polymer nanocomposites at ambient temperature
  34. Preparation and morphological studies of tin sulfide nanoparticles and use as efficient photocatalysts for the degradation of rhodamine B and phenol
  35. Polyethyleneimine-impregnated activated carbon nanofiber composited graphene-derived rice husk char for efficient post-combustion CO2 capture
  36. Electrospun nanofibers of Co3O4 nanocrystals encapsulated in cyclized-polyacrylonitrile for lithium storage
  37. Pitting corrosion induced on high-strength high carbon steel wire in high alkaline deaerated chloride electrolyte
  38. Formulation of polymeric nanoparticles loaded sorafenib; evaluation of cytotoxicity, molecular evaluation, and gene expression studies in lung and breast cancer cell lines
  39. Engineered nanocomposites in asphalt binders
  40. Influence of loading voltage, domain ratio, and additional load on the actuation of dielectric elastomer
  41. Thermally induced hex-graphene transitions in 2D carbon crystals
  42. The surface modification effect on the interfacial properties of glass fiber-reinforced epoxy: A molecular dynamics study
  43. Molecular dynamics study of deformation mechanism of interfacial microzone of Cu/Al2Cu/Al composites under tension
  44. Nanocolloid simulators of luminescent solar concentrator photovoltaic windows
  45. Compressive strength and anti-chloride ion penetration assessment of geopolymer mortar merging PVA fiber and nano-SiO2 using RBF–BP composite neural network
  46. Effect of 3-mercapto-1-propane sulfonate sulfonic acid and polyvinylpyrrolidone on the growth of cobalt pillar by electrodeposition
  47. Dynamics of convective slippery constraints on hybrid radiative Sutterby nanofluid flow by Galerkin finite element simulation
  48. Preparation of vanadium by the magnesiothermic self-propagating reduction and process control
  49. Microstructure-dependent photoelectrocatalytic activity of heterogeneous ZnO–ZnS nanosheets
  50. Cytotoxic and pro-inflammatory effects of molybdenum and tungsten disulphide on human bronchial cells
  51. Improving recycled aggregate concrete by compression casting and nano-silica
  52. Chemically reactive Maxwell nanoliquid flow by a stretching surface in the frames of Newtonian heating, nonlinear convection and radiative flux: Nanopolymer flow processing simulation
  53. Nonlinear dynamic and crack behaviors of carbon nanotubes-reinforced composites with various geometries
  54. Biosynthesis of copper oxide nanoparticles and its therapeutic efficacy against colon cancer
  55. Synthesis and characterization of smart stimuli-responsive herbal drug-encapsulated nanoniosome particles for efficient treatment of breast cancer
  56. Homotopic simulation for heat transport phenomenon of the Burgers nanofluids flow over a stretching cylinder with thermal convective and zero mass flux conditions
  57. Incorporation of copper and strontium ions in TiO2 nanotubes via dopamine to enhance hemocompatibility and cytocompatibility
  58. Mechanical, thermal, and barrier properties of starch films incorporated with chitosan nanoparticles
  59. Mechanical properties and microstructure of nano-strengthened recycled aggregate concrete
  60. Glucose-responsive nanogels efficiently maintain the stability and activity of therapeutic enzymes
  61. Tunning matrix rheology and mechanical performance of ultra-high performance concrete using cellulose nanofibers
  62. Flexible MXene/copper/cellulose nanofiber heat spreader films with enhanced thermal conductivity
  63. Promoted charge separation and specific surface area via interlacing of N-doped titanium dioxide nanotubes on carbon nitride nanosheets for photocatalytic degradation of Rhodamine B
  64. Elucidating the role of silicon dioxide and titanium dioxide nanoparticles in mitigating the disease of the eggplant caused by Phomopsis vexans, Ralstonia solanacearum, and root-knot nematode Meloidogyne incognita
  65. An implication of magnetic dipole in Carreau Yasuda liquid influenced by engine oil using ternary hybrid nanomaterial
  66. Robust synthesis of a composite phase of copper vanadium oxide with enhanced performance for durable aqueous Zn-ion batteries
  67. Tunning self-assembled phases of bovine serum albumin via hydrothermal process to synthesize novel functional hydrogel for skin protection against UVB
  68. A comparative experimental study on damping properties of epoxy nanocomposite beams reinforced with carbon nanotubes and graphene nanoplatelets
  69. Lightweight and hydrophobic Ni/GO/PVA composite aerogels for ultrahigh performance electromagnetic interference shielding
  70. Research on the auxetic behavior and mechanical properties of periodically rotating graphene nanostructures
  71. Repairing performances of novel cement mortar modified with graphene oxide and polyacrylate polymer
  72. Closed-loop recycling and fabrication of hydrophilic CNT films with high performance
  73. Design of thin-film configuration of SnO2–Ag2O composites for NO2 gas-sensing applications
  74. Study on stress distribution of SiC/Al composites based on microstructure models with microns and nanoparticles
  75. PVDF green nanofibers as potential carriers for improving self-healing and mechanical properties of carbon fiber/epoxy prepregs
  76. Osteogenesis capability of three-dimensionally printed poly(lactic acid)-halloysite nanotube scaffolds containing strontium ranelate
  77. Silver nanoparticles induce mitochondria-dependent apoptosis and late non-canonical autophagy in HT-29 colon cancer cells
  78. Preparation and bonding mechanisms of polymer/metal hybrid composite by nano molding technology
  79. Damage self-sensing and strain monitoring of glass-reinforced epoxy composite impregnated with graphene nanoplatelet and multiwalled carbon nanotubes
  80. Thermal analysis characterisation of solar-powered ship using Oldroyd hybrid nanofluids in parabolic trough solar collector: An optimal thermal application
  81. Pyrene-functionalized halloysite nanotubes for simultaneously detecting and separating Hg(ii) in aqueous media: A comprehensive comparison on interparticle and intraparticle excimers
  82. Fabrication of self-assembly CNT flexible film and its piezoresistive sensing behaviors
  83. Thermal valuation and entropy inspection of second-grade nanoscale fluid flow over a stretching surface by applying Koo–Kleinstreuer–Li relation
  84. Mechanical properties and microstructure of nano-SiO2 and basalt-fiber-reinforced recycled aggregate concrete
  85. Characterization and tribology performance of polyaniline-coated nanodiamond lubricant additives
  86. Combined impact of Marangoni convection and thermophoretic particle deposition on chemically reactive transport of nanofluid flow over a stretching surface
  87. Spark plasma extrusion of binder free hydroxyapatite powder
  88. An investigation on thermo-mechanical performance of graphene-oxide-reinforced shape memory polymer
  89. Effect of nanoadditives on the novel leather fiber/recycled poly(ethylene-vinyl-acetate) polymer composites for multifunctional applications: Fabrication, characterizations, and multiobjective optimization using central composite design
  90. Design selection for a hemispherical dimple core sandwich panel using hybrid multi-criteria decision-making methods
  91. Improving tensile strength and impact toughness of plasticized poly(lactic acid) biocomposites by incorporating nanofibrillated cellulose
  92. Green synthesis of spinel copper ferrite (CuFe2O4) nanoparticles and their toxicity
  93. The effect of TaC and NbC hybrid and mono-nanoparticles on AA2024 nanocomposites: Microstructure, strengthening, and artificial aging
  94. Excited-state geometry relaxation of pyrene-modified cellulose nanocrystals under UV-light excitation for detecting Fe3+
  95. Effect of CNTs and MEA on the creep of face-slab concrete at an early age
  96. Effect of deformation conditions on compression phase transformation of AZ31
  97. Application of MXene as a new generation of highly conductive coating materials for electromembrane-surrounded solid-phase microextraction
  98. A comparative study of the elasto-plastic properties for ceramic nanocomposites filled by graphene or graphene oxide nanoplates
  99. Encapsulation strategies for improving the biological behavior of CdS@ZIF-8 nanocomposites
  100. Biosynthesis of ZnO NPs from pumpkin seeds’ extract and elucidation of its anticancer potential against breast cancer
  101. Preliminary trials of the gold nanoparticles conjugated chrysin: An assessment of anti-oxidant, anti-microbial, and in vitro cytotoxic activities of a nanoformulated flavonoid
  102. Effect of micron-scale pores increased by nano-SiO2 sol modification on the strength of cement mortar
  103. Fractional simulations for thermal flow of hybrid nanofluid with aluminum oxide and titanium oxide nanoparticles with water and blood base fluids
  104. The effect of graphene nano-powder on the viscosity of water: An experimental study and artificial neural network modeling
  105. Development of a novel heat- and shear-resistant nano-silica gelling agent
  106. Characterization, biocompatibility and in vivo of nominal MnO2-containing wollastonite glass-ceramic
  107. Entropy production simulation of second-grade magnetic nanomaterials flowing across an expanding surface with viscidness dissipative flux
  108. Enhancement in structural, morphological, and optical properties of copper oxide for optoelectronic device applications
  109. Aptamer-functionalized chitosan-coated gold nanoparticle complex as a suitable targeted drug carrier for improved breast cancer treatment
  110. Performance and overall evaluation of nano-alumina-modified asphalt mixture
  111. Analysis of pure nanofluid (GO/engine oil) and hybrid nanofluid (GO–Fe3O4/engine oil): Novel thermal and magnetic features
  112. Synthesis of Ag@AgCl modified anatase/rutile/brookite mixed phase TiO2 and their photocatalytic property
  113. Mechanisms and influential variables on the abrasion resistance hydraulic concrete
  114. Synergistic reinforcement mechanism of basalt fiber/cellulose nanocrystals/polypropylene composites
  115. Achieving excellent oxidation resistance and mechanical properties of TiB2–B4C/carbon aerogel composites by quick-gelation and mechanical mixing
  116. Microwave-assisted sol–gel template-free synthesis and characterization of silica nanoparticles obtained from South African coal fly ash
  117. Pulsed laser-assisted synthesis of nano nickel(ii) oxide-anchored graphitic carbon nitride: Characterizations and their potential antibacterial/anti-biofilm applications
  118. Effects of nano-ZrSi2 on thermal stability of phenolic resin and thermal reusability of quartz–phenolic composites
  119. Benzaldehyde derivatives on tin electroplating as corrosion resistance for fabricating copper circuit
  120. Mechanical and heat transfer properties of 4D-printed shape memory graphene oxide/epoxy acrylate composites
  121. Coupling the vanadium-induced amorphous/crystalline NiFe2O4 with phosphide heterojunction toward active oxygen evolution reaction catalysts
  122. Graphene-oxide-reinforced cement composites mechanical and microstructural characteristics at elevated temperatures
  123. Gray correlation analysis of factors influencing compressive strength and durability of nano-SiO2 and PVA fiber reinforced geopolymer mortar
  124. Preparation of layered gradient Cu–Cr–Ti alloy with excellent mechanical properties, thermal stability, and electrical conductivity
  125. Recovery of Cr from chrome-containing leather wastes to develop aluminum-based composite material along with Al2O3 ceramic particles: An ingenious approach
  126. Mechanisms of the improved stiffness of flexible polymers under impact loading
  127. Anticancer potential of gold nanoparticles (AuNPs) using a battery of in vitro tests
  128. Review Articles
  129. Proposed approaches for coronaviruses elimination from wastewater: Membrane techniques and nanotechnology solutions
  130. Application of Pickering emulsion in oil drilling and production
  131. The contribution of microfluidics to the fight against tuberculosis
  132. Graphene-based biosensors for disease theranostics: Development, applications, and recent advancements
  133. Synthesis and encapsulation of iron oxide nanorods for application in magnetic hyperthermia and photothermal therapy
  134. Contemporary nano-architectured drugs and leads for ανβ3 integrin-based chemotherapy: Rationale and retrospect
  135. State-of-the-art review of fabrication, application, and mechanical properties of functionally graded porous nanocomposite materials
  136. Insights on magnetic spinel ferrites for targeted drug delivery and hyperthermia applications
  137. A review on heterogeneous oxidation of acetaminophen based on micro and nanoparticles catalyzed by different activators
  138. Early diagnosis of lung cancer using magnetic nanoparticles-integrated systems
  139. Advances in ZnO: Manipulation of defects for enhancing their technological potentials
  140. Efficacious nanomedicine track toward combating COVID-19
  141. A review of the design, processes, and properties of Mg-based composites
  142. Green synthesis of nanoparticles for varied applications: Green renewable resources and energy-efficient synthetic routes
  143. Two-dimensional nanomaterial-based polymer composites: Fundamentals and applications
  144. Recent progress and challenges in plasmonic nanomaterials
  145. Apoptotic cell-derived micro/nanosized extracellular vesicles in tissue regeneration
  146. Electronic noses based on metal oxide nanowires: A review
  147. Framework materials for supercapacitors
  148. An overview on the reproductive toxicity of graphene derivatives: Highlighting the importance
  149. Antibacterial nanomaterials: Upcoming hope to overcome antibiotic resistance crisis
  150. Research progress of carbon materials in the field of three-dimensional printing polymer nanocomposites
  151. A review of atomic layer deposition modelling and simulation methodologies: Density functional theory and molecular dynamics
  152. Recent advances in the preparation of PVDF-based piezoelectric materials
  153. Recent developments in tensile properties of friction welding of carbon fiber-reinforced composite: A review
  154. Comprehensive review of the properties of fly ash-based geopolymer with additive of nano-SiO2
  155. Perspectives in biopolymer/graphene-based composite application: Advances, challenges, and recommendations
  156. Graphene-based nanocomposite using new modeling molecular dynamic simulations for proposed neutralizing mechanism and real-time sensing of COVID-19
  157. Nanotechnology application on bamboo materials: A review
  158. Recent developments and future perspectives of biorenewable nanocomposites for advanced applications
  159. Nanostructured lipid carrier system: A compendium of their formulation development approaches, optimization strategies by quality by design, and recent applications in drug delivery
  160. 3D printing customized design of human bone tissue implant and its application
  161. Design, preparation, and functionalization of nanobiomaterials for enhanced efficacy in current and future biomedical applications
  162. A brief review of nanoparticles-doped PEDOT:PSS nanocomposite for OLED and OPV
  163. Nanotechnology interventions as a putative tool for the treatment of dental afflictions
  164. Recent advancements in metal–organic frameworks integrating quantum dots (QDs@MOF) and their potential applications
  165. A focused review of short electrospun nanofiber preparation techniques for composite reinforcement
  166. Microstructural characteristics and nano-modification of interfacial transition zone in concrete: A review
  167. Latest developments in the upconversion nanotechnology for the rapid detection of food safety: A review
  168. Strategic applications of nano-fertilizers for sustainable agriculture: Benefits and bottlenecks
  169. Molecular dynamics application of cocrystal energetic materials: A review
  170. Synthesis and application of nanometer hydroxyapatite in biomedicine
  171. Cutting-edge development in waste-recycled nanomaterials for energy storage and conversion applications
  172. Biological applications of ternary quantum dots: A review
  173. Nanotherapeutics for hydrogen sulfide-involved treatment: An emerging approach for cancer therapy
  174. Application of antibacterial nanoparticles in orthodontic materials
  175. Effect of natural-based biological hydrogels combined with growth factors on skin wound healing
  176. Nanozymes – A route to overcome microbial resistance: A viewpoint
  177. Recent developments and applications of smart nanoparticles in biomedicine
  178. Contemporary review on carbon nanotube (CNT) composites and their impact on multifarious applications
  179. Interfacial interactions and reinforcing mechanisms of cellulose and chitin nanomaterials and starch derivatives for cement and concrete strength and durability enhancement: A review
  180. Diamond-like carbon films for tribological modification of rubber
  181. Layered double hydroxides (LDHs) modified cement-based materials: A systematic review
  182. Recent research progress and advanced applications of silica/polymer nanocomposites
  183. Modeling of supramolecular biopolymers: Leading the in silico revolution of tissue engineering and nanomedicine
  184. Recent advances in perovskites-based optoelectronics
  185. Biogenic synthesis of palladium nanoparticles: New production methods and applications
  186. A comprehensive review of nanofluids with fractional derivatives: Modeling and application
  187. Electrospinning of marine polysaccharides: Processing and chemical aspects, challenges, and future prospects
  188. Electrohydrodynamic printing for demanding devices: A review of processing and applications
  189. Rapid Communications
  190. Structural material with designed thermal twist for a simple actuation
  191. Recent advances in photothermal materials for solar-driven crude oil adsorption
https://doi.org/10.1515/ntrev-2022-0151
Keywords for this article
plane strain compression; uniaxial compression; temperature; strain rate; phase transformation
Creative Commons
BY 4.0

Articles in the same Issue

  1. Research Articles
  2. Theoretical and experimental investigation of MWCNT dispersion effect on the elastic modulus of flexible PDMS/MWCNT nanocomposites
  3. Mechanical, morphological, and fracture-deformation behavior of MWCNTs-reinforced (Al–Cu–Mg–T351) alloy cast nanocomposites fabricated by optimized mechanical milling and powder metallurgy techniques
  4. Flammability and physical stability of sugar palm crystalline nanocellulose reinforced thermoplastic sugar palm starch/poly(lactic acid) blend bionanocomposites
  5. Glutathione-loaded non-ionic surfactant niosomes: A new approach to improve oral bioavailability and hepatoprotective efficacy of glutathione
  6. Relationship between mechano-bactericidal activity and nanoblades density on chemically strengthened glass
  7. In situ regulation of microstructure and microwave-absorbing properties of FeSiAl through HNO3 oxidation
  8. Research on a mechanical model of magnetorheological fluid different diameter particles
  9. Nanomechanical and dynamic mechanical properties of rubber–wood–plastic composites
  10. Investigative properties of CeO2 doped with niobium: A combined characterization and DFT studies
  11. Miniaturized peptidomimetics and nano-vesiculation in endothelin types through probable nano-disk formation and structure property relationships of endothelins’ fragments
  12. N/S co-doped CoSe/C nanocubes as anode materials for Li-ion batteries
  13. Synergistic effects of halloysite nanotubes with metal and phosphorus additives on the optimal design of eco-friendly sandwich panels with maximum flame resistance and minimum weight
  14. Octreotide-conjugated silver nanoparticles for active targeting of somatostatin receptors and their application in a nebulized rat model
  15. Controllable morphology of Bi2S3 nanostructures formed via hydrothermal vulcanization of Bi2O3 thin-film layer and their photoelectrocatalytic performances
  16. Development of (−)-epigallocatechin-3-gallate-loaded folate receptor-targeted nanoparticles for prostate cancer treatment
  17. Enhancement of the mechanical properties of HDPE mineral nanocomposites by filler particles modulation of the matrix plastic/elastic behavior
  18. Effect of plasticizers on the properties of sugar palm nanocellulose/cinnamon essential oil reinforced starch bionanocomposite films
  19. Optimization of nano coating to reduce the thermal deformation of ball screws
  20. Preparation of efficient piezoelectric PVDF–HFP/Ni composite films by high electric field poling
  21. MHD dissipative Casson nanofluid liquid film flow due to an unsteady stretching sheet with radiation influence and slip velocity phenomenon
  22. Effects of nano-SiO2 modification on rubberised mortar and concrete with recycled coarse aggregates
  23. Mechanical and microscopic properties of fiber-reinforced coal gangue-based geopolymer concrete
  24. Effect of morphology and size on the thermodynamic stability of cerium oxide nanoparticles: Experiment and molecular dynamics calculation
  25. Mechanical performance of a CFRP composite reinforced via gelatin-CNTs: A study on fiber interfacial enhancement and matrix enhancement
  26. A practical review over surface modification, nanopatterns, emerging materials, drug delivery systems, and their biophysiochemical properties for dental implants: Recent progresses and advances
  27. HTR: An ultra-high speed algorithm for cage recognition of clathrate hydrates
  28. Effects of microalloying elements added by in situ synthesis on the microstructure of WCu composites
  29. A highly sensitive nanobiosensor based on aptamer-conjugated graphene-decorated rhodium nanoparticles for detection of HER2-positive circulating tumor cells
  30. Progressive collapse performance of shear strengthened RC frames by nano CFRP
  31. Core–shell heterostructured composites of carbon nanotubes and imine-linked hyperbranched polymers as metal-free Li-ion anodes
  32. A Galerkin strategy for tri-hybridized mixture in ethylene glycol comprising variable diffusion and thermal conductivity using non-Fourier’s theory
  33. Simple models for tensile modulus of shape memory polymer nanocomposites at ambient temperature
  34. Preparation and morphological studies of tin sulfide nanoparticles and use as efficient photocatalysts for the degradation of rhodamine B and phenol
  35. Polyethyleneimine-impregnated activated carbon nanofiber composited graphene-derived rice husk char for efficient post-combustion CO2 capture
  36. Electrospun nanofibers of Co3O4 nanocrystals encapsulated in cyclized-polyacrylonitrile for lithium storage
  37. Pitting corrosion induced on high-strength high carbon steel wire in high alkaline deaerated chloride electrolyte
  38. Formulation of polymeric nanoparticles loaded sorafenib; evaluation of cytotoxicity, molecular evaluation, and gene expression studies in lung and breast cancer cell lines
  39. Engineered nanocomposites in asphalt binders
  40. Influence of loading voltage, domain ratio, and additional load on the actuation of dielectric elastomer
  41. Thermally induced hex-graphene transitions in 2D carbon crystals
  42. The surface modification effect on the interfacial properties of glass fiber-reinforced epoxy: A molecular dynamics study
  43. Molecular dynamics study of deformation mechanism of interfacial microzone of Cu/Al2Cu/Al composites under tension
  44. Nanocolloid simulators of luminescent solar concentrator photovoltaic windows
  45. Compressive strength and anti-chloride ion penetration assessment of geopolymer mortar merging PVA fiber and nano-SiO2 using RBF–BP composite neural network
  46. Effect of 3-mercapto-1-propane sulfonate sulfonic acid and polyvinylpyrrolidone on the growth of cobalt pillar by electrodeposition
  47. Dynamics of convective slippery constraints on hybrid radiative Sutterby nanofluid flow by Galerkin finite element simulation
  48. Preparation of vanadium by the magnesiothermic self-propagating reduction and process control
  49. Microstructure-dependent photoelectrocatalytic activity of heterogeneous ZnO–ZnS nanosheets
  50. Cytotoxic and pro-inflammatory effects of molybdenum and tungsten disulphide on human bronchial cells
  51. Improving recycled aggregate concrete by compression casting and nano-silica
  52. Chemically reactive Maxwell nanoliquid flow by a stretching surface in the frames of Newtonian heating, nonlinear convection and radiative flux: Nanopolymer flow processing simulation
  53. Nonlinear dynamic and crack behaviors of carbon nanotubes-reinforced composites with various geometries
  54. Biosynthesis of copper oxide nanoparticles and its therapeutic efficacy against colon cancer
  55. Synthesis and characterization of smart stimuli-responsive herbal drug-encapsulated nanoniosome particles for efficient treatment of breast cancer
  56. Homotopic simulation for heat transport phenomenon of the Burgers nanofluids flow over a stretching cylinder with thermal convective and zero mass flux conditions
  57. Incorporation of copper and strontium ions in TiO2 nanotubes via dopamine to enhance hemocompatibility and cytocompatibility
  58. Mechanical, thermal, and barrier properties of starch films incorporated with chitosan nanoparticles
  59. Mechanical properties and microstructure of nano-strengthened recycled aggregate concrete
  60. Glucose-responsive nanogels efficiently maintain the stability and activity of therapeutic enzymes
  61. Tunning matrix rheology and mechanical performance of ultra-high performance concrete using cellulose nanofibers
  62. Flexible MXene/copper/cellulose nanofiber heat spreader films with enhanced thermal conductivity
  63. Promoted charge separation and specific surface area via interlacing of N-doped titanium dioxide nanotubes on carbon nitride nanosheets for photocatalytic degradation of Rhodamine B
  64. Elucidating the role of silicon dioxide and titanium dioxide nanoparticles in mitigating the disease of the eggplant caused by Phomopsis vexans, Ralstonia solanacearum, and root-knot nematode Meloidogyne incognita
  65. An implication of magnetic dipole in Carreau Yasuda liquid influenced by engine oil using ternary hybrid nanomaterial
  66. Robust synthesis of a composite phase of copper vanadium oxide with enhanced performance for durable aqueous Zn-ion batteries
  67. Tunning self-assembled phases of bovine serum albumin via hydrothermal process to synthesize novel functional hydrogel for skin protection against UVB
  68. A comparative experimental study on damping properties of epoxy nanocomposite beams reinforced with carbon nanotubes and graphene nanoplatelets
  69. Lightweight and hydrophobic Ni/GO/PVA composite aerogels for ultrahigh performance electromagnetic interference shielding
  70. Research on the auxetic behavior and mechanical properties of periodically rotating graphene nanostructures
  71. Repairing performances of novel cement mortar modified with graphene oxide and polyacrylate polymer
  72. Closed-loop recycling and fabrication of hydrophilic CNT films with high performance
  73. Design of thin-film configuration of SnO2–Ag2O composites for NO2 gas-sensing applications
  74. Study on stress distribution of SiC/Al composites based on microstructure models with microns and nanoparticles
  75. PVDF green nanofibers as potential carriers for improving self-healing and mechanical properties of carbon fiber/epoxy prepregs
  76. Osteogenesis capability of three-dimensionally printed poly(lactic acid)-halloysite nanotube scaffolds containing strontium ranelate
  77. Silver nanoparticles induce mitochondria-dependent apoptosis and late non-canonical autophagy in HT-29 colon cancer cells
  78. Preparation and bonding mechanisms of polymer/metal hybrid composite by nano molding technology
  79. Damage self-sensing and strain monitoring of glass-reinforced epoxy composite impregnated with graphene nanoplatelet and multiwalled carbon nanotubes
  80. Thermal analysis characterisation of solar-powered ship using Oldroyd hybrid nanofluids in parabolic trough solar collector: An optimal thermal application
  81. Pyrene-functionalized halloysite nanotubes for simultaneously detecting and separating Hg(ii) in aqueous media: A comprehensive comparison on interparticle and intraparticle excimers
  82. Fabrication of self-assembly CNT flexible film and its piezoresistive sensing behaviors
  83. Thermal valuation and entropy inspection of second-grade nanoscale fluid flow over a stretching surface by applying Koo–Kleinstreuer–Li relation
  84. Mechanical properties and microstructure of nano-SiO2 and basalt-fiber-reinforced recycled aggregate concrete
  85. Characterization and tribology performance of polyaniline-coated nanodiamond lubricant additives
  86. Combined impact of Marangoni convection and thermophoretic particle deposition on chemically reactive transport of nanofluid flow over a stretching surface
  87. Spark plasma extrusion of binder free hydroxyapatite powder
  88. An investigation on thermo-mechanical performance of graphene-oxide-reinforced shape memory polymer
  89. Effect of nanoadditives on the novel leather fiber/recycled poly(ethylene-vinyl-acetate) polymer composites for multifunctional applications: Fabrication, characterizations, and multiobjective optimization using central composite design
  90. Design selection for a hemispherical dimple core sandwich panel using hybrid multi-criteria decision-making methods
  91. Improving tensile strength and impact toughness of plasticized poly(lactic acid) biocomposites by incorporating nanofibrillated cellulose
  92. Green synthesis of spinel copper ferrite (CuFe2O4) nanoparticles and their toxicity
  93. The effect of TaC and NbC hybrid and mono-nanoparticles on AA2024 nanocomposites: Microstructure, strengthening, and artificial aging
  94. Excited-state geometry relaxation of pyrene-modified cellulose nanocrystals under UV-light excitation for detecting Fe3+
  95. Effect of CNTs and MEA on the creep of face-slab concrete at an early age
  96. Effect of deformation conditions on compression phase transformation of AZ31
  97. Application of MXene as a new generation of highly conductive coating materials for electromembrane-surrounded solid-phase microextraction
  98. A comparative study of the elasto-plastic properties for ceramic nanocomposites filled by graphene or graphene oxide nanoplates
  99. Encapsulation strategies for improving the biological behavior of CdS@ZIF-8 nanocomposites
  100. Biosynthesis of ZnO NPs from pumpkin seeds’ extract and elucidation of its anticancer potential against breast cancer
  101. Preliminary trials of the gold nanoparticles conjugated chrysin: An assessment of anti-oxidant, anti-microbial, and in vitro cytotoxic activities of a nanoformulated flavonoid
  102. Effect of micron-scale pores increased by nano-SiO2 sol modification on the strength of cement mortar
  103. Fractional simulations for thermal flow of hybrid nanofluid with aluminum oxide and titanium oxide nanoparticles with water and blood base fluids
  104. The effect of graphene nano-powder on the viscosity of water: An experimental study and artificial neural network modeling
  105. Development of a novel heat- and shear-resistant nano-silica gelling agent
  106. Characterization, biocompatibility and in vivo of nominal MnO2-containing wollastonite glass-ceramic
  107. Entropy production simulation of second-grade magnetic nanomaterials flowing across an expanding surface with viscidness dissipative flux
  108. Enhancement in structural, morphological, and optical properties of copper oxide for optoelectronic device applications
  109. Aptamer-functionalized chitosan-coated gold nanoparticle complex as a suitable targeted drug carrier for improved breast cancer treatment
  110. Performance and overall evaluation of nano-alumina-modified asphalt mixture
  111. Analysis of pure nanofluid (GO/engine oil) and hybrid nanofluid (GO–Fe3O4/engine oil): Novel thermal and magnetic features
  112. Synthesis of Ag@AgCl modified anatase/rutile/brookite mixed phase TiO2 and their photocatalytic property
  113. Mechanisms and influential variables on the abrasion resistance hydraulic concrete
  114. Synergistic reinforcement mechanism of basalt fiber/cellulose nanocrystals/polypropylene composites
  115. Achieving excellent oxidation resistance and mechanical properties of TiB2–B4C/carbon aerogel composites by quick-gelation and mechanical mixing
  116. Microwave-assisted sol–gel template-free synthesis and characterization of silica nanoparticles obtained from South African coal fly ash
  117. Pulsed laser-assisted synthesis of nano nickel(ii) oxide-anchored graphitic carbon nitride: Characterizations and their potential antibacterial/anti-biofilm applications
  118. Effects of nano-ZrSi2 on thermal stability of phenolic resin and thermal reusability of quartz–phenolic composites
  119. Benzaldehyde derivatives on tin electroplating as corrosion resistance for fabricating copper circuit
  120. Mechanical and heat transfer properties of 4D-printed shape memory graphene oxide/epoxy acrylate composites
  121. Coupling the vanadium-induced amorphous/crystalline NiFe2O4 with phosphide heterojunction toward active oxygen evolution reaction catalysts
  122. Graphene-oxide-reinforced cement composites mechanical and microstructural characteristics at elevated temperatures
  123. Gray correlation analysis of factors influencing compressive strength and durability of nano-SiO2 and PVA fiber reinforced geopolymer mortar
  124. Preparation of layered gradient Cu–Cr–Ti alloy with excellent mechanical properties, thermal stability, and electrical conductivity
  125. Recovery of Cr from chrome-containing leather wastes to develop aluminum-based composite material along with Al2O3 ceramic particles: An ingenious approach
  126. Mechanisms of the improved stiffness of flexible polymers under impact loading
  127. Anticancer potential of gold nanoparticles (AuNPs) using a battery of in vitro tests
  128. Review Articles
  129. Proposed approaches for coronaviruses elimination from wastewater: Membrane techniques and nanotechnology solutions
  130. Application of Pickering emulsion in oil drilling and production
  131. The contribution of microfluidics to the fight against tuberculosis
  132. Graphene-based biosensors for disease theranostics: Development, applications, and recent advancements
  133. Synthesis and encapsulation of iron oxide nanorods for application in magnetic hyperthermia and photothermal therapy
  134. Contemporary nano-architectured drugs and leads for ανβ3 integrin-based chemotherapy: Rationale and retrospect
  135. State-of-the-art review of fabrication, application, and mechanical properties of functionally graded porous nanocomposite materials
  136. Insights on magnetic spinel ferrites for targeted drug delivery and hyperthermia applications
  137. A review on heterogeneous oxidation of acetaminophen based on micro and nanoparticles catalyzed by different activators
  138. Early diagnosis of lung cancer using magnetic nanoparticles-integrated systems
  139. Advances in ZnO: Manipulation of defects for enhancing their technological potentials
  140. Efficacious nanomedicine track toward combating COVID-19
  141. A review of the design, processes, and properties of Mg-based composites
  142. Green synthesis of nanoparticles for varied applications: Green renewable resources and energy-efficient synthetic routes
  143. Two-dimensional nanomaterial-based polymer composites: Fundamentals and applications
  144. Recent progress and challenges in plasmonic nanomaterials
  145. Apoptotic cell-derived micro/nanosized extracellular vesicles in tissue regeneration
  146. Electronic noses based on metal oxide nanowires: A review
  147. Framework materials for supercapacitors
  148. An overview on the reproductive toxicity of graphene derivatives: Highlighting the importance
  149. Antibacterial nanomaterials: Upcoming hope to overcome antibiotic resistance crisis
  150. Research progress of carbon materials in the field of three-dimensional printing polymer nanocomposites
  151. A review of atomic layer deposition modelling and simulation methodologies: Density functional theory and molecular dynamics
  152. Recent advances in the preparation of PVDF-based piezoelectric materials
  153. Recent developments in tensile properties of friction welding of carbon fiber-reinforced composite: A review
  154. Comprehensive review of the properties of fly ash-based geopolymer with additive of nano-SiO2
  155. Perspectives in biopolymer/graphene-based composite application: Advances, challenges, and recommendations
  156. Graphene-based nanocomposite using new modeling molecular dynamic simulations for proposed neutralizing mechanism and real-time sensing of COVID-19
  157. Nanotechnology application on bamboo materials: A review
  158. Recent developments and future perspectives of biorenewable nanocomposites for advanced applications
  159. Nanostructured lipid carrier system: A compendium of their formulation development approaches, optimization strategies by quality by design, and recent applications in drug delivery
  160. 3D printing customized design of human bone tissue implant and its application
  161. Design, preparation, and functionalization of nanobiomaterials for enhanced efficacy in current and future biomedical applications
  162. A brief review of nanoparticles-doped PEDOT:PSS nanocomposite for OLED and OPV
  163. Nanotechnology interventions as a putative tool for the treatment of dental afflictions
  164. Recent advancements in metal–organic frameworks integrating quantum dots (QDs@MOF) and their potential applications
  165. A focused review of short electrospun nanofiber preparation techniques for composite reinforcement
  166. Microstructural characteristics and nano-modification of interfacial transition zone in concrete: A review
  167. Latest developments in the upconversion nanotechnology for the rapid detection of food safety: A review
  168. Strategic applications of nano-fertilizers for sustainable agriculture: Benefits and bottlenecks
  169. Molecular dynamics application of cocrystal energetic materials: A review
  170. Synthesis and application of nanometer hydroxyapatite in biomedicine
  171. Cutting-edge development in waste-recycled nanomaterials for energy storage and conversion applications
  172. Biological applications of ternary quantum dots: A review
  173. Nanotherapeutics for hydrogen sulfide-involved treatment: An emerging approach for cancer therapy
  174. Application of antibacterial nanoparticles in orthodontic materials
  175. Effect of natural-based biological hydrogels combined with growth factors on skin wound healing
  176. Nanozymes – A route to overcome microbial resistance: A viewpoint
  177. Recent developments and applications of smart nanoparticles in biomedicine
  178. Contemporary review on carbon nanotube (CNT) composites and their impact on multifarious applications
  179. Interfacial interactions and reinforcing mechanisms of cellulose and chitin nanomaterials and starch derivatives for cement and concrete strength and durability enhancement: A review
  180. Diamond-like carbon films for tribological modification of rubber
  181. Layered double hydroxides (LDHs) modified cement-based materials: A systematic review
  182. Recent research progress and advanced applications of silica/polymer nanocomposites
  183. Modeling of supramolecular biopolymers: Leading the in silico revolution of tissue engineering and nanomedicine
  184. Recent advances in perovskites-based optoelectronics
  185. Biogenic synthesis of palladium nanoparticles: New production methods and applications
  186. A comprehensive review of nanofluids with fractional derivatives: Modeling and application
  187. Electrospinning of marine polysaccharides: Processing and chemical aspects, challenges, and future prospects
  188. Electrohydrodynamic printing for demanding devices: A review of processing and applications
  189. Rapid Communications
  190. Structural material with designed thermal twist for a simple actuation
  191. Recent advances in photothermal materials for solar-driven crude oil adsorption
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 6.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/ntrev-2022-0151/html
Scroll to top button