Startseite Technik Construction vibration risk assessment of engineering projects based on nonlinear feature algorithm
Artikel Open Access

Construction vibration risk assessment of engineering projects based on nonlinear feature algorithm

  • Li Liu EMAIL logo
Veröffentlicht/Copyright: 2. November 2022
Artikel downloaden (PDF)
Veröffentlichen auch Sie bei De Gruyter Brill
Manuskript einreichen Informationen für Autor*innen
Nonlinear Engineering
Aus der Zeitschrift Nonlinear Engineering Band 11 Heft 1

Abstract

In order to study the vibration engineering project construction risk assessment, algorithms based on nonlinear characteristics, a nonlinear feature extraction local linear embedding (LLE) combined with adaptive neuro-fuzzy inference system (ANFIS) assessment of risk assessment methods have been proposed. This method is first utilized by the LLE manifold method to extract a number of sample construction vibration risk assessment factors of high-dimensional data vector of the nonlinear components. The nonlinear component is then used as the input for ANFIS evaluation method to evaluate and classify construction vibration risk samples. An example shows that this method can effectively improve the accuracy of risk assessment and reduce the error rate to less than 10%. Applying it to practical projects can provide effective decision-making information for construction managers and improve the credibility of decision-making. The identification results prove that the method in this article improves the accuracy of feature extraction and vibration risk assessment, and can as a vibration risk assessment method, be applied to the actual engineering vibration risk assessment.

Keywords: nonlinear; engineering project; construction vibration risk

1 Introduction

In the early stage of engineering construction, in order to provide auxiliary information for project managers to make risk decisions in the project planning stage, environmental risk assessment of construction vibration is carried out for engineering projects that may produce construction vibration, construction vibration risk evaluation [1]. Previous studies did not consider the impact of construction vibration from the perspective of risk or from the perspective of project managers, but paid much attention to the quantitative evaluation of the measured data on the engineering site. In order to avoid the complexity of previous quantitative evaluation methods, lag in evaluation, and strict requirements on data, and make full use of expert knowledge and experience in the field, this article proposes a new method for qualitative evaluation of construction vibration risk based on fuzzy logic theory [2]. The construction vibration risk assessment knowledge system is composed of the factors considered by experts in risk assessment and established on the basis of literature collection and expert investigation. According to the spreading process of construction vibration environmental risk, construction vibration risk is divided into building risk and occupant risk, and the building risk is divided into building settlement risk and building vibration risk. According to the construction vibration environmental risk model, the risk module, vulnerability module, and importance module are integrated into risk [3]. There are a lot of uncertainties in the complex dynamic system composed of vibration sources, soil, and buildings, which are difficult to calculate accurately and quantitatively. Assessing the environmental risks brought by construction vibration is a process involving foundation and foundation engineering, soil dynamics, and structural dynamics. It is difficult to quantitatively and scientifically evaluate construction vibration risks. In the past, quantitative methods were mainly used to evaluate the environmental impact of construction vibration. In view of this, from the perspective of risk, an expert system based on fuzzy logic is constructed to qualitatively assess the environmental risk of construction vibration.

In view of this, from the perspective of risk, an expert system based on fuzzy logic is constructed to qualitatively assess the environmental risk of construction vibration. Fuzzy logic can imitate the uncertainty concept judgment and reasoning way of thinking of the human brain to solve the uncertain problems that are difficult to obtain with mathematical models and simulate with computers. On the one hand, vibration transmission by soil, caused by the vibration source, may result in ground soil densification, in turn, causing the ground foundation settlement of surrounding buildings, and on the other hand, the interaction between the soil and building foundation make building structure vibrate in response, thereby causing damage to the buildings or occupants and precision instruments. According to different risk objectives, construction vibration risk is divided into three parts: building settlement risk, building vibration risk, and inhabitant risk.

2 Literature review

Risk can be expressed as R (risk) = P (probability) × C (consequence), that is, the possibility of loss occurring. According to the definition of risk, Engineering vibration environmental risk is defined as the possibility of construction vibration affecting or damaging the surrounding environment. Among them, precision instruments are considered as occupants with special attributes and classified as occupants’ risk. The construction vibration risk assessment knowledge system is composed of the influential factors considered by experts in risk assessment, and is based on literature collection and expert investigation. It was built according to the transmission process of environmental risk of construction vibration. The construction vibration risk is divided into building risk and occupant risk, and the building risk is divided into building settlement risk and building vibration risk. According to the construction vibration environmental risk model, the risk module, vulnerability module, and importance module are integrated as risks. The knowledge framework of the construction vibration risk assessment index system is shown in Figure 1.

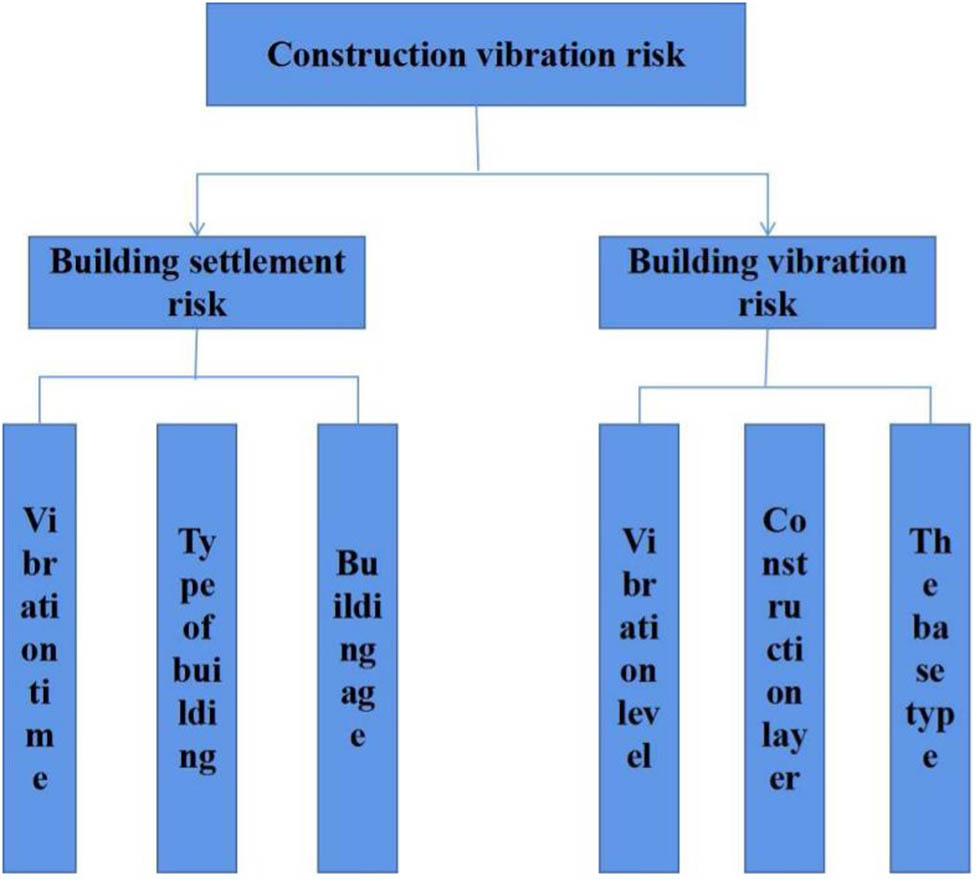
Figure 1 Index system of construction vibration risk assessment model.
Figure 1

Index system of construction vibration risk assessment model.

Khanh and Kim discussed the impact of uneven deformation of deceptive foundation on the cracking of box culvert roof and the specific causes of cracking of clamp culvert by using AN-SYS software [4]. Portugal-Pereira et al. analyzed various working conditions of underpass project through finite element software and monitoring data. The impact degree of high-speed railway facilities and equipment is also presented, and effective measures to reduce risks are given [5]. Wibowo and Taufik analyzed the settlement of roadbed caused by jacking of existing railway under frame bridge by establishing three-dimensional numerical distress type and field monitoring values and obtained the risk situation in the construction process [6]. Liu evaluated the construction quality of the existing railway under the large span box culverts by analyzing the actual chaff data of the deviation of the central axis of the box culverts, and established a risk evaluation model of the existing railway under the box culverts based on support vector theory by using the risk management method in project management [7]. Yoo et al. developed a building safety index evaluation tool based on scientific research methods, a checklist is formulated in detail, and the safety management of the site is quantitatively evaluated and scored from the three aspects of procedures, personnel, and policies [8].

Based on the comprehensive analysis of the construction risk factors affecting the railway jacking under box culvert, a new construction risk evaluation model based on nonlinear fuzzy analytic hierarchy process (AHP) is proposed in this article. AHP is used to calculate the weight of construction risk factors of jacking railway under box culvert, and the membership vector is obtained by combining the expert evaluation method to construct the fuzzy relation matrix. Then, a nonlinear fuzzy operator is introduced to comprehensively calculate the risk weight and fuzzy relation matrix. Finally, according to the principle of maximum membership degree and risk evaluation standard, the final risk evaluation grade is obtained. The new model is applied to the jacking method construction of Jingjilu – Longhai railway overpass project to further verify the correctness and rationality of the method.

3 Engineering case analysis

Through Jiulu – Longhai railway overpass project, located in the west side of the east railway station, box shaped overpass adopts five-hole reinforced concrete structure, along the central line of the entire 146 m long bridge, the overall view is trapezoidal. The overpass has a positive width of 50.5 m and a slant width of 56.45 m. Under this project, there are six existing or renovated railway lines, and the height of each rail top varies greatly, causing great traffic disturbance. The structure of the underground overpass is 26.5° oblique with railway, jacking, and cast-in-place intersect, and the overhead system is frequently converted and the construction is complicated. From south to north, the overpass is divided into 11 sections, including the 2nd special block, 1#–9# and S6. The first section goes through the main line of Longhai road, and the fifth section goes through the reconstruction of two lines of Longhai road up-line and right line, and adopts the jacking method for construction. The first section has a self-weight of 3757.7 t and a maximum of 5,261 t; The fifth section has a dead weight of 6,095 t and a maximum jacking force of 8,533 t. The jacking section is located in the saturated soft loess bad geological layer, making construction difficult. In addition, the project involves the transformation and transition protection of more than 180 railway 4-power equipment, and the construction of 360 24 m long manual digging piles and 77 40 m dewatering wells has a great impact on the railway operation safety and high risk of safety control.

3.1 Weight calculation

The AHP can be used to solve the weight vector to obtain the corresponding weight vector of each risk factor set in the construction risk evaluation of jacking railway under box culvert, as shown in Table 1.

Table 1

Weight vector calculated values of risk factor sets

Risk factor set The weight vector
Level 1 indicator risk W 1 = [0.2772, 0.4673, 0.0954, 0.1601]
Secondary index risk Geological risk W 2 = [0.4308, 0.2021, 0.3671]
Environmental risk W 3 = [0.5695, 0.3332, 0.0974]
Equipment risk W 4 = [0.1732, 0.2728, 0.4271, 0.0506, 0.0763]
Existing railway risk W 5 = [0.4428, 0.2487, 0.1299, 0.1786]

3.2 Construction of fuzzy relation matrix

Combined with nine roads and Longhai railway overpass project box culvert under actual situation in railway jacking construction site, the expert evaluation method, respectively, for the nine roads and Longhai railway overpass project under the box culvert in railway jacking construction of various risk factors in the evaluation of risk scores, can get the corresponding membership values, as shown in Table 2.

Table 2

Risk index

Category Category 1 Category 2 Category 3 Category 4
Category 1 (10 groups) 10 1 10 0
Category 2 (10 groups) 0 0 0 10
Category 3 (10 groups) 1 9 0 1
Category 4 (10 groups) 0 0 9 0

The evaluation matrix of risk factors at all levels is obtained according to Table 3, and then transformed into the evaluation matrix for nonlinear fuzzy comprehensive calculation through formula r ′ i j = 10 × r i j (as shown in Figure 2).

Table 3

Values of prominent influence coefficient vectors of risk factor sets at all levels

Risk factor set The weight vector
Level 1 indicator risk A = (3.5, 4.5, 1.5, 2.5)
Secondary index risk Geological risk A 1 = (4.0, 2.5, 3.5)
Environmental risk A 2 = (4.5, 4.0, 1.5)
Equipment risk A 3 = (3.0, 3.0, 3.5, 1.0, 1.0)
Existing railway risk A 4 = (4.0, 3.0, 2.0, 2.5)
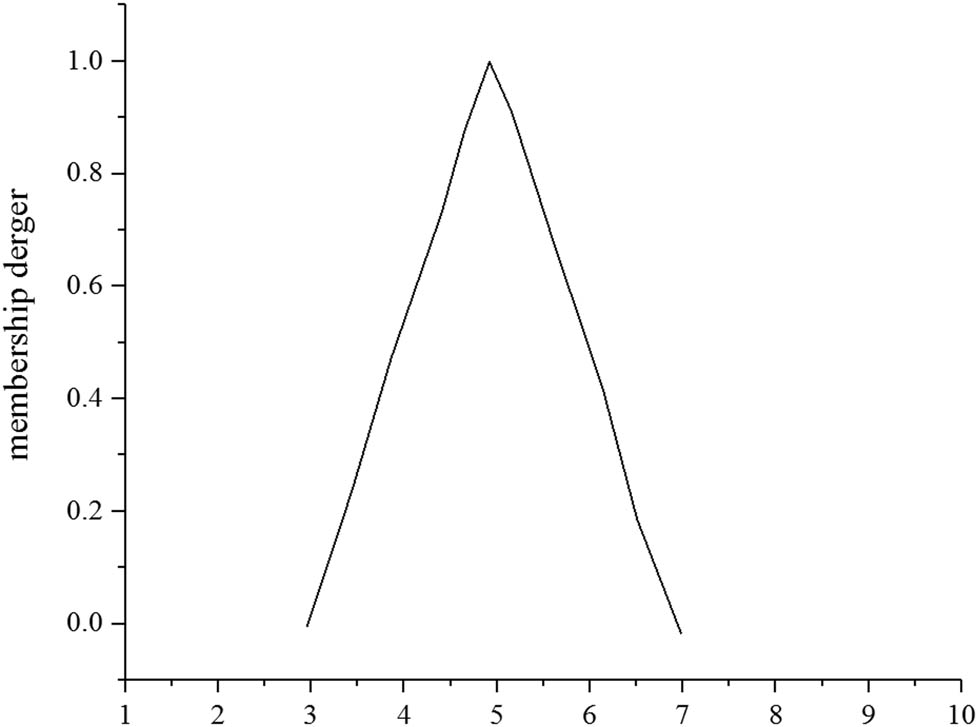
Figure 2 Triangle membership function.
Figure 2

Triangle membership function.

The nonlinear fuzzy evaluation matrix formed by each risk factor in geological risk is

(1) R 1 = 0 0 1 1 3 6 0 0 3 8 1 0 0 7 0 .

The nonlinear fuzzy evaluation matrix formed by various risk factors in the surrounding environmental risks is

(2) R 2 = 0 0 0 8 2 0 0 1 8 1 1 7 2 0 0 .

The nonlinear fuzzy evaluation matrix formed by all risk factors in equipment risk is

(3) R 3 = 0 0 5 5 0 0 1 2 7 0 0 0 2 8 0 2 7 1 0 0 1 6 3 0 0 .

The nonlinear fuzzy evaluation matrix formed by various risk factors in the existing railway risks is

(4) R 4 = 0 0 1 8 1 0 0 4 6 0 1 3 6 0 0 1 2 7 0 0 .

3.3 Determining the prominent influence coefficient of risk factor indicators

According to the value of outburst influence coefficient, the outburst influence coefficient vectors corresponding to each nonlinear fuzzy evaluation matrix are constructed. The values of the prominent influence coefficient vectors are shown in Table 3.

3.4 Level 1 nonlinear fuzzy comprehensive evaluation

According to the expert evaluation method, the membership degree vector of fuzzy comprehensive evaluation calculation of jacking construction risk of underpass railway box culvert is constructed. Several experts with rich practical experience and high academic level were selected to set up an evaluation group, and then on the quantitative and qualitative basis, each index with concentrated risk factors was scored according to the five risk levels of the risk evaluation standard in Table 3. The membership vector of any risk factor in the risk evaluation index system can be obtained as follows:

(5) R 1 = [ r i l , r i 2 , r i 3 , r i 4 , r i 5 ] .

According to the principle of membership degree vector construction, the membership degree vector of each risk factor in the jacking construction risk evaluation of railway under box culvert can be obtained, respectively. Then, the membership vector of risk factors corresponding to each risk factor set is combined to obtain the fuzzy relation matrix corresponding to each risk factor set.

The specific form of fuzzy comprehensive evaluation calculation for jacking construction risk of railway under box culvert by using nonlinear fuzzy operator is as follows:

(6) f ( w 1 , w 2 , ⋯ , w n , x 1 , x 2 , ⋯ , x n , Λ ) = ( w 1 x 1 λ 1 + w 2 x 2 λ 2 + ⋯ w n x n λ n ) .

According to the weight vector W 1–4 of risk factors, the nonlinear fuzzy evaluation matrix R 1–4, and the prominent influence coefficient vector A 1–4 calculated above, formula (6) is used to conduct first-order nonlinear fuzzy comprehensive evaluation. According to the principle of maximum membership degree, the jacking construction risk grade is four, which is a high risk. The risks with greater impact are the surrounding environment risk and geological risk, while the risks with lesser impact are the equipment risk and existing railway risk. Jingjilu – Longhai Railway overpass engineering box culvert underpass railway jacking project 2 is located in saturated soft loess bad geological layer, the construction needs a large area of precipitation treatment, and the project runs Longhai railway and a number of busy trunk railways, the surrounding buildings are dense. Precipitation and jacking construction may cause excessive ground settlement, and the existing structures and pavement around the foundation pit will be greatly deformed, which will affect the safety of railway and existing buildings. According to the constructed model, the risk assessment of the construction process of the project is carried out. The results show that the surrounding environment has the greatest risk, which is consistent with the actual situation of the site construction, and verifies the correctness and rationality of the new model.

4 Numerical results and discussion

4.1 Local linear embedding (LLE) nonlinear feature extraction method

Based on expert system to extract multiple samples of construction vibration risk provided you can get a set of feature vector set, the feature vector set contains some redundancy of having nothing to do with the construction of the vibration characteristic information, and the characteristics of linear combination of the body is piled up, and how to get to reflect the nonlinear characteristic of the vibration characteristics of the construction is a problem to be solved. On this basis, we adopt the local linear embedding (LLE) algorithm to extract the nonlinear features from the linear feature dataset. The following will first introduce the local linear feature embedding algorithm for subsequent application. The LLE algorithm assumes that the data structure in the local sense is linear on the premise of the overall nonlinearity of the data, and it is a manifold algorithm that approximates the overall nonlinearity based on the local linearity [9]. In this algorithm, local neighborhoods are overlapped with each other to provide global feature information after dimensionality reduction in high-dimensional data, while keeping local geometric characteristics unchanged.

The essence of LLE algorithm is to map high-dimensional feature dataset A = { a 1 , a 2 , … , a n } , a i ∈ R D to low-dimensional feature dataset B = { b 1 , b 2 , … , b n } , b i ∈ R d ( D > d ) .

4.2 Adaptive fuzzy neural network reasoning system (ANFIS)

Adaptive neuro-fuzzy inference system (ANFIS) is an integrated system combining neural network and fuzzy theory proposed by JyH-Skiing Roger Jang in 1993. The system uses the topology structure of neural network to express fuzzy reasoning system and realizes various fuzzy operations through its neurons. A hybrid algorithm combining error back propagation and least square estimation in neural network theory is used to adaptively adjust system parameters and approximate the implicit relationship between input and output data. This fuzzy neural network system has fuzzy reasoning function and mapping approximation ability, and has been tried and applied in many fields such as system identification [10].

ANFIS uses a hybrid algorithm combining error back propagation and least square estimation to adjust the variable parameters of the system. For the adaptive network with adjustable parameters, the linear parameters can be identified by the least square method, while the nonlinear parameters can be identified by the error back propagation algorithm. As can be seen from the network structure of ANFIS, when the conditional parameters are fixed, the output of the system can be expressed as a linear combination of the conclusion parameters, namely,

(7) f = w 1 w 1 + w 2 f 1 + w 2 w 1 + w 2 f 2 .

Therefore, a hybrid algorithm combining error back propagation and least square estimation can be used to adjust the parameters of ANFIS. In each iteration, when the system input is forward transfer, the conditional parameters are fixed and the conclusion parameters are adjusted by the least square estimation method. When the output error propagates back, the conclusion parameters are fixed and the condition parameters are adjusted by gradient descent method. For known conditional parameters, the globally optimal conclusion parameters can be obtained in this way, which can not only reduce the dimension of the search space in ladder descent method, but also significantly improve the convergence rate.

LLE method extracted the low-dimensional nonlinear feature representing the multi-dimensional feature vector of the vibration construction risk characteristic index system, and reduced the dimension of the feature vector representing the high-dimensional feature index system to obtain the low-dimensional nonlinear feature vector of vibration construction risk. The vector input of ANFIS learning method is used to evaluate the construction vibration risk of different sites. The specific implementation steps of this method are as follows:

  1. Take a series of actual construction projects as the research object, extract specific indicators representing construction vibration risk according to the indicator system shown, and obtain a set of high-dimensional feature vectors representing construction vibration risk [11,12,13].

  2. Each component of each high-dimensional feature vector is normalized to form a normalized high-dimensional feature vector representing the construction vibration risk of the project.

  3. Calculate the low-dimensional nonlinear features of high-dimensional feature vectors according to the formula L ( B ) = min ∑ i = 1 n b i − ∑ j = 1 k w j ( j ) b j 2 , which are used as the input feature vectors of ANFIS method [14,15,16,17].

  4. The low-dimensional nonlinear features of engineering samples with known construction vibration risk levels are used as training samples to train ANFIS neural network, and then the low-dimensional nonlinear feature vector-values of verification samples are input into ANFIS neural network to obtain the classification results of construction vibration risk rating of samples.

    For construction vibration, soil and rock, foundation, and structure form are all factors affecting the response mode of structure, which together constitute a dynamic system. The vibration is transmitted to the building foundation by the strata around the engineering site, and the soil interacts with the building foundation, causing the building to respond. Ground vibration wavelengths can range from a few meters to hundreds of meters, and shorter wavelengths cause complex building responses. However, except for the high-frequency vibration source, the size of civil building base is smaller than the characteristic wavelength of the vibration source. If the source of the vibration is a transient load, the building will respond at its natural frequency (free vibration) [18,19,20,21,22]. If the source is harmonic load, the building will vibrate at the same frequency (forced vibration), and if the vibration frequency is close to the natural frequency of the building, resonance may occur. The closer the excitation frequency is to the natural frequency of the building, the greater the response of the building structure. Generally, the earthquake frequency is closer to the natural frequency of the building, so the earthquake is generally more destructive, especially the earthquake of 0.5–8 Hz is easy to cause the resonance damage of the building [23,24,25,26,27].

  5. LE method extracts the low-dimensional nonlinear features which represent the multi-dimensional feature vectors of the characteristic index system of vibration construction risk, and will represent the high-dimensional features. The nonlinear feature vector of vibration construction risk with lower dimension is obtained by dimensionality reduction in feature vector of feature index system. The vector input of ANFIS learning method is used to evaluate the construction vibration risk of different sites. The specific implementation steps of this method are as follows:

Each component of each high-dimensional feature vector is normalized to form a normalized high-dimensional feature vector representing the construction vibration risk of the project according to formula (8) [28].

(8) L ( B ) = min ∑ i = 1 m b i − ∑ j = 1 k w j b j = t r .

The low-dimensional nonlinear features of high-dimensional eigenvectors are calculated as the input eigenvectors of ANFIS method [29].

5 Conclusion and prospects

An ANFIS vibration risk assessment method based on LLE nonlinear characteristics is proposed. This method integrates more information, and not only makes the information contained in the original vibration risk index fully reflected by non-linear low-dimensional feature components but also simplifies the interference or coupling of feature information between systems. Based on the in-depth analysis of the risk factors affecting the jacking construction of railway under box culvert, the risk evaluation index system established can reflect the actual situation of all levels of risk in the jacking construction of railway under box culvert comprehensively. According to the established nonlinear fuzzy AHP model, quantitative and qualitative evaluation is carried out on the jacking construction of railway under box culvert, and the evaluation results are basically consistent with the field construction. It is feasible to apply the new model to risk analysis in actual construction. Using nonlinear fuzzy AHP to wear under the box culvert railway jacking construction risk fuzzy comprehensive evaluation, not only can we solve the box culvert under wear railway jacking construction risk factors in the process of risk assessment of the problems of randomness, fuzziness but can also solve the prominent influence factors in railway under the box culvert jacking construction risk evaluation results, the influence of the evaluation results more reasonable. In terms of bridge construction, countermeasures for pile hole construction, lifting operations, gantry crane construction, and profile beam installation have been formulated. In terms of tunnel engineering, four levels of countermeasures are put forward, including tunnel intrusion cement treatment, tunnel engineering construction safety assurance, emergency rescue of tunnel construction accidents, and treatment of fault fractured areas, so as to reduce or avoid safety risks during the construction of expressway tunnel engineering.

This article proposes a risk assessment method of ANFIS construction vibration based on LLE nonlinear characteristics. This method integrates more information, and not only makes the information contained in the original vibration risk index fully reflected by nonlinear low-dimensional feature components but also simplifies the interference or coupling of feature information between systems. Finally, ANFIS neural network classifier, the method, and the traditional vibration risk characteristics parameters identification method of feature extraction and recognition results proved that the method improves the accuracy of feature extraction and vibration risk assessment, can serve as a kind of vibration risk assessment method and can be applied to practical engineering vibration risk assessment.

Due to the limitation of knowledge level and vision, the deficiencies in the article still need to be improved. As for the specific understanding of security risks, the risk resource database will continue to be supplemented because of the places that I cannot consider and some uncertain places; if those uncertain risk factors are continued to be classified, the obtained risk assessment results will also be better, to be accurate.

  1. Funding information: The author states no funding involved.

  2. Author contributions: The author has accepted responsibility for the entire content of this manuscript and approved its submission.

  3. Conflict of interest: The author states no conflict of interest.

References

[1] Deng X, Wang R, Xu T. Risk assessment of tunnel portals in the construction stage based on fuzzy analytic hierarchy process. Arch Civ Eng. 2018;64(4PT.1):69–87.10.2478/ace-2018-0045Suche in Google Scholar

[2] Antwi-Afari MF, Li H. Fall risk assessment of construction workers based on biomechanical gait stability parameters using wearable insole pressure system. Adv Eng Inform. 2018;38(OCT):683–94.10.1016/j.aei.2018.10.002Suche in Google Scholar

[3] Guo Q, Li Y, Meng X, Guo G, Lv X. Instability risk assessment of expressway construction site above an abandoned goaf: a case study in China. Environ Earth Sci. 2019;78(20):588.10.1007/s12665-019-8599-zSuche in Google Scholar

[4] Khanh HD, Kim SY. A survey on production planning system in construction projects based on last planner system. KSCE J Civ Eng. 2016;20(1):1–11.10.1007/s12205-015-1412-ySuche in Google Scholar

[5] Portugal-Pereira J, Ferreira P, Cunha J, Szklo A, Schaeffer R, Araujo M. Better late than never, but never late is better: risk assessment of nuclear power construction projects. Energy Policy. 2018;120(SEP):158–66.10.1016/j.enpol.2018.05.041Suche in Google Scholar

[6] Wibowo A, Taufik J. Developing a self-assessment model of risk management maturity for client organizations of public construction projects: Indonesian context. Proc Eng. 2017;171(Complete):274–81.10.1016/j.proeng.2017.01.335Suche in Google Scholar

[7] Liu Y, Dang J, Igarashi A. Implications of bidirectional interaction on nonlinear seismic response of steel piers. J Constr Steel Res. 2019;160(SEP):289–300.10.1016/j.jcsr.2019.05.044Suche in Google Scholar

[8] Yoo WS, Yang J, Kang S, Lee S. Development of a computerized risk management system for international NPP EPC projects. KSCE J Civ Eng. 2017;21(1):11–26.10.1007/s12205-016-0784-ySuche in Google Scholar

[9] Jung JH, Kim DY, Lee HK. The computer-based contingency estimation through analysis cost overrun risk of public construction project. KSCE J Civ Eng. 2016;20(4):1119–30.10.1007/s12205-015-0184-8Suche in Google Scholar

[10] Mahanipour A, Nezamabadi-Pour H. A multiple feature construction method based on gravitational search algorithm. Expert Syst Appl. 2019;127(AUG):199–209.10.1016/j.eswa.2019.03.015Suche in Google Scholar

[11] Yi L, Ji S, Ren L, Su R, Liang Y. A nonlinear feature fusion-based rating prediction algorithm in heterogeneous network. IEEE Trans Comput Soc Syst. 2021;99:1–9.10.1109/TCSS.2020.3046772Suche in Google Scholar

[12] Wang G, Karnan L, Hassan FM. Face feature point detection based on nonlinear high-dimensional space. Int J Syst Assur Eng Manag. 2021;13(Suppl 1):312–21.10.1007/s13198-021-01406-2Suche in Google Scholar

[13] Wei P, Wang BO, Almalki MA, Dai X, Zhang X. A facial expression recognition method using local nonlinear features. Fractals. 2022;30(2):2240105–34.10.1142/S0218348X22401053Suche in Google Scholar

[14] Gao J, Li F, Wang B, Liang H. Unsupervised nonlinear adaptive manifold learning for global and local information. Tsinghua Sci Technol. 2021;26(2):31–9.10.26599/TST.2019.9010049Suche in Google Scholar

[15] Liang T, Lu H. A novel method based on multi-island genetic algorithm improved variational mode decomposition and multi-features for fault diagnosis of rolling bearing. Entropy. 2020;22(9):995.10.3390/e22090995Suche in Google Scholar PubMed PubMed Central

[16] Du XF, Wang JS, Sun WZ. UNet retinal blood vessel segmentation algorithm based on improved pyramid pooling method and attention mechanism. Phys Med Biol. 2021;66(17):175013 (13pp).10.1088/1361-6560/ac1c4cSuche in Google Scholar PubMed

[17] Fatemi M, Daliri MR. Nonlinear sparse partial least squares: an investigation of the effect of nonlinearity and sparsity on the decoding of intracranial data. J Neural Eng. 2020;17(1):016055.1–9.10.1088/1741-2552/ab5d47Suche in Google Scholar PubMed

[18] Wang X, Xie W, Liangqun LI. Labeled multi-Bernoulli maneuvering target tracking algorithm via TSK iterative regression model. Chin J Electron. 2022;31(2):227–39.10.1049/cje.2020.00.156Suche in Google Scholar

[19] Galkin MG, Smagin AS. Implementation of the nonlinear programming algorithm when optimizing the final turning mode. IOP Conf Series Mater Sci Eng. 2020;862(3):032009 (7pp).10.1088/1757-899X/862/3/032009Suche in Google Scholar

[20] Segera D, Buthia MM, Nyete A. An innovative excited-ACS-IDGWO algorithm for optimal biomedical data feature selection. BioMed Res Int. 2020;2020(3):8506365.10.1155/2020/8506365Suche in Google Scholar PubMed PubMed Central

[21] Lou F, Key NL. Compressor stall warning using nonlinear feature extraction algorithms. J Eng Gas Turbines Power. 2020;142(12):121005.10.1115/GT2020-14247Suche in Google Scholar

[22] Hashempour Z, Agahi H, Mahmoodzadeh A. A novel method for fault diagnosis in rolling bearings based on bispectrum signals and combined feature extraction algorithms. Signal Image Video Process. 2021;16(4):1043–51.10.1007/s11760-021-02053-7Suche in Google Scholar

[23] Wang D, Song W, Pedrycz W, Cai L. An integrated neural network with nonlinear output structure for interval-valued data. J Intell Fuzzy Syst. 2020;40(1):1–11.10.3233/JIFS-200500Suche in Google Scholar

[24] Hashempour Z, Agahi H, Mahmoodzadeh A. A novel method for fault diagnosis in rolling bearings based on bispectrum signals and combined feature extraction algorithms. Signal Image Video Process. 2022;16(4):1043–51.10.1007/s11760-021-02053-7Suche in Google Scholar

[25] Leon-Medina JX, Anaya M, Pozo F, Tibaduiza D. Nonlinear feature extraction through manifold learning in an electronic tongue classification task. Sensors. 2020;20(17):4834.10.3390/s20174834Suche in Google Scholar PubMed PubMed Central

[26] Stepanov OA, Vasiliev VA, Basin MV, Tupysev VA, Litvinenko YA. Efficiency analysis of polynomial filtering algorithms in navigation data processing for a class of nonlinear discrete dynamical systems. IET Control Theory Appl. 2020;15:3.10.1049/cth2.12036Suche in Google Scholar

[27] Hashim HA. Guaranteed performance nonlinear observer for simultaneous localization and mapping. IEEE Control Syst Lett. 2021;5(1):91–6.10.1109/LCSYS.2020.3000266Suche in Google Scholar

[28] Dhiman G, Kumar V, Kaur A, Sharma A. Don: deep learning and optimization-based framework for detection of novel coronavirus disease using x-ray images. Interdiscip Sci Comput Life Sci. 2021;13:260–72.10.1007/s12539-021-00418-7Suche in Google Scholar PubMed PubMed Central

[29] Kaabar M, Kalvandi V, Eghbali N, Samei M, Siri Z, Martínez F. A generalized ML-Hyers-Ulam stability of quadratic fractional integral equation. Nonlinear Eng. 2021;10(1):414–27.10.1515/nleng-2021-0033Suche in Google Scholar
Received: 2021-12-08
Revised: 2022-07-04
Accepted: 2022-07-05
Published Online: 2022-11-02

© 2022 Li Liu, published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

  1. Research Articles
  2. Fractal approach to the fluidity of a cement mortar
  3. Novel results on conformable Bessel functions
  4. The role of relaxation and retardation phenomenon of Oldroyd-B fluid flow through Stehfest’s and Tzou’s algorithms
  5. Damage identification of wind turbine blades based on dynamic characteristics
  6. Improving nonlinear behavior and tensile and compressive strengths of sustainable lightweight concrete using waste glass powder, nanosilica, and recycled polypropylene fiber
  7. Two-point nonlocal nonlinear fractional boundary value problem with Caputo derivative: Analysis and numerical solution
  8. Construction of optical solitons of Radhakrishnan–Kundu–Lakshmanan equation in birefringent fibers
  9. Dynamics and simulations of discretized Caputo-conformable fractional-order Lotka–Volterra models
  10. Research on facial expression recognition based on an improved fusion algorithm
  11. N-dimensional quintic B-spline functions for solving n-dimensional partial differential equations
  12. Solution of two-dimensional fractional diffusion equation by a novel hybrid D(TQ) method
  13. Investigation of three-dimensional hybrid nanofluid flow affected by nonuniform MHD over exponential stretching/shrinking plate
  14. Solution for a rotational pendulum system by the Rach–Adomian–Meyers decomposition method
  15. Study on the technical parameters model of the functional components of cone crushers
  16. Using Krasnoselskii's theorem to investigate the Cauchy and neutral fractional q-integro-differential equation via numerical technique
  17. Smear character recognition method of side-end power meter based on PCA image enhancement
  18. Significance of adding titanium dioxide nanoparticles to an existing distilled water conveying aluminum oxide and zinc oxide nanoparticles: Scrutinization of chemical reactive ternary-hybrid nanofluid due to bioconvection on a convectively heated surface
  19. An analytical approach for Shehu transform on fractional coupled 1D, 2D and 3D Burgers’ equations
  20. Exploration of the dynamics of hyperbolic tangent fluid through a tapered asymmetric porous channel
  21. Bond behavior of recycled coarse aggregate concrete with rebar after freeze–thaw cycles: Finite element nonlinear analysis
  22. Edge detection using nonlinear structure tensor
  23. Synchronizing a synchronverter to an unbalanced power grid using sequence component decomposition
  24. Distinguishability criteria of conformable hybrid linear systems
  25. A new computational investigation to the new exact solutions of (3 + 1)-dimensional WKdV equations via two novel procedures arising in shallow water magnetohydrodynamics
  26. A passive verses active exposure of mathematical smoking model: A role for optimal and dynamical control
  27. A new analytical method to simulate the mutual impact of space-time memory indices embedded in (1 + 2)-physical models
  28. Exploration of peristaltic pumping of Casson fluid flow through a porous peripheral layer in a channel
  29. Investigation of optimized ELM using Invasive Weed-optimization and Cuckoo-Search optimization
  30. Analytical analysis for non-homogeneous two-layer functionally graded material
  31. Investigation of critical load of structures using modified energy method in nonlinear-geometry solid mechanics problems
  32. Thermal and multi-boiling analysis of a rectangular porous fin: A spectral approach
  33. The path planning of collision avoidance for an unmanned ship navigating in waterways based on an artificial neural network
  34. Shear bond and compressive strength of clay stabilised with lime/cement jet grouting and deep mixing: A case of Norvik, Nynäshamn
  35. Communication
  36. Results for the heat transfer of a fin with exponential-law temperature-dependent thermal conductivity and power-law temperature-dependent heat transfer coefficients
  37. Special Issue: Recent trends and emergence of technology in nonlinear engineering and its applications - Part I
  38. Research on fault detection and identification methods of nonlinear dynamic process based on ICA
  39. Multi-objective optimization design of steel structure building energy consumption simulation based on genetic algorithm
  40. Study on modal parameter identification of engineering structures based on nonlinear characteristics
  41. On-line monitoring of steel ball stamping by mechatronics cold heading equipment based on PVDF polymer sensing material
  42. Vibration signal acquisition and computer simulation detection of mechanical equipment failure
  43. Development of a CPU-GPU heterogeneous platform based on a nonlinear parallel algorithm
  44. A GA-BP neural network for nonlinear time-series forecasting and its application in cigarette sales forecast
  45. Analysis of radiation effects of semiconductor devices based on numerical simulation Fermi–Dirac
  46. Design of motion-assisted training control system based on nonlinear mechanics
  47. Nonlinear discrete system model of tobacco supply chain information
  48. Performance degradation detection method of aeroengine fuel metering device
  49. Research on contour feature extraction method of multiple sports images based on nonlinear mechanics
  50. Design and implementation of Internet-of-Things software monitoring and early warning system based on nonlinear technology
  51. Application of nonlinear adaptive technology in GPS positioning trajectory of ship navigation
  52. Real-time control of laboratory information system based on nonlinear programming
  53. Software engineering defect detection and classification system based on artificial intelligence
  54. Vibration signal collection and analysis of mechanical equipment failure based on computer simulation detection
  55. Fractal analysis of retinal vasculature in relation with retinal diseases – an machine learning approach
  56. Application of programmable logic control in the nonlinear machine automation control using numerical control technology
  57. Application of nonlinear recursion equation in network security risk detection
  58. Study on mechanical maintenance method of ballasted track of high-speed railway based on nonlinear discrete element theory
  59. Optimal control and nonlinear numerical simulation analysis of tunnel rock deformation parameters
  60. Nonlinear reliability of urban rail transit network connectivity based on computer aided design and topology
  61. Optimization of target acquisition and sorting for object-finding multi-manipulator based on open MV vision
  62. Nonlinear numerical simulation of dynamic response of pile site and pile foundation under earthquake
  63. Research on stability of hydraulic system based on nonlinear PID control
  64. Design and simulation of vehicle vibration test based on virtual reality technology
  65. Nonlinear parameter optimization method for high-resolution monitoring of marine environment
  66. Mobile app for COVID-19 patient education – Development process using the analysis, design, development, implementation, and evaluation models
  67. Internet of Things-based smart vehicles design of bio-inspired algorithms using artificial intelligence charging system
  68. Construction vibration risk assessment of engineering projects based on nonlinear feature algorithm
  69. Application of third-order nonlinear optical materials in complex crystalline chemical reactions of borates
  70. Evaluation of LoRa nodes for long-range communication
  71. Secret information security system in computer network based on Bayesian classification and nonlinear algorithm
  72. Experimental and simulation research on the difference in motion technology levels based on nonlinear characteristics
  73. Research on computer 3D image encryption processing based on the nonlinear algorithm
  74. Outage probability for a multiuser NOMA-based network using energy harvesting relays
https://doi.org/10.1515/nleng-2022-0221
Schlagwörter für diesen Artikel
nonlinear; engineering project; construction vibration risk
Creative Commons
BY 4.0

Artikel in diesem Heft

  1. Research Articles
  2. Fractal approach to the fluidity of a cement mortar
  3. Novel results on conformable Bessel functions
  4. The role of relaxation and retardation phenomenon of Oldroyd-B fluid flow through Stehfest’s and Tzou’s algorithms
  5. Damage identification of wind turbine blades based on dynamic characteristics
  6. Improving nonlinear behavior and tensile and compressive strengths of sustainable lightweight concrete using waste glass powder, nanosilica, and recycled polypropylene fiber
  7. Two-point nonlocal nonlinear fractional boundary value problem with Caputo derivative: Analysis and numerical solution
  8. Construction of optical solitons of Radhakrishnan–Kundu–Lakshmanan equation in birefringent fibers
  9. Dynamics and simulations of discretized Caputo-conformable fractional-order Lotka–Volterra models
  10. Research on facial expression recognition based on an improved fusion algorithm
  11. N-dimensional quintic B-spline functions for solving n-dimensional partial differential equations
  12. Solution of two-dimensional fractional diffusion equation by a novel hybrid D(TQ) method
  13. Investigation of three-dimensional hybrid nanofluid flow affected by nonuniform MHD over exponential stretching/shrinking plate
  14. Solution for a rotational pendulum system by the Rach–Adomian–Meyers decomposition method
  15. Study on the technical parameters model of the functional components of cone crushers
  16. Using Krasnoselskii's theorem to investigate the Cauchy and neutral fractional q-integro-differential equation via numerical technique
  17. Smear character recognition method of side-end power meter based on PCA image enhancement
  18. Significance of adding titanium dioxide nanoparticles to an existing distilled water conveying aluminum oxide and zinc oxide nanoparticles: Scrutinization of chemical reactive ternary-hybrid nanofluid due to bioconvection on a convectively heated surface
  19. An analytical approach for Shehu transform on fractional coupled 1D, 2D and 3D Burgers’ equations
  20. Exploration of the dynamics of hyperbolic tangent fluid through a tapered asymmetric porous channel
  21. Bond behavior of recycled coarse aggregate concrete with rebar after freeze–thaw cycles: Finite element nonlinear analysis
  22. Edge detection using nonlinear structure tensor
  23. Synchronizing a synchronverter to an unbalanced power grid using sequence component decomposition
  24. Distinguishability criteria of conformable hybrid linear systems
  25. A new computational investigation to the new exact solutions of (3 + 1)-dimensional WKdV equations via two novel procedures arising in shallow water magnetohydrodynamics
  26. A passive verses active exposure of mathematical smoking model: A role for optimal and dynamical control
  27. A new analytical method to simulate the mutual impact of space-time memory indices embedded in (1 + 2)-physical models
  28. Exploration of peristaltic pumping of Casson fluid flow through a porous peripheral layer in a channel
  29. Investigation of optimized ELM using Invasive Weed-optimization and Cuckoo-Search optimization
  30. Analytical analysis for non-homogeneous two-layer functionally graded material
  31. Investigation of critical load of structures using modified energy method in nonlinear-geometry solid mechanics problems
  32. Thermal and multi-boiling analysis of a rectangular porous fin: A spectral approach
  33. The path planning of collision avoidance for an unmanned ship navigating in waterways based on an artificial neural network
  34. Shear bond and compressive strength of clay stabilised with lime/cement jet grouting and deep mixing: A case of Norvik, Nynäshamn
  35. Communication
  36. Results for the heat transfer of a fin with exponential-law temperature-dependent thermal conductivity and power-law temperature-dependent heat transfer coefficients
  37. Special Issue: Recent trends and emergence of technology in nonlinear engineering and its applications - Part I
  38. Research on fault detection and identification methods of nonlinear dynamic process based on ICA
  39. Multi-objective optimization design of steel structure building energy consumption simulation based on genetic algorithm
  40. Study on modal parameter identification of engineering structures based on nonlinear characteristics
  41. On-line monitoring of steel ball stamping by mechatronics cold heading equipment based on PVDF polymer sensing material
  42. Vibration signal acquisition and computer simulation detection of mechanical equipment failure
  43. Development of a CPU-GPU heterogeneous platform based on a nonlinear parallel algorithm
  44. A GA-BP neural network for nonlinear time-series forecasting and its application in cigarette sales forecast
  45. Analysis of radiation effects of semiconductor devices based on numerical simulation Fermi–Dirac
  46. Design of motion-assisted training control system based on nonlinear mechanics
  47. Nonlinear discrete system model of tobacco supply chain information
  48. Performance degradation detection method of aeroengine fuel metering device
  49. Research on contour feature extraction method of multiple sports images based on nonlinear mechanics
  50. Design and implementation of Internet-of-Things software monitoring and early warning system based on nonlinear technology
  51. Application of nonlinear adaptive technology in GPS positioning trajectory of ship navigation
  52. Real-time control of laboratory information system based on nonlinear programming
  53. Software engineering defect detection and classification system based on artificial intelligence
  54. Vibration signal collection and analysis of mechanical equipment failure based on computer simulation detection
  55. Fractal analysis of retinal vasculature in relation with retinal diseases – an machine learning approach
  56. Application of programmable logic control in the nonlinear machine automation control using numerical control technology
  57. Application of nonlinear recursion equation in network security risk detection
  58. Study on mechanical maintenance method of ballasted track of high-speed railway based on nonlinear discrete element theory
  59. Optimal control and nonlinear numerical simulation analysis of tunnel rock deformation parameters
  60. Nonlinear reliability of urban rail transit network connectivity based on computer aided design and topology
  61. Optimization of target acquisition and sorting for object-finding multi-manipulator based on open MV vision
  62. Nonlinear numerical simulation of dynamic response of pile site and pile foundation under earthquake
  63. Research on stability of hydraulic system based on nonlinear PID control
  64. Design and simulation of vehicle vibration test based on virtual reality technology
  65. Nonlinear parameter optimization method for high-resolution monitoring of marine environment
  66. Mobile app for COVID-19 patient education – Development process using the analysis, design, development, implementation, and evaluation models
  67. Internet of Things-based smart vehicles design of bio-inspired algorithms using artificial intelligence charging system
  68. Construction vibration risk assessment of engineering projects based on nonlinear feature algorithm
  69. Application of third-order nonlinear optical materials in complex crystalline chemical reactions of borates
  70. Evaluation of LoRa nodes for long-range communication
  71. Secret information security system in computer network based on Bayesian classification and nonlinear algorithm
  72. Experimental and simulation research on the difference in motion technology levels based on nonlinear characteristics
  73. Research on computer 3D image encryption processing based on the nonlinear algorithm
  74. Outage probability for a multiuser NOMA-based network using energy harvesting relays
Jetzt anmelden und 20% sparen
Institutioneller Zugang
Wie funktioniert Authentifizierung?
Haben Sie eine Idee, wie wir unsere Website verbessern können?
Bitte schreiben Sie uns.
© 2025 De Gruyter Brill
Heruntergeladen am 30.12.2025 von https://www.degruyterbrill.com/document/doi/10.1515/nleng-2022-0221/html
Button zum nach oben scrollen