Significance of adding titanium dioxide nanoparticles to an existing distilled water conveying aluminum oxide and zinc oxide nanoparticles: Scrutinization of chemical reactive ternary-hybrid nanofluid due to bioconvection on a convectively heated surface
-
Gadamsetty Revathi
, Venkata Subrahmanyam Sajja
Abstract
With the emphasis on the properties of titanium dioxide nanoparticles and numerous applications of chemical reactive distilled water due to bioconvection in the industries, nothing is known about the significance of adding titanium dioxide nanoparticles to an existing distilled water conveying aluminum oxide and zinc oxide nanoparticles when viscous dissipation, heat source, and higher buoyancy forces and thermal radiation are substantial. The governing partial differential equations that model the motion of both transport phenomena mentioned earlier were transformed into ordinary differential equations using appropriate similarity transmutations and solved with bvp4c (MATLAB built-in function). Multiple linear regression (i.e., a statistical tool used to explain outcomes related to engineering parameters of interest) was adopted for a deep scrutinization and exploration. The outcome of the analysis suggests that the thermal radiation parameter can be used to control the heat transferred via convection in the fluid flow. It is detected that the magnetic field parameter and volume fraction of nanoparticle parameters are useful to reduce the shear stress near the surface. The heat source ameliorates the fluid temperature, and the concentration of the fluid decreases with the rise in the chemical reaction parameter. Worthy to conclude that the Peclet and Schmidt number escalates the density number of motile microorganisms.
1 Background information
Titanium dioxide is one of the most fundamental elements in our daily lives. Titanium dioxide is one of the most studied crystalline oxides in the field of metal oxide surface science due to its capabilities as a photocatalyst with reasonably high efficiency for water breakdown et al. [1]. Titanium dioxide powders possess varieties of applications, owing to its capacity to impart whiteness and opacity to a variety of items, including paints, papers, and cosmetics. Titanium dioxide, for example, is approved as a food and pharmaceutical addition by Rowe et al. [2]. In the United States, titanium dioxide is considered an inert ingredient useful for oral capsules, cutaneous treatments, dental paste, nonparenteral medications, tablets, and suspensions by the Food and Drug Administration. The mechanistic toxicity investigations on titanium dioxide nanoparticles were discussed by Skocaj et al. [3]. The majority of the negative effects of titanium dioxide nanoparticles are caused by oxidative stress. Because the physicochemical qualities of particles are proportional to their size, the majority of materials including titanium dioxide nanoparticles are chemically more reactive at the nanometer level. Fujishima et al. [4] explicitly presented more information on the outstanding photocatalyst material of titanium dioxide for environmental purification. Although, according to the study by Kang et al. [5], high overpotential, slow migration, and quick recombination of photogenerated electron/hole pairs are important characteristics that limit the applicability of titanium dioxide. Ziental et al. [6] introduced titanium dioxide nanoparticles as photosensitizing agents for the treatment of malignant tumors and the photodynamic inactivation of antibiotic-resistant bacteria. Titanium dioxide nanoparticles, in particular, can be used as photosensitizers on their own or in composites and combinations with other chemicals or biomolecules. In a comparative analysis of water conveying copper oxide (CuO) nanoparticles, gold (Ag) nanoparticles, alumina (Al2O3) nanoparticles, copper (Cu) nanoparticles, and titania TiO2 nanoparticles by Animasaun et al. [7], the thermal conductivity of titanium dioxide nanoparticles is 8.9538 W m K−1, while its density is 4,250 kg m−3 and heat capacity is around 686.2 J kg−1 K.
Nanofluids are generally employed as coolants in heat transfer equipment such as heat exchangers, electronic cooling systems, and radiators due to their increased thermal characteristics. In recent years, there has been a focus on heat transmission over a flat plate. Nanofluids have been introduced as a new interesting kind of heat transfer fluids to replace regular fluids in industrial processes. Nanofluids may diminish erosion and corrosion significantly owing to their small size. Nanofluids have a broad range of applications, including refrigeration, heat exchangers, and cooling electronic devices. The use of nanoparticles is becoming more fascinating as the demand for high thermal performance in industries grows Khan et al. [8]. The dynamics of non-Newtonian Eyring Powell liquid substance conveying not only nanoparticles but also gyrotactic microorganisms through the porous medium on Riga surface was examined by Khan et al. [9]. Consequently, Algehyne et al. [10] explained Darcy–Forchheimer of radiative alumina–water nanofluid, and Wakif et al. [11,12] explored the dynamics of 40% water conveying alumina nanoparticles and the dynamics of 60% ethylene glycol conveying alumina nanoparticles, mixed convection flow of non-Newtonian Walters-b fluid conveying tiny particles experiencing haphazard motion, and thermo-migration when Lorentz force and movement of gyrotactic microorganisms is significant. In another report, in the case of metallic and metallic oxide nanomaterials, Nayak et al. [13] explored nanofluid flows over an isothermal thin needle due to mixed convection.
A hybrid nanofluid is a revised kind of a mono nanofluid in which more than one nanoparticle is present. As a result, hybrid fluids outperform mono fluids in terms of heat transfer. These are used in various applications, including military equipment and solar collectors. Mustafa et al. [14] investigated heat transfer along the vertical rough surface of the sinusoidal wall beneath the nanofluid made up of interactions between alumina and silver nanoparticles subjected to an external magnetic field in the presence of internal heat generation. Because of the increased concentration of silver and alumina nanoparticles, it was discovered that skin friction increases while the Nusselt number decreases. The dynamics of non-Newtonian micropolar fluid conveying magnesium oxide and molybdenum disulfide nanoparticles experiencing Cattaneo–Christov heat flux was studied by Reddy and Shehzad [15]. The motion of couple stress hybrid nanofluids experiencing electroosmosis-induced alterations and peristaltic pumping through microchannel was examined by Tripathi et al. [16]. In another related study, the non-Newtonian Carreau hybrid nanofluid experiencing convective heat and non-Newtonian micropolar fluid conveying ferromagnetic and titanium alloy nanoparticles was examined by Kumar et al. [17] and Shehzad et al. [18] respectively.
Ternary hybrid nanofluid (THNF) is best described as a blend of three nanomaterials and a base fluid; see the studies by Elnaqeeb et al. [19], Animasaun et al. [20], and Saleem et al. [21]. In other words, THNF is described as the colloidal mixture of three different types of nanoparticles with a single base fluid. It exhibits greater thermal conductivity compared to binary hybrid nanofluid (one base fluid + two nanomaterials), as the name suggests. Sahoo and Kumar [22] experimentally prepared a THNF (Al2O3 + CuO + TiO2/H2O) and discussed its viscosity with different nanoparticle volume fractions. A linear relationship was discovered between dynamic viscosity and nanoparticle volume fraction. Boroomandpour et al. [23] prepared a water-ethylene glycol-based THNF and concluded that thermal conductivity and nanoparticle volume fraction have a linear relationship. In a recent study by Cao et al. [24] on thermo-migration, the haphazard motion of platelet alumina nanoparticles, spherical carbon nanotubes, and cylindrical graphene in the dynamics of water induced by free convection, forced convection, and mixed convection, it was discovered that rising thermo-migration of spherical carbon nanotubes, cylindrical graphene, and platelet alumina nanoparticles cause the heat and mass transfer across the ternary-hybrid nanofluid to diminish. Several researchers like Yang et al. [25], Ahmed et al. [26], Sundar et al. [27], and Manjunatha et al. [28] have recently contributed to the experimental and theoretical analyses of various ternary-hybrid nanofluid flows. Within the scope of rheology, distilled water conveying aluminum oxide, zinc oxide, and titanium dioxide possess a thermal conductivity, that is, 69% more than the thermal conductivity of distilled water.
Based on the aforementioned facts, it is important to discuss the impact of quadratic thermal radiation on the slip flow of THNF by an elongating sheet with higher order chemical reaction after carefully considering the preceding writing. The results are provided for two cases, ternary and binary hybrid nanofluids. Multiple linear regression is used to determine the effects of various parameters on surface drag force and heat transfer rate. Furthermore, a high level of agreement is observed in the validation between the current results and previous outcomes. The purpose of this study was to find answers to the following connected research questions:
At different levels of Lorentz force, volume fraction, and mixed convection, how does the velocity of the dynamics of chemical reactive distilled water conveying aluminum oxide and zinc oxide nanoparticles differ from the case of water conveying aluminum oxide, zinc oxide, and titanium dioxide nanoparticles?
At various levels of thermal radiation, volume fraction of the overall ternary-hybrid nanofluid, viscous dissipation, and heat source, to what extent does the addition of titanium dioxide nanoparticles to the existing chemical reactive distilled water conveying aluminum oxide and zinc oxide nanoparticles affects the distribution of temperature across the domain?
What is the difference in the concentration of chemical reactive distilled water conveying aluminum oxide, zinc oxide nanoparticles and chemical reactive distilled water conveying aluminum oxide, zinc oxide, and titanium dioxide nanoparticles?
2 Research methodology
This study investigates the laminar and two-dimensional chemically reactive and bioconvective flow of the THNF through a stretching sheet with quadratic thermal radiation and heat source.
2.1 Mathematical formulation
It is assumed that the stretching sheet is positioned along x-axis and y-axis is perpendicular to it. The sheet is assumed to be stretching at a speed of u w (x) = bx. The strength of the magnetic field B 0 was applied perpendicular to the flow; see Figure 1. Ambient temperature and concentrations are denoted by T ∞ and C ∞, respectively, and the surface temperature and concentrations are denoted by T w and C w , respectively. Values of the thermophysical properties of base fluid and nanomaterials are presented in Table 1. Furthermore, it is assumed that the induced magnetic field is insignificant. By using these assumptions, the governing equations for this study are as follows (Al-Kouz et al. [29], Al-Hossainy and Eid [30], Wakif et al. [31], and Ali et al. [32]):
with the conditions

Graphical illustration of the transport phenomenon.
The thermo-physical properties of distilled water conveying aluminum oxide, zinc oxide, and titanium dioxide
| S.No. | DW (f) | Al2O3 (s1) | ZnO (s2) | TiO2 (s3) | |
|---|---|---|---|---|---|
| 1 | ρ (kg m−3) | 998.203 | 3,970 | 5,600 | 4,250 |
| 2 | C p (J kg K−1) | 4,182 | 765 | 495.2 | 686.2 |
| 3 | k (W m K−1) | 0.613 | 40 | 13 | 8.953 |
Source: Ahmed et al. [33].
Following Manjunatha et al. [28], the heat capacity, viscosity, density, and thermal conductivity of the ternary-hybrid nanofluid (distilled water conveying aluminum oxide, zinc oxide, and titanium dioxide nanoparticles) are expressed as follows:
In agreement with the theory by Nasr et al. [34], the radiative heat flux q R can be defined as follows:
With the aid of Taylor’s series expansion about T ∞, T 4 can be expressed as follows:
Considering truncating the series after the second-order term and substituting it in Eq. (7), we can obtain the quadratic thermal radiation term. Then
Substituting Eq. (8) into Eq. (7) to obtain
With this, Eq. (3) becomes,
Similarity transformations (Ali et al. [32] and Pal et al. [35]) are expressed as follows:
satisfies continuity Eq. (1), and Eq. (2), Eqs. (4)–(5), and Eq. (9) are transformed as follows:
and the conditions in Eq. (6) are changed as follows:
where
and
The mass transfer rate of motile microorganisms, mass transfer rate of species, heat transfer rate (Nn x , Sh x , and Nu x ), and surface drag force C fx are indicated as follows:
where
By using Eq. (10), we can rewrite Eq. (16) as follows:
2.2 Numerical procedure and validation
In-built function MATLAB, bvp4c, is utilized to solve the transmuted Eqs. (11)–(14) with the conditions (15). It is simple to use because it is a built-in function. It is imperative first to make the following assumptions before we can write code (Waini et al. [36]):
Then, using Eqs. (11)–(14) and conditions (15), we can construct a subsequent system of first-order ordinary differential equations:
with the conditions
Next stage is to run the aforementioned system after conversion to MATLAB code and obtain the desired results in graphs. Table 2 presents the verification of our results with the previous outcomes under special circumstances, which revealed a good concordance.
Verification of our results with previously published results in exceptional circumstances, such as ϕ 1 = ϕ 2 = ϕ 3 = 0
| Pr | −θ′(0) | |
|---|---|---|
| Manjunatha et al. [28] | Current outcomes | |
| 2 | 0.9113 | 0.911320 |
| 6.13 | 1.7597 | 1.759701 |
| 7 | 1.8954 | 1.895449 |
| 20 | 1.3539 | 1.353909 |
3 Analysis of results and discussion
The results of this study are shown for two cases: THNF (DW + Al2O3 + ZnO + TiO2) and binary hybrid nanofluid (DW + Al2O3 + ZnO). The motion of the fluid is affected by the applied magnetic field. The particles of the liquid structure a chain turn toward the course of the applied attractive field. During this time, the particles are collided with one another, forming a barrier to the fluid flow. Fluid velocity decreases due to the increased viscosity, which is illustrated by Figure 2. It is clear from Figure 3 that the fluid velocity enriches with the increase in ϕ 1. Note that the velocity profiles are looking high in the case of THNF flow compared to binary hybrid nanofluid flow. An increase in the mixed convective parameter minimizes the viscous forces. As a result, the fluid velocity increases, as shown in Figure 4. An increase in the Biot number increases the convective heat transfer to the fluid flow. As a result, the fluid temperature increases (Figure 5). Thermal radiation can be transmitted without the use of an intermediate medium. Growing thermal radiation parameter as shown in Figure 6, on the other hand, quickly indicates a higher process in which energy is radiated in all directions by a heated surface and travels at the speed of light to its absorption location. The temperature of the fluid rises as a result of particle collisions, as shown in Figure 6. More collisions between fluid particles occur as the volume fraction of the nanoparticles improves. Consequently, the fluid temperature rises, as shown in Figure 7. More kinetic energy is converted as internal energy in the fluid flow as the Eckert number improves. As a result, the temperature increases as shown in Figure 8. Figure 9 shows how the heat source changes the temperature profile. When the heat source increases, the fluid absorbs more heat energy from the source, which causes the escalation in the fluid temperature. The temperature profiles in the case of THNF flow appear to be higher than in the case of binary hybrid nanofluid flow, as seen in these graphs. As shown in Figure 10, as the chemical reaction parameter goes up, the concentration usually goes down. This behavior could be explained by the increased entropy generation.

Increasing effects of M on f′(η).

Increasing effects of ϕ 1 on f′(η).

Increasing effects of δ on f′(η).
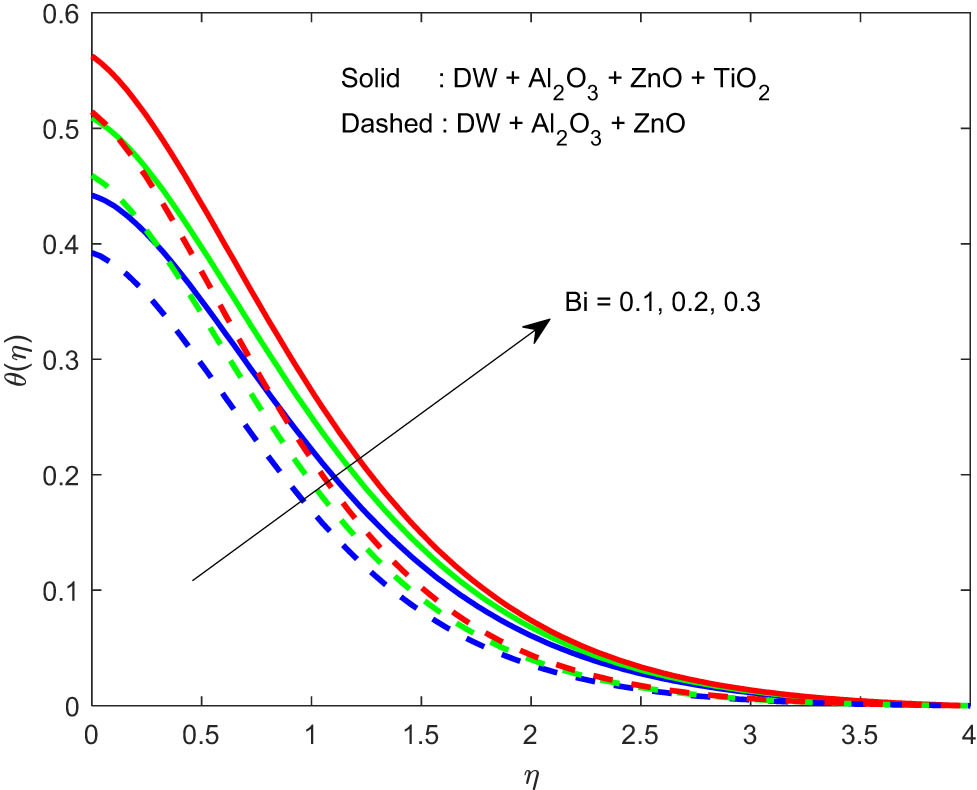
Increasing effects of Bi on θ(η).

Increasing effects of R a on θ(η).

Increasing effects of ϕ 1 on θ(η).
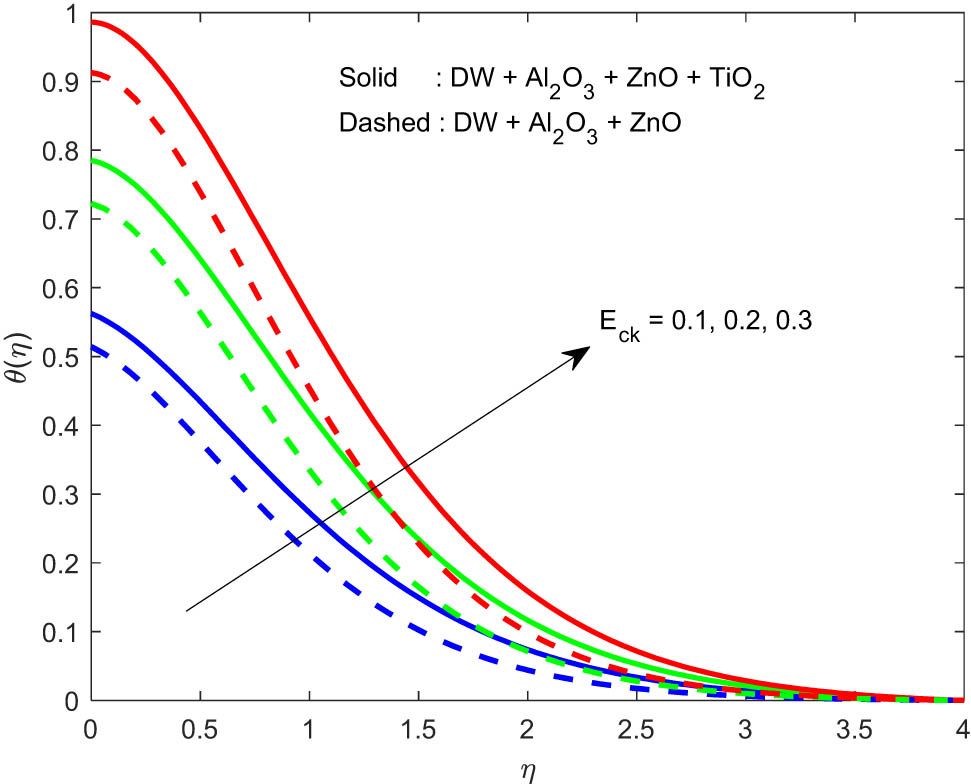
Increasing effects of E ck on θ(η).

Increasing effects of Q t on θ(η).

Increasing effects of k r on Φ(η).
The effect of Le on the concentration profile is shown in Figure 11. When Le increases, momentum diffusivity far exceeds mass diffusivity, implying that the fluid moves at a high velocity and the fluid concentration decreases. Figures 12 and 13 show that the concentration of motile microorganisms minifies with the rise in S c and P e .

Increasing effects of Le on Φ(η).

Increasing effects of S c on χ(η).

Increasing effects of P e on χ(η).
3.1 Multiple linear regression
Multiple linear regression is a statistical technique for estimating the correlation among at least two independent and one dependent variables. The formula for multiple linear regression is expressed as follows:
where y is the dependent variable, x i is the independent variable, a 0 – y – intercept, and a i – regression coefficient of x i for i = 1,2,…, n. While obtaining the values of a i ’s, if p value is less than 0.05, then the relation between y and x i is significant. In this work, we used the following models to know the relationship among the engineering parameters of concern including the heat transfer rate and the parameters including radiation.
With the aid of 21 sets of values for each equation, we obtain the following results:
It is noticed from Eq. (22) that M and ϕ 1 are having a negative impact on surface drag force. This means that surface drag force minimizes with the amelioration in M and ϕ 1. Eq. (23) exhibited that the radiation, heat source, and viscous dissipation parameters have a negative influence on the Nusselt number. This means that the heat transfer rate minimizes with the escalation in those parameters. From Eq. (24), it is clear that there is a positive relation among Sherwood number and k r , Le. It is clear from Eq. (25) that the escalation in Schmidt number and Peclet numbers enriches motile microorganisms’ mass transfer rate.
4 Conclusion
In this report, the dynamics of chemical reactive distilled water conveying aluminum oxide, zinc oxide, and titanium dioxide due to bioconvection on a convectively heated surface when there is a significant viscous dissipation, heat source, and higher buoyancy forces and thermal radiation had been investigated. The engineering parameters, including heat transfer rate, have been discussed using multilinear regression. Based on the analysis of the new observations, it is worthy to conclude that
the volume fraction of nanoparticles lessens the shear stress near the surface.
heat source parameter ameliorates the temperature of the fluid.
radiation and Eckert number have a negative impact on the Nusselt number.
the mass transfer rate is positively influenced by the larger Lewis number and chemical reaction parameter.
the Peclet number enriches the density number of motile microorganisms.
the concentration of motile microorganisms minifies with bigger Schmidt number.
magnetic field parameter is used to control the fluid velocity.
Nomenclature
- μ
-
dynamic viscosity of the fluid (kg m−1 s−1)
- ρ
-
density of the fluid (kg m−3)
- β T
-
volumetric coefficient of thermal expansion (K−1)
- β C
-
volumetric coefficient of diffusion expansion of species (m−3)
- β N
-
volumetric coefficient of diffusion expansion of microorganisms (m−3)
- g
-
acceleration of gravity (m s−2)
- υ
-
kinematic viscosity (m2 s−1)
- T
-
dimensional temperature of fluid (K)
- k
-
thermal conductivity (W m−1 K−1)
- f'
-
dimensionless velocity
- θ
-
dimensionless temperature of fluid
- C p
-
specific heat capacitance (J kg−1 K−1)
- u, v
-
velocity components in x, y directions (m s−1)
- η
-
similarity variable
- Pr
-
Prandtl number
- E ck
-
Eckert number
- θ w
-
temperature ratio parameter
- D n
-
microorganism diffusivity (m2 s−1)
- N ∞
-
difference parameter of microorganisms concentration (mol m−3)
- S c
-
Schmidt number
- Le
-
Lewis number
- n
-
order of chemical reaction
- Q 0
-
dimensional heat source parameter (W m−3 K−1)
- Re x
-
Local Reynold’s number
- Gr T
-
Grashoff number related to thermal
- Gr C
-
Grashoff number related toconcentration of species
- Gr N
-
Grashoff number related to concentration of microorganisms
- λ 1
-
nonlinear convection parameter related to temperature
- λ 2
-
Buoyancy ratio parameter related to concentration of species
- λ 3
-
Buoyancy ratio parameter related to concentration of microorganisms
- δ
-
mixed convection parameter
- M
-
magnetic field parameter
- σ*
-
Stefan–Boltzman constant (W m−2 K−4)
- k*
-
mean absorption constant (m−1)
- f
-
dimensionless Stream function
- χ
-
dimensionless concentration of microorganisms
- N
-
dimensional concentration of microorganisms
- W c
-
maximum speed of swimming cell (km h−1)
- k r
-
chemical reaction parameter (s−1)
- h
-
convective heat transfer Coefficient (W m−2 K−1)
- P e
-
Peclet number
- b*
-
Chemotaxis constant
- Bi
-
biot number subscripts
- f
-
fluid
- nf
-
nanofluid
- hnf
-
Binary hybrid nanofluid
- thnf
-
ternary hybrid nanofluid
Acknowledgment
Special thanks to the anonymous Reviewers for their valuable suggestions and comments.
-
Funding information: The authors state no funding involved.
-
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
-
Conflict of interest: The authors declare that there are no conflict of interests regarding the publication of this paper.
-
Data availability statement: The results of this study are available only within the paper to support the data.
References
[1] Xiong L-B, Li J-L, Yang B, Yu Y. Ti??+ in the Surface of Titanium Dioxide: Generation, Properties and Photocatalytic Application. Nanostruct Layers Catalytic Appl. 2012;2012:1–13. Article ID 831524. 10.1155/2012/831524.Search in Google Scholar
[2] Rowe RC, Sheskey PJ, Weller PJ. Handbook of pharmaceutical excipients. 4th ed. London: Pharmaceutical Press, London, United Kingdom, and the American Pharmaceutical Association; 2003.Search in Google Scholar
[3] Skocaj M, Filipic M, Petkovic J, Novak S. Titanium dioxide in our everyday life; is it safe? Radiol Oncol. 2011;45(4):227–47. 10.2478/v10019-011-0037-0.Search in Google Scholar
[4] Fujishima A, Rao TN, Tryk DA. Titanium dioxide photocatalysis. J Photochem Photobiol C Photochem Rev. 2000;1(1):1–21. 10.1016/s1389-5567(00)00002-2.Search in Google Scholar
[5] Kang X, Liu S, Dai Z, He Y, Song X, Tan Z. Titanium dioxide: from engineering to applications. Catalysts. 2019;9(2):191. 10.3390/catal9020191.Search in Google Scholar
[6] Ziental D, Czarczynska-Goslinska B, Mlynarczyk DT, Glowacka-Sobotta A, Stanisz B, Goslinski T, et al. Titanium dioxide nanoparticles: prospects and applications in medicine. Nanomaterials. 2020;10(2):387. 10.3390/nano10020387.Search in Google Scholar PubMed PubMed Central
[7] Animasaun IL, Shah NA, Wakif A, Mahanthesh B, Sivaraj R, Koriko OK. Ratio of momentum diffusivity to thermal diffusivity: introduction, meta-analysis, and scrutinization. New York: Chapman and Hall/CRC; 2022. ISBN-13: 978-1032108520, ISBN-10: 1032108525, ISBN9781003217374.10.1201/9781003217374Search in Google Scholar
[8] Khan SU, Al-Khaled K, Hussain SM, Ghaffari A, Khan MI, Ahmed MW. Implication of arrhenius activation energy and temperature-dependent viscosity on non-newtonian nanomaterial bio-convective flow with partial slip. Arab J Sci Eng. 2021;47:1–2. 10.1007/s13369-021-06274-3.Search in Google Scholar
[9] Khan MI, Shah F, Khan SU, Ghaffari A, Chu YM. Heat and mass transfer analysis for bioconvective flow of Eyring Powell nanofluid over a Riga surface with nonlinear thermal features. Numer Methods Partial Differ Equ. 2020;38(4):777–93. 10.1002/num.22696.Search in Google Scholar
[10] Algehyne EA, Wakif A, Rasool G, Saeed A, Ghouli Z. Significance of Darcy-Forchheimer and Lorentz forces on radiative alumina-water nanofluid flows over a slippery curved geometry under multiple convective constraints: a renovated Buongiorno’s model with validated thermophysical correlations. Waves Random Complex Media. 2022;1–30. 10.1080/17455030.2022.2074570.Search in Google Scholar
[11] Wakif A, Zaydan M, Alshomrani AS, Muhammad T, Sehaqui R. New insights into the dynamics of alumina-(60% ethylene glycol + 40% water) over an isothermal stretching sheet using a renovated Buongiorno’s approach: A numerical GDQLLM analysis. Int Commun Heat Mass Transf. 2022;133:105937. 10.1016/j.icheatmasstransfer.2022.105937.Search in Google Scholar
[12] Wakif A, Animasaun IL, Khan U, Shah NA, Thumma T. Dynamics of radiative-reactive Walters-b fluid due to mixed convection conveying gyrotactic microorganisms, tiny particles experience haphazard motion, thermo-migration, and Lorentz force. Phys Scr. 2021;96(12):125239. 10.1088/1402-4896/ac2b4b.Search in Google Scholar
[13] Nayak MK, Wakif A, Animasaun IL, Alaoui M. Numerical differential quadrature examination of steady mixed convection nanofluid flows over an isothermal thin needle conveying metallic and metallic oxide nanomaterials: a comparative investigation. Arab J Sci Eng. 2020;45(7):5331–46. 10.1007/s13369-020-04420-x.Search in Google Scholar
[14] Mustafa I, Javed T, Ghaffari A. Hydromagnetic natural convection flow of water-based nanofluid along a vertical wavy surface with heat generation. J Mol Liq. 2017;229:246–54. 10.1016/j.molliq.2016.12.079.Search in Google Scholar
[15] Reddy MG, Shehzad SA. Molybdenum disulfide and magnesium oxide nanoparticle performance on micropolar Cattaneo-Christov heat flux model. Appl Math Mech. 2021;42(4):541–52. 10.1007/s10483-021-2713-9.Search in Google Scholar
[16] Tripathi D, Prakash J, Gnaneswara Reddy M, Kumar R. Numerical study of electroosmosis-induced alterations in peristaltic pumping of couple stress hybrid nanofluids through microchannel. Indian J Phys. 2021;95(11):2411–21. 10.1007/s12648-020-01906-0.Search in Google Scholar
[17] Kumar KG, Reddy MG, Aldalbahi A, Rahimi-Gorji M, Rahaman M. Application of different hybrid nanofluids in convective heat transport of Carreau fluid. Chaos Solitons Fractals. 2020;141:110350. 10.1016/j.chaos.2020.110350.Search in Google Scholar
[18] Shehzad SA, Reddy MG, VIjayakumari P, Tlili I. Behavior of ferromagnetic Fe2SO4 and titanium alloy Ti6Al4v nanoparticles in micropolar fluid flow. Int Commun Heat Mass Transf. 2020;117:104769. 10.1016/j.icheatmasstransfer.2020.104769.Search in Google Scholar
[19] Elnaqeeb T, Animasaun IL, Shah NA. Ternary-hybrid nanofluids: significance of suction and dual-stretching on three-dimensional flow of water conveying nanoparticles with various shapes and densities. Z für Naturforschung A. 2021;76(3):231–43. 10.1515/zna-2020-0317.Search in Google Scholar
[20] Animasaun IL, Yook SJ, Muhammad T, Mathew A. Dynamics of ternary-hybrid nanofluid subject to magnetic flux density and heat source or sink on a convectively heated surface. Surf Interfaces. 2022;28:101654. 10.1016/j.surfin.2021.101654.Search in Google Scholar
[21] Saleem S, Animasaun IL, Yook SJ, Al-Mdallal QM, Shah NA, Faisal M. Insight into the motion of water conveying three kinds of nanoparticles shapes on a horizontal surface: Significance of thermo-migration and Brownian motion. Surf Interfaces. 2022;30:101854. 10.1016/j.surfin.2022.101854.Search in Google Scholar
[22] Sahoo RR, Kumar V. Development of a new correlation to determine the viscosity of ternary hybrid nanofluid. Int Commun Heat Mass Transf. 2020;111:104451. 10.1016/j.icheatmasstransfer.2019.104451.Search in Google Scholar
[23] Boroomandpour A, Toghraie D, Hashemian M. A comprehensive experimental investigation of thermal conductivity of a ternary hybrid nanofluid containing MWCNTs-titania-zinc oxide/water-ethylene glycol (80: 20) as well as binary and mono nanofluids. Synth Met. 2020;268:116501. 10.1016/j.synthmet.2020.116501.Search in Google Scholar
[24] Cao W, Animasaun IL, Yook SJ, Oladipupo VA, Ji X. Simulation of the dynamics of colloidal mixture of water with various nanoparticles at different levels of partial slip: Ternary-hybrid nanofluid. Int Commun Heat Mass Transf. 2022;135:106069. 10.1016/j.icheatmasstransfer.2022.106069.Search in Google Scholar
[25] Yang X, Boroomandpour A, Wen S, Toghraie D, Soltani F. Applying Artificial Neural Networks (ANNs) for prediction of the thermal characteristics of water/ethylene glycol-based mono, binary and ternary nanofluids containing MWCNTs, titania, and zinc oxide. Powder Technol. 2021;388:418–24. 10.1016/j.powtec.2021.04.093.Search in Google Scholar
[26] Ahmed W, Kazi SN, Chowdhury ZZ, Johan MR, Mehmood S, Soudagar ME, et al. Heat transfer growth of sonochemically synthesized novel mixed metal oxide ZnO + Al2O3 + TiO2/DW based ternary hybrid nanofluids in a square flow conduit. Renew Sustain Energy Rev. 2021;145:111025. 10.1016/j.rser.2021.111025.Search in Google Scholar
[27] Sundar LS, Chandra Mouli KV, Said Z, Sousa AC. Heat transfer and second law analysis of ethylene glycol-based ternary hybrid nanofluid under laminar flow. J Therm Sci Eng Appl. 2021;13(5):051021. 10.1115/1.4050228.Search in Google Scholar
[28] Manjunatha S, Puneeth V, Gireesha BJ, Chamkha A. Theoretical study of convective heat transfer in ternary nanofluid flowing past a stretching sheet. J Appl Computational Mech. 2021;1–8. 10.22055/jacm.2021.37698.3067.Search in Google Scholar
[29] Al-Kouz W, Mahanthesh B, Alqarni MS, Thriveni K. A study of quadratic thermal radiation and quadratic convection on viscoelastic material flow with two different heat source modulations. Int Commun Heat Mass Transf. 2021;126:105364. 10.1016/j.icheatmasstransfer.2021.105364.Search in Google Scholar
[30] Al-Hossainy AF, Eid MR. Combined experimental thin films, TDDFT-DFT theoretical method, and spin effect on [PEG-H2O/ZrO2 + MgO] h hybrid nanofluid flow with higher chemical rate. Surf Interfaces. 2021;23:100971. 10.1016/j.surfin.2021.100971.Search in Google Scholar
[31] Wakif A. A novel numerical procedure for simulating steady MHD convective flows of radiative Casson fluids over a horizontal stretching sheet with irregular geometry under the combined influence of temperature-dependent viscosity and thermal conductivity. Math Probl Eng. 2020;2020:2020. 10.1155/2020/1675350.Search in Google Scholar
[32] Ali L, Liu X, Ali B, Mujeed S, Abdal S. Finite element simulation of multi-slip effects on unsteady MHD bioconvective micropolar nanofluid flow over a sheet with solutal and thermal convective boundary conditions. Coatings. 2019;9(12):842. 10.3390/coatings9120842.Search in Google Scholar
[33] Ahmed W, Kazi SN, Chowdhury ZZ, Johan MR, Soudagar ME, Mujtaba MA, et al. Ultrasonic assisted new Al2O3@ TiO2-ZnO/DW ternary composites nanofluids for enhanced energy transportation in a closed horizontal circular flow passage. Int Commun Heat Mass Transf. 2021;120:105018.10.1016/j.icheatmasstransfer.2020.105018Search in Google Scholar
[34] Nasr ME, Gnaneswara Reddy M, Abbas W, Megahed AM, Awwad E, Khalil KM. Analysis of non-linear radiation and activation energy analysis on hydromagnetic Reiner–Philippoff fluid flow with Cattaneo–Christov double diffusions. Mathematics. 2022;10(9):1534. 10.3390/math10091534.Search in Google Scholar
[35] Pal D, Mondal S, Mondal H. Entropy generation on MHD Jeffrey nanofluid over a stretching sheet with nonlinear thermal radiation using spectral quasilinearisation method. Int J Ambient Energy. 2021;42(15):1712–26.10.1080/01430750.2019.1614984Search in Google Scholar
[36] Waini I, Ishak A, Pop I. Hybrid nanofluid flow past a permeable moving thin needle. Mathematics. 2020;8(4):612. 10.3390/math8040612.Search in Google Scholar
© 2022 Gadamsetty Revathi et al., published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Research Articles
- Fractal approach to the fluidity of a cement mortar
- Novel results on conformable Bessel functions
- The role of relaxation and retardation phenomenon of Oldroyd-B fluid flow through Stehfest’s and Tzou’s algorithms
- Damage identification of wind turbine blades based on dynamic characteristics
- Improving nonlinear behavior and tensile and compressive strengths of sustainable lightweight concrete using waste glass powder, nanosilica, and recycled polypropylene fiber
- Two-point nonlocal nonlinear fractional boundary value problem with Caputo derivative: Analysis and numerical solution
- Construction of optical solitons of Radhakrishnan–Kundu–Lakshmanan equation in birefringent fibers
- Dynamics and simulations of discretized Caputo-conformable fractional-order Lotka–Volterra models
- Research on facial expression recognition based on an improved fusion algorithm
- N-dimensional quintic B-spline functions for solving n-dimensional partial differential equations
- Solution of two-dimensional fractional diffusion equation by a novel hybrid D(TQ) method
- Investigation of three-dimensional hybrid nanofluid flow affected by nonuniform MHD over exponential stretching/shrinking plate
- Solution for a rotational pendulum system by the Rach–Adomian–Meyers decomposition method
- Study on the technical parameters model of the functional components of cone crushers
- Using Krasnoselskii's theorem to investigate the Cauchy and neutral fractional q-integro-differential equation via numerical technique
- Smear character recognition method of side-end power meter based on PCA image enhancement
- Significance of adding titanium dioxide nanoparticles to an existing distilled water conveying aluminum oxide and zinc oxide nanoparticles: Scrutinization of chemical reactive ternary-hybrid nanofluid due to bioconvection on a convectively heated surface
- An analytical approach for Shehu transform on fractional coupled 1D, 2D and 3D Burgers’ equations
- Exploration of the dynamics of hyperbolic tangent fluid through a tapered asymmetric porous channel
- Bond behavior of recycled coarse aggregate concrete with rebar after freeze–thaw cycles: Finite element nonlinear analysis
- Edge detection using nonlinear structure tensor
- Synchronizing a synchronverter to an unbalanced power grid using sequence component decomposition
- Distinguishability criteria of conformable hybrid linear systems
- A new computational investigation to the new exact solutions of (3 + 1)-dimensional WKdV equations via two novel procedures arising in shallow water magnetohydrodynamics
- A passive verses active exposure of mathematical smoking model: A role for optimal and dynamical control
- A new analytical method to simulate the mutual impact of space-time memory indices embedded in (1 + 2)-physical models
- Exploration of peristaltic pumping of Casson fluid flow through a porous peripheral layer in a channel
- Investigation of optimized ELM using Invasive Weed-optimization and Cuckoo-Search optimization
- Analytical analysis for non-homogeneous two-layer functionally graded material
- Investigation of critical load of structures using modified energy method in nonlinear-geometry solid mechanics problems
- Thermal and multi-boiling analysis of a rectangular porous fin: A spectral approach
- The path planning of collision avoidance for an unmanned ship navigating in waterways based on an artificial neural network
- Shear bond and compressive strength of clay stabilised with lime/cement jet grouting and deep mixing: A case of Norvik, Nynäshamn
- Communication
- Results for the heat transfer of a fin with exponential-law temperature-dependent thermal conductivity and power-law temperature-dependent heat transfer coefficients
- Special Issue: Recent trends and emergence of technology in nonlinear engineering and its applications - Part I
- Research on fault detection and identification methods of nonlinear dynamic process based on ICA
- Multi-objective optimization design of steel structure building energy consumption simulation based on genetic algorithm
- Study on modal parameter identification of engineering structures based on nonlinear characteristics
- On-line monitoring of steel ball stamping by mechatronics cold heading equipment based on PVDF polymer sensing material
- Vibration signal acquisition and computer simulation detection of mechanical equipment failure
- Development of a CPU-GPU heterogeneous platform based on a nonlinear parallel algorithm
- A GA-BP neural network for nonlinear time-series forecasting and its application in cigarette sales forecast
- Analysis of radiation effects of semiconductor devices based on numerical simulation Fermi–Dirac
- Design of motion-assisted training control system based on nonlinear mechanics
- Nonlinear discrete system model of tobacco supply chain information
- Performance degradation detection method of aeroengine fuel metering device
- Research on contour feature extraction method of multiple sports images based on nonlinear mechanics
- Design and implementation of Internet-of-Things software monitoring and early warning system based on nonlinear technology
- Application of nonlinear adaptive technology in GPS positioning trajectory of ship navigation
- Real-time control of laboratory information system based on nonlinear programming
- Software engineering defect detection and classification system based on artificial intelligence
- Vibration signal collection and analysis of mechanical equipment failure based on computer simulation detection
- Fractal analysis of retinal vasculature in relation with retinal diseases – an machine learning approach
- Application of programmable logic control in the nonlinear machine automation control using numerical control technology
- Application of nonlinear recursion equation in network security risk detection
- Study on mechanical maintenance method of ballasted track of high-speed railway based on nonlinear discrete element theory
- Optimal control and nonlinear numerical simulation analysis of tunnel rock deformation parameters
- Nonlinear reliability of urban rail transit network connectivity based on computer aided design and topology
- Optimization of target acquisition and sorting for object-finding multi-manipulator based on open MV vision
- Nonlinear numerical simulation of dynamic response of pile site and pile foundation under earthquake
- Research on stability of hydraulic system based on nonlinear PID control
- Design and simulation of vehicle vibration test based on virtual reality technology
- Nonlinear parameter optimization method for high-resolution monitoring of marine environment
- Mobile app for COVID-19 patient education – Development process using the analysis, design, development, implementation, and evaluation models
- Internet of Things-based smart vehicles design of bio-inspired algorithms using artificial intelligence charging system
- Construction vibration risk assessment of engineering projects based on nonlinear feature algorithm
- Application of third-order nonlinear optical materials in complex crystalline chemical reactions of borates
- Evaluation of LoRa nodes for long-range communication
- Secret information security system in computer network based on Bayesian classification and nonlinear algorithm
- Experimental and simulation research on the difference in motion technology levels based on nonlinear characteristics
- Research on computer 3D image encryption processing based on the nonlinear algorithm
- Outage probability for a multiuser NOMA-based network using energy harvesting relays
Articles in the same Issue
- Research Articles
- Fractal approach to the fluidity of a cement mortar
- Novel results on conformable Bessel functions
- The role of relaxation and retardation phenomenon of Oldroyd-B fluid flow through Stehfest’s and Tzou’s algorithms
- Damage identification of wind turbine blades based on dynamic characteristics
- Improving nonlinear behavior and tensile and compressive strengths of sustainable lightweight concrete using waste glass powder, nanosilica, and recycled polypropylene fiber
- Two-point nonlocal nonlinear fractional boundary value problem with Caputo derivative: Analysis and numerical solution
- Construction of optical solitons of Radhakrishnan–Kundu–Lakshmanan equation in birefringent fibers
- Dynamics and simulations of discretized Caputo-conformable fractional-order Lotka–Volterra models
- Research on facial expression recognition based on an improved fusion algorithm
- N-dimensional quintic B-spline functions for solving n-dimensional partial differential equations
- Solution of two-dimensional fractional diffusion equation by a novel hybrid D(TQ) method
- Investigation of three-dimensional hybrid nanofluid flow affected by nonuniform MHD over exponential stretching/shrinking plate
- Solution for a rotational pendulum system by the Rach–Adomian–Meyers decomposition method
- Study on the technical parameters model of the functional components of cone crushers
- Using Krasnoselskii's theorem to investigate the Cauchy and neutral fractional q-integro-differential equation via numerical technique
- Smear character recognition method of side-end power meter based on PCA image enhancement
- Significance of adding titanium dioxide nanoparticles to an existing distilled water conveying aluminum oxide and zinc oxide nanoparticles: Scrutinization of chemical reactive ternary-hybrid nanofluid due to bioconvection on a convectively heated surface
- An analytical approach for Shehu transform on fractional coupled 1D, 2D and 3D Burgers’ equations
- Exploration of the dynamics of hyperbolic tangent fluid through a tapered asymmetric porous channel
- Bond behavior of recycled coarse aggregate concrete with rebar after freeze–thaw cycles: Finite element nonlinear analysis
- Edge detection using nonlinear structure tensor
- Synchronizing a synchronverter to an unbalanced power grid using sequence component decomposition
- Distinguishability criteria of conformable hybrid linear systems
- A new computational investigation to the new exact solutions of (3 + 1)-dimensional WKdV equations via two novel procedures arising in shallow water magnetohydrodynamics
- A passive verses active exposure of mathematical smoking model: A role for optimal and dynamical control
- A new analytical method to simulate the mutual impact of space-time memory indices embedded in (1 + 2)-physical models
- Exploration of peristaltic pumping of Casson fluid flow through a porous peripheral layer in a channel
- Investigation of optimized ELM using Invasive Weed-optimization and Cuckoo-Search optimization
- Analytical analysis for non-homogeneous two-layer functionally graded material
- Investigation of critical load of structures using modified energy method in nonlinear-geometry solid mechanics problems
- Thermal and multi-boiling analysis of a rectangular porous fin: A spectral approach
- The path planning of collision avoidance for an unmanned ship navigating in waterways based on an artificial neural network
- Shear bond and compressive strength of clay stabilised with lime/cement jet grouting and deep mixing: A case of Norvik, Nynäshamn
- Communication
- Results for the heat transfer of a fin with exponential-law temperature-dependent thermal conductivity and power-law temperature-dependent heat transfer coefficients
- Special Issue: Recent trends and emergence of technology in nonlinear engineering and its applications - Part I
- Research on fault detection and identification methods of nonlinear dynamic process based on ICA
- Multi-objective optimization design of steel structure building energy consumption simulation based on genetic algorithm
- Study on modal parameter identification of engineering structures based on nonlinear characteristics
- On-line monitoring of steel ball stamping by mechatronics cold heading equipment based on PVDF polymer sensing material
- Vibration signal acquisition and computer simulation detection of mechanical equipment failure
- Development of a CPU-GPU heterogeneous platform based on a nonlinear parallel algorithm
- A GA-BP neural network for nonlinear time-series forecasting and its application in cigarette sales forecast
- Analysis of radiation effects of semiconductor devices based on numerical simulation Fermi–Dirac
- Design of motion-assisted training control system based on nonlinear mechanics
- Nonlinear discrete system model of tobacco supply chain information
- Performance degradation detection method of aeroengine fuel metering device
- Research on contour feature extraction method of multiple sports images based on nonlinear mechanics
- Design and implementation of Internet-of-Things software monitoring and early warning system based on nonlinear technology
- Application of nonlinear adaptive technology in GPS positioning trajectory of ship navigation
- Real-time control of laboratory information system based on nonlinear programming
- Software engineering defect detection and classification system based on artificial intelligence
- Vibration signal collection and analysis of mechanical equipment failure based on computer simulation detection
- Fractal analysis of retinal vasculature in relation with retinal diseases – an machine learning approach
- Application of programmable logic control in the nonlinear machine automation control using numerical control technology
- Application of nonlinear recursion equation in network security risk detection
- Study on mechanical maintenance method of ballasted track of high-speed railway based on nonlinear discrete element theory
- Optimal control and nonlinear numerical simulation analysis of tunnel rock deformation parameters
- Nonlinear reliability of urban rail transit network connectivity based on computer aided design and topology
- Optimization of target acquisition and sorting for object-finding multi-manipulator based on open MV vision
- Nonlinear numerical simulation of dynamic response of pile site and pile foundation under earthquake
- Research on stability of hydraulic system based on nonlinear PID control
- Design and simulation of vehicle vibration test based on virtual reality technology
- Nonlinear parameter optimization method for high-resolution monitoring of marine environment
- Mobile app for COVID-19 patient education – Development process using the analysis, design, development, implementation, and evaluation models
- Internet of Things-based smart vehicles design of bio-inspired algorithms using artificial intelligence charging system
- Construction vibration risk assessment of engineering projects based on nonlinear feature algorithm
- Application of third-order nonlinear optical materials in complex crystalline chemical reactions of borates
- Evaluation of LoRa nodes for long-range communication
- Secret information security system in computer network based on Bayesian classification and nonlinear algorithm
- Experimental and simulation research on the difference in motion technology levels based on nonlinear characteristics
- Research on computer 3D image encryption processing based on the nonlinear algorithm
- Outage probability for a multiuser NOMA-based network using energy harvesting relays

