Startseite Technik N-dimensional quintic B-spline functions for solving n-dimensional partial differential equations
Artikel Open Access

N-dimensional quintic B-spline functions for solving n-dimensional partial differential equations

  • K. R. Raslan , Khalid K. Ali EMAIL logo und Hind K. Al-Jeaid
Veröffentlicht/Copyright: 18. April 2022
Artikel downloaden (PDF)
Veröffentlichen auch Sie bei De Gruyter Brill
Manuskript einreichen Informationen für Autor*innen
Nonlinear Engineering
Aus der Zeitschrift Nonlinear Engineering Band 11 Heft 1

Abstract

In continuation to what we started from developing the B-spline functions and putting them in n-dimensional to solve mathematical models in n-dimensions, we present in this article a new structure for the quintic B-spline collocation algorithm in n-dimensional. The quintic B-spline collocation algorithm is shown in three different formats: one, two, and three dimensional. These constructs are critical for solving mathematical models in different fields. The proposed method’s efficiency and accuracy are illustrated by their application to a few two- and three-dimensional test problems. We use other numerical methods available in the literature to make comparisons.

Keywords: collocation method; n-dimensional B-spline functions; mathematical models

1 Introduction

Solving n-dimensional mathematical models is the main concern of most researchers now due to the importance of these models in the physical, engineering, chemical, fluid mechanics, plasma, and other sciences. Many researchers have tried to solve these models analytically by using some analytical and approximate methods as we see in [1,2,3, 4,5,6, 7,8,9, 10,11]. Recently, a problem has emerged that most of the mathematical models in some sciences, including fluid mechanics and physics, are difficult to deal with analytically, so some researchers began to think about solving these models numerically. One of the methods that have been used in solving n-dimensional models is the finite difference method, as we see in [12,13]. Some researchers also tried to develop some methods that were used to solve mathematical models in a dimension to be suitable for solving n-dimensional models, such as spectral methods [14,15]. However, there was difficulty in using spectral methods to solve most nonlinear models. From here Gardner and Gardner introduced a two-dimensional bi-cubic B-spline finite element to solve two-dimensional equations [16]. Some researchers used the bi-cubic B-spline finite element method to solve some different mathematical models [17,18,19]. Raslan and Ali started thinking about generalizing all forms of B-spline functions. They presented on n-dimensional quadratic B-splines [20], new structure formulations for cubic B-spline collocation method in three and four dimensions [21], construct extended cubic B-Splines in n-dimensional for solving n-dimensional partial differential equations [22], and a new structure to n-dimensional trigonometric cubic B-spline functions for solving n-dimensional partial differential equations [23].

In this work, we continue developing the B-spline collocation functions. We present the quintic B-spline collocation algorithm in n-dimensional with some numerical examples to investigate the method’s efficacy and accuracy.

This article is structured as follows. Section 2 presents quintic B-spline formulations in n-dimensional. Section 3 contains the error estimates. Numerical examples are introduced in Section 4. Finally, the conclusion part is given.

2 N-dimensional quintic B-spline functions

In this section, we present the n-dimensional quintic B-splines.

2.1 One dimension quintic B-spline [24,25]

Let l ≤ x ≤ m and ℧ i ( x ) be those quintic B-spline with knots at the points x ϱ . Then the set of quintic B-splines ℧ − 2 ( x ) , ℧ − 1 ( x ) , ℧ 0 ( x ) , … , ℧ N − 1 ( x ) , ℧ N ( x ) , ℧ N + 1 ( x ) , ℧ N + 2 ( x ) , serves as a basis for functions specified over a range of values. The H N ( x ) approximation to H ( x ) , which uses these splines as:

(1) H N ( x ) = ∑ ϱ = − 2 N + 2 γ ϱ ℧ ϱ ( x ) ,

where γ ϱ is the unknown term. The formulations of H ϱ , d H ϱ d x , d 2 H ϱ d x 2 are given by:

(2) H ϱ = γ ϱ − 2 + 26 γ ϱ − 1 + 66 γ ϱ + 26 γ ϱ + 1 + γ ϱ + 2 , d H ϱ d x = − 5 ( γ ϱ − 2 + 10 γ ϱ − 1 − 10 γ ϱ + 1 − γ ϱ + 2 ) h , d 2 H ϱ d x 2 = 20 ( γ ϱ − 2 + 2 γ ϱ − 1 − 6 γ ϱ + 2 γ ϱ + 1 + γ ϱ + 2 ) h 2 .

The above analysis yields the following theorem:

Theorem 1

The solution of one dimension differential equation (DE) using the collocation method with basis quintic B-spline can be determined by Eq. (2).

2.2 Two-dimensional quintic B-spline

This subsection shows the formula for a two-dimensional quintic B-spline on a rectangular grid divided into regular rectangular finite elements on both sides. h = Δ x , k = Δ y by the knots ( x ϱ , y τ ) , where ϱ = 0 , 1 , … , N , τ = 0 , 1 , … , M . The approximation H N ( x , y ) to H ( x , y ) is given by:

(3) H N ( x , y ) = ∑ ϱ = − 2 N + 2 ∑ τ = − 2 M + 2 γ ϱ , τ Θ ϱ , τ ( x , y ) ,

where γ ϱ , τ are the amplitudes of the quintic B-splines Θ ϱ , τ ( x , y ) given by

Θ ϱ , τ ( x , y ) = ℧ ϱ ( x ) ℧ τ ( y ) .

Which peaks on the knot ( x ϱ , y τ ) and ℧ τ ( x ) , ℧ n ( y ) are identical in form to the one-dimension quintic B-splines. Then the formulations of H ϱ , τ , ∂ H ϱ , τ ∂ x , ∂ H ϱ , τ ∂ y , ∂ 2 H ϱ , τ ∂ x 2 , ∂ 2 H ϱ , τ ∂ y 2 , ∂ 2 H ϱ , τ ∂ x ∂ y , … are given by:

(4) H ϱ , τ = γ ϱ − 2 , τ − 2 + 26 γ ϱ − 2 , τ − 1 + 66 γ ϱ − 2 , τ + 26 γ ϱ − 2 , τ + 1 + γ ϱ − 2 , τ + 2 + 26 γ ϱ − 1 , τ − 2 + 676 γ ϱ − 1 , τ − 1 + 1,716 γ ϱ − 1 , τ + 676 γ ϱ − 1 , τ + 1 + 26 γ ϱ − 1 , τ + 2 + 66 γ ϱ , τ − 2 + 1,716 γ ϱ , τ − 1 + 4,356 γ ϱ , τ + 1,716 γ ϱ , τ + 1 + 66 γ ϱ , τ + 2 + 26 γ ϱ + 1 , τ − 2 + 676 γ ϱ + 1 , τ − 1 + 1,716 γ ϱ + 1 , τ + 676 γ ϱ + 1 , τ + 1 + 26 γ ϱ + 1 , τ + 2 + γ ϱ + 2 , τ − 2 + 26 γ ϱ + 2 , τ − 1 + 66 γ ϱ + 2 , τ + 26 γ ϱ + 2 , τ + 1 + γ ϱ + 2 , τ + 2 ,

(5) ∂ H ϱ , τ ∂ x = − 5 h ( γ ϱ − 2 , τ − 2 + 26 γ ϱ − 2 , τ − 1 + 66 γ ϱ − 2 , τ + 26 γ ϱ − 2 , τ + 1 + γ ϱ − 2 , τ + 2 + 10 γ ϱ − 1 , τ − 2 + 260 γ ϱ − 1 , τ − 1 + 660 γ ϱ − 1 , τ + 260 γ ϱ − 1 , τ + 1 + 10 γ ϱ − 1 , τ + 2 − 10 γ ϱ + 1 , τ − 2 − 260 γ ϱ + 1 , τ − 1 − 660 γ ϱ + 1 , τ − 260 γ ϱ + 1 , τ + 1 − 10 γ ϱ + 1 , τ + 2 − γ ϱ + 2 , τ − 2 − 26 γ ϱ + 2 , τ − 1 − 66 γ ϱ + 2 , τ − 26 γ ϱ + 2 , τ + 1 − γ ϱ + 2 , τ + 2 ) , ∂ H ϱ , τ ∂ y = − 5 k ( γ ϱ − 2 , τ − 2 + 10 γ ϱ − 2 , τ − 1 − 10 γ ϱ − 2 , τ + 1 − γ ϱ − 2 , τ + 2 + 26 γ ϱ − 1 , τ − 2 + 260 γ ϱ − 1 , τ − 1 − 260 γ ϱ − 1 , τ + 1 − 26 γ ϱ − 1 , τ + 2 + 66 γ ϱ , τ − 2 + 660 γ ϱ , τ − 1 − 660 γ ϱ , τ + 1 − 66 γ ϱ , τ + 2 + 26 γ ϱ + 1 , τ − 2 + 260 γ ϱ + 1 , τ − 1 − 260 γ ϱ + 1 , τ + 1 − 26 γ ϱ + 1 , τ + 2 + γ ϱ + 2 , τ − 2 + 10 γ ϱ + 2 , τ − 1 − 10 γ ϱ + 2 , τ + 1 − γ ϱ + 2 , τ + 2 ) .

(6) ∂ 2 H ϱ , τ ∂ x 2 = 20 h 2 ( γ ϱ − 2 , τ − 2 + 26 γ ϱ − 2 , τ − 1 + 66 γ ϱ − 2 , τ + 26 γ ϱ − 2 , τ + 1 + γ ϱ − 2 , τ + 2 + 2 γ ϱ − 1 , τ − 2 + 52 γ ϱ − 1 , τ − 1 + 132 γ ϱ − 1 , τ + 52 γ ϱ − 1 , τ + 1 + 2 γ ϱ − 1 , τ + 2 − 6 γ ϱ , τ − 2 − 156 γ ϱ , τ − 1 − 396 γ ϱ , τ − 156 γ ϱ , τ + 1 − 6 γ ϱ , τ + 2 + 2 γ ϱ + 1 , τ − 2 + 52 γ ϱ + 1 , τ − 1 + 132 γ ϱ + 1 , τ + 52 γ ϱ + 1 , τ + 1 + 2 γ ϱ + 1 , τ + 2 + γ ϱ + 2 , τ − 2 + 26 γ ϱ + 2 , τ − 1 + 66 γ ϱ + 2 , τ + 26 γ ϱ + 2 , τ + 1 + γ ϱ + 2 , τ + 2 ) , ∂ 2 H ϱ , τ ∂ y 2 = 20 k 2 ( γ ϱ − 2 , τ − 2 + 2 γ ϱ − 2 , τ − 1 − 6 γ ϱ − 2 , τ + 2 γ ϱ − 2 , τ + 1 + γ ϱ − 2 , τ + 2 + 26 γ ϱ − 1 , τ − 2 + 52 γ ϱ − 1 , τ − 1 − 156 γ ϱ − 1 , τ + 52 γ ϱ − 1 , τ + 1 + 26 γ ϱ − 1 , τ + 2 + 66 γ ϱ , τ − 2 + 132 γ ϱ , τ − 1 − 396 γ ϱ , τ + 132 γ ϱ , τ + 1 + 66 γ ϱ , τ + 2 + 26 γ ϱ + 1 , τ − 2 + 52 γ ϱ + 1 , τ − 1 − 156 γ ϱ + 1 , τ + 52 γ ϱ + 1 , τ + 1 + 26 γ ϱ + 1 , τ + 2 + γ ϱ + 2 , τ − 2 + 2 γ ϱ + 2 , τ − 1 − 6 γ ϱ + 2 , τ + 2 γ ϱ + 2 , τ + 1 + γ ϱ + 2 , τ + 2 ) , ⋮

The above analysis yields the following theorem:

Theorem 2

The solution of two-dimensional DE using the collocation method with basis quintic B-spline can be determined by Eqs. (4)–(6).

2.3 The three-dimensional quintic B-spline

Now, we obtain the quintic B-spline in three measurement approximates on a framework divided into limited components of sides h = Δ x , k = Δ y , q = Δ z by the knots ( x ϱ , y τ , z σ ) , where ϱ = 0 , 1 , … , N , τ = 0 , 1 , … , M , σ = 0 , 1 , … , R can be interpolated in terms of piecewise quintic B-splines. If H ( x , y , z ) is a function of x , y , and z , it can be shown that there exists a unique approximation H N ( x , y , z ) as

(7) H N ( x , y , z ) = ∑ ϱ = − 2 N + 2 ∑ τ = − 2 M + 2 ∑ σ = − 2 R + 2 γ ϱ , τ , σ B ϱ , τ , σ ( x , y , z ) ,

where χ ϱ , τ , σ are the quintic B-spline amplitudes B ϱ , τ , σ ( x , y , z ) given by

B ϱ , τ , σ ( x , y , z ) = ℧ ϱ ( x ) ℧ τ ( y ) ℧ σ ( z ) .

Also, ϕ ϱ ( x ) , ϕ τ ( y ) , and ϕ σ ( z ) have the same shape as quintic B-splines in one dimension. The compositions of H ϱ , τ , σ , ∂ H ϱ , τ , σ ∂ x , ∂ H ϱ , τ , σ ∂ y , ∂ H ϱ , τ , σ ∂ z , ∂ 2 H ϱ , τ , σ ∂ x 2 , ∂ 2 H ϱ , τ , σ ∂ y 2 , ∂ 2 H ϱ , τ , σ ∂ z 2 , ∂ 2 H ϱ , τ , σ ∂ x ∂ y , ∂ 2 H ϱ , τ , σ ∂ x ∂ z , … , are given in terms of the γ ϱ , τ , σ by:

H ϱ , τ , σ = γ ϱ − 2 , τ − 2 , σ − 2 + 26 γ ϱ − 2 , τ − 2 , σ − 1 + 66 γ ϱ − 2 , τ − 2 , σ + 26 γ ϱ − 2 , τ − 2 , σ + 1 + γ ϱ − 2 , τ − 2 , σ + 2 + 26 γ ϱ − 2 , τ − 1 , σ − 2 + 676 γ ϱ − 2 , τ − 1 , σ − 1 + 1,716 γ ϱ − 2 , τ − 1 , σ + 676 γ ϱ − 2 , τ − 1 , σ + 1 + 26 γ ϱ − 2 , τ − 1 , σ + 2 + 66 γ ϱ − 2 , τ , σ − 2 + 1,716 γ ϱ − 2 , τ , σ − 1 + 4,356 γ ϱ − 2 , τ , σ + 1,716 γ ϱ − 2 , τ , σ + 1 + 66 γ ϱ − 2 , τ , σ + 2 + 26 γ ϱ − 2 , τ + 1 , σ − 2 + 676 γ ϱ − 2 , τ + 1 , σ − 1 + 1,716 γ ϱ − 2 , τ + 1 , σ + 676 γ ϱ − 2 , τ + 1 , σ + 1 + 26 γ ϱ − 2 , τ + 1 , σ + 2 + γ ϱ − 2 , τ + 2 , σ − 2 + 26 γ ϱ − 2 , τ + 2 , σ − 1 + 66 γ ϱ − 2 , τ + 2 , σ + 26 γ ϱ − 2 , τ + 2 , σ + 1 + γ ϱ − 2 , τ + 2 , σ + 2 + 26 γ ϱ − 1 , τ − 2 , σ − 2 + 676 γ ϱ − 1 , τ − 2 , σ − 1 + 1,716 γ ϱ − 1 , τ − 2 , σ + 676 γ ϱ − 1 , τ − 2 , σ + 1 + 26 γ ϱ − 1 , τ − 2 , σ + 2

(8) + 676 γ ϱ − 1 , τ − 1 , σ − 2 + 17,576 γ ϱ − 1 , τ − 1 , σ − 1 + 44,616 γ ϱ − 1 , τ − 1 , σ + 17,576 γ ϱ − 1 , τ − 1 , σ + 1 + 676 γ ϱ − 1 , τ − 1 , σ + 2 + 1,716 γ ϱ − 1 , τ , σ − 2 + 44,616 γ ϱ − 1 , τ , σ − 1 + 113,256 γ ϱ − 1 , τ , σ + 44,616 γ ϱ − 1 , τ , σ + 1 + 1,716 γ ϱ − 1 , τ , σ + 2 + 676 γ ϱ − 1 , τ + 1 , σ − 2 + 17,576 γ ϱ − 1 , τ + 1 , σ − 1 + 44,616 γ ϱ − 1 , τ + 1 , σ + 17,576 γ ϱ − 1 , τ + 1 , σ + 1 + 676 γ ϱ − 1 , τ + 1 , σ + 2 + 26 γ ϱ − 1 , τ + 2 , σ − 2 + 676 γ ϱ − 1 , τ + 2 , σ − 1 + 1,716 γ ϱ − 1 , τ + 2 , σ + 676 γ ϱ − 1 , τ + 2 , σ + 1 + 26 γ ϱ − 1 , τ + 2 , σ + 2 + 66 γ ϱ , τ − 2 , σ − 2 + 1,716 γ ϱ , τ − 2 , σ − 1 + 4,356 γ ϱ , τ − 2 , σ + 1,716 γ ϱ , τ − 2 , σ + 1 + 66 γ ϱ , τ − 2 , σ + 2 + 1,716 γ ϱ , τ − 1 , σ − 2 + 44,616 γ ϱ , τ − 1 , σ − 1 + 113,256 γ ϱ , τ − 1 , σ + 44,616 γ ϱ , τ − 1 , σ + 1 + 1,716 γ ϱ , τ − 1 , σ + 2 + 4,356 γ ϱ , τ , σ − 2 + 113,256 γ ϱ , τ , σ − 1 + 287,496 γ ϱ , τ , σ + 113,256 γ ϱ , τ , σ + 1 + 4,356 γ ϱ , τ , σ + 2 + 1,716 γ ϱ , τ + 1 , σ − 2 + 44,616 γ ϱ , τ + 1 , σ − 1 + 113,256 γ ϱ , τ + 1 , σ + 44,616 γ ϱ , τ + 1 , σ + 1 + 1,716 γ ϱ , τ + 1 , σ + 2 + 66 γ ϱ , τ + 2 , σ − 2 + 1,716 γ ϱ , τ + 2 , σ − 1 + 4,356 γ ϱ , τ + 2 , σ + 1,716 γ ϱ , τ + 2 , σ + 1 + 66 γ ϱ , τ + 2 , σ + 2 + 26 γ ϱ + 1 , τ − 2 , σ − 2 + 676 γ ϱ + 1 , τ − 2 , σ − 1 + 1,716 γ ϱ + 1 , τ − 2 , σ + 676 γ ϱ + 1 , τ − 2 , σ + 1 + 26 γ ϱ + 1 , τ − 2 , σ + 2 + 676 γ ϱ + 1 , τ − 1 , σ − 2 + 17,576 γ ϱ + 1 , τ − 1 , σ − 1 + 44,616 γ ϱ + 1 , τ − 1 , σ + 17,576 γ ϱ + 1 , τ − 1 , σ + 1 + 676 γ ϱ + 1 , τ − 1 , σ + 2 + 1,716 γ ϱ + 1 , τ , σ − 2 + 44,616 γ ϱ + 1 , τ , σ − 1 + 113,256 γ ϱ + 1 , τ , σ + 44,616 γ ϱ + 1 , τ , σ + 1 + 1,716 γ ϱ + 1 , τ , σ + 2 + 676 γ ϱ + 1 , τ + 1 , σ − 2 + 17,576 γ ϱ + 1 , τ + 1 , σ − 1 + 44,616 γ ϱ + 1 , τ + 1 , σ + 17,576 γ ϱ + 1 , τ + 1 , σ + 1 + 676 γ ϱ + 1 , τ + 1 , σ + 2 + 26 γ ϱ + 1 , τ + 2 , σ − 2 + 676 γ ϱ + 1 , τ + 2 , σ − 1 + 1,716 γ ϱ + 1 , τ + 2 , σ + 676 γ ϱ + 1 , τ + 2 , σ + 1 + 26 γ ϱ + 1 , τ + 2 , σ + 2 + γ ϱ + 2 , τ − 2 , σ − 2 + 26 γ ϱ + 2 , τ − 2 , σ − 1 + 66 γ ϱ + 2 , τ − 2 , σ + 26 γ ϱ + 2 , τ − 2 , σ + 1 + γ ϱ + 2 , τ − 2 , σ + 2 + 26 γ ϱ + 2 , τ − 1 , σ − 2 + 676 γ ϱ + 2 , τ − 1 , σ − 1 + 1,716 γ ϱ + 2 , τ − 1 , σ + 676 γ ϱ + 2 , τ − 1 , σ + 1 + 26 γ ϱ + 2 , τ − 1 , σ + 2 + 66 γ ϱ + 2 , τ , σ − 2 + 1,716 γ ϱ + 2 , τ , σ − 1 + 4,356 γ ϱ + 2 , τ , σ + 1,716 γ ϱ + 2 , τ , σ + 1 + 66 γ ϱ + 2 , τ , σ + 2 + 26 γ ϱ + 2 , τ + 1 , σ − 2 + 676 γ ϱ + 2 , τ + 1 , σ − 1 + 1,716 γ ϱ + 2 , τ + 1 , σ + 676 γ ϱ + 2 , τ + 1 , σ + 1 + 26 γ ϱ + 2 , τ + 1 , σ + 2 + γ ϱ + 2 , τ + 2 , σ − 2 + 26 γ ϱ + 2 , τ + 2 , σ − 1 + 66 γ ϱ + 2 , τ + 2 , σ + 26 γ ϱ + 2 , τ + 2 , σ + 1 + γ ϱ + 2 , τ + 2 , σ + 2 .

(9) ∂ H ϱ , τ , σ ∂ x = − 5 h ( γ ϱ − 2 , τ − 2 , σ − 2 + 26 γ ϱ − 2 , τ − 2 , σ − 1 + 66 γ ϱ − 2 , τ − 2 , σ + 26 γ ϱ − 2 , τ − 2 , σ + 1 + γ ϱ − 2 , τ − 2 , σ + 2 + 26 γ ϱ − 2 , τ − 1 , σ − 2 + 676 γ ϱ − 2 , τ − 1 , σ − 1 + 1,716 γ ϱ − 2 , τ − 1 , σ + 676 γ ϱ − 2 , τ − 1 , σ + 1 + 26 γ ϱ − 2 , τ − 1 , σ + 2 + 66 γ ϱ − 2 , τ , σ − 2 + 1,716 γ ϱ − 2 , τ , σ − 1 + 4,356 γ ϱ − 2 , τ , σ + 1,716 γ ϱ − 2 , τ , σ + 1 + 66 γ ϱ − 2 , τ , σ + 2 + 26 γ ϱ − 2 , τ + 1 , σ − 2 + 676 γ ϱ − 2 , τ + 1 , σ − 1 + 1,716 γ ϱ − 2 , τ + 1 , σ + 676 γ ϱ − 2 , τ + 1 , σ + 1 + 26 γ ϱ − 2 , τ + 1 , σ + 2 + γ ϱ − 2 , τ + 2 , σ − 2 + 26 γ ϱ − 2 , τ + 2 , σ − 1 + 66 γ ϱ − 2 , τ + 2 , σ + 26 γ ϱ − 2 , τ + 2 , σ + 1 + γ ϱ − 2 , τ + 2 , σ + 2 + 10 γ ϱ − 1 , τ − 2 , σ − 2 + 260 γ ϱ − 1 , τ − 2 , σ − 1 + 660 γ ϱ − 1 , τ − 2 , σ + 260 γ ϱ − 1 , τ − 2 , σ + 1 + 10 γ ϱ − 1 , τ − 2 , σ + 2 + 260 γ ϱ − 1 , τ − 1 , σ − 2 + 6,760 γ ϱ − 1 , τ − 1 , σ − 1 + 1,716 0 γ ϱ − 1 , τ − 1 , σ + 6,760 γ ϱ − 1 , τ − 1 , σ + 1 + 260 γ ϱ − 1 , τ − 1 , σ + 2 + 660 γ ϱ − 1 , τ , σ − 2 + 1,716 0 γ ϱ − 1 , τ , σ − 1 + 43,560 γ ϱ − 1 , τ , σ + 1,716 0 γ ϱ − 1 , τ , σ + 1 + 660 γ ϱ − 1 , τ , σ + 2 + 260 γ ϱ − 1 , τ + 1 , σ − 2 + 6,760 γ ϱ − 1 , τ + 1 , σ − 1 + 1,716 0 γ ϱ − 1 , τ + 1 , σ + 6,760 γ ϱ − 1 , τ + 1 , σ + 1 + 260 γ ϱ − 1 , τ + 1 , σ + 2 + 10 γ ϱ − 1 , τ + 2 , σ − 2 + 260 γ ϱ − 1 , τ + 2 , σ − 1 + 660 γ ϱ − 1 , τ + 2 , σ + 260 γ ϱ − 1 , τ + 2 , σ + 1 + 10 γ ϱ − 1 , τ + 2 , σ + 2 − 10 γ ϱ + 1 , τ − 2 , σ − 2 − 260 γ ϱ + 1 , τ − 2 , σ − 1 − 660 γ ϱ + 1 , τ − 2 , σ − 260 γ ϱ + 1 , τ − 2 , σ + 1 − 10 γ ϱ + 1 , τ − 2 , σ + 2 − 260 γ ϱ + 1 , τ − 1 , σ − 2 − 6,760 γ ϱ + 1 , τ − 1 , σ − 1 − 1,716 0 γ ϱ + 1 , τ − 1 , σ − 6,760 γ ϱ + 1 , τ − 1 , σ + 1 − 260 γ ϱ + 1 , τ − 1 , σ + 2 − 660 γ ϱ + 1 , τ , σ − 2 − 1,716 0 γ ϱ + 1 , τ , σ − 1 − 43,560 γ ϱ + 1 , τ , σ − 1,716 0 γ ϱ + 1 , τ , σ + 1 − 660 γ ϱ + 1 , τ , σ + 2 − 260 γ ϱ + 1 , τ + 1 , σ − 2 − 6,760 γ ϱ + 1 , τ + 1 , σ − 1 − 1,716 0 γ ϱ + 1 , τ + 1 , σ − 6,760 γ ϱ + 1 , τ + 1 , σ + 1 − 260 γ ϱ + 1 , τ + 1 , σ + 2 − 10 γ ϱ + 1 , τ + 2 , σ − 2 − 260 γ ϱ + 1 , τ + 2 , σ − 1 − 660 γ ϱ + 1 , τ + 2 , σ − 260 γ ϱ + 1 , τ + 2 , σ + 1 − 10 γ ϱ + 1 , τ + 2 , σ + 2 − γ ϱ + 2 , τ − 2 , σ − 2 − 26 γ ϱ + 2 , τ − 2 , σ − 1 − 66 γ ϱ + 2 , τ − 2 , σ − 26 γ ϱ + 2 , τ − 2 , σ + 1 − γ ϱ + 2 , τ − 2 , σ + 2 − 26 γ ϱ + 2 , τ − 1 , σ − 2 − 676 γ ϱ + 2 , τ − 1 , σ − 1 − 1,716 γ ϱ + 2 , τ − 1 , σ − 676 γ ϱ + 2 , τ − 1 , σ + 1 − 26 γ ϱ + 2 , τ − 1 , σ + 2 − 66 γ ϱ + 2 , τ , σ − 2 − 1,716 γ ϱ + 2 , τ , σ − 1 − 4,356 γ ϱ + 2 , τ , σ − 1,716 γ ϱ + 2 , τ , σ + 1 − 66 γ ϱ + 2 , τ , σ + 2 − 26 γ ϱ + 2 , τ + 1 , σ − 2 − 676 γ ϱ + 2 , τ + 1 , σ − 1 − 1,716 γ ϱ + 2 , τ + 1 , σ − 676 γ ϱ + 2 , τ + 1 , σ + 1 − 26 γ ϱ + 2 , τ + 1 , σ + 2 − γ ϱ + 2 , τ + 2 , σ − 2 − 26 γ ϱ + 2 , τ + 2 , σ − 1 − 66 γ ϱ + 2 , τ + 2 , σ − 26 γ ϱ + 2 , τ + 2 , σ + 1 − γ ϱ + 2 , τ + 2 , σ + 2 ) ,

(10) ∂ H ϱ , τ , σ ∂ y = − 5 k ( γ ϱ − 2 , τ − 2 , σ − 2 + 26 γ ϱ − 2 , τ − 2 , σ − 1 + 66 γ ϱ − 2 , τ − 2 , σ + 26 γ ϱ − 2 , τ − 2 , σ + 1 + γ ϱ − 2 , τ − 2 , σ + 2 + 10 γ ϱ − 2 , τ − 1 , σ − 2 + 260 γ ϱ − 2 , τ − 1 , σ − 1 + 660 γ ϱ − 2 , τ − 1 , σ + 260 γ ϱ − 2 , τ − 1 , σ + 1 + 10 γ ϱ − 2 , τ − 1 , σ + 2 − 10 γ ϱ − 2 , τ + 1 , σ − 2 − 260 γ ϱ − 2 , τ + 1 , σ − 1 − 660 γ ϱ − 2 , τ + 1 , σ − 260 γ ϱ − 2 , τ + 1 , σ + 1 − 10 γ ϱ − 2 , τ + 1 , σ + 2 − γ ϱ − 2 , τ + 2 , σ − 2 − 26 γ ϱ − 2 , τ + 2 , σ − 1 − 66 γ ϱ − 2 , τ + 2 , σ − 26 γ ϱ − 2 , τ + 2 , σ + 1 − γ ϱ − 2 , τ + 2 , σ + 2 + 26 γ ϱ − 1 , τ − 2 , σ − 2 + 676 γ ϱ − 1 , τ − 2 , σ − 1 + 1,716 γ ϱ − 1 , τ − 2 , σ + 676 γ ϱ − 1 , τ − 2 , σ + 1 + 26 γ ϱ − 1 , τ − 2 , σ + 2 + 260 γ ϱ − 1 , τ − 1 , σ − 2 + 6,760 γ ϱ − 1 , τ − 1 , σ − 1 + 1,716 0 γ ϱ − 1 , τ − 1 , σ + 6,760 γ ϱ − 1 , τ − 1 , σ + 1 + 260 γ ϱ − 1 , τ − 1 , σ + 2 − 260 γ ϱ − 1 , τ + 1 , σ − 2 − 6,760 γ ϱ − 1 , τ + 1 , σ − 1 − 1,716 0 γ ϱ − 1 , τ + 1 , σ − 6,760 γ ϱ − 1 , τ + 1 , σ + 1 − 260 γ ϱ − 1 , τ + 1 , σ + 2 − 26 γ ϱ − 1 , τ + 2 , σ − 2 − 676 γ ϱ − 1 , τ + 2 , σ − 1 − 1,716 γ ϱ − 1 , τ + 2 , σ − 676 γ ϱ − 1 , τ + 2 , σ + 1 − 26 γ ϱ − 1 , τ + 2 , σ + 2 + 66 γ ϱ , τ − 2 , σ − 2 + 1,716 γ ϱ , τ − 2 , σ − 1 + 4,356 γ ϱ , τ − 2 , σ + 1,716 γ ϱ , τ − 2 , σ + 1 + 66 γ ϱ , τ − 2 , σ + 2 + 660 γ ϱ , τ − 1 , σ − 2 + 1,716 0 γ ϱ , τ − 1 , σ − 1 + 43,560 γ ϱ , τ − 1 , σ + 1,716 0 γ ϱ , τ − 1 , σ + 1 + 660 γ ϱ , τ − 1 , σ + 2 − 660 γ ϱ , τ + 1 , σ − 2 − 1,716 0 γ ϱ , τ + 1 , σ − 1 − 43,560 γ ϱ , τ + 1 , σ − 1,716 0 γ ϱ , τ + 1 , σ + 1 − 660 γ ϱ , τ + 1 , σ + 2 − 66 γ ϱ , τ + 2 , σ − 2 − 1,716 γ ϱ , τ + 2 , σ − 1 − 4,356 γ ϱ , τ + 2 , σ − 1,716 γ ϱ , τ + 2 , σ + 1 − 66 γ ϱ , τ + 2 , σ + 2 + 26 γ ϱ + 1 , τ − 2 , σ − 2 + 676 γ ϱ + 1 , τ − 2 , σ − 1 + 1,716 γ ϱ + 1 , τ − 2 , σ + 676 γ ϱ + 1 , τ − 2 , σ + 1 + 26 γ ϱ + 1 , τ − 2 , σ + 2 + 260 γ ϱ + 1 , τ − 1 , σ − 2 + 6,760 γ ϱ + 1 , τ − 1 , σ − 1 + 1,716 0 γ ϱ + 1 , τ − 1 , σ + 6,760 γ ϱ + 1 , τ − 1 , σ + 1 + 260 γ ϱ + 1 , τ − 1 , σ + 2 − 260 γ ϱ + 1 , τ + 1 , σ − 2 − 6,760 γ ϱ + 1 , τ + 1 , σ − 1 − 1,716 0 γ ϱ + 1 , τ + 1 , σ − 6,760 γ ϱ + 1 , τ + 1 , σ + 1 − 260 γ ϱ + 1 , τ + 1 , σ + 2 − 26 γ ϱ + 1 , τ + 2 , σ − 2 − 676 γ ϱ + 1 , τ + 2 , σ − 1 − 1,716 γ ϱ + 1 , τ + 2 , σ − 676 γ ϱ + 1 , τ + 2 , σ + 1 − 26 γ ϱ + 1 , τ + 2 , σ + 2 + γ ϱ + 2 , τ − 2 , σ − 2 + 26 γ ϱ + 2 , τ − 2 , σ − 1 + 66 γ ϱ + 2 , τ − 2 , σ + 26 γ ϱ + 2 , τ − 2 , σ + 1 + γ ϱ + 2 , τ − 2 , σ + 2 + 10 γ ϱ + 2 , τ − 1 , σ − 2 + 260 γ ϱ + 2 , τ − 1 , σ − 1 + 660 γ ϱ + 2 , τ − 1 , σ + 260 γ ϱ + 2 , τ − 1 , σ + 1 + 10 γ ϱ + 2 , τ − 1 , σ + 2 − 10 γ ϱ + 2 , τ + 1 , σ − 2 − 260 γ ϱ + 2 , τ + 1 , σ − 1 − 660 γ ϱ + 2 , τ + 1 , σ − 260 γ ϱ + 2 , τ + 1 , σ + 1 − 10 γ ϱ + 2 , τ + 1 , σ + 2 − γ ϱ + 2 , τ + 2 , σ − 2 − 26 γ ϱ + 2 , τ + 2 , σ − 1 − 66 γ ϱ + 2 , τ + 2 , σ − 26 γ ϱ + 2 , τ + 2 , σ + 1 − γ ϱ + 2 , τ + 2 , σ + 2 ) ,

(11) ∂ H ϱ , τ , σ ∂ z = − 5 q ( γ ϱ − 2 , τ − 2 , σ − 2 + 10 γ ϱ − 2 , τ − 2 , σ − 1 − 10 γ ϱ − 2 , τ − 2 , σ + 1 − γ ϱ − 2 , τ − 2 , σ + 2 + 26 γ ϱ − 2 , τ − 1 , σ − 2 + 260 γ ϱ − 2 , τ − 1 , σ − 1 − 260 γ ϱ − 2 , τ − 1 , σ + 1 − 26 γ ϱ − 2 , τ − 1 , σ + 2 + 66 γ ϱ − 2 , τ , σ − 2 + 660 γ ϱ − 2 , τ , σ − 1 − 660 γ ϱ − 2 , τ , σ + 1 − 66 γ ϱ − 2 , τ , σ + 2 + 26 γ ϱ − 2 , τ + 1 , σ − 2 + 260 γ ϱ − 2 , τ + 1 , σ − 1 − 260 γ ϱ − 2 , τ + 1 , σ + 1 − 26 γ ϱ − 2 , τ + 1 , σ + 2 + γ ϱ − 2 , τ + 2 , σ − 2 + 10 γ ϱ − 2 , τ + 2 , σ − 1 − 10 γ ϱ − 2 , τ + 2 , σ + 1 − γ ϱ − 2 , τ + 2 , σ + 2 + 26 γ ϱ − 1 , τ − 2 , σ − 2 + 260 γ ϱ − 1 , τ − 2 , σ − 1 − 260 γ ϱ − 1 , τ − 2 , σ + 1 − 26 γ ϱ − 1 , τ − 2 , σ + 2 + 676 γ ϱ − 1 , τ − 1 , σ − 2 + 6,760 γ ϱ − 1 , τ − 1 , σ − 1 − 6,760 γ ϱ − 1 , τ − 1 , σ + 1 − 676 γ ϱ − 1 , τ − 1 , σ + 2 + 1,716 γ ϱ − 1 , τ , σ − 2 + 1,716 0 γ ϱ − 1 , τ , σ − 1 − 1,716 0 γ ϱ − 1 , τ , σ + 1 − 1,716 γ ϱ − 1 , τ , σ + 2 + 676 γ ϱ − 1 , τ + 1 , σ − 2 + 6,760 γ ϱ − 1 , τ + 1 , σ − 1 − 6,760 γ ϱ − 1 , τ + 1 , σ + 1 − 676 γ ϱ − 1 , τ + 1 , σ + 2 + 26 γ ϱ − 1 , τ + 2 , σ − 2 + 260 γ ϱ − 1 , τ + 2 , σ − 1 − 260 γ ϱ − 1 , τ + 2 , σ + 1 − 26 γ ϱ − 1 , τ + 2 , σ + 2 + 66 γ ϱ , τ − 2 , σ − 2 + 660 γ ϱ , τ − 2 , σ − 1 − 660 γ ϱ , τ − 2 , σ + 1 − 66 γ ϱ , τ − 2 , σ + 2 + 1,716 γ ϱ , τ − 1 , σ − 2 + 1,716 0 γ ϱ , τ − 1 , σ − 1 − 1,716 0 γ ϱ , τ − 1 , σ + 1 − 1,716 γ ϱ , τ − 1 , σ + 2 + 4,356 γ ϱ , τ , σ − 2 + 43,560 γ ϱ , τ , σ − 1 − 43,560 γ ϱ , τ , σ + 1 − 4,356 γ ϱ , τ , σ + 2 + 1,716 γ ϱ , τ + 1 , σ − 2 + 1,716 0 γ ϱ , τ + 1 , σ − 1 − 1,716 0 γ ϱ , τ + 1 , σ + 1 − 1,716 γ ϱ , τ + 1 , σ + 2 + 66 γ ϱ , τ + 2 , σ − 2 + 660 γ ϱ , τ + 2 , σ − 1 − 660 γ ϱ , τ + 2 , σ + 1 − 66 γ ϱ , τ + 2 , σ + 2 + 26 γ ϱ + 1 , τ − 2 , σ − 2 + 260 γ ϱ + 1 , τ − 2 , σ − 1 − 260 γ ϱ + 1 , τ − 2 , σ + 1 − 26 γ ϱ + 1 , τ − 2 , σ + 2 + 676 γ ϱ + 1 , τ − 1 , σ − 2 + 6,760 γ ϱ + 1 , τ − 1 , σ − 1 − 6,760 γ ϱ + 1 , τ − 1 , σ + 1 − 676 γ ϱ + 1 , τ − 1 , σ + 2 + 1,716 γ ϱ + 1 , τ , σ − 2 + 1,716 0 γ ϱ + 1 , τ , σ − 1 − 1,716 0 γ ϱ + 1 , τ , σ + 1 − 1,716 γ ϱ + 1 , τ , σ + 2 + 676 γ ϱ + 1 , τ + 1 , σ − 2 + 6,760 γ ϱ + 1 , τ + 1 , σ − 1 − 6,760 γ ϱ + 1 , τ + 1 , σ + 1 − 676 γ ϱ + 1 , τ + 1 , σ + 2 + 26 γ ϱ + 1 , τ + 2 , σ − 2 + 260 γ ϱ + 1 , τ + 2 , σ − 1 − 260 γ ϱ + 1 , τ + 2 , σ + 1 − 26 γ ϱ + 1 , τ + 2 , σ + 2 + γ ϱ + 2 , τ − 2 , σ − 2 + 10 γ ϱ + 2 , τ − 2 , σ − 1 − 10 γ ϱ + 2 , τ − 2 , σ + 1 − γ ϱ + 2 , τ − 2 , σ + 2 + 26 γ ϱ + 2 , τ − 1 , σ − 2 + 260 γ ϱ + 2 , τ − 1 , σ − 1 − 260 γ ϱ + 2 , τ − 1 , σ + 1 − 26 γ ϱ + 2 , τ − 1 , σ + 2 + 66 γ ϱ + 2 , τ , σ − 2 + 660 γ ϱ + 2 , τ , σ − 1 − 660 γ ϱ + 2 , τ , σ + 1 − 66 γ ϱ + 2 , τ , σ + 2 + 26 γ ϱ + 2 , τ + 1 , σ − 2 + 260 γ ϱ + 2 , τ + 1 , σ − 1 − 260 γ ϱ + 2 , τ + 1 , σ + 1 − 26 γ ϱ + 2 , τ + 1 , σ + 2 + γ ϱ + 2 , τ + 2 , σ − 2 + 10 γ ϱ + 2 , τ + 2 , σ − 1 − 10 γ ϱ + 2 , τ + 2 , σ + 1 − γ ϱ + 2 , τ + 2 , σ + 2 ) .

(12) ∂ 3 U m , n , r ∂ x ∂ y ∂ z = − 125 h k q ( γ ϱ − 2 , τ − 2 , σ − 2 + 10 γ ϱ − 2 , τ − 2 , σ − 1 − 10 γ ϱ − 2 , τ − 2 , σ + 1 − γ ϱ − 2 , τ − 2 , σ + 2 + 10 γ ϱ − 2 , τ − 1 , σ − 2 + 100 γ ϱ − 2 , τ − 1 , σ − 1 − 100 γ ϱ − 2 , τ − 1 , σ + 1 − 10 γ ϱ − 2 , τ − 1 , σ + 2 − 10 γ ϱ − 2 , τ + 1 , σ − 2 − 100 γ ϱ − 2 , τ + 1 , σ − 1 + 100 γ ϱ − 2 , τ + 1 , σ + 1 + 10 γ ϱ − 2 , τ + 1 , σ + 2 − γ ϱ − 2 , τ + 2 , σ − 2 − 10 γ ϱ − 2 , τ + 2 , σ − 1 + 10 γ ϱ − 2 , τ + 2 , σ + 1 + γ ϱ − 2 , τ + 2 , σ + 2 + 10 γ ϱ − 1 , τ − 2 , σ − 2 + 100 γ ϱ − 1 , τ − 2 , σ − 1 − 100 γ ϱ − 1 , τ − 2 , σ + 1 − 10 γ ϱ − 1 , τ − 2 , σ + 2 + 100 γ ϱ − 1 , τ − 1 , σ − 2 + 1,000 γ ϱ − 1 , τ − 1 , σ − 1 − 1,000 γ ϱ − 1 , τ − 1 , σ + 1 − 100 γ ϱ − 1 , τ − 1 , σ + 2 − 100 γ ϱ − 1 , τ + 1 , σ − 2 − 1,000 γ ϱ − 1 , τ + 1 , σ − 1 + 1,000 γ ϱ − 1 , τ + 1 , σ + 1 + 100 γ ϱ − 1 , τ + 1 , σ + 2 − 10 γ ϱ − 1 , τ + 2 , σ − 2 − 100 γ ϱ − 1 , τ + 2 , σ − 1 + 100 γ ϱ − 1 , τ + 2 , σ + 1 + 10 γ ϱ − 1 , τ + 2 , σ + 2 − 10 γ ϱ + 1 , τ − 2 , σ − 2 − 100 γ ϱ + 1 , τ − 2 , σ − 1 + 100 γ ϱ + 1 , τ − 2 , σ + 1 + 10 γ ϱ + 1 , τ − 2 , σ + 2 − 100 γ ϱ + 1 , τ − 1 , σ − 2 − 1,000 γ ϱ + 1 , τ − 1 , σ − 1 + 1,000 γ ϱ + 1 , τ − 1 , σ + 1 + 100 γ ϱ + 1 , τ − 1 , σ + 2 + 100 γ ϱ + 1 , τ + 1 , σ − 2 + 1,000 γ ϱ + 1 , τ + 1 , σ − 1 − 1,000 γ ϱ + 1 , τ + 1 , σ + 1 − 100 γ ϱ + 1 , τ + 1 , σ + 2 + 10 γ ϱ + 1 , τ + 2 , σ − 2 + 100 γ ϱ + 1 , τ + 2 , σ − 1 − 100 γ ϱ + 1 , τ + 2 , σ + 1 − 10 γ ϱ + 1 , τ + 2 , σ + 2 − γ ϱ + 2 , τ − 2 , σ − 2 − 10 γ ϱ + 2 , τ − 2 , σ − 1 + 10 γ ϱ + 2 , τ − 2 , σ + 1 + γ ϱ + 2 , τ − 2 , σ + 2 − 10 γ ϱ + 2 , τ − 1 , σ − 2 − 100 γ ϱ + 2 , τ − 1 , σ − 1 + 100 γ ϱ + 2 , τ − 1 , σ + 1 + 10 γ ϱ + 2 , τ − 1 , σ + 2 + 10 γ ϱ + 2 , τ + 1 , σ − 2 + 100 γ ϱ + 2 , τ + 1 , σ − 1 − 100 γ ϱ + 2 , τ + 1 , σ + 1 − 10 γ ϱ + 2 , τ + 1 , σ + 2 + γ ϱ + 2 , τ + 2 , σ − 2 + 10 γ ϱ + 2 , τ + 2 , σ − 1 − 10 γ ϱ + 2 , τ + 2 , σ + 1 − γ ϱ + 2 , τ + 2 , σ + 2 ) , ⋮

(13) ∂ 2 H ϱ , τ , σ ∂ x 2 = 20 h 2 ( γ ϱ − 2 , τ − 2 , σ − 2 + 26 γ ϱ − 2 , τ − 2 , σ − 1 + 66 γ ϱ − 2 , τ − 2 , σ + 26 γ ϱ − 2 , τ − 2 , σ + 1 + γ ϱ − 2 , τ − 2 , σ + 2 + 26 γ ϱ − 2 , τ − 1 , σ − 2 + 676 γ ϱ − 2 , τ − 1 , σ − 1 + 1,716 γ ϱ − 2 , τ − 1 , σ + 676 γ ϱ − 2 , τ − 1 , σ + 1 + 26 γ ϱ − 2 , τ − 1 , σ + 2 + 66 γ ϱ − 2 , τ , σ − 2 + 1,716 γ ϱ − 2 , τ , σ − 1 + 4,356 γ ϱ − 2 , τ , σ + 1,716 γ ϱ − 2 , τ , σ + 1 + 66 γ ϱ − 2 , τ , σ + 2 + 26 γ ϱ − 2 , τ + 1 , σ − 2 + 676 γ ϱ − 2 , τ + 1 , σ − 1 + 1,716 γ ϱ − 2 , τ + 1 , σ + 676 γ ϱ − 2 , τ + 1 , σ + 1 + 26 γ ϱ − 2 , τ + 1 , σ + 2 + γ ϱ − 2 , τ + 2 , σ − 2 + 26 γ ϱ − 2 , τ + 2 , σ − 1 + 66 γ ϱ − 2 , τ + 2 , σ + 26 γ ϱ − 2 , τ + 2 , σ + 1 + γ ϱ − 2 , τ + 2 , σ + 2 + 2 γ ϱ − 1 , τ − 2 , σ − 2 + 52 γ ϱ − 1 , τ − 2 , σ − 1 + 132 γ ϱ − 1 , τ − 2 , σ + 52 γ ϱ − 1 , τ − 2 , σ + 1 + 2 γ ϱ − 1 , τ − 2 , σ + 2 + 52 γ ϱ − 1 , τ − 1 , σ − 2 + 1,352 γ ϱ − 1 , τ − 1 , σ − 1 + 3,432 γ ϱ − 1 , τ − 1 , σ + 1,352 γ ϱ − 1 , τ − 1 , σ + 1 + 52 γ ϱ − 1 , τ − 1 , σ + 2 + 132 γ ϱ − 1 , τ , σ − 2 + 3,432 γ ϱ − 1 , τ , σ − 1 + 8,712 γ ϱ − 1 , τ , σ + 3,432 γ ϱ − 1 , τ , σ + 1 + 132 γ ϱ − 1 , τ , σ + 2 + 52 γ ϱ − 1 , τ + 1 , σ − 2 + 1,352 γ ϱ − 1 , τ + 1 , σ − 1 + 3,432 γ ϱ − 1 , τ + 1 , σ + 1,352 γ ϱ − 1 , τ + 1 , σ + 1 + 52 γ ϱ − 1 , τ + 1 , σ + 2 + 2 γ ϱ − 1 , τ + 2 , σ − 2 + 52 γ ϱ − 1 , τ + 2 , σ − 1 + 132 γ ϱ − 1 , τ + 2 , σ + 52 γ ϱ − 1 , τ + 2 , σ + 1 + 2 γ ϱ − 1 , τ + 2 , σ + 2 − 6 γ ϱ , τ − 2 , σ − 2 − 156 γ ϱ , τ − 2 , σ − 1 − 396 γ ϱ , τ − 2 , σ − 156 γ ϱ , τ − 2 , σ + 1 − 6 γ ϱ , τ − 2 , σ + 2 − 156 γ ϱ , τ − 1 , σ − 2 − 4,056 γ ϱ , τ − 1 , σ − 1 − 10,296 γ ϱ , τ − 1 , σ − 4,056 γ ϱ , τ − 1 , σ + 1 − 156 γ ϱ , τ − 1 , σ + 2 − 396 γ ϱ , τ , σ − 2 − 10,296 γ ϱ , τ , σ − 1 − 26,136 γ ϱ , τ , σ − 10,296 γ ϱ , τ , σ + 1 − 396 γ ϱ , τ , σ + 2 − 156 γ ϱ , τ + 1 , σ − 2 − 4,056 γ ϱ , τ + 1 , σ − 1 − 10,296 γ ϱ , τ + 1 , σ − 4,056 γ ϱ , τ + 1 , σ + 1 − 156 γ ϱ , τ + 1 , σ + 2 − 6 γ ϱ , τ + 2 , σ − 2 − 156 γ ϱ , τ + 2 , σ − 1 − 396 γ ϱ , τ + 2 , σ − 156 γ ϱ , τ + 2 , σ + 1 − 6 γ ϱ , τ + 2 , σ + 2 + 2 γ ϱ + 1 , τ − 2 , σ − 2 + 52 γ ϱ + 1 , τ − 2 , σ − 1 + 132 γ ϱ + 1 , τ − 2 , σ + 52 γ ϱ + 1 , τ − 2 , σ + 1 + 2 γ ϱ + 1 , τ − 2 , σ + 2 + 52 γ ϱ + 1 , τ − 1 , σ − 2 + 1,352 γ ϱ + 1 , τ − 1 , σ − 1 + 3,432 γ ϱ + 1 , τ − 1 , σ + 1,352 γ ϱ + 1 , τ − 1 , σ + 1 + 52 γ ϱ + 1 , τ − 1 , σ + 2 + 132 γ ϱ + 1 , τ , σ − 2 + 3,432 γ ϱ + 1 , τ , σ − 1 + 8,712 γ ϱ + 1 , τ , σ + 3,432 γ ϱ + 1 , τ , σ + 1 + 132 γ ϱ + 1 , τ , σ + 2 + 52 γ ϱ + 1 , τ + 1 , σ − 2 + 1,352 γ ϱ + 1 , τ + 1 , σ − 1 + 3,432 γ ϱ + 1 , τ + 1 , σ + 1,352 γ ϱ + 1 , τ + 1 , σ + 1 + 52 γ ϱ + 1 , τ + 1 , σ + 2 + 2 γ ϱ + 1 , τ + 2 , σ − 2 + 52 γ ϱ + 1 , τ + 2 , σ − 1 + 132 γ ϱ + 1 , τ + 2 , σ + 52 γ ϱ + 1 , τ + 2 , σ + 1 + 2 γ ϱ + 1 , τ + 2 , σ + 2 + γ ϱ + 2 , τ − 2 , σ − 2 + 26 γ ϱ + 2 , τ − 2 , σ − 1 + 66 γ ϱ + 2 , τ − 2 , σ + 26 γ ϱ + 2 , τ − 2 , σ + 1 + γ ϱ + 2 , τ − 2 , σ + 2 + 26 γ ϱ + 2 , τ − 1 , σ − 2 + 676 γ ϱ + 2 , τ − 1 , σ − 1 + 1,716 γ ϱ + 2 , τ − 1 , σ + 676 γ ϱ + 2 , τ − 1 , σ + 1 + 26 γ ϱ + 2 , τ − 1 , σ + 2 + 66 γ ϱ + 2 , τ , σ − 2 + 1,716 γ ϱ + 2 , τ , σ − 1 + 4,356 γ ϱ + 2 , τ , σ + 1,716 γ ϱ + 2 , τ , σ + 1 + 66 γ ϱ + 2 , τ , σ + 2 + 26 γ ϱ + 2 , τ + 1 , σ − 2 + 676 γ ϱ + 2 , τ + 1 , σ − 1 + 1,716 γ ϱ + 2 , τ + 1 , σ + 676 γ ϱ + 2 , τ + 1 , σ + 1 + 26 γ ϱ + 2 , τ + 1 , σ + 2 + γ ϱ + 2 , τ + 2 , σ − 2 + 26 γ ϱ + 2 , τ + 2 , σ − 1 + 66 γ ϱ + 2 , τ + 2 , σ + 26 γ ϱ + 2 , τ + 2 , σ + 1 + γ ϱ + 2 , τ + 2 , σ + 2 ) .

(14) ∂ 2 H ϱ , τ , σ ∂ y 2 = 20 k 2 ( γ ϱ − 2 , τ − 2 , σ − 2 + 26 γ ϱ − 2 , τ − 2 , σ − 1 + 66 γ ϱ − 2 , τ − 2 , σ + 26 γ ϱ − 2 , τ − 2 , σ + 1 + γ ϱ − 2 , τ − 2 , σ + 2 + 2 γ ϱ − 2 , τ − 1 , σ − 2 + 52 γ ϱ − 2 , τ − 1 , σ − 1 + 132 γ ϱ − 2 , τ − 1 , σ + 52 γ ϱ − 2 , τ − 1 , σ + 1 + 2 γ ϱ − 2 , τ − 1 , σ + 2 − 6 γ ϱ − 2 , τ , σ − 2 − 156 γ ϱ − 2 , τ , σ − 1 − 396 γ ϱ − 2 , τ , σ − 156 γ ϱ − 2 , τ , σ + 1 − 6 γ ϱ − 2 , τ , σ + 2 + 2 γ ϱ − 2 , τ + 1 , σ − 2 + 52 γ ϱ − 2 , τ + 1 , σ − 1 + 132 γ ϱ − 2 , τ + 1 , σ + 52 γ ϱ − 2 , τ + 1 , σ + 1 + 2 γ ϱ − 2 , τ + 1 , σ + 2 + γ ϱ − 2 , τ + 2 , σ − 2 + 26 γ ϱ − 2 , τ + 2 , σ − 1 + 66 γ ϱ − 2 , τ + 2 , σ + 26 γ ϱ − 2 , τ + 2 , σ + 1 + γ ϱ − 2 , τ + 2 , σ + 2 + 26 γ ϱ − 1 , τ − 2 , σ − 2 + 676 γ ϱ − 1 , τ − 2 , σ − 1 + 1,716 γ ϱ − 1 , τ − 2 , σ + 676 γ ϱ − 1 , τ − 2 , σ + 1 + 26 γ ϱ − 1 , τ − 2 , σ + 2 + 52 γ ϱ − 1 , τ − 1 , σ − 2 + 1,352 γ ϱ − 1 , τ − 1 , σ − 1 + 3,432 γ ϱ − 1 , τ − 1 , σ + 1,352 γ ϱ − 1 , τ − 1 , σ + 1 + 52 γ ϱ − 1 , τ − 1 , σ + 2 − 156 γ ϱ − 1 , τ , σ − 2 − 4,056 γ ϱ − 1 , τ , σ − 1 − 10,296 γ ϱ − 1 , τ , σ − 4,056 γ ϱ − 1 , τ , σ + 1 − 156 γ ϱ − 1 , τ , σ + 2 + 52 γ ϱ − 1 , τ + 1 , σ − 2 + 1,352 γ ϱ − 1 , τ + 1 , σ − 1 + 3,432 γ ϱ − 1 , τ + 1 , σ + 1,352 γ ϱ − 1 , τ + 1 , σ + 1 + 52 γ ϱ − 1 , τ + 1 , σ + 2 + 26 γ ϱ − 1 , τ + 2 , σ − 2 + 676 γ ϱ − 1 , τ + 2 , σ − 1 + 1,716 γ ϱ − 1 , τ + 2 , σ + 676 γ ϱ − 1 , τ + 2 , σ + 1 + 26 γ ϱ − 1 , τ + 2 , σ + 2 + 66 γ ϱ , τ − 2 , σ − 2 + 1,716 γ ϱ , τ − 2 , σ − 1 + 4,356 γ ϱ , τ − 2 , σ + 1,716 γ ϱ , τ − 2 , σ + 1 + 66 γ ϱ , τ − 2 , σ + 2 + 132 γ ϱ , τ − 1 , σ − 2 + 3,432 γ ϱ , τ − 1 , σ − 1 + 8,712 γ ϱ , τ − 1 , σ + 3,432 γ ϱ , τ − 1 , σ + 1 + 132 γ ϱ , τ − 1 , σ + 2 − 396 γ ϱ , τ , σ − 2 − 10,296 γ ϱ , τ , σ − 1 − 26,136 γ ϱ , τ , σ − 10,296 γ ϱ , τ , σ + 1 − 396 γ ϱ , τ , σ + 2 + 132 γ ϱ , τ + 1 , σ − 2 + 3,432 γ ϱ , τ + 1 , σ − 1 + 8,712 γ ϱ , τ + 1 , σ + 3,432 γ ϱ , τ + 1 , σ + 1 + 132 γ ϱ , τ + 1 , σ + 2 + 66 γ ϱ , τ + 2 , σ − 2 + 1,716 γ ϱ , τ + 2 , σ − 1 + 4,356 γ ϱ , τ + 2 , σ + 1,716 γ ϱ , τ + 2 , σ + 1 + 66 γ ϱ , τ + 2 , σ + 2 + 26 γ ϱ + 1 , τ − 2 , σ − 2 + 676 γ ϱ + 1 , τ − 2 , σ − 1 + 1,716 γ ϱ + 1 , τ − 2 , σ + 676 γ ϱ + 1 , τ − 2 , σ + 1 + 26 γ ϱ + 1 , τ − 2 , σ + 2 + 52 γ ϱ + 1 , τ − 1 , σ − 2

+ 1,352 γ ϱ + 1 , τ − 1 , σ − 1 + 3,432 γ ϱ + 1 , τ − 1 , σ + 1,352 γ ϱ + 1 , τ − 1 , σ + 1 + 52 γ ϱ + 1 , τ − 1 , σ + 2 − 156 γ ϱ + 1 , τ , σ − 2 − 4,056 γ ϱ + 1 , τ , σ − 1 − 10,296 γ ϱ + 1 , τ , σ − 4,056 γ ϱ + 1 , τ , σ + 1 − 156 γ ϱ + 1 , τ , σ + 2 + 52 γ ϱ + 1 , τ + 1 , σ − 2 + 1,352 γ ϱ + 1 , τ + 1 , σ − 1 + 3,432 γ ϱ + 1 , τ + 1 , σ + 1,352 γ ϱ + 1 , τ + 1 , σ + 1 + 52 γ ϱ + 1 , τ + 1 , σ + 2 + 26 γ ϱ + 1 , τ + 2 , σ − 2 + 676 γ ϱ + 1 , τ + 2 , σ − 1 + 1,716 γ ϱ + 1 , τ + 2 , σ + 676 γ ϱ + 1 , τ + 2 , σ + 1 + 26 γ ϱ + 1 , τ + 2 , σ + 2 + γ ϱ + 2 , τ − 2 , σ − 2 + 26 γ ϱ + 2 , τ − 2 , σ − 1 + 66 γ ϱ + 2 , τ − 2 , σ + 26 γ ϱ + 2 , τ − 2 , σ + 1 + γ ϱ + 2 , τ − 2 , σ + 2 + 2 γ ϱ + 2 , τ − 1 , σ − 2 + 52 γ ϱ + 2 , τ − 1 , σ − 1 + 132 γ ϱ + 2 , τ − 1 , σ + 52 γ ϱ + 2 , τ − 1 , σ + 1 + 2 γ ϱ + 2 , τ − 1 , σ + 2 − 6 γ ϱ + 2 , τ , σ − 2 − 156 γ ϱ + 2 , τ , σ − 1 − 396 γ ϱ + 2 , τ , σ − 156 γ ϱ + 2 , τ , σ + 1 − 6 γ ϱ + 2 , τ , σ + 2 + 2 γ ϱ + 2 , τ + 1 , σ − 2 + 52 γ ϱ + 2 , τ + 1 , σ − 1 + 132 γ ϱ + 2 , τ + 1 , σ + 52 γ ϱ + 2 , τ + 1 , σ + 1 + 2 γ ϱ + 2 , τ + 1 , σ + 2 + γ ϱ + 2 , τ + 2 , σ − 2 + 26 γ ϱ + 2 , τ + 2 , σ − 1 + 66 γ ϱ + 2 , τ + 2 , σ + 26 γ ϱ + 2 , τ + 2 , σ + 1 + γ ϱ + 2 , τ + 2 , σ + 2 ) .

(15) ∂ 2 U m , n , r ∂ z 2 = 20 q 2 ( γ ϱ − 2 , τ − 2 , σ − 2 + 2 γ ϱ − 2 , τ − 2 , σ − 1 − 6 γ ϱ − 2 , τ − 2 , σ + 2 γ ϱ − 2 , τ − 2 , σ + 1 + γ ϱ − 2 , τ − 2 , σ + 2 + 26 γ ϱ − 2 , τ − 1 , σ − 2 + 52 γ ϱ − 2 , τ − 1 , σ − 1 − 156 γ ϱ − 2 , τ − 1 , σ + 52 γ ϱ − 2 , τ − 1 , σ + 1 + 26 γ ϱ − 2 , τ − 1 , σ + 2 + 66 γ ϱ − 2 , τ , σ − 2 + 132 γ ϱ − 2 , τ , σ − 1 − 396 γ ϱ − 2 , τ , σ + 132 γ ϱ − 2 , τ , σ + 1 + 66 γ ϱ − 2 , τ , σ + 2 + 26 γ ϱ − 2 , τ + 1 , σ − 2 + 52 γ ϱ − 2 , τ + 1 , σ − 1 − 156 γ ϱ − 2 , τ + 1 , σ + 52 γ ϱ − 2 , τ + 1 , σ + 1 + 26 γ ϱ − 2 , τ + 1 , σ + 2 + γ ϱ − 2 , τ + 2 , σ − 2 + 2 γ ϱ − 2 , τ + 2 , σ − 1 − 6 γ ϱ − 2 , τ + 2 , σ + 2 γ ϱ − 2 , τ + 2 , σ + 1 + γ ϱ − 2 , τ + 2 , σ + 2 + 26 γ ϱ − 1 , τ − 2 , σ − 2 + 52 γ ϱ − 1 , τ − 2 , σ − 1 − 156 γ ϱ − 1 , τ − 2 , σ + 52 γ ϱ − 1 , τ − 2 , σ + 1 + 26 γ ϱ − 1 , τ − 2 , σ + 2 + 676 γ ϱ − 1 , τ − 1 , σ − 2 + 1,352 γ ϱ − 1 , τ − 1 , σ − 1 − 4,056 γ ϱ − 1 , τ − 1 , σ + 1,352 γ ϱ − 1 , τ − 1 , σ + 1 + 676 γ ϱ − 1 , τ − 1 , σ + 2 + 1,716 γ ϱ − 1 , τ , σ − 2 + 3,432 γ ϱ − 1 , τ , σ − 1 − 10,296 γ ϱ − 1 , τ , σ + 3,432 γ ϱ − 1 , τ , σ + 1 + 1,716 γ ϱ − 1 , τ , σ + 2 + 676 γ ϱ − 1 , τ + 1 , σ − 2 + 1,352 γ ϱ − 1 , τ + 1 , σ − 1 − 4,056 γ ϱ − 1 , τ + 1 , σ + 1,352 γ ϱ − 1 , τ + 1 , σ + 1 + 676 γ ϱ − 1 , τ + 1 , σ + 2 + 26 γ ϱ − 1 , τ + 2 , σ − 2 + 52 γ ϱ − 1 , τ + 2 , σ − 1 − 156 γ ϱ − 1 , τ + 2 , σ + 52 γ ϱ − 1 , τ + 2 , σ + 1 + 26 γ ϱ − 1 , τ + 2 , σ + 2 + 66 γ ϱ , τ − 2 , σ − 2 + 132 γ ϱ , τ − 2 , σ − 1 − 396 γ ϱ , τ − 2 , σ + 132 γ ϱ , τ − 2 , σ + 1 + 66 γ ϱ , τ − 2 , σ + 2 + 1,716 γ ϱ , τ − 1 , σ − 2 + 3,432 γ ϱ , τ − 1 , σ − 1 − 10,296 γ ϱ , τ − 1 , σ + 3,432 γ ϱ , τ − 1 , σ + 1 + 1,716 γ ϱ , τ − 1 , σ + 2 + 4,356 γ ϱ , τ , σ − 2 + 8,712 γ ϱ , τ , σ − 1 − 26,136 γ ϱ , τ , σ + 8,712 γ ϱ , τ , σ + 1 + 4,356 γ ϱ , τ , σ + 2 + 1,716 γ ϱ , τ + 1 , σ − 2 + 3,432 γ ϱ , τ + 1 , σ − 1 − 10,296 γ ϱ , τ + 1 , σ + 3,432 γ ϱ , τ + 1 , σ + 1 + 1,716 γ ϱ , τ + 1 , σ + 2 + 66 γ ϱ , τ + 2 , σ − 2 + 132 γ ϱ , τ + 2 , σ − 1 − 396 γ ϱ , τ + 2 , σ + 132 γ ϱ , τ + 2 , σ + 1 + 66 γ ϱ , τ + 2 , σ + 2 + 26 γ ϱ + 1 , τ − 2 , σ − 2 + 52 γ ϱ + 1 , τ − 2 , σ − 1 − 156 γ ϱ + 1 , τ − 2 , σ + 52 γ ϱ + 1 , τ − 2 , σ + 1 + 26 γ ϱ + 1 , τ − 2 , σ + 2 + 676 γ ϱ + 1 , τ − 1 , σ − 2 + 1,352 γ ϱ + 1 , τ − 1 , σ − 1 − 4,056 γ ϱ + 1 , τ − 1 , σ + 1,352 γ ϱ + 1 , τ − 1 , σ + 1 + 676 γ ϱ + 1 , τ − 1 , σ + 2 + 1,716 γ ϱ + 1 , τ , σ − 2 + 3,432 γ ϱ + 1 , τ , σ − 1 − 10,296 γ ϱ + 1 , τ , σ + 3,432 γ ϱ + 1 , τ , σ + 1 + 1,716 γ ϱ + 1 , τ , σ + 2 + 676 γ ϱ + 1 , τ + 1 , σ − 2 + 1,352 γ ϱ + 1 , τ + 1 , σ − 1 − 4,056 γ ϱ + 1 , τ + 1 , σ + 1,352 γ ϱ + 1 , τ + 1 , σ + 1 + 676 γ ϱ + 1 , τ + 1 , σ + 2 + 26 γ ϱ + 1 , τ + 2 , σ − 2 + 52 γ ϱ + 1 , τ + 2 , σ − 1 − 156 γ ϱ + 1 , τ + 2 , σ + 52 γ ϱ + 1 , τ + 2 , σ + 1 + 26 γ ϱ + 1 , τ + 2 , σ + 2 + γ ϱ + 2 , τ − 2 , σ − 2 + 2 γ ϱ + 2 , τ − 2 , σ − 1 − 6 γ ϱ + 2 , τ − 2 , σ + 2 γ ϱ + 2 , τ − 2 , σ + 1 + γ ϱ + 2 , τ − 2 , σ + 2 + 26 γ ϱ + 2 , τ − 1 , σ − 2 + 52 γ ϱ + 2 , τ − 1 , σ − 1 − 156 γ ϱ + 2 , τ − 1 , σ + 52 γ ϱ + 2 , τ − 1 , σ + 1 + 26 γ ϱ + 2 , τ − 1 , σ + 2 + 66 γ ϱ + 2 , τ , σ − 2 + 132 γ ϱ + 2 , τ , σ − 1 − 396 γ ϱ + 2 , τ , σ + 132 γ ϱ + 2 , τ , σ + 1 + 66 γ ϱ + 2 , τ , σ + 2 + 26 γ ϱ + 2 , τ + 1 , σ − 2 + 52 γ ϱ + 2 , τ + 1 , σ − 1 − 156 γ ϱ + 2 , τ + 1 , σ + 52 γ ϱ + 2 , τ + 1 , σ + 1 + 26 γ ϱ + 2 , τ + 1 , σ + 2 + γ ϱ + 2 , τ + 2 , σ − 2 + 2 γ ϱ + 2 , τ + 2 , σ − 1 − 6 γ ϱ + 2 , τ + 2 , σ + 2 γ ϱ + 2 , τ + 2 , σ + 1 + γ ϱ + 2 , τ + 2 , σ + 2 ) .

The above analysis yields the following theorem:

Theorem 3

The solution of three-dimensional DE using the collocation method with basis quintic B-spline can be determined by Eqs. (8)–(15).

3 The numerical outcomes

Now, we must know whether this method, which was developed by presenting its constructions in different dimensions, is accurate and effective or not. To prove that this method is of high accuracy, we present in this section various numerical examples in different dimensional. We also show some figures of the results obtained. In addition provide comparisons of our results with pre-existing results.

The first test problem: [20]

We take the test problem in the two-dimensional in the following form:

(16) h x x ( x , y ) + h y y ( x , y ) + h x ( x , y ) + h y ( x , y ) − 3 e 2 x + 3 y ( x 2 ( 18 y 2 − 4 y − 5 ) + x ( 5 − 8 y 2 − 6 y ) − 3 y 2 + 3 y ) = 0 , x , y ∈ [ l , m ] .

The exact solution to that problem is given as follows:

(17) h ( x , y ) = 3 e 2 x + 3 y ( x − x 2 ) ( y − y 2 ) .

We take the boundary conditions of the first problem in the following form:

(18) h ( l , y ) = h ( x , l ) = α , h ( m , y ) = h ( x , m ) = β .

By substituting from (4)–(6) into (16) with (18) we obtain the numerical results as in Table 1.

Table 1

The computational results to the problem at y = 0.5 , x , y ∈ [ 0 , 1 ]

x Numerical results Exact results Absolute error Quadratic B-Spline [20]
0.1 0.36844 0.36949 1.04272 × 1 0 − 3 1.06992 × 1 0 − 3
0.2 0.80013 0.80230 2.16802 × 1 0 − 3 2.32385 × 1 0 − 3
0.3 1.28303 1.28617 3.13752 × 1 0 − 3 3.40917 × 1 0 − 3
0.4 1.79142 1.79535 3.93387 × 1 0 − 3 4.31609 × 1 0 − 3
0.5 2.27968 2.28422 4.53888 × 1 0 − 3 5.04294 × 1 0 − 3
0.6 2.67341 2.67835 4.94235 × 1 0 − 3 5.60652 × 1 0 − 3
0.7 2.85727 2.86243 5.15340 × 1 0 − 3 6.05466 × 1 0 − 3
0.8 2.65855 2.66375 5.20654 × 1 0 − 3 6.46809 × 1 0 − 3
0.9 1.82495 1.83010 5.15163 × 1 0 − 3 6.93102 × 1 0 − 3

We contrasted the exact solutions with the results of the two-dimensional quintic B-spline technique using a mesh divided into 50 × 50 in Table 1. Figures 1 and 2 display numerical results with exact results at y = 0.5 and x = 0.5 , respectively. The three-dimensional graph for numerical results is shown in Figure 3.

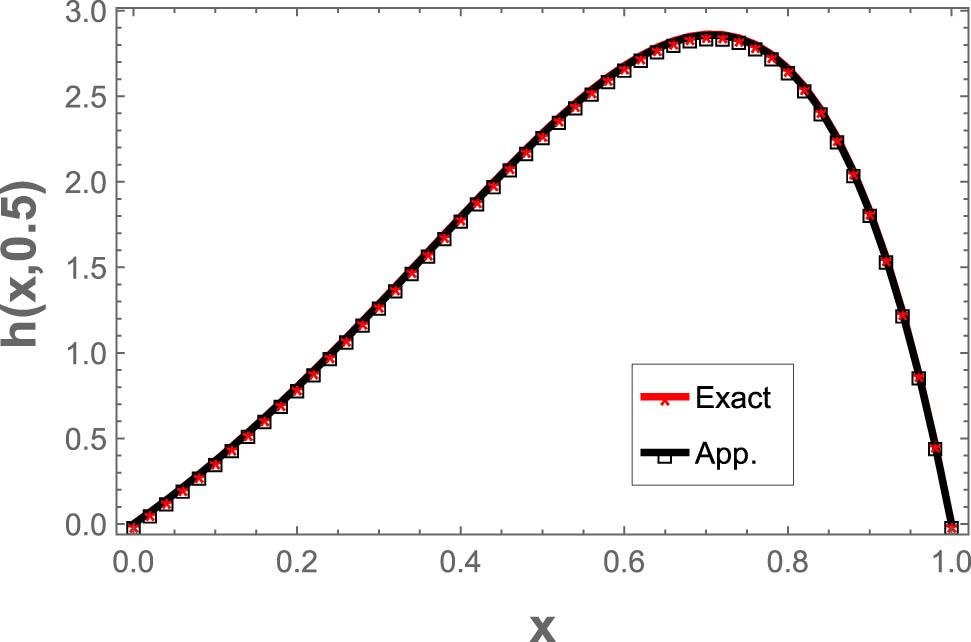
Figure 1 The exact results at y = 0.5 y=0.5 and the numerical results.
Figure 1

The exact results at y = 0.5 and the numerical results.

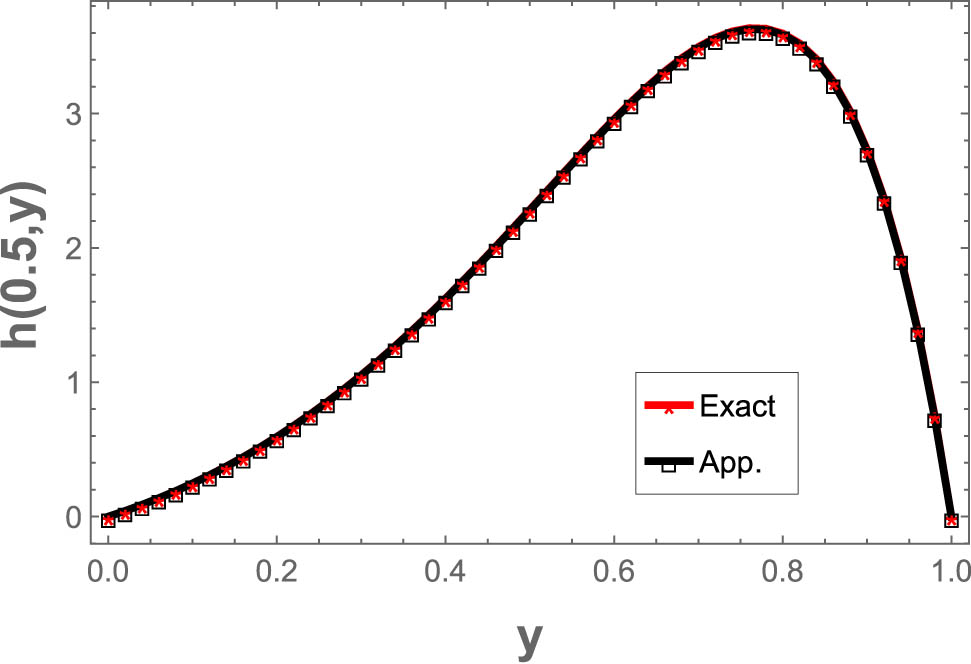
Figure 2 The exact results at x = 0.5 x=0.5 and the numerical results.
Figure 2

The exact results at x = 0.5 and the numerical results.

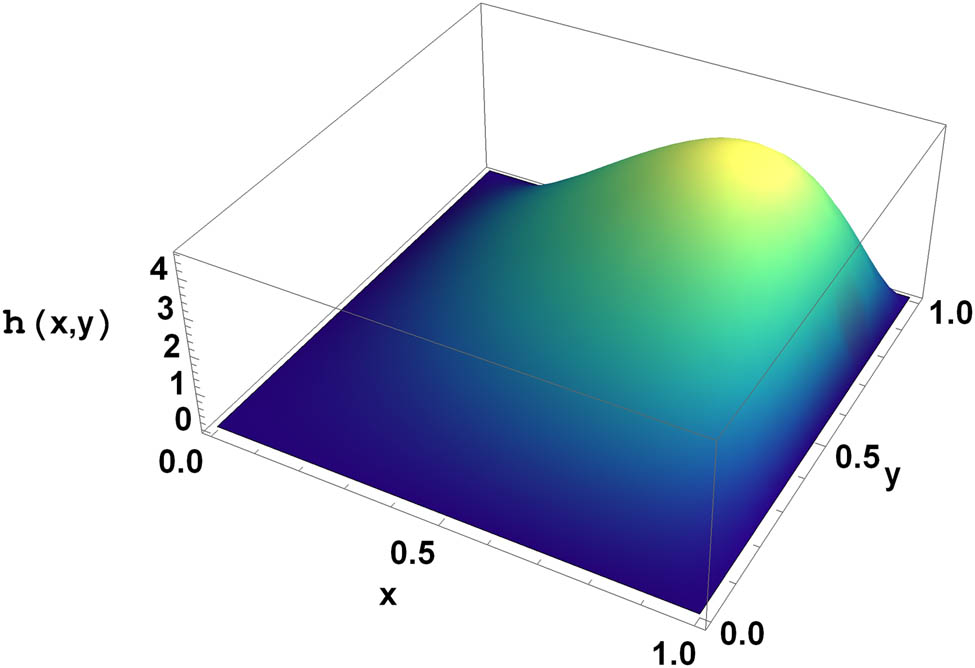
Figure 3 Three-dimensional graph for numerical results.
Figure 3

Three-dimensional graph for numerical results.

The second test problem: [14,15,19,20,26]

We take the test problem in the two-dimensional in the following form:

(19) h x x ( x , y ) + h y y ( x , y ) − sin ( π x ) sin ( π y ) = 0 , x , y ∈ [ l , m ] .

The following is the exact solution to that problem:

(20) h ( x , y ) = − sin ( π x ) sin ( π y ) 2 π 2 .

We take the boundary conditions to the third problem in the following form:

(21) h ( l , y ) = h ( x , l ) = α , h ( m , y ) = h ( x , m ) = β .

By substituting from (4)–(6) into (19) with (21) we obtain the numerical results as in Table 2.

Table 2

The numerical results for the problem are available at y = 0.4 , x , y ∈ [ 0 , 1 ]

x Numerical results Exact results Absolute error
0.2 − 0.028320 − 0.028320 7.63952 × 1 0 − 8
0.4 − 0.045822 − 0.045822 1.23610 × 1 0 − 7
0.6 − 0.045822 − 0.045822 1.23610 × 1 0 − 7
0.8 − 0.028320 − 0.028320 7.63952 × 1 0 − 8

Table 2 presents the results of the two-dimensional quintic B-spline technique at 15 × 15 . In terms of results, we can assume that the results are acceptable. Figures 4 and 5 display the numerical results with exact results at y = 0.4 . The three-dimensional graph for numerical results is shown in Figure 6.

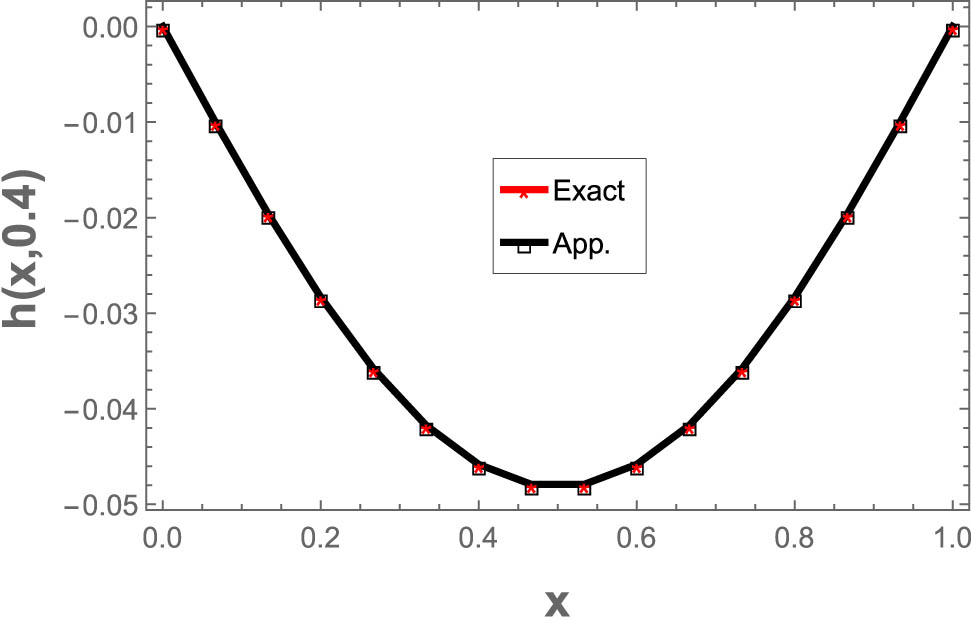
Figure 4 The numerical results are compared to the exact results at y = 0.4 y=0.4 .
Figure 4

The numerical results are compared to the exact results at y = 0.4 .

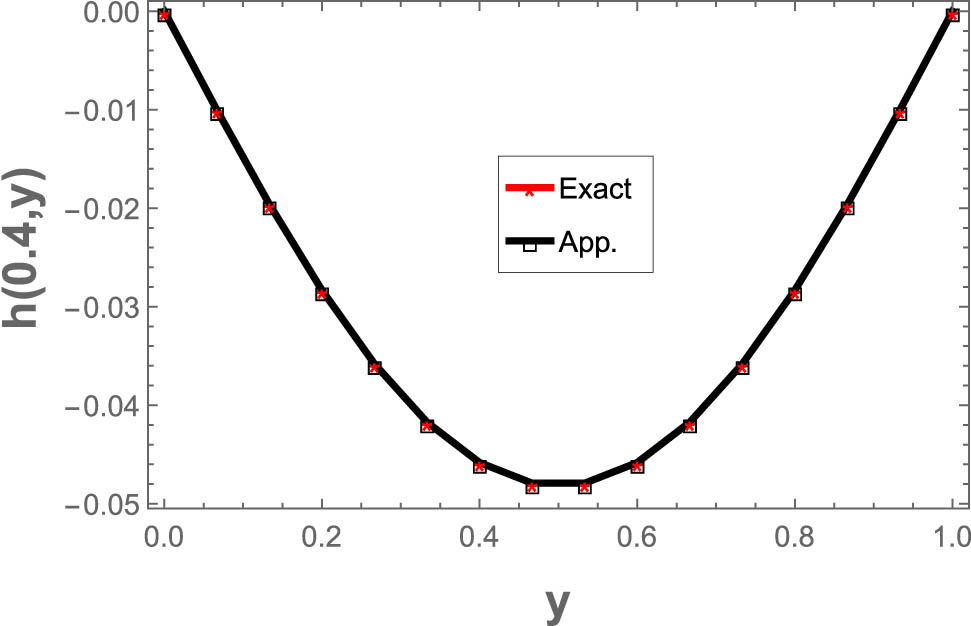
Figure 5 The numerical results are compared to the exact results at x = 0.4 x=0.4 .
Figure 5

The numerical results are compared to the exact results at x = 0.4 .

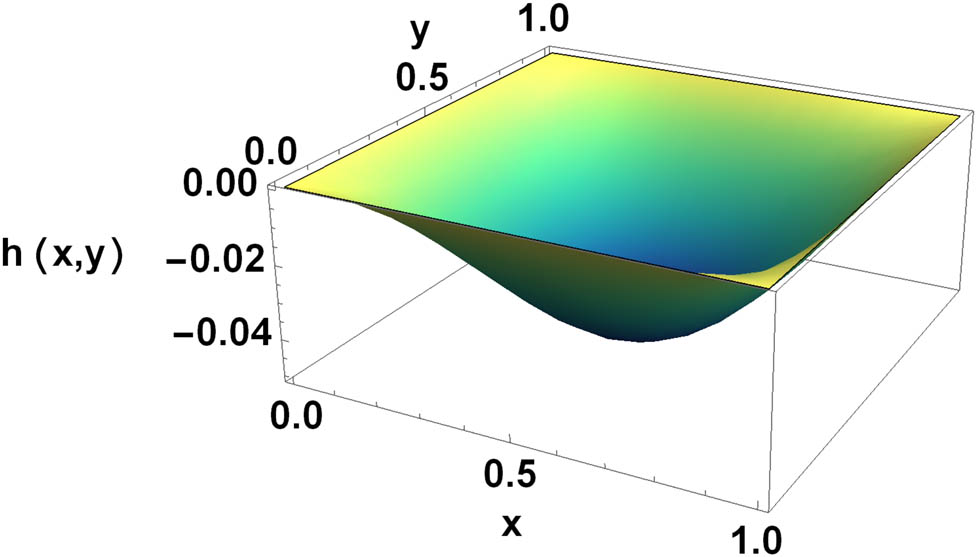
Figure 6 Three-dimensional graph for numerical results.
Figure 6

Three-dimensional graph for numerical results.

We compare the results of the proposed method to the results of various methods [14,15,19,20,26] that are shown in Table 5 using mesh 15 × 15 grid points.

Table 3 shows the maximum absolute error based on the approach used to solve the problem.

Table 3

The maximum absolute error

The proposed method Quadratic B-spline approach [20] MCBDQM approach [19] Spline-based DQM approach [26] Haar wavelet approach [14] Spectral collocation approach based on Haarwavelets [15]
7.63 × 1 0 − 8 3.72 × 1 0 − 5 2.11 × 1 0 − 5 1.62 × 1 0 − 4 3.08 × 1 0 − 4 3.08 × 1 0 − 4

MCBDQM: modified cubic B-spline differential quadrature method; DQM: B-spline differential quadrature method.

The third test problem: [20]

We take the test problem in the three-dimensional in the following form:

(22) h x x ( x , y , z ) + h y y ( x , y , z ) + h z z ( x , y , z ) − x y z ( e x + y + z ) ( 3 y x z + y x + z x − 5 x + z y − 5 y − 5 z + 9 ) = 0 , x , y , z ∈ [ l , m ] .

The exact solution to that problem is given as follows:

(23) h ( x , y , z ) = ( x − x 2 ) ( y − y 2 ) ( z − z 2 ) e x + y + z .

We take the boundary conditions to the fourth problem in the following form:

(24) h ( l , y , z ) = h ( x , l , z ) = h ( x , y , l ) = α , h ( m , y , z ) = h ( x , m , z ) = h ( x , y , m ) = β .

By substituting from (8)–(15) into (22) with (24) we obtain the numerical results as in Table 4.

Table 4

The numerical results for test problem at z = y = 0.5 , x , y , z ∈ [ 0 , 1 ]

x Numerical solution Exact solution Absolute error Quadratic B-spline method [20]
0.1 0.016868 0.0168984 3.00290 × 1 0 − 5 3.24947 × 1 0 − 5
0.2 0.033142 0.0332012 5.91336 × 1 0 − 5 6.49943 × 1 0 − 5
0.3 0.048073 0.0481595 8.64991 × 1 0 − 5 9.65554 × 1 0 − 5
0.4 0.060716 0.0608280 1.11772 × 1 0 − 4 1.27075 × 1 0 − 4
0.5 0.069891 0.0700264 1.35404 × 1 0 − 4 1.57835 × 1 0 − 4
0.6 0.074136 0.0742955 1.59207 × 1 0 − 4 1.92337 × 1 0 − 4
0.7 0.071658 0.0718456 1.87092 × 1 0 − 4 2.37433 × 1 0 − 4
0.8 0.060271 0.0604965 2.25422 × 1 0 − 4 3.04639 × 1 0 − 4
0.9 0.050423 0.0376082 2.56119 × 1 0 − 4 4.11161 × 1 0 − 4

Table 4 presents comparison between our results with the results of Quadratic B-spline technique using mesh 20 × 20 . In terms of the results based on our observations, we can see that the results are acceptable. Figure 7 shows the numerical results with exact solutions at y = z = 0.5 . The three-dimensional graph for numerical results is shown in Figure 8.

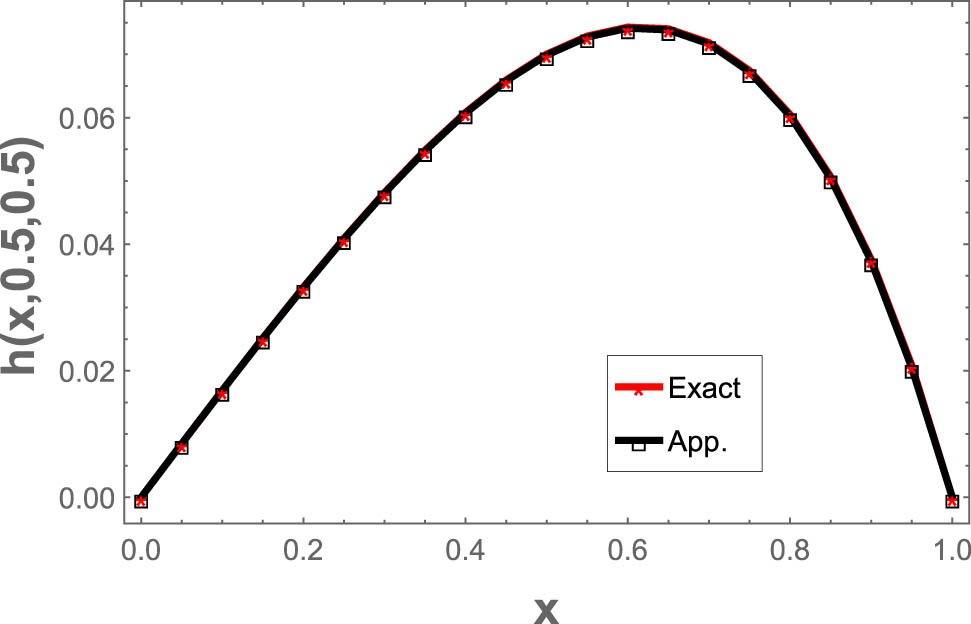
Figure 7 The numerical results with exact results at y = z = 0.5 y=z=0.5 .
Figure 7

The numerical results with exact results at y = z = 0.5 .

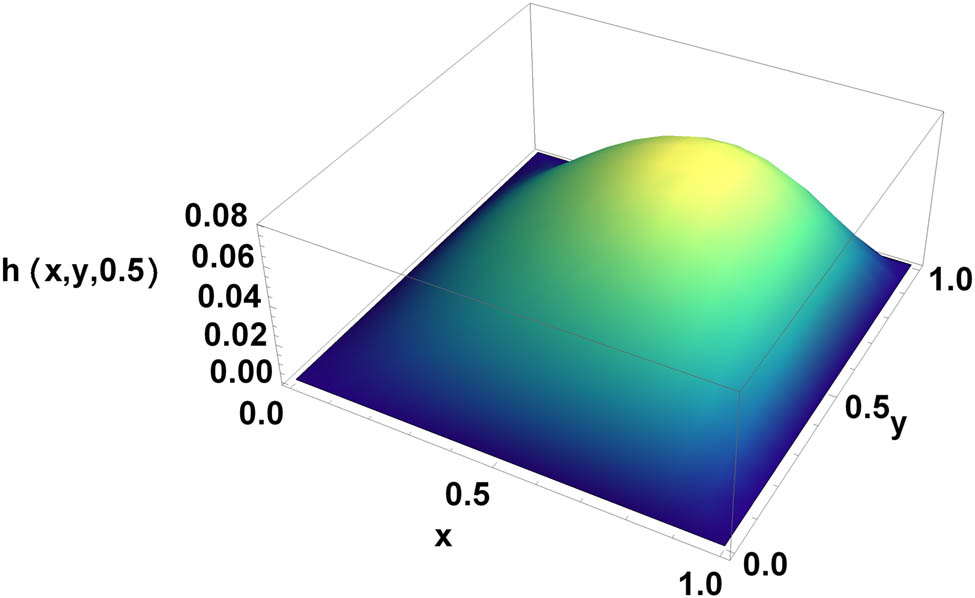
Figure 8 Three-dimensional graph for numerical results.
Figure 8

Three-dimensional graph for numerical results.

The fourth test problem: [15]

We take the test problem in the two-dimensional in the following form:

(25) h x x ( x , y , z ) + h y y ( x , y , z ) + h z z ( x , y , z ) − sin ( π x ) sin ( π y ) sin ( π z ) = 0 , x , y , z ∈ [ l , m ] .

The following is the exact solution to that problem:

(26) h ( x , y , z ) = − sin ( π x ) sin ( π y ) sin ( π z ) 2 π 2 .

We take the boundary conditions to the third problem in the following form:

(27) h ( l , y , z ) = h ( x , l , z ) = h ( x , y , l ) = α , h ( m , y , z ) = h ( x , m , z ) = h ( x , y , m ) = β .

By substituting from (8)–(15) into (25) with (27) we obtain the numerical results as in Table 5.

Table 5

The numerical results for the test problem are available at y = z = 0.5 , x , y , z ∈ [ 0 , 1 ]

x Numerical results Exact results Absolute error Maximum absolute error of our method Maximum absolute error [15]
0.2 − 0.0198517 − 0.0198517 1.68747 × 1 0 − 8 4.96665 × 1 0 − 5 8.9227 × 1 0 − 4
0.4 − 0.0321207 − 0.0321207 2.73039 × 1 0 − 8 — —
0.6 − 0.0321207 − 0.0321207 2.73039 × 1 0 − 8 — —
0.8 − 0.0198517 − 0.0198517 1.68747 × 1 0 − 8 — —

In Table 5 we present our results of the two-dimensional quintic B-spline technique using mesh 15 × 15 . In terms of observation, we can see that the results are acceptable. Figure 9 displays the numerical results with exact results at y = z = 0.5 . The three-dimensional graph for numerical results is shown in Figure 10.

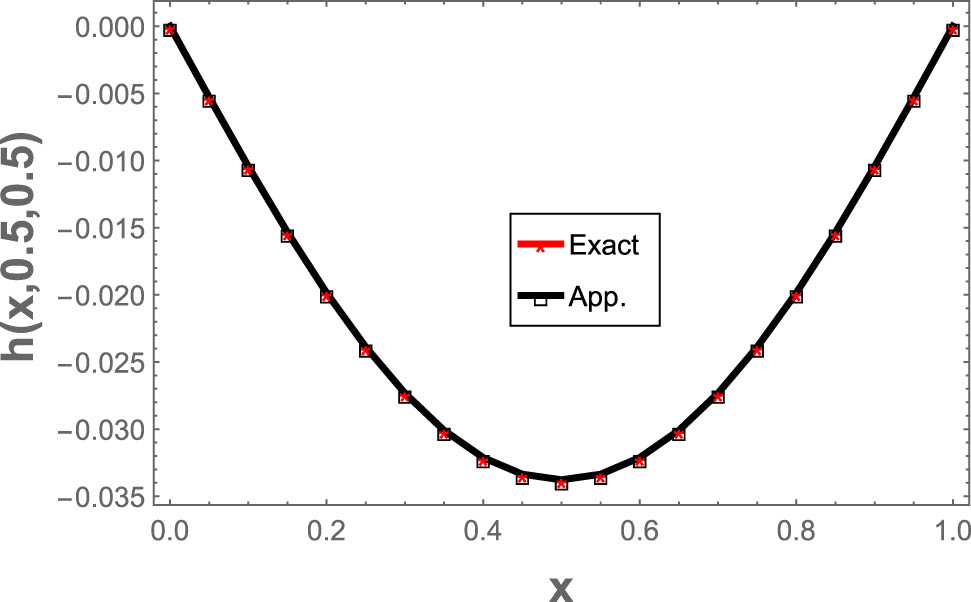
Figure 9 The numerical results are compared to the exact results at y = z = 0.5 y=z=0.5 .
Figure 9

The numerical results are compared to the exact results at y = z = 0.5 .

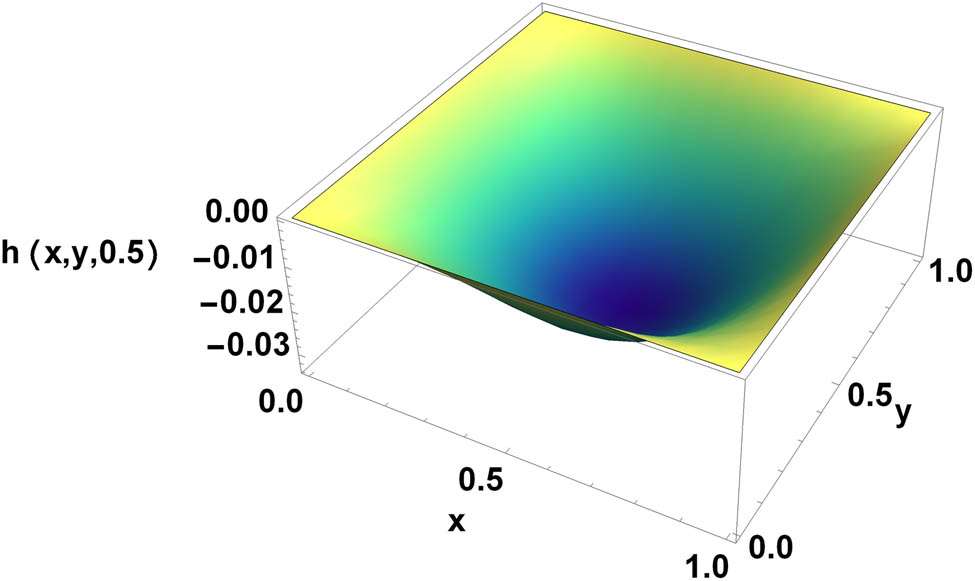
Figure 10 Three-dimensional graph for numerical results.
Figure 10

Three-dimensional graph for numerical results.

4 Conclusion

Perhaps by the end of this project, we will have made a significant contribution to tackling some of the challenges that most academics in various domains have when dealing with n-dimensional mathematical models. The research problem is really important, and we feel that the majority of scholars are eagerly awaiting the findings. After watching some researchers discuss their findings on partial differential equation solutions in one, two, and three dimensions, we realized how difficult it is for them to cope with these models as the dimension grows. As a result, we chose to extend the quintic B-spline method, which had previously been utilized to answer one-dimensional mathematical problems, and we were able to present it in two and three dimensions. We used numerical examples of various dimensional to assess the correctness and efficacy of the produced forms. When the numerical results were compared to the actual solution, we find that the formulas that were determined are efficient. We think that a major contribution has been made toward solving problems involving partial differential equations in various dimensional from this perspective. As part of our long-term research, we would generalize a few other B-Splines shapes to serve as solutions to differential equations in n-dimensional.

Acknowledgments

All authors thank the editor chief of the journal, the editor who follows up the paper, and all employees of the journal.

  1. Funding information: Not applicable.

  2. Author contributions: The authors declare that the study was realized in collaboration with equal responsibility. All authors read and approved the final manuscript.

  3. Conflict of interest: The authors declare that they have no conflict of interests.

  4. Data availability statement: Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.

References

[1] Ali KK, Mehanna MS. Analytical and numerical solutions to the (3+1)-dimensional Date-Jimbo-Kashiwara-Miwa with time-dependent coefficients. Alexandr Eng J. 2021;60(6):5275–85. 10.1016/j.aej.2021.04.045Suche in Google Scholar

[2] Ali KK, Mehanna MS. On some new soliton solutions of (3+1)-dimensional Boiti-Leon-Manna-Pempinelli equation using two different methods. Arab J Basic Appl Sci. 2021;28(1):234–43. 10.1080/25765299.2021.1927498Suche in Google Scholar

[3] Ali KK, Wazwaz A-M, Mehanna MS, Osman MS. On short-range pulse propagation described by (2+1)-dimensional Schrödinger’s hyperbolic equation in nonlinear optical fibers. Physica Scripta. 2020;95(2020):075203. 10.1088/1402-4896/ab8d57Suche in Google Scholar

[4] Abdelwahab AM, Mekheimer KhS, Ali KK, EL-Kholy A, Sweed NS, Numerical simulation of electroosmotic force on micropolar pulsatile bloodstream through aneurysm and stenosis of carotid. Waves in Random and Complex Media 2021;1–32. 10.1080/17455030.2021.1989517. Suche in Google Scholar

[5] Almusawa H, Ali KK, Wazwaz A-M, Mehanna MS, Baleanu D, Osman MS, et al. Protracted study on a real physical phenomenon generated by media inhomogeneities. Results Phys. 2021;31:104933. 10.1016/j.rinp.2021.104933Suche in Google Scholar

[6] GaziKarakoc SB, Ali KK. Analytical and computational approaches on solitary wave solutions of the generalized equal width equation. Appl Math Comput. 2020;371:124933. 10.1016/j.amc.2019.124933Suche in Google Scholar

[7] Battal Gazi Karako S, Zeybek H. Solitary-wave solutions of the GRLW equation using septic B-spline collocation method. Appl Math Comput. 2016;289:159–71. 10.1016/j.amc.2016.05.021Suche in Google Scholar

[8] BattalGaziKarakoc S, Ali KK. New exact solutions and numerical approximations of the generalized KdV equation. Comput Meth Differ Equ. 2021;9(3):670–91. Suche in Google Scholar

[9] Ali KK, GaziKarakoc B, Rezazadeh H. Optical soliton solution of the fractional perturbed nonlinear Schrödinger equation. TWMS J App Eng Math. 2020;10(4):930–9. Suche in Google Scholar

[10] BattalGaziKarakoc S, Geyikli T, Bashan A. A numerical solution of the modified regularized long wave (MRLW) equation using quartic B-splines. TWMS J App Eng Math. 2013;3(2):231–44. 10.1186/1687-2770-2013-27Suche in Google Scholar

[11] Zeybek H, BattalGaziKarakoç S. A numerical investigation of the GRLW equation using lumped Galerkin approach with cubic B-spline. SpringerPlus 2016;5:199. 10.1186/s40064-016-1773-9Suche in Google Scholar

[12] Fana C-M, Lia P-W. Generalized finite difference method for solving two-dimensional Burgers’ equations. Proc Eng. 2014;79:55–60. 10.1016/j.proeng.2014.06.310Suche in Google Scholar

[13] Raslan KR and Ali KK. Numerical study of MHD-duct flow using the two-dimensional finite difference method. Appl Math Inf Sci. 2020;14(4):1–5. 10.18576/amis/140417Suche in Google Scholar

[14] Zhi S, Yong-yan C, Qing J. Solving 2D and 3D Poisson equations and biharmonic equations by the Haar wavelet method. Appl Math Model. 2012;36(11):5134–61. 10.1016/j.apm.2011.11.078Suche in Google Scholar

[15] Singh I, Kumar Sh. Wavelet methods for solving three-dimensional partial differential equations. Math Sci. 2017;11:145–54. 10.1007/s40096-017-0220-6Suche in Google Scholar

[16] Gardner LRT, Gardner GA. A two dimensional cubic B-spline finite element: used in a study of MHD-duct flow. Comput Meth Appl Mech Eng. 1995;124:365–75. 10.1016/0045-7825(94)00760-KSuche in Google Scholar

[17] Arora R, Singh S, Singh S. Numerical solution of second-order two-dimensional hyperbolic equation by bi-cubic B-spline collocation method. Math Sci. 2020;14:201–13. 10.1007/s40096-020-00331-ySuche in Google Scholar

[18] Mittal RC, Tripathi A. Numerical solutions of two-dimensional unsteady convection-diffusion problems using modified bicubic B-spline finite elements. Int J Comp Math. 2017;94(1):1–21. 10.1080/00207160.2015.1085976Suche in Google Scholar

[19] Elsherbeny AM, El-hassani RMI, El-badry H, Abdallah MI. Solving 2D-poisson equation using modified cubic B-spline differential quadrature method. Ain Shams Eng J. 2018;9(4):2879–85. 10.1016/j.asej.2017.12.001Suche in Google Scholar

[20] Raslan KR and Ali KK. On n-dimensional quadratic B-splines. Numer Meth Partial Differ Equ. 2021;37(2):1057–71. 10.1002/num.22566Suche in Google Scholar

[21] Raslan KR, Ali KK. A new structure formulations for cubic B-spline collocation method in three and four-dimensions. Nonlinear Eng. 2020;9:432–48. 10.1515/nleng-2020-0027Suche in Google Scholar

[22] Raslan KR, Ali KK, Al-Bayatti HM. Construct extended cubic B-splines in n-dimensional for solving n-dimensional partial differential equations. Appl Math Inform Sci. 2021;15(5):599–611. 10.18576/amis/150508Suche in Google Scholar

[23] Raslan KR, Ali KK, Mohamed MS, Hadhoud AR. A new structure to n-dimensional trigonometric cubic B-spline functions for solving n-dimensional partial differential equations. Adv Differ Equ. 2021;2021(1):442. 10.1186/s13662-021-03596-2Suche in Google Scholar

[24] Raslan KR, El-Danaf TS, Ali KK. Collocation method with quintic B-spline method for solving the Hirota equation. J Abstract Comput Math. 2016;1:1–12. 10.17654/AM096010055Suche in Google Scholar

[25] Raslan KR, El-Danaf TS, Ali KK. Collocation method with Quantic b-spline method for solving Hirota-Satsuma coupled KDV equation. Int J Appl Math Res. 2016;5(2):123–31. 10.14419/ijamr.v5i2.6138Suche in Google Scholar

[26] Mohammad G. Spline-based DQM for multi-dimensional PDEs: application to biharmonic and Poisson equations in 2D and 3D. Comput Math Appl. 2017;73(7):1576–92. 10.1016/j.camwa.2017.02.006Suche in Google Scholar
Received: 2022-01-18
Revised: 2022-03-16
Accepted: 2022-03-28
Published Online: 2022-04-18

© 2022 K. R. Raslan et al., published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

  1. Research Articles
  2. Fractal approach to the fluidity of a cement mortar
  3. Novel results on conformable Bessel functions
  4. The role of relaxation and retardation phenomenon of Oldroyd-B fluid flow through Stehfest’s and Tzou’s algorithms
  5. Damage identification of wind turbine blades based on dynamic characteristics
  6. Improving nonlinear behavior and tensile and compressive strengths of sustainable lightweight concrete using waste glass powder, nanosilica, and recycled polypropylene fiber
  7. Two-point nonlocal nonlinear fractional boundary value problem with Caputo derivative: Analysis and numerical solution
  8. Construction of optical solitons of Radhakrishnan–Kundu–Lakshmanan equation in birefringent fibers
  9. Dynamics and simulations of discretized Caputo-conformable fractional-order Lotka–Volterra models
  10. Research on facial expression recognition based on an improved fusion algorithm
  11. N-dimensional quintic B-spline functions for solving n-dimensional partial differential equations
  12. Solution of two-dimensional fractional diffusion equation by a novel hybrid D(TQ) method
  13. Investigation of three-dimensional hybrid nanofluid flow affected by nonuniform MHD over exponential stretching/shrinking plate
  14. Solution for a rotational pendulum system by the Rach–Adomian–Meyers decomposition method
  15. Study on the technical parameters model of the functional components of cone crushers
  16. Using Krasnoselskii's theorem to investigate the Cauchy and neutral fractional q-integro-differential equation via numerical technique
  17. Smear character recognition method of side-end power meter based on PCA image enhancement
  18. Significance of adding titanium dioxide nanoparticles to an existing distilled water conveying aluminum oxide and zinc oxide nanoparticles: Scrutinization of chemical reactive ternary-hybrid nanofluid due to bioconvection on a convectively heated surface
  19. An analytical approach for Shehu transform on fractional coupled 1D, 2D and 3D Burgers’ equations
  20. Exploration of the dynamics of hyperbolic tangent fluid through a tapered asymmetric porous channel
  21. Bond behavior of recycled coarse aggregate concrete with rebar after freeze–thaw cycles: Finite element nonlinear analysis
  22. Edge detection using nonlinear structure tensor
  23. Synchronizing a synchronverter to an unbalanced power grid using sequence component decomposition
  24. Distinguishability criteria of conformable hybrid linear systems
  25. A new computational investigation to the new exact solutions of (3 + 1)-dimensional WKdV equations via two novel procedures arising in shallow water magnetohydrodynamics
  26. A passive verses active exposure of mathematical smoking model: A role for optimal and dynamical control
  27. A new analytical method to simulate the mutual impact of space-time memory indices embedded in (1 + 2)-physical models
  28. Exploration of peristaltic pumping of Casson fluid flow through a porous peripheral layer in a channel
  29. Investigation of optimized ELM using Invasive Weed-optimization and Cuckoo-Search optimization
  30. Analytical analysis for non-homogeneous two-layer functionally graded material
  31. Investigation of critical load of structures using modified energy method in nonlinear-geometry solid mechanics problems
  32. Thermal and multi-boiling analysis of a rectangular porous fin: A spectral approach
  33. The path planning of collision avoidance for an unmanned ship navigating in waterways based on an artificial neural network
  34. Shear bond and compressive strength of clay stabilised with lime/cement jet grouting and deep mixing: A case of Norvik, Nynäshamn
  35. Communication
  36. Results for the heat transfer of a fin with exponential-law temperature-dependent thermal conductivity and power-law temperature-dependent heat transfer coefficients
  37. Special Issue: Recent trends and emergence of technology in nonlinear engineering and its applications - Part I
  38. Research on fault detection and identification methods of nonlinear dynamic process based on ICA
  39. Multi-objective optimization design of steel structure building energy consumption simulation based on genetic algorithm
  40. Study on modal parameter identification of engineering structures based on nonlinear characteristics
  41. On-line monitoring of steel ball stamping by mechatronics cold heading equipment based on PVDF polymer sensing material
  42. Vibration signal acquisition and computer simulation detection of mechanical equipment failure
  43. Development of a CPU-GPU heterogeneous platform based on a nonlinear parallel algorithm
  44. A GA-BP neural network for nonlinear time-series forecasting and its application in cigarette sales forecast
  45. Analysis of radiation effects of semiconductor devices based on numerical simulation Fermi–Dirac
  46. Design of motion-assisted training control system based on nonlinear mechanics
  47. Nonlinear discrete system model of tobacco supply chain information
  48. Performance degradation detection method of aeroengine fuel metering device
  49. Research on contour feature extraction method of multiple sports images based on nonlinear mechanics
  50. Design and implementation of Internet-of-Things software monitoring and early warning system based on nonlinear technology
  51. Application of nonlinear adaptive technology in GPS positioning trajectory of ship navigation
  52. Real-time control of laboratory information system based on nonlinear programming
  53. Software engineering defect detection and classification system based on artificial intelligence
  54. Vibration signal collection and analysis of mechanical equipment failure based on computer simulation detection
  55. Fractal analysis of retinal vasculature in relation with retinal diseases – an machine learning approach
  56. Application of programmable logic control in the nonlinear machine automation control using numerical control technology
  57. Application of nonlinear recursion equation in network security risk detection
  58. Study on mechanical maintenance method of ballasted track of high-speed railway based on nonlinear discrete element theory
  59. Optimal control and nonlinear numerical simulation analysis of tunnel rock deformation parameters
  60. Nonlinear reliability of urban rail transit network connectivity based on computer aided design and topology
  61. Optimization of target acquisition and sorting for object-finding multi-manipulator based on open MV vision
  62. Nonlinear numerical simulation of dynamic response of pile site and pile foundation under earthquake
  63. Research on stability of hydraulic system based on nonlinear PID control
  64. Design and simulation of vehicle vibration test based on virtual reality technology
  65. Nonlinear parameter optimization method for high-resolution monitoring of marine environment
  66. Mobile app for COVID-19 patient education – Development process using the analysis, design, development, implementation, and evaluation models
  67. Internet of Things-based smart vehicles design of bio-inspired algorithms using artificial intelligence charging system
  68. Construction vibration risk assessment of engineering projects based on nonlinear feature algorithm
  69. Application of third-order nonlinear optical materials in complex crystalline chemical reactions of borates
  70. Evaluation of LoRa nodes for long-range communication
  71. Secret information security system in computer network based on Bayesian classification and nonlinear algorithm
  72. Experimental and simulation research on the difference in motion technology levels based on nonlinear characteristics
  73. Research on computer 3D image encryption processing based on the nonlinear algorithm
  74. Outage probability for a multiuser NOMA-based network using energy harvesting relays
https://doi.org/10.1515/nleng-2022-0016
Schlagwörter für diesen Artikel
collocation method; n-dimensional B-spline functions; mathematical models
Creative Commons
BY 4.0

Artikel in diesem Heft

  1. Research Articles
  2. Fractal approach to the fluidity of a cement mortar
  3. Novel results on conformable Bessel functions
  4. The role of relaxation and retardation phenomenon of Oldroyd-B fluid flow through Stehfest’s and Tzou’s algorithms
  5. Damage identification of wind turbine blades based on dynamic characteristics
  6. Improving nonlinear behavior and tensile and compressive strengths of sustainable lightweight concrete using waste glass powder, nanosilica, and recycled polypropylene fiber
  7. Two-point nonlocal nonlinear fractional boundary value problem with Caputo derivative: Analysis and numerical solution
  8. Construction of optical solitons of Radhakrishnan–Kundu–Lakshmanan equation in birefringent fibers
  9. Dynamics and simulations of discretized Caputo-conformable fractional-order Lotka–Volterra models
  10. Research on facial expression recognition based on an improved fusion algorithm
  11. N-dimensional quintic B-spline functions for solving n-dimensional partial differential equations
  12. Solution of two-dimensional fractional diffusion equation by a novel hybrid D(TQ) method
  13. Investigation of three-dimensional hybrid nanofluid flow affected by nonuniform MHD over exponential stretching/shrinking plate
  14. Solution for a rotational pendulum system by the Rach–Adomian–Meyers decomposition method
  15. Study on the technical parameters model of the functional components of cone crushers
  16. Using Krasnoselskii's theorem to investigate the Cauchy and neutral fractional q-integro-differential equation via numerical technique
  17. Smear character recognition method of side-end power meter based on PCA image enhancement
  18. Significance of adding titanium dioxide nanoparticles to an existing distilled water conveying aluminum oxide and zinc oxide nanoparticles: Scrutinization of chemical reactive ternary-hybrid nanofluid due to bioconvection on a convectively heated surface
  19. An analytical approach for Shehu transform on fractional coupled 1D, 2D and 3D Burgers’ equations
  20. Exploration of the dynamics of hyperbolic tangent fluid through a tapered asymmetric porous channel
  21. Bond behavior of recycled coarse aggregate concrete with rebar after freeze–thaw cycles: Finite element nonlinear analysis
  22. Edge detection using nonlinear structure tensor
  23. Synchronizing a synchronverter to an unbalanced power grid using sequence component decomposition
  24. Distinguishability criteria of conformable hybrid linear systems
  25. A new computational investigation to the new exact solutions of (3 + 1)-dimensional WKdV equations via two novel procedures arising in shallow water magnetohydrodynamics
  26. A passive verses active exposure of mathematical smoking model: A role for optimal and dynamical control
  27. A new analytical method to simulate the mutual impact of space-time memory indices embedded in (1 + 2)-physical models
  28. Exploration of peristaltic pumping of Casson fluid flow through a porous peripheral layer in a channel
  29. Investigation of optimized ELM using Invasive Weed-optimization and Cuckoo-Search optimization
  30. Analytical analysis for non-homogeneous two-layer functionally graded material
  31. Investigation of critical load of structures using modified energy method in nonlinear-geometry solid mechanics problems
  32. Thermal and multi-boiling analysis of a rectangular porous fin: A spectral approach
  33. The path planning of collision avoidance for an unmanned ship navigating in waterways based on an artificial neural network
  34. Shear bond and compressive strength of clay stabilised with lime/cement jet grouting and deep mixing: A case of Norvik, Nynäshamn
  35. Communication
  36. Results for the heat transfer of a fin with exponential-law temperature-dependent thermal conductivity and power-law temperature-dependent heat transfer coefficients
  37. Special Issue: Recent trends and emergence of technology in nonlinear engineering and its applications - Part I
  38. Research on fault detection and identification methods of nonlinear dynamic process based on ICA
  39. Multi-objective optimization design of steel structure building energy consumption simulation based on genetic algorithm
  40. Study on modal parameter identification of engineering structures based on nonlinear characteristics
  41. On-line monitoring of steel ball stamping by mechatronics cold heading equipment based on PVDF polymer sensing material
  42. Vibration signal acquisition and computer simulation detection of mechanical equipment failure
  43. Development of a CPU-GPU heterogeneous platform based on a nonlinear parallel algorithm
  44. A GA-BP neural network for nonlinear time-series forecasting and its application in cigarette sales forecast
  45. Analysis of radiation effects of semiconductor devices based on numerical simulation Fermi–Dirac
  46. Design of motion-assisted training control system based on nonlinear mechanics
  47. Nonlinear discrete system model of tobacco supply chain information
  48. Performance degradation detection method of aeroengine fuel metering device
  49. Research on contour feature extraction method of multiple sports images based on nonlinear mechanics
  50. Design and implementation of Internet-of-Things software monitoring and early warning system based on nonlinear technology
  51. Application of nonlinear adaptive technology in GPS positioning trajectory of ship navigation
  52. Real-time control of laboratory information system based on nonlinear programming
  53. Software engineering defect detection and classification system based on artificial intelligence
  54. Vibration signal collection and analysis of mechanical equipment failure based on computer simulation detection
  55. Fractal analysis of retinal vasculature in relation with retinal diseases – an machine learning approach
  56. Application of programmable logic control in the nonlinear machine automation control using numerical control technology
  57. Application of nonlinear recursion equation in network security risk detection
  58. Study on mechanical maintenance method of ballasted track of high-speed railway based on nonlinear discrete element theory
  59. Optimal control and nonlinear numerical simulation analysis of tunnel rock deformation parameters
  60. Nonlinear reliability of urban rail transit network connectivity based on computer aided design and topology
  61. Optimization of target acquisition and sorting for object-finding multi-manipulator based on open MV vision
  62. Nonlinear numerical simulation of dynamic response of pile site and pile foundation under earthquake
  63. Research on stability of hydraulic system based on nonlinear PID control
  64. Design and simulation of vehicle vibration test based on virtual reality technology
  65. Nonlinear parameter optimization method for high-resolution monitoring of marine environment
  66. Mobile app for COVID-19 patient education – Development process using the analysis, design, development, implementation, and evaluation models
  67. Internet of Things-based smart vehicles design of bio-inspired algorithms using artificial intelligence charging system
  68. Construction vibration risk assessment of engineering projects based on nonlinear feature algorithm
  69. Application of third-order nonlinear optical materials in complex crystalline chemical reactions of borates
  70. Evaluation of LoRa nodes for long-range communication
  71. Secret information security system in computer network based on Bayesian classification and nonlinear algorithm
  72. Experimental and simulation research on the difference in motion technology levels based on nonlinear characteristics
  73. Research on computer 3D image encryption processing based on the nonlinear algorithm
  74. Outage probability for a multiuser NOMA-based network using energy harvesting relays
Jetzt anmelden und 20% sparen
Institutioneller Zugang
Wie funktioniert Authentifizierung?
Haben Sie eine Idee, wie wir unsere Website verbessern können?
Bitte schreiben Sie uns.
© 2025 De Gruyter Brill
Heruntergeladen am 30.12.2025 von https://www.degruyterbrill.com/document/doi/10.1515/nleng-2022-0016/html
Button zum nach oben scrollen