Home Optimal control and nonlinear numerical simulation analysis of tunnel rock deformation parameters
Article Open Access

Optimal control and nonlinear numerical simulation analysis of tunnel rock deformation parameters

  • Li Guo EMAIL logo and Yi He
Published/Copyright: September 8, 2022
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
Nonlinear Engineering
From the journal Nonlinear Engineering Volume 11 Issue 1

Abstract

In order to study the influence of nonlinear numerical simulation on the optimal control of the tunnel rock deformation parameters, the author proposes a numerical simulation study of the deformation characteristics of the layered rock tunnel, and determines the calculation model according to the thickness of the rock mass. The estimated thicknesses of the dolomite limestone surrounding the tunnel are 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, and 0.9 m. Select the vertical displacement to analyze as a result of the calculation. In order to study the influence of the structural slope on the tunnel stability, the thickness of the rock layer was 0.6 m, and the structural slopes of 5°, 15°, 30°, 45°, 60°, 75°, and 85° were used for simulation calculations. During on-site construction, focus on monitoring the tunnel section deformation before the construction of the secondary lining. Every 10–20 m and at the change of the surrounding rock, the observation section of the surrounding convergence and vault settlement shall be arranged, according to the observed deformation, the peripheral displacement rate and the vault subsidence rate are calculated. The results show that the vertical displacement of the top of the tunnel is generally in a “V” shape, that is, the maximum settlement in the tunnel; when the layer thickness is 0.3 m, the maximum vertical displacement of the rock layer is 7.2 mm, and the total settlement in the lining support tunnel is 8.23 mm. When the layer thickness is 0.9 m, the vertical displacement of the rock layer is 5.14 mm, and the total settlement in the lining support tunnel is 5.22 mm. When the layer thickness is from 0.9 to 0.3 m, the maximum vertical displacement of the rock layer increases by 140%, and the settlement at the vault increases by 158%. The focus of tunnel support at this time is the two sides of the lining structure and the vault with large vertical settlement. For the YK51 + 032 section, the phenomenon of first decreasing and then increasing is due to the sudden mud on the surrounding YK51 + 040, which causes the short-term deformation to increase. Only the ZK49 + 356 sections at the entrance of the spider has very good deformation due to the thin overlying stratum, and other sections are similar, which shows the reliability of the calculation results.

Keywords: tunnel; rock deformation; nonlinear numerical simulation; layered rock mass; dip angle

1 Introduction

At this stage, the deformation control of tunnel construction is still unsatisfactory, especially the deformation problems of tunnels with high ground stress and weak surrounding rock are still relatively prominent, it is manifested as rapid deformation, large deformation, and long-lasting deformation, which is easy to cause the support to be dismantled and replaced due to intrusion or damage, and the construction safety risk is high. It often leads to delays in construction period and increased investment, which brings great risks and challenges to tunnel survey, design, construction, and management [1]. The existing supporting technology is summarized and analyzed, construct a tunnel support system based on active deformation control, and study its support mechanism and key support technologies. In order to ensure the safe construction of railway tunnels, it is of certain significance to innovate the theory and method of railway tunnel support. Figure 1 shows the solution of the online monitoring system for tunnel deformation. To solve the deformation problem, scientists have used methods such as field experiments, mathematical simulations, and theoretical analysis [2].

Figure 1 Solution of online monitoring system for tunnel deformation.
Figure 1

Solution of online monitoring system for tunnel deformation.

At present, there are certain deficiencies in the active control and support of surrounding rock deformation of railway tunnels in China, which are mainly manifested as follows: railway tunnel support is generally a passive support system; at present, railway tunnel support generally emphasizes the deformation control of passive support members such as steel frames, and the support construction cannot effectively strengthen the surrounding rock. The support system based on passive support is suitable for tunnels with good surrounding rock, but under difficult conditions such as poor self-supporting capacity of surrounding rock and high in situ stress, it is difficult to control deformation only by passive support; the supporting structure is easily deformed and damaged, and accidents such as tunnel collapse occur [3]. The concept of active support is still not unified, in the construction of railway tunnels for many years, the importance of active deformation control has been generally realized, and it is emphasized that active support should be used to prevent active deformation, the bearing capacity of the surrounding rock is fully utilized to control the deformation, and the supporting measures such as pre-stressed bolts (cables) and grouting reinforcement of the stratum have been extensively studied and applied. However, at present, there is no unified understanding of the support concept, application conditions, and scope of application of active deformation control [4]. The key technologies of the active support system need further innovation, the effect of active support depends on high-performance support materials; at present, the mechanical properties of support materials or components are generally low, if the support force performance cannot be fully exerted, high-performance shotcrete material technology, new anchoring material technology, and non-destructive testing technology for initial support construction quality should be studied, achieve rapid construction, and timely effect of tunnel support [5].

2 Literature review

In terms of weather and hydrology, weather and hydrology conditions are important factors in causing tunnel collapse. In response to this research problem, Nedelescu et al. proposed the concept of active control deformation. Bolt (cable) support and surrounding rock grouting are considered to be active support, while steel frame support, shotcrete support, and secondary lining are passive support [6]. According to the mechanism of tunnel support, Pal divided the types of tunnel support into two categories, namely active support and passive support. Passive support is passively applied to the surrounding rock; it is a support system that has relatively little effect on controlling the mechanical properties of the surrounding rock [7]. Li et al. put forward the mechanical support theory of soft rock engineering, systematically introduced the definition, basic properties, and continuity generalization of soft surrounding rock, and proposed the determination of deformation mechanics mechanism, support load determination, and support design method [8]. Luo et al. proposed the release-constrained balance method, the deformation of surrounding rock is controlled from two aspects of releasing in situ stress and optimizing support. The main measures for stress release are reserved deformation and advanced pilot holes. Optimized support includes measures such as strengthening support, strengthening locking feet, timely closure, and dynamic reinforcement [9]. Wu et al. proposed the classification of weak surrounding rock, tunnel section, and span classification, and established a tunnel structure system with weak surrounding rock [10]. Li et al. proposed a stability classification method for large-section tunnels, and based on the face wedge failure mode and limit equilibrium theory, the advanced support design method of the tunnel full-section method construction face is proposed, which provides a theoretical guarantee for the tunnel full-section method construction face [11]. Liu et al., through their research on micro- and macro-non-photorealistic rendering (NPR) materials and structures, as well as their application in practical engineering, for the first time in the field of rock mechanics, the scientific problem of the concept and mechanical behavior of NPR support structure was proposed, and on this basis, it is proposed that “no matter what kind of engineering geological structure the rock mass has, after the NPR support is embedded, it will have the same constitutive relationship as the NPR bolt/cable” [12]. Wu et al. studied the structure, constitutive model, and energy absorption characteristics of NPR anchor cables, and used Flac3D to establish NPR anchor cable constitutive numerical simulation experiments, the actual deformation characteristics of the NPR cable were fitted [13]. Zhang et al. used Flac3D to simulate and analyze deep tunnels and their supports [14]. Matyushkin proposed a variety of methods to simulate the mechanical behavior of surrounding rock and bolts, which promoted the application of Flac3D in tunnel engineering [15]. On the basis of the existing research, the author proposes nonlinear numerical simulation analysis to optimize the deformation parameters of the tunnel rock layer, and uses the ANSYS finite element software to analyze the stress and deformation characteristics of the surrounding rock and foundation after the tunnel layer is excavated. ANSYS software is a large-scale general-purpose finite element analysis (FEA) software developed by ANSYS Company, USA. It is the fastest growing computer-aided engineering software in the world. It can interface with most computer-aided design software. Realize data sharing and exchange, such as Creo, NASTRAN, Algor, I-DEAS, AutoCAD, etc. It is a large-scale general-purpose FEA software that integrates the analysis of structure, fluid, electric field, magnetic field, and sound field. It has a wide range of applications in nuclear industry, railway, petrochemical, aerospace, machinery manufacturing, energy, automobile transportation, defense industry, electronics, civil engineering, shipbuilding, biomedicine, light industry, geology and mining, water conservancy, household appliances, etc. With powerful functions and simple and convenient operation, ANSYS has become the most popular FEA software in the world, ranking first in FEA evaluations over the years. There is obvious inhomogeneity because the displacement on one side of the rock layer slope is smaller than that on the other side. Therefore, the roughness first increases and then decreases. The slope angle increases most obviously at 45°, and gradually stabilizes when it is greater than 60°; the displacement of the arch and wall is less affected by the change of the slope. The design and construction of layered rock tunnel support should avoid accidents caused by excessive deformation and uneven deformation of the tunnel.

3 Methods

3.1 Computational model

Since only the influence of surrounding rock changes was studied, a two-dimensional plane model was established. In order to reduce the adverse effect of boundary effects, the final size of the model was determined to be 100 m × 100 m. The thickness of the weak interlayer between rock layers is calculated as 2 cm. The origin of the coordinates is 10 m directly below the tunnel arch bottom, and the rest of the depth is converted into the pressure load of the corresponding layer thickness. The pressure load applied in the dip model is the self-weight load of the rock and soil in each half-time. The lower boundary fixes the horizontal and vertical displacement, and the left and right only constrain the horizontal displacement [16]. The mechanized construction method of tunnel drilling and blasting method is based on high-efficiency large-scale machinery in the whole process, and is a technical method to solve the construction problems of safety, high quality, high efficiency, and economy of the complex mountainous Changshanling tunnel. All geological construction technology, face stability evaluation method, face advance active support technology, “quantitative” precise design technology of face advance support, low pre-stressed bolt active support technology, and early high-intensity injection The key technologies of tunnel drilling and blasting mechanized construction design with the core of concrete active support technology, initial support rapid ring-forming and sealing technology, and surrounding rock deformation pressure calculation method provide technical support for the popularization and application of tunnel drilling and blasting mechanized construction method.

3.2 Calculation parameters

The physical and non-physical compositions of the selected materials are shown in Table 1, using the normalized calculations of the planar and D–P models.

Table 1

Physical and mechanical parameters of main materials

Category Elastic modulus, E (GPa) Poisson’s ratio, v Severe, γ/(kg m−3) Friction angle ϕ (°) Cohesion, C (MPa)
Mezzanine 0.185 0.24 1,800 37 0.5
Surrounding rock 39.54 0.19 2,702 –/– –/–
Initial lining 20 0.2 2,201 –/– –/–
Second block 25 0.2 2,201 –/– –/–

3.3 Construction of NPR anchor cable constitutive model

The disadvantage of ordinary anchor cable relative to NPR anchor cable is that its deformation is small, under the condition of large deformation or impact of surrounding rock, the anchor cable is damaged due to excessive deformation [17]. NPR anchor cable can not only adapt to large deformation surrounding rock, but also provide effective high constant resistance. It is necessary to redefine the anchor cable element (geometry, material parameters, and anchoring agent properties) using Fish language in Flac3D, the NPR anchor cable is an elastic–plastic body, its characteristics are described by a one-dimensional constitutive model, and its axial stiffness K can be expressed as:

(1) K = A E L .

In the above formula, A is the reinforcement cross-sectional area (m2), E is the elastic modulus (GPa), and L is the member length (m).

In Flac3D, the tensile yield strength F t and compressive strength F c of the anchor cable can be specified, and these two limits cannot be exceeded in the application of the constitutive model [18]. The parameters that govern the performance of NPR cables are tensile strength and tightening parameters, PR (normal) cables reaching their tensile strength limit due to pulling, or failure of the fasteners when installing NPR anchors. The strength of the anchor cable unit and the tightening agent is adjusted to be greater than the tensile strength of the anchor cable, which is rigidly connected with the surrounding rock, and the free end of the anchor cable is also adjusted to be rigidly connected with its surroundings, imitating stones, and shelves. By adjusting the high deformation of the anchor cable when a constant resistance value is reached, it is possible to lengthen the anchor cable, filter the distance between the free end and the anchor end using the built-in Fish language, and control the anchor cable anchor force. When the anchor cable and the deformation value reach a predetermined value, the anchor cable unit is loosened [19].

4 Results and analysis

4.1 Analysis of the influence of the thickness of the layered rock mass on the tunnel

When studying the effect of layered rock mass on the tunnel stability, the thickness of the dolomite limestone around, assuming that the dip angles of the stratigraphic structure were 0, 0.5, 0.6, 0.7, 0.8, and 0.9 m. In the calculation results, select vertical displacement for analysis. When the inclination of the rock formation is zero, layered rock mass can be regarded as a flexural member bearing uniformly distributed loads, no matter how the layer thickness changes, the vault is the part where the vertical displacement of the tunnel changes the most [20]. Therefore, when the layered jointed rock layer is horizontal, the key point of lining support should be the dome position during tunnel excavation construction [21]. Select the vertical displacement of rock layers with different thicknesses and lining support arch tops with a horizontal length of 15 m directly above the vault, and draw the vertical settlement curves of the rock layers and the cumulative value of vault settlement at different layer thicknesses, as shown in Figures 2 and 3.

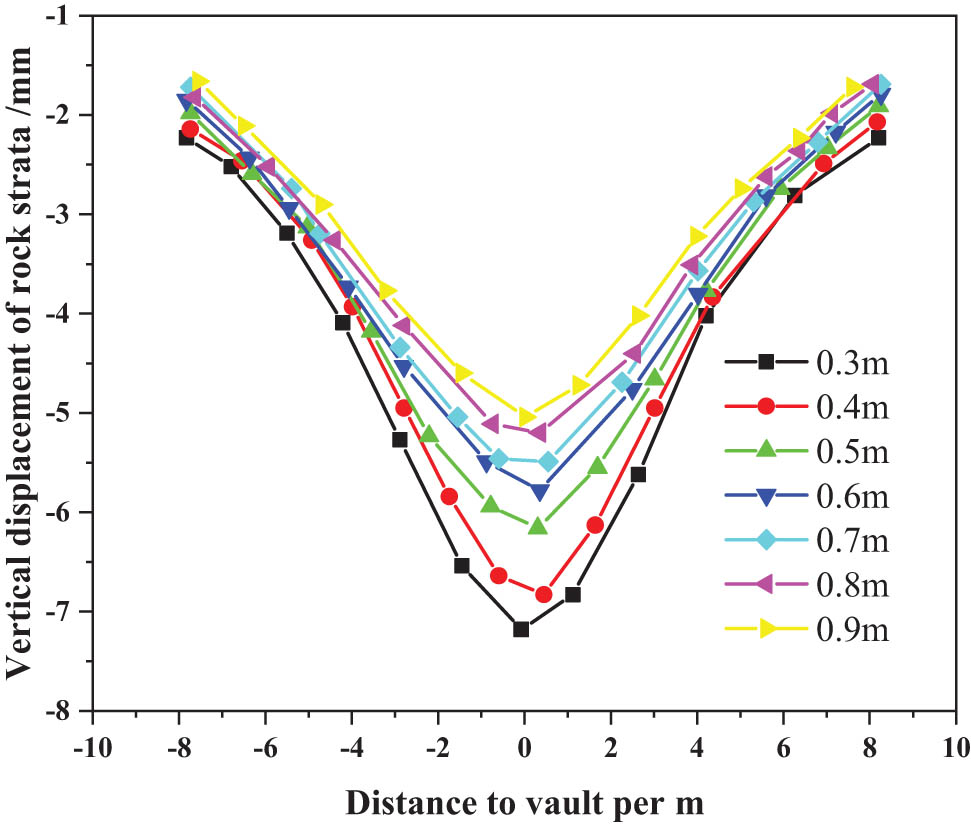
Figure 2 Vertical displacement curves of different thick rock layers.
Figure 2

Vertical displacement curves of different thick rock layers.

Figure 3 Cumulative value curve of settlement at the vault with different layer thickness.
Figure 3

Cumulative value curve of settlement at the vault with different layer thickness.

In Figure 2, the origin of the abscissa in the tunnel, the left side of the tunnel is positive and the right side is negative, the result of longitudinal displacement ignores the mode settlement caused by self-weight load. It can be seen that the vertical displacement of the top of the tunnel is generally V-shaped, that is, the maximum settlement in the tunnel [22]. The perpendicularity of the lining support frame is 5.22 mm; from 0.9 to 0.3 m, the maximum vertical displacement of the formation increased by 140%, and the settlement in the tunnel increased by 158%. It is clear that the stability of the tunnel is greatly affected by the thickness of the rock layers. As the thickness of the rock increases, the deformation of the upper part of the tunnel gradually decreases. If the thickness is 0.4–0.6 m, the vertical displacement decreases rapidly, but if the thickness is greater than 0.6 m, the displacement does not change much [23–27].

4.2 Analysis of the influence of the inclination angle of the rock stratum structure on the tunnel

Since 0.6 m is the critical layer thickness of the deformation speed, the rock layer thickness of 0.6 m is selected when studying the plane dip angle characteristics of the tunnel stability, and the standard plane dip angles are 5°, 15°, 30°, 45°, 60°, 75°, and 85° for simulation calculation. The displacement on one side of the rock stratum is smaller than that on the other side. The asymmetry of the displacement cloud map first increases and then decreases, when the rock formation dip angle is close to 90°, this asymmetry will disappear. The deformation point with the largest settlement displacement for the lining structure is always the vault of the tunnel. It can be concluded that the dome position is the key point of lining support when the tunnel layer is excavated [28]. According to the distribution characteristics of the vertical displacement of the lining, six main points of the rock and lining around the tunnel are selected: the vertical displacement of the main point obtained from the tunnel, and the corner. The bottoms of the left and right reverse arches and basement arches are shown in Figures 4 and 5.

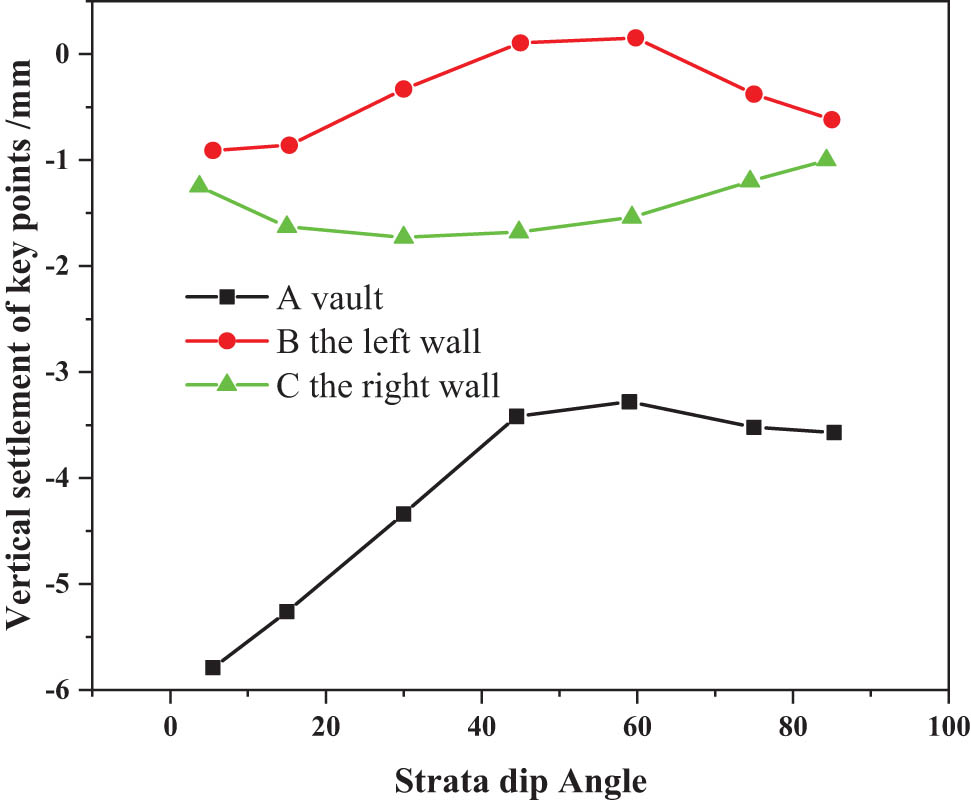
Figure 4 Vertical displacement curve 1 of key points.
Figure 4

Vertical displacement curve 1 of key points.

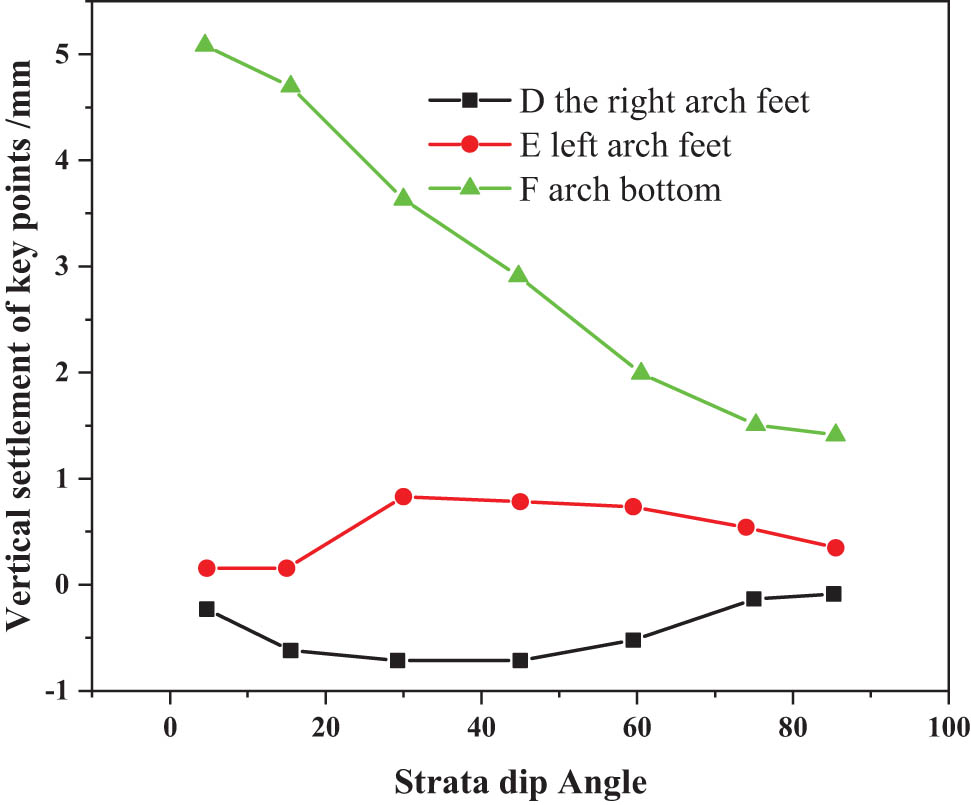
Figure 5 Vertical displacement curve 2 of key points.
Figure 5

Vertical displacement curve 2 of key points.

From Figure 4, the vertical displacement and settlement of key points A (vault top) and F (vault bottom) decrease with the gradual increase of rock inclination from 5° to 85°, especially when the inclination angle of the rock formation is from 5° to 45°, the variation of the vertical displacement and settlement is large [28]. Moreover, with the increase of the inclination angle of the rock structure, the difference in displacement and settlement of key points at the same height first increases and then decreases, such as points B and C and points D and E. Since the inclination of the rock formation increases from the right side, the inclination angle of the rock structure plane gradually increases from 5° to 45°. The difference between the settlements on both sides increases, and the displacement of the rock mass on both sides increases gradually asymmetrically. As a result, the relative sliding tendency between the rock layers on the left and right sides will also increase. Also, it may even lead to the damage of the lining structures. The inclination angle θ of the rock structure plane increases gradually from 45° to 85°. The difference between the settlements on both sides decreases, and the displacement of the rock mass on both sides decreases gradually asymmetrically.

From Figure 5, it can also be determined that when the depth is constant and the inclination angle is gradually increased, due to the balance of the left and right sides of the lining, the dislocation of the balls causes friction. Therefore, it was decided to excavate the tunnel at an inclined position, with the support core on both sides of the structural lining and the vault with the larger vertical settlement.

4.3 On-site monitoring and analysis

During on-site construction, focus on monitoring the tunnel section deformation before the construction of the secondary lining. Peripheral convergence and vault settlement detection sections are set every 10–20 m, and the door body value is calculated according to the visible deformation. Due to space limitations, the peripheral convergence and the distribution range of the vault displacement rate for one observation period of some sections are listed, as shown in Tables 2 and 3.

Table 2

The distribution range of the convergence displacement rate of the BC survey line in some sections

Station (1.5) (0.2,1] ≤0.2
ZK49 + 356 8.5–8.9 8.09–8.19 8.19–9.24
ZK49 + 380 9.5–9.1 9.1–9.14 9.14–9.24
YK49 + 330 — 8.14–8.22 8.22–9.24
YK49 + 340 — 8.19–8.219 8.29–9.29
ZK51 + 020 8.2–8.28 8.28–9.29 9.29–9.23
ZK51 + 040 −8.14 to 8.17 8.09–8.19 8.19–9.16
YK51 + 032 9.22–8.24 8.17–9.24 8.24–9.22
YK51 + 050 — 9.09–8.18 8.18–8.24
Table 3

Distribution range of displacement rate of partial section vault

Station (1.5) (0.2,1] ≤0.2
ZK49 + 356 8.59–8.26 8.26–8.3 8.3–10.4
ZK49 + 380 9.59–9.11 9.11–9.17 9.17–10.28
YK49 + 330 8.14–8.18 8.18–8.23 8.23–10.5
YK49 + 340 8.19–8.26 8.26–8.29 8.29–10.1
ZK51 + 020 8.19–8.30 8.3–9.29 9.29–10.1
ZK51 + 040 8.09–8.17 8.17–8.29 8.19–10.3
YK51 + 032 8.17–8.24 8.24–8.3 8.3–10.13
YK51 + 025 9.1–9.21 9.21–9.24 9.24–10.13

4.4 Discussion

It can be seen from Tables 2 and 3 that, except for the YK51 + 032 sections, the deformation rate of each section at the inlet and outlet gradually decreases with time. For the YK51 + 032 section, the phenomenon of first decreasing and then increasing is due to the sudden mud on the surrounding YK51 + 040, which causes the short-term deformation to increase. The layer thickness varies from 0.3 to 0.6 m, comparing the simulation results of tunnel vault settlement in Table 3 and Figures 2–5, only the ZK49 + 356 section at the entrance of the left line is greatly deformed due to the thin overlying strata, and other sections are relatively consistent, indicating the reliability of the calculation results.

5 Conclusion

The optimal monitoring and nonlinear numerical simulation analysis of tunnel rock deformation parameters are proposed, and the surrounding rock, basement stress, and deformation characteristics after excavation of layered dolomite limestone are analyzed by using ANSYS end element software. The vertical movement of the opening is divided into a “V” shape, and the maximum vertical rotation occurs on the ground. As the thickness of the stone layer increases, the maximum vertical displacement decreases with increasing rock thickness. The thickness of the rock formation is greater than 0.6 m. This is the defined critical thickness; it is clear that the displacement of the rock mass and lining around the slope tunnel will be non-uniform. The displacement of one side of the rock layer is smaller than that of the other side, and the unevenness increases first with the increase of the drop and decreases later. The angle is most obvious when the slope is 45°, and gradually stabilizes when the slope is greater than 60°. The planning and construction of layered rock tunnel support should avoid accidents caused by excessive deformation and uneven deformation of the tunnel. In the future, it is necessary to analyze several factors causing large deformation of surrounding rock, study other factors and their relationship, disaster mechanism, quantitative evaluation index of each factor, and standard for determining the stability of surrounding rock. Further improvement is required. Further research on the creep and strength development law of loose rock in high pressure environment, the rheological mechanism of loose surrounding rock tunnel, and the design structure of surrounding rock is of great significance for longevity.

  1. Funding information: The authors state no funding involved.

  2. Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.

  3. Conflict of interest: The authors state no conflict of interest.

References

[1] Li G, Ma W, Tian S, Zhou H, Zou W. Groundwater inrush control and parameters optimization of curtain grouting reinforcement for the Jingzhai tunnel. Geofluids. 2021;2021(7):1–10.10.1155/2021/6634513Search in Google Scholar

[2] Zhou G, Zhao Z, Song Z, Wang H. Stability analysis and protection measures of large section tunnel in coal rich weak rock stratum. Geofluids. 2021;2021(2):1–15.10.1155/2021/9394145Search in Google Scholar

[3] Sun X, Zhao C, Tao Z, Kang H, He M. Failure mechanism and control technology of large deformation for muzhailing tunnel in stratified rock masses. Bull Eng Geol Environ. 2021;80(1):1–20.10.1007/s10064-021-02222-5Search in Google Scholar

[4] Li C, Liang S, Wang Y, Li L, Liu D. Attenuation parameters of blasting vibration by fuzzy nonlinear regression analysis. J Beijing Inst Technol. 2020;29(4):89–94.Search in Google Scholar

[5] Yang Y, Xia Y, Zheng H, Liu Z. Investigation of rock slope stability using a 3D nonlinear strength-reduction numerical manifold method. Eng Geol. 2021;292(6):106285.10.1016/j.enggeo.2021.106285Search in Google Scholar

[6] Nedelescu C, Chiru A, Vrabie P, Trusca D. The analysis of kinematic parameters of the vehicle occupants on impact with a rigid barrier. IOP Conf Ser Mater Sci Eng. 2022;1220(1):012052.10.1088/1757-899X/1220/1/012052Search in Google Scholar

[7] Pal AK. Stability analysis of a delayed predator–prey model with nonlinear harvesting efforts using imprecise biological parameters. Z Naturforsch A. 2021;76(10):909–21.10.1515/zna-2021-0131Search in Google Scholar

[8] Li G, Hu Y, Tian SM, Ma W, Huang HL. Analysis of deformation control mechanism of prestressed anchor on jointed soft rock in large cross-section tunnel. Bull Eng Geol Environ. 2021;80(12):9089–103.10.1007/s10064-021-02470-5Search in Google Scholar

[9] Luo Y, Chen J, Shi Z, Zhang S, Li Y. Mechanical and deformation characteristics and optimization of support parameters for superlarge-span tunnel: a case study from Laohushan tunnel. Adv Civ Eng. 2020;2020(1):1–17.10.1155/2020/8882019Search in Google Scholar

[10] Wu X, Ren F, Zhu S. Deformation monitoring and numerical simulation analysis of ultra-deep working well. IOP Conf Ser Earth Environ Sci. 2021:634(1):012141.10.1088/1755-1315/634/1/012141Search in Google Scholar

[11] Li C, Zhang W, Huo T, Yu R, Luo M. Failure analysis of deep composite roof roadway and support optimization of anchor cable parameters. Geofluids. 2021;2021(1):1–13.10.1155/2021/5610058Search in Google Scholar

[12] Liu Q, Guo J, Liu L, Huang K, Li X. Optimization analysis of smart steel-plastic geogrid support for tunnel. Adv Civ Eng. 2020;2020(1):1–11.10.1155/2020/6661807Search in Google Scholar

[13] Wu C, Qin T, Wang L, Liu Z. Research on surrounding rock control technology of dongbaowei deep mining roadway. Adv Civ Eng. 2021;2021(5):1–10.10.1155/2021/6660989Search in Google Scholar

[14] Zhang C, Zhang Q, Pei Z, Song Z, Wang J. Construction sequence optimization and settlement control countermeasures of metro tunnels underpassing expressway. Adv Civ Eng. 2021;2021(21):1–17.10.1155/2021/8834368Search in Google Scholar

[15] Matyushkin IV. Nonlinear dynamic approach to the analysis of memristor parameters instability. Izvestiya Vysshikh Uchebnykh Zavedenii Materialy Elektronnoi Tekhniki = Mater Electron Eng. 2020;22(4):253–61.10.17073/1609-3577-2019-4-253-261Search in Google Scholar

[16] Sinyavsky O, Kisten V, Solomko N. Optimization of nonlinear pulse systems of automatic control with astatic objects. Energy Autom. 2020;1(53):61–70.10.31548/energiya2021.01.061Search in Google Scholar

[17] Akbas M, Zaslan B, Khanbabazadeh H, Yisan R. Numerical study using stiffness parameters on the nonlinear behavior of rca pavements under heavy traffic loads. Transp Geotech. 2021;29(1):100582.10.1016/j.trgeo.2021.100582Search in Google Scholar

[18] Da M, Su Z. Stress and deformation analysis of concrete-facing sand–gravel dam based on inversion parameters. Geotech Geol Eng. 2021;39(11):1–10.10.1007/s10706-020-01565-2Search in Google Scholar

[19] Dhiman G, Kumar V, Kaur A, Sharma A. Don: deep learning and optimization-based framework for detection of novel coronavirus disease using x-ray images. Interdiscip Sci Comput Life Sci. 2021;13(2):260–72.10.1007/s12539-021-00418-7Search in Google Scholar PubMed PubMed Central

[20] Rasheed M, Shihab S, Mohammed OY, Al-Adili A. Parameters estimation of photovoltaic model using nonlinear algorithms. J Phys Conf Ser. 2021:1795(1):012058.10.1088/1742-6596/1795/1/012058Search in Google Scholar

[21] Selva D, Nagaraj B, Pelusi D, Arunkumar R, Nair A. Intelligent network intrusion prevention feature collection and classification algorithms. Algorithms. 2021;14:224.10.3390/a14080224Search in Google Scholar

[22] Erguler ZA, Karaku H, Ediz G, Ensüt C. Assessment of design parameters and the slope stability analysis of weak clay-bearing rock masses and associated spoil piles at tunbilek basin. Arab J Geosci. 2020;13(1):1–11.10.1007/s12517-019-5030-8Search in Google Scholar

[23] Le L, Yongfa D, Xin L. Ce–Mn mixed oxides supported on glass-fiber for low-temperature selective catalytic reduction of NO with NH3. J Rare Earths. 2014;5:409–15.10.1016/S1002-0721(14)60086-7Search in Google Scholar

[24] Hillier C, Balyan V. Error detection and correction on-board nanosatellites using hamming codes. J Electr Comput Eng. 2019;2019(6):1–15. 10.1155/2019/3905094.Search in Google Scholar

[25] Babalola OP, Balyan V. Efficient channel coding for dimmable visible light communications system. IEEE Access. 2020;8:215100–6. 10.1109/ACCESS.2020.3041431.Search in Google Scholar

[26] Balyan V, Daniels R. Resource allocation for NOMA based networks using relays: cell centre and cell edge users. Int J Smart Sens Intell Syst. 2020;13(1):18.10.21307/ijssis-2020-031Search in Google Scholar

[27] Balyan V. Outage probability of cognitive radio network utilizing non orthogonal multiple access. 7th International Conference on Signal Processing and Integrated Networks (SPIN); 2020 Feb 27–28; Noida, India. IEEE; 2020. p. 751–5.10.1109/SPIN48934.2020.9071401Search in Google Scholar

[28] Huang R. Framework for a smart adult education environment. World Trans Eng Technol Educ. 2015;13(4):637–41.Search in Google Scholar
Received: 2022-03-25
Revised: 2022-07-03
Accepted: 2022-07-12
Published Online: 2022-09-08

© 2022 Li Guo and Yi He, published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Research Articles
  2. Fractal approach to the fluidity of a cement mortar
  3. Novel results on conformable Bessel functions
  4. The role of relaxation and retardation phenomenon of Oldroyd-B fluid flow through Stehfest’s and Tzou’s algorithms
  5. Damage identification of wind turbine blades based on dynamic characteristics
  6. Improving nonlinear behavior and tensile and compressive strengths of sustainable lightweight concrete using waste glass powder, nanosilica, and recycled polypropylene fiber
  7. Two-point nonlocal nonlinear fractional boundary value problem with Caputo derivative: Analysis and numerical solution
  8. Construction of optical solitons of Radhakrishnan–Kundu–Lakshmanan equation in birefringent fibers
  9. Dynamics and simulations of discretized Caputo-conformable fractional-order Lotka–Volterra models
  10. Research on facial expression recognition based on an improved fusion algorithm
  11. N-dimensional quintic B-spline functions for solving n-dimensional partial differential equations
  12. Solution of two-dimensional fractional diffusion equation by a novel hybrid D(TQ) method
  13. Investigation of three-dimensional hybrid nanofluid flow affected by nonuniform MHD over exponential stretching/shrinking plate
  14. Solution for a rotational pendulum system by the Rach–Adomian–Meyers decomposition method
  15. Study on the technical parameters model of the functional components of cone crushers
  16. Using Krasnoselskii's theorem to investigate the Cauchy and neutral fractional q-integro-differential equation via numerical technique
  17. Smear character recognition method of side-end power meter based on PCA image enhancement
  18. Significance of adding titanium dioxide nanoparticles to an existing distilled water conveying aluminum oxide and zinc oxide nanoparticles: Scrutinization of chemical reactive ternary-hybrid nanofluid due to bioconvection on a convectively heated surface
  19. An analytical approach for Shehu transform on fractional coupled 1D, 2D and 3D Burgers’ equations
  20. Exploration of the dynamics of hyperbolic tangent fluid through a tapered asymmetric porous channel
  21. Bond behavior of recycled coarse aggregate concrete with rebar after freeze–thaw cycles: Finite element nonlinear analysis
  22. Edge detection using nonlinear structure tensor
  23. Synchronizing a synchronverter to an unbalanced power grid using sequence component decomposition
  24. Distinguishability criteria of conformable hybrid linear systems
  25. A new computational investigation to the new exact solutions of (3 + 1)-dimensional WKdV equations via two novel procedures arising in shallow water magnetohydrodynamics
  26. A passive verses active exposure of mathematical smoking model: A role for optimal and dynamical control
  27. A new analytical method to simulate the mutual impact of space-time memory indices embedded in (1 + 2)-physical models
  28. Exploration of peristaltic pumping of Casson fluid flow through a porous peripheral layer in a channel
  29. Investigation of optimized ELM using Invasive Weed-optimization and Cuckoo-Search optimization
  30. Analytical analysis for non-homogeneous two-layer functionally graded material
  31. Investigation of critical load of structures using modified energy method in nonlinear-geometry solid mechanics problems
  32. Thermal and multi-boiling analysis of a rectangular porous fin: A spectral approach
  33. The path planning of collision avoidance for an unmanned ship navigating in waterways based on an artificial neural network
  34. Shear bond and compressive strength of clay stabilised with lime/cement jet grouting and deep mixing: A case of Norvik, Nynäshamn
  35. Communication
  36. Results for the heat transfer of a fin with exponential-law temperature-dependent thermal conductivity and power-law temperature-dependent heat transfer coefficients
  37. Special Issue: Recent trends and emergence of technology in nonlinear engineering and its applications - Part I
  38. Research on fault detection and identification methods of nonlinear dynamic process based on ICA
  39. Multi-objective optimization design of steel structure building energy consumption simulation based on genetic algorithm
  40. Study on modal parameter identification of engineering structures based on nonlinear characteristics
  41. On-line monitoring of steel ball stamping by mechatronics cold heading equipment based on PVDF polymer sensing material
  42. Vibration signal acquisition and computer simulation detection of mechanical equipment failure
  43. Development of a CPU-GPU heterogeneous platform based on a nonlinear parallel algorithm
  44. A GA-BP neural network for nonlinear time-series forecasting and its application in cigarette sales forecast
  45. Analysis of radiation effects of semiconductor devices based on numerical simulation Fermi–Dirac
  46. Design of motion-assisted training control system based on nonlinear mechanics
  47. Nonlinear discrete system model of tobacco supply chain information
  48. Performance degradation detection method of aeroengine fuel metering device
  49. Research on contour feature extraction method of multiple sports images based on nonlinear mechanics
  50. Design and implementation of Internet-of-Things software monitoring and early warning system based on nonlinear technology
  51. Application of nonlinear adaptive technology in GPS positioning trajectory of ship navigation
  52. Real-time control of laboratory information system based on nonlinear programming
  53. Software engineering defect detection and classification system based on artificial intelligence
  54. Vibration signal collection and analysis of mechanical equipment failure based on computer simulation detection
  55. Fractal analysis of retinal vasculature in relation with retinal diseases – an machine learning approach
  56. Application of programmable logic control in the nonlinear machine automation control using numerical control technology
  57. Application of nonlinear recursion equation in network security risk detection
  58. Study on mechanical maintenance method of ballasted track of high-speed railway based on nonlinear discrete element theory
  59. Optimal control and nonlinear numerical simulation analysis of tunnel rock deformation parameters
  60. Nonlinear reliability of urban rail transit network connectivity based on computer aided design and topology
  61. Optimization of target acquisition and sorting for object-finding multi-manipulator based on open MV vision
  62. Nonlinear numerical simulation of dynamic response of pile site and pile foundation under earthquake
  63. Research on stability of hydraulic system based on nonlinear PID control
  64. Design and simulation of vehicle vibration test based on virtual reality technology
  65. Nonlinear parameter optimization method for high-resolution monitoring of marine environment
  66. Mobile app for COVID-19 patient education – Development process using the analysis, design, development, implementation, and evaluation models
  67. Internet of Things-based smart vehicles design of bio-inspired algorithms using artificial intelligence charging system
  68. Construction vibration risk assessment of engineering projects based on nonlinear feature algorithm
  69. Application of third-order nonlinear optical materials in complex crystalline chemical reactions of borates
  70. Evaluation of LoRa nodes for long-range communication
  71. Secret information security system in computer network based on Bayesian classification and nonlinear algorithm
  72. Experimental and simulation research on the difference in motion technology levels based on nonlinear characteristics
  73. Research on computer 3D image encryption processing based on the nonlinear algorithm
  74. Outage probability for a multiuser NOMA-based network using energy harvesting relays
https://doi.org/10.1515/nleng-2022-0223
Keywords for this article
tunnel; rock deformation; nonlinear numerical simulation; layered rock mass; dip angle
Creative Commons
BY 4.0

Articles in the same Issue

  1. Research Articles
  2. Fractal approach to the fluidity of a cement mortar
  3. Novel results on conformable Bessel functions
  4. The role of relaxation and retardation phenomenon of Oldroyd-B fluid flow through Stehfest’s and Tzou’s algorithms
  5. Damage identification of wind turbine blades based on dynamic characteristics
  6. Improving nonlinear behavior and tensile and compressive strengths of sustainable lightweight concrete using waste glass powder, nanosilica, and recycled polypropylene fiber
  7. Two-point nonlocal nonlinear fractional boundary value problem with Caputo derivative: Analysis and numerical solution
  8. Construction of optical solitons of Radhakrishnan–Kundu–Lakshmanan equation in birefringent fibers
  9. Dynamics and simulations of discretized Caputo-conformable fractional-order Lotka–Volterra models
  10. Research on facial expression recognition based on an improved fusion algorithm
  11. N-dimensional quintic B-spline functions for solving n-dimensional partial differential equations
  12. Solution of two-dimensional fractional diffusion equation by a novel hybrid D(TQ) method
  13. Investigation of three-dimensional hybrid nanofluid flow affected by nonuniform MHD over exponential stretching/shrinking plate
  14. Solution for a rotational pendulum system by the Rach–Adomian–Meyers decomposition method
  15. Study on the technical parameters model of the functional components of cone crushers
  16. Using Krasnoselskii's theorem to investigate the Cauchy and neutral fractional q-integro-differential equation via numerical technique
  17. Smear character recognition method of side-end power meter based on PCA image enhancement
  18. Significance of adding titanium dioxide nanoparticles to an existing distilled water conveying aluminum oxide and zinc oxide nanoparticles: Scrutinization of chemical reactive ternary-hybrid nanofluid due to bioconvection on a convectively heated surface
  19. An analytical approach for Shehu transform on fractional coupled 1D, 2D and 3D Burgers’ equations
  20. Exploration of the dynamics of hyperbolic tangent fluid through a tapered asymmetric porous channel
  21. Bond behavior of recycled coarse aggregate concrete with rebar after freeze–thaw cycles: Finite element nonlinear analysis
  22. Edge detection using nonlinear structure tensor
  23. Synchronizing a synchronverter to an unbalanced power grid using sequence component decomposition
  24. Distinguishability criteria of conformable hybrid linear systems
  25. A new computational investigation to the new exact solutions of (3 + 1)-dimensional WKdV equations via two novel procedures arising in shallow water magnetohydrodynamics
  26. A passive verses active exposure of mathematical smoking model: A role for optimal and dynamical control
  27. A new analytical method to simulate the mutual impact of space-time memory indices embedded in (1 + 2)-physical models
  28. Exploration of peristaltic pumping of Casson fluid flow through a porous peripheral layer in a channel
  29. Investigation of optimized ELM using Invasive Weed-optimization and Cuckoo-Search optimization
  30. Analytical analysis for non-homogeneous two-layer functionally graded material
  31. Investigation of critical load of structures using modified energy method in nonlinear-geometry solid mechanics problems
  32. Thermal and multi-boiling analysis of a rectangular porous fin: A spectral approach
  33. The path planning of collision avoidance for an unmanned ship navigating in waterways based on an artificial neural network
  34. Shear bond and compressive strength of clay stabilised with lime/cement jet grouting and deep mixing: A case of Norvik, Nynäshamn
  35. Communication
  36. Results for the heat transfer of a fin with exponential-law temperature-dependent thermal conductivity and power-law temperature-dependent heat transfer coefficients
  37. Special Issue: Recent trends and emergence of technology in nonlinear engineering and its applications - Part I
  38. Research on fault detection and identification methods of nonlinear dynamic process based on ICA
  39. Multi-objective optimization design of steel structure building energy consumption simulation based on genetic algorithm
  40. Study on modal parameter identification of engineering structures based on nonlinear characteristics
  41. On-line monitoring of steel ball stamping by mechatronics cold heading equipment based on PVDF polymer sensing material
  42. Vibration signal acquisition and computer simulation detection of mechanical equipment failure
  43. Development of a CPU-GPU heterogeneous platform based on a nonlinear parallel algorithm
  44. A GA-BP neural network for nonlinear time-series forecasting and its application in cigarette sales forecast
  45. Analysis of radiation effects of semiconductor devices based on numerical simulation Fermi–Dirac
  46. Design of motion-assisted training control system based on nonlinear mechanics
  47. Nonlinear discrete system model of tobacco supply chain information
  48. Performance degradation detection method of aeroengine fuel metering device
  49. Research on contour feature extraction method of multiple sports images based on nonlinear mechanics
  50. Design and implementation of Internet-of-Things software monitoring and early warning system based on nonlinear technology
  51. Application of nonlinear adaptive technology in GPS positioning trajectory of ship navigation
  52. Real-time control of laboratory information system based on nonlinear programming
  53. Software engineering defect detection and classification system based on artificial intelligence
  54. Vibration signal collection and analysis of mechanical equipment failure based on computer simulation detection
  55. Fractal analysis of retinal vasculature in relation with retinal diseases – an machine learning approach
  56. Application of programmable logic control in the nonlinear machine automation control using numerical control technology
  57. Application of nonlinear recursion equation in network security risk detection
  58. Study on mechanical maintenance method of ballasted track of high-speed railway based on nonlinear discrete element theory
  59. Optimal control and nonlinear numerical simulation analysis of tunnel rock deformation parameters
  60. Nonlinear reliability of urban rail transit network connectivity based on computer aided design and topology
  61. Optimization of target acquisition and sorting for object-finding multi-manipulator based on open MV vision
  62. Nonlinear numerical simulation of dynamic response of pile site and pile foundation under earthquake
  63. Research on stability of hydraulic system based on nonlinear PID control
  64. Design and simulation of vehicle vibration test based on virtual reality technology
  65. Nonlinear parameter optimization method for high-resolution monitoring of marine environment
  66. Mobile app for COVID-19 patient education – Development process using the analysis, design, development, implementation, and evaluation models
  67. Internet of Things-based smart vehicles design of bio-inspired algorithms using artificial intelligence charging system
  68. Construction vibration risk assessment of engineering projects based on nonlinear feature algorithm
  69. Application of third-order nonlinear optical materials in complex crystalline chemical reactions of borates
  70. Evaluation of LoRa nodes for long-range communication
  71. Secret information security system in computer network based on Bayesian classification and nonlinear algorithm
  72. Experimental and simulation research on the difference in motion technology levels based on nonlinear characteristics
  73. Research on computer 3D image encryption processing based on the nonlinear algorithm
  74. Outage probability for a multiuser NOMA-based network using energy harvesting relays
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 14.10.2025 from https://www.degruyterbrill.com/document/doi/10.1515/nleng-2022-0223/html
Scroll to top button