Exploration of peristaltic pumping of Casson fluid flow through a porous peripheral layer in a channel

A. Rushi Kesava; A. N. S. Srinivas

doi:10.1515/nleng-2022-0247

Article Open Access

Exploration of peristaltic pumping of Casson fluid flow through a porous peripheral layer in a channel

A. Rushi Kesava and A. N. S. Srinivas

Published/Copyright: October 10, 2022

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Nonlinear Engineering Volume 11 Issue 1

Abstract

This article is aimed to investigate the peristaltic pumping of a two-layered model in a two-dimensional channel. The core region occupies Casson fluid, while the porous medium occupies the peripheral region. The fluid flow in a porous medium was described with a suitable model using the Brinkman-extended Darcy equation. In the interface between fluid and porous medium, a shear stress jump boundary condition was applied. Closed-form solutions were obtained in both regions (core and peripheral). The physical quantities of peristaltic flow, such as axial velocity, pumping and change in the interface, were derived and explained. The fluid flow was analyzed by different physical parameters such as viscosity, permeability, porosity, Casson parameter and Darcy number. It is observed that the peristalsis mechanism has greater pressure in a two-layered model containing a non-Newtonian fluid in contact with a porous medium compared to a viscous fluid in the peripheral layer. It was observed that pumping decreased with the increase in Darcy number and an increase in shear stress jump constant resulted in increasing the pumping. The outcomes of the pumping phenomenon may be helpful for understanding the fluid flow aspects of blood flow in capillaries.

Keywords: Casson fluid; peristaltic transport; porous medium; interface

1 Introduction

The transportation of physiological fluids pumped from one place in the body to another place with a wavelike muscle contraction and relaxation is called peristalsis. Intensive research has been carried out on the peristaltic flow of biological fluids. The study of biological fluids is very important in understanding physiological systems such as esophagus, ureter, stomach, blood vessels and bile duct. Porous walls and deformable porous layers have been noticed in many biological applications. Some of the examples are capillary walls, gastrointestinal tract and intra-pleural membrane. The capillary walls are also surrounded by a layer of flattened endothelial cells, which is porous in nature [1]. The transport in and around the capillary walls plays a beneficial role in maintaining metabolism as well as fluid balance. Hou et al. [2] discussed a two-fluid model in a channel having viscous fluid as synovial fluid and a porous layer as articular cartilage. The gastrointestinal tract absorbs nutrients from food as well as fluids passing through it. Here, the epithelial cells are held responsible for absorbing water from the intestine. Furthermore, there are pores through the tight junction of them. It is quite significant to study the peristaltic behavior of two-layered systems with porous peripheral layers as well as the porous boundaries of a channel.

In order to explore the importance of peristalsis, various theoretical and experimental works were carried out by many researchers. The importance of peristaltic transport using theoretical fluid mechanics and experimental studies was reviewed by Jaffrin and Shapiro [3], Rath [4] and Srivastava and Srivastava [5]. The first attempt at experimental work of peristaltic transport is made by Latham [6]. The experiments made by Bugliarello and Sevilla [7], Cockelet [8] and Scott Blair [9] reveal that blood is a non-Newtonian fluid in many situations. To understand the rheological properties of blood, many models were developed, and among them, the Casson fluid model gave better results.

Two-fluid model considerations become very important in understanding biofluid flow analysis in physiological systems. The influence of the outer layer with different viscosities on the flow rate of Newtonian fluids was studied by Brasseur et al. [10]. Studies have been carried out by Mishra and Pandey [11] on peristaltic transport of blood flow in a small vessel by considering the Casson fluid in the central region but the Newtonian fluid in the outer region. The peristaltic transport of both viscous fluids in a tube was studied by Ramachandra Rao and Usha [12]. For analyzing the results, Ochaoa-Tapia and Whitaker [14] considered shear stress jump boundary conditions at porous as well as fluid boundary regions. El Shehawey and Hussseny [15] analyzed the properties of porous boundaries on peristaltic pumping through a porous medium in a channel. Magnetohydrodynamic flow effects in peristaltic transport through a porous medium were studied by Mekheimer [16]. Furthermore, the peristaltic flow of fluids at the interface of a fluid layer and a porous medium was explained by Alazmi and Vafai [17] by considering two-fluid models. The peristaltic movement of Casson fluid with a symmetrical tube was described by Mernone et al. [18] and considered perturbation methods to explain the fluid flow in terms of amplitude ratio. Peristaltic flow in the gastrointestinal tract was explained by Mishra and Ramachandra Rao [19]. Vajravelu et al. [13,20,21] and Sreenadh et al. [22] explained some of the two-layered models by considering Newtonian/non-Newtonian fluids in core as well as peripheral regions.

Ponalagusamy and Tamil Selvi [23] investigated a two-fluid model in blood flow by arterial stenosis under the impact of magnetic field and heat transfer. As suction and internal heat generation (exponentially decaying) are significant, the behavior of Casson fluid flow over an exponentially stretching surface was examined. Animasaun et al. [24] showed an increase in the variable plastic dynamic viscosity parameter of Casson fluid with an increase in the velocity profiles. However, there is a decrease in temperature throughout the boundary layer. Thumma et al. [25] recently studied generalized differential quadrature analysis of unsteady Casson fluid and discovered that increasing the Casson parameter decreases the axial velocities in both directions significantly. Recently, some researchers have worked on peristaltic transport of different biofluid flows in different geometries with permeable boundaries [26,27,28,29,30,31,36,37]. Kesava and Srinivas [32] analyzed the peristaltic pumping of viscous fluid through a porous peripheral layer in a channel with an external magnetic field.

Two-layered peristaltic pumping in a channel having non-Newtonian Casson fluid in the inner layer and a porous medium in the outer layer is proposed. In both regions, closed-form solutions were derived. Computational outcomes show the existence of porous medium in the peripheral layer that affects the flow field significantly.

2 Problem formulation by governing equations

Consider peristaltic transport in a two-dimensional channel filled with a non-Newtonian fluid in the core region and a porous medium in the peripheral region. The fluids are immiscible. An infinite sinusoidal wave of amplitude ( b ) and axial wavelength ( λ ) with a constant velocity c passes through the flexible walls of the channel. The walls taken are Y = ± a ± b sin 2 π λ ( X − c t ) , having t as the time. Here, 2 a is the mean width of the channel as well as the interface equation, which is denoted by Y = H 1 ( x ) (Figure 1).

Figure 1

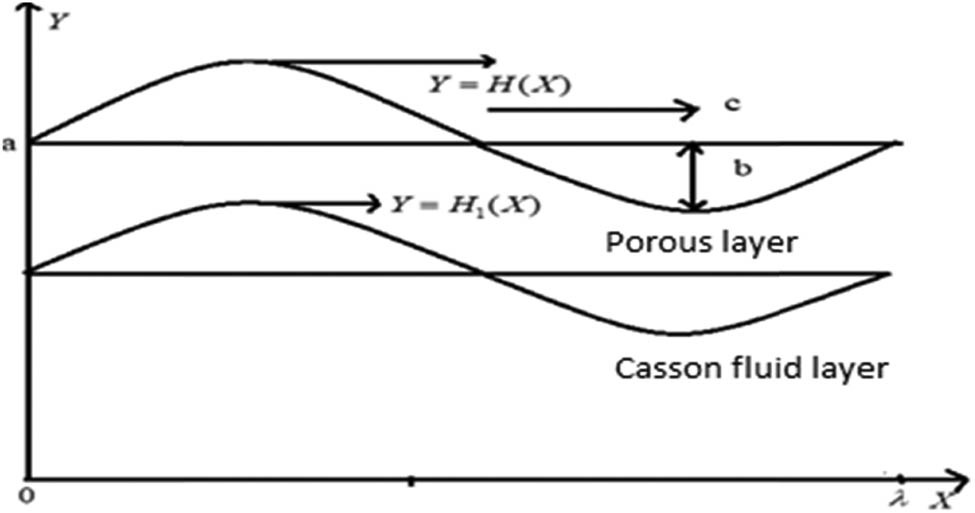
Sketch of the flow pattern.

We assume that the length of the conduit is an integral multiple of the wavelength. The porous medium is assumed to be homogeneous and isotropic. Across the boundaries of the channel, a constant pressure difference was considered. The flow is unsteady in the lab frame taking the Cartesian coordinate system (X, Y) and the flow becomes steady in a wave frame of reference (x, y) by moving along with velocity c in the wave propagation direction.

The fixed and wave frames of reference were coupled together by using the transformation of equations as follows (Brasseur et al. [10]):

(1) v i = V i ; x = X − c t ; p i ( x ) = P i ( X , t ) ; u i = U i − c ; y = Y ,

where (U _i, V _i) and (u _i,v _i) are velocity coordinates along the transverse and axial directions. The pressure coordinates along transverse and fixed frames were considered as p _i and P _i. The core and peripheral sections are denoted by the subscripts i = 1 , 2 .

For an isotropic as well as incompressible transfer of Casson fluid, the rheological equation in accordance with Nakamura and Sawada [33], Mukopadhyay [34], Selvi and Srinivas [35] is given as follows:

(2) τ i j = 2 p y 2 π + μ B e i j , π > π c , 2 p y 2 π c + μ B e i j , π < π c ,

where P y , μ B and π are yield stress, plastic dynamic viscosity and product of the components, respectively. Furthermore, the deformation component product is represented as π = e i j e i j , where e i j is the ( i , j ) th component, π c is the critical value of the non-Newtonian model.

The governing equations of motions in the fluid (core) region and porous (peripheral) region that describes the flow in the moving frame are (Mishra and Ramachandra Rao [19]).

2.1 Core region

(3) ρ 1 u 1 ∂ u 1 ∂ x + v 1 ∂ u 1 ∂ y = − ∂ p 1 ∂ x + μ 1 1 + 1 β 2 ∂ 2 u 1 ∂ y 2 + ∂ 2 u 1 ∂ x 2 ,

(4) ρ 1 u 1 ∂ v 1 ∂ x + v 1 ∂ v 1 ∂ y = − ∂ p 1 ∂ y + μ 1 1 + 1 β 2 ∂ 2 v 1 ∂ y 2 + ∂ 2 v 1 ∂ x 2 ,

(5) ∂ u 1 ∂ x + ∂ v 1 ∂ y = 0 .

2.2 Peripheral region

(6) ρ 2 u 2 ∂ u 2 ∂ x + v 2 ∂ u 2 ∂ y = − ∂ p 2 ∂ x + μ 2 ε ∂ 2 u 2 ∂ y 2 + ∂ 2 u 2 ∂ x 2 − μ 2 k u 2 ,

(7) ρ 2 u 2 ∂ v 2 ∂ x + v 2 ∂ v 2 ∂ y = − ∂ p 2 ∂ y + μ 2 ε ∂ 2 v 2 ∂ y 2 + ∂ 2 v 2 ∂ x 2 − μ 2 k v 2 ,

(8) ∂ u 2 ∂ x + ∂ v 2 ∂ y = 0 ,

where µ ₁ and µ ₂ are viscosities in the inner and outer regions; ρ _1, ρ ₂ are densities in the core and peripheral regions and ε and k are the porosity and permeability in the porous medium as non-dimensional parameters.

By considering the following dimensionless variables,

(9) μ = μ 2 / μ 1 , u ¯ i = u i / c , x ¯ = x / λ , t ¯ = c t / λ , p ¯ i = a 2 p i / μ 1 c λ , v ¯ i = v ¯ i / c δ , y ¯ = y / a , ψ ¯ i = ψ i / a c , Re = ρ 1 c a / μ 1 , h = H / a , δ = a / λ , ρ = ρ 2 / ρ 1 , ϕ = b / a , D a = k / a 2 , h 1 = H 1 / a ,

in the governing Eqs. (3)–(8) and in terms of the stream function, we obtain

(10) δ Re ( ψ 1 y ψ 1 y x − ψ 1 x ψ 1 y y ) = − P 1 x + ( δ 2 ψ 1 y x x + ψ 1 y y y ) 1 + 1 β 2 , δ 3 Re ( ψ 1 y ψ 1 x x − ψ 1 x ψ 1 y x ) = P 1 y + δ 2 ( δ 2 ψ 1 x x x + ψ 1 x y y ) 1 + 1 β 2 ,

(11) δ ρ Re ( ψ 2 y x ψ 2 y − ψ 2 y y ψ 2 x ) = − P 2 x + ( δ 2 ψ 2 y x x + ψ 2 y y y ) μ ε − μ Da ψ 2 y , δ 3 ρ Re ( ψ 2 x x ψ 2 y − ψ 2 x y ψ 2 x ) = P 2 y + ( δ 2 ψ 2 x x x + ψ 2 x y y ) μ δ 2 ε − μ δ 2 Da ψ 2 x .

Let us define u i = ψ y i ; v i = − ψ x i .

Approximating very negligible inertial forces compared to viscous forces Re → 0 and long wavelength δ ≪ 1 , Eqs. (10) and (11) are reduced (bars removed) to

(12) ψ 1 y 1 + 1 β 2 ψ 1 y y = P , 0 ≤ y ≤ h 1 ,

(13) ψ 2 y y y y = A 2 ψ 2 y y , h 1 ≤ y ≤ h .

The associated non-dimensional boundary conditions then become

(14) at y = h ( x ) : ∂ ψ 2 ∂ y = − 1 , ψ 2 = q ,

(15) at y = 0 : ψ 1 = 0 , ∂ 2 ψ 1 ∂ y 2 = 0 ,

(16) at y = h 1 ( x ) : ψ 2 = ψ 1 = q 1 ,

(17) at y = h 1 ( x ) : ∂ ψ 1 ∂ y = ∂ ψ 2 ∂ y ,

(18) at y = h 1 ( x ) : 1 + 1 β 2 ∂ 2 ψ 1 ∂ y 2 = μ ε ∂ 2 ψ 2 ∂ y 2 − β 1 ∂ ψ 2 ∂ y ,

(19) at y = h 1 ( x ) : 1 + 1 β 2 ∂ 3 ψ 1 ∂ y 3 = μ ε ∂ 3 ψ 2 ∂ y 3 − A 2 ∂ ψ 2 ∂ y ,

where A 2 = ε Da , β 1 = β ε Da and μ ε = μ ε in Eq. (14), q represents the total flux. In Eq. (16), q 1 represents the core flux. Moreover, it is observed that the limit Da → ∞ and β 2 → ∞ in the governing equations and boundary conditions are reduced by Brasseur et al. [10].

3 Solution

The stream function for the flow within the two layers is determined by solving Eqs. (12) and (13) with boundary conditions (14)–(19) to obtain

(20) ψ 1 = A 2 β 2 μ ε 6 ( β 2 + 1 ) ( AC 1 cosh A h + AC 2 sinh A h + 1 ) y 3 + β 2 ( β 2 + 1 ) B 1 y , 0 ≤ y ≤ h 1 ( x ) ,

(21) ψ 2 = q + h − y + C 1 { sinh A y − sinh A h + A cosh A h ( h − y ) } + C 2 { cosh A y − cosh A h + A sinh A h ( h − y ) } . h 1 ≤ y ≤ h .

In Appendix I, the constants C 1 , C 2 , B 1 are given.

Substituting (20) and (21) in the momentum equations, we obtain the pressure gradient as follows:

(22) d p d x = A 2 μ ε ( 1 + AC 1 cosh A h + AC 2 sinh A h ) .

The dimensionless flux Q at any axial station in the fixed frame and the flux q in the wave frame of reference are connected by

(23) Q = ∫ 0 h ( 1 + u ) d y = h + q .

The time average yields to ( T = λ / c )

(24) Q ¯ = 1 T ∫ 0 T Q d t = 1 T ∫ 0 T ( q + h ) d t = q + ∫ 0 1 h d t = q + 1 .

The expression for the interface h 1 is also determined from Eq. (16) by using any of the conditions ψ 2 = q 1 or ψ 1 = q 1 at y = h 1 ( x ) . The equation governing the interface is as follows:

(25) k ( h 1 ) = − ( q + h ) + q 1 + h 1 − C 1 { A cosh A h ( h − h 1 ) + sinh A h 1 − sinh A h } − C 2 { A sinh A h ( h − h 1 ) + cosh A h 1 − cosh A h } = 0 .

The constants q and q 1 do not depend on x. By proposing the conditions h 1 = γ at x = 0 in Eq. (25), we obtain

(26) q 1 = ( Q ¯ − γ ) H 2 H 8 + H 3 H 8 H 10 − H 7 ( H 2 H 9 + H 1 H 10 ) ( H 8 − H 9 ) H 2 − H 1 H 10 .

In Appendix II, the constants H j , j = 1 , … , 10 are given.

Suppose we integrate Eq. (22) over one non-dimensional wavelength, then

(27) Δ p = ∫ 0 1 d p d x d x = ∫ 0 1 A 2 μ ε { A C 4 Sin h ( A h ) + A C 3 Cos h ( A h ) + 1 } d x .

4 Results and discussion

Peristaltic flow of Casson fluid in the core region and porous material in the peripheral region is explained by considering the two-layered system. The equations for pressure difference, stream functions, velocities and interface were derived in both core and peripheral regions. We have discussed about the important physical quantities in peristaltic transport like axial velocity, pumping and interface for different pertinent parameters governing the flow like Casson parameter, Darcy number, stress jump constant, porosity, viscosity and amplitude ratio. Ochoa-Tapia and Whitaker [14] used shear stress jump conditions between fluid and porous layers. The transcendental interface equation is calculated and solved. For assessing the quantitative effects of various parameters involved in the problem, the numerical computations can be carried out by using the software MATLAB, and graphs are plotted in origin. The governing equation and boundary conditions of this study are reduced to Brasseur et al. [10] with a few limitations.

The interface was considered as a streamline. Figure 2(a)–(d) shows the change in the shape of the interface for various parameters such as μ , Da , β 2 and ϕ . Figure 2(b) shows the shape of the interface for different Da. It was found that an increase in Darcy number (Da) became a cause for the thinner peripheral layer in the dilated regime. Figure 2(c) shows the variation of interface with the Casson parameter β 2 , and it was found that increasing the Casson parameter increases the thickness of the layer in the crystal part of the channel, while the reverse performance is observed in the trough regions of the channel. Figure 2(a) and (d) shows the amplitude and viscosity ratios at the interface. From the graphs, one can see that an increase in amplitude and viscosity ratios gives rise to thinner peripheral layers in the constricted region of the pump.

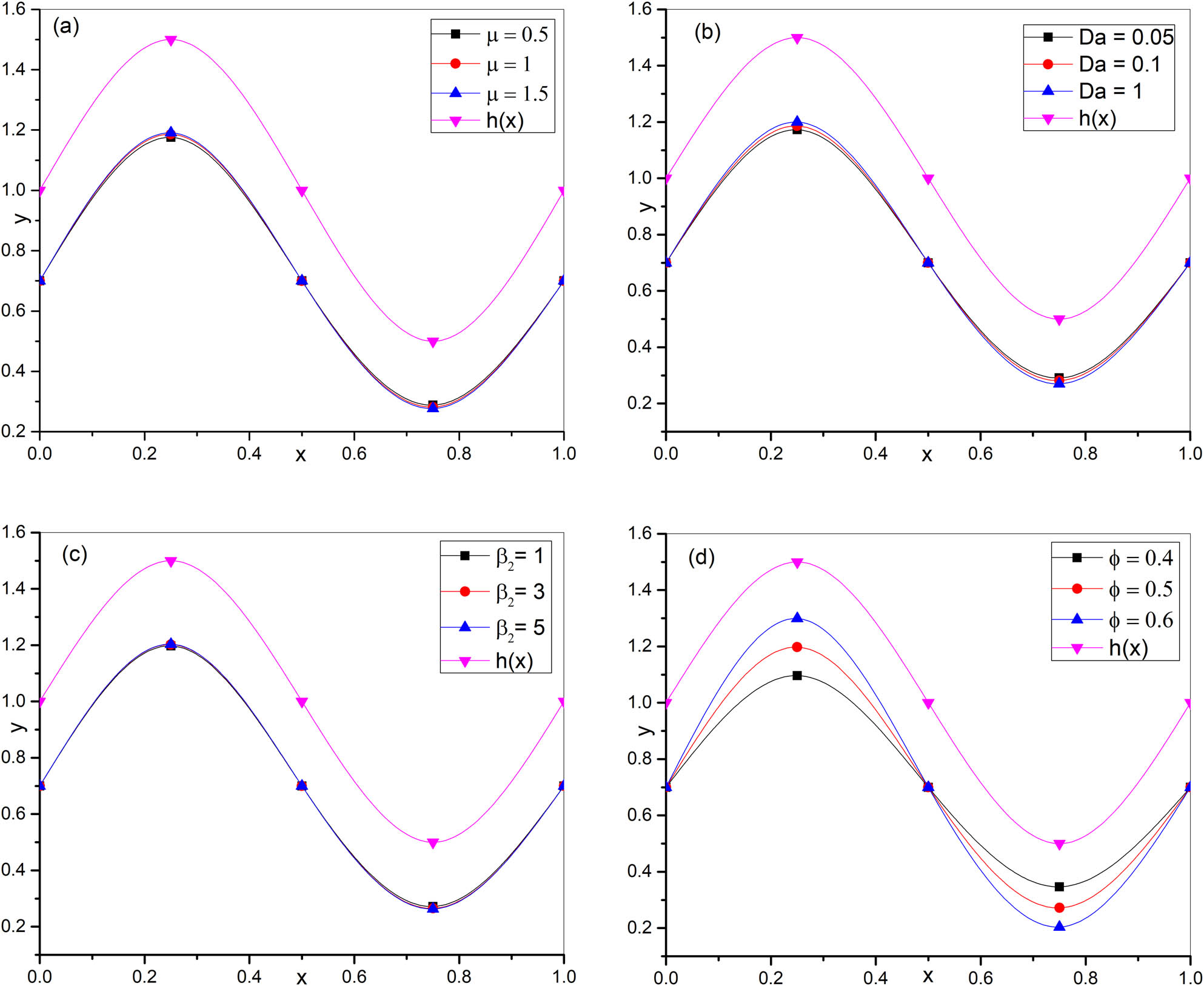
$Figure 2 Variation in the shape of the interface for μ , Da , β 2 \mu ,\text{Da},{\beta }_{2} and ϕ \phi . (a) ϕ = 0.5 , Da = 1 , β 2 = 0.9 , ε = 0.7 , β = 0.5 , γ = 0.7 \phi =0.5,\text{Da}=1,{\beta }_{2}=0.9,\varepsilon =0.7,\beta =0.5,\gamma =0.7 . (b) ϕ = 0.5 , β 2 = 0.9 , ε = 0.7 , μ = 1 , β = 0.5 , γ = 0.7 \phi =0.5,{\beta }_{2}=0.9,\varepsilon =0.7,\mu =1,\beta =0.5,\gamma =0.7 . (c) ϕ = 0.5 , Da = 1 , ε = 0.7 , μ = 1 , β = 0.5 , γ = 0.7 \phi =0.5,\text{Da}=1,\varepsilon =0.7,\mu =1,\beta =0.5,\gamma =0.7 . (d) Da = 1 , β 2 = 0.9 , ε = 0.7 , μ = 1 , β = 0.5 , γ = 0.7 \text{Da}=1,{\beta }_{2}=0.9,\varepsilon =0.7,\mu =1,\beta =0.5,\gamma =0.7 .$

Figure 2

Variation in the shape of the interface for μ , Da , β 2 and ϕ . (a) ϕ = 0.5 , Da = 1 , β 2 = 0.9 , ε = 0.7 , β = 0.5 , γ = 0.7 . (b) ϕ = 0.5 , β 2 = 0.9 , ε = 0.7 , μ = 1 , β = 0.5 , γ = 0.7 . (c) ϕ = 0.5 , Da = 1 , ε = 0.7 , μ = 1 , β = 0.5 , γ = 0.7 . (d) Da = 1 , β 2 = 0.9 , ε = 0.7 , μ = 1 , β = 0.5 , γ = 0.7 .

The variation of Δp with Q ¯ is given by solving Eq. (27) using MATLAB. Figure 3(a)–(f) shows the graphical representation of pumping parameters for different parameters. The pumping features are drawn as graphs for different parameters such as amplitude and viscosity ratios, Darcy number, Casson parameter, stress jump constant and porosity by keeping other parameters constant. Figure 3(a) shows that the pumping speed decreased with the increase of the Casson factor for constant Δp. Figure 3(b) shows the effect of Darcy number Da on the pumping factor. It can be observed from the figures that an increase in Darcy number increases permeability, which causes a decrease in pumping. These results indicate that the growing values of Darcy number decrease the pressure rise, which opposes the working of the pump. At a constant flux Q ¯ , the growing values of Darcy number decrease the pressure rise.

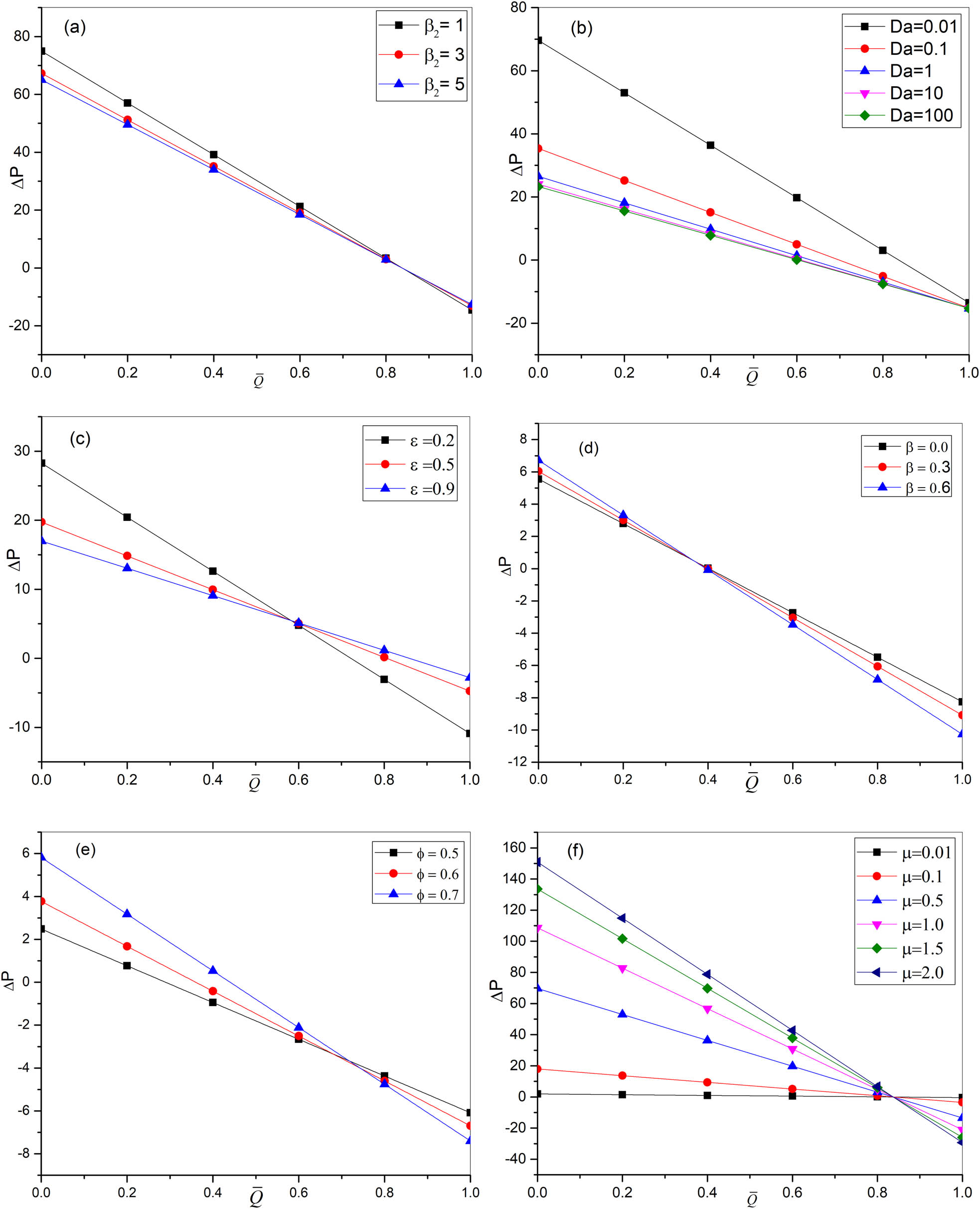
$Figure 3 Variation of Δp with Q ¯ \bar{Q} for β 2 , D a , ε , β , ϕ {\beta }_{2},Da,\varepsilon ,\beta ,\phi and μ \mu . (a) ϕ = 0.5 , ε = 0.7 , β = 1 , Da = 1 , μ = 2 . \phi =0.5,\varepsilon =0.7,\beta =1,\text{Da}=1,\mu =2. (b) ϕ = 0.5 , ε = 0.7 , β = 1 , β 2 = 0.5 , μ = 2 . \phi =0.5,\varepsilon =0.7,\beta =1,{\beta }_{2}=0.5,\mu =2. (c) ϕ = 0.5 , Da = 1 , β = 1 , β 2 = 0.5 , μ = 2 . \phi =0.5,\text{Da}=1,\beta =1,{\beta }_{2}=0.5,\mu =2. (d) ϕ = 0.5 , ε = 0.7 , Da = 1 , β 2 = 0.5 , μ = 2 . \phi =0.5,\varepsilon =0.7,\text{Da}=1,{\beta }_{2}=0.5,\mu =2. (e) β = 1 , ε = 0.7 , Da = 1 , β 2 = 0.5 , μ = 2 . \beta =1,\varepsilon =0.7,\text{Da}=1,{\beta }_{2}=0.5,\mu =2. (f) ϕ = 0.5 , ε = 0.7 , β = 1 , β 2 = 0.5 , Da = 0.1 . \phi =0.5,\varepsilon =0.7,\beta =1,{\beta }_{2}=0.5,\text{Da}=0.1.$

Figure 3

Variation of Δp with Q ¯ for β 2 , D a , ε , β , ϕ and μ . (a) ϕ = 0.5 , ε = 0.7 , β = 1 , Da = 1 , μ = 2 . (b) ϕ = 0.5 , ε = 0.7 , β = 1 , β 2 = 0.5 , μ = 2 . (c) ϕ = 0.5 , Da = 1 , β = 1 , β 2 = 0.5 , μ = 2 . (d) ϕ = 0.5 , ε = 0.7 , Da = 1 , β 2 = 0.5 , μ = 2 . (e) β = 1 , ε = 0.7 , Da = 1 , β 2 = 0.5 , μ = 2 . (f) ϕ = 0.5 , ε = 0.7 , β = 1 , β 2 = 0.5 , Da = 0.1 .

The relationship between porosity and pumping was explained using Figure 3(c). We observe that the pumping decreases as the porosity ( ε ) increases. Thus, for large values of porosity ( ε ) , more flux is observed in free pumping as well as co-pumping. The influence of shear stress jump constant ( β ) on pumping is represented in Figure 3(d). For large values of shear stress jump constant, the flow rate increases in the free pumping region and the co-pumping region. Figure 3(e) shows a change in flux with ϕ , and it was found that at a constant Δp, an increase in flux increases ϕ . Figure 3(f) shows the effect of the viscosity ratio on flow rate. The flux increases as the viscosity ratio ( μ ) increases in the pumping region. The pumping is better with μ > 1 compared to μ < 1 , which is similar to the outcomes of Brasseur et al. [10]. Hence, it is concluded that for a given pressure rise, a better time-averaged flux with a porous peripheral layer having a large shear stress jump constant, high effective viscosity and small Darcy number is related to two Newtonian fluid layers.

Figure 4(a)–(d) shows the change in axial velocity at a constant axial station ( x = 0.25 ) for various Darcy numbers (Da), shear stress jump constant (β), viscosity ratio (μ) and Casson parameter ( β 2 ). From Figure 4(a), it is observed that in the core region, an increase in the jump constant (β) decreases the axial velocity. But a reverse trend was observed in the peripheral region, as shown in Figure 4(a). Figure 4(b) shows the relationship between the axial velocity (along y) and the Casson parameter ( β 2 ). From the figure, one can understand that fluid velocity increases with the increase in the Casson parameter ( β 2 ).

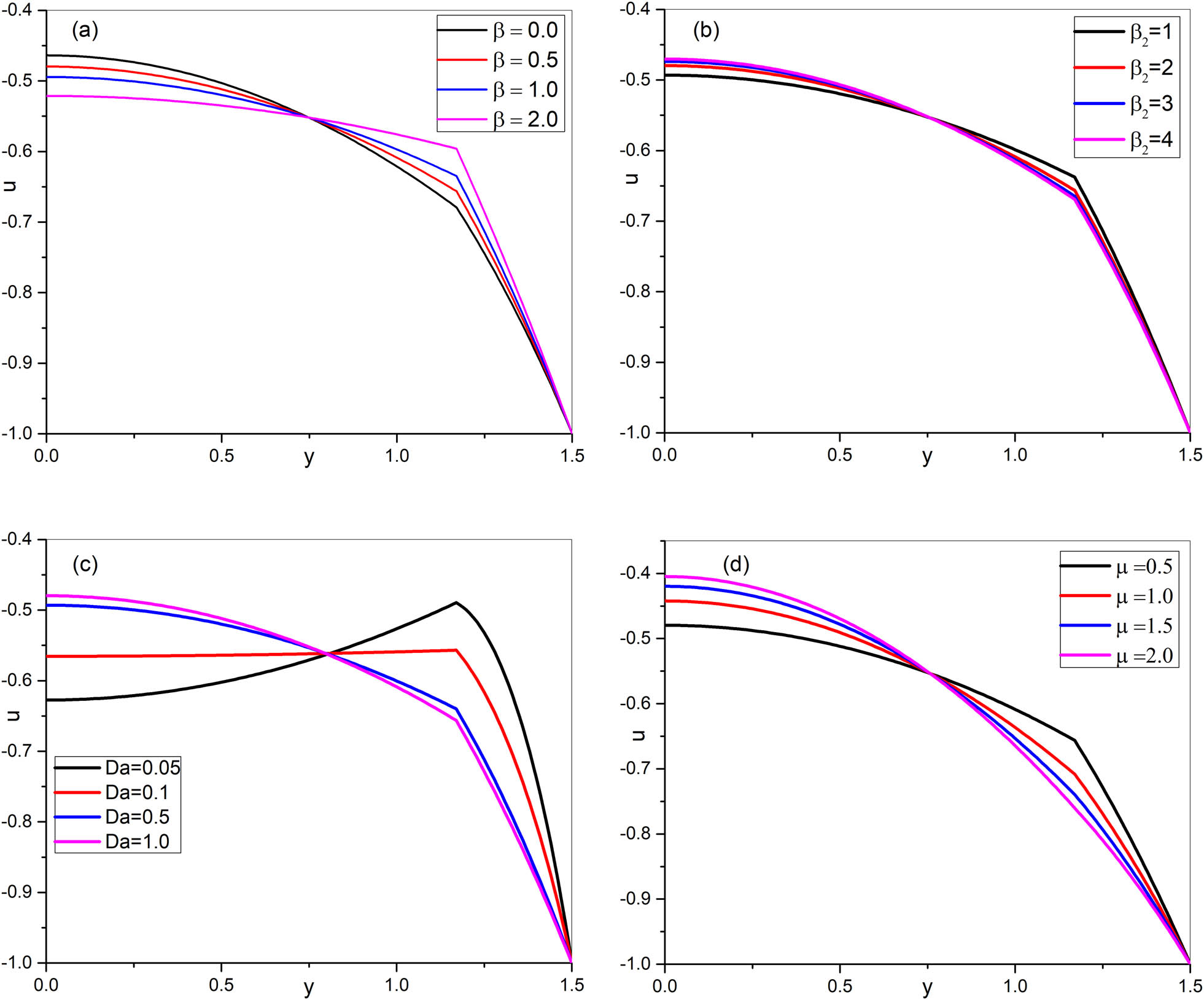
$Figure 4 Velocity profiles u ( y ) u(y) for (a) Da = 0.5 , M = 2 , μ = 1 , ϕ = 0.5 , Q ¯ = 0.1 , ε = 0.7 , γ = 0.7 \text{Da}=0.5,\hspace{.25em}M=2,\hspace{.25em}\mu =1,\hspace{.25em}\phi =0.5,\hspace{.25em}\bar{Q}=0.1,\hspace{.25em}\varepsilon =0.7,\hspace{.25em}\gamma =0.7 . (b) β = 0.5 , M = 2 , μ = 1 , ϕ = 0.5 , Q ¯ = 0.1 , ε = 0.7 , γ = 0.7 \beta \hspace{-.16em}=\hspace{-.16em}0.5,M\hspace{-.16em}=\hspace{-.16em}2,\mu \hspace{-.16em}=\hspace{-.16em}1,\phi \hspace{-.16em}=\hspace{-.16em}0.5,\bar{Q}\hspace{-.16em}=\hspace{-.16em}0.1,\varepsilon \hspace{-.16em}=\hspace{-.16em}0.7,\gamma \hspace{-.16em}=\hspace{-.16em}0.7 . (c) Da = 0.5 , β = 0.5 , μ = 1 , ϕ = 0.5 , Q ¯ = 0.1 , ε = 0.7 , γ = 0.7 \text{Da}\hspace{-.16em}=\hspace{-.16em}0.5,\beta \hspace{-.16em}=\hspace{-.16em}0.5,\mu =1,\phi =0.5,\bar{Q}=0.1,\varepsilon =0.7,\gamma =0.7 (d) Da = 0.5 , M = 2 , β = 0.5 , ϕ = 0.5 , Q ¯ = 0.1 , ε = 0.7 , γ = 0.7 \text{Da}=0.5,M=2,\beta =0.5,\phi =0.5,\bar{Q}=0.1,\varepsilon =0.7,\gamma =0.7 .$

Figure 4

Velocity profiles u ( y ) for (a) Da = 0.5 , M = 2 , μ = 1 , ϕ = 0.5 , Q ¯ = 0.1 , ε = 0.7 , γ = 0.7 . (b) β = 0.5 , M = 2 , μ = 1 , ϕ = 0.5 , Q ¯ = 0.1 , ε = 0.7 , γ = 0.7 . (c) Da = 0.5 , β = 0.5 , μ = 1 , ϕ = 0.5 , Q ¯ = 0.1 , ε = 0.7 , γ = 0.7 (d) Da = 0.5 , M = 2 , β = 0.5 , ϕ = 0.5 , Q ¯ = 0.1 , ε = 0.7 , γ = 0.7 .

But surprisingly, quite the opposite results were found in the peripheral region, i.e., fluid velocity increased with a decrease in Casson parameter ( β 2 ). Figure 4(c) shows the relation between the axial velocity and Darcy number (Da), and it was found that axial velocity is directly proportional to Darcy number, which is a clear indication of flow reversal in the core section reflecting a possible reflux. But the results are quite opposite in the peripheral region. Figure 4(d) indicates the relation between axial velocity and viscosity ratio, and from this figure, one can observe that axial velocity increases with the viscosity ratio parameter. But these results are quite the opposite in the core and peripheral regions.

5 Conclusions

The study on peristaltic transport of a two-layered system with a porous medium in the peripheral layer in a channel may represent the blood flow in capillaries and gastrointestinal tract. In this study, we investigated two-layered peristaltic pumping in a channel with non-Newtonian fluid in the inner layer and a porous medium in the outer layer. In the interface between the fluid and porous layers, a shear stress jump boundary condition is considered. The interface and pumping phenomena are observed for various physical parameters that govern the flow, such as Darcy number, porosity and shear stress jump constant. At a constant flux Q ¯ , an increase in Darcy number decreases the pressure rise. It is concluded that for a given pressure rise, the flux Q ¯ is better with a small Darcy number, the values of shear stress jump constant are larger and the viscosity is higher compared to two Newtonian fluid layers.

tel: +91-8903312379

Acknowledgments

The authors express their gratitude to the referees and the subject Editor for their valuable suggestions in the improvement of the paper.

Funding information: The authors state no funding involved.
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors state no conflict of interest.

Appendix I:

C 1 = ( q + h − h 1 − M 7 ) M 2 + M 3 M 10 ( M 8 − M 9 ) M 2 − M 1 M 10 , C 2 = C 1 M 1 + M 3 M 2 , B 1 = C 1 ( M 2 M 5 + M 1 M 6 ) + M 3 M 6 − M 2 M 4 K M 2 , K = β 2 β 2 + 1 , M 1 = sinh A h 1 − h 1 A K cosh A h − β 1 A ( cosh A h 1 − cosh A h ) ,

M 2 = β 1 A ( sinh A h 1 − sinh A h ) − cosh A h 1 + h 1 A K sinh A h , M 3 = β 1 A 2 − K h 1 , M 4 = 1 + K A 2 μ ε h 1 2 2 , M 5 = A cosh A h 1 − A M 4 cosh A h , M 6 = A sinh A h 1 − A M 4 sinh A h , M 7 = A 2 μ ε K h 1 3 6 M 2 ( M 2 + M 3 A sinh A h ) + h 1 M 2 ( M 3 M 6 − M 2 M 4 ) , M 8 = A 2 μ ε K h 1 3 6 M 2 ( M 2 A cosh A h + M 1 A sinh A h ) + h 1 M 2 ( M 1 M 6 + M 2 M 5 ) , M 9 = sinh A h 1 ± sinh A h + ( h − h 1 ) A cosh A h , M 10 = cosh A h 1 − cosh A h + ( h − h 1 ) A sinh A h .

Appendix II:

H 1 = sinh A γ − γ A K cosh A − β 1 A ( cosh A γ − cosh A ) , H 2 = γ A K sinh A − cosh A γ + β 1 A ( sinh A γ − sinh A ) , H 3 = β 1 A 2 − K γ , H 4 = 1 + K A 2 μ ε γ 2 2 , H 5 = A ( cosh A γ − H 4 cosh A ) , H 6 = A ( sinh A γ − H 4 sinh A ) , H 7 = A 2 μ ε K γ 3 6 H 2 ( H 2 + H 3 A sinh A ) + γ H 2 ( H 3 H 6 − H 2 H 4 ) , H 8 = A 2 μ ε K γ 3 6 H 2 ( H 2 A cosh A + H 1 A sinh A ) + γ H 2 ( H 1 H 6 + H 2 H 5 ) ,

H 9 = sinh A γ − sinh A + ( 1 − γ ) A cosh A , H 10 = cosh A γ − cosh A + ( 1 − γ ) A sinh A .

References

[1] Bergel DH. Cardiovascular fluid dynamics. London: Academic Press; 1972.Search in Google Scholar

[2] Hou JS, Holmes MH, Lai WM, Mow VC. Boundary conditions at the cartilage-synovial fluid interface for joint lubrication and theoretical verifications. Trans ASME J Bio Mech Eng. 1989;111:78–87.10.1115/1.3168343Search in Google Scholar

[3] Jaffrin MY, Shapiro AH. Peristaltic pumping. Ann Rev Fluid Mech. 1971;3:13–36.10.1146/annurev.fl.03.010171.000305Search in Google Scholar

[4] Rath HJ. Peristaltis chestromungen. Berlin: Springer; 1980.10.1007/978-3-642-81452-5Search in Google Scholar

[5] Srivastava LM, Srivastava VP. Peristaltic transport of a blood: Casson model: II. J Biomech. 1984;17:821–30.10.1016/0021-9290(84)90140-4Search in Google Scholar

[6] Latham TW. Fluid motions in peristaltic pump [dissertation]. Cambridge: MIT; 1966.Search in Google Scholar

[7] Bugliarello G, Sevilla J. Velocity distribution and other characteristics of steady and pulsatile blood flow in fine glass tubes. Biorheology. 1970;7:85–107.10.3233/BIR-1970-7202Search in Google Scholar

[8] Cokelet GR. The rheology of human blood. Y. C. Fung (Eds.), Biomechanics. Englewood Cliffs: Prentice-Hall; 1972. p. 63–103.Search in Google Scholar

[9] Scott Blair GW. An equation for the flow of blood plasma and serum through glass capillaries. Nature. 1959;185:613–4.10.1038/183613a0Search in Google Scholar

[10] Brasseur JG, Corrsin S, Lu NQ. The influence of a peripheral layer of different viscosity on peristaltic pumping with Newtonian fluids. J Fluid Mech. 1987;174:495–519.10.1017/S0022112087000211Search in Google Scholar

[11] Misra JC, Pandey SK. Peristaltic transport of blood in small vessels: Study of a mathematical model. An Int J Comput Math Appl. 2000;43:1183–93.10.1016/S0898-1221(02)80022-0Search in Google Scholar

[12] Ramachandra Rao A, Usha S. Peristaltic transport of two immiscible viscous fluid in a circular tube. J Fluid Mech. 1995;298:271–85.10.1017/S0022112095003302Search in Google Scholar

[13] Vajravelu K, Sreenadh S, Babu VR. Peristaltic transport of a Herschel–Bulkley fluid in contact with a Newtonian fluid. Q Appl Math. 2006;64:593–604.10.1090/S0033-569X-06-01020-9Search in Google Scholar

[14] Ochoa-Tapia JA, Whitaker S. Momentum transfer at the boundary between a porous medium and a homogenous fluid: Theoretical development. Int J Heat Mass Transf. 1995;38:2635–46.10.1016/0017-9310(94)00346-WSearch in Google Scholar

[15] EI Shehawey EF, Husseny SZA. Effects of porous boundaries on peristaltic transport through a porous medium. Acta Mechanica. 2000;143:165–77.10.1007/BF01170946Search in Google Scholar

[16] Mekheimer KS. Nonlinear peristaltic transport through a porous medium in an inclined planar channel. J Porous Media. 2003;6(3):1–13.10.1615/JPorMedia.v6.i3.40Search in Google Scholar

[17] Alazmi B, Vafai K. Analysis of fluid flow and heat transfer inter-facial conditions between a porous medium and a fluid layer. Int J Heat Mass Transf. 2001;44:1735–49.10.1016/S0017-9310(00)00217-9Search in Google Scholar

[18] Mernone AV, Mazumdar JN, Lucas SK. A mathematical study of peristaltic transport of a Casson fluid. Math Comput Model. 2002;35:895–912.10.1016/S0895-7177(02)00058-4Search in Google Scholar

[19] Mishra M, Ramachandra Rao A. Peristaltic transport in a channel with a porous peripheral layer: Model of a flow in gastrointestinal tract. J Biomech. 2005;38:779–89.10.1016/j.jbiomech.2004.05.017Search in Google Scholar PubMed

[20] Vajravelu K, Sreenadh S, Hemadri Reddy R, Murugesan K. Peristaltic transport of a Casson fluid in contact with a Newtonian fluid in a circular tube with permeable wall. Int J Fluid Mech Res. 2009;36:244–54.10.1615/InterJFluidMechRes.v36.i3.40Search in Google Scholar

[21] Vajravelu K, Sreenadh S, Saravana R. Influence of velocity slip and temperature jump conditions on the peristaltic flow of a Jeffrey fluid in contact with a Newtonian fluid. Appl Math Nonlinear Sci. 2017;2:429–42.10.21042/AMNS.2017.2.00034Search in Google Scholar

[22] Sreenadh S, Komala K, Srinivas ANS. Peristaltic pumping of a power – Law fluid in contact with a Jeffrey fluid in an inclined channel with permeable walls. Ain Shams Eng J. 2017;8:605–11.10.1016/j.asej.2015.08.019Search in Google Scholar

[23] Ponalagusamy R, Tamil Selvi R. Influence of magnetic field and heat transfer on two-phase fluid model for oscillatory blood flow in an arterial stenosis. Meccanica. 2015;50:927–43.10.1007/s11012-014-9990-1Search in Google Scholar

[24] Animasaun IL, Adebile EA, Fagbade AI. Casson fluid flow with variable thermo-physical property along exponentially stretching sheet with suction and exponentially decaying internal heat generation using the homotopy analysis method. J Nigerian Math Soc. 2016;35(1):1–17.10.1016/j.jnnms.2015.02.001Search in Google Scholar

[25] Thumma T, Wakif A, Animasaun IL. Generalized differential quadrature analysis of unsteady three-dimensional MHD radiating dissipative Casson fluid conveying tiny particles. Heat Transf. 2020;49(5):2595–626.10.1002/htj.21736Search in Google Scholar

[26] Ramachandra Rao A, Mishra M. Peristaltic transport of a power-law fluid in a porous tube. J Non-Newtonian Fluid Mech. 2004;121:163–74.10.1016/j.jnnfm.2004.06.006Search in Google Scholar

[27] Nadeem S, Shahzadi I. Mathematical analysis for peristaltic flow of two phase nanofluid in a curved channel. Comm Theor Phys. 2015;64:547–54.10.1088/0253-6102/64/5/547Search in Google Scholar

[28] Sadiq MA, Hayat T. Characterization of Marangoni forced convection in Casson nano liquid flow with joule heating and irreversibility. Entropy. 2020;22:433.10.3390/e22040433Search in Google Scholar PubMed PubMed Central

[29] Shukla JB, Parihar RS, Rao BRP, Gupta SP. Effects of peripheral-layer viscosity on peristaltic transport of a bio-fluid. J Fluid Mech. 1980;97:225–37.10.1017/S0022112080002534Search in Google Scholar

[30] Srivastava LM, Srivastava VP. Peristaltic transport of a non-Newtonian fluid: applications to the vas deferens and small intestine. Ann Biomed Eng. 1985;13:137–53.10.1007/BF02584235Search in Google Scholar PubMed

[31] Usha S, Ramachandra Rao A. Peristaltic transport of two-layered power-law fluids. J Biomech Eng. 1997;119:483–8.10.1115/1.2798297Search in Google Scholar PubMed

[32] Kesava AR, Srinivas ANS. Peristaltic flow of a two-layer system in a channel with a porous peripheral layer under action of magnetic field. Spec Top Rev Porous Media An Int J. 2021;12:93–106.10.1615/SpecialTopicsRevPorousMedia.2021035098Search in Google Scholar

[33] Nakamura M, Sawada T. Numerical study on the flow of a Non-Newtonian fluid through an axisymmetric stenosis. J Biomech Eng. 1988;110:137–43.10.1115/1.3108418Search in Google Scholar PubMed

[34] Mukhopadhyay S. Casson fluid flow and heat transfer over a nonlinearly stretching surface. Chin Phys B. 2013;22:074701.10.1088/1674-1056/22/7/074701Search in Google Scholar

[35] Selvi CK, Srinivas ANS. Oscillatory flow of a Casson fluid in an elastic tube with variable cross section. Applied Mathematics and Nonlinear. Sciences. 2018;3:571–82.10.2478/AMNS.2018.2.00044Search in Google Scholar

[36] Gireesha BJ, Sindhu S. MHD natural convection flow of Casson fluid in an annular microchannel containing porous medium with heat generation/absorption. Nonlinear Eng. 2020;9:223–32.10.1515/nleng-2020-0010Search in Google Scholar

[37] Alali E, Megahed AM. MHD dissipative Casson nano fluid liquid film flow due to an unsteady stretching sheet with radiation influence and slip velocity phenomenon. Nonlinear Eng. 2022;11:463–72.10.1515/ntrev-2022-0031Search in Google Scholar

Received: 2021-12-11

Revised: 2022-08-14

Accepted: 2022-08-23

Published Online: 2022-10-10

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/nleng-2022-0247

Keywords for this article

Casson fluid; peristaltic transport; porous medium; interface

Creative Commons

BY 4.0