A new computational investigation to the new exact solutions of (3 + 1)-dimensional WKdV equations via two novel procedures arising in shallow water magnetohydrodynamics

Maojie Zhou; Arzu Akbulut; Melike Kaplan; Mohammed K. A. Kaabar; Xiao-Guang Yue

doi:10.1515/nleng-2022-0041

Article Open Access

A new computational investigation to the new exact solutions of (3 + 1)-dimensional WKdV equations via two novel procedures arising in shallow water magnetohydrodynamics

Maojie Zhou , Arzu Akbulut , Melike Kaplan , Mohammed K. A. Kaabar and Xiao-Guang Yue

Published/Copyright: September 21, 2022

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Nonlinear Engineering Volume 11 Issue 1

Abstract

Various new exact solutions to ( 3 + 1 ) -dimensional Wazwaz–KdV equations are obtained in this work via two techniques: the modified Kudryashov procedure and modified simple equation method. The 3D plots, contour plots, and 2D plots of some obtained solutions are provided to describe the dynamic characteristics of the obtained solutions. Our employed techniques are very helpful in constructing new exact solutions to several nonlinear models encountered in ocean scientific phenomena arising in stratified flows, shallow water, plasma physics, and internal waves.

Keywords: exact solutions; (3 + 1)-dimensional modified Wazwaz–KdV equations; modified Kudryashov procedure; modified simple equation method

1 Introduction

In many physical phenomena, nonlinear partial differential equations (NPDEs) are apparent in modeling these phenomena [1]. To understand the dynamic behaviour of these models, several research studies have been dedicated to study the exact solutions of NLPDEqs using a variety of procedures such as the enhanced Kudryashov’s (KdV) technique [2], general projective Riccati equations technique [2], sine-Gordon expansion technique [3,4], sinh-Gordon expansion technique [5,6], Hirota bilinear approach [7], Riccati–Bernoulli sub ordinary differential equation (ODE) technique [8], modified simple equation (MSE) technique [9], KdV and exponential techniques [10,11,12], and improved F-expansion technique [13]. In addition, some studies have formulated some of NPDEs in the sense of fractional calculus such as the fractional-order Kaup–Boussinesq and generalized Hirota Satsuma-coupled KdV systems [14], ( 3 + 1 ) -dimensional conformable Wazwaz–Benjamin–Bona–Mahony equation [15], and nonlinear fractional Schrödinger equation [16] (see also ref. [17]).

For the fractional version of NPDEs and other types of differential equations, a newly proposed definition of generalized fractional derivative, named Abu-Shady–Kaabar fractional derivative, [18], can be utilized further in studying these equations due to the simplicity and efficiency of obtained analytical solutions using this new definition.

This article is organized as follows: Basic preliminaries about our adapted algorithms are reviewed in Section 2. The utilized procedures, particularly the modified KdV and MSE procedures, are discussed in Section 3. The illustrations of some obtained solutions are represented graphically in Section 4. A conclusion is drawn in Section 5.

2 Adopted algorithms

The needed tools are presented here to help in a NPDE’s reduction to an ODE. We suppose that NPDE is expressed as follows:

(1) P ( u , u t , u x , u y , u z , u t t , u x t , u x x , … ) = 0 ,

where P is a polynomial of u and its partial derivatives.

We will take a transformation as follows:

(2) ξ = k x + r y + s z − w t .

Here, k , r , s , and w are constants. By substituting Eq. (2) to Eq. (1), we obtain an ODE as follows, which will be integrated with respect to ξ possible times [19].

(3) Q ( u , u ′ , u ″ , u ‴ , … ) = 0 .

In Sections 2.1 and 2.2, we describe the modified KdV and the modified simple eqaution (MSE) procedures, respectively.

2.1 The procedure of modified Kudryashov

The exact solutions of Eq. (3) are assumed as follows follows:

(4) u ( ξ ) = ∑ n = 0 m α i ( ϕ ( ξ ) ) n .

Here, α n ( n = 0 , 1 , … , m ) are constants to be obtained later, and α m ≠ 0 . The balancing term is represented by m . ϕ ( ξ ) is written as follows:

(5) ϕ ( ξ ) = 1 1 + δ a ξ ,

and Eq. (5) satisfies:

(6) ϕ ′ ( ξ ) = ϕ ( ξ ) ( ϕ ( ξ ) − 1 ) ln a .

Nonlinear algebraic equations’ system is obtained for α n ( n = 0 , … , m ) , a , k , r , s , and w by substituting Eq. (4) into Eq. (3) associated with Eq. (6) and then setting the collection of all the coefficients of ϕ n ( ξ ) to be 0. By solving the obtained system via MAPLE, a variety of exact solutions [20,21,22] is found.

2.2 The method of MSE

We present the MSE method’s main steps along with its fundamental ideas [27]. Through the transformation Eq. (2), Eq. (1) can be changed into Eq. (3). This procedure benefits from choosing the solution of Eq. (3) as follows:

(7) u ( ξ ) = ∑ m n = 0 a n ϕ ′ ( ξ ) ϕ ( ξ ) n ,

where a n , ( n = 0 , 1 , 2 , 3 , … , m ) are arbitrary constants to be found later ∋ a m ≠ 0 , and ϕ ( ξ ) is an unknown function to be found later ∋ ϕ ′ ( ξ ) ≠ 0 . We may calculate the positive integer m occur in Eq. (7) via the homogeneous balance principle. Substituting Eq. (7) into Eq. (3), a polynomial in ϕ ( ξ ) can be obtained, and then by setting all the coefficients of ϕ j ( ξ ) ( j = … , − 2 , − 1 , 0 ) to 0 obtains nonlinear algebraic equation’s system for a n , ( n = 0 , 1 , 2 , 3 , … , m ) and ϕ ( ξ ) . A variety of exact solutions is constructed for the desired equation via solving the obtained system.

Remark 1

The obtained solution via the tanh-function method, G ′ G -expansion method, and exp-function method is expressed in the terms of some predefined functions, but in the MSE method, ϕ is not predefined or not a solution of any predefined equation. Therefore, novel solutions are obtained via this technique.

3 The modified version of (3 + 1)-dimensional KdV equations

The modified (3 + 1)-dimensional KdV equations’ exact solutions are presented in this section. These equations are expressed as follows [23,24]:

(8) u t + 6 u 2 u x + u x y z = 0 .

(9) u t + 6 u 2 u y + u x y z = 0 .

(10) u t + 6 u 2 u z + u x y z = 0 .

The above equations are essential in mathematical physics topics. The first equation is given by Hereman [25], while the second and third equations are given by Wazwaz [26].

3.1 Application of the modified Kudryashov procedure

We will employ the modified KdV procedure to the adopted equations.

3.1.1 First equation’s exact solutions

Let the wave variable: ξ = k x + r y + s z − w t be applied to Eq. (8). Then, by integrating the obtained ODE, we obtain:

(11) − w u + 2 k u 3 + k r s u ″ = 0 .

Here, according to the homogeneous balance principle, the balancing number is 1. So, the ODE’s solution is written as follows:

(12) u ( ξ ) = a 0 + a 1 ϕ ( ξ ) .

Eq. (12) is substituted via Eq. (6)’s help into Eq. (11). Then, by collecting all terms with the same power of ϕ ( ξ ) , we obtain:

(13) ( ϕ ( ξ ) ) 3 : 2 ln ( a ) 2 k r s a 1 + 2 k a 1 3 , ( ϕ ( ξ ) ) 2 : − 3 ln ( a ) 2 k r s a 1 + 6 k a 0 a 1 2 , ( ϕ ( ξ ) ) 1 : ln ( a ) 2 k r s a 1 + 6 k a 0 2 a 1 − a 1 w , ( ϕ ( ξ ) ) 0 : 2 k a 0 3 − w a 0 .

The exact solutions are obtained by solving the aforementioned system as follows:

(14) a 0 = ± − r s ln ( a ) 2 , a 1 = ± r s ln ( a ) − r s , w = − k s r ln ( a ) 2 2 .

Then, Eq. (8)’s exact solutions are expressed as follows:

(15) u 1 , 2 ( x , y , z , t ) = ± − r s ln ( a ) 2 ± r s ln ( a ) − r s 1 + δ a k x + r y + s z + k s r ln ( a ) 2 2 t .

3.1.2 The second equation’s exact solutions

Let the wave variable: ξ = k x + r y + s z − w t be applied to Eq. (9). Then, by integrating the obtained ODE, we obtain:

(16) − w u + 2 r u 3 + k r s u ″ = 0 .

Here, the balancing number is 1. So, the ODE’s solution is same as Eq. (12). Eq. (12) is substituted via Eq. (6)’s help into Eq. (16). Then, by collecting all terms with the same power of ϕ ( ξ ) , we obtain:

( ϕ ( ξ ) ) 3 : 2 ln ( a ) 2 k r s a 1 + 2 r a 1 3 , ( ϕ ( ξ ) ) 2 : − 3 ln ( a ) 2 k r s a 1 + 6 r a 0 a 1 2 , ( ϕ ( ξ ) ) 1 : ln ( a ) 2 k r s a 1 + 6 r a 0 2 a 1 − a 1 w , ( ϕ ( ξ ) ) 0 : 2 r a 0 3 − w a 0 .

If we solve the aforementioned system, we obtain following values of the constant:

(17) a 0 = ± − k s ln ( a ) 2 , a 1 = ± k s ln ( a ) − k s , w = − k s r ln ( a ) 2 2 .

Then, Eq. (9)’s exact solutions are expressed as follows:

(18) u 1 , 2 ( x , y , z , t ) = ± − k s ln ( a ) 2 ± k s ln ( a ) − k s 1 + δ a k x + r y + s z + k s r ln ( a ) 2 2 t .

3.1.3 The third equation’s exact solutions

Let the wave variable: ξ = k x + r y + s z − w t be applied to Eq. (10), and we obtain:

(19) − w u + 2 s u 3 + k r s u ″ = 0 .

Here, the balancing number is 1. So, the ODE’s solution is same as Eq. (12). Eq. (12) is substituted via Eq. (6)’s help into Eq. (19). Then, by collecting all terms with the same power of ϕ ( ξ ) , we obtain:

( ϕ ( ξ ) ) 3 : 2 ln ( a ) 2 k r s a 1 + 2 s a 1 3 , ( ϕ ( ξ ) ) 2 : − 3 ln ( a ) 2 k r s a 1 + 6 s a 0 a 1 2 , ( ϕ ( ξ ) ) 1 : ln ( a ) 2 k r s a 1 + 6 s a 0 2 a 1 − a 1 w , ( ϕ ( ξ ) ) 0 : 2 s a 0 3 − w a 0 .

The values of constants are obtained by solving the aforementioned system as follows:

a 0 = ± − k s ln ( a ) 2 , a 1 = ± k s ln ( a ) − k s , w = − k s r ln ( a ) 2 2 .

Thus, the third equation’s exact solutions are expressed as follows:

(20) u 1 , 2 ( x , y , z , t ) = ± − k r ln ( a ) 2 ± k r ln ( a ) − k r 1 + δ a k x + r y + s z + k s r ln ( a ) 2 2 t .

3.2 Application of the modified simple equation procedure

We will employ the MSE procedure to the adopted equations.

3.2.1 The first equation’s exact solutions

From the employed technique, Eq. (11)’s exact solution is assumed as follows:

(21) u ( ξ ) = a 0 + a 1 ϕ ′ ( ξ ) ϕ ( ξ ) .

Eq. (21) is substituted into Eq. (11), and all terms with the same power of ϕ ( ξ ) are collected. Then, we obtain:

(22) ( ϕ ( ξ ) ) − 3 : 2 k a 1 3 + 2 k r s a 1 = 0 ,

(23) ( ϕ ( ξ ) ) − 2 : 6 k a 0 a 1 2 ϕ ′ ( ξ ) − 3 k r s a 1 ϕ ″ ( ξ ) = 0 ,

(24) ( ϕ ( ξ ) ) − 1 : 6 k a 1 a 0 2 ϕ ′ ( ξ ) + k r s a 1 ϕ ‴ ( ξ ) − w a 1 ϕ ′ ( ξ ) = 0 ,

(25) ( ϕ ( ξ ) ) 0 : 2 k a 0 3 − w a 0 = 0 .

By solving Eqs. (25) and (22), we obtain the following values of the constants:

(26) a 0 = a 0 , a 1 = ± − r s , w = 2 a 0 2 k .

If we substitute Eq. (26) in Eqs. (23)–(24), we obtain:

(27) ϕ ( ξ ) = C 1 + C 2 e ± 2 a 0 − r s ξ r s ,

and, Eq. (8)’s exact solutions are expressed as follows:

(28) u 3 , 4 ( x , y , z , t ) = a 0 − 2 C 2 a 0 e ± 2 a 0 − r s ξ r s C 1 + C 2 e ± 2 a 0 − r s ξ r s .

3.2.2 The second equation’s exact solutions

From the employed technique, Eq. (16)’s exact solution is assumed as follows:

(29) u ( ξ ) = a 0 + a 1 ϕ ′ ( ξ ) ϕ ( ξ ) .

Eq. (29) is substituted into Eq. (16), and all terms with the same power of ϕ ( ξ ) are collected. Then, we obtain:

(30) ( ϕ ( ξ ) ) − 3 : 2 r a 1 3 + 2 k r s a 1 = 0 ,

(31) ( ϕ ( ξ ) ) − 2 : 6 r a 0 a 1 2 ϕ ′ ( ξ ) − 3 k r s a 1 ϕ ″ ( ξ ) = 0 ,

(32) ( ϕ ( ξ ) ) − 1 : 6 r a 1 a 0 2 ϕ ′ ( ξ ) + k r s a 1 ϕ ‴ ( ξ ) − w a 1 ϕ ′ ( ξ ) = 0 ,

(33) ( ϕ ( ξ ) ) 0 : 2 r a 0 3 − w a 0 = 0 .

By solving Eqs. (30) and (33), we obtain the following values of the constants:

(34) a 0 = a 0 , a 1 = ± − k s , w = 2 a 0 2 r .

If we substitute Eq. (34) into Eqs. (31) and (32), we obtain:

(35) ϕ ( ξ ) = C 1 + C 2 e ± 2 a 0 − k s ξ k s ,

and, Eq. (9)’s exact solutions are as follows:

(36) u 3 , 4 ( x , y , z , t ) = a 0 − 2 C 2 a 0 e ± 2 a 0 − k s ξ r s C 1 + C 2 e ± 2 a 0 − k s ξ r s .

3.2.3 The third equation’s exact solutions

From the employed technique, Eq. (19)’s exact solution is assumed as follows:

(37) u ( ξ ) = a 0 + a 1 ϕ ′ ( ξ ) ϕ ( ξ ) .

Eq. (37) is substituted into Eq. (19), and all terms with the same power of ϕ ( ξ ) are collected. Then, we obtain:

(38) ( ϕ ( ξ ) ) − 3 : 2 s a 1 3 + 2 k r s a 1 = 0 ,

(39) ( ϕ ( ξ ) ) − 2 : 6 s a 0 a 1 2 ϕ ′ ( ξ ) − 3 k r s a 1 ϕ ″ ( ξ ) = 0 ,

(40) ( ϕ ( ξ ) ) − 1 : 6 s a 1 a 0 2 ϕ ′ ( ξ ) + k r s a 1 ϕ ‴ ( ξ ) − w a 1 ϕ ′ ( ξ ) = 0 ,

(41) ( ϕ ( ξ ) ) 0 : 2 s a 0 3 − w a 0 = 0 .

Solving Eqs. (38) and (41), we obtain the following values of the constants:

(42) a 0 = a 0 , a 1 = ± − k r , w = 2 a 0 2 s .

If we substitute Eq. (42) in Eqs. (39) and (40), we obtain:

(43) ϕ ( ξ ) = C 1 + C 2 e ± 2 a 0 − k r ξ k r ,

and Eq. (10)’s exact solutions are as follows:

(44) u 3 , 4 ( x , y , z , t ) = a 0 − 2 C 2 a 0 e ± 2 a 0 − k r ξ k r C 1 + C 2 e ± 2 a 0 − k r ξ k r .

Remark 2

Here, we did not consider the case of a 0 = 0 as it leads to zero solutions.

4 Graphical representation of the obtained solutions

The figures of some obtained solutions are given in this section, which are obtained by the discussed methods. We give graphical illustrations by 3D plots, contour plots, and 2D plots.

First, we have given graphs for solution (8) in Figure 1. Figure 1(a) and (b) show 3D and contour plots, respectively. We have plotted them when y = 1 , z = 1 , k = 2.1 , r = − 0.5 , s = 1.7 , a = 2.7 , and δ = 5 . Figure 1(c) shows the 2D plot which is plotted when y = 1 , z = 1 , k = 2.1 , r = − 0.5 , s = 1.7 , a = 2.7 , and δ = 5 . Red line is plotted when t = 0 , green line is plotted when t = 0.5 , and blue line is plotted when t = 1 .

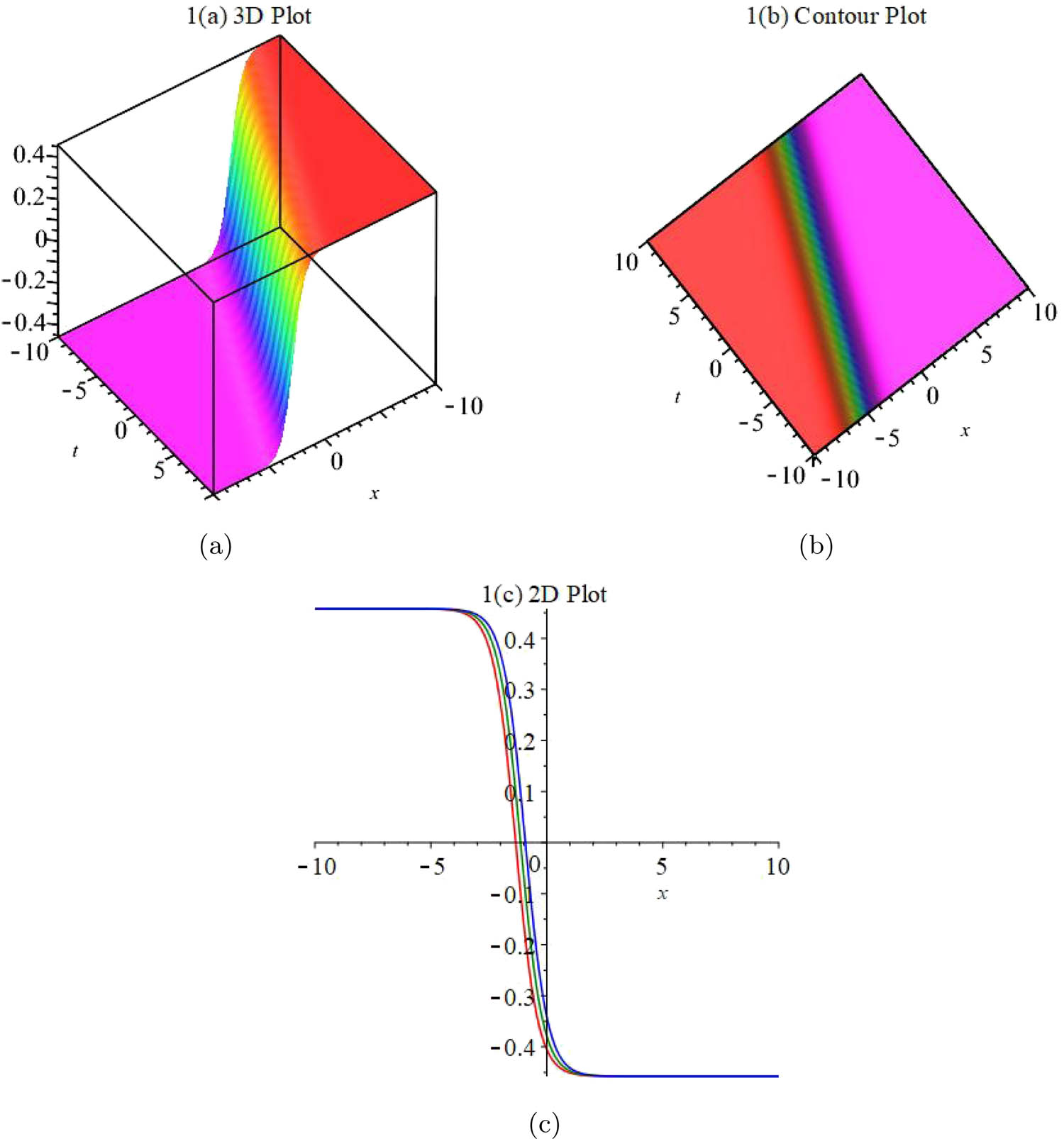
$Figure 1 Graphical representations of (a) and (b) when y = 1 y=1 , z = 1 z=1 , k = 2.1 k=2.1 , r = − 0.5 r=-0.5 , s = 1.7 s=1.7 , a = 2.7 a=2.7 , δ = 5 \delta =5 ; and (c) when y = 1 y=1 , z = 1 z=1 , k = 2.1 k=2.1 , r = − 0.5 r=-0.5 , s = 1.7 s=1.7 , a = 2.7 a=2.7 , δ = 5 \delta =5 . (a) 3D representation, (b) contour representation, and (c) 2D representation.$

Figure 1

Graphical representations of (a) and (b) when y = 1 , z = 1 , k = 2.1 , r = − 0.5 , s = 1.7 , a = 2.7 , δ = 5 ; and (c) when y = 1 , z = 1 , k = 2.1 , r = − 0.5 , s = 1.7 , a = 2.7 , δ = 5 . (a) 3D representation, (b) contour representation, and (c) 2D representation.

Then, we have given graphs for solution (28) in Figure 2. Figure 2(a) and (b) show 3D and contour plots, respectively. We have plotted them when y = 1 , z = 1 , k = 2.1 , r = − 3.5 , s = 1.7 , C 1 = 0.3 , C 2 = 0.8 , a 0 = 2.1 . Figure 2(c) shows the 2D plot, which is plotted when y = 1 , z = 1 , k = 2.1 , r = − 3.5 , s = 1.7 , C 1 = 0.3 , C 2 = 0.8 , and a 0 = 2.1 . Red line is plotted when t = 0 , green line is plotted when t = 0.5 , and blue line is plotted when t = 1 .

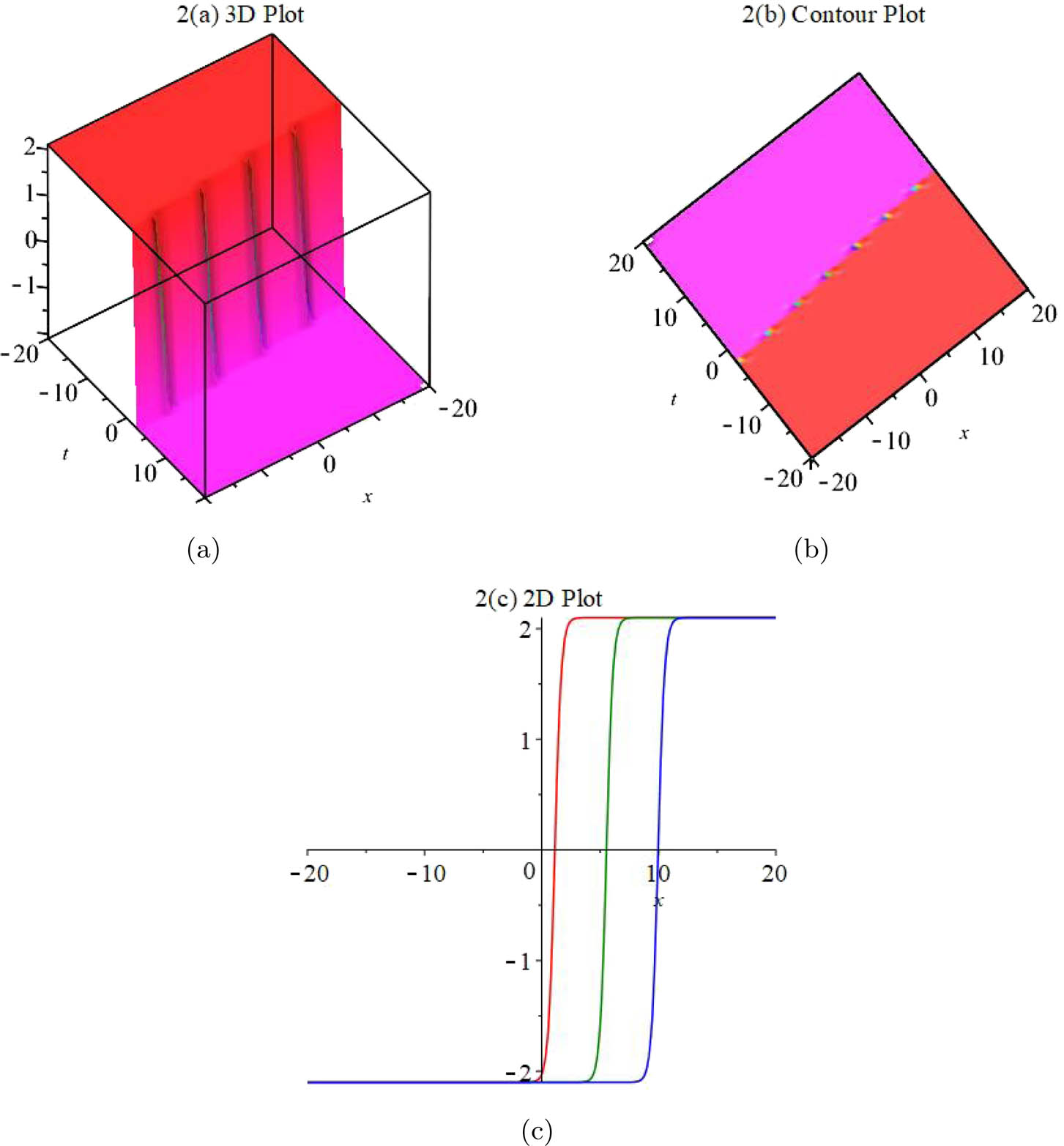
$Figure 2 Graphical representations of (a) and (b) when y = 1 y=1 , z = 1 z=1 , k = 2.1 k=2.1 , r = − 3.5 r=-3.5 , s = 1.7 s=1.7 , C 1 = 0.3 {C}_{1}=0.3 , C 2 = 0.8 {C}_{2}=0.8 , a 0 = 2.1 {a}_{0}=2.1 ; and (c) when y = 1 y=1 , z = 1 z=1 , k = 2.1 k=2.1 , r = − 3.5 r=-3.5 , s = 1.7 s=1.7 , C 1 = 0.3 {C}_{1}=0.3 , C 2 = 0.8 {C}_{2}=0.8 , a 0 = 2.1 {a}_{0}=2.1 . (a) 3D representation, (b) contour representation, and (c) 2D representation.$

Figure 2

Graphical representations of (a) and (b) when y = 1 , z = 1 , k = 2.1 , r = − 3.5 , s = 1.7 , C 1 = 0.3 , C 2 = 0.8 , a 0 = 2.1 ; and (c) when y = 1 , z = 1 , k = 2.1 , r = − 3.5 , s = 1.7 , C 1 = 0.3 , C 2 = 0.8 , a 0 = 2.1 . (a) 3D representation, (b) contour representation, and (c) 2D representation.

5 Conclusion

Exploring the exact solutions of NPDEs is essential in studying various modeling scenarios. In our work, we have obtained the ( 3 + 1 ) -dimensional Wazwaz-KdV (WKdV) equations’ new exact solutions via the modified Kudryashov procedure and the MSE method. The graphical representations involving 3D plots, contour plots and 2D plots have been provided for some obtained solutions to understand the nonlinear model’s behavior. These investigated techniques can provide exact solutions to many nonlinear models in physics and engineering. Future research works can be based on our results by extending this work to study the fractional version of ( 3 + 1 ) -dimensional WKdV equations via some new fractional definitions such as Abu-Shady–Kaabar fractional derivative [18].

Acknowledgments

This work has been supported by Guilin Science and Technology Research and Development Project (20180102-2, 20170220), Guangxi Science and Technology Plan Project (guikeAB17195028),and Guangxi University Young and Middle-Aged Teachers' Basic Scientific Research Ability Improvement Project (2021KY1675).

Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: On behalf of all authors, the corresponding author states that there is no conflict of interest.
Data availability statement: No data were used in this study.

References

[1] Jaradat I, Alquran M, Sulaiman TA, Yusuf A. Analytic simulation of the synergy of spatial-temporal memory indices with proportional time delay. Chaos Solitons Fractals. 2022;156:111818. 10.1016/j.chaos.2022.111818Search in Google Scholar

[2] Arnous AH, Mirzazadeh M, Akinyemi L, Akbulut A. New solitary waves and exact solutions for the fifth-order nonlinear wave equation using two integration techniques. J Ocean Eng Sci. 2022. 10.1016/j.joes.2022.02.012. Search in Google Scholar

[3] Baskonus HM, Bulut H, Sulaiman TA. Investigation of various travelling wave solutions to the extended (2+1)-dimensional quantum ZK equation. Eur Phys J Plus. 2017;132:482. 10.1140/epjp/i2017-11778-ySearch in Google Scholar

[4] Bulut H, Aksan EN, Kayhan M, Sulaiman TA. New solitary wave structures to the (3+1) dimensional Kadomtsev-Petviashvili and Schrödinger equation. J Ocean Eng Sci. 2019;4(4):373–8. 10.1016/j.joes.2019.06.002Search in Google Scholar

[5] Sulaiman TA, Bulut H, Baskonus HM. On the exact solutions to some system of complex nonlinear models. Appl Math Nonlinear Sci. 2021;6(1):29–42. 10.2478/amns.2020.2.00007Search in Google Scholar

[6] Sulaiman TA. Three-component coupled nonlinear Schrödinger equation: optical soliton and modulation instability analysis. Phys Scr. 2020;95:065201. 10.1088/1402-4896/ab7c77Search in Google Scholar

[7] Sulaiman TA, Yusuf A, Atangana A. New lump, lump-kink, breather waves and other interaction solutions to the (3+1)-dimensional soliton equation. Commun Theoret Phys. 2020;72(8):085004. 10.1088/1572-9494/ab8a21Search in Google Scholar

[8] Ozdemir N, Esen H, Secer A, Bayram M, Yusuf A, Sulaiman TA. Optical solitons and other solutions to the Hirota-Maccari system with conformable, M-truncated and beta derivatives. Modern Phys Lett B. 2022;36(11):2150625. 10.1142/S0217984921506259Search in Google Scholar

[9] Akbulut A, Kaplan M, Kaabar MKA. New conservation laws and exact solutions of the special case of the fifth-order KdV equation. J Ocean Eng Sci. 2021. 10.1016/j.joes.2021.09.010. Search in Google Scholar

[10] Hosseini H, Akbulut A, Baleanu D, Salahshour S. The Sharma-Tasso-Olver-Burgers equation: Its conservation laws and kink solitons. Commun Theoret Phys. 2022;74:025001. 10.1088/1572-9494/ac4411Search in Google Scholar

[11] Jaradat I, Alquran M, Qureshi S, Sulaiman TA, Yusuf A. Convex-rogue, half-kink, cusp-soliton and other bidirectional wave-solutions to the generalized Pochhammer-Chree equation. Phys Scr. 2022;97(5):055203. 10.1088/1402-4896/ac5f25Search in Google Scholar

[12] Usman Y, Bilal M, Sulaiman TA, Ren J, Yusuf A. On the exact soliton solutions and different wave structures to the double dispersive equation. Opt Quantum Electron. 2022;54(2):1–22. 10.1007/s11082-021-03445-2Search in Google Scholar

[13] Mirzazadeh M, Akbulut A, Taşcan F, Akinyemi L. A novel integration approach to study the perturbed Biswas-Milovic equation with Kudryashov’s law of refractive index. Optik. 2022;252:168529. 10.1016/j.ijleo.2021.168529Search in Google Scholar

[14] Wang X, Yue XG, Kaabar MKA, Akbulut A, Kaplan M. A unique computational investigation of the exact traveling wave solutions for the fractional-order Kaup-Boussinesq and generalized Hirota Satsuma coupled KdV systems arising from water waves and interaction of long waves. J Ocean Eng Sci. 2022. 10.1016/j.joes.2022.03.012. Search in Google Scholar

[15] Kaabar MKA, Kaplan M, Siri Z. New exact soliton solutions of the (3+1)-dimensional conformable Wazwaz-Benjamin-Bona-Mahony equation via two novel techniques. J Function Spaces. 2021;4659905:1–13. 10.1155/2021/4659905Search in Google Scholar

[16] Kaabar MKA, Martínez F, Gómez-Aguilar JF, Ghanbari B, Kaplan M, Günerhan H. New approximate analytical solutions for the nonlinear fractional Schrödinger equation with second-order spatio-temporal dispersion via double Laplace transform method. Math Methods Appl Sci. 2021;44(14):11138–56. 10.1002/mma.7476Search in Google Scholar

[17] Bhanotar SA, Kaabar MKA. Analytical solutions for the nonlinear partial differential equations using the conformable triple Laplace transform decomposition method. Int J Differ Equ. 2021;2021:1–18. 10.1155/2021/9988160Search in Google Scholar

[18] Abu-Shady M, Kaabar MKA. A generalized definition of the fractional derivative with applications. Math Probl Eng. 2021;9444803:1–9. 10.1155/2021/9444803Search in Google Scholar

[19] Hereman W, Nuseir A. Symbolic methods to construct exact solutions of nonlinear partial differential equations. Math Comput Simulat. 2021;43(1):13–27. 10.1016/S0378-4754(96)00053-5Search in Google Scholar

[20] Hosseini K, Ansari R. New exact solutions of nonlinear conformable time-fractional Boussinesq equations using the modified Kudryashov method. Waves Random Complex Media. 2017;27(4):628–36. 10.1080/17455030.2017.1296983Search in Google Scholar

[21] Zayed EME, Alurrfi KAE. The modified Kudryashov method for solving some seventh order nonlinear PDEs in mathematical physics. World J Modell Simulat. 2015;11(4):308–19. Search in Google Scholar

[22] Hosseini K, Akbulut A, Baleanu D, Salahshour S. The Sharma-Tasso-Olver-Burgers equation: Its conservation laws and kink solitons. Commun Theoret Phys. 2021;74:025001. 10.1088/1572-9494/ac4411. Search in Google Scholar

[23] Akbulut A, Rezazadeh H, Hashemi MS, Tascan F. The (3+1)-dimensional Wazwaz-KdV equations: the conservation laws and exact solutions. IJNSNS. 2021. 10.1515/ijnsns-2021-0161. Search in Google Scholar

[24] Nuruddeen RI. Multiple soliton solutions for the (3+1) conformable space-time fractional modified Korteweg-de-Vries equations. J Ocean Eng Sci. 2018;3:11–8. 10.1016/j.joes.2017.11.004Search in Google Scholar

[25] Hereman, W. Exact solutions of nonlinear partial differential equations the tanh/sech method. Champaign. Illinois: Wolfram Res Acade Intern Program Inc.; 2000. p. 1–14. Search in Google Scholar

[26] Wazwaz AM. Exact soliton and kink solutions for new (3+1)-dimensional nonlinear modified equations of wave propagation. Open Eng. 2017;7:169–74. 10.1515/eng-2017-0023Search in Google Scholar

[27] Kaplan M, Bekir A. The modified simple equation method for solving some fractional-order nonlinear equations. Pramana. 2016;87(1):1–5. 10.1007/s12043-016-1205-ySearch in Google Scholar

[28] Kaplan M, Mayeli P, Hosseini K. Exact traveling wave solutions of the Wu-Zhang system describing (1+1)-dimensional dispersive long wave. Opt Quant Electron. 2017;49:404. 10.1007/s11082-017-1231-0Search in Google Scholar

Received: 2022-04-25

Revised: 2022-06-13

Accepted: 2022-07-12

Published Online: 2022-09-21

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/nleng-2022-0041

Keywords for this article

exact solutions; (3 + 1)-dimensional modified Wazwaz–KdV equations; modified Kudryashov procedure; modified simple equation method

Creative Commons

BY 4.0