Home Outage probability for a multiuser NOMA-based network using energy harvesting relays
Article Open Access

Outage probability for a multiuser NOMA-based network using energy harvesting relays

  • Rifqah Press and Vipin Balyan EMAIL logo
Published/Copyright: December 21, 2022
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
Nonlinear Engineering
From the journal Nonlinear Engineering Volume 11 Issue 1

Abstract

This article evaluates the energy-harvesting capabilities of a multiuser non-orthogonal multiple access-based system, where energy harvesting relays utilise the power splitting relaying protocol to harvest energy and amplify-and-forward protocol to forward the signals to the connected users. The expressions for each user’s energy harvesting outage probability are calculated and compared to the same system model without energy harvesting. Simulation results show the effectiveness of the energy-harvesting relay nodes and the improved outage probability of each user.

Keywords: NOMA; energy harvesting; power splitting protocol; amplify-and-forward; outage probability

1 Introduction

Energy harvesting in wireless communication networks has garnered much attention recently; it is a proposed solution to self-sustaining and lifetime extension of wireless networks. It is argued that battery replacement and charging can be done; however, it can be costly and inconvenient, especially if the location of the batteries is not ideal. There are environmental energy-harvesting techniques such as wind, solar, and vibration; however, radio frequency (RF) wireless energy transfer is a more controlled, convenient, and safer way to harvest energy from the environment. RF signals contain information and energy; thus, an energy-harvesting node can simultaneously harvest and process information. A relay in a cooperative wireless network needs to have sufficient energy to stay active; therefore, a relay node with energy-harvesting capabilities is an excellent advantage in a wireless network [1,2].

Research in cooperative networks shows the benefits of energy-harvesting nodes, such as an increase in the life span of the nodes and the self-sustainability of a communication network, especially for 5G applications. The energy-harvesting employs different receiver architectures, power splitting, and time switching, thus enabling two protocols: power splitting relaying (PSR) and time switching relaying (TSR). The authors of refs [3,4,5,6] utilise the most widely used PSR protocol, whereas ref. [7] utilises the TSR protocol. However, refs [8] and [2] utilise both protocols and evaluate the performance of each. Moreover, ref. [8] reports the superiority of the PSR protocol, whereas ref. [2] reports that the latter is superior. Many researchers only implement one energy-harvesting scheme into their system model; however, refs [3] and [9] implement three different relay schemes. To explore the comparison of the proposed schemes, [3] implements adaptable PSR schemes, whereas [9] increases the security of the communication system. The previous studies [9,10] focus on the physical layer security of the communication system, where the base station transmits a jamming signal to mitigate interference from the eavesdropper node.

2 System model

The system model is similar to that shown in ref. [11]; however, the two relays employ energy-harvesting capabilities. This article follows the layout and the method presented in ref. [11]: the system model in which user connections, time subslots, power allocation, decoding order, and outage probability conditions are the same, thus avoiding repetition.

2.1 Time sub-slot t s 1

The active users in the network are UE 1 , UE 2 , UE 3 , and UE 4 . The status of these users in t s 1 is according to their locations, as shown in Figure 1: UE 1 and UE 2 are cell centre users connected directly to the base station and UE 3 and UE 4 are cell edge users connected to relay r 2 and r 1 , respectively. The base station transmits the superimposed signal to the connected UEs given by Eq. (1) from [11]:

(1) x s ( t s 1 ) = P 1 t s 1 P s x 1 ( t s 1 ) + P 2 t s 1 P s x 2 ( t s 1 ) + P 3 t s 1 P s x 3 ( t s 1 ) + P 4 t s 1 P s x 4 ( t s 1 ) .

Figure 1 System model 1.
Figure 1

System model 1.

The received signals at UE 1 , UE 2 , r 1 , and r 2 are given by Eq. (2) from [11]:

(2) y 1 ( t s 1 ) = h 1 BS x s ( t s 1 ) + N 1 ,

(3) y 2 ( t s 1 ) = h 2 BS x s ( t s 1 ) + N 2 ,

(4) y r 1 ( t s 1 ) = h r 1 BS x s ( t s 1 ) + N r 1 ,

(5) y r 2 ( t s 1 ) = h r 2 BS x s ( t s 1 ) + N r 2 .

The decoding order follows that of ref. [11], for time sub-slot t s 1 . The decoded SINRs at UE 1 are given by Eq. (3) from refs. [11,12], with the decoded SINR of UE 1 given by Eq. (4) from ref. [11]:

(6) SINR t s 1 4 − 1 = P 4 t s 1 P s ∣ h 1 BS ∣ 2 ∑ j = 1 3 P j t s 1 P s ∣ h 1 BS ∣ 2 + σ 1 2 ,

(7) SINR t s 1 3 − 1 = P 3 t s 1 P s ∣ h 1 BS ∣ 2 ∑ j = 1 2 P j t s 1 P s ∣ h 1 BS ∣ 2 + σ 1 2 ,

(8) SINR t s 1 2 − 1 = P 2 t s 1 P s ∣ h 1 BS ∣ 2 P 1 t s 1 P s ∣ h 1 BS ∣ 2 + σ 1 2 ,

(9) SINR t s 1 1 − 1 = P 1 t s 1 P s ∣ h 1 BS ∣ 2 σ 1 2 .

The decoded SINRs at UE 2 are given by Eq. (7) from [11], with the decoded SINR of UE 2 given by Eq. (8) from [11]

(10) SINR t s 1 4 − 2 = P 4 t s 1 P s ∣ h 2 BS ∣ 2 ∑ j = 1 3 P j t s 1 P s ∣ h 2 BS ∣ 2 + σ 2 2 ,

(11) SINR t s 1 3 − 2 = P 3 t s 1 P s ∣ h 2 BS ∣ 2 ∑ j = 1 2 P j t s 1 P s ∣ h 2 BS ∣ 2 + σ 2 2 ,

(12) SINR t s 1 2 − 2 = P 2 t s 1 P s ∣ h 2 BS ∣ 2 P 1 t s 1 P s ∣ h 2 BS ∣ 2 + σ 2 2 .

The energy-harvesting does not affect UE 1 and UE 2 as it is not connected to a relay. The PSR splits the received superimposed signal by a portion ρ y r i ( t s 1 ) utilised by the energy-harvesting receiver, given by Eq. (13), for i = 1 , 2 .

(13) ρ y r i ( t s 1 ) = ρ P 1 t s 1 P s x 1 ( t s 1 ) h r i BS + ρ P 2 t s 1 P s x 2 ( t s 1 ) h r i BS + ρ P 3 t s 1 P s x 3 ( t s 1 ) h r i BS + ρ P 4 t s 1 P s x 4 ( t s 1 ) h r i BS + ρ N r i .

With the remaining power of the received signal ( 1 − ρ ) y r i ( t s 1 ) utilised by the information receiver, given by

(14) ( 1 − ρ ) y r i ( t s 1 ) = ( 1 − ρ ) P 1 t s 1 P s x 1 ( t s 1 ) h r i BS + ( 1 − ρ ) P 2 t s 1 P s x 2 ( t s 1 ) h r i BS + ( 1 − ρ ) P 3 t s 1 P s x 3 ( t s 1 ) h r i BS + ( 1 − ρ ) P 4 t s 1 P s x 4 ( t s 1 ) h r i BS + ( 1 − ρ ) N r i .

The decoded SINR at relays r 1 and r 2 are given by

(15) SINR t s 1 4 − r 1 = ( 1 − ρ ) P 4 t s 1 P s ∣ h r 1 BS ∣ 2 ∑ j = 1 3 ( 1 − ρ ) P j t s 1 P s ∣ h r 1 BS ∣ 2 + ( 1 − ρ ) σ r 1 2 ,

(16) SINR t s 1 4 − r 2 = ( 1 − ρ ) P 4 t s 1 P s ∣ h r 2 BS ∣ 2 ∑ j = 1 3 ( 1 − ρ ) P j t s 1 P s ∣ h r 2 BS ∣ 2 + ( 1 − ρ ) σ r 2 2 ,

(17) SINR t s 1 3 − r 2 = ( 1 − ρ ) P 3 t s 1 P s ∣ h r 2 BS ∣ 2 ∑ j = 1 2 ( 1 − ρ ) P j t s 1 P s ∣ h r 2 BS ∣ 2 + ( 1 − ρ ) σ r 2 2 .

In the first block-time, the energy-harvesting receiver at r 1 and r 2 harvests the energy from the received signal given by Eq. (18), for i = 1 , 2 . The energy conversion efficiency is η with values between 0 < η < 1 .

(18) EH r i = η ρ P s ∣ h r i BS ∣ 2 ( P 1 t s 1 + P 2 t s 1 + P 3 t s 1 + P 4 t s 1 ) T / 2 = η ρ P s ∣ h r i BS ∣ 2 T / 2 .

The harvested energy is used to power the relays; thus, the relay power is given by

(19) P r i = EH r i T / 2 = η ρ P s ∣ h r i BS ∣ 2 .

2.2 Time sub-slot t s 2

In the second block-time, the amplify-and-forward (AF) protocol utilises an amplifying factor G r i given by

(20) G r i = 1 ( 1 − ρ ) P s ∣ h r i BS ∣ 2 ( P 1 t s 1 + P 2 t s 1 + P 3 t s 1 + P 4 t s 1 ) + σ R i 2 = 1 ( 1 − ρ ) P s ∣ h r i BS ∣ 2 + σ R i 2 .

The relays regenerate the signals for the users connected to it with the amplification given by Eqs. (21) and (22).

(21) x s r 1 ( t s 2 ) = ( 1 − ρ ) P 4 t s 2 G r 1 P s P r 1 x 4 ( t s 1 ) h r 1 BS ,

(22) x s r 2 ( t s 2 ) = ( 1 − ρ ) P 3 t s 2 G r 2 P s P r 2 x 3 ( t s 1 ) h r 2 BS .

The received signals of UE 3 and UE 4 are given by Eqs. (23) and (24).

(23) y 3 ( t s 2 ) = h 3 r 2 x s r 2 ( t s 2 ) + N 3 ,

(24) y 4 ( t s 2 ) = h 4 r 1 x s r 1 ( t s 2 ) + N 4 .

Combining Eqs. (19)–(24), the decoded SINRs at UE 3 and UE 4 are given by

(25) SINR t s 2 3 − 3 = ( 1 − ρ ) η ρ P 3 t s 2 P s 2 ( ∣ h r 2 BS ∣ 2 ) 2 ∣ h 3 r 2 ∣ 2 ( 1 − ρ ) P s ∣ h r 2 BS ∣ 2 σ 3 2 + σ R 2 2 σ 3 2 ,

(26) SINR t s 2 4 − 4 = ( 1 − ρ ) η ρ P 4 t s 2 P s 2 ( ∣ h r 1 BS ∣ 2 ) 2 ∣ h 4 r 1 ∣ 2 ( 1 − ρ ) P s ∣ h r 1 BS ∣ 2 σ 4 2 + σ R 1 2 σ 4 2 .

2.3 Time sub-slot t s 3

In this time sub-slot, the UEs status changes according to their new locations as shown in Figure 2, with the following connections: UE 1 is a cell centre user connected directly to the base station and UE 2 , UE 3 , and UE 4 are cell edge users with UE 3 connected to r 1 , and UE 2 and UE 4 connected to r 2 . The base station transmits the superimposed signal to the connected UEs given by

(27) x s ( t s 3 ) = P 1 t s 3 P s x 1 ( t s 3 ) + P 2 t s 3 P s x 2 ( t s 3 ) + P 3 t s 3 P s x 3 ( t s 3 ) + P 4 t s 3 P s x 4 ( t s 3 ) .

Figure 2 System model 2.
Figure 2

System model 2.

The received signals at UE 1 , r 1 , and r 2 are given by Eqs. (28)–(30).

(28) y 1 ( t s 3 ) = h 1 BS x s ( t s 3 ) + N 1 ,

(29) y r 1 ( t s 3 ) = h r 1 BS x s ( t s 3 ) + N r 1 ,

(30) y r 2 ( t s 3 ) = h r 2 BS x s ( t s 3 ) + N r 2 .

The decoded SINRs at UE 1 are given by Eqs. (31)–(34)

(31) SINR t s 3 3 − 1 = P 3 t s 3 P s ∣ h 1 BS ∣ 2 ∑ j = 1 2 P j t s 3 P s ∣ h 1 BS ∣ 2 + P 4 t s 3 P s ∣ h 1 BS ∣ 2 + σ 1 2 ,

(32) SINR t s 3 4 − 1 = P 4 t s 3 P s ∣ h 1 BS ∣ 2 ∑ j = 1 2 P j t s 3 P s ∣ h 1 B S ∣ 2 + σ 1 2 ,

(33) SINR t s 3 2 − 1 = P 2 t s 3 P s ∣ h 1 BS ∣ 2 P 1 t s 3 P s ∣ h 1 BS ∣ 2 + σ 1 2 ,

(34) SINR t s 3 1 − 1 = P 1 t s 3 P s ∣ h 1 BS ∣ 2 σ 1 2 .

As previously stated in Section 2.1, the PSR protocol splits the received signal by ρ : ( 1 − ρ ) , resulting in Eqs. (35) and (36), for i = 1 , 2 .

(35) ρ y r i ( t s 3 ) = ρ P 1 t s 3 P s x 1 ( t s 3 ) h r i BS + ρ P 2 t s 3 P s x 2 ( t s 3 ) h r i BS + ρ P 3 t s 3 P s x 3 ( t s 3 ) h r i BS + ρ P 4 t s 3 P s x 4 ( t s 3 ) h r i BS + ρ N r i ,

(36) ( 1 − ρ ) y r i ( t s 3 ) = ( 1 − ρ ) P 1 t s 3 P s x 1 ( t s 3 ) h r i BS + ( 1 − ρ ) P 2 t s 3 P s x 2 ( t s 3 ) h r i BS + ( 1 − ρ ) P 3 t s 3 P s x 3 ( t s 3 ) h r i BS + ( 1 − ρ ) P 4 t s 3 P s x 4 ( t s 3 ) h r i BS + ( 1 − ρ ) N r i .

Eqs. (37)–(40) give the decoded SINR at the relays in time sub-slot t s 3 .

(37) SINR t s 3 3 − r 1 = ( 1 − ρ ) P 3 t s 3 P s ∣ h r 1 BS ∣ 2 ∑ j = 1 2 ( 1 − ρ ) P j t s 3 P s ∣ h r 1 BS ∣ 2 + ( 1 − ρ ) P 4 t s 3 P s ∣ h r 1 BS ∣ 2 + ( 1 − ρ ) σ r 1 2 ,

(38) SINR t s 3 3 − r 2 = ( 1 − ρ ) P 3 t s 3 P s ∣ h r 2 BS ∣ 2 ∑ j = 1 2 ( 1 − ρ ) P j t s 3 P s ∣ h r 2 BS ∣ 2 + ( 1 − ρ ) P 4 t s 3 P s ∣ h r 2 BS ∣ 2 + ( 1 − ρ ) σ r 2 2 ,

(39) SINR t s 3 4 − r 2 = ( 1 − ρ ) P 4 t s 3 P s ∣ h r 2 BS ∣ 2 ∑ j = 1 2 ( 1 − ρ ) P j t s 3 P s ∣ h r 2 BS ∣ 2 + ( 1 − ρ ) σ r 2 2 ,

(40) SINR t s 3 2 − r 2 = ( 1 − ρ ) P 2 t s 3 P s ∣ h r 2 B S ∣ 2 ( 1 − ρ ) P 1 t s 3 P s ∣ h r 2 BS ∣ 2 + ( 1 − ρ ) σ r 2 2 .

The energy-harvesting equations in Section 2.1 are not time dependent; thus, they are utilised in this time sub-slot as well.

2.4 Time sub-slot t s 4

The relays regenerate the signals for the users connected to it, given by the following equations:

(41) x s r 1 ( t s 4 ) = ( 1 − ρ ) P 3 t s 4 G r 1 P s P r 1 x 3 ( t s 3 ) h r 1 BS ,

(42) x s r 2 ( t s 4 ) = ( 1 − ρ ) P 2 t s 4 G r 2 P s P r 2 x 2 ( t s 3 ) h r 2 BS + ( 1 − ρ ) P 4 t s 4 G r 2 P s P r 2 x 4 ( t s 3 ) h r 2 BS .

The received signals of UE 2 , UE 3 , and UE 4 are given by Eqs. (43)–(45).

(43) y 2 ( t s 4 ) = h 2 r 2 x s r 2 ( t s 4 ) + N 2 ,

(44) y 3 ( t s 4 ) = h 3 r 1 x s r 1 ( t s 4 ) + N 3 ,

(45) y 4 ( t s 4 ) = h 4 r 2 x s r 2 ( t s 4 ) + N 4 .

The decoded SINRs at UE 2 , UE 3 , and UE 4 are given by Eqs. (46)–(49).

(46) SINR t s 4 4 − 2 = ( 1 − ρ ) η ρ P 4 t s 4 P s 2 ( ∣ h r 2 BS ∣ 2 ) 2 ∣ h 2 r 2 ∣ 2 ( 1 − ρ ) η ρ P 2 t s 4 P s 2 ( ∣ h r 2 BS ∣ 2 ) 2 ∣ h 2 r 2 ∣ 2 + ( 1 − ρ ) P s ∣ h r 2 BS ∣ 2 σ 2 2 + σ R 2 2 σ 2 2 ,

(47) SINR t s 4 2 − 2 = ( 1 − ρ ) η ρ P 2 t s 4 P s 2 ( ∣ h r 2 BS ∣ 2 ) 2 ∣ h 2 r 2 ∣ 2 ( 1 − ρ ) P s ∣ h r 2 BS ∣ 2 σ 2 2 + σ R 2 2 σ 2 2 ,

(48) SINR t s 4 3 − 3 = ( 1 − ρ ) η ρ P 3 t s 4 P s 2 ( ∣ h r 1 BS ∣ 2 ) 2 ∣ h 3 r 1 ∣ 2 ( 1 − ρ ) P s ∣ h r 1 BS ∣ 2 σ 3 2 + σ R 1 2 σ 3 2 ,

(49) SINR t s 4 4 − 4 = ( 1 − ρ ) P 4 t s 4 η ρ P s 2 ( ∣ h r 2 BS ∣ 2 ) 2 ∣ h 4 r 2 ∣ 2 ( 1 − ρ ) η ρ P 2 t s 4 P s 2 ( ∣ h r 2 BS ∣ 2 ) 2 ∣ h 4 r 2 ∣ 2 + ( 1 − ρ ) P s ∣ h r 2 BS ∣ 2 σ 4 2 + σ R 2 2 σ 4 2 .

3 Energy-harvesting outage probability

The outage probability for energy harvesting is similar to that presented in ref. [11]. For generality, the conditions for communication interruption or an outage event may occur if one of the following conditions hold:

  1. If a user cannot detect the signals of higher-powered users.

  2. If a relay cannot detect the signals of higher-powered users.

  3. If a relay cannot detect the signals of the users connected to it.

  4. If the user throughput is not able to achieve the target rate

See reference [11] for more details.

3.1 Outage probability for UE 1

Outage probability for UE 1 in t s 1 :

(50) P 1 , t s 1 = P r [ OE 1 , t s 1 ] = P r [ OE r 4 − 1 t s 1 ∪ OE r 3 − 1 t s 1 ∪ OE r 2 − 1 t s 1 ∪ OE r 1 − 1 t s 1 ] = 1 − [ 1 − F R r 4 − 1 t s 1 ( R ) ] [ 1 − F R r 3 − 1 t s 1 ( R ) ] [ 1 − F R r 2 − 1 t s 1 ( R ) ] [ 1 − F R r 1 − 1 t s 1 ( R ) ] ,

(51) P 1 , t s 1 = 1 − e − β t s 1 σ 2 λ 1 BS P s 1 P 1 t s 1 + 1 P 2 t s 1 − P 1 t s 1 β t s 1 + 1 P 3 t s 1 − ∑ j = 1 2 P j t s 1 β t s 1 + 1 P 4 t s 1 − ∑ j = 1 3 P j t s 1 β t s 1 , 0 < β t s 1 < P 4 t s 1 ∑ j = 1 3 P j t s 1 ∪ P 3 t s 1 ∑ j = 1 2 P j t s 1 ∪ P 2 t s 1 P 1 t s 1 1 , else .

Outage probability for UE 1 in t s 3 :

(52) P 1 , t s 3 = P r [ OE 1 , t s 3 ] = P r [ OE r 3 − 1 t s 3 ∪ OE r 4 − 1 t s 3 ∪ OE r 2 − 1 t s 3 ∪ OE r 1 − 1 t s 3 ] = 1 − [ 1 − F R r 3 − 1 t s 3 ( R ) ] [ 1 − F R r 4 − 1 t s 3 ( R ) ] [ 1 − F R r 2 − 1 t s 3 ( R ) ] [ 1 − F R r 1 − 1 t s 3 ( R ) ] ,

(53) P 1 , t s 3 = 1 − e − β t s 3 σ 2 λ 1 B S P s 1 P 1 t s 3 + 1 P 2 t s 3 − P 1 t s 3 β t s 3 + 1 P 3 t s 3 − ∑ j = 1 2 P j t s 3 + P 4 t s 3 β t s 3 + 1 P 4 t s 3 − ∑ j = 1 2 P j t s 3 β t s 3 , 0 < β t s 3 < P 4 t s 3 ∑ j = 1 2 P j t s 3 ∪ P 3 t s 3 ∑ j = 1 2 P j t s 3 + P 4 t s 3 ∪ P 2 t s 3 P 1 t s 3 1 , else .

3.2 Outage probability for UE 2

Outage probability for UE 2 in t s 1 :

(54) P 2 , t s 1 = P r [ OE 2 , t s 1 ] = P r [ OE r 4 − 2 t s 1 ∪ OE r 3 − 2 t s 1 ∪ OE r 2 − 2 t s 1 ] = 1 − [ 1 − F R r 4 − 2 t s 1 ( R ) ] [ 1 − F R r 3 − 2 t s 1 ( R ) ] [ 1 − F R r 2 − 2 t s 1 ( R ) ] ,

(55) P 2 , t s 1 = 1 − e − β t s 1 σ 2 λ 2 BS P s 1 P 2 t s 1 − P 1 t s 1 β t s 1 + 1 P 3 t s 1 − ∑ j = 1 2 P j t s 1 β t s 1 + 1 P 4 t s 1 − ∑ j = 1 3 P j t s 1 β t s 1 , 0 < β t s 1 < P 4 t s 1 ∑ j = 1 3 P j t s 1 ∪ P 3 t s 1 ∑ j = 1 2 P j t s 1 ∪ P 2 t s 1 P 1 t s 1 1 , else .

Outage probability for UE 2 in t s 3 and t s 4 :

(56) P 2 , t s 4 = P r [ OE 2 , t s 4 ] = P r [ OE r 3 − r 2 t s 3 ∪ OE r 4 − r 2 t s 3 ∪ OE r 2 − r 2 t s 3 ∪ OE r 4 − 2 t s 4 ∪ OE r 2 − 2 t s 4 ] = 1 − [ 1 − F R r 3 − r 2 t s 3 ( R ) ] [ 1 − F R r 4 − r 2 t s 3 ( R ) ] [ 1 − F R r 2 − r 2 t s 3 ( R ) ] [ 1 − F R r 4 − 2 t s 4 ( R ) ] [ 1 − F R r 2 − 2 t s 4 ( R ) ] ,

(57) P 2 , t s 4 = 1 − e − λ r 2 BS P s σ 2 β t s 4 η ρ ∣ h 2 r 2 ∣ 2 1 P 2 t s 4 + 1 [ P 4 t s 4 − P 2 t s 4 β t s 4 ] + β t s 3 1 [ P 2 t s 3 − P 1 t s 3 β t s 3 ] + 1 P 4 t s 3 − ∑ j = 1 2 P j t s 3 β t s 3 + 1 P 3 t s 3 − ∑ j = 1 2 P j t s 3 + P 4 t s 3 β t s 3 , 0 < β t s 4 < P 4 t s 4 P 2 t s 4 ∪ β t s 3 < P 2 t s 3 P 1 t s 3 ∪ P 4 t s 3 ∑ j = 1 2 P j t s 3 ∪ P 3 t s 3 ∑ j = 1 2 P j t s 3 + P 4 t s 3 1 , else .

3.3 Outage probability for UE 3

Outage probability for UE 3 in t s 1 and t s 2 :

(58) P 3 , t s 2 = P r [ OE 3 , t s 2 ] = P r [ OE r 4 − r 2 t s 1 ∪ OE r 3 − r 2 t s 1 ∪ OE r 3 − 3 t s 2 ] = 1 − [ 1 − F R r 4 − r 2 t s 1 ( R ) ] [ 1 − F R r 3 − r 2 t s 1 ( R ) ] [ 1 − F R r 3 − 3 t s 2 ( R ) ] ,

(59) P 3 , t s 2 = 1 − e − σ 2 β t s 2 λ 3 r 2 P s η ρ P 3 t s 2 ∣ h r 2 BS ∣ 2 + β t s 1 λ r 2 B S P s 1 P 3 t s 1 − ∑ j = 1 2 P j t s 1 β t s 1 + 1 P 4 t s 1 − ∑ j = 1 3 P j t s 1 β t s 1 , 0 < β t s 2 ∪ β t s 1 < P 3 t s 1 ∑ j = 1 2 P j t s 1 ∪ P 4 t s 1 ∑ j = 1 3 P j t s 1 1 , else .

Outage probability for UE 3 in t s 3 and t s 4 :

(60) P 3 , t s 4 = P r [ OE 3 , t s 4 ] = P r [ OE r 3 − r 1 t s 3 ∪ OE r 3 − 3 t s 4 ] = 1 − [ 1 − F R r 3 − r 1 t s 3 ( R ) ] [ 1 − F R r 3 − r 1 t s 3 ( R ) ] ,

(61) P 3 , t s 4 = 1 − e − σ 2 β t s 4 λ 3 r 1 P s [ η ρ P 3 t s 4 ∣ h r 1 BS ∣ 2 ] + β t s 3 λ r 1 BS P s 1 P 3 t s 3 − ∑ j = 1 2 P j t s 3 + P 4 t s 3 β t s 3 , 0 < β t s 4 ∪ β t s 3 < P 3 t s 3 ∑ j = 1 2 P j t s 3 + P 4 t s 3 1 , else .

3.4 Outage probability for UE 4

Outage probability for UE 4 in t s 1 and t s 2 :

(62) P 4 , t s 2 = P r [ OE 4 , t s 2 ] = P r [ OE r 4 − r 1 t s 1 ∪ OE r 4 − 4 t s 2 ] = 1 − [ 1 − F R r 4 − r 1 t s 1 ( R ) ] [ 1 − F R r 4 − 4 t s 2 ( R ) ] ,

(63) P 4 , t s 2 = 1 − e − σ 2 β t s 2 λ 4 r 1 P s η ρ P 4 t s 2 ∣ h r 1 B S ∣ 2 + β t s 1 λ r 1 B S P s 1 P 4 t s 1 − ∑ j = 1 3 P j t s 1 β t s 1 , 0 < β t s 2 ∪ β t s 1 < P 4 t s 1 ∑ j = 1 3 P j t s 1 1 , else .

Outage probability for UE 4 in t s 3 and t s 4 :

(64) P 4 , t s 4 = P r [ OE 4 , t s 4 ] = P r [ OE r 3 − r 2 t s 3 ∪ OE r 4 − r 2 t s 3 ∪ OE r 4 − 4 t s 4 ] = 1 − [ 1 − F R r 3 − r 2 t s 3 ( R ) ] [ 1 − F R r 4 − r 2 t s 3 ( R ) ] [ 1 − F R r 4 − 4 t s 4 ( R ) ] ,

(65) P 4 , t s 4 = 1 − e − σ 2 β t s 4 λ 4 r 2 P s η ρ ∣ h r 2 BS ∣ 2 1 [ P 4 t s 4 − P 2 t s 4 β t s 4 ] + β t s 3 λ r 2 BS P s 1 P 4 t s 3 − ∑ j = 1 2 P j t s 3 β t s 3 + 1 P 3 t s 3 − ∑ j = 1 2 P j t s 3 + P 4 t s 3 β t s 3 , 0 < β t s 4 < P 4 t s 4 P 2 t s 4 ∪ β t s 3 < P 4 t s 3 ∑ j = 1 2 P j t s 3 ∪ P 3 t s 3 ∑ j = 1 2 P j t s 3 + P 4 t s 3 1 , else .

4 Simulation results

The simulation model is shown in Figures 1 and 2, with the energy-harvesting relay nodes. The system model has one BS, two relays ( r 1 and r 2 ) , and four users ( UE 1 , UE 2 , UE 3 , and UE 4 ) . The relay works in half-duplex mode. For t s 1 and t s 2 time sub-slots, UE 1 and UE 2 are cell centre users, while UE 3 and UE 4 are cell edge users using relays r 2 and r 1 . For t s 3 and t s 4 time sub-slots, UE 1 is a cell centre user, while UE 2 , UE 3 , and UE 4 are cell edge users. The UE 2 and UE 2 are connected to relay r 2 and UE 3 is connected to relay r 1 . The relays harvest energy from the received signal and employ the AF protocol to forward the intended signals to the connected users. The system parameters for the energy-harvesting non-orthogonal multiple access (NOMA)-based system are given in Table 1. Simulation results compare the four-user NOMA-based network proposed by ref. [11] with and with energy-harvesting relay capabilities.

Table 1

System parameters

P s = 25 − 50 dB Base station power
λ 1 BS = 1 − 4 , λ 2 BS = 0.8 − 4 , λ r 1 BS = 0.4 − 4 , λ r 2 BS = 0.5 − 4 , λ 3 r 2 = 0.3 − 4 , λ 4 r 1 = 0.3 − 4 Figure 1 channel variances
λ 1 BS = 1 − 4 , λ r 1 BS = 0.4 − 4 , λ r 2 BS = 0.5 − 4 , λ 2 r 2 = 0.3 − 4 , λ 3 r 1 = 0.3 − 4 , λ 4 r 2 = 0.4 − 4 Figure 2 channel variances
R = 0.3 bps/Hz Target rate
ρ = 0.5 Power splitting coefficient
η = 1 Energy conversion efficiency
P s = 10 − 20 dB Transmit power

The simulation results show the outage probability of UEs in the various time sub-slots. Figure 3 shows the outage probability of UE 1 in t s 1 and t s 3 , with and without energy-harvesting relays. The energy harvesting does not affect UE 1 as it is always a cell-centre user and connects directly to the base station. The figure also shows a slight change in the outage probability of UE 1 from t s 1 to t s 3 .

Figure 3 Outage probability of user 1.
Figure 3

Outage probability of user 1.

Figure 4 shows the outage probability of UE 2 in t s 1 and t s 3 − 4 . During time sub-slot 1, UE 2 is a cell centre user, and therefore the energy harvesting does not affect this user. However, for time sub-slot t s 3 − 4 , the outage probability of UE 2 improves; because UE 2 is a cell-edge user and connected to an energy harvesting relay.

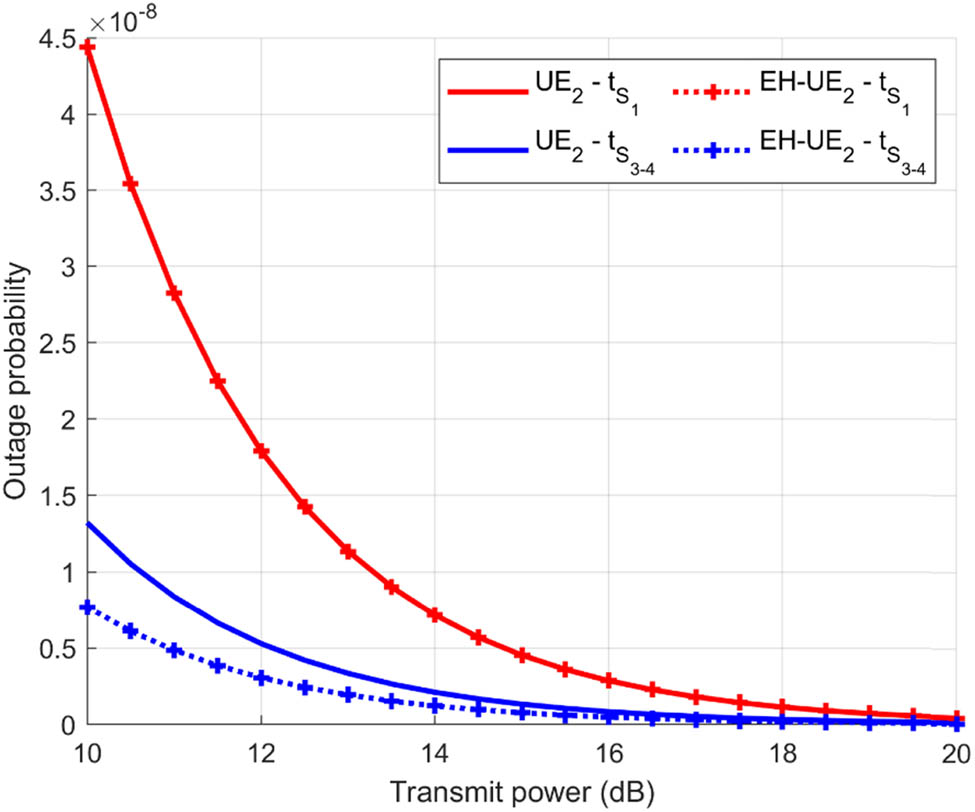
Figure 4 Outage probability of user 2.
Figure 4

Outage probability of user 2.

Figures 5 and 6 show the outage probability of UE 3 and UE 4 , respectively. These UEs are cell edge users in both time slots; therefore, they benefit from the energy-harvesting relays where their outage probabilities improve. The change in positions shows a noticeable difference between the outage probability of UE 3 and UE 4 . For the first time slot ( t s 1 − 2 ) , UE 3 is connected to relay 2 with the second highest allocated power, whereas UE 4 is connected to relay 1 with the highest allocated power. However, in time slot ( t s 3 − 4 ) , UE 3 is connected to relay 1 with the highest allocated power and UE 4 shares a relay with UE 2 .

Figure 5 Outage probability of user 3.
Figure 5

Outage probability of user 3.

Figure 6 Outage probability of user 4.
Figure 6

Outage probability of user 4.

5 Conclusion

This article evaluated the effectiveness of the energy-harvesting relay nodes on the user’s outage probability. The four-user NOMA-based network utilises energy-harvesting relays to communicate with the base station. This research is an adaptation and extension of the research presented by ref. [11], utilising the same methods and procedures to derive the outage probability expressions. The results simply show the impact of the energy harvesting on the outage probability of the users as well as their positions in the network. The cell edge users connected to the relays benefit from the harvested energy by receiving more power than the network without harvesting, which can be seen in the results. Future works may include the physical layer security of the energy-harvesting network by implementing a jamming signal to mitigate eavesdropping.

  1. Funding information: The authors state no funding involved.

  2. Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.

  3. Conflict of interest: The authors state no conflict of interest.

References

[1] Shi L, Zhao L, Liang K. Power allocation for wireless powered MIMO transmissions with non-linear RF energy conversion models. China Commun. 2017;4(2):57–64.10.1109/CC.2017.7868175Search in Google Scholar

[2] Nasir AA, Zhou X, Durrani S, Kennedy RA. Relaying protocols for wireless energy harvesting and information processing. IEEE Trans Wirel Commun. 2013;12(17):3622–36.10.1109/TWC.2013.062413.122042Search in Google Scholar

[3] Mondal S, Dharroy S, Kundu S. Adaptive energy harvesting with relay selection schemes in an ordered NOMA network; In 2020 National Conference on Communications; 2020 Feb 21–24; Kharagpur, India. IEEE, 2020. p. 1–6.10.1109/NCC48643.2020.9056072Search in Google Scholar

[4] Guo C, Xin J, Zhao L, Chu X. Performance analysis of cooperative NOMA with energy harvesting in multi-cell networks. China Commun. 2019;16(11):120–9.10.23919/JCC.2019.11.010Search in Google Scholar

[5] Alsharoa A, Ghazzai H, Kamal AE, Kadri A. Near optimal power splitting protocol for energy harvesting based two way multiple relay systems; 2017 IEEE Wireless Communications and Networking Conference (WCNC); 2017 Mar 19–22; San Francisco (CA), USA. IEEE, 2017. p. 1–6.10.1109/WCNC.2017.7925700Search in Google Scholar

[6] Wang T, Lu G, Ye Y, Ren Y. Dynamic power splitting strategy for SWIPT based two-way multiplicative AF relay networks with nonlinear energy harvesting model. Wirel Commun Mob Comput. 2018;2018:1–9.10.1155/2018/1802063Search in Google Scholar

[7] Li F, Jiang H, Fan R, Tan P. Cognitive Non-Orthogonal Multiple Access With Energy Harvesting: An Optimal Resource Allocation Approach. IEEE Trans Veh Technol. 2019;68(7):7080–95.10.1109/TVT.2019.2919261Search in Google Scholar

[8] Du G, Xiong K, Qiu Z. Outage analysis of cooperative transmission with energy harvesting relay: Time switching versus power splitting. Math Probl Eng. 2015;2015:598290.10.1155/2015/598290Search in Google Scholar

[9] Salem A, Musavian L, Jorswieck E, Aissa S. Secrecy outage probability of energy-harvesting cooperative NOMA transmissions with relay selection. IEEE Trans Green Commun Netw. 2020;4(4):1130–48.10.1109/TGCN.2020.2999815Search in Google Scholar

[10] Le TA, Kong HY. Evaluating the performance of cooperative NOMA with energy harvesting under physical layer security. Wirel Pers Commun. 2019 Sep 4;108(2):1037–54.10.1007/s11277-019-06452-5Search in Google Scholar

[11] Balyan V, Daniels R. Resource allocation for NOMA based networks using relays: cell centre and cell edge users. Int J Smart Sens Intell Syst. 2020;13(1):1–18.10.21307/ijssis-2020-031Search in Google Scholar

[12] Balyan V. Cooperative relay to relay communication using NOMA for energy efficient wireless communication. Springer Telecommun Syst. 2021;76(2):14.10.1007/s11235-021-00756-3Search in Google Scholar
Received: 2022-04-15
Revised: 2022-07-29
Accepted: 2022-08-15
Published Online: 2022-12-21

© 2022 the author(s), published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Research Articles
  2. Fractal approach to the fluidity of a cement mortar
  3. Novel results on conformable Bessel functions
  4. The role of relaxation and retardation phenomenon of Oldroyd-B fluid flow through Stehfest’s and Tzou’s algorithms
  5. Damage identification of wind turbine blades based on dynamic characteristics
  6. Improving nonlinear behavior and tensile and compressive strengths of sustainable lightweight concrete using waste glass powder, nanosilica, and recycled polypropylene fiber
  7. Two-point nonlocal nonlinear fractional boundary value problem with Caputo derivative: Analysis and numerical solution
  8. Construction of optical solitons of Radhakrishnan–Kundu–Lakshmanan equation in birefringent fibers
  9. Dynamics and simulations of discretized Caputo-conformable fractional-order Lotka–Volterra models
  10. Research on facial expression recognition based on an improved fusion algorithm
  11. N-dimensional quintic B-spline functions for solving n-dimensional partial differential equations
  12. Solution of two-dimensional fractional diffusion equation by a novel hybrid D(TQ) method
  13. Investigation of three-dimensional hybrid nanofluid flow affected by nonuniform MHD over exponential stretching/shrinking plate
  14. Solution for a rotational pendulum system by the Rach–Adomian–Meyers decomposition method
  15. Study on the technical parameters model of the functional components of cone crushers
  16. Using Krasnoselskii's theorem to investigate the Cauchy and neutral fractional q-integro-differential equation via numerical technique
  17. Smear character recognition method of side-end power meter based on PCA image enhancement
  18. Significance of adding titanium dioxide nanoparticles to an existing distilled water conveying aluminum oxide and zinc oxide nanoparticles: Scrutinization of chemical reactive ternary-hybrid nanofluid due to bioconvection on a convectively heated surface
  19. An analytical approach for Shehu transform on fractional coupled 1D, 2D and 3D Burgers’ equations
  20. Exploration of the dynamics of hyperbolic tangent fluid through a tapered asymmetric porous channel
  21. Bond behavior of recycled coarse aggregate concrete with rebar after freeze–thaw cycles: Finite element nonlinear analysis
  22. Edge detection using nonlinear structure tensor
  23. Synchronizing a synchronverter to an unbalanced power grid using sequence component decomposition
  24. Distinguishability criteria of conformable hybrid linear systems
  25. A new computational investigation to the new exact solutions of (3 + 1)-dimensional WKdV equations via two novel procedures arising in shallow water magnetohydrodynamics
  26. A passive verses active exposure of mathematical smoking model: A role for optimal and dynamical control
  27. A new analytical method to simulate the mutual impact of space-time memory indices embedded in (1 + 2)-physical models
  28. Exploration of peristaltic pumping of Casson fluid flow through a porous peripheral layer in a channel
  29. Investigation of optimized ELM using Invasive Weed-optimization and Cuckoo-Search optimization
  30. Analytical analysis for non-homogeneous two-layer functionally graded material
  31. Investigation of critical load of structures using modified energy method in nonlinear-geometry solid mechanics problems
  32. Thermal and multi-boiling analysis of a rectangular porous fin: A spectral approach
  33. The path planning of collision avoidance for an unmanned ship navigating in waterways based on an artificial neural network
  34. Shear bond and compressive strength of clay stabilised with lime/cement jet grouting and deep mixing: A case of Norvik, Nynäshamn
  35. Communication
  36. Results for the heat transfer of a fin with exponential-law temperature-dependent thermal conductivity and power-law temperature-dependent heat transfer coefficients
  37. Special Issue: Recent trends and emergence of technology in nonlinear engineering and its applications - Part I
  38. Research on fault detection and identification methods of nonlinear dynamic process based on ICA
  39. Multi-objective optimization design of steel structure building energy consumption simulation based on genetic algorithm
  40. Study on modal parameter identification of engineering structures based on nonlinear characteristics
  41. On-line monitoring of steel ball stamping by mechatronics cold heading equipment based on PVDF polymer sensing material
  42. Vibration signal acquisition and computer simulation detection of mechanical equipment failure
  43. Development of a CPU-GPU heterogeneous platform based on a nonlinear parallel algorithm
  44. A GA-BP neural network for nonlinear time-series forecasting and its application in cigarette sales forecast
  45. Analysis of radiation effects of semiconductor devices based on numerical simulation Fermi–Dirac
  46. Design of motion-assisted training control system based on nonlinear mechanics
  47. Nonlinear discrete system model of tobacco supply chain information
  48. Performance degradation detection method of aeroengine fuel metering device
  49. Research on contour feature extraction method of multiple sports images based on nonlinear mechanics
  50. Design and implementation of Internet-of-Things software monitoring and early warning system based on nonlinear technology
  51. Application of nonlinear adaptive technology in GPS positioning trajectory of ship navigation
  52. Real-time control of laboratory information system based on nonlinear programming
  53. Software engineering defect detection and classification system based on artificial intelligence
  54. Vibration signal collection and analysis of mechanical equipment failure based on computer simulation detection
  55. Fractal analysis of retinal vasculature in relation with retinal diseases – an machine learning approach
  56. Application of programmable logic control in the nonlinear machine automation control using numerical control technology
  57. Application of nonlinear recursion equation in network security risk detection
  58. Study on mechanical maintenance method of ballasted track of high-speed railway based on nonlinear discrete element theory
  59. Optimal control and nonlinear numerical simulation analysis of tunnel rock deformation parameters
  60. Nonlinear reliability of urban rail transit network connectivity based on computer aided design and topology
  61. Optimization of target acquisition and sorting for object-finding multi-manipulator based on open MV vision
  62. Nonlinear numerical simulation of dynamic response of pile site and pile foundation under earthquake
  63. Research on stability of hydraulic system based on nonlinear PID control
  64. Design and simulation of vehicle vibration test based on virtual reality technology
  65. Nonlinear parameter optimization method for high-resolution monitoring of marine environment
  66. Mobile app for COVID-19 patient education – Development process using the analysis, design, development, implementation, and evaluation models
  67. Internet of Things-based smart vehicles design of bio-inspired algorithms using artificial intelligence charging system
  68. Construction vibration risk assessment of engineering projects based on nonlinear feature algorithm
  69. Application of third-order nonlinear optical materials in complex crystalline chemical reactions of borates
  70. Evaluation of LoRa nodes for long-range communication
  71. Secret information security system in computer network based on Bayesian classification and nonlinear algorithm
  72. Experimental and simulation research on the difference in motion technology levels based on nonlinear characteristics
  73. Research on computer 3D image encryption processing based on the nonlinear algorithm
  74. Outage probability for a multiuser NOMA-based network using energy harvesting relays
https://doi.org/10.1515/nleng-2022-0240
Keywords for this article
NOMA; energy harvesting; power splitting protocol; amplify-and-forward; outage probability
Creative Commons
BY 4.0

Articles in the same Issue

  1. Research Articles
  2. Fractal approach to the fluidity of a cement mortar
  3. Novel results on conformable Bessel functions
  4. The role of relaxation and retardation phenomenon of Oldroyd-B fluid flow through Stehfest’s and Tzou’s algorithms
  5. Damage identification of wind turbine blades based on dynamic characteristics
  6. Improving nonlinear behavior and tensile and compressive strengths of sustainable lightweight concrete using waste glass powder, nanosilica, and recycled polypropylene fiber
  7. Two-point nonlocal nonlinear fractional boundary value problem with Caputo derivative: Analysis and numerical solution
  8. Construction of optical solitons of Radhakrishnan–Kundu–Lakshmanan equation in birefringent fibers
  9. Dynamics and simulations of discretized Caputo-conformable fractional-order Lotka–Volterra models
  10. Research on facial expression recognition based on an improved fusion algorithm
  11. N-dimensional quintic B-spline functions for solving n-dimensional partial differential equations
  12. Solution of two-dimensional fractional diffusion equation by a novel hybrid D(TQ) method
  13. Investigation of three-dimensional hybrid nanofluid flow affected by nonuniform MHD over exponential stretching/shrinking plate
  14. Solution for a rotational pendulum system by the Rach–Adomian–Meyers decomposition method
  15. Study on the technical parameters model of the functional components of cone crushers
  16. Using Krasnoselskii's theorem to investigate the Cauchy and neutral fractional q-integro-differential equation via numerical technique
  17. Smear character recognition method of side-end power meter based on PCA image enhancement
  18. Significance of adding titanium dioxide nanoparticles to an existing distilled water conveying aluminum oxide and zinc oxide nanoparticles: Scrutinization of chemical reactive ternary-hybrid nanofluid due to bioconvection on a convectively heated surface
  19. An analytical approach for Shehu transform on fractional coupled 1D, 2D and 3D Burgers’ equations
  20. Exploration of the dynamics of hyperbolic tangent fluid through a tapered asymmetric porous channel
  21. Bond behavior of recycled coarse aggregate concrete with rebar after freeze–thaw cycles: Finite element nonlinear analysis
  22. Edge detection using nonlinear structure tensor
  23. Synchronizing a synchronverter to an unbalanced power grid using sequence component decomposition
  24. Distinguishability criteria of conformable hybrid linear systems
  25. A new computational investigation to the new exact solutions of (3 + 1)-dimensional WKdV equations via two novel procedures arising in shallow water magnetohydrodynamics
  26. A passive verses active exposure of mathematical smoking model: A role for optimal and dynamical control
  27. A new analytical method to simulate the mutual impact of space-time memory indices embedded in (1 + 2)-physical models
  28. Exploration of peristaltic pumping of Casson fluid flow through a porous peripheral layer in a channel
  29. Investigation of optimized ELM using Invasive Weed-optimization and Cuckoo-Search optimization
  30. Analytical analysis for non-homogeneous two-layer functionally graded material
  31. Investigation of critical load of structures using modified energy method in nonlinear-geometry solid mechanics problems
  32. Thermal and multi-boiling analysis of a rectangular porous fin: A spectral approach
  33. The path planning of collision avoidance for an unmanned ship navigating in waterways based on an artificial neural network
  34. Shear bond and compressive strength of clay stabilised with lime/cement jet grouting and deep mixing: A case of Norvik, Nynäshamn
  35. Communication
  36. Results for the heat transfer of a fin with exponential-law temperature-dependent thermal conductivity and power-law temperature-dependent heat transfer coefficients
  37. Special Issue: Recent trends and emergence of technology in nonlinear engineering and its applications - Part I
  38. Research on fault detection and identification methods of nonlinear dynamic process based on ICA
  39. Multi-objective optimization design of steel structure building energy consumption simulation based on genetic algorithm
  40. Study on modal parameter identification of engineering structures based on nonlinear characteristics
  41. On-line monitoring of steel ball stamping by mechatronics cold heading equipment based on PVDF polymer sensing material
  42. Vibration signal acquisition and computer simulation detection of mechanical equipment failure
  43. Development of a CPU-GPU heterogeneous platform based on a nonlinear parallel algorithm
  44. A GA-BP neural network for nonlinear time-series forecasting and its application in cigarette sales forecast
  45. Analysis of radiation effects of semiconductor devices based on numerical simulation Fermi–Dirac
  46. Design of motion-assisted training control system based on nonlinear mechanics
  47. Nonlinear discrete system model of tobacco supply chain information
  48. Performance degradation detection method of aeroengine fuel metering device
  49. Research on contour feature extraction method of multiple sports images based on nonlinear mechanics
  50. Design and implementation of Internet-of-Things software monitoring and early warning system based on nonlinear technology
  51. Application of nonlinear adaptive technology in GPS positioning trajectory of ship navigation
  52. Real-time control of laboratory information system based on nonlinear programming
  53. Software engineering defect detection and classification system based on artificial intelligence
  54. Vibration signal collection and analysis of mechanical equipment failure based on computer simulation detection
  55. Fractal analysis of retinal vasculature in relation with retinal diseases – an machine learning approach
  56. Application of programmable logic control in the nonlinear machine automation control using numerical control technology
  57. Application of nonlinear recursion equation in network security risk detection
  58. Study on mechanical maintenance method of ballasted track of high-speed railway based on nonlinear discrete element theory
  59. Optimal control and nonlinear numerical simulation analysis of tunnel rock deformation parameters
  60. Nonlinear reliability of urban rail transit network connectivity based on computer aided design and topology
  61. Optimization of target acquisition and sorting for object-finding multi-manipulator based on open MV vision
  62. Nonlinear numerical simulation of dynamic response of pile site and pile foundation under earthquake
  63. Research on stability of hydraulic system based on nonlinear PID control
  64. Design and simulation of vehicle vibration test based on virtual reality technology
  65. Nonlinear parameter optimization method for high-resolution monitoring of marine environment
  66. Mobile app for COVID-19 patient education – Development process using the analysis, design, development, implementation, and evaluation models
  67. Internet of Things-based smart vehicles design of bio-inspired algorithms using artificial intelligence charging system
  68. Construction vibration risk assessment of engineering projects based on nonlinear feature algorithm
  69. Application of third-order nonlinear optical materials in complex crystalline chemical reactions of borates
  70. Evaluation of LoRa nodes for long-range communication
  71. Secret information security system in computer network based on Bayesian classification and nonlinear algorithm
  72. Experimental and simulation research on the difference in motion technology levels based on nonlinear characteristics
  73. Research on computer 3D image encryption processing based on the nonlinear algorithm
  74. Outage probability for a multiuser NOMA-based network using energy harvesting relays
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 23.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/nleng-2022-0240/html?lang=en
Scroll to top button