Surface waves on a coated incompressible elastic half-space

Saad Althobaiti

doi:10.1515/phys-2022-0213

Article Open Access

Surface waves on a coated incompressible elastic half-space

Saad Althobaiti

Published/Copyright: November 8, 2022

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

From the journal Open Physics Volume 20 Issue 1

Abstract

Recently, Khajiyeva et al. (2018) studied the dynamics of surface wave propagation in a pre-stressed incompressible half-space when accompanied by both vertical and tangential loads. In this study, however, we extend the work of Khajiyeva et al. to include the presence of a coating layer above the half-space, upon which the loads are acted. Moreover, we prescribe sufficient perfect continuity conditions between the two layers, resulting in an inhomogeneous composite structure. Furthermore, related effective boundary conditions within the long-wave assumption are acquired for the model through the application of the asymptotic approximation method. Finally, approximate uncoupled pseudo-differential equations are derived on the surface, thereby admitting all the results of Khajiyeva et al. as limiting cases of concern.

Keywords: coated half-space; incompressible; pre-stress; surface waves

1 Introduction

Propagation of waves in assorted structural arrangements has been expansively investigated since long ago owing to its immense happening in a variety of science and technological applications. In this regard, one can easily find some pertinent areas of real applications that involve the production and examination of elastic waves, such areas include seismology, materials science, earthquake, fluid dynamics, elastodynamics, biomechanics, geophysics, and geology [1,2, 3,4] to state a few. More so, there exist other fields from modern-day engineering that hugely enjoy massive contributions from the governing phenomena, including, for instance, structural engineering, transportation engineering, aeronautical engineering, and metallurgical engineering, just to mention a few [5,6, 7,8]. Structure-wise, various studies have been reported with regard to the propagation of different wave forms in disparate structural bodies and shapes, comprising singled-layered media [9,10,11], composite structures [12,13, 14,15], and the generalized multilayered bodies [16,17, 18,19,20, 21,22]. Besides, the case of the propagation of waves in singled-layered media is actually the classical consideration of different situations. One would read the book of Achenbach [23] for dissimilar scenarios about the propagation of waves in different elastic solids. Dutta [24] examined the longitudinal vibration of elastic disturbance associated with linear excitation by parameters. Bhattacharyya and Bera [25] made use of the legendary Adomian’s method to examine the propagation of waves in single elastic bars with linear and random material constituents. Moreover, Ahmad and Zaman [26] examined the case of a propagating wave in an isotropic nonhomogeneous single rod via exact and asymptotic methods. We also recall the latest work of Alzaidi et al. [27] for the study of the influence of non-integer temporal variation on the propagation of waves on an inhomogeneous finite elastic substrate.

Equally, for composites and multilayered structures, including coated media, there exist ample related examinations in both the past and recent works of the literature, with regard to the propagation and dispersion of elastic waves in such media. Moreover, such structural formations are realized in the present-day designs and inventions; take a look at the wings of an aeroplane, photovoltaic solar panels, metamaterials, multilayered petitioning timbers, nano-indentation tests, and laminated glazing glasses to refer to a few, see ref. [28] and references therein. Thus, upon putting more weights behind the coated media, since their applications are numerous, as we further recall some of their significance in seismic protection, rail transportation, and highway engineering, refer refs [29,30,31]. More so, their fundamental impacts are to protect material surfaces from external agents such as chemicals, thereby causing the whole structure to deteriorate [32]; read also about their relevance in the design and construction of biomaterials, such as implantations [33,34].

Nevertheless, stating some of the latest findings with regard to the dynamics of waves in coated media, Mubaraki et al. [35] examined the influence of certain external excitations, including rotation, and the gravitational and magnetic field forces on the vibration of surface waves on a viscoelastic-coated half-plane. Mubaraki et al. [36] determined the approximate explicit equations for the propagation of elastic waves on an elastic half-plane endowed with a thin-coating strip; read also ref. [37] for the study of Rayleigh waves’ effect on the propagation of surface waves on such media amidst the influence of prescribed stresses and gravity. In addition, a doubly coated inhomogeneous half-space was equally examined in ref. [38] with regard to the implication of rotation in the media, and on the other hand, the impact of the material inhomogeneity in the half-space; adequate approximate effective boundary conditions were constructed, which successfully approximated the derived secular equation with high precision. Additionally, the recent works of Manna et al. [39,40] on the propagation of Love-type wave on coated extended medium within the setting of orthotropic and anisotropic materials, respectively, are quite relevant in this arena; read also the study of Selim and Althobaiti [41] about the vibration of waves in supported walled carbon nanotubes by utilizing the wave-based method.

However, the present study aims at extending the recent work of Khajiyeva et al. [42] for the determination of approximate equations of motion with regard to the propagation of surface waves in a pre-stressed incompressible half-space, by incorporating a single coating layer with sufficient perfect continuity conditions in-between. Additionally, the present inhomogeneous composite structure is further assumed to be exerted by vertical and tangential loads from the other end of the coating. Furthermore, the related effective boundary conditions within the long-wave will be acquired for the model through the application of the asymptotic approximation method [37]. More so, the resulting approximate uncoupled pseudo-differential equations will be derived on the surface, thereby generalizing the results of Khajiyeva et al. [42], as all their results serve as limiting cases of the current study; for more relevant and recent considerations on the propagation of waves on coated and other related media, comprising the methodology of hyperbolic-elliptic types of Rayleigh waves, the consideration of surface waves in a coated half-space with Dirichlet-type boundary conditions, the extension to arbitrary anisotropy, and others; read refs [43,44,45, 46,47,48, 49,50] and references therein. Besides, the present study will be useful in the construction of medical biomaterials, which improves the quality of lives, in particular, in addition to its usefulness in addition to its usefulness in the modeling and analysis of coated media in modern technological inventions; see the frontier references cited in refs [1,2,3, 4,5,6, 7,8] and in refs [33,34] as an instance.

Finally, we organize the present article as follows: Section 2 gives the formulation of the governing problem. Section 3 derived the related appropriate effective boundary conditions; while Section 4 derives the asymptotic approximation for the propagation of surface waves by acquiring the resulting pseudo-differential equations. Finally, Section 5 gives some concluding notes and future perspectives.

2 Problem formulation

Consider a homogeneous, incompressible elastic coating of constant thickness h , subject to vertical and tangential loads, overlying a homogeneous elastic body B , which when a natural unstressed occupies the configuration B u . Purely homogeneous state deformations are imposed to produce a pre-stress equilibrium upon B e . The position vectors of a representative particle are denoted by X and x ( X ) in B u and B e , respectively. The deformation between them can be described by the mapping φ , so that

(1) x = φ ( X ) , X ∈ B u ,

where φ is assumed to be one-to-one mapping and at least twice continuously differentiable. We further consider an infinitesimal time-dependent motion u i ( X A , t ) , which is then superimposed upon B e , resulting in B t that occupies new time-dependent deformations. The position vectors of representative particle are denoted by X A , x i ( X A ) , and x ˜ i ( X A , t ) in B u , B e , and B t , respectively. The position vector x ˜ i ( X A , t ) may therefore be expressible in the form

(2) x ˜ i ( X A , t ) = x i ( X A ) + u i ( X A , t ) .

A Cartesian coordinate system O x 1 x 2 is chosen to be coincident with the deformed principal axes in B e , the Cartesian axes, O x 1 lies on the upper surface of the coating and O x 2 is located between the coating and half-plane (Figure 1).

Figure 1

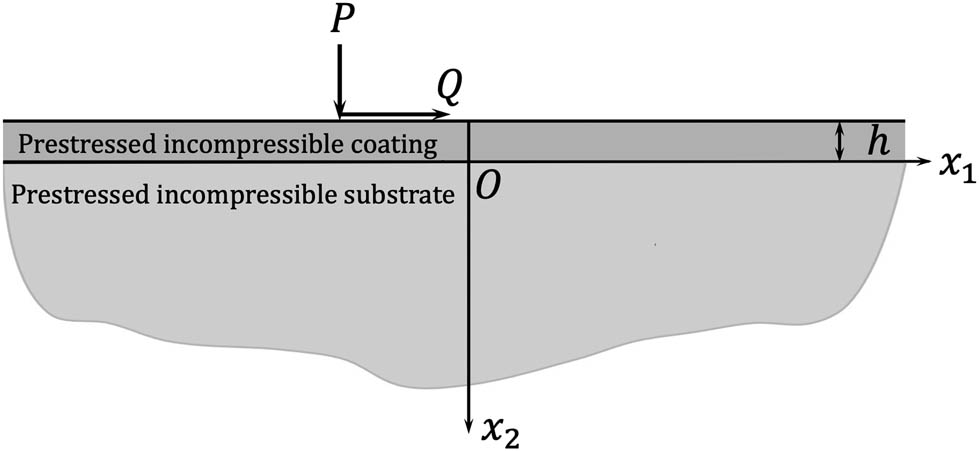
The tangential and vertical loads acting on a half-plane coated by a pre-stressed incompressible elastic layer.

In addition, the linearized measures of incremental tractions, associated with a surface having outward unit normals along O x 1 and O x 2 in B e , are obtained in the component forms as follows:

(3) τ 11 = ( A 1111 + p ¯ ) u 1 , 1 + A 1122 u 2 , 2 − p t , τ 12 = ( A 1221 + p ¯ ) u 1 , 2 + A 1212 u 2 , 1 , τ 21 = A 2121 u 1 , 2 + ( A 1221 + p ¯ ) u 2 , 1 , τ 22 = A 1122 u 1 , 1 + ( A 2222 + p ¯ ) u 2 , 2 − p t ,

where p ¯ is a static pressure in the configuration B e , that is, taken of the form

p ¯ = A 2121 − A 1221 − σ 2 ,

with σ 2 denoting the principal Cauchy stresses in B e , and p t is the associated time-dependent incremental component of pressure arising due to the incompressibility conditions, given by

(4) u 1 , 1 + u 2 , 2 = 0 .

Here and below, the comma indicates the differentiation with respect to the appropriate variables.

Then, the two coupled non-trivial equations of motion are thus given by

(5) A 1111 u 1 , 11 + A 2121 u 1 , 22 + δ u 2 , 12 − p t , 1 = ρ e u 1 , t t , A 1212 u 2 , 11 + A 2222 u 2 , 22 + δ u 1 , 12 − p t , 2 = ρ e u 2 , t t ,

in which

δ = A 1122 + A 1221 ,

and ρ e is the material density per unit volume of B e , while A i j k l are components of the fourth-order elasticity tensor. We assume the material parameters of the coating ( − h ≤ x 2 ≤ 0 ) are ρ e 0 , A i i j j 0 , A i j i j 0 , δ 0 , and p ¯ 0 . More so, the boundary conditions at the surface of the coating ( x 2 = − h ) are the prescribed tangential and vertical loads given as follows:

(6) τ 21 = − P ( x 1 , t ) , and τ 22 = − Q ( x 1 , t ) ,

while perfect continuity conditions involving all the displacements and stresses τ 2 i for i = 1 , 2 are assumed along the interface ( x 2 = 0 ) . Accordingly, we set the following boundary conditions:

(7) u i = v i ,

where v i = v i ( x 1 , t ) , i = 1 , 2 are displacements in the substrate at x 2 = 0 .

3 Effective boundary conditions

The derivation of effective boundary conditions goes by first introducing a small asymptotic parameter ε within the long-wave assumption as follows:

(8) ε = h λ ≪ 1 ,

where h is the thickness of the coating, while λ is the wave length. Next, we make use of the following scaling:

(9) ξ = x 1 λ , η = x 2 + h h , τ = c 0 λ t ,

along with the following dimensionless quantities:

(10) u i ∗ = 1 λ u i , v i ∗ = 1 λ v i , p t ∗ = p t γ 0 , p ∗ = λ h γ 0 P , q ∗ = λ h γ 0 Q ,

where γ 0 = A 2121 0 , and c 0 is the wave speed, defined as c 0 = γ 0 ∕ ρ e 0 .

In addition, the equations of motion expressed in Eq. (5) can now be rewritten as:

(11) γ 0 u 1 , η η ∗ + ε δ 0 u 2 , ξ η ∗ + ε 2 ( A 1111 0 u 1 , ξ ξ ∗ − γ 0 ( p t , ξ ∗ + u 1 , τ τ ∗ ) ) = 0 , A 2222 0 u 2 , η η ∗ + ε ( δ 0 u 1 , ξ η ∗ − γ 0 p t , η ∗ ) + ε 2 ( A 1212 0 u 2 , ξ ξ ∗ − γ 0 u 2 , τ τ ∗ ) = 0 ,

along with the transformed incompressibility equation as follows:

(12) u 2 , η ∗ + ε u 1 , ξ ∗ = 0 ,

where δ 0 = A 1122 0 + A 1221 o .

Furthermore, the prescribed boundary conditions in Eqs. (6) and (7) are transformed based on the above development to the following dimensionless forms:

(13) γ 0 u 1 , η ∗ + ε ( A 1221 0 + p ¯ 0 ) u 2 , ξ ∗ = − ε 2 γ 0 p ∗ , at η = 0 , ( A 2222 0 + p ¯ 0 ) u 2 , η ∗ + ε ( A 1122 0 u 1 , ξ ∗ − γ 0 p t ∗ ) = − ε 2 γ 0 q ∗ , at η = 0 , u i ∗ = v i ∗ , at η = 1 .

Next, the components of displacements u i ∗ and the pressure p t ∗ may be written by asymptotic series in terms of the small parameter ε as

(14) u i ∗ = u i ( 0 ) + ε u i ( 1 ) + … , and p t ∗ = p t ( 0 ) + ε p t ( 1 ) + … .

Therefore, at O ( 1 ) , we obtain

(15) u i , η η ( 0 ) = 0 , u 2 , η ∗ = 0 , u i , η ( 0 ) = 0 , at η = 0 , u i ( 0 ) = v i ∗ , at η = 1 ,

such that the above system admits the following solution:

(16) u i ( 0 ) = v i ∗ .

Going further to order O ( ε ) , we obtain

(17) γ 0 u 1 , η η ( 1 ) + δ 0 u 2 , ξ η ( 0 ) = 0 , A 2222 0 u 2 , η η ( 1 ) + δ 0 u 1 , ξ η ( 0 ) − γ 0 p t , η ( 0 ) = 0 , u 2 , η ( 1 ) + u 1 , ξ ( 0 ) = 0 ,

associated with

(18) γ 0 u 1 , η ( 1 ) + ( A 1221 0 + p ¯ 0 ) u 2 , ξ ( 0 ) = 0 , at η = 0 , ( A 2222 0 + p ¯ 0 ) u 2 , η ( 1 ) + ( A 1122 0 u 1 , ξ ( 0 ) − γ 0 p t ( 0 ) ) = 0 , at η = 0 , u i ( 1 ) = 0 , at η = 1 .

More so, the displacement components u 1 ( 1 ) and u 2 ( 1 ) are determined by solving Eqs. ( 17 ) 1 and ( 17 ) 3 , together with Eqs. (16), ( 18 ) 1 , and ( 18 ) 3 to obtain

(19) u 1 ( 1 ) = 1 γ 0 ( 1 − η ) ( A 1221 0 + p ¯ 0 ) v 2 , ξ ∗

and

(20) u 2 ( 1 ) = ( 1 − η ) v 1 , ξ ∗ .

Also, the pressure p t ( 0 ) is obtained from Eqs. ( 17 ) 2 and (19) along with the boundary condition given in Eq. ( 18 ) 2 as

(21) p t ( 0 ) = 1 γ 0 ( A 1122 0 − ( A 2222 0 + p ¯ 0 ) ) v 1 , ξ ∗ .

The next order O ( ε 2 ) gives

(22) γ 0 u 1 , η η ( 2 ) + δ 0 u 2 , ξ η ( 1 ) + A 1111 0 u 1 , ξ ξ ( 0 ) − γ 0 ( p t , ξ ( 0 ) + u 1 , τ τ ( 0 ) ) = 0 , A 2222 0 u 2 , η η ( 2 ) + δ 0 u 1 , ξ η ( 1 ) − γ 0 p t , η ( 1 ) + A 1212 0 u 2 , ξ ξ ( 0 ) − γ 0 u 2 , τ τ ( 0 ) = 0 , u 2 , η ( 2 ) + u 1 , ξ ( 1 ) = 0 ,

subject to

(23) γ 0 A 2121 0 u 1 , η ( 2 ) + ( A 1221 0 + p ¯ 0 ) u 2 , ξ ( 1 ) = − γ 0 p ∗ , at η = 0 , ( A 2222 0 + p ¯ 0 ) u 2 , η ( 2 ) + A 1122 0 u 1 , ξ ( 1 ) − γ 0 p t ( 1 ) = − γ 0 q ∗ , at η = 0 , u i ( 2 ) = 0 , at η = 1 .

The solution of this system may be obtained as follows:

(24) u 1 ( 2 ) = 1 2 ( 1 − η ) 2 γ 0 ( A 1221 0 + p ¯ 0 ) − ( 1 + η ) δ 1 v 1 , ξ ξ ∗ − ( 1 + η ) v 1 , τ τ ∗ + 2 p ∗ ,

(25) u 2 ( 2 ) = 1 2 γ 0 ( 1 − η ) 2 ( A 1221 0 + p ¯ 0 ) v 2 , ξ ξ ∗

and

(26) p t ( 1 ) = 1 γ 0 ( η δ 2 + δ 3 ) v 2 , ξ ξ ∗ − η v 2 , τ τ ∗ + q ∗ ,

wherein

δ 1 = δ 0 + A 1122 0 − A 1111 0 − A 2222 0 − p ¯ 0 , δ 2 = 1 γ 0 ( A 1221 0 + p ¯ 0 ) ( A 2222 0 − δ 0 ) + A 1212 0 , δ 3 = 1 γ 0 ( A 1221 0 + p ¯ 0 ) ( A 1122 0 − A 2222 0 − p ¯ 0 ) .

Hence, the incremental tractions τ 21 and τ 22 are represented as

(27) τ 21 = ε [ ( δ 1 − A 1221 0 − p ¯ 0 ) η v 1 , ξ ξ ∗ + γ 0 ( η v 1 , τ τ ∗ − p ∗ ) ] + O ( ε 2 ) , τ 22 = ε γ 0 η v 2 , τ τ ∗ + 1 γ 0 ( A 1221 0 + p ¯ 0 ) ( A 1122 0 − A 2222 0 − p ¯ 0 ) ( 1 − η ) − ( η δ 2 + δ 3 ) v 2 , ξ ξ ∗ − γ 0 q ∗ + O ( ε 2 ) .

Finally, upon returning to the original dimensional variables, the effective boundary conditions at the interface ( x 2 = 0 ) eventually become

(28) τ 21 = h ( γ 0 c 0 − 2 v 1 , t t + δ 4 v 1 , 11 ) − P , τ 22 = h ( γ 0 c 0 − 2 v 2 , t t + δ 5 v 2 , 11 ) − Q ,

where

δ 4 = 2 A 1122 0 − A 1111 0 − A 2222 0 − 2 p ¯ 0 , and δ 5 = 1 γ 0 ( A 1221 0 + p ¯ 0 ) 2 − A 1212 0 .

4 Asymptotic formulation for surface waves

Here, having successfully determined the effective boundary conditions in Eq. (28), we now proceed further to derive a pseudo-differential equation for the vertical and longitudinal displacements of the substrate, thereby generalizing the forgoing results to case of the pre-stressed incompressible elastic half-plane, and extending the hyperbolic-elliptic equation in the study of Khajiyeva et al. [42]. To begin with, we follow the consideration in the study of Dowaikh and Ogden [51] by considering the displacement components – via the Cauchy–Riemann identities, to be of the following forms:

(29) u 1 = ψ , 2 and u 2 = − ψ 1 ,

where ψ is the potential function, which satisfies the incompressibility condition. Thus, the coupled equations of motion expressed in Eq. (5) would now be rewritten in terms of the potential function ψ as follows:

(30) A 1111 ψ , 112 + A 2222 ψ , 222 − δ ψ , 112 − p t , 1 = ρ e ψ , 2 t t , A 1212 ψ , 111 + A 2222 ψ , 122 − δ ψ , 122 + p t , 2 = ρ e ψ , 1 t t .

Then, upon eliminating p t from the above equation, we obtain

(31) α ψ , 1111 + 2 β ψ , 1122 + γ ψ , 2222 = ρ e ( ψ , 11 t t + ψ , 22 t t ) ,

where

α = A 1212 γ = A 2121 , 2 β = A 1111 + A 2222 − 2 δ ,

and satisfying

α > 0 and β + α γ > 0 ,

such that the obtained traction boundary conditions in Eq. (28) are also expressed at the interface ( x 2 = 0 ) as follows:

(32) γ ψ , 22 − ( γ − σ 2 ) ψ , 11 = h ( γ 0 c 0 − 2 ψ , 2 t t + δ 4 ψ , 112 ) − P , ( 2 β + γ − σ 2 ) ψ , 112 + γ ψ , 222 − ρ e ψ , 2 t t = h ( γ 0 c 0 − 2 ψ , 11 t t + δ 5 ψ , 1111 ) + Q , 1 .

Now, let us introduce the slow-time perturbation scheme, by introducing the following dimensionless variables:

(33) ξ ˆ = x 1 − c R t λ , η ˆ = x 2 λ , τ ˆ = c R ε λ t ,

where τ ˆ is the slow time, λ is the typical wave length, and c R denotes the Rayleigh wave speed.

Then Eq. (31) is re-cast in terms of a single fourth order partial differential equation (PDE) as follows:

(34) ( α − ρ e c R 2 ) ψ , ξ ˆ ξ ˆ ξ ˆ ξ ˆ + ( 2 β − ρ e c R 2 ) ψ , ξ ˆ ξ ˆ η ˆ η ˆ + γ ψ , η ˆ η ˆ η ˆ η ˆ + 2 ε ρ e c R 2 ( ψ , ξ ˆ ξ ˆ ξ ˆ τ ˆ + ψ , ξ ˆ η ˆ η ˆ τ ˆ ) − ε 2 ρ e c R 2 ( ψ , ξ ˆ ξ ˆ τ ˆ τ ˆ + ψ , η ˆ η ˆ τ ˆ τ ˆ ) = 0 ,

subject to

(35) γ ψ , η ˆ η ˆ − ( γ − σ 2 ) ψ , ξ ˆ ξ ˆ − ε ( γ 0 k 0 + δ 4 ) ψ , ξ ˆ ξ ˆ η ˆ + γ 0 c R 2 c 0 2 ( 2 ε 2 ψ , ξ ˆ η ˆ τ ˆ − ε 3 ψ , η ˆ τ ˆ τ ˆ ) = − λ 2 P , ( 2 β + γ − σ 2 − ρ e c R 2 ) ψ , ξ ˆ ξ ˆ η ˆ + γ ψ , η ˆ η ˆ η ˆ + ε [ 2 ε ρ e c R 2 ψ , ξ ˆ η ˆ τ ˆ − ( γ 0 k 0 + δ 5 ) ψ , ξ ˆ ξ ˆ ξ ˆ ξ ˆ ] + ε 2 [ 2 γ 0 c 0 − 2 c R 2 ψ , ξ ˆ ξ ˆ ξ ˆ τ ˆ − ρ e c R 2 ψ , η ˆ τ ˆ τ ˆ ] − ε 3 γ 0 c 0 − 2 ψ , ξ ˆ ξ ˆ τ ˆ τ ˆ = λ 2 Q , ξ ˆ ,

where

k 0 2 = c R 2 c 0 2 .

Let us now expand the displacements ψ via asymptotic series as follows:

ψ = λ 2 ε ( ψ ( 0 ) ( ξ ˆ , η ˆ , τ ˆ ) + ε ψ ( 1 ) ( ξ ˆ , η ˆ , τ ˆ ) + … ) ,

then, at the leading order, Eq. (34) becomes

(36) ( α − ρ e c R 2 ) ψ , ξ ˆ ξ ˆ ξ ˆ ξ ˆ ( 0 ) + ( 2 β − ρ e c R 2 ) ψ , ξ ˆ ξ ˆ η ˆ η ˆ ( 0 ) + γ ψ , η ˆ η ˆ η ˆ η ˆ ( 0 ) = 0 ,

this PDE is elliptic, hence, it can be represented in operator form as

(37) Δ 1 Δ 2 ψ ( 0 ) = 0 ,

where

(38) κ ˆ 1 2 κ ˆ 2 2 = 1 γ ( α − ρ e c R 2 ) κ ˆ 1 2 + κ ˆ 1 2 = 1 γ ( 2 β − ρ e c R 2 ) .

For each κ ˆ i 2 > 0 , the solution of Eq. (37) can be expressed in terms of a pair of plane harmonic functions as

(39) ψ ( 0 ) = ∑ i = 1 2 ψ i ( 0 ) ( ξ ˆ , κ ˆ i 2 η ˆ , τ ˆ ) ,

where ψ i ( 0 ) ( ξ ˆ , κ ˆ i 2 η ˆ , τ ˆ ) are the arbitrary harmonic functions in the first two arguments. Substituting these solutions given in Eq. (39) into the boundary conditions expressed in Eq. (35) at leading order, and implying the Cauchy–Riemann identities expressed earlier, and further integrating the second boundary condition with respect to ξ , we arrive at

(40) ∑ i = 1 2 c 1 i ψ i , ξ ˆ ξ ˆ ( 0 ) = 0 , and ∑ i = 1 2 c 2 i ψ i , ξ ˆ ξ ˆ ( 0 ) = 0 ,

where

c 1 i = γ ( κ ˆ i 2 + 1 ) − σ 2 , c 2 i = κ ˆ i ( 2 β − ρ e c R 2 − σ 2 + γ ( 1 − κ ˆ i 2 ) ) ,

then, the classical Rayleigh wave equation follows as a solvability condition

(41) c 22 c 11 − c 12 c 21 = 0 ,

with the relation between the potentials, given as

(42) ψ 1 ( 0 ) = ϑ ψ 2 ( 0 ) , at η ˆ = 0 ,

where

ϑ = − c 11 c 12 .

At the next order, the general solution of the potential function ψ is obtained by Khajiyeva et al. [42] as follows:

(43) ψ ( 1 ) ( ξ ˆ , η ˆ , τ ˆ ) = ∑ i = 1 2 ( ψ i ( 1 , 0 ) + η ˆ e i ψ ¯ i , τ ˆ ( 0 ) ) ,

with

e i = ρ e c R 2 ( κ ˆ i 2 − 1 ) γ κ ˆ i − ( κ ˆ j − κ ˆ i ) , i ≠ j = 1 , 2 ,

where ψ i ( 1 , 0 ) = ψ i ( 1 , 0 ) ( ξ ˆ , κ ˆ i 2 η ˆ , τ ˆ ) are once again arbitrary plane harmonic functions in the first two arguments and bar denote a harmonic conjugate.

More so, at the next order, the boundary conditions given in Eq. (35) at η ˆ = 0 yield

(44) γ ψ , η ˆ η ˆ ( 1 ) − ( γ − σ 2 ) ψ , ξ ˆ ξ ˆ ( 1 ) − ( γ 0 k 0 2 + δ 4 ) ψ , ξ ˆ ξ ˆ η ˆ ( 0 ) = − P , ( 2 β + γ − σ 2 − ρ e c R 2 ) ψ , ξ ˆ ξ ˆ η ˆ ( 1 ) + γ ψ , η ˆ η ˆ η ˆ ( 1 ) + 2 ρ e c R ψ , ξ ˆ γ ˆ τ ˆ ( 0 ) − ( γ 0 k 0 2 + δ 5 ) ψ , ξ ˆ ξ ˆ ξ ˆ ξ ˆ ( 0 ) = Q , ξ ˆ .

Therefore, upon inserting Eqs (39) and (43) into conditions (44), and thereafter making use of the Cauchy–Riemann identities, we arrive at η ˆ = 0 the following:

(45) ∑ i = 1 2 { − c 1 i ψ i , ξ ˆ ξ ˆ ( 1 , 0 ) + 2 γ e i κ ˆ i ψ i , ξ ˆ τ ˆ ( 0 ) + κ ˆ i ( γ 0 k 0 2 + δ 4 ) ψ ¯ i , ξ ˆ ξ ˆ ξ ˆ ( 0 ) } = − P , ∑ i = 1 2 { c 2 i ψ i , ξ ˆ ξ ˆ ( 1 , 0 ) − g i ψ i , ξ ˆ τ ˆ ( 0 ) − ( γ 0 k 0 2 + δ 5 ) ψ ¯ i , ξ ˆ ξ ˆ ξ ˆ ( 0 ) } = Q ¯ , ξ ˆ ,

where

g i = e i ( 2 β − ρ e c R 2 − σ 2 + γ ( 1 − 3 κ ˆ i 2 ) ) − 2 κ ˆ i ρ e c R .

Next, plugging the relation determined in Eq. (42) into (45), we obtain at η ˆ = 0 as follows:

(46) − c 11 ψ 1 , ξ ˆ ξ ˆ ( 1 , 0 ) − c 12 ψ 2 , ξ ˆ ξ ˆ ( 1 , 0 ) + b 1 ψ 1 , ξ ˆ τ ˆ ( 0 ) + ( κ ˆ 1 + ϑ κ ˆ 2 ) × ( γ 0 k 0 2 + δ 4 ) ψ ¯ 1 , ξ ˆ ξ ˆ ξ ˆ ( 0 ) = − P , c 21 ψ 1 , ξ ˆ ξ ˆ ( 1 , 0 ) + c 22 ψ 2 , ξ ˆ ξ ˆ ( 1 , 0 ) − b 2 ψ 1 , ξ ˆ τ ˆ ( 0 ) − ( 1 + ϑ ) × ( γ 0 k 0 2 + δ 5 ) ψ ¯ 1 , ξ ˆ ξ ˆ ξ ˆ ( 0 ) = Q ¯ ,

where

b 1 = 2 γ ( e 1 κ ˆ 1 + ϑ e 2 κ ˆ 2 ) , and b 2 = g 1 + ϑ g 2 .

Furthermore, upon combining the previous equations, we have at η ˆ = 0

(47) ( c 22 c 11 − c 12 c 21 ) ψ 2 , ξ ˆ ξ ˆ ( 1 , 0 ) + ( c 21 b 1 − c 11 b 2 ) ψ 1 , ξ ˆ τ ˆ ( 0 ) − [ c 11 ( 1 + ϑ ) ( γ 0 k 0 2 + δ 5 ) − c 21 ( κ ˆ 1 + ϑ κ ˆ 2 ) ( γ 0 k 0 2 + δ 4 ) ] ψ ¯ 1 , ξ ˆ ξ ˆ ξ ˆ ( 0 ) = − ( c 21 P − c 11 Q ¯ ) .

Moreover, from the solvability condition given in Eq. (41), the first term in Eq. (47) vanishes, therefore, we deduce

(48) ψ 1 , ξ ˆ τ ˆ ( 0 ) + c R b 0 2 κ ˆ 1 ψ 1 , ξ ˆ ξ ˆ η ˆ ( 0 ) = − c R 2 B ( c 21 P − c 11 Q ¯ ) , at η ˆ = 0 ,

where

B = c R 2 ( c 21 b 1 − c 11 b 2 )

and

(49) b 0 = 1 B [ c 11 ( 1 + ϑ ) ( γ 0 k 0 2 + δ 5 ) − c 21 ( κ ˆ 1 + ϑ κ ˆ 2 ) ( γ 0 k 0 2 + δ 4 ) ] .

In addition, Eq. (48) is rearranged in terms of the original variables ( x 1 , x 2 , t ) as follows:

(50) ψ 1 , 11 − 1 c R 2 ψ 1 , t t + h b 0 κ ˆ 1 ψ 1 , 112 = − 1 B ( c 21 P − c 11 Q ¯ ) , at x 2 = 0 ,

where the elliptic equation for the potential ψ 1 is obtained as

(51) [ ∂ 22 2 + κ ˆ 1 2 ∂ 11 2 ] ψ 1 = 0 ,

over the interior, along with the boundary condition on the surface of the substrate ( x 2 = 0 ) given in (50). Then, Eq. (50) can be expressed in terms of the surface displacements u i ( x 1 , 0 , t ) as follows:

(52) u 1 , 11 − 1 c R 2 u 1 , t t + h b 0 κ ˆ 1 u 1 , 112 = ( κ ˆ 1 + ϑ κ ˆ 2 ) B ( c 21 P ¯ , 1 + c 11 Q , 1 )

and

(53) u 2 , 11 − 1 c R 2 u 1 , t t + h b 0 κ ˆ 1 u 2 , 112 = ( 1 + ϑ ) B ( c 21 P , 1 − c 11 Q ¯ , 1 ) .

Next, Eqs (52) and (53) may be expressed in the form of a pseudo-differential equations on the surface as follows:

(54) u 1 , 11 − 1 c R 2 u 1 , t t − h b 0 − ∂ 11 u 1 , 11 = ( κ ˆ 1 + ϑ κ ˆ 2 ) B ˆ ( c 21 P ¯ , 1 + c 11 Q , 1 ) , at x 2 = 0 ,

and

(55) u 2 , 11 − 1 c R 2 u 2 , t t − h b 0 − ∂ 11 u 2 , 11 = ( 1 + ϑ ) B ( c 21 P , 1 − c 11 Q ¯ , 1 ) , at x 2 = 0 .

Note that, for instance, the case of tangential loading of Eq. (52) may be reduced to linear isotropic elasticity as

(56) u 1 , 11 − 1 c R 2 u 1 , t t + h b 0 k 2 u 1 , 112 = ( 1 − k 2 4 ) 4 μ B Q , 1 ,

where in the absence of deformation ( λ 1 = λ 2 = λ 3 = 1 ) , we find k 1 = 1 and k 2 = κ ˆ 1 , and then the constants b 0 and B become

B = k 2 4 − k 2 − 1 + k 2 − 1 and b 0 = ( 1 − k 2 4 ) 4 B ρ c c R 2 μ c ( 1 − 2 k 2 − k 2 2 ) + 8 k 2 ,

where

k 1 = 1 − ρ s c R 2 λ s + 2 μ s , and k 2 = 1 − ρ s c R 2 μ s ,

with λ q and μ q the elastic constants, and ρ q are the densities for q = c , s where c indicates the coating layer and s the half-space.

Finally, in the case of no coating, Eqs. (54) and (55) coincide with the recent results reported by Khajiyeva et al. [42] for the dynamics of surface waves in a pre-stressed incompressible half-space. Thus, as the present investigation extended the results of the above-mentioned reference, various directions could be taken to extend the study of Khajiyeva et al. [42]; at the same time, it also serves as a benchmark reference for comparative examination.

5 Conclusion

As a concluding note, the present study analyzed a plane inhomogeneous dynamic problem with regard to a coated pre-stressed incompressible half-space. Sufficient perfect continuity conditions are prescribed between the coating layer and the half-space, while the other end surface of the coating is being excited by both the vertical and tangential loads. Moreover, we acquired the related effective boundary conditions within the long-wave assumption via the application of the asymptotic approximation method. In addition, the uncoupled pseudo-differential equations are approximately revealed on the surface; these approximate equations serve as the overall postulate for the propagation of surface waves in the governing coated structure. More conceivably, all the results presented recently by Khajiyeva et al. [42] could be obtained easily from the presented results as limiting cases of concern upon ignoring the presence and effect of the coating layer. Finally, the present examination can be extended to multiply-coated structures amidst the presence of external forces; in addition, the case of a generalized anisotropic medium can equally be considered as an interesting case of universal concern. Besides, this study is useful in the construction of medical biomaterials – including implants/implantation, which improves the quality of lives, as a particular case of great concern, in addition to its usefulness in the modeling and analysis of coated media.

Funding information: This research was supported by Taif University Researchers Sup porting Project number (TURSP-2020/305), Taif University, Taif, Saudi Arabia.
Author contributions: The author has accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The author states no conflict of interest.

References

[1] Kaplunov JD, Kossovich LY, Nolde EV. Dynamics of thin walled elastic bodies. San Diego, CA, USA: Academic Press; 1998. Search in Google Scholar

[2] Andrianov IV, Awrejcewicz J, Danishevs’kyy VV, Ivankov OA. Asymptotic methods in the theory of plates with mixed boundary conditions. Hoboken, NJ, USA: John Wiley & Sons, Ltd; 2014. 10.1002/9781118725184Search in Google Scholar

[3] Ewing WM, Jardetzky WS, Press F, Beiser A. Elastic waves in layered media. Phy Today; 1957;10(12):27. 10.1063/1.3060203Search in Google Scholar

[4] Daniel IM, Ishai O, Daniel IM, Daniel I. Engineering mechanics of composite materials. New York, NY, USA: Oxford University Press; 2006. Search in Google Scholar

[5] Padture NP, Gell M, Jordan EH. Thermal barrier coatings for gas-turbine engine application. Science. 2002;296:280–4. 10.1126/science.1068609Search in Google Scholar PubMed

[6] Palermo A, Krodel S, Marzani A, Daraio C. Engineered metabarrier as shield from seismic surface waves. Sci Rep. 2016;6:1–10. 10.1038/srep39356Search in Google Scholar PubMed PubMed Central

[7] Cho YS. Non-destructive testing of high strength concrete using spectral analysis of surface waves. NDT Int. 2003;36:229–35. 10.1016/S0963-8695(02)00067-1Search in Google Scholar

[8] Krylov VV. Noise and vibration from high-speed trains. London, UK: Thomas Telford; 2001. 10.1680/navfht.29637Search in Google Scholar

[9] Yigit G, Sahin A, Bayram M. Modelling of vibration for functionally graded beams. Open Math. 2016;14:661–71. 10.1515/math-2016-0057Search in Google Scholar

[10] Althobaiti S, Hawwa MA. Flexural edge waves in a thick piezoelectric film resting on a Winkler foundation. Crystals. 2022;12(5):640. 10.3390/cryst12050640Search in Google Scholar

[11] Erbas B, Kaplunov J, Nobili A, Kilic G. Dispersion of elastic waves in a layer interacting with a Winkler foundation. J Acoust Soc Am. 2018;144:2918–25. 10.1121/1.5079640Search in Google Scholar PubMed

[12] Mandi A, Kundu S, Chandra P, Pati P. An analytic study on the dispersion of Love wave propagation in double layers lying over inhomogeneous half-space. J Solid Mech. 2019:11:570–80. Search in Google Scholar

[13] Abd-Alla AM, Abo-Dahab SM, Khan A. Rotational effects on magneto-thermoelastic Stoneley, Love, and Rayleigh waves in fibre-reinforced anisotropic general viscoelastic media of higher order. Comp Math Continua. 2017;53:49–72. 10.12989/sem.2017.61.2.221Search in Google Scholar

[14] Alam P, Kundu S. Influences of heterogeneities and initial stresses on the propagation of love-type waves in a transversely isotropic layer over an inhomogeneous half-space. J Solid Mech. 2017:9:783–93. Search in Google Scholar

[15] Althobaiti S, Mubaraki A, Nuruddeen RI, Gomez-Aguilar JF. Wave propagation in an elastic coaxial hollow cylinder when exposed to thermal heating and external load. Results Phys. 2022;38:105582. 10.1016/j.rinp.2022.105582Search in Google Scholar

[16] Nuruddeen RI, Nawaz R, Zia ZQM. Effects of thermal stress, magnetic field and rotation on the dispersion of elastic waves in an inhomogeneous five-layered plate with alternating components. Sci Prog. 2020;103:0036850420940469. 10.1177/0036850420940469Search in Google Scholar PubMed

[17] Kaplunov J, Prikazchikov DA, Prikazchikov LA, Sergushova O. The lowest vibration spectra of multi-component structures with contrast material properties. J Sound Vib. 2019;445:132–47. 10.1016/j.jsv.2019.01.013Search in Google Scholar

[18] Wang YZ, Li MF, Kishimoto K. Thermal effects on vibration properties of double-layered nanoplates at small scales. Composites B Eng. 2011;42:1311–7. 10.1016/j.compositesb.2011.01.001Search in Google Scholar

[19] Kundu S, Kumari A. Torsional wave propagation in an initially stressed anisotropic heterogeneous crustal layer lying over a viscoelastic half-space. Procedia Eng. 2017;173:980–7. 10.1016/j.proeng.2016.12.166Search in Google Scholar

[20] Kaplunov J, Prikazchikova L, Alkinidri M. Antiplane shear of an asymmetric sandwich plate. Contin Mech Thermodyn. 2021;33:1247–62. 10.1007/s00161-021-00969-6Search in Google Scholar

[21] Vinson J. The Behavior of Sandwich Structures of Isotropic and Composite Materials. London, UK: Routledge; 2018. 10.1201/9780203737101Search in Google Scholar

[22] Asif M, Nawaz R, Nuruddeen RI. Dispersion of elastic waves in an inhomogenous multilayered plate over a Winkler elastic foundation with imperfect interfacial conditions. Phys Scr. 2021;96:125026. 10.1088/1402-4896/ac36a1Search in Google Scholar

[23] Achenbach JD. Wave propagation in elastic solids, eight impression. Amsterdam, Netherlands: Elsevier; 1999. Search in Google Scholar

[24] Dutta AN. Longitudinal propagation of elastic disturbance for linear vibrations of elastic parameters. Indian J Theor Phys. 1965;4:43–60. Search in Google Scholar

[25] Bhattacharyya RK, Bera RK. Application of Adomian method on the solution of the elastic wave propagation in elastic bars of finite length with randomly and linearly varying Young’s modulus. Appl Math Let. 2004;17:703–9. 10.1016/S0893-9659(04)90108-5Search in Google Scholar

[26] Ahmad F, Zaman FD. Exact and asymptotic solutions of the elastic wave propagation problem in a rod. Int J Pure Appl Math. 2006;27:123–7. Search in Google Scholar

[27] Alzaidi ASM, Mubaraki AM, Nuruddeen RI. Effect of fractional temporal variation on the vibration of waves on elastic substrates with spatial non-homogeneity. AIMS Math. 2022;7:13746–62. 10.3934/math.2022757Search in Google Scholar

[28] Kaplunov J, Prikazchikov D, Prikazchikova L. Dispersion of elastic waves in a strongly inhomogeneous three-layered plate. Int J Solids Struct. 2017;113:169–79. 10.1016/j.ijsolstr.2017.01.042Search in Google Scholar

[29] Dai HH, Kaplunov J, Prikachikov DA. A long-wave model for the surface wave in a coated half-space. Proc R Soc A Math Phy Eng Sci. 2010;466:3097–116. doi: 10.1098/rsta.2019.0111. 10.1098/rspa.2010.0125Search in Google Scholar

[30] Vinh PC, Linh NTK. An approximate secular equation of Rayleigh waves propagating in an orthotropic elastic half-space coated by a thin orthotropic elastic layer. Wave Motion. 2012;49:681–9. 10.1016/j.wavemoti.2012.04.005Search in Google Scholar

[31] Vinh PC, Anh VTN, Thanh VP. Rayleigh waves in an isotropic elastic half-space coated by a thin isotropic elastic layer with smooth contact. Wave Motion. 2014;51:496–504. 10.1016/j.wavemoti.2013.11.008Search in Google Scholar

[32] Mubaraki A. Asymptotic models for surface waves in coated elastic solids. Ph.D. Thesis. Keele, UK, Keel University; 2021. Search in Google Scholar

[33] Tiainen VM. Amorphous carbon as a bio-mechanical coating-mechanical properties and biological applications. Diamond Rel Mat. 2001;10:153–60. 10.1016/S0925-9635(00)00462-3Search in Google Scholar

[34] Li M, Liu Q, Jia Z, Xu X, Cheng Y, Zheng Y, et al. Graphene oxide/hydroxyapatite composite coatings fabricated by electrophoretic nanotechnology for biological applications. Carbon. 2014;67:185–97. 10.1016/j.carbon.2013.09.080Search in Google Scholar

[35] Mubaraki A, Althobaiti S, Nuruddeen RI. Propagation of surface waves in a rotating coated viscoelastic half-space under the influence of magnetic field and gravitational forces. Fractal Fract. 2021;5:1–16. 10.3390/fractalfract5040250Search in Google Scholar

[36] Mubaraki A, Prikazchikov D, Kudaibergenov A. Explicit model for surface waves on an elastic half-space coated by a thin vertically inhomogeneous layer. Dyn Syst Theo Appl. 2019:267–75. 10.1007/978-3-030-77306-9_23Search in Google Scholar

[37] Mubariki A, Prikazchikov D. On Rayleigh wave field induced by surface stresses under the effect of gravity. Math Mech Solids 2020;27:1–12. doi: 10.1177/0812865221080550. 10.1177/10812865221080550Search in Google Scholar

[38] Mubaraki AM, Helmi MM, Nuruddeen RI. Surface wave propagation in a rotating doubly coated nonhomogeneous half space with application. Symmetry. 2022;14:1000. 10.3390/sym14051000Search in Google Scholar

[39] Manna S, Halder T, Althobaiti SN. Dispersion of Love-type wave and its limitation in a nonlocal elastic model of nonhomogeneous layer upon an orthotropic extended medium. Soil Dyn Earthquake Eng. 2022;153:107117. 10.1016/j.soildyn.2021.107117Search in Google Scholar

[40] Manna S, Pramanik D, Althobaiti SN. Love-type surface wave propagation due to interior impulsive point source in a homogenous-coated anisotropic poroelastic layer over a non-homogenous extended substance. Waves Random Complex Media. 2022;1–37. 10.1080/17455030.2022.2081737Search in Google Scholar

[41] Selim MM, Althobaiti S. Wave-based method for longitudinal vibration analysis for irregular single-walled carbon nanotube with elastic-support boundary conditions. Alexandria Eng J. 2022;61:12129–38. 10.1016/j.aej.2022.06.001Search in Google Scholar

[42] Khajiyeva LA, Prikazchikov DA, Prikazchikova LA. Hyperbolic-elliptic model for surface wave in pre-stressed incompressible elastic half-space. Mech Res Comm. 2018;92:49–53. doi: 10.1016/j.mecherescom.2018.07.006. 10.1016/j.mechrescom.2018.07.006Search in Google Scholar

[43] Kaplunov J, Prikazchikov DA. Asymptotic theory for Rayleigh and Rayleigh-type waves. Adv Appl Mech. 2017;50:1–106. 10.1016/bs.aams.2017.01.001Search in Google Scholar

[44] Kaplunov J, Prikazchikov D, Sultanova L. Rayleigh-type waves on a coated elastic half-space with a clamped surface. Phil Transc Royal Soc A. 2019;377:20190111. 10.1098/rsta.2019.0111Search in Google Scholar PubMed

[45] Fu Y, Kaplunov J, Prikazchikov D. Reduced model for the surface dynamics of a generally anisotropic elastic half-space. Proc Royal Soc A. 2020;476:20190590. 10.1098/rspa.2019.0590Search in Google Scholar

[46] Singh AK, Pal MK, Negi A, Mistri KC. Analytical study on dynamic response due to a moving load on distinctly characterized orthotropic half-spaces under different physical conditions with comparative approach. Arab J Sci Eng. 2019;44:4863–83. doi: 10.1007/s13369-018-3577-4. 10.1007/s13369-018-3577-4Search in Google Scholar

[47] Pal MK, Singh AK. On the characteristics of reflected waves in Rotating Functionally graded initially stressed piezoelectric-orthotropic half-space. Waves Random Complex Media. 2021;1–15. doi: 10.1080/17455030.2021.1892239. 10.1080/17455030.2021.1892239Search in Google Scholar

[48] Pal MK, Singh AK. Analysis of reflection and transmission phenomenon at distinct bonding interfaces in a rotating pre-stressed functionally graded piezoelectric-orthotropic structure. Appl Math Comput. 2021;15:126398. doi: 10.1016/j.amc.2021.126398. 10.1016/j.amc.2021.126398Search in Google Scholar

[49] Mubaraki AM, Althobaiti S, Nuruddeen RI. Heat and wave interactions in a thermoelastic coaxial solid cylinder driven by laser heating sources. Case Stud Thermal Eng. 2022;38:102338. doi: 10.1016/j.csite.2022.102338. 10.1016/j.csite.2022.102338Search in Google Scholar

[50] Sahin O, Ege N. Surface displacement field of a coated elastic half-space under the influence of a moving distributional load. Anadolu Universitesi Bilim Ve Teknoloji Dergisi-B Teorik Bilimler. 2017;5:77–90. 10.20290/aubtdb.282613Search in Google Scholar

[51] Dowaikh MA, Ogden RW. On surface waves and deformation in a pre-stressed incompressible elastic solid. IMA J Appl Math. 1990;44:261–84. 10.1093/imamat/44.3.261Search in Google Scholar

Received: 2022-08-11

Revised: 2022-09-27

Accepted: 2022-10-20

Published Online: 2022-11-08

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/phys-2022-0213

Keywords for this article

coated half-space; incompressible; pre-stress; surface waves

Creative Commons

BY 4.0