Home Extended warranty decision model of failure dependence wind turbine system based on cost-effectiveness analysis
Article Open Access

Extended warranty decision model of failure dependence wind turbine system based on cost-effectiveness analysis

  • Enzhi Dong , Zhonghua Cheng EMAIL logo , Rongcai Wang and Yuexing Zhang
Published/Copyright: July 12, 2022
Download Article (PDF)
Open Physics
From the journal Open Physics Volume 20 Issue 1

Abstract

The wind turbine system is the core equipment of wind power generation. Scientific formulation of an extended warranty (EW) scheme to optimize the cost-effectiveness ratio per unit time for a wind turbine system is one of the key concerns both for users and manufacturers. Based on the failure dependence analysis of the multi-component system, the EW cost model and availability model of the multi-component system are established. Based on the EW cost model and availability model, the cost-effectiveness ratio model per unit time is constructed. Through the case study, the optimal EW scheme of the wind turbine system is obtained via genetic algorithm, so as to minimize the cost-effectiveness ratio per unit time. The results of fitting prediction analysis and flexible decision analysis show that the model can excellently predict the minimum warranty cost and maximum availability of failure dependence wind turbine systems and can supply different EW schemes for users and manufacturers to choose from under a specific cost–effectiveness ratio. Through sensitivity analysis, reasonable suggestions for optimizing the EW scheme of the wind turbine system are proposed.

Keywords: failure dependence; wind turbine system; preventive maintenance; extended warranty; cost-efficiency ratio

1 Introduction

At present, a large number of modern technological equipment are used in various fields of industrial production. This equipment has a complex structure and high integration, and is a typical mechanical electrical and hydraulic integration system [1]. The failure dependence between components is more obvious, which increases the difficulty of equipment maintenance and daily management. A wind turbine system is typical modern technological equipment. With the continuous progress of productivity, people’s demand for electric energy is gradually increasing. Compared with traditional hydropower and thermal power generation, wind power generation has more advantages, which are clean, pollution-free, renewable, short capital construction cycle, and good environmental benefits. The wind turbine system is the core equipment of wind power generation.

The wind turbine system is composed of more than ten complex subsystems such as transmission system, pitch system, wind wheel system, braking system, and yaw system. Each subsystem is composed of many components, so its structure is very complex. In fact, the failure among the components of the wind turbine system is related. For example, the wear of the main shaft will aggravate the vibration of the gearbox and increase the failure rate of the gearbox. Therefore, the warranty decision model based on failure dependence is more in line with the engineering practice to a certain extent. During the basic warranty period, it is difficult for users to form independent support capability for this equipment, so it is very necessary to rely on manufacturers to carry out equipment extended warranty (EW). In the research of EW, it is one of the hotspots of current research to scientifically formulate EW schemes, reduce EW costs, and maintain availability.

EW means that after the basic warranty, the user and the manufacturer sign a warranty service contract, and the manufacturer carries out the follow-up service for a certain period of time. Generally, the user needs to pay a certain fee separately. For manufacturers, EW is an effective means to enhance product competitiveness and has become a new source of profit for manufacturers. For users, EW ensures that the product can be repaired in time in case of failure. In addition, EW is also a sign of product quality. Generally speaking, it is more common for manufacturers to provide EW services for products with good quality and high reliability.

In the existing research on EW decision-making, most of its decision-making objectives are the lowest cost of EW [2]. The reduction of EW costs can make manufacturers obtain more profits, which is beneficial to them [3]. Wang [4] established a warranty cost model based on customer utilization and product failure history to calculate the manufacturer’s expected warranty cost and expected profit, so as to determine the optimal warranty price. Tong et al. [5] studied the best maintenance degree during the EW period based on the dynamic utilization rate of consumers to reduce the EW cost; Su and Wang [6] introduced the preventive maintenance (PM) strategy on the basis of Tong et al. [5] and optimized the maintenance strategy with the goal of minimizing the cost of product EW.

Other studies consider the availability of warranty objects. For users, the improvement of the availability of warranty objects means the reduction of unexpected failure, which is the ideal state expected by users. Song et al. [7] formulated the equipment maintenance plan with the minimum maintenance cost per unit time in the replacement cycle as the goal and the availability as the constraint and verified the effectiveness of the model through an example analysis. On the premise of ensuring that the equipment availability meets the military requirements, Yang et al. [8] took the lowest equipment warranty cost as the goal to obtain the optimal PM scheme of equipment under partial outsourcing and complete outsourcing modes, respectively; Huang et al. [9] classified different users according to their usage during the initial warranty period, provided differentiated EW schemes for different types of users and improved consumer satisfaction and marketing competitiveness by maximizing the availability of products; ref. [10] takes the maximum availability of two-dimensional warranty products as the optimization objective and uses a numerical algorithm and particle swarm optimization algorithm to obtain the optimal PM interval, which provides a scientific basis for manufacturers to formulate two-dimensional warranty strategy. Authors of ref. [11] studied the system with competitive failure mode, comprehensively considered the availability and average long-term cost rate, and obtained the optimal periodic inspection and imperfect maintenance strategy of the system. The ratio of input cost to output benefit is known as the cost-effectiveness ratio. As a result, users and producers alike strive for a lower cost-effectiveness ratio. Reference may be found in the research of warranty decisions based on cost-effectiveness analysis [12,13,14,15].

Through literature review, it can be seen that although the current academic circles have carried out some research on EW cost optimization, availability optimization, and cost-effectiveness ratio optimization, most of the research objects are single-component systems, ignoring the failure dependence between multiple components. To some extent, it affects and restricts the formulation of EW strategy.

Failure dependence mainly refers to that in a multi-component system, the occurrence of a component failure will lead to a change in the overall environment of the system and then affect the state of other components, resulting in the increase of failure [16,17]. Sun et al. [18] introduced the concept of interactive failure, established a model for quantitative analysis of failure interaction between components, and gave an experimental derivation method of the failure correlation coefficient between components, which belongs to the earlier research on failure dependence. Zhang et al. [19] studied the periodic inspection strategy for a class of k-out-of-n systems with Class I failure dependence. The highly degraded or failed components are replaced. The short-term and long-term maintenance costs of the system are derived based on the Markov renewal process. Han [20] calculated the inherent reliability and comprehensive reliability of the subsystem respectively based on the failure dependence analysis and full probability formula of the wind turbine, further calculated the failure rate of the subsystem, and studied the optimal maintenance scheme of the wind turbine based on the failure rate of the subsystem. Qian and Jiang [21] studied the PM strategy of the multi-component system with one-way failure correlation based on the Class II failure dependence between multiple components and established the PM task grouping optimization model with the PM interval as the decision variable and the minimum maintenance cost within the specified operation time as the goal; Wang et al. [22] used the failure chain to describe the failure dependence between components, implemented the grouping maintenance strategy of the indefinite cycle for components with the goal of minimum maintenance time and cost, and optimized the maintenance plan by using genetic algorithm.

Based on the above analysis, this article mainly carries out EW research for failure dependence multi-component systems. Considering the failure dependence between components, aiming at minimizing the cost-effectiveness ratio per unit time, this article solves the optimal EW period and PM interval, which is acceptable to both manufacturers and users. It provides a quantitative basis for the formulation of the EW scheme of failure dependence multi-component system. The case study takes the wind turbine system as the research object and obtains the optimal EW decision-making scheme for the wind turbine system through the method established in this study.

The organizational structure of the rest of this article is as follows: Section 2 puts forward the model description and assumptions. In Section 3, the cost model and the availability model are constructed. The case analysis is carried out in Section 4, and Section 5 draws the conclusion of the article.

2 Model description and assumptions

2.1 Failure dependence analysis

Failure dependence can be divided into unidirectional failure dependence and bidirectional failure dependence. According to the failure chain model [23], if a component actively affects other components, the component is the failure starting point. If a component not only passively receives the effect of other components but also actively affects other components, it is called the failure midpoint. If a component only passively receives the effect of other components, it is called the failure ending point. This article mainly considers the case related to unidirectional failure dependence. The unidirectional failure dependence model is shown in Figure 1.

Figure 1 Unidirectional failure dependence model.
Figure 1

Unidirectional failure dependence model.

In Figure 1, A is the failure starting point, B and C are the failure midpoint, and D is the failure ending point. The actual failure rate of each component during operation is influenced by two factors in a multi-component system with failure dependence: intrinsic failure rate and related failure rate. The intrinsic failure rate of the component is defined by design and manufacture; the failure rate induced by the failure of other components in the system is referred to as the related failure rate [24]. The real failure rate of each component of a multi-component system with numerous components may be stated in the following matrix form [20] under the condition of failure dependence:

(1) h a ( t ) = h a 0 ( t ) + ∑ a b [ ω a b ( t ) ] [ h a b ( t ) ] ,

where h a ( t ) represents the actual failure rate of a single component, 1 ≤ a ≤ q and a ∈ N + ; h a 0 ( t ) represents the intrinsic failure rate of each component; [ h a b ( t ) ] is a p × 1 -dimensional matrix, 1 ≤ p ≤ q , b ∈ { b | b = 1 , 2 , 3 , … , q and b ≠ a } , and [ h a b ( t ) ] represents the related failure rate caused by component b to component a ; [ ω a b ( t ) ] is the 1 × p -dimensional non-negative real matrix, [ ω a b ( t ) ] represents the failure influence coefficient of component b on component a , 0 ≤ ω a b ( t ) ≤ 1 . When ω a b ( t ) value is 0, it indicates that there is no interaction between components, and when ω a b ( t ) value is 1, it indicates that component b failure leads to component a failure.

2.2 Model description

This article mainly studies the failure dependence of a two-component system, which can be regarded as a failure dependence multi-component system composed of the key component and the subsystem. The warranty strategy is that we implement the minimum maintenance after failure for the multi-component system in the basic warranty period, the imperfect PM for the system in the EW period, and the minimum maintenance for unexpected failure. The failure rate of the key component and the subsystem are expressed by h ψ ( t ) and h s ( t ) , respectively. The failure of the key component will increase the failure rate of the subsystem to a certain extent. Taking PM interval and EW period as decision variables, the cost model, availability model, and cost-effectiveness model of per unit time for equipment multi-component system in EW period are established respectively, and case analysis and optimization solution are carried out.

2.3 Model assumptions

For the convenience of research, the establishment of the model is mainly based on the assumption that

  1. The system only carries out the minimum maintenance after a failure during the basic warranty period. Imperfect PM shall be adopted during the EW period, and the minimum maintenance after failure shall be adopted within the interval of PM during the EW period.

  2. The system failure rate increases with time.

  3. The PM cost does not change with the change of PM time and times.

  4. The minimum maintenance cost is fixed.

  5. Minimum maintenance does not change the failure rate of components.

3 Model construction

3.1 Imperfect PM strategy

The effect of imperfect PM is between “good as new” and “bad as old” [25]. This article uses the virtual age method to describe the effect of imperfect PM; that is, each imperfect PM will reduce the actual age of the equipment for a period of time [26,27,28]. Let δ indicates the improvement factor of imperfect PM. Assuming that the kth imperfect PM is performed at time t, the failure rate of the equipment in the k-the PM interval can be expressed as:

(2) h ( t ) = h ( t − δ ( k − 1 ) T 0 ) .

T 0 is the interval of imperfect PM. Using the virtual age method, the change in equipment failure rate after each imperfect PM is shown in Figure 2.

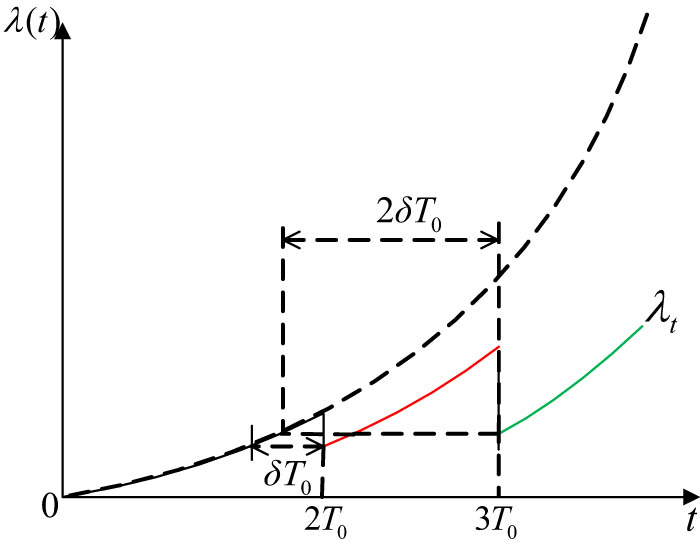
Figure 2 Schematic diagram of virtual age method.
Figure 2

Schematic diagram of virtual age method.

3.2 Minimum maintenance strategy

The minimum maintenance strategy is adopted for the failure of components within the basic warranty period and PM interval. The characteristic of the minimum maintenance is that the arrival of failure follows the Non-Homogeneous Poisson Process [29,30]. The expected number of failures of the system in a period of time is as follows:

(3) E [ N ( t ) ] = ∫ 0 t h ( s ) d s ,

where N ( t ) is the number of system failures in time [ 0 , t ] , and h ( s ) is the system failure rate.

3.3 Warranty cost model

The number of imperfect PM of the multi-component system during the EW period is as follows:

(4) m = int [ ( W E − W ) / ( T + T p ) ] ,

where “int” represents the downward rounding function, and T p represents the time required for an imperfect PM. W E represents the EW ending period, and W represents the basic warranty ending period.

Then the warranty cost EC ( T , W , W e ) of the multi-component system during the EW period can be expressed as:

(5) E C ( T , W , W E ) = m C p + ∑ k = 1 m E C f k ( T ) + E C f ( W + m ( T + T p ) , W E ) ,

where E C f ( W + m ( T + T p ) , W E ) represents the expected minimum maintenance cost in time [W + m(T + T p ), W E ], that is, the expected minimum maintenance cost in the last PM interval; E C f k ( T ) is the expected minimum maintenance cost in the kth PM interval.

The failure rate function of the key component in the kth PM interval can be expressed as:

(6) h k ψ ( t ) = h ψ ( t ) k = 1 h ψ [ t − δ ( W +( k − 1 ) T ] k = 2 , 3 , 4 , … , m .

The failure of the key component will increase the failure rate of subsystem to a certain extent. According to the failure dependence analysis in 1.1, it can be obtained that the failure rate function of subsystem in the kth PM interval is [31]:

(7) h k s ( t ) = h s ( t ) + ω 2 l k ψ h k ψ ( t ) k = 1 h s [ t − δ ( W +( k − 1 ) T ) ] + ω { ∑ i = 1 k [ l i ψ h ψ ( t − δ ( W +( i − 1 ) T ) ) ] − 1 2 l k ψ h k ψ ( t ) } k = 2 , 3 , 4 , … , m ,

where l k ψ represents the number of failures of the key component in the kth PM interval.

Therefore, it can be concluded that in the kth PM interval, the total expected cost of failure minimum maintenance of the multi-component system is as follows:

(8) E C f k ( T ) = ∫ W + ( k − 1 ) ( T + T p ) W + k T + ( k − 1 ) T p h k ψ ( t ) d t C f 1 + ∫ W + ( k − 1 ) ( T + T p ) W + k T + ( k − 1 ) T p h k s ( t ) d t C f 2 ,

where C f 1 represents the minimum maintenance cost of the key component and C f 2 represents the minimum maintenance cost of the subsystem.

Similarly, the minimum maintenance cost of the expected failure of the multi-component system in [ W + m ( T + T p ) , W E ] is:

(9) EC f ( W + m ( T + T p ) , W E ) = ∫ W + m ( T + T p ) W E h ( m + 1 ) ψ ( t ) d t C f 1 + ∫ W + m ( T + T p ) W E h ( m + 1 ) s ( t ) d t , C f 2 .

To sum up, the total expected warranty cost of the multi-component system within the EW period is:

(10) EC ( T , W , W E ) = m C p + C f 1 ∑ k = 1 m ∫ W + ( k − 1 ) ( T + T p ) W + k T + ( k − 1 ) T p h k ψ ( t ) d t + ∫ W + m ( T + T p ) W e h ( m + 1 ) ψ ( t ) d t ] + C f 2 ∑ k = 1 m ∫ W + ( k − 1 ) ( T + T p ) W + k T + ( k − 1 ) T p h k s ( t ) d t + ∫ W + m ( T + T p ) W E h ( m + 1 ) s ( t ) d t .

3.4 Multi-component system availability model

If the expected total downtime ED ( T , W , W E ) during ( W , W E ) can be obtained, the availability of the multi-component system during the EW period can be calculated by the following formula [32]:

(11) EA ( T , W , W E ) = ( W E − W ) − E D ( T , W , W E ) W E − W ,

ED ( T , W , W E ) can be expressed in a similar way to EC ( T , W , W E ) , as long as C p , C f 1 , and C f 2 in formula (10) are replaced with T p , T f 1 , and T f 2 , respectively.

(12) ED ( T , W , W E ) = m T p + T f 1 ∑ k = 1 m ∫ W + ( k − 1 ) ( T + T p ) W + k T + ( k − 1 ) T p h k ψ ( t ) d t + ∫ W + m ( T + T p ) W E h ( m + 1 ) ψ ( t ) d t + T f 2 ∑ k = 1 m ∫ W + ( k − 1 ) ( T + T p ) W + k T + ( k − 1 ) T p h k s ( t ) d t + ∫ W + m ( T + T p ) W E h ( m + 1 ) s ( t ) d t .

According to the above model, the maximum availability of the system in the EW period can be obtained by solving the PM interval under different EW periods.

3.5 Cost-effectiveness ratio model of per unit time

The EW cost and availability of the multi-component systems are a pair of mutually restrictive contradictions. For manufacturers, the lower the EW cost of the multi-component system, the better. However, the availability of the multi-component system cannot be guaranteed to be the highest; for users, the higher the availability of the multi-component system, the better. At this time, the warranty cost of the multi-component system cannot be guaranteed to be the lowest. From this point, it is one-sided to only emphasize the warranty cost or system availability. It is a more scientific and acceptable way for manufacturers and users to ensure the availability on the basis of controlling the warranty cost. The cost-effectiveness ratio function V per unit time is adopted to comprehensively weigh the warranty cost and availability.

Cost-effectiveness ratio per unit time refers to the ratio of warranty cost per unit time to availability within the EW period. The cost-effectiveness ratio per unit time considers both warranty cost and system availability quantitatively, which can be used as an important basis for warranty decision-making. The cost-effectiveness ratio function of per unit time can be expressed as [32]:

(13) V = E C ( T , W , W E ) W E − W 1 E A ( T , W , W E ) .

4 Case analysis

4.1 Problem description

There is unidirectional failure dependence between the main shaft and gearbox of the wind turbine system. The main shaft can be regarded as the key component, and the gearbox can be regarded as the subsystem. When the wear of the main shaft exceeds the failure threshold, it will aggravate the vibration of the gearbox and increase the failure rate of the gearbox. Through the investigation, during the basic warranty period, the user cannot fully form the independent maintenance ability for the main shaft and gearbox. It is necessary to introduce the maintenance force of the manufacturer to carry out technical services during the EW period. Since the failure rate of the main shaft and gearbox during the basic warranty period is low, only the minimum maintenance after failure is considered. During the EW period, the main shaft and gearbox have been in service for a period of time, and the failure rate has increased significantly. Besides the minimum maintenance after failure, it is very necessary to carry out imperfect PM. It is assumed that the main shaft failure follows the following two-parameter Weibull distribution:

(14) λ ψ ( t ) = α β t β α − 1 ,

where the shape parameter α = 3 and the scale parameter W = 2 years. It is known that the basic warranty period of the equipment W is 2 years, the failure rate of the gearbox λ s is 6 × 10 − 4 /day, the minimum maintenance time of the main shaft T f 1 is 4 days, and the cost is 900 CNY. The minimum maintenance time of gearbox T f 2 = 6 days , the cost is 1,300 CNY. The PM time T p = 3 days, the cost is 600 CNY, and the improvement factor of imperfect PM within the EW period δ = 0.8 . According to the maintenance experience and data analysis, the failure of the main shaft will increase the failure rate of the gearbox, and the failure influence coefficient ω = 0.5 . By minimizing the cost-effectiveness ratio per unit time for the wind turbine system, the optimal EW period and PM interval of the wind turbine system are obtained, and then, an EW scheme of the wind turbine system acceptable to both manufacturers and users is formed.

4.2 Numerical algorithm

According to the investigation, the EW period of the wind turbine system generally does not exceed 10 years. Therefore, the value range of the EW period W E is set as [3 years, 10 years], and the value range of the PM interval is [0.1 years, 3 years]. The value steps of PM interval and EW period are 0.1 years. The numerical algorithm is used to calculate the EW cost, availability, and cost-effectiveness ratio per unit time for the multi-component system corresponding to any combination of W E and T . The algorithm flowchart is shown in Figure 3.

Figure 3 Flowchart of numerical algorithm.
Figure 3

Flowchart of numerical algorithm.

Using the stored combination of W E and T and the EW cost, availability, and cost-effectiveness ratio per unit time for the multi-component system corresponding to the combination of W E and T , the change trend diagram of EW cost, availability, and cost-effectiveness ratio per unit time for the multi-component system can be drawn.

In order to study the variation law of EW cost, availability, and cost-effectiveness ratio per unit time for the wind turbine system with EW period W E and PM interval T , and to analyze the three-dimensional graphics intuitively, we make dimension-reduced analysis of the three-dimensional graphics here.

Figure 4a–c respectively shows the corresponding changes in EW cost, availability, and cost-effectiveness ratio per unit time with the EW period under the determined imperfect PM interval; Figure 4d–f respectively represent the corresponding changes of EW cost, availability, and cost-effectiveness ratio per unit time with the imperfect PM interval when the warranty period is a certain value. It can be seen intuitively from Figure 5 that when the imperfect PM is a certain value, with the extension of the EW period, the corresponding EW cost will increase, the availability will decrease, and the cost-effectiveness ratio per unit time will increase. When the EW period is a certain value and the imperfect PM interval changes, there are optimal values for the EW cost, availability, and cost-effectiveness ratio per unit time.

Figure 4 Dimension reduction analysis. (a) Schematic diagram of EC changing with We; (b) Schematic diagram of EA changing with We; (c) Schematic diagram of V changing with We; (d) Schematic diagram of EC changing with T; (e) Schematic diagram of EA changing with T; (f) Schematic diagram of V changing with T.
Figure 4

Dimension reduction analysis. (a) Schematic diagram of EC changing with We; (b) Schematic diagram of EA changing with We; (c) Schematic diagram of V changing with We; (d) Schematic diagram of EC changing with T; (e) Schematic diagram of EA changing with T; (f) Schematic diagram of V changing with T.

Figure 5 Change trend of cost-effectiveness ratio per unit time.
Figure 5

Change trend of cost-effectiveness ratio per unit time.

4.3 Genetic algorithm

Genetic algorithm is an adaptive global optimization probability search algorithm formed by simulating the genetic and evolution process of organisms in the natural environment. Its principle is that organisms maintain excellent genes and promote population evolution through selection, heredity, and mutation. Genetic algorithm has the outstanding advantages of population parallel search function and not easy to fall into local convergence. The algorithm flow is as follows:

Step 1 Coding, designing the objective function, and determining the fitness function. Designing the convergence condition or iteration times, setting the GA parameters, and establishing the initial population.

Step 2 Calculating the fitness function to judge whether the convergence conditions or the number of iterations are met. If yes, the optimal individual is output as the result, otherwise enter step 3.

Step 3 Completing the replication of new species.

Step 4 Completing the mating of new species.

Step 5 New species, gene mutation within the group, return to step 2.

In this example, the specific parameter settings of the genetic algorithm are shown in Table 1.

Table 1

Parameter setting

Parameters Value
Population size 50
Elite count 3
Crossover fraction 0.8
Stopping criteria 200

Figure 6 shows the iterative process of genetic algorithm. When taking the lowest EW cost as the decision goal, that is, Eq. (10) as the fitness function, the optimal EW period is 1,081 days and the optimal PM interval is 180 days. The EW cost is 1097.6 CNY, and the availability is 0.9869; When taking the highest availability as the decision goal, that is, when Eq. (11) is the fitness function, the optimal EW period is 1,241 days and the optimal PM interval is 259 days. At this time, the EW cost is 1653.2 CNY and the availability is 0.988; When the EW cost and availability are comprehensively considered and the cost-effectiveness ratio per unit time is the minimum, the optimal EW period is 1,224 days, and the optimal PM interval is 250 days. At this time, the EW cost is 1446.6 CNY, and the availability is 0.987.

Because this article takes the lowest cost-effectiveness ratio per unit time as the goal, the optimal EW scheme is 1,224 days of EW period and 250 days of PM interval.

Figure 6 Schematic diagram of genetic algorithm iteration. (a) Aim at the lowest warranty cost; (b) Aim at the highest availability; (c) Aiming at the lowest cost-effectiveness ratio.
Figure 6

Schematic diagram of genetic algorithm iteration. (a) Aim at the lowest warranty cost; (b) Aim at the highest availability; (c) Aiming at the lowest cost-effectiveness ratio.

4.4 Result analysis

4.4.1 Scheme comparison and analysis

Based on the above analysis, the EW period is considered to be 1,224 days. When the wind turbine system does not carry out imperfect PM during the EW period, that is, set the PM interval to the same 1,224 days, the corresponding EW cost, availability and cost-effectiveness ratio per unit time can be obtained as follows:

W E = T = 1 , 224 days, EC = 2176.4 CNY, EA = 0.94 , V = 4.6 .

When the imperfect PM strategy is considered to be adopted in the EW period, the warranty cost, system availability, and cost-effectiveness ratio per unit time within the EW period are as follows:

W E = 1 , 224 days , T = 252 days, EC = 1446.6 CNY, EA = 0.987 , V = 2.9034 .

As shown in Figure 7, after adopting the imperfect PM strategy, the EW cost is reduced by 34%, the availability is increased by 5.2%, and the cost-effectiveness ratio per unit time is reduced by 37%. It can be seen that the imperfect PM strategy is a win–win strategy for the manufacturer and users.

(2) This article considers the failure dependence between the main shaft and gearbox. If the failure dependence between components is ignored, assuming that the failure between components is independent, the optimal PM interval can be obtained on the basis of 1,224 days of EW period, and the corresponding data of EW cost, system availability, and cost-effectiveness ratio per unit time can be obtained as follows:

W E = 1 , 224 days , T = 324 days , EC = 1092.4 CNY, EA = 0.99 , V = 2.19 .

Figure 7 Comparison between with and without PM.
Figure 7

Comparison between with and without PM.

As shown in Figure 8, by comparing the data considering the failure dependence between components, it is found that assuming that the failure between components is independent, the calculated EW cost is lower, the system availability is higher and the cost-effectiveness ratio is smaller. Although the data seems better than when considering the failure dependence between components, the assumption of independent failure is unrealistic, so the calculated results are inconsistent with the actual situation. This also proves that ignoring failure dependence will lead to unacceptable analysis errors, which will reduce the manufacturer’s cost expectation and improve the user’s expectation of system availability. In the actual warranty practice, the EW scheme and transaction contract based on the failure independence assumption will increase the manufacturer’s cost risk, and the system will have more failures in the use stage, reducing the user’s favor for the equipment and then reducing the user’s loyalty to the equipment.

Figure 8 Comparison between considering and not considering failure dependence.
Figure 8

Comparison between considering and not considering failure dependence.

Figure 9 Change trend of system EW cost.
Figure 9

Change trend of system EW cost.

4.4.2 Regression fitting analysis

Based on the above calculation results, combined with Figures 5, 9, and 10, the maximum availability of the wind turbine system and corresponding optimal PM interval under different EW periods can be solved, as well as the cost-effectiveness ratio per unit time under this scheme, as shown in Table 2.

Table 2

Optimal EW scheme under different EW periods

Scheme W E /Days T*/Days EC (CNY) EA V
1 1,080 180 1094.2 0.9879 3.0767
2 1,152 216 1260.9 0.9884 2.9531
3 1,224 252 1446.6 0.9886 2.9034
4 1,296 288 1653.2 0.9886 2.9033
5 1,368 324 1882.8 0.9884 2.9395
6 1,440 360 2137.4 0.9882 3.0041
7 1,512 396 2419.3 0.9878 3.0924
8 1,584 432 2730.9 0.9874 3.2013
9 1,656 468 3074.8 0.9869 3.3287
10 1,728 504 3453.2 0.9863 3.4735
11 1,800 360 3807.4 0.9858 3.5761
12 1,872 396 4258.1 0.9851 3.7520
13 1,944 432 4763.8 0.9843 3.9540
14 2,016 432 5059.2 0.9843 3.9661
15 2,088 468 5653.5 0.9833 4.2028
16 2,160 360 6048.2 0.9830 4.2727
17 2,232 504 6688.8 0.9821 4.5044
18 2,304 396 7150.7 0.9817 4.5984
19 2,376 432 8068.6 0.9802 4.9705
20 2,448 432 8449.6 0.9801 4.9889
21 2,520 360 9087.4 0.9795 5.1543
22 2,592 468 9969.4 0.9783 5.4434
23 2,664 324 10597.6 0.9778 5.5751
24 2,736 288 11480.3 0.9768 5.8297
25 2,808 360 12746.9 0.9751 6.2608
26 2,880 360 13183.3 0.9751 6.2592
27 2,952 324 14406.9 0.9737 6.6294
28 3,024 288 15181.1 0.9731 6.7711
29 3,096 396 16374.7 0.9718 7.0916
30 3,168 360 18093.2 0.9697 7.6216
31 3,240 360 18625.2 0.9697 7.6215
32 3,312 288 19785.5 0.9688 7.8794
33 3,384 252 22520.5 0.9659 8.7567
34 3,456 252 23019.3 0.9655 8.7137
35 3,528 216 24306.8 0.9646 8.9742
36 3,600 288 25458.6 0.9637 9.1723

*Optimal preventive maintenance interval under different extended warranty periods.

In Table 2, T* stands for the optimal PM interval, EC stands for the EW cost of the wind turbine system, EA represents the availability of the wind turbine system, and V represents the cost-effectiveness ratio per unit time under the EW scheme. Table 2 shows that with the growing of W E , the EW cost increases and the availability decreases. There is an obvious positive correlation between W E and EC, while there is an obvious negative correlation between W E and EA. Based on the data in Table 2, the relationship between W E , EC, and EA is analyzed by regression analysis. MATLAB data fitting toolbox is used to fit the EW period and EW cost data. The fitting method is polynomial, and the maximum power is 2. The regression function can be expressed as follows:

E C = 0.003758 W E 2 − 8.118 W E + 5 , 987 .

As shown in Figure 11, the correlation coefficient between W E and EC is 0.9976, and the fitting effect of the model is good. The same method is used to fit the EW period and system availability data. At this time, the regression function can be expressed as follows:

E A = − 3.295 exp ( − 9 ) W E 2 + 5.147 exp ( − 6 ) W E + 0.987 .

As shown in Figure 12, the correlation coefficient between W E and EA is 0.9942, and the fitting effect of the model is good. In practical application, the optimal warranty cost and system availability under different warranty periods can be estimated, which provides a scientific basis for formulating the warranty strategy of the wind turbine system.

4.4.3 Flexible decision analysis

It can be found from Figure 10 that the cost-effectiveness ratio per unit time may be the same under different combinations of EW period and PM interval. Based on this, the equal cost-effectiveness ratio per unit time curve under different combinations of EW period and PM interval is drawn, as shown in Figure 13.

Figure 10 Change trend of system availability.
Figure 10

Change trend of system availability.

Figure 11 Fitting curve of W E and EC.
Figure 11

Fitting curve of W E and EC.

Figure 12 Fitting curve of W E and EA.
Figure 12

Fitting curve of W E and EA.

Figure 13 The equal cost-effectiveness ratio per unit time curve.
Figure 13

The equal cost-effectiveness ratio per unit time curve.

According to the equal cost-effectiveness ratio per unit time curve, a more flexible warranty period and PM interval scheme can be provided for both manufacturers and users to choose from on the premise that the cost-effectiveness ratio of per unit time of the system does not increase. For example, when V = 5.8417, different combinations of W E and T can be obtained from the corresponding equal cost-effectiveness ratio per unit time curve. Under these combinations, the cost-effectiveness ratio per unit time is 5.8417. The user and the manufacturer can choose any scheme according to the actual situation to meet the needs of both parties.

4.5 Sensitivity analysis

In the model established in this article, failure dependence coefficient ω and imperfect PM improvement factor δ will have a certain impact on the cost-effectiveness ratio per unit time. In order to test the impact of failure dependence coefficient ω and imperfect PM improvement factor δ on cost-effectiveness ratio per unit time, sensitivity analysis is carried out for ω and δ respectively, and the change trend of cost-effectiveness ratio per unit time for the wind turbine system is observed when the two parameters change.

4.5.1 Sensitivity analysis of failure dependence coefficient ω

The failure dependence coefficient ω indicates the failure dependence degree between two components. The larger the ω is, the stronger the failure dependence between the two components is. On the contrary, the failure dependence between the two components is weaker. In order to further verify the impact of failure dependence coefficient on the cost-effectiveness ratio per unit time of the system, based on the fixed PM interval T and EW period W E , the cost-effectiveness ratio per unit time corresponding to different values of ω is calculated, and the T–V curve and the W E –V curve are drawn, respectively.

Figure 14(a) and (b) shows the variation trend of system cost-effectiveness ratio per unit time with failure dependence coefficient when W E is 2,340 days and T is 576 days, respectively. It can be seen from the image that the cost-effectiveness ratio per unit time for the system increases with the increase in the failure dependence coefficient. The failure dependence coefficient is generally determined in the design stage of the system. Therefore, in the design stage, manufacturers should focus on the failure dependence between components and strive to reduce the failure dependence coefficient. Only in this way can the cost-effectiveness ratio per unit time for the system be reduced during the warranty period.

Figure 14 Sensitivity analysis of ω. (a) Sensitivity analysis of ω when We is fixed; (b) Sensitivity analysis of ω when T is fixed.
Figure 14

Sensitivity analysis of ω. (a) Sensitivity analysis of ω when We is fixed; (b) Sensitivity analysis of ω when T is fixed.

4.5.2 Sensitivity analysis of improvement factor δ

Imperfect PM improvement factor δ indicates the degree of imperfect PM. The larger the δ is, the better the effect of imperfect PM on reducing the system failure rate is. On the contrary, the effect of imperfect PM on reducing the system failure rate is worse. In order to further verify the impact of imperfect PM improvement factors on the cost-effectiveness ratio per unit time for the system, on the basis of fixed PM interval T and EW period W E , the cost-effectiveness ratio per unit time corresponding to different values of δ is calculated, and the T–V curve and the W E –V curve are drawn, respectively

Figure 15(a) and (b) shows the variation trend of the system cost-effectiveness ratio per unit time with the imperfect PM improvement factor δ when W E is 1,260 days and T is 576 days, respectively. It can be seen from the image that the cost-effectiveness ratio per unit time of the system decreases with the increase in the imperfect PM improvement factor δ. The imperfect PM improvement factor δ generally reflects the maintenance level of the manufacturer. The manufacturer could pursue a higher imperfect PM improvement factor δ by improving the quality of maintenance workers, improving maintenance technology, and strengthening technological innovation, so as to reduce the cost-effectiveness ratio per unit time for the system.

Figure 15 Sensitivity analysis of δ. (a) Sensitivity analysis of δ when We is fixed; (b) Sensitivity analysis of δ when T is fixed.
Figure 15

Sensitivity analysis of δ. (a) Sensitivity analysis of δ when We is fixed; (b) Sensitivity analysis of δ when T is fixed.

5 Conclusion

Considering the failure dependence between components, the imperfect PM and minimum maintenance strategy are used to obtain the optimal EW scheme of the wind turbine system in this article. Through the result analysis, the following conclusions can be drawn:

  1. The optimal EW scheme of the system can be obtained accurately and effectively by using the genetic algorithm.

  2. The PM is necessary. The EW cost is reduced by 34%, the availability is increased by 5.2%, and the cost-effectiveness ratio per unit time is reduced by 37% with PM.

  3. Ignoring failure dependence will lead to unacceptable analysis errors.

  4. The model established in this article can provide a quantitative analysis method for EW decision-making of failure dependence wind turbine system.

    In the future, there are many interesting research directions on this topic:

  5. More complex failure dependence relationships among system components can be considered, such as common cause failure, interactive failure, and reserve redundancy, and the corresponding EW decision model can be established.

  6. It can also study the formulation of EW scheme for failure dependence multi-component system under two-dimensional warranty strategy.

  7. Through the field data of the wind turbine system, the failure distribution of the system is determined by regression fitting, and the failure rate function and parameters of the system are obtained, and then, the warranty period model and PM interval model of the system are determined.

tel: +86-18733131820

Acknowledgments

The authors thank the reviewers for their valuable comments, which greatly helped to improve the quality of this article.

  1. Funding information: This research was funded by the National Natural Science Foundation of China (no. 71871219).

  2. Author contributions: Conceptualization: Zhonghua Cheng; methodology: Zhonghua Cheng; writing-original draft preparation: Enzhi Dong; writing-review and editing: Zhonghua Cheng, Rongcai Wang, Yuexing Zhang; supervision: Liqing Rong; all authors have accepted responsibility for the entire content of this manuscript and approved its submission.

  3. Conflict of interest: The authors state no conflict of interest.

  4. Data availability statement: All data generated or analysed during this study are included in this published article.

Appendix

The derivation process of formula (1)

Assuming that the multi-component system contains Z components, h a 0 ( t ) represents the independent failure rate of component a, h a ( t ) represents the actual failure rate of components, and h a b ( t ) B represents the relevant failure rate of all components that affect component a. Therefore, the actual failure rate function of each component is as follows:

h 1 ( t ) = κ 1 [ h 10 ( t ) , h 1 b ( t ) B , t ] h 2 ( t ) = κ 2 [ h 20 ( t ) , h 2 b ( t ) B , t ] ⋮ h a ( t ) = κ a [ h a 0 ( t ) , h a b ( t ) B , t ] ⋮ h Z ( t ) = κ Z [ h Z 0 ( t ) , h Z b ( t ) B , t ] .

By expanding the function of the above formula through the Taylor series expansion theorem, the analytical formula of the actual failure rate function of component a can be obtained.

h a ( t ) = κ a [ h a 0 ( t ) , h a b ( t ) B , t ] = κ a ∣ h a b ( t ) B → = 0 + ∑ a b ∂ κ a ∂ h a b h a b ( t ) B → = 0 h a b ( t ) B + ∑ a b , a c ∂ 2 κ a 2 ∂ h a b h a c h a b ( t ) B → = 0 h a b ( t ) B h a c ( t ) B + ∑ a b ∂ 2 κ a ∂ h a b 2 h a b ( t ) B → = 0 h a b 2 ( t ) B + … .

Merging h a b ( t ) B with similar items to obtain:

h a ( t ) = κ a ∣ h a b ( t ) B → = 0 + ∑ a b ∂ κ a ∂ h a b h a b ( t ) B → = 0 + ∑ a c ∂ 2 κ a 2 ∂ h a b h a c h a b ( t ) B → = 0 h a c ( t ) B + ∂ 2 κ a ∂ h a b 2 h a b ( t ) B → = 0 h a b ( t ) B + … × h a b ( t ) B .

Let h a b ( t ) B = 0 , indicating that component a is not affected by other components, so κ a ∣ h a b ( t ) B → = h a 0 ( t ) .

Let:

ω a b ( t ) = ∂ κ a ∂ h a b ∣ h a b ( t ) B → = 0 + ∑ a c ∂ 2 κ a 2 ∂ h a b h a c ∣ h a b ( t ) B → = 0 h a c ( t ) B + ∂ 2 κ a ∂ h a b 2 ∣ h a b ( t ) B → = 0 h a b ( t ) B + … .

Then:

h a ( t ) = h a 0 ( t ) + ∑ a b [ ω a b ( t ) ] [ h a b ( t ) ] .

References

[1] Gao WK, Zhang ZS, Liu Y, Chen X. Reliability modeling and dynamic replacement strategy of fault related two component parallel system. Computer Integr Manuf Syst. 2015;21(2):510–8.Search in Google Scholar

[2] Afsahi M, Kashan AH, Ostadi B. A hybrid approach for joint optimization of base and extended warranty decisions considering out-of-warranty products. Appl Math Model. 2021;95:176–99.10.1016/j.apm.2021.01.051Search in Google Scholar

[3] Wang D, He Z, He S, Zhang Z, Zhang Y. Dynamic pricing of two-dimensional extended warranty considering the impacts of product price fluctuations and repair learning. Reliab Eng Syst Safe. 2021;210:107516.10.1016/j.ress.2021.107516Search in Google Scholar

[4] Wang X, Ye ZS. Design of customized two-dimensional extended warranties considering use rate and heterogeneity. IISE Trans. 2020;53(3):341–51.10.1080/24725854.2020.1768455Search in Google Scholar

[5] Tong P, Song X, Zixian L. A maintenance strategy for two-dimensional extended warranty based on dynamic usage rate. Int J Prod Res. 2017;55(19):5743–59.10.1080/00207543.2017.1330573Search in Google Scholar

[6] Su C, Wang X. A two-stage preventive maintenance optimization model incorporating two-dimensional extended warranty. Reliab Eng Syst Safe. 2016;155:169–78.10.1016/j.ress.2016.07.004Search in Google Scholar

[7] Song ZJ, Yang ZX, Zhao YZ, Hou GB. VIP Maintenance decision model under availability and dynamic maintenance cost. Ind Eng. 2014;17(2):17–22.Search in Google Scholar

[8] Yang ZY, Cheng ZH, Deng LJ. Equipment extended warranty purchase decision based on cost-effectiveness analysis. Fire CommControl. 2016;41(2):18–22 + 27.Search in Google Scholar

[9] Huang YS, Huang CD, Ho JW. A customized two-dimensional extended warranty with preventive maintenance. Eur J Oper Res. 2017;257(3):971–8.10.1016/j.ejor.2016.07.034Search in Google Scholar

[10] Wang R, Cheng Z, Rong L, Bai Y, Wang Q. Availability optimization of two-dimensional warranty products under imperfect preventive maintenance. IEEE Access. 2021;9:8099–109.10.1109/ACCESS.2021.3049441Search in Google Scholar

[11] Qiu Q, Liu B, Lin C, Wang J. Availability analysis and maintenance optimization for multiple failure mode systems considering imperfect repair. P I Mech Eng O-J Ris. 2021;235:982–97.10.1177/1748006X211012792Search in Google Scholar

[12] Lam Y, Lam PKW. An extended warranty policy with options open to consumers. Eur J Oper Res. 2001;131(3):514–29.10.1016/S0377-2217(00)00091-6Search in Google Scholar

[13] Jack N, Murthy DNP. A flexible extended warranty and related optimal strategies. J Oper Res Soc. 2007;58(12):1612–20.10.1057/palgrave.jors.2602326Search in Google Scholar

[14] Hu DC, Ouyang ZH, Chen QH, Fan HJ. Optimization method of special vehicle maintenance strategy based on reliability and cost-effectiveness ratio. Ordnance Ind Autom. 2021;40(7):72–7 + 83.Search in Google Scholar

[15] Zhu DX, Shi XM, Ding SH, Situ CY. Task differentiation of military civilian integrated equipment maintenance support based on cost-effectiveness ratio. CommControl Simul. 2018;40(3):41–5.Search in Google Scholar

[16] Peng W, Zhang X, Huang HZ. A failure rate interaction model for two-component systems based on copula function. P I Mech Eng O-J Ris. 2016;230(3):278–84.10.1177/1748006X16629855Search in Google Scholar

[17] Sun Y. Reliability prediction of complex repairable systems: an engineering approach. Queensland, Australia: Queensland University of Technology; 2006.Search in Google Scholar

[18] Sun Y, Ma L, Mathew J, Zhang S. An analytical model for interactive failures. Reliab Eng Syst Safe. 2006;91(5):495–504.10.1016/j.ress.2005.03.014Search in Google Scholar

[19] Zhang N, Fouladirad M, Barros A, Zhang J. Condition-based maintenance for a K-out-of-N deteriorating system under periodic inspection with failure dependence. Eur J Oper Res. 2020;287(1):159–67.10.1016/j.ejor.2020.04.041Search in Google Scholar

[20] Han S. Research on condition based opportunistic maintenance strategy of doubly fed wind turbine considering fault correlation. Lanzhou, China: Lanzhou Jiaotong University; 2017.Search in Google Scholar

[21] Qian Q, Jiang Z. Maintenance strategy of multi-component system considering preventive maintenance time and correlation. Ind Worker Cheng. 2020;23(6):95–100.Search in Google Scholar

[22] Wang H, Du WX, Liu ZL, Yang XY, Li ZX. Multi component system maintenance of EMU based on joint fault and economic correlation. J Shanghai Jiaotong Univ. 2016;50(5):660–7.Search in Google Scholar

[23] Gao P, Xie L, Pan J. Reliability and Availability Models of Belt Drive Systems Considering Failure Dependence. Chin J Mech Eng-En. 2019;32(1):1–12.10.1186/s10033-019-0342-xSearch in Google Scholar

[24] Yang GJ, Wang H, He Y, Xiong L, Wang HY. Dynamic group maintenance strategy of EMU system under fault and economic correlation. Railw Sect J Sci Eng. 2021;18(1):31–7.Search in Google Scholar

[25] Tong P, Liu Z, Men F, Cao L. Designing and pricing of two-dimensional extended warranty contracts based on usage rate. Int J Prod Res. 2014;52(21):6362–80.10.1080/00207543.2014.940073Search in Google Scholar

[26] Zhao X, Xie M. Using accelerated life tests data to predict warranty cost under imperfect repair. Comput Ind Eng. 2017;107:223–34.10.1016/j.cie.2017.03.021Search in Google Scholar

[27] Pham H, Wang H. Imperfect maintenance. Eur J Oper Res. 1996;94(3):425–38.10.1016/S0377-2217(96)00099-9Search in Google Scholar

[28] Wu S, Zuo MJ. Linear and Nonlinear Preventive Maintenance Models. IEEE T Reliab. 2010;59(1):242–9.10.1109/TR.2010.2041972Search in Google Scholar

[29] Wang Y, Liu Z, Liu Y. Optimal preventive maintenance strategy for repairable items under two-dimensional warranty. Reliab Eng Syst Safe. 2015;142:326–33.10.1016/j.ress.2015.06.003Search in Google Scholar

[30] Wang L. Research on warranty period of high-tech equipment under preventive warranty strategy. Master’s thesis. Shijiazhuang, China: Ordnance Engineering College. 2010.Search in Google Scholar

[31] He Z, Wang D, He S, Zhang Y, Dai A. Two-dimensional extended warranty strategy including maintenance level and purchase time: A win-win perspective. Comput Ind Eng. 2020;141:106294.10.1016/j.cie.2020.106294Search in Google Scholar

[32] Zhao X, Zhao XN, Quan XY, Xie XY, Liu Y. Calculation method of cost-effectiveness ratio of campaign tactical weapons. J Ordnance Eng. 2020;41(S2):257–64.Search in Google Scholar
Received: 2022-02-22
Revised: 2022-05-07
Accepted: 2022-05-27
Published Online: 2022-07-12

© 2022 Enzhi Dong et al., published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Regular Articles
  2. Test influence of screen thickness on double-N six-light-screen sky screen target
  3. Analysis on the speed properties of the shock wave in light curtain
  4. Abundant accurate analytical and semi-analytical solutions of the positive Gardner–Kadomtsev–Petviashvili equation
  5. Measured distribution of cloud chamber tracks from radioactive decay: A new empirical approach to investigating the quantum measurement problem
  6. Nuclear radiation detection based on the convolutional neural network under public surveillance scenarios
  7. Effect of process parameters on density and mechanical behaviour of a selective laser melted 17-4PH stainless steel alloy
  8. Performance evaluation of self-mixing interferometer with the ceramic type piezoelectric accelerometers
  9. Effect of geometry error on the non-Newtonian flow in the ceramic microchannel molded by SLA
  10. Numerical investigation of ozone decomposition by self-excited oscillation cavitation jet
  11. Modeling electrostatic potential in FDSOI MOSFETS: An approach based on homotopy perturbations
  12. Modeling analysis of microenvironment of 3D cell mechanics based on machine vision
  13. Numerical solution for two-dimensional partial differential equations using SM’s method
  14. Multiple velocity composition in the standard synchronization
  15. Electroosmotic flow for Eyring fluid with Navier slip boundary condition under high zeta potential in a parallel microchannel
  16. Soliton solutions of Calogero–Degasperis–Fokas dynamical equation via modified mathematical methods
  17. Performance evaluation of a high-performance offshore cementing wastes accelerating agent
  18. Sapphire irradiation by phosphorus as an approach to improve its optical properties
  19. A physical model for calculating cementing quality based on the XGboost algorithm
  20. Experimental investigation and numerical analysis of stress concentration distribution at the typical slots for stiffeners
  21. An analytical model for solute transport from blood to tissue
  22. Finite-size effects in one-dimensional Bose–Einstein condensation of photons
  23. Drying kinetics of Pleurotus eryngii slices during hot air drying
  24. Computer-aided measurement technology for Cu2ZnSnS4 thin-film solar cell characteristics
  25. QCD phase diagram in a finite volume in the PNJL model
  26. Study on abundant analytical solutions of the new coupled Konno–Oono equation in the magnetic field
  27. Experimental analysis of a laser beam propagating in angular turbulence
  28. Numerical investigation of heat transfer in the nanofluids under the impact of length and radius of carbon nanotubes
  29. Multiple rogue wave solutions of a generalized (3+1)-dimensional variable-coefficient Kadomtsev--Petviashvili equation
  30. Optical properties and thermal stability of the H+-implanted Dy3+/Tm3+-codoped GeS2–Ga2S3–PbI2 chalcohalide glass waveguide
  31. Nonlinear dynamics for different nonautonomous wave structure solutions
  32. Numerical analysis of bioconvection-MHD flow of Williamson nanofluid with gyrotactic microbes and thermal radiation: New iterative method
  33. Modeling extreme value data with an upside down bathtub-shaped failure rate model
  34. Abundant optical soliton structures to the Fokas system arising in monomode optical fibers
  35. Analysis of the partially ionized kerosene oil-based ternary nanofluid flow over a convectively heated rotating surface
  36. Multiple-scale analysis of the parametric-driven sine-Gordon equation with phase shifts
  37. Magnetofluid unsteady electroosmotic flow of Jeffrey fluid at high zeta potential in parallel microchannels
  38. Effect of plasma-activated water on microbial quality and physicochemical properties of fresh beef
  39. The finite element modeling of the impacting process of hard particles on pump components
  40. Analysis of respiratory mechanics models with different kernels
  41. Extended warranty decision model of failure dependence wind turbine system based on cost-effectiveness analysis
  42. Breather wave and double-periodic soliton solutions for a (2+1)-dimensional generalized Hirota–Satsuma–Ito equation
  43. First-principle calculation of electronic structure and optical properties of (P, Ga, P–Ga) doped graphene
  44. Numerical simulation of nanofluid flow between two parallel disks using 3-stage Lobatto III-A formula
  45. Optimization method for detection a flying bullet
  46. Angle error control model of laser profilometer contact measurement
  47. Numerical study on flue gas–liquid flow with side-entering mixing
  48. Travelling waves solutions of the KP equation in weakly dispersive media
  49. Characterization of damage morphology of structural SiO2 film induced by nanosecond pulsed laser
  50. A study of generalized hypergeometric Matrix functions via two-parameter Mittag–Leffler matrix function
  51. Study of the length and influencing factors of air plasma ignition time
  52. Analysis of parametric effects in the wave profile of the variant Boussinesq equation through two analytical approaches
  53. The nonlinear vibration and dispersive wave systems with extended homoclinic breather wave solutions
  54. Generalized notion of integral inequalities of variables
  55. The seasonal variation in the polarization (Ex/Ey) of the characteristic wave in ionosphere plasma
  56. Impact of COVID 19 on the demand for an inventory model under preservation technology and advance payment facility
  57. Approximate solution of linear integral equations by Taylor ordering method: Applied mathematical approach
  58. Exploring the new optical solitons to the time-fractional integrable generalized (2+1)-dimensional nonlinear Schrödinger system via three different methods
  59. Irreversibility analysis in time-dependent Darcy–Forchheimer flow of viscous fluid with diffusion-thermo and thermo-diffusion effects
  60. Double diffusion in a combined cavity occupied by a nanofluid and heterogeneous porous media
  61. NTIM solution of the fractional order parabolic partial differential equations
  62. Jointly Rayleigh lifetime products in the presence of competing risks model
  63. Abundant exact solutions of higher-order dispersion variable coefficient KdV equation
  64. Laser cutting tobacco slice experiment: Effects of cutting power and cutting speed
  65. Performance evaluation of common-aperture visible and long-wave infrared imaging system based on a comprehensive resolution
  66. Diesel engine small-sample transfer learning fault diagnosis algorithm based on STFT time–frequency image and hyperparameter autonomous optimization deep convolutional network improved by PSO–GWO–BPNN surrogate model
  67. Analyses of electrokinetic energy conversion for periodic electromagnetohydrodynamic (EMHD) nanofluid through the rectangular microchannel under the Hall effects
  68. Propagation properties of cosh-Airy beams in an inhomogeneous medium with Gaussian PT-symmetric potentials
  69. Dynamics investigation on a Kadomtsev–Petviashvili equation with variable coefficients
  70. Study on fine characterization and reconstruction modeling of porous media based on spatially-resolved nuclear magnetic resonance technology
  71. Optimal block replacement policy for two-dimensional products considering imperfect maintenance with improved Salp swarm algorithm
  72. A hybrid forecasting model based on the group method of data handling and wavelet decomposition for monthly rivers streamflow data sets
  73. Hybrid pencil beam model based on photon characteristic line algorithm for lung radiotherapy in small fields
  74. Surface waves on a coated incompressible elastic half-space
  75. Radiation dose measurement on bone scintigraphy and planning clinical management
  76. Lie symmetry analysis for generalized short pulse equation
  77. Spectroscopic characteristics and dissociation of nitrogen trifluoride under external electric fields: Theoretical study
  78. Cross electromagnetic nanofluid flow examination with infinite shear rate viscosity and melting heat through Skan-Falkner wedge
  79. Convection heat–mass transfer of generalized Maxwell fluid with radiation effect, exponential heating, and chemical reaction using fractional Caputo–Fabrizio derivatives
  80. Weak nonlinear analysis of nanofluid convection with g-jitter using the Ginzburg--Landau model
  81. Strip waveguides in Yb3+-doped silicate glass formed by combination of He+ ion implantation and precise ultrashort pulse laser ablation
  82. Best selected forecasting models for COVID-19 pandemic
  83. Research on attenuation motion test at oblique incidence based on double-N six-light-screen system
  84. Review Articles
  85. Progress in epitaxial growth of stanene
  86. Review and validation of photovoltaic solar simulation tools/software based on case study
  87. Brief Report
  88. The Debye–Scherrer technique – rapid detection for applications
  89. Rapid Communication
  90. Radial oscillations of an electron in a Coulomb attracting field
  91. Special Issue on Novel Numerical and Analytical Techniques for Fractional Nonlinear Schrodinger Type - Part II
  92. The exact solutions of the stochastic fractional-space Allen–Cahn equation
  93. Propagation of some new traveling wave patterns of the double dispersive equation
  94. A new modified technique to study the dynamics of fractional hyperbolic-telegraph equations
  95. An orthotropic thermo-viscoelastic infinite medium with a cylindrical cavity of temperature dependent properties via MGT thermoelasticity
  96. Modeling of hepatitis B epidemic model with fractional operator
  97. Special Issue on Transport phenomena and thermal analysis in micro/nano-scale structure surfaces - Part III
  98. Investigation of effective thermal conductivity of SiC foam ceramics with various pore densities
  99. Nonlocal magneto-thermoelastic infinite half-space due to a periodically varying heat flow under Caputo–Fabrizio fractional derivative heat equation
  100. The flow and heat transfer characteristics of DPF porous media with different structures based on LBM
  101. Homotopy analysis method with application to thin-film flow of couple stress fluid through a vertical cylinder
  102. Special Issue on Advanced Topics on the Modelling and Assessment of Complicated Physical Phenomena - Part II
  103. Asymptotic analysis of hepatitis B epidemic model using Caputo Fabrizio fractional operator
  104. Influence of chemical reaction on MHD Newtonian fluid flow on vertical plate in porous medium in conjunction with thermal radiation
  105. Structure of analytical ion-acoustic solitary wave solutions for the dynamical system of nonlinear wave propagation
  106. Evaluation of ESBL resistance dynamics in Escherichia coli isolates by mathematical modeling
  107. On theoretical analysis of nonlinear fractional order partial Benney equations under nonsingular kernel
  108. The solutions of nonlinear fractional partial differential equations by using a novel technique
  109. Modelling and graphing the Wi-Fi wave field using the shape function
  110. Generalized invexity and duality in multiobjective variational problems involving non-singular fractional derivative
  111. Impact of the convergent geometric profile on boundary layer separation in the supersonic over-expanded nozzle
  112. Variable stepsize construction of a two-step optimized hybrid block method with relative stability
  113. Thermal transport with nanoparticles of fractional Oldroyd-B fluid under the effects of magnetic field, radiations, and viscous dissipation: Entropy generation; via finite difference method
  114. Special Issue on Advanced Energy Materials - Part I
  115. Voltage regulation and power-saving method of asynchronous motor based on fuzzy control theory
  116. The structure design of mobile charging piles
  117. Analysis and modeling of pitaya slices in a heat pump drying system
  118. Design of pulse laser high-precision ranging algorithm under low signal-to-noise ratio
  119. Special Issue on Geological Modeling and Geospatial Data Analysis
  120. Determination of luminescent characteristics of organometallic complex in land and coal mining
  121. InSAR terrain mapping error sources based on satellite interferometry
https://doi.org/10.1515/phys-2022-0057
Keywords for this article
failure dependence; wind turbine system; preventive maintenance; extended warranty; cost-efficiency ratio
Creative Commons
BY 4.0

Articles in the same Issue

  1. Regular Articles
  2. Test influence of screen thickness on double-N six-light-screen sky screen target
  3. Analysis on the speed properties of the shock wave in light curtain
  4. Abundant accurate analytical and semi-analytical solutions of the positive Gardner–Kadomtsev–Petviashvili equation
  5. Measured distribution of cloud chamber tracks from radioactive decay: A new empirical approach to investigating the quantum measurement problem
  6. Nuclear radiation detection based on the convolutional neural network under public surveillance scenarios
  7. Effect of process parameters on density and mechanical behaviour of a selective laser melted 17-4PH stainless steel alloy
  8. Performance evaluation of self-mixing interferometer with the ceramic type piezoelectric accelerometers
  9. Effect of geometry error on the non-Newtonian flow in the ceramic microchannel molded by SLA
  10. Numerical investigation of ozone decomposition by self-excited oscillation cavitation jet
  11. Modeling electrostatic potential in FDSOI MOSFETS: An approach based on homotopy perturbations
  12. Modeling analysis of microenvironment of 3D cell mechanics based on machine vision
  13. Numerical solution for two-dimensional partial differential equations using SM’s method
  14. Multiple velocity composition in the standard synchronization
  15. Electroosmotic flow for Eyring fluid with Navier slip boundary condition under high zeta potential in a parallel microchannel
  16. Soliton solutions of Calogero–Degasperis–Fokas dynamical equation via modified mathematical methods
  17. Performance evaluation of a high-performance offshore cementing wastes accelerating agent
  18. Sapphire irradiation by phosphorus as an approach to improve its optical properties
  19. A physical model for calculating cementing quality based on the XGboost algorithm
  20. Experimental investigation and numerical analysis of stress concentration distribution at the typical slots for stiffeners
  21. An analytical model for solute transport from blood to tissue
  22. Finite-size effects in one-dimensional Bose–Einstein condensation of photons
  23. Drying kinetics of Pleurotus eryngii slices during hot air drying
  24. Computer-aided measurement technology for Cu2ZnSnS4 thin-film solar cell characteristics
  25. QCD phase diagram in a finite volume in the PNJL model
  26. Study on abundant analytical solutions of the new coupled Konno–Oono equation in the magnetic field
  27. Experimental analysis of a laser beam propagating in angular turbulence
  28. Numerical investigation of heat transfer in the nanofluids under the impact of length and radius of carbon nanotubes
  29. Multiple rogue wave solutions of a generalized (3+1)-dimensional variable-coefficient Kadomtsev--Petviashvili equation
  30. Optical properties and thermal stability of the H+-implanted Dy3+/Tm3+-codoped GeS2–Ga2S3–PbI2 chalcohalide glass waveguide
  31. Nonlinear dynamics for different nonautonomous wave structure solutions
  32. Numerical analysis of bioconvection-MHD flow of Williamson nanofluid with gyrotactic microbes and thermal radiation: New iterative method
  33. Modeling extreme value data with an upside down bathtub-shaped failure rate model
  34. Abundant optical soliton structures to the Fokas system arising in monomode optical fibers
  35. Analysis of the partially ionized kerosene oil-based ternary nanofluid flow over a convectively heated rotating surface
  36. Multiple-scale analysis of the parametric-driven sine-Gordon equation with phase shifts
  37. Magnetofluid unsteady electroosmotic flow of Jeffrey fluid at high zeta potential in parallel microchannels
  38. Effect of plasma-activated water on microbial quality and physicochemical properties of fresh beef
  39. The finite element modeling of the impacting process of hard particles on pump components
  40. Analysis of respiratory mechanics models with different kernels
  41. Extended warranty decision model of failure dependence wind turbine system based on cost-effectiveness analysis
  42. Breather wave and double-periodic soliton solutions for a (2+1)-dimensional generalized Hirota–Satsuma–Ito equation
  43. First-principle calculation of electronic structure and optical properties of (P, Ga, P–Ga) doped graphene
  44. Numerical simulation of nanofluid flow between two parallel disks using 3-stage Lobatto III-A formula
  45. Optimization method for detection a flying bullet
  46. Angle error control model of laser profilometer contact measurement
  47. Numerical study on flue gas–liquid flow with side-entering mixing
  48. Travelling waves solutions of the KP equation in weakly dispersive media
  49. Characterization of damage morphology of structural SiO2 film induced by nanosecond pulsed laser
  50. A study of generalized hypergeometric Matrix functions via two-parameter Mittag–Leffler matrix function
  51. Study of the length and influencing factors of air plasma ignition time
  52. Analysis of parametric effects in the wave profile of the variant Boussinesq equation through two analytical approaches
  53. The nonlinear vibration and dispersive wave systems with extended homoclinic breather wave solutions
  54. Generalized notion of integral inequalities of variables
  55. The seasonal variation in the polarization (Ex/Ey) of the characteristic wave in ionosphere plasma
  56. Impact of COVID 19 on the demand for an inventory model under preservation technology and advance payment facility
  57. Approximate solution of linear integral equations by Taylor ordering method: Applied mathematical approach
  58. Exploring the new optical solitons to the time-fractional integrable generalized (2+1)-dimensional nonlinear Schrödinger system via three different methods
  59. Irreversibility analysis in time-dependent Darcy–Forchheimer flow of viscous fluid with diffusion-thermo and thermo-diffusion effects
  60. Double diffusion in a combined cavity occupied by a nanofluid and heterogeneous porous media
  61. NTIM solution of the fractional order parabolic partial differential equations
  62. Jointly Rayleigh lifetime products in the presence of competing risks model
  63. Abundant exact solutions of higher-order dispersion variable coefficient KdV equation
  64. Laser cutting tobacco slice experiment: Effects of cutting power and cutting speed
  65. Performance evaluation of common-aperture visible and long-wave infrared imaging system based on a comprehensive resolution
  66. Diesel engine small-sample transfer learning fault diagnosis algorithm based on STFT time–frequency image and hyperparameter autonomous optimization deep convolutional network improved by PSO–GWO–BPNN surrogate model
  67. Analyses of electrokinetic energy conversion for periodic electromagnetohydrodynamic (EMHD) nanofluid through the rectangular microchannel under the Hall effects
  68. Propagation properties of cosh-Airy beams in an inhomogeneous medium with Gaussian PT-symmetric potentials
  69. Dynamics investigation on a Kadomtsev–Petviashvili equation with variable coefficients
  70. Study on fine characterization and reconstruction modeling of porous media based on spatially-resolved nuclear magnetic resonance technology
  71. Optimal block replacement policy for two-dimensional products considering imperfect maintenance with improved Salp swarm algorithm
  72. A hybrid forecasting model based on the group method of data handling and wavelet decomposition for monthly rivers streamflow data sets
  73. Hybrid pencil beam model based on photon characteristic line algorithm for lung radiotherapy in small fields
  74. Surface waves on a coated incompressible elastic half-space
  75. Radiation dose measurement on bone scintigraphy and planning clinical management
  76. Lie symmetry analysis for generalized short pulse equation
  77. Spectroscopic characteristics and dissociation of nitrogen trifluoride under external electric fields: Theoretical study
  78. Cross electromagnetic nanofluid flow examination with infinite shear rate viscosity and melting heat through Skan-Falkner wedge
  79. Convection heat–mass transfer of generalized Maxwell fluid with radiation effect, exponential heating, and chemical reaction using fractional Caputo–Fabrizio derivatives
  80. Weak nonlinear analysis of nanofluid convection with g-jitter using the Ginzburg--Landau model
  81. Strip waveguides in Yb3+-doped silicate glass formed by combination of He+ ion implantation and precise ultrashort pulse laser ablation
  82. Best selected forecasting models for COVID-19 pandemic
  83. Research on attenuation motion test at oblique incidence based on double-N six-light-screen system
  84. Review Articles
  85. Progress in epitaxial growth of stanene
  86. Review and validation of photovoltaic solar simulation tools/software based on case study
  87. Brief Report
  88. The Debye–Scherrer technique – rapid detection for applications
  89. Rapid Communication
  90. Radial oscillations of an electron in a Coulomb attracting field
  91. Special Issue on Novel Numerical and Analytical Techniques for Fractional Nonlinear Schrodinger Type - Part II
  92. The exact solutions of the stochastic fractional-space Allen–Cahn equation
  93. Propagation of some new traveling wave patterns of the double dispersive equation
  94. A new modified technique to study the dynamics of fractional hyperbolic-telegraph equations
  95. An orthotropic thermo-viscoelastic infinite medium with a cylindrical cavity of temperature dependent properties via MGT thermoelasticity
  96. Modeling of hepatitis B epidemic model with fractional operator
  97. Special Issue on Transport phenomena and thermal analysis in micro/nano-scale structure surfaces - Part III
  98. Investigation of effective thermal conductivity of SiC foam ceramics with various pore densities
  99. Nonlocal magneto-thermoelastic infinite half-space due to a periodically varying heat flow under Caputo–Fabrizio fractional derivative heat equation
  100. The flow and heat transfer characteristics of DPF porous media with different structures based on LBM
  101. Homotopy analysis method with application to thin-film flow of couple stress fluid through a vertical cylinder
  102. Special Issue on Advanced Topics on the Modelling and Assessment of Complicated Physical Phenomena - Part II
  103. Asymptotic analysis of hepatitis B epidemic model using Caputo Fabrizio fractional operator
  104. Influence of chemical reaction on MHD Newtonian fluid flow on vertical plate in porous medium in conjunction with thermal radiation
  105. Structure of analytical ion-acoustic solitary wave solutions for the dynamical system of nonlinear wave propagation
  106. Evaluation of ESBL resistance dynamics in Escherichia coli isolates by mathematical modeling
  107. On theoretical analysis of nonlinear fractional order partial Benney equations under nonsingular kernel
  108. The solutions of nonlinear fractional partial differential equations by using a novel technique
  109. Modelling and graphing the Wi-Fi wave field using the shape function
  110. Generalized invexity and duality in multiobjective variational problems involving non-singular fractional derivative
  111. Impact of the convergent geometric profile on boundary layer separation in the supersonic over-expanded nozzle
  112. Variable stepsize construction of a two-step optimized hybrid block method with relative stability
  113. Thermal transport with nanoparticles of fractional Oldroyd-B fluid under the effects of magnetic field, radiations, and viscous dissipation: Entropy generation; via finite difference method
  114. Special Issue on Advanced Energy Materials - Part I
  115. Voltage regulation and power-saving method of asynchronous motor based on fuzzy control theory
  116. The structure design of mobile charging piles
  117. Analysis and modeling of pitaya slices in a heat pump drying system
  118. Design of pulse laser high-precision ranging algorithm under low signal-to-noise ratio
  119. Special Issue on Geological Modeling and Geospatial Data Analysis
  120. Determination of luminescent characteristics of organometallic complex in land and coal mining
  121. InSAR terrain mapping error sources based on satellite interferometry
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 13.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/phys-2022-0057/html
Scroll to top button