The solutions of nonlinear fractional partial differential equations by using a novel technique

Aisha Abdullah Alderremy; Hassan Khan; Qasim Khan; Poom Kumam; Shaban Aly; Said Ahmad; Kanokwan Sitthithakerngkiet

doi:10.1515/phys-2022-0069

Artikel Open Access

The solutions of nonlinear fractional partial differential equations by using a novel technique

Aisha Abdullah Alderremy , Hassan Khan , Qasim Khan , Poom Kumam , Shaban Aly , Said Ahmad und Kanokwan Sitthithakerngkiet

Veröffentlicht/Copyright: 9. August 2022

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen Erkunden Sie dieses Fachgebiet

Aus der Zeitschrift Open Physics Band 20 Heft 1

Abstract

In this article, the solutions of higher nonlinear partial differential equations (PDEs) with the Caputo operator are presented. The fractional PDEs are modern tools to model various phenomena more accurately. The residual power series method (RPSM) is used for the solution analysis of fractional partial differential equations (FPDEs), which has direct implementation for the solutions of fractional partial differential equations. In this work, the solutions to a few nonlinear FPDEs are handled by the proposed technique. The general and particular schemes of RPSM are constructed and implemented successfully. The fractional solutions of PDEs have provided many useful dynamics of the targeted problems. The RPSM results for both integer and fractional-order FPDEs are further explained and elaborated by using graphs and tables. It is observed that the higher accuracy of RPSM is achieved with fewer calculations. Graphs and tables for fractional-order solutions are presented, which confirm the convergence phenomena of fractional solutions toward integer order solutions of each problem. The suggested method can be extended to the solutions of other nonlinear fractional partial differential equations.

Keywords: fractional partial differential equations; Caputo derivative operator; residual power series method; analytical technique

1 Introduction

The generalization of the derivative and integral to arbitrary orders is known as fractional calculus (FC). It is an extension of ordinary calculus. Many physical phenomena are accurately modeled when compared to ordinary calculus. FC has gained prominence in recent decades due to its numerous applications in fields such as electrodynamics [1], tuberculosis [2], immunogenic tumor dynamics [3], cholera infection model [4], hepatitis B virus [5], pine wilt disease [6], diabetes [7], and so on. In FC, fractional partial differential equations (FPDEs) are regarded as the most precise techniques for developing mathematical models in applied mathematics, such as damping laws, rheology, diffusion, electrostatics, electrodynamics, fluid flows, and so on [8,9, 10,11]. Several methods are used to solve FPDEs and system of FPDEs, for example, Laplace Adomin decomposition method [12], Laplace variational homotopy perturbation method [13], Chebyshev wavelet method [14], Elzaki transform method [15], natural transform decomposition method [16], finite element method [17], finite difference method [18], q-homotopy analysis method [19], matrix approximation technique [20], modified predictor–corrector method [21], and corrected Fourier series and fractional complex transformation [22,23,24]. In the same context, Erturk et al. have implemented fractional Lagrangian approach to describe the motion of a beam on a nanowire [25].

The residual power series method (RPSM) is an analytical procedure and is used to solve FPDEs and system FPDEs. Arqub introduced the RPSM in ref. [26], which was utilized to solve first- and second-order fuzzy differential equations. RPSM is a simple and accurate tool for mathematicians to obtain the series form solutions to a variety of differential equations. RPSM is based on the power series expansion and can be applied efficiently without the use of discretization, perturbation, or linearization [18,27]. RPSM is based on residual error concepts, which derive power series coefficients in a chain of algebraic equations with one or two variables. Furthermore, RPSM is a simple and accurate tool for solving various fractional differential equations and FPDEs as well. In the literature, RPSM was used to find the solution to Lane Emeden equations [28]. It has been usefully applied to other equations [29], including the fractional foam drainage equation [30], fractional diffusion equations [31], fuzzy type differential equations [26], Boussinesq–Burgers equations [32], fractional-order Burger types equations [33], the nonlinear KdV-Burgers equation [18], initial value problems of higher order [34], nonlinear coupled Boussinesq–Burgers equations [35], system of Fredhlom integral equations [36], system of multipantograph differential equations [37], the Lane–Emden equations [38], the Whitham–Broer–Kaup equations [39], fractional model of vibration equation [40], system evolutionary having two-component equation [41], the black-Scholes European option pricing equations [42], the nonlinear gas dynamics equations [43], the Schrödinger equations in one dimension space [44], Benney-Lin equation arising in falling film problems [45], and time fractional heat like PDEs [46]. In ref. [47], the researchers looked at the analysis and modeling of FPDEs for use in the reaction-diffusion model [48] and analytic approximation solutions of diffusion equations arising in oil pollution.

In the current research task, the analytical solutions of fractional-order time and space PDEs are calculated by using RPSM. The generalized RPSM algorithms are successfully constructed for the solution of all problems. The RPSM implementation is completed for a few numerical examples of the targeted problems. Graphs and tables are used to display the RPSM results. Despite the fact that only a few terms are used in the solution, RPSM provides a higher level of accuracy. The proposed method requires fewer calculations and does not rely on additional parameters or discratization. For fractional-order and integer order problems, the exact and RPSM solutions are in close contact. Furthermore, the RPSM methodology and accuracy have allowed it to be used for other fractional problems as well.

Finally, this article is structured as follows: Section 1 is devoted to some basic introductions related to the current work. Basic definitions are defined in Section 2. Section 3 discusses the specifics of the RPSM formulation for fractional partial differential equations. Section 4 contains some numerical examples with solutions and their graphs as well. Section 5 presents the Conclusion.

2 Basic definitions

2.1 Definitions

The fractional-order Caputo derivative of order δ > 0 is defined by ref. [16]

D ℑ δ μ ( ζ , ℑ ) = 1 Γ ( m − δ ) ∫ 0 ℑ ( ℑ − ℑ o ) m − δ − 1 ∂ m μ ( ζ , ℑ ) ∂ ℑ m d ℑ , if m − 1 < δ ≤ m ,

if δ = m , for m ∈ N , then,

D ℑ δ μ ( ζ , ℑ ) = ∂ m μ ( ζ , ℑ ) ∂ ℑ m .

2.2 Definitions

The fractional power series (FPS) is represented by ref. [18]

∑ m = 0 ∞ P m ( ℑ − ℑ o ) m δ = P o + P 1 ( ℑ − ℑ o ) δ + P 2 ( ℑ − ℑ o ) 2 δ + … , m − 1 < δ ≤ m , ℑ ≤ ℑ o ,

where P m are the constant coefficients of the series. If ℑ o = 0 , then FPS become fractional Maclaurin series.

2.3 Theorem

The FPS expansion for μ ( ζ , ℑ ) at ℑ = ℑ o can be expressed as ref. [18]:

μ ( ζ , ℑ ) = ∑ m = 0 ∞ P m ( ζ ) ( ℑ − ℑ o ) m δ .

If D ℑ m δ μ ( ζ , ℑ ) are continuous for m = 0 , 1 , … , then

P m ( ζ ) = D ℑ m δ μ ( ζ , ℑ ) Γ ( 1 + m δ ) ,

where ζ ∈ I , ℑ o ≤ ℑ < ℑ + R .

The FPS expansion of μ ( ζ , ℑ ) can be expressed as follows:

μ ( ζ , ℑ ) = ∑ m = 0 ∞ D ℑ m δ μ ( ζ , ℑ ) Γ ( 1 + m δ ) ( ℑ − ℑ o ) m δ ,

which is called generalization Taylor expansion. If δ = 1 , then it will be converted into Taylor series.

2.4 Definitions

The fractional derivatives D δ ( ℑ ) m δ is describe as suggested in ref. [18]

D ℑ δ ( ℑ ) m δ = Γ ( m δ + 1 ) Γ ( m δ − δ + 1 ) ( ℑ ) m δ − δ ,

where, 0 < δ ≤ 1 and m = 1 , 2 , … .

3 RPSM methodology

To understand the RPSM procedure [1], we will take to solve time and space fractional partial differential equations (FPDEs).

(1) D ℑ δ μ ( ζ , ℑ ) + μ ( ζ , ℑ ) D ζ ρ μ ( ζ , ℑ ) = H ( ζ ) , 0 < δ ≤ 1 and 0 < ρ ≤ 1 ,

having initial condition

(2) μ ( ζ , 0 ) = f ( ζ ) ,

and the truncated series of Eq. (1) is

(3) μ k ( ζ , ℑ ) = f ( ζ ) + ∑ m = 1 k f m ( ℑ ) m δ Γ ( 1 + m δ ) .

Residual function of Eq. (1) is given by

(4) Res μ ( ζ , ℑ ) = D ℑ δ μ ( ζ , ℑ ) + μ ( ζ , ℑ ) D ζ ρ μ ( ζ , ℑ ) = H ( ζ ) ,

and the k th -residual function is defined as follows:

(5) Res μ , k ( ζ , ℑ ) = D ℑ δ μ k ( ζ , ℑ ) + μ k ( ζ , ℑ ) D ζ ρ μ k ( ζ , ℑ ) − H ( ζ ) .

For first approximation putting k = 1 , Eqs. (3) and (5) can be simplified as follows:

(6) μ 1 ( ζ , ℑ ) = f ( ζ ) + f 1 ( ζ ) ( ℑ ) δ Γ ( 1 + δ ) ,

(7) Res μ , 1 ( ζ , ℑ ) = D ℑ δ μ 1 ( ζ , ℑ ) + μ 1 ( ζ , ℑ ) D ζ ρ μ 1 ( ζ , ℑ ) − H ( ζ ) .

By putting Eq. (14) in Eq. (15), we obtain,

(8) Res μ , 1 ( ζ , ℑ ) = f 1 ( ζ ) + f ( ζ ) D ζ ρ f ( ζ ) − H ( ζ ) ,

using Res μ , 1 ( ζ , 0 ) =0, to obtained,

(9) f 1 ( ζ ) = H ( ζ ) − f ( ζ ) D ζ ρ f ( ζ ) .

first RPSM approximation is expressed as follows:

(10) μ 1 ( ζ , ℑ ) = f ( ζ ) + ( H ( ζ ) − f ( ζ ) D ζ ρ f ( ζ ) ) ( ℑ ) δ Γ ( 1 + δ ) .

For k = 2 , Eqs. (3) and (5) can be written as follows:

(11) μ 2 ( ζ , ℑ ) = f ( ζ ) + ( H ( ζ ) − f ( ζ ) D ζ ρ f ( ζ ) ) ( ℑ ) δ Γ ( 1 + δ ) + f 2 ( ζ ) ( ℑ ) 2 δ Γ ( 1 + 2 δ ) ,

(12) Res μ , 2 ( ζ , ℑ ) = D ℑ δ μ 2 ( ζ , ℑ ) + μ 2 ( ζ , ℑ ) D ζ ρ μ 2 ( ζ , ℑ ) − H ( ζ ) ,

and by putting Eq. (11) in Eq. (12), we obtain

(13) Res μ , 2 ( ζ , ℑ ) = D ℑ δ f ( ζ ) + ( H ( ζ ) − f ( ζ ) D ζ ρ f ( ζ ) ) ( ℑ ) δ Γ ( 1 + δ ) + f 2 ( ζ ) ( ℑ ) 2 δ Γ ( 1 + 2 δ ) + f ( ζ ) + ( H ( ζ ) − f ( ζ ) D ζ ρ f ( ζ ) ) ( ℑ ) δ Γ ( 1 + δ ) + f 2 ( ζ ) ( ℑ ) 2 δ Γ ( 1 + 2 δ ) × D ζ ρ f ( ζ ) + ( H ( ζ ) − f ( ζ ) D ζ ρ f ( ζ ) ) ( ℑ ) δ Γ ( 1 + δ ) + f 2 ( ζ ) ( ℑ ) 2 δ Γ ( 1 + 2 δ ) − H ( ζ ) .

By using D ℑ δ in Eq. (13) and then using D ℑ δ Res μ , 2 ( ζ , 0 ) = 0 , we obtain

(14) f 2 ( ζ ) = − f ( ζ ) D ζ ρ f ( ζ ) − [ H ( ζ ) − f ( ζ ) D ζ ρ f ( ζ ) ] D ζ ρ f ( ζ ) − f ( ζ ) [ D ζ ρ H ( ζ ) − D ζ ρ ( f ( ζ ) D ζ ρ f ( ζ ) ) ] .

Second RPSM approximation is expressed as follows:

(15) μ 2 ( ζ , ℑ ) = f ( ζ ) + ( H ( ζ ) − f ( ζ ) D ζ ρ f ( ζ ) ) ( ℑ ) δ Γ ( 1 + δ ) + ( − f ( ζ ) D ζ ρ f ( ζ ) − [ H ( ζ ) − f ( ζ ) D ζ ρ f ( ζ ) ] × D ζ ρ f ( ζ ) − f ( ζ ) [ D ζ ρ H ( ζ ) − D ζ ρ ( f ( ζ ) D ζ ρ f ( ζ ) ) ] ) ( ℑ ) δ Γ ( 1 + δ ) .

In general, f m ( ζ ) for k ≥ 3 is calculated by putting Eq. (3) in Eq. (5) and then computing D ℑ ( k − 1 ) δ o f Res μ , k ( ζ , ℑ ) . Therefore, f m ( ζ ) are calculated by using the following algebraic equations.

(16) D ℑ ( k − 1 ) δ Res μ , k ( ζ , 0 ) = 0 , k = 1 , 2 , … .

4 Numerical examples

4.1 Example

Take a look at the fractional partial differential equation [49],

(17) D ℑ δ μ ( ζ , ℑ ) + μ ( ζ , ℑ ) D ζ ρ μ ( ζ , ℑ ) = ζ , 0 < δ ≤ 1 and 0 < ρ ≤ 1 ,

having initial condition

(18) μ ( ζ , 0 ) = 1 ,

and the truncated series of Eq. (17) is

(19) μ k ( ζ , ℑ ) = 1 + ∑ m = 1 k C m ( ℑ ) m δ Γ ( 1 + m δ ) ,

and the residual function for Eq. (17) is define as follows:

(20) Res μ , k ( ζ , ℑ ) = D ℑ δ μ k ( ζ , ℑ ) + μ k ( ζ , ℑ ) D ζ ρ μ k ( ζ , ℑ ) − ζ .

For k = 1 , Eqs. (19) and (20) can be simplified as follows:

(21) μ 1 ( ζ , ℑ ) = 1 + C 1 ( ℑ ) δ Γ ( 1 + δ ) ,

(22) Res μ , 1 ( ζ , ℑ ) = D ℑ δ μ 1 ( ζ , ℑ ) + μ 1 ( ζ , ℑ ) D ζ ρ μ 1 ( ζ , ℑ ) − ζ .

By putting Eq. (21) in Eq. (22), we obtain

(23) Res μ , 1 ( ζ , ℑ ) = C 1 − ζ ,

and by using Res μ , 1 ( ζ , 0 ) = 0 , we obtain

(24) C 1 = ζ .

First RPSM approximation is expressed as follows:

(25) μ 1 ( ζ , ℑ ) = 1 + ζ ( ℑ ) δ Γ ( 1 + δ ) .

For k = 2 , Eqs. (19) and (20) can be written as follows:

(26) μ 2 ( ζ , ℑ ) = 1 + ζ ( ℑ ) δ Γ ( 1 + δ ) + C 2 ( ℑ ) 2 δ Γ ( 1 + 2 δ ) ,

(27) Res μ , 2 ( ζ , ℑ ) = D ℑ δ μ 2 ( ζ , ℑ ) + μ 2 ( ζ , ℑ ) D ζ ρ μ 2 ( ζ , ℑ ) − ζ .

By putting Eq. (26) in Eq. (27), we obtain

(28) Res μ , 2 ( ζ , ℑ ) = ζ + C 2 ( ℑ ) δ Γ ( 1 + δ ) + 1 + ζ ( ℑ ) δ Γ ( 1 + δ ) + C 2 ( ℑ ) 2 δ Γ ( 1 + 2 δ ) × ζ ( 1 − ρ ) ℑ δ Γ ( 2 − ρ ) Γ ( 1 + δ ) − ζ .

By using D ℑ δ in Eq. (28) and then using D ℑ δ Res μ , 2 ( ζ , 0 ) = 0 , we have

(29) C 2 = − ζ ( 1 − ρ ) Γ ( 2 − ρ ) .

Second RPSM approximation is expressed as follows:

(30) μ 2 ( ζ , ℑ ) = 1 + ζ ( ℑ ) δ Γ ( 1 + δ ) − ζ ( 1 − ρ ) Γ ( 2 − ρ ) ( ℑ ) 2 δ Γ ( 1 + 2 δ ) .

Similarly, for k = 3 , Eqs. (19) and (20) can be simplified as follows:

(31) μ 3 ( ζ , ℑ ) = 1 + ζ ( ℑ ) δ Γ ( 1 + δ ) − ζ ( 1 − ρ ) Γ ( 2 − ρ ) ( ℑ ) 2 δ Γ ( 1 + 2 δ ) + C 3 ( ℑ ) 3 δ Γ ( 1 + 3 δ ) ,

(32) Res μ , 3 ( ζ , ℑ ) = D ℑ δ μ 3 ( ζ , ℑ ) + μ 3 ( ζ , ℑ ) D ζ ρ μ 3 ( ζ , ℑ ) − ζ .

By putting Eq. (31) in Eq. (32), we obtain

(33) Res μ , 3 ( ζ , ℑ ) = ζ − ζ ( 1 − ρ ) ℑ δ Γ ( 2 − ρ ) Γ ( 1 + δ ) + C 3 ( ℑ ) 2 δ Γ ( 1 + 2 δ ) + 1 + ζ ( ℑ ) δ Γ ( 1 + δ ) − ζ ( 1 − ρ ) Γ ( 2 − ρ ) ( ℑ ) 2 δ Γ ( 1 + 2 δ ) + C 3 ( ℑ ) 3 δ Γ ( 1 + 3 δ ) ζ ( 1 − ρ ) ℑ δ Γ ( 2 − ρ ) Γ ( 1 + δ ) − ζ ( 1 − 2 ρ ) ℑ 2 δ Γ ( 2 − 2 ρ ) Γ ( 1 + 2 δ ) − ζ .

By applying D ℑ 2 δ both sides of Eq. (33) and then using D ℑ 2 δ Res μ , 3 ( ζ , 0 ) = 0 , we have

(34) C 3 = − 2 ζ ( 2 − ρ ) Γ ( 2 − ρ ) .

Third RPSM approximation is expressed as follows:

(35) μ 3 ( ζ , ℑ ) = 1 + ζ ( ℑ ) δ Γ ( 1 + δ ) − ζ ( 1 − ρ ) Γ ( 2 − ρ ) ( ℑ ) 2 δ Γ ( 1 + 2 δ ) − 2 ζ ( 2 − ρ ) Γ ( 2 − ρ ) ( ℑ ) 3 δ Γ ( 1 + 3 δ ) .

By putting δ = ρ = 1 , we obtain the closed form solution of the problem:

(36) μ ( ζ , ℑ ) = ζ tanh ( ℑ ) + sech ( ℑ ) .

4.2 Example

Take a look at the fractional partial differential equation of the form [49],

(37) D ℑ δ μ ( ζ , ℑ ) + μ ( ζ , ℑ ) D ζ ρ μ ( ζ , ℑ ) = 1 , 0 < δ ≤ 1 and 0 < ρ ≤ 1

having initial condition

(38) μ ( ζ , 0 ) = − ζ ,

and the truncated series of Eq. (37) is expressed as follows:

(39) μ k ( ζ , ℑ ) = − ζ + ∑ m = 1 k C m ( ℑ ) m δ Γ ( 1 + m δ ) .

The residual function for Eq. (37) is define as follows:

(40) Res μ , k ( ζ , ℑ ) = D ℑ δ μ k ( ζ , ℑ ) + μ k ( ζ , ℑ ) D ζ ρ μ k ( ζ , ℑ ) − 1 .

For k = 1 , Eqs. (39) and (40) can be simplified as follows:

(41) μ 1 ( ζ , ℑ ) = − ζ + C 1 ( ℑ ) δ Γ ( 1 + δ ) ,

(42) Res μ , 1 ( ζ , ℑ ) = D ℑ δ μ 1 ( ζ , ℑ ) + μ 1 ( ζ , ℑ ) D ζ ρ μ 1 ( ζ , ℑ ) − 1 .

By putting Eq. (41) in Eq. (46), we obtain

(43) Res μ , 1 ( ζ , ℑ ) = C 1 + − ζ + C 1 ( ℑ ) δ Γ ( 1 + δ ) − ζ 1 − ρ Γ ( 2 − ρ ) − 1 ,

and using Res μ , 1 ( ζ , 0 ) = 0 , we obtain

(44) C 1 = Γ ( 2 − ρ ) − ζ ( 2 − ρ ) Γ ( 2 − ρ ) .

First RPSM approximation defined as follows:

(45) μ 1 ( ζ , ℑ ) = − ζ + Γ ( 2 − ρ ) − ζ ( 2 − ρ ) Γ ( 2 − ρ ) ( ℑ ) δ Γ ( 1 + δ ) .

For k = 2 , Eqs. (39) and (40) can be written as follows:

(46) μ 2 ( ζ , ℑ ) = − ζ + Γ ( 2 − ρ ) − ζ ( 2 − ρ ) Γ ( 2 − ρ ) ( ℑ ) δ Γ ( 1 + δ ) + C 2 ( ℑ ) 2 δ Γ ( 1 + 2 δ ) ,

(47) Res μ , 2 ( ζ , ℑ ) = D ℑ δ μ 2 ( ζ , ℑ ) + μ 2 ( ζ , ℑ ) D ζ ρ μ 2 ( ζ , ℑ ) − 1 .

By putting Eq. (46) in Eq. (40), we obtain

(48) Res μ , 2 ( ζ , ℑ ) = ( 2 − ρ ) − ζ ( 2 − ρ ) Γ ( 2 − ρ ) + C 2 ( ℑ ) δ Γ ( 1 + δ ) + − ζ + Γ ( 2 − ρ ) − ζ ( 2 − ρ ) Γ ( 2 − ρ ) ( ℑ ) δ Γ ( 1 + δ ) + C 2 ( ℑ ) 2 δ Γ ( 1 + 2 δ ) − ζ ( 1 − ρ ) Γ ( 2 − ρ ) − Γ ( 3 − ρ ) ζ ( 2 − 2 ρ ) Γ ( 3 − 2 ρ ) ( ℑ ) δ Γ ( 1 + δ ) − 1 ,

By substituting D ℑ δ into Eq. (48) and then using D ℑ δ Res μ , 2 ( ζ , 0 ) = 0 , we obtain

(49) C 2 = − Γ ( 3 − ρ ) ζ ( 3 − 2 ρ ) Γ ( 3 − 2 ρ ) + ζ ( 3 − 2 ρ ) − Γ ( 2 − ρ ) ζ ( 1 − ρ ) Γ ( 2 − ρ ) Γ ( 2 − ρ ) .

Second RPSM approximation is expressed as follows:

(50) μ 2 ( ζ , ℑ ) = − ζ + Γ ( 2 − ρ ) − ζ ( 2 − ρ ) Γ ( 2 − ρ ) ( ℑ ) δ Γ ( 1 + δ ) − Γ ( 3 − ρ ) ζ ( 3 − 2 ρ ) Γ ( 3 − 2 ρ ) + ζ ( 3 − 2 ρ ) − Γ ( 2 − ρ ) ζ ( 1 − ρ ) Γ ( 2 − ρ ) Γ ( 2 − ρ ) ( ℑ ) 2 δ Γ ( 1 + 2 δ ) .

Similarly, for k = 3 , Eqs. (39) and (40) can be simplified as follows:

(51) μ 3 ( ζ , ℑ ) = − ζ + Γ ( 2 − ρ ) − ζ ( 2 − ρ ) Γ ( 2 − ρ ) ( ℑ ) δ Γ ( 1 + δ ) − Γ ( 3 − ρ ) ζ ( 3 − 2 ρ ) Γ ( 3 − 2 ρ ) + ζ ( 3 − 2 ρ ) − Γ ( 2 − ρ ) ζ ( 1 − ρ ) Γ ( 2 − ρ ) Γ ( 2 − ρ ) × ( ℑ ) 2 δ Γ ( 1 + 2 δ ) + C 3 ( ℑ ) 3 δ Γ ( 1 + 3 δ ) ,

(52) Res μ , 3 ( ζ , ℑ ) = D ℑ δ μ 3 ( ζ , ℑ ) + μ 3 ( ζ , ℑ ) D ζ ρ μ 3 ( ζ , ℑ ) − 1 .

By putting Eq. (51) in Eq. (52), we obtain

Res μ , 3 ( ζ , ℑ ) = Γ ( 2 − ρ ) − ζ ( 2 − ρ ) Γ ( 2 − ρ ) − Γ ( 3 − ρ ) ζ ( 3 − 2 ρ ) Γ ( 3 − 2 ρ ) + ζ ( 3 − 2 ρ ) − Γ ( 2 − ρ ) ζ ( 1 − ρ ) Γ ( 2 − ρ ) Γ ( 2 − ρ ) × ( ℑ ) δ Γ ( 1 + δ ) + C 3 ( ℑ ) 2 δ Γ ( 1 + 2 δ ) + − ζ + Γ ( 2 − ρ ) − ζ ( 2 − ρ ) Γ ( 2 − ρ ) ( ℑ ) δ Γ ( 1 + δ ) − Γ ( 3 − ρ ) ζ ( 3 − 2 ρ ) Γ ( 3 − 2 ρ ) + ζ ( 3 − 2 ρ ) − Γ ( 2 − ρ ) ζ ( 1 − ρ ) Γ ( 2 − ρ ) Γ ( 2 − ρ ) × ( ℑ ) 2 δ Γ ( 1 + 2 δ ) + C 3 ( ℑ ) 3 δ Γ ( 1 + 3 δ ) − ζ ( 1 − ρ ) Γ ( 2 − ρ ) + − Γ ( 3 − ρ ) ζ ( 2 − 2 ρ ) Γ ( 3 − 2 ρ ) Γ ( 2 − ρ ) × ( ℑ ) δ Γ ( 1 + δ ) − Γ ( 3 − ρ ) Γ ( 4 − 2 ρ ) ζ ( 3 − 3 ρ ) Γ ( 4 − 3 ρ ) Γ ( 3 − 2 ρ ) + Γ ( 4 − 2 ρ ) ζ ( 3 − 3 ρ ) Γ ( 4 − 3 ρ ) Γ ( 2 − ρ ) Γ ( 2 − ρ ) − ζ ( 1 − 2 ρ ) Γ ( 2 − 2 ρ ) ( ℑ ) 2 δ Γ ( 1 + 2 δ ) − 1 .

By applying D ℑ 2 δ both sides of Eq. (53) and then using D ℑ 2 δ Res μ , 3 ( ζ , 0 ) = 0 , we have,

C 3 = − Γ ( 3 − ρ ) Γ ( 4 − 2 ρ ) ζ ( 4 − 3 ρ ) Γ ( 4 − 3 ρ ) Γ ( 3 − 2 ρ ) + Γ ( 4 − 2 ρ ) ζ ( 4 − 3 ρ ) Γ ( 4 − 3 ρ ) Γ ( 2 − ρ ) 2 − 2 Γ ( 2 − ρ ) Γ ( 3 − ρ ) ζ ( 2 − 2 ρ ) − Γ ( 3 − ρ ) ζ ( 4 − 3 ρ ) Γ ( 2 − ρ ) 2 Γ ( 3 − 2 ρ ) + Γ ( 3 − ρ ) ζ ( 4 − 3 ρ ) Γ ( 2 − ρ ) Γ ( 3 − 2 ρ ) + ζ ( 4 − 3 ρ ) Γ ( 2 − ρ ) 3 − Γ ( 2 − ρ ) ζ ( 2 − 2 ρ ) Γ ( 2 − ρ ) 3 .

Third RPSM approximation is expressed as follows:

μ 3 ( ζ , ℑ ) = − ζ + Γ ( 2 − ρ ) − ζ ( 2 − ρ ) Γ ( 2 − ρ ) ( ℑ ) δ Γ ( 1 + δ ) − Γ ( 3 − ρ ) ζ ( 3 − 2 ρ ) Γ ( 3 − 2 ρ ) + ζ ( 3 − 2 ρ ) − Γ ( 2 − ρ ) ζ ( 1 − ρ ) Γ ( 2 − ρ ) Γ ( 2 − ρ ) × ( ℑ ) 2 δ Γ ( 1 + 2 δ ) − Γ ( 3 − ρ ) Γ ( 4 − 2 ρ ) ζ ( 4 − 3 ρ ) Γ ( 4 − 3 ρ ) Γ ( 3 − 2 ρ ) + Γ ( 4 − 2 ρ ) ζ ( 4 − 3 ρ ) Γ ( 4 − 3 ρ ) Γ ( 2 − ρ ) 2 − 2 Γ ( 2 − ρ ) Γ ( 3 − ρ ) ζ ( 2 − 2 ρ ) − Γ ( 3 − ρ ) ζ ( 4 − 3 ρ ) Γ ( 2 − ρ ) 2 Γ ( 3 − 2 ρ ) + Γ ( 3 − ρ ) ζ ( 4 − 3 ρ ) Γ ( 2 − ρ ) Γ ( 3 − 2 ρ ) + ζ ( 4 − 3 ρ ) Γ ( 2 − ρ ) 3 − Γ ( 2 − ρ ) ζ ( 2 − 2 ρ ) Γ ( 2 − ρ ) 3 ( ℑ ) 3 δ Γ ( 1 + 3 δ ) .

By putting δ = ρ = 1 , we obtain the closed form solution of the problem:

(53) μ ( ζ , ℑ ) = 2 ζ − 2 ℑ + ℑ 2 2 ( ℑ − 1 ) .

4.3 Example

Let us consider the fractional partial differential equation of the form [49],

(54) D ℑ δ μ ( ζ , ℑ ) + μ ( ζ , ℑ ) D ζ ρ μ ( ζ , ℑ ) = 0 , 0 < δ ≤ 1 and 0 < ρ ≤ 1 ,

having initial condition

(55) μ ( ζ , 0 ) = ζ + 1 .

The truncated series of Eq. (54) is expressed as follows:

(56) μ k ( ζ , ℑ ) = ζ + 1 + ∑ m = 1 k C m ( ℑ ) m δ Γ ( 1 + m δ ) .

The residual function for Eq. (54) is define as follows:

(57) Res μ , k ( ζ , ℑ ) = D ℑ δ μ k ( ζ , ℑ ) + μ k ( ζ , ℑ ) D ζ ρ μ k ( ζ , ℑ ) .

For k = 1 , Eqs. (56) and (57) can be simplified as follows:

(58) μ 1 ( ζ , ℑ ) = ζ + 1 + C 1 ( ℑ ) δ Γ ( 1 + δ ) ,

(59) Res μ , 1 ( ζ , ℑ ) = D ℑ δ μ 1 ( ζ , ℑ ) + μ 1 ( ζ , ℑ ) D ζ ρ μ 1 ( ζ , ℑ ) .

By putting Eq. (58) in Eq. (59), we obtain

(60) Res μ , 1 ( ζ , ℑ ) = C 1 + ζ + 1 + C 1 ( ℑ ) δ Γ ( 1 + δ ) ζ 1 − ρ Γ ( 2 − ρ ) ,

and by using Res μ , 1 ( ζ , 0 ) = 0 , we obtain

(61) C 1 = − ζ ( 2 − ρ ) + ζ ( 1 − ρ ) Γ ( 2 − ρ ) .

First RPSM approximation is defined as follows:

(62) μ 1 ( ζ , ℑ ) = ζ + 1 − ζ ( 2 − ρ ) + ζ ( 1 − ρ ) Γ ( 2 − ρ ) ( ℑ ) δ Γ ( 1 + δ ) .

For k = 2 , Eqs. (56) and (57) can be written as follows:

(63) μ 2 ( ζ , ℑ ) = ζ + 1 − ζ ( 2 − ρ ) + ζ ( 1 − ρ ) Γ ( 2 − ρ ) ( ℑ ) δ Γ ( 1 + δ ) + C 2 ( ℑ ) 2 δ Γ ( 1 + 2 δ ) ,

(64) Res μ , 2 ( ζ , ℑ ) = D ℑ δ μ 2 ( ζ , ℑ ) + μ 2 ( ζ , ℑ ) D ζ ρ μ 2 ( ζ , ℑ ) .

By putting Eq. (63) in Eq. (64), we obtain

(65) Res μ , 2 ( ζ , ℑ ) = − ζ ( 2 − ρ ) + ζ ( 1 − ρ ) Γ ( 2 − ρ ) + C 2 ( ℑ ) δ Γ ( 1 + δ ) + ζ + 1 − ζ ( 2 − ρ ) + ζ ( 1 − ρ ) Γ ( 2 − ρ ) ( ℑ ) δ Γ ( 1 + δ ) + C 2 ( ℑ ) 2 δ Γ ( 1 + 2 δ ) × ζ ( 1 − ρ ) Γ ( 2 − ρ ) − Γ ( 3 − ρ ) ζ ( 2 − 2 ρ ) Γ ( 2 − ρ ) Γ ( 3 − 2 ρ ) + ζ ( 1 − 2 ρ ) Γ ( 2 − 2 ρ ) ( ℑ ) δ Γ ( 1 + δ ) .

By using D ℑ δ into Eq. (65) and then using D ℑ δ Res μ , 2 ( ζ , 0 ) = 0 , we obtain,

(66) C 2 = Γ ( 3 − ρ ) ζ ( 3 − 2 ρ ) + Γ ( 3 − ρ ) ζ ( 2 − 2 ρ ) Γ ( 2 − ρ ) Γ ( 3 − 2 ρ ) + ζ ( 3 − 2 ρ ) + ζ ( 2 − 2 ρ ) Γ ( 2 − ρ ) 2 .

Second RPSM approximation is expressed as follows:

μ 2 ( ζ , ℑ ) = ζ + 1 − ζ ( 2 − ρ ) + ζ ( 1 − ρ ) Γ ( 2 − ρ ) ( ℑ ) δ Γ ( 1 + δ ) + Γ ( 3 − ρ ) ζ ( 3 − 2 ρ ) + Γ ( 3 − ρ ) ζ ( 2 − 2 ρ ) Γ ( 2 − ρ ) Γ ( 3 − 2 ρ ) + ζ ( 3 − 2 ρ ) + ζ ( 2 − 2 ρ ) Γ ( 2 − ρ ) 2 × ( ℑ ) 2 δ Γ ( 1 + 2 δ ) .

Similarly, for k = 3 , Eqs. (56) and (57) can be simplified as follows:

(67) μ 3 ( ζ , ℑ ) = ζ + 1 − ζ ( 2 − ρ ) + ζ ( 1 − ρ ) Γ ( 2 − ρ ) ( ℑ ) δ Γ ( 1 + δ ) + Γ ( 3 − ρ ) ζ ( 3 − 2 ρ ) + Γ ( 3 − ρ ) ζ ( 2 − 2 ρ ) Γ ( 2 − ρ ) Γ ( 3 − 2 ρ ) + ζ ( 3 − 2 ρ ) + ζ ( 2 − 2 ρ ) Γ ( 2 − ρ ) 2 × ( ℑ ) 2 δ Γ ( 1 + 2 δ ) + C 3 ( ℑ ) 3 δ Γ ( 1 + 3 δ ) ,

(68) Res μ , 3 ( ζ , ℑ ) = D ℑ δ μ 3 ( ζ , ℑ ) + μ 3 ( ζ , ℑ ) D ζ ρ μ 3 ( ζ , ℑ ) .

By putting Eq. (67) in Eq. (68), we obtain

Res μ , 3 ( ζ , ℑ ) = − ζ ( 2 − ρ ) + ζ ( 1 − ρ ) Γ ( 2 − ρ ) + Γ ( 3 − ρ ) ζ ( 3 − 2 ρ ) + Γ ( 3 − ρ ) ζ ( 2 − 2 ρ ) Γ ( 2 − ρ ) Γ ( 3 − 2 ρ ) + ζ ( 3 − 2 ρ ) + ζ ( 2 − 2 ρ ) Γ ( 2 − ρ ) 2 × ( ℑ ) δ Γ ( 1 + δ ) + C 3 ( ℑ ) 2 δ Γ ( 1 + 2 δ ) + ζ + 1 − ζ ( 2 − ρ ) + ζ ( 1 − ρ ) Γ ( 2 − ρ ) ( ℑ ) δ Γ ( 1 + δ ) + Γ ( 3 − ρ ) ζ ( 3 − 2 ρ ) + Γ ( 3 − ρ ) ζ ( 2 − 2 ρ ) Γ ( 2 − ρ ) Γ ( 3 − 2 ρ ) + ζ ( 3 − 2 ρ ) + ζ ( 2 − 2 ρ ) Γ ( 2 − ρ ) 2 ( ℑ ) 2 δ Γ ( 1 + 2 δ ) + C 3 ( ℑ ) 3 δ Γ ( 1 + 3 δ ) × ζ ( 1 − ρ ) Γ ( 2 − ρ ) − Γ ( 3 − ρ ) ζ ( 2 − 2 ρ ) Γ ( 2 − ρ ) Γ ( 3 − 2 ρ ) + ζ ( 1 − 2 ρ ) Γ ( 2 − 2 ρ ) ( ℑ ) δ Γ ( 1 + δ ) + Γ ( 3 − ρ ) Γ ( 4 − 2 ρ ) ζ ( 3 − 3 ρ ) Γ ( 2 − ρ ) Γ ( 3 − 2 ρ ) Γ ( 4 − 3 ρ ) + Γ ( 3 − ρ ) ζ ( 2 − 3 ρ ) Γ ( 2 − ρ ) Γ ( 3 − 3 ρ ) + Γ ( 4 − 2 ρ ) ζ ( 3 − 3 ρ ) Γ ( 2 − ρ ) 2 Γ ( 4 − 3 ρ ) + Γ ( 3 − 2 ρ ) ζ ( 2 − 3 ρ ) Γ ( 2 − ρ ) 2 Γ ( 3 − 3 ρ ) ( ℑ ) 2 δ Γ ( 1 + 2 δ ) ,

and applying D ℑ 2 δ and then using D ℑ 2 δ Res μ , 3 ( ζ , 0 ) = 0 , we obtain

C 3 = − ( ζ + 1 ) Γ ( 3 − ρ ) Γ ( 4 − 2 ρ ) ζ ( 3 − 3 ρ ) Γ ( 2 − ρ ) Γ ( 3 − 2 ρ ) Γ ( 4 − 3 ρ ) + Γ ( 4 − 2 ρ ) ζ ( 3 − 3 ρ ) Γ ( 2 − ρ ) 2 Γ ( 4 − 3 ρ ) + − Γ ( 3 − ρ ) ζ ( 2 − 2 ρ ) Γ ( 2 − ρ ) Γ ( 3 − 2 ρ ) × − ζ ( 2 − ρ ) − ζ ( 1 − ρ ) Γ ( 2 − ρ ) + ζ ( 1 − ρ ) Γ ( 2 − ρ ) × Γ ( 3 − ρ ) ζ ( 3 − 2 ρ ) + Γ ( 3 − ρ ) ζ ( 2 − 2 ρ ) Γ ( 2 − ρ ) Γ ( 3 − 2 ρ ) + ζ ( 3 − 2 ρ ) + ζ ( 2 − 2 ρ ) Γ ( 2 − ρ ) 2 + − ζ ( 2 − ρ ) − ζ ( 1 − ρ ) Γ ( 2 − ρ ) − Γ ( 3 − ρ ) ζ ( 2 − 2 ρ ) Γ ( 2 − ρ ) Γ ( 3 − 2 ρ ) .

Third RPSM approximation is expressed as follows:

(69) μ 3 ( ζ , ℑ ) = ζ + 1 − ζ ( 2 − ρ ) + ζ ( 1 − ρ ) Γ ( 2 − ρ ) ( ℑ ) δ Γ ( 1 + δ ) + Γ ( 3 − ρ ) ζ ( 3 − 2 ρ ) + Γ ( 3 − ρ ) ζ ( 2 − 2 ρ ) Γ ( 2 − ρ ) Γ ( 3 − 2 ρ ) + ζ ( 3 − 2 ρ ) + ζ ( 2 − 2 ρ ) Γ ( 2 − ρ ) 2 ( ℑ ) 2 δ Γ ( 1 + 2 δ ) − ( ζ + 1 ) Γ ( 3 − ρ ) Γ ( 4 − 2 ρ ) ζ ( 3 − 3 ρ ) Γ ( 2 − ρ ) Γ ( 3 − 2 ρ ) Γ ( 4 − 3 ρ ) + Γ ( 4 − 2 ρ ) ζ ( 3 − 3 ρ ) Γ ( 2 − ρ ) 2 Γ ( 4 − 3 ρ ) + − Γ ( 3 − ρ ) ζ ( 2 − 2 ρ ) Γ ( 2 − ρ ) Γ ( 3 − 2 ρ ) × − ζ ( 2 − ρ ) − ζ ( 1 − ρ ) Γ ( 2 − ρ ) + ζ ( 1 − ρ ) Γ ( 2 − ρ ) Γ ( 3 − ρ ) ζ ( 3 − 2 ρ ) + Γ ( 3 − ρ ) ζ ( 2 − 2 ρ ) Γ ( 2 − ρ ) Γ ( 3 − 2 ρ ) + ζ ( 3 − 2 ρ ) + ζ ( 2 − 2 ρ ) Γ ( 2 − ρ ) 2 + − ζ ( 2 − ρ ) − ζ ( 1 − ρ ) Γ ( 2 − ρ ) − Γ ( 3 − ρ ) ζ ( 2 − 2 ρ ) Γ ( 2 − ρ ) Γ ( 3 − 2 ρ ) ( ℑ ) 3 δ Γ ( 1 + 3 δ ) .

By substituting δ = ρ = 1 in Eq. (69), we obtain

(70) μ ( ζ , ℑ ) = 1 + ζ 1 + ℑ ,

which is the closed form solution of Example 4.3.

5 Results and discussion

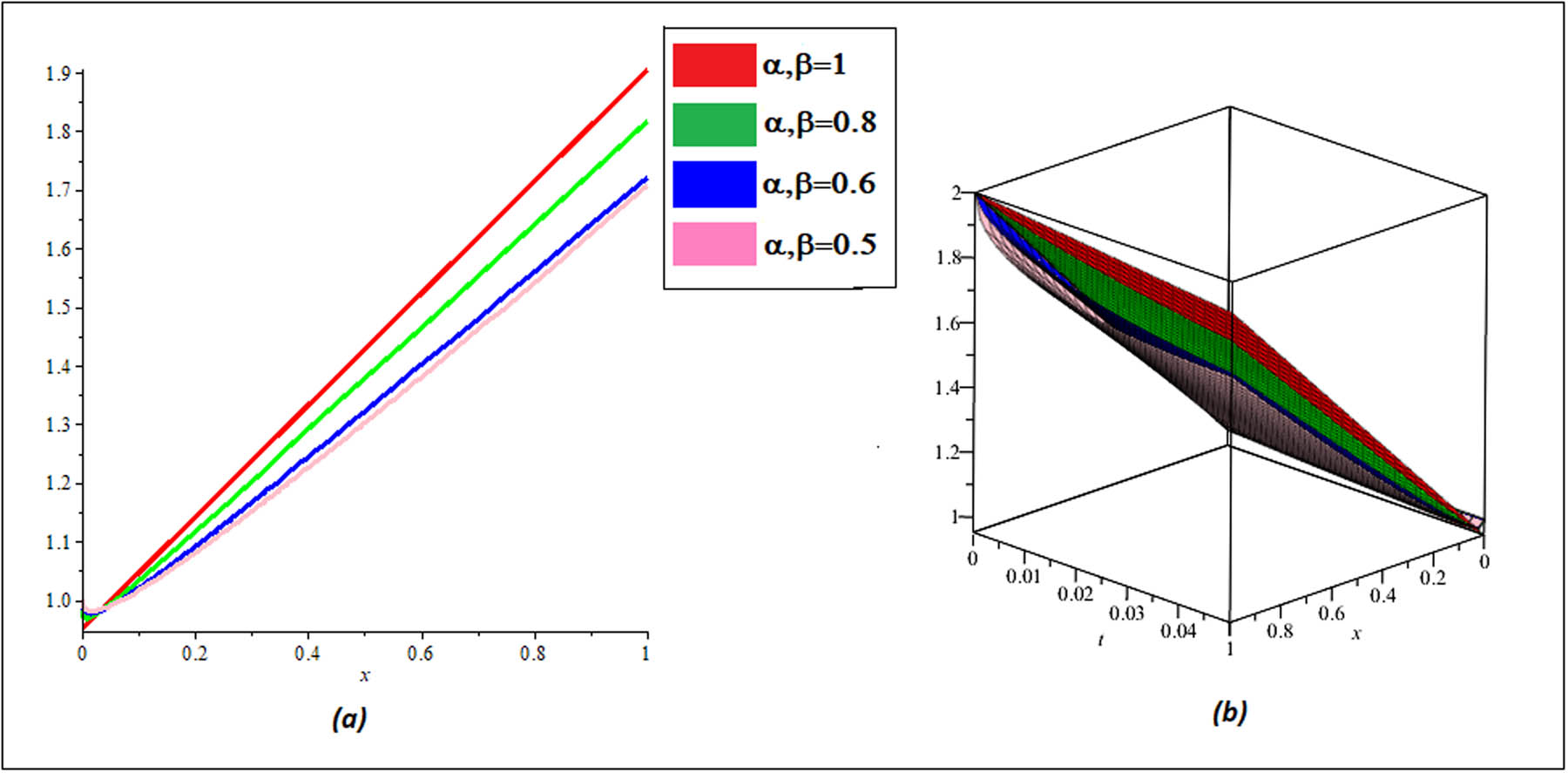
Figures 1 and 2 depict the 3D and 2D comparison plots of the exact and RPSM solutions, respectively, while Figure 3 depicts the 2D and 3D plots of Example 4.1 for various fractional-order δ . Figures 4 and 5 show the 3D and 2D comparison plots of the exact and RPSM-solution, respectively, while Figure 6 shows the 2D and 3D plots of Example 4.2 for different fractional-order δ . Figures 7 and Figure 8 show the 3D and 2D comparison plots of the Exact and RPSM solutions, respectively, while Figure 9 shows the 2D and 3D plots of Example 4.3 for different fractional-order δ . Tables 1, 2, and 3 are the absolute error (AE) tables for different spaces of Examples 4.1–4.3, respectively.

$Figure 1 3D solution graph, at δ \delta and ρ = 1 \rho =1 of Example 4.1.$

Figure 1

3D solution graph, at δ and ρ = 1 of Example 4.1.

$Figure 2 2D solution graph, at δ \delta and ρ = 1 \rho =1 of Example 4.1.$

Figure 2

2D solution graph, at δ and ρ = 1 of Example 4.1.

$Figure 3 2D and 3D plots exact and RPSM solutions of Example 4.1 for different values of δ \delta .$

Figure 3

2D and 3D plots exact and RPSM solutions of Example 4.1 for different values of δ .

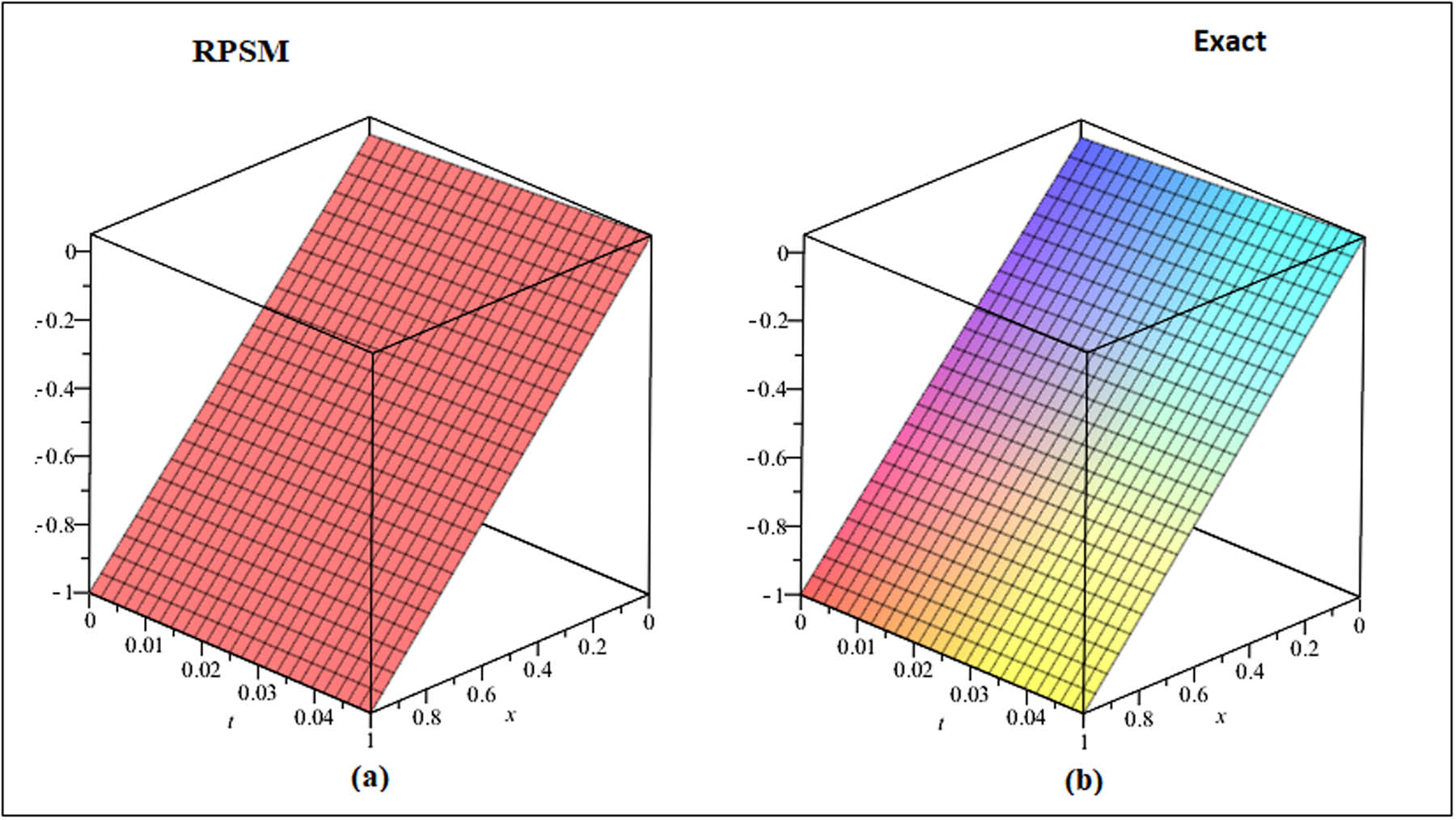
$Figure 4 3D (a) RPSM solution and (b) exact solution graph, at δ \delta and ρ = 1 \rho =1 of Example 4.2.$

Figure 4

3D (a) RPSM solution and (b) exact solution graph, at δ and ρ = 1 of Example 4.2.

$Figure 5 2D (a) RPSM solution (b) exact solution graph, at δ \delta and ρ = 1 \rho =1 of Example 4.2.$

Figure 5

2D (a) RPSM solution (b) exact solution graph, at δ and ρ = 1 of Example 4.2.

$Figure 6 2D and 3D plots for RPSM solution of Example 4.2 for different values of δ \delta .$

Figure 6

2D and 3D plots for RPSM solution of Example 4.2 for different values of δ .

$Figure 7 3D solution comparison graph, at δ \delta and ρ = 1 \rho =1 of Example 4.3.$

Figure 7

3D solution comparison graph, at δ and ρ = 1 of Example 4.3.

$Figure 8 2D solution comparison graph, at δ \delta and ρ = 1 \rho =1 of Example 4.3.$

Figure 8

2D solution comparison graph, at δ and ρ = 1 of Example 4.3.

$Figure 9 2D and 3D plots for RPSM solution of Example 4.3 for different values of δ \delta .$

Figure 9

2D and 3D plots for RPSM solution of Example 4.3 for different values of δ .

Table 1

AE of Example 1, at ℑ = 0.05 and δ , ρ = 1

	Exact–RPSM	Exact–RPSM	Exact–RPSM
ζ	K = 1	K = 2	K = 3
0.1	1.252861704 × 1 0 − 3	2.861704 × 1 0 − 6	1.305 × 1 0 − 6
0.2	1.257024208 × 1 0 − 3	7.024208 × 1 0 − 6	1.309 × 1 0 − 6
0.3	1.261186712 × 1 0 − 3	1.1186712 × 1 0 − 5	1.313 × 1 0 − 6
0.4	1.265349216 × 1 0 − 3	1.5349216 × 1 0 − 5	1.318 × 1 0 − 6
0.5	1.269511720 × 1 0 − 3	1.9511720 × 1 0 − 5	1.321 × 1 0 − 6
0.6	1.273674224 × 1 0 − 3	2.3674224 × 1 0 − 5	1.326 × 1 0 − 6
0.7	1.277836728 × 1 0 − 3	2.7836728 × 1 0 − 5	1.330 × 1 0 − 6
0.8	1.281999232 × 1 0 − 3	3.1999232 × 1 0 − 5	1.334 × 1 0 − 6
0.9	1.286161736 × 1 0 − 3	3.6161736 × 1 0 − 5	1.338 × 1 0 − 6
1	1.29032424 × 1 0 − 3	4.0324240 × 1 0 − 5	1.343 × 1 0 − 6

Table 2

AE comparison of RPSM and ADM [49] for Example 4.2

t	ζ	RPSM	ADM
0.01	0.3	2.0 × 1 0 − 9	2.9798 × 1 0 − 9
	0.6	1.0 × 1 0 − 9	6.0101 × 1 0 − 9
	0.9	4.0 × 1 0 − 9	9.04041 × 1 0 − 9
0.05	0.3	1.31580 × 1 0 − 6	1.80921 × 1 0 − 6
	0.6	6.5790 × 1 0 − 7	3.78289 × 1 0 − 6
	0.9	2.63160 × 1 0 − 6	5.75658 × 1 0 − 6
0.1	0.3	2.222220 × 1 0 − 5	2.77778 × 1 0 − 5
	0.6	1.111120 × 1 0 − 5	6.11111 × 1 0 − 5
	0.9	4.444450 × 1 0 − 5	9.44444 × 1 0 − 5

Table 3

AE of Example 4.3, at ℑ = 0.05 and δ , ρ = 1

	Exact–RPSM	Exact–RPSM	Exact–RPSM
ζ	K = 1	K = 2	K = 3
0.1	2.6190476 × 1 0 − 3	1.3095236 × 1 0 − 4	6.5476 × 1 0 − 6
0.2	2.8571428 × 1 0 − 3	1.4285712 × 1 0 − 4	7.1428 × 1 0 − 6
0.3	3.0952380 × 1 0 − 3	1.5476188 × 1 0 − 4	7.7380 × 1 0 − 6
0.4	3.3333332 × 1 0 − 3	1.6666664 × 1 0 − 4	8.3332 × 1 0 − 6
0.5	3.5714284 × 1 0 − 3	1.7857140 × 1 0 − 4	8.9284 × 1 0 − 6
0.6	3.8095236 × 1 0 − 3	1.9047616 × 1 0 − 4	9.5236 × 1 0 − 6
0.7	4.0476188 × 1 0 − 3	2.0238092 × 1 0 − 4	1.01188 × 1 0 − 5
0.8	4.2857140 × 1 0 − 3	2.1428568 × 1 0 − 4	1.07140 × 1 0 − 5
0.9	4.5238092 × 1 0 − 3	2.2619044 × 1 0 − 4	1.13092 × 1 0 − 5
1	4.7619044 × 1 0 − 3	2.380952 × 1 0 − 4	1.19044 × 1 0 − 5

6 Conclusion

The solutions of nonlinear systems are generally very difficult to investigate. In the present work, the solutions of some illustrative nonlinear problems of fractional partial differential equations are handled in a very simple and straightforward procedure. The fractional and integer order solutions to the targeted problems are analyzed by using graphs and tables. It is noted that RPSM has a direct and simple implementation to obtain solutions to the problems. The graphs and tables have confirmed the sufficient degree of accuracy of RPSM. In Figures 3, 6, and 9, the solutions at various fractional-orders of time and space are shown. The RPSM solutions are compared with adomian decomposition method (ADM) solutions, and the dominant accuracy of RPSM is confirmed over ADM. It is also investigated that the integer order solutions are in close contact with the exact solutions of each problem. The fractional solutions are obtained and found to be in strong agreement with the actual solutions to the problems. The proposed technique is very effective for nonlinear cases and thus supports a better way for solving FPDEs that arise frequently in science and engineering.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Saudi Arabia for founding this work through Research Groups program under grant number (R.G.P2./41/43).

Funding information: This research was funded by National Science, Research and Innovation Fund (NSRF), and King Mongkut’s University of Technology North Bangkok with Contract no. KMUTNB-FF-65-24. The authors acknowledge the financial support provided by the Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT.
Author contributions: A. A. Alderremy: project administrator; Hassan Khan: supervision; Qasim khan: methodology; Poom Kumam: funding, draft writing; Shaban Aly: investigation; Said Ahmad: methodology. All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors state no conflict of interest.
Data availability statement: Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.

References

[1] Arafa A, Elmahdy G. Application of residual power series method to fractional coupled physical equations arising in fluids flow. Int J Differ Equ. 2018;2018. 10.1155/2018/7692849Suche in Google Scholar

[2] Khan MA, Ullah S, Farooq M. A new fractional model for tuberculosis with relapse via Atangana-Baleanu derivative. Chaos Solitons Fractals. 2018;116:227–38. 10.1016/j.chaos.2018.09.039Suche in Google Scholar

[3] Jajarmi A, Baleanu D, ZarghamiVahid K, Mobayen S. A general fractional formulation and tracking control for immunogenic tumor dynamics. Math Meth Appl Sci. 2022;45(2):667–80. 10.1002/mma.7804Suche in Google Scholar

[4] Baleanu D, Ghassabzade FA, Nieto JJ, Jajarmi A. On a new and generalized fractional model for a real cholera outbreak. Alexandria Eng J. 2022;61(11):9175–86. 10.1016/j.aej.2022.02.054Suche in Google Scholar

[5] Ullah S, Khan MA, Farooq M. A new fractional model for the dynamics of the hepatitis B virus using the Caputo-Fabrizio derivative. Europ Phys J Plus. 2018;133(6):1–14. 10.1140/epjp/i2018-12072-4Suche in Google Scholar

[6] Khan MA, Ullah S, Okosun KO, Shah K. A fractional-order pine wilt disease model with Caputo-Fabrizio derivative. Adv Differ Equ. 2018;2018(1):1–8. 10.1186/s13662-018-1868-4Suche in Google Scholar

[7] Singh J, Kumar D, Baleanu D. On the analysis of fractional diabetes model with exponential law. Adv Differ Equ. 2018;2018(1):1–15. 10.1186/s13662-018-1680-1Suche in Google Scholar

[8] Baleanu D, Diethelm K, Scalas E, Trujillo JJ. Fractional calculus: models and numerical methods. Vol. 3. World Scientifc; 2012. 10.1142/8180Suche in Google Scholar

[9] Zaslavsky GM. Chaos, fractional kinetics, and anomalous transport. Physics reports 2002;371(6):460–580. 10.1016/S0370-1573(02)00331-9Suche in Google Scholar

[10] Hirota R. Exact envelope-soliton solutions of a nonlinear wave equation. J Math Phys. 1973;14(7):805–9. 10.1063/1.1666399Suche in Google Scholar

[11] Kumar S, Kumar D, Singh J. Numerical computation of fractional Black-Scholes equation arising in fnancial market. Egyptian J Basic Appl Sci. 2014;1(3–4):177–83. 10.1016/j.ejbas.2014.10.003Suche in Google Scholar

[12] Mahmood S, Shah R, Arif M. Laplace adomian decomposition method for multi dimensional time fractional model of Navier-Stokes equation. Symmetry. 2019;11(2):149. 10.3390/sym11020149Suche in Google Scholar

[13] Ali I, Khan H, Shah R, Baleanu D, Kumam P, Arif M. Fractional view analysis of acoustic wave equations, using fractional-order differential equations. Appl Sci. 2020;10(2):610. 10.3390/app10020610Suche in Google Scholar

[14] Khan H, Arif M, Mohyud-Din ST. Numerical solution of fractional boundary value problems by using Chebyshev wavelet method. Matrix Sci Math. 2019;3(1):13–16. 10.26480/msmk.01.2019.13.16Suche in Google Scholar

[15] Khan H, Khan A, Kumam P, Baleanu D, Arif M. An approximate analytical solution of the Navier-Stokes equations within Caputo operator and Elzaki transform decomposition method. Adv Differ Equ. 2020;2020(1):1–23. 10.1186/s13662-020-03058-1Suche in Google Scholar

[16] Shah R, Khan H, Mustafa S, Kumam P, Arif M. Analytical solutions of fractional-order diffusion equations by natural transform decomposition method. Entropy. 2019;21(6):557. 10.3390/e21060557Suche in Google Scholar PubMed PubMed Central

[17] Ford NJ, Xiao J, Yan Y. A finite element method for time fractional partial differential equations. Fractional Calculus Appl Anal. 2011;14(3):454–74. 10.2478/s13540-011-0028-2Suche in Google Scholar

[18] El-Ajou A, Arqub OA, Momani S. Approximate analytical solution of the nonlinear fractional KdV-Burgers equation: a new iterative algorithm. J Comput Phys. 2015;293:81–95. 10.1016/j.jcp.2014.08.004Suche in Google Scholar

[19] Veeresha P, Ilhan E, Prakasha DG, Baskonus HM, Gao W. A new numerical investigation of fractional-order susceptible-infected-recovered epidemic model of childhood disease. Alexandria Eng J 2022;61(2):1747–56. 10.1016/j.aej.2021.07.015Suche in Google Scholar

[20] Jajarmi A, Baleanu D, Vahid KZ, Pirouz HM, Asad JH. A new and general fractional Lagrangian approach: a capacitor microphone case study. Results Phys. 2021;31:104950. 10.1016/j.rinp.2021.104950Suche in Google Scholar

[21] Baleanu D, Abadi MH, Jajarmi A, Vahid KZ, Nieto JJ. A new comparative study on the general fractional model of COVID-19 with isolation and quarantine effects. Alexandria Eng J. 2022;61(6):4779–91. 10.1016/j.aej.2021.10.030Suche in Google Scholar

[22] Hemeda AA. Homotopy perturbation method for solving systems of nonlinear coupled equations. Appl Math Sci. 2012;6(96):4787–800. Suche in Google Scholar

[23] Wazwaz AM. The variational iteration method for solving linear and nonlinear ODEs and scientific models with variable coefficients. Central Europ J Eng. 2014;4(1):64–71. 10.2478/s13531-013-0141-6Suche in Google Scholar

[24] Liao S. Homotopy analysis method in nonlinear differential equations. Beijing: Higher Education Press; 2012. p. 153–65. 10.1007/978-3-642-25132-0Suche in Google Scholar

[25] Erturk VS, Godwe E, Baleanu D, Kumar P, Asad J, Jajarmi A. Novel fractional-order Lagrangian to describe motion of beam on nanowire. Acta Physica Polonica A. 2021;140(3):265–72. 10.12693/APhysPolA.140.265Suche in Google Scholar

[26] Arqub OA. Series solution of fuzzy differential equations under strongly generalized differentiability. J Adv Res Appl Math. 2013;5(1):31–52. 10.5373/jaram.1447.051912Suche in Google Scholar

[27] El-Ajou A, Arqub OA, Zhour ZA, Momani S. New results on fractional power series: theories and applications. Entropy. 2013;15(12):5305–23. 10.3390/e15125305Suche in Google Scholar

[28] Abu Arqub O, El-Ajou A, Bataineh AS, Hashim I. A representation of the exact solution of generalized Lane-Emden equations using a new analytical method. In: Abstract and Applied Analysis. Vol. 2013. Hindawi; 2013. 10.1155/2013/378593Suche in Google Scholar

[29] Arqub OA, El-Ajou A, Al Zhour Z, Momani S. Multiple solutions of nonlinear boundary value problems of fractional-order: a new analytic iterative technique. Entropy. 2014;16(1):471–93. 10.3390/e16010471Suche in Google Scholar

[30] Alquran M. Analytical solutions of fractional foam drainage equation by residual power series method. Math Sci. 2014;8(4):153–60. 10.1007/s40096-015-0141-1Suche in Google Scholar

[31] Kumar A, Kumar S, Yan SP. Residual power series method for fractional diffusion equations. Fund Inform. 2017;151:213–30. 10.3233/FI-2017-1488Suche in Google Scholar

[32] Mahmood BA, Yousif MA. A residual power series technique for solving Boussinesq-Burgers equations. Cogent Math Stat. 2017;4:1279398. 10.1080/23311835.2017.1279398Suche in Google Scholar

[33] Kumar A, Kumar S. Residual power series method for fractional Burger types equations. Nonlinear Eng. 2016;5:235–44. 10.1515/nleng-2016-0028Suche in Google Scholar

[34] Abu Arqub O, Abo-Hammour Z, Al-Badarneh R, Momani S. A reliable analytical method for solving higher-order initial value problems. Discret Dyn Nat Soc. 2013;2013:1–12. 10.1155/2013/673829Suche in Google Scholar

[35] Kumar S, Kumar A, Baleanu D. Two analytical methods for time-fractional nonlinear coupled Boussinesq-Burgeras equations arise in propagation of shallow water waves, Nonlinear Dyn. 2016;85:699–715. 10.1007/s11071-016-2716-2Suche in Google Scholar

[36] Komashynska I, Al-Smadi M, Ateiwi A, Al-Obaidy S. Approximate analytical solution by residual power series method for system of Fredholm integral equations. Appl Math Inf Sci. 2016;10:1–11. 10.18576/amis/100315Suche in Google Scholar

[37] Komashynska I, Al-Smadi M, Al-Habahbeh A, Ateiwi A. Analytical approximate solutions of systems of multi-pantograph delay differential equations using residual power-series method. 2016. arXiv: http://arXiv.org/abs/arXiv:1611.05485. Suche in Google Scholar

[38] Abu Arqub O, El-Ajou A, Bataineh AS, Hashim I. A representation of the exact solution of generalized Lane-Emden equations using a new analytical method. In: Abstract and Applied Analysis. Vol. 2013. Hindawi; 2013. 10.1155/2013/378593Suche in Google Scholar

[39] Wang L, Chen X. Approximate analytical solutions of time fractional Whitham-Broer-Kaup equations by a residual power series method. Entropy 2015;17:6519–33. 10.3390/e17096519Suche in Google Scholar

[40] Jena RM, Chakraverty S. Residual power series method for solving time-fractional model of vibration equation of large membranes. J Appl Comput Mech. 2019;5:603–15. Suche in Google Scholar

[41] Alquran M. Analytical solution of time-fractional two-component evolutionary system of order 2 by residual power series method. J Appl Anal Comput. 2015;5(4):589–99. 10.11948/2015046Suche in Google Scholar

[42] Dubey VP, Kumar R, Kumar D. A reliable treatment of residual power series method for time-fractional BlackScholes European option pricing equations. Phys A Statist Mechanic Appl. 2019;533:122040. 10.1016/j.physa.2019.122040Suche in Google Scholar

[43] Rao TR. Application of residual power series method to time fractional gas dynamics equations. J Phys Conf Ser. 2018;1139:012007. 10.1088/1742-6596/1139/1/012007Suche in Google Scholar

[44] Abu Arqub O. Application of residual power series method for the solution of time-fractional Schrödinger equations in one-dimensional space. Fundamenta Informaticae. 2019;166(2):87–110. 10.3233/FI-2019-1795Suche in Google Scholar

[45] Tariq H, Akram G. Residual power series method for solving time-space-fractional Benney-Lin equation arising in falling film problems. J Appl Math Comput. 2017;55(1):683–708. 10.1007/s12190-016-1056-1Suche in Google Scholar

[46] Demir A, Bayrak MA. A new approach for the solution of space-time fractional-order heat-like partial differential equations by residual power series method. Commun Math Appl. 2019;10(3):585–97. 10.26713/cma.v10i3.626Suche in Google Scholar

[47] Ahmad H, Khan TA, Durur H, Ismail GM, Yokus A. Analytic approximate solutions of diffusion equations arising in oil pollution. J Ocean Eng Sci. 2021;6(1):62–9. 10.1016/j.joes.2020.05.002Suche in Google Scholar

[48] Owolabi KM, Atangana A, Akgul A. Modelling and analysis of fractal-fractional partial differential equations: Application to reaction-diffusion model. Alexandria Eng J. 2020;59:2477–90. 10.1016/j.aej.2020.03.022Suche in Google Scholar

[49] Javed I, Ahmad A, Hussain M, Iqbal S. Some solutions of fractional-order partial differ-ential equations using adomian decomposition method. 2017. arXiv: http://arXiv.org/abs/arXiv:1712.09207. Suche in Google Scholar

Received: 2022-05-13

Revised: 2022-06-07

Accepted: 2022-06-16

Published Online: 2022-08-09

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

https://doi.org/10.1515/phys-2022-0069

Schlagwörter für diesen Artikel

fractional partial differential equations; Caputo derivative operator; residual power series method; analytical technique

Creative Commons

BY 4.0