Effect of geometry error on the non-Newtonian flow in the ceramic microchannel molded by SLA

Jie Zhang; Hai Gu; Jianhua Sun; Bin Li; Jie Jiang; Weiwei Wu

doi:10.1515/phys-2022-0004

Article Open Access

Effect of geometry error on the non-Newtonian flow in the ceramic microchannel molded by SLA

Jie Zhang , Hai Gu , Jianhua Sun , Bin Li , Jie Jiang and Weiwei Wu

Published/Copyright: February 10, 2022

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

From the journal Open Physics Volume 20 Issue 1

Abstract

The ceramic microchannel manufactured by stereolithography (SLA) can be used in many engineering cases. SLA is an accurate 3D printing technology, while the small geometry error is inevitable. The involved flow is always non-Newtonian fluids. Therefore, it is necessary to analyze Bingham fluids flow in the ceramic microchannel with geometry errors. To conduct the numerical simulations, a modified lattice Boltzmann (LB) model is presented. Then, the good consistency between the theoretical and numerical solutions demonstrates the effectiveness of the improved method. The required cases are analyzed by using the proposed method. Both the streamlines and outlet velocity distribution show that the geometry error increases the outlet velocity. The Bingham parameters are important factors in the flow of the microchannel.

Keywords: geometry error; ceramic; microchannel; Bingham fluids

1 Introduction

Stereolithography (SLA), as a type of high-precision 3D printing technology, has been widely used to mold various parts [1,2,3]. The commonly used material is photosensitive resin. In recent years, to broaden the application, some experiments have been done to develop new suitable materials. The photosensitive resin is always selected as the basic material and other materials (such as polyimide, ceramics) are mixed with it. The ultraviolet solidifies the resin and then the other materials are wrapped by the solidified resin [4,5,6]. In this way, the parts can be manufactured easily. If the content of the resin is small, additional post-processing is not required; otherwise, a degreasing process is necessary. When the ceramic materials are applied to SLA, the high solid content of the ceramic powders is essential and the resin is also required to improve the flowability [7,8], therefore, the degrease is included in the processes to increase the content of the ceramics and decrease the resin.

The ceramics have the advantages of perfect stability, high strength, and hardness, and have been widely applied to many engineering areas. However, it is difficult to mold into parts by using conventional CNC manufacturing. SLA provides a new way for the molding process. Based on the high precision, SLA can be used to print the ceramic microchannel [9]. However, when 3D printing is compared with traditional machining technologies, such as CNC machining, the main disadvantages are the poorer accuracy and mechanical performances. Particularly, poor accuracy is more obvious for printing micro parts. The layer thickness results in the inevitable stair-stepping effect. The dimension shrinkage always occurs in the phase transition. The nozzle dimension, laser power, extrusion speed, and scanning speed have been confirmed to affect the printing performances. The lack of accuracy may affect applications such as the fluids flow and heat transfer in the microchannel.

In the present work, the non-Newtonian flow in the ceramic microchannel manufactured by SLA is investigated and the effect of the geometry error is considered in detail. To realize the abovementioned analysis, the numerical simulation is adopted here. Fluent, as a common commercial computational fluids dynamic analysis software, has been widely used to solve the fluids flow [10,11,12]. However, secondary development is always required in complicated cases, which increases the difficulty in the solving process. Lattice Boltzmann method (LBM) is a program method which has a clear and convenient physical computational process, and can be used to solve many complex fluid dynamics cases [13,14]. Based on the advantage, it is used to solve the micro non-Newtonian flow mentioned above. Chen and Shu proposed a simplified LB model for power-law fluids flow, which adopts the corrector predicting scheme [15]. Li and Tian presented a hybrid immersed boundary LB model and finite differential method to analyze the non-Newtonian fluids [16]. Weiwei et al. proposed a universal improved model for common non-Newtonian fluids flow based on the multiple-relaxation-time (MRT) LBM [17]. Rezaie and Norouzi conducted the numerical investigation of magnet hydrodynamics non-Newtonian fluids flow over a circular cylinder by using LBM [18]. Li et al. proposed an axisymmetric LB model for power-law fluids flow, and the effectiveness is also demonstrated [19]. Kefayati proposed an immersed boundary LBM to solve the thermal and thermos-solutal case, which can be efficiently applied to both Newtonian and non-Newtonian fluids flow [20]. Adam and Premnath numerically investigated non-Newtonian fluids flow by proposing a cascaded central moment LBM [21]. Chiappini proposed a LB free surface model to simulate the injection molding process for non-Newtonian fluids [22]. Wang et al. employed a diffusive interface LB model with a lattice advection-diffusion scheme to analyze the viscoelastic non-Newtonian drop flow [23]. In most of the above cases, the LBM is modified with some models, which is mainly caused by the changeable located relaxation parameters [24]. The modified LBM can improve the stability in solving the non-Newtonian fluids flow.

The work is organized as follows. In Section 2, an improved LB model for Bingham fluids is proposed and the effectiveness is validated. In Section 3, the geometrical model of the microchannel is introduced, the geometry error is described, and then the required simulations are conducted. In Section 4, the discussion and conclusion are given.

2 Numerical simulation method

2.1 Improved LB model for Bingham fluids

In this section, the flow analysis method is introduced and validated. As mentioned above, LBM has been used in many engineering cases. To improve the stability and accuracy of the numerical method, LBM is modified based on the standard LB model containing an external force. The standard expression is shown as follows [25]:

(1) f ( r + e i δ t , t + δ t ) − f ( r , t ) = − 1 τ [ f ( r , t ) − f eq ( r , t ) ] + δ t F ′ ,

where r denotes the displacement vector, τ denotes the relaxation time, δt is the time step, which is equal to 1. e _i denotes the discrete velocity, which is expressed as:

(2) e i = ( 0 , 0 ) , i = 0 , c cos i − 1 2 π , sin i − 1 2 π , i = 1 , 2 , 3 , 4 , 2 c cos 2 i − 9 4 π , sin 2 i − 9 4 π , i = 5 , 6 , 7 , 8 ,

where c is the lattice speed, which is defined by c = δx/δt, δx is the lattice step, which is always set to 1, thus, c is equal to 1. f and f ^eq denote the general and equilibrium distribution functions, respectively, where f ^eq is expressed as follows:

(3) f eq ( r , t ) = ω i ρ 1 + ( e i ⋅ u ) c s 2 + ( e i ⋅ u ) 2 2 c s 4 − u 2 2 c s 2 ,

where c _s is the lattice sound speed, which is described as c 3 2 = c 2 / 3 , u denotes the velocity vector, ω _i denotes the weight coefficient, which is given by ω ₀ = 4/9 for i = 0, ω _i = 1/9 for i = 1–4 and ω _i = 1/36 for i = 5–8.

The strain rate tensor S _αβ for the power-law fluid can be calculated as:

(4) S α β = − 1 2 ρ τ c s 2 ∑ i = 0 8 e i α e i β ( f i − f i eq ) ,

where ρ denotes the numerical density.

Then, the second invariant of strain rate tensor D _II can be calculated as:

(5) D II = ∑ α , β = 1 l S α β S α β .

The shearing rate can be further obtained according to the following expression.

(6) γ ̇ = 2 D II .

There is the following description based on the isotropic constraint condition.

(7) ∑ i = 1 9 f i e q e i α e i β = ρ u α u β + P δ α β = ρ u α u β + 1 3 ρ δ α β ,

where δ _αβ denotes the Kronecker delta.

The general distribution function and momentum flux tensor can be expanded based on the Champ–Enskog expansion rule. The specific equations are expressed as follows:

(8) f i ≈ f i e q + ε f i ( 1 ) + ε 2 f i ( 2 ) , Π α β ≈ Π α β ( 0 ) + Π α β ( 1 ) ,

where ∏ α β and ∏ α β ( 0 ) stand for the equilibrium and non-equilibrium momentum flux tensors, respectively. They can be obtained by solving the first moment of the velocity.

(9) ∏ α β ( 0 ) ∑ i e i α e i β f i eq = − P δ α β + ρ u α u β , Π α β ( 1 ) = ∑ i = 0 8 e i α e i β 1 − 1 2 τ f i ( 1 ) .

Substituting equation (9) in equation (8), the specific expression for the momentum flux tensor can be obtained as follows:

(10) ∏ α β = − P δ α β + ρ u α u β + 2 μ b S α β ,

where μ _b denotes the dynamic viscosity for the Bingham fluids, which is described by the standard form as follows:

(11) μ b = μ b 0 + τ b 0 | γ ̇ | [ 1 − exp ( − m | γ ̇ | ) ] ,

where μ _b0 is the viscosity coefficient and m is a stress-related factor, which is set to 400 here. Bingham fluids are similar to Newtonian fluids, the biggest difference is that Bingham fluids exhibit the yielding behavior, only when the yielding stress is larger than the initial yielding stress, the effective flow occurs. Therefore, the rheological equation is always truncated and equation (11) is a modified equation for convenient calculation. The relaxation time τ can be calculated by the following:

(12) τ = μ b ρ δ t c s 2 + 1 2 .

If the fluids discussed here is assumed to be incompressible fluids, then the general momentum flux tensor can also be described as follows:

(13) ∏ α β = ρ u α u β − σ α β .

The stressor tensor can be further calculated based on equations (10) and (13).

(14) σ α β = − P δ α β + 2 μ b 0 S α β + 2 μ b 0 1 + τ b 0 μ b 0 | γ ̇ | [ 1 − exp ( − m | γ ̇ | ) ] − 1 S α β .

Considering the N–S equation at the incompressible limit, the following equation can be obtained based on the Chapman–Enskog expansion.

(15) ρ ∂ t ( u β ) + ( ρ u α ) ∂ α u β = − ∂ β P + 2 μ b 0 ∂ α S α β + 2 μ b 0 1 + τ b 0 μ b 0 | γ ̇ | [ 1 − exp ( − m | γ ̇ | ) ] − 1 ∂ α S α β = − ∂ β P + 2 μ p 0 ∂ α S α β + F ¯ .

Therefore, the description of F ¯ can be obtained as follows:

(16) F ¯ = 2 μ b 0 1 + τ b 0 μ b 0 | γ ̇ | [ 1 − exp ( − m | γ ̇ | ) ] − 1 ∂ α S α β .

For the general LB model with the external force, the relative item is expressed as follows:

(17) F i ' = ω i 1 - δ t τ e i − u c s 2 + ( e i ⋅ u ) c s 4 ⋅ e i F ¯ .

Substituting equation (16) in equation (17), the modified equation used to describe the non-Newtonian effect for power-law fluids can be expressed as follows:

(18) F i ' = 2 μ b 0 ω i 1 − δ t τ e i − u c s 2 + ( e i ⋅ u ) c s 4 ⋅ e i × 1 + τ b 0 μ b 0 | γ ̇ | [ 1 − exp ( − m | γ ̇ | ) ] − 1 ∂ α S α β .

2.2 Validation

When the effectiveness of a numerical simulation method is required to be validated, the known cases in the literature and the theoretical solutions of certain cases can be used for comparison. Poiseuille flow is a classical fluids flow case, which owns the theoretical solutions for most of the generalized Newtonian fluids. For Bingham fluids, the solution is expressed as follows:

(19) u b ( y ) = 1 2 − 1 μ b 0 ∂ P ∂ x H 2 2 − y b τ 2 − τ b 0 μ b 0 H 2 − y b τ , 0 ≤ ∣ y ∣ ≤ y b τ , 1 2 − 1 μ b 0 ∂ P ∂ x H 2 2 − ∣ y ∣ 2 − τ b 0 μ b 0 H 2 − ∣ y ∣ , y b τ < ∣ y ∣ ≤ H 2 ,

where H is the distance between two plates, y denotes the distance between a certain point and the middle position, ∂ P / ∂ x is the pressure gradient, y _bτ is the critical value because of the initial yielding stress, which is calculated as:

(20) y b τ = − τ b 0 ∂ p / ∂ x .

In the simulation and the theoretical calculation, the relevant parameters are set as follows. H is equal to 1, ∂ P / ∂ x is set to −2 × 10⁻⁴, μ _b0 is 0.01, lattice nodes are 150 × 150, and the initial yielding stresses are set to 4 × 10⁻⁵, 5 × 10⁻⁵, and 6 × 10⁻⁵. The comparisons between the theoretical and numerical solutions are figured in Figure 1. The result shows that the numerical solution of each case is well consistent with the theoretical solution, which demonstrates that the proposed numerical method is effective.

Figure 1

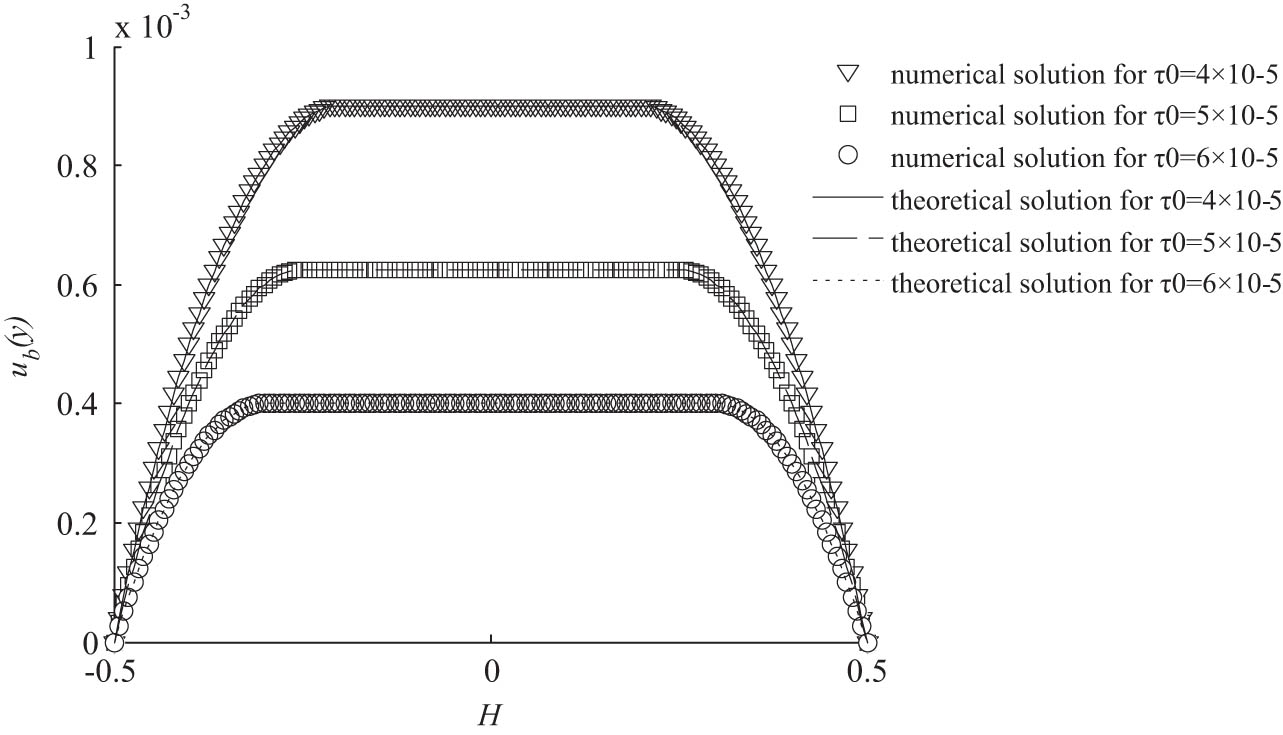
Validation by theoretical solutions of Poiseuille flow.

3 Bingham fluids flow in the ceramic microchannel manufactured by SLA

3.1 The ceramic microchannel

It is assumed that the condition of the manufactured ceramic microchannel is shown in Figure 2(a). In the printing process, many factors may cause the geometrical error and the randomly distributed rectangles are used to describe the possible errors (Figure 2[b]). The different dimensions of the rectangles are considered for various Bingham parameters to analyze the flow. The fluids flow from the left to the right.

Figure 2

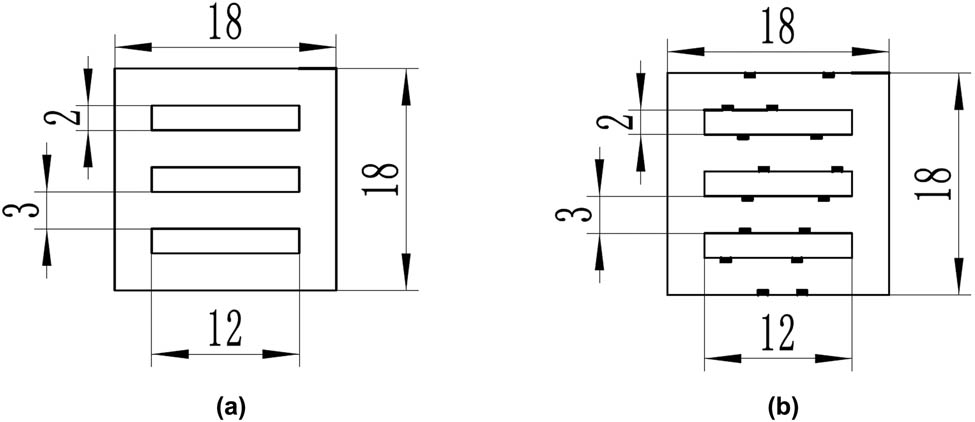
Designed microchannel: (a) without geometry error and (b) with geometry error.

3.2 Numerical simulations

To explore the effects of the geometry error and Bingham parameters on the flow, six cases are conducted for the analysis. The lattice nodes are set to 360 × 360 and the inlet velocity is set as a parabola form, whose maximum value is 1 m/s. When the printed microchannel is accurate enough, the simulated model is set as case 1, which is shown in Figure 2(a). The Bingham parameters are set as follows. The viscosity coefficient μ _b0 is 0.005 and the initial yielding stress τ _b0 is 4 × 10⁻⁵ Pa. The streamlines are shown in Figure 3(a). The red color represents the high-velocity area and the blue color corresponds to the low-velocity area. The active flow mainly involves the flow channels and the high-velocity flow concentrates in the middle positions. Once the fluids flow out from the baffles, the flow rapidly expands into a bell mouth form.

Figure 3

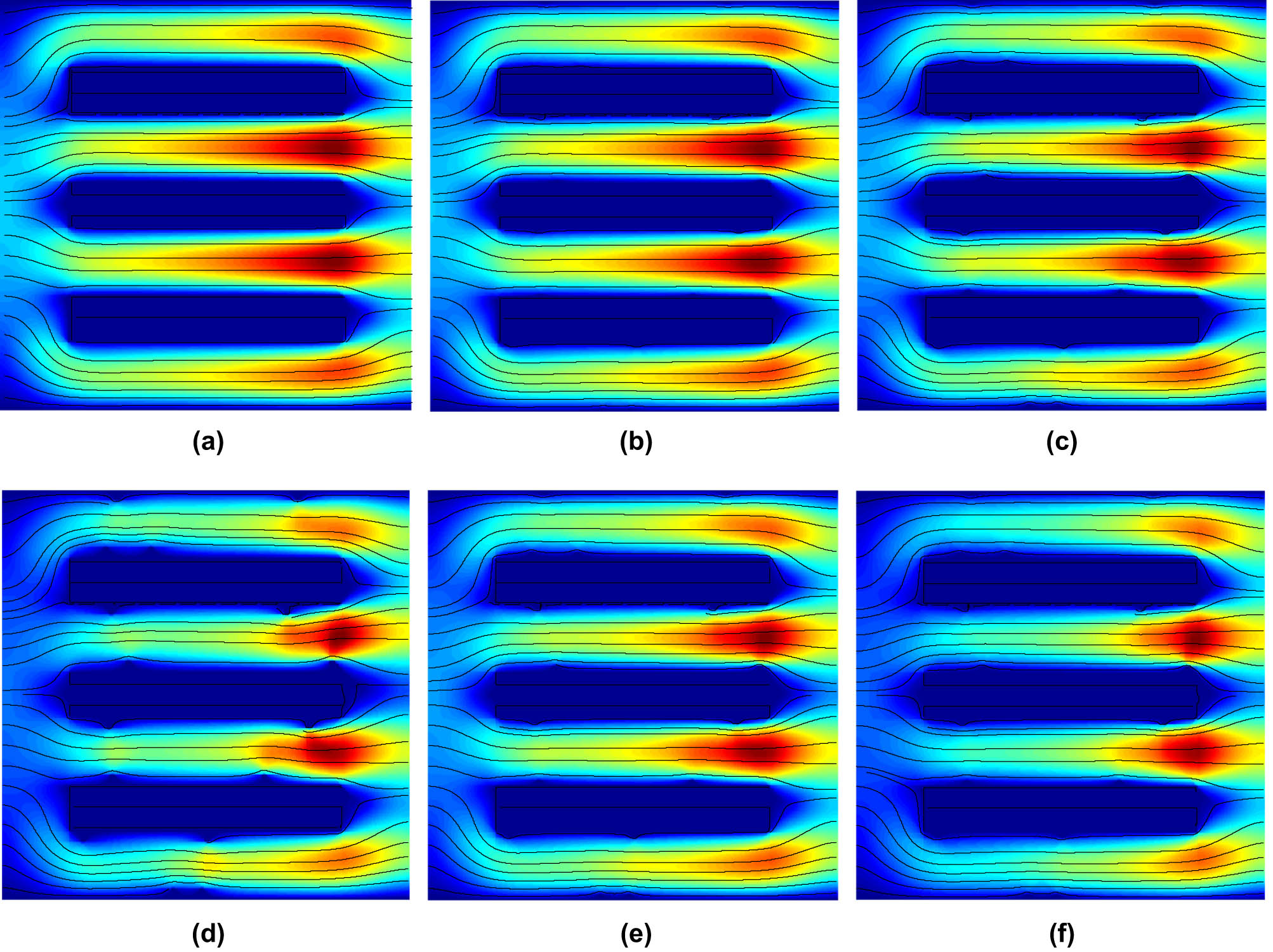
Streamlines of six cases: (a) streamlines of case 1, (b) streamlines of case 2, (c) streamlines of case 3, (d) streamlines of case 4, (e) streamlines of case 5, and (f) streamlines of case 6; case 1: without geometry error, the viscosity coefficient is 0.01 and the initial yielding stress is 4 × 10⁻⁵ Pa; case 2: with geometry error of 0.1 mm, the viscosity coefficient is 0.01 and the initial yielding stress is 4 × 10⁻⁵ Pa; case 3: with geometry error of 0.2 mm, the viscosity coefficient is 0.01 and the initial yielding stress is 4 × 10⁻⁵ Pa; case 4: with geometry error of 0.4 mm, the viscosity coefficient is 0.01 and the initial yielding stress is 4 × 10⁻⁵ Pa; case 5: with geometry error of 0.2 mm, the viscosity coefficient is 0.1 and the initial yielding stress is 4 × 10⁻⁵ Pa; and case 6: with geometry error of 0.2 mm, the viscosity coefficient is 0.01 and the initial yielding stress is 5 × 10⁻⁵ Pa.

In cases 2–4, the geometry errors of the microchannel are considered as 0.1, 0.2, and 0.4 mm, respectively, and the errors are described as random rectangles, whose positions are kept unchanged. The simulated results are shown in Figure 3(b)–(d). A similar phenomenon is that when the flow encounters the rectangle, a slight deformation occurs. The obvious deflection of the flow appears in Figure 3(d) while the error is large enough. Therefore, the geometry error must affect the flow. In case 5, the viscosity coefficient is increased to 0.1, and the other parameters are the same as that of case 3. The streamlines show that the dark red area is smaller than that in case 3. The initial yielding stress is increased to 5 × 10⁻⁵ Pa in case 6 and the other parameters are the same as that of case 3. The result shows that the high-velocity area is much smaller than that in case 3. Both cases 5 and 6 illustrate that Bingham parameters also have significant effects on the flow.

In addition, the outlet velocities of six cases are given in Figure 4 for comparison. The outlet velocity of each case has severely increased. The outlet velocity exhibits the oscillation form. The minimum velocity occurs near the boundary, which is negative. From the horizontal position, the peak area corresponds to the channel position, while the valley area corresponds to the baffle position. The curve of case 4 is different from others, which further validates that the increase in the error may affect the outflow. According to the velocity distribution, the increase in the error results in a larger outlet velocity. As the Bingham parameters increase, the outlet velocity also becomes larger.

Figure 4

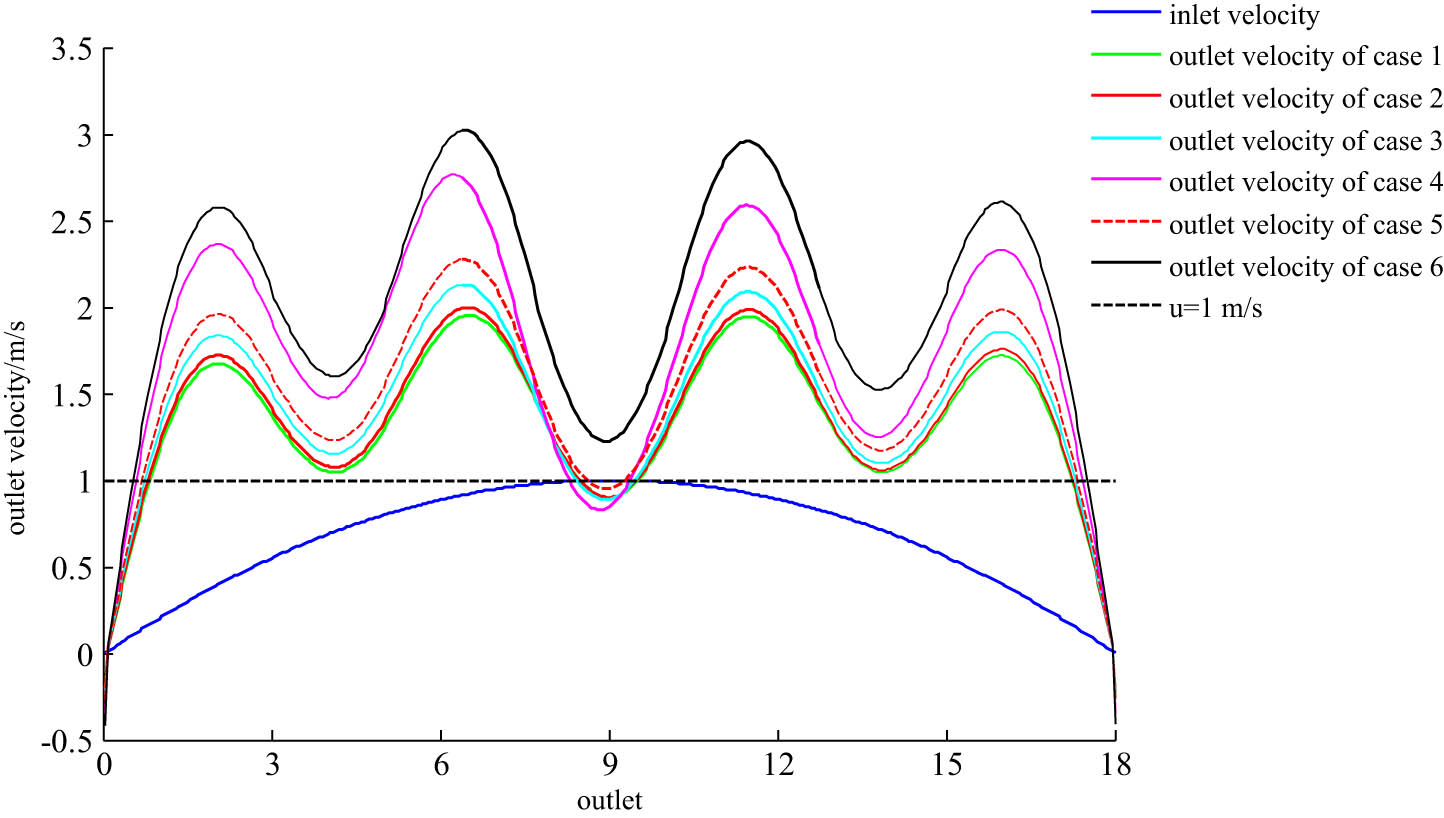
Outlet velocity distribution of six cases.

4 Discussion and conclusion

The Bingham flow in the ceramic microchannel manufactured by SLA is analyzed. To achieve the non-Newtonian flow simulation, a modified LB model is proposed and validated by the theoretical solutions of Poiseuille flow. Then, six cases are considered and analyzed to explain the Bingham flow in the microchannel. The results show that the geometry error and Bingham parameters (viscosity coefficient and initial yielding stress) affect the flow. The random distribution of the rectangles is used to describe the error. The outlet velocity in Figure 3(a) significantly increases when compared with the inlet velocity. The oscillation of the velocity mainly depends on the positions of the baffle and channel.

When the error is small, the effect on the flow process is also weak. As the error increases, the flow changes obviously and the dark red area is slightly shrunk. Further, the deflection of the flow direction also occurs to some extent. Regarding the outlet velocity, it increases with the increase in the geometry error.

The Bingham parameters are also considered. When the viscosity coefficient is increased from 0.01 to 0.1, the outlet velocity also increases. When the initial yielding stress is slightly increased, the velocity is increased severely and the dark red area is shrunk obviously. Therefore, the change in the Bingham parameters must affect the flow.

In summary, when considering the flow in the ceramic microchannel manufactured by SLA, the surface finish is an important factor for the flow process and the velocity distribution, and then the non-Newtonian behavior also has an obvious effect on the flow. Thus, when the microchannel is designed and molded, the above factors should be taken into consideration to contribute to obtaining the expected outflow.

Funding information: This work was financially supported by Key University Science Research Project of Jiangsu Province (Grant No. 18KJA460006), Top-notch Academic Programs Project of Jiangsu Higher Education Institutions (Grant No. 2020-9), Key R&D Plan of Jiangsu Province (Grant Nos. BE2018010-4 and BY2020545), Science and Technology Project of Nantong (Grant Nos. JCZ20056, JC2020155, and JC2020132), and Key Laboratory of Laser Processing and Metal Additive of Provincial Science and Technology Service Platform Cultivation project of Nantong Institute of Technology (Grant No. XQPT202101).
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors state no conflict of interest.
Data availability statement: The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

[1] Manapat JZ , Chen Q , Ye P , Advincula RC . 3D Printing of polymer nanocomposites via stereolithography. Macromol Mater Eng. 2017;302(9):1600553.10.1002/mame.201600553Search in Google Scholar

[2] Park JY , Kim HY , Kim JH , Kim JH , Kim WC . Comparison of prosthetic models produced by traditional and additive manufacturing methods. J Adv Prosthodont. 2015;7(4):294–302.10.4047/jap.2015.7.4.294Search in Google Scholar PubMed PubMed Central

[3] Yang Q , Lu Z , Zhou J , Miao K , Li D . A novel method for improving surface finish of stereolithography apparatus. Int J Adv Manuf Tech. 2017;93(5–8):1537–44.10.1007/s00170-017-0529-1Search in Google Scholar

[4] Sahin S , Nahar NK , Sertel K . Dielectric properties of low-loss polymers for mmW and THz Applications. J Infrared Millim Te. 2019;40(5):557–73.10.1007/s10762-019-00584-2Search in Google Scholar

[5] Esposito Corcione C , Montagna F , Greco A , Licciulli A , Maffezzoli A . Free form fabrication of silica moulds for aluminium casting by stereolithography. Rapid Prototyp J. 2006;12(4):184–8.10.1108/13552540610682688Search in Google Scholar

[6] Dehurtevent M , Robberecht L , Hornez JC , Thuault A , Deveaux E , Béhin P . Stereolithography: A new method for processing dental ceramics by additive computer-aided manufacturing. Dent mater. 2017;33(5):477–85.10.1016/j.dental.2017.01.018Search in Google Scholar PubMed

[7] Zhang C , Jiang Z , Zhao L , Guo W , Gao X . Stability, rheological behaviors, and curing properties of 3Y-ZrO2 and 3Y-ZrO2/GO ceramic suspensions in stereolithography applied for dental implants. Ceram Int. 2021;47(10):13344–50.10.1016/j.ceramint.2021.01.191Search in Google Scholar

[8] Li KH , Zhao Z . The effect of the surfactants on the formulation of UV-curable SLA alumina suspension. Ceram Int. 2017;43(6):4761–7.10.1016/j.ceramint.2016.11.143Search in Google Scholar

[9] Nawrot W , Malecha K . Additive manufacturing revolution in ceramic microsystems. Microelectron Int. 2020;37(2):79–85.10.1108/MI-11-2019-0073Search in Google Scholar

[10] Khalil I , Pratt Q . MATLAB/FLUENT model for studying the uncertainty quantification of spent nuclear fuel heat transfer. Nucl Technol. 2019;205(7):987–91.10.1080/00295450.2018.1554026Search in Google Scholar

[11] Ariza C , Casado C , Wang RQ , Adams E , Marugán J . Comparative evaluation of OpenFOAM (R) and ANSYS (R) Fluent for the modeling of annular reactors. Chem Eng Technol. 2018;41(7):1473–83.10.1002/ceat.201700455Search in Google Scholar

[12] Ridha H , Al-Azawy MG . Effect of wall heat transfer on the fluidization process. Int J Heat Technol. 2021;39(2):615–20.10.18280/ijht.390232Search in Google Scholar

[13] Menni Y , Ameur H , Yao SW , Amine Amraoui M , Inc M , Lorenzini G , et al. Computational fluid dynamic simulations and heat transfer characteristic comparisons of various arc-baffled channels. Open Phys. 2021;19(1):51–60.10.1515/phys-2021-0005Search in Google Scholar

[14] Zhang Y , Xu F , Li B , Kim YS , Zhao W , Xie G , et al. Three phase heat and mass transfer model for unsaturated soil freezing process: Part 2 – model validation. Open Phys. 2018;16(1):84–92.10.1515/phys-2018-0015Search in Google Scholar

[15] Chen Z , Shu C . Simplified lattice Boltzmann method for non‐Newtonian power-law fluid flows. Int J Numer Meth Fl. 2020;92(1):38–54.10.1002/fld.4771Search in Google Scholar

[16] Li W , Tian FB . Heat transfer in non-Newtonian flows by a hybrid immersed boundary-lattice Boltzmann and finite difference method. Appl Sci-Basel. 2018;8(4):559.10.3390/app8040559Search in Google Scholar

[17] Weiwei W , Shouli S , Zhouzhou W , Shuang D . A universal modified MRT LBM for common non-Newtonian fluids and their applications. Mech Mater. 2019;139:103187.10.1016/j.mechmat.2019.103187Search in Google Scholar

[18] Rezaie MR , Norouzi M . Numerical investigation of MHD flow of non-Newtonian fluid over confined circular cylinder: a lattice Boltzmann approach. J Braz Soc Mech Sci. 2018;40(4):185.10.1007/s40430-018-1128-2Search in Google Scholar

[19] Li Y , Zhuo Q , You W . Axisymmetric lattice Boltzmann method for non-Newtonian flows. Int J Numer Meth Fl. 2018;88(10–11):47992–492.10.1002/fld.4676Search in Google Scholar

[20] Kefayati G . An immersed boundary-lattice Boltzmann method for thermal and thermo-solutal problems of Newtonian and non-Newtonian fluids. Phys Fluids. 2020;32(7):073103.10.1063/5.0013977Search in Google Scholar

[21] Adam S , Premnath KN . Numerical investigation of the cascaded central moment lattice Boltzmann method for non-Newtonian fluid flows. J Non-Newton Fluid. 2019;274:104188.10.1016/j.jnnfm.2019.104188Search in Google Scholar

[22] Chiappini D . A lattice-Boltzmann free surface model for injection moulding of a non-Newtonian fluid. Philos T R Soc A. 2020;378(2175):20190407.10.1098/rsta.2019.0407Search in Google Scholar PubMed

[23] Wang D , Tan D , Nhan P . A lattice Boltzmann method for simulating viscoelastic drops. Phys Fluids. 2019;31(7):073101.10.1063/1.5100327Search in Google Scholar

[24] Gabbanelli S , Drazer G , Koplik J . Lattice Boltzmann method for non-Newtonian (power-law) fluids. Phys Rev E. 2005;72(4 Pt 2):046312.10.1103/PhysRevE.72.046312Search in Google Scholar PubMed

[25] Guo Z , Zheng C , Shi B . Discrete lattice effects on the forcing term in the lattice Boltzmann method. Phys Rev E. 2002;65(4):046308.10.1103/PhysRevE.65.046308Search in Google Scholar PubMed

Received: 2021-12-21

Revised: 2022-01-08

Accepted: 2022-01-10

Published Online: 2022-02-10

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/phys-2022-0004

Keywords for this article

geometry error; ceramic; microchannel; Bingham fluids

Creative Commons

BY 4.0