Experimental analysis of a laser beam propagating in angular turbulence

Gareth Daniel Enoch; Naven Chetty

doi:10.1515/phys-2022-0038

Article Open Access

Experimental analysis of a laser beam propagating in angular turbulence

Gareth Daniel Enoch and Naven Chetty

Published/Copyright: May 26, 2022

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

From the journal Open Physics Volume 20 Issue 1

Abstract

In this work, a Gaussian laser beam is propagated through a thermally turbulent region before passing through a point diffraction interferometer to produce a circular interferogram. This was done to ascertain how turbulent windstreams of various wind speeds and temperatures affect a laser beam when directed at different angles to the beam axis. The interferometric results portray a clear dependence on the angle of application. That is, deviations away from 90° result in increased wavefront fluctuations. The refractive index structure constant, Rytov variance, and Fried’s parameter were computed to quantify each turbulent model. The attributed strength regimes of these atmospheric parameters were in varying degrees of agreement with the interferometric data. These contradictions and resulting conclusions were discussed in full.

Keywords: turbulence; Gaussian laser beam; point diffraction interferometer; refractive index structure constant; Rytov variance; Fried’s parameter

1 Introduction

The study of the interactions of light within inhomogeneous media has been a robust field within the scientific world [1]. These interactions, known as optical turbulence, occur when light propagates through an inhomogeneous medium such as the earth’s atmosphere [2,3]. As such, the atmosphere exhibits fluctuations in its refractive index, with its intensity decreasing as altitude increases [1,4]. In addition to these fluctuations, other factors influencing a beam’s propagation are scattering via dust and fog as well as absorption via water vapour [5,6]. Refractive index fluctuations are attributed to the turbulent nature of the atmosphere due to the nonuniformity of its constituent temperatures and pressures [6]. Although the fluctuations of the refractive index at a single point in space are small, the accrual of these fluctuations on light over vast distances is substantial [4,7]. Thus, a laser beam that is propagating through a turbulent region will experience erratic changes in its wavefronts such as beam wander, beam spread, scintillation, and beam distortion [4,8,9,10,11,12].

Airflow is categorized as either laminar or turbulent, where laminar airflow is characterized by a uniformity in flow and a velocity that is uniform or changes in a consistent manner, whilst turbulent airflow undergoes unsystematic mixing with nonuniform velocities [4]. Due to the random nature of turbulence, a statistical model was formulated by Kolmogorov [13]. According to the Kolmogorov spectrum, refractive index fluctuations occur only within vortices, known as turbulent eddies, of sizes L ₀ to l ₀ with corresponding velocities of V ₀ to v ₀, respectively. The region bounded by L ₀ to l ₀ is known as the inertial subrange [4]. Fields such as radar, satellite communication, remote sensing, military and terrestrial communications rely strongly on information gathered from the study of electromagnetic waves propagating through the atmosphere [14,15,16,17,18]. In addition, it has been found that mammalian tissue exhibits refractive index variations [19]. Given the above applications, further research into how light interacts with inhomogeneous media is of utmost importance. For example, proper modelling may lead to reduced collateral damage for laser-guided military weapons as opposed to conventional weaponry.

Figure 1 depicts the experimental setup, which will be discussed in Section 3. The experimental setup is based on Ndlovu and Chetty’s works [20,21] and was later modified by Augustine and Chetty on two occasions [22,23]. The turbulent models used by Ndlovu and Chetty were a butane-fuelled flame and Dust Off spray, whilst Augustine and Chetty utilized an automated heating plate and later a wind tunnel while making an addition to the equipment by placing a highly sensitive differential pressure sensor within the turbulent region [20,21,22,23]. Their work has produced strong results despite being incredibly low in cost compared to other interferometric setups.

Figure 1

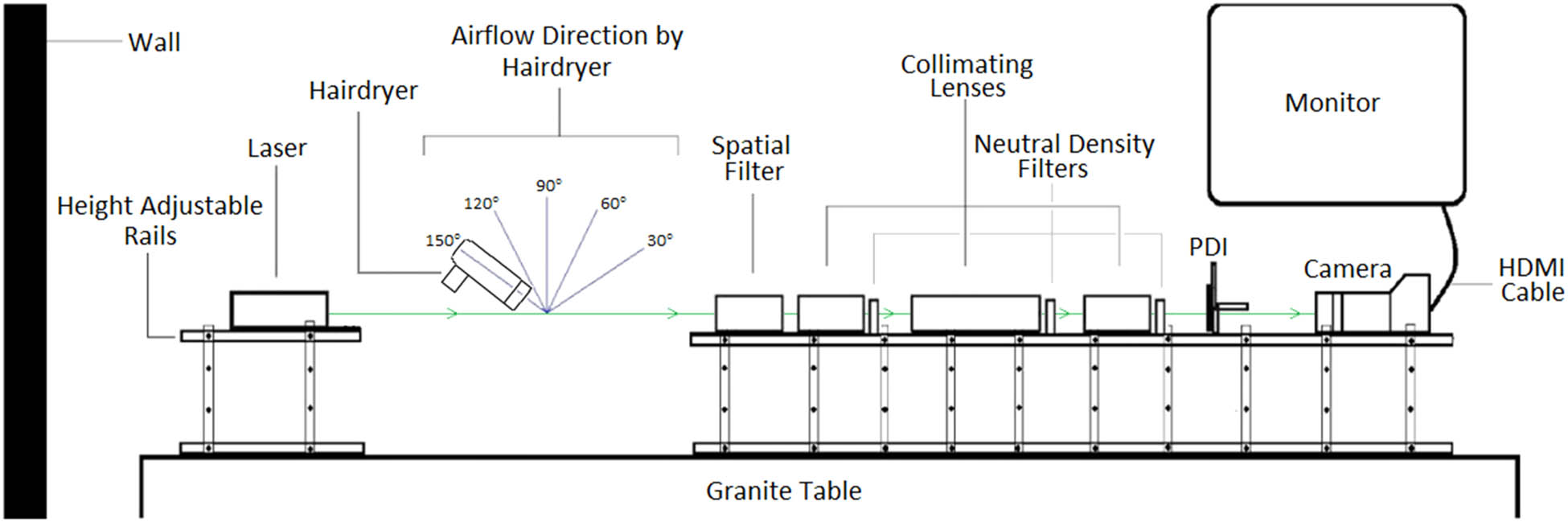
2D front view of the experimental setup.

2 Theory

Our atmosphere is classified as turbulent near the surface due to the energetic mixing of gases occurring within. These energetic mixings yield unsystematic sub-flows called eddies, with each eddy varying in size and velocity. As a result, a specific eddy has an associated refractive index. The accumulation of eddies over vast distances leads to an increase of aberrations experienced on the wavefronts. In the Kolmogorov power-law spectrum, it is only amongst eddies of an inertial range K (rad · m⁻¹) – which are locally isotropic and locally homogeneous – that refractive index fluctuations occur [13,24]:

(1) Φ n ( K ) = 0.033 C n 2 K − 11 / 3 , 2 π L 0 − 1 ≪ K ≪ 2 π l 0 − 1 ,

where C n 2 is the refractive index structure constant (m^−2/3), l ₀ is the inner turbulence scale, and L ₀ is the outer turbulence scale with values of l ₀ and L ₀ near the earth being on the orders of millimetres and metres, respectively.

The path through which light propagates depends on whether its medium is homogeneous or inhomogeneous. In a homogeneous medium with a constant refractive index, a laser beam will propagate in a straight path to the receiver with no erratic alterations to its wavefronts. In an inhomogeneous medium – such as our atmosphere or a water mass – a laser beam will exhibit various changes due to the perturbations initiated by the refractive index fluctuations occurring within. The pathway of the laser beam in a random medium will deviate from its initial aligned path (beam wander) as well as undergo other alterations to its wavefront such as energy redistribution/beam spread, loss of spatial coherence, and irradiance fluctuations/scintillations [4,25]. Scintillation strengths are commonly characterised using the Rytov variance of a plane wave [4]:

(2) σ R 2 = 1.23 C n 2 k 7 / 6 L 11 / 6 ,

where L is the beam path length within the turbulent region and k is the wavenumber. Scintillations are regarded as weak when σ R 2 < 1, moderate when σ R 2 ∼ 1, and strong when σ R 2 > 1.

The refractive index structure constant quantifies the degree to which a medium’s refractive index fluctuates. Weak turbulence is associated with values on the order of 10⁻¹⁷ m^−2/3 and lower whilst strong turbulence is associated with values on the order of 10⁻¹³ m^−2/3 and higher. Thus, the region of moderate turbulence is 10⁻¹⁷ m^−2/3 < C n 2 < 10⁻¹³ m^−2/3 [4]. As mentioned above, the degree of turbulence is higher at lower altitudes. This results in higher values of C n 2 closer to the ground. The refractive index structure constant is defined as follows [4,13]:

(3) C n 2 = 79.0 × 10 − 6 P T 2 C T 2 ,

where P, T, and C T 2 are the pressure (mbar), temperature (K), and temperature structure constant within the turbulence model. The temperature structure constant is defined as

(4) C T 2 = 〈 ( T ( x 0 ) − T ( x 0 + x ) ) 2 〉 x 2 / 3 ,

where T (K) is the temperature potential and x ₀ and x (m) are the position and separation vector, respectively. The parentheses (…) specify a time average, and the separation vector must be within the order of the inertial subrange [26,27].

When dealing with lasers in a turbulent region, it is useful to determine the atmospheric coherence diameter (or Fried’s parameter) r ₀, which is a measurement of the quality of the image received and the strength of the applied turbulence [12,28,29]. Standard values of r ₀ for outer space observatories are 5 cm for relatively poor visual conditions and 20 cm for remarkably good visual conditions, with an average value potentially being 10 cm [30]. Hence, values of r ₀ obtained below 5 cm indicate strong turbulence. According to Goodman [30], the atmospheric coherence diameter is defined as

(5) r 0 = 0.185 λ 2 ∫ 0 z C n 2 ( ξ ) d ξ 3 / 5 ,

where λ is the wavelength of the beam, z is the propagation path length within the turbulent region and ξ is an element of length.

3 Experimental setup

For this work, a 29.4 mW TEM00 He–Ne 532 nm laser beam was propagated through a turbulent region and a series of optical components (a spatial filter, an objective lens, reflective neutral density filters, and collimators) before striking a point diffraction interferometer (PDI) to produce a circular interferogram. The turbulence source used in this experiment was a multi-setting Toni & Guy 1800W hairdryer, as it produces a stream of wind that maintains a constant velocity and temperature whilst being low on cost. It features three temperature settings ranging from around 45°C, 110°C, and 136°C and two wind speed settings of 5.7 and 8.8 m · s⁻¹. It should be noted that upon decreasing the temperature to the first setting, the lowest wind speed increases to 6.8 m · s⁻¹. The wind speed was measured using a Brunton ADC Wind 21 cm away. The mentioned wind speeds correlate with a moderate breeze as determined by the device’s in-built Beaufort wind scale value of 4. The hairdryer creates several turbulent models by directing its flow at various angles to the beam axis. The hairdryer was secured on a retort stand to maintain a constant pressure and temperature profile at the required angle. Additionally, a concentrator nozzle was attached to the hairdryer outlet, which allowed a focus windstream to interact with the laser beam. A sensitive differential pressure sensor and a TM Electronics manufactured K-type thermocouple rod were mounted at the centre of the expanded laser beam. The differential pressure sensor was set to its lowest detection range of 0–0.100 kPa, while the thermometer, manufactured by Techgear (model code: TG732TK), detected temperatures at a 1 decimal place precision in degrees celsius. The ambient pressure was measured using an Xplorer GLX fitted with a barometer sensor and was set to a 1 decimal place precision in millibars. Readings were only taken once the fluctuations in the measured temperature and pressure within the turbulence region reduced, which indicated that the system had reached a maximised stabilisation point. A more detailed description of each component displayed in Figure 1 can be found in Augustine and Chetty’s work [22].

4 Experimental procedure

The optical components mentioned above were cleaned off of any dust that may have accumulated with methanol and Kimtech Delicate Task Wipers because the presence of dust dramatically augmented the profile of the interferograms in the presence of discontinuities due to scattered light falling on the detector. The collimators and reflective neutral density filters, 50 mm × 50 mm × 2.0 mm of 2.5 optical density, were then adjusted along the optical pathway to produce a focused beam of a reduced diameter to propagate through a selected pinhole of the PDI. The reflective neutral density filters served to reduce the intensity of the beam to allow the procurement of a clear circular interferogram depicting a Gaussian intensity profile that was then captured by the DSLR camera and projected onto a nearby monitor. Due to the highly sensitive nature of the experiment, extreme care was taken to not excessively touch the adjustable height rails and optical components once their placements were set. Perturbations were applied to the laser beam by incrementing the hair dryer’s temperature and wind speed settings at each prescribed angle (30°, 60°, 90°, 120°, and 150°). The angle of the hairdryer was measured using a large protractor with a thin rod aligning the hairdryer by swivelling about the protractor centre. The protractor was firmly attached to an elevated stand and aligned by a spirit level. The distance between the beam and the flow nozzle was kept constant by lowering the hairdryer towards the centre of the said protractor. The captured interferograms were inspected using image analysis software “ImageJ” to produce a cross-sectional intensity profile to graphically examine the extent of the fluctuations. Intensity profiles were then replotted using “Microsoft Excel” for readability. In Figure 2, an unperturbed interferogram is portrayed with arrows indicating where the cross-sectional intensity profile was procured.

Figure 2

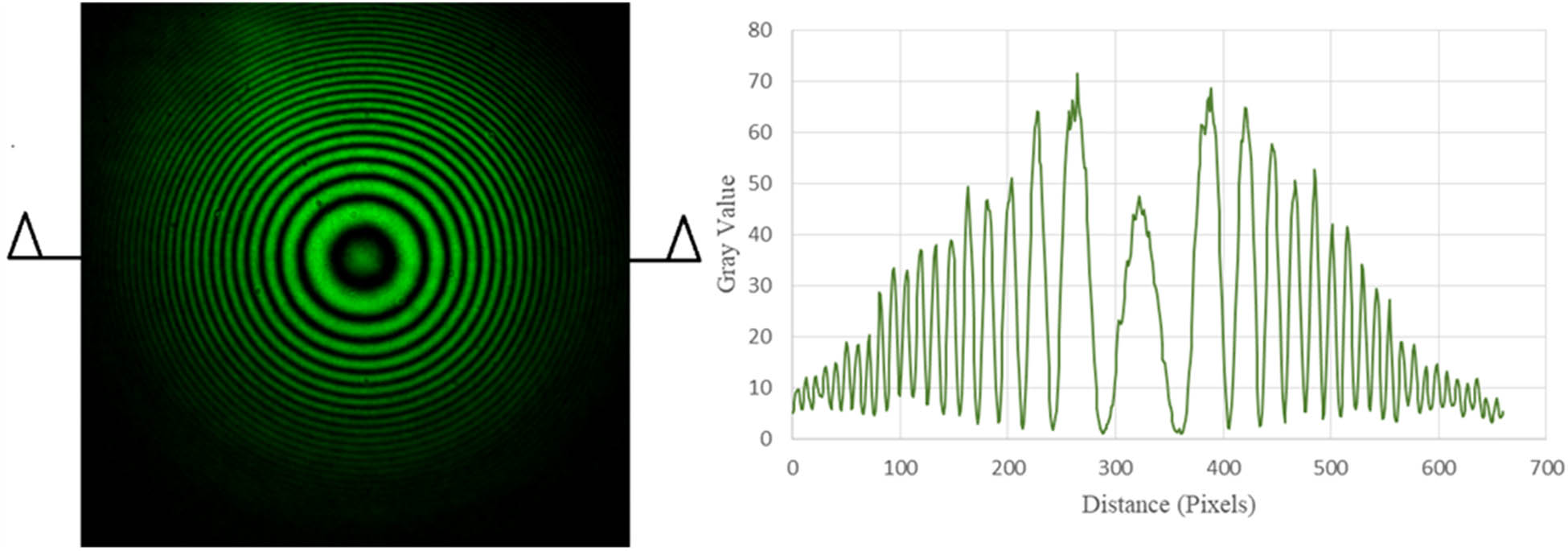
Unperturbed interferogram and its respective cross-sectional intensity profile.

During a particular run, pressure and temperature profiles were measured simultaneously across the turbulent region. This was achieved by initially measuring the ambient temperature and pressure with Xplorer GLX, and then attaching a K-type thermocouple and a differential pressure tube to a retort stand. The thermocouple and differential pressure sensor were then placed within the turbulent region and methodically manoeuvred across the optical pathway – “Distance (mm)” on the x-axis – in segments of 50 or 100 mbar depending on the windspeed setting of the run. The resulting profiles were used in determining C T 2 and C n 2 ; and hence, σ R 2 and r ₀. It should be noted that Augustine and Chetty [22,23] maintained a constant separation r in their calculation of C T 2 due to the set positioning and hence area of applied turbulence. In contrast, the turbulence width for this work either broadened or narrowed depending on the angle and wind speed setting used. Thus, the partition of the base and the peak of the temperature profiles were used. Peak values of the pressure and temperature profiles, together with C T 2 , were then used to calculate C n 2 . The now calculated C n 2 was then used to calculate σ R 2 and r ₀, where the path length was 2.52 m. Although every precautionary measure was taken to keep the laboratory as dust-free as possible by selecting a room with no windows, blocking all ventilation outlets, and continually cleaning the room of dust, the nature of the applied turbulence created a gust within the room, resulting in the upliftment of dust particles that would attach onto the optical components during each run.

5 Results

Measurements were recorded with ambient temperatures ranging from 22.2 to 25.6°C and atmospheric pressures of 938.7–955.1 mbar. During measurements for the temperature and pressure profiles, the door to the room was left ajar to avoid increasing ambient temperatures. For the sake of simplicity, the notation “(t/T/s/S)” will be used to indicate [low temperature/high temperature/low windspeed/high windspeed].

5.1 30° to the beam

For measured results for turbulence at 30°, see Table 1.

Table 1

Measured results for turbulence at 30°

Reading	C n 2 /× 10⁻¹¹ m^−2/3	σ R 2 /× 10⁻²	r ₀ (cm)
1	0.97	1.16	1.27
2	15.88	18.95	0.24

5.1.1 Reading 1 (t/s)

Interferogram, intensity, pressure, and temperature profiles at low temperature and low windspeed settings for 30° are given in Figure 3.

Figure 3

Interferogram, intensity, pressure, and temperature profiles at low temperature and low windspeed settings for 30°.

5.1.2 Reading 2 (T/S)

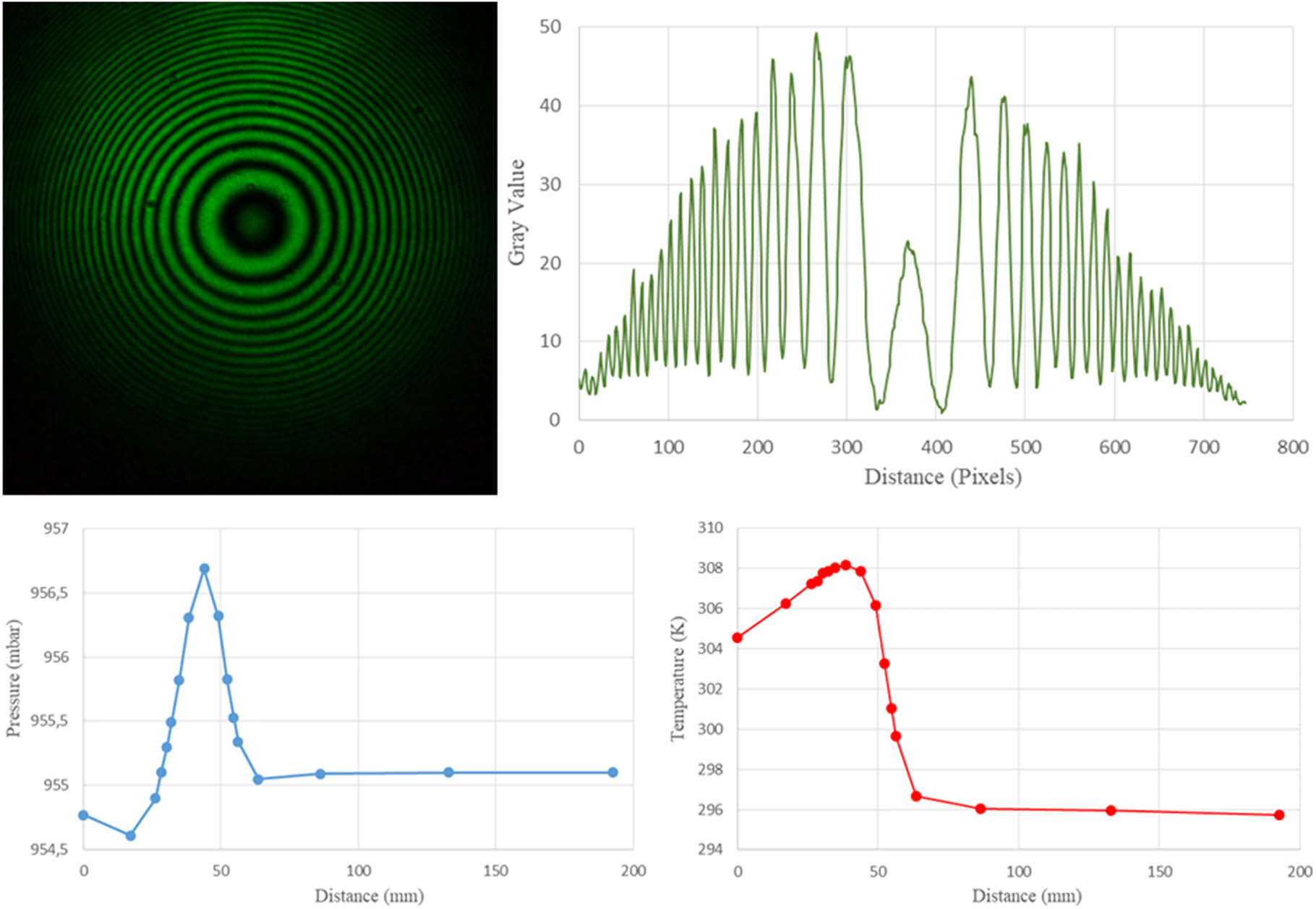
Interferogram, intensity, pressure, and temperature profiles at high temperature and high windspeed settings for 30° are given in Figure 4.

Figure 4

Interferogram, intensity, pressure, and temperature profiles at high temperature and high windspeed settings for 30°.

5.2 60° to the beam

For measured results for turbulence at 60°, see Table 2.

Table 2

Measured results for turbulence at 60°

Reading	C n 2 /× 10⁻¹¹ m^−2/3	σ R 2 /× 10⁻²	r ₀ (cm)
3	2.78	3.32	0.68
4	29.19	34.83	0.17

5.2.1 Reading 3 (t/s)

Interferogram, intensity, pressure, and temperature profiles at low temperature and low windspeed settings for 60° are given in Figure 5.

Figure 5

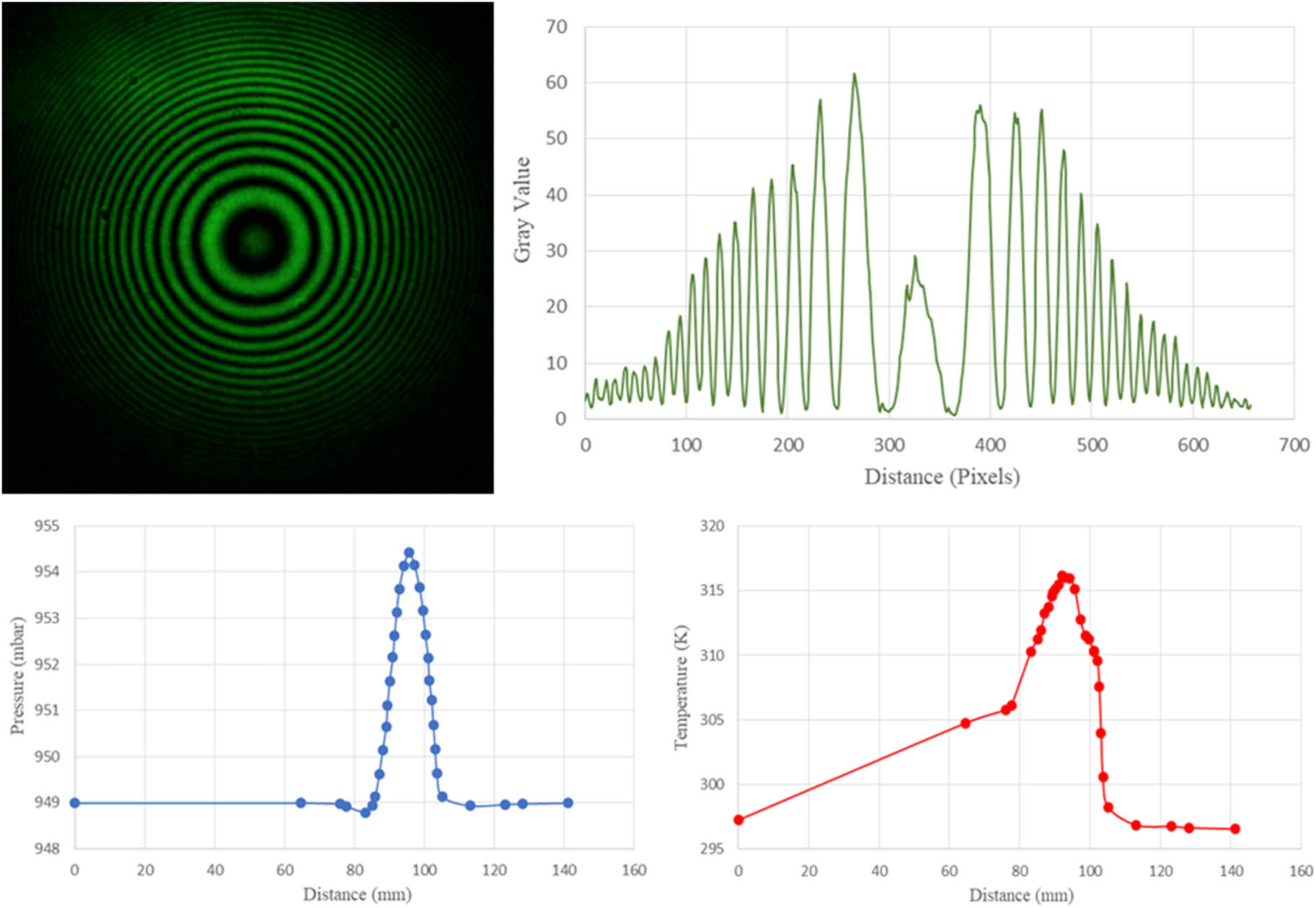
Interferogram, intensity, pressure, and temperature profiles at low temperature and low windspeed settings for 60°.

5.2.2 Reading 4 (T/s)

Interferogram, intensity, pressure, and temperature profiles at high temperature and high windspeed settings for 60° are given in Figure 6.

Figure 6

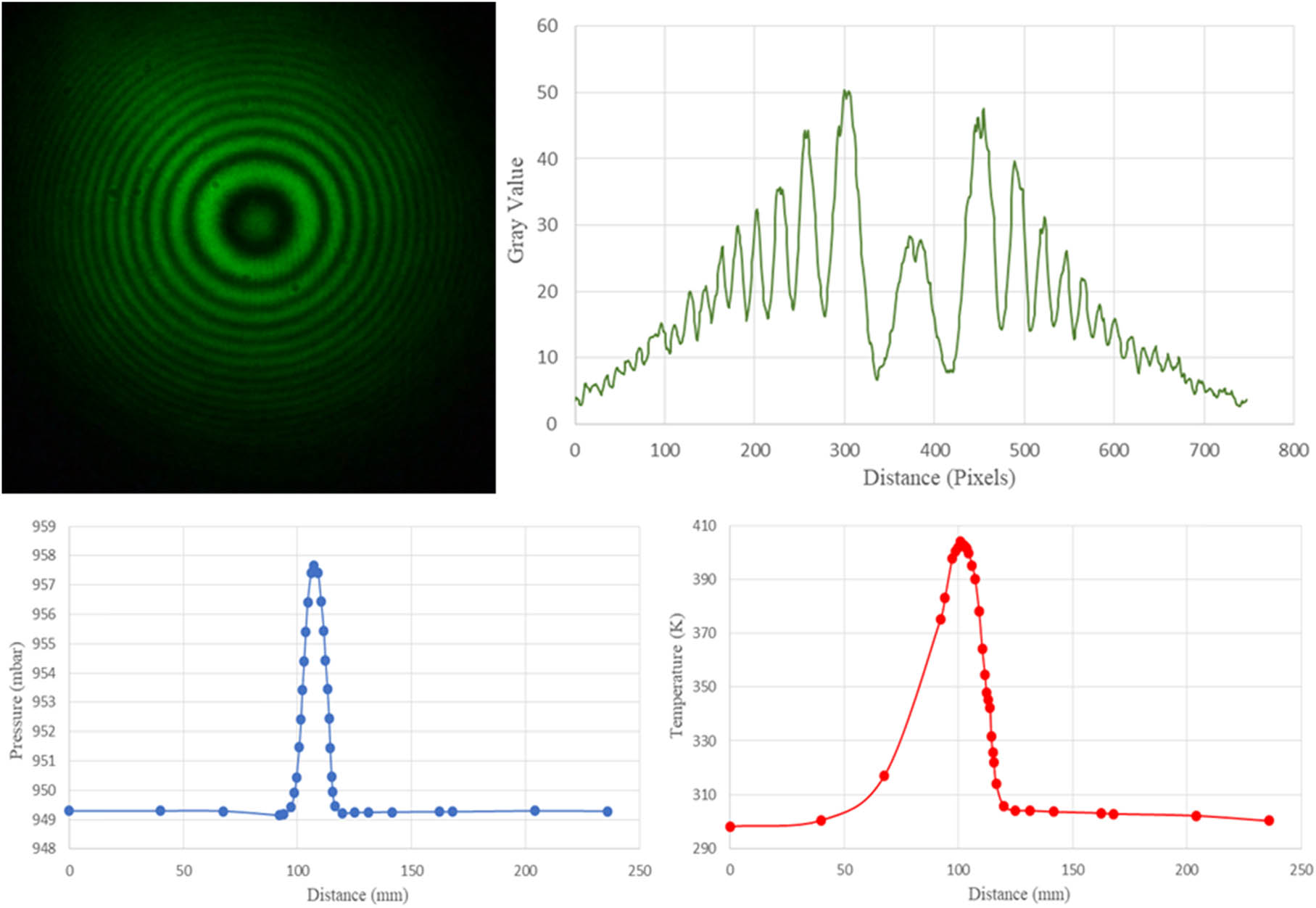
Interferogram, intensity, pressure, and temperature profiles at high temperature and high windspeed settings for 60°.

5.3 90° to the beam

For measured results for turbulence at 90°, see Table 3.

Table 3

Measured results for turbulence at 90°

Reading	C n 2 /× 10⁻¹¹ m^−2/3	σ R 2 /× 10⁻²	r ₀ (cm)
5	3.27	3.90	0.61
6	31.04	37.04	0.16

5.3.1 Reading 5 (t/s)

Interferogram, intensity, pressure, and temperature profiles at low temperature and low windspeed settings for 90° are given in Figure 7.

Figure 7

Interferogram, intensity, pressure, and temperature profiles at low temperature and low windspeed settings for 90°.

5.3.2 Reading 6 (T/s)

Interferogram, intensity, pressure, and temperature profiles at high temperature and high windspeed settings for 90° aregiven in Figure 8.

Figure 8

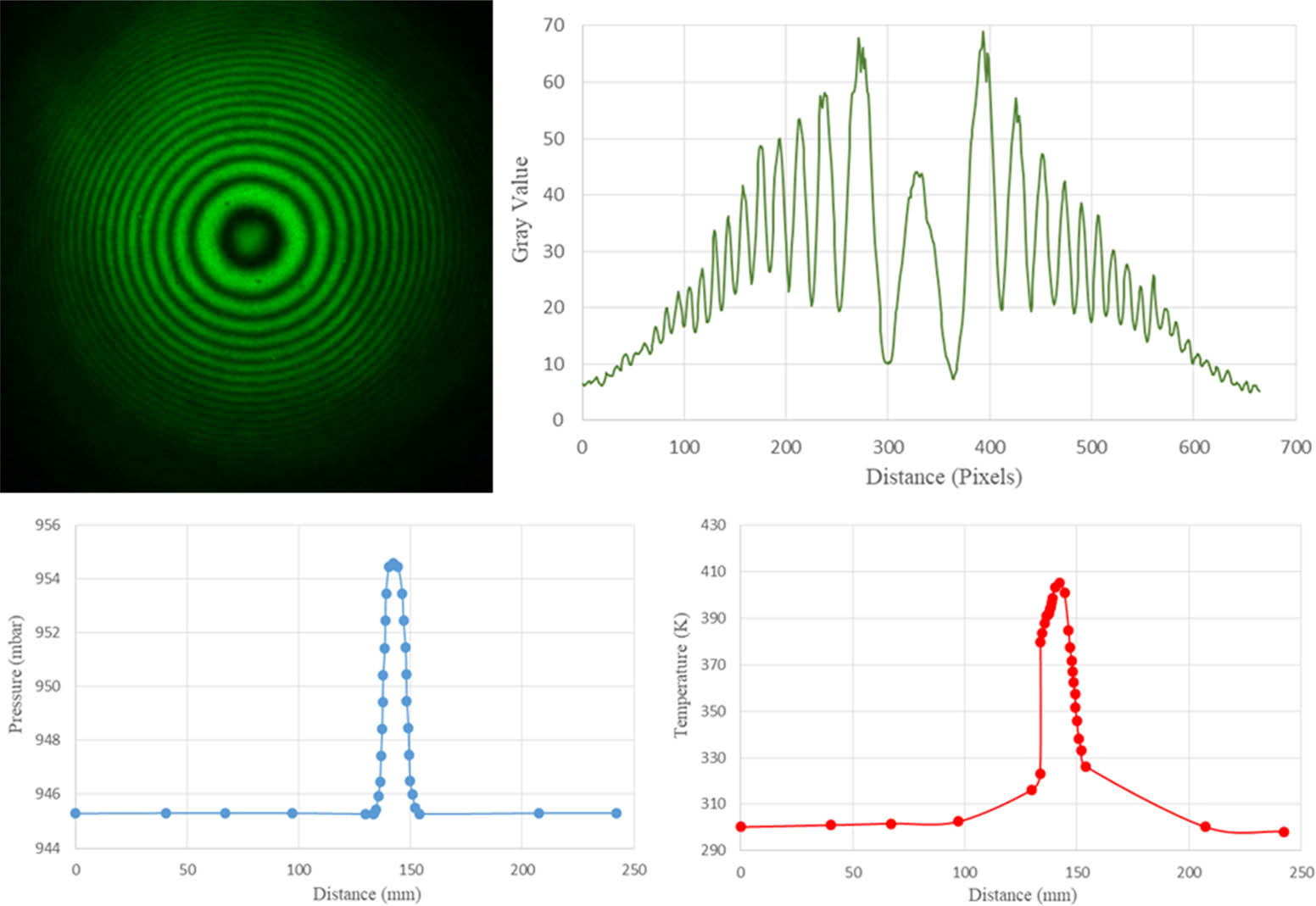
Interferogram, intensity, pressure, and temperature profiles at high temperature and high windspeed settings for 90°.

5.4 120° to the beam

For measured results for turbulence at 120°, see Table 4.

Table 4

Measured results for turbulence at 120°

Reading	C n 2 /× 10⁻¹¹ m^−2/3	σ R 2 /× 10⁻²	r ₀ (cm)
7	2.91	3.48	0.66
8	28.24	33.70	0.17

5.4.1 Reading 7 (t/s)

Interferogram, intensity, pressure, and temperature profiles at low temperature and low windspeed settings for 120° are given in Figure 9.

Figure 9

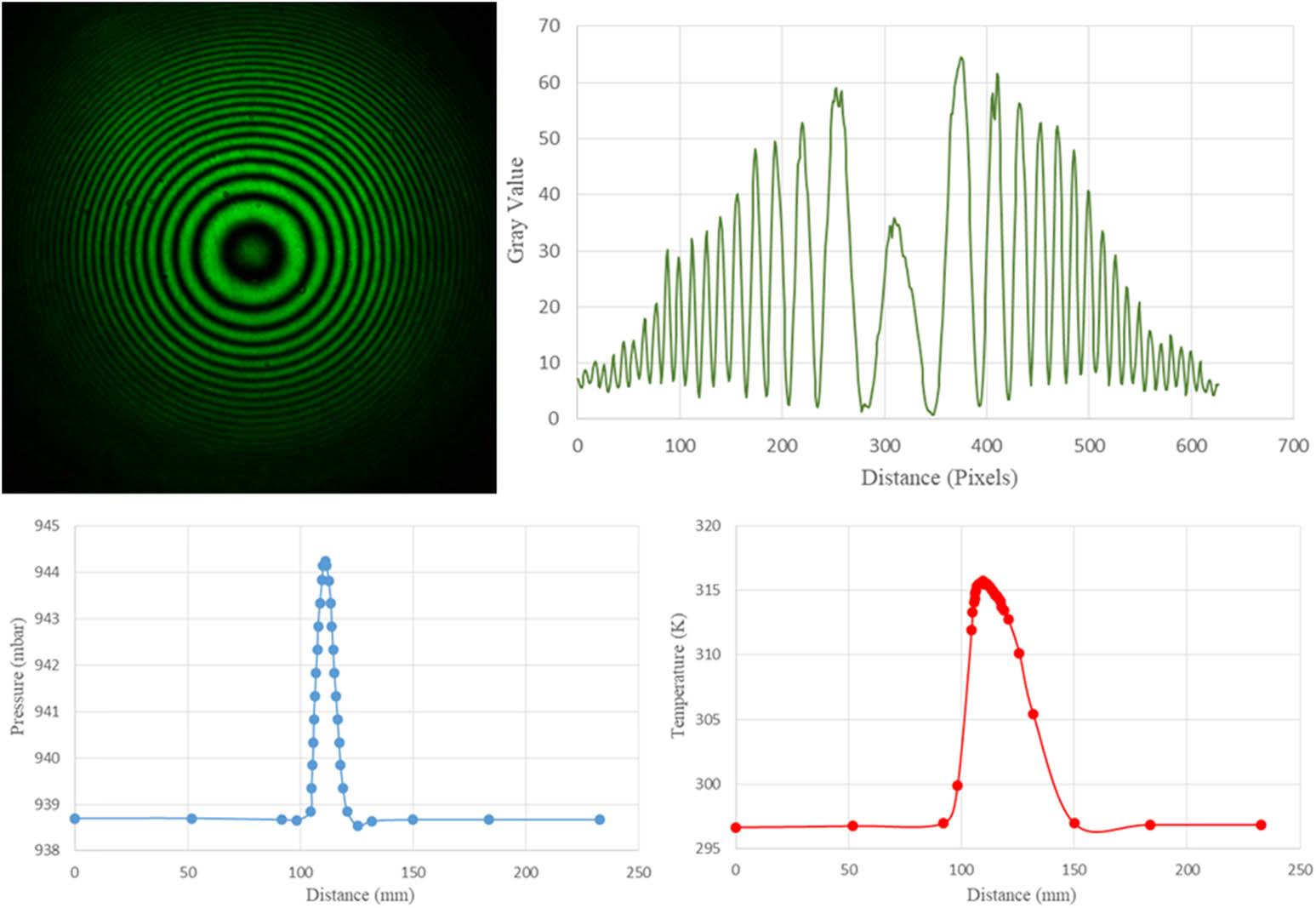
Interferogram, intensity, pressure, and temperature profiles at low temperature and low windspeed settings for 120°.

5.4.2 Reading 8 (T/s)

Interferogram, intensity, pressure, and temperature profiles at high temperature and high windspeed settings for 120° are given in Figure 10.

Figure 10

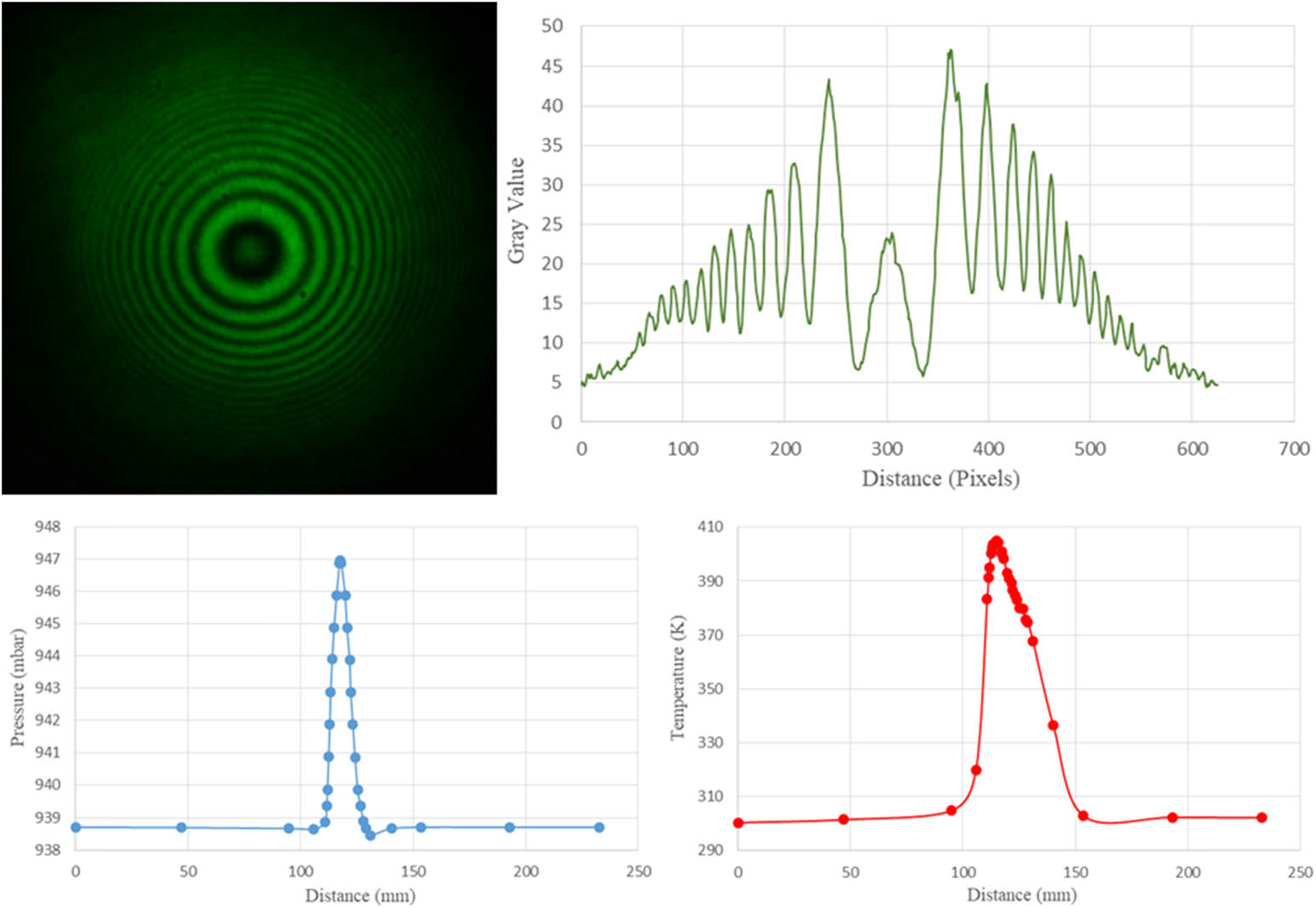
Interferogram, intensity, pressure, and temperature profiles at high temperature and high windspeed settings for 120°.

5.5 150° to the beam

For measured results for turbulence at 150°, see Table 5.

Table 5

Measured results for turbulence at 150°

Reading	C n 2 /× 10⁻¹¹ m^−2/3	σ R 2 /× 10⁻²	r ₀ (cm)
9	1.35	1.61	1.04
10	16.06	19.16	0.24

5.5.1 Reading 9 (t/s)

Interferogram, intensity, pressure, and temperature profiles at low temperature and low windspeed settings for 150° are given in Figure 11.

Figure 11

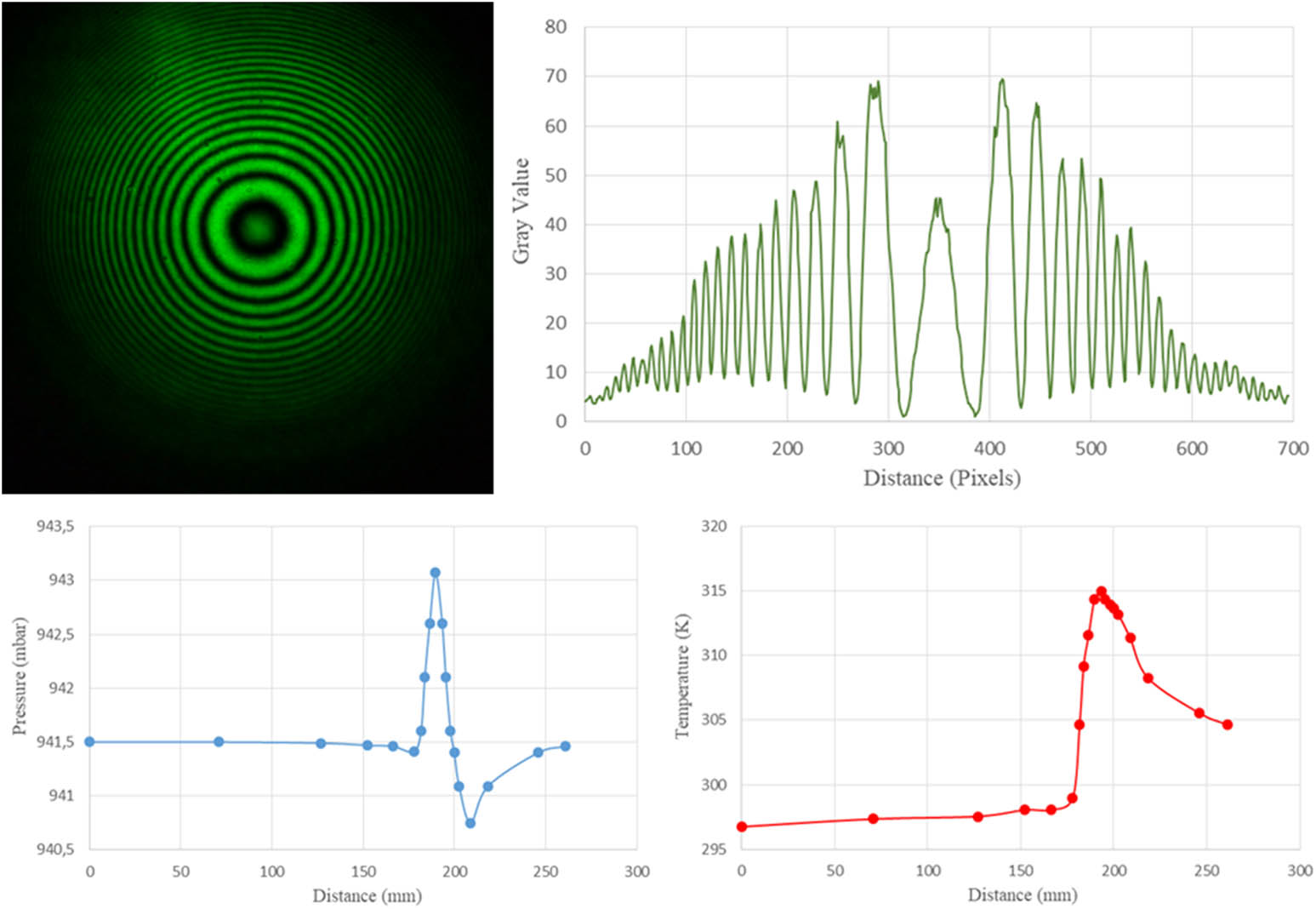
Interferogram, intensity, pressure, and temperature profiles at low temperature and low windspeed settings for 150°.

5.5.2 Reading 10 (T/s)

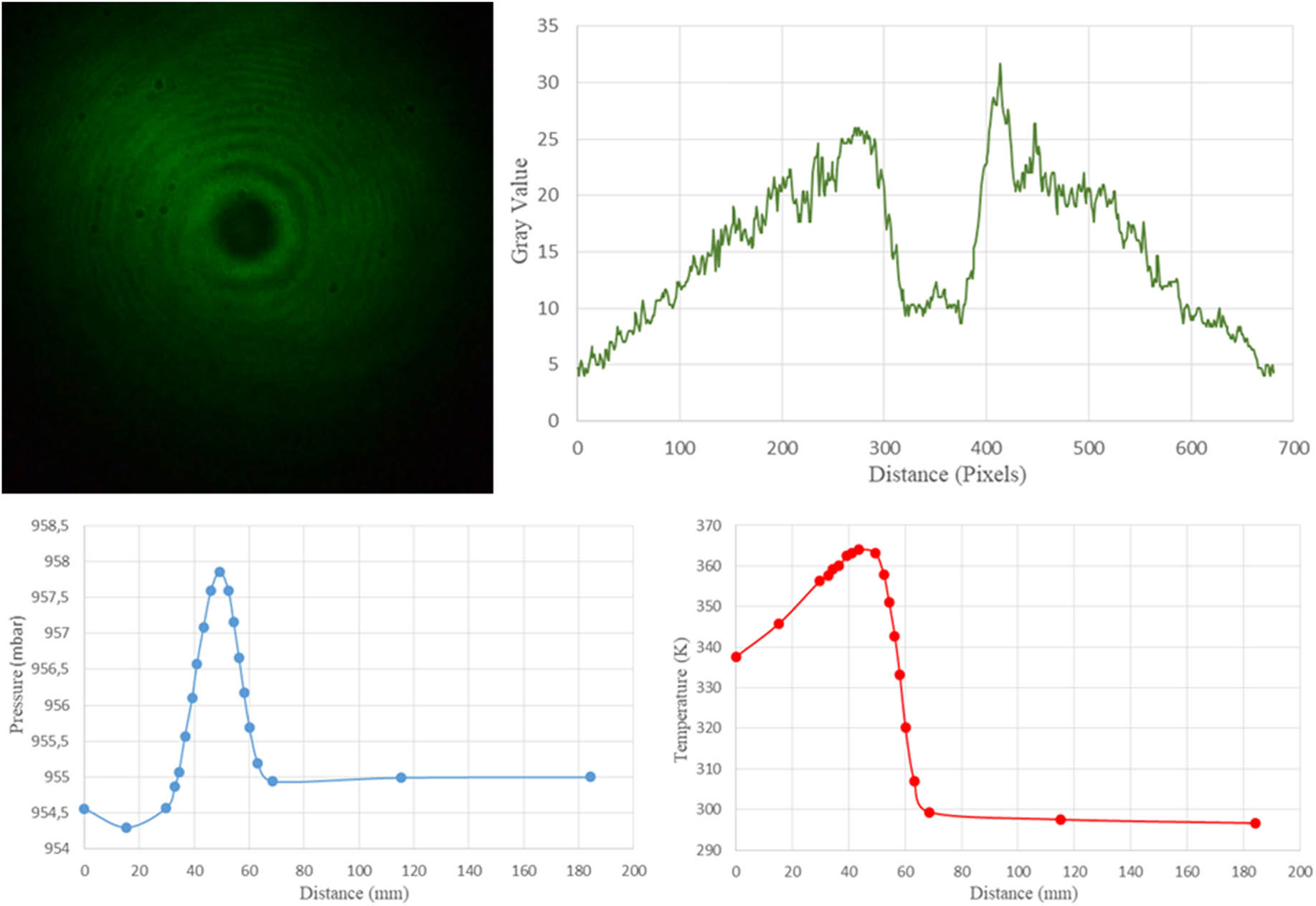
Interferogram, intensity, pressure, and temperature profiles at high temperature and high windspeed settings for 150° are given in Figure 12.

Figure 12

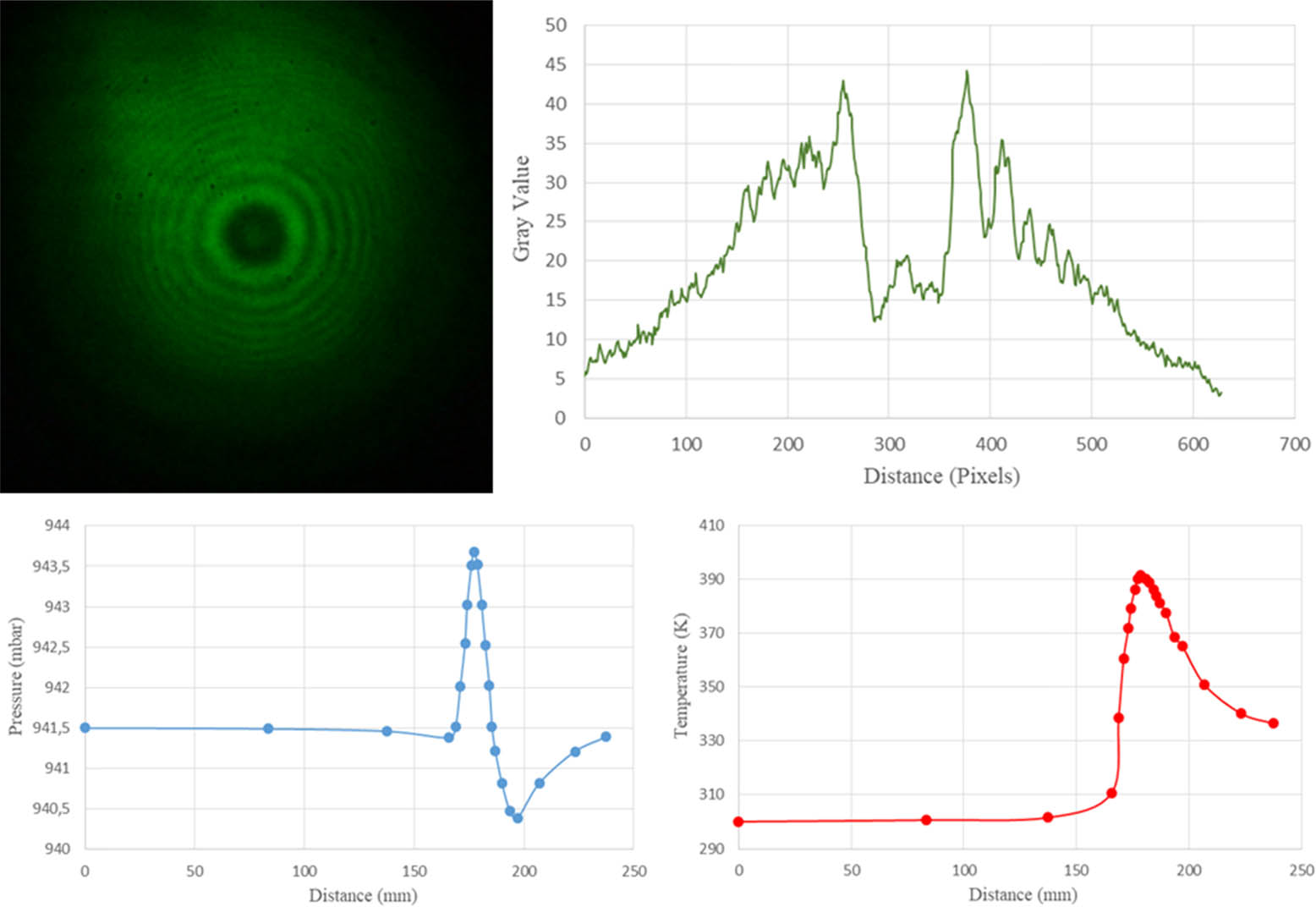
Interferogram, intensity, pressure, and temperature profiles at high temperature and high windspeed settings for 150°.

6 Analysis

6.1 Error evaluation

The Bruton ADC Wind quotes an accuracy better than ±5% for windspeeds above 3 m · s⁻¹, however, its readings were not vital in the calculations of the atmospheric parameters and may be neglected. Each value of the refractive structure constants and, hence, the other atmospheric parameters were averaged and varied by 5.44%. This is inevitably due to parallax error and estimations occurring during the horizontal measurements for the temperature and pressure profiles. The K-type thermocouple quotes a maximum possible error of 0.25% (±1.5 K) whilst the thermometer cites a maximum error of 0.3% (±1 K). Together, temperature readings have the highest possible error of 0.55%. The Xplorer GLX barometer sensor cites an error of approximately 0.11% (±0.03 inHg) – where 1 mbar = 0.02953 in Hg – whilst the differential pressure sensor quotes the highest possible error of 1% (±0.1 Pa). Thus, the combined error for the pressure is therefore 1.11%. Therefore, the total error for this work is 7.1%. As a result, the corrected ranges for the atmospheric parameters are tabulated as follows (Table 6):

6.2 Discussion

From the interferograms and the respective intensity profiles, it is evident that at constant temperature and wind speed, the extent of aberrations experienced by a laser beam is highly dependent on the angle of applied turbulence. As the angle of applied turbulence deviates away from the normal (90°), the aberrations depicted by the interferograms and intensity profiles increase. Despite this trend, the interferometric data (ID) yielded for turbulence setting (t/s) show minor occurrences of image blur (beam spread) and image jitter (beam wander) [4]. The amplification of temperature and windspeed (turbulence setting [T/S]) aggravates the degree of image blur and jitter. Image blur portrayed in the interferograms is depicted as energy redistribution in the intensity profiles. The ID produced for the turbulence setting (T/S) show an immense increase in wavefront aberrations, with fringes being near indistinguishable at the outer region and considerably diminished and sprawled in the inner region. The difference in shape (where symmetry is to be expected) between the intensity profiles of readings 2 and 10 is due to the presence of the wall, as depicted in Figure 1. Airflow for turbulence applied at 30° to the beam axis is aimed more so in the direction of the wall. This results in a higher concentration of thermal energy within the turbulence region. As such, higher wavefront fluctuations occur.

There is a common trend displayed in relation to the pressure and temperature profiles. For turbulence applications 90° to the beam (readings 5 and 6), the pressure profiles adopt a tall Gaussian formation with the peak value increasing as the wind speed increases. The corresponding temperature profiles depict sharp peaks, which amplify as temperature increases and broaden in the lower temperature region in a logarithmic fashion. This broadening is due to the obstruction of the granite table on which the experimental setup rests, as it disperses the thermally charged windstream horizontally. The ensuing dispersion allowed for sufficient energy cascade to occur resulting in eddies on the order of the first Fresnel zone. Such eddies are predominantly responsible for irradiance fluctuations, while eddies larger than the beam diameter induce beam wander [4]. All atmospheric profile peaks are measurements recorded closest to the turbulence source. It should be noted that seasonal conditions influenced the formation of the temperature profiles, with summer/spring periods increasing the ambient temperature and vice versa for winter/autumn.

The temperature and pressure profiles depict a clear dependency on the angle of applied turbulence. Deviations away from the normal give rise to a gradual broadening of both profile types as well as a reduction in peak values. With regard to the pressure profiles, the shape not only illustrates signs of broadening but also indicates a negative differential pressure, which increases in strength and broadens in width as the angle of turbulence application tends to 30° or 150°. This infers the presence of an upward draft that intensifies as the wind speed increases. The upward draft is due chiefly to the bottom optical bench plates rested on the granite table since the wind direction is downward in nature. Not surprisingly, the shape of the temperature profiles as the angle deviates from 90° broadens primarily in the direction of the windstream. With reference to Figure 1, when 90° > θ ≥ 30° say, the wind is directed to the left of the turbulent region, creating a concentration of heat energy to the left as opposed to the right. This likewise applies to the positioning of the negative differential pressure regions.

With reference to Table 6, value ranges for the atmospheric parameters were found to be 0.90 × 10⁻¹¹ m^−2/3 ≤ C n 2 ≤ 33.25 × 10⁻¹¹ m^−2/3, 1.08 × 10⁻² ≤ σ R 2 ≤ 39.68 × 10⁻², and 0.15 cm ≤ r ₀ ≤ 1.36 cm. All values obtained for C n 2 correspond to the strong turbulence regime ( C n 2 ≥ 10⁻¹³ m^−2/3). An increase in C n 2 ensues as perturbations advance closer to the normal, as depicted in Figure 13. This is due to P being measured perpendicularly to the horizon. In addition, the incrementation of the temperature and wind speed settings results in further C n 2 growth. This strength regime is due to the steep temperature gradients present in the turbulent regions (yielding high C T 2 values) and P being directly proportional to the wind speed.

Table 6

Atmospheric parameter ranges for each temperature and windspeed variation

Setting	C n 2 / × 10⁻¹¹ m^−2/3	σ R 2 / × 10⁻²	r ₀ (cm)
(t/s)	2.20 ± 1.30	2.63 ± 1.55	0.97 ± 0.39
(T/S)	24.00 ± 9.25	28.64 ± 11.04	0.20 ± 0.05

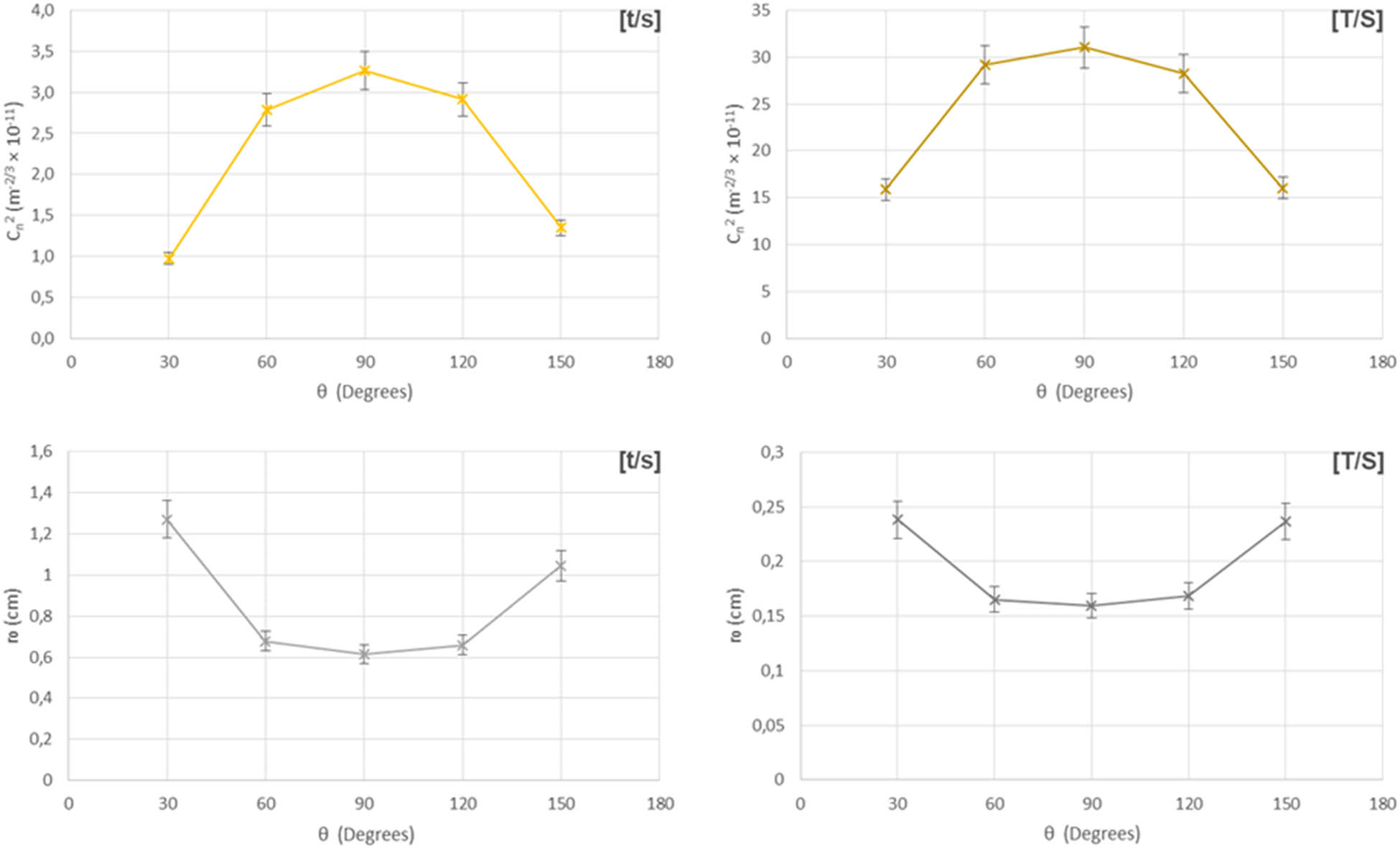
$Figure 13 Relationships of C n 2 {C}_{n}^{2} and r 0 with θ for each turbulence setting.$

Figure 13

Relationships of C n 2 and r ₀ with θ for each turbulence setting.

Recalling that weak scintillations are associated with σ R 2 < 1, the values obtained for σ R 2 indicate weak scintillations for all turbulence settings. In addition, σ R 2 follows the same trend across θ as C n 2 due to proportionality. This necessitates an increase in σ R 2 for the turbulence setting (T/S). The discrepancy of the strength regime of σ R 2 , as opposed to that of C n 2 , is attributed to the short optical path length within the turbulence region since such measurements are typically obtained over vast distances [22]. All values obtained for r ₀ indicate poor visual conditions (strong turbulence), with the extent being proportional to the strength of applied turbulence. Turbulence settings (t/s) and (T/S) produce r ₀ values with percentage differences of 72.8–88.4% and 95.0–97.0%, respectively, below the accepted minimum (r ₀ = 5 cm). Since r ₀ is inversely proportional to C n 2 , values obtained decrease as the degree of applied turbulence increases.

Bringing the above together and with reference to Figure 13, it is clear that as the angle of applied turbulence deviates away from the normal, values of the atmospheric parameters subside, given that pressure is measured vertically. In contrast, the ID obtained undoubtedly depicts a rise in the degree of wavefront aberrations as the angle of applied turbulence approaches 30° or 150° from the normal. According to the readings obtained for turbulence applications at 90°, both temperature and pressure profiles indicate intense yet narrow perturbations to the beam resulting in higher values in C n 2 . Accordingly, this results in a higher σ R 2 and lower r ₀ by virtue of proportionality and inverse proportionality, respectively. Although deviations away from the normal result in a decrease in C n 2 for the above-mentioned reasons, there is a broadening of the temperature and pressure profiles across the optical path length as this shift progresses. As such, it may be deduced that light propagating through an increasingly broadened temperature and pressure profile experiences higher degrees of aberrations on its wavefront despite the reduction of the maximum temperatures and pressures, thus confirming the literature [4,7]. In addition, it confirms the literature that for a localised region, such as the region perturbed at 90°, a highly intense turbulence model is needed to exhibit similar effects to those with weak turbulence that span over greater distances [20].

The ID are in varying degrees of agreement with the atmospheric parameter’s strength regimes. The inability of σ R 2 to quantify the strong turbulence associated with the wavefront aberrations of the turbulence setting (T/S) is attributed to the use of a Gaussian beam in addition to the short optical path length [4]. The inability of C n 2 and r ₀ to confirm the weak wavefront aberrations of the turbulence setting (t/s) gives rise to two possible outcomes: that lowest order Gaussian beams propagate well under strong cool turbulence conditions, or the parameters lack the ability to account for weak turbulence under low thermal settings. This may be attributed to steep temperature gradients of the turbulence model ( C T 2 ) and the fact that 150 m is regarded as a short path length for C n 2 , whilst the general equation used for r ₀ is employed for astronomical purposes [30].

7 Conclusion

The effects of a hairdryer functioning as a turbulence source have been analysed with the use of a point diffraction interferometer. This produced distinct results compared to those of previous works [20,21,22,23]. Perturbations varied in wind speed, temperature, and angle from the beam axis in a downward manner. The resulting perturbed interferograms were analysed using image processing software ImageJ to achieve subsequent intensity profiles. Pressure and temperature profiles were measured along the optical path length within the turbulent region in order to properly model the turbulence. The atmospheric parameters C n 2 , σ R 2 , and r ₀ were then computed.

A visible trend in wavefront aberrations was apparent as the angle of turbulence deviated from the axial normal (see Figure 13). Additionally, perturbations for turbulence settings (t/s) and (T/S) produced weak and strong wavefront aberrations, respectively. This was in the form of scintillation, beam wander, and beam spread. For a specific turbulence setting, wavefront aberrations were minimal at 90° and would progressively increase as the angle tended towards 30° or 150°. Values for C n 2 (and σ R 2 due to proportionality) decreased as perturbations deviated from 90°, whilst r ₀ increased due to inverse proportionality. It was determined that the increased size of the pressure and temperature profiles spanning the optical pathway as the angle of turbulence deviated further from the normal was, in part, responsible for the discrepancy between the ID and the trends of the atmospheric parameters. The other is that pressure is measured perpendicularly to the horizon, resulting in flows being in direct line of sight of the sensor. This compels higher C n 2 values due to proportionality with pressure.

The atmospheric parameter strength regimes exhibited varying degrees of agreement with the obtained ID (Table 7). C n 2 and r ₀ classified both turbulence settings in the strong turbulence regime. Consequently, all r ₀ values inferred poor visual conditions. These discrepancies of C n 2 and r ₀ – to the weak wavefront aberrations of turbulence setting (t/s) – are attributed to the short optical path length and steep temperature gradients or that TEM₀₀ Gaussian beams propagate well in strong cool turbulence. σ R 2 classified both turbulence settings in the weak strength regime, thus implying weak scintillations. This discrepancy to the strong wavefront aberrations of turbulence setting (T/S) was attributed to the short optical path length and σ R 2 being ill-equipped for use with Gaussian beams. Future work may entail using water as a random medium from various accessible sources such as tap, distilled, river, and beach water. Monitoring these different water types whilst systematically introducing heat and motion may produce robust results for analysis. Another experiment may utilize a greenhouse gas at different concentrations, wind speeds and temperatures to gauge the effects that they may have on received light. As alluded, the refractivity threshold of the fundamental Gaussian beam subjected to various strong cool turbulences could be determined in the future work by altering the turbulence pathlengths.

Table 7

Comparison of atmospheric parameter strengths with wavefront aberrations for each turbulence setting

Turbulence setting	C n 2 Strength	σ R 2 Strength	r ₀ Strength	Wavefront aberrations
(t/s)	Strong	Weak	Strong	Weak
(T/S)	Strong	Weak	Strong	Strong

Funding information: The authors state no funding involved.
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors state no conflict of interest.

References

[1] Ishimaru A. Theory of optical propagation in the atmosphere. Opt Eng. 1981;20(1):63–70. 10.1117/12.7972665.Search in Google Scholar

[2] Miller WB, Ricklin JC, Andrews LC. Log-amplitude variance and wave structure function: a new perspective for gaussian beams. J Opt Soc Am A. 1993;10(4):661–72. 10.1364/JOSAA.10.000661.Search in Google Scholar

[3] Schulz TJ. Optimal beams for propagation through random media. Opt Lett. 2005;30(10):1093–5. 10.1364/OL.30.001093.Search in Google Scholar

[4] Andrews LC, Phillips RL. Laser beam propagation through random media. 2nd edn. Bellingham: SPIE Press; 2005.10.1117/3.626196Search in Google Scholar

[5] Buck AL. Effects of the atmosphere on laser beam propagation. Appl Opt. 1967;6(4):703–8. 10.1364/AO.6.000703.Search in Google Scholar PubMed

[6] Fernández MM, Vilnrotter VA, Mukai R, Hassibi B. Coherent optical array receiver experiment: design, implementation, and BER performance of a multichannel coherent optical receiver for PPM signals under atmospheric turbulence. Proceedings of the Free-Space Laser Communication Technologies XVIII Conference; 2006 Jan 21–26; San Jose, USA. Bellingham: SPIE; 2006.10.1117/12.660253Search in Google Scholar

[7] Shaik KS. Atmospheric propagation effects relevant to optical communications. In: Posner EC, editor. The Telecommunications and Data Acquisition Progress Report 42-94. Pasadena: NASA Technical Reports Server; 1988. p. 180–200.Search in Google Scholar

[8] Yuksel H. Studies of the effects of atmospheric turbulence on free space optical communications. Empirical Dissertation. College Park, MD: University of Maryland; 2005.Search in Google Scholar

[9] Berman GP, Chumak AA, Gorshkov VN. Beam wandering in the atmosphere: The effect of partial coherence. Phys Rev E. 2007;76(5):056606-1-7. 10.1103/PhysRevE.76.056606.Search in Google Scholar PubMed

[10] Consortini A, O’Donnell KA. Beam wandering of thin parallel beams through atmospheric turbulence. Wave Random Media. 2006;1(3):S11–28. 10.1088/0959-7174/1/3/002.Search in Google Scholar

[11] Fu S, Gao C. Influences of atmospheric turbulence effects on the orbital angular momentum spectra of vortex beams. Photon Res. 2016;4(5):B1–4. 10.1364/PRJ.4.0000B1.Search in Google Scholar

[12] Fried DL. Optical resolution through a randomly inhomogeneous medium for very long and very short exposures. J Opt Soc Am. 1966;56(10):1372–9. 10.1364/JOSA.56.001372.Search in Google Scholar

[13] Clifford SF. The classical theory of wave propagation in a turbulent medium. In: Strohbehn JW, editor. Laser beam propagation in the atmosphere. Berlin Heidelberg: Springer-Verlag; 1978. p. 9–43.10.1007/3540088121_16Search in Google Scholar

[14] McMillan RW. Atmospheric turbulence effects on radar systems. Proceedings of the IEEE 2010 National Aerospace & Electronics Conference; 2010 Jul 14–16. Ohio, New York, USA: IEEE Xplore; 2010.10.1109/NAECON.2010.5712909Search in Google Scholar

[15] Arnon S, Kopeika NS, Kedar D, Zilberman A, Arbel D, Livne A, et al. Performance limitation of laser satellite communication due to vibrations and atmospheric turbulence: down‐link scenario. Int J Satell Comm N. 2003;21(6):561–73. 10.1002/sat.769.Search in Google Scholar

[16] Hanada T, Fujisaki K, Tateiba M. Theoretical analysis of effects of atmospheric turbulence on bit error rate for satellite communications in Ka-band. In: Karimi M, editor. Advances in Satellite Communications. Rijeka: InTech; 2011. p. 29–52.10.5772/21643Search in Google Scholar

[17] Shin RT, Kong JA. Radiative transfer theory for active remote sensing of two-layer random medium. PIER. 1989;1:359–417.10.1016/B978-0-444-01490-0.50010-6Search in Google Scholar

[18] Titterton DH. Development of infrared countermeasure technology and systems. In: Krier A, editor. Mid-infrared semiconductor optoelectronics. London: Springer-Verlag; 2006. p. 635–71.10.1007/1-84628-209-8_20Search in Google Scholar

[19] Schmitt JM, Kumar G. Turbulent nature of refractive-index variations in biological tissue. Opt Lett. 1996;21(16):1310–2. 10.1364/OL.21.001310.Search in Google Scholar

[20] Ndlovu SC, Chetty N. Analysis of the fluctuations of a laser beam due to thermal turbulence. Centr Eur J Phys. 2014;12(7):466–72. 10.2478/s11534-014-0479-2.Search in Google Scholar

[21] Ndlovu SC, Chetty N. Experimental determination of thermal turbulence effects on a propagating laser beam. Open Phys. 2015;13(1):226–31. 10.1515/phys-2015-0028.Search in Google Scholar

[22] Augustine SM, Chetty N. Experimental verification of the turbulent effects on laser beam propagation in space. Atmósfera. 2014;27(4):385–401. 10.1016/S0187-6236(14)70037-2.Search in Google Scholar

[23] Augustine SM, Chetty N. Wind tunnel simulations to detect and quantify the turbulent effects of a propagating He–Ne laser beam in air. Atmósfera. 2017;30(1):27–38. 10.20937/ATM.2017.30.01.03.Search in Google Scholar

[24] Lutomirski RF, Yura HT. Wave structure function and mutual coherence function of an optical wave in a turbulent atmosphere. J Opt Soc Am. 1971;61(4):482–7. 10.1364/JOSA.61.000482.Search in Google Scholar

[25] Isterling WM. Electro-optic propagation through highly aberrant media. Empirical Thesis. Adelaide: The University of Adelaide; 2010.Search in Google Scholar

[26] Thiermann V, Kohnle A. A simple model for the structure constant of temperature fluctuations in the lower atmosphere. J Phys D: Appl Phys. 1988;21(10S):S37–40. 10.1088/0022-3727/21/10 S/011.Search in Google Scholar

[27] Wyngaard JC, Izumi Y, Collins SA. Behavior of the refractive-index-structure parameter near the ground. J Opt Soc Am. 1971;61(12):1646–50. 10.1364/JOSA.61.001646.Search in Google Scholar

[28] Roddier F. The effects of atmospheric turbulence in optical astronomy. In: Wolf E, editor. Progress in optics. Vol 19. Amsterdam: Elsevier; 1981. p. 281–376.10.1016/S0079-6638(08)70204-XSearch in Google Scholar

[29] Magee EP, Welsh BM. Characterization of laboratory-generated turbulence by optical phase measurements. Opt Eng. 1994;33(11):3810–7. 10.1117/12.181180.Search in Google Scholar

[30] Goodman JW. Statistical optics. Toronto: Wiley Classics Library; 2000.Search in Google Scholar

Received: 2021-08-04

Revised: 2022-01-10

Accepted: 2022-02-22

Published Online: 2022-05-26

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/phys-2022-0038

Keywords for this article

turbulence; Gaussian laser beam; point diffraction interferometer; refractive index structure constant; Rytov variance; Fried’s parameter

Creative Commons

BY 4.0