Propagation properties of cosh-Airy beams in an inhomogeneous medium with Gaussian PT-symmetric potentials

Yangbao Deng; Bing Wen; Liezun Chen; Saiwen Zhang; Guangfu Zhang; Cuixiu Xiong; Xiaoling Leng

doi:10.1515/phys-2022-0202

Article Open Access

Propagation properties of cosh-Airy beams in an inhomogeneous medium with Gaussian PT-symmetric potentials

Yangbao Deng , Bing Wen , Liezun Chen , Saiwen Zhang , Guangfu Zhang , Cuixiu Xiong and Xiaoling Leng

Published/Copyright: October 18, 2022

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information Explore this Subject

From the journal Open Physics Volume 20 Issue 1

Abstract

We numerically investigate and statistically analyze the impact of medium parameters (modulation depth P, modulation factor ω, and gain/loss strength W ₀) and beam parameters (truncation coefficient a and distribution factor χ ₀) on the propagation characteristics of a cosh-Airy beam in the Gaussian parity-time (PT)-symmetric potential. It is demonstrated that the main lobe of a cosh-Airy beam is captured as a soliton, which varies periodically during propagation. The residual beam self-accelerates along a parabolic trajectory due to the self-healing property. With increment in P, the period of a trapped soliton decreases almost monotonically, while the peak power of a trapped soliton increases monotonically. With the increase in ω or decrease in the absolute value of W ₀, the period and peak power of a trapped soliton decrease rapidly and then almost remain unchanged. Moreover, it is indicated that the period of a trapped soliton remains basically unchanged no matter a and χ ₀ increase or decrease. The peak power of a trapped soliton increases with increment of a, but the peak power of a trapped soliton stays relatively constant irrespective of variation in χ ₀.

Keywords: cosh-Airy beams; Gaussian PT-symmetric potential; trapped solitons; propagation properties

1 Introduction

In 1979, Berry and Balazs deduced a non-diffracting Airy wave packet solution in Schrödinger equation [1]. In 2007, Christodoulides et al. first reported the generation of a finite-energy Airy beam in experiment. Then, the Airy beam has attracted significant attention due to its unique properties, such as non-diffraction, self-acceleration, and self-healing [1,2,3,4,5,6]. Because of these properties, an Airy beam has important applications in plasma waveguides [7], optical micromanipulation [8], light bullet [9,10], plasmonic energy routing [11], and so on. An Airy beam propagating in different kinds of medium has been investigated in recent years [12,13,14,15,16,17,18,19,20,21,22]. Combing Airy beams with other shaped beams, some novel beams have been proposed and studied, including Airy–Gaussian beams [23], Airy–Bessel beams [24], Airy–Vortex beams [25], Airy–Laguerre–Gaussian beams [26], Airy–Ince–Gaussian beams [27], and Airy–Hermite–Gaussian beams [28]. Recently, a cosh-Airy beam was proposed by superposition of two Airy beams with different truncation coefficients [29]. The beam propagation factor of a cosh-Airy beam has been studied by the second-order moments [30]. The propagation characteristics of the cosh-Airy beam is similar to that of an Airy beam, except that the cosh-Airy beam has more manipulation degrees of freedom [29]. Additionally, the self-healing ability of the cosh-Airy beam is higher than that of an Airy beam [31]. Moreover, few works reported on the propagation of the cosh-Airy beam in uniaxial crystals orthogonal to the optical axis [32], quadratic-index inhomogeneous medium [33], and parabolic potential [34].

With the rapid development of material technology, lots of new nonlinear materials have been discovered, such as the parity-time (PT)-symmetric medium [35]. PT-symmetric medium is a kind of typical inhomogeneous medium. PT-symmetric demonstrates that the real and imaginary part of a complex potential must be an even function and an odd function, respectively [36]. Christodoulides et al. creatively introduced the PT-symmetric into optics field [37]. Adding the periodic gain/loss to an optical lattice, the distribution function of refractive index is an even function and the distribution function of gain/loss is an odd function, so a PT-symmetric optical lattice is constructed [38]. The PT-symmetric medium with some unique properties supports an optical soliton generation. Therefore, generation and propagation of a variety of PT soliton in different types of PT-symmetric potentials have been investigated extensively, for example periodic potentials [39], hyperbolic potentials [40], Bessel potentials [41], parabolic potentials [42], and Gaussian potentials [43].

The Gaussian PT-symmetric profile has an explicit expression, the real part is refractive index modulation, and the imaginary part plays a role in phase modulation. Therefore, research on the Gaussian PT-symmetric medium is particularly important. To the best of our knowledge, there are few research reports about cosh-Airy beams; however, the previous research works have not investigated the influence of PT-symmetric medium with Gaussian potential on the propagation properties of a cosh-Airy beam. In this work, we study the propagation characteristics of a cosh-Airy beam in an inhomogeneous medium with Gaussian PT-symmetric potential. Our simulation result illustrates that a trapped soliton is generated from the main lobe of a cosh-Airy beam, the residual part can also self-accelerate along a parabolic trajectory. The propagation characteristics of a cosh-Airy beam are controlled by the Gaussian PT-symmetric potential parameters and the cosh-Airy beam parameters. This work is organized as follows. In Section 2, the model describing a cosh-Airy beam propagating in the Gaussian PT-symmetric potential is displayed. In Section 3, the influence of modulation depth, modulation factor, gain/loss strength, truncation coefficient, and distribution factor on the propagation properties of a cosh-Airy beam is analyzed and discussed in details. Conclusion is presented in Section 4.

2 Theoretical model

When a beam propagates in a one-dimensional PT-symmetric optical lattice, the refractive index has the following form:

(1) n ( X ) = n 0 + n R ( X ) + i n I ( X ) + n 2 ∣ φ ∣ 2 ,

where φ is the amplitude of a beam, n ₀ is the linear refractive index, and n ₂ is the nonlinear index coefficient. n ₂ is positive or negative, which represents the self-focusing or self-defocusing nonlinear effect, respectively. n _R(X) and n _I(X) are the real and imaginary parts of the complex refractive index, representing the refractive index distribution and gain/loss distribution of an optical lattice, respectively. To satisfy the PT-symmetry condition, the complex refractive index is written as follows:

(2) n R ( X ) = n R ( − X ) , n I ( X ) = − n I ( − X ) .

According to the Eq. (2), it is demonstrated that the refractive index distribution must be an even function, and the gain/loss distribution must be an odd function. In other words, the real and imaginary parts of the complex refractive index must be even and odd symmetric, respectively. Without Kerr nonlinearity, we consider the (1 + 1)-D normalized nonlinear Schrodinger equation for a cosh-Airy beam propagating in a Gaussian PT-symmetric potential [43].

(3) i ∂ φ ∂ z + 1 2 ∂ 2 φ ∂ x 2 + P [ V ( x ) + W ( x ) ] φ = 0 ,

where φ(x, z) is the field envelop, and z represents the normalized longitudinal coordinate. x = X/X ₀ is the dimensionless transverse coordinate, and X ₀ is the beam width. V(x) and W(x) represent the real and imaginary parts of a PT-symmetric potential, respectively. P is the modulation depth of a PT-symmetric potential. The Gaussian PT-symmetric potential is presented as follows [43]:

(4) V ( x ) = exp ( − ( ω x ) 2 ) ,

(5) W ( x ) = i W 0 ( ω x ) exp ( − ( ω x ) 2 ) ,

where ω is a modulation factor of the Gaussian PT-symmetric potential. W ₀ is the gain/loss strength. For the complex Gaussian PT-symmetric potential, all eigenvalues are real when the refractive index strength is stronger than the gain/loss strength, otherwise, the eigenvalues are mixed [43]. The initial field distribution of a cosh-Airy beam is taken as

(6) φ ( z = 0 , x ) = A i ( x ) exp ( a x ) cosh ( χ 0 x ) ,

where a is a truncation coefficient that must satisfy the condition 0 < a < 1 to ensure the physical realization of a finite energy cosh-Airy beam [1]. The side lobes of the cosh-Airy beam become more and more obvious when a is close to 0. The cosh-Airy beam becomes a Gaussian beam if a is close to 1. χ ₀ is a distribution factor, Eq. (6) stands for an Airy beam for χ ₀ = 0. Ai(·) represents an Airy function.

The cosh-Airy beam is regarded as the result of superposition of two Airy beams with different truncation coefficients [29], so Eq. (6) is expressed as

(7) φ ( z = 0 , x ) = 1 2 [ A i ( x ) exp ( a + x ) + A i ( x ) exp ( a − x ) ] ,

where

(8a) a + = a + χ 0 ,

(8b) a − = a − χ 0 .

When the modulation depth and the gain/loss strength are set as P = 1 and W ₀ = 1, Figure 1 displays the refractive index distribution function V(x) and the gain/loss distribution function W(x) for various values of ω and the initial cosh-Airy curve with different χ ₀. In Figure 1(a), it is presented that real part V(x) is even symmetry and imaginary part W(x) is odd symmetry, which satisfies the PT-symmetric condition. From the real part V(x), it is illustrated that the value of V(x) is positive and is maximum at x = 0. The value of V(x) is gradually close to 0 as x increases or decreases. The center refractive index of a Gaussian PT-symmetric potential is the largest, while the refractive index gradually decreases to 0 away from the center position. From the imaginary part W(x), it is shown that the value of V(x) is positive for x > 0, V(x) is negative for x < 0, and the maximum absolute value of W(x) occurs around x = 0. The value of W(x) is gradually close to 0 as x increases or decreases. The Gaussian PT-symmetric potential generates loss and gain for x < 0 and x > 0, respectively. In Figure 1(b), it is shown that the side lobe intensity of a cosh-Airy beam with truncation coefficient a = 0.1 gradually increases with increment of χ _0; however, the main lobe intensity varies little.

Figure 1

Profiles of a Gaussian PT-symmetric for different values of ω and initial cosh-Airy curve with different χ ₀: (a) real part V(x) (red solid line) and imaginary part W(x) (red dotted line) of a Gaussian PT-symmetric potential for ω = 1, and real part V(x) (blue solid line) and imaginary part W(x) (blue dotted line) for ω = 0.1; (b) different cosh-Airy beam curves with truncation coefficient a = 0.1 for χ ₀ = 0 (blue solid line), χ ₀ = 1.5 (red solid line), and χ ₀ = 2 (green solid line).

From Figure 1, it is also found that the cosh-Airy beam will be constrained due to the highest refractive index in the Gaussian PT-symmetry center. Meanwhile, the power of a cosh-Airy beam will generate oscillation because the gain/loss of imaginary part are inconsistent near the Gaussian PT-symmetry center. The modulation range is wide enough to control the entire cosh-Airy beam for ω = 0.1 (blue cure). However, the potential width or modulation range is much narrower that merely covers the main lobe of a cosh-Airy beam for ω = 1.0 (red curve). A more complicated inhomogeneous medium can be composed by superposition and combination of these different unique properties medium. Therefore, the influence of a Gaussian PT potential on the propagation characteristics of a cosh-Airy beam may be different due to different modulation ranges.

3 Results and discussion

Based on Eq. (3), we numerically simulate the propagation process of a cosh-Airy beam in the Gaussian PT-symmetric potential by considering the effect of modulation depth P, modulation factor ω, gain/loss strength W ₀, truncation coefficient a, and distribution factor χ ₀.

At ω = 1, W ₀ = 0.9, a = 0.1, and χ ₀ = 0.02, Figure 2 presents the propagation properties of a cosh-Airy beam in the Gaussian PT-symmetric potential for P = 1.6, 2.0, 2.5, and 3.5, respectively. In Figure 2(a)–(d), it is illustrated that the main lobe of a cosh-Airy beam is captured as a soliton, i.e., trapped soliton, because the refractive index in the PT-symmetric center is higher than that of others. The trapped soliton varies periodically during propagation. The remaining part of the cosh-Airy beam is still able to self-accelerate along a parabolic trajectory due to the self-healing property. The refractive index of Gaussian PT-symmetric potential in the center position increases gradually with increment in modulation depth P, which shows that the restraint ability of a beam increases gradually. On increasing the modulation depth P, the peak power of a trapped soliton increases and the period of a trapped soliton becomes short in Figure 2(a)–(e).

Figure 2

Propagation of a cosh-Airy beam in Gaussian PT-symmetric potential with different modulation depth: (a) P = 1.6, (b) P = 2.0, (c) P = 2.5, and (d) P = 3.5. (e) Variation in peak power of a trapped soliton with propagation distance for different modulation depths.

When we set P = 2.5, W ₀ = 0.9, a = 0.1, and χ ₀ = 0.02, Figure 3 shows the propagation properties of the cosh-Airy beam in Gaussian PT-symmetric potential for ω = 0.8, 1.1, 1.3, and 1.5, respectively. The potential width is much narrower for ω = 1 that is equal to the main lobe width of the cosh-Airy beam (Figure 1(a)). With increasing modulation factor ω, the potential width decreases gradually that is narrower than the main lobe width of the cosh-Airy beam. It is indicated that the restraint ability of a beam decreases gradually with increment in ω. Since the refractive index in the center of a Gaussian PT-symmetric potential is the highest, the main lobe of the cosh-Airy beam is also captured as a soliton in Figure 3(a)–(d). The trapped soliton still varies periodically in the process of propagation. The remaining part of the cosh-Airy beam is still able to self-accelerate along a parabolic trajectory due to the self-healing properties (Figure 3(a)–(d)). In Figure 3(a)–(e), we find that the peak power of a trapped soliton decreases and the period of a trapped soliton becomes short with increase in ω.

Figure 3

The change in the cosh-Airy beam as a function of propagation distance for different modulation factors: (a) ω = 0.8, (b) ω = 1.1, (c) ω = 1.3, and (d) ω = 1.5. (e) Peak power of a trapped soliton changes with propagation distance for different modulation factors.

The propagation characteristics of the cosh-Airy beam in Gaussian PT-symmetric potential with different gain/loss strength W ₀ are shown in Figure 4 for P = 2.5, ω = 1, a = 0.1, and χ ₀ = 0.02. For W ₀ > 0, the Gaussian PT-symmetric potential generates loss at x < 0, while the gain appears at x > 0 (Figure 1(a)). However, for W ₀ < 0, the Gaussian PT-symmetric potential generates gain at x < 0, and the loss appears at x > 0. It is presented that a soliton sheds from the main lobe of the cosh-Airy beam because of the effect of Gaussian PT-symmetric potential and propagates periodically in Figure 4. The remaining part of the cosh-Airy beam is also able to self-accelerate along a parabolic trajectory due to the self-healing properties. Comparing Figure 4(a1–d1 and a2–d2) shows that the deflection direction of a trapped soliton is opposite. On increasing the absolute value of W ₀, the peak power of a trapped soliton increases and the period of a trapped soliton becomes long in Figure 4(e1) and (e2).

Figure 4

Propagation of a cosh-Airy beam in Gaussian PT-symmetric potential with different gain/loss strength: (a1 and a2) W ₀ = ±0.4, (b1 and b2) W ₀ = ±0.6, (c1 and c2) W ₀ = ±0.8, and (d1 and d2) W ₀ = ±1. (e1) and (e2) Peak power of a trapped soliton varies with propagation distance for different gain/loss strengths.

The effect of Gaussian PT-symmetric potential parameters on the propagation properties of a trapped soliton is statistically analyzed. Variation in the peak power and period of a trapped soliton with modulation depth P, modulation factor ω, and gain/loss strength W ₀ is depicted in Figure 5. It is demonstrated that the period of a trapped soliton decreases almost monotonically with increase in P, while the peak power of a trapped soliton increases monotonically with increment of P (Figure 5(a)). On increasing ω or decreasing the absolute value of W ₀, the period and peak power of a trapped soliton decrease rapidly and then almost tend to be stable (Figure 5(b) and (c)). Thus, we found that a trapped soliton shedding from a cosh-Airy beam can be manipulated by changing the Gaussian PT-symmetric potential parameters.

Figure 5

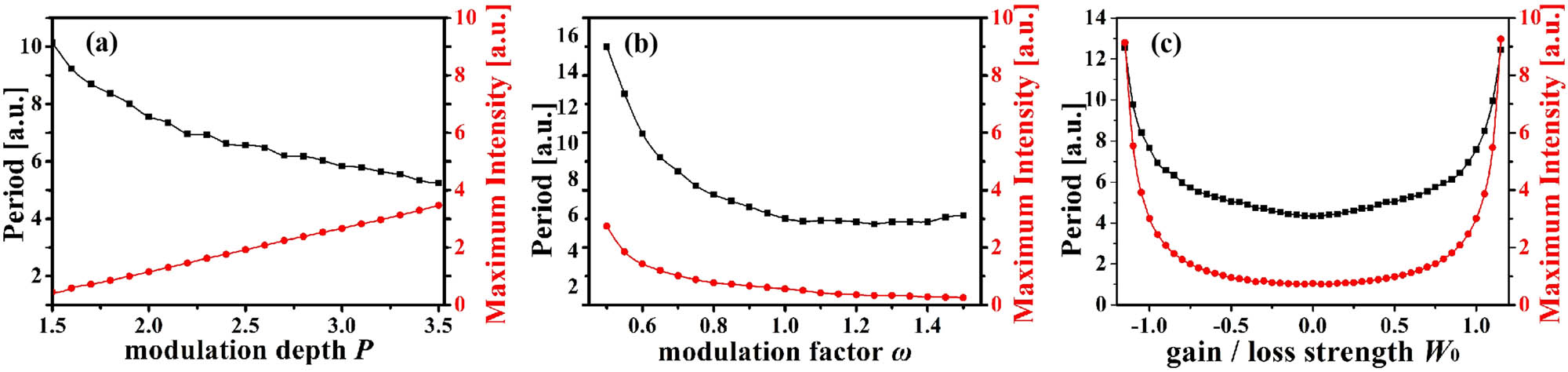
Statistical diagram of the influence of modulation depth P, modulation factor ω, and gain/loss strength W ₀ on the peak power and period of a trapped soliton.

Truncation coefficient a is an important parameter used to manipulate the waveform of a cosh-Airy beam. Figure 6 presents the propagation characteristics of a cosh-Airy beam in a Gaussian PT-symmetric potential for three truncation coefficients under the condition of P = 1.5, ω = 1, W ₀ = 0.9, and χ ₀ = 0.01. In Figure 6(a), the initial spatial shape of the cosh-Airy beam is asymmetric oscillation structure with multi-peak. When the truncation coefficient is smaller (a = 0.05), a trapped soliton generates from the main lobe of the cosh-Airy beam due to the effect of Gaussian PT-symmetric potential and propagates periodically. The remaining part of the cosh-Airy beam is also able to self-accelerate along a parabolic trajectory because of the self-healing properties. In Figure 6(b), the side lobes of the cosh-Airy beam decreases rapidly and the main lobe is also captured as a soliton with increase in a to 0.25. In Figure 6(c), when the truncation coefficient becomes much large (a = 0.35), the side lobes disappear slowly and the cosh-Airy beam evolves almost into a Gaussian beam, so the property of transverse self-acceleration almost loses. In addition, a trapped soliton also generates from the cosh-Airy beam and propagates periodically. As the truncation coefficient increases, the peak power of the trapped soliton increases, but the period the trapped soliton almost remains unchanged (Figure 6(a)–(d)).

Figure 6

Variation in a cosh-Airy beam with propagation distance for different truncation coefficients: (a) a = 0.05, (b) a = 0.25, and (c) a = 0.35. (d) Variation in peak power of a trapped soliton with propagation distance for different truncation coefficients.

Distribution factor χ ₀ is another important parameter to control the waveform of the cosh-Airy beam. For P = 1.5, ω = 1, W ₀ = 0.9, and a = 0.3, the propagation properties of the cosh-Airy beam in a Gaussian PT-symmetric potential with three distribution factors is displayed in Figure 7. Distribution factor can be used to control the side lobe intensity of the cosh-Airy beam, but has little effect on the main lobe intensity (Figure 1(b)). In Figure 7(a)–(c), when the distribution factor χ ₀ increases gradually, it is illustrated that a soliton sheds from the main lobe of the cosh-Airy beam and propagates periodically, meanwhile the property of transverse self-acceleration recovers gradually due to the increase in the side lobe energy. In Figure 7(d), it is found that the peak power and period of a trapped soliton almost remains unchanged with increment of χ ₀.

Figure 7

Propagation of a cosh-Airy beam in Gaussian PT-symmetric potential with different distribution factors: (a) χ ₀ = 0, (b) χ ₀ = 0.15, and (c) χ ₀ = 0.25. (d) The change in peak power of a trapped soliton as a function of propagation distance for different distribution factor.

The influence of beam parameters on the propagation characteristics of a trapped soliton is statistically analyzed. Figure 8 shows the peak power and period of a trapped soliton varying with truncation coefficient a and distribution factor χ ₀. It is illustrated that the period of a trapped soliton remains basically unchanged irrespective of increase or decrease in a and χ ₀ (Figure 8(a) and (b)). The peak power of a trapped soliton increases with increment of a; however, the peak power of a trapped soliton stays relatively constant in spite of variations in χ ₀ (Figure 8(a) and (b)). Consequently, we found that a trapped soliton shedding from a cosh-Airy beam can be controlled by changing the beam parameter a, while another beam parameter χ ₀ has little effect on the propagation properties of the trapped soliton.

Figure 8

Statistical diagram of the impact of truncation coefficient a and distribution factor χ ₀ on the peak power and period of a trapped soliton.

4 Conclusion

In conclusion, the propagation characteristics of a cosh-Airy beam in the inhomogeneous nonlinear medium with Gaussian PT-symmetric potential is numerically investigated in detail. It is found that a trapped soliton sheds from the main lobe of a cosh-Airy beam and propagates periodically, while the residual part can also self-accelerate along a parabolic trajectory because of the self-healing property. Furthermore, the influence of Gaussian PT-symmetric potential parameters and beam parameters on the propagation properties of a cosh-Airy beam is statistically analyzed. It is presented that the period of a trapped soliton decreases almost monotonically with increase in the modulation depth P, while the peak power of a trapped soliton increases monotonically with increment in the modulation depth P. On increasing the modulation factor ω or decreasing the absolute value of gain/loss strength W ₀, the period and peak power of a trapped soliton decrease rapidly and then almost stays relatively constant. Moreover, it is illustrated that the period of a trapped soliton remains basically unchanged irrespective of variation in truncation coefficient a and distribution factor χ ₀. The peak power of a trapped soliton increases with the increment in the truncation coefficient a; however, the peak power of a trapped soliton remains unchanged in spite of increase or decrease in the distribution factor χ ₀. Hence, we found that the propagation properties of a trapped soliton shedding from a cosh-Airy beam can be manipulated by appropriately choosing the Gaussian PT-symmetric potential parameters and beam parameters.

Funding information: This work was partially supported by the National Natural Science Foundation of China (No. 11947088), the Hunan Provincial Natural Science Foundation of China (No. 2022JJ50276 and 2021JJ40020), and the Scientific Research Fund of Hunan Provincial Education Department (No. 21A0499, 20B107, and 19B098).
Author contributions: Y.B. Deng: conceptualization, writing, review and editing; B. Wen: data curation and methodology; L.Z. Chen: conceptualization and supervision; S.W. Zhang: validation; G.F. Zhang: methodology; C.X. Xiong: investigation and software; X.L. Leng: data curation and software. All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors state no conflict of interest.

References

[1] Berry MV, Balazs NL. Nonspreading wave packets. Am J Phys. 1979;47(3):264–7.10.1119/1.11855Search in Google Scholar

[2] Siviloglou GA, Broky J, Dogariu A, Christodoulides DN. Observation of accelerating Airy beams. Phys Rev Lett. 2007;99(21):213901.10.1103/PhysRevLett.99.213901Search in Google Scholar PubMed

[3] Kaminer I, Bekenstein R, Nemirovsky J, Segev M. Nondiffracting accelerating wave packets of Maxwells equations. Phys Rev Lett. 2012;108(16):163901.10.1103/PhysRevLett.108.163901Search in Google Scholar PubMed

[4] Siviloglou GA, Christodoulides DN. Accelerating finite energy Airy beams. Opt Lett. 2007;32(8):979–81.10.1364/OL.32.000979Search in Google Scholar

[5] Siviloglou GA, Broky J, Dogariu A, Christodoulides DN. Ballistic dynamics of Airy beams. Opt Lett. 2008;33(3):207–9.10.1364/OL.33.000207Search in Google Scholar

[6] Zhao JY, Zhang P, Deng DM, Liu JJ, Gao YM, Chremmos ID, et al. Observation of self-accelerating Bessel-like optical beams along arbitrary trajectories. Opt Lett. 2013;38(4):498–500.10.1364/OL.38.000498Search in Google Scholar PubMed

[7] Polynkin P, Kolesik M, Moloney JV, Siviloglou GA, Christodoulides DN. Curved plasma channel generation using ultraintense Airy beams. Science. 2009;324(5924):229–32.10.1126/science.1169544Search in Google Scholar PubMed

[8] Baumgartl J, Mazilu M, Dholakia K. Optically mediated particle clearing using Airy wavepackets. Nat Photonics. 2008;2:675–8.10.1038/nphoton.2008.201Search in Google Scholar

[9] Abdollahpour D, Suntsov S, Papazoglou DG, Tzortzakis S. Spatiotemporal Airy light bullets in the linear and nonlinear regimes. Phys Rev Lett. 2010;105(25):253901.10.1103/PhysRevLett.105.253901Search in Google Scholar PubMed

[10] Panagiotopoulos P, Papazoglou DG, Couairon A, Tzortzakis S. Sharply autofocused ring-Airy beams transforming into non-linear intense light bullets. Nat Commun. 2013;4:2622.10.1038/ncomms3622Search in Google Scholar PubMed

[11] Salandrino A, Christodoulides DN. Airy plasmon: A nondiffracting surface wave. Opt Lett. 2010;35(15):2082–4.10.1364/OL.35.002082Search in Google Scholar PubMed

[12] Polynkin P, Kolesik M, Moloney J. Filamentation of femtosecond laser Airy beams in water. Phys Rev Lett. 2009;103(12):123902.10.1103/PhysRevLett.103.123902Search in Google Scholar PubMed

[13] Jia S, Lee J, Fleischer JW, Siviloglou GA, Christodoulides DN. Diffusion-trapped Airy beams in photorefractive media. Phys Rev Lett. 2010;104(25):253904.10.1103/PhysRevLett.104.253904Search in Google Scholar PubMed

[14] Chu XX. Evolution of an Airy beam in turbulence. Opt Lett. 2011;36(14):2701–3.10.1364/OL.36.002701Search in Google Scholar PubMed

[15] Zhou GQ, Chen RP, Chu XX. Propagation of Airy beams in uniaxial crystals orthogonal to the optical axis. Opt Express. 2012;20(3):2196–205.10.1364/OE.20.002196Search in Google Scholar PubMed

[16] Xiao FJ, Li BR, Wang MR, Zhu WR, Zhang P, Liu S, et al. Optical Bloch oscillations of an Airy beam in a photonic lattice with a linear transverse index gradient. Opt Express. 2014;22(19):22763–70.10.1364/OE.22.022763Search in Google Scholar PubMed

[17] Chen RP, Chew KH, Zhao TY, Li PG, Li CR. Evolution of an Airy beam in a saturated medium. Laser Phys. 2014;24(11):115402.10.1088/1054-660X/24/11/115402Search in Google Scholar

[18] Zhang YQ, Belić MR, Zhang L, Zhong WP, Zhu DY, Wang RM, et al. Periodic inversion and phase transition of finite energy Airy beams in a medium with parabolic potential. Opt Express. 2015;23(8):10467–80.10.1364/OE.23.010467Search in Google Scholar PubMed

[19] Huang SM, Shi XH, Bai YF, Fu XQ. Multi-solitons shedding from truncated Airy beam in nonlocal nonlinear media. IEEE Photonics Technol Lett. 2016;28(15):1621–4.10.1109/LPT.2016.2564999Search in Google Scholar

[20] Jin Y, Hu MJ, Luo M, Luo Y, Mi XW, Zou CJ, et al. Beam wander of a partially coherent Airy beam in oceanic turbulence. J Opt Soc Am A. 2018;35(8):1457–64.10.1364/JOSAA.35.001457Search in Google Scholar PubMed

[21] Wang XN, Fu XQ, Huang XW, Yang YJ, Bai YF. The robustness of truncated Airy beam in PT Gaussian potentials media. Opt Commun. 2018;410:717–22.10.1016/j.optcom.2017.11.038Search in Google Scholar

[22] Li HH, Tang MM, Wang JG, Cao JX, Li XZ. Spin hall effect of Airy beam in inhomogeneous medium. Appl Phys B. 2019;125(51):1–8.10.1007/s00340-019-7163-6Search in Google Scholar

[23] Bandres MA, Gutiérrez-Vega JC. Airy-Gauss beams and their transformation by paraxial optical systems. Opt Exp. 2007;15(25):16719–28.10.1364/OE.15.016719Search in Google Scholar PubMed

[24] Chong A, Renninger WH, Christodoulides DN, Wise FW. Airy-Bessel wave packets as versatile linear light bullets. Nat Photonics. 2010;4:103–6.10.1038/nphoton.2009.264Search in Google Scholar

[25] Dai HT, Liu YJ, Luo D, Sun XW. Propagation dynamics of an optical vortex imposed on an Airy beam. Opt Lett. 2010;35(23):4075–7.10.1364/OL.35.004075Search in Google Scholar PubMed

[26] Zhong WP, Belić M, Zhang YQ. Three-dimensional localized Airy-Laguerre-Gaussian wave packets in free space. Opt Exp. 2015;23(18):23867–76.10.1364/OE.23.023867Search in Google Scholar PubMed

[27] Peng YL, Chen B, Peng X, Zhou ML, Zhang LP, Li DD, et al. Self-accelerating Airy-Ince-Gaussian and Airy-Helical-Ince-Gaussian light bullets in free space. Opt Exp. 2016;24(17):18973–85.10.1364/OE.24.018973Search in Google Scholar PubMed

[28] Deng F, Deng DM. Three-dimensional localized Airy-Hermite-Gaussian and Airy-Helical-Hermite-Gaussian wave packets in free space. Opt Exp. 2016;24(5):5478–86.10.1364/OE.24.005478Search in Google Scholar PubMed

[29] Li HH, Wang JG, Tang MM, Li XZ. Propagation properties of cosh-Airy beams. J Mod Opt. 2018;65(3):314–20.10.1080/09500340.2017.1393572Search in Google Scholar

[30] Zhou YM, Xu YQ, Zhou GQ. Beam propagation factor of a cosh-Airy beam. Appl Sci. 2019;9(9):1817.10.3390/app9091817Search in Google Scholar

[31] Zhou GQ, Chu XX, Chen RP, Zhou YM. Self-healing properties of cosh-Airy beams. Laser Phys. 2019;29(2):025001.10.1088/1555-6611/aaf641Search in Google Scholar

[32] Zhou GQ, Chen RP, Chu XX. Propagation of cosh-Airy beams in uniaxial crystals orthogonal to the optical axis. Opt Laser Technol. 2019;116:72–82.10.1016/j.optlastec.2019.03.016Search in Google Scholar

[33] Li HH, Wang JG, Tang MM, Cao JX, Li XZ. Phase transition of cosh-Airy beams in inhomogeneous media. Opt Commun. 2018;427:147–51.10.1016/j.optcom.2018.06.045Search in Google Scholar

[34] Zhou YM, Xu YQ, Chu XX, Zhou GQ. Propagation of cosh-Airy and cos-Airy beams in parabolic potential. Appl Sci. 2019;9(24):5530.10.3390/app9245530Search in Google Scholar

[35] Regensburger A, Bersch C, Miri MA, Onishchukov G, Christodoulides DN, Peschel U. Parity-time synthetic photonic lattices. Nature. 2012;488:167–71.10.1038/nature11298Search in Google Scholar PubMed

[36] Bender CM, Boettcher S. Real spectra in non-Hermitian Hamiltonians having PT symmetry. Phys Rev Lett. 1998;80(24):5243–6.10.1103/PhysRevLett.80.5243Search in Google Scholar

[37] Ganainy RE, Makris KG, Christodoulides DN, Musslimani ZH. Theory of coupled optical PT symmetric structures. Opt Lett. 2007;32(17):2632–4.10.1364/OL.32.002632Search in Google Scholar PubMed

[38] Dmitriev SV, Sukhorukov AA, Kivshar YS. Binary parity-time-symmetric nonlinear lattices with balanced gain and loss. Opt Lett. 2010;35(17):2976–8.10.1364/OL.35.002976Search in Google Scholar PubMed

[39] Miri MA, Aceves AB, Kottos T, Kovanis V, Christodoulides DN. Bragg solitons in nonlinear PT-symmetric periodic potentials. Phys Rev A. 2012;86(3):033801.10.1103/PhysRevA.86.033801Search in Google Scholar

[40] Midya B, Roychoudhury R. Nonlinear localized modes in PT-symmetric optical media with competing gain and loss. Ann Phys. 2014;341:12–20.10.1016/j.aop.2013.11.011Search in Google Scholar

[41] Hu SM, Hu W. Optical solitons in the parity-time-symmetric Bessel complex potential. J Phys B Mol Opt Phys. 2012;45(22):225401.10.1088/0953-4075/45/22/225401Search in Google Scholar

[42] Zezyulin DA, Konotop VV. Nonlinear modes in the harmonic PT-symmetric potential. Phys Rev A. 2012;85(4):043840.10.1103/PhysRevA.85.043840Search in Google Scholar

[43] Hu, SM, Ma XK, Lu DQ, Yang ZJ, Zheng YZ, Hu W. Solitons supported by complex PT symmetric Gaussian potentials. Phys Rev A. 2011;84(4):043818.10.1103/PhysRevA.84.043818Search in Google Scholar

Received: 2022-06-26

Revised: 2022-08-13

Accepted: 2022-08-15

Published Online: 2022-10-18

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/phys-2022-0202

Keywords for this article

cosh-Airy beams; Gaussian PT-symmetric potential; trapped solitons; propagation properties

Creative Commons

BY 4.0