New approach to analysis of railway track dynamics – Rail head vibrations

Włodzimierz Czyczuła; Dorota Błaszkiewicz-Juszczęć; Małgorzata Urbanek

doi:10.1515/eng-2021-0119

40% Rabatt

auf Fachbücher bei De Gruyter Brill *

Artikel Open Access

New approach to analysis of railway track dynamics – Rail head vibrations

Włodzimierz Czyczuła , Dorota Błaszkiewicz-Juszczęć und Małgorzata Urbanek

Veröffentlicht/Copyright: 31. Dezember 2021

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen

Aus der Zeitschrift Open Engineering Band 11 Heft 1

Abstract

The article presents an original approach to the analysis of railway track dynamics. The “beam-inside-beam” concept is introduced as a dynamic generalisation of the static head-on-web effect, based on the two-layer model of rail. Rail head is a distinguished element of the rail. The system of distributed moving loads excites rail head as a beam supported by the rail web being considered as a viscoelastic layer. Rail head vibration is a kinematic excitation of the whole rail profile, including the rail head. The whole rail is also considered as a beam on viscoelastic foundation with parameters used in typical analyses of railway track dynamics. Vibrations of the whole rail obtained from the analysis of the two-layer “beam-inside-beam” model are compared with vibrations of typical one-layer track model. It is known that the static head-on-web effect is very limited. The range of significant rail head displacements covers nearly 0.6 m of area centred around the wheel position. This observation is also valid in the case of moving constant load. In other words, the dynamic effect of rail head vibrations in the case without imperfections type of track-vehicle is practically the same as in the static head-on-web case. Nevertheless, the analysis of track imperfections impact with various factors influencing the system behaviour, like the axles load and configuration, the track elastic parameters, the length of imperfection, or the train speed, show that the head-on-web effect is significant and should be analysed in more detail. For this purpose, a new model “beam-inside-beam” is proposed. The Fourier series are used to solve the two considered models. The load and unknown functions in the models’ solutions are expanded in the arbitrarily assumed interval which practically covers non-zero track response for the analysed system of parameters (group of wheels). This solving method for equation of motion was experimentally validated in the paper by Czyczula et al. (2017). Validation of the “beam-inside-beam” model is considered as future work and the current article should be recognised as a preliminary study of the analysed effects under assumption of being purely theoretical investigation so far, although forming hierarchically organised building of more complex rail models is possible to partially verify in further steps of modelling process.

Keywords: railway track; moving load; train axles configuration; track imperfections

1 Introduction

The problem of dynamic response of the track under a moving load is the subject of many theoretical and experimental studies.

Under some assumptions, the beam on elastic foundation can be considered as a typical track model. It is worth to mention that the first study of beams on Winkler foundation subjected to a concentrated force moving with constant speed was initiated by Timoshenko [1]. The first solution to a simple stationary case of the Bernoulli–Euler beam on an elastic foundation was properly obtained by Ludwig [2]. The case of moving and oscillating force was formulated and partly solved by Mathews [3]. The case of varying moving force was studied by Fryba [4] and Bogacz and Krzyżyński [5]. The model of load moving along a sectional structure (varying along the space variable) was analysed by Bogacz [6].

Many papers are devoted to study the various effects of generalised models:

Analysis of the Timoshenko beam under a moving constant and varying load [7,8,9],
Analysis of beam vibration on elastic half-space [10],
Beam response on non-linear foundation [7,10,11] and non-linear spring contact between wheel and rail [23,24]
Beam dynamic response on random foundation [12,13]
Dynamic response of track considered as a multilayer structure, e.g. refs. [14,15] – analytical approach and [16] – numerical approach;
Analysis of a set of distributed moving forces, described with Heaviside functions (e.g. ref. [8]), cosine square formula [9], or rectangular and Gauss functions [15];
Effect of axial force on dynamic response [15,17];
Analysis of a set of forces varying harmonically and associated with track imperfections – including phase of sine function for particular axles (numerically in refs. [16,18,19] and analytical approach in ref. [15]).

In all the above described generalisations of classical approach, the track response model is composed of rail (as the beam) and viscoelastic or elastic foundation. The sleepers and the ballast are modelled as additional layers.

The rail head effect in a static load case was studied analytically by Orringer et al. [20]. In this article, the effects of rail head vibrations on track response are studied in a steady state case. In the model, both the rail head and the whole rail profile are described as the Bernoulli–Euler beams. The moving load is modelled by a set of distributed forces moving with constant velocity.

2 Rail head as beam on elastic web – static analysis using numerical approach

In the paper by Orringer et al. [20], the rail head is modelled as the Bernoulli–Euler beam with the moment of inertia determined numerically (for US rail only). The stiffness of the web, treated as the head foundation, is described by the formula:

(1) k h = t h ⋅ E ,

where t – rail web thickness; h – rail web height, and E – Young’s modulus of rail steel.

As rail web thickness is changing and its height is difficult to determine, the numerical analysis is carried out to determine both the rail head foundation and the rail head geometrical parameters. Figure 1 presents cross section of the most popular rail i.e. the 60E1 type. Rail head is selected arbitrarily and the following parameters are used:

moment of inertia in vertical plane: I _h = 43.84 × 10⁻⁸ m⁴;
cross section area: A _h = 2,990 × 10⁻⁶ m²;
unit mass: m _h = 23.3 kg/m.

Figure 1

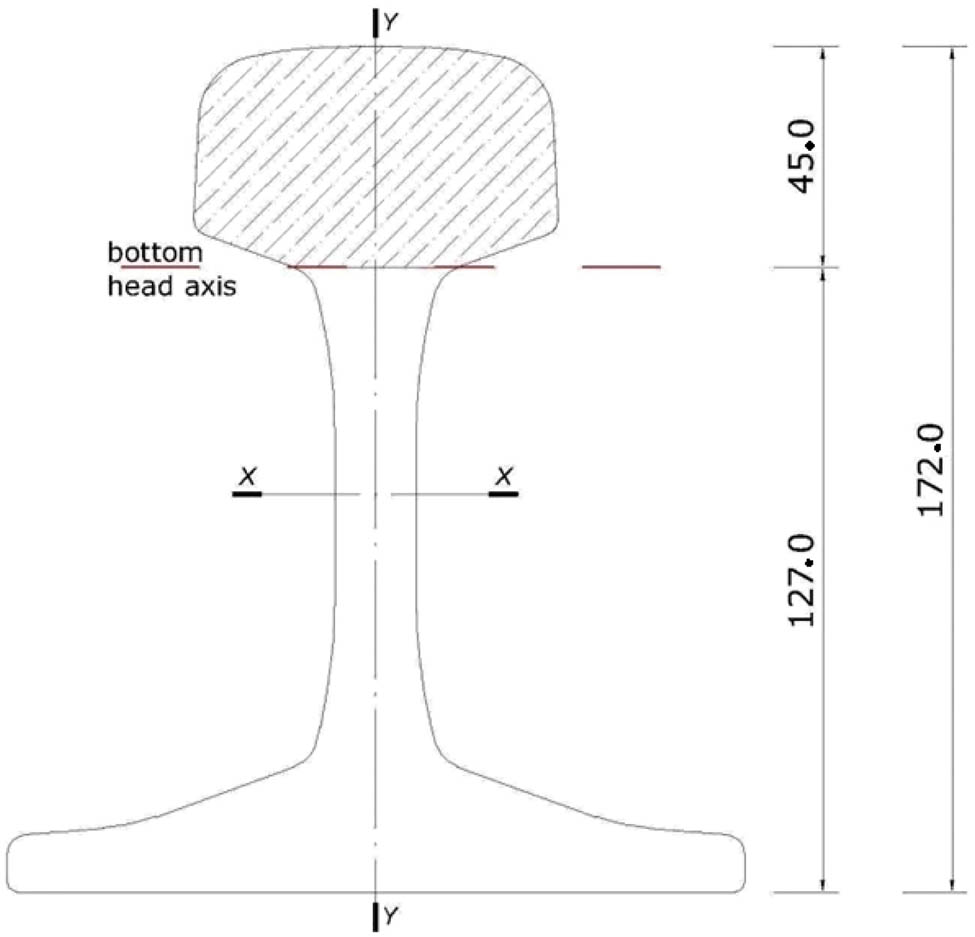
Rail cross section with the rail head separation.

To determine the stiffness of rail head foundation, a 3D numerical model is analysed. A 1 m long 60E1 rail considered as an elastic body is fixed at the bottom, and loaded along the top of the rail by vertical distributed forces with density q = 78.328 kN/m. The rail head foundation stiffness can be calculated with the following simple formula:

(2) k h = q y av ,

where y _av is the average vertical displacement of the rail head neutral axis. The rail head foundation stiffness obtained by numerical experiment, according to formula (2), is equal to 0.19 E which is very close to the value 0.2 E obtained by Orringer with the use of equation (1).

3 Steady state response in vertical direction using the two-layer “beam-inside-beam” model

The problem of rail head vibration as “beam-inside-beam” model was mentioned in the paper by Czyczula et al. [21] presenting non-linear formulation of the problem; however, without finalized solution. In this article, a two-layer track model is considered, in which a rail head is distinguished, but not separated from the whole rail profile. The rail head is described as a layer, the vibrations of which are a kinematic excitation of rail longitudinal axis. It is assumed that both the rail head and the whole rail are the Bernoulli–Euler beams with the following parameters:

E = E _h = E _r – Young’s modulus of rail steel (N/m²);

I _h and I _r – moments of inertia of rail head and the whole rail profile, respectively (m⁴);

m _h and m _r – unit mass of rail head and the whole rail profile, respectively (kg/m);

N _h and N _r – axial forces in rail head and the whole rail profile, respectively (should be considered as constant along the track) (N). Assuming that (k _h [N/m²], c _h [Ns/m²]) is viscoelastic constraint describing rail head foundation (rail web) properties, and (k _r [N/m²], c _r [Ns/m²]) describing viscoelastic properties of rail foundation, the “beam-inside-beam” system can be described by the following system of equations:

(3) EI h ∂ 4 y h ∂ x 4 + N h ∂ 2 y h ∂ x 2 + m h ∂ 2 y h ∂ t 2 + c h ∂ y h ∂ t − ∂ y r ∂ t + k h ( y h − y r ) = q ( x , t ) , EI r ∂ 4 y r ∂ x 4 + N r ∂ 2 y r ∂ x 2 + m r ∂ 2 y r ∂ t 2 + c r ∂ y r ∂ t + k r y r = c h ∂ y h ∂ t − ∂ y r ∂ t + k h ( y h − y r ) ,

where q(x, t) is a unit load acting on a rail head (N/m).

After introducing the moving coordinate system (η = y, χ = y _h, ξ = x − vt), equation (3) can be written as follows:

(4) EI h ∂ 4 y h ∂ ξ 4 + N h ∂ 2 y h ∂ ξ 2 + m h ∂ 2 y h ∂ t 2 − 2 v ∂ 2 y h ∂ t ∂ ξ + v 2 ∂ 2 y h ∂ ξ 2 + c h ∂ y h ∂ t − v ∂ y h ∂ ξ − ∂ y r ∂ t + v ∂ y r ∂ ξ + k h ( y h − y r ) = q ( ξ , t ) EI r ∂ 4 y r ∂ ξ 4 + N r ∂ 2 y r ∂ ξ 2 + m r ∂ 2 y r ∂ t 2 − 2 v ∂ 2 y r ∂ t ∂ ξ + v 2 ∂ 2 y r ∂ ξ 2 + c r ∂ y r ∂ t − ∂ y r ∂ ξ + k r y r = c h ∂ y h ∂ t − v ∂ y h ∂ ξ − ∂ y r ∂ t + v ∂ y r ∂ ξ + k h ( y h − y r ) .

For a set of moving distributed forces changing harmonically in time with circular frequency ω, the load q(ξ, t) can be expressed as:

(5) q ( ξ , t ) = q c ( ξ ) ⋅ cos ω t + q s ( ξ ) ⋅ sin ω t ,

where q _c and q _s are cosine and sine parts of the load, respectively.

The steady state solution of (4) can also be described as cosine and sine parts of the rail head and the whole rail profile displacements:

(6) y h ( ξ , t ) = Y hc ( ξ ) ⋅ cos ω t + Y hs ( ξ ) ⋅ sin ω t y r ( ξ , t ) = Y rc ( ξ ) ⋅ cos ω t + Y rs ( ξ ) ⋅ sin ω t .

By differentiating equation (6) and substituting together with equation (5), equation (4) becomes a set of ordinary equations associated with the cosine (cos ωt) and the sine (sin ωt) parts:

(7) L 1 ( Y hc , Y hs , Y rc , Y rs , P ) ⋅ cos ω t = q c ⋅ cos ω t L 2 ( Y hc , Y hs , Y rc , Y rs , P ) ⋅ sin ω t = q s ⋅ sin ω t L 3 ( Y hc , Y hs , Y rc , Y rs , P ) ⋅ cos ω t = 0 ⋅ cos ω t L 4 ( Y hc , Y hs , Y rc , Y rs , P ) ⋅ sin ω t = 0 ⋅ sin ω t ,

where L ₁,…,L ₄ are linear operators of functions Y _hc, Y _hs, Y _rc, Y _rs, and their derivatives, while P denotes a set of model parameters. E.g. operator L ₁ has the following form:

(8) L 1 = EI h d 4 Y hc d ξ 4 − m h ω 2 Y hc − 2 m h v ω d Y hs d ξ + ( N h + m h v 2 ) d 2 Y hc d ξ 2 + c h ω Y hs − c h v d Y hc d ξ − c h ω Y rs + c h v d Y rc d ξ + k h Y hc − k h Y rc .

In order to solve the considered system, a method similar to that presented in the paper by Czyczula et al. [15] can be applied. The distributed loads q _c(ξ) and q _s(ξ) and the unknown functions Y _hc , Y _hs, Y _rc and Y _rs are expanded by the Fourier series in the assumed interval [0, λ], which should cover significantly different from zero response of the track for the analysed group of wheels:

(9) q c ( ξ ) = a 0 2 + ∑ i = 1 ∞ ( a i ⋅ cos Ω i ξ + b i ⋅ sin Ω i ξ ) ; q s ( ξ ) = c 0 2 + ∑ i = 1 ∞ ( c i ⋅ cos Ω i ξ + d i ⋅ sin Ω i ξ ) ; Y hc ( ξ ) = Y h 01 2 + ∑ i = 1 ∞ ( A i ⋅ cos Ω i ξ + B i ⋅ sin Ω i ξ ) ; Y hs ( ξ ) = Y h 02 2 + ∑ i = 1 ∞ ( C i ⋅ cos Ω i ξ + D i ⋅ sin Ω i ξ ) ;

Y rc ( ξ ) = Y r 01 2 + ∑ i = 1 ∞ ( E i ⋅ cos Ω i ξ + F i ⋅ sin Ω i ξ ) ; Y rs ( ξ ) = Y r 02 2 + ∑ i = 1 ∞ ( G i ⋅ cos Ω i ξ + H i ⋅ sin Ω i ξ ) ξ ∈ [ 0 , λ ] ; Ω i = 2 π ⋅ i λ . .

Differentiating functions (9) and substituting the obtained expressions to the set of equation (7) lead to the solution of the system of algebraic equations with unknown coefficients A _i , B _i , C _i, D _i, E _i , F _i , G _i, and H _i, which can be found by comparison of quantities with the sine and cosine ith series:

(10) A i ⋅ P 1 + B i ⋅ ( − P 2 ) + C i ⋅ P 3 + D i ⋅ ( − P 4 ) + E i ⋅ P 5 + F i ⋅ P 2 + G i ⋅ ( − P 3 ) + H i ⋅ P 6 = a i A i ⋅ P 2 + B i ⋅ P 1 + C i ⋅ P 4 + D i ⋅ P 3 + E i ⋅ ( − P 2 ) + F i ⋅ ( − P 5 ) + G i ⋅ P 6 + H i ⋅ ( − P 3 ) = b i A i ⋅ ( − P 3 ) + B i ⋅ P 4 + C i ⋅ P 1 + D i ⋅ ( − P 2 ) + E i ⋅ P 3 + F i ⋅ P 6 + G i ⋅ ( − P 5 ) + H i ⋅ P 2 = c i A i ⋅ ( − P 4 ) + B i ⋅ ( − P 3 ) + C i ⋅ P 2 + D i ⋅ P 1 + E i ⋅ P 6 + F i ⋅ P 3 + G i ⋅ ( − P 2 ) + H i ⋅ ( − P 5 ) = d i A i ⋅ ( − P 5 ) + B i ⋅ P 2 + C i ⋅ ( − P 3 ) + D i ⋅ P 6 + E i ⋅ P 7 + F i ⋅ ( − P 8 ) + G i ⋅ P 9 + H i ⋅ ( − P 10 ) = 0 A i ⋅ ( − P 2 ) + B i ⋅ ( − P 5 ) + C i ⋅ P 6 + D i ⋅ ( − P 3 ) + E i ⋅ P 8 + F i ⋅ P 7 + G i ⋅ P 10 + H i ⋅ P 9 = 0 A i ⋅ P 3 + B i ⋅ P 6 + C i ⋅ ( − P 5 ) + D i ⋅ P 2 + E i ⋅ ( − P 9 ) + F i ⋅ P 10 + G i ⋅ P 7 + H i ⋅ ( − P 8 ) = 0 A i ⋅ P 6 + B i ⋅ P 3 + C i ⋅ ( − P 2 ) + D i ⋅ ( − P 5 ) + E i ⋅ ( − P 10 ) + F i ⋅ ( − P 9 ) + G i ⋅ P 8 + H i ⋅ P 7 = 0 .

In the system (10), the following new parameters are introduced:

(11) P 1 = EI h Ω i 4 − m h ω 2 − ( N h + m h v 2 ) Ω i 2 + k h P 2 = c h v Ω i P 3 = c h ω P 4 = 2 m h v ω Ω i P 5 = k h P 6 = 0 P 7 = EI r Ω i 4 − m r ω 2 − ( N r + m r v 2 ) Ω i 2 + k r + k h P 8 = ( c r + c h ) v Ω i P 9 = ( c r + c h ) ω P 10 = 2 m r v ω Ω i .

The constants Y _h01, Y _h02, Y _r01, and Y _r02 (equation [9]) are calculated from the set of equations:

(12) Y h 01 ⋅ ( k h − m h ω 2 ) + Y h 02 ( c h ω ) + Y r 01 ( − k h ) + Y r 02 ( − c h ω ) = a 0 Y h 01 ⋅ ( − c h ω 2 ) + Y h 02 ( k h − m h ω 2 ) + Y r 01 ( c h ω ) + Y r 02 ( − k h ) = c 0 Y h 01 ⋅ ( − k h ) + Y h 02 ( − c h ω ) + Y r 01 ( k r + k h − m r ω 2 ) + Y r 02 ( c r ω + c h ω ) = 0 Y h 01 ⋅ ( c h ω ) + Y h 02 ( − k h ) + Y r 01 ( − c h ω − c r ω ) + Y r 02 ( k r + k h − m r ω 2 ) = 0 .

Vibrations of the whole rail profile obtained from the analysis of the two-layer model described above can be compared to the vibrations of rail modelled by one-beam equation (cf. e.g. ref. [15]):

(13) EI r ∂ 4 y r ∂ x 4 + N r ∂ 2 y r ∂ x 2 + m r ∂ 2 y r ∂ t 2 + c r ∂ y r ∂ t + k r y r = q ( x , t ) ,

where all parameters are similar to those in equation (3).

4 Numerical examples

The following track and load parameters are used in computational examples:

Rail type of 60E1: Young’s modulus E = 2.1 × 10⁸ kN/m²; moment of inertia in vertical plane I _r = 3,055 × 10⁻⁸ m⁴; unit mass m _r = 60 kg/m; and longitudinal force in rail N _r ≡ 0;
Rail head (60E1 rail): moment of inertia in vertical plane I _h = 43.84 × 10⁻⁸ m⁴; unit mass m _h = 23.3 kg/m (cf. Section 2), and longitudinal force in rail head N _h ≡ 0;
Rail head foundation: stiffness k _h = 0.19 E × 10¹⁰ kN/m² and damping coefficient c _h = 0; 20 Ns/m²;
Rail foundation: k _r = 91.2 × 10⁶ N/m² (reference value), also 0.3 and 0.1 of the reference value and c _r = 3,950 Ns/m²;
Track irregularities: cosine type – the depth of 10 μm at the length of 0.3 and 0.6 m;
Rail head/wheel contact stiffness: k _c = 10⁶ kN/m (cf. ref. [15]);
Load configuration: two wheels of Thalys train with a static load P _st = 80,000 N at the distance of 3 m one from another (cf. ref. [16]); four wheels of EMU-250 (Pendolino) train with average static load P _st = 78,329 N with distances between them: 2.7, 7.2, and 9.9 m (cf. ref. [22]), four wheels of coal wagons Falns 441 VA with static load P _st = 112,500 N; and distances: 1.8, 5.04 and 6.84 m;
Train speed: up to 300 km/h;
Distributed forces approximation: Gauss function (cf. ref. [15]); number of Fourier series coefficients: 2,000–3,000.

It is assumed that the “rail head – wheel” contact is continuous and vibration occurs with a change in the length of contact spring.

Figure 2 shows the difference between a rail head and a whole rail vertical displacements in the case of the Pendolino EMU-250 train in the region of the first axle and with the train speed of 300 km/h. Only forces constant in time are taken into account (corresponding to a track without imperfections). It can be seen that the effect of the head-on-web displacement is relatively small (0.018 mm) and it possesses a local nature. It can be said that displacements of the rail head and the whole rail are practically the same at a distance of more than approximately 0.3 m from the wheel. This conclusion, however, is valid for moving forces constant in time only.

Figure 2

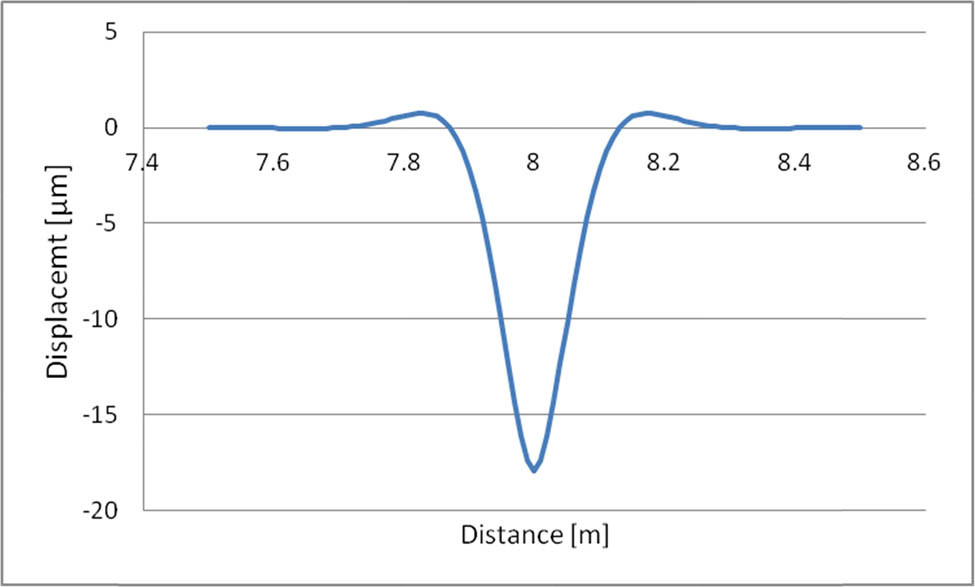
Difference between rail head and whole rail vertical displacements.

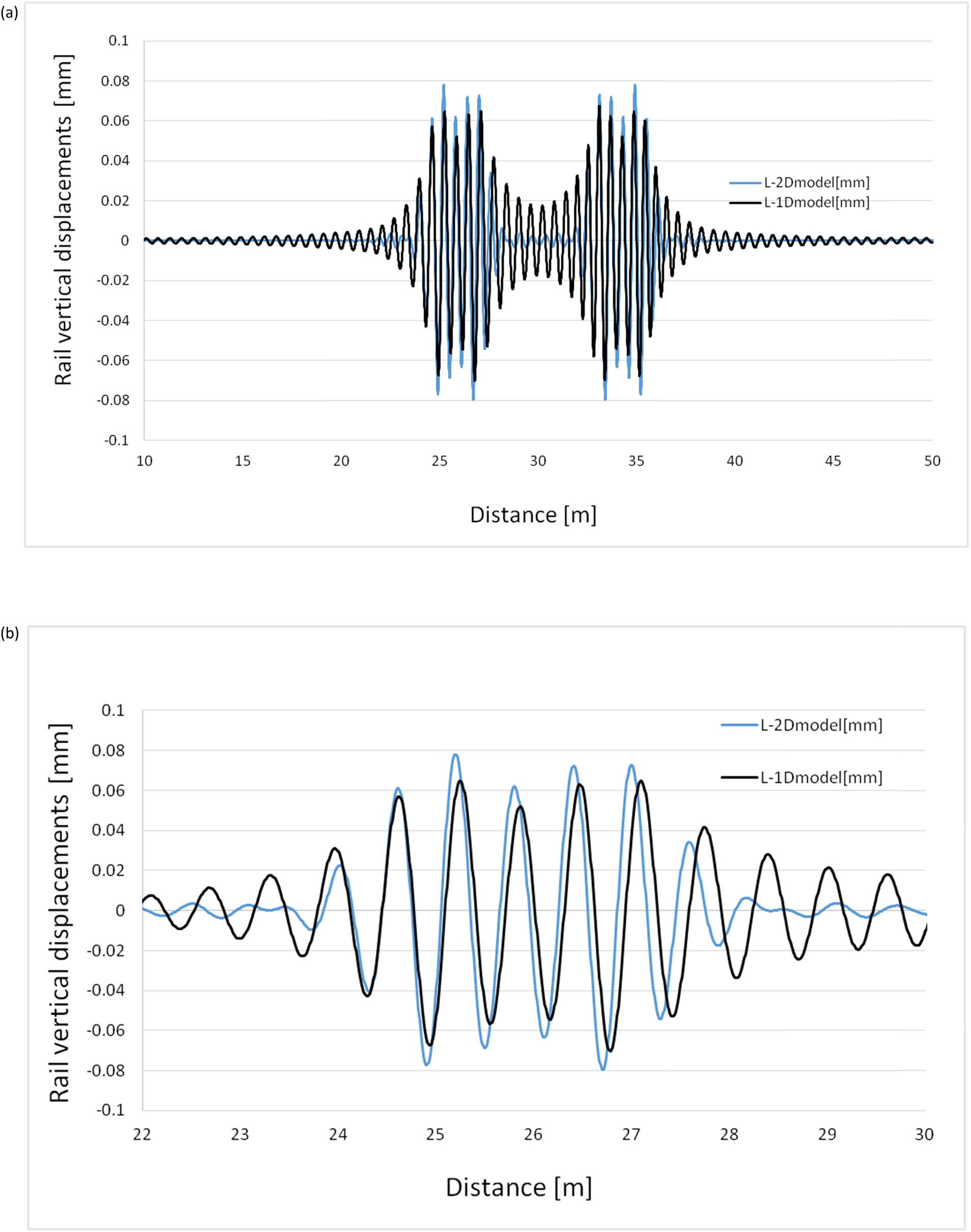
Both Figure 3a and b present rail displacements obtained in the case of the two-layer “beam-inside-beam” model and the one-layer model, with the second one (Figure 3b) as a “zoomed” fragment shown for better recognition of the pattern details. The calculations are carried out for the Pendolino train moving with the speed of 300 km/h along a track with a 10 μm imperfection with the cosine wave with a length of 0.6 m and the track stiffness k _r = 91.1 kN/m². In this case, the difference reaches 0.05 mm and it is spread over 5 m in length. Therefore, the effect of head-on-web should not be considered as local.

Figure 3

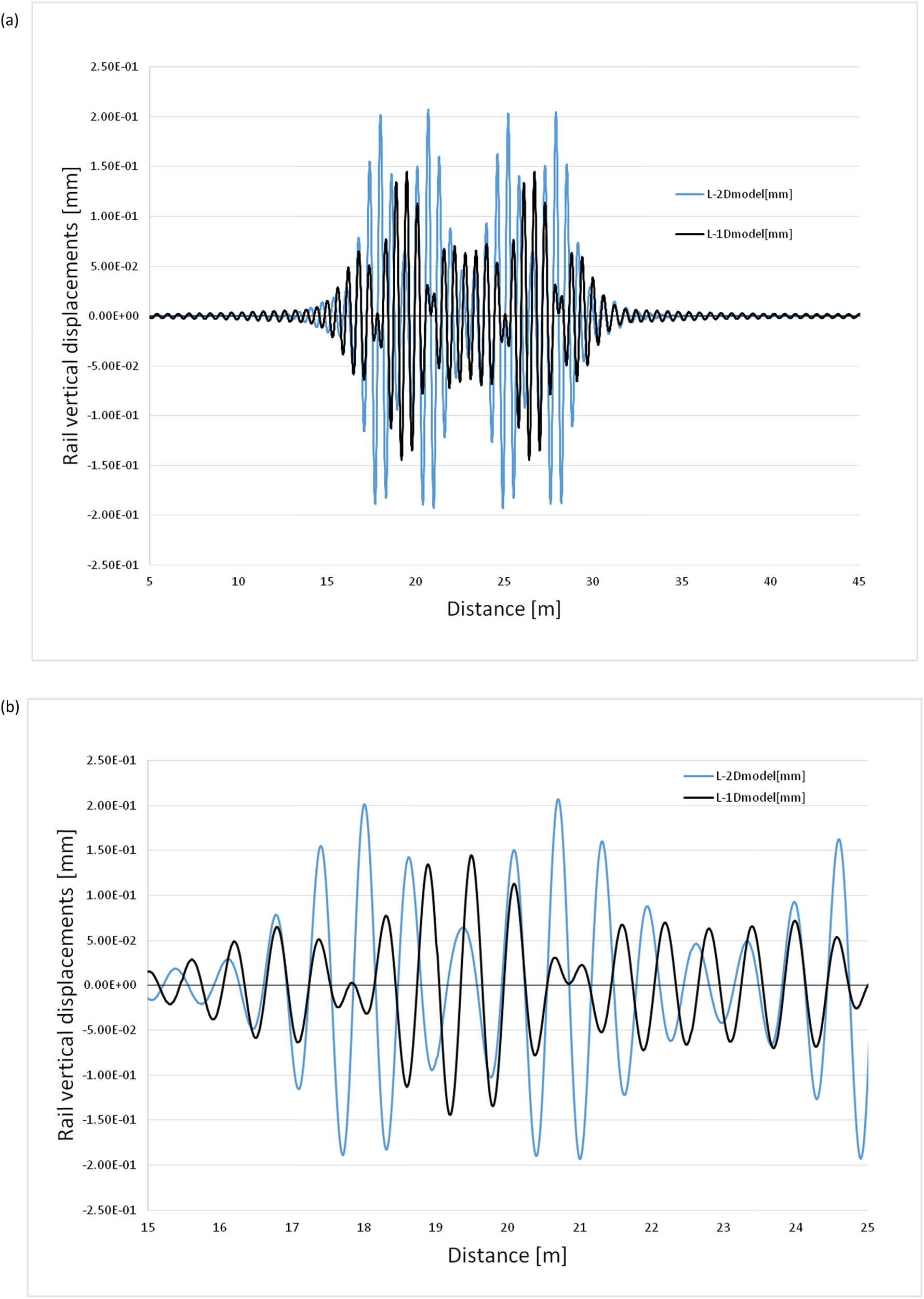
(a) The whole rail displacements for a two-layer (L-2D model) and a one-layer (L-1D model) models (Pendolino train, v = 300 km/h, k _r = 91.1 MPa, imperfection s = 10 μm, and L _n = 0.6 m) and (b) “Zoomed” graph of a part of (a) solution.

One should mention that an introduction of imperfection in both the considered models leads to the necessity of the analysed distance enlargement due to the increasing range of the response significantly different from zero. Therefore, the interval (0, λ) must be modified according to the particular cases.

Similarly prepared examples are shown in Figures 4 and 5, with second graphs presenting zoomed fragments of the response history in time.

Figure 4

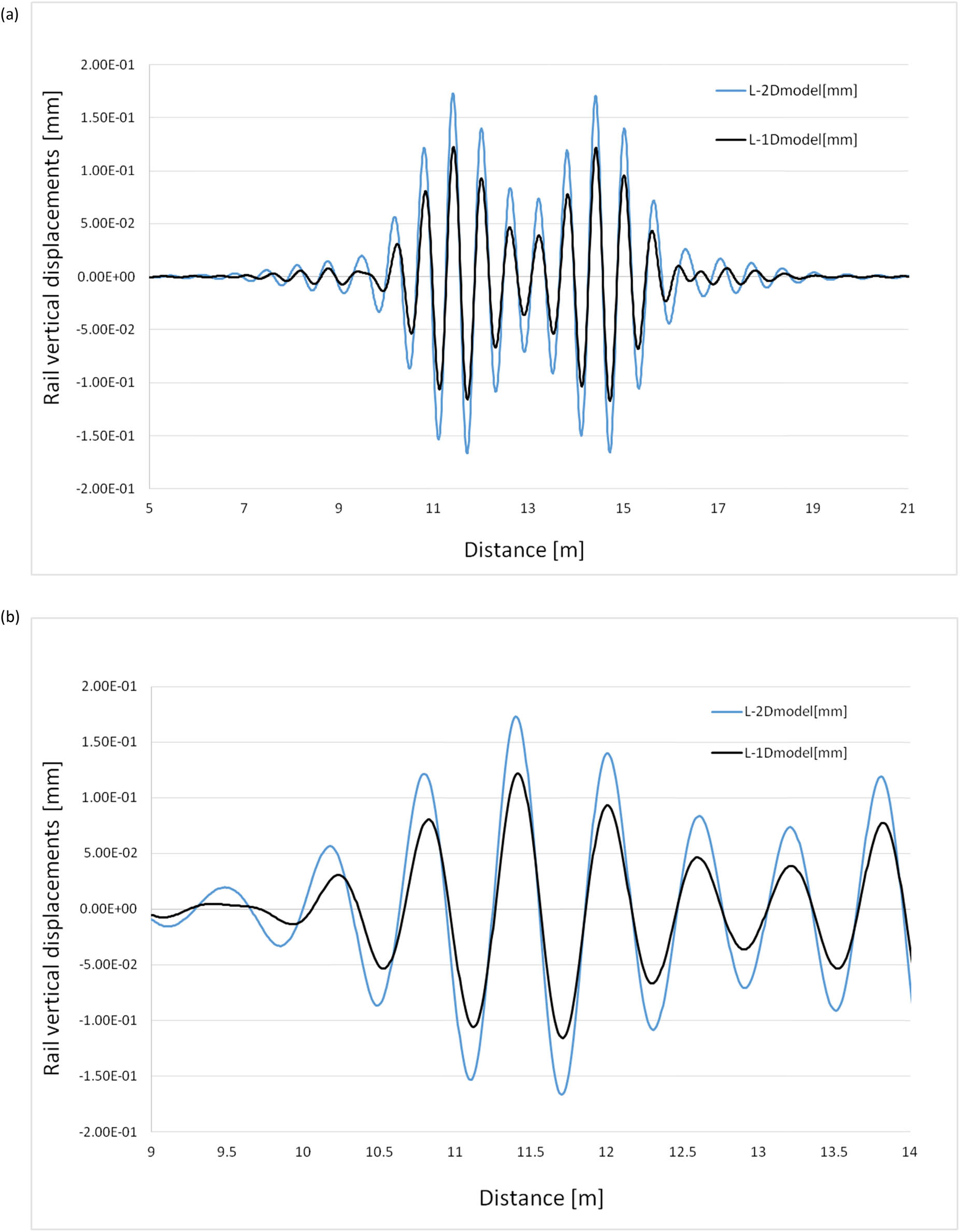
(a) The whole rail displacements for a two-layer (L-2D model) and a one-layer (L-1D model) models (Thalys train, v = 200 km/h, k _r = 91.1 MPa, imperfection s = 10 μm, and L _n = 0.6 m) and (b) “Zoomed” graph of a part of (a) solution.

Figure 5

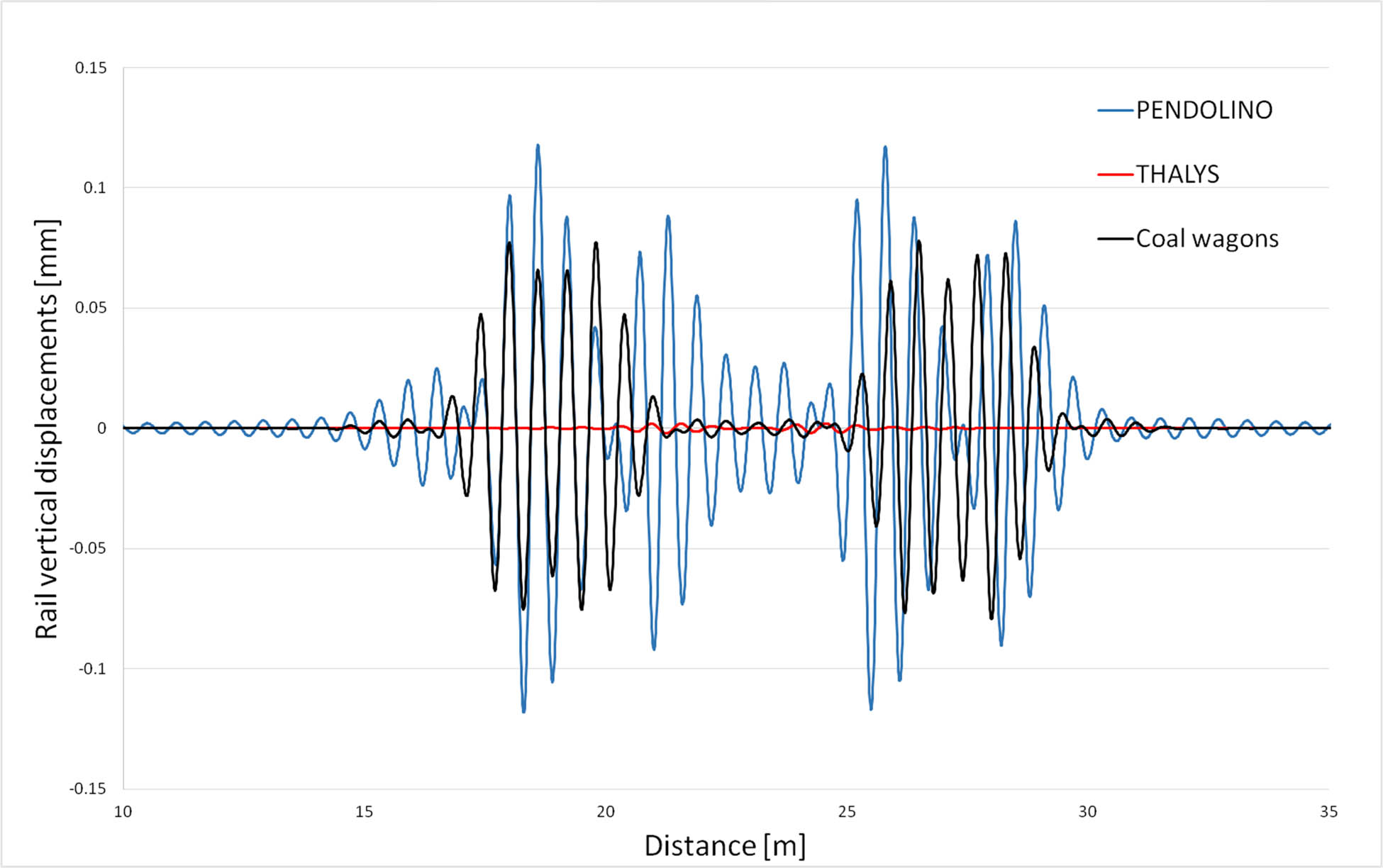
(a) Whole rail displacements for a two-layer (L-2D model) and a one-layer (L-1D model) models (coal wagon, v = 100 km/h, k _r = 91.1 MPa, imperfection s = 10 μm, and L _n = 0.6 m) and (b) “Zoomed” graph of a part of (a) solution.

Both Figure 4a and b present the difference between the two-layer and one-layer rail responses for the Thalys train moving with the speed of 200 km/h on a track with imperfections of 10 μm represented by the cosine wave with a length of 0.3 m and the track stiffness k _r = 91.1 kN/m². In this case, there is also a significant difference between the maximum displacements obtained using both models.

Another example, for a coal wagons, is shown in Figure 5a and b confirming the previously described observations. Here, additionally, a phase shift can be observed which makes the necessity of the head-on-web problem analysis even stronger. However, physical reasons of this phenomena for the considered system of parameters remain an open problem.

Figure 6 shows the maximum difference of displacements between the two-layer and the one-layer cases obtained for the three considered vehicles but for the same set of track parameters and speed v = 100 km/h. This is an example justifying the necessity of more detailed analysis of the analysed phenomenon, taking into account various scenarios of track loads and other track parameters. Results of such a preliminary analysis are gathered in Tables 1–3 showing that the difference in question significantly depends on the selected parameters, i.e. the train speed, the type of train (axle configuration and load characteristics), the track stiffness, and the length of track imperfection.

Figure 6

Maximum difference of a two-layer (2-L) and a one-layer (1-L) model displacements (v = 100 km/h, k _r = 91.1 MPa, imperfection s = 10 μm, and L _n = 0.6 m).

Table 1

The amplitude differences for the two considered models (Pendolino)

Pendolino
	Track stiffness
	k _r = 91.2 × 10⁶ (N/m²)		k _r = 0.3 × 91.2 × 10⁶ (N/m²)		k _r = 0.1 × 91.2 × 10⁶ (N/m²)
	Length of cosine wave
	L _n = 0.3 (m)	L _n = 0.6 (m)	L _n = 0.3 (m)	L _n = 0.6 (m)	L _n = 0.3 (m)	L _n = 0.6 (m)
v = 100 (km/h)	0.164	0.002	2.209	0.019	0.215	0.745
v = 200 (km/h)	0.601	0.009	0.195	1.729	0.31	0.568
v = 300 (km/h)	0.295	0.054	0.117	0.312	0.256	0.384

Table 2

The amplitude differences for the two considered models (Thalys)

Thalys
	Track stiffness
	k _r = 91.2 × 10⁶ (N/m²)		k _r = 0.3 × 91.2 × 10⁶ (N/m²)		k _r = 0.1 × 91.2 × 10⁶ (N/m²)
	Length of cosine wave
	L _n = 0.3 (m)	L _n = 0.6 (m)	L _n = 0.3 (m)	L _n = 0.6 (m)	L _n = 0.3 (m)	L _n = 0.6 (m)
v = 100 (km/h)	0.008	0.118	2.384	0.365	0.252	1.366
v = 200 (km/h)	0.743	0.145	0.260	1.747	0.431	1.119
v = 300 (km/h)	0.304	0.253	0.113	1.031	0.265	1.580

Table 3

The amplitude differences for the two considered models (coal wagons)

Coal wagons
	Track stiffness
	k _r = 91.2 × 10⁶ (N/m²)		k _r = 0.3 × 91.2 × 10⁶ (N/m²)		k _r = 0.1 × 91.2 × 10⁶ (N/m²)
	Length of cosine wave
	L _n = 0.3 (m)	L _n = 0.6 (m)	L _n = 0.3 (m)	L _n = 0.6 (m)	L _n = 0.3 (m)	L _n = 0.6 (m)
v = 100 (km/h)	0.135	0.062	2.655	0.216	0.899	1.397
v = 50 (km/h)	0.110	0.059	0.372	0.180	2.196	0.544
v = 20 (km/h)	0.105	0.059	0.307	0.172	0.873	0.468

One can observe that the length of imperfections significantly influences the investigated characteristics when analysing the two discussed models. One should also underline that the dynamic “head-on-web” effect becomes stronger with increasing train speed and changes with rail foundation stiffness variation.

5 Conclusion

The rail head vibrations effect is described and studied as a new approach to the analysis of the track response under load in vertical direction moving along the track. The analysis is carried out for various train axle configurations, train speeds, lengths of track imperfections, and track foundation stiffness. The main conclusions can be formulated as follows:

The rail head vibrations effect is significant which is confirmed by a comparative study of the track response in the case of the two-layer “beam-inside-beam” model and the one-layer (the whole rail profile). The response difference between these two cases can reach 2 mm and occurs even at the distance of a few meters around a source of the load. It means that the rail head should be considered as a separated part of rail when one deals with more advanced discussions regarding the railway track dynamic response to moving vehicles.
The rail head foundation effect changes with decreasing rail foundation stiffness and with increasing train speed.
Train axle configurations (track load characteristics) and track imperfection parameters influence the difference between the rail response in the cases of the two-layer “beam-inside-beam” and the one-layer (the whole rail profile) models.
Although the new model itself still needs to be verified by experimental measurements, the method of solution was previously checked and validated in the cases of one-layer model and the two-layer track model, which is used for the “beam-inside-beam” concept introduced in the current article.
The article can be recognised as a preliminary study of the analysed effects under assumption of being purely theoretical investigation so far. Nevertheless, a proposed structure of this investigation follows the idea of hierarchical extension process leading to a building of more advanced rail models available for partial verification in consecutive steps of modelling process.

Further investigations should be directed, besides the experimental verification supported by an application of other computational techniques, towards the model extensions, including an introduction of the sleeper and ballast layers and non-linear properties of track and foundation parameters. In addition, the head-on-web effect should be analysed in lateral and longitudinal directions, leading to a 3D system characteristics.

Acknowledgements

We would like to give our sincere thanks and gratitude to Professor Piotr Kozioł for his invaluable assistance and advice during our work on this manuscript.

Conflict of interest: Authors state no conflict of interest.

References

[1] Timoshenko S. Method of analysis of static and dynamic stresses in rail. Proceedings of 2nd International Congress on Applied Mechanics. Zurich: 1926. p. 407–18.Suche in Google Scholar

[2] Ludwig K. Deformation of rail elasticity supported of infinite length by load moving at a constant velocity. Proceedings of 5th Internatiional Congress Applied Mechanics; 1938. p. 650–5.Suche in Google Scholar

[3] Mathews PM. Vibration of beam on elastic foundation. ZAMM J Appl Math Mech. 1958;38(3–4):105–15.10.1002/zamm.19580380305Suche in Google Scholar

[4] Fryba L. Vibration of solids and structures under moving loads. ZAMM J Appl Math Mech. 1979;59(9):489–9.10.1002/zamm.19790590925Suche in Google Scholar

[5] Bogacz R, Krzyżynski T. On the Bernoulli-Euler beam on the visco-elastic foundation under moving oscillating load. IPPT Polish Academy of Science Reports; 1986. p. 38. In Polish.Suche in Google Scholar

[6] Bogacz R. Dynamics of continuous systems subjected to traveling loads. Appl Mech Mater. 1998;9:509–16.10.4028/www.scientific.net/AMM.9.31Suche in Google Scholar

[7] Kargarnovin MH, Younesian D, Thompson DJ, Jones CJ. Response of beams on nonlinear viscoelastic foundations to harmonic moving loads. Computers Struct. 2005;83:1865–77.10.1016/j.compstruc.2005.03.003Suche in Google Scholar

[8] Bogacz R, Czyczula W. Response of beam on visco-elastic foundation to moving distributed load. J Theor Appl Mech. 2008;46(4):763–75.Suche in Google Scholar

[9] Koziol P, Hryniewicz Z. Dynamic response of a beam resting on a nonlinear foundation to a moving load: Coiflet-based solution. Shock Vib. 2012;19:995–1007.10.1155/2012/525643Suche in Google Scholar

[10] Koziol P, Mares C. Wavelet approach for vibration analysis of fast moving load on a viscoelastic medium. Shock Vib. 2010;17(4–5):461–72.10.1155/2010/278538Suche in Google Scholar

[11] Dahlberg T. Dynamic interaction between train and nonlinear railway model. Proceedings of Fourth International Conference on Structural Dynamics. Munich(2): 2002 September 2–5.Suche in Google Scholar

[12] Koziol P, Mares C, Esat I. A wavelet approach for the analysis of bending waves in a beam on viscoelastic random foundation. Proceedings of the 6th International Conference on Modern Practice in Stress and Vibration Analysis. Applied Mechanics and Materials. Vol. 5–6; 2006 September 5–6. p. 239–46.10.4028/www.scientific.net/AMM.5-6.239Suche in Google Scholar

[13] Koziol P, Hryniewicz Z. Vibrations of beams on a random foundation due to a moving load: wavelet approach. Proceedings of the Twelfth International Conference on Civil, Structural and Environmental Engineering Computing. CC2009. Funchal, Madeira; 2009 September 1–4. p. 42. 10.4203/ccp.91.42):1-16.Suche in Google Scholar

[14] Koziol P, Neves MM. Multilayered infinite medium subject to a moving load: dynamic response and optimization using Coiflet expansion. Shock Vib. 2012;19:1009–18.10.1155/2012/257608Suche in Google Scholar

[15] Czyczula W, Koziol P, Kudla D, Lisowski S. Analytical evaluation of track response in vertical direction due to moving load. J Vib Control. 2017;23(18):2989–3006.10.1177/1077546315625823Suche in Google Scholar

[16] Lombaert G, Degrande J, Kogut J, François S. The experimental validation of a numerical model for the prediction of railway induced vibrations. J Sound Vib. 2006;297(3–5):512–35.10.1016/j.jsv.2006.03.048Suche in Google Scholar

[17] Kerr AD. The continuously supported rail subjected to axial force and moving load. Int J Mech Sci. 1972;14:71–8.10.1016/0020-7403(72)90007-0Suche in Google Scholar

[18] Ferrara R, Leonardi G, Jourdan F. A two-dimensional numerical model to analyse the critical velocity of high speed infrastructure. Proceedings of XIV-th International Conference on Civil, Structural and Environmental Engineering Computing. Cagliar, Italy: 2013 Oct 15.Suche in Google Scholar

[19] Zhai W, Xia H, Cai C, Gao M, Li X, Guo X, et al. High-speed train-track-bridge dynamic interactions – Part I: theoretical model and numerical simulation, Part II: experimental validation and engineering application. Int J Rail Transport. 2013;1(1–2):3–41.10.1080/23248378.2013.791498Suche in Google Scholar

[20] Orringer O, Morris JM, Joeng DY. Detail fracture growth in rails: test results. Theor Appl Fract Mech. 1986;5(2):63–95.10.1016/0167-8442(86)90019-4Suche in Google Scholar

[21] Czyczula W, Koziol P, Urbanek M. Effect of rail head vibrations: nonlinear “beam-inside-beam” model. Proceedings of ICEDyn2017. International Conference on Structural Engineering Dynamics. Ericeira, Portugal; 2017 July 3–5.Suche in Google Scholar

[22] Czyczuła W, Tatara T, Bohatkiewicz J, Hałucha M, Stecz P, Chełmecki J, et al. Field investigation of track response under EMU-250 (Pendolino) high speed train). Krakow: Krakow University of Technology Reports; 2014. In Polish.Suche in Google Scholar

[23] Sadeghi J, Khajehdezfuly A, Esmaeili M, Poorveis D. An efficient algorithm for nonlinear analysis of vehicle/track interaction problems. Int J Struct Stab Dyn. 2016;16(8):1550040.10.1142/S0219455415500406Suche in Google Scholar

[24] Sadeghi J, Fesharaki M. Importance of nonlinearity of track support system in modeling of railway track dynamics. Int J Struct Stab Dyn. 2013;13(1):1350008.10.1142/S0219455413500089Suche in Google Scholar

Received: 2021-02-05

Revised: 2021-11-30

Accepted: 2021-12-01

Published Online: 2021-12-31

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

https://doi.org/10.1515/eng-2021-0119

Schlagwörter für diesen Artikel

railway track; moving load; train axles configuration; track imperfections

Creative Commons

BY 4.0