Simulation assessment of the half-power bandwidth method in testing shock absorbers

Zbigniew Lozia; Piotr Zdanowicz

doi:10.1515/eng-2021-0011

Artikel Open Access

Simulation assessment of the half-power bandwidth method in testing shock absorbers

Zbigniew Lozia und Piotr Zdanowicz

Veröffentlicht/Copyright: 12. Dezember 2020

Veröffentlicht von

Veröffentlichen auch Sie bei De Gruyter Brill

Manuskript einreichen Informationen für Autor*innen

Aus der Zeitschrift Open Engineering Band 11 Heft 1

Abstract

The work deals with usability of the half-power bandwidth method in the diagnostic testing of automotive shock absorbers. In all the simulation tests, the front and rear suspension system of a present-day medium-classmotor car was considered. At the first stage, calculations were made in the frequency domain for a linear “quarter-car” model with two degrees of freedom; then, simulations were carried out in the time domain with using a similar but strongly nonlinear model. In the latter case, actual characteristics (corresponding to those obtained from test rig measurements) of shock absorber damping, suspension and tire elasticity, sliding friction in the suspension, and “wheel hop” were considered. The calculations were carried out every time for twelve levels of viscous damping in the suspension system, which made 48 calculation series in total. The factors of gain in the vertical force between the tester’s vibration plate and the vehicle tire (relative to the input force applied) and the dimensionless coefficients of viscous damping in the suspension system, determined by the half-power bandwidth method, were thoroughly analyzed. The calculation results were presented in graphical form. Attention was also paid to the distortions caused by the force of inertia of the tester’s vibration plate.

Keywords: suspension; damping coefficient; peak-picking method

1 Introduction

The technical condition of automotive shock absorbers is essential for vehicle motion safety and occupants’ comfort.With the development of damping components of suspension systems, newer and better methods of diagnosing such parts are sought. The “on-vehicle” tests are particularly useful thanks to their low cost and short time. Predominantly, “forced vibration tests” are used for this purpose [1, 2]. At present, efforts are made to adopt in Europe a uniform (standard) method of forcing the vibration for all the shock absorber testers. As one of the peculiarities of such a method, the stroke of the tester’s vibration plate is to be constant, equal to e.g. 6 mm, as it is in the case of the EUSAMA machines [1, 2, 3, 4]. Unfortunately, such testers, which are most popular, suffer from a major drawback: the final test result strongly depends on tire inflation pressure (i.e. tire stiffness), sprung mass, sliding friction in the suspension system, test conditions, and tester characteristics [1, 2, 4, 5]. In consideration of the above, the authors, when searching for new “on-vehicle” shock absorber assessment methods and having reviewed the literature, paid particular attention to publications [3, 6], where a suggestion was made to introduce some modifications to the EUSAMA testers and to use the half-power bandwidth method for determining the dimensionless coefficients of damping in the motor vehicle suspension system. This method is derived from modal analysis [7]. However, it is applied to systems with a single degree of freedom and with low damping (where the dimensionless damping coefficients are below 0.1 – see also e.g. [8]). The authors decided to assess the usability of this method in diagnostic testing of automotive suspension systems, where the relative damping coefficient reaches and even exceeds a value of 0.3. A novelty in relation to publications [3, 6] is here the use of a linear and a strongly nonlinear quarter-car model.

2 The half-power bandwidth method in the testing of automotive shock absorbers

The authors of publication [3] have shown that the said half-power bandwidth method [7] may be used to determine the dimensionless coefficient of damping in the suspension system. They used a modified EUSAMA tester (with a system to measure the vertical force under the vibration plate, at a sinusoidal input with a constant amplitude of 3 mm), but with the test duration time being significantly extended (to 140 s). Thus, small changes in the input frequency were obtained (from 25 Hz to 0, with a rate of 0.18 Hz/s) and, in consequence, quasi-state conditions of motion were ensured for the core phase of the test. Additionally, the vertical displacement of the tester’s vibration plate was measured. Thus, with using the fast Fourier transform, factors of gain in the vertical force measured under the EUSAMA tester’s vibration plate (relative to the input force), i.e. the absolute values of their transmittance (for linear systems), may be determined. By analyzing the curves representing these quantities close to the second natural frequency of the undamped system and with using the half-power bandwidth method (Figure 1), the estimated value of the coefficient of viscous damping in the motor vehicle suspension system may be determined from formula (1) [3, 7]:

Figure 1

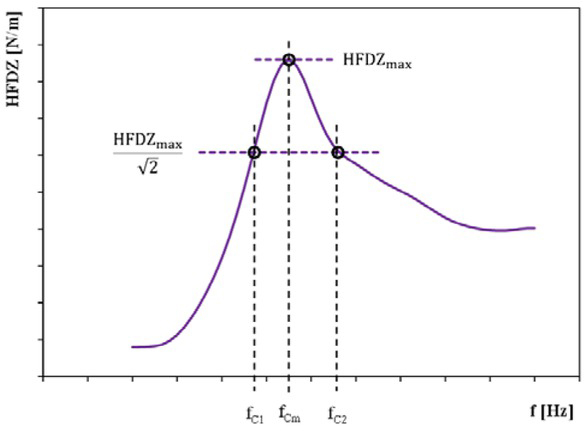
Illustration showing the characteristic points of the factor of gain in the force measured in the tester (HFDZ) in the half-power bandwidth method

(1) ϑ C 1 = f C 2 2 − f C 1 2 4 ⋅ f C m 2

where: f_Cm is the frequency corresponding to the maximum value of the factor of gain in the force measured in the tester (HFDZ_max) and f_C1 and f_C2 √are the frequencies corresponding to the value H F D Z m a x / 2 (see Figure 1).

The considerations presented in publication [3] were continued in [6] (by the same authors). It was ascertained that shock absorbers might be tested with making use of the effect of amplification of the vertical force (measured under the tester’s vibration plate) in the resonance area, for the first natural frequency. In this connection, the input frequency should decline in the core phase of the test from 3Hz to 0 for a period of 30 s (with a rate of 0.1 Hz/s). For the suspension deflection rates during the test to be similar to those occurring in typical road conditions, the amplitude of the sinusoidal input was increased to 12.5 mm. Additionally, an assumption was made that the curves used as characteristics of the factor of gain in the force measured in the tester were symmetrical and, therefore, a simplified equation (2) might be applied here:

(2) ϑ C 2 = f C 2 − f C 1 2 ⋅ f C m ≈ ϑ C 1

3 Simulation models used

The usability of the half-power bandwidth method in the diagnostic testing of automotive shock absorbers was assessed in two stages. At first, simulations were carried out in the frequency domain with using a linear quarter-car model placed on a suspension tester (Figure 2a). Next, time domain simulations were performed using an analogous, highly non-linear model (Figure 2b and 2c).

Figure 2

Quarter-car model on a diagnostic shock absorber tester: a) general structure of linear version; b) general structure of nonlinear version; c) force system in nonlinear version

3.1 Linear model

In this representation (Figure 2a), sprung mass m₁, unsprung mass m₂, and mass m₃ of tester’s vibration plate were taken into account. The vertical displacements of model bodies relative to their equilibrium positions (for the exciter, i.e. the vibration plate, being in its rest position) are denoted here by z₁ and z₂; ζ is the time-varying kinematic input applied by the exciter. The stiffness and damping of the suspension system are denoted by k₁ and c₁, respectively, and the radial stiffness and damping of the tire are denoted by k₂ and c₂, respectively. To check the distorting impact of the inertia of tester’s vibration plate (exciter) on the final shock absorber test results, the dynamic component of the normal reaction at the tire-exciter contact point (F_dz) and the dynamic component of the force measured in the tester (F_md) were distinguished.

The equations of motion were derived in accordance with the principle of dynamic force analysis (see [9]), with taking into account the forces of inertia of individual mass elements. The equations in their full and concise matrix form have been shown below (3):

(3) m 1 0 0 m 2 ⋅ z ¨ 1 z ¨ 2 + c 1 − c 1 − c 1 c 1 + c 2 ⋅ z ˙ 1 z ˙ 2 + + k 1 − k 1 − k 1 k 1 + k 2 ⋅ z 1 z 2 = 0 c 2 ⋅ ζ ˙ + 0 k 2 ⋅ ζ M ⋅ q ¨ + C ⋅ q ˙ + K ⋅ q = C ζ ⋅ ζ ˙ + K ζ ⋅ ζ

where: M, C, K, C_ζ , and K_ζ are, respectively, the matrices of inertia, viscous damping, stiffness, and matrices representing the excitation impact exerted through the tire damping and the radial stiffness of the tire; q , q ˙ , and q ¨ are the vectors of generalized displacements, velocities, and accelerations, respectively.

The Laplace transform of (3) at zero initial conditions and some subsequent transformations have resulted in the obtaining of equation (4) and its solution (5):

(4) M ⋅ s 2 + C ⋅ s + K ⋅ q s = C ζ ⋅ s + K ζ ⋅ ζ s

(5) q s = M ⋅ s 2 + C ⋅ s + K − 1 ⋅ C ζ ⋅ s + K ζ ⋅ ζ s

The operational transmittances (transfer functions) for displacements, velocities, and accelerations were expressed by relations (6), (7), (8) as the ratios of the Laplace transform of the output signal to the Laplace transform of the input signal (excitation):

(6) H q s = H q 1 s H q 2 s = q s ζ s = = M ⋅ s 2 + C ⋅ s + K − 1 ⋅ C ζ ⋅ s + K ζ

(7) H q ˙ s = H q ˙ 1 s H q ˙ 2 s = q ˙ s ζ s = s ⋅ H q s

(8) H q ¨ s = H q ¨ 1 s H q ¨ 2 s = q ¨ s ζ s = s 2 ⋅ H q s

To pass from the Laplace transform to the Fourier transform, it will be enough to pass from domain s to parameter i · ω (with assuming that the real part is equal to zero). For the linear model used here, the Fourier transform of the dynamic component of the vertical force at the tire-exciter contact point was described by (9):

(9) F d z i ⋅ ω = c 2 ⋅ ζ ˙ i ⋅ ω − z ˙ 2 i ⋅ ω + + k 2 ⋅ ζ i ⋅ ω − z 2 i ⋅ ω

Based on equations (6)–(9) and in result of appropriate transformations, a compact end form of the spectral transmittance for the dynamic vertical force at the tire-exciter contact point was finally obtained (with remembering that q₁ = z₁ and q₂ = z₂):

(10) H F d z i ⋅ ω = F d z i ⋅ ω ζ i ⋅ ω = = i ⋅ c 2 ⋅ ω + k 2 ⋅ 1 − H q 2 i ⋅ ω

The difference between the dynamic component of the force measured in the tester (F_md) and the dynamic vertical force at the tire-exciter contact point (F_dz) arises from the force of inertia of tester’s vibration plate (exciter):

(11) H F m d i ⋅ ω = F m d i ⋅ ω ζ i ⋅ ω H F m d i ⋅ ω = F d z i ⋅ ω + m 3 ⋅ ζ ¨ i ⋅ ω ζ i ⋅ ω H F m d i ⋅ ω = F d z i ⋅ ω − m 3 ⋅ ω 2 ⋅ ζ i ⋅ ω ζ i ⋅ ω H F m d i ⋅ ω = i ⋅ c 2 ⋅ ω + k 2 ⋅ 1 − H q 2 i ⋅ ω − m 3 ⋅ ω 2 H F m d i ⋅ ω = H F d z i ⋅ ω − m 3 ⋅ ω 2

The quantities describing the properties of the linear model, i.e. the Hertz and radian natural frequency (f_01/02 and ω_01/02, respectively) of the undamped system (12), critical damping coefficient c_kr1 (13), and relative damping coefficient ϑ₁ (14) were also used:

(12) ω 01 / 02 2 = k 1 ⋅ m 2 + k 1 + k 2 ⋅ m 1 2 ⋅ m 1 ⋅ m 2 ∓ ∓ k 1 ⋅ m 2 + k 1 + k 2 ⋅ m 1 2 ⋅ m 1 ⋅ m 2 2 − k 1 ⋅ k 2 m 1 ⋅ m 2 = = 2 π ⋅ f 01 / 02 2

(13) c k r 1 = 2 ⋅ k 1 ⋅ k 2 ⋅ m 1 k 2 + k 1 ⋅ 1 + m 2 m 1 c k r 1 ≈ 2 ⋅ k 1 ⋅ k 2 ⋅ m 1 k 2 + k 1 for m 1 ≫ m 2

(14) ϑ 1 = c 1 c k r 1

3.2 Nonlinear model

At the second stage, numerical computations were carried out in the time domain with using a strongly nonlinear quarter-car model (Figure 2b and 2c). Force F_st balances the weight of system masses (m₁·g, m₂·g, m₃·g). The dynamic components F_md and F_dz were taken separately to compare the results obtained for the two models.

The actual elasticity characteristics of vehicle suspension and tires, sliding friction in the suspension system, and tire separation from the ground were taken into account. The description of these properties was exactly consistent with the results of test rig measurements of the real system. The equations of motion (15) of the nonlinear quarter-car model were derived according to the principle of dynamic force analysis.

(15) ζ ¨ 1 = F s 1 + F t s 1 + F t 1 m 1 − g ζ ¨ 2 = − F s 1 − F t s 1 − F t 1 + F s 2 + F t 2 m 2 − g

where: ζ ¨ 1 and ζ ¨ 2 are accelerations of the sprung and unsprung mass; Fs₁, Fts₁, and Ft₁ are forces of elasticity, sliding friction, and viscous damping in the suspension system; Fs₂ and Ft₂ are forces of elasticity and damping in the tire; and g is acceleration of gravity.

The elasticity force in the suspension system was approximated by a linear function and a 2^nd or 3^rd degree polynomial:

(16) F s 1 = A 1 s 1 ⋅ u 1 for u 1 ≤ u 1 g r A 2 s 1 ⋅ u 1 3 + B 2 s 1 ⋅ u 1 2 + + C 2 s 1 ⋅ u 1 + D 2 s 1 for u 1 > u 1 g r

where: A1s₁ and A2s₁ to D2s₁ are coefficients of the functions that describe the elasticity force in the suspension system at low and high deflection values, respectively; u_1gris boundary between areas of different descriptions of the elasticity force; u₁ is deflection of the suspension system, according to (17):

(17) u 1 = ζ 2 − ζ 1 + o m 0

where: om₀ is the difference between coordinates ζ₁ and ζ₂ at which Fs₁ = 0.

The force of sliding friction in the suspension system is represented as follows:

(18) F t s 1 = A t s 1 ⋅ s g n u ˙ 1 for u ˙ 1 > u ˙ 1 g r A t s 1 ⋅ u ˙ 1 u ˙ 1 g r for u ˙ 1 ≤ u ˙ 1 g r

where: Ats₁ is amplitude of the force of sliding friction in the suspension system and u ˙ 1 g r is boundary value of the suspension system deflection rate, see (19):

(19) u ˙ 1 = ζ ˙ 2 − ζ ˙ 1

The force of viscous damping in the suspension system is described by (20):

(20) F t 1 = − i z ⋅ c o ⋅ − u ˙ 1 ⋅ i z W o for u ˙ 1 < 0 i z ⋅ c u ⋅ u ˙ 1 ⋅ i z W u for u ˙ 1 ≥ 0

where: i_z is a coefficient describing the kinematic relations in the suspension system; c₀ and c_u are shock absorber damping coefficients for the rebound and compression stroke; Wo and Wu are exponents of the function that describes the shock absorber damping for the rebound and compression stroke.

The tire elasticity force was approximated by a 3^rd degree polynomial:

(21) F s 2 = A s 2 ⋅ u 2 3 + B s 2 ⋅ u 2 2 + C s 2 ⋅ u 2

where: As₂ to Cs₂ are coefficients of the polynomial that describes the tire elasticity force and u₂ is radial deflection of the tire, according to (22):

(22) u 2 = ζ − ζ 2 + R for ζ − ζ 2 + R ≥ 0 0 for ζ − ζ 2 + R < 0

where: R is free radius of the pneumatic tire.

According to equation (23), the damping force in the tire model is a linear function of the rate of tire deflection in the radial direction:

(23) F t 2 = c 2 ⋅ u ˙ 2

where: c₂ is damping coefficient and u₂ is deflection rate, according to (24):

(24) u ˙ 2 = ζ ˙ − ζ ˙ 2 for ζ − ζ 2 + R ≥ 0 0 for ζ − ζ 2 + R < 0

The solutions of the equations of motion (15) were obtained in the time domain by approximate techniques involving numerical integration, with using an authorial program built in the Matlab-Simulink environment [2].

4 Parameters of the models and of the test conditions

All the simulation tests were carried out for nominal parameters of the front and rear “quarter” of the selected medium-class car (Tables 1 and 2), which had been previously subjected to test rig measurements.

Table 1

Parameters of the linear model

Symbol	Unit	Value for the front “quarter car”	Value for the rear “quarter car”
m₁	kg	346	160
m₂	kg	36	35
k₁	N/m	25570	24882
k₂	N/m	253161	206526
c₂	N·s/m	150	150
f₀₁	Hz	1.30 (8.19)	1.87 (11.77)
(ω₀₁)	(rad/s)
f₀₂	Hz	14.01 (88.03)	12.96 (81.42)
(ω₀₂)	(rad/s)
c_kr1	N·s/m	5669	3770

Table 2

Additional parameters of the nonlinear model and the diagnostic tester

Symbol	Unit	Value for the front “quarter car”	Value for the rear “quarter car”
A1s₁	N/m	2.267E+05	4.400E+05
A2s₁	N/m³	0	7.290E+05
B2s₁	N/m²	1.852E+04	−5.037E+04
C2s₁	N/m	2.310E+04	2.155E+04
D2s₁	N	1.526E+03	4.094E+02
u_1gr	m	0.0075	0.001
om₀	m	0.337	0.309
Ats₁	N	200	40
ü_1gr	m/s	0.005	0.005
c_u	N·s^Wu/m^Wu	975	850
c_o	N·s^Wo/m^Wo	1700	3200
Wu	-	0.8	0.65
Wo	-	1	1.2
i_z	-	0.9936	0.7068
As₂	N/m³	−9.367E+07	−3.021E+07
Bs₂	N/m²	5.653E+06	3.592E+06
Cs₂	N/m	1.525E+05	1.553E+05
R	m	0.311	0.311
m₃	kg	14.5	14.5
ζ_max	m	0.025 or 0.006	0.025 or 0.006

In pursuance of the objective of this work, only the viscous damping in the suspension system was changed, with using the dimensionless (relative) coefficient (14) and with applying every time 12 values of this parameter, ranging from 0.04 to 0.48 (with Δϑ₁ = 0, 04).

For the nonlinear model, the force of viscous damping in the suspension system was reproduced from the nominal characteristic curve, with multiplying it by a percentage factor appropriately selected so that the energy dissipated in a single cycle in the shock absorber being simulated was equal to that dissipated in the corresponding linear element of the model.

The analysis was focused on the factors of gain in the vertical force at the tire-exciter contact point (relative to the input force) and on the relative coefficients of viscous damping in the suspension system, determined by the half-power bandwidth method. The distortions caused by the force of exciter’s inertia were also shown if deemed significant.

5 Results of simulation computations

The spectral characteristic curves obtained from the simulation tests carried out with using the linear model of the front “quarter car” were almost symmetrical, especially when the value of the dimensionless coefficient of damping in the suspension system did not exceed 0.24 (Figures 3a, 4a, and 5a). Close to the first natural frequency, the diagnostic parameters ϑ_C1 and ϑ_C2 (equations (1) and (2)) could be determined but only for the 6 lowest damping levels (of the range 0.04÷0.24). Close to the second natural frequency, in turn, the use of the half-power bandwidth method was reasonable in 7 of 12 cases. In contrast, the values of ϑ_C1 and ϑ_C2 could be estimated for all the damping levels under consideration (Figure 5a), if the factors of gain in the force under the tester’s vibration plate (measured by means of real diagnostic testers) were used. For the calculations carried out with using the nonlinear model of the front “quarter car”, the results obtained were less optimistic. The spectral characteristic curves showed some symmetry, but only close to the second natural frequency. For the curves presented in Figures 3b, 4b, and 5b, the parameters ϑ_C1m and ϑ_C2m could only be estimated for the first 2, first 5, and all the damping levels in question, respectively.

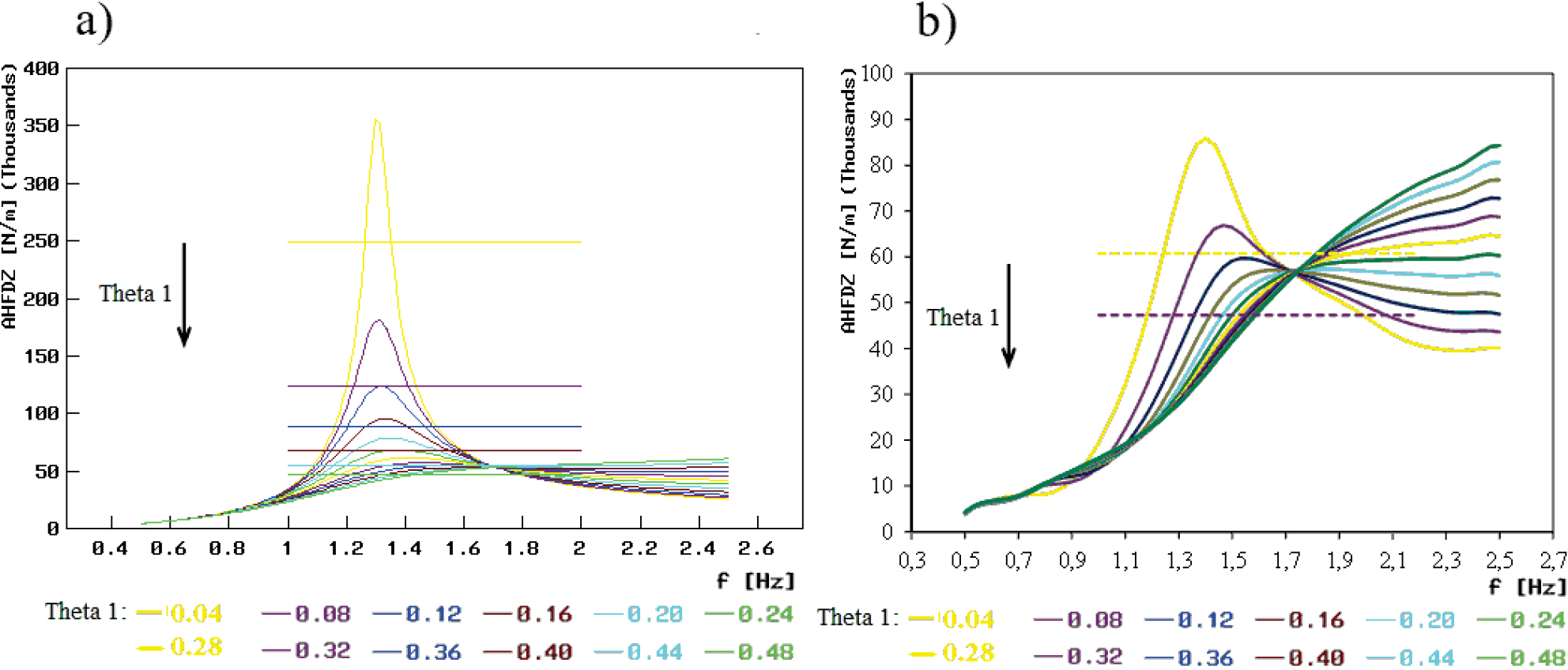
$Figure 3 Factors of gain (AHFDZ) in the vertical force at the tire-exciter contact point (relative to the input force) close to the first natural frequency of the front “quarter car” for various damping values ϑ1 (Theta1): The horizontal lines represent the values of A H F D Z m a x / 2 ; ${AHFDZ}_{max}/\sqrt{2};$ a) results for the linear model; b) results for the nonlinear model$

Figure 3

Factors of gain (AHFDZ) in the vertical force at the tire-exciter contact point (relative to the input force) close to the first natural frequency of the front “quarter car” for various damping values ϑ₁ (Theta1): The horizontal lines represent the values of A H F D Z m a x / 2 ; a) results for the linear model; b) results for the nonlinear model

$Figure 4 Factors of gain (AHFDZ) in the vertical force at the tire-exciter contact point (relative to the input force) close to the second natural frequency of the front “quarter car” for various damping values ϑ1 (Theta1): the horizontal lines represent the values of A H F D Z m a x / 2 ; ${AHFDZ}_{max}/\sqrt{2};$ a) results for the linear model; b) results for the nonlinear model$

Figure 4

Factors of gain (AHFDZ) in the vertical force at the tire-exciter contact point (relative to the input force) close to the second natural frequency of the front “quarter car” for various damping values ϑ₁ (Theta1): the horizontal lines represent the values of A H F D Z m a x / 2 ; a) results for the linear model; b) results for the nonlinear model

$Figure 5 Factors of gain (AHFDZM) in the force measured by the real diagnostic tester, i.e. under the exciter (relative to the input force), close to the second natural frequency of the front “quarter car” for various damping values ϑ1 (Theta1): the horizontal lines represent the values of A H F D Z m a x / 2 ; ${AHFDZ}_{max}/\sqrt{2};$ a) results for the linear model; b) results for the nonlinear model$

Figure 5

Factors of gain (AHFDZM) in the force measured by the real diagnostic tester, i.e. under the exciter (relative to the input force), close to the second natural frequency of the front “quarter car” for various damping values ϑ₁ (Theta1): the horizontal lines represent the values of A H F D Z m a x / 2 ; a) results for the linear model; b) results for the nonlinear model

The final simulation results, determined from the spectral characteristic curves close to the first natural frequency of the linear model corresponded to the applied values of the dimensionless coefficient of damping of the range 0.04÷0.24 (Figures 6a and 9a). For higher values of this coefficient, a trend to overestimate the values of ϑ_C1 and ϑ_C2 (even by about 25%) was noticed or the values could not be determined at all.

Figure 6

Values of diagnostic parameters ϑ_C1 (Theta_C1) and ϑ_C2 (Theta_C2) as functions of the dimensionless coefficient of damping in the suspension system ϑ₁ (Theta1), obtained from an analysis of the factor of gain in the vertical force at the tire-exciter contact point (relative to the input force) close to the first natural frequency of the front “quarter car”: a) results for the linear model; b) results for the nonlinear model

Figure 7

Values of diagnostic parameters ϑ_C1 (Theta_C1) and ϑ_C2 (Theta_C2) as functions of the dimensionless coefficient of damping in the suspension system ϑ₁ (Theta1), obtained from an analysis of the factor of gain in the vertical force at the tire-exciter contact point (relative to the input force) close to the second natural frequency of the front “quarter car”: a) results for the linear model; b) results for the nonlinear model

Figure 8

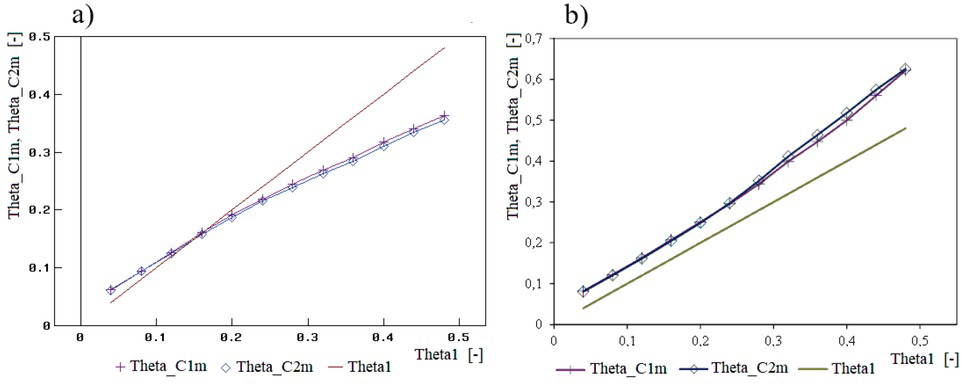
Values of diagnostic parameters ϑ_C1m (Theta_C1m) and ϑ_C2m (Theta_C2m) as functions of the dimensionless coefficient of damping in the suspension system ϑ₁ (Theta1), obtained from an analysis of the factor of gain in the force measured by the real diagnostic tester, i.e. under the exciter (relative to the input force), close to the second natural frequency of the front “quarter car”: a) results for the linear model; b) results for the nonlinear model

Figure 9

Values of diagnostic parameters ϑ_C1 (Theta_C1) and ϑ_C2 (Theta_C2) as functions of the dimensionless coefficient of damping in the suspension system ϑ₁ (Theta1), obtained from an analysis of the factor of gain in the vertical force at the tire-exciter contact point (relative to the input force) close to the first natural frequency of the rear “quarter car”: a) results for the linear model; b) results for the nonlinear model

For the nonlinear model of the front “quarter car”, in turn, high sliding friction forces in the suspension system prevented the obtaining of final test results except for the tests with the two lowest damping levels, where the results were several times overestimated at that (Figure 6b). Somewhat better results were obtained for the rear suspension system (Figure 8b). However, the ϑ_C1 and ϑ_C2 values could only be determined for the five lowest damping levels and the values corresponding to the levels of 0.04 and 0.2 were overestimated even by as much as several ten percent.

In the case of using the factors of gain in the vertical force at the tire-exciter contact point (relative to the input force) close to the second natural frequency of the front “quarter car”, quite good conformity was obtained between the final test results and the predefined values, but only when the latter were relatively low (Figures 7a and 10a). For the front suspension system, significant over-estimation of parameters ϑ_C1 and ϑ_C2 (even by as much as several ten percent) was observed when the damping level exceeded 0.16. For the rear suspension system, the value of this threshold was 0.28.

Figure 10

Values of diagnostic parameters ϑ_C1 (Theta_C1) and ϑ_C2 (Theta_C2) as functions of the dimensionless coefficient of damping in the suspension system ϑ₁ (Theta1), obtained from an analysis of the factor of gain in the vertical force at the tire-exciter contact point (relative to the input force) close to the second natural frequency of the rear “quarter car”: a) results for the linear model; b) results for the nonlinear model

For the nonlinear front “quarter car” model, the calculations produced test results overestimated by several ten to about two hundred percent in the whole range of changes in the damping (Figure 7b). The results obtained in this case were markedly better for the rear suspension system (Figure 10b). Parameters ϑ_C1 and ϑ_C2 adequately described the shock absorber condition, but only within the medium damping range. For very low and very high damping levels (0.04÷0.12 and above 0.36), the overestimation of the final test results reached a few ten percent. The phenomenon of tire separation from the exciter (“bouncing”) resulted in conspicuous distortions of the initial parts of the curves plotted (Figures 10b and 11b).

Figure 11

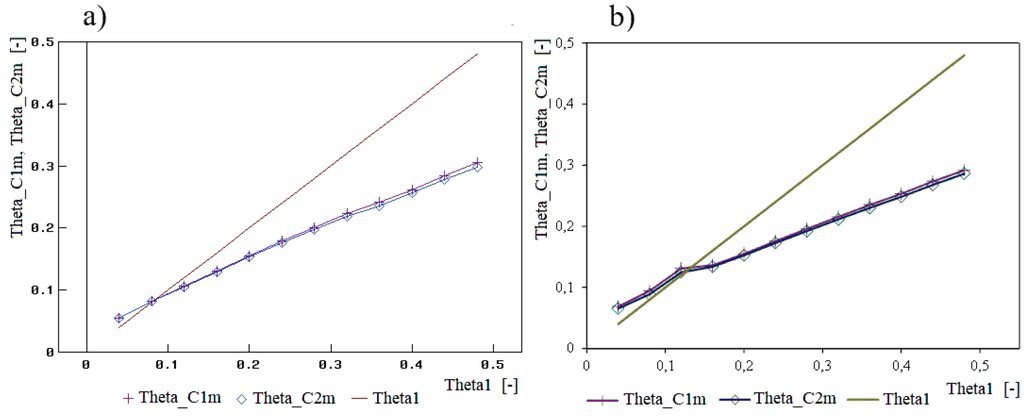
Values of diagnostic parameters ϑ_C1m (Theta_C1m) and ϑ_C2m (Theta_C2m) as functions of the dimensionless coefficient of damping in the suspension system ϑ₁ (Theta1), obtained from an analysis of the factor of gain in the force measured by the real diagnostic tester, i.e. under the exciter (relative to the input force), close to the second natural frequency of the rear “quarter car”: a) results for the linear model; b) results for the nonlinear model

Wherever the calculations made for the front “quarter car” were based on the factors of gain in the force measured under the tester’s vibration plate, their results better represented the suspension damping applied, in comparison with the case that the vertical force at the tire-exciter contact point was taken as a basis (see Figures 7 and 8). For the linear model, the diagnostic parameters were generally underestimated (by up to about 25%); conversely, those obtained for the nonlinear representation remained overestimated, but definitely less than it can be seen in Figure 7b. A different situation was observed for the rear suspension system: here, the ϑ_C1m and ϑ_C2m values represented the suspension damping levels worse than ϑ_C1 and ϑ_C2 did and they were underestimated in most cases (see Figures 10 and 11).

6 Recapitulation

Based on the simulation tests carried out, the usability of the half-power bandwidth method in the diagnostic testing of automotive shock absorbers was found to be limited.

The final calculation results were approximately in conformity with expectations but in general, this was only true for low suspension system damping values. However, such cases, occurring when the shock absorbers are in poor condition, are most important in the practical applications of this method. At high damping levels, overestimation of the diagnostic parameters was usually observed, although different situations occurred as well.

A distorting impact of sliding friction in the suspension system on the final test results was noticed. The cases have also been shown where the new diagnostic parameters proposed cannot be determined at all.

The results presented indicate the usability of the linear model, although many important characteristics of a real object are not taken into account in such a model.

In authors’ opinion, experimental verification of the results obtained is necessary because in practice, at low-frequency input (even if the input amplitude is raised to 12.5 mm), the extremum of the response of the system under test becomes hardly distinguishable. Moreover, the shock absorber under test usually fails to function in such conditions if the sliding friction in the suspension system is strong enough.

Acknowledgement

The work was done within project “UNILINE QUANTUM (...)” sponsored by the European Union within the European Regional Development Fund, Smart Growth Operational Programme, Sub-measure 1.1.1. Project No: POIR.01.01.01-00-0949/15. Task carried out by the authors for UNIMETAL Sp. z o.o. in Złotów.

References

[1] Stańczyk TL, Jurecki R. [Comparative analysis of testing methods of hydraulic shock absorbers]. Proceedings of the Institute of Vehicles, Warsaw University of Technology. 2014;4(100):25-45. Polish.Suche in Google Scholar

[2] Zdanowicz P. Assessment of vehicle shock-absorbers’ condition having considered dry friction in the suspension [dissertation]. Warsaw: Warsaw University of Technology; 2012.Suche in Google Scholar

[3] Calvo JA, Diaz V, San Román JL. Establishing inspection criteria to verify the dynamic behaviour of the vehicle suspension system by a platform vibrating test bench. International Journal of Vehicle Design. 2005;38(4):290-306.10.1504/IJVD.2005.007623Suche in Google Scholar

[4] Lozia Z, Zdanowicz P. Simulation assessment of the impact of inertia of the vibration plate of a diagnostic suspension tester on results of the EUSAMA test of shock absorbers mounted in a vehicle. IOP Conference Series: Materials Science and Engineering. 2018;421(2):1-10.10.1088/1757-899X/421/2/022018Suche in Google Scholar

[5] Lozia Z, Mikołajczuk J. Ocena przydatności testu diagnostycznego stanu amortyzatorów zamontowanych w pojeździe, wykorzystującego wymuszenie kinematyczne w kontakcie koła z podłożem. The Archives of Automotive Engineering. 1997;2:3-24. Polish.Suche in Google Scholar

[6] Calvo JA, San Román JL, Alvarez-Caldas C. Procedure to verify the suspension system on periodical motor vehicle inspection. International Journal of Vehicle Design. 2013;63(1):1-17.10.1504/IJVD.2013.055497Suche in Google Scholar

[7] He J, Fu ZF. Modal analysis. 1st ed. Woburn: Butterworth-Heinemann; 2001.10.1016/B978-075065079-3/50001-2Suche in Google Scholar

[8] Pugi L, Reatti A, Corti F. Application of modal analysis methods to the design of wireless power transfer systems. Meccanica. 2019;54:321–31.10.1007/s11012-018-00940-xSuche in Google Scholar

[9] Lozia Z. The use of a linear quarter-car model to optimize the damping in a passive automotive suspension system – a follow-on from many authors’ works of the recent 40 years. The Archives of Automotive Engineering. 2016;71(1):33-65.10.14669/AM.VOL71.ART3Suche in Google Scholar

Received: 2020-07-13

Accepted: 2020-09-28

Published Online: 2020-12-12

This work is licensed under the Creative Commons Attribution 4.0 International License.

Artikel in diesem Heft

https://doi.org/10.1515/eng-2021-0011

Schlagwörter für diesen Artikel

suspension; damping coefficient; peak-picking method

Creative Commons

BY 4.0